Основные элементы автоматизированных систем обработки данных

Вид материала

Документы

Содержание Методы схематизации случайных процессов при амплитудном анализе Анализ статистической независимости случайных значений: критерий серий Анализ статистической независимости случайных значений: критерий инверсий Методики проверки стационарности случайного процесса Методы построения эмпирических закономерностей: метод узловых точек Обнаружение и устранение трендов в случайном процессе Методики вычисления усреднённого спектра случайного процесса Методики с интенсивным использованием ЭВМ: «Бутстрэп» метод Методики с интенсивным использованием ЭВМ: «Джекнайт» метод АЦП и его погрешности Теорема Котельникова

Подобный материал:

• Понятия о базах данных и системах управления ими. Классификация баз данных. Основные, 222.31kb.
• План занятий третьего года обучения, по специальности «Программное обеспечение вычислительной, 103.35kb.
• Ы, включают методы обработки данных многих ранее су­ществовавших автоматизированных, 3469.84kb.
• Пример рабочей программы дисциплины ооп основы построения современных систем, 65.27kb.
• Доклад Тема: «Информационные технологии», 58.36kb.
• К рабочей программе учебной дисциплины «Безопасность систем баз данных», 28.21kb.
• Методы анализа данных, 17.8kb.
• Методические указания к курсовому проектированию по дисциплине проектирование автоматизированных, 1086.71kb.
• Рабочая программа по дисциплине "Организация ЭВМ и систем" для специальности 230102, 93.42kb.
• Г. И. Ревунков Научно-образовательный материал «Электронное учебно-методическое пособие, 306.81kb.

Основные элементы автоматизированных систем обработки данных


Самописец



Д₁


ПУ₁


Ф₁


АЦП₁


УО



Д₂



…


Д_к

АЦП₂




ИУ

…


Д_i-1

ПУ_z

Ф_к-1


АЦП_m





Д_i

Ф_к


Магнитограф

Д – датчик ПУ – предусилитель У – усилитель Ф – фильтр

АЦП – аналого-цифровой преобразователь Магнитограф – устройство, которое записывает в аналогов виде некоторые сигналы. Самописец – печать на ленту текущих значений

УО – устройство отображения ИУ – исполнительное устройство


Методы схематизации случайных процессов при амплитудном анализе


метод текущих значений


X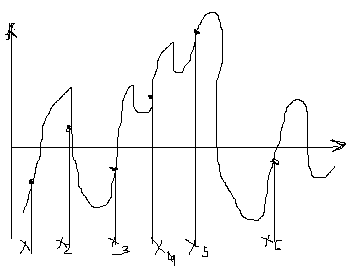_i – текущие значения. Могут быть как положительны, так и отрицательны.

метод размахов вниз (вверх)


X_i – текущие перепады, которые будут зарегистрированы.



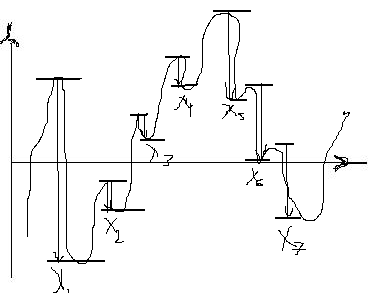
метод экстремумов

X_i – текущие перепады, которые будут зарегистрированы.



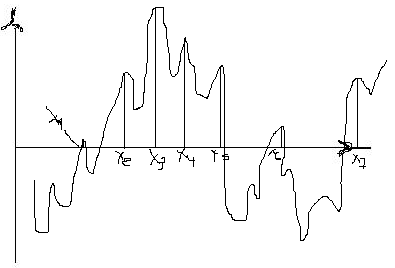
метод главных экстремумов

X_i – текущие перепады, которые будут зарегистрированы.



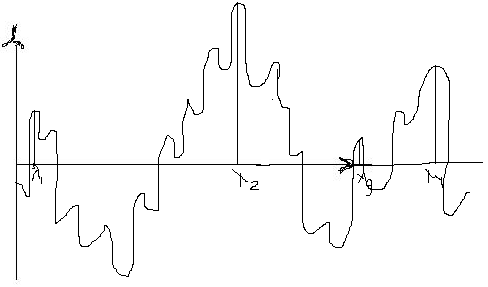
метод полных циклов вверх (вниз). Метод дождя





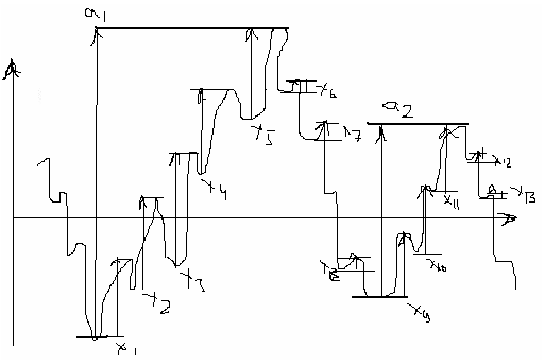
А₁ и А₂ – «главные» перепады

X_i – текущие перепады, которые будут зарегистрированы.


Анализ статистической независимости случайных значений: критерий серий


Берется несколько экспериментальных значений, и считается среднее (не арифметическое) после этого каждому значению противопоставляется (+) или (-). Серией называется последовательность однотипных наблюдений, перед и после которой следуют наблюдения противоположного знака или их вообще нет. После этого мы с некоторой вероятностью говорим, что этот процесс независимый или нет на основании таблицы (в таблице берется N/2 значение!).


Анализ статистической независимости случайных значений: критерий инверсий


Берется несколько экспериментальных значений. Считаем, сколько раз имело место неравенство: x_i>x_j при i

Методики проверки стационарности случайного процесса


Дан процесс. Бьём его на N частей. В каждом разбиении считает математическое ожидание и среднеквадратическое отклонение


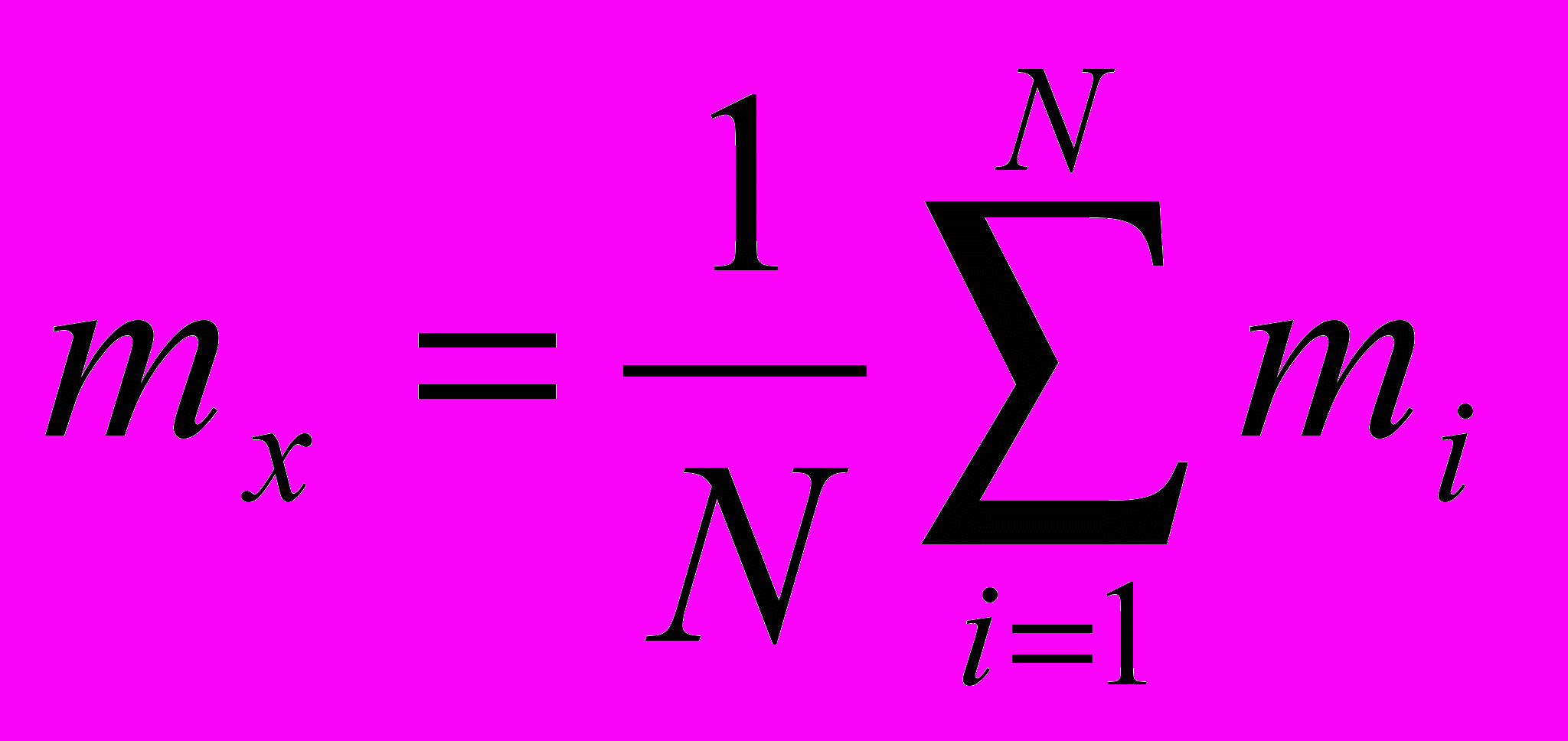
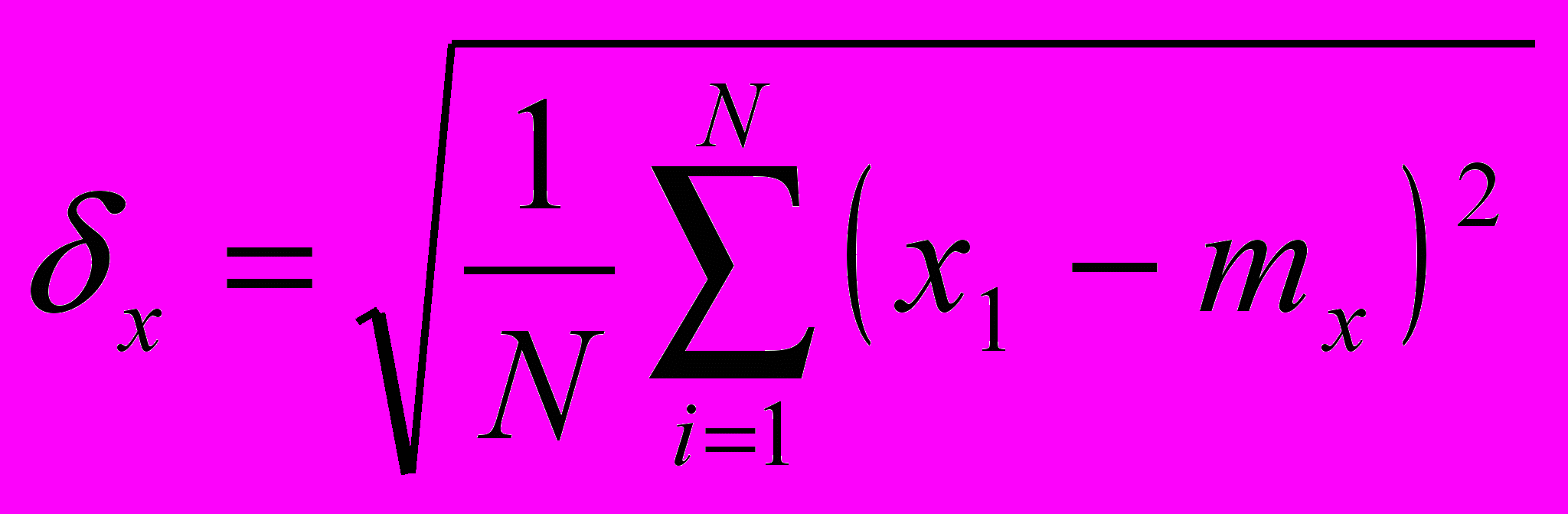
процесс считается стационарным только в том случае, если двойная проверка (серий и инверсий) каждой величины не обнаружила статистической зависимости.


Методы построения эмпирических закономерностей: метод узловых точек


Дано: 4 точки с координатами (0;2), (3;6), (8,х), (6;12).

Вывести формулу кривой, которая их соединяет.

Решение: уравнение прямой, проходящей через 4 точки – 3-его порядка в общем виде: y=a+bx+cx²+dx³

получаем систему линейных уравнений размерностью 4х4




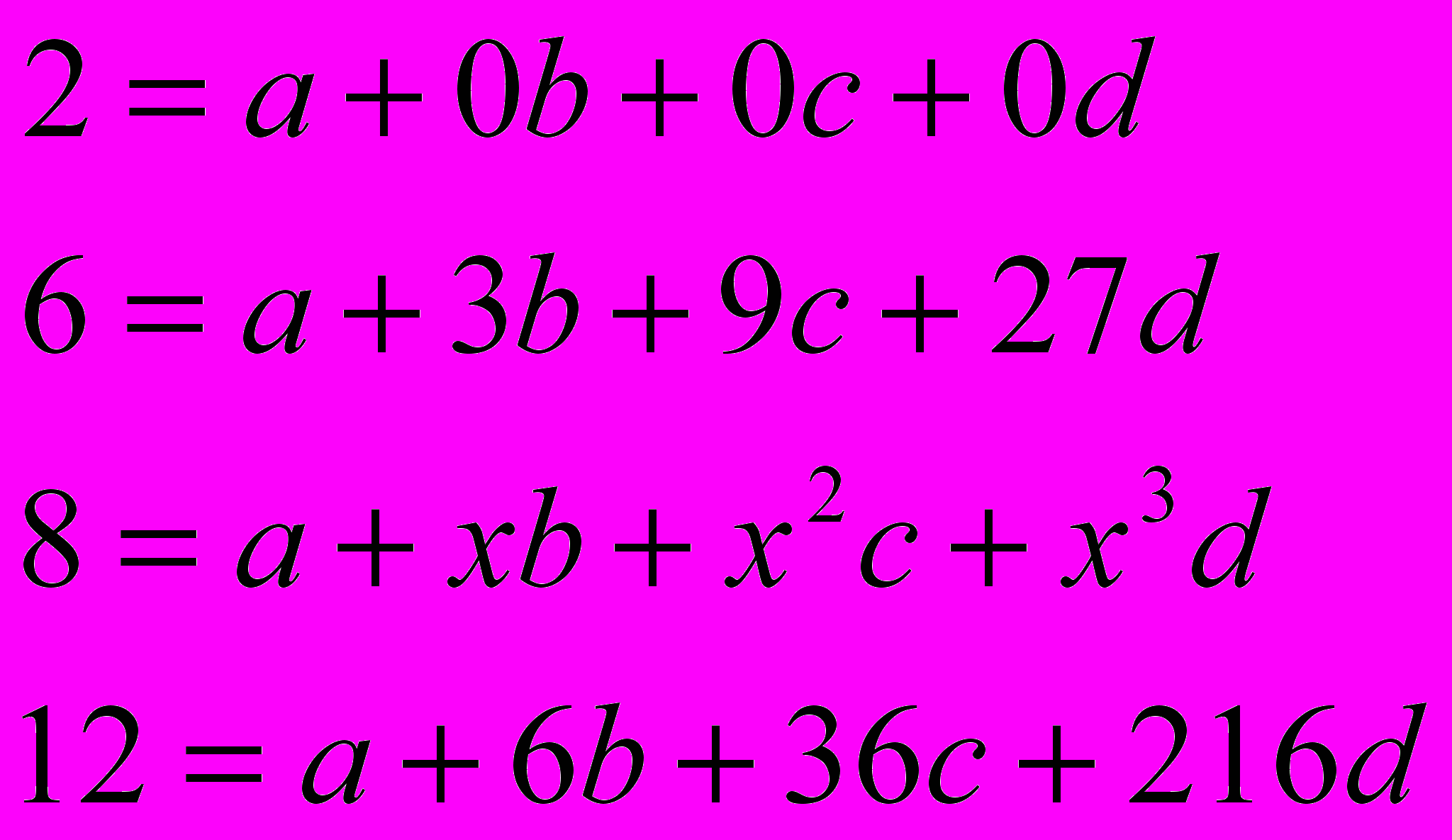
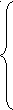
в результате получаем коэффициенты «А», «В», «С», «Д»


Методы построения эмпирических закономерностей: метод наименьших квадратов


Построение функции отражающей характерные особенности зарегистрированных данных.

С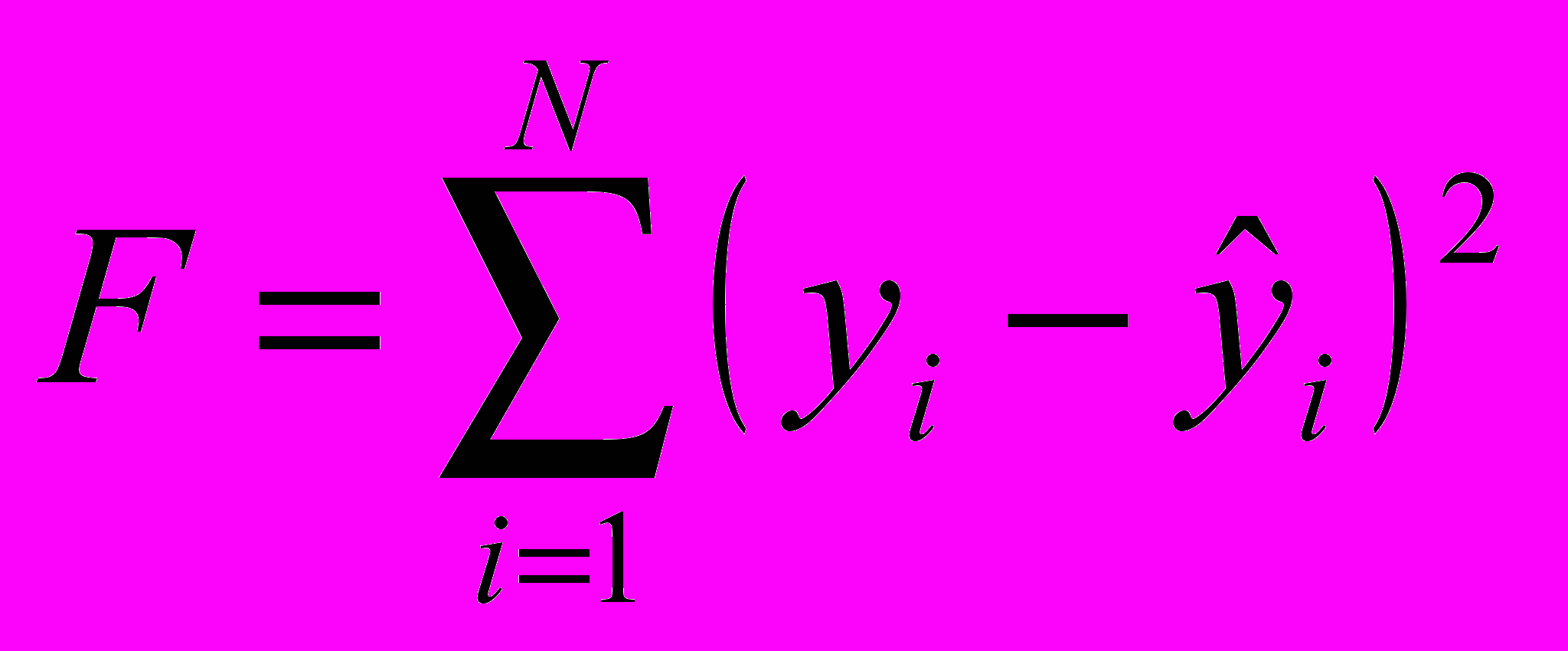умма квадратов отклонений должна быть минимальна.


Для тренда первого порядка: Для тренда третьего порядка:










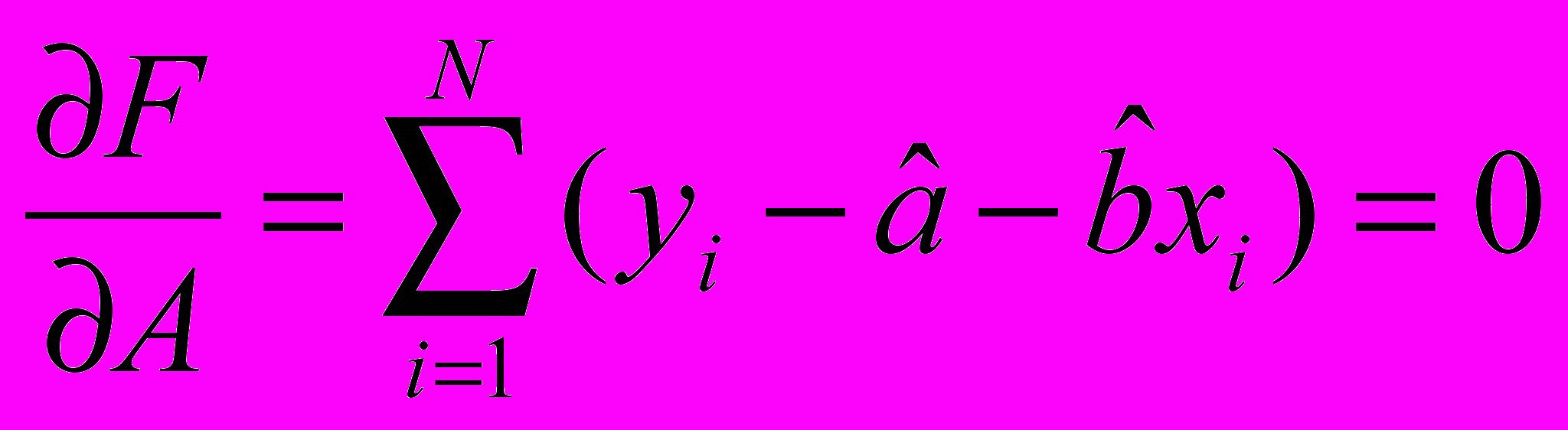
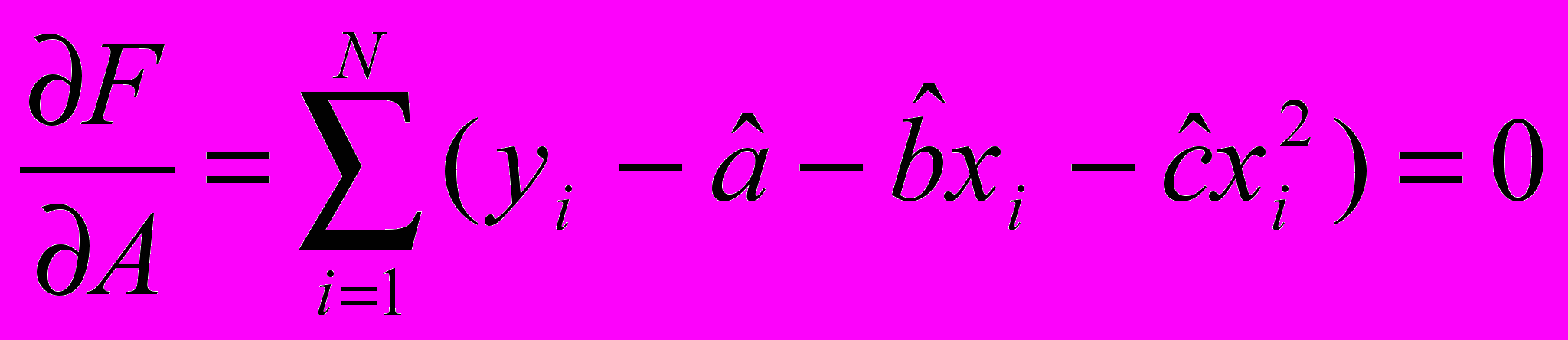
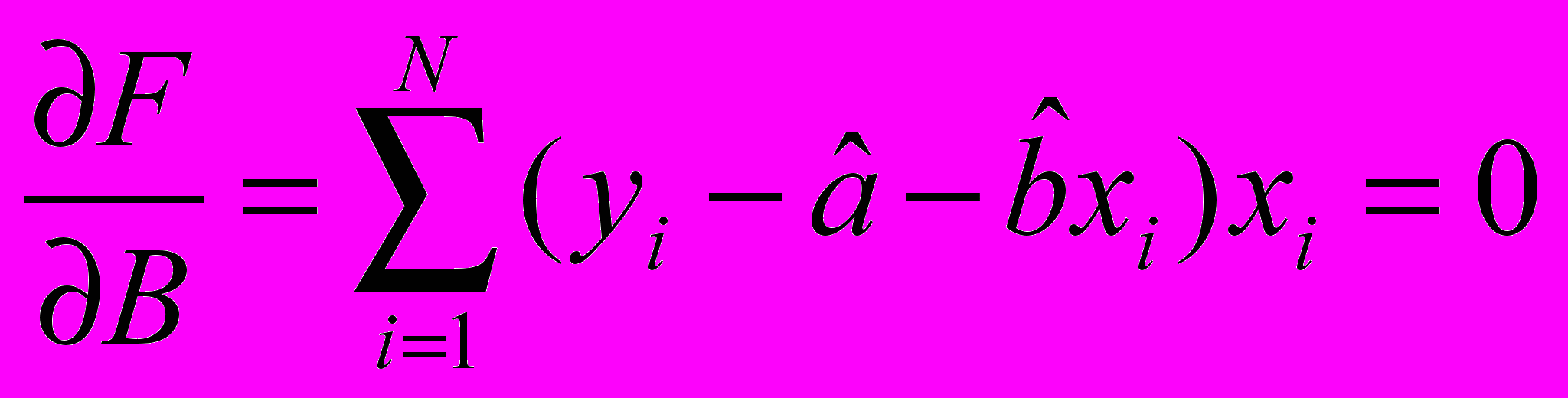
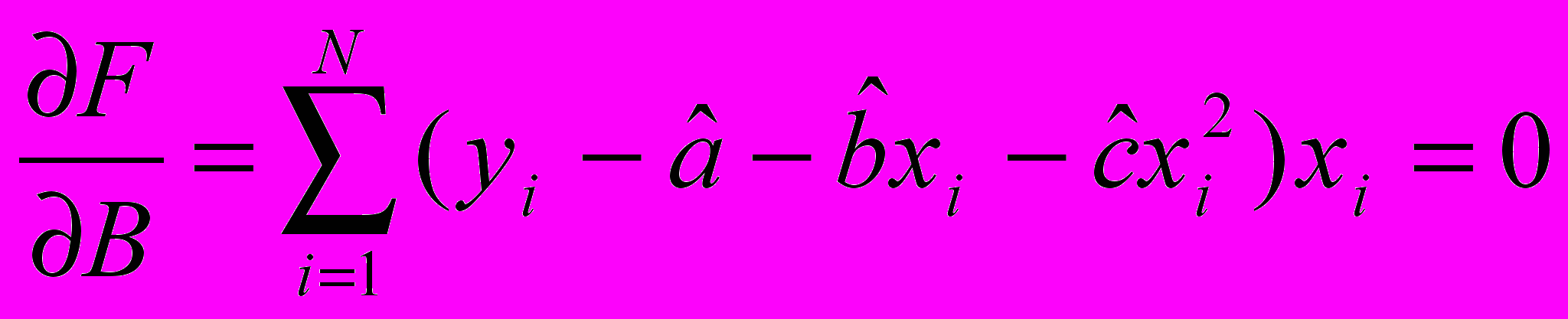
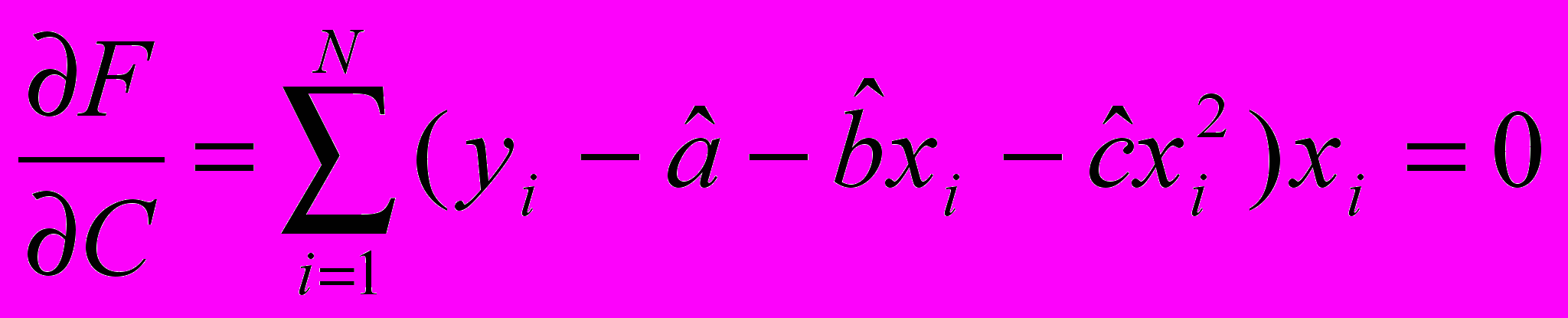
Обнаружение и устранение трендов в случайном процессе


Если по анализу статистической независимости какой-либо опыт показал зависимость то в функции содержится тренд.

Предполагаем что это тренд первого порядка и получаем систему уравнений:




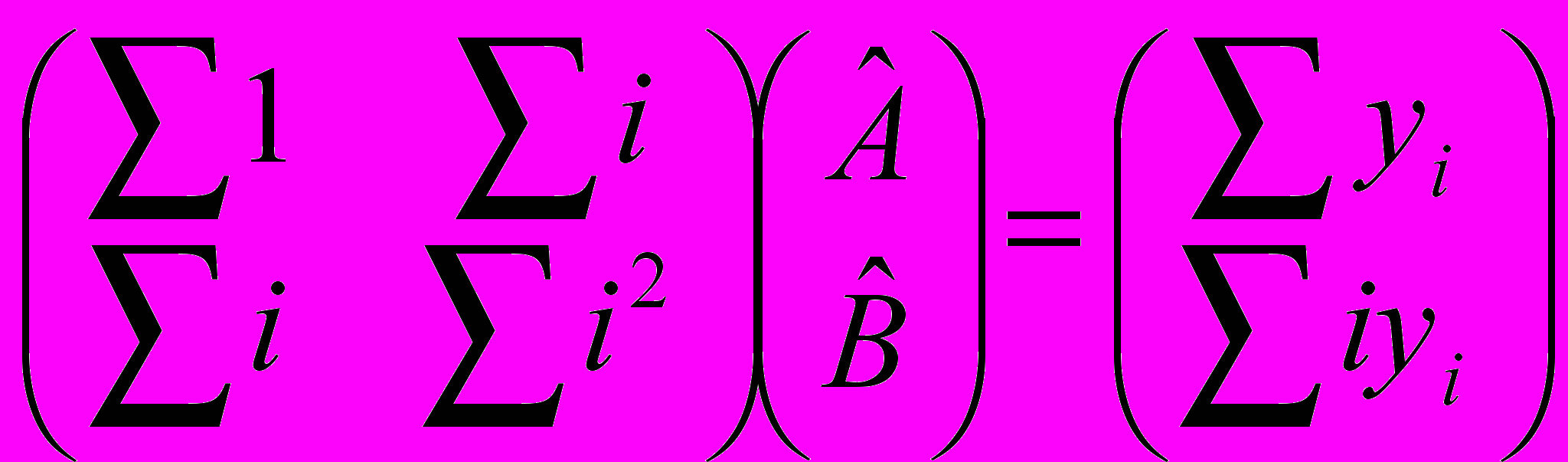
В результате получаем коэффициенты «А» и «В» - строим функцию y=a+bx и вычитаем эту функцию из исходных данных после чего проверяем на независимость.

Если всё хорошо – то говорим, что тренд был первого порядка и он успешно удалён, иначе предполагаем что там тренд 2-ого порядка:




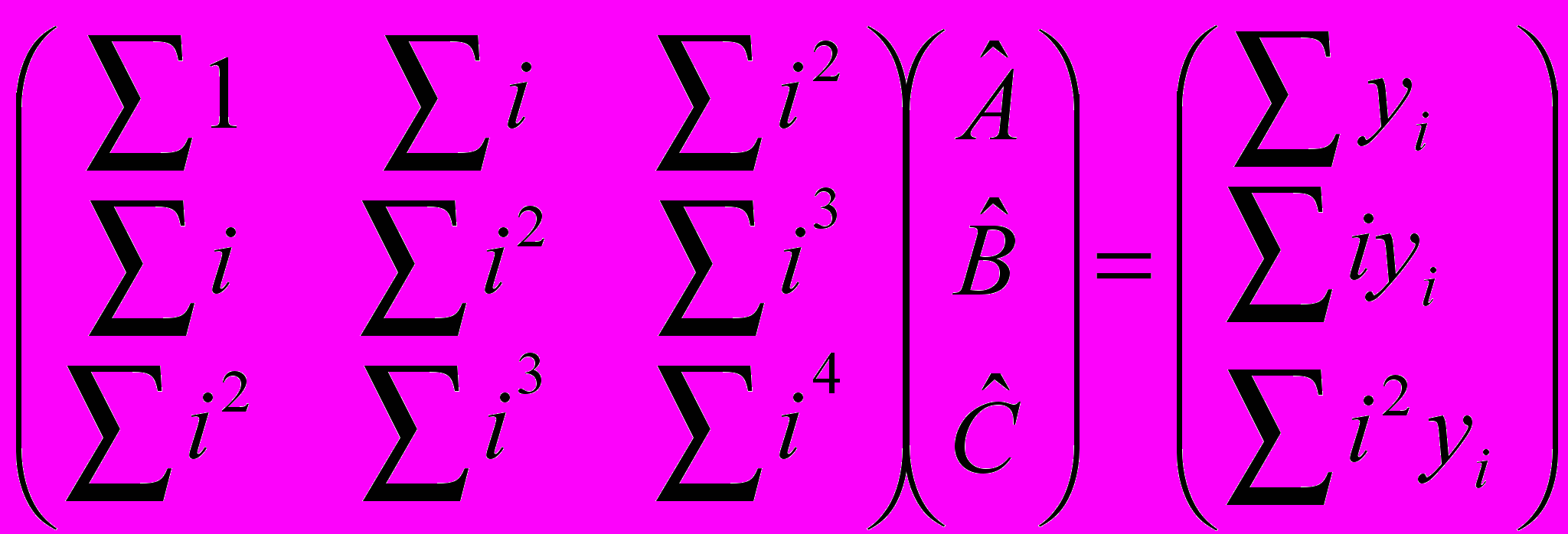
В результате получаем коэффициенты «А», «В» и «С» - строим функцию y=a+bx+cx² и вычитаем эту функцию из исходных данных после чего проверяем на независимость.


Если всё хорошо – то говорим, что тренд был первого второго и он успешно удалён, иначе говорим, что тренд удалить не представляется возможным.


Автокорреляционная функция, её свойства и способы вычисления (АКФ)


АКФ – зависимость внутри функции

Свойства:

1. |АКФ| < 1
   
2. АКФ [0] = 1
   
3. АКФ - симметрична
   

Взаимная корреляционная функция, её свойства и способы вычисления (ВКФ)

Вычисляется, когда оба процесса оптимизированы, выбирается из N/2 точек и сдвигается на N/4.

В результате получаем функцию взаимосвязи двух функций.

ВКФ показывает наличие линейных взаимосвязей между двумя функциями.




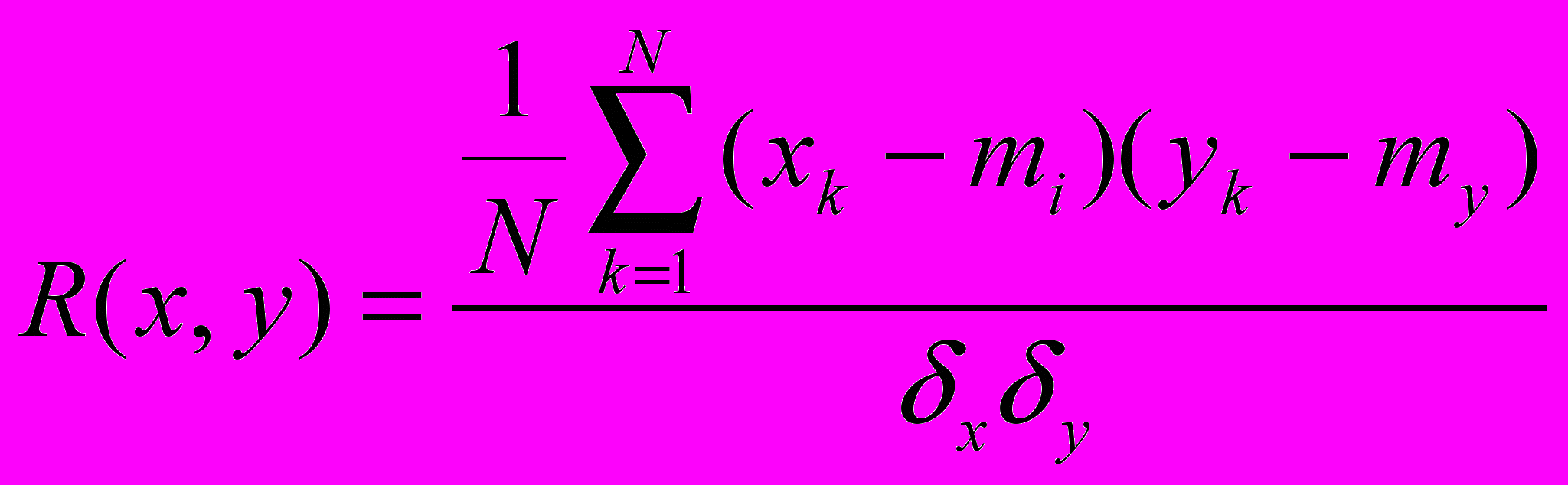
Свойства: |ВКФ| < 1





Методики вычисления усреднённого спектра случайного процесса


Во-первых усреднять можно только спектр мощности и плотности!

Берём спектр, делим его на N частей и вычисляем N мгновенных спектров.




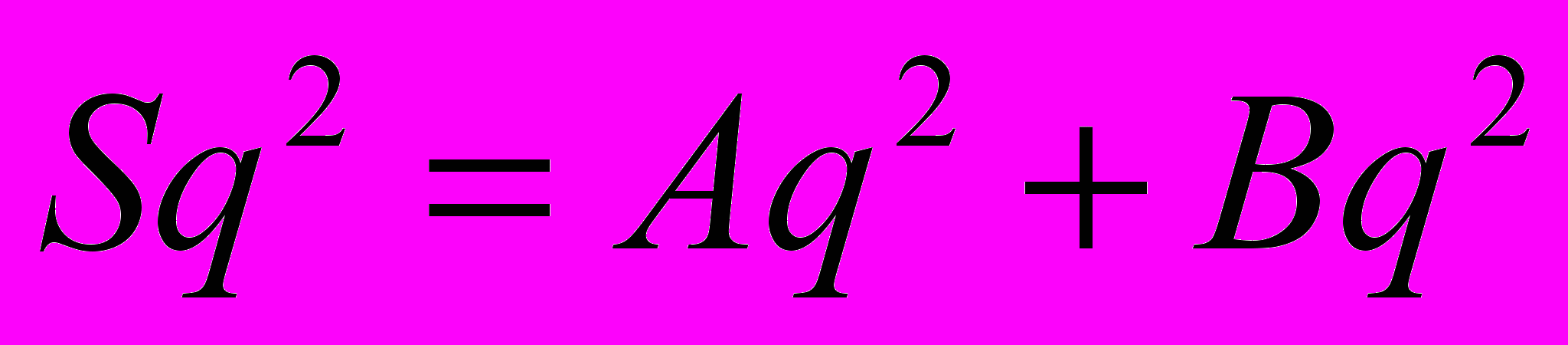
- амплитудный спектр (энергетический)





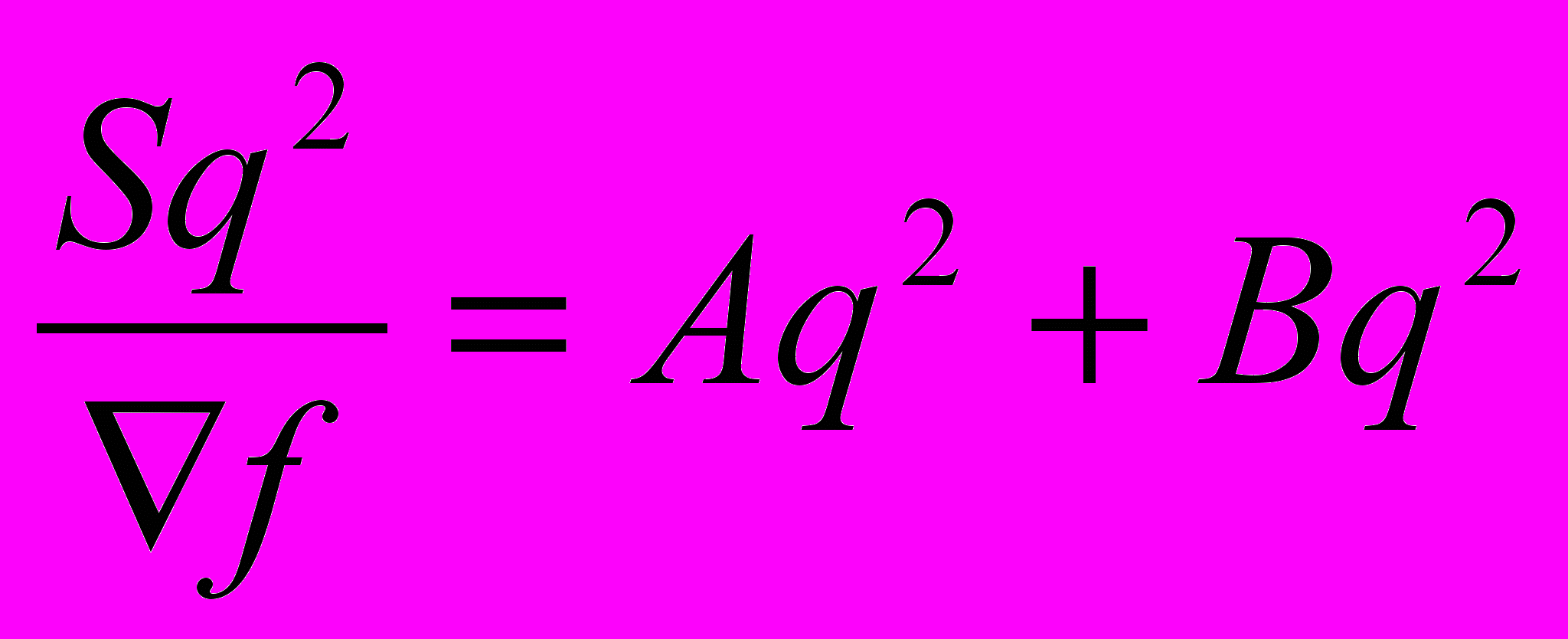
- спектр мощности


После этого суммируем и делим на N – получаем усреднённый спектр




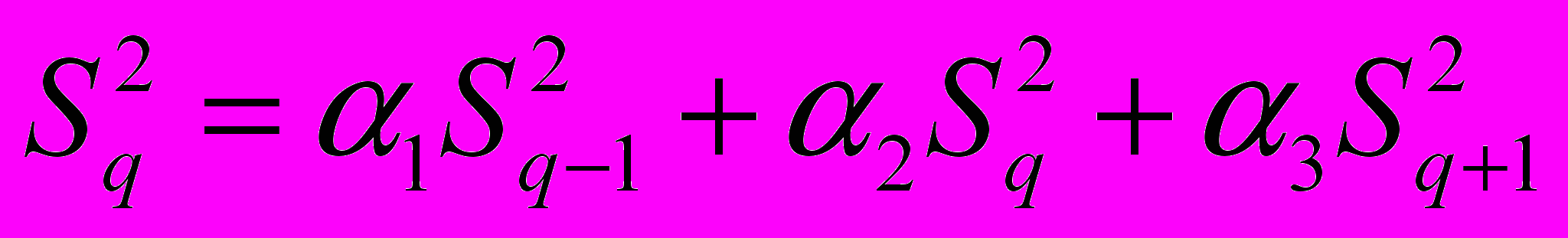
После этого сглаживаем

Методики с интенсивным использованием ЭВМ: «Бутстрэп» метод


Если мы не можем оценить погрешность – то вместо N элементов берём N-к элементов и считаем m раз. В результате получаем разброс и оцениваем n среднее.

Если берут разные исходные данные – можно получить довольно большой разброс


Методики с интенсивным использованием ЭВМ: «Джекнайт» метод


Если мы не можем оценить погрешность – то вместо N элементов берём N-1 элементов и считаем m раз. В результате получаем разброс и оцениваем n среднее.

- ответ всегда один и тот же.


АЦП и его погрешности

U_max




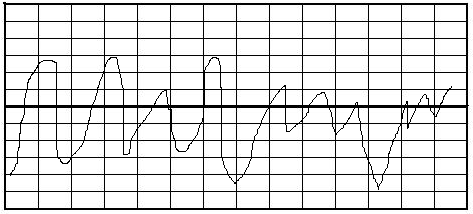
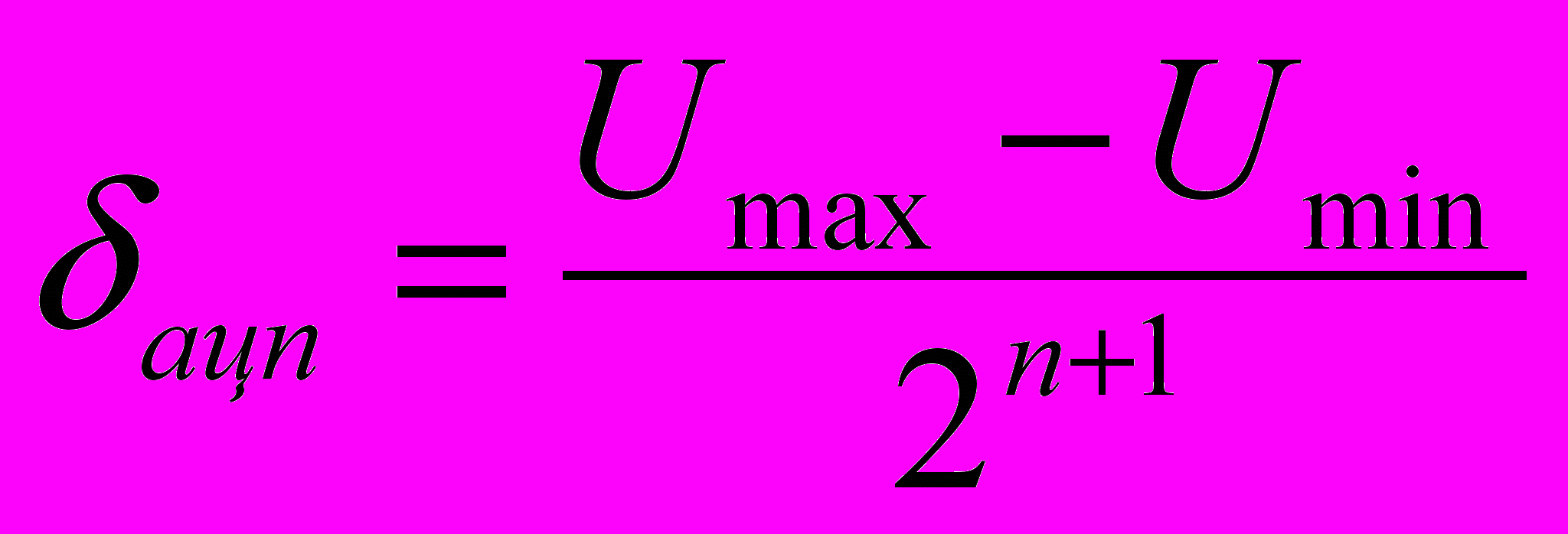
n –разрядность сетки
U_min


Основные характеристики случайного процесса


Случайный процесс – это процесс, значение которого в общем неизвестно, но может быть предсказано.

процессы делятся на:

• стационарные – процесс, который на зарегистрированном отрезке не меняет свои свойства
  
• Нестационарный – процесс, который на зарегистрированном отрезке меняет свои свойства: среднее значение, среднеквадратическое отклонение, состав.
  

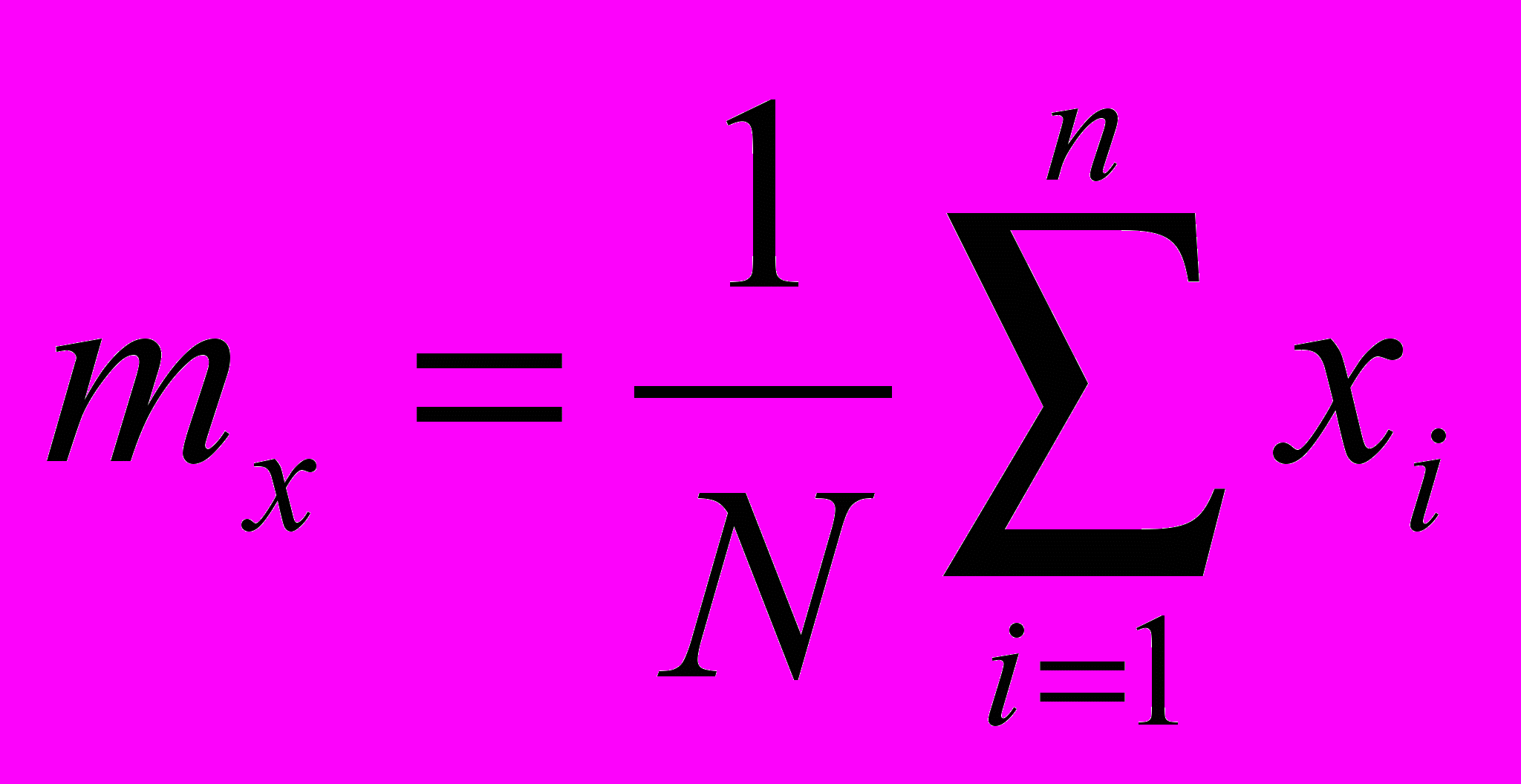
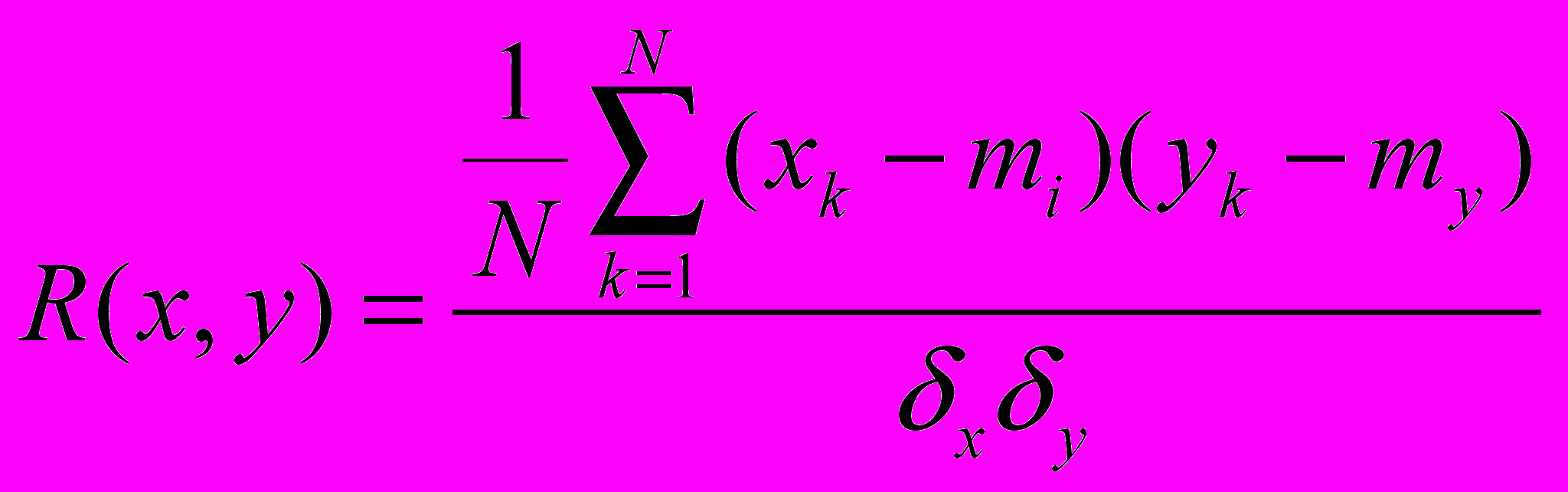
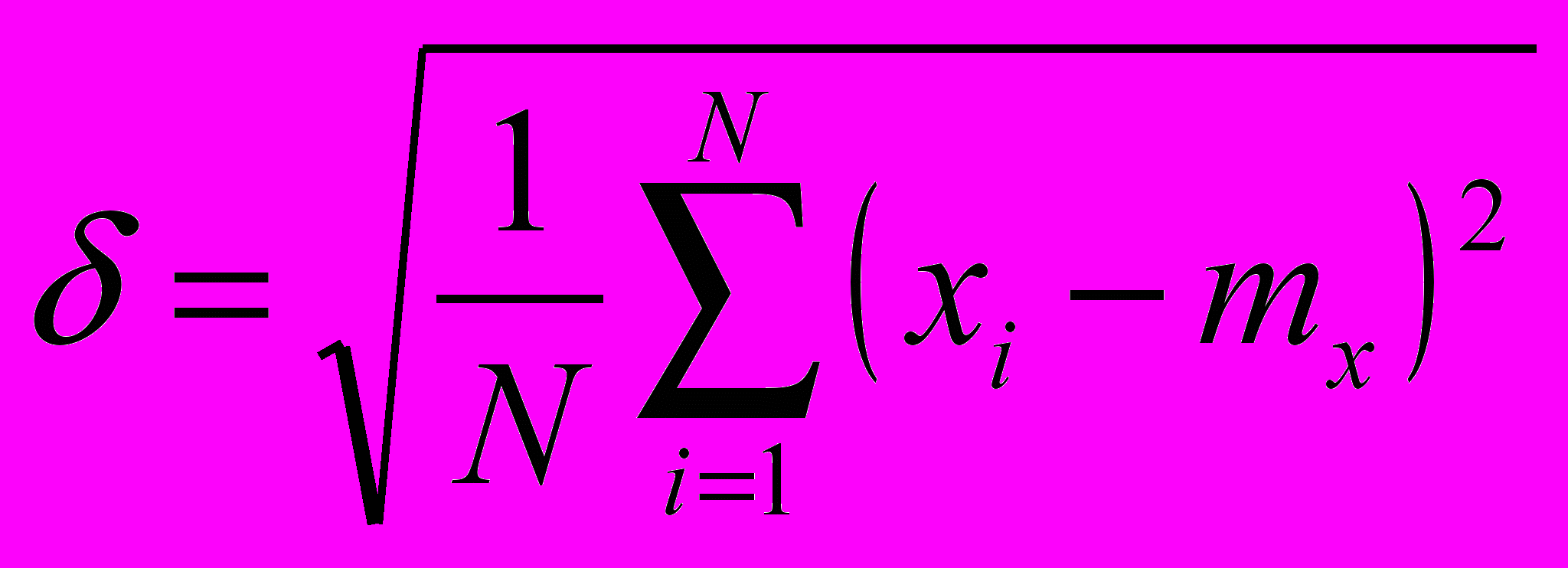
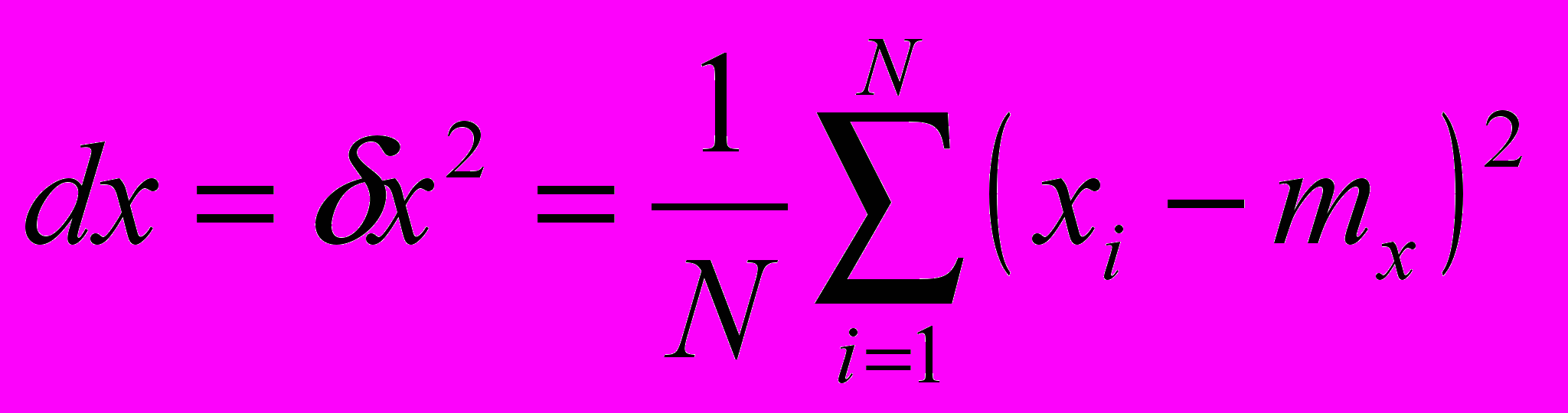
Авторегрессионная функция

1. Генерируется 6*N элементов (N – сколько элементов мы в результате хотим получить)
   
2. Суммируем по 6 элементов, в результате получаем массив из N элементов
   
3. Вычитаем из каждого элемента m_x
   
4. Считаем среднеквадратическое отклонение, и делим на него каждый элемент нового массива
   

Моделирование процессов с заданными свойствами


Моделирование процессов с заданными свойствами осуществляется 2 способами:

1. авторегрессионное моделирование. Спектр, который мы получаем широкополосный.
   

Генерируется 6*N элементов (N – сколько элементов мы в результате хотим получить)

Суммируем по 6 элементов, в результате получаем массив из N элементов

Вычитаем из каждого элемента m_x

Считаем среднеквадратическое отклонение, и делим на него каждый элемент нового массива

Поле этого по формуле

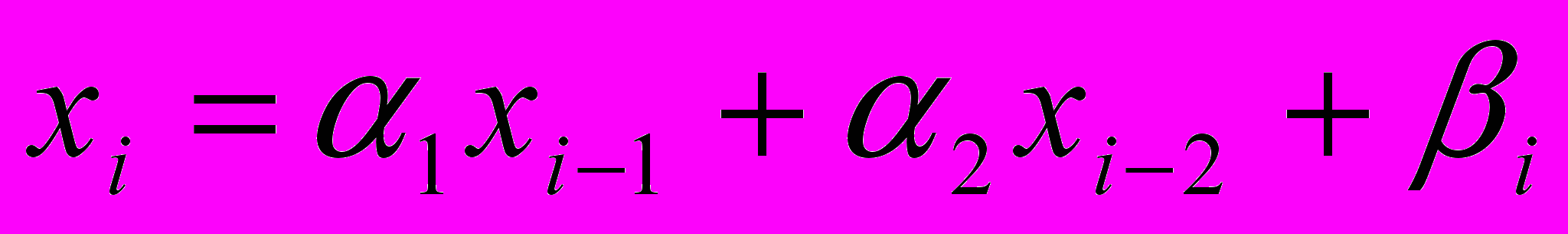
п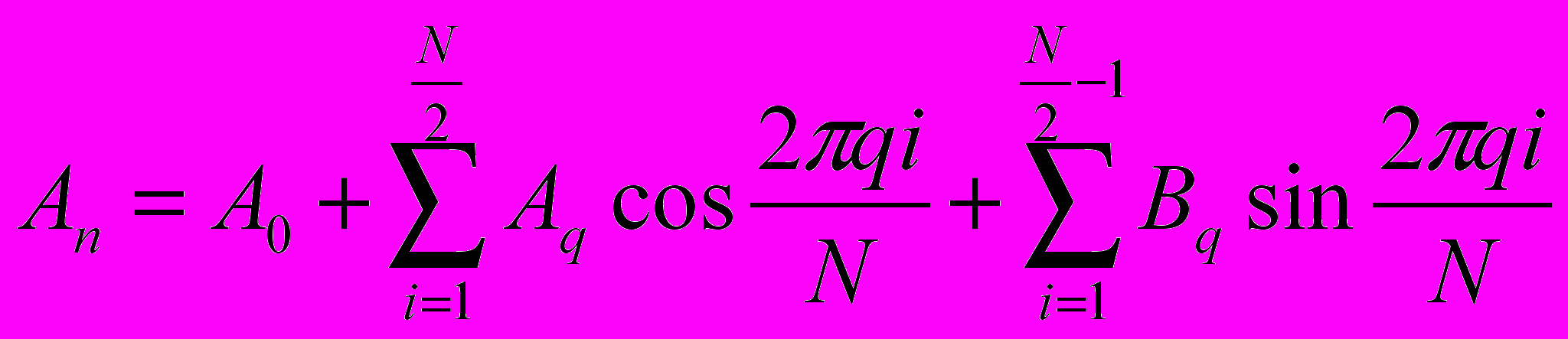олучаем массив x_i

2. гармонический синтез (ряд Фурье)
   

Основные систематические погрешности в спектре


Недостатки такие:

• недостаточное количество периодов гармоники на длину выборки, при достаточно точном описании периода
  
• недостаточное количество точек, описывающих соответствующие гармоники, при большом количестве периодов
  

Теорема Котельникова


т.Котельникова гласит о том, что: частота дискретизации исследуемого сигнала должна быть как минимум вдвое больше максимальной частотной составляющей этого сигнала.


Ф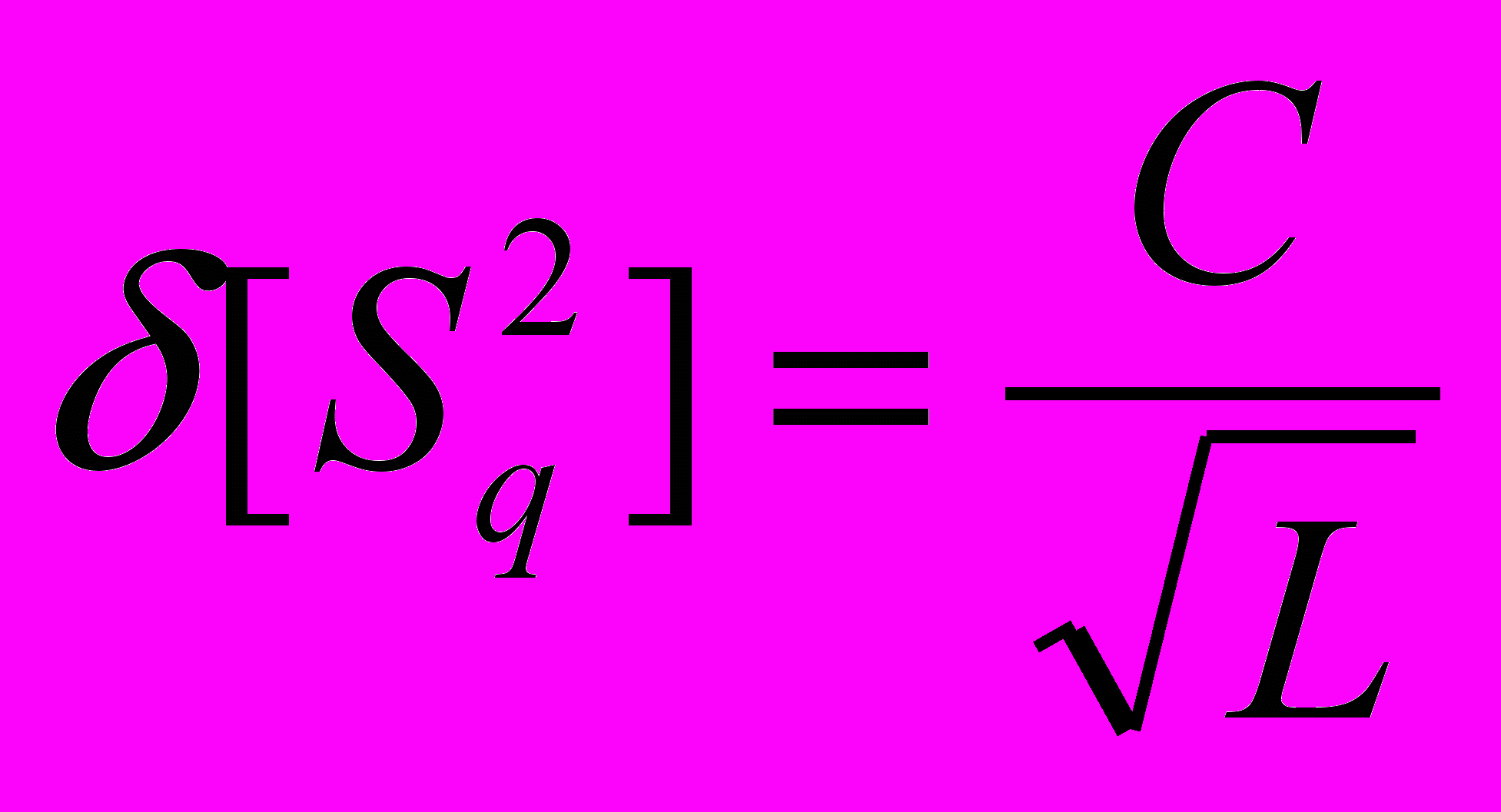ОРМУЛЫ:


- относительная погрешность; С – тип окна (1; 0,75; 0,64)





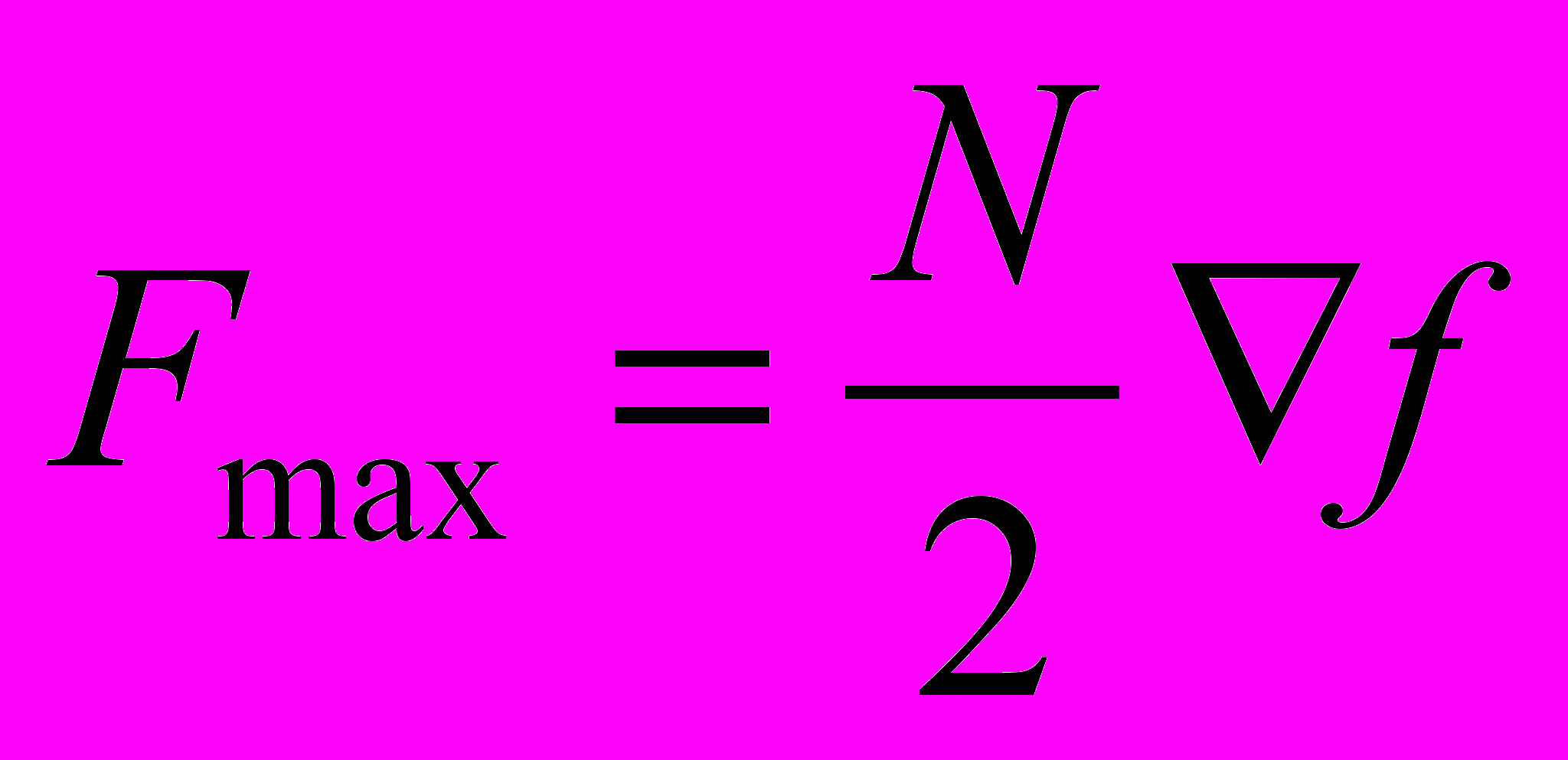
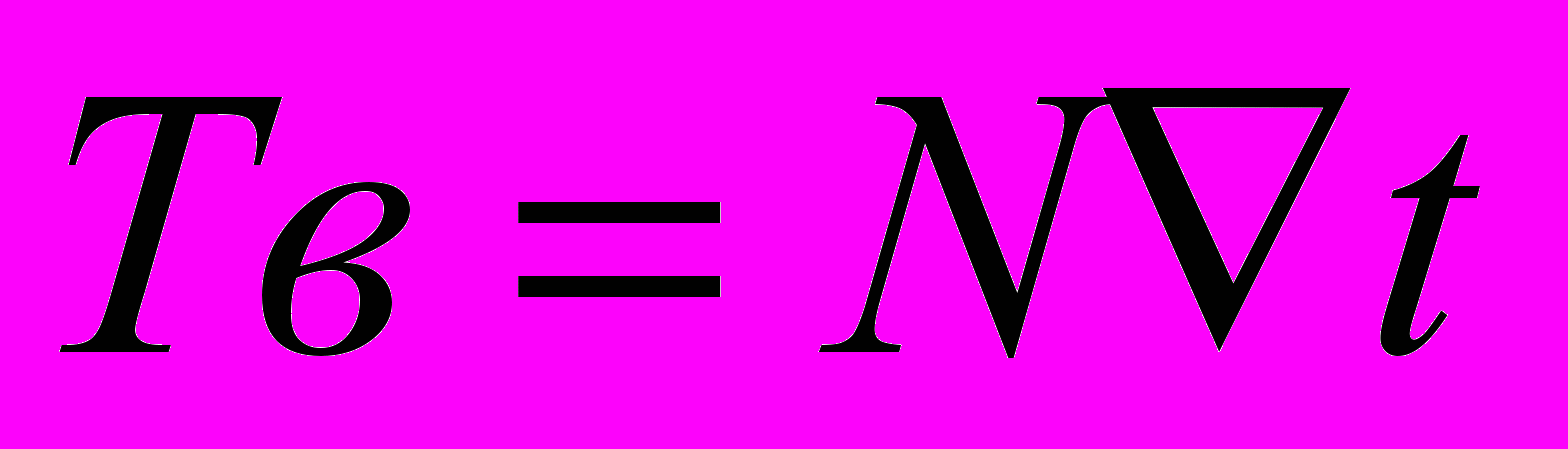
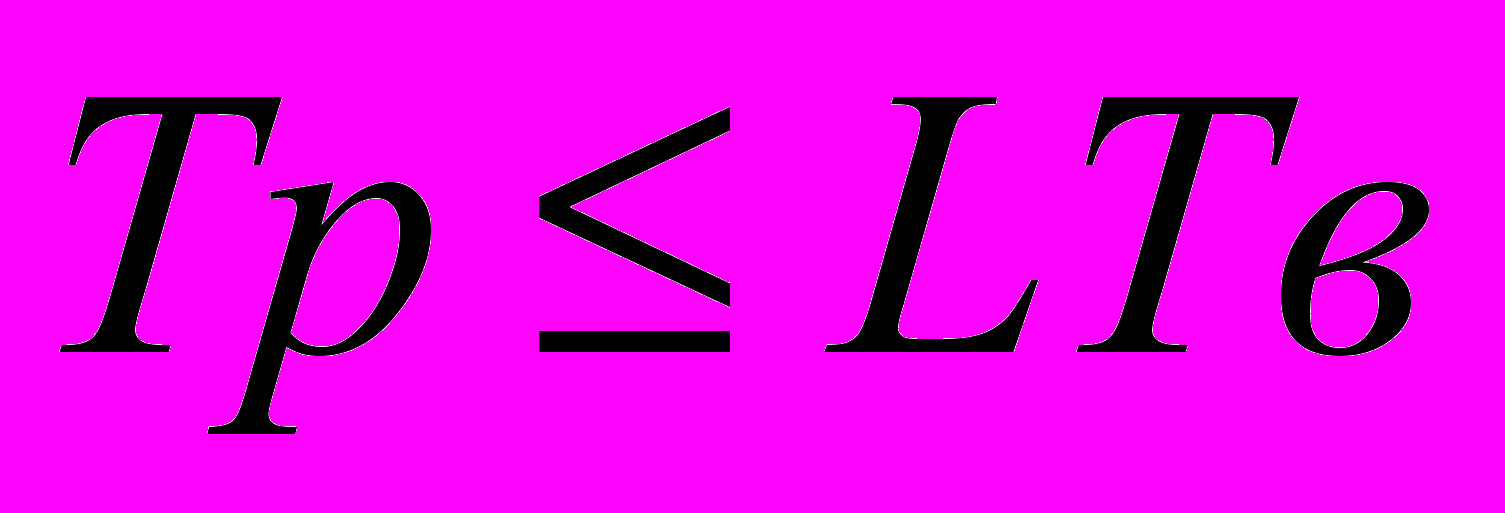
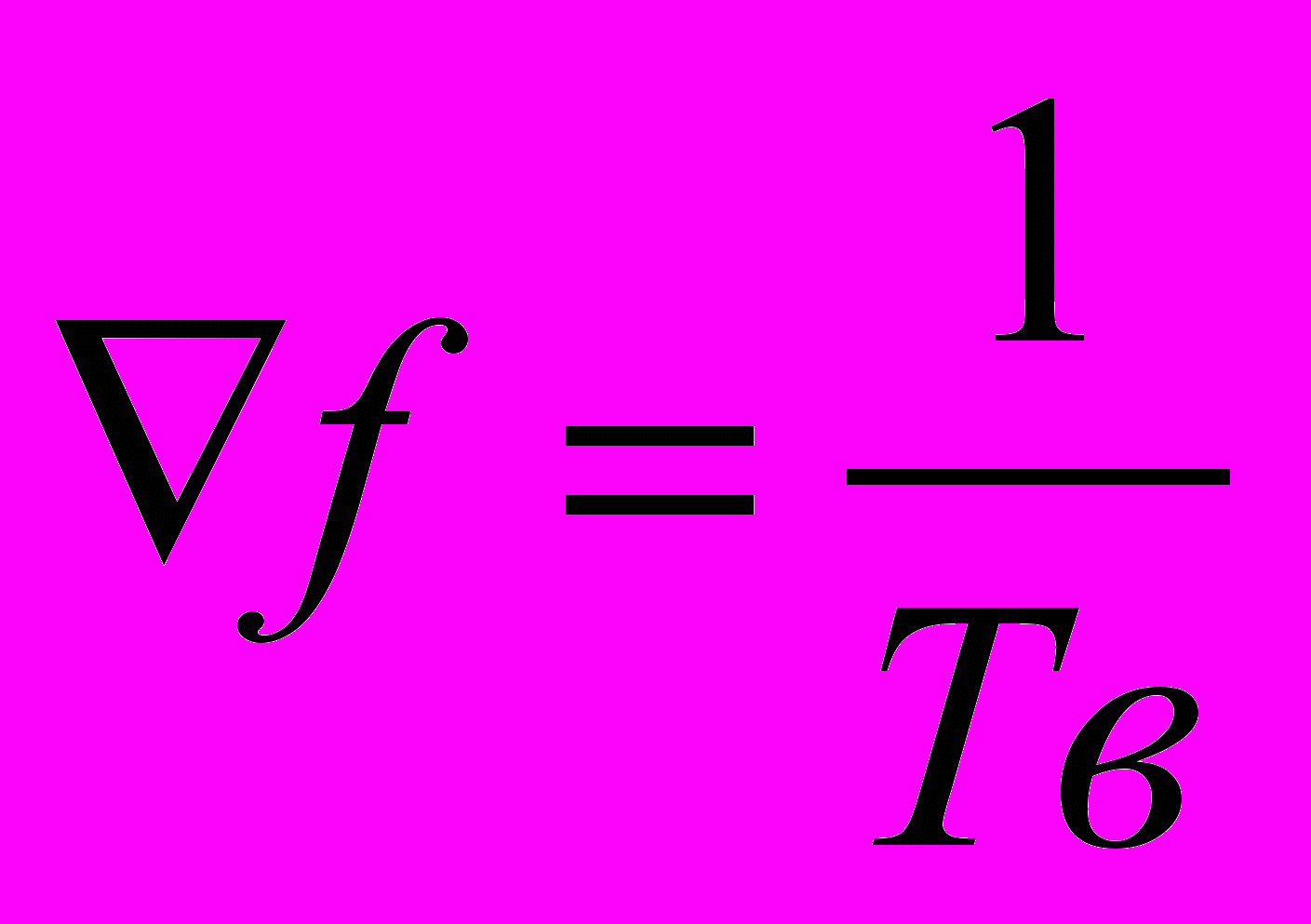- частота дискретизации


- время реализации


- зависимость частоты дискретизации от времени выборки


- время выборки