14. Элементы квантовой статистики и зонной теории твердого тела

Вид материала

Лекция

Содержание 14.7.1. Уровень Ферми, поверхность Ферми 14.7.2. Электронный газ и его некоторые свойства 14.7.3. Температура вырождения 14.7.4. Влияние температуры на электронную теплоемкость 18.8. Электронная зонная структура и волны Блоха 14.8.1. Разрешенные и запрещенные электронные энергетические зоны в кристаллах 14.8.3. Металлы, полупроводники, диэлектрики

Подобный материал:

• Рабочая программа дисциплины «теория представлений групп в физике твердого тела», 52.74kb.
• Программа дисциплины дпп. В. 03 «Физика твердого тела» Специальность 032200., 165.38kb.
• Рабочая программа дисциплины «Физика твердого тела», 72.99kb.
• Учебно-методический комплекс дисциплина «физика твёрдого тела» Челябинск, 194.36kb.
• Ix международная научная конференция «химия твердого тела: монокристаллы, наноматериалы,, 81.75kb.
• Его работы относятся к термодинамике, теории теплового излучения, теории относительности,, 26.02kb.
• Программа курса «квантовая химия твердого тела», 18.91kb.
• Программа курса общей физики для I курса этф осенний семестр 2011, 58.04kb.
• Малюкин Сергей Яковлевич. Физика 11 класс моу «сош с. Ивантеевка» Ивантеевский район, 102.46kb.
• Процедура восполнения напряжений при решении нелинейных краевых задач механики деформируемого, 69.02kb.

14.7. Квантовая теория свободных электронов в металле.


В настоящее время отсутствуют методы точного решения динамической задачи для системы многих частиц. Поэтому использование уравнения Шредингера для задачи о взаимодействии множества электронов и ядер в твердом теле не позволяет найти точных решений. Эта задача решается приближенно, путем сведения задачи многих частиц к одноэлектронной задаче об одном электроне, движущемся в заданном внешнем поле. Подобный путь приводит к зонной теории твердого тела. Но прежде рассмотрим основные понятия квантовой теории свободных электронов в металле.


14.7.1. Уровень Ферми, поверхность Ферми

Согласно модели свободных электронов валентные электроны атомов металла могут свободно перемещаться в пределах образца. Именно валентные электроны обусло­вливают электропроводность металла, и по этой причине их называют электронами проводимости. Допустим, что электроны проводимости движутся в пределах образца металла совершенно свободно. Положив в уравнении Шрёдингера




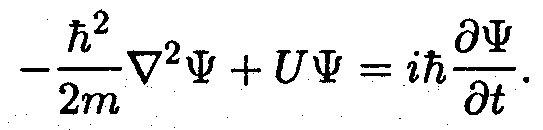
U = 0, получим уравнение Шрёдингера для свободного электрона:

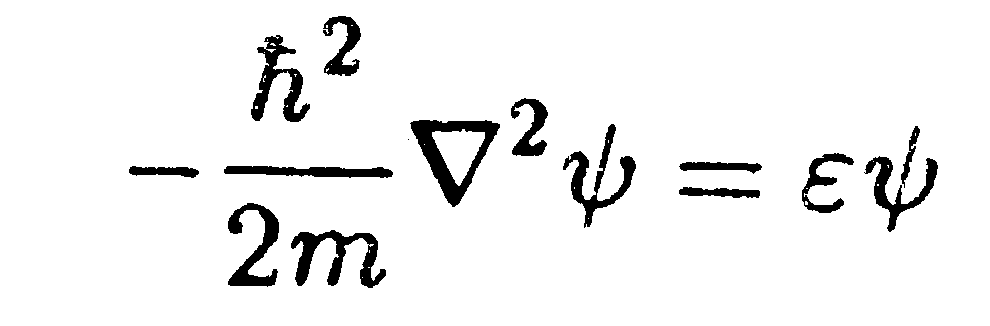(14.38)

(m — масса, ε — энергия электрона).

Решение уравнения (14.38) имеет вид

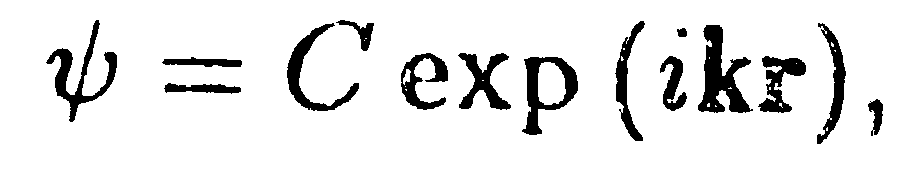(14.39)

где k = p/ћ есть волновой вектор электрона, связанный с энергией соотношением

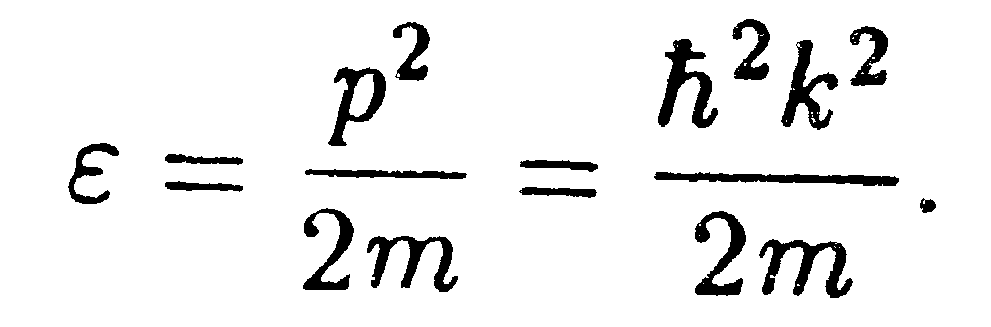(14.40)

Пусть число свободных электронов в единице объема металла равно n. Тогда в образце металла будет содержаться nV свободных электронов. Вследствие принципа Паули при абсолютном нуле эти электроны расположатся по одному в каждом состоянии на самых низких энергетических уровнях. Поэтому все состояния с энергией ε, меньшей некоторого значения ε _F (0) , будут заполнены электронами, состояния же с ε > ε _F (0) будут вакантными. Энергия ε _F (0) называется уровнем Ферми при абсолютном н у л е. Уровень Ферми играет роль параметра ε _F в распределении электронов по состояниям с различной энергией. Этот параметр слабо зависит от температуры (см. ниже). Величина ε _F (0) представляет собой значение параметра ε _F при Т = 0 К.

Поверхность постоянной энергии в k-пространстве (или, что то же самое, в p-пространстве; р = ћk), соответствующая значению энергии, равному ε _F , носит название поверхности Ферми. В случае свободных электронов эта поверхность описывается уравнением

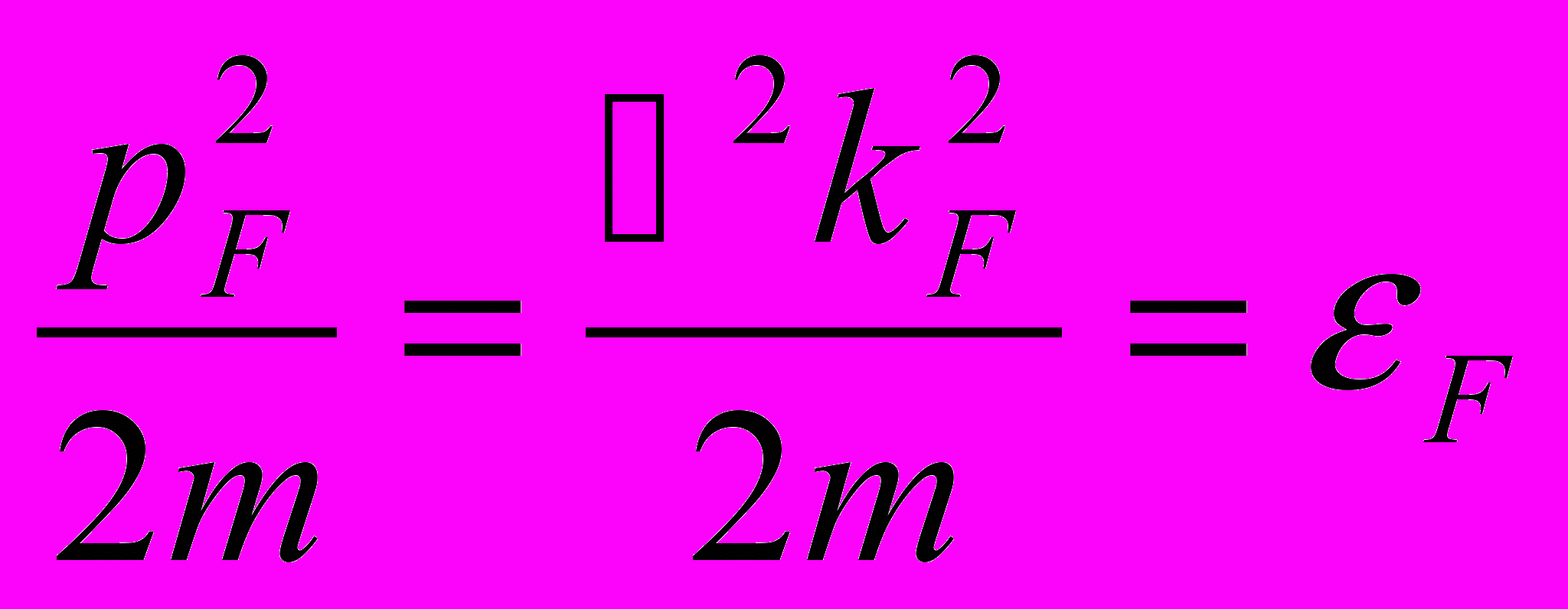(14.41)

(см. (14.40)) и, следовательно, имеет форму сферы. При аб­солютном нуле температуры поверхность Ферми отделяет состояния, заполненные электронами, от незаполненных состояний.


14.7.2. Электронный газ и его некоторые свойства

В приближении свободных электронов электроны рассматриваются как идеальный газ. Металлический образец представляет собой для электронов трехмерную потенциальную яму. Реше­ние уравнения Шрёдингера для частицы, находящейся в такой яме, показывает, что энергия частицы может иметь только дискретные (квантованные) значения. Электроны являются фермионами (их спин равен 1/2); поэтому распределение электронов по энергетическим уровням описывается функцией распределения Ферми-Дирака. При выводе этой формулы (14.12) мы считали уровни энергии невырожденными, т. е. не учитывали возможности того, что данной энергии могут соответствовать несколько различных квантовых состояний частицы. Электроны обладают одной и той же энергией в двух состояниях, различающихся ориентацией спина (т. е. значениями квантового числа m_s, которое может быть равно ±1/2). В связи с этим среднее число электронов, находящихся на уровне энергии ε_i , определяется выражением

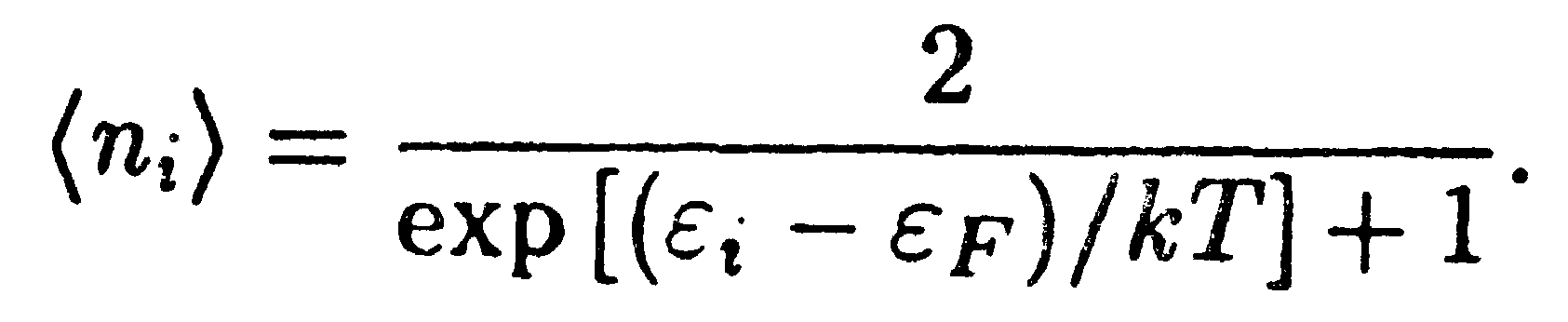(14.42)

Имеющий размерность энергии параметр μ в формуле (14.12) часто обозначают через ε _F и называют уровнем Ферми или энергией Ферми, что и было использовано в формуле (14.42). Отметим, что ε _F > 0, иначе некоторые числа заполнения обращались бы при Т → 0 К в нуль.

При абсолютном нуле электроны располагаются попарно на самых низких доступных для 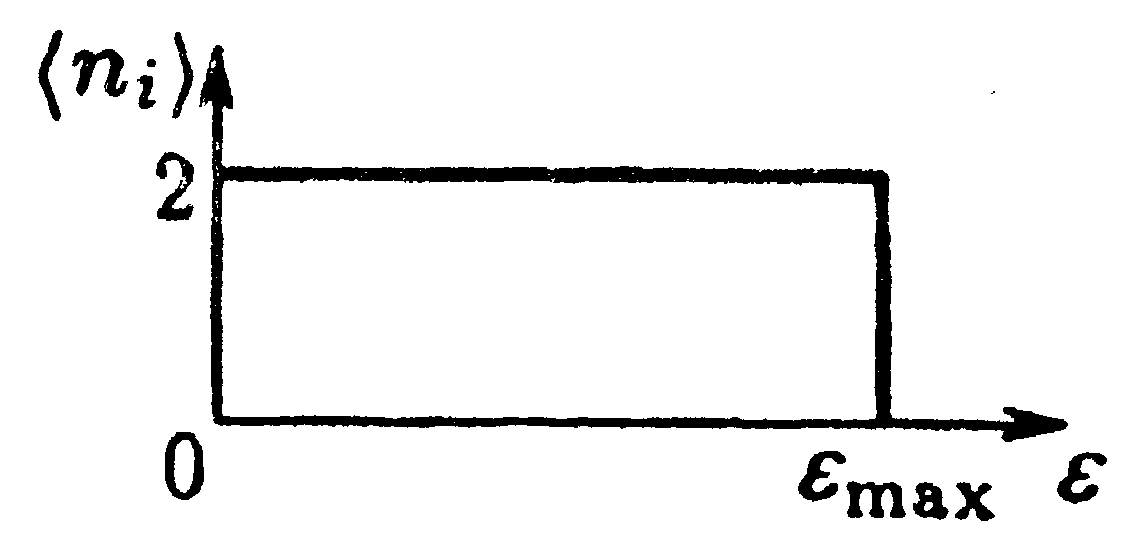них уровнях. В соответствии с этим зависимость _i> от ε_i имеет вид, показанный на рис. 14.5. Вследствие дискретности уровней горизонтальный участок графика состоит из отдельных точек. Однако уровни расположены столь густо, что изображающие их точки сливаются в непрерывную линию.

Рис. 14.5.


Каждой ячейке фазового пространства соответствуют два состояния электрона, различающиеся направлением спина. Поэтому, как и в случае фотонов, число состояний в тонком энергетическом слое объема ∆τ_i определяется формулой (см. (14.19))

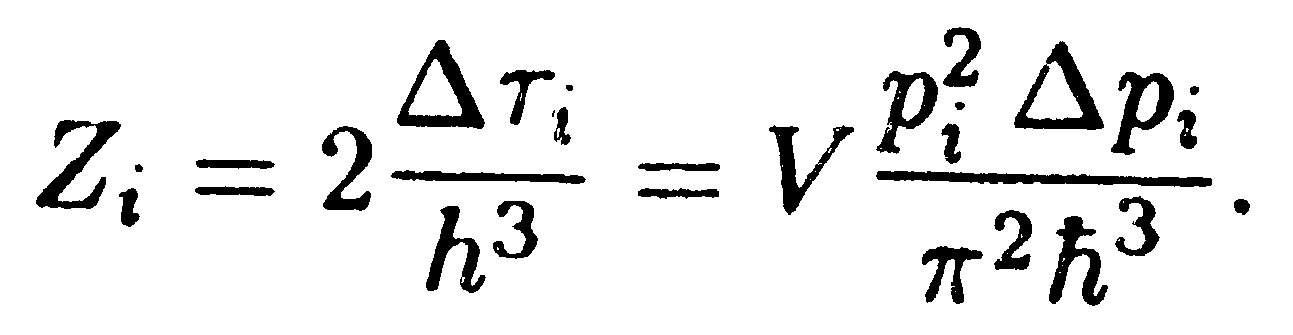(14.43)

Импульс электрона связан с его энергией соотношением ε_i = р²/2m. Отсюда p_i = (2mε_i)^1/2, а p_i ∆p_i = m ∆ε_i . Перемножив эти выражения, найдем, что



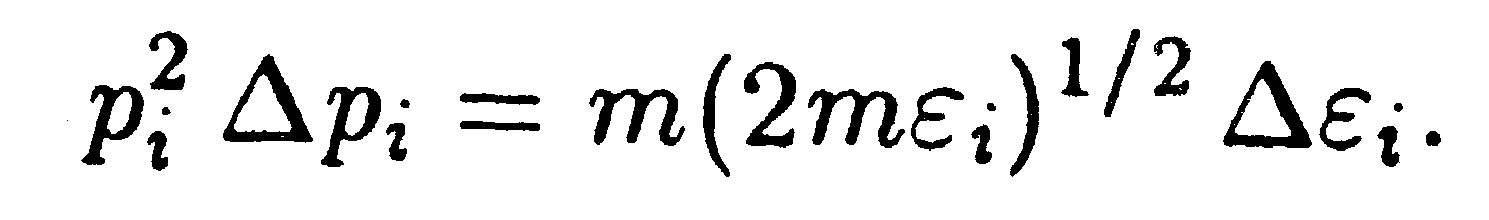
Произведя в (14.43) такую замену, получим

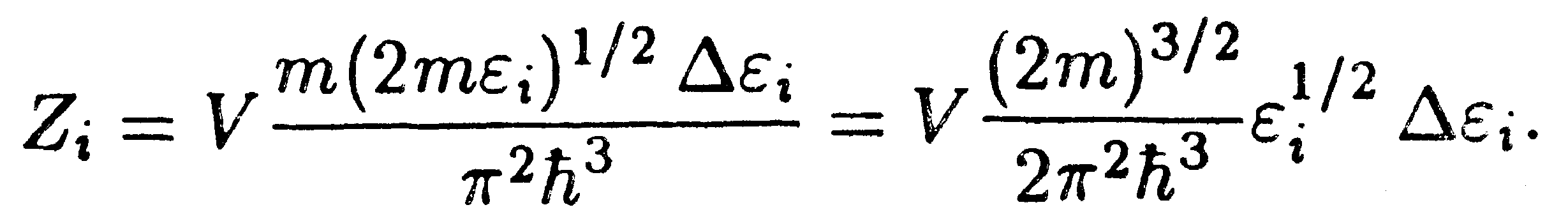(14.44)

Введя обозначения

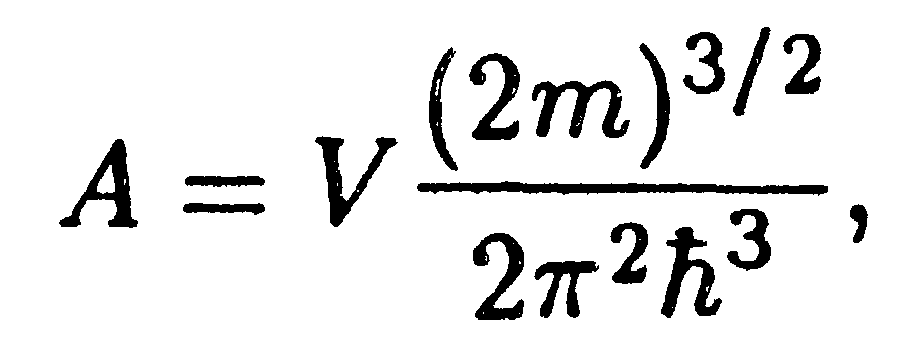(14.45)

представим формулу (14.44) в виде

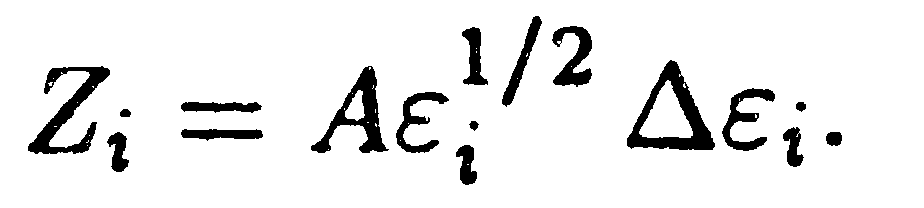(14.46)

При абсолютном нуле заполнены N нижних состоя­ний, где N — число электронов в данном образце металла. Следовательно, сумма чисел Z_i, соответствующих энергиям от 0 до ε_mах, должна быть равна N:

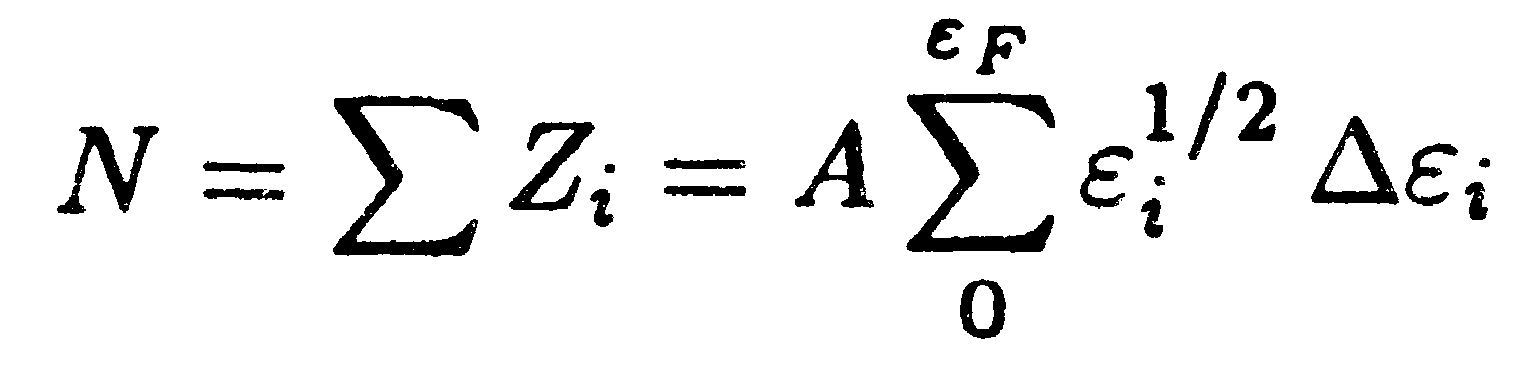(14.47)

(учли, что при абсолютном нуле ε_mах = ε _F). Приняв во внимание, что ∆ε_i << ε_i, можно в формуле (14.47) заменить суммирование интегрированием. Тогда

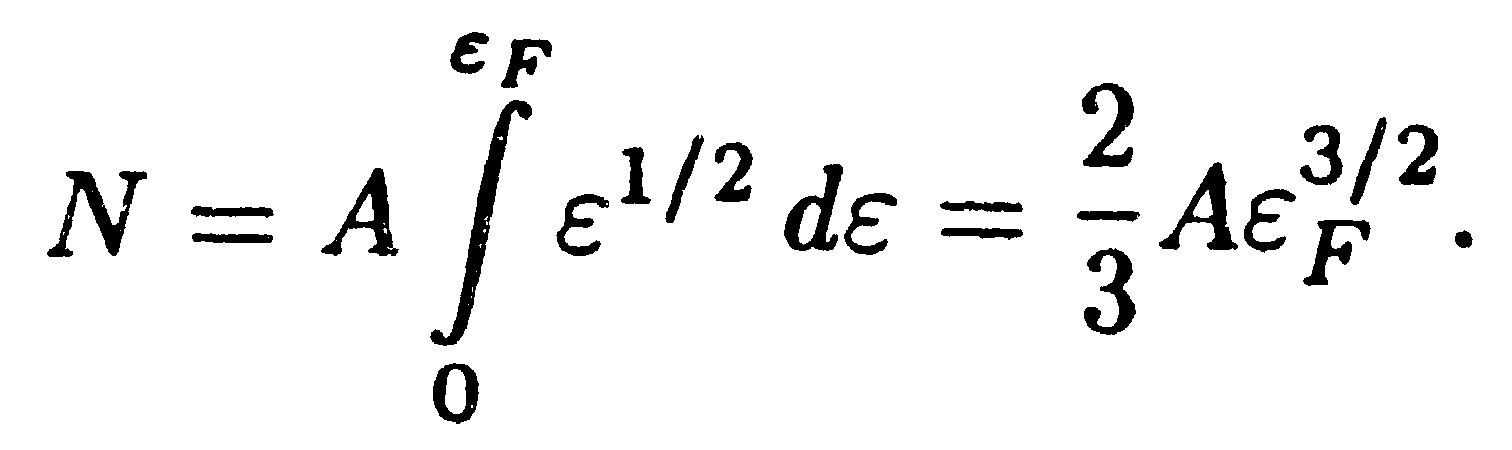(14.48)

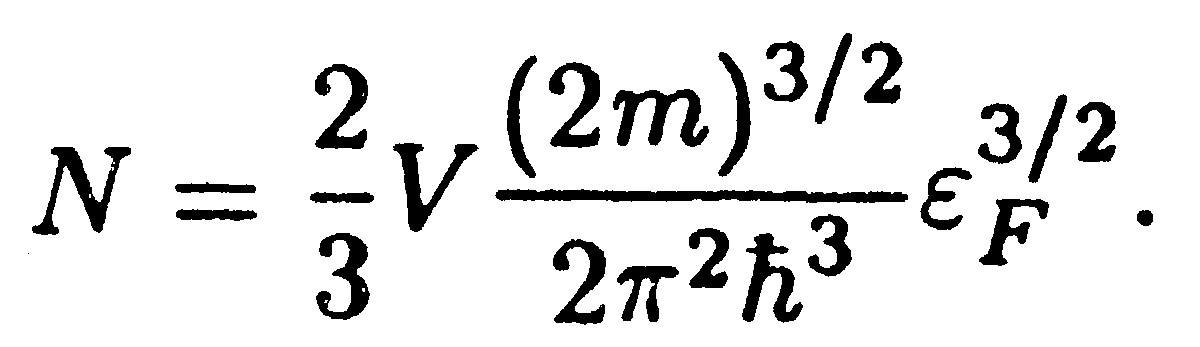
Подстановка выражения (14.45) для А дает

Отсюда с учетом того, что N/V = п есть концентрация свободных электронов, т. е. их число в единице объема металла, получается для уровня Ферми при абсолютном нуле формула

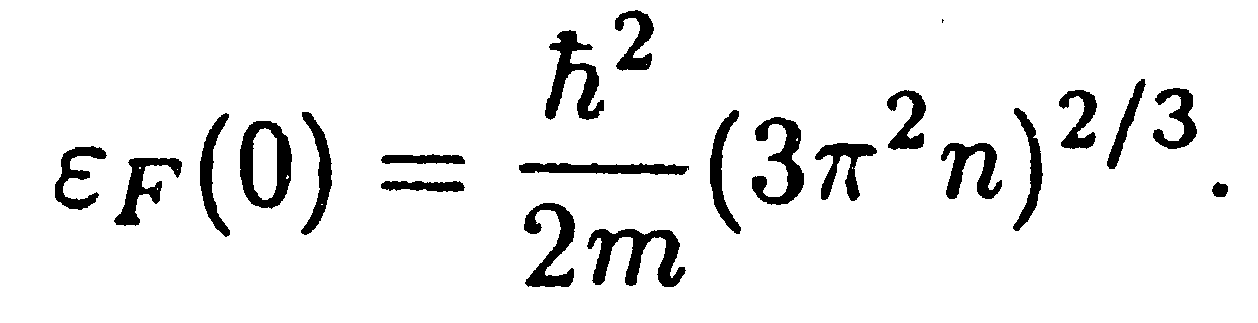(14.49)

Оценка дает для ε _F(0) примерно 5 эВ в случае характерного значения n = 5∙10²⁸ м^-3.

Величина

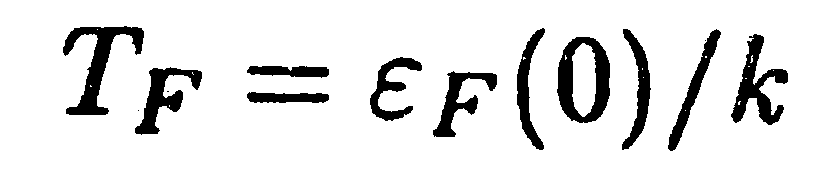(14.50)

называется температурой Ферми. Для ε _F(0) = 5 эВ температура Ферми равна примерно 60 000 К, т. е. в 200 раз превышает комнатную температуру.




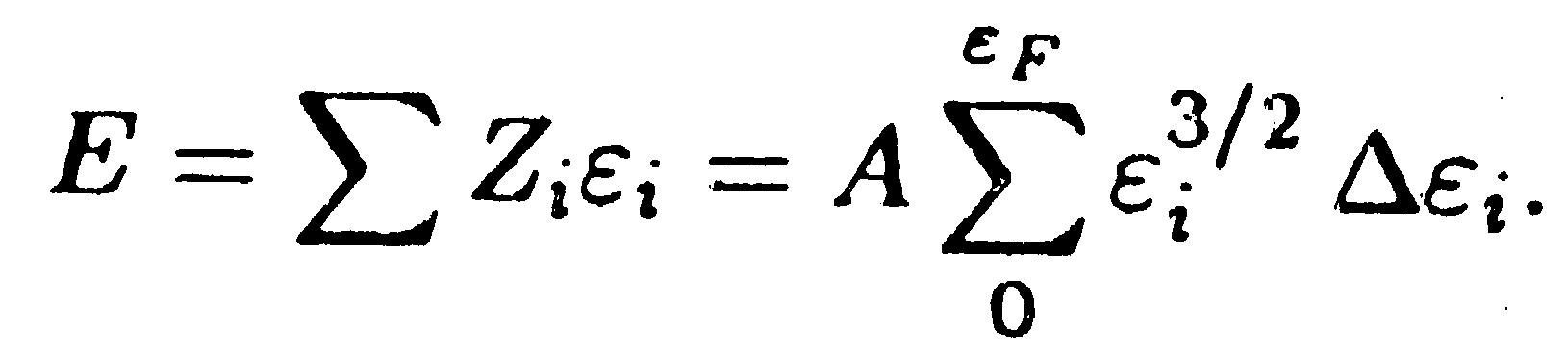
Теперь можно найти среднюю энергию электронов при абсолютном нуле. Для этого нужно умножить число состояний Z_i, на энергию ε_i и просуммировать произведения по соответствующим значениям индекса i. В результате получится суммарная энергия Е свободных электронов, заключенных в объеме V:

Замена суммирования интегрированием дает

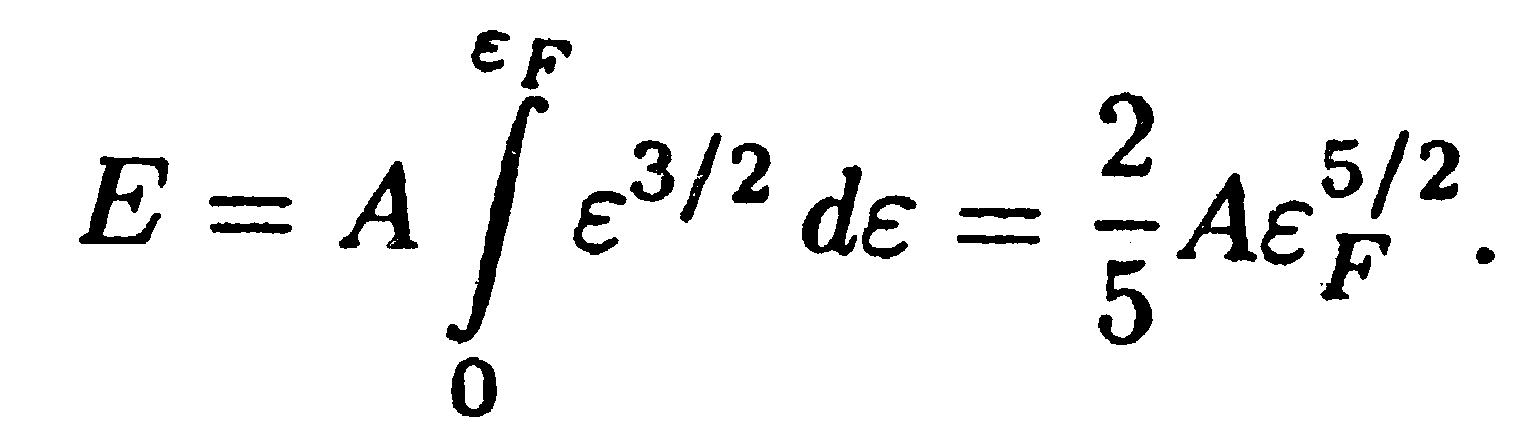(14.51)

Разделив суммарную энергию Е на число электронов N, т. е. взяв отношение выражений (14.51) и (14.48), найдем среднюю энергию свободных электронов при абсолютном нуле:

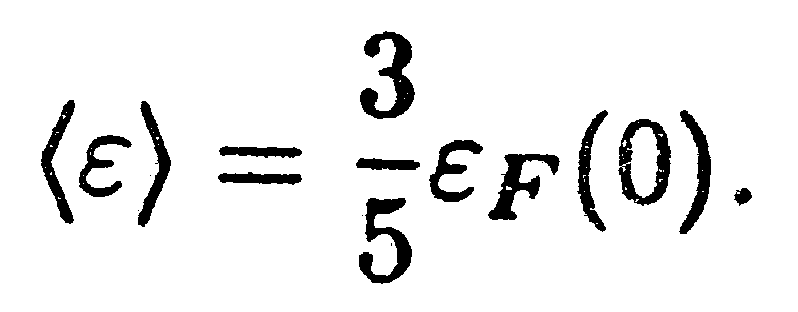(14.52)

14.7.3. Температура вырождения

Уровень Ферми, хотя и очень слабо, но зависит от температуры. Для температур, удовлетворяющих условию kТ < ε_F, эта зависимость описывается приближенной формулой

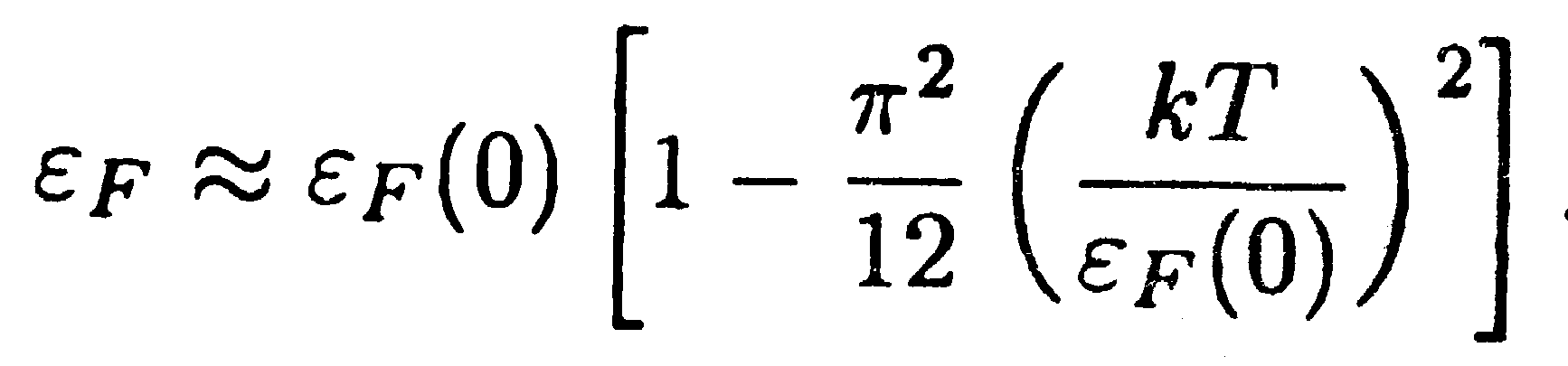(14.53)

Для комнатных температур kТ ≈ 0,025 эВ, в то время как ε _F(0) ≈ 5 эВ. Следовательно, при температуре порядка 300 К ε _F отличается от ε _F(0) лишь на 0,002 %. Поэтому во многих случаях можно полагать ε _F равным ε _F(0). Однако для понимания некоторых явлений зависимость ε _F от Т имеет принципиальное значение.

При температурах, отличных от нуля, график функции (14.42) имеет вид, показанный на рис. 14.6. Заметное отличие от графика, изображенного на рис. 14.5, наблюдается лишь в области порядка kТ. Чем выше температура, тем более полого идет ниспадающий участок кривой.




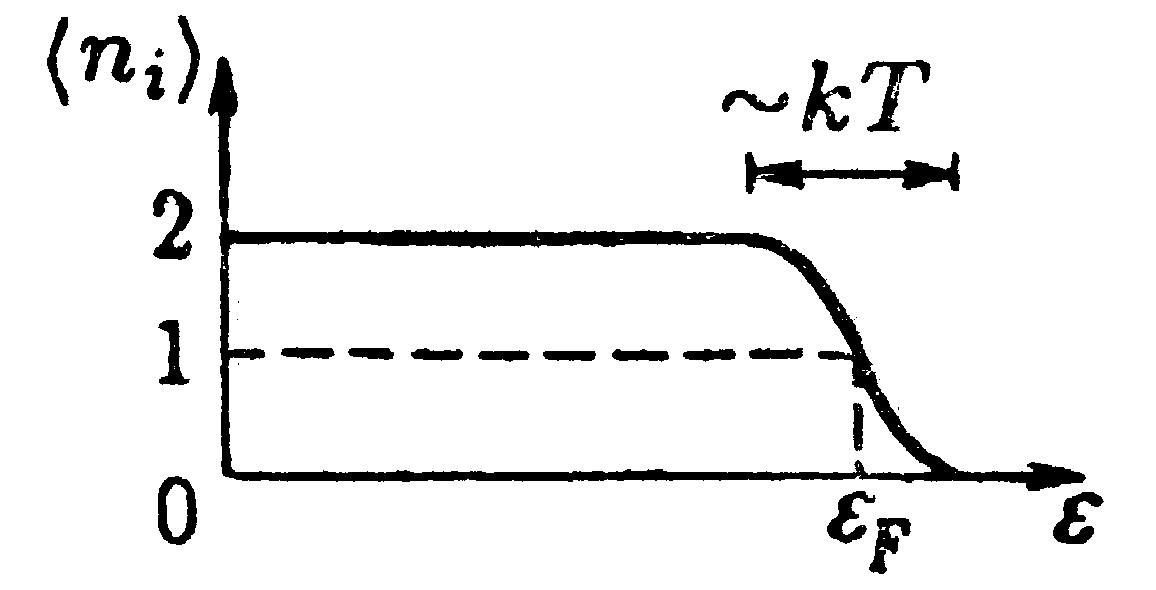
Рис.14.6.


Поведение электронного газа в сильной степени зависит от соотношения между температурой кристалла и температурой Ферми (см. (14.50)).

Различают два предельных случая.

1. Если Т << T_F , т. е. kТ << ε _F, электронный газ называется вырожденным.
   
2. Если Т >> T_F , т. е. kТ >> ε _F, электронный газ называется невырожденным.
   

Температура Ферми для металлов составляет несколько десятков тысяч кельвин. Поэтому даже при температуре, близкой к температуре плавления металла (порядка 10³ К), электронный газ в металле является вырожденным. В полупроводниках концентрация свободных электронов оказывается много меньшей, чем в металлах. Соответственно уровень Ферми мал (согласно (14.49) ε _F пропорционально n ^2/3 ). Поэтому уже при комнатной температуре электронный газ во многих полупроводниках является невырожденным и подчиняется классической статистике.


14.7.4. Влияние температуры на электронную теплоемкость


Теперь можно объяснить, почему электронный газ вно­ит очень малый вклад в теплоемкость металлов. Средняя энергия теплового движения, равная по порядку величины kТ, составляет при комнатной температуре (1/40) эВ. Такая энергия может возбудить только электроны, находящиеся на самых верхних уровнях, примыкающих к уровню Ферми. Напомним, что переход электрона при возбуждении должен быть из занятого в свободное состояние, т.е. выше уровня Ферми. Основная масса электронов, размещенных на более глубоких уровнях, останется в прежних состояниях и поглощать энергию при нагревании не будет. Таким образом, в процессе нагревания металла участвует лишь незначительная часть электронов проводимости, чем и объясняется малая теплоемкость электронного газа в металлах.


18.8. Электронная зонная структура и волны Блоха


В основе зонной теории твердого тела лежит так называемое адиабатическое приближение. Квантовомеханическая система разделяется на тяжелые и легкие частицы - ядра и электроны. Поскольку массы и скорости этих частиц значительно различаются, можно считать, что движение электронов происходит в поле неподвижных ядер, а медленно движущиеся ядра находятся в усредненном поле всех электронов. Принимая, что ядра в узлах кристаллической решетки неподвижны, движение электрона рассматривается в постоянном периодическом поле ядер.

Далее используется приближение самосогласованного поля. Взаимодействие данного электрона со всеми другими электронами заменяется действием на него эффективного электрического поля, обладающего периодичностью кристаллической решетки. Это поле создается зарядом всех других электронов и всех ядер.

14.8.1. Разрешенные и запрещенные электронные энергетические зоны в кристаллах

Рассмотрим мысленно «процесс образования» твердого тела из изолированных атомов одного типа. Энергетические уровни какого-либо валентного электрона в одном

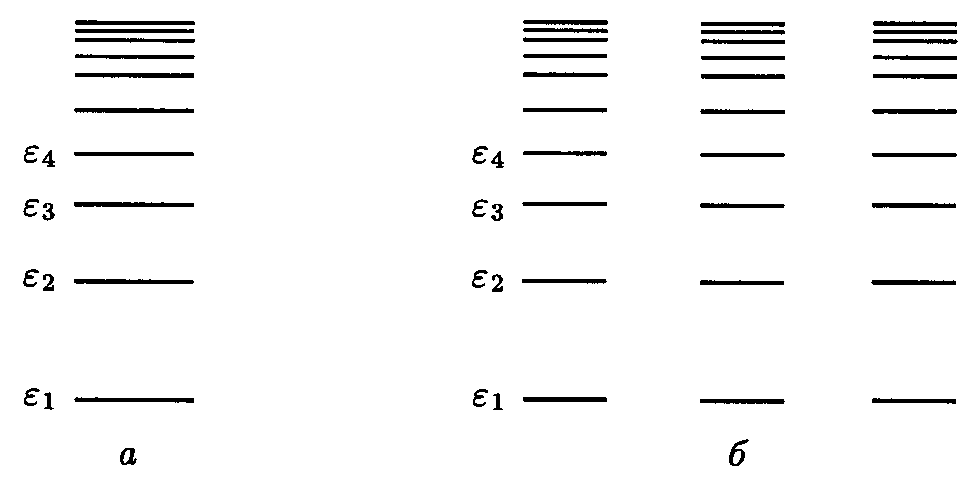изолированном атоме представлены на схематическом рис. 14.7 а. Для простоты будем считать их простыми, т. е. невырожденными. Рассмотрим теперь N тождественных атомов, удаленных друг от друга настолько далеко, что их взаимодействием можно полностью пренебречь. Энергетические уровни того же валентного электрона системы N невзаимодействующих атомов получатся, если рис. 14.7 а повторить N раз — столько, сколько содержится атомов в системе (рис. 14.7 б). Теперь каждый простой уровень превращается в уровень кратности N.


Рис. 14.7.


Будем сближать атомы друг с другом, чтобы они образовали кристаллическую решетку.

Т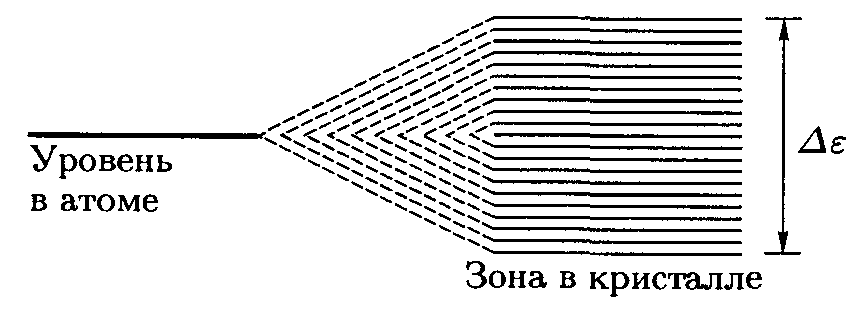огда из-за взаимодействия между атомами каждый кратный энергетический уровень расщепится на N простых уровней (рис. 14.8).


Рис. 14.8.


Совокупность энергетических уровней, на которые расщепляется кратный уровень, называется энергетической зоной или просто зоной кристалла (см. рис. 14.9). Ввиду того, что N очень велико, расстояния между уровнями одной и той же зоны крайне малы, так что требуется ничтожная энергия, чтобы перевести электрон в пределах зоны с одного энергетического уровня на соседний. В этом смысле энергетические уровни каждой зоны ведут себя практически так, как если бы они были непрерывны. Однако соседние энергетические зоны, вообще говоря, разделены конечными интервалами энергии. Эти интервалы называются запрещенными зонами, так как энергия электрона не может

п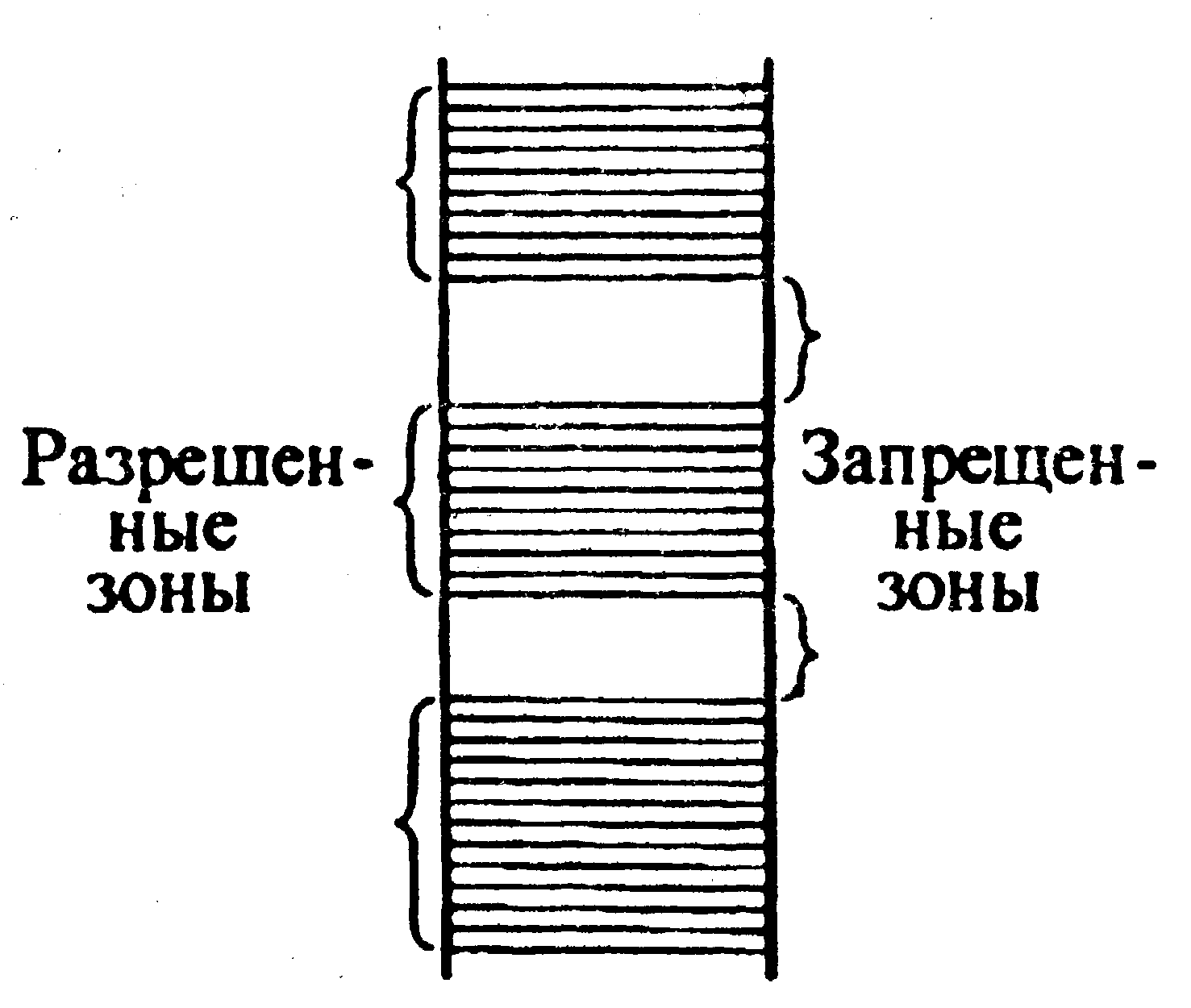ринимать значения, лежащие в пределах таких интервалов. Зоны с дозволенными значениями энергии называются разрешенными. Величина расщепления для разных уровней не одина­кова. Сильнее возмущаются уровни, заполненные в атоме внешними электронами.


Рис. 14.9.


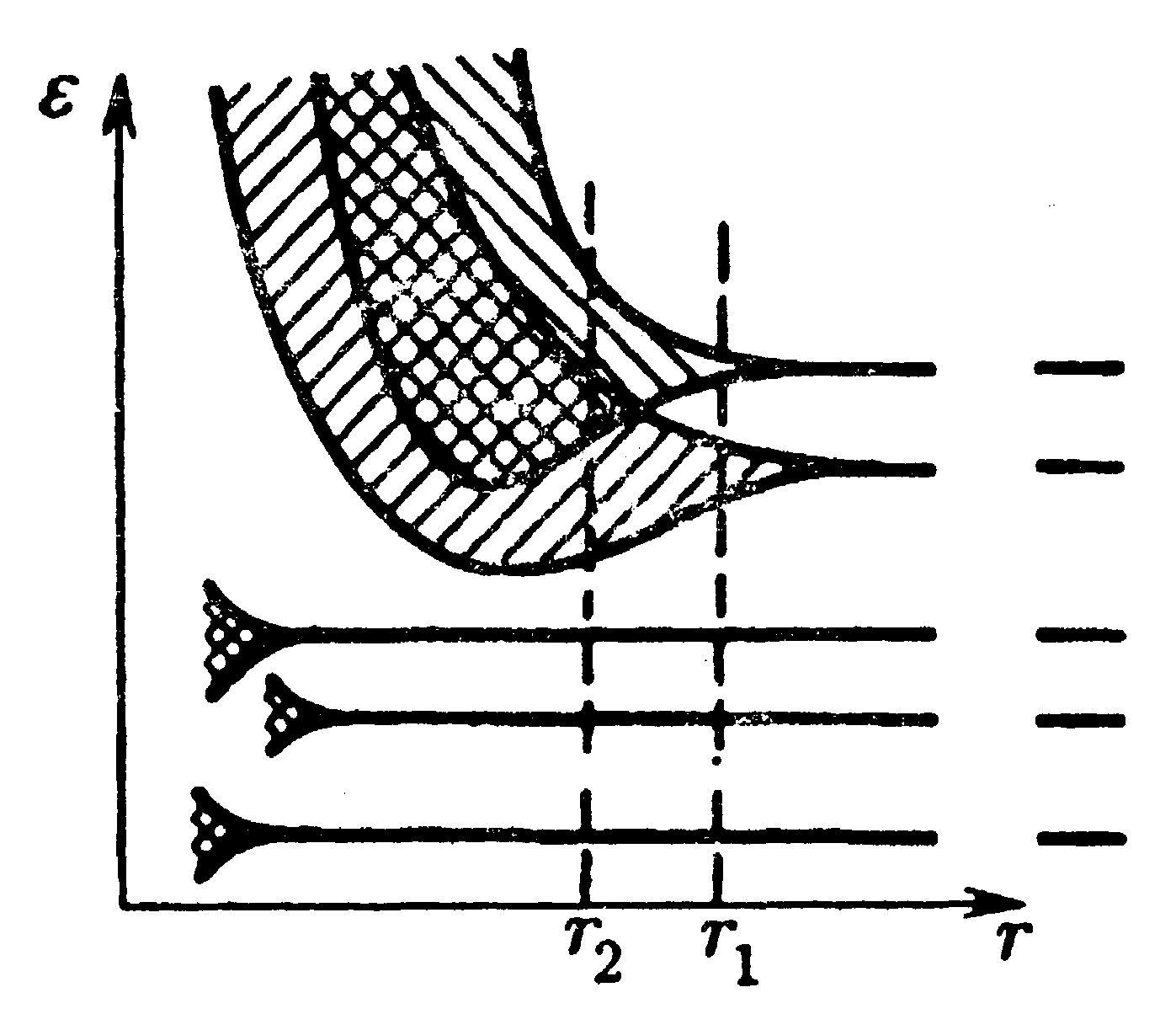Уровни, заполненные внутренними электронами, возмущаются мало. На рис. 14.10 показано расщепление уровней как функция расстояния r между атомами. Из схемы видно, что возникающее в кристалле расщепление уровней, занятых внутренними электронами, очень мало. Заметно расщепляются лишь уровни, занимаемые валентными электронами. Такому же расщеплению подвергаются и более высокие уровни, не занятые электронами в основном состоянии атома. В зависимости от конкретных свойств атомов равновесное расстояние между соседними атомами в кристалле может быть либо типа r₁, либо типа r₂ (см. рис. 14.10).


Рис. 14.10.


При расстоянии типа r₁ между разрешенными зонами, возникшими из соседних уровней атома, имеется запрещенная зона, показанная на рис. 14.11 а. При расстоянии типа r₂ происходит перекрывание соседних зон, как на рис. 14.11 б. Число уровней в такой слившейся зоне равно сумме количеств уровней, на которые расщепляются оба уровня атома. На рис. 14.11 в показан случай не полностью заполненной зоны в металле.








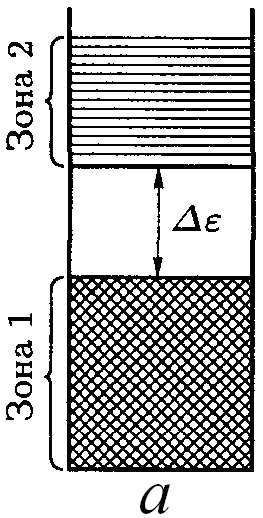
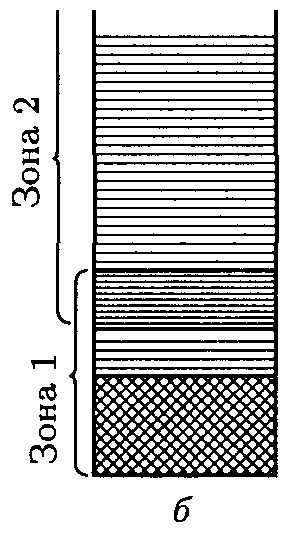
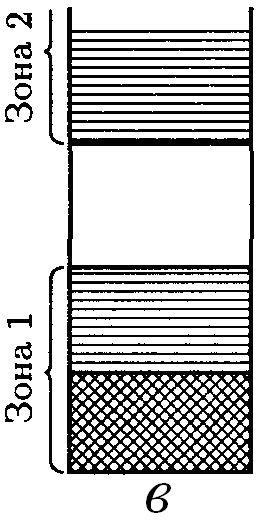
Рис. 14.11.


14.8.2. Функции Блоха и зоны Бриллюэна

Зонная структура энергетических уровней получается непосредственно из решения уравнения Шрёдингера для электрона, движущегося в периодическом силовом поле. Это поле создается решеткой кристалла. Уравнение Шрёдингера, учитывающее поле решетки, имеет вид








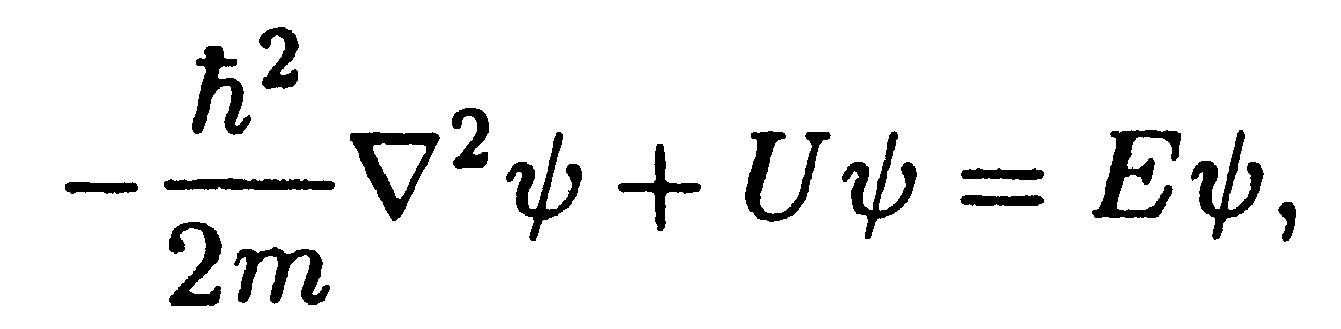
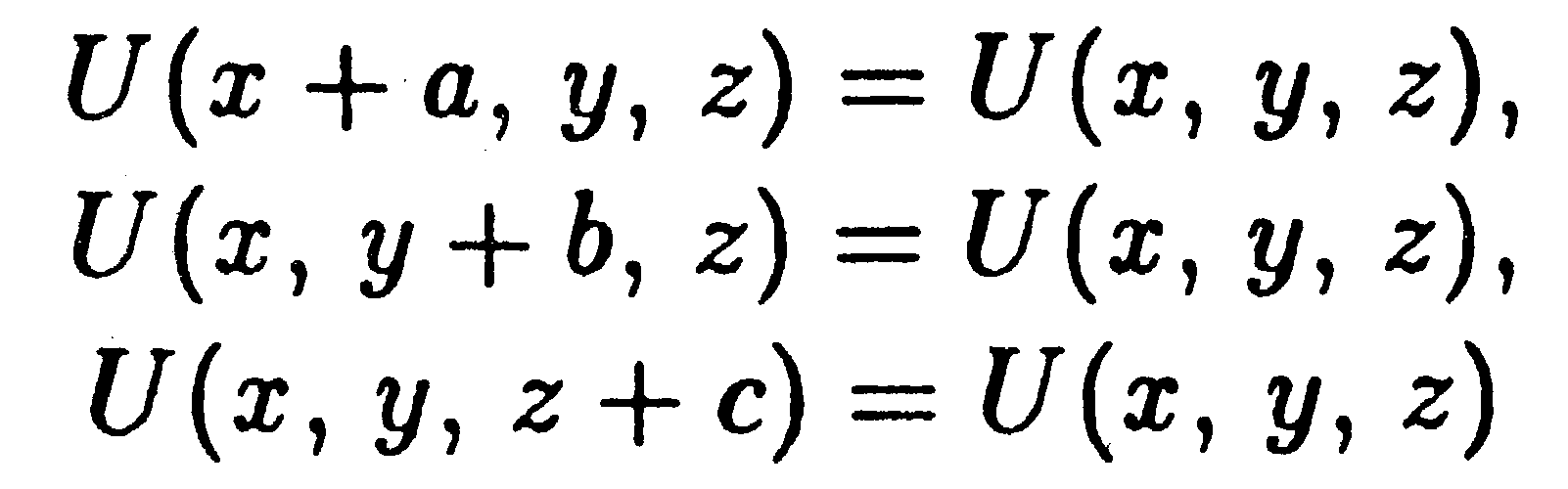
где U — функция, обладающая свойствами:

(а, 6, с — периоды решетки вдоль осей x, y, z).

Блох доказал, что решение уравнения Шрёдингера с периодическим потенциалом имеет вид

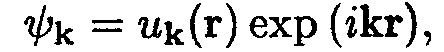(14.54)

где u_k(r) — функция, имеющая периодичность потенциала, т. е. периодичность решетки. Решения (14.54) называются функциями Блоха. Они отличаются от (14.39) наличием периодического множителя u_k(r).

Г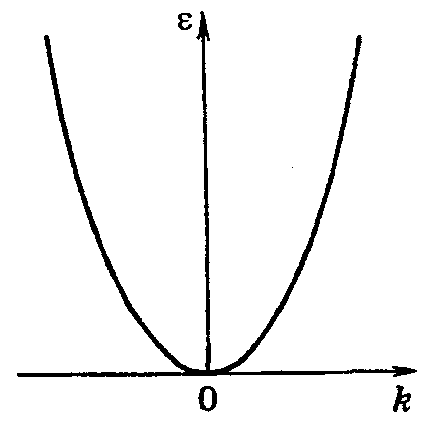рафик зависимости энергии частицы ε от модуля волнового вектора k, т. е. график функции ε(k)называется дисперсионной кривой. В приближении свободных электронов дисперсионная кривая имеет вид, показанный на рис. 14.12 (см. формулу (14.40)). Значения энергии образуют квазинепрерывную последовательность. Следовательно, график ε(k) состоит из дискретных точек. Однако эти точки расположены так густо, что зрительно сливаются в сплошную кривую.


Рис. 14.12.


В случае периодического поля дисперсионная кривая имеет вид, показанный на рис. 14.13. Из рисунка видно, что изображенные сплошными линиями зоны квазинепрерывно изменяющейся энергии (разрешенные зоны) чередуются с запрещенными зонами. Каждая разрешенная зона состоит из близкорасположенных дискретных уровней, число которых равно числу атомов в образце кристалла.

О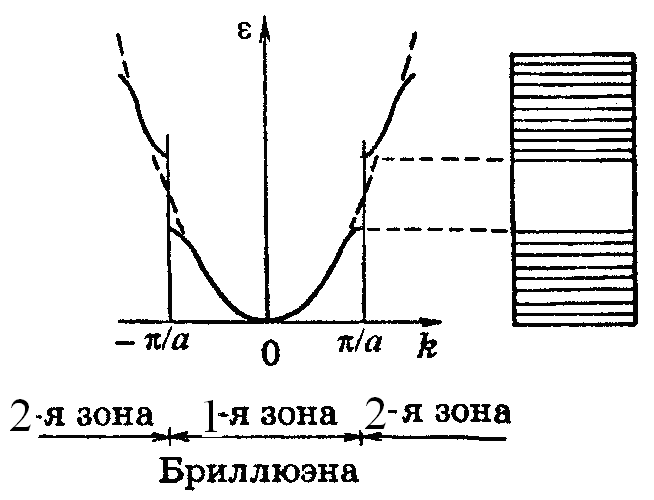бласть k-пространства, внутри которой энергия электрона в кристалле изменяется квазинепрерывно, называется зоной Бриллюэна. На границах зон энергия терпит разрыв. Рисунок 14.13 изображает зоны Бриллюэна в случае одномерного кристалла. Для трехмерных кристаллов границами зон Бриллюэна являются замкнутые многогранные поверхности, заключенные одна внутри другой. В случае свободных электронов поверхность Ферми имеет форму сферы. В общем случае форма поверхности Ферми для электронов проводимости металла зависит от свойств кристаллической решетки и имеет сложный, подчас причудливый вид.


Рис. 14.13.


Поверхность Ферми является важной характеристикой металла. Форма этой поверхности определяет характер движения электронов с энергией, близкой к ε_F. Характер же движения электронов, в свою очередь, определяет физику различных явлений, наблюдаемых при воздействии на металл магнитного поля.

Итак, спектр возможных значений энергии валентных электронов в кристалле распадается на ряд разрешенных и запрещенных зон. Ширина зон не зависит от размеров кристалла. Таким образом, чем больше атомов содержит кристалл, тем теснее располагаются уровни в зоне. Ширина разрешенных зон имеет величину порядка нескольких электронвольт. Следовательно, если кристалл содержит 10²³ атомов, расстояние между соседними уровнями в зоне составляет ~ 10^-23 эВ.

Каждый энергетический уровень отвечает определен­ному значению k. Поскольку квантовое число т_s может принимать два значения, на любом разрешенном уровне могут находиться два электрона, обладающие противопо­ложными спинами.


14.8.3. Металлы, полупроводники, диэлектрики


Существование энергетических зон позволяет объяснить с единой точки зрения существование металлов, полупроводников и диэлектриков.

Р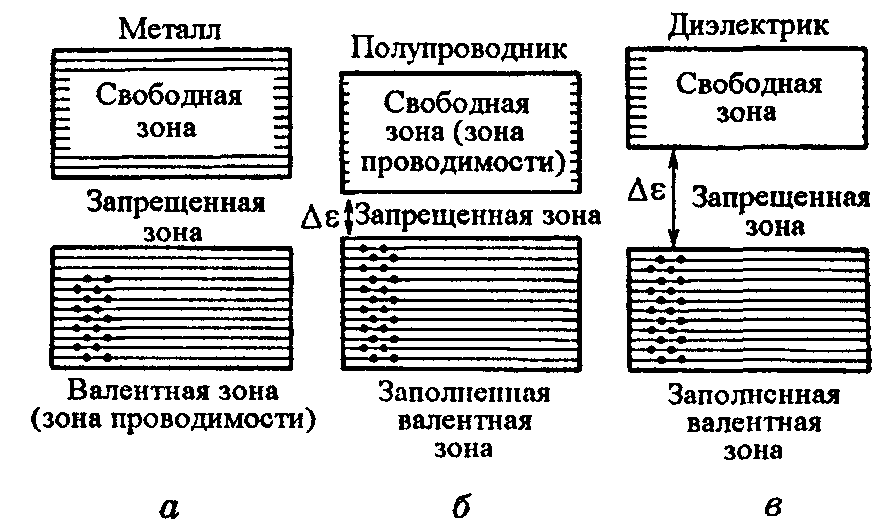азрешенную зону, возникшую из того уровня, на котором находятся валентные электроны в основном состо­янии атома, мы будем называть валентной зоной. При абсолютном нуле валентные электроны заполняют по­парно нижние уровни валентной зоны. Более высокие разрешенные зоны будут от электронов свободны. В зависимости от степени заполнения валентной зоны электро­нами и ширины запрещенной зоны возможны три случая, изображенные на рис. 14.14. В случае рис. 14.14 а электроны заполняют валентную зону не полностью. Поэтому достаточно сообщить электронам, находящимся на

Рис. 14.14

верхних уровнях, совсем небольшую энергию (10^-23 – 10^-22 эВ), для того чтобы перевести их на более высокие уровни. Энергия теплового движения (kТ) составляет при 1 К величину порядка 10^-4 эВ. Следовательно, при температурах, отличных от абсолютного нуля, часть

электронов перево­дится на более высокие уровни. Дополнительная энергия, названная действием на электрон электрического поля, также оказывается достаточной для перевода электрона на более высокие уровни. Поэтому электроны могут ускоряться

электрическим полем и приобретать дополнительную скорость в направлении, противоположном направлению поля. Таким образом, кристалл с подобной схемой энергетических уровней будет представлять собою металл.

Частичное заполнение валентной зоны (в случае ме­талла ее называют также зоной проводимости) наблюдается в тех случаях, когда на последнем занятом уровне в атоме находится только один электрон или когда имеет место перекрывание зон (см. рис. 14.11 б и рис. 14.10 расстояние r₂). В первом случае N электронов проводимости заполняют попарно только половину уровней валентной зоны. Во втором случае число уровней в зоне проводимости будет больше N.

В случаях б и в (см. рис. 14.14) уровни валентной зоны полностью заняты электронами — зона заполнена. Для того чтобы увеличить энергию электрона, необходимо сообщить ему количество энергии, не меньшее, чем ширина запрещенной зоны ∆ε. Электрическое поле (во всяком случае, такой напряженности, при которой не происходит электрический пробой кристалла) сообщить электрону та­кую энергию не в состоянии. При этих условиях электрические свойства кристалла определяются шириной запрещенной зоны ∆ε. Если эта ширина невелика (порядка несколь­ких десятых электронвольт), энергия теплового движения оказывается достаточной для того, чтобы перевести часть электронов в верхнюю свободную зону. Эти электроны будут находиться в условиях, аналогичных тем, в которых находятся валентные электроны в металле. Свободная зона окажется для них зоной проводимости. Одновременно станет возможным переход электронов валентной зоны на ее освободившиеся верхние уровни. Такое вещество называется собственным полупроводником.

Если ширина запрещенной зоны ∆ε велика (порядка нескольких электронвольт), тепловое движение не сможет забросить в свободную зону заметное число электронов. В этом случае кристалл оказывается диэлектриком.