Спорта Республики Молдова Академия Экономических Знаний Кафедра : " Кибернетики и экономической информатики". курсовая

Вид материала

Курсовая

Содержание 8. Государственное регулирование экономического роста. Практическая часть Общее описание программы. Библиотечные классы Структура программы Items . А момент времени равный нулю как Caption. Проверяем значения параметров

Подобный материал:

• Проблемы кибернетики и информатики” (pci’2010), 57.04kb.
• М. В. Ломоносова Факультет вычислительной математики и кибернетики Кафедра математической, 6.81kb.
• Костромская Государственная Сельскохозяйственная Академия кафедра экономической кибернетики, 297.18kb.
• Персональные данные, 17.92kb.
• Приказ об утверждении Регламента по таможенному оформлению имущества, перемещаемого, 426.88kb.
• Г. В. Плеханова Кафедра экономической географии Курсовая, 477.09kb.
• Знаний Кафедра «Финансы и страхование», 45.96kb.
• Государственный Университет Физкультуры и Спорта статья, 150.79kb.
• Н. И. Лобачевского Экономический факультет Кафедра экономической информатики, 861.83kb.
• Закон республики молдова уголовный кодекс Республики Молдова n 985-xv от 18. 04. 2002, 1622.88kb.

 8. Государственное регулирование экономического роста.

Государство играет значительную роль в регулировании экономического роста и следует рассмотреть такие меры государственного регулирования, которые наилучшем образом могут стимулировать этот процесс.

1. Кейнсианцы рассматривают экономический рост преимущественно с точки зрения факторов спроса. Обычно они объясняют низкие темпы роста неадекватным уровнем  совокупных расходов, которые не обеспечивают необходимого прироста ВНП. Поэтому они проповедуют низкие ставки процента (политику “дешевых денег”) как  средство  стимулирования капиталовложений. При  необходимости  финансово-бюджетная политика может использоваться для ограничения правительственных расходов и потребления, с тем,  чтобы  высокий уровень капиталовложений не приводил к инфляции.

2. В  противоположность  кейнсианцам, сторонники “экономики  предложения”  делают упор  на  факторы, повышающие производственный потенциал экономической системы. В частности, они призывают к снижению налогов как к средству, стимулирующему  сбережения и капиталовложения, поощряющему трудовые усилия и предпринимательский риск. Например, снижение или отмена налога на доход от процентов приведет к увеличению отдачи от сбережений. Аналогичным образом, если облагать подоходным налогом суммы, идущие на  выплаты  по  процентам, это приведет  к  ограничению потребления и стимулированию сбережений. Некоторые экономисты выступают за введение единого налога на потребление в качестве  полной или частичной замены личного подоходного налога. Смысл этого  предложения состоит в ограничении потребления и стимулировании сбережений. В  отношении капиталовложений эти экономисты обычно предлагают уменьшить или отменить налог  на прибыли корпораций, в частности предоставить значительные налоговые льготы на инвестиции. Было бы правомерно сказать, что кейнсианцы уделяют  больше  внимания  краткосрочным целям, а именно поддержанию высокого уровня реального ВНП, воздействия на совокупные расходы. В отличие от них, сторонники “экономики предложения”  отдают  предпочтения долгосрочным перспективам, делая упор на факторы, обеспечивающие рост  общественного  продукта  при полной занятости и полной загрузке производственных мощностей.

3. Экономисты  разных  теоретических направлений рекомендуют и другие возможные методы  стимулирования  экономического роста. Например, некоторые ученые пропагандируют  индустриальную  политику, посредством  которой  правительство взяло бы на себя прямую активную роль в формировании структуры промышленности для поощрения экономического роста. Правительство могло бы принять меры, ускоряющие развитие высокопроизводительных  отраслей и способствующие  перемещению  ресурсов из низко производительных  отраслей. Правительство  также  могло бы увеличить  свои расходы на фундаментальные  исследования  и разработки, стимулируя технический прогресс. Рост расходов на образования также может способствовать повышению качества рабочей силы и  росту  производительности труда.

При  всей  многочисленности и сложности  возможных методов стимулирования экономического  роста  большинство  экономистов едины в том, что увеличение темпов экономического роста является весьма непростой задачей, - капиталоемкость и склонность  к  сбережениям нелегко поддаются мерам регулирования.


ЗАКЛЮЧЕНИЕ

Итак, проанализировав различную специальную литературу, сделаем выводы, исходя из целей исследования.

Под экономическим ростом принято понимать уве­личение валового национального продукта (ВНП) обыч­но за год. Этот рост исчисляется в продуктах к пред­ыдущему году (в неизменных ценах), а также как аб­солютный прирост объемов ВНП этого года по сравне­нию с предшествующим. Экономическая динамика, выражающаяся в росте объемов качества результатов производства, является объективной тенденцией развития. Экономический рост показатель мощи страны, центральная задача всех государств.

Возможности экономического роста могут быть связаны с количеством основных факторов производства - труда, капитала и природных ресурсов.

По мере развития экономической теории складывались основные модели макроэкономической динамики: кейнсианская и неоклассические (Р. Солоу).

Кейнсианская модель, как и учение в целом, основаны на гла­венствующей роли спроса в обеспечении мак­роэкономического равновесия. Решающий эле­мент спроса — инвестиции, которые посред­ством мультипликатора увеличивают прибыль. Одновременно они сами вызваны к жизни ростом прибыли, так как капитальные вложения представляют собой функцию увеличения прибыли.

Неокейнсианцы (Э. Домар и Р. Харрод прежде всего) создали свой тип моде­лей экономического роста. Они рассматривают эконо­мику как нестабильную по своей природе и для ком­пенсации “провалов рынка” считают необходимым обес­печивать инвестиции, учитывать роль сбережений.

Рассмотрев модель Домара, отметим, что в ней, в отличие от первоначальных кейнсианских моделей, инвестиции — фактор создания не только дохода, но и новых мощностей. Динамическая сбалан­сированность спроса и предложения, по Домару, определяется динамикой капитальных вложений, которые образуют новые мощ­ности и новые доходы. Следовательно, задача сводится к опреде­лению объема и динамики инвестиций. Домар предложил для решения систему из трех уравнений: уравнение предложения, уравнение спроса, уравнение спроса и предложения совместно.

Модель Е. Домара не претендовала на роль теории роста. Это была попытка расширить условия краткосрочного кейнсианского равновесия на более длительный период и выяснить, какими будут эти условия для развивающейся системы.

Развитием модели Домара выступает модель Харрода. Как и в предыдущей модели, норма уравновешенного роста является функцией со­отношения поста походов и капитальных вло­жений, что дает повод называть эти модели моделями Харрода— Домара. Однако если модель Домара базируется на использовании мультипликатора, то в основе модели Харрода лежит теория акселератора, и, следовательно, она определяет норму сбалан­сированного роста доходов, с которой связаны капитальные вложения. Модель Харрода позволяет на базе теории акселера­тора исследовать инвестиционные решения предпринимателей, где а — ускорение. Харрод исходит из двух посылок. Во-первых, накопление представляет постоянную долю национального до­хода, оно растет темпами, равными темпами роста доходов, предельная и средняя склонность к накоплению равны между собой. Во-вторых, объем осуществляемых капиталовложений есть функция прироста дохода или спроса между двумя периодами. Согласно основному уравнению Кейнса, для равновесия сумма сбережений должна быть равна сумме инвестиций. Отсюда следует, что норма роста, умноженная на капитальный коэффи­циент, равна удельному весу накоплений в национальном до­ходе.

Для различных норм роста Харрод выдвигает следующее по­ложение: система свободного предпринимательства (к которой идет наша страна) будет эффективно функционировать, если до­ходы будут расти ускоренными темпами. Инвестиции должны предвосхищать динамику потребительского спроса. Равновесие по этой модели весьма неустойчиво. Отсюда следует, что необ­ходимо вмешательство государства через финансовую политику. Модель Харрода послужила толчком для разработки моделей Д.Хикса, Р.Гудвина и др.

Примечания

¹ См.: D о m а r Е. D. Capital Expansion, Rate of Growth and Employment.- Econometrica 14 (April 1946), p. 137-147, и Expansion and Employment.- American Economic Review 37 (March 1947), p. 34-55. Обе эти статьи были перепечатаны в качестве очерков в кн.: D о m а r Е. D. Essays in the Theory of Economic Growth. New York, Oxford University Press, 1957, гл. З и 4.

² См. статью: Harrod R.F.An Essay in Dynamic Theory.- Economic Journal 49 (March 1939), p. 14-33, перепечатанную в: Harrod. Economic Essays. London, Macmillan & Co., 1952, p. 254-277, и Towards a Dynamic Economics. London, Macmillan & Co., 1948, особенно лекцию 3.

³ Обозначим через Y_f уровень национального продукта, соответствующий полной занятости трудовых ресурсов, L. Кроме того, пусть Р представляет собой объем продукции, приходящийся на один отработанный человеко-час в условиях полной занятости; другими словами, Р = Y_f/L. Соответственно в период t Y_f(t) = L(t) · P(t). Допустим теперь, что рост предложения труда (выраженного в человеко-часах) носит экзогенный характер; будем полагать, что предложение расширяется с одной и той же заданной скоростью, скажем, со скоростью n процентов. С помощью формул экспоненциального роста это можно математически выразить следующим образом: L (t) = L₀·e^nt. Положим далее, что производительность труда непрерывно повышается, и скорость такого роста составляет g процентов. Как и предшествующее уравнение, это соотношение можно записать в виде экспоненциальной функции: P(t) = P₀e^gi. Подставив два последних уравнения в первое, прологарифмировав полученное выражение, а затем дифференцируя его по t, получим темп роста, Y_f(t), или естественный темп роста, по Харроду, равный n + g.

⁴ Поскольку все фигурирующие в модели величины заданы в реальном выражении и вводить денежную заработную" плату, определяющую уровень цен, нет особой нужды, в настоящее время Харрод (а также ряд других авторов) мог бы трактовать этот процесс как относительный рост цен в сфере потребления. На протяжении последних лет Харрод высказывался в поддержку предложений, предусматривающих осуществление "политики доходов".

⁵ Подробный разбор различных предпосылок, позволяющих использовать величину s в качестве переменной, содержится в кн. Hamberg D. Models of Economic Growth. New York, Harper & Row, 1971, p. 128-135.


Практическая часть

Свою практическую часть я осуществил, благодаря языку программирования С++ Builder . Прежде всего она направлена на то, чтобы рассчитать динамику изменения национального дохода .Естественно, это опять –таки касается модели мною изучаемой в данной работе – модель экономического роста Харрода-Домара.

Общее описание программы.

Программа позволяет работать с формой. То есть можно задавать параметры , получить необходимые данные и уже работать над их анализом . При этом демонстрируются особенности применения объектно-ориентированной методики программирования.

Программа состоит из следующих модулей:

* undiagram.h — декларируются использумые кнопки , а соответсвенно и их функции ;

* undiagram.cpp — реализация функций использумых кнопок;

* unmain.h — декларируется основные показатели , которые будут использованы в модели ;

* unmain.h — реализация исчесления основных показателей .


Остальные модули (Ecircle.cpp, Ecircle.res, Ecircle.obj, Undiagram.obj , Unmain.obj) относятся к среде программирования Borland C++ Builder и были сгенерированны автоматически этой средой. В этих модулях описывается главная форма программы и при возникновении определенных событий управление передается контроллеру.

Библиотечные классы

В программе используются следующие библиотечные классы:

* TСomponent - позволяет фиксацию исходной компоненты ;

* TList - позволяет хранить список указателей, и используется для

хранения списков;

* Tobject – оперирует с объектами (в моём случае параметрами

факторов модели).

Структура программы

Логически программу можно разделить на две части: модель данных и контроллер . Модель описывает графические сущности (кнопки , «кассетки») формы, причем каждая сущность «умеет» отображать себя на экране предоставлять о себе данные необходимые для работы с вводимыми данными. Контроллер управляет поведением формы при взаимодействии с пользователем.

Блок-схема .

TList

TUndiagram

TMain

TObject

TComponent

ECircle

Из схемы видна связь между основными модулями , использованными в программе .Основное подчинение идёт к TList . И иерархический порядок позволяет виртуально оценить и пронаблюдать связи между ними .

Undiagram.cpp

#include

#pragma hdrstop


#include "unDiagram.h"


#pragma package(smart_init)

#pragma resource "*.dfm"

TfmDiagram *fmDiagram;

// определяется переменные fmDiagram


__fastcall TfmDiagram::TfmDiagram(TComponent* Owner)

// перегружается при функции __fastcall


: TForm(Owner)

{

}

// активирует возможность реального вывода формы при помощи метода //ShowDiagram


void TfmDiagram::ShowDiagram(TListView* lv)

{

int I;

double X,Y;

// вводятся переменные X,Y для подсчёта количества циклов


chDiagram->Series[0]->Clear();

for(I=0; IItems->Count; I++){

X=StrToInt(lv->Items->Item[I]->Caption);

Y=StrToFloat(lv->Items->Item[I]->SubItems->Strings[0]);

chDiagram->Series[0]->AddXY(X,Y,"",clTeeColor);

}

fmDiagram->Show();

}


Хотелось бы отметить то , что первоначальные значения национального дохода описываются как Items . А момент времени равный нулю как Caption.


Undiagram.h


#ifndef unMainH

#define unMainH

#include

#include

#include

#include

#include

class TfmMain : public TForm

{__published: // IDE-managed Components

TEdit *edC0;

TEdit *edI0;

TLabel *Label1;

TLabel *Label2;

TEdit *edS;

TEdit *edV;

TLabel *Label3;

TLabel *Label4;

TEdit *edY0;

TEdit *edY1;

TLabel *Label5;

TLabel *Label6;

TEdit *edCircleCount;

TLabel *Label7;

TButton *btCalculate;

TListView *lvResults;

TButton *btDiagram;

void __fastcall btCalculateClick(TObject *Sender);

void __fastcall btDiagramClick(TObject *Sender);

private: // User declarations

public: // User declarations

__fastcall TfmMain(TComponent* Owner);

};

extern PACKAGE TfmMain *fmMain;

#endif


Работа с активацией и созданием кнопок .Используются возможности методов :

-Tlabel – надпись на форме ;

- Tedit –её редактирование ;

-Tbutton – определение кнопки;

-TListView *lvResults – вывод (вид) построенной формы .


undiagram.cpp


#include

#pragma hdrstop


#include "unMain.h"

#include "unDiagram.h"


#pragma package(smart_init)

#pragma resource "*.dfm"

TfmMain *fmMain;


__fastcall TfmMain::TfmMain(TComponent* Owner)

: TForm(Owner)

{

}


void __fastcall TfmMain::btCalculateClick(TObject *Sender)

{

double C0,I0;

double S,V;

double Y_t_2,Y_t_1,Y_t;

int CCount,I;

TListItem* LI;


// Проверяем значения параметров

C0=StrToFloat(edC0->Text);

I0=StrToFloat(edI0->Text);

S=StrToFloat(edS->Text);

V=StrToFloat(edV->Text);

Y_t_2=StrToFloat(edY0->Text);

Y_t_1=StrToFloat(edY1->Text);

CCount=StrToInt(edCircleCount->Text);


if (S<0 || S>1) {

ShowMessage("0
edS->SetFocus();

return;

}

if (V<0 || V>1-S) {

ShowMessage("0
edV->SetFocus();

return;

}

if (CCount<2) {

ShowMessage("Кол-во циклов >= 2");

edCircleCount->SetFocus();

return;

}


lvResults->Items->Clear();

LI=lvResults->Items->Add();

LI->Caption="0";

LI->SubItems->Add(FloatToStr(Y_t_2));

LI=lvResults->Items->Add();

LI->Caption="1";

LI->SubItems->Add(FloatToStr(Y_t_1));

// Рассчитываем

for (I=2; I<=CCount; I++)

{

lvResults->Items->Add();

LI->Caption=IntToStr(I);

LI->SubItems->Add(FloatToStr(Y_t));


Y_t_2=Y_t_1;

Y_t_1=Y_t;

}

}


void __fastcall TfmMain::btDiagramClick(TObject *Sender)

{

fmDiagram->ShowDiagram(lvResults);

}


Данный этап предпологает уже определение кнопок , их функций , надписи на них . Так же проверяются входные (задаваемые) пользователем

данные (значения v и s , не превышающие установленных коцепцией ) .


unmain.h


#ifndef unDiagramH

#define unDiagramH


#include

#include

#include

#include

#include

#include

#include

#include

#include

#include


class TfmDiagram : public TForm

{

__published: // IDE-managed Components

TChart *chDiagram;

TLineSeries *Series1;

private: // User declarations

public: // User declarations

__fastcall TfmDiagram(TComponent* Owner);

void ShowDiagram(TListView* lv);

};


extern PACKAGE TfmDiagram *fmDiagram;


#endif------

Эта программа выясняет параметры , и диаграммы . То есть её построение уже по результирующим данным .

Ecircle.cpp

#include

#pragma hdrstop

USERES("ECircle.res");

USEFORM("unMain.cpp", fmMain);

USEFORM("unDiagram.cpp", fmDiagram);


WINAPI WinMain(HINSTANCE, HINSTANCE, LPSTR, int)

{

try

{

Application->Initialize();

Application->CreateForm(__classid(TfmMain), &fmMain);

Application->CreateForm(__classid(TfmDiagram), &fmDiagram);

Application->Run();

}

catch (Exception &exception)

{

Application->ShowException(&exception);

}

return 0;

}


Наблюдается сложение связей между скорректированной формой данных с её «запуском» на экране .Естественно , учтена и взаимосвязь диаграммы (графика) с ней . Всё это будет выведено благодаря Application->ShowException .

Форма

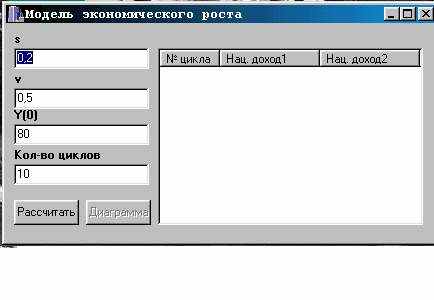
Данная форма является своеобразным буфером для уточнения и , естественно , заполнения показателями при которых требуется вывести зависимость национального дохода от мультипликатора , акселератора .Иными словами всего того , что предусмотрено при анализе модели экономического роста Домара-Харрода. На рисунке в «кассетках» отмечают те исходные данные при которых интересует динамика изменения Y(t) :

YO- национальные доходы в первоначальном периоде;

v- акселератор;

s- норма накопления .

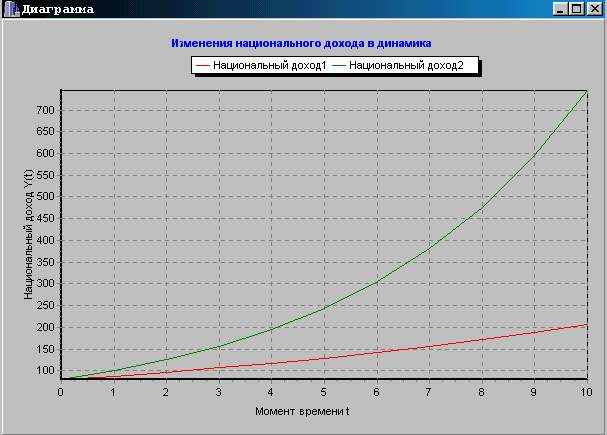
Следовательно , при заполнении нужно лишь учитывать «коридор» изменений параметров , установленный ещё изначально при определении самой модели .При нажатии на кнопку «Рассчитать» получу в нижерасположенном окошке данные результирующие уже при расчёте национального дохода . Что касается кнопки «Диаграмма» , то она рассчитана на наглядное (графическое) изображение исчислений.

Список используемой литературы.

1 А.Ф.Гамецкий ,Д.И.Соломон Математическое моделирование

макроэкономических процессов .Еврика ,1997.

2. Борисов Е. Ф. Экономическая теория: Учебник. — М.: Юрист, 1997г.

3. Самуэльсон П. Экономика. В 2-х т. Т. 2. — М.: Машиностроение, 1997г.

4. Экономика: Учебник / Под ред. доц. А. С. Булатова. 1997г.

5. Агапова. Т.А., Серегина  С.В. Макроэкономика. Учебник ,1999г.

6. роста Денисом Э. Исследование различий в темпах экономического. — М., 1971.