Пояснительная записка к курсовой работе на тему «Исследование математических методов построения изолиний» по дисциплине
| Вид материала | Пояснительная записка |
- Пояснительная записка к курсовой работе на тему: «Активный полосовой фильтр» по дисциплине, 342.06kb.
- Пояснительная записка к курсовой работе по дисциплине: «Электроника и микросхемотехника», 171.54kb.
- Пояснительная записка к курсовой работе по дисциплине «Обработка изображения, распознавание, 186.43kb.
- Пояснительная записка к курсовой работе по дисциплине: «Теория чисел», 275.76kb.
- Пояснительная записка к курсовой работе по предмету «Языки и технологии программирования», 353.31kb.
- Пояснительная записка к курсовой работе по курсу: "Техническая механика" на тему: "Анализ, 279.44kb.
- Пояснительная записка к курсовой работе по дисциплине "Системное программное обеспечение", 277.1kb.
- Пояснительная записка к курсовой работе по газогидродинамике на тему: Студенты:, 268.12kb.
- Пояснительная записка к курсовой работе по дисциплине "Гидромашины и компрессоры", 200.01kb.
- Пояснительная записка к курсовой работе по дисциплине "Информатика" кр 030500. 12., 163.99kb.
В связи с этим существует острая необходимость разработки оптимальных методов построения ЦМР. Тем более, что в России практически не существует публикаций на подобные темы.
Краткий обзор ГИС, используемых в России.
В России используются ГИС, как профессионального уровня, так и специализированные. Программные продукты формируются на основе модульного принципа. Обычно выделяют базовый модуль и модули расширения (или приложения). В базовом модуле содержатся функции, реализующие основные операции ГИС, в том числе программная поддержка устройств ввода-вывода, экспорт и импорт данных и т.д. Следует отметить, что программные продукты разных фирм имеют много общего, так как производители вынуждены заимствовать друг у друга те или иные технологические разработки. В настоящее время на рынке представлено около 20 хорошо известных ГИС-пакетов, которые можно отнести к полнофункциональным.
Характеризуя свойства полнофункциональных ГИС можно отметить их общие черты. Все системы работают на платформе Windows. Только некоторые из них имеют версии, работающие под управлением других операционных систем («Горизонт» - MS DOS, Unix, Linux, MC BC, Free BSD, Solaris, ИНТРОС; ПАРК – MS DOS; Arc GIS Arc Info-Solaris, Digital Unix, AIX и др.; ArcView GIS – Unix) [7].
Все системы поддерживают обмен пространственной информацией (экспорт и импорт) со многими ГИС и САПР через основные обменные форматы.
Еще более однородными являются возможности по работе с атрибутивной информацией. Большинство систем обеспечивают работу со всеми основными СУБД через драйверы ODBC, BDE. Первой в ряду поддерживаемых или используемых СУБД стоит Oracle.
В преобладающем большинстве случаев современные полнофункциональные ГИС позволяют расширять свои возможности. Основным способом расширения возможностей является программирование на языках высокого уровня (MS Visual Basic, MS Visual C++, Borland Delphy, Borland C++ Builder) с подключением DLL и OCX-библиотек (ActiveX). Естественно имеются и исключения. Такие системы как MapInfo Professional используют Map Basic, а системы AricView GIS - Avenue [7].
Наиболее распространенными зарубежными системами по разным причинам являются ArcView GIS, MapInfo Professioal, MicroStation/J. Аналогичный перечень отечественных систем возглавляют ГеоГраф, Панорама (Карта 2000), ПАРК, GeoLink [7].
Коротко охарактеризуем наиболее распространенные программные продукты, отмечая особенности и области применения.
ArcGIS ArcInfo (разработчик фирма ESRI, США). Полнофункциональная ГИС, состоящая из двух независимо устанавливаемых программных пакетов – ArcInfo Workstation и ArcInfo Desktop. Первый состоит из трех базовых модулей: ArcMap – отображение, редактирование и анализ данных, ArcCatalog – доступ к данным и управление ими, ArcToolbox – инструмент расширенного пространственного анализа, управление проекциями и конвертацией данных. Дополнительные модули обеспечивают решение следующих задач:
- Arc COGO – набор средств и функций для работы с геодезическими данными;
- Arc GRID – имеет мощный набор средств анализа и управления непрерывно распределенными числовыми и качественными признаками, представляемыми в виде регулярных моделей, а также моделирования сложных процессов;
- ARC TIN – предназначен для моделирования топографических поверхностей;
- Arc NETWORK – для моделирования и анализа топологически связанных объектов в виде пространственных сетей, оценки и управление ресурсами, распределенными по сетям, и процессами в таких сетях.
ArcInfo обеспечивает создание геоинформационных систем, создание и ведение земельных, лесных, геологических и других кадастров, проектирование транспортных сетей, оценку природных ресурсов.
ArcGIS ArcView (разработчик фирма ESRI, США). Настольная ГИС, которая предоставляет пользователю средства выбора и просмотра разнообразных геоданных, их редактирования, анализа и вывода (бизнес, наука, образование, управление, социология, демография, экология, транспорт, городское хозяйство).
Все продукты ArcGis могут использовать дополнительные модули для решения специализированных задач пространственного анализа:
- ArcGIS Spatial Analyst – программный модуль для работы с растровыми поверхностями. Позволяет анализировать характеристики поверхности, а также интерполировать пространственно распределенные данные для визуализации и анализа процессов;
- ArcGis 3D Analyst – программа для создания, визуализации и анализа трехмерных объектов и поверхностей;
- ArcGIS Geostatistical Analyst – новый модуль для интерполяции поверхностей на основе статистического анализа пространственно распределенных данных;
- ArcView поддерживает реляционные СУБД, имеет развитую деловую графику (форма просмотра, табличная форма, форма диаграмм, создание макета), предусматривает создание профессионально оформленной картографической информации и разработку собственных приложений.
MapInfo Professional (разработка фирмы MapInfo Corp.США), одна из самых распространенных настольных ГИС в России. MapInfo специально спроектирован для обработки и анализа информации, имеющей адресную или пространственную привязку.
В MapInfo реализованы:
- поиск географических объектов;
- работа с базами данных;
- геометрические функции: расчеты площадей, длин, периметров, объемов, заключенных между поверхностями;
- построение буферных зон вокруг любого объекта или группы объектов;
- расширенный язык запросов SQL, запросы основываются на выражениях, осуществляют объединение, отображают доступные поля, позволяют делать подзапросы, объединения из нескольких таблиц и географические объединения.
- компьютерный дизайн и подготовку к изданию картографических документов.
ГеоГраф [4] (разработка Центра информационных исследований Института географии РАН, Россия). Дает возможность создавать электронные тематические атласы и композиции карт на основе слоев цифровых карт и связанных с ними таблиц атрибутивных данных. Основные возможности ГеоГраф следующие:
- создание пространственных объектов в виде косметических слоев с привязкой к ним таблиц атрибутивных данных;
- подсистема управления атрибутивными данными, включая подсоединение таблиц, редактирование, выборку, сортировку, запросы по образцу и т.д.
- электронное тематическое картографирование и др.
Панорама (Россия) [4] Построение и обработка цифровых и электронных карт, ведение картографической и атрибутивной баз данных.
Отдельно следует выделить профессиональные многофункциональные инструментальные ГИС, обеспечивающие возможность непосредственной обработки данных ДЗ. К ним относятся ERDAS IMAGINE, ERMapper и др.
ER Mapper (разработка ER Mapper) Обработка больших объёмов фотограмметрической информации, тематическое картографирование (геофизика, природные ресурсы, лесное хозяйство). Точность, печать карт, визуализация трёхмерного изображения, библиотека алгоритмов.
ERDAS IMAGINE (разработка Leica) – программный пакет, разработанный специально для обработки и анализа данных дистанционного зондирования, предоставляет полный набор инструментов для анализа данных из любого источника и представление результатов в различных формах – от печатных карт до трехмерных моделей. ERDAS IMAGINE построен по модульному принципу в виде базовых комплектов – IMAGINE Essential, IMAGINE Advantage и IMAGINE Professional.
В ERDAS IMAGINE реализованы:
- широкие возможности по визуализации и импорту данных (поддерживает более 100 форматов);
- геометрическая коррекция;
- улучшающие преобразования и ГИС-анализ;
- дешифрирование снимков;
- инструменты обработки изображений и построение алгоритмов пространственных вычислений;
- создание карт.
Постановка задачи исследования и используемые методы.
В рамках данной работы выполнен анализ трех математических методов, направленных на восстановление оптимальной исходной функции. А также проведено исследование на возможность применения данных методов для построения изолиний в геоинформационных системах.
При непосредственном участии научного руководителя были выбраны следующие методы:
- Интерполяция с помощью полинома Лагранжа;
- Оптимизация функции методом градиентного спуска;
- Сплайн-интерполяция.
Первый метод был выбран в связи с его простой реализацией. Т.к. всем известно, что методы интерполяции с помощью полиномов Лагранжа и Ньютона, являются самыми элементарными.
Второй метод выбран из соображений, что простые методы интерполяции не могут рационально обработать большое количество исходных данных. В случае большого количества исходных точек интерполятор выбирает далеко не самую оптимальную функцию, хотя она и проходит через все исходные точки. Поэтому был выбран метод оптимизации функции.
Третий же метод был выбран, т.к. он довольно часто применяется для построения изолиний в ГИС. Конечно, при реализации данного метода рассмотрен один из наипростейших случаев, в связи с ограниченным временем проектирования.
В результате, проанализирована эффективность каждого метода для решения поставленной задачи, а также планируется внедрение разработанного программного продукта в учебный процесс на кафедре геодезии нашего университета.
Для разработки программного продукта использовалась программная среда Visual Studio 2005 и язык программирования С#.
В последнее время С и С++ становятся наиболее используемыми языками при разработке коммерческих и бизнес-приложений. Эти языки устраивают многих разработчиков, но в действительности не обеспечивают должной продуктивности разработки. К примеру, процесс написания приложения на С++ часто занимает гораздо больше времени, чем разработка эквивалентного приложения на Visual Basic. Сейчас существуют языки, увеличивающие продуктивность разработки за счет потери в гибкости, которая так привычна и необходима программистам на С/С++. Подобные решения весьма неудобны для разработчиков и нередко предлагают значительно меньшие возможности. Эти языки также не ориентированы на взаимодействие с появляющимися сегодня системами и очень часто не соответствуют существующей практике программирования для Web. Многие разработчики хотели бы использовать современный язык, который позволял бы писать, читать и сопровождать программы с простотой Visual Basic и в то же время давал мощь и гибкость С++, обеспечивал доступ ко всем функциональным возможностям системы, взаимодействовал с существующими программами и легко работал с возникающими Web-стандартами.
Учитывая все подобные пожелания, Microsoft разработала новый язык – С#. Он имеет массу преимуществ: простота, объектная ориентированность, типовая защищенность, «сборка мусора», поддержка совместимости версий и многое другое. Данные возможности позволяют быстро и легко разрабатывать приложения. При создании С# его авторы учитывали достижения многих других языков программирования: С++, С, Java, Visual Basic т.д. Надо заметить, что поскольку С# разрабатывался, что называется, «с нуля», у его авторов была возможность не переносить в него все неудачные особенности любого из предшествующих языков. Особенно это касается проблемы совместимости с предыдущими версиями. В результате получился действительно простой, удобный и современный язык, который по мощности не уступает С++, но существенно повышает продуктивность разработок [15].
Ввиду высокой объектной ориентированности, язык С# великолепно подходит для быстрого конструирования различных компонентов – от высокоуровневой бизнес-логики до системных приложений, использующих низкоуровневый код. Также следует отметить, что С# является и Web-ориентированным – с помощью простых встроенных конструкций языка ваши компоненты легко превратятся в Web-сервисы, к которым можно будет обращаться из Интернета, используя любой язык на любой операционной системе. Дополнительные возможности и преимущества С# перед другими языками приносит использование современных Web-технологий, таких как: XML (Extensible Markup Language) и SOAP (Simple Object Access Protocol). Удобные методы для разработки Web-приложений позволяют программистам, владеющим навыками объектно-проектированного программирования, легко освоиться в разработке Web-сервисов [15].
Рассмотрим перечисленные выше методы:
Интерполяция полиномом Лагранжа [13]:
Пусть на отрезке [a, b] даны n + 1 различных значений аргумента: x, x, ..., xn и известны для функции y = f(х) соответствующие значения выражений
| f(x0) = y0, f(x1) = y1, . . ., f(xn) = yn. | (1) |
Требуется построить полином Ln(x) степени не выше n, имеющий в заданных узлах x, x, ..., xn те же значения, что и функция f(х), т. е. тaкой, что
Ln(xi) = yi (i = 0, 1, ..., n)
Будем искать Ln(x) в виде:
| Ln(x)=l(x)+ l(x)+...+ ln(x), | (6) |
где li(x) - полином степени n, причем
| li(xk) =  | (7) |
Очевидно, что требование (7) с учетом (6) обеспечивает выполнение условий (3) (Рисунок 2).
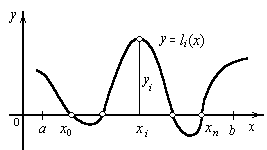
Рисунок 4. li (x) - полином степени n
Так как искомый полином li(x) обращaется в нуль в n точках x,…, xi - , xi + , ..., xn, то он имеет вид
| li(x) = Ci (x - x) (x - x) … (x - xi-) (x - xi +) ... (x - xn) | (8) |
где Сi - постоянный коэффициент. Полагая в формуле (8) х = xi и учитывая, что li(xi) = yi, получим:
yi = Ci (xi - x)(xi - x) ... (xi - xi -)(xi - xi +) ... (xi - xn).
Отсюда
Сi =
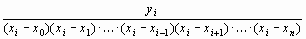 .
.Заметим, что ни один из множителей не равен нулю. Подставляя Сi a (8), а также с учетом (6), окончaтельно имеем:
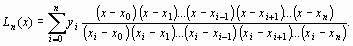 | (9) |
Это и есть интерполяционная формула Лагранжа.
Формуле (9) можно придать более сжатый вид, используя обознaчение
In+(х) = (x - x0) (x - x1) … (x - xn). (10)
Aифференцируя по х это произведение, получим:
I' n+(х) =
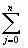 (x - x) ... (x - xj - ) (x - x j + ) ... (x - xn).
(x - x) ... (x - xj - ) (x - x j + ) ... (x - xn).Полагая х = хi (i = , , ..., n), получим:
I' n+(хi)= (xi - x) …(xi - xi -) (xi - xi +) ... (xi - xn). (11)
Подставляя выражения (10) и (11) в формулу (9), получим
| Ln(x) = In+(х) 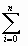 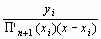 | (9’) |
Пример 1. Положим n = 1. Ясно, что мы имеем в этом случае две точки и интерполяционная формула Лагранжа дает уравнение прямой, проходящей через две заданные точки. Обозначив абсциссы этих точек через a и b, получим интерполяционный полином в виде
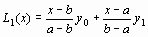 .
.Примем n = 2. Тогда получим уравнение параболы, проходящей через три точки. Если обозначить x0 = a, x1 = b, x2 = c, то искомое уравнение имеет вид
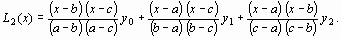
Пример 2. Пусть заданы значения x0 =1, x1 =3, x2 =7, x3 =12 и y0 =5.6, y1 =6.7, y2 =8.1, y3 =10.3 определить значение неизвестной функции для х = 6,5.
Для данного случая, когда мы имеем четыре значения функции, интерполяционная формула Лагранжа представляется так:
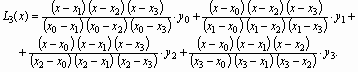
После подстановки заданных значений в формулу Лагранжа получаем:

Определим значение f(х) при х = 6,5:
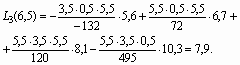
Кубическая сплайн-интерполяция [16].
Пусть на
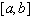 задана сетка
задана сетка 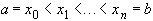 , в узлах которой известны значения функции
, в узлах которой известны значения функции 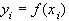 . Сплайн третьей степени
. Сплайн третьей степени 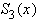 , интерполирующий заданную функцию
, интерполирующий заданную функцию 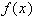 , определяется как функция, удовлетворяющая условиям:
, определяется как функция, удовлетворяющая условиям:1)

2) Для любого частичного промежутка
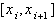
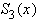 -многочлен третьей степени
-многочлен третьей степени 3)
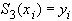
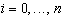
Для задания
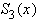 надо определить 4 коэффициента для каждого промежутка
надо определить 4 коэффициента для каждого промежутка 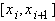 , т.е.
, т.е. 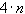 параметров.
параметров.Условия 1) требуют чтобы во внутренних узлах сплайн и его производные до 2-го порядка были непрерывны.
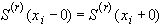
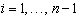
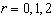
Это дает
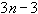 условия для определения параметров, еще
условия для определения параметров, еще 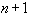 условие содержится в 3).
условие содержится в 3).Итого имеем
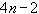 условия. Еще 2 условия, необходимые для однозначного определения сплайна, обычно задаются в виде граничных условий, т.е. условий в точках
условия. Еще 2 условия, необходимые для однозначного определения сплайна, обычно задаются в виде граничных условий, т.е. условий в точках 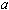 и
и  .
.Возьмем в качестве граничных условия
4)
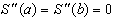
Для построения кубического интерполяционного сплайна могут быть использованы различные подходы. Проведем построение сплайна, исходя из условий 1) - 4). Из 1) и 2) следует, что S(x) непрерывная функция, линейная на каждом
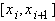 т.е. S(x) - линейный сплайн.
т.е. S(x) - линейный сплайн.Обозначив
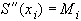 , получаем
, получаем 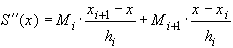 (33)
(33)для
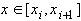 .
.Интегрируя (5), получаем
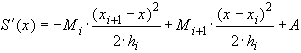 (34)
(34)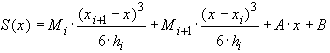 (35)
(35) и
и  - постоянные интегрирования.
- постоянные интегрирования.Условия 3) дают:
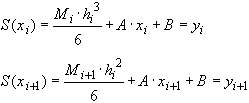 (36)
(36)Из (36) получаем:
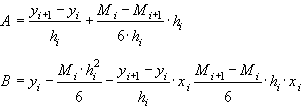
Подставляя
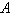 и
и 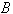 в (7), получаем:
в (7), получаем:
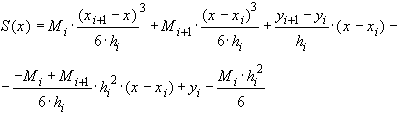 (37)
(37)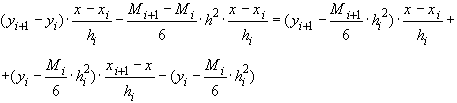
После преобразования
из (37) получаем
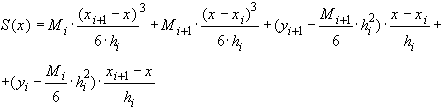 (38)
(38)Из (34) получаем
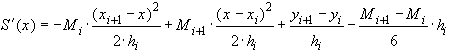 (39)
(39)Из (39) находим односторонние пределы производной для узла
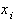 ,
, 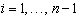
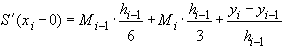 (40)
(40)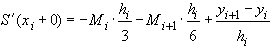 (41)
(41)Подставляя (40) и (41) в условие непрерывности
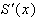 в узле
в узле 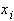 получаем :
получаем :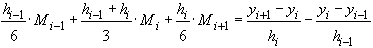 (42)
(42)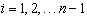
Дополняя (42) равенствами из условия 4) :
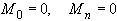 , получаем систему уравнений относительно
, получаем систему уравнений относительно 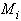 вида :
вида :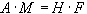 (43)
(43)с квадратной матрицей
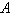 .
.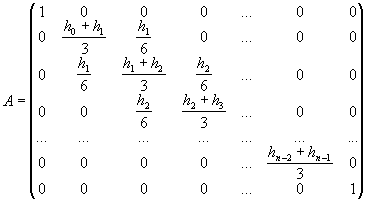
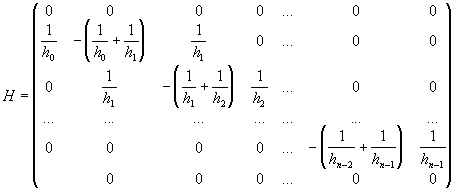
и квадратной матрицей
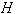
Координатами вектора
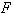 являются значения
являются значения 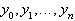 .
.Для матрицы
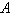 ненулевые элементы расположены на главной диагонали и двух соседних с ней. Такие матрицы называются трехдиагональными. Для
ненулевые элементы расположены на главной диагонали и двух соседних с ней. Такие матрицы называются трехдиагональными. Для 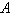 выполнено условие диагонального преобладания.
выполнено условие диагонального преобладания.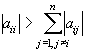
Матрица с диагональным преобладанием невырождена. Следовательно, система (42) однозначно разрешима, т.е. существует единственный кубический интерполяционный сплайн. Кроме условий 4) - условий "свободного провисания" интерполяционной кривой в точках
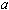 и
и  , могут быть известны наклоны интерполяционной кривой в граничных точках. Тогда условия на границах имеют вид:
, могут быть известны наклоны интерполяционной кривой в граничных точках. Тогда условия на границах имеют вид: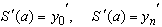 (44)
(44)Могут быть использованы и другие варианты.
Вид граничных условий меняет некоторые элементы матрицы
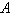 , но в любом случае она остается матрицей с диагональным преобладанием.
, но в любом случае она остается матрицей с диагональным преобладанием.Решение системы (43) с трехдиагональной матрицей
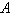 может быть найдено посредством специального варианта метода последовательного исключения неизвестных, который называется методом прогонки.
может быть найдено посредством специального варианта метода последовательного исключения неизвестных, который называется методом прогонки.Относительно оценки погрешности и сходимости интерполяций кубическими сплайнами имеют место следующие результаты:
если
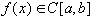 , то
, то 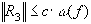 , где
, где 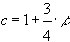 ,
, 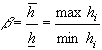 ,
,если
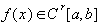 ,
, 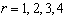 , то оценка имеет вид для
, то оценка имеет вид для 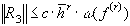 .
.Из этих оценок следует сходимость интерполяционного процесса на последовательности сеток
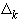 .
.Аппроксимация методом градиентного спуска [16].
