Пояснительная записка к курсовой работе по дисциплине «Обработка изображения, распознавание образов, мультимедиа»

Вид материала

Пояснительная записка

Содержание 1. Основные характеристики программы 2. Простейшие преобразования 3.1. Восстанавливающие фильтры 4. Преобразование Фурье 5. Быстрое преобразование Уолша, упорядоченное по Адамару Приложение. ОБРАБОТКА СИГНАЛОВ А. Разложение функции в ряд Фурье (с коэффициентами Ак, Вк) В. Разложение функции в ряд Фурье (с коэффициентами Dn) С. Разложение функции в ряд Фурье в комплексной форме D. Полином Лежандра Е. Преобразование Фурье для непрерывных сигналов F. Взаимная корреляция G. Быстрое преобразование Фурье (БПФ)

Подобный материал:

• Пояснительная записка к курсовой работе на тему: «Активный полосовой фильтр» по дисциплине, 342.06kb.
• Лабораторная работа № Нейросетевое распознавание печатных символов. Дисциплина: «Распознавание, 74.04kb.
• Пояснительная записка к курсовой работе по дисциплине: «Электроника и микросхемотехника», 171.54kb.
• Пояснительная записка к курсовой работе по дисциплине: «Теория чисел», 275.76kb.
• Пояснительная записка к курсовой работе по дисциплине "Системное программное обеспечение", 277.1kb.
• Пояснительная записка курсовой работы "Обработка экономической информации с помощью, 269.69kb.
• Распознавание и преобразование образов указатель документов описания первоисточников., 52.79kb.
• Программа по дисциплине "Распознавание образов/(по выбору)" для подготовки студентов, 89.53kb.
• Средства мультимедиа. Мультимедиа, 53.29kb.
• Пояснительная записка к курсовой работе по дисциплине "Гидромашины и компрессоры", 200.01kb.

Министерство образования РФ


Владимирский государственный университет


Кафедра вычислительной техники

Пояснительная записка
к курсовой работе по дисциплине
«Обработка изображения, распознавание образов, мультимедиа»

Выполнил: студент гр. ИВТ-199

Евстюничев С.М.

Принял: Жирков В.Ф.


Владимир, 2003 г.


Настоящая курсовая работа выполнена как результат прослушивания курса лекций и выполнения ряда лабораторных работ по дисциплине «Обработка изображений, распознавание образов и мультимедиа». Целью ее является создание программы, позволяющей наглядно рассмотреть некоторые приёмы работы с изображениями.


В задании предлагается спроектировать программу, выполняющую простейшие преобразования изображения, реализовать фильтры выделения границ, восстанавливающие фильтры, преобразования Фурье и Уолша-Адамара. Окончательно это было реализовано в виде исполнимого файла Imager.exe. Программа предназначена для операционных систем: Windows 95/98/2000/XP.


Настоящая пояснительная записка является наиболее полной документацией к выполненной курсовой работе. Она содержит 16 страниц машинописного текста. Листинг программы представлен на магнитном носителе.


Содержание



1.Основные характеристики программы . . . . . . . . . . . . . .4

2.Простейшие преобразования . . . . . . . . . . . ……. . . . . . .5

3.Фильтры . . . . . . . . . . . . . . . . . . . . . . . ………………. . . .9

3.1.Восстанавливающие фильтры. . . . . . . . . …... . . . . .12

4.Преобразования Фурье. . . . . . . . . . . . . . . . …...….. . ... 13

5.Быстрое преобразование Уолша, упорядоченное

по Адамару. . . . . . . . . . . . . . . . . . . . . . . .…………….. . .14

Источники информации. . . . . . . . . . . . ……… . . . . . . . . .15

Приложение. Обработка сигналов. . . . . …. . . . . . . . . . . .16

1. Основные характеристики программы

В ходе выполнения курсовой работы были программно реализованы следующие функции:

• Считывание файла формата Windows Bitmap (*.bmp);
  
• Гистограммы, отображающие распределение цветов по слоям и яркости;
  
• ПреобразованиЯ:
  

• яркости;
  
• контраста;
  
• бинаризация;
  
• негатив;
  
• оттенки серого;
  

• Фильтры выделения границ:
  

• Фильтр Собела;
  
• Фильтр Уоллиса;
  
• Фильтр Робертса;
  
• Фильтр Кирша;
  
• Фильтр Лапласа;
  

• Восстанавливающие фильтры:
  

• Одномерный и двумерный медианные фильтры;
  
• Одномерный и двумерный сглаживающие фильтры;
  

• Одномерное и двумерное преобразование Фурье;
  
• Одномерное и двумерное преобразование Уолша-Адамара;
  
• Выделение текстовых символов для последующего распознавания.
  

2. Простейшие преобразования

Внизу окна реализовано управление диаграммами цветности (левая диаграмма относится к полученному изображению, правая – к предыдущему.) При установке радиокнопки на соответствующий цвет меняется показание диаграмм. При включенном чекбоксе «Отображать» диаграммы отрисовываются заново после каждого преобразования рисунка.


Преобразования.


1) Преобразование яркости изображения происходит по формулам:


г
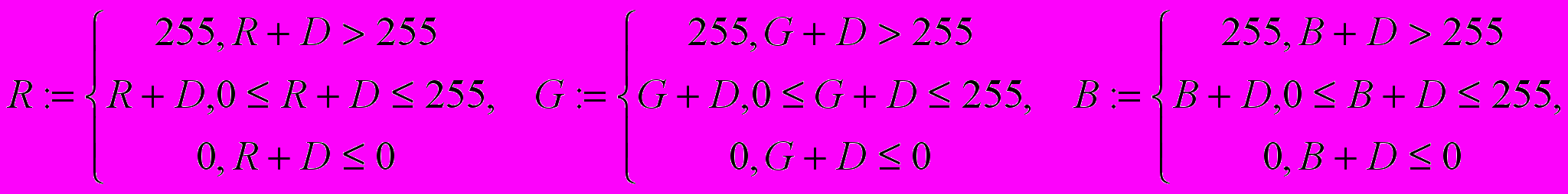
де: R, G, B – яркости соответствующих каналов пиксела,

D – приращение яркости.


Исходное изображение приведено на рис. 1.





Результат преобразования яркости при приращении D=128 показан на рис. 2.

2. Преобразование контраста происходит по формуле для каждого цветового канала:
   

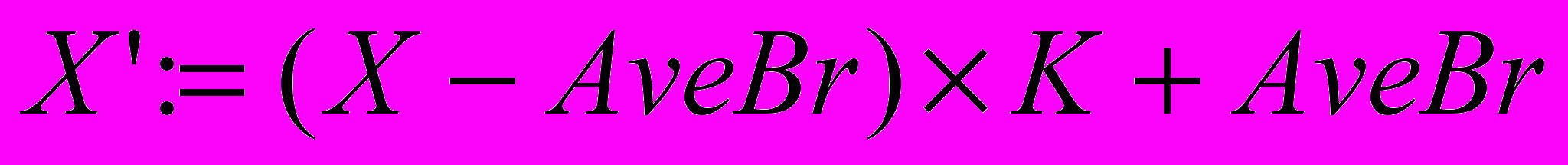
Где: X’ – новое значение яркости точки,

X – прежнее значение яркости точки,

AveBr – среднее значение яркости изображения по каналу,

К – задаваемый коэффициент контраста.


Результат преобразования контраста при коэффициенте К=2.5 показан на рис. 3.





3) Бинаризация изображения проводится по следующим правилам:





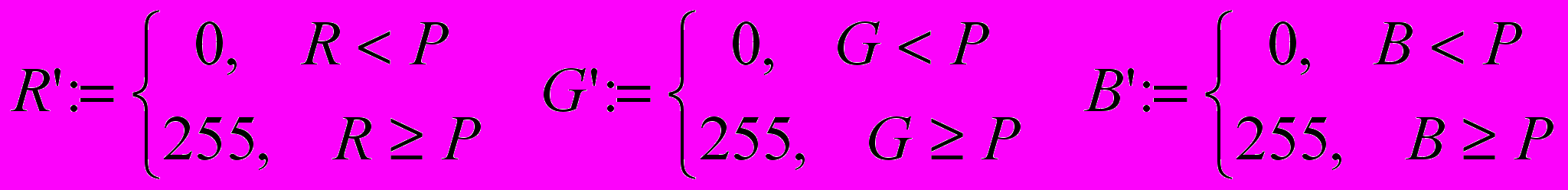
Где: R, G, B – прежние значения яркости точки по каналам;

R’, G’, B’ – новые значения яркости точки по каналам;

Р – порог бинаризации.


Результат бинаризации при пороге P=128 показан на рис. 4.





4) Негативное изображение получается по формулам:





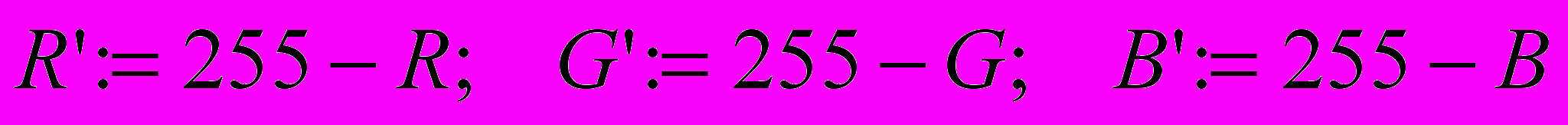
Где: R, G, B – прежние значения яркости точки по каналам;

R’, G’, B’ – новые значения яркости точки по каналам;


Результирующее изображение показано на рис. 5.





5) Оттенки серого.

Перевод цветного изображения в оттенки серого производится по следующим формулам:

Г
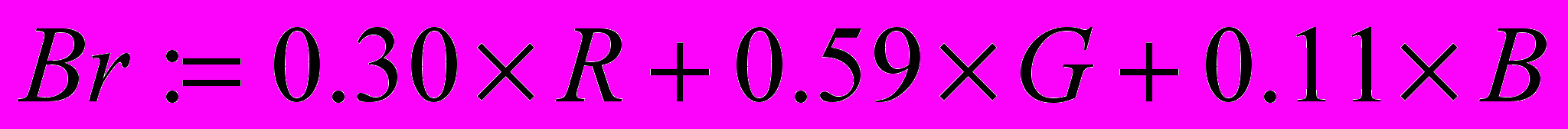
де: Br – результирующая яркость для каждого канала цвета точки,

R, G, B – прежние значения яркости точки по каналам.


Результирующее изображение показано на рис. 6.




3. Фильтры


В данной работе были рассмотрены и реализованы некоторые двумерные фильтры: фильтры выделения границ и восстанавливающие фильтры. Фильтры выделения границ позволяют четко обозначить границу смены цветов. К ним относятся фильтры Робертса, Собела, Кирша, Уоллиса, Лапласа. Эти фильтры действуют на основе анализа информации о яркостях соседних точек в пределе некоторой зоны, называемой окном фильтра, или его апертурой.

1. Фильтр Робертса.
   

Окно фильтра 2х2.

Работа фильтра описывается следующей формулой:





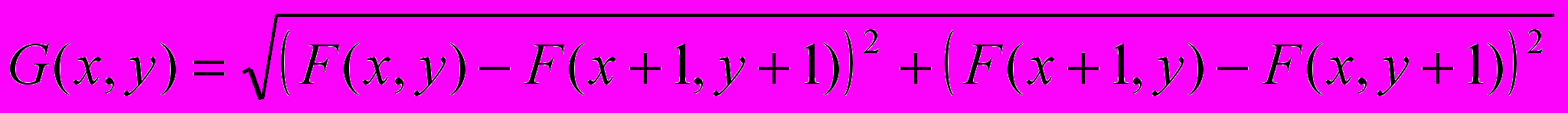
Результат работы фильтра Робертса показан на рис. 7.

2. Фильтр Кирша.
   

Окно фильтра 3х3.

Работа фильтра описывается следующими формулами:





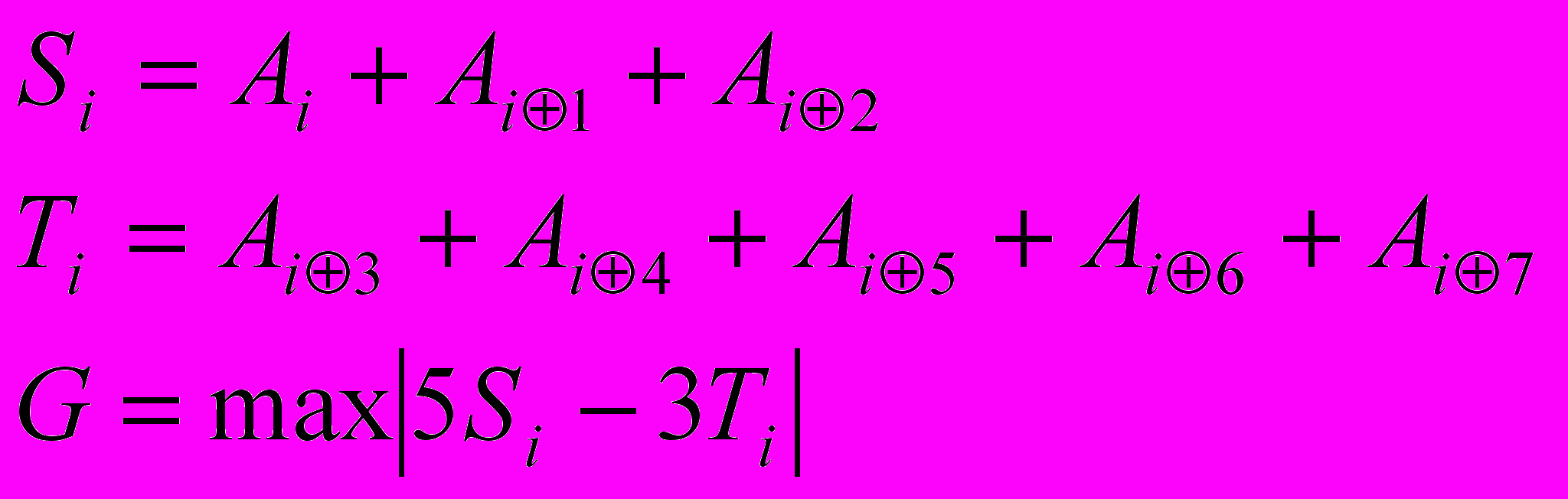
Результат работы фильтра Кирша показан на рис. 8.





3) Фильтр Собела.

Окно фильтра 3х3.

Р
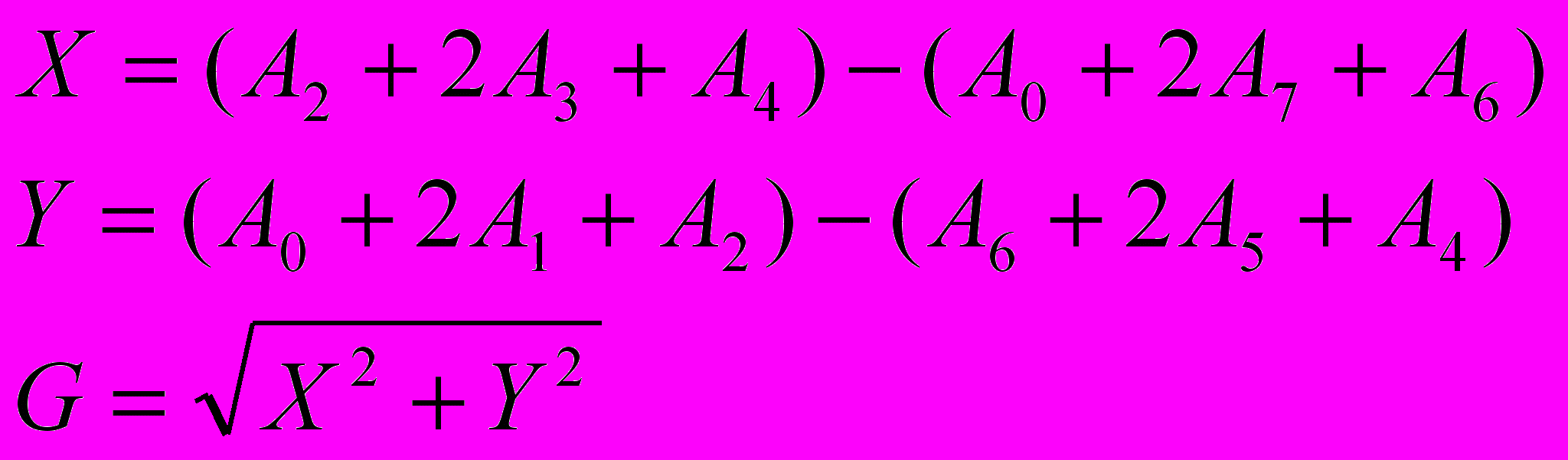
абота фильтра описывается следующими формулами:


Результат работы фильтра Собела показан на рис. 9.





4) Фильтр Уоллеса.

Окно фильтра 3х3.

Р
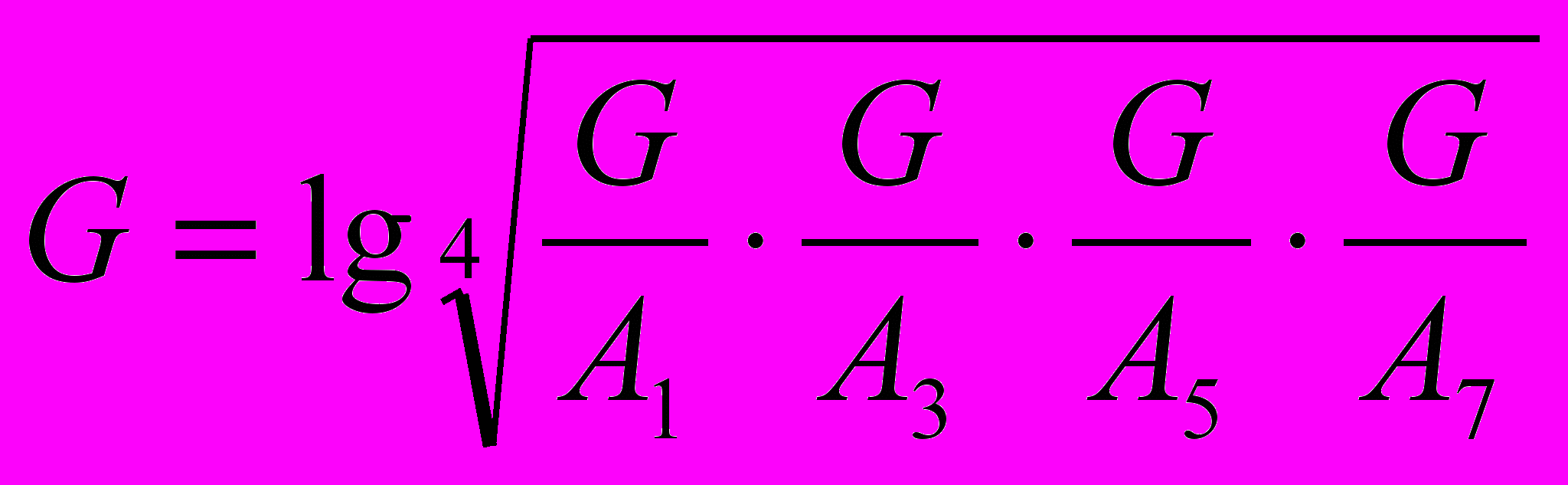
абота фильтра описывается следующей формулой:


Результат работы фильтра Уоллеса показан на рис. 10.

5. Фильтр Лапласа.
   

О
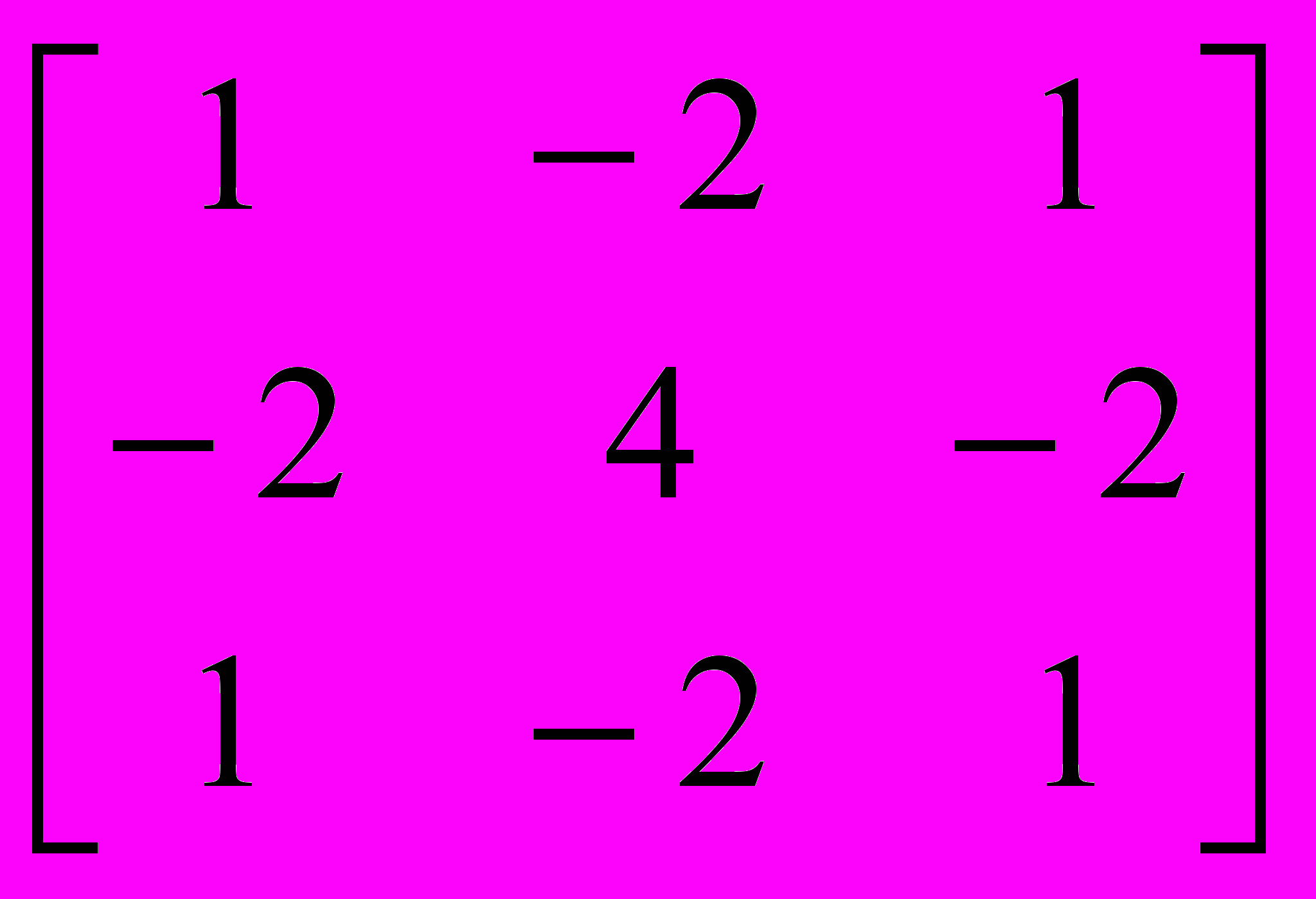
кно фильтра:


Результат работы фильтра Лапласа показан на рис. 11.

3.1. Восстанавливающие фильтры

Основным параметром фильтра является его апертура А, определяющая, сколько точек, окружая данную будет использовано для вычисления нового значения данной точки. Для линейных фильтров это означает, что для точки Х[i,j] будут использоваться точки в диапазоне от X[i-A div 2, j] до X[i+A div 2, j], не исключая данную точку. Для двумерных фильтров это означает, что будут использованы точки от X[i-A div 2, j-A div 2] до

X[i+A div 2, j+A div 2].

При применении сглаживающего фильтра вычисление нового значения каждой из трёх компонентов точки происходит по формуле: NewBr = AveBr, где NewBr – новое значение яркости компонента, АveBr – средняя яркость канала.

При применении линейного медианного фильтра формула та же, но переменная AveBr имеет другой смысл: здесь это значение элемента с индексом [A div 2 +1] в отсортированном массиве яркостей точек канала, участвующих в вычислении. При применении двумерного медианного фильтра сначала вычисляются медианы строк матрицы преобразования. Затем на основании полученных значений снова вычисляется медиана, и найденное число становится новым значением данной точки.

Результаты работы одномерного и двумерного сглаживающих фильтров (после 10 применений) показаны на рис. 12 и 13, соответственно.

4. Преобразование Фурье

Для реализации дискретного преобразования Фурье берется часть исходного изображения размером 128Х128 пикселей. Такой размер выбран ввиду того, что преобразование требует значительного времени на старых машинах.

Цель прямого преобразования – получить последовательность комплексных чисел, имея исходную последовательность действительных чисел по правилам:





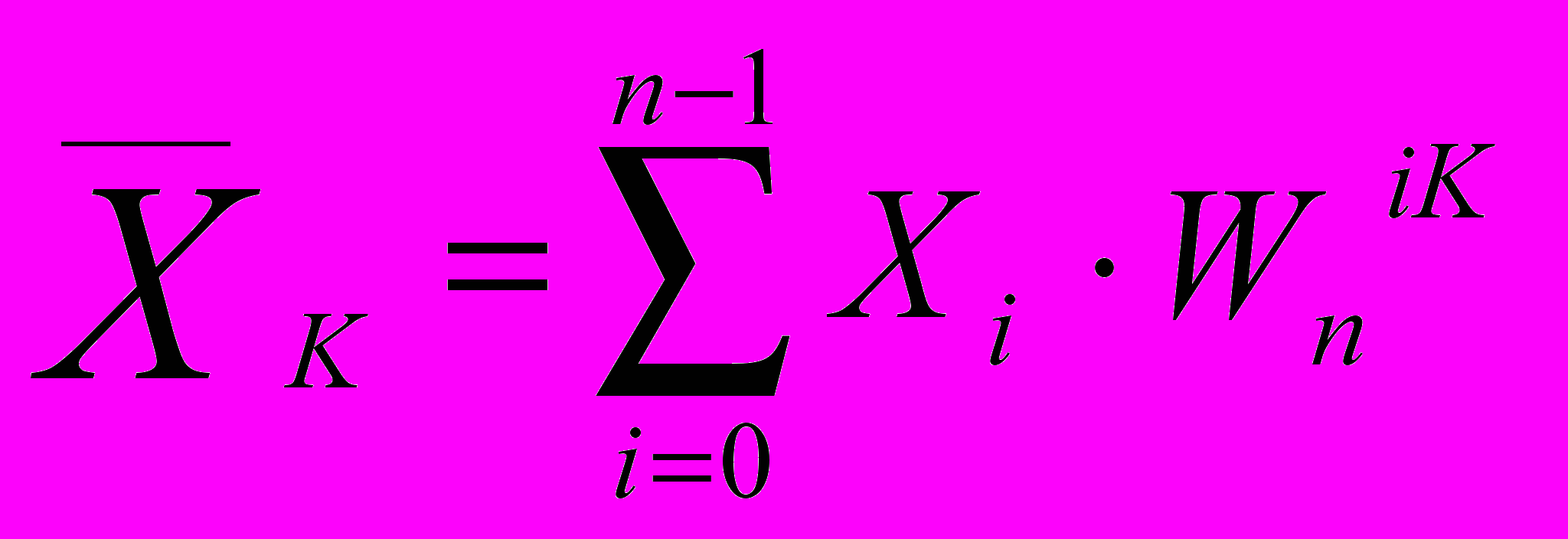
г
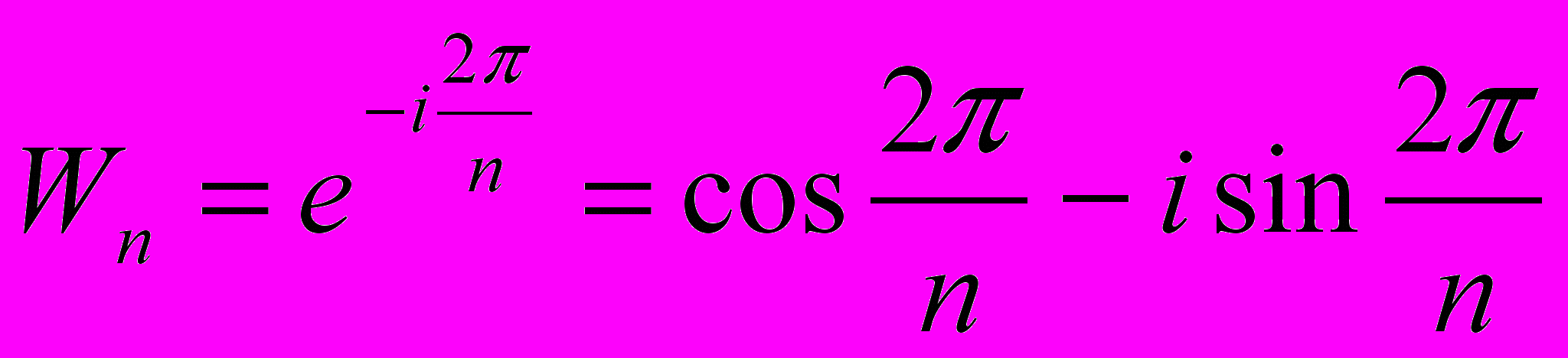
де


Цель обратного преобразования – получить исходную последовательность действительных чисел, имея последовательность комплексных чисел.



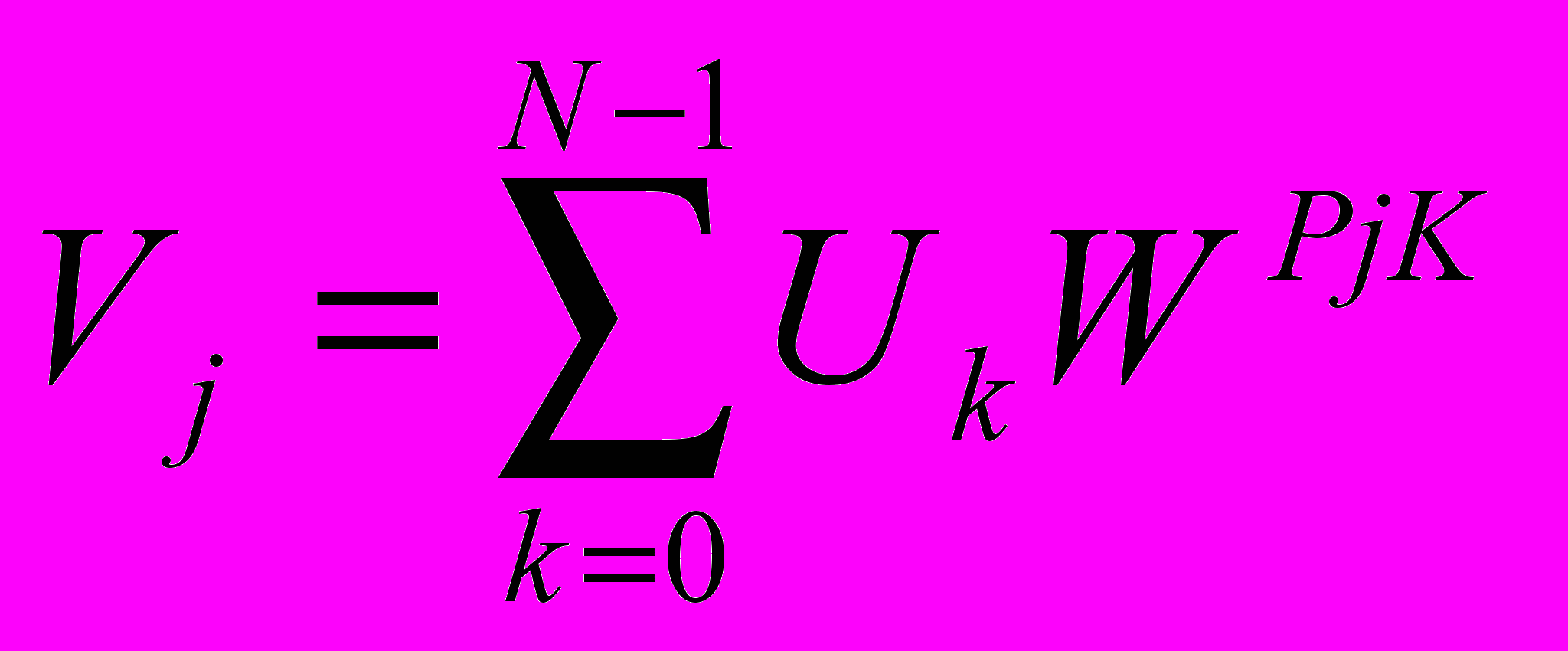
Формула, использовавшаяся при реализации одномерного преобразования:


Для прямого преобразования: P=-1; U_K=X_K; V_j=NC_K.

Для обратного преобразования: P=1; U_K=С_K; V_j=Х_K.



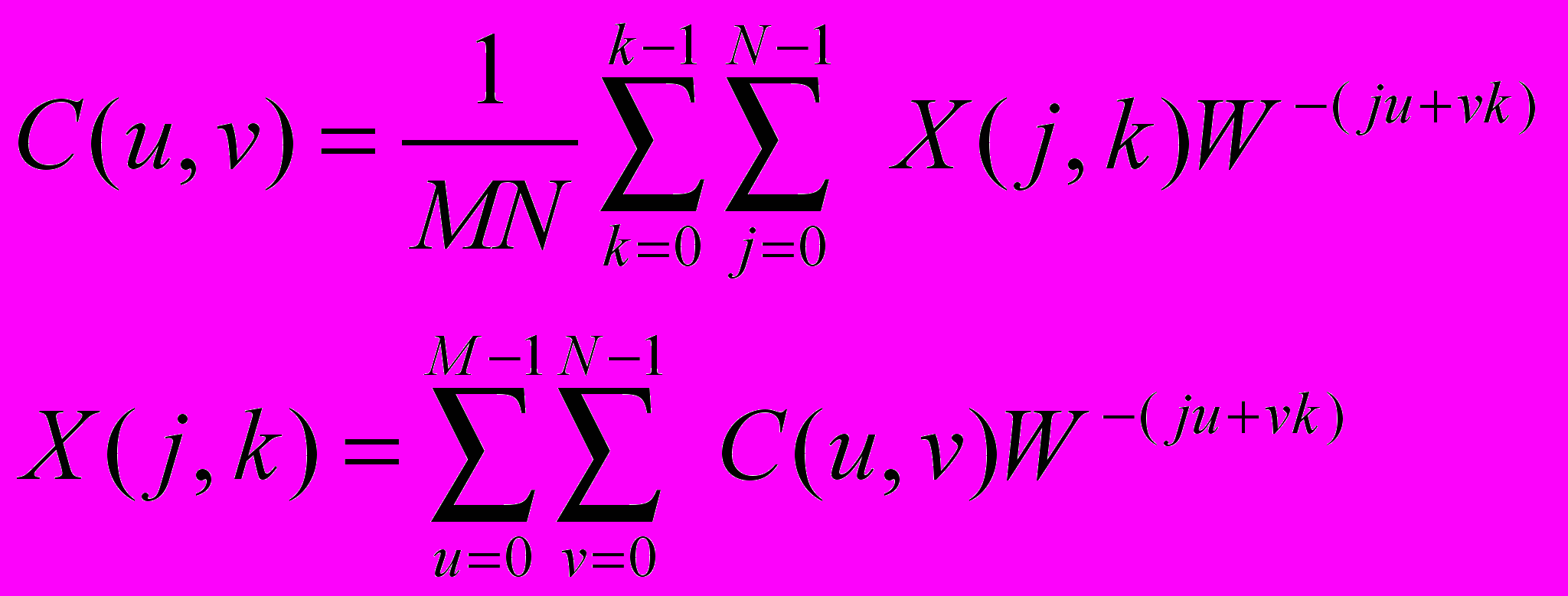
Формула, использовавшаяся при реализации двумерного преобразования:


Результаты работы одномерного и двумерного преобразований Фурье (левый верхний угол размером 128х128) показаны на рис. 14 и 15, соответственно.



5. Быстрое преобразование Уолша, упорядоченное по Адамару


В основе ДПУ лежит система дискретных функций Уолша. Эти функции являются отсчётами непрерывных функций Уолша. Каждый отсчет расположен в середине связанного с ним элемента функции. Длительность элемента равна 1/N от интервала [0;1], на котором и определены непрерывные функции Уолша, здесь N- натуральное число – количество функций Уолша в системе. Функции Уолша в системе из N функций могут быть упорядочены различным образом. При реализации в работе упорядочивание проводилось по Адамару. Размер системы функций Уолша всегда равен целой степени двойки.


А
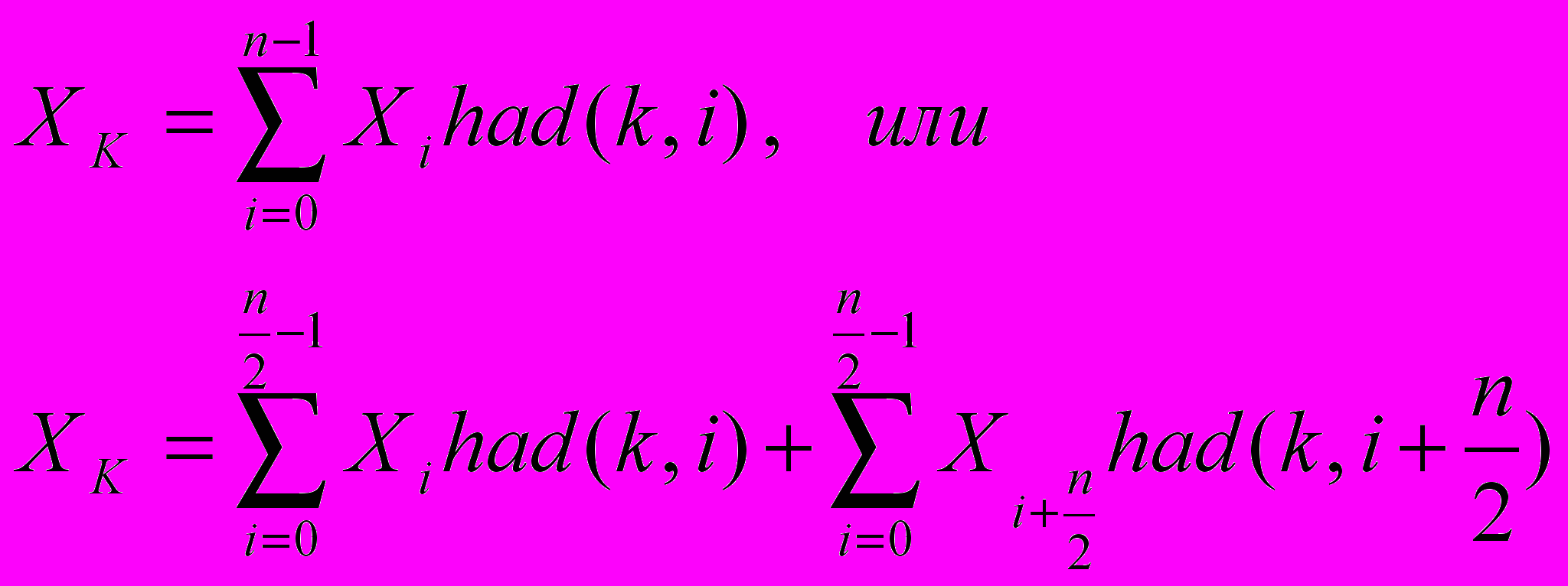
лгоритм быстрого ДПУ:


Размер последовательности: 128 строк X 128 столбцов.

Схема реализации (при 8 значениях):

Р
езультат прямого одномерного преобразования (левый верхний угол размером 128х128) представлен на рис. 16, результат двумерного – на рис.17.







Источники информации


1) Лекции по обработке изображений.

2) Круглински Д., Уингоу С., Шеферд Дж. Программирование на

Microsoft Visual C++ 6.0 /Пер. с англ. – СПб: Питер.

3) Франка П. С++: Учебный курс – СПб: Питер 1999.

4) Вопросы и ответы по С и С++ - Москва: «МикроАрт», 1997

Cервисный центр, №2-9 2001.

Приложение. ОБРАБОТКА СИГНАЛОВ

А. Разложение функции в ряд Фурье (с коэффициентами Ак, Вк)

Задана периодическая функция X(t) на интервале [-Т, T]. Ее можно представить как сумму некоторых базисных функций {U_n (t)}={sin nw_ot, cos nw_ot }, где n= 0, 1, 2 ... w_o=2/Т. Коэффициенты разложения определяются по формулам:








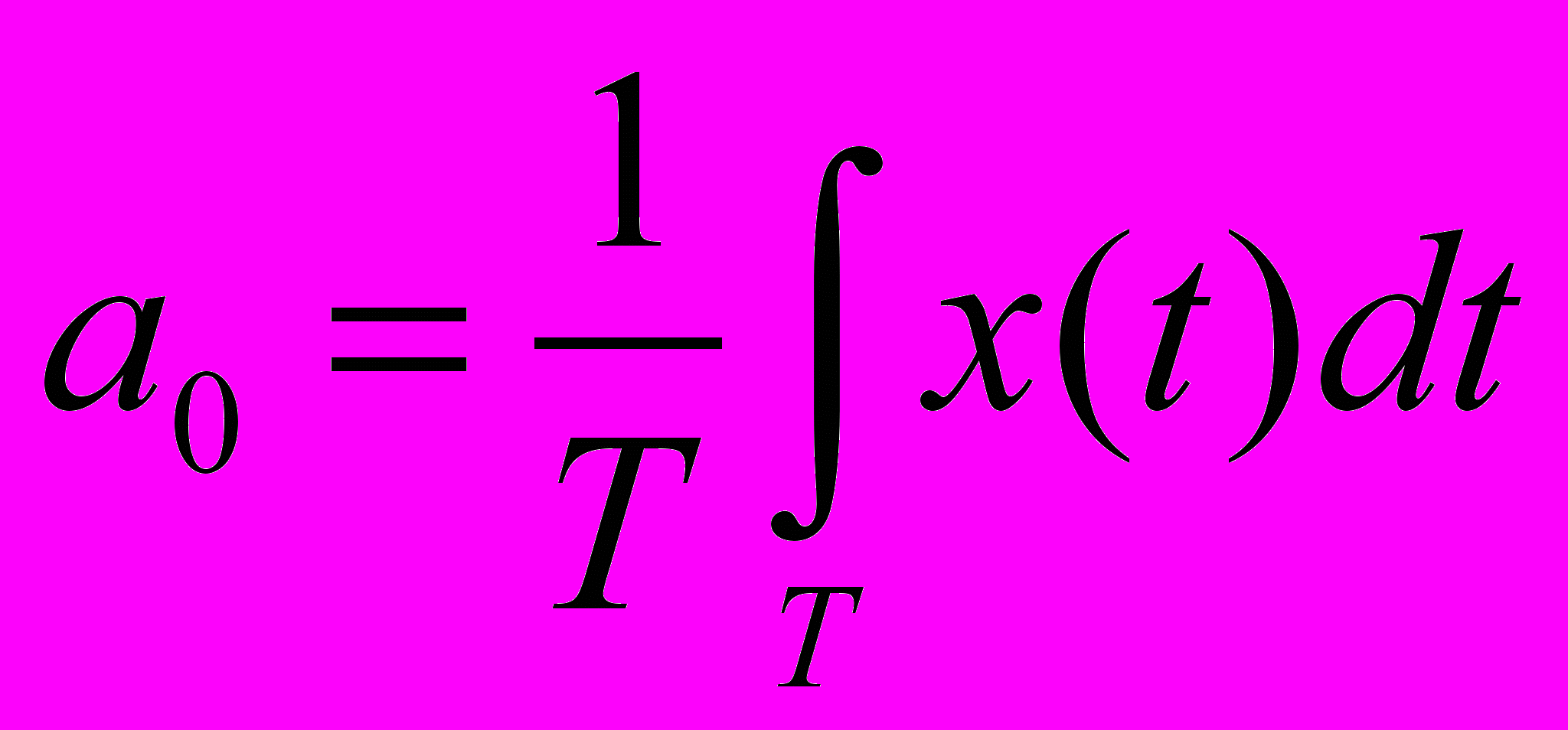
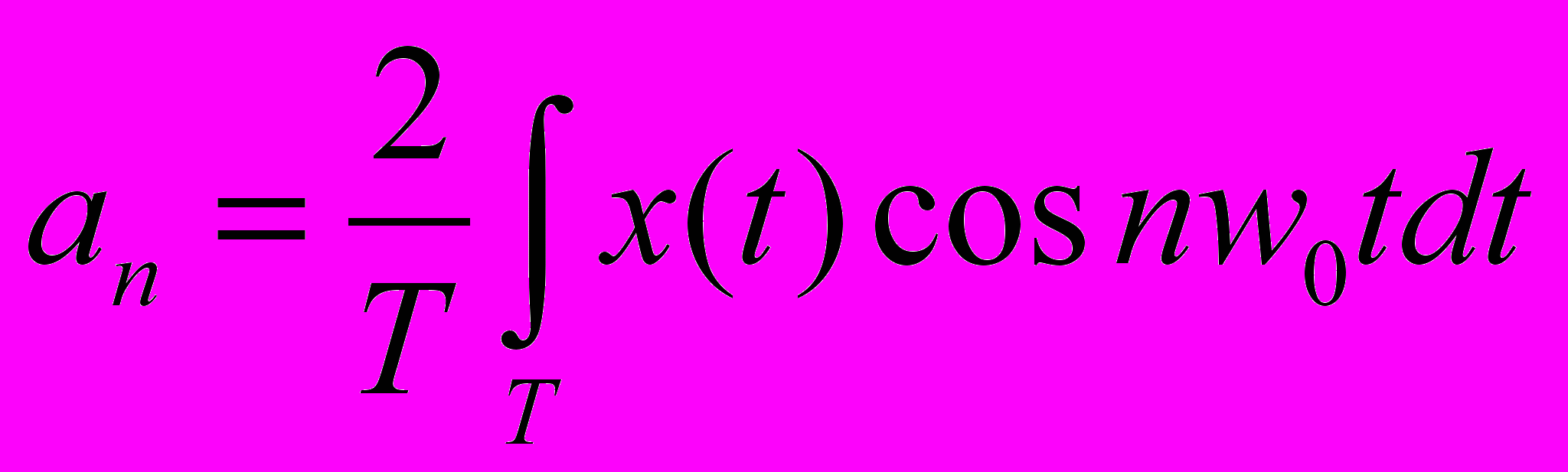
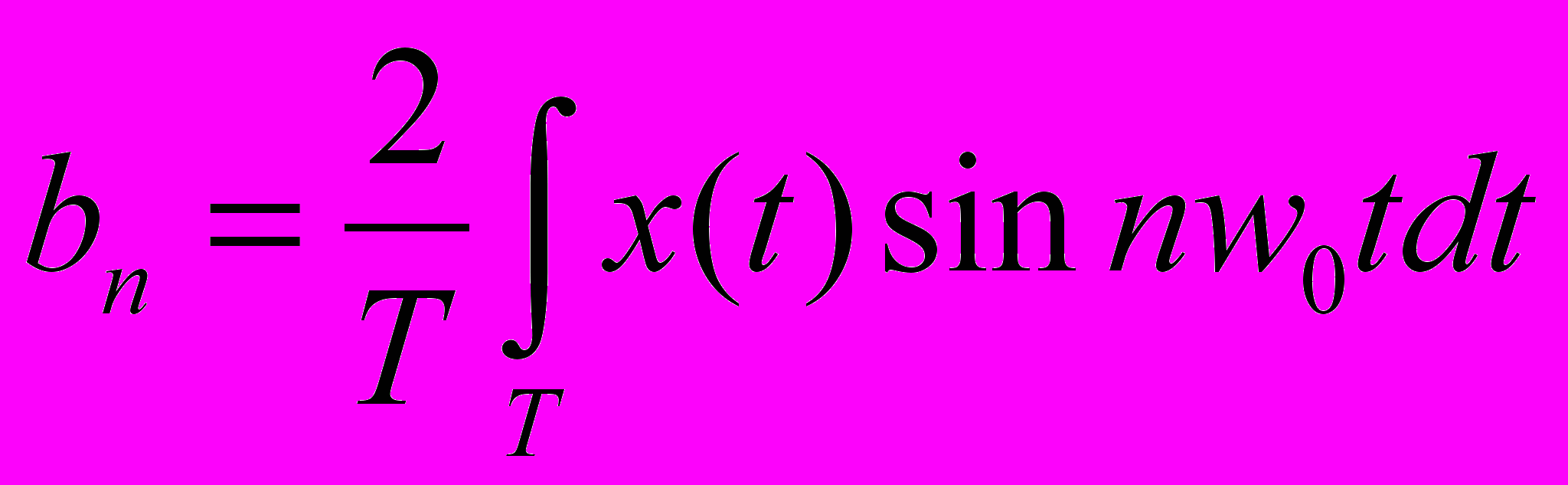
Тогда разложение функции будет выглядеть:





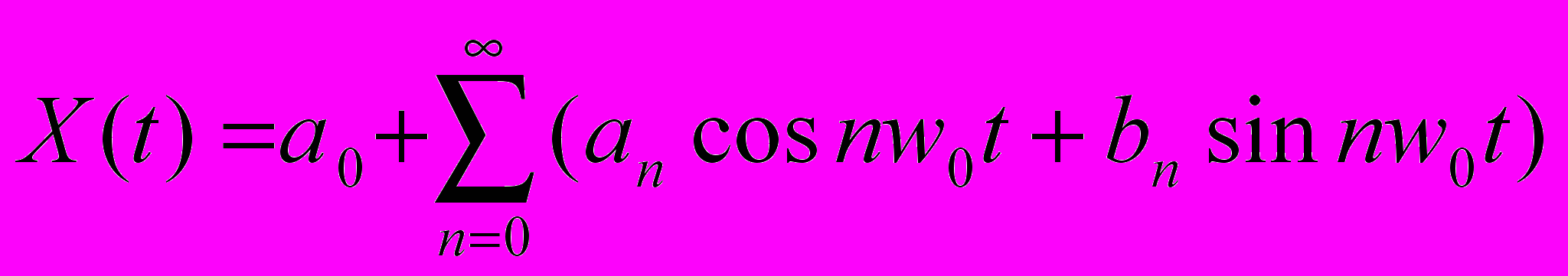
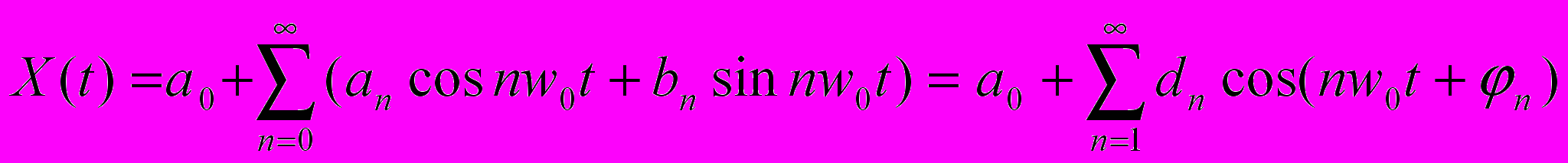
В
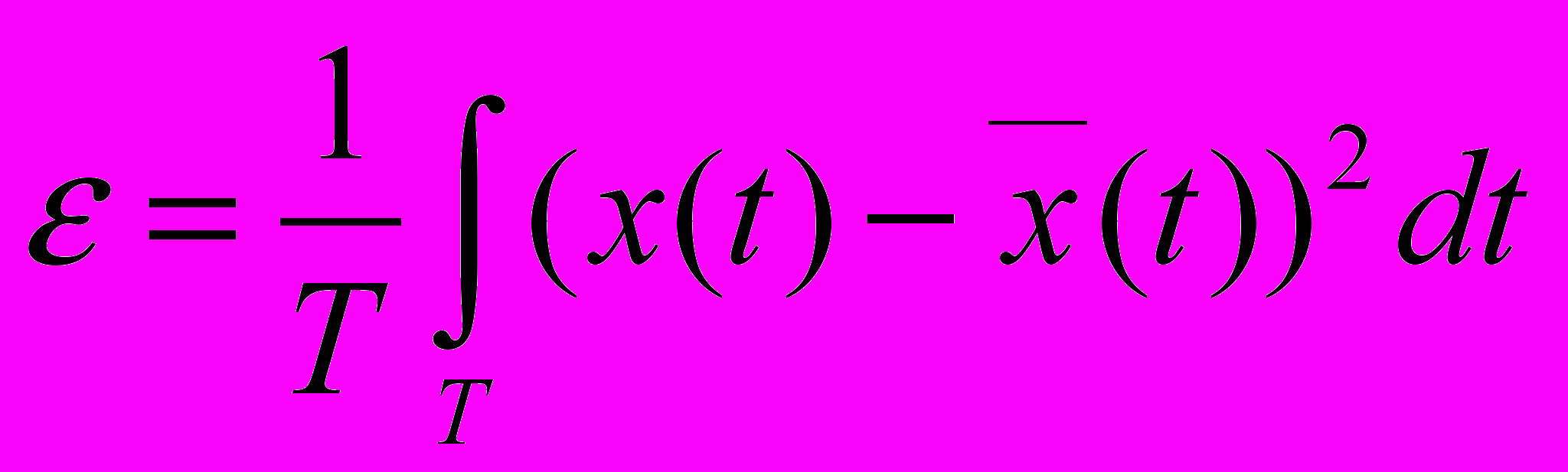
ычисление ошибки:


Где X(t)- исходная функция, а 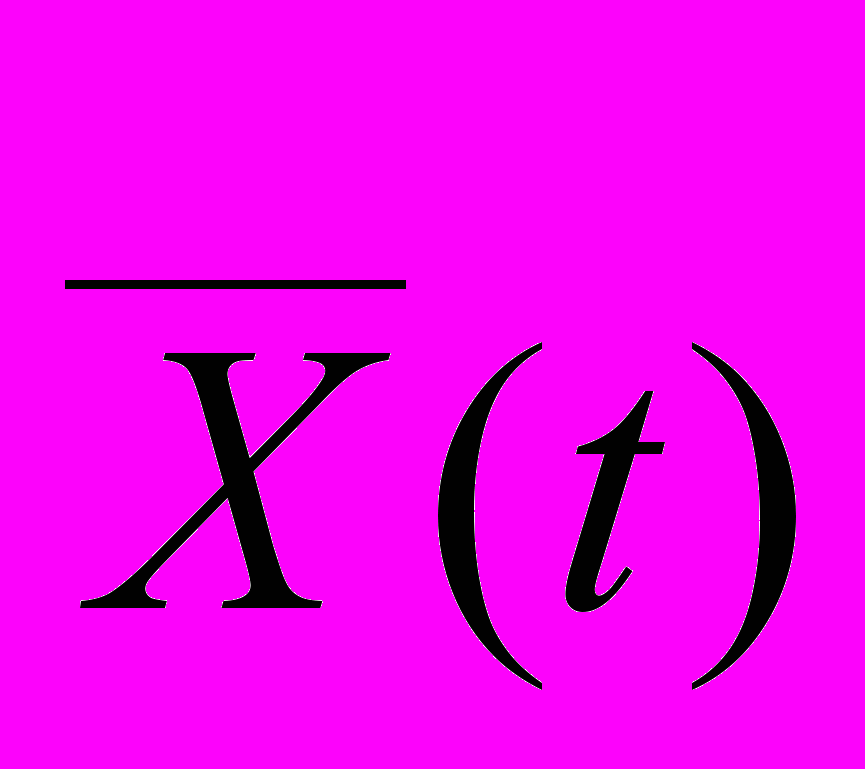функция разложения с заданным n.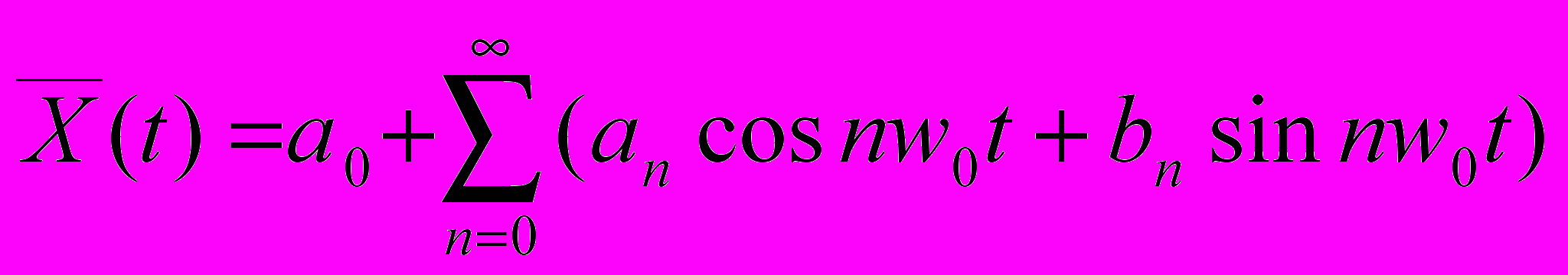

В. Разложение функции в ряд Фурье (с коэффициентами Dn)

Разложении функции можно представить в другом виде


Где

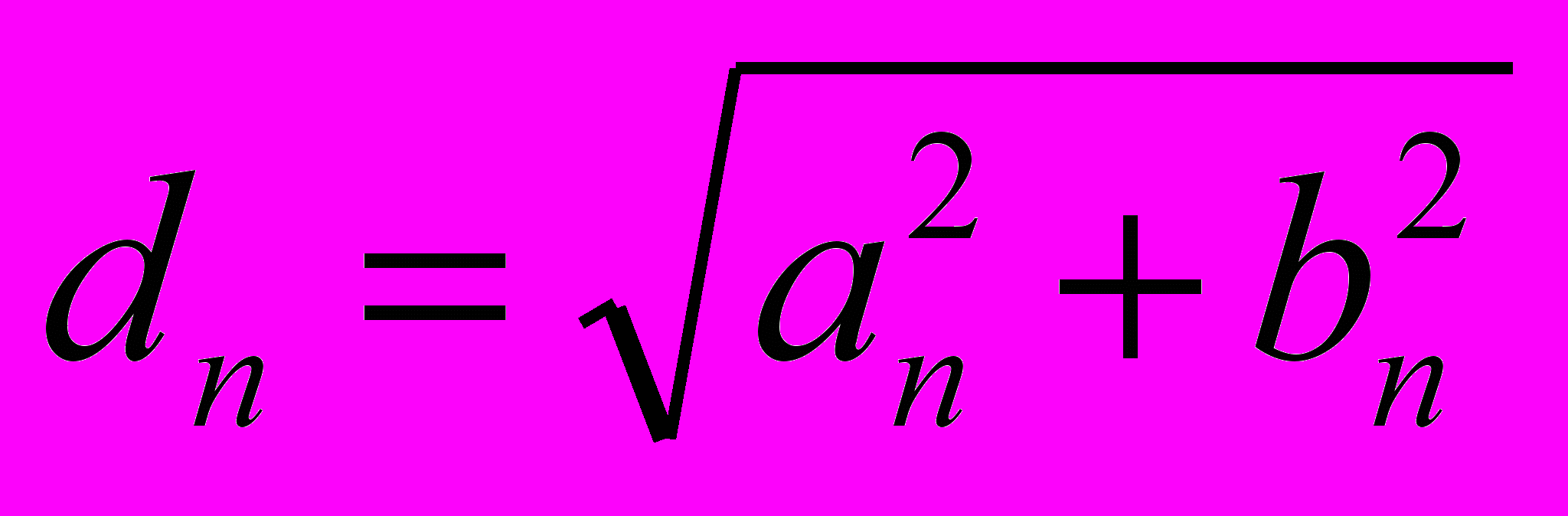
С. Разложение функции в ряд Фурье в комплексной форме

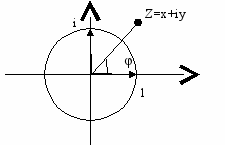Все точки на окружности представляют как (Рис.1.):


Представление комплексных чисел.




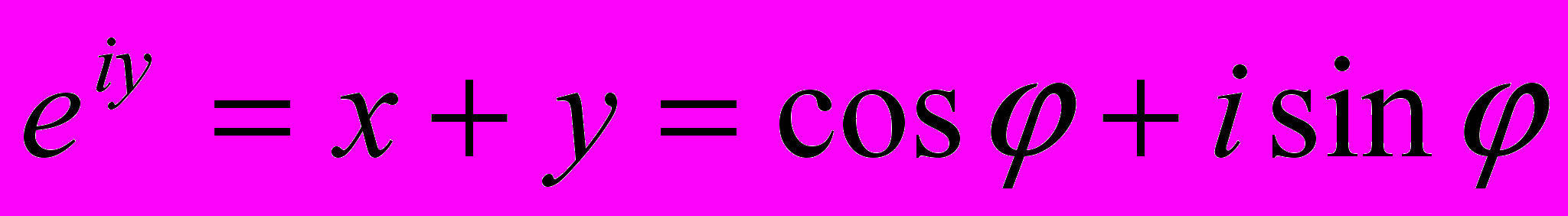
Т
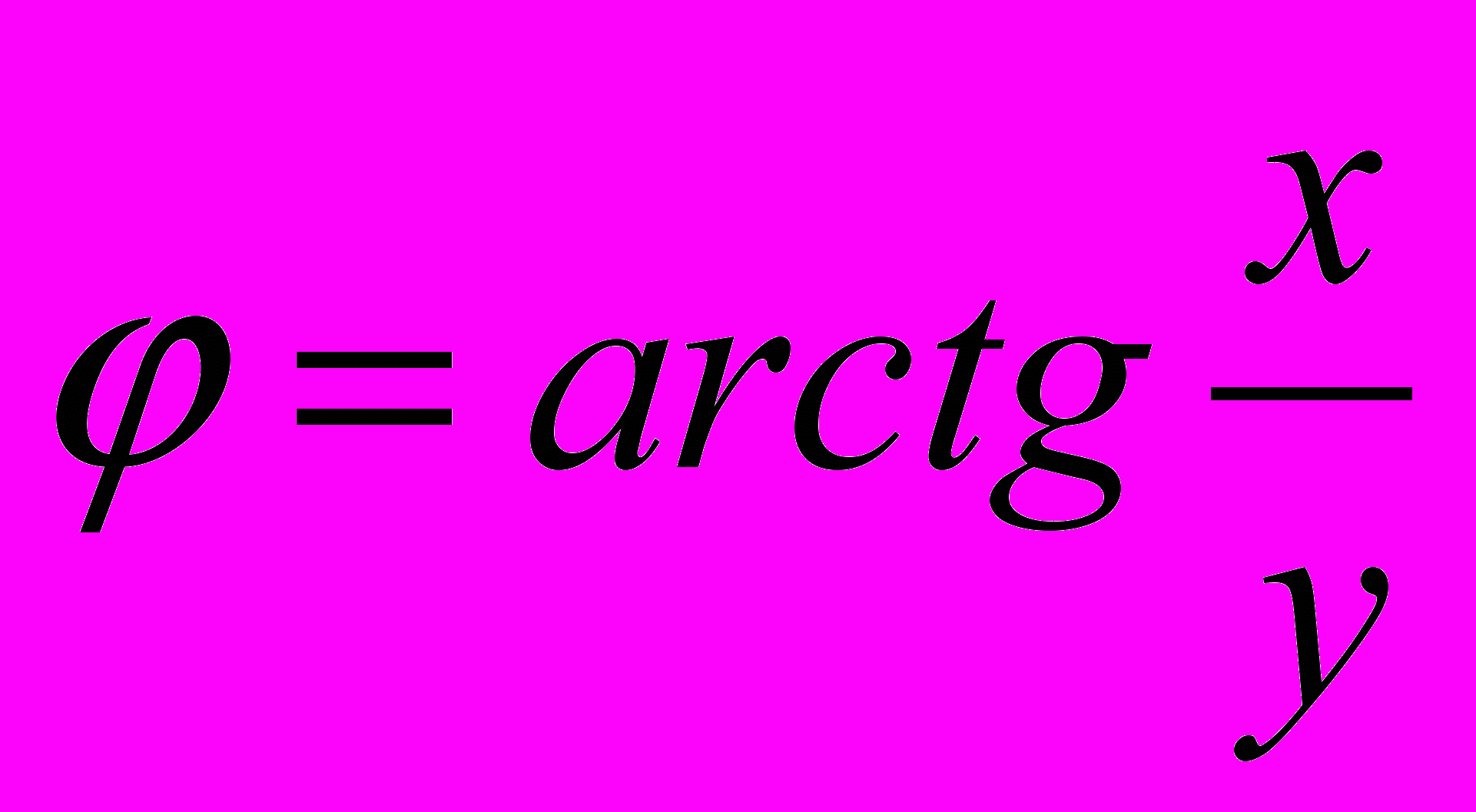
огда комплексное число Z можно представить:



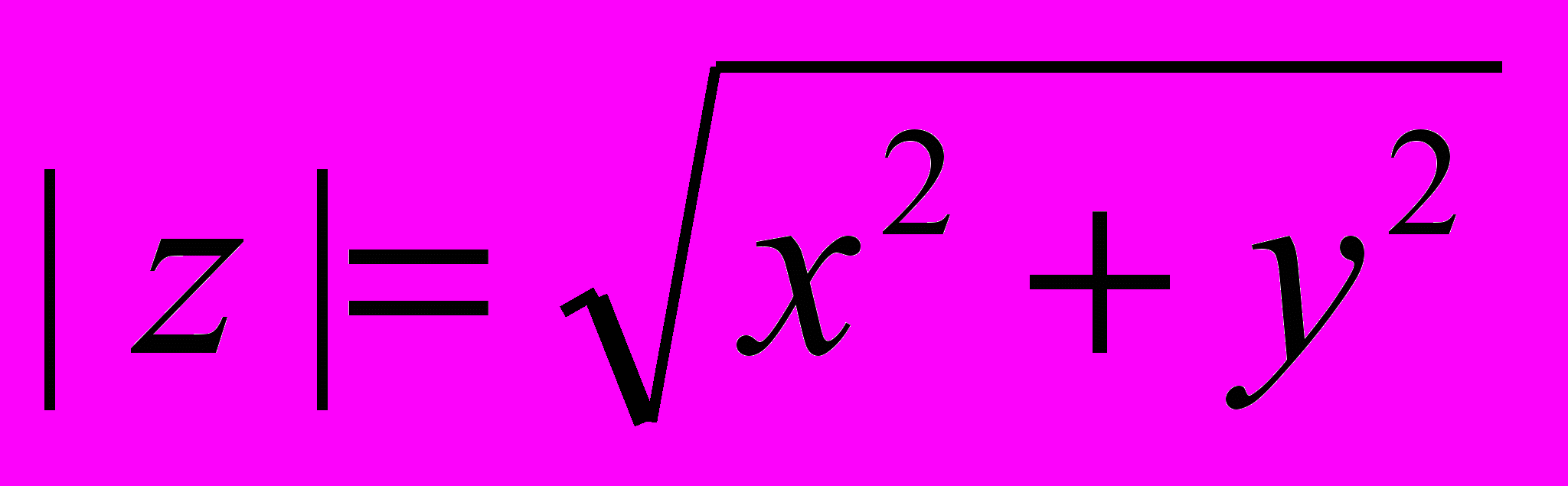
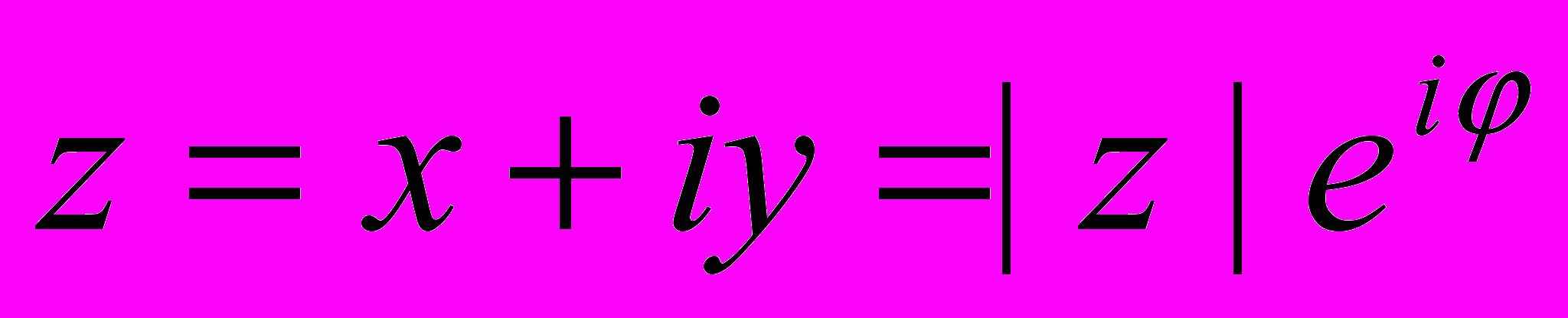
Рис.1.

С
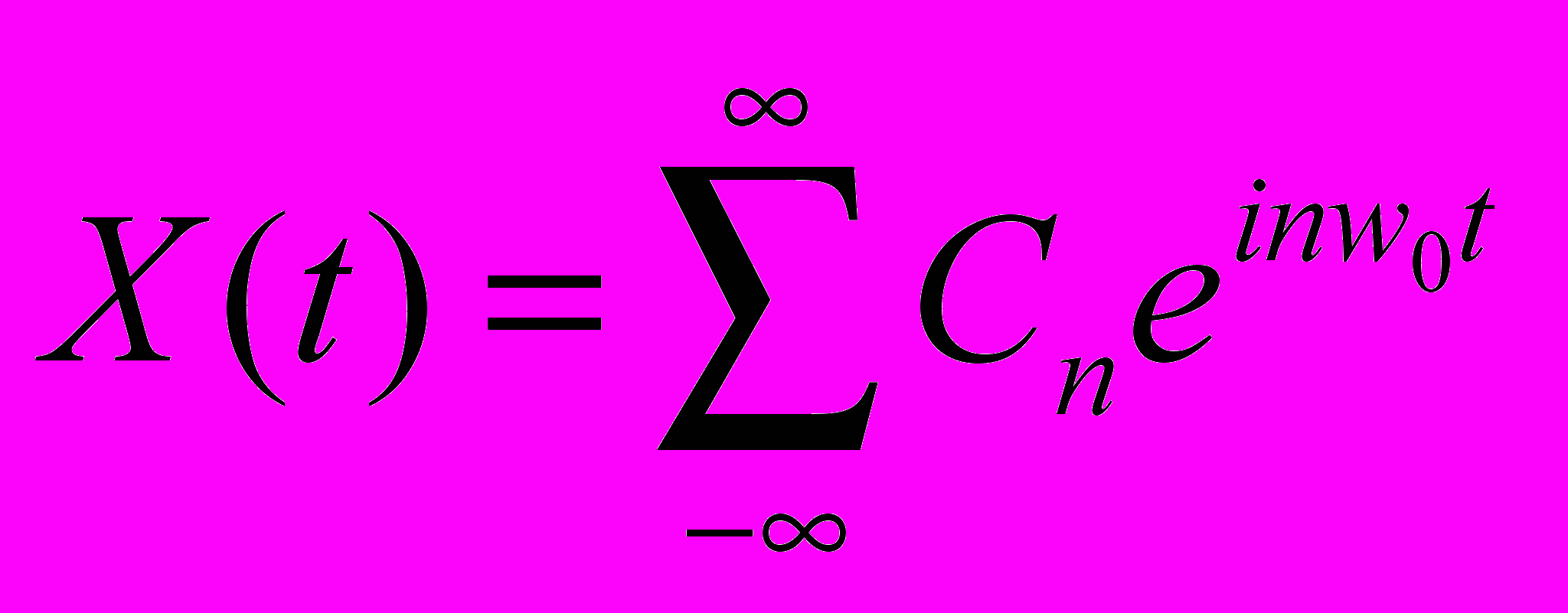
использованием комплексных величин можно разложить заданную функцию X(t) в ряд Фурье. Где

D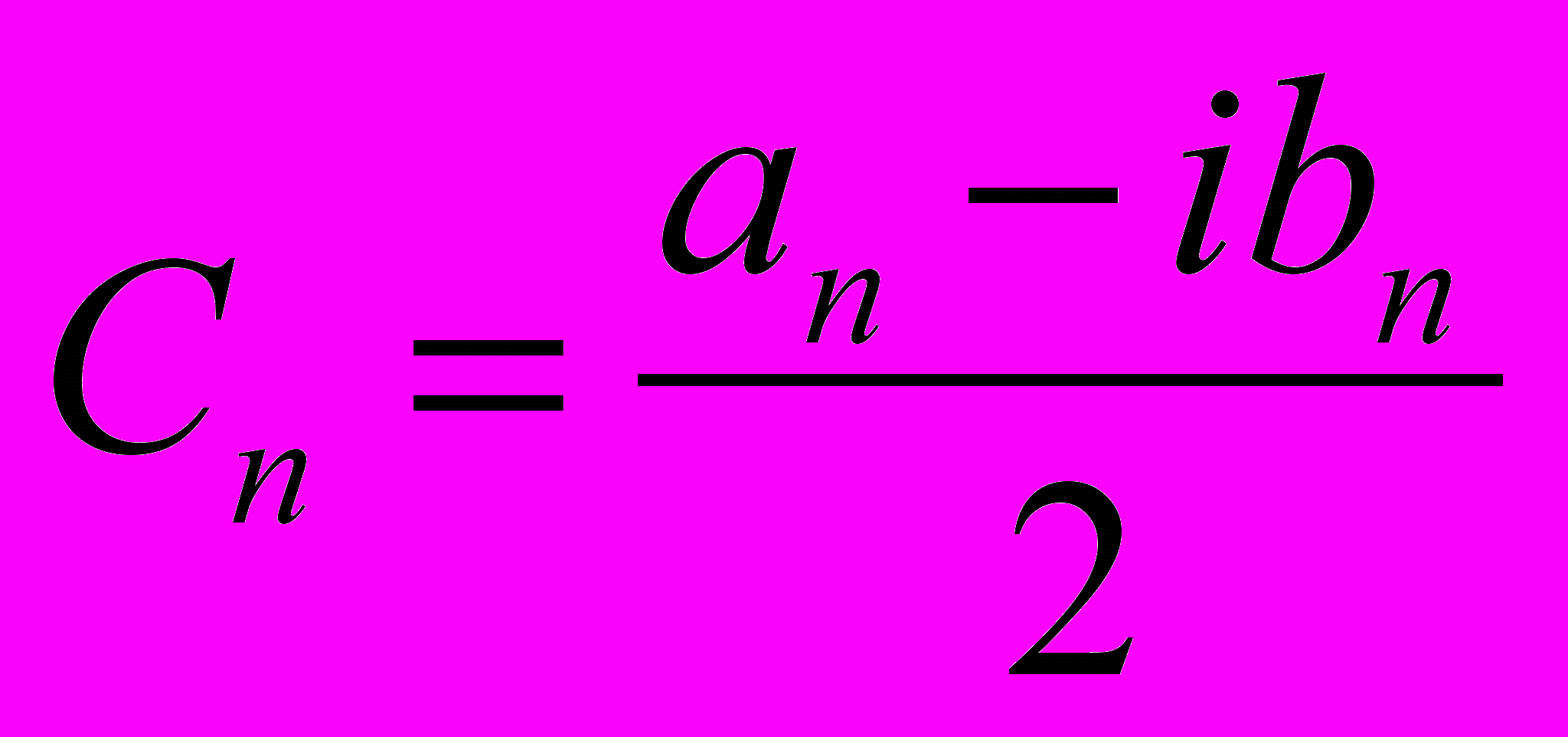. Полином Лежандра

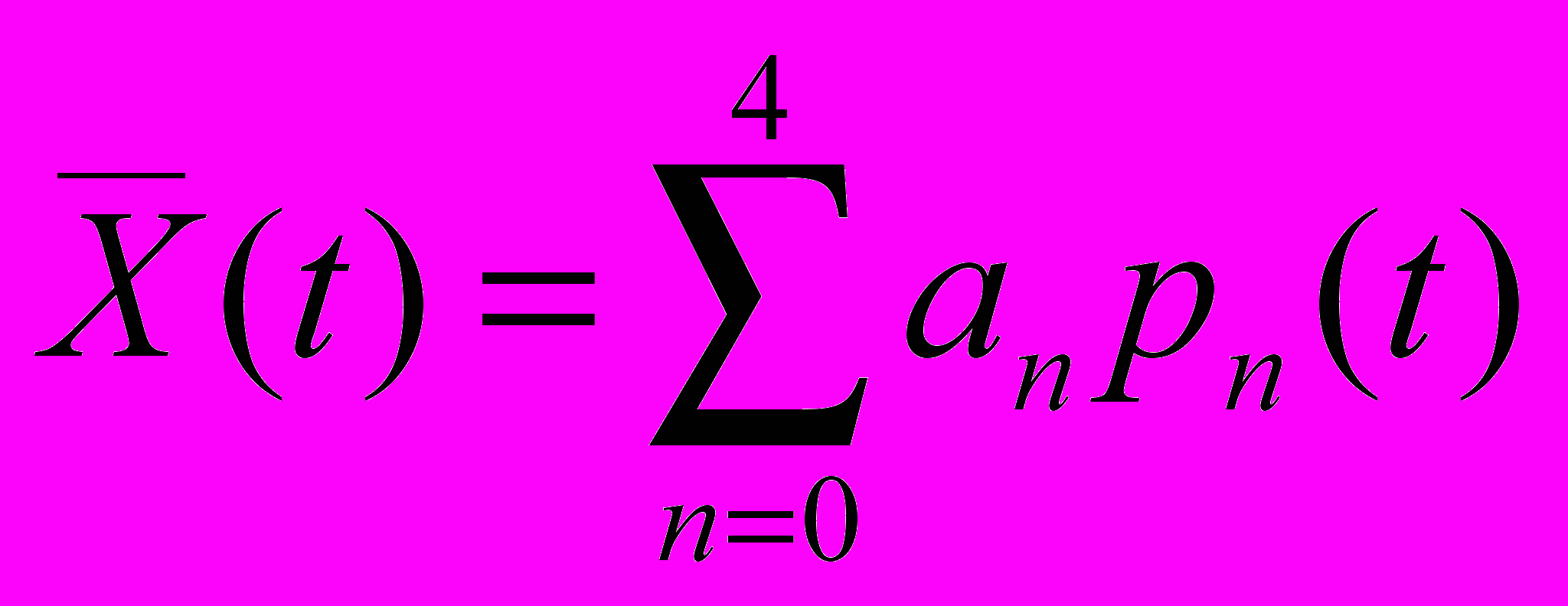
Задана функция X(t), t [-1,1]. Разложение функции по полиному Лежандра будет:

Г
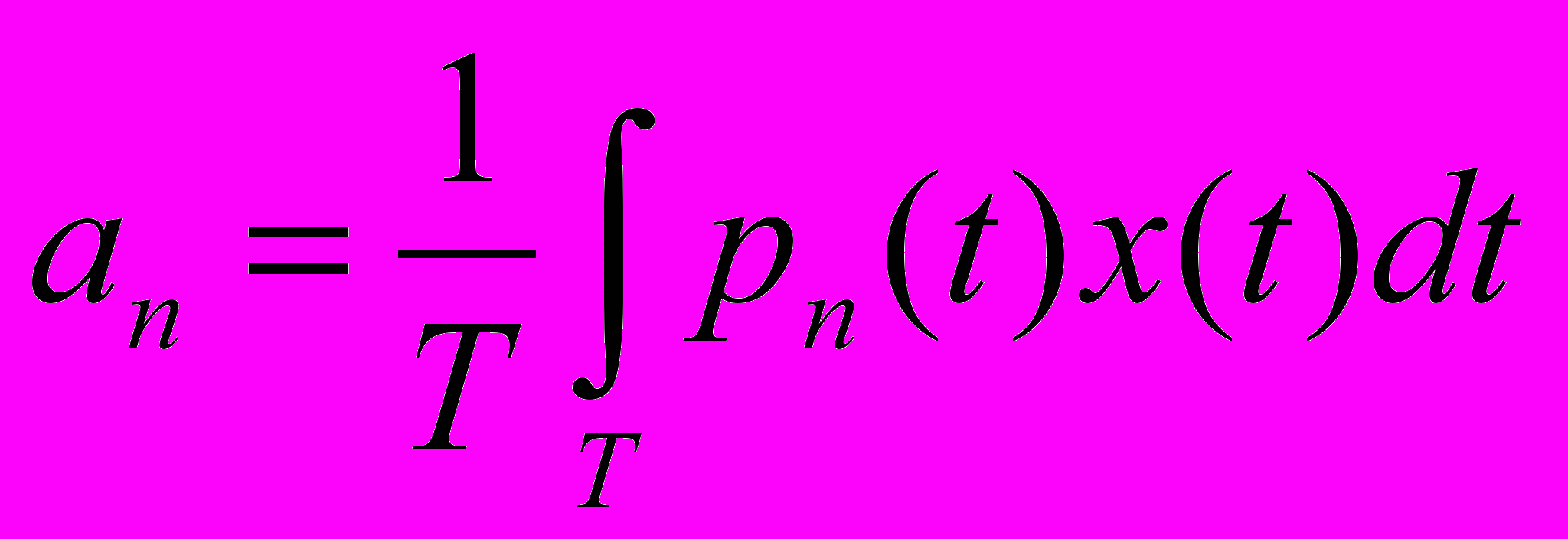
де весовые коэффициенты

Коэффициенты разложения определяются:

P₀(t)=1; P₁(t)=t

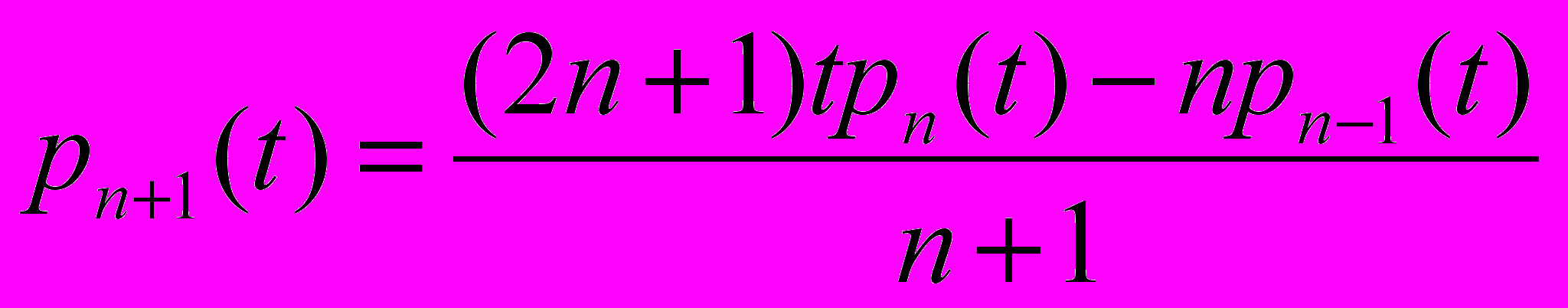
Е. Преобразование Фурье для непрерывных сигналов

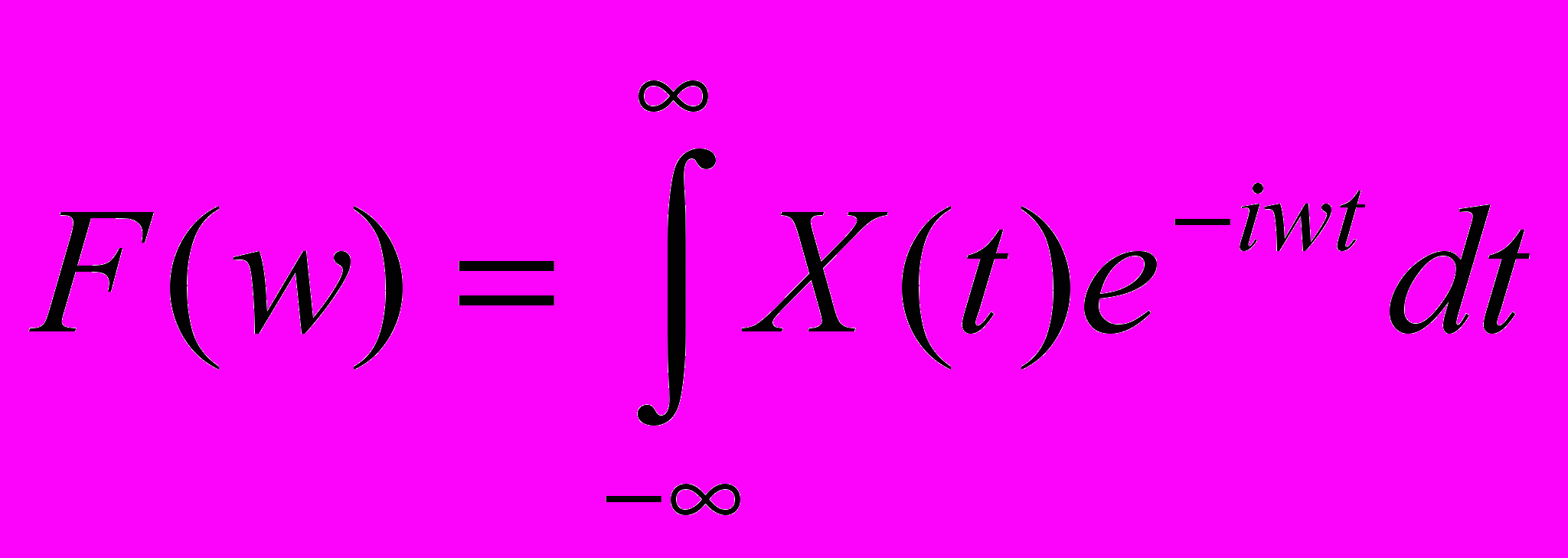
Для заданной непериодической функции X(t) прямое преобразование Фурье будет:

Обратное преобразование:

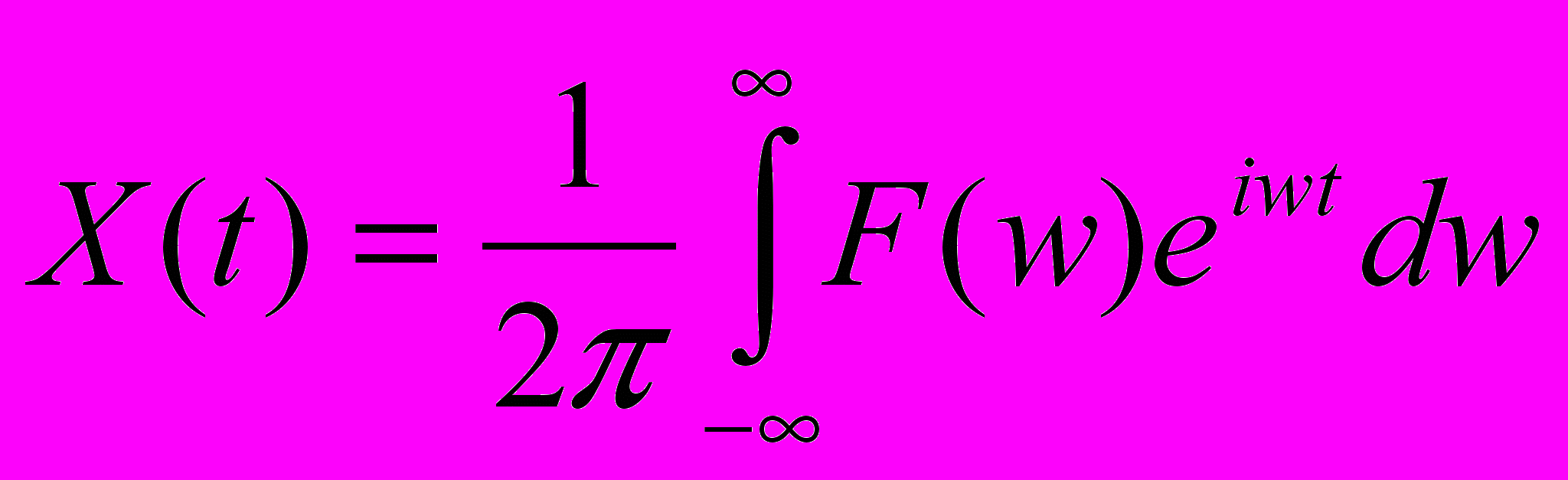
F. Взаимная корреляция

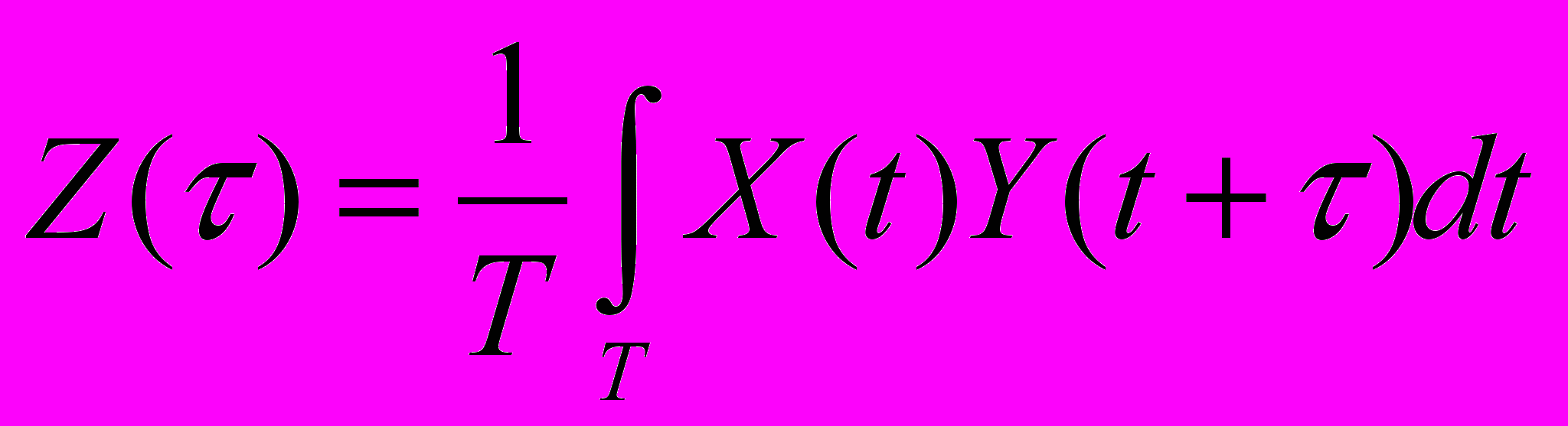
Если заданы две функции X(t) и Y(t), то их взаимная корреляция вычисляется по формуле:

G. Быстрое преобразование Фурье (БПФ)

Пусть N=2^v, целое число. Разложим ДП x(n), n[0,N-1], на четные и нечетные отсчеты:


x(n)















0 1 2 3 4 5 6 7 8… n




x(2r) x(2r+1)


0 2 4 6 8 n 1 3 5 7 n 0 1 2 3 4 r 0 1 2 3 r


X_N(n)=X_N/2(n)+X_N/2(n)=X(n=2r)+X(n=2r+1)

четн.n нечет.n

N-1 N/2-1 N/2-1

X(k)= X(n)W ^nk = X(n)W^nk +X(n)W^nk = X(2r)W^2rk + X(2r+1)W^(2r+1) =

^{n=0 N n-нечетн. N n-четн. N r = 0 N r = 0 N}

N/2-1 N/2-1

= X(2r)(W²)^rk +  X(2r+1)(W²)^rk W<sup>k

r = 0 N r = 0 N</sup>



Так как W²_N = e ^{–j (2П/ (N/2))} = W_N/2 ,то

_{N/2-1 N/2-1}

X(k) = X(2r)W^rk + W^k X(2r+1)W^rk = G(k) + W^kH(k) ,

^{r = 0 N/2 N r = 0 N/2 N}

где G(k) и H(k) – N/2 точечные ДПФ четных и нечетных отсчетов. Каждая из

сумм G(k) и H(k) требует вычисления k от 0 (N/2)-1, хотя k[0, N-1].

Пример: Вычисление ДПФ при N=8.


ДПФ N/2 = 4


четных


X(n) = X(2r)
ДПФ N = 8

X(0) G(0) X(0) = G(0) + W⁰H(0)

X(2) G(1) X(1) = G(1) + W¹H(1)

X(4) G(2) X(2) = G(2) + W²H(2)

X(6) G(3) X(3) = G(3) + W³H(3)




ДПФ N/2 = 4


нечетных


X(n)=X(2r+1)

X(1) H(0) X(4) = G(4) + W⁴H(4) = G(0) + W⁴H(0)

X(3) H(1) X(5) = G(5) + W⁵H(5) = G(1) + W⁵H(1)

X(5) H(2) X(6) = G(6) + W⁶H(6) = G(2) + W⁶H(2)

X(7) H(3) X(7) = G(7) + W⁷H(7) = G(3) + W⁷H(3)







Видно, что в данном случае вычислительные затраты составляют: 2(N/2)²

комплексных умножений и 2(N/2)² комплексных сложений (для N\2-точечных ДПФ G(k)

и H(k)), N комплексных умножений (W^kH(k)) и N комплексных сложений (G(k)+W^kH(k)).

Считая умножение самой медленной операцией, оцениваем длительность выполнения

БПФ числом комплексных умножений:

t_БПФ  [N + (N/2)²] t₀  N²t₀ = t_ДПФ ,

где t₀ – длительность выполнения одной операции умножения.

Процесс прореживания по времени можно продолжить, так как N\2–четное число.

Каждое N/2-точечное ДПФ вычисляется в виде суммы двух N/4-точечных ДПФ.


_{N/2 –1 N/4 –1 N/4 –1 N/4 –1 N/4 –1}

<sup>G(k) = g(r)Wrk = g(2l)W2lk+g(2l+1)W(2l+1)k =g(2l)Wlk + g(2l+1)Wlk

r = 0 N/2 l = 0 N/2 l = 0 N/2 l = 0 N/4 l = 0 N/4</sup>




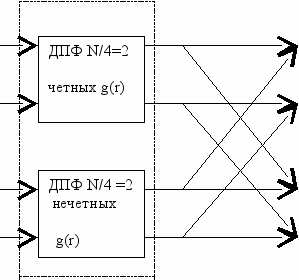
<sub>ДПФ N/2=4

X(0) G(0)

W</sub>⁰ ₌₁

^N\2

<sub>X(4) G(1)

W</sub>¹ _{= W}<sup>2

N\2 N</sup>


<sub>X(2) G(2)

W</sub>² _{= W}<sup>4

N/2 N</sup>

_{X(6) G(3)}

W³ = W⁶



_{N/4 –1 N/4 –1}

Аналогично H(k) =h(2l) W^lk + W^k h(2l+1) W<sup>lk

l = 0 N/4 N/2 l = 0 N/4</sup>

Разбиение X(n) продолжается до тех пор, пока не дойдем до N/2=2 (двухточечное

ДПФ). Граф двухточечного ДПФ («бабочка») имеет вид:


X(0) X(0) + W⁰ X(4) = X(0) + X(4)

W⁰ = 1 <sup>N/4

N/4</sup>

X(4) X(0) + W¹ X(4) = X(0) – X(4)

^N/4

W¹ = W⁴ = W^N/2 = 1

^{N/4 N N}

A(k) A(k) + W^k B(k)

+


_

B(k)

A(k) - W^k B(k)


Базовая операция БПФВ включает в себя одно комплексное умножение

и два комплексных сложения. Всего этапов БПФВ L = log₂N. На каждом этапе БПФВ

выполняется N/2 базовых операции (в данном примере четыре). Таким образом, на

выполнение БПФВ требуется N/2 * log₂ комплексных умножений.


Полный граф восьмиточечного БПФВ (N=8)

x(0) x(0) + X(0)

W⁰ W^{0 W0}

x(1) x(4) X(1)

W⁴ W² W¹

x(2) x(2) + X(2)

W⁰ W⁴ W²

x(3) x(6) X(3)

W⁴ W⁶ W³

x(4) x(1) + X(4)

_W⁰ _W⁰ W⁴

x(5) x(5) X(5)

_W⁴ _W² W⁵

x(6) x(3) + X(6)

_W⁰ _W⁴ W⁶

x(7) x(7) X(7)

_{Этап 1 W}⁴ _{Этап2 W}⁶ _{Этап 3 W}⁷


При вычислении БПФВ для получения естественного порядка следования

выходов ДП X(k): X(0),X(1),…X(N-1) необходимо перетасовать входные отсчеты x(n)

по закону двоичной инверсии кода индексов n.

nестеств	nестеств. двоичн.	nдвоичн. инверсн.	nтреб.
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	110	3
7	111	111	7

<sub>x(0) x(1) x(2) x(3) x(4) x(5) x(6) x(7)




x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7)</sub>


Число разрядов кода n равно L=log₂N. Перестановку x(n) производятся с

замещением, меняя в парах числа с прямыми и двоично-инверсными номерами и используя

лишь одну вспомогательную ячейку памяти.


Блок схема программы двоично-инверсного счетчика





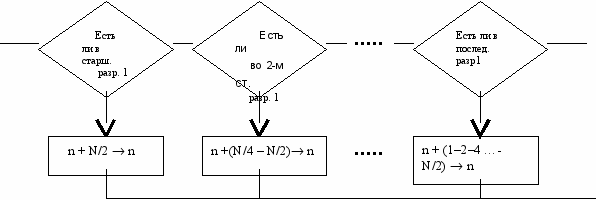
Пример:(N=8)

ni	Двоичный код	n i+1	двоично-инверсный код
0	000	0+8/2=4	100
4	100	4+(8/4-8/2)=2	010
2	010	2+8/2=6	110
6	110	6+(8/8-8/4-8/2)=1	001