Geum.ru

Построение нечетких графовых моделей на основе гис дулин С. К., д т. н., профессор s dulin@gismps ru Розенберг И. Н

Вид материалаДокументы

Содержание


Третьей особенностью
Рис. 1. Пример расположения зон технического обслуживания
Рис. 2. Граф для задачи размещения
Рис. 3. Пример топологии железнодорожной сети
Пятую особенность
Рис. 4. К определению нечетких значений высоты
Select r2.
GetLinvValue( double Distance, double MembershipRestriction)
Подобный материал:
ПОСТРОЕНИЕ НЕЧЕТКИХ ГРАФОВЫХ МОДЕЛЕЙ НА ОСНОВЕ ГИС


Дулин С.К., д.т.н., профессор

s.dulin@gismps.ru

Розенберг И.Н., д.т.н.

Открытое акционерное общество «Научно-исследовательский и проектно-конструкторский институт информатизации, автоматизации и связи на железнодорожном транспорте» (ОАО «НИИАС»)


В представленном докладе анализируются возможности построения нечетких графовых моделей. Цель анализа – выявить причины использования нечетких категорий и источники информации в среде ГИС для их формального описания.

Электронные карты, планы и схемы являются универсальным средством хранения, поиска информации, моделирования процессов, позволяют формировать емкие по смыслу визуальные образы. Эти и другие свойства определили широкий спектр применения ГИС в автоматизированных системах на железнодорожном транспорте. Карты и схемы являются первичным рабочим инструментом специалистов, с его помощью решаются оперативные и стратегические задачи управления перевозками, технического обслуживания подвижного состава, ликвидации аварийных ситуаций.

Анализируя практику решения задач с помощью ГИС, нельзя не обратить внимания на неформальность постановки подавляющего большинства задач [1, 2]. Эксперт-аналитик обращается к картам и схемам, имея зачастую лишь интуитивное представление о плане предстоящих действий. Это обуславливается как недостатком исходных данных, так и огромным разнообразием реально складывающихся ситуаций. Например, при ликвидации аварийной ситуации, вызванной сходом состава, требуется строго следовать соответствующей инструкции, но при этом учитывать пространственное размещение путей и станций, возможности подъезда к месту аварии, производственную и жилую инфраструктуру района, наличие опасных объектов, состояние природной среды. Зачастую требуется прогнозировать тенденции ближайшего изменения различных факторов – накопления загрязняющих веществ, простои других видов транспорта, оползни, лесные пожары, и т.д.

Подготовить заранее решения относительно возможных аварийных ситуаций и поместить их в ГИС даже для такого относительно небольшого участка практически невозможно. Поэтому в условиях трудной формализуемости задач роль ГИС сводится не к выдаче готовых решений, а предоставлении программного инструментария для формирования решений. Инструменты должны охватывать действия от простого просмотра участков карты, выполнения вспомогательных геометрических построений до выдачи экспертных рекомендаций.

Взгляд на ГИС как систему, позволяющую решать разнообразные проблемы, известен [3]. Можно выделить следующие особенности применения ГИС в системах, требующих принятия решений:

  1. исходные данные для решения любых задач и их результаты являются картами, полученными отбором, созданием и модификацией картографических объектов [4];
  2. для решения конкретной задачи строится рабочая область общей карты, хранимой в системе. Пользователь отбирает из всего доступного множества картографических материалов все то существенное, что с требуемой точностью отображает реальную действительность. Здесь выполняются все этапы, характерные для картографического анализа [1], выполняются построения, необходимые для пространственного, статистического, морфометрического и других видов анализа [5];
  3. результат решения задачи получается интерпретацией содержимого рабочей области. Важную роль в этом случае играет визуальный анализ рабочей области, манипулирование изображением – изменение масштаба, ракурса, точек зрения, комбинаций активных слоев. Решение аналитик получает не напрямую, а через осмысление образа, порожденного картографическим изображением. Возможны модификации рабочей области соответственно логике решаемой проблемы.

Как показал анализ, решение задач на транспорте обладает всеми перечисленными выше особенностями. Причина заключается в сложности карт, схем и планов, отображающих реальные объекты транспортной системы. Соотношение «часть» и «целое» таково, что не позволяет сохранить причинно-следственные связи иначе, чем через метапредставление, которым и является электронная карта.

Масштабы отображаемых на экране фрагментов подчас отличаются более чем на порядок. Можно видеть, насколько расходятся представление и смысл каждого из изображений, не позволяющие вывести свойства станции в целом из свойств отдельного фрагмента.

Объективно сложность обусловлена следующими факторами:
    1. существующая железнодорожная сеть и сопутствующая инфраструктура представляют собой сложные в пространственном отношении объекты, описываемые сложными электронными картами в векторном формате с обширными атрибутивными данными;
    2. информационная среда системы железнодорожного транспорта образована сетью, включающей тысячи компьютеров и охватывающей громадную территорию. ГИС, работающая в такой среде, неизбежно будет связываться с разнородными информационными источниками различной точности, формата представления, содержания и качества;
    3. геоинформация в ГИС ЖД непрерывно накапливается, что свойственно любой ГИС [6]. Динамика изменения пространственных объектов достаточно велика, что обуславливает непрерывное пополнение системы данными пространственно-временного характера.

Важно отметить, что современные программные оболочки ГИС, ориентированные на поддержку процедур принятия решений, включают программные инструменты решения оптимизационных задач на «топологиях» – специальных структурах данных [7, 8]. Топологические структуры данных включают в себя точечные, линейные и площадные объекты, но дополняют их описанием отношений между объектами. Соответственно, растет уровень операций над данными: топологии могут комбинироваться, дают возможность поиска элементов карты со сложными свойствами, позволяют делать специальные построения. В частности, топологии естественным образом отображают графовые структуры. Последняя версия аналитического приложения ARCINFO Spatial Analist позволяет находить центры обслуживания, максимальные потоки, потоки минимальной стоимости. Таким образом, современный ГИС-инструментарий поддерживает механизмы решения задач на графах. Насколько эффективно этот механизм используется, определяется двумя основными причинами:
  • качеством картографической основы. Поскольку электронная карта – образно-знаковая модель реальности, ей объективно присущи погрешности пространственного, временного и семантического характера, которые определяют адекватность графовой модели;
  • свойствами рабочей области для анализа. Она может быть построена не единственным образом, что может существенно повлиять на результат оптимизации.

Основа любого графического изображения – графический примитив векторного или растрового формата [3], [8], [11], [2]. Четкость описания и толкования свойств примитива не вызывает сомнений: координаты точек, цвет, ссылки отображаются числами, над которыми выполняются традиционные четкие арифметические операции. Однако, известно, что преимущества ГИС становятся все более явными, когда электронная карта наполняется содержанием – между примитивами устанавливаются отношения и фиксируются в базе данных, что приводит к появлению картографических объектов [3]. Этот переход неизбежно использует предположения, упрощения реальности и добавляет условности, необходимые для связывания смысла с множеством графических примитивов. Охватить все аспекты представления картографических объектов невозможно, возникает неполнота и недоопределенность описания. Например, вес участка железнодорожного полотна произвольной длины определить с заданной точностью невозможно: если длина рельса еще может быть измерена по карте, то данные о вспомогательной арматуре, количестве и весе отдельных шпал попросту недоступны. Таким образом, картографические объекты приобретают свойства, не выводимые из их графических изображений. Эти свойства нечетко определяются экспертами-пользователями. Можно заключить, что первой особенностью картографических объектов является нечеткость определения их свойств.

Применение процедуры генерализации при построении любой карты является второй особенностью, заставляющей применять нечеткие категории при решении задач в картографической среде. Эффекты генерализации все сильней ощущаются по мере уменьшения масштаба карты [1]. Потери качества информации неизбежны. Например, условности визуального представления делают невозможным проведение измерений ввиду утрирования формы объектов. Вполне естественным окажется ситуация, когда оценки взаимного расположения протяженных объектов, выполненные на топопланах масштаба 1:500 и картах масштаба 1:100000 будут существенно различаться. Полезным для расчетов могло бы быть знание точности, гарантируемое генерализацией на карте более мелкого масштаба, однако получить такую информацию от автора карты невозможно принципиально – генерализация субъективна и зависит от опыта и квалификации картографа [1].

Третьей особенностью, диктующей применение специфических (нечетких) операций при оптимизации, является необходимость применения адекватных расчетных соотношений для вычисления производных показателей от нечетких свойств объектов. Построение графовой модели для решения прикладной задачи требует абстрагирования. Пространственные объекты должны быть представлены точками или дугами, веса которых отображают существенно важные свойства объекта. Для задач размещения – одного из наиболее часто встречающегося класса задач [10] – непосредственное использование карты ГИС порождает неоднозначность. На рис. 1 приведен фрагмент плана, на котором решается задача наилучшего размещения оборудования, использующегося для текущего обслуживания железнодорожного пути.



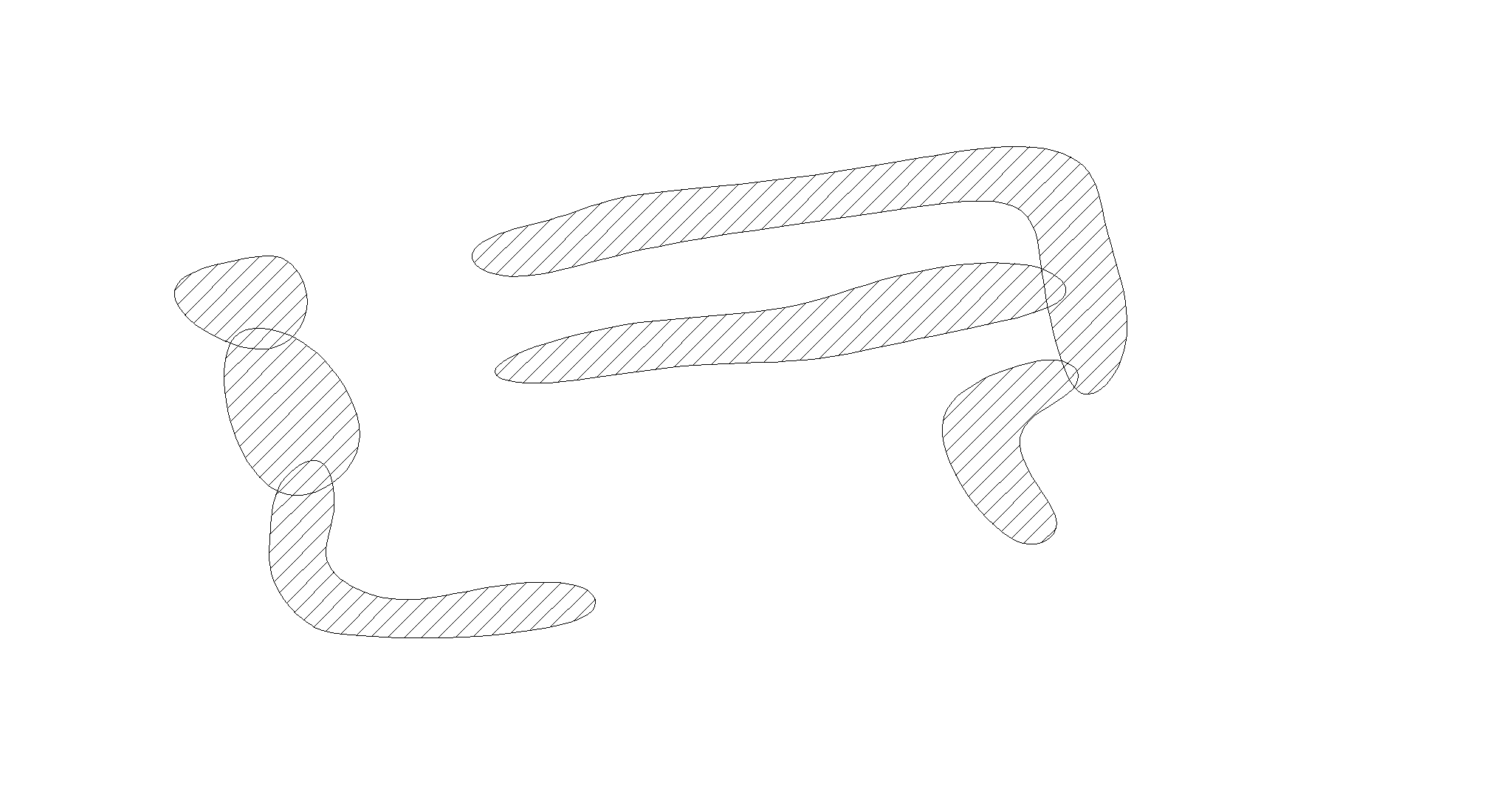
Рис. 1. Пример расположения зон технического обслуживания


Участки доступа к точкам технического обслуживания, показаны заштрихованными полигонами. Критерием качества размещения является минимум суммарного расстояния от места, в котором расположено оборудование, до точек технического обслуживания. В четкой постановке получение графа предполагает сопоставление каждому участку вершины и соединение вершин дугами, соответствующими наличию пути между участками. Попытка сопоставить дугам веса (расстояния между участками) требует ответа на вопрос – как его измерить? Очевидны проблемы:
  • расстояние между участками является непрерывной величиной. Для получения дискретного значения расстояния следует установить допущения о нахождении центроида полигона, влиянии на его размещение пересечения с соседними полигонами, и т.д.
  • границы участков на самом деле не имеют той четкой границы, которая показана экспертом на карте. Здесь упущены некоторые тонкие детали возможного размещения, о которых можно говорить в смысле возможности либо вероятности.

Получить четкую графовую модель (рис. 2) значит, игнорировать эти особенности и вести дальнейшую оптимизацию лишь усугубляя последствия упрощений применением соответствующих математических методов.



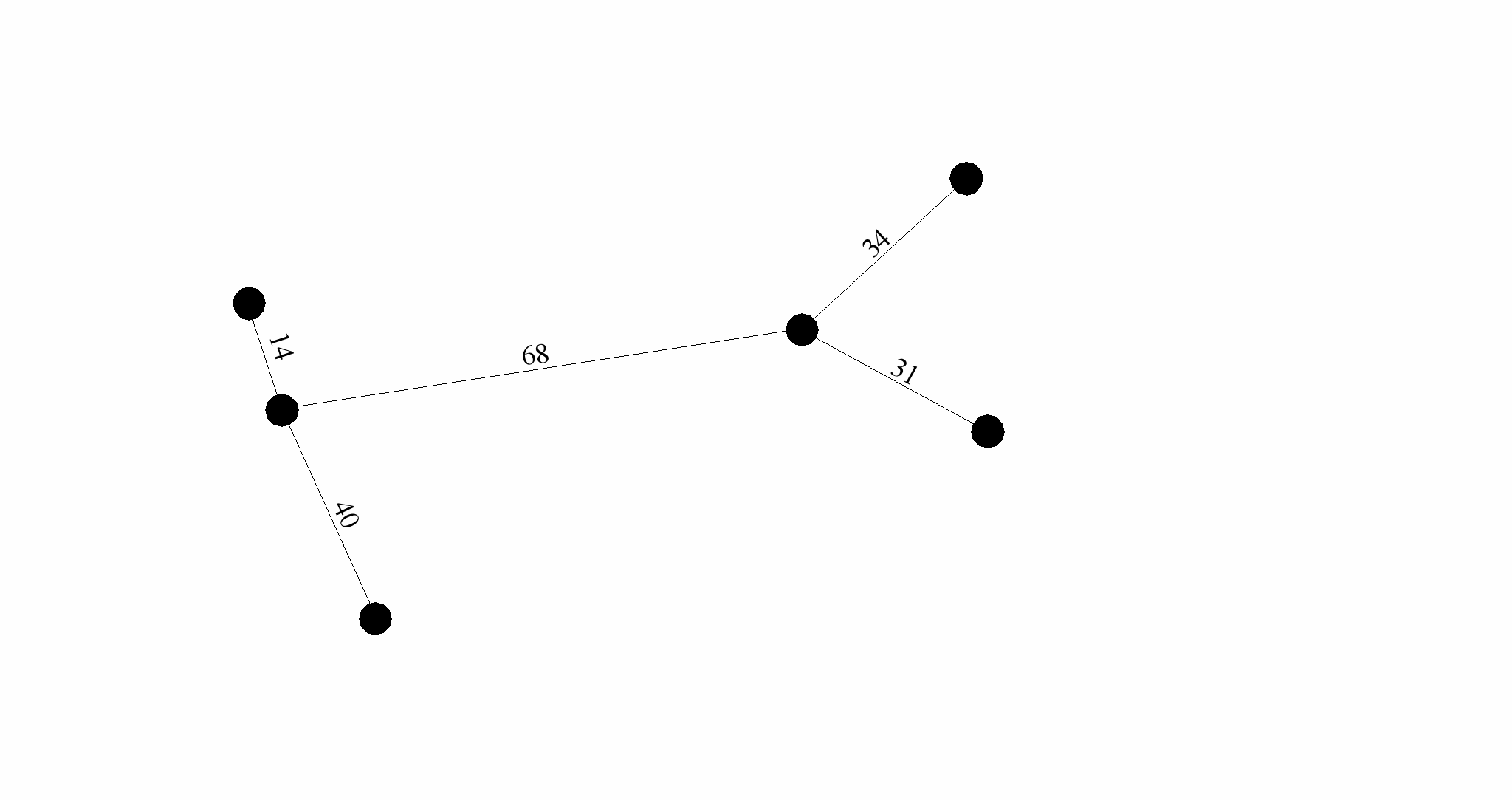
Рис. 2. Граф для задачи размещения


Топологические структуры данных ГИС (точечная, сетевая, полигональная) создаются для отображения отношений между картографическими объектами [3]. На сетевых топологиях решается ряд оптимизационных задач из теории графов: нахождение кратчайшего расстояния, определение степени связности, размещения медиан и т.д. Вместе с тем, как показывает анализ, результаты, полученные на топологиях, требуют дополнительной интерпретации, процедуры которой по сложности сравнимы со сложностью процедур поиска решения.



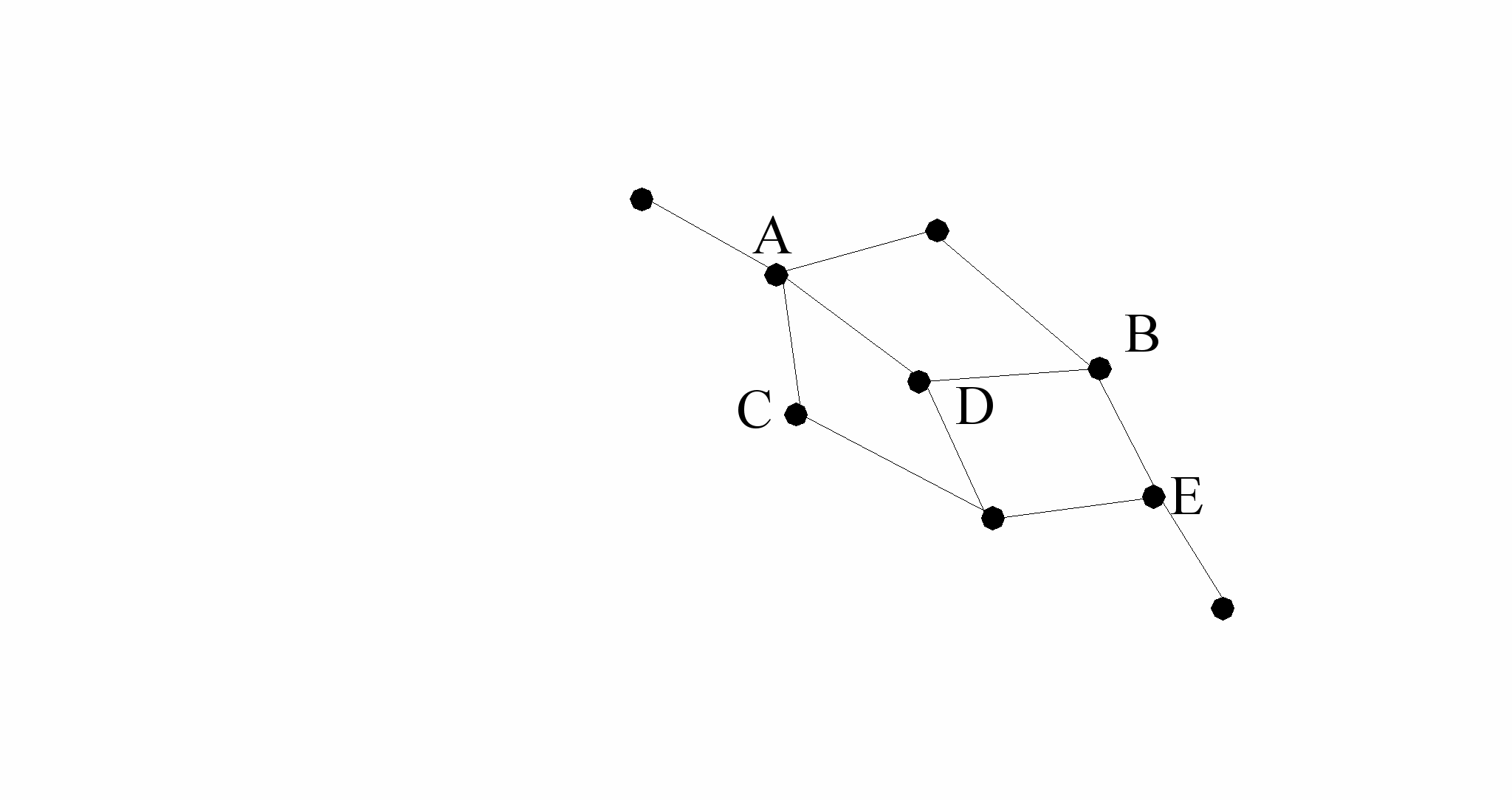
Рис. 3. Пример топологии железнодорожной сети


Например, имея сетевую топологию железнодорожной сети (рис. 3), анализ потоков между узлами А и Е нельзя проводить без учета текущего и прогнозируемого на ближайшее время технического состояния, экспертных оценок сезонного колебания интенсивностей потоков, опыта разрешения критических ситуаций и некоторых других факторов. Их значения обладают ограниченной достоверностью и актуальностью. На практике это приводит к тому, что из-за сложности связей и факторов можно лишь утверждать, что участок между узлами А и В по совокупности причин «на ближайшее время» обеспечит «невысокую пропускную способность» и его трафик «будет распределяться между» ветками АС и АД. Полученные точные (четкие) решения должны интерпретироваться дополнительно, что является четвертой особенностью решения задач на графах в среде ГИС.

Пятую особенность информационной основы ГИС, которая влияет на поиск оптимальных решений, следует связать с актуальностью хранимых данных. Не вызывает сомнений изменчивость внешнего мира и то, что эти изменения своевременно не могут быть отражены в базе данных ГИС. Фактор времени заставляет о многих объектах рассуждать в терминах нечеткости и это естественно для ГИС. Например, анализируя надежность участка железнодорожного пути, пользуются данными периодических осмотров. Учитывая ограниченное качество осмотров и возможные нарушения режимов эксплуатации, объективно оценить состояние пути в промежутках между осмотрами невозможно. Оценки вида «состояние пути хорошее», «состояние пути удовлетворительное», «состояние пути опасное», являются тем материалом, который реально может использоваться для оптимизации.

Таким образом, перечисленные особенности представления картографической информации в ГИС диктуют необходимость использования нечетких категорий в оптимизационных процедурах. Получить нечеткие данные можно различными путями [7]:

  1. фазификацией четких значений, измеренных на карте или считанных как внешние атрибуты объектов. Для этого ГИС должна хранить некоторые эталонные описания нечетких величин. На рис. 4 проиллюстрирован пример определения нечеткого значения высоты над уровнем моря в заданной точке между изолиниями.

Неопределенность в данном случае отображается зависимостью степени принадлежности (m) от нормированного расстояния (L*) между двумя соседними изогипсами:

L* = (Lmax-Lmin)/Lmax,

где Lmax – ближайшее расстояние от точки определения высоты до изогипсы с большим значением высоты, Lmin – с меньшим значением высоты. Множество {<m /Lmin>, <m /Lmax >} характеризует нечеткое значение высоты в указанной точке. Описание нечетких величин может храниться, например, в реляционной базе данных как совокупность отношений:

R0(ИмяКартографическогоОбраза, ВидНечеткойВеличины)

R1(ВидНечеткойВеличины,ВидОписания,СсылкаНаТаблицуЗначений)

R2(СсылкаИзR1,ЗначениеПараметра,ЗначениеФункцииПринадлежности,ЛингвистическоеЗначение).





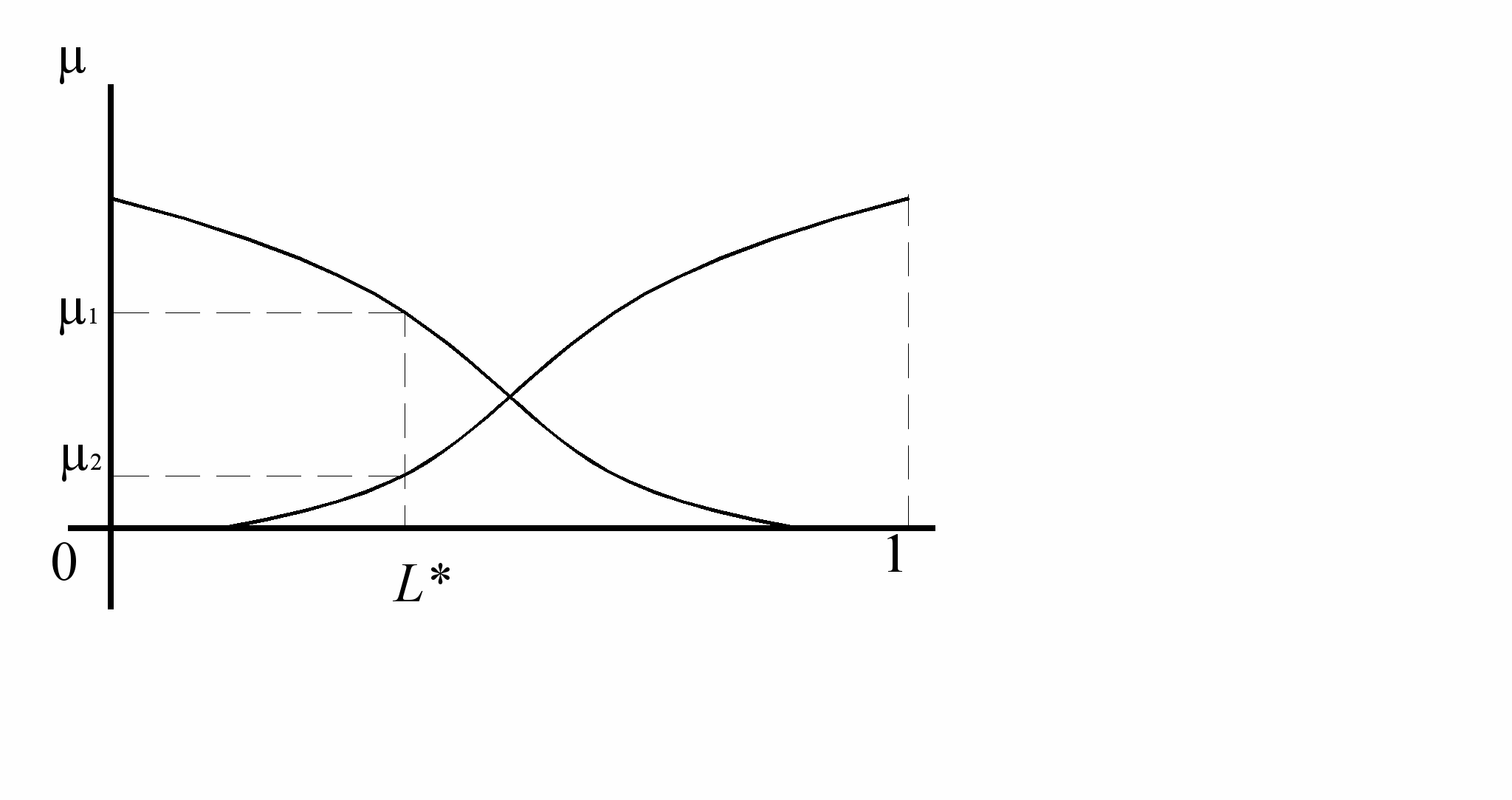
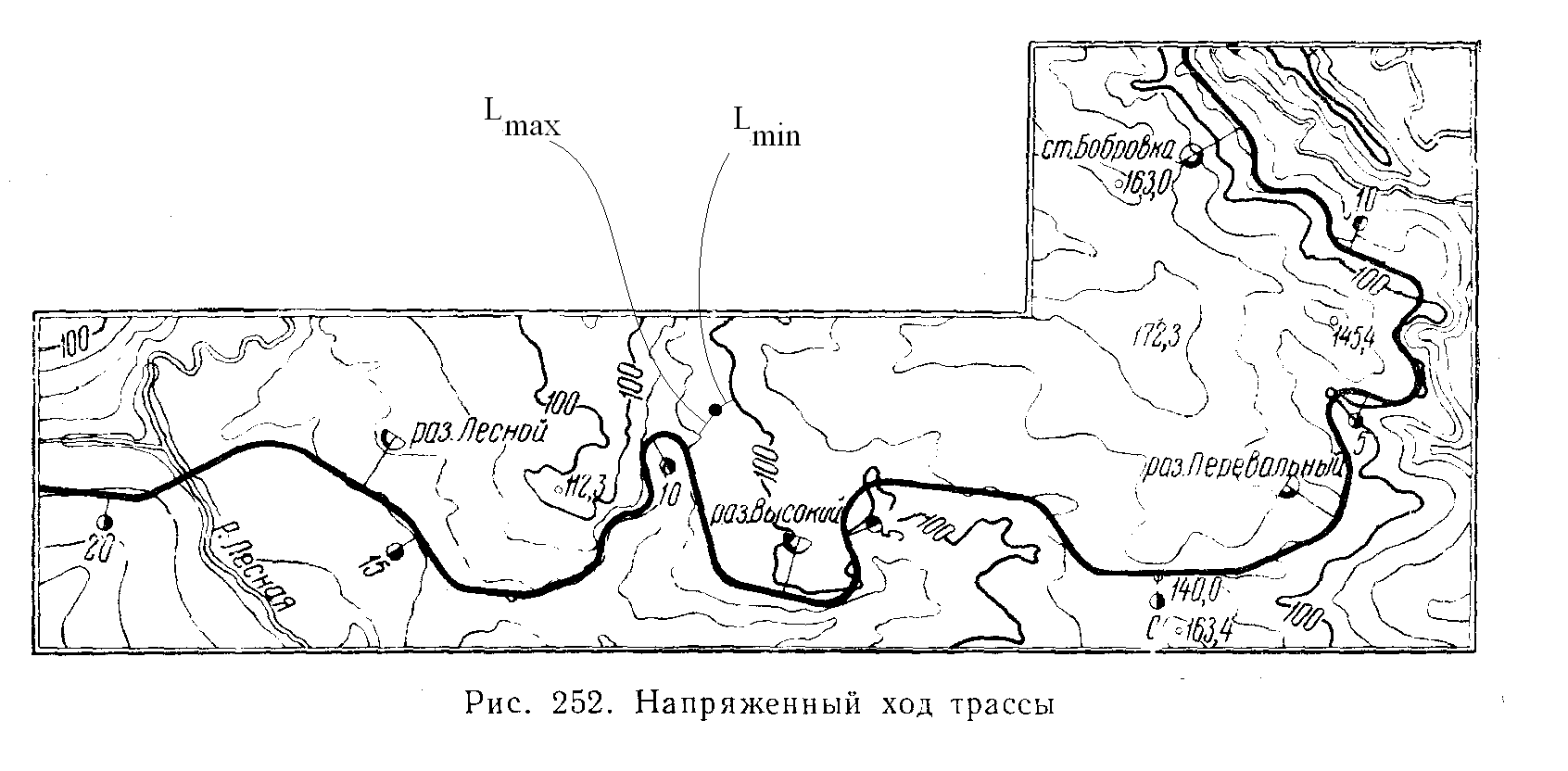
Рис. 4. К определению нечетких значений высоты


Отношение R0 связывает каждый картографический образ со специфическими нечеткими величинами, начиная с координат расположения и заканчивая атрибутивными данными. Отношение R1 определяет связь вида нечеткой величины со способом ее задания – алгоритмическим, табличным или некоторым промежуточным. С помощью отношения R3 получают лингвистические значения по известному четкому значению параметра. Использование подобной реляционной модели дает возможность получать, например, лингвистическое значение по заданной величине параметра SQL-запросом

SELECT R2.ЛингвистическоеЗначение FROM R0,R1,R2 WHERE R0.ИмяКартографическогоОбраза=’Наилучшее размещение участков’ AND R0.ВидНечеткойВеличины=’Площадь’ AND R0.ВидНечеткойВеличины= R1.ВидНечеткойВеличины AND R1.ВидОписания=’Табличный’ AND R1. СсылкаНаТаблицуЗначенийВR2=R2. СсылкаИзR1 AND R2. ЗначениеПараметра=15.52 AND R2. ЗначениеФункцииПринадлежности>0.7;
  1. явным хранением лингвистических значений, привязанных к объектам ГИС. Исследования в области баз данных должны привести к появлению стандартов на хранение и доступ к лингвистическим значениям [10, 11], но уже в настоящее время объектные СУБД предоставляют возможность хранения объектов с заданной схемой. Например, лингвистическая переменная «Расстояние между станциями» может быть описана как класс (на псевдокоде)

class DistanceBetweenStation

{ public:

//конструктор лингвистической переменной

DistanceBetweenStation();

//метод получения лингвистического значения по значению расстояния

GetLinvValue( double Distance, double MembershipRestriction);

//метод установки лингвистического значения по степени принадлежности

SetLinvValue(MembershipValue);

private:

//перечисление допустимых значений

enum LinvValue = {“очень малое”,”небольшое”,”среднее”,”больше среднего”,”большое”};

// вектор степени принадлежности

vector< double > MembershipValue;

// ассоциативный список лингвистических значений и степеней принадлежности

map< LingvValue , vector< double > > LingvVar;}

При конструировании лингвистической переменной класса DistanceBetweenStation описание степеней принадлежности должно быть введено пользователем класса. Очевидно, что эти величины будут зависеть от контекста использования и связаны с картографическим образом. Однажды созданная и сохраненная как объект, лингвистическая переменная затем может многократно использоваться при оптимизации размещения;
  1. из использовавшихся ранее графовых моделей, описание которых сохранено в ГИС на уровне информационного ресурса. Механизм геокодирования предоставляет возможность связывать пространственные координаты и объекты с конкретными экземплярами графовых моделей. Таким образом, повторным использованием уже формализованных нечетких сущностей можно сократить затраты на проведение оптимизации. Перспективным может стать применением экспертных систем, позволяющих новые модели строить по аналогии с существующими [12].

Литература

  1. Берлянт А.М. Образ пространства: карта и информация. – М.: Мысль, 1986.
  2. Бугаевский Л.М., Цветков В.Я. Геоинформационные системы. – М.: ″Златоус″, 2000.
  3. Майкл де Мерс Географические информационные системы. Основы/ Перевод с английского. – М.: Дата+, 1999.
  4. Максудова Л.Г., Савиных В.П., Цветков В.Я. Интеграция наук об окружающем мире в геоинформатике// Исследование Земли из космоса. – 2000. – №1. – С.40-45.
  5. Розенберг И.Н. Новые информационные технологии управления инфраструктурой железнодорожного транспорта// Труды восьмой научно-практической конференции «Информационные технологии в железнодорожном транспорте». «ИНФОТРАНС-2003» (Санкт-Петербург, 8-11 октября, 2003). – С.71-82.
  6. Розенберг И.Н., Духин С.В. Геоинформационные технологии – важнейшая составляющая современных информационных систем// Журнал «Автоматика, связь, информатика». –2005. – №7. – С.8-12.
  7. Дулин С.К., Розенберг И.Н. Концепция комбинированных картографических образов – основа снижения избыточности единой геоинформационной системы// Системы и средства информатики. Специальный выпуск «Геоинформационные технологии». – 2008. – С.175-203.
  8. Розенберг И.Н., Цветков В.Я., Матвеев С.И., Дулин С.К. Интегрированная система управления железной дорогой /под ред. В.И.Якунина. – М.: ИПЦ «Дизайн. Информация. Картография», 2008.
  9. Дулин С.К., Розенберг И.Н. Интеллектуальные информационные технологии согласованного сопровождения геоинформационного портала отрасли// Материалы 5-й Международной научно-практической конференции «Геопространственные технологии и сферы их применения». – М.: Информационное агентство «Гром», 2009. – С.35-38.
  10. Bershtein L.S., Bozhenyuk A.V., Rozenberg I.N. Definition of Optimum Allocation of the Service Centers// Proceedings of International Conference on Fuzzy Sets and Soft Computing in Economics and Finance. FSSCEF2004 (Saint-Petersburg, June 17-20). – 2004. –Vol.1. – P.283-290.
  11. Дулин С.К., Розенберг И.Н. Об одном подходе к структурной согласованности геоданных// Мир транспорта. – 2005. – № 3. – С.16-29.
  12. Дулин С.К., Розенберг И.Н. О развитии методологических основ и концепций геоинформатики// Системы и средства информатики. Специальный выпуск: «Научно – методологические проблемы информатики». – М.: ИПИ РАН, 2006. – С.201-256.