Тема: Система упражнений и задач основа реализации технологического подхода в обучении

Вид материала

Документы

Содержание 4.Задания для выполнения. Подготовительный этап. Этап непосредственного обучения понятию.

Подобный материал:

• Тема: «Интеграл» (заключительный урок), 49.41kb.
• Проблемные упражнения в обучении каменщиков, 240.16kb.
• Моу «Камызякская средняя общеобразовательная школа №4», 308.03kb.
• Математика. Пояснительная записка, 718.48kb.
• Урок-сказка по математике. Тема: Решение упражнений, 44.09kb.
• Омпетенция и компетентностный подход в образовании, сформулированы задачи реализации, 139.99kb.
• Личностно-ориентированный урок решения задач по теме, 160.57kb.
• Г. Г. Кравцов Принцип единства аффекта и интеллекта как основа личностного подхода, 227.3kb.
• Программа развития моу сош с. Красная Горка «Развитие личности школьников на основе, 786.75kb.
• Использование системно-деятельностного подхода в обучении химии, 194.1kb.

Разработчик: к.п.н., доцент каф. дидактики и частных методик Грекова С.В.

Практическое занятие №1(2 часа).

Тема: Система упражнений и задач – основа реализации технологического подхода в обучении.

Цель: рассмотреть частнометодические аспекты реализации технологического подхода в обучении математике через специальным образом разработанную систему упражнений и задач.

План:

1. Технологический подход к обучению в историческом аспекте.
   
2. Современная трактовка понятия «технология обучения».
   
3. Технология обучения и методика преподавания предмета.
   
4. Основные принципы реализации технологического подхода в обучении.
   

Задания для выполнения.

В социальную сферу термин «технология» пришёл из производственных процессов, где обозначал алгоритм создания того или иного изделия с заданными параметрами. С философской же точки зрения «технология» означает наилучшую деятельность любого вида в конкретных условиях. Педагогическая наука и методика вносит свои коррективы в толкование данного термина.

В отечественной методике термин «технология» является относительно новым. В зарубежном же преподавании он стал активно употребляться уже в 50-х гг. ХХ столетия, обозначая направление, которое ставило целью повышение эффективности учебного процесса и гарантию достижения учащимися запланированных результатов обучения. Приход «технологии» в педагогику и методику был связан, прежде всего, с желанием педагогов сделать процесс усвоения учащимися знаний управляемым.

Первой попыткой создания такой целостной методики, с помощью которой можно управлять процессом обучения и усвоения знаний учащимися, было возникновение в 70-х гг. прошлого века в США, а затем и в Западной Европе, программированного обучения как педагогического метода.

Программированное обучение получило широкое распространение и в нашей стране. Однако постепенно интерес к программированному обучению упал из-за невозможности решить с его помощью вопросы, связанные с различиями в способностях учащихся, в уровне их подготовленности, в сформированности учебных действий.

Современная педагогическая наука оперирует следующими понятиями: педагогическая технология, образовательная технология, технология обучения, частнопредметная технология, локальная технология, которые рассматриваются в рамках общего технологического подхода, заключающегося в построении и осуществлении оптимальной педагогической деятельности, результат которой должен максимально соответствовать поставленной цели.

Современное понимание этих терминов существенно отличается от соответсвующих терминов, употребляемых в прошлом веке в педагогической науке.

Обучение математике, имея свои характерные особенности, которые связаны со спецификой математического содержания, является частью общего процесса обучения, но и говоря о технологиях обучения математике, нельзя говорить об этом изолированно от построения всего процесса обучения в целом.

В общем виде требования к технологии обучения, и технологии обучения математике в частности, можно считать следующие:

1. В основе построения любой технологии обучения должны лежать результаты научных исследований, связанных с осуществлением процесса обучения конкретному предмету.

2. Любая технология должна представлять собой подробно описанную последовательность шагов.

3. Каждый шаг в последовательности обязательно сопровождается проведением диагностики, сравнения с предполагаемыми результатами и коррекции дальнейших мер.

4. Любая технология обучения должна предусматривать наличие обратной связи между учениками и учителем.

5. Любая технология обучения гарантирует достижение определённого для данной технологии результата.

6. Любая технология воспроизводима любым учителем в соответствующих условиях с гарантией достижения результата.

Самыми существенными отличиями технологии от методики являются требования гарантированности достижения результата и воспроизводимости её любым учителем с сохранением достигаемого результата.

В соответствии с этими требованиями выделяют критерии технологичности осуществляемого процесса обучении и процесса обучения математике в частности:

- диагностично заданная цель и способы диагностики её достижения;

- представление учебного материала в системы познавательных и практических задач с ориентирами и способами их решения;

- достаточно жёсткая логика этапов усвоения учебного материала;

- адекватная система способов взаимодействия на каждом этапе участников учебного процесса друг с другом и с информационной техникой;

- указание границ допустимого отступления от целесообразной и от свободной творческой деятельности учителя;

- применение в учебном процессе новейших средств и способов продоставления информации.

Отмечается, что наиболее важный этап при разработке любой технологии – это определение системы целей, которая должна быть диагностична. Для диагностируемости целей нужно осуществить переход от цели обучения, выраженной в общих терминах, к той цели обучения, достижение которой можно проверить. Заметим, что к целям, которые отражают развитие личности ребёнка в процессе обучения математике, нужно подходить очень осторожно. В этом случае, говорить о технологии, вероятно, уже нельзя.

Реализация технологического подхода в обучении требует от учителя качественно иной подготовки к проведению урока и к осуществлению всего процесса обучения учащихся математике. Учитель становится не только исполнителем разработанных локальных технологических сценариев обучения, но и сам может выступить в роли разработчика частнопредметных и локальных технологий. Такая роль учителя предполагает переосмысление всей его профессиональной деятельности и выхода её на качественно иной уровень - уровень профессиональной компетентности.

Важным в свете требований, предъявляемых к технологичности процесса обучения, является активизация следующих направлений саморазвития педагога как профессионала:

1. Усиление теоретической подготовки учителя математики в области педагогики и особенно психологии обучения математики.
   
2. Повышение алгоритмической культуры учителя математики.
   
3. Формирование методологической компетенции учителя математики в области целеполагания, организации, проведения и обработки результатов педагогического эксперимента.
   
4. Активизировать деятельность по обмену опытом между учителями математики.
   
5. Усилить конкретность деятельности учителя как с точки зрения организации процесса обучения математики, так и сточки зрения диагностируемости результатов этой деятельности.
   

В связи с чем, предлагаем подумать и обсудить следующие вопросы:

1. В чём вы видите существенные признаки реализации технологического подхода в обучении математике?

2. По каким признакам урока математики можно судить о применении на нём технологий обучения?

3. Какие технологии обучения Вы применяете сами? Какие испытываете трудности при этом? В чём видите пути их преодоления?

Задание: Изучить традиционные требования, которые предъявляются к системе упражнений и задач по математике, и выявить специфику этих требований в свете технологизации процесса обучения.

ЛИТЕРАТУРА:

1. Грудёнов Я.И. Психолого-дидактические основы методики обучения математике/ Я.И.Грудёнов.-М.:Педагогика, 1987.
   
2. Саранцев Г.И. Упражнения в обучении математике/Г.И.Саранцев.- М.:Просвещение, 1995.
   
3. Беспалько В.П. Педагогика и прогрессивные технологии обучения.-М.:Педагогика, 1995.
   
4. Селевко Г.К. Современные образовательные технологии.-М.: Народное образование, 1998.
   
5. Якиманская И.С. Технология личностно-ориентированного образования.-М.: Сентябрь,2000.
   
6. Методика и технология обучения математике. Курс лекций: пособие для вузов/ Под научн. Ред. Н.Л. Стефановой, Н.С. Подходовой. – М.:Дрофа, 2005.
   

Практическое занятие №2(2 часа).

Тема: Технологические схемы обучения элементам математического содержания.

Цель: рассмотреть частнометодические аспекты реализации технологического подхода в обучении математике через специальным образом разработанную систему упражнений и задач.

ПЛАН:

1.Структура содержания школьного курса математики.

2.Технологическая схема обучения основным элементам математического содержания (математическое понятие).

3.Технологическая схема обучения основным элементам математического содержания (математическое утверждение).

4.Задания для выполнения.

В содержании школьного курса математики можно выделить следующие элементы:

1) математические понятия;

2) математические утверждения;

3) законы, правила, алгоритмы.

Рассматривая проблему построения технологической схемы обучения тому или иному элементу математического содержания, нужно учитывать специфику математической науки: специфику содержания, особенности деятельности учащегося по его освоению, особенности возможностей учителя по организации этой деятельности.

На основе анализа соответствия между этапами процесса обучения и этапами освоения понятия выделяют следующие этапы реализации технологического подхода в обучении понятиям:

1. Подготовительный этап.
   

На этом этапе осуществляется методическая работа учителя в следующих направлениях:

- постановка целей;

- разработка системы диагностический задач и критериев оценки;

- отбор теоретического содержания;

- анализ отобранного теоретического содержания;

- разработка систем задач, которые целесообразно использовать на различных этапах работы с понятием;

- разработка системы диагностических задач, используемых на каждом этапе;

- выбор или разработка технологии реализации содержания;

- методическая обработка систем задач с учётом выбранной или разработанной технологии и уровня сформированности общеучебных и специальных умений учащихся.

2. Этап непосредственного обучения понятию.

3. Этап диагностики.

ПРИМЕР: технология введения понятия параллелограмм

(для класса среднего уровня не только математической подготовки, но и сформированности общеучебных и специальных умений и навыков; при этом есть учащиеся, уровень знаний которых выше среднего, проявляющие интерес к математике).

«Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны». (Л.С.Атанасян и др. Геометрия 7-9.-М.:Просвещение, 1990.)

На подготовительном этапе проводится отбор теоретического содержания. Выделяются актуализируемые теоретические знания, вводимые теоретические знания. Определяется возможность пропедевтики. Поводится анализ отобранного теоретического содержания: устанавливается вид определения, его структура, родословная. Определяется система задач, которую целесообразно использовать на этапе актуализации знаний, и варианты работы с ней. Затем осуществляется выбор или разработка технологии реализации содержания.

Цель работы: ввести новое понятие параллелограмма (сформулировать без предварительной подготовки), закрепить его, показать применение вновь введённого понятия при решении простейших задач.

На этапе обучения понятию необходимо:

1. сформулировать тему и цели урока;
   
2. предложить прочитать по учебнику определение параллелограмма;
   
3. выделить в определении определяемое понятие, родовое понятие, видовые отличия;
   
4. обсудить ответ на вопрос: «Является ли параллелограмм выпуклым четырёхугольником?»;
   
5. Решить задачу: «Доказать, что если в четырёхугольнике АВСД угол ВСА равен углу САД, а угол ВАС равен углу АСД, то он является параллелограммом» (при работе с этой задачей: предложить выдвинуть гипотезу - затем прочитать готовое доказательство этого утверждения, например, в учебнике);
   
6. Решить задачу: «Существование каких свойств параллелограмма можно предположить?» (при работе с этой задачей: по рисунку сформулировать условие и требование задачи - выделить в определении свойство параллелограмма - подумать, чем можно воспользоваться при доказательстве параллельности противоположных сторон четырёхугольника – самостоятельно вспомнить известные свойства параллельных прямых, соотнести каждый с условием задачи с целью установления возможности или невозможности его использования, продумать вариант доказательства – провести доказательство).
   
7. Решить задачу: «Даны три точки А,В и С, являющиеся вершинами параллелограмма. Построить этот параллелограмм. Определить, сколько решений имеет задача» ( при работе с этой задачей: выбрать инструменты, которыми можно пользоваться при построении параллелограмма – выполнить построение (один ученик работает у доски)).
   

Технологии обучения понятиям, определение которых сформулированы в другом виде, разрабатываются аналогично.

При разработке технологических схем работы с математическими утверждениями большое внимание должно уделяться мотивационному компоненту, а также поиску доказательства и обоснованности получаемых в процессе доказательства выводов.

При работе с алгоритмами можно выделить следующие основные этапы работы учителя по разработке технологической схемы его изучения и усвоения:

1. подготовительный этап; 2) этап обучения алгоритму; 3) этап диагностики.
   

Задание 1: Разработайте и реализуйте технологические схемы обучения различным элементам школьного курса математики (математическим понятиям, теоремам, законам, правилам, алгоритмам).

ПРИМЕР: Исследовательский проект как форма реализации технологического подхода к обучению

математике.

Главная цель данной технологии исследовательского обучения – активизировать обучение, придав ему исследовательский, творческий характер, передать инициативу учащимся в познавательной деятельности. Самостоятельная исследовательская работа учащихся является важнейшим фактором развития творческих способностей. «В исследовательском методе знание не дается как готовое, а получается в результате работы самих детей над тем или иным жизненным материалом» (Б.В.Всесвятский). Известный специалист в области исследовательского обучения Дж. Брунер подчеркивал: «Умственная деятельность ученого, сделавшего эпохальное открытие, и умственная деятельность ребенка, познающего новое, идентичны по своей внутренней «механике»».

В педагогике выделяется три уровня реализации исследовательского обучения:

• преподаватель ставит проблему и намечает стратегию и тактику ее решения, само решение предстоит самостоятельно найти учащемуся;
  
• преподаватель ставит проблему, но метод ее решения ученик ищет самостоятельно (допускается коллективный поиск);
  
• постановка проблемы, поиск методов ее исследования и разработка решения осуществляется учащимися самостоятельно.
  

Рассмотрим одну из наиболее актуальных технологий обучения, применяющихся на уроке математике – исследовательский проект.

Исследовательские проекты, выполняемые самими учащимися, могут различаться по продукту деятельности:

1. проект – получение новых знаний о некотором объекте;
   
2. проект – обобщение и систематизация уже имеющихся знаний;
   
3. проект – открытие новых понятий;
   
4. проект – открытие новых теорем.
   

Исследовательский проект может быть разработан учителем математики по следующей схеме:

- цель проекта (формулирование вопроса исследования);

- объект и предмет исследования;

- оборудование;

- план исследования (наблюдений, эксперимента);

- план обсуждения результатов исследования;

- формулирование вывода;

- презентация итогов проекта.

«Исследовательский проект «Взаимно простые числа».

Цель - сформулировать и усвоить понятие взаимно простых чисел.

Объект исследования: натуральные числа.

Предмет исследования: пары натуральных чисел и их НОД.

Оборудование: учитель заранее готовит для учащихся карточки, на которых заданы пары натуральных чисел. Среди них есть пары чисел, имеющие НОД, равный 1.

План исследования: учитель предлагает учащимся найти НОД каждой пары чисел.

План обсуждения результатов исследования: учитель предлагает учащимся, после проверки нахождения всех НОД ответить на следующие вопросы:

* на какие две группы можно разбить все пары чисел в зависимости от величины НОД этих чисел?

* чему равен НОД чисел в каждой группе?

* какая группа имеет НОД равный для всех пар чисел?

* чему он равен?

Формулирование вывода: учитель говорит, что такие пары чисел называют взаимно простыми и просит учащихся самостоятельно сформулировать определение этих пар чисел (при необходимости учитель корректирует определение учащихся).

Презентация итогов проекта: можно вывесить плакат с определением взаимно простых чисел или предложить учащимся самим изобразить в виде схемы или таблицы сущность определения взаимно простых чисел.»

Задание 2: Разработайте какую-либо локальную технологию обучения, применимую на уроке математики.

ЛИТЕРАТУРА:

1. Волович М.Б. Ключ к пониманию алгебры.-М.:Аквариум,1996.
   
2. Волович М.Б. Ключ к пониманию геометрии.-М.:Аквариум,1996.
   
3. Лабораторные и практические работы по методике преподавания математики/Под ред. Е.И.Лященко.-М.: Просвещение, 1988.
   
4. Селевко Г.К. Педагогика и прогрессивные технологии обучения.-М.:Народное образование, 1995.
   

Практическое занятие №3(2 часа).

Тема: Логико-математический анализ определения математического понятия.

Цель: актуализация знаний по логико-математическому анализу определений математических понятий.

ПЛАН:

1. Процесс формирования понятия.
   
2. Конъюнктивная структура определения понятия.
   
3. Дизъюнктивная структура определения понятия.
   
4. Методические рекомендации по работе с понятием на уроке математики.
   
5. Задания для выполнения.
   

Формирование понятий – сложный психологический процесс, нередко начинающийся с образования простейших форм познания – ощущений, и протекающий по следующей схеме: ощущения – восприятие – представление - понятие. Чувственная ступень в процессе формирования понятия соответствует первому этапу пути познания, то есть «живому созерцанию». Поэтому осуществление этой ступени требует применение средств наглядности. Так формируются первые математические понятия. С развитием науки образование новых понятий может идти и другим путём. Они могут формироваться на базе уже существующих, процесс их формирования может далеко уходить за пределы известных данных, являться результатом их активной творческой переработки, обусловленной исторической практикой, в том числе и практикой научной деятельности. В связи с чем, обычно, различают две ступени процесса формирования понятия: чувственную - состоящую в образовании ощущений, восприятий и представлений, и логическую – заключающуюся в переходе от представления к понятию с помощью обобщения и абстрагирования.

Ключевым моментом в процессе формирования понятия является его определение. Определение понятия – условное соглашение, разумно выбираемое, исходя из реальных свойств того или иного понятия, или в соответствии с теми или иными требованиями процесса обучения. В связи с чем нужно, чтобы учащиеся понимали, что никакие определения не доказываются. Особенно часто желание доказать то или иное определение возникает у учащихся по отношению к определениям, принятым по соглашению.

Перед введением определения математического понятия на уроке математики учитель должен проделать большую подготовительную работу теоретического характера: выяснить вид определения математического понятия (родо-видовое, генетическое, по соглашению и т.д.), его логическую структуру, построить по необходимости родословную понятия.

Под логической структурой определения, построенного по схеме: A(x)  B(x), понимают структуру его правой части, т.е. предложения «В». В школьной математике встречаются определения различной структуры, порой довольно сложной, и, чем сложнее структура определения, тем более тщательной должна быть работа по его разъяснению, по предупреждению его формального усвоения.

Одна из наиболее распространённых структур определений – конъюнктивная структура, имеющая вид: xA  P₁(x) и P₂(x) и ... и P_n(x).

Выявленная таким образом конъюнктивная структура определения во многом задаёт методику работы с этим определением на уроке математики. Учитель здесь должен подчеркнуть перед учащимися, что данный объект x будет принадлежать классу А, если он обладает всеми свойствами P₁ и P₂ и ... и P_n, и не принадлежит этому классу, если не обладает хотя бы одним из этих свойств.

Для распознавания математических понятий, имеющих конъюнктивную структуру, для их усвоения и для проведения закрепления таких понятий в сознании учащихся полезно разработать соответствующую систему упражнений. На этом этапе каждое существенное свойство, используемое в определении понятия, делается специальным объектом усвоения.

При формировании геометрических понятий удобно для упражнений на распознавание объектов, принадлежащих изучаемому понятию, использовать готовые рисунки. При этом учащиеся усваивают и такие действия, как вычленение на рисунках объектов, принадлежащих данному понятию, рассмотрение объектов с точки зрения других понятий.

Встречаются определения и дизъюнктивной структуры, имеющие вид: xA  P₁(x) или P₂(x) или ... или P_n(x).

В этом случае в процессе обучения нужно подчеркнуть, что данный объект принадлежит классу А, если он обладает хотя бы одним из свойств P₁, P₂, ... P_n, и не принадлежит этому классу, если не обладает ни одним из этих свойств.

Для определения дизъюнктивной структуры полезно провести работу, аналогичную как и для определения, имеющего конъюнктивную структуру, т.е. выделить его логическую структуру, состав существенных свойств, входящих в определение и составить соответствующую систему упражнений для распознавания понятия, для закрепления этого понятия в сознании учащихся.

После проведённой таким образом работы, можно приступать к разработке методики введения данного понятия на уроке математики через его определение.

В зависимости от места расположения формулировки определения в процессе введения понятия в методике преподавания математики выделяют конкретно-индуктивный и абстрактно-дедуктивный методы.

При конкретно-индуктивном методе введения понятия само определение понятия появляется в конце рассуждений. Учитель вместе с учащимися начинает с рассмотрения конкретных примеров и путём мыслительных операций приводит учащихся к образованию нового понятия. При умелом, продуманном проведении этого процесса учащиеся почти всегда сами способны сформулировать определение нового понятия. В случае надобности определение может быть откорректировано до правильной логической формы учителем.

При введении понятия конкретно-индуктивным методом обычно придерживаются следующей схемы:

1. отыскание ярких практических примеров, показывающих целесообразность изучения этого понятия;
   
2. выявление различных существенных и несущественных признаков данного понятия;
   
3. введение термина, обозначающее это понятие;
   
4. рассмотрение, если имеются, особых случаев;
   
5. мотивация термина, обозначающее данное понятие;
   
6. отбор существенных свойств данного понятия и первичная формулировка определения этого понятия;
   
7. внесение поправок; вторичное определение; коррекция определения; чёткое формулирование определения; повторение определения;
   
8. иллюстрация понятия конкретными примерами; демонстрация моделей понятия; контрпримеры; символическое обозначение.
   

При абстрактно-дедуктивном введении понятия определение понятия сообщается учащимся сразу, без особой предварительной подготовки. Этот метод введения понятия применяется тогда, когда новое понятие полностью подготовлено изучением предыдущих понятий, органически связано с уже известными учащимся понятиями или тогда, когда объективно сложно организовать процесс выделения существенных свойств у рассматриваемых объектов.

При абстрактно-дедуктивном методе введения понятия придерживаются обычно следующей схемы:

1. дать определение нового понятия, мотивируя обозначающий его термин;
   
2. рассмотреть частные (особые) случаи выражения этого понятия;
   
3. привести некоторые контрпримеры этого понятия;
   
4. проиллюстрировать введённое понятие конкретными примерами, всякий раз проверяя, удовлетворяет ли каждый из конкретных примеров вводимому определению,
   
5. привести конкретные примеры приложений этого понятия в других научных областях.
   

При разработке того или иного метода введения понятия на уроке математики нужно учитывать объективно меняющиеся условия обучения учащихся и динамично сокращать или дополнять приведённые выше схемы с целью повысить эффективность обучения математике учащихся.

Выбор учителем математики метода введения математического понятия на уроке может быть обычно обусловлен следующими факторами: степенью абстракции самого понятия, психолого-физиологическими возрастными особенностями учащихся, включая и уровень их математической подготовки. На выбор метода введения некоторых математических понятий на уроке математики могут повлиять и исторические процессы развития математической науки.

При введении математического понятия на уроке математики любым методом нельзя забывать о мотивации его введения. Сущность мотивации заключается в подчёркивании важности изучаемого понятия, в побуждении школьников к целенаправленной и активной деятельности, в возбуждении интереса к изучению рассматриваемых понятий. Одним из средств мотивации является выполнение упражнений практического, физического, биологического, химического и т.д. характера.

Мотивация введения понятия может быть осуществлена не только посредством упражнений, что, кстати, не всегда удаётся. Она может быть обусловлена и чисто теоретическими потребностями самой математики.

Также большую помощь в разработке методики введения определения понятия на уроке математики может оказать родословная понятия – логическое «дерево» происхождения понятия, если при классификации делят объём самого понятия и идут от подчиняющего понятия (родового) к подчинённым (видовым), то есть к более узким понятиям ( в направлении ограничения их объёма), то при составлении «родословной» идут в противоположном направлении – расширении объёма понятия. При этом интересует не объём понятия, а его определение, то есть через какие понятия (родовое и упоминающиеся в видовых признаках) выражается данное понятие.

Чёткость понятий и их отношений – один из признаков высокого уровня научности учебного предмета. Математические понятия в этом отношении являются лучшими образцами и представляют прекрасный материал для отработки основных методологических умений. При работе с математическими понятиями учитель должен помнить, что целью качественного математического образования учащихся является формирование в их сознании не отдельных математических понятий, а системы понятий.

Задание:

выбрать из школьного курса математики какие-либо математические понятия и провести их логико-математический анализ, включающий классификацию понятия и его родословную.

ЛИТЕРАТУРА:

1. Столяр А.А. Педагогика математики /А.А.Столяр. – Минск, Издательство «Вышейшая школа»,1968.
   
2. Фридман Л.М. Теоретические основы методики обучения математике: Уебное пособие. Изд. 2-е, испр. и доп./Л.М.Фридман. – М.: Едиториал УРСС, 2005.
   
3. Лабораторные и практические работы по методике преподавания математики/Под ред. Е.И.Лященко.-М.: Просвещение, 1988.
   

Практическое занятие №4(2 часа).

Тема: Логико-математический анализ теоремы.

Цель: актуализация знаний по логико-математическому анализу теоремы.

ПЛАН:

1. Логическая структура теоремы.
   
2. Примеры теорем и их логико-математический анализ.
   
3. Задания для выполнения.
   

Теоретической основой логической грамотности учителя математики является математическая логика. С точки зрения математической логики теорема является высказыванием следующего вида: хМ, А(х)В(х), где М – некоторое множество элементов, относительно которых сформулирована теорема. В самом общем виде практически любая теорема носит, говорят, импликативную структуру. В связи с чем, во многих учебных пособиях по методике преподавания математики структуру теоремы указывают в виде: АВ.

Заметно, что в этом случае упущен один из принципиально важных для понимания сути теоремы компонентов её логической структуры – множество М, называемое разъяснительной частью теоремы. Именно введение в структуру теоремы этого множества позволяет проследить путь её образования.

Изначально рассматриваются некоторые элементы множества М, про которые замечается наличие у них некоторого свойства А, при чём, если рассматривать все объекты множества М, то зафиксированным свойством А объект может как обладать, так и не обладать. В связи с чем, можно говорить о задании на множестве М предиката А(х).

ПРИМЕР. Рассмотрим множество всех треугольников. Некоторые из ни имеют только две равные стороны. Такие треугольники в геометрии имеют особое название – равнобедренные треугольники. Таким образом, можно говорить о предикате А(х): «треугольник х – равнобедренный», где х – элемент множества всех треугольников.

Аналогично замечается, что некоторые из элементов множества М обладают свойством В, тогда можно говорить о предикате, заданном на множестве М – В(х).

Вообще говоря, отношения между множеством элементов, обладающих свойством А, и множеством элементов, обладающих свойством В, может быть различно. Принципиально важными являются случаи, когда эти множества не имеют общих элементов, и, когда они совпадают. В первом случае, правда, можно констатировать, что данные множества не пересекаются, а, следовательно, и сочетание свойств А и В в одном объекте х множества М – невозможно. Во втором случае, например, замечается, что как только элемент множества М стал обладать свойством А, так он сразу же стал обладать и свойством В. Этот факт, как правило и фиксируется в теореме.

ПРИМЕР. Было замечено, что как только треугольник стал обладать двумя равными сторонами, так в нем сразу же всегда найдутся два равных угла, прилегающих к этим сторонам. Этот факт и фиксируется в теореме: «В равнобедренном треугольнике два угла при основании равны», акцентируя внимание на том, что такое происходит со всяким равнобедренным треугольником.

Таким образом, отбрасывание в логической структуре теоремы её разъяснительной части мы лишаем, так сказать, теорему истории. Не даём возможности ни учителю, а тем более ученику глубже понять её и изучить.

Однако, выделение этой разъяснительной части по уже имеющейся формулировке теоремы порой представляет непростую задачу даже для опытного учителя. Рассмотрим несколько примеров.

ТЕОРЕМА 1: «В равнобедренном треугольнике углы при основании равны».

Студенты часто допускают ошибку и говорят, что разъяснительной частью этой теоремы является множество равнобедренных треугольников. В этом случае происходит смешение в объекте его родовидовых отличий. Разъяснительной частью этой теоремы является множество произвольных треугольников. Теорема трактуется так: как только в треугольнике нашлись две равные стороны, так в нём сразу же обнаружатся и два равных угла.

ТЕОРЕМА 2:

«Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине».

Разъяснительной частью этой теоремы является множество отрезков. Однако такой ответ нарушает существующее общее правило, принятое в теории методики преподавания математики при переходе от рода объекта к его виду. Имеется в виду договорённость о том, что от рода объекта, например, при классификации какого-либо математического понятия, переходить к ближайшему его виду; и, наоборот, от вида, например, при формулировании родовидового определения понятия, переходить к ближайшему роду. В нашем же случае, множество произвольных отрезков как род не является ближайшим к множеству средних линий отрезка как вид. Правильный ответ подсказывает формулировка теоремы. Разъяснительной частью здесь является множество отрезков с концами на двух данных сторонах треугольника. Теорему можно трактовать так: как только отрезок, с концами на двух данных сторонах треугольника стал его средней линией, так он сразу же стал параллелен третьей стороне и равен её половине.

В этих теоремах разъяснительная часть состояла из моносоставных элементов: множество треугольников, множество отрезков. При этом структура самого объекта во внимание не принималась. К тому же можно заметить, и даже особо подчеркнуть, что предикаты А(х) и В(х) являются заданными на одном и том же множестве М. Например, для теоремы об углах в равнобедренном треугольнике предикаты: А(х): « треугольник х – равнобедренный», В(х): «треугольник х – имеет два равных угла»

заданы на одном и том же множестве М – множестве произвольных треугольников. С этой точки зрения, формулировка теоремы говорит о том, что, если предикат А(х) принял значение «истинно» для некоторого треугольника, то для этого же треугольника предикат В(х) так же примет значение «истинно». И этот факт будет иметь место для любого треугольника.

Теорема 3: «Если внутренние накрест лежащие углы равны, то прямые параллельны» (Погорелов А.В. Геометрия: Учебное пособие 7-11классов сред. шк. -М.:Просвещение, 1990.)

Для выяснения разъяснительной части этой теоремы нужно вспомнить условия образования накрест лежащих углов: берутся две прямые (a и b) и пересекаются третьей прямой (с), называемой секущей (рис.1).




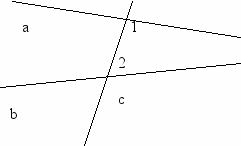
Углы, например, 1 и 2 будут внутренними накрест лежащими. Формулировка теоремы и её разъяснительная часть при первом рассмотрении вызывает недоумение: в условии теоремы говориться об углах, в заключении - о прямых. Возникает вопрос: неужели возможно, что предикат-условие теоремы задаётся на одном множестве, а предикат-заключение – на другом. Конечно, нет. Всё становится ясным, если допустить, что множество М может состоять из элементов различной структуры, в том числе и такой, как в этой теореме. Разъяснительная часть этой теоремы состоит из конструкций, в состав которых входят две прямые и пересекающая их третья прямая, а также внутренние накрест лежащие углы, расположенные при точках пересечений этих прямых. Обозначим прямые, которые пересекаются третьей прямой, х и y, а внутренние накрест лежащие углы за 1 и 2. Таким образом, можно говорить, что множество М состоит из элементов вида (х, y, 1, 2). То есть является элементом некоторого 4-х мерного пространства. В этом случае теорема трактуется так: как только в этой конструкции прямых и углов, углы стали равными, так сразу же в той же самой конструкции прямые стали параллельны. И так выполняется для любых прямых и углов в данной конструкции. Предикаты А(х) и В(х) в этом случае могут быть заданы следующим образом: А(х, у, 1, 2): «углы 1 и 2 равны», В(х, у, 1, ): «прямые х и у параллельны».

С этой точки зрения более удачной можно признать формулировку соответствующей теоремы в учебнике геометрии Л.С.Атанасяна (Геометрия: Учеб. Для 7-9 кл. общеобразоват. учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.-5-е изд.-М.:Просвещение,1995.): «Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны», которая более раскрывает смысл факта, сформулированного в теореме.

Знание разъяснительной части теоремы заметно облегчает формулирование теоремы, обратной к данной. Классической ошибкой при формулировании теоремы, обратной к теореме о свойстве равнобедренного треугольника является формулировка: «Если углы в треугольнике при основании равны, то такой треугольник равнобедренный». Часто забывают о том, что множество объектов, относительно которых сформулирована теорема одно и то же и для предиката-условия, и для предиката-заключения. И в процессе истории возникновения формулировке теоремы, обратной к данной, так же как и в прямой теореме, рассматриваются, вообще говоря, произвольные треугольники, у которых не выделено основание. Основание в треугольнике рассматривается только у равнобедренных. Следовательно, говорить об углах при основании произвольного треугольника, вообще говоря, некорректно. Учитывая содержательный аспект формулирования обратной теоремы к теореме о свойстве равнобедренного треугольника, и общее строение теоремы ВА, обратной к данной АВ, получим следующую формулировку: если в треугольнике найдутся два равных угла, то этот треугольник будет равнобедренным, а прилегающие к этим углам стороны – равными; или «если в треугольнике какие - либо два угла равны, то треугольник равнобедренный».

Задание: выберите из школьного курса математики какие-либо теоремы и проведите их логико-математический анализ.

ЛИТЕРАТУРА:

1. Фридан Л.М.Теоретические основы методики обучения математике: Учебное пособие. Изд.2-е, исп. И доп.-М.:Едиториал УРСС, 2005.
   
2. Хинчин А.Я. Педагогические статьи.-М: 1963.
   
3. Столяр А.А. Педагогика математики /А.А.Столяр. – Минск, Издательство «Вышейшая школа»,1968
   
4. Лабораторные и практические работы по методике преподавания математики/Под ред. Е.И.Лященко.-М.: Просвещение, 1988.