Тема Средние величины

Вид материала

Документы

Содержание 3.2. Cреднее гармоническое 3.3. Среднее геометрическое 3.5. Свойства среднего арифметического 3.6. Мода и медиана ряда распределения Вклады, грн Процент высо Тема 4. Показатели вариации и формы распределения Пример 4.1. Рост 6 игроков баскетбольной команды определяется выборкой (в см) Согласно (3.1) и (4.3) получим 4.2. Среднеквадратическое отклонение (СКО) Число установок 4.4. Показатели формы распределения Коэффициент асимметрии Коэффициент эксцесса – Число семей Номинал, грн Число акций Контрольные вопросы

Подобный материал:

• Тема: Абсолютные, относительные и средние величины, 185.25kb.
• Понятие статистики и краткие сведения из ее истории, 29.13kb.
• И отн сред величины, сравнение, группировки, церные подстановки, баланс), матем (сравнение,, 288.04kb.
• План: Характеристика основных видов относительной величины. Требования к статическому, 91.5kb.
• Вопросы для самоконтроля знаний студентов по дисциплине «Комплексный экономический, 39.33kb.
• Линейная регрессия и метод наименьших квадратов, 177.63kb.
• Программа обсуждена на заседании кафедры Математики фнти, 75.2kb.
• 1 Оплата труда в бюджетном секторе, 3504.84kb.
• Бухгалтерский отчёт План счетов Первичный документ Вкачестве регистраторов могут выступать, 109.43kb.
• В реализации данного проекта принимают участие все средние школы и профессиональные, 229.41kb.

Тема 3. Средние величины


Наиболее распространенными и информативными статистическими показателями являются средние величины. Как правило, первым результа-том обработки статистических данных является вычисление среднего значения изучаемой совокупности. Зная средний процент работоспособного населения, можно правильно планировать и распоряжаться трудовыми ресу-рсами. Средняя стоимость жилья позволяет оценивать возможные прибыли жилого строительства, а ввода и эксплуатации цифрового сотового телефона – прибыли телефонной компании. Чтобы рассчитать кубатуру большого лес-ного массива, не надо пересчитывать все деревья, достаточно знать среднюю плотность и площадь леса.

При вычислении средних величин не следует забывать, что изучаемая выборочная совокупность наблюдения должна быть репрезентативной и однородной. Хороший пример нарушения одного из условий: усредняя состояния одного миллиардера и тысячи нищих, заключаем, что в среднем все миллионеры.

В общей теории статистики принято рассматривать различные типы усреднения, приводящие к средним арифметическим, гармоническим, геометрическим, квадратичным величинам.


3.1. Среднее арифметическое


Д
ля выборочной совокупности {x_i}⁽ⁿ⁾={x₁,x₂,x₃,…,x_n} среднее ариф-метическое определяется как




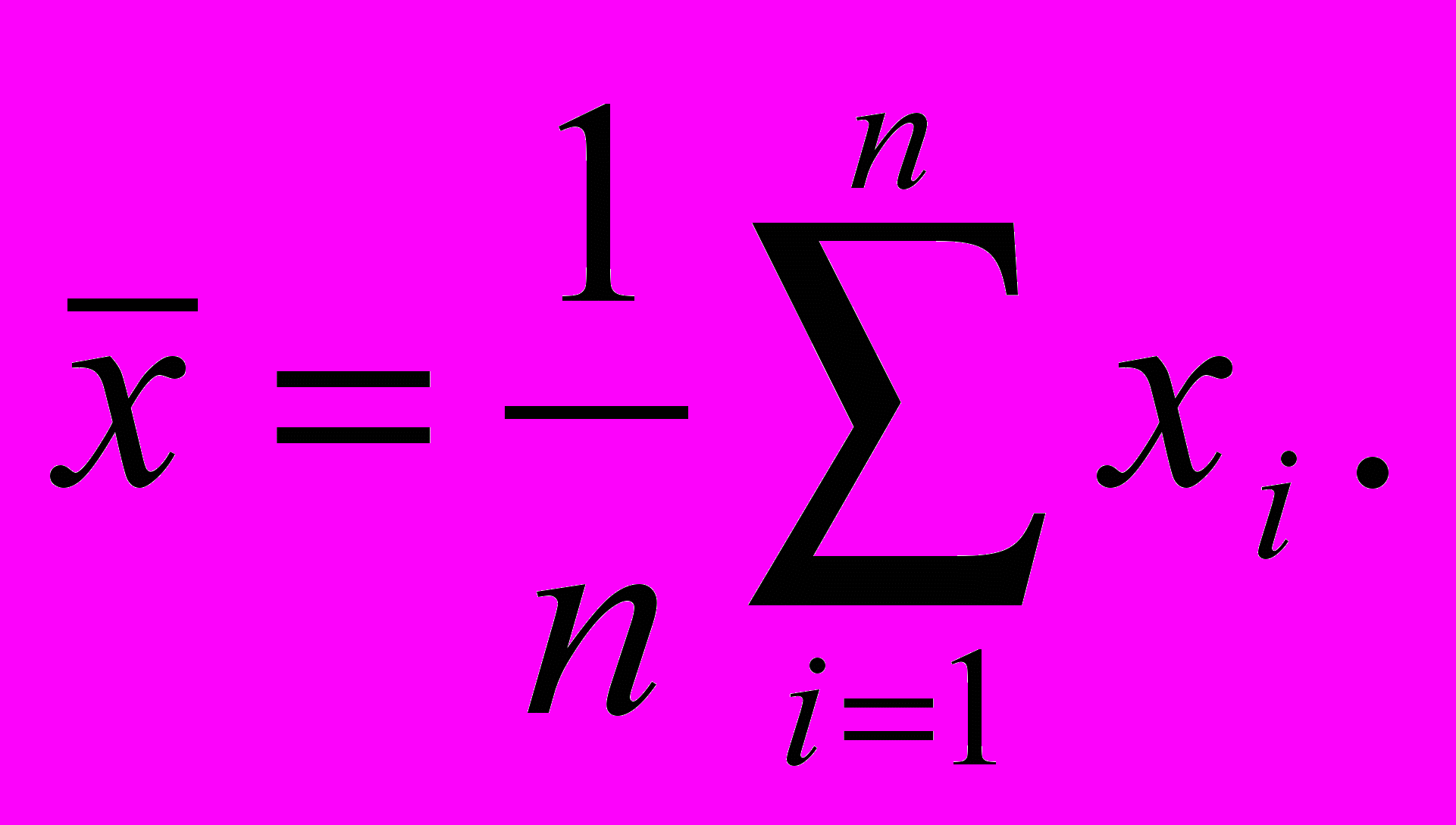
Э
та формула определяет так называемое невзвешенное среднее. При группировании выборки на m дискретных значений (для полигонов распре-деления) или m интервалов со средними точками х_k получим взвешенное среднее арифметическое





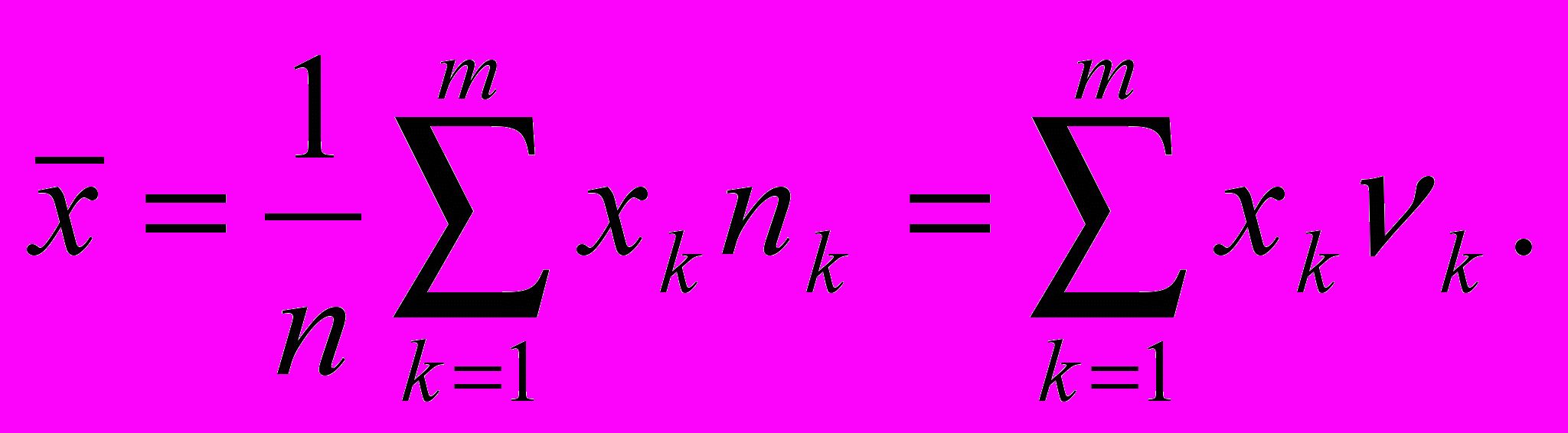
Здесь, как и ранее, n_k и _k – частоты и относительные частоты к-го значения дискретной величины (для полигонов распределения) или к-го ин-тервала непрерывной величины (для гистограммы). Формулы (3.1), (3.2) еще называют выборочными средними.

Пример 3.1. Результаты сдачи экзамена по “Статистике” группой из 26 студентов: “отлично” – 4 студента, “хорошо” – 9 судентов, “удовлетвори-тельно” – 10 студентов, “неудовлетворительно” – 2 студента. Определить средний балл.

С
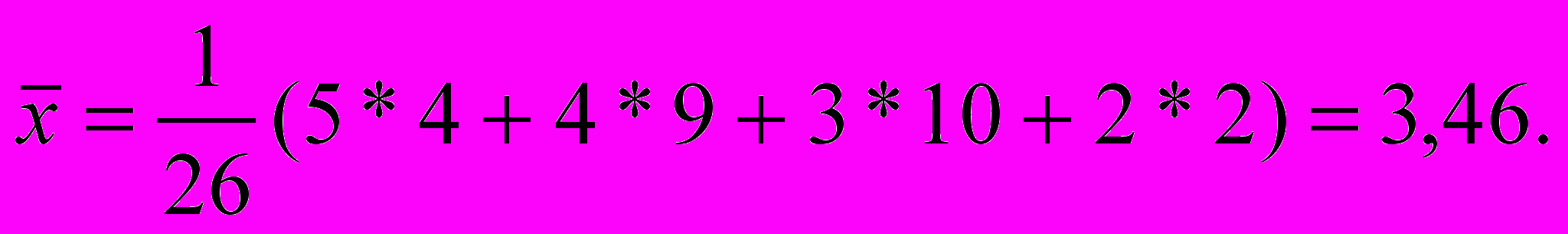
огласно (3.2) получим

Пример 3.2. Распределение доходов D (грн) 40 работников фирмы задано таблицей

D	100 - 200	200 - 300	300 - 400	400 - 500	500 – 600
nk	4	8	15	10	3

Определить средний доход работника.

П
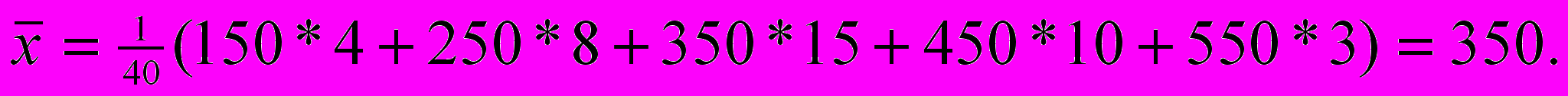
о формуле (3.2) имеем


Выборочное среднее в математической статистике рассматривается как оценка математического ожидания, тем более точная, чем больше объем выборки n.


3.2. Cреднее гармоническое


С
реднее гармоническое определяется формулами







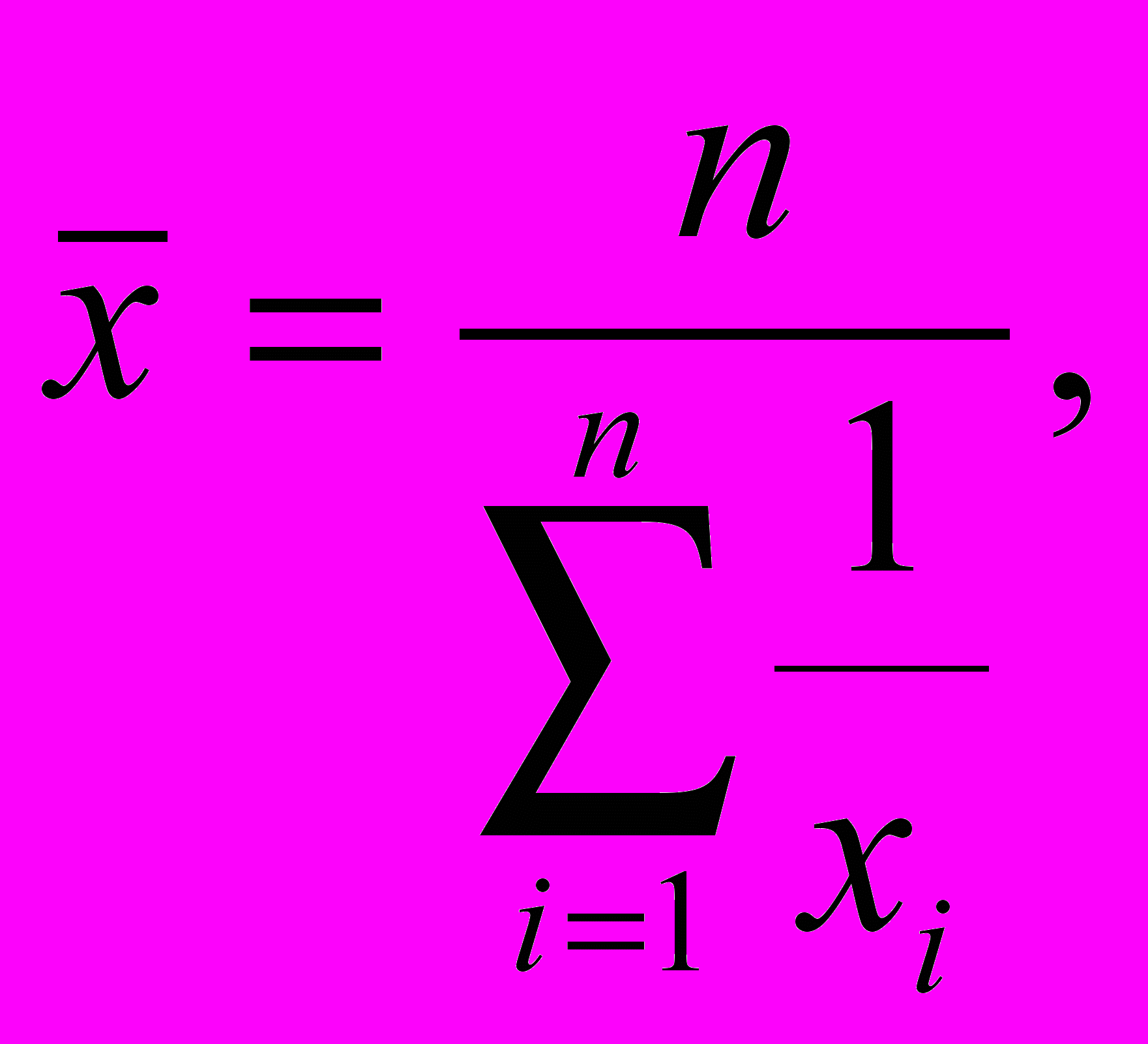
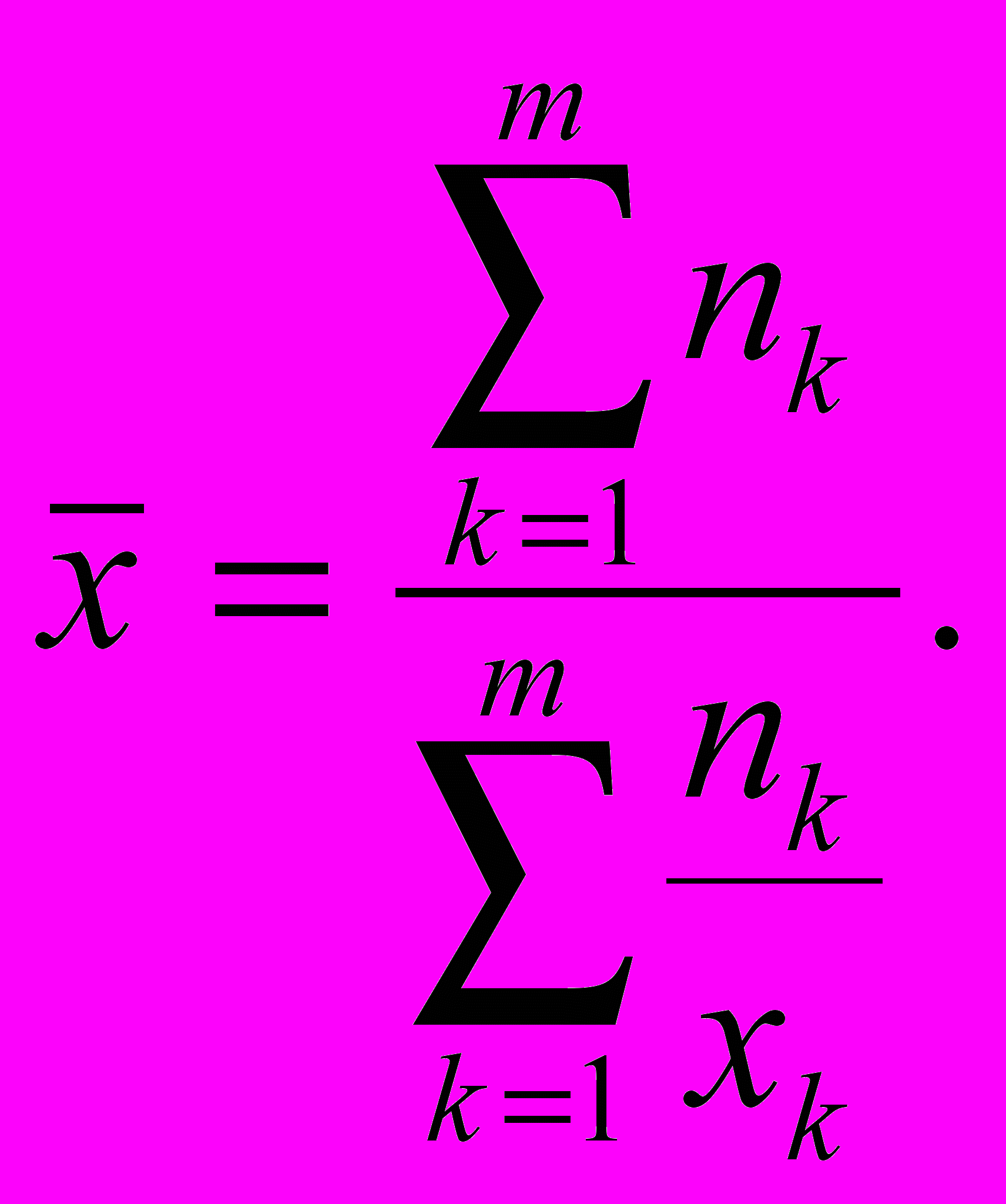
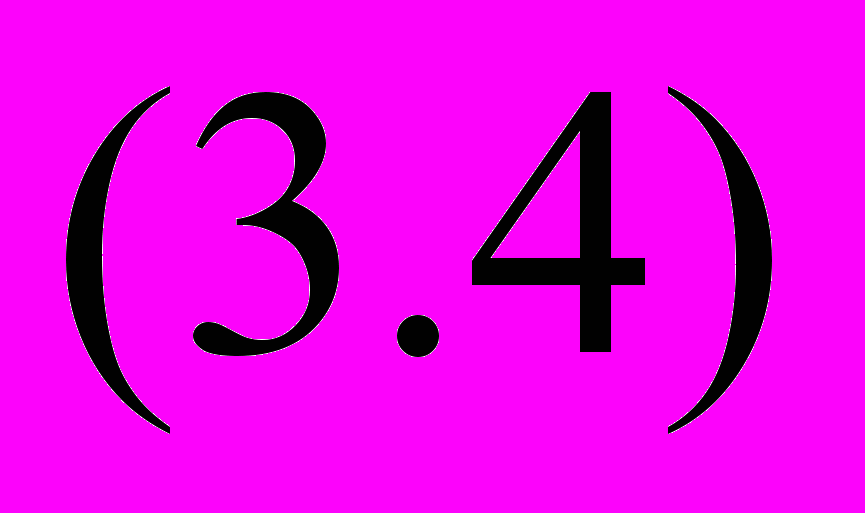
Здесь (3.3) определяет невзвешенное, а (3.4) – взвешенное среднее.

Появление этого типа усреднения связано с двумя аспектами. С одной стороны, среднее гармоническое возникает при вычислении средней про-изводительности при фиксации времени. Другое приложение – при вычис-лении обратных показателей. Рассмотрим примеры.

Пример 3.4. Из Киева до Белой Церкви грузовой автомобиль едет со скоростью V₁=80 км/час, а обратно со скоростью V₂= 60 км/час. Какова средняя скорость?

Среднее арифметическое, очевидно, равно 70 км/час. Если, однако, ввести условие одинакового времени при движении с заданными и со сред-ней скоростью, то результат будет иным. Действительно, время в пути туда S/V₁ и обратно S/V₂ должно равняться времени движения 2S/V_ср со средней скоростью V_ср, то есть


S/V₁+S/V₂=2S/V_cp  V_cp=2/(1/V₁+1/V₂)=2/(1/80+1/60)=68,6 км/час.


Отсюда видно, что средняя скорость определяется как среднее гармо-ническое (3.3).

С другой стороны, эта формула справедлива при вычислении так назы-ваемых обратных показателей. Обратными называют относительные пока-затели, имеющие обратные размерности. Например, измеряя произво-дительность труда величиной х [деталей/час], можно пользоваться и обрат-ным показателем х ^-1[час/деталь], определяющим трудозатраты времени на производство одной детали. Другие примеры: затраты капитала в единицу времени [грн/час] и время оборота денежной единицы [час/грн]; число заявок на обслуживание[заявок/час] и период времени поступления заявок [час/заявка]. Вычисляя прямой показатель как среднее арифметическое (3.1) и принимая





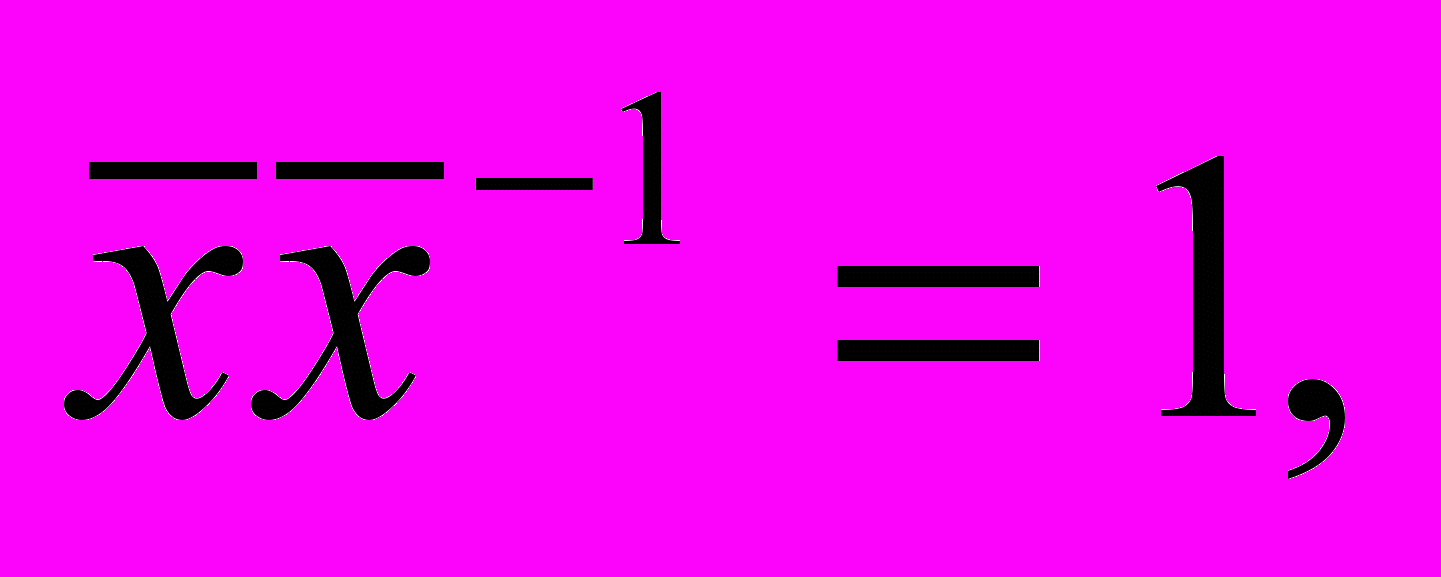
получим для обратного показателя





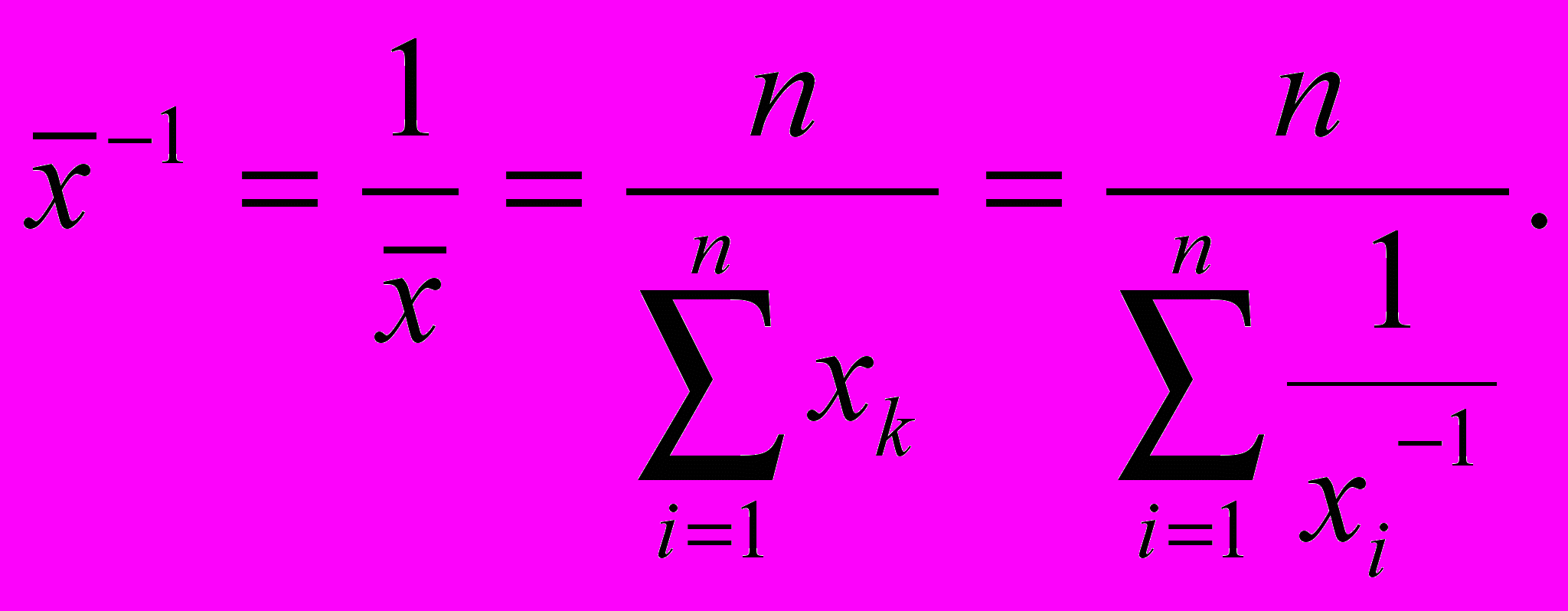
Пример 3.5. Производительность труда Артема х₁=2 дет/час, Бориса х₂=3 дет/час и Влада – 7 дет/час. Каково среднее время выработки одной детали ?

Так как средняя производительность этой бригады (2+3+7)/3=4 дет/час, то время на изготовление одной детали ¼ часа или 15 мин/дет. Тот же резу-льтат получим с помощью (3.3)





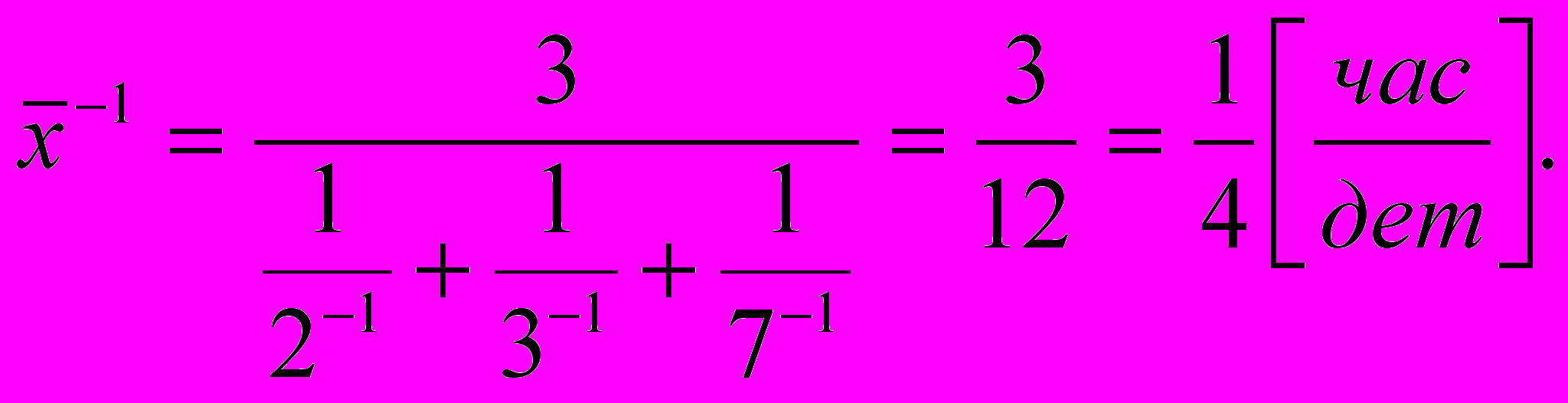
Иначе говоря, здесь среднее гармоническое есть не что иное, как обратное значение среднего арифметического.


3.3. Среднее геометрическое


В ряде случаев относительные показатели (например, темпы роста) не складываются, а перемножаются. В этом случае используется среднее геоме-трическое





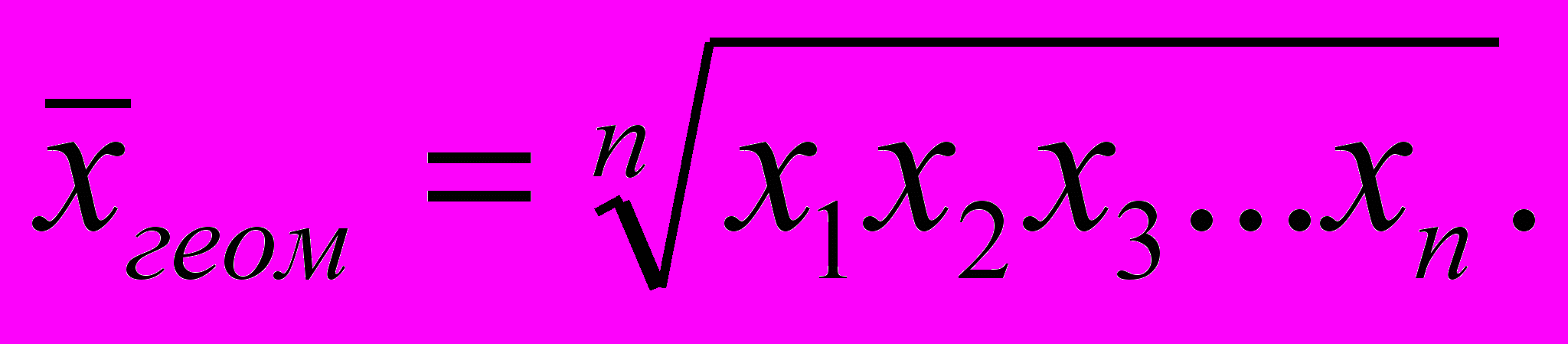
Этот вид усреднения встретится далее в теме “Индексы”.


3.4. Среднеквадратичное


О
перацию арифметического усреднения применяют не только к исхо-дным величинам x_i выборки, но и к квадратам x_i², в результате получим средний квадрат





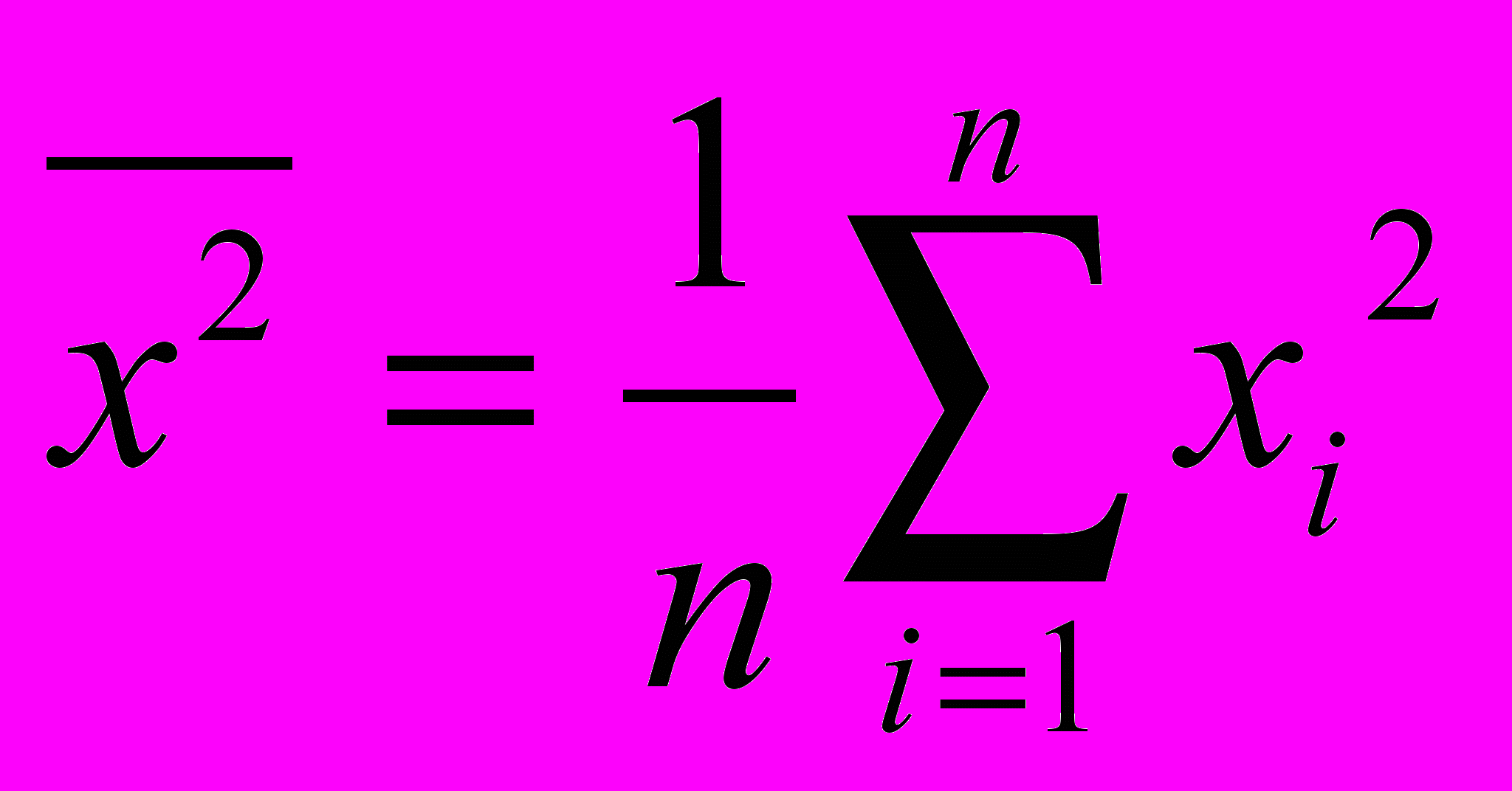
при невзвешенном усреднении или






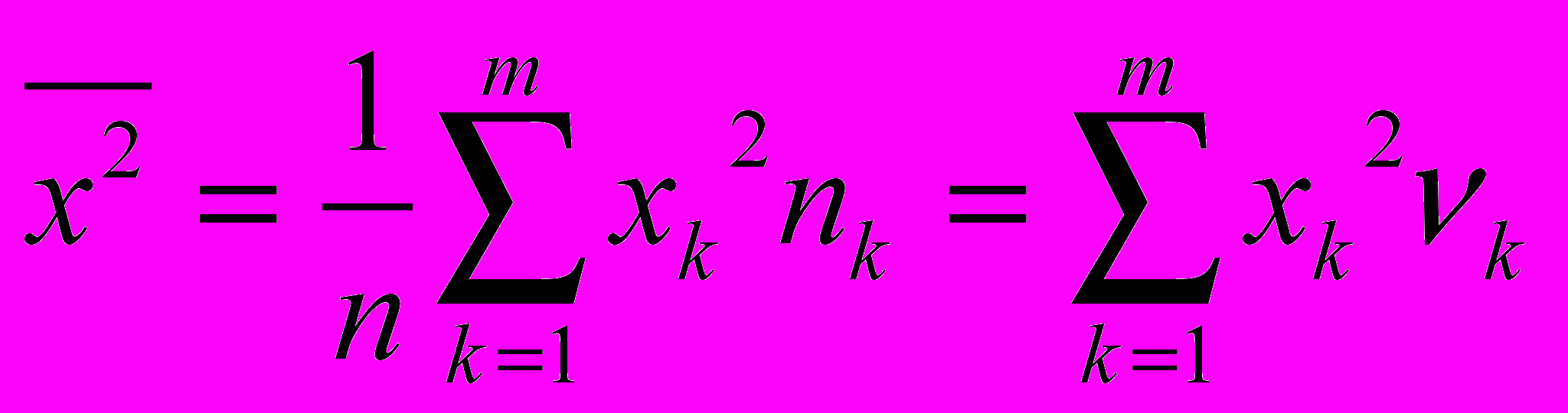
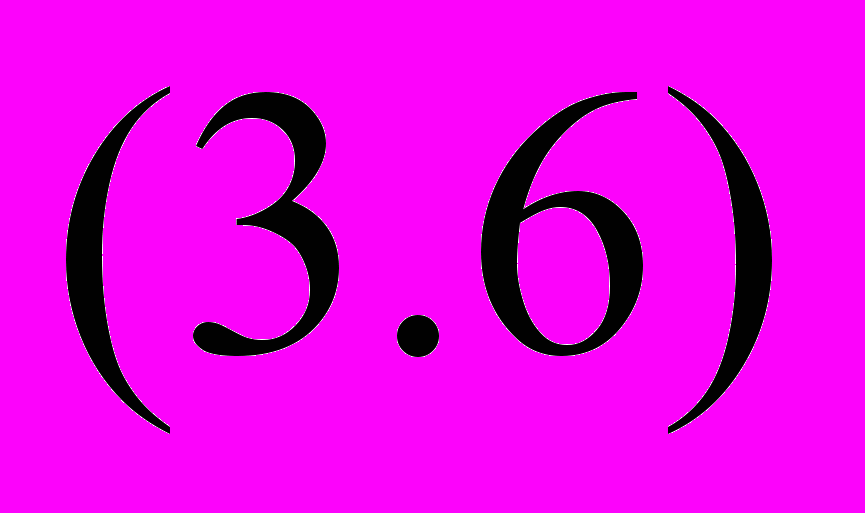
при взвешенном. Поскольку размерность среднего квадрата равна квадрату размерности х, возврат к исходной размерности х осуществляется извлечением квадратного корня из (3.5), (3.6)

Э
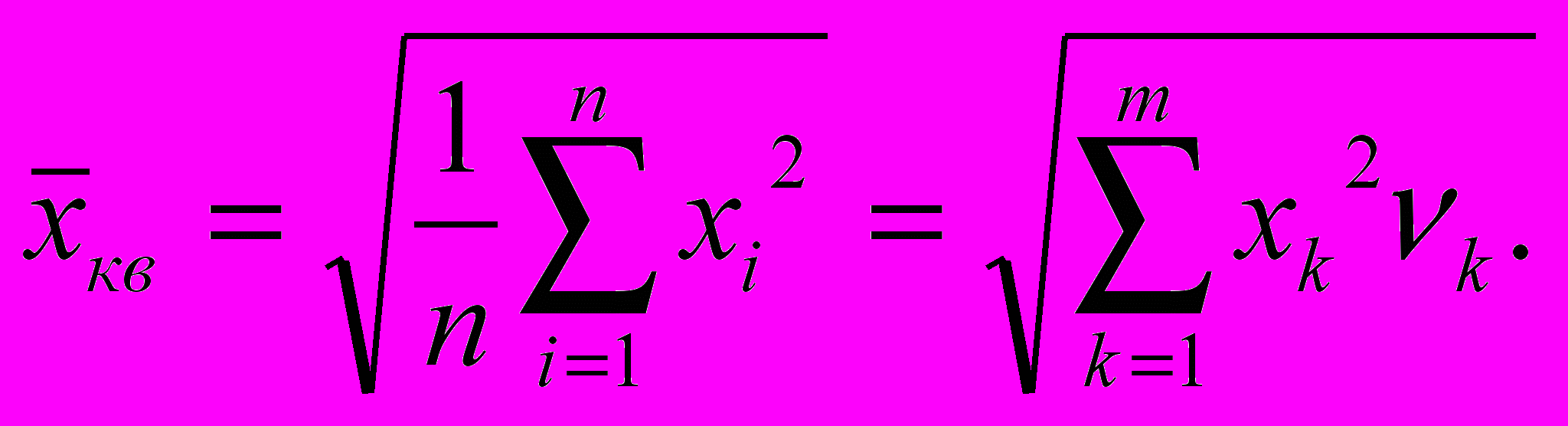
та средняя величина называется среднеквадратичной. Она наиболее часто используется при оценке ошибок измерений.

Имеет место следующее соотношение между средними величинами для одной и той же выборки

С
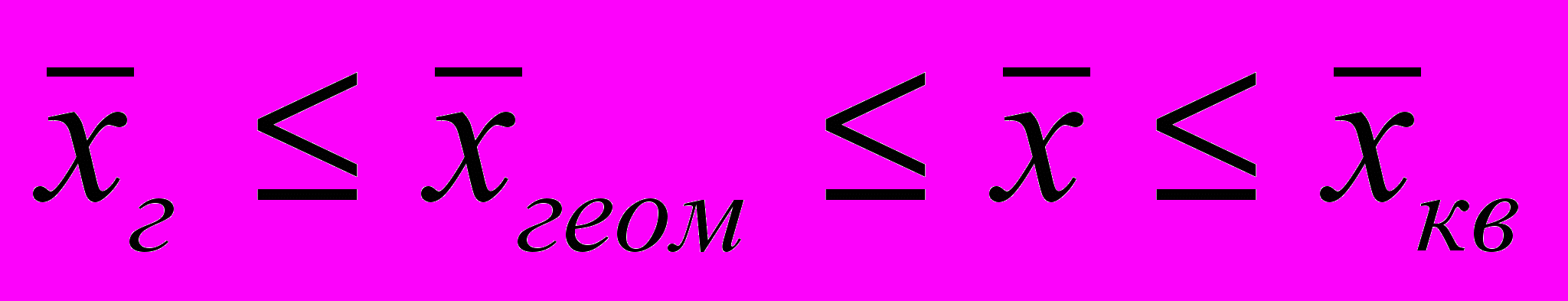
ледует отметить, что в подавляющем большинстве случаев в стати-стике используется среднее арифметическое. Эта величина наиболее проста и имеет ряд замечательных свойств.


3.5. Свойства среднего арифметического

1. Среднее арифметическое центрированных величин равно 0, т.е.
   
2. Д
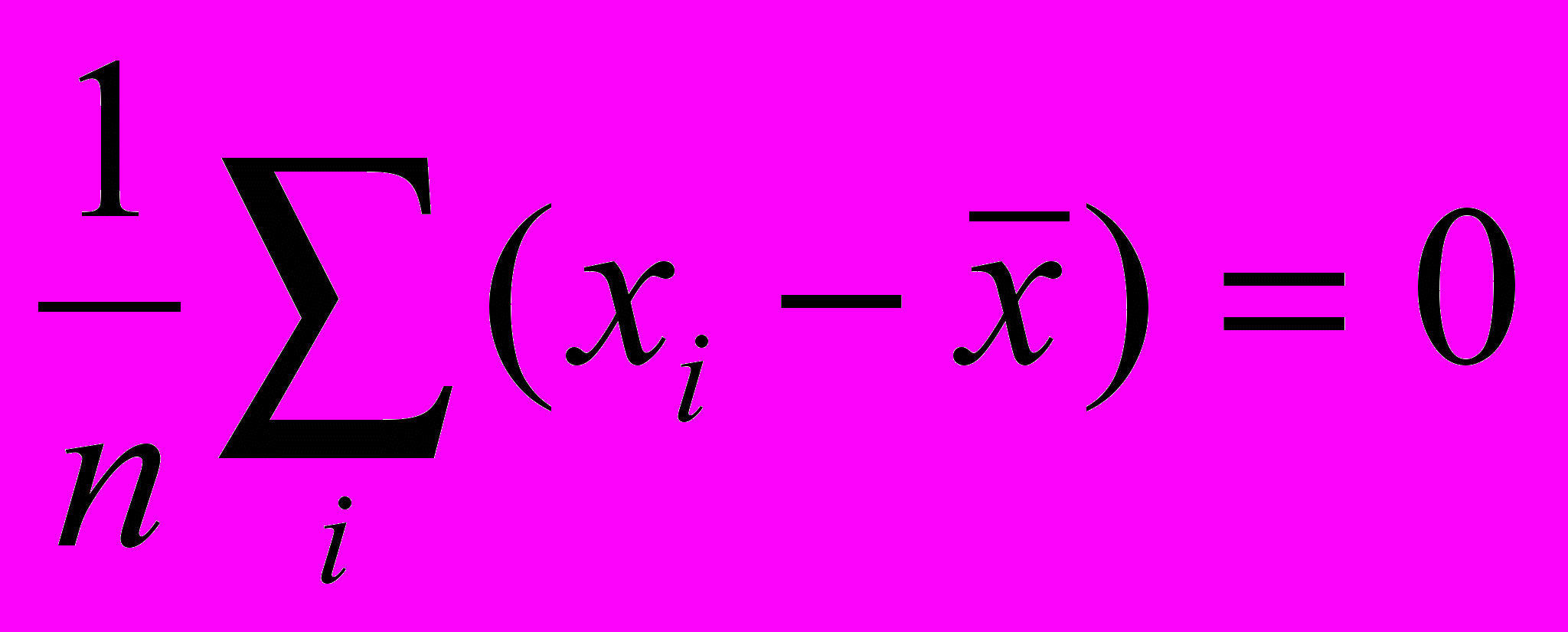
   обавление постоянной а к каждому элементу x_i изменяет среднее значение на ту же величину
   

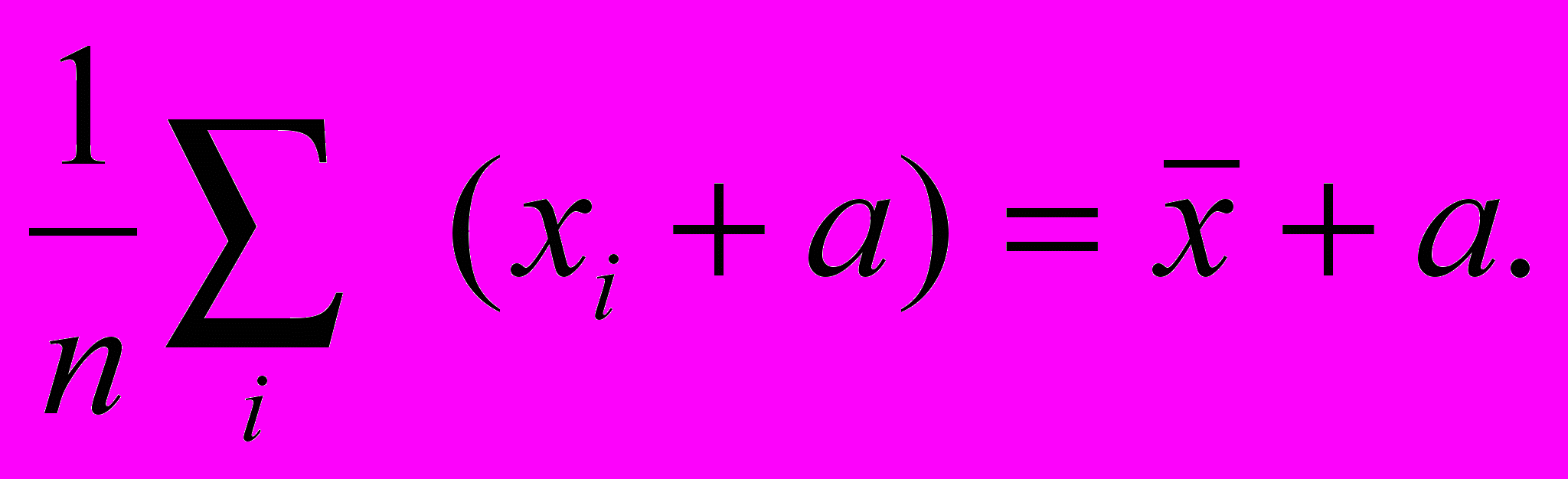
3. Умножение каждого элемента х_i на постоянную величину а изме- няет среднее арифметическое в а раз

4
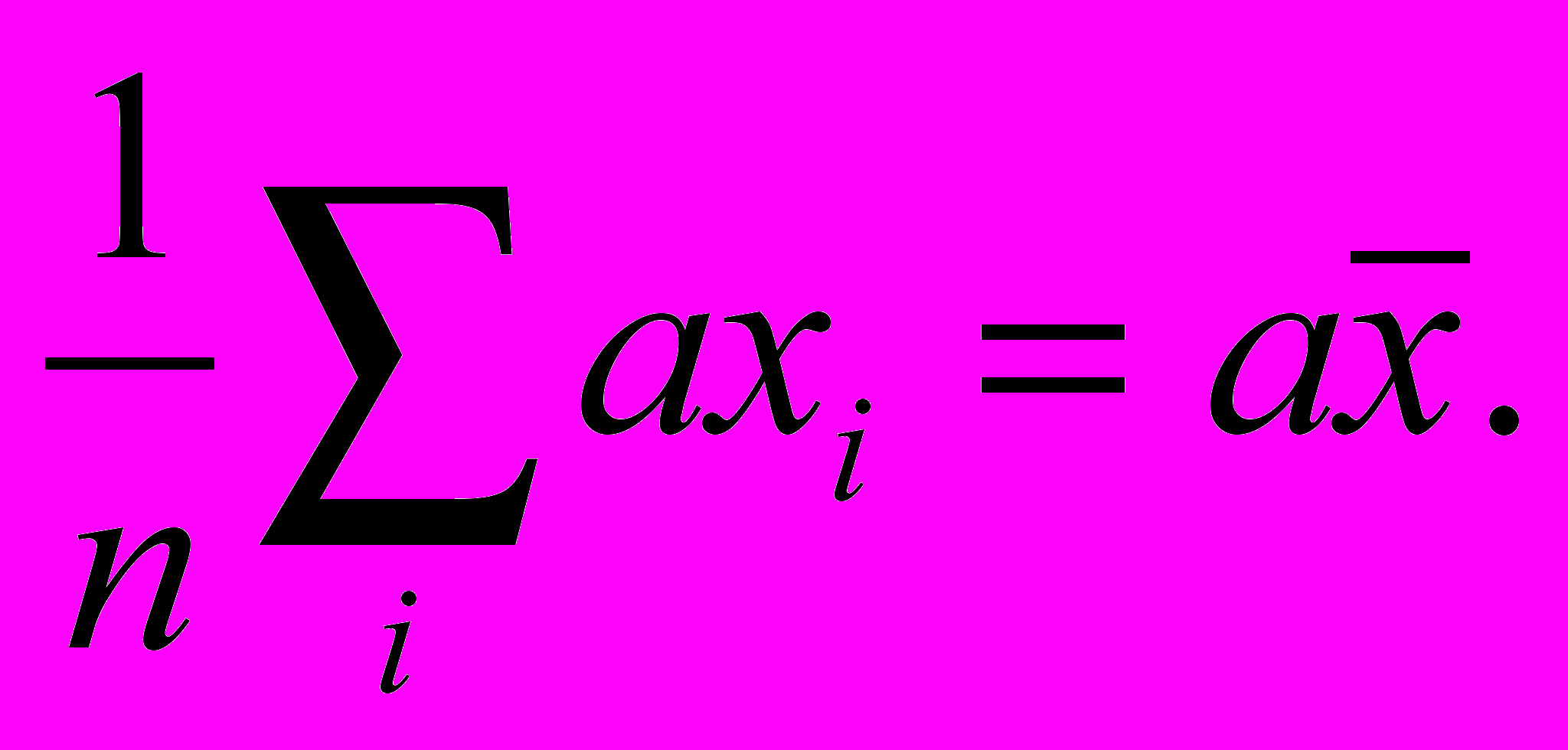
. Среднее арифметическое сумм двух выборок одинакового объема n равна сумме средних (свойство аддитивности)


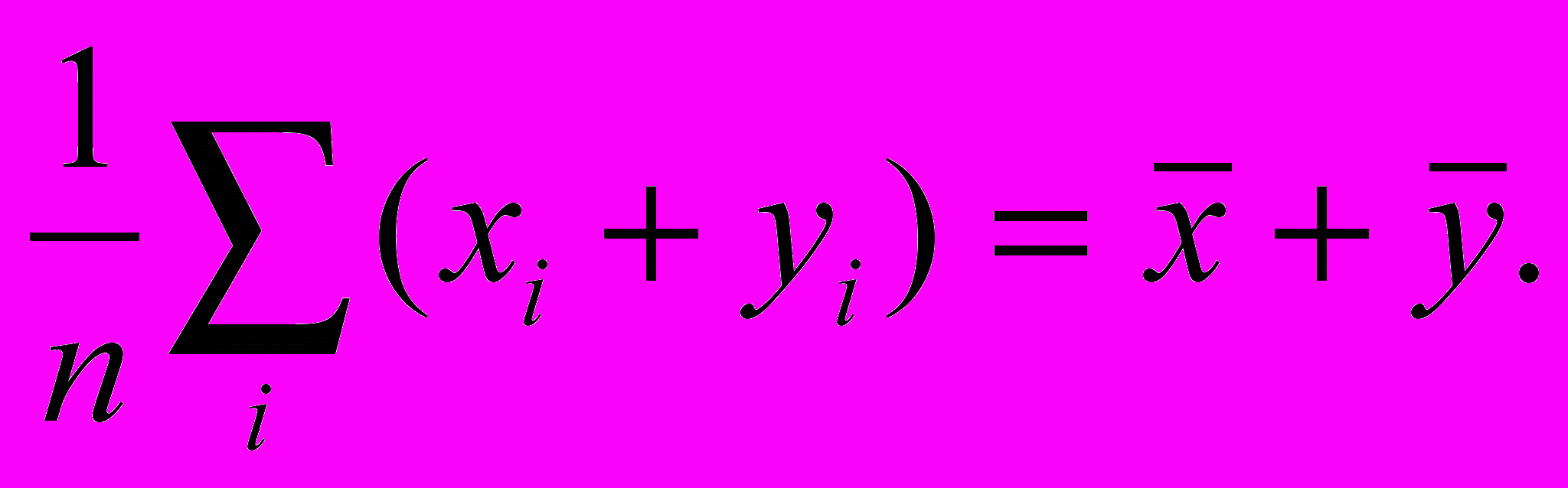
Кроме этих достаточно очевидных свойств в математической статистике выборочное среднее (3.1), (3.2) рассматривается как оценка математического ожидания и обладает свойствами несмещенной, состоя-тельной и эффективной оценки. Это значит, что с ростом объема выборки среднее арифметическое приближается к математическому ожиданию и, кроме того, является наиболее точной оценкой. Все отмеченные свойства и предопределили широкое применение средней арифметической величины в статистике.


3.6. Мода и медиана ряда распределения


Кроме средних значений, характеристиками центра распределения принято считать также моду и медиану.

Мода – это значение признака х, при котором значение ряда распре-деления максимально.

Для полигонов, характеризующих распределения дискретных призна-ков, мода М₀ определяется достаточно просто. Например, значение моды распределения размеров обуви группы из 20 студенток, заданного таблицей 3.1, равно М₀=37.

Таблица 3.1

xk	35	36	37	38	39	
nk	2	5	9	3	1	20

В

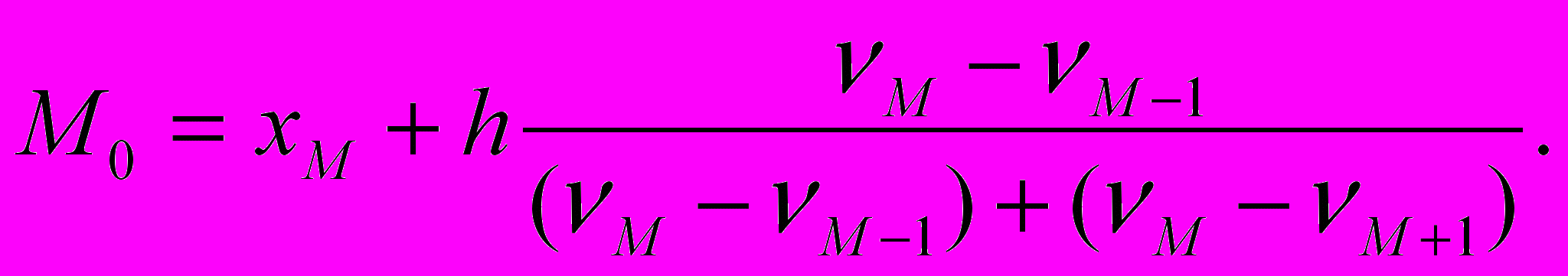
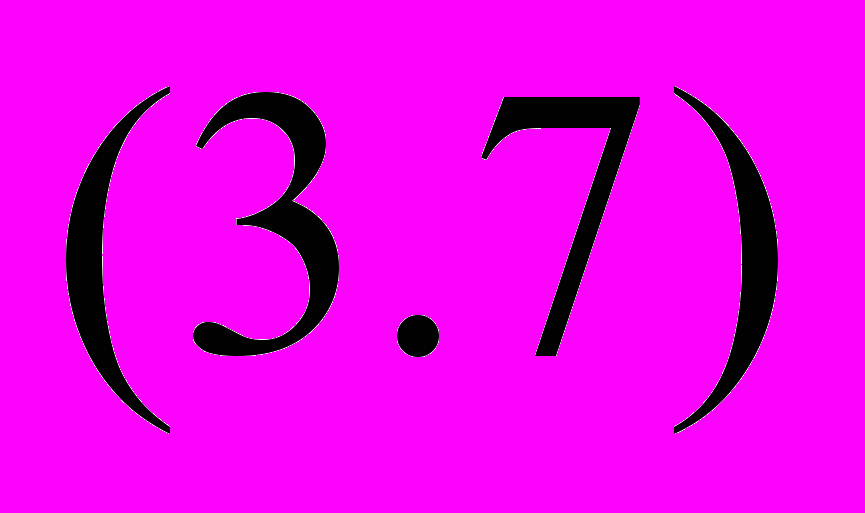
гистограмме значение моды определяется внутри модального интер-вала [x_M ,x_M+1] формулой Орженцкого (1863 – 1923)


Точка на оси х, определяющая это значение, может быть легко найдена графически как абсцисса точки пересечения двух прямых, проведенных в модальном интервале так, как показано на рис. 3.1.




_k


_М







_М+1

_М-1





₁




h



x₁ x₂ x _M-1 x_M M₀ x_M+1 x


Рис.3.1

М

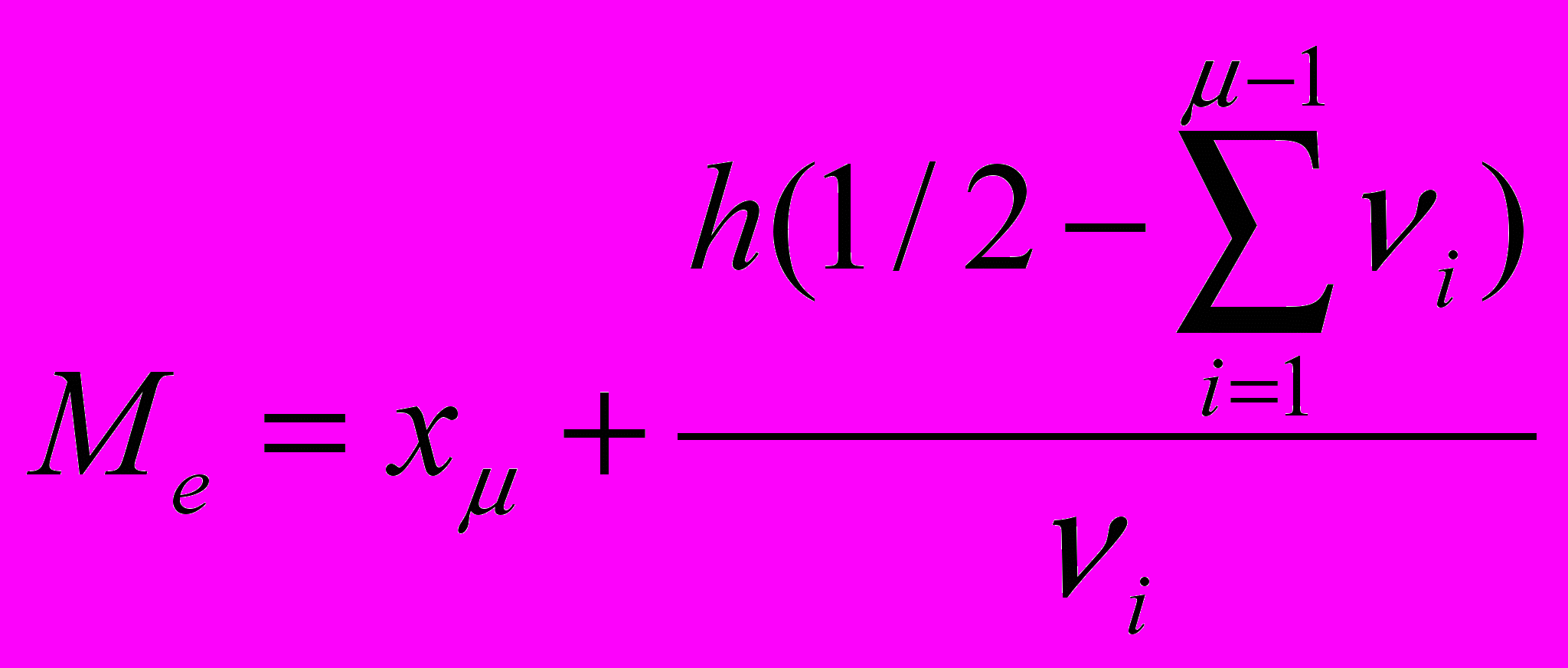
едиана – это значение признака х=М_е, которое делит площадь гистограммы пополам. Если обозначить х_ левую границу медианного инте-рвала, то значение медианы гистограммы с равными интервалами ширины h определяется формулой

Пример 3.7. Распределение вкладов в банке представлено таблицей

Вклады, грн	<1000	1000-1999	2000-2999	3000-3999	>4000
k, %	19	34	25	13	9

Определить моду и медиану распределения.

О
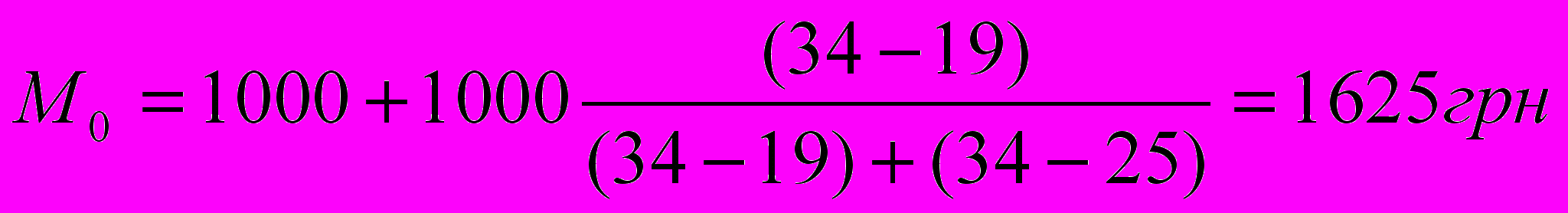
чевидно, модальный интервал лежит в области значений 1000-1999 грн. Согласно (3.7) получим значение моды

М
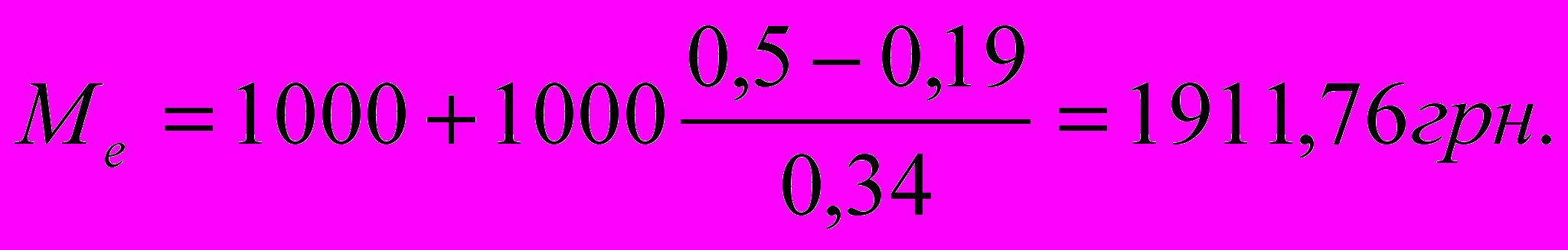
едиана этого распределения расположена в том же интервале и в соответствии с (3.8) равна

При симметричных рядах распределений все три параметра центра распределения – среднее арифметическое, мода и медиана – совпадают. В остальных случаях, которые, очевидно, преобладают, приходится произ-водить отдельные расчеты для каждого параметра.


Задачи

1. Имеются отчетные данные 20 заводов отрасли по объему валовой продукции (ОВП) за год (в млн. грн.)
   

{х_i}⁽²⁰⁾={4,5; 3,5;12,0; 3,4; 10,0; 8,8; 3,6; 9,5; 2,8; 6,5; 13,3; 9,9; 9,3; 8,7; 7,2; 6,2; 2,6; 3,7; 4,4; 4,1}.

Произвести группировку заводов по этому признаку с разбиением на 4 равных интервала. Построить гистограмму распределения ОВП для частот n_k и относительных частот 100_k%, определить средний ОВП, моду и медиану распределения.

2. Данные о заработной плате работников двух цехов приведены в таблице
   

Но- Мер Цеха	Январь		Февраль
	Средняя зар- плата, грн	Фонд зар- платы, грн	Средняя зар- плата, грн	Число работ- ников
1	380	41800	350	110
2	420	50400	400	130

Вычислить среднюю зарплату по заводу за январь, февраль и за два месяца.

3. Распределение работников двух отраслей А и В по уровню квалификации характеризуется данными, %
   

Отрасль	Тарифный разряд
	2	3	4	5	6
А	9	20	35	22	12
В	5	17	30	29	19

Для каждой отрасли определить средний уровень квалификации (по тарифному разряду) и моды распределений.

4. По проценту высоколиквидных активов среди всех активов 20 банков распределяются следующим образом
   

Процент высо- Коликвидных Активов	0 -10	10-20	20-30	30-40	40-50	50-60	60-70	>70
Число банков	1	4	7	3	3	1	1	0

Определить средний процент высоколиквидных активов, моду и медиану распределения.

5.Денежный оборот 3-х фирм оценивается данными: 200; 300; 700 грн/час. Определить среднее арифметическое и среднее гармоническое значение оборота. Каков финансовый смысл этих двух показателей?


Контрольные вопросы

1. Какие виды усреднения используются в статистике?
   
2. Напишите выражения для вычисления среднего арифметического (невзвешенного и взвешенного по частотам). В чем специфика определения среднего на основе гистограммы по сравнению с полигоном распределения? Приведите примеры средних величин в социально-экономических явлениях.
   
3. Дайте математическое определение среднего гармонического. В каких условиях используется этот вид средней велечины? Приведите примеры.
   
4. Напишите формулы вычисления среднего геометрического и среднеквадратичной величины. Когда они используются?
   
5. Определите соотношение между различными средними величинами (арифметическим, гармоническим, геометрическим и среднеквадратичным).
   
6. Дайте определение моды распределения. Напишите формулу вычисления моды для гистограммы. Как определить моду графиче-ски?
   
7. Дайте определение медианы распределения. Напишите выражение для вычисления медианы непрерывной величины.
   
8. При каких распределениях среднее арифметическое, мода и медиана совпадают?
   
9. Сформулируйте свойства среднего арифметического. Почему этот показатель является самым распространенным в статистике?
   

Тема 4. Показатели вариации и формы распределения


Представляется очевидным, что одним параметром, хоть и самым информативным – средней величиной – нельзя оценить все свойства массо-вого явления. Если средний срок жизни 75 лет, то это вовсе не значит, что в этом возрасте обязательно нужно отправляться на кладбище (хотя в Японии в старину это было принято). Если уровень жизни в среднем по стране очень низок, то это не говорит о том, что нет очень богатых. Естественным образом возникает необходимость в показателе, оценивающем степень отклонения от среднего. Такие показатели в статистике называют показателями (параметрами) вариации (лат.variatio – изменение). Они характеризуют степень неоднородности совокупности. Наиболее распространенными в статистике параметрами вариации являются размах вариации R=x_max-x_min, дисперсия ², среднеквадратичное отклонение  (СКО), среднее линейное отклонение d (СЛО).

Разумеется, вариационные показатели тоже являются частными характеристиками социально-экономического явления. По форме ряда распределения можно судить, например, о том, какие значения признака более вероятны (чаще встречаются), чем средние значения. При этом может появиться право- или левосторонняя асимметрия, которые измеряются коэффициентом асимметрии. Распределения бывают сравнительно равномерные (плосковерхие), что свидетельствует об отсутствии выраженных предпочтений в значениях признака, и островерхие, которые выражают степень таких предпочтений. Оценка этих свойств осуществляется с помощью коэффициента эксцесса.


4.1. Дисперсия


О
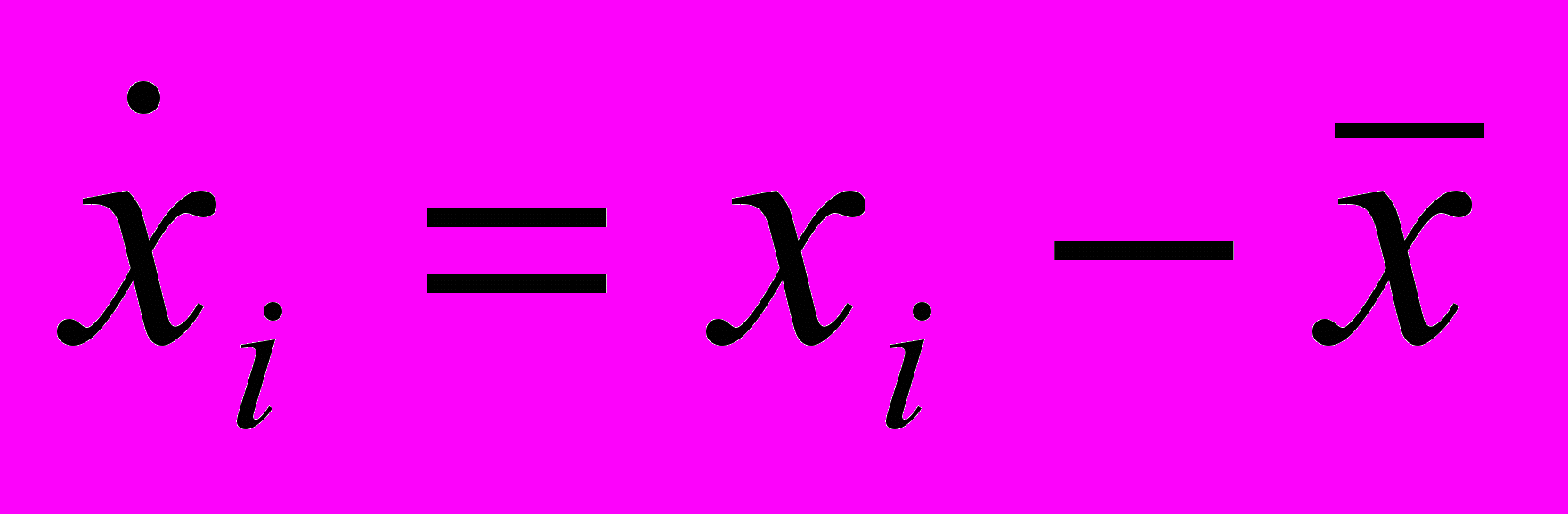
тклонения от среднего значения имеют как положительные, так и отрицательные знаки. К примеру, отличники на сессии получают оценки выше среднего балла (положительные отклонения), а аутсайдеры учебы – ниже среднего. Разность

называется центрированной величиной. Среднее значение центриро-ванной величины, как следует из первого свойства арифметического среднего (см. п.3.5) равно 0, поэтому для определения степени отклонения от среднего следует усреднять неотрицательные значения. Наиболее часто для этого усредняют квадраты центрированных величин, после чего возвращение к исходной размерности осуществляют извлечением корня квадратного (положительного).

К-м центральным моментом выборки {x_i}⁽ⁿ⁾ называется величина






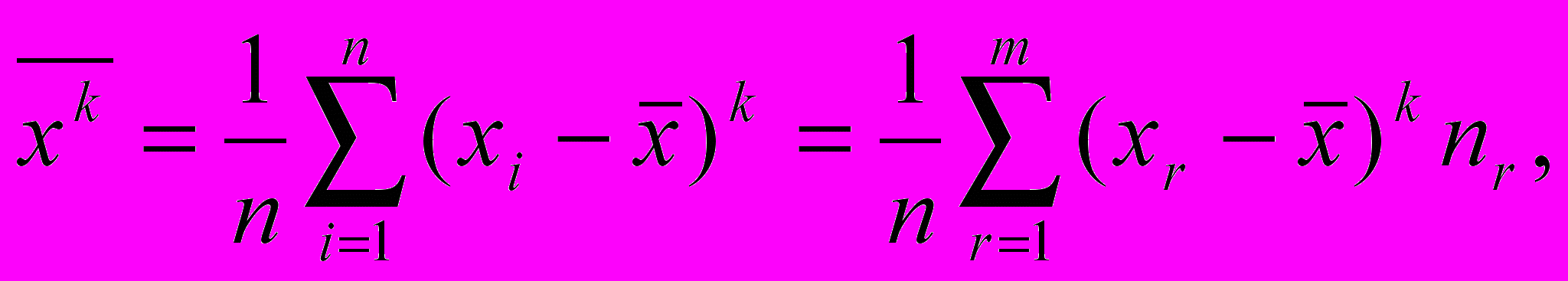
г
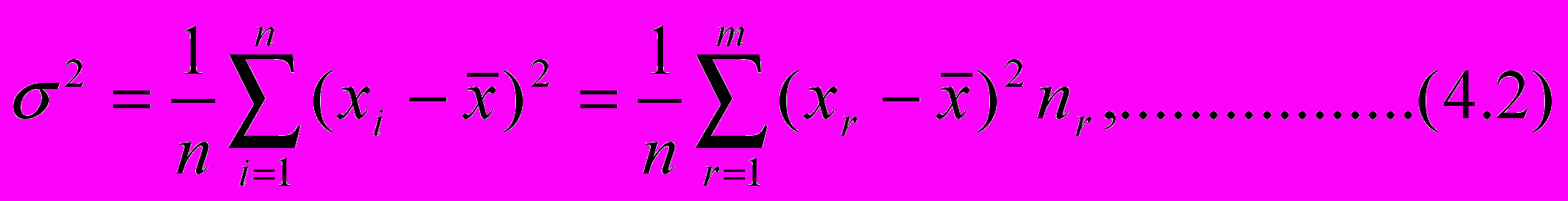
де слева дано выражение для невзвешенного, а справа – взвешенного k-го момента с группировкой выборки на m групп. Центральный момент 2-го порядка

называется выборочной дисперсией. Для оценки степени отклонения от среднего в принципе можно использовать любой момент четного порядка, так как слагаемые в (4.2) для них положительны. Дисперсия получила распространение для подобной оценки в связи с тем, что она является моментом минимального четного (k=2) порядка.

Р
аскрывая скобки в (4.2) и учитывая свойства среднего арифметиче-ского (см. п.3.5), легко получить более простое выражение для дисперсии





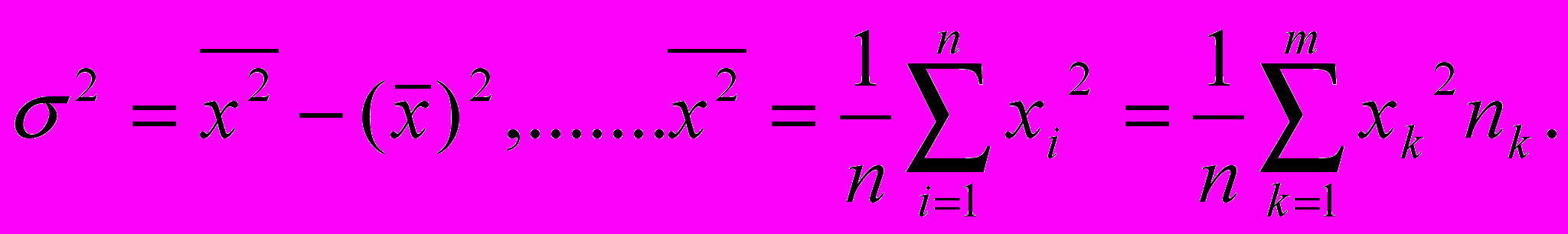
Здесь дисперсия определена как разность между средним квадратом и квадратом средней величины. Если перед определением дисперсии среднее значение уже вычислено, то обычно пользуются для расчета формулой (4.3).

Основные свойства дисперсии:

1. ²0, причем дисперсия равна 0 лишь при x_i=c, i=1,…,n, т.е. все элементы выборки одинаковы и равны постоянной с;
   
2. Изменение всех элементов выборки в а раз приводит к изменению дисперсии в а² раз
   

²_ax=a²²_x;

3. Для двух независимых выборок {x_i}⁽ⁿ⁾ и {y_i}⁽ⁿ⁾ дисперсия суммы равна сумме дисперсий, т.е.
   

²_x+y= _x²+_y².

Если Х и Y – статистически зависимые (коррелированные) величины, то в последнем свойстве к сумме двух дисперсий добавляется момент корреляции К_xy. Он определен в теме 6.

Пример 4.1. Рост 6 игроков баскетбольной команды определяется выборкой (в см)

{x_i}={206, 214, 195, 198, 208, 201}.

Определить средний рост и дисперсию этой выборки.

Согласно (3.1) и (4.3) получим

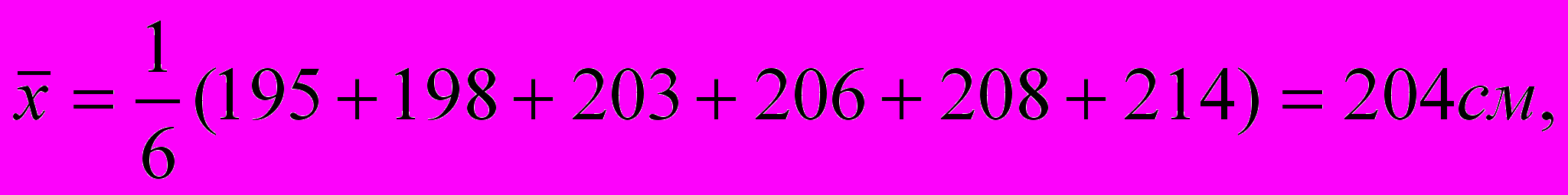
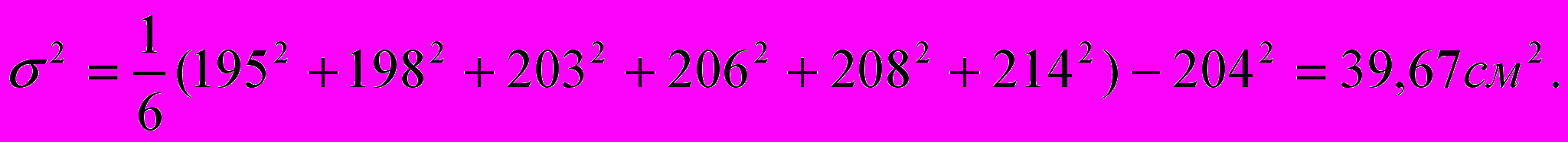
Как мера отклонения от среднего дисперсия является промежуточной характеристикой, так как ее размерность равна квадрату размерности средней величины и, следовательно, среднее и дисперсия не сравнимы. Поэтому для сопоставления со средней величиной пользуются корнем квад-ратным из дисперсии.

4.2. Среднеквадратическое отклонение (СКО)


Э

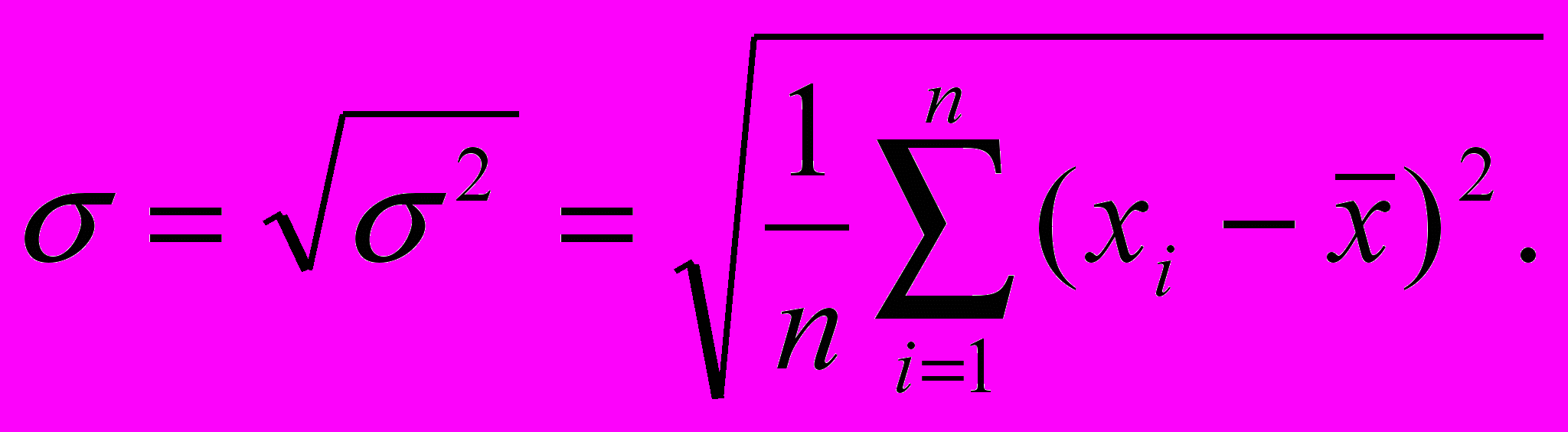
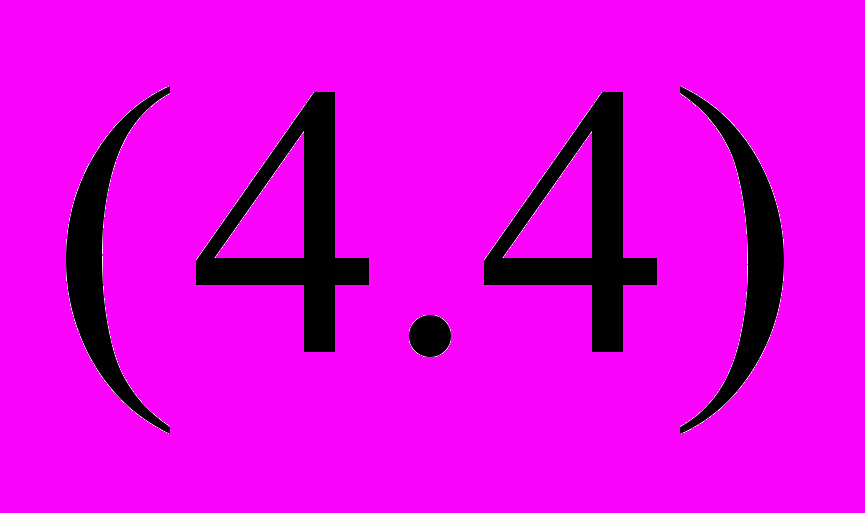
тот параметр определяется как

С
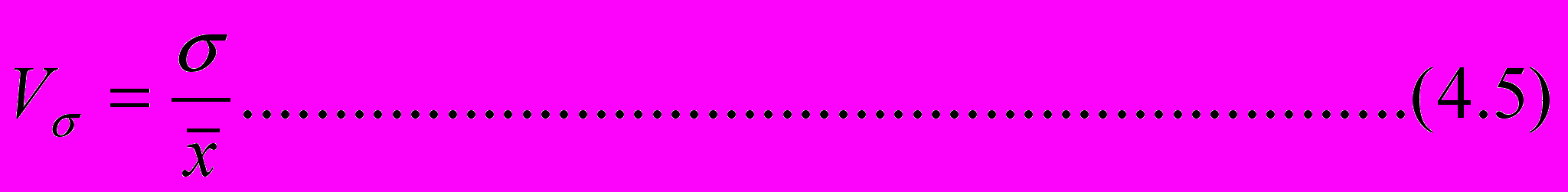
КО как параметр широко используется при оценке ошибок выбороч-ного наблюдения (см. тему 5), а также при оценке неоднородности выборки. Для этого введем относительный параметр – коэффициент вариации

Принято считать, что при V_<1/3 совокупность однородна, в против-ном случае – неоднородна.

В
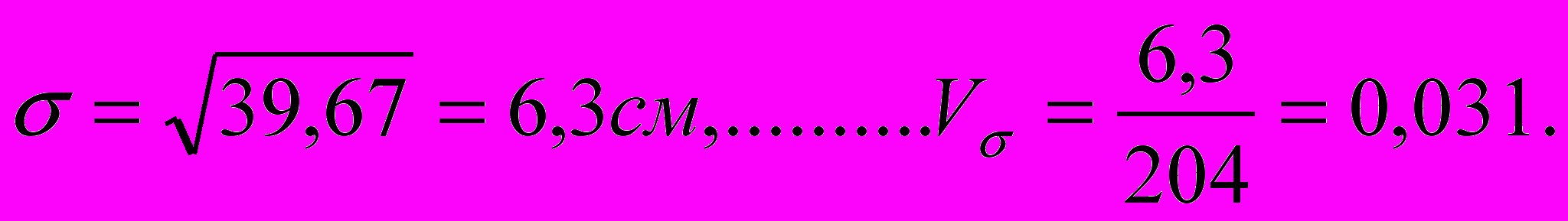
продолжение примера 4.1 определим СКО и коэффициент вариации

Мы видим из этого примера, что отклонение от среднего роста баскет-болистов-великанов невелико и выборку вполне можно считать однородной.

3. Среднее линейное отклонение (СЛО)
   

Иногда вместо СКО в качестве меры отклонения используют среднее значение абсолютных отклонений

г
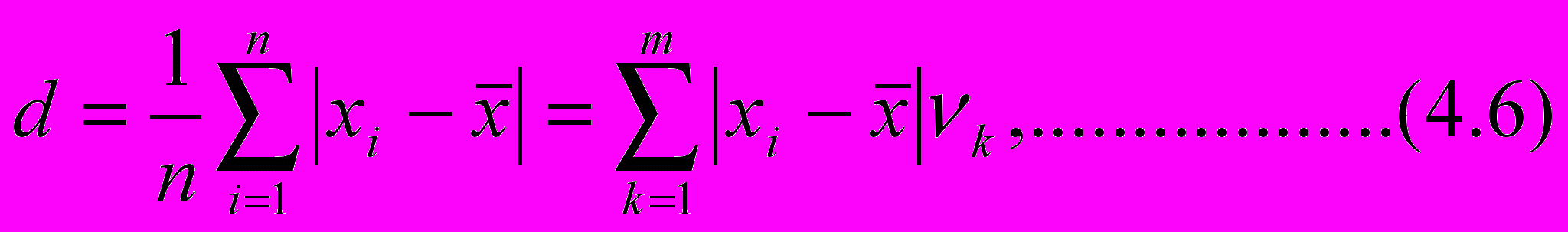
де, как и прежде, слева записано невзвешенное, а справа – взвешенное выражение среднего линейного отклонения. По аналогии с (4.5) определим коэффициент линейной вариации

И
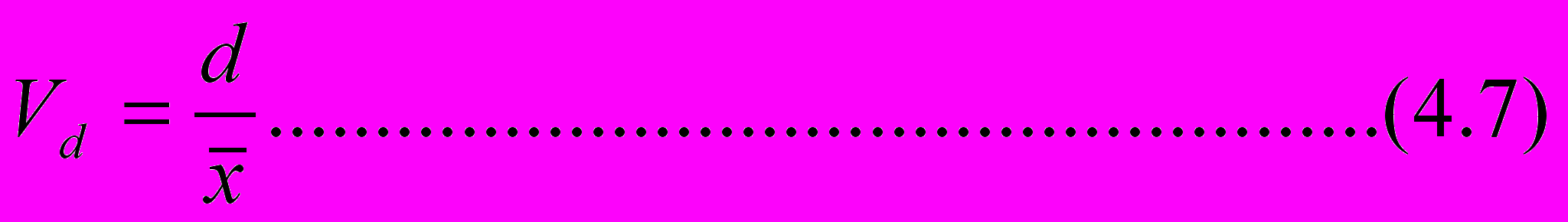
з математической статистики известно, что d< и, следовательно, V_d. Убедимся в этом на примере 4.1. Вычисления по (4.6), (4.7) дают

d=(|195-204|+|198-204|+|203-204|+|206-204|+|208-204|+|214-204|)/6=

5,33см,

V_d=5,33/204=0,026.

Отметим, что СКО используется гораздо чаще, чем СЛО. Это вызвано тем, что свойства дисперсии и СКО обеспечивают сравнительно более простой анализ многофакторных явлений.

Пример 4.2. Коэффициент использования энергетического оборудова-ния (в %) для 50 установок предприятия имеет распределение

Коэффициент использования,%	<60	60 – 70	70 – 80	>80
Число установок	3	9	23	15

Требуется определить средний показатель коэффициента использова-ния, СКО и СЛО, коэффициенты вариации и линейной вариации.

П

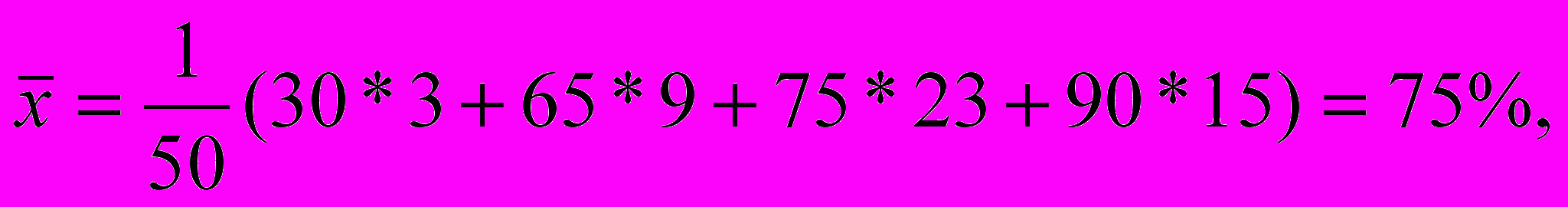
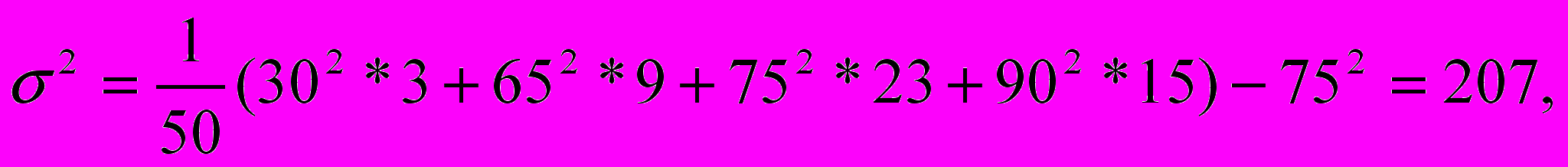
оскольку задано распределение с неравными интервалами h_k, в формулах взвешенного усреднения x_k - средние точки интервалов, равные 30, 65, 75 и 90 %. Согласно (3.1), (4.3), (4.4) и (4.6) получим






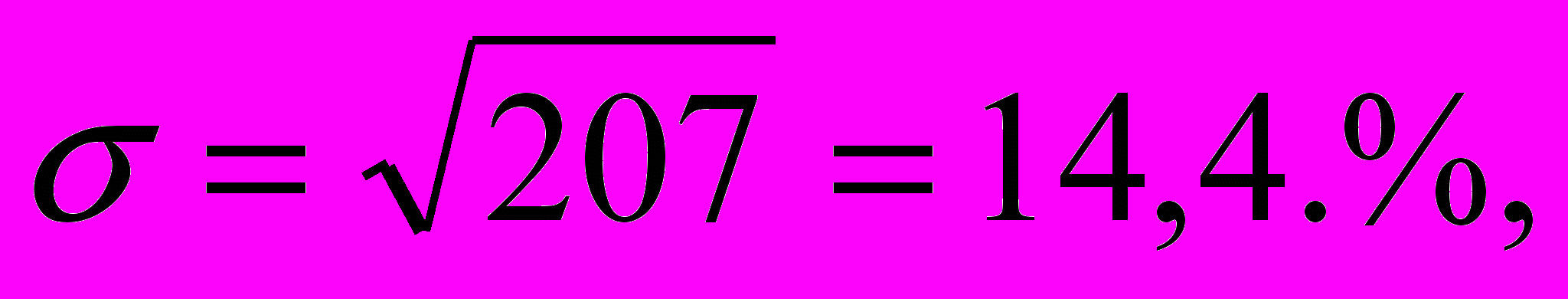
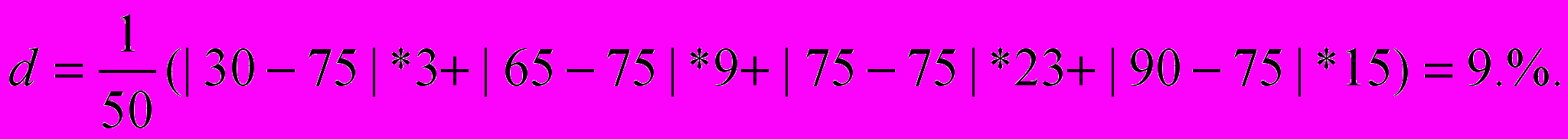
В результате коэффициент вариации (4.5) равен V_=14,4/75=0,192, а коэффициент (4.7) линейной вариации V_d=9/75=0,12. Данную совокупность энергетических установок можно считать однородной.


4.4. Показатели формы распределения


К эим показателям обычно относят:

• коэффициент асимметрии A_s;
  
• коэффициент эксцесса E.
  

О
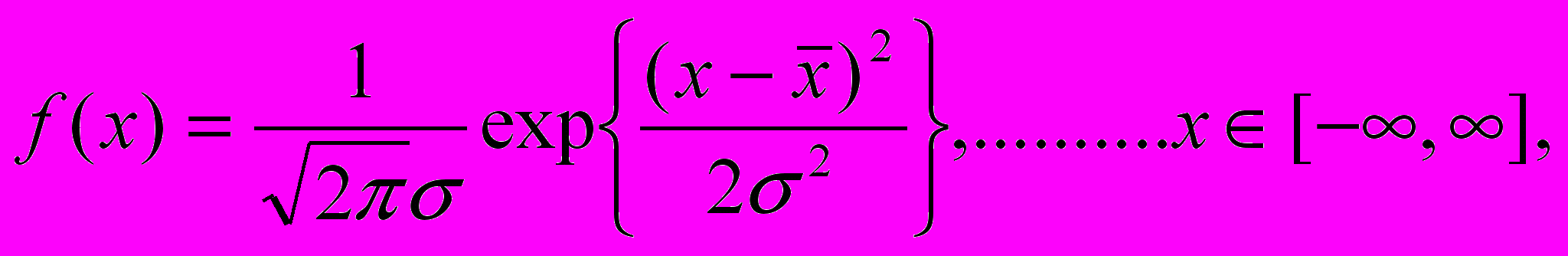
ни характеризуют степень отклонения ряда распределения от нормального закона распределения, который еще называют законом Гаусса

где f(x) – плотность вероятности непрерывной случайной величины Х.

График нормального распределения изображен на рис.4.1. Он симметричен относительно средней величины и имеет вид колоколообразной кривой. С

ростом объема выборки n ряд распределения асимптотически стремится к вероятностному распределению (ряду вероятностей для дискретной величины или плотности вероятности – для непрерывной). Большое число реальных явлений или процессов можно с приемлемой точностью аппро-ксимировать нормальным законом. Он по сути утверждает, что наиболее часто появляются значения совокупности, равные среднему, а по мере отклонения от среднего в обе стороны частота случайных величин снижается

тем быстрей, чем больше это отклонение. Например, распределение людей по росту, весу, доходам в определенных пределах может быть близко к нор-

мальному. Нормальный закон симметричен относительно среднего, для него






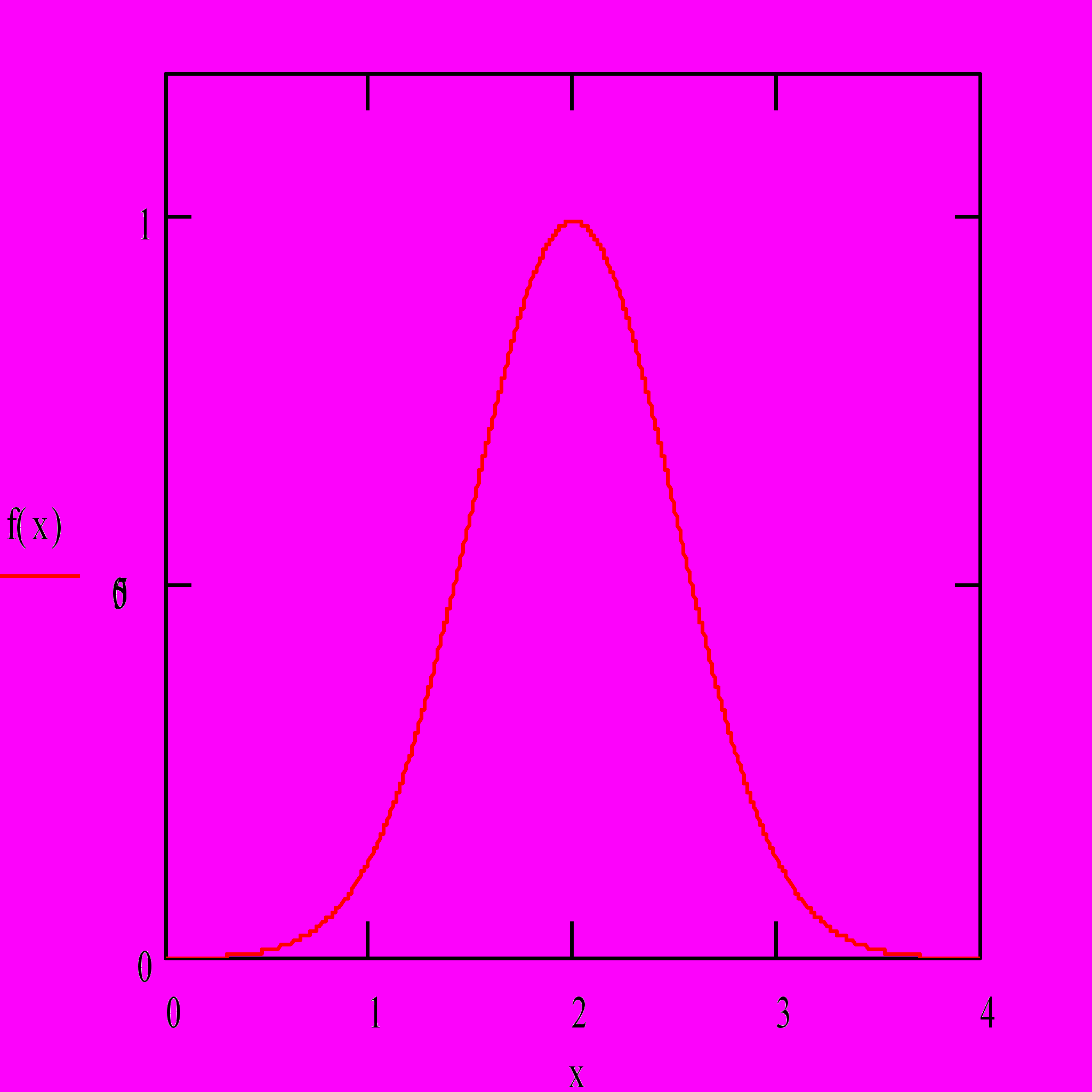
Рис.4.1


коэффициенты асимметрии и эксцесса равны 0. В статистике он служит эта-лоном, с которым сравниваются другие распределения.

Коэффициент асимметрии

определяется как отношение 3-го центрального момента к кубу СКО.

Д
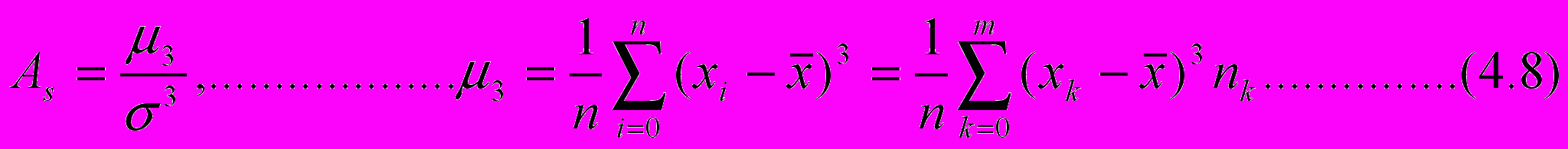
ля любого симметричного распределения A_s=0, так как третий (и вообще нечетный) момент такого распределения равен 0. Это связано с тем, что под знаком суммы образуется нечетная функция отклонений от среднего, дающая в результате суммирования 0. Для асимметричных распределений при A_s>0 имеет место правосторонняя асимметрия, при A_s<0 – левосторон-няя, рис.4.2а,б.

f(x) (а) f(x) (б)

A_s>0 A_s<0













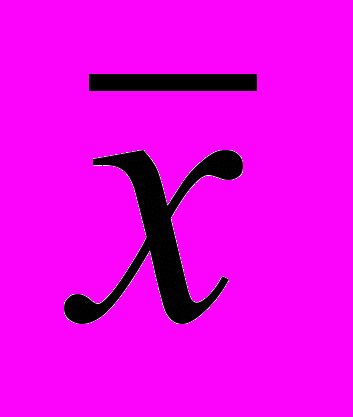
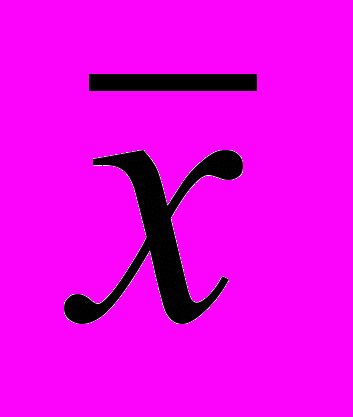
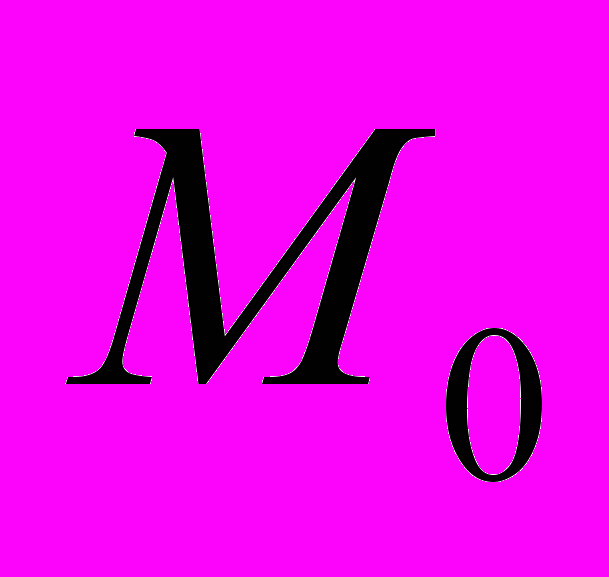
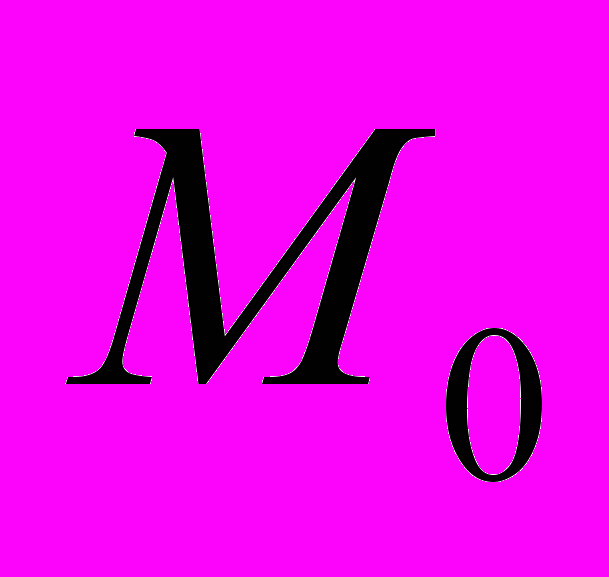
Рис.4.2


Пример 4.3. В конце года коэффициенты ликвидности предприятий- должников имели распределение

Коэффициент ликвидности	<1,5	1,5–1,7	1,7 – 1,9	1,9 – 2,1	>2,1
Частость предприятий,%	3	9	21	47	20

Определить средний коэффициент ликвидности, СКО, коэффициенты вариации и асимметрии.

В статистике принято ширину открытого интервала (в примере это крайние интервалы) принимать равными соседним интервалам. Поэтому {x_k}={1,4; 1,6; 1,8; 2,0; 2,2) и согласно (3.1), (4. 3 – 4.5), (4.8) получим











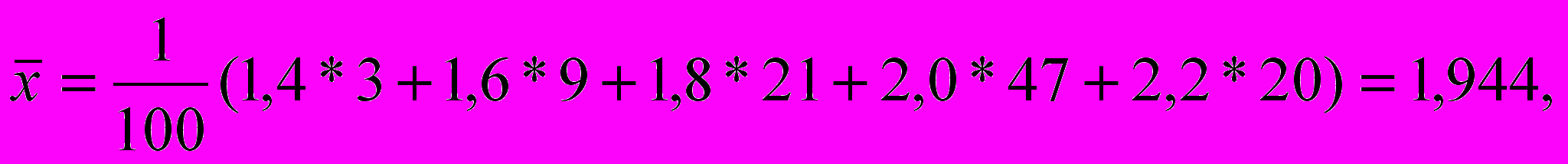
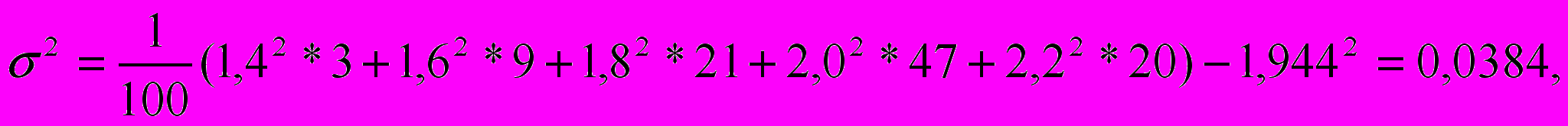
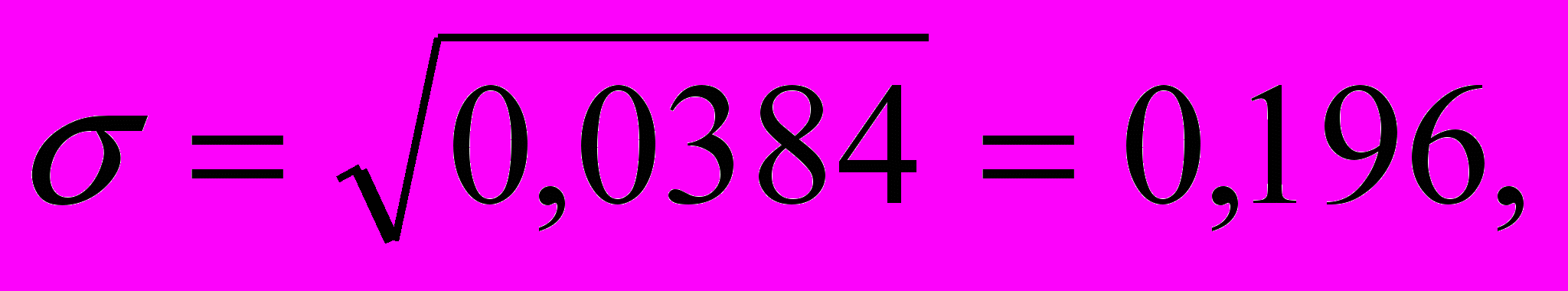
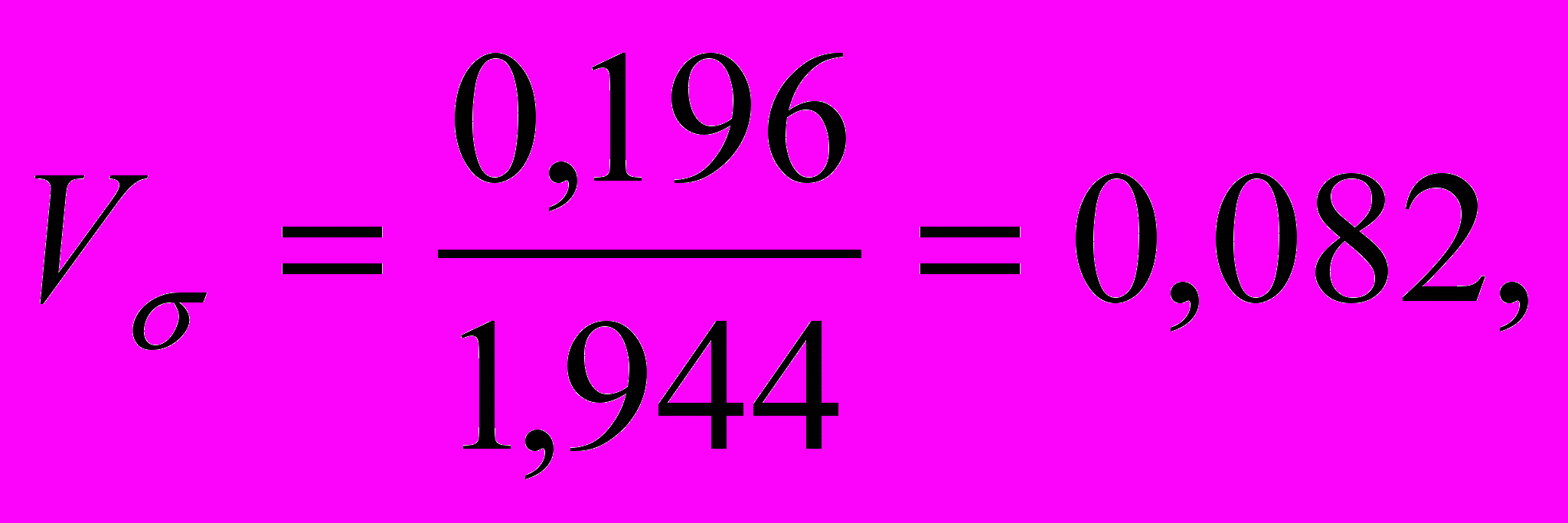
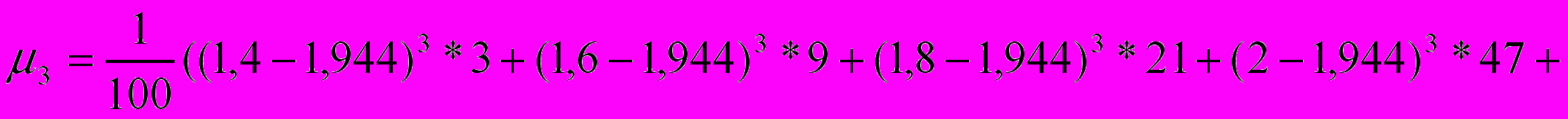
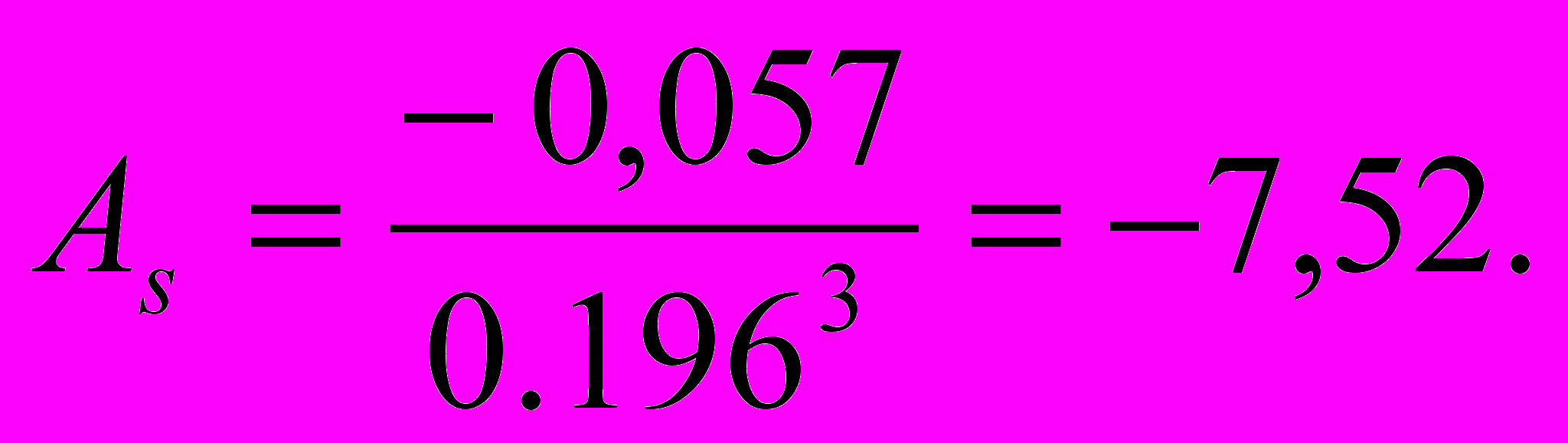
Вывод: данная выборка является весьма однородной, но с существен-ной левосторонней асимметрией.

Коэффициент эксцесса – это отношение четвертого центрального мо-мента к четвертой степени СКО минус 3, т.е.

Э
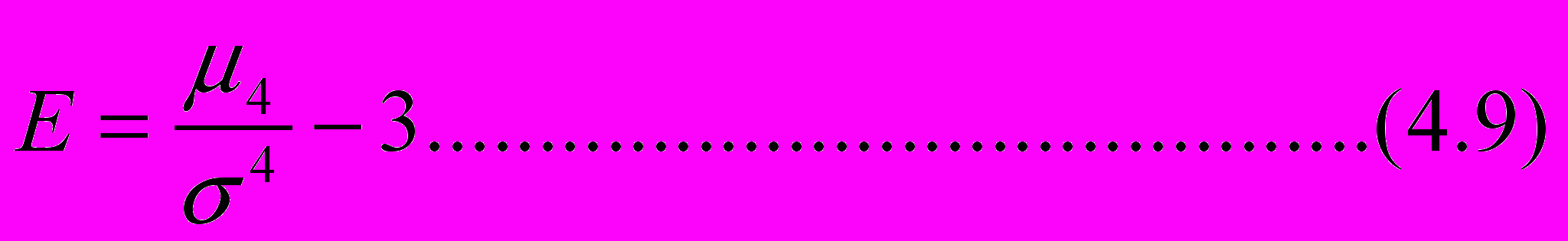
тот показатель характеризует степень островерхости распределения по сравнению с нормальным распределением, для которого Е=0. Как показано на рис.4.3, при Е>0 говорят, что распределение островерхое, а при Е<0 – плосковерхое.




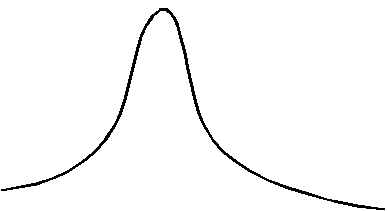
f(x)

E>0





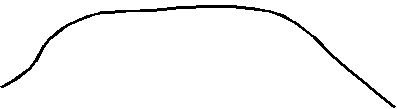
E<0





x

Рис.4.3


Пример 4.4. По данным примера 4.3 определить коэффициент эксцесса.

Согласно (4.9)





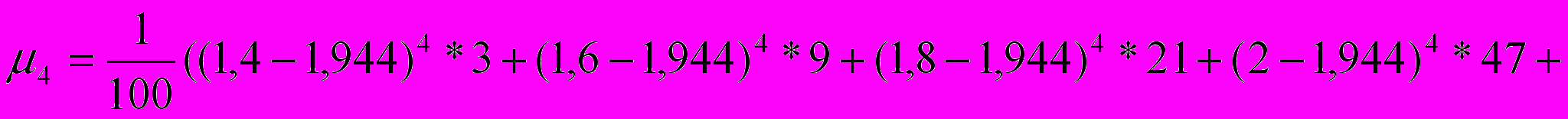
Т

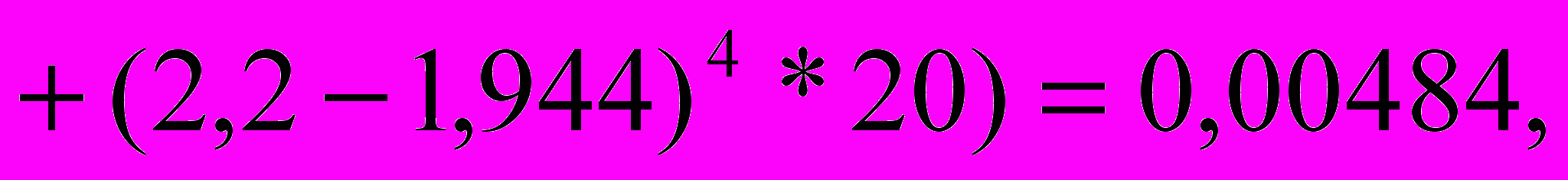
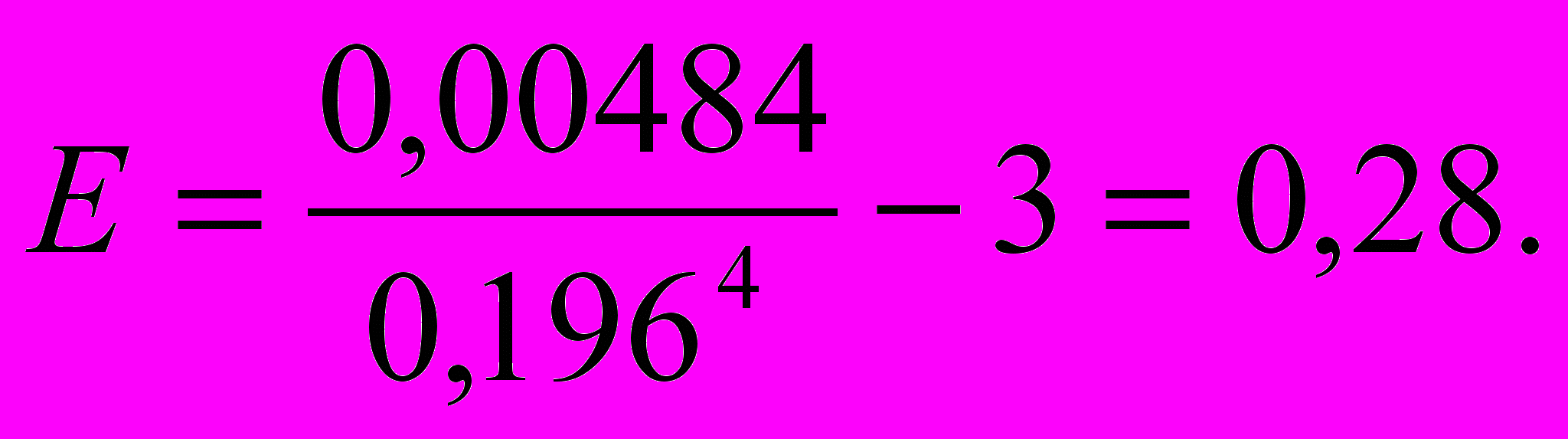
аким образом, приведенное в примере 4.3 распределение обладает некоторой островерхостью по сравнению с нормальным.

Задачи

1. В выборке из 200 семей жилплощадь на одного человека (в м²) рас-пределена следующим образом
   

Жилплощадь, м2	<7	5-7	7-9	9-11	11-13	13-15	>15
Число семей	12	34	47	50	26	18	13

Определить среднюю величину, СКО, коэффициенты вариации и асимметрии.

2. Время изготовления детали по данным 12 измерений составило (мин)
   

{26, 24, 23, 28, 25, 21, 30, 24, 29, 27, 26, 23}.

Определить среднее время изготовления детали, СКО, СЛО, коэффициенты вариации, линейной вариации и асимметрии.

3. В зависимости от номинала акции банка имеют распределение
   

Номинал, грн	<100	100-150	150-200	200-250	>250
Число акций, %	5	10	30	45	10

Определить средний номинал акций, коэффициенты вариации, асимме-трии и эксцесса.

4. Тарифные (квалификационные) разряды в отраслях А и В рас-пределяются как
   

Тарифный разряд	2	3	4	5	6
Отрасль А	9	20	35	24	12
Отрасль В	5	17	30	29	19

Для каждой отрасли определить средние значения разрядов, СКО, СЛО, коэффициенты вариации и линейной вариации. Сравнить эти показатели по отраслям и сделать выводы.

5. Процент работоспособного населения по районам страны определяется выборкой
   

{x_i}={80,2; 68,0; 72,2; 83,4; 79,1; 76,7; 85,8; 81,2; 75,5; 65,1}.

Определить показатели вариации R, CKO, СЛО, коэффициенты вариации, асимметрии и эксцесса.

Контрольные вопросы

1. Перечислите основные показатели вариации и формы распреде-ления.
   
2. Напишите выражения для определения дисперсии и СКО. Что хара-ктеризуют эти показатели. Приведите примеры. Перечислите основные свойства дисперсии.
   
3. Напишите формулу определения среднего линейного отклонения. Какое имеет место соотношение между СКО и СЛО.
   
4. Как определяются коэффициенты вариации и линейной вариации. Какая совокупность считается однородной?
   
5. В чем различие операций усреднения для сгруппированных и не-сгруппированных выборок, для дискретных и непрерывных величин (признаков)?
   
6. Дайте определение к-го центрального момента. При каких значени-ях к моменты могут быть отрицательными?
   
7. Напишите выражения для определения коэффициента асимметрии и эксцесса.
   
8. В каком случае имеет место правосторонняя и левосторонняя асимметрия?
   
9. Какими коэффициентами эксцесса характеризуются островерхие и плосковерхие распределения?
   

10.Как изменятся показатели вариации ², СКО, коэффициенты вариации и асимметрии при:

• удвоении значений всех элементов совокупности?
  
• увеличении вдвое средней величины?
  
• удвоении размаха вариации (с фиксацией левой границы)?