Программ Control System Toolbox и предназначен для анализа линейных стационарных систем

Вид материала

Документы

Содержание Simulink LTI-Viewer 11.2. Настройка Simulink LTI-Viewer Style). На данной вкладке можно выполнить настройку шрифтов окна Simulink LTI-Viewer 11.3. Экспорт модели A = имя_структуры.aB = имя_структуры.bC = имя_структуры.cD = имя_структуры.d D могут использоваться для дальнейших преобразований (создание LTI 3), an, …, a1 – значения коэффициентов полинома A в (3 1. Параллельное соединение 2. Последовательное соединение – 3. Обратная связь L определяется на основе решения алгебраического матричного уравнения Риккати. Например, при Н L и новая матрица коэффициентов обратных связей М P, являющаяся решением уравнения Риккати и собственные значения e P, являющаяся решением уравнения Риккати и собственные значения e Ts, возвращаются значения матрицы K С симметрична. На практике целесообразно решать обратную задачу. Выбирают какую-либо положительно определенную положительную мат Q также положительно определена. (Необходимое условие устойчивости матрицы А H – произвольная положительно-определенная симметричная матрица. Для определенности в уравнении (4.5) матрицу H Описание функций K, определяющая закон управления u ... Полное содержание

Подобный материал:

• Учебная программа профилирующей дисциплины теория автоматического управления, 36.13kb.
• Обработка и передача измерительной информации, 182.05kb.
• Программа учебной дисциплины «Теория линейных систем» Специальности 071500, 013900, 64.99kb.
• Обзор средств matlab и ToolBox'ов для приближения данных, 622.57kb.
• Операции с матрицами Решение систем линейных уравнений с помощью матриц Операции, 131.32kb.
• Окно элементов управления toolbox окно элементов управления ToolBox, 76.09kb.
• Isbn 5-7262-0634 нейроинформатика 2006, 93.81kb.
• Тодологию upms (unified project management system), которая предполагает интеграцию, 39.1kb.
• The Conception of Control of Projects System disupir, 167.3kb.
• Дидактические единицы гос оп по дисциплине тау, 12.23kb.

ponenta.ru/

И.В.Черных. "Simulink: Инструмент моделирования динамических систем"

11. Использование Simulink LTI-Viewer для анализа динамических систем

Инструмент Simulink LTI-Viewer входит в состав пакета прикладных программ Control System Toolbox и предназначен для анализа линейных стационарных систем. С помощью данного инструмента можно легко построить частотные характеристики исследуемой системы, получить ее отклики на единичные ступенчатое и импульсное воздействия, найти нули и полюса системы и т.д.

Краткий алгоритм работы с Simulink LTI-Viewer приведен ниже.

11.1. Работа с Simulink LTI-Viewer

1. Выполнить команду Tools\Linear Analysis... окна Simulink-модели.

В результате выполнения команды откроется окно Model_Inputs_and_Outputs как это показано на рис. 11.1, а также пустое окно Simulink LTI-Viewer .



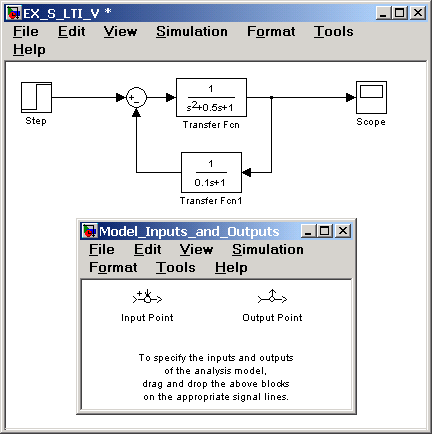
Рис. 11.1 Исследуемая модель и окно Model_Inputs_and_Outputs инструмента Simulink LTI-Viewer

2. Установить блок Input Point на входе и блок Output Point на выходе исследуемой системы, как это показано на рис. 11.2.



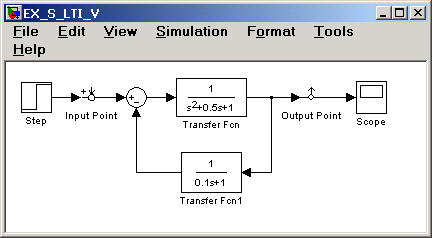
Рис. 11.2 Исследуемая модель с установленными блоками

Input Point и Output Point

3. В окне LTI Viewer выполнить команду Simulink\Get Linearized Model.

Данная команда выполняет линеаризацию модели и строит реакцию системы на единичное ступенчатое воздействие. Результат выполнения данного пункта показан на рис. 11.3



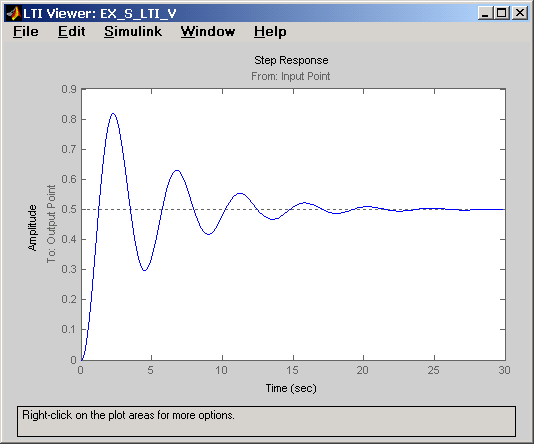
Рис. 11.3 Реакция системы на единичное ступенчатое воздействие.

Если система имеет несколько входов и выходов и для всех них установлены блоки Input Point и Output Point, то на графике будет отображено несколько окон показывающих реакцию на каждом выходе при воздействии на каждый вход.

5. Для получения остальных характеристик системы необходимо выполнить команду Edit\Plot Configuration... в окне LTI Viewer. В результате выполнения этой команды откроется окно Plot Configuration, показанное на рис. 11.4.



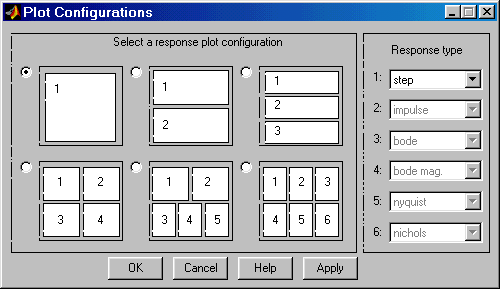
Рис. 11.4 Окно Plot Configuration

В открывшемся окне можно выбрать число отображаемых графиков (панель Select a response plot configuration) и вид отображаемых графиков (панель Response type). Для построения доступны следующие графики (диаграммы):

• step – Реакция на единичное ступенчатое воздействие.
  
• impulse – Реакция на единичное импульсное воздействие.
  
• bode – Логарифмические амплитудная и фазовая частотные характеристики.
  
• bode mag – Логарифмическая амплитудная частотная характеристика.
  
• nyquist – Диаграмма Найквиста.
  
• nichols – Годограф Николса.
  
• sigma – Сингулярные числа.
  
• pole/zero – Нули и полюса системы.
  

На рис. 11.5 приведен пример окна Simulink LTI-Viewer с несколькими различными характеристиками исследуемой системы.



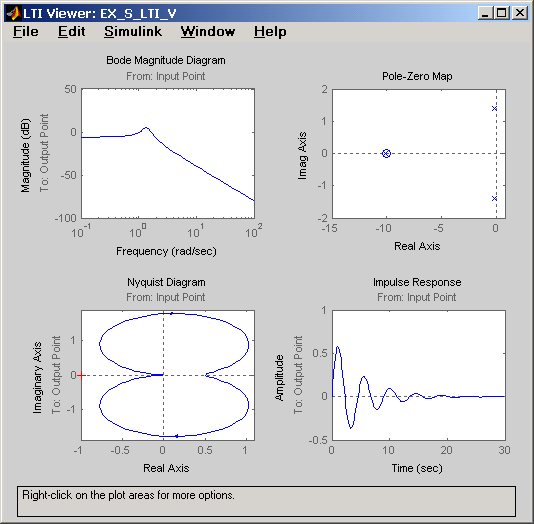
Рис. 11.5 Окно Simulink LTI-Viewer с несколькими графиками.

Настройку внешнего вида графиков можно выполнить с помощью команды Edit\Line Styles… (установка вида и цвета линий, вида маркеров).

ссылка скрыта

11.2. Настройка Simulink LTI-Viewer

С помощью команды Edit\Viewer Preferences… выполняются следующие виды настройки:

1. Установка единиц измерения (вкладка Units). Вид окна при настройке единиц измерения показан на рис. 11.6.



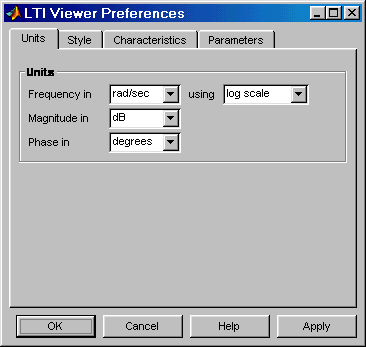
Рис. 11.6 Вкладка Units

Вкладка Units окна позволяет задать единицы измерения частоты (рад/c или Гц), уровня (dB или абсолютные единицы), фазы (градусы или радианы), а также установить вид шкалы частоты (логарифмический или линейный).

2. Установка стиля графиков (вкладка Style). На данной вкладке можно выполнить настройку шрифтов окна Simulink LTI-Viewer (панель Fonts), выбрать цвет осей графиков (панель Colors), а также задать нанесение линий сетки на графики (флажок Show grids). Внешний вид вкладки Style показан на рис. 11.7.



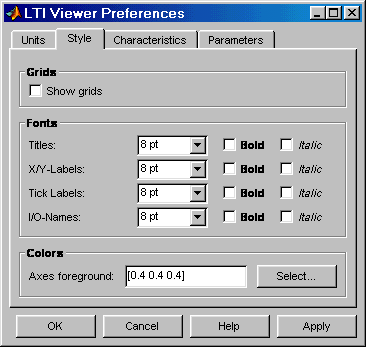
Рис. 11.7 Вкладка Style

3. Установка параметров расчета переходного процесса (вкладка Characteristics). Данная вкладка позволяет задать параметры установленные "по умолчанию" для вычисления времени нарастания и времени переходного процесса. По умолчанию Simulink LTI-Viewer вычисляет время переходного процесса как время, когда переходная функция входит в 2% зону и больше не выходит из нее (параметр Show setting time within). Также можно изменить параметры для вычисления времени переходного процесса (Show rise time from). На данной вкладке имеется также флажок Unwrap phase, установка которого позволяет избежать отображения разрывов в фазо-частотной характеристике, связанных с областью определения функции arctg, вычисляющей фазовый сдвиг. Внешний вид вкладки Characteristics показан на рис. 11.8.



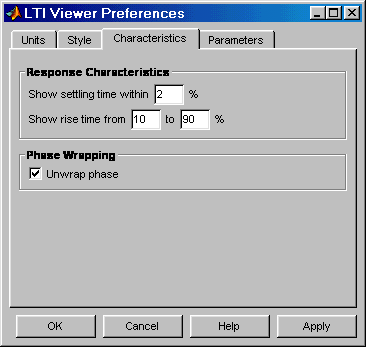
Рис. 11.7 Вкладка Characteristics

4. Установка интервалов времени и частоты (вкладка Parameters). На данной вкладке задается временной интервал для расчета переходного процесса (панель Time Vector), а также интервал частот для расчета частотных характеристик (панель Frequency Vector). Внешний вид вкладки Parameters показан на рис. 11.8.



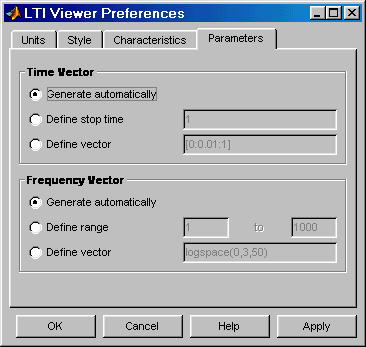
Рис. 11.8. Вкладка Parameters

Векторы времени и частоты можно вычислять в автоматическом режиме (Generate automatically), ввести конкретное значение для времени окончания расчета (Define stop time) или диапазон значений по частоте (Define range), либо задать непосредственно вектор значений времени или частоты (Define vector).

11.3. Экспорт модели

Команда File/Export позволяет выполнить экспорт модели в виде матриц уравнений пространства состояния в рабочую область MATLAB или в файл. При выполнении этой команды открывается окно диалога (см. рис. 11.9) в котором необходимо выбрать вариант экспорта.



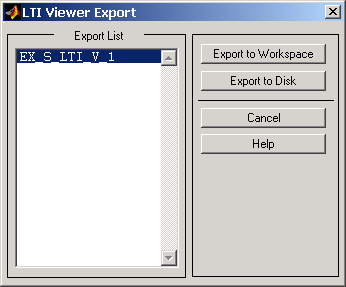
Рис. 11.9. Окно диалога при экспорте модели.

В случае экспорта в рабочую область MATLAB в ней появляется структура с именем имя_модели_1 (при последующих операциях экспорта имя_модели_2, имя_модели_3 и т.д.). Для рассматриваемой модели с именем EX_S_LTI_V.mdl имя структуры будет EX_S_LTI_V_1 . Для просмотра значений матриц уравнений пространства состояния необходимо ввести в командной строке MATLAB имя структуры и нажать клавишу Enter на клавиатуре. В командном окне появится распечатка значений матриц:

>> EX_S_LTI_V_1 % Ввод с клавиатуры (символы >> не вводятся)

a =
                 EX_S_LTI_V/T  EX_S_LTI_V/T  EX_S_LTI_V/T
   EX_S_LTI_V/T        -0.5            -1           -10
   EX_S_LTI_V/T             1             0               0
   EX_S_LTI_V/T             0             1           -10

b = 
                 Input Point
   EX_S_LTI_V/T            1
   EX_S_LTI_V/T            0
   EX_S_LTI_V/T            0

c = 
                 EX_S_LTI_V/T  EX_S_LTI_V/T  EX_S_LTI_V/T
   Output Point               0             1             0

d = 
                 Input Point
   Output Point              0

Continuous-time model.

Для работы с матрицами удобно извлечь их из структуры командами вида:

A = имя_структуры.a
B = имя_структуры.b
C = имя_структуры.c
D = имя_структуры.d

Применительно к рассматриваемой модели эти команды будут выглядеть следующим образом:

>> A=EX_S_LTI_V_1.a              % Ввод с клавиатуры (символы >> не вводятся)
A =
   -0.5000   -1.0000  -10.0000
    1.0000              0              0
             0     1.0000  -10.0000

>> B=EX_S_LTI_V_1.b              % Ввод с клавиатуры (символы >> не вводятся)
B =
    1.0000
             0
             0

>> C=EX_S_LTI_V_1.c              % Ввод с клавиатуры (символы >> не вводятся)
C =
             0    1.0000             0

>> D=EX_S_LTI_V_1.d              % Ввод с клавиатуры (символы >> не вводятся)
D =
             0

Сформированные в рабочей области матрицы A, B, C и D могут использоваться для дальнейших преобразований (создание LTI-объектов, переход к передаточным функциям, переход к дискретным моделям и т.д.).


Е.В.Никульчев. Пособие "Control System Toolbox"
Динамические и частотные характеристики систем автоматического управления

Краткие сведения из теории

Рассмотрим систему автоматического управления (САУ), описываемую линейным (линеаризованным) дифференциальным уравнением вида:

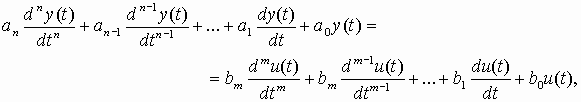   (1)

где u(t) – входной процесс, y(t) – выходной процесс, a_i, b_j, (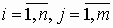) – постоянные коэффициенты,
n, m (n >=m) – постоянные числа. В операторной форме выражение (1) может быть записано –

.

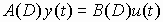Здесь D – оператор дифференцирования 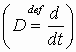. Отсюда преобразование “вход-выход” системы –

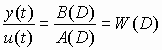,                                                                                                      (2)

W(D) называется операторной передаточной функции.

Один из способов моделирования систем заключается в представлении преобразования “вход-выход” в виде комплексной передаточной функции:

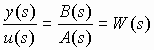,                                                                                                            (3)

которая получается путем применения преобразования Лапласа к (2) при начальных нулевых условиях. Здесь s - комплексная переменная. Связь между операторной (2) и комплексной (3) передаточными функциями можно записать в виде

.

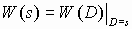Комплексные числа, являющиеся корнями многочлена В(s), называются нулями передаточной функции, а корни многочлена A(s) – полюсами.

Динамические свойства систем характеризуют реакции на входные воздействия специального вида. В частности анализ выхода системы на единичный скачок и  -функцию (дельта-функцию).

Пусть u(t) = 1(t), то есть на вход системы подается функция Хевисайда (единичный скачок), определяемая



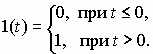
График функции Хевисайда приведен на рис. 1.1. Реакция САУ на единичный скачок называется переходной функцией системы и обозначается h(t).



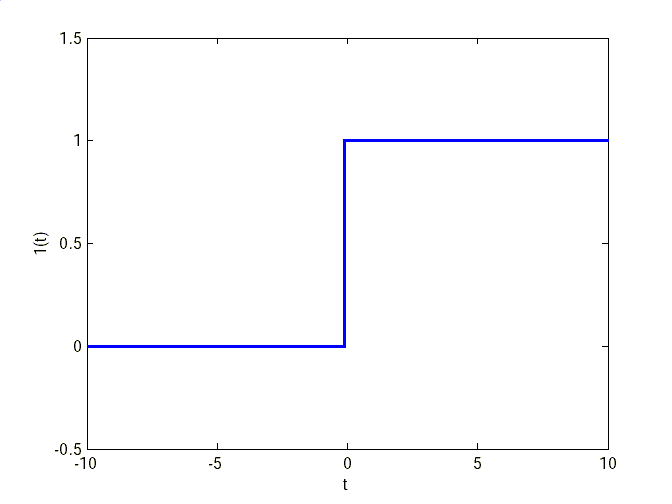
Рис. 1.1. Функция Хевисайда


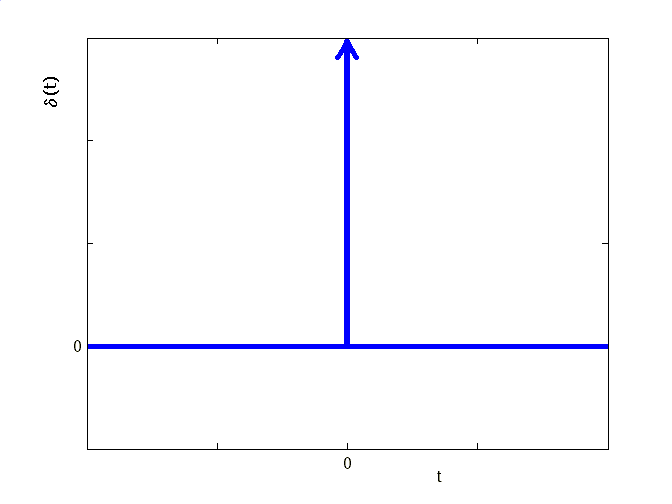
Рис. 1.2. Функция Дирака

Если u(t) =  (t), то есть на вход системы поступает функция Дирака ( -функция, импульсная функция, рис. 1.2) определяемая



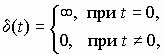
то реакция САУ называется импульсной переходной функцией системы и обозначается w(t).

Импульсная и переходная функции системы связаны соотношением:

.

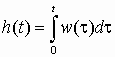Благодаря широкому применению при исследовании устойчивости динамических систем и проектировании регуляторов получили распространение частотные характеристики.

Пусть на вход системы с передаточной функцией W(s) подается гармонический сигнал

u(t) = a_u cos( t), t >0.

В этих условиях справедлива следующая теорема: Если звено является устойчивым, то установившаяся реакция y(t) на гармоническое воздействие является функцией той же частоты с амплитудой

a_y = a_u |W(i )|,

и относительным сдвигом по фазе

y = arg W(i ).

Таким образом:

y(t) = a_u |W(i )| cos( t + arg W(i )),

где i – комплексная единица, 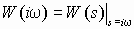– частотная характеристика.

Частотной характеристикой W(i ) стационарной динамической системы называется преобразование Фурье переходной функции:

,

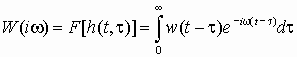где w(t –  ) – импульсная переходная функция.

Связь между комплексной передаточной функцией и частотной характеристикой определяется соотношением:



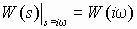
При фиксированном значении w частотная характеристика является комплексным числом, и, следовательно, может быть представлена в виде

.

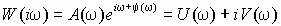Здесь

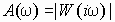– амплитудно-частотная характеристика (АЧХ);

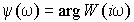– фазово-частотная характеристика (ФЧХ);

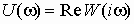– вещественная частотная характеристика (ВЧХ);

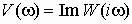– мнимая частотная характеристика (МЧХ).

Геометрическое место точек W(i ) на комплексной плоскости при изменении   от  ₀ до от  ₁ (обычно
 ₀ = 0,  ₁ = 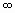 ), называется амплитудно-фазовой характеристикой (АФХ) или частотным годографом Найквиста.

Имеет широкое практическое значение диаграмма Боде (логарифмическая амплитудная характеристика, ЛАХ), которая определяется как L = 20 lg A( ), измеряется в децибелах и строится как функция от lg ..

Получение характеристик САУ

Постановка задачи

В качестве объекта исследования выступают линейные (линеаризованные) динамические стационарные системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов

.

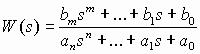Необходимо:

1. Определить полюса и нули передаточной функции
   

, .

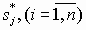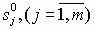2. Построить графики переходной и импульсно-переходной функции:
   

h(t), w(t).

3. Построить логарифмические частотные характеристики
   

L ( ).

4. Построить частотный годограф Найквиста
   

W(i ), w = [0, ].

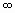Для решения задачи используется пакет прикладных программ (ППП) Control System Toolbox 5 [ссылка скрыта] системы инженерных расчетов MatLab. ППП предназначен для работы с LTI-моделями (Linear Time Invariant Models) систем управления.

В Control System Toolbox имеется тип данных, определяющих динамическую систему в виде комплексной передаточной функции. Синтаксис команды, создающий LTI-систему c одним входом и одним выходом, в виде передаточной функции:

TF([b_m, …, b₁, b₀], [a_n, …, a₁, a₀]),

b_m, …, b₁ – значения коэффициентов полинома В в ( 3),

a_n, …, a₁ – значения коэффициентов полинома A в (3).

Таблица 1. Некоторые команды Control System Toolbox

Синтаксис	Описание
pole()	Вычисление полюсов передаточной функции
zero()	Вычисление нулей передаточной функции
step()	Построение графика переходного процесса
impulse()	Построение графика импульсной переходной функции
bode()	Построение логарифмических частотных характеристик (диаграммы Боде)
nyquist()	Построение частотного годографа Найквиста

Для определения корней полиномов степени k   может также применяться команда MatLab

roots(P),

которая в качестве аргумента P получает матрицу коэффициентов полинома [p_k, …, p₀].

Другим вариантом получения графиков динамических характеристик САУ является использование графического интерфейса ППП CST – LTI viewer, вызов которого осуществляется командой

ltiviewer,

которой в качестве параметра можно указать имя переменной, содержащей LTI-объект.

Пример

Пусть задана передаточная функция САУ

.

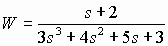Найдем ее динамические и частотные характеристики с использованием ППП Control System Toolbox системы MatLab. Будем работать в командном режиме.

1. Создадим LTI-объект с именем w, для этого выполним:



2. Найдем полюса и нули передаточной функции с использованием команд pole, zero.



3. Построим переходную функцию командой step(w). Результат ее выполнения приведен на рис. 1.3.



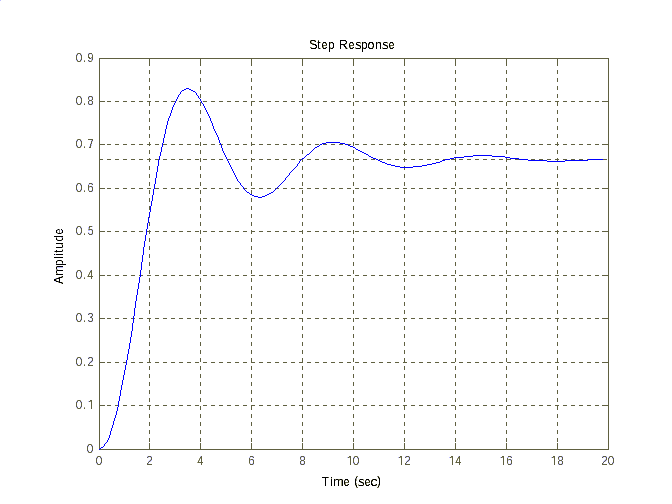
Рис.1.3. Переходная функция h(t)

4. Построим импульсную переходную функцию командой impulse(w). Результат показан на рис. 1.4.



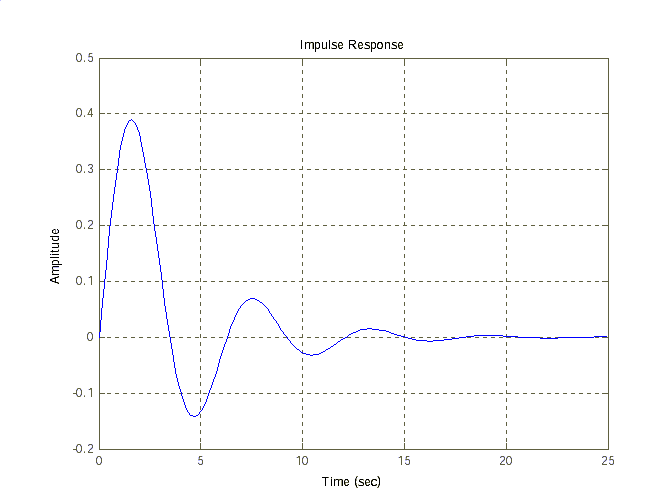
Рис 1.4. Импульсная переходная функция

5. Диаграмму Боде получим, используя команду bode(w) – рис. 1.5.



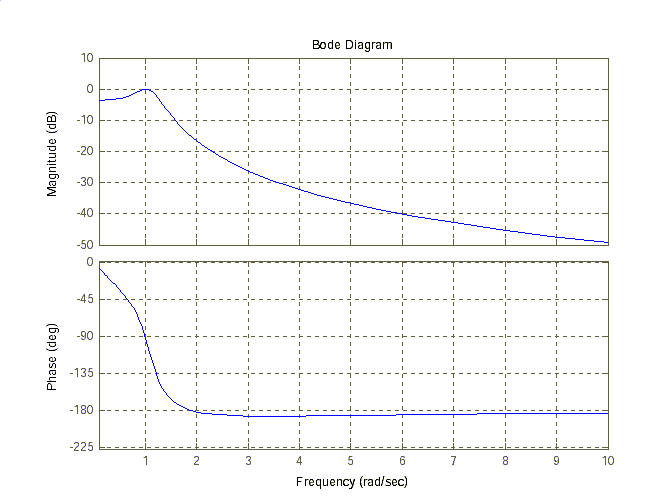
Рис. 1.5. Логарифмические частотные характеристики

6. Определим частотный годограф Найквиста, выполнив команду nyuivist(w) – рис. 1.6.



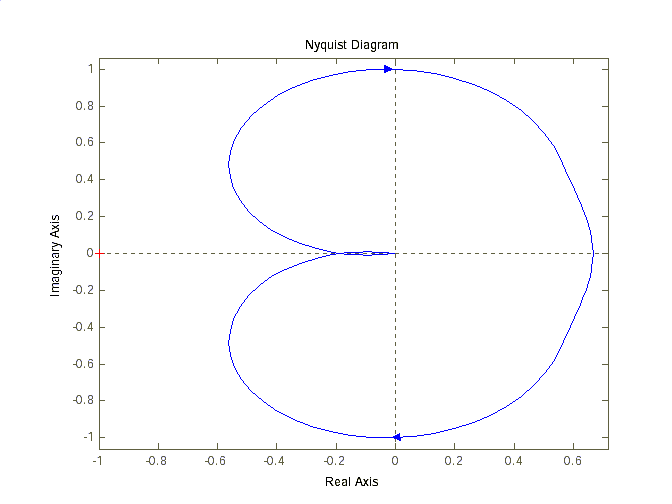
Рис. 1.6. Частотный годограф

Аналогичные результаты (рис. 1.7) можно получить, используя команду ltiviewer(w), с соответствующими настройками в меню “Plot Configuration".



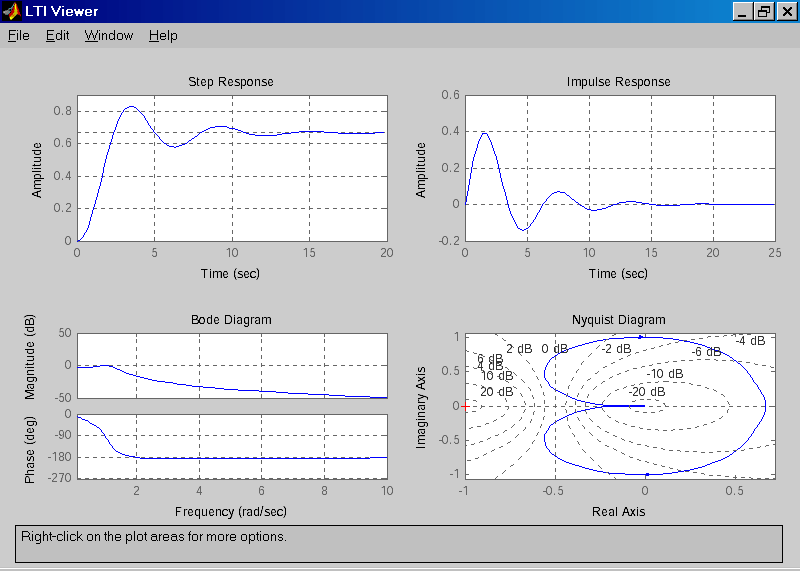
Рис. 1.7. LTI-viewer

Краткие сведения из теории

В ряде случаев, имеющих практическое значение, модель линейной системы автоматического управления (САУ) задается в виде структурной схемы, состоящей из типовых звеньев, математическое описание которых задано в операторной форме. Связь между входом и выходом системы задается в виде передаточной функции W(s) [ссылка скрыта]. B общем виде передаточную функцию W(s) можно представить в виде:

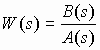                                                                                                           (1)

где s – комплексная переменная, B(s) – полином степени m; A(s) – полином степени n.

Для физически реализуемых САУ m <= n. Коэффициенты указанных полиномов действительные числа.

Применение метода корневого годографа (КГ) обусловлено фундаментальной зависимостью поведения линейной САУ от полюсов и нулей ее передаточной функции. Под полюсами подразумеваются корни полинома - знаменателя A(s), а под нулями - корни полинома числителя B(s). Полином A(s) называется также характеристическим многочленом передаточной функции W(s).

Положение полюсов W(s) на комплексной плоскости определяет устойчивость САУ, а в совокупности с нулями вид импульсной переходной функции w(t) и переходной функции h(t).

Метод корневого годографа позволяет находить полюса и нули передаточной функции замкнутой системы, располагая полюсами и нулями разомкнутой системы при изменении коэффициента усиления разомкнутой системы k.

Передаточную функцию разомкнутой системы W_p(s) представим в виде:

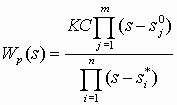,                                                                                                               (2)

где 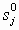– нули передаточной функции W_p(s), (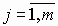); 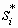– полюса передаточной функции W_p(s), (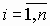), n  и m – порядки знаменателя и числителя; K - коэффициент усиления разомкнутой системы; C - коэффициент представления.

Передаточная функция разомкнутой системы, как правило, задается в виде отношения произведений передаточных функций стандартных (типовых) звеньев, при описании которых используются выражения трех видов:

Ts                                                                                                                                    (3)

Ts +1                                                                                                                               (4)

T ²s ² + 2T  s + 1                                                                                                             (5)

Здесь Т - постоянная времени [с].

Если выражения (3), (4), (5) стоят в знаменателе передаточных функций звеньев (в числителе 1), то звенья называются соответственно интегрирующим, апериодическим, колебательным. Для колебательного звена  - безразмерный коэффициент затухания (0< <1). Если выражения (3), (4), (5) стоят в числителе передаточных функций звеньев (1), то звенья называются соответственно дифференцирующим, форсирующим первого порядка, форсирующим второго порядка.

Для перехода от стандартной формы записи к формуле (2) необходимо вычислить полюса и нули соответствующих типовых звеньев.

Для передаточных функций, использующих выражение (3) –

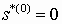,                                                                                                                                         (6)

использующих выражение (4) –

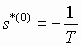,                                                                                                                                     (7)

использующих выражение (5) –

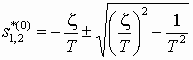,                                                                                                         (8)

или

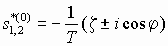                                                                                                                (9)

где j = arcsin  .

Коэффициент представления C вычисляется по формуле

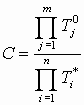                                                                                                                                     (10)

Для звеньев, использующих выражение (5), соответствующая постоянная времени входит в выражение (10) в квадрате.

При замыкании системы с передаточной функцией W_p(s) единичной обратной связью передаточная функция замкнутой системы W_з(s) принимает вид:

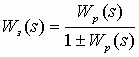,                                                                                                                      (11)

где знак "+" соответствует отрицательной обратной связи; знак "–" соответствует положительной обратной связи.

Структурная схема системы с обратной связью приведена на рис. 2.1.

 



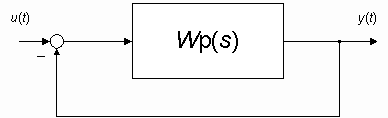
Рис. 2.1. Структурная схема САУ

Из (11) следует, что нули передаточной функции замкнутой системы равны нулям передаточной функции разомкнутой системы.

Для определения полюсов замкнутой системы необходимо решить уравнение:

W_p(s) = – 1.                                                                                        (12)

Так как W_p(s) является функцией комплексного переменного s, то уравнение (12) распадается на два уравнения:

– уравнение модулей:

|W(s)|=1                                                                                                                                              (13)

– уравнение аргументов:

arg W(s) = ± (2 +1) ,  =0, 1, 2, …                                                                                                      (14а)

для отрицательной обратной связи и

arg W(s) = ± 2 ,  =0, 1, 2, …                                                                                                                (14б)

для положительной обратной связи.

Уравнения (14) имеют наглядный геометрический смысл. Если точка s является полюсом замкнутой системы, то проведя в точку s вектора из всех нулей W_p(s) (обозначим аргументы этих векторов 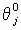) и вектора из всех полюсов W_p(s) (обозначим аргументы этих векторов 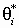), уравнение (14а) можно записать в следующем виде:

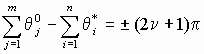,   = 0, 1, 2, …                                                                              (15a)

а уравнение (14б) в виде:

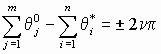,  = 0, 1, 2, …                                                                                             (15б)

Углы  отсчитываются от положительного направления действительной оси. Знак угла "+" соответствует повороту против часовой стрелки, знак угла "–" соответствует повороту по часовой стрелке.

Геометрическое место точек на комплексной плоскости “s”, удовлетворяющее выражениям (15а) и (15б) называется корневым годографом.

Как следует из (15), конфигурация корневого годографа не зависит от коэффициента усиления K, но каждому конкретному значению K однозначно соответствуют точки на корневом годографе.

Для определения этого соответствия достаточно воспользоваться уравнением (13) в следующей интерпретации:

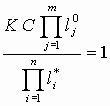,                                                                                                                             (16)

где – модуль (длина) вектора, проведенного из j-нуля в точку s   КГ; 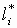– модуль вектора, проведенного из i-полюса в ту же точку s.

Для систем небольшого порядка m, n <  5 - 7 построение КГ можно осуществлять “вручную” (с помощью транспортира и линейки).

Приведем свойства корневых годографов (случай отрицательной обратной связи):

1. Ветви корневого годографа непрерывны и расположены на комплексной плоскости симметрично относительно действительной оси.

2. Число ветвей КГ равно порядку системы n. Ветви начинаются в n полюсах разомкнутой системы при K = 0. При возрастании K от 0 до бесконечности полюса замкнутой системы двигаются по ветвям КГ.

3. Отрезки действительной оси, по которым перемещаются действительные полюса замкнутой системы являются действительными ветвями корневого годографа. Эти ветви находятся в тех частях действительной оси, справа от которых расположено нечетное общее число действительных полюсов и нулей разомкнутой системы.

4. m ветвей КГ при возрастании K от 0 до бесконечности заканчиваются в m нулях W_p(s), a (n – m) ветвей при K, стремящемся к бесконечности, удаляются от полюсов вдоль асимптот.

5. Асимптоты в виде звезды из (n – m) полупрямых выходят из точки с координатой



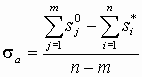
на действительной оси под углами



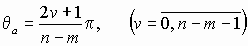
к действительной оси.

6. Угол выхода 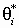ветви КГ из полюса 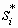определяется из уравнения (15а), примененного к данному полюсу. Аналогично определяется угол входа ветви КГ в нуль .

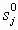7. При расположении ветвей корневого годографа в левой полуплоскости s САУ устойчива. При пересечении ветвей КГ мнимой оси слева направо САУ становится неустойчивой. Пусть при K = K^кр пересечение КГ с мнимой осью произойдет в некоторой точке i ^кр. Назовем это значение коэффициента усиления критическим K^кр, а величину    ^кр критической угловой частотой, на которой система становится неустойчивой.

Метод КГ позволяет выбрать коэффициент усиления САУ, подобрать расположение полюсов и нулей передаточной функции корректирующих звеньев, определить параметры доминирующих полюсов САУ (ближайших к началу координат плоскости s).

В качестве примеров, приведем КГ для двух систем автоматического управления.

На рисунке 2.2а приведен корневой годограф САУ, передаточная функция разомкнутой системы, которой равна:

.

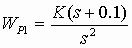Рисунок 2.2б иллюстрирует КГ САУ с передаточной функцией разомкнутой системы вида:

.



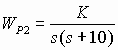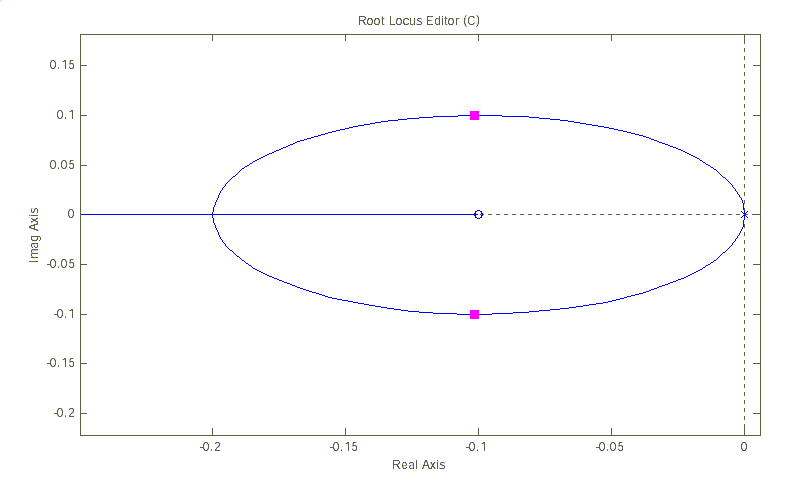
а)



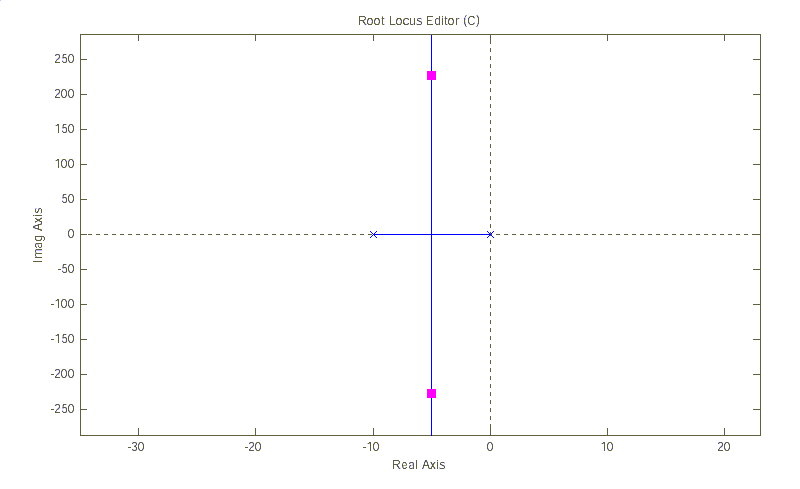
б)

Рис.2.2. Примеры корневых годографов

Построение корневых годографов

Постановка задачи

Дана модель разомкнутой системы, записанная в виде отношения произведений типовых звеньев.

Необходимо:

1. Построить корневой годограф.
   
2. Получить коэффициент усиления K^кр, при котором система находится на границе устойчивости.
   
3. Вычислить частоту   ^кр, при которой в системе возникают незатухающие колебания.
   

Для решения задачи используется GUI-интерфейс “SISO-Design Tool” из пакета прикладных программ Control System Toolbox [ссылка скрыта] системы инженерных расчетов MatLab.

Графический интерфейс предназначен для анализа и синтеза одномерных линейных (линеаризованных) систем автоматического управления (SISO - Single Input/Single Output).

В Control System Toolbox имеется тип данных, определяющих динамическую систему в виде набора полюсов, нулей и коэффициента усиления передаточной функции. Синтаксис команды, создающий LTI (Linear Time Invariant)-систему в виде объекта ZPK (zero-pole-gain) c одним входом и одним выходом

ZP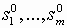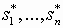K([], [], K)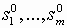

– значения нулей системы, 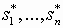– значения полюсов системы, K – коэффициент усиления.

Более естественным является вариант, при котором с помощью функции ZPK создается символьная переменная 's', которая затем используется для определения передаточной функции в виде отношения (2). Например, после выполнения команд

s = zpk('s'); W1 = (s+0.1)/(s2)

произойдет создание переменной W1 типа ZPK, определяющей передаточную функцию вида .

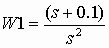Запуск графического интерфейса SISO-Design Tool осуществляется командой

sisotool

или выбором соответствующего пункта в окне “Launch Pad".

Необходимо выбрать в меню View пункт Root Locus (корневой годограф), для отображения редактора Root Locus Editor. В правом верхнем углу SISO-Design Tool можно менять тип обратной связи (кнопка '+/–') и структурную схему САУ. Предполагается наличие отрицательной обратной связи, и структурной схемы, показанной на рис.2.1.

Для загрузки данных из рабочего пространства MatLab необходимо использовать меню “File/Import”, в результате чего появляется диалог Import System Data. Необходимо, чтобы в результате импортирования данных получилась рассматриваемая схема САУ (рис.2.1).  Изменение динамических и частотных характеристик замкнутой системы при изменении К можно проследить используя меню "Tools/Loop Responses".

Пример

Пусть необходимо исследовать САУ с передаточной функцией разомкнутой системы:

.

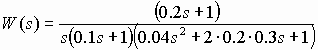1. Создадим ZPK-объект, найдем полюса и нули разомкнутой системы:



2. Запустим SISO-Design Tool, настроим параметры и импортируем ZPK-объект из рабочего пространства MatLab (рис.2.3). В окне Root Locus Editor интерфейса SISO-Design Tool построится корневой годограф (рис. 2.4).



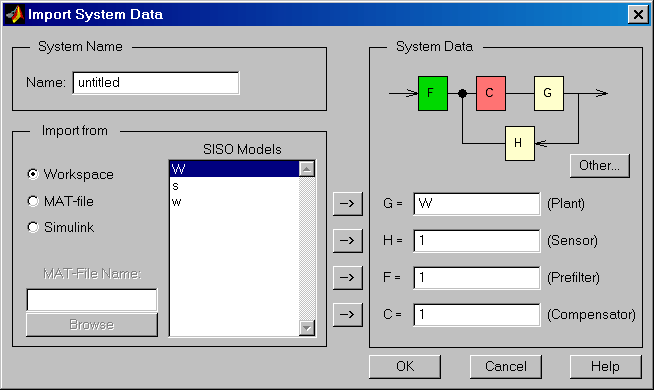
Рис. 2.3. Диалог импортирования данных в SISO-Design Tool



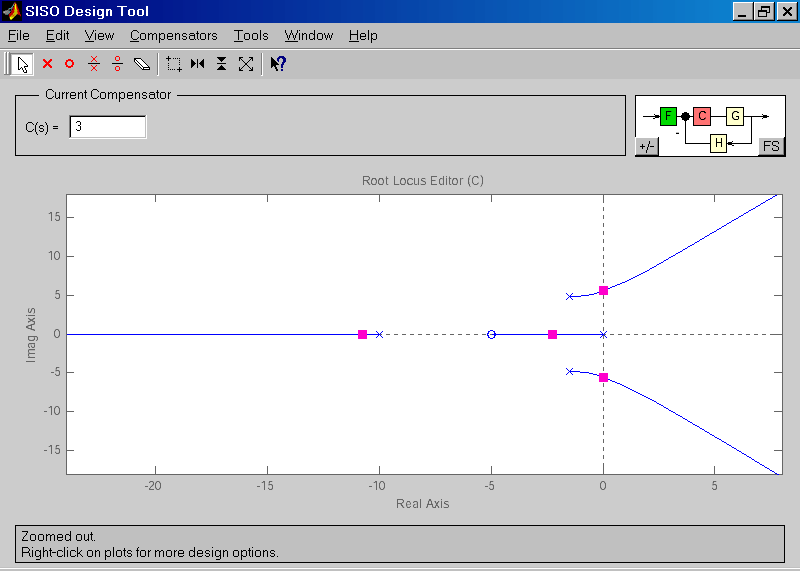
Рис 2.4. SISO-Design Tool

3. Двигая красным курсором по корневому годографу до пересечения ветвей с мнимой осью, определить значение K^кр (рис. 2.5). В данном случае K^кр » 3. Значение  ^кр соответствует мнимой координате пересечения КГ мнимой оси. Просмотреть это значение можно в нижней части интерфейса или выбрав меню "View/Closed-Loop Poles" (рис. 2.6).



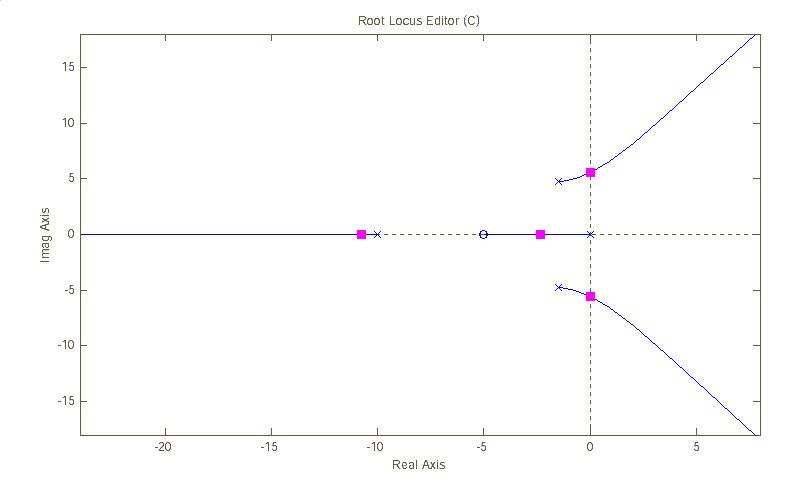
Рис. 2.5. Корневой годограф с нанесенным значением K^кр   



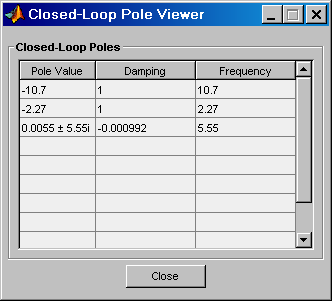
Рис. 2.6. Closed-Loop Poles Viewer

Постановка задачи

Даны математические модели трех систем и структурная схема, представляющая собой соединение этих систем. Необходимо:

• получить модель результирующей системы в пространстве состояний,
  
• исследовать наблюдаемость и управляемость трех подсистем в отдельности, и общей системы.
  

Многомерные системы, в отличие от одномерных имеют несколько входов и несколько выходов.

Для описания таких систем используются три набора параметров (три вектора), см рис.1:

1. вектор входных воздействий (управлений);
   
2. вектор переменных состояний;
   
3. вектор выходных параметров
   

и двумя преобразованиями:

1. Преобразование “входы-состояния”
   
2. Преобразование “состояния-выходы”.
   

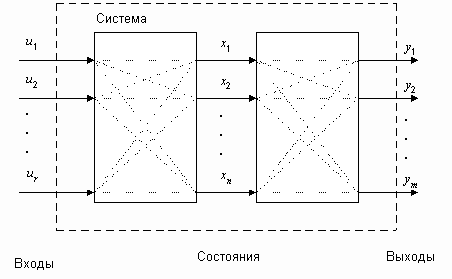
Рис.1. Многомерные системы

Широкое распространение, обусловленное разработанным математическим аппаратом, получили линейные модели многомерных систем в пространстве состояний, которые имеют вид:

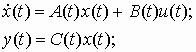                                 (1)

первое соотношение называется уравнением состояния, второе – уравнением выхода. Здесь x = (x₁, x₂, …, x_n)^T  Rⁿ – вектор переменных состояний; u = (u₁, u₂, …, u_r)^T  U  Rⁿ – вектор управлений; y = (y₁, y₂, …, y_m)^T  Rⁿ – вектор измеряемых параметров; t – время; A(t), B(t), C(t) – матрицы размерности (n n), (n r), (m n) соответственно. Предполагается, что известны начальные состояния x(t₀) = x₀, где t₀ – начальный момент времени.

Если матрицы A(t), B(t), C(t) не зависят от времени t, то система называется стационарной. В пакете предполагается, что системы стационарны.

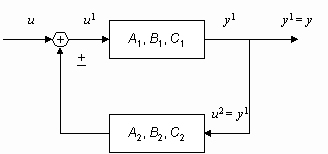
Рассмотрим задачи соединения двух подсистем в систему. При соединении возможны три варианта (рис. 2): параллельное (а), последовательное (б) и в обратной связи (в). Предполагается, что обе системы описываются в пространстве состояний соотношениями:

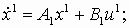y¹ = C x¹;

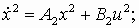y² = C x²;

где x¹, u¹, y¹ – векторы состояний, управлений, выходов первой системы, x², u², y² – второй. Необходимо по известным матрицам A₁, B₁, C₁, A₂, B₂, C₂ получить матрицы A, B, C (рис. 2.г).



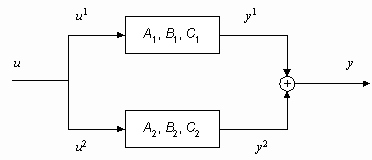
a)



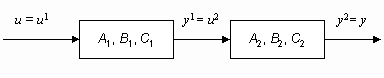
б)



в)



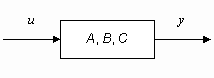
г)

Рис. 2. Соединение двух систем