Задача курсовой работы состоит в изучении выборочным методом производственных и финансовых показателей

Вид материала

Задача

Содержание 1. Понятие о выборочном наблюдении, его применение в статистике. 2. Преимущества выборочного метода 3. Примеры применения выборочного метода 4. Основные проблемы выборочного обследования 5. Практическая часть Список используемой литературы.

Подобный материал:

• Методические рекомендации по выполнению курсовой работы Целями данной курсовой работы, 260.08kb.
• 3 Прогнозирование дополнительных финансовых потребностей, 207.95kb.
• Елью данной курсовой работы является изучение издержек производства, их сущности, путей, 380.64kb.
• Методические указания по выполнению курсовой работы. По изучении дисциплин «Финансовое, 108.28kb.
• Оформляется отчёт о курсовой работе. Проводится защита курсовой работы, 33.31kb.
• Моделирование финансовых кризисов. Цель курсовой работы, 193.64kb.
• Пояснительная записка курсовой работы "Обработка экономической информации с помощью, 269.69kb.
• Методические рекоммендации по написанию курсовой работы по направлению «Финансовое, 48.95kb.
• Состав и содержание курсовой работы, 8.25kb.
• Методические указания по выполнению курсовой работы по дисциплине сд. 01 «Бухгалтерский, 869.3kb.

Содержание

Введение

Выборочное наблюдение – одно из наиболее современных видов статистического наблюдения. Выборочное наблюдение – это такое наблюдение, при котором обследованию подвергается часть единиц изучаемой совокупности, отобранных на основе научно разработанных принципов, обеспечивающих получение достаточного количества достоверных данных, для того чтобы охарактеризовать всю совокупность в целом.

Средние и относительные показатели, полученные на основе выборочных данных, должны достаточно полно воспроизводить или репрезентатировать соответствующие показатели совокупности в целом.

Задача курсовой работы состоит в изучении выборочным методом производственных и финансовых показателей.

В первой части работы мы даем определение выборочному методу в статистике, затем рассматриваем основные преимущества и проблемы применения выборочного метода в статистике и приводим примеры использования этого метода в реально жизни.

В практической части работы решается задача нахождения средних значений при помощи выборочного метода.

1. Понятие о выборочном наблюдении, его применение в статистике.

Выборочное наблюдение - это вид не сплошного наблюдения, при котором обследуется часть единиц совокупности, отобранной на основе научно разработанных принципов и результат распространяется на всю изучаемую совокупность.

Особенностью выборочного метода наблюдения является то, что при отборе единиц в выборочную совокупность обеспечивается равная возможность каждой единицы наблюдения попасть в выборку, а также вычислить ошибку выборки или ошибку репрезентативности.

Разработка метода выборочного наблюдения основана на законе больших чисел, теории Бернули, Чебышева, Ляпунова¹.

Преимущества выборочного метода перед сплошным:

1. экономия времени, труда, материальных и денежных затрат,
   
2. в ряде случаев не возможно применять сплошное наблюдение,
   
3. выборочное наблюдение обеспечивает расширенные программы наблюдения,
   
4. сокращает сроки получения конечного результата,
   
5. повышает достоверность результата обследования.
   

Применение выборочного метода на практике:

1. контроль качества продукции,
   
2. изучение занятости населения и проблем безработицы,
   
3. для изучения малых предприятий,
   
4. при изучении уровня цен, расчет индекса потребительских цен,
   
5. при формировании рынка ценных бумаг,
   
6. исследование бюджета семей рабочих и служащих
   

2. Преимущества выборочного метода

Наши знания, суждения и поступки в очень большой мере основаны на выборочных данных. Это утверждение одинаково справедливо как для повседневной жизни, так и для научных исследований. Впечатление об учреждении, в котором ежедневно производятся тысячи различных операций, складывается часто на основании лишь одного или двух посещений этого учреждения за несколько лет. Путешественник, проведя десять дней в чужой стране, собирается написать книгу и в ней посоветовать жителям этой страны, как оживить промышленность, преобразовать политическую систему, сбалансировать бюджет и улучшить питание в гостиницах. Это - персонаж анекдотический. Но на самом деле, от ученого-обществоведа, который прожил 20 лет в этой стране, изучая ее, он отличается лишь тем, что основывает свои выводы на гораздо меньшем числе наблюдений, да еще, вероятно, меньше осведомлен о степени своего невежества. И в науке и в житейских делах нам доступен для изучения лишь фрагмент той общей картины, которая должна расширить наши знания².

Тому, как правильно получить выборку и как сделать по ее данным обоснованные выводы, еще лет 30 назад не уделяли внимания. Эти проблемы не играли бы особой роли, если бы материал, из которого мы производим отбор, был однороден, так что любая выборка дала бы приблизительно одинаковые результаты. Заключение о состоянии нашего здоровья делается по нескольким каплям крови, проанализированным в лаборатории. Такой метод основан на предположении, что циркулирующая кровь всегда хорошо перемешана и каждая ее капля несет одинаковую информацию, - предположении, в правильность которого мы, будучи неспециалистами, свято верим. Однако, когда изучаемый материал далеко не однороден, как это часто и бывает, способ получения выборки приобретает решающее значение, а изучение методов, позволяющих получить достоверные сведения, становится весьма важным.

3. Примеры применения выборочного метода

Выявление главных факторов, влияющих на качество продукции позволяет увязать показатели производственного качества с каким-либо показателем, характеризующим потребительское качество.

В результате специально организованных наблюдений за результатами носки обуви и последующей статистической обработки полученных данных, было установлено, что срок службы обуви (у), зависит от двух переменных: плотности материала подошвы в г/см³ (х1) и предела прочности сцепления подошвы с верхом обуви в кг/см² (х2). Вариация этих факторов на 84,6% объясняет вариацию результативного признака (множественный коэффициент коррекции R = 0,92), а уравнение регрессии имеет вид:

у = 6,0 + 4,0 * х1 + 12 * х2

Таким образом, уже в процессе производства зная характеристики факторов х1 и х2 можно прогнозировать срок службы обуви. Улучшая вышеназванные параметры, можно увеличить срок носки обуви. Исходя из необходимого срока службы обуви, можно выбирать технологически допустимые и экономически оптимальные уровни признаков производственного качества.

Наибольшее практическое распространение имеет характеристика качества изучаемого процесса путем оценки качества результата этого процесса. В этом случае речь о контроле качества изделий, деталей, получаемых на той или иной операции. Наибольшее распространение имеют несплошные методы контроля, а наиболее эффективны те из них, которые базируются на теории выборочного метода наблюдения.

На электроламповом заводе цех производит электролампочки.

Для проверки качеств ламп отбирают совокупность 25 штук и подвергают испытанию на специальном стенде (меняется напряжение, стенд подвергается вибрации и т. д.). Каждый час снимают показания о продолжительности горения ламп. Получены следующие результаты:

6; 6; 4; 5; 7;

5; 6; 6; 7; 8;

5; 7; 7; 6; 4;

5; 6; 8; 7; 5;

7; 6; 5; 6; 6.

Прежде всего необходимо построить ряд распределения.

Продолжительность горения (х)	частота (f)	x*f		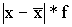	В % к итогу	Накопленный процент
4	2	8	4	8	8	8
5	6	30	6	6	24	32
6	9	54	0	0	36	68
7	6	42	6	6	24	92
8	2	16	4	8	8	100
	25	150	20	28	100	–

Затем следует определить

1) среднюю продолжительность горения ламп:

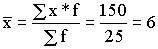часов;

2) Моду (вариант, который чаще всего встречается в статистическом ряду). Она равна 6;

3) Медиану (значение, которое расположено в середине ряди. Это такое значение ряда, которое делит его численность на две равные части). Медиана равна, также 6.

Построим кривую распределения (полигон).



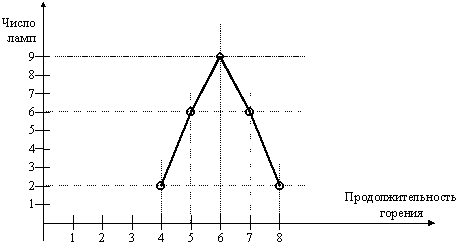
Рис. 1 Распределение ламп по продолжительности горения

Определим размах:

R = Х_max – Х_min = 4 часа.

Он характеризует пределы изменения варьирующего признака. Среднее абсолютное отклонение:

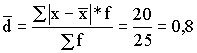часа.

Это средняя мера отклонения каждого значения признака от средней.

Среднее квадратическое отклонение:

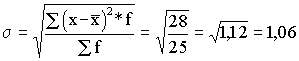часа.

Рассчитаем коэффициенты вариации:

1) по размаху:

;

2) по среднему абсолютному отклонению:

;

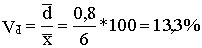3) по среднему квадратическому отношению:

.

С точки зрения качества продукции, коэффициенты вариации должны быть минимальными.

Так как завод интересует не качество контрольных ламп, а всех ламп, возникает вопрос о расчете средней ошибки выборки:

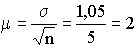часа,

а от числа от отобранных единиц  которая зависит от колеблемости признака ( (n).

 = Предельная ошибка выборки . Доверительное число t показывает, что расхождение не превышаетt* кратную ему ошибку выборки. С вероятностью 0,954 можно утверждать, что разность между выборочной и генеральной не превысит двух величин средней ошибки выборки, то есть в 954 случаях ошибка репрезентативности не выйдет за 2

;



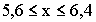
Таким образом, с вероятностью 0,954 ожидается, что средняя продолжительность горения будет не меньше, чем 5,6 часа и не больше, чем 6,4 часа. С точки зрения качества продукции необходимо стремиться к уменьшению этих отклонений.

Обычно при статистическом контроле качества допустимый уровень качества, который определяется количеством изделий, прошедших контроль и имевших качество ниже минимально приемлемого, колеблется от 0,5% до 1% изделий. Однако, для компаний, которые стремятся выпускать продукцию только высшего качества, этот уровень может быть недостаточным. Статистический контроль качества в первую очередь применяется в отделениях фирмы, где продукция изготавливается партиями. Большую роль в обеспечении качества играет статистический приемочный контроль.

4. Основные проблемы выборочного обследования

Прежде чем рассматривать роль, которую играет теория в выборочном обследовании, полезно вкратце охарактеризовать основные проблемы, связанные с планированием и проведением обследования. Обследования могут сильно различаться по их сложности. Взять выборку из 5000 карточек, пронумерованных и аккуратно расставленных в картотеке, нетрудно. Совсем другое дело получить выборку жителей района, где средством сообщения служат реки, протекающие в лесах, где карты отсутствуют, жители говорят на 15 разных диалектах и весьма подозрительно относятся к любопытным незнакомцам. Проблемы, вызывающие затруднения в одном обследовании, могут оказаться несущественными или совсем не возникнуть в другом.

Основные проблемы, связанные с обследованием, сгруппированы более или менее произвольно в следующие 11 пунктов³.

Цели обследования.

Чрезвычайно полезна четкая формулировка целей обследования. Без нее, погружаясь в детали планирования сложного обследования, легко забыть о его общих целях и принять решения, расходящиеся с ними.

Совокупность, из которой производится отбор.

Словом совокупность пользуются для обозначения множества объектов, из которого извлекается выборка. Определение совокупности может не представлять никакой трудности, как, например, в случае, когда отбирается партия электрических лампочек для оценки среднего времени их горения. Напротив, при выборочном исследовании совокупности ферм необходимо сформулировать правила, позволяющие выделить ферму и отграничить одну из них от другой. Такие правила должны быть практичными: нужно, чтобы в ходе работы обследователь был в состоянии без особых колебаний определять, принадлежит ли сомнительный объект к совокупности или нет.

Совокупность, из которой производится отбор (обследуемая совокупность), должна совпадать с совокупностью, о которой мы хотим собрать сведения (изучаемая совокупность). Иногда по практическим соображениям или ради удобства обследуемая совокупность суживается по сравнению с изучаемой. В этом случае следует помнить, что выводы, сделанные по выборке, относятся лишь к обследуемой совокупности. 'Суждение о степени применимости этих выводов также и к изучаемой совокупности должно основываться на других источниках сведений. Может оказаться полезной любая доступная дополнительная информация о характере различий между обследуемой и изучаемой совокупностями.

Собираемые данные.

Необходимо убедиться в том, что все собираемые данные соответствуют целям обследования и никаких важных данных не пропущено. Существует распространенная тенденция, особенно при обследовании совокупностей людей, задавать слишком много вопросов, часть которых впоследствии вовсе не анализируется. Перегруженный опросный лист ухудшает качество ответов, как на важные, так и на второстепенные вопросы.

Желательная степень точности.

Результаты выборочных обследований всегда отчасти неопределенны. Это происходит потому, что исследуется только часть всей совокупности, и измерения производятся с ошибками. Эту неопределенность можно уменьшить, извлекая выборки большего объема и производя более точные измерения. Но это обычно увеличивает затраты времени и средств. Следовательно, важный момент состоит в определении желательной степени точности результатов⁴. Ответственность за это несет лицо, которое будет пользоваться собранными данными. Принятие решения относительно желательной точности может оказаться затруднительным, поскольку многие практические работники не привыкли мыслить в терминах величины погрешностей, допустимой при получении оценок и тем не менее дающей возможность принять правильное решение. Статистик часто может оказать им помощь на этом этапе.

Способы наблюдения.

Существует большой выбор средств и методов изучения совокупности. Данные о состоянии здоровья человека могут быть получены либо с его слов, либо по результатам медицинского исследования. При обследовании можно предоставить опрашиваемому самому заполнять опросный лист или поручить обследователям задавать стандартный набор вопросов в определенной форме или же вести опрос в виде беседы, при которой вопросы задают в различной форме и в произвольном порядке. Обследование можно произвести по почте, по телефону, путем личного посещения или же, так или иначе, сочетая эти способы.

Значительная часть предварительной работы состоит в разработке форм документов, в которых будут содержаться вопросы и куда нужно будет записывать ответы. Если опросные листы сравнительно просты, то возможные ответы можно иногда заранее закодировать, т. е. записать в таком виде, чтобы потом их легко было преобразовать для машинной обработки. Для разработки удачного инструментария обследования необходимо отчетливо представлять структуру таблиц с итоговыми данными, которыми будут пользоваться при анализе материалов обследования.

Основа выборки.

Прежде чем производить отбор, необходимо разбить совокупность на части, которые называются единицами отбора или просто единицами. Эти единицы должны вместе исчерпывать всю совокупность и не должны перекрывать одна другую, т. е. каждый элемент совокупности должен принадлежать одной и только одной единице. Иногда единицы отбора выделяются очевидным образом, как, например, в совокупности электрических лампочек, где единицей отбора служит отдельная лампочка. Иногда приходится выбирать из нескольких возможных единиц отбора. Например, при обследовании людей в городе единицей отбора может быть отдельный человек, члены одной семьи или же все жители Уродского квартала. При выборочном изучении урожая сельскохозяйственных культур единицами отбора могут служить поля, фермы или же участки земли, форма и размеры которых заранее известны.

Построение такого перечня единиц отбора, называемого основой сборки, на практике часто бывает одной из главных задач. Наученные горьким опытом организаторы обследований с недоверием относятся к спискам, составленным ранее для других целей. Несмотря на заверения в обратном, такие списки часто оказываются неполными оценки, получаемой с помощью того или иного способа отбора, определяется на основании распределения частот этой оценки, которое получается, если соответствующий способ многократно применять к одной и той же совокупности. Это, конечно, обычный прием суждения о точности в статистической теории.

Можно ввести еще одно упрощение. Для выборок того объема, который обычно встречается на практике, часто есть все основания полагать, что выборочные оценки имеют приблизительно нормальное распределение. Для нормально распределенных оценок вид распределения частот полностью известен, если известны среднее значение и среднее квадратичное отклонение ( или дисперсия). Значительная часть теории выборочного метода посвящена нахождению формул для таких средних и дисперсий⁵.

Существует некоторое различие между теорией выборочных обследований и классической теорией выборочного метода, заключающееся в том, что при обследованиях совокупности состоят из конечного числа единиц. Когда отбор производится из конечной, а не из бесконечной совокупности, методы доказательства теорем иные и результаты несколько более сложны. Для практических целей эти различия в результатах для конечных и для бесконечных совокупностей обычно не имеют значения. Если объем выборки (по числу первичных единиц отбора) мал по сравнению с объемом всей совокупности, то вполне применимы результаты, полученные для бесконечной совокупности. В основном в этой книге излагаются результаты, относящиеся к конечным совокупностям. В некоторых, более сложных вопросах, чтобы упростить изложение, мы будем пользоваться теорией для бесконечных совокупностей.

5. Практическая часть

Имеются следующие данные по 30 строительным организациям региона (выборка 10%-ная, механическая) об объеме выполненных работ и численности рабочих за год:


Табл.1

Номер предприятия	Численность рабочих, чел.	Обьем выполненных работ,млн. руб.
1	110	19
2	123	17
3	133	24
4	142	25
5	135	25
6	128	21
7	131	23
8	139	28
9	126	20
10	138	26
11	115	22
12	108	16
13	129	21
14	140	23
15	98	16
16	125	17
17	114	18
18	118	25
19	98	14
20	140	22
21	160	25
22	124	18
23	117	23
24	80	12
25	112	20
26	143	25
27	102	17
28	127	21
29	132	24
30	130	23

Признак - объем выполненных работ

Число групп - четыре


Задание:

По данным таблицы 1 с вероятностью 0,954 определить:

1. Ошибку выборки среднего объема выполненных работ и границы, в которых будет находиться средний объем выполненных работ в генеральной совокупности
   
2. Ошибку выборки доли предприятий с объемом работ 20 и более млн рублей и границы, в которых будет находиться генеральная доля.
   

Решение


1. Сначала определяем длину интервала по формуле:

е= (х _max – x _min ) /k,

где k – число выделенных интервалов.

е = (28 – 12) / 4 =4 млн. руб .

12 - 16, 16 - 20, 20 - 24, 24 - 28.

Распределение предприятий по сумме выполненных работ, млн. руб.

№ группы	Группировка предприятий по сумме выполненных работ, млн. руб.	№ предприятия	Обьем выполненных работ, млн. руб.
I	12 -16	24	12
		19	14
		15	16
		12	16
II	16 - 20	2	17
		1	19
		9	20
		16	17
		17	18
		22	18
		25	20
		27	17
III	20 - 24	3	24
		6	21
		7	23
		11	22
		13	21
		14	23
		20	22
		23	23
		28	21
		29	24
		30	23
IV	24 -28	4	25
		5	25
		8	28
		10	26
		18	25
		21	25
		26	25

Рассчитываем характеристику ряда распределения предприятий по сумме выполненных работ, для этого составим расчетную таблицу:

Группы предприятий по сумме выполненных работ, млн. руб.	Число предприятий f шт.	Середина интервала Х млн. руб.	xf млн. руб.	X 2 f млн2. руб.
12 – 16	4	14	56	784
16 – 20	8	18	144	2592
20 – 24	11	22	242	5324
24 – 28	7	26	182	4732
E	30	------	624	13432

Средняя арифметическая: = 624: 30 = 20,8 млн. руб.

Среднее квадратическое отклонение: 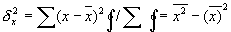получаем:

Определяем среднее квадратическое отклонение для определения коэффициента вариации. Коэффициент вариации: u _х = ( d _х * 100%) / x получаем: u _х =3,9 * 100%: 20,8 = 18,75 % так как u _х = 18,75 % < 33% то можно сделать вывод, что совокупность однородная, а средняя величина типичная ее характеристика.

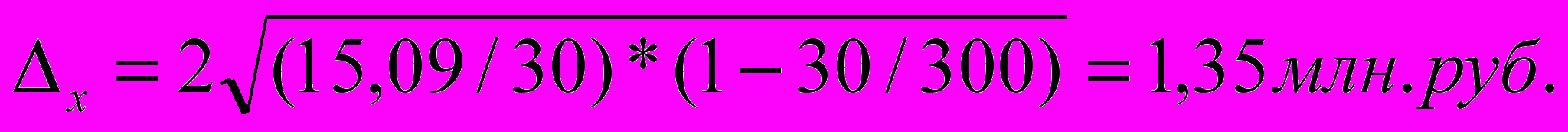Определяем ошибку выборки (выборка механическая) для средней суммы выполненных работ на одно предприятие по следующей формуле: если Р=0,954 то t=2 ошибка выборки для средней суммы выполненных работ на одно предприятие Dх = 1,35 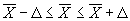Средняя сумма выполненных работ будет находиться в границах которые мы находим по формуле: получаем: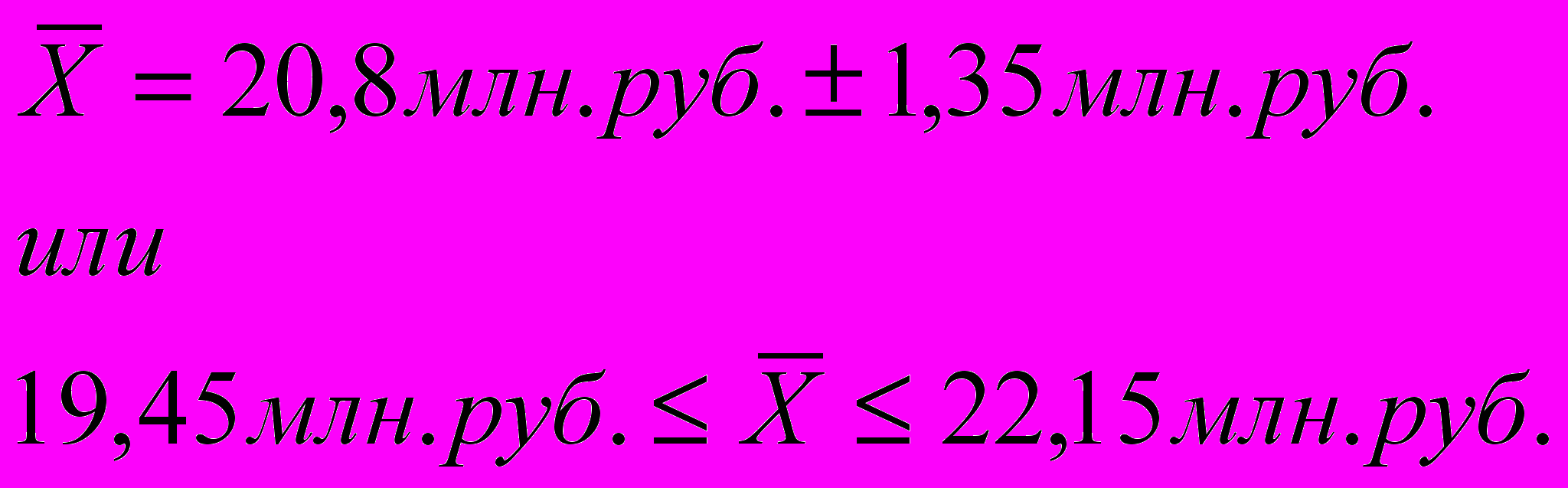



С вероятностью 0,954 можно утверждать, что средняя сумма выполненных работ одного предприятия заключается в пределах: 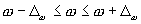Доля предприятий со средней суммой выполненных работ 20 млн. руб. и более находится в пределах:

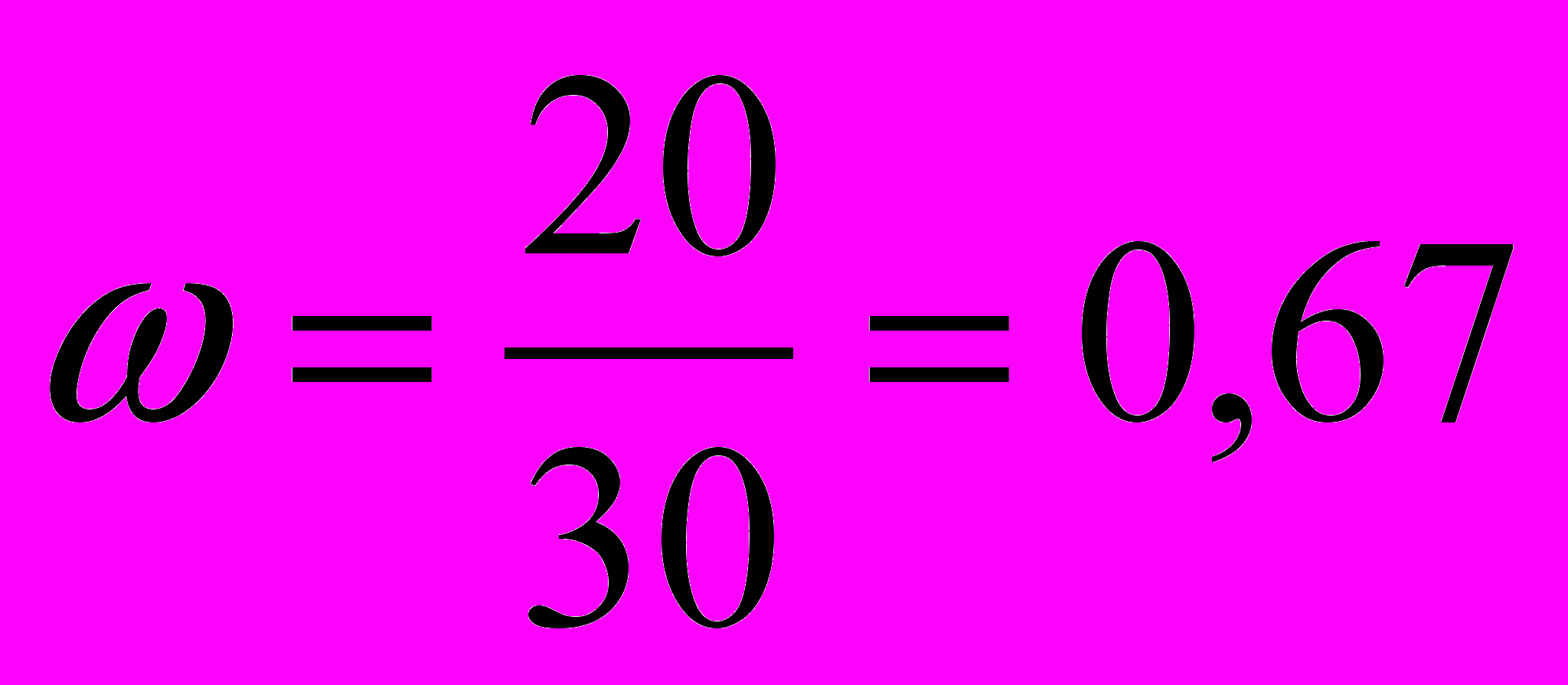Выборочная доля составит: 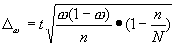Ошибку выборки определяем по формуле:, где N – объем генеральной совокупности.

Также объем генеральной совокупности можно определить из условия задачи, так как выборка 10% -тная и в выборку вошло 30 предприятий: 30 предприятий – 10% Х – 100% 10х=3000 х=300 предприятий, следовательно, N=300



подставляем данные в формулу: Следовательно, с вероятностью 0,954 можно утверждать, что доля предприятий со средней суммой выполненных работ 20 млн. руб. будет находиться в следующих пределах: 67 % ± 16,3% или

Заключение

Чтобы получить исчерпывающую информацию о состоянии той или иной статистической совокупности, нужно учесть весь ее состав без исключения.

Однако в силу разных обстоятельств, не всегда приходится прибегать к сплошному обследованию изучаемых совокупностей. Во-первых, потому, что эта работа сопряжена с большими затратами труда и времени, не говоря уже о больших затратах материальных средств, а во-вторых, ввиду практической невозможности или нецелесообразности полного учета всех членов совокупности.

Вследствие этого и в целях экономии времени и средств вместо сплошного учета всех членов изучаемой совокупности анализу подвергается обычно какая-то ее часть, по которой и судят о состоянии всей совокупности в целом. Отсюда идут понятия о генеральной (общей) и выборочной совокупности, исследуемых с точки зрения интересующего нас признака (или признаков).

Сущность выборочного метода заключается в том, чтобы по свойствам части (выборки) судить о численных характеристиках целого (генеральной совокупности), по отдельным группам вариант—об их общей совокупности, которая иногда мыслится как совокупность неограниченно большого объема. Основу выборочного метода составляет та внутренняя связь, которая существует в популяциях между единичным и общим, частью и целым.

Список используемой литературы.

1. Вайнберг Дж., Шумекер Дж. Статистика. – М.: Наука, 1979
   
2. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Экмо-Пресс, 2005
   
3. Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики. – М.: Юнити, 2002.
   
4. Маслов П.П. Техника работы с цифрами. – М.: Наука, 1977
   
5. Плешко Б.Т., Елисеева И.И. История статистики. – М.: Просвещение, 1990
   
6. Рейхман У.Дж. Применение статистики. – М.: Наука 1969
   
7. Общая теория статистики: Учебное пособие. \ Под ред. А.Я.Боярского. – М.: Наука, 1985
   
8. Практикум по теории статистики: Учеб. Пособие. \ Под ред. Р.А. Шмойловой. – М.: Дело, 2003
   
9. Социально-экономическая статистика: Учебник. \ Под ред. Г.М. Громыко. – М.: Просвещение, 1994
   
10. Экономическая статистика: Учебник. \ Под ред. Ю.Н. Иванова. – М.: Дело, 2002.