Встатье рассмотрены основные методы оценки параметров производственных функций малых и средних предприятий, которые могут быть применены на практике
| Вид материала | Документы |
СодержаниеГришин А.Ф., Кочерова Е.В. |
- Лекция 14. Основные методы интегрирования (продолжение), 72.42kb.
- Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
- Встатье рассмотрены различные методы оценки экономической конкурентоспособности региона, 97.28kb.
- Уважаемые руководители малых и средних предприятий Катав-Ивановского муниципального, 18.01kb.
- Система микрофинансирования на Северном Кавказе, 20.29kb.
- Северо-Кавказский банк Сбербанка России, 21.88kb.
- Управление интеллектуальной собственностью и инновационным процессом. Роль малых, 218.32kb.
- Интегрированные системы менеджмента на мсп содержание, 1296.18kb.
- И. С. Савельева Научный центр акушерства, гинекологии и перинатологии рамн, Москва, 107.97kb.
- Активизация участия малых и средних предприятий в глобальных производственных цепочках, 23.43kb.
| | Москаленко Н.И. к. ф.-м. н., доцент кафедры естественнонаучных дисциплин Белгородского университета потребительской кооперации |
ОЦЕНКА ПАРАМЕТРОВ производственных функций малых и средних предприятий
В статье рассмотрены основные методы оценки параметров производственных функций малых и средних предприятий, которые могут быть применены на практике. Приведен пример оценки параметров линейной производственной функции по данным деятельности предприятия «Экотранс» г. Белгорода.
Производственные функции малых и средних предприятий моделируют те связи, которые имеют место в реальной производственной сфере.
Практическое применение производственных функций в деятельности малых и средних предприятий может идти по следующим направлениям: прогнозирование и планирование уровня важнейших показателей производства; проведение углубленного экономического анализа; поиск оптимального сочетания факторов производства.
При решении этих и других задач необходимо получить аналитические выражения для производственных функций. Для этого разработаны различные методы оценки параметров производственной функции и проверки качества уравнения полученной зависимости.
Линейная производственная функция, содержащая один параметр
, имеет вид: 
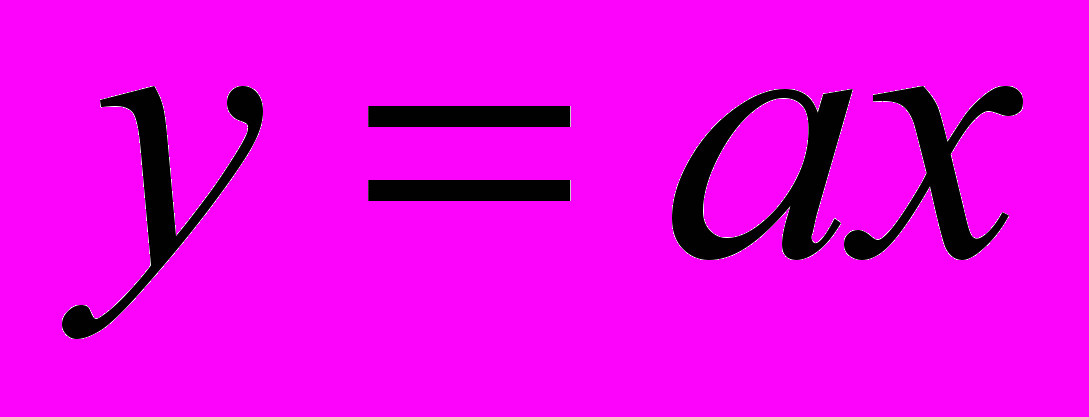. Она моделирует зависимость результатов производства 
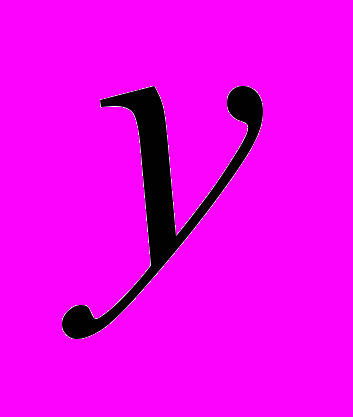от одного фактора 
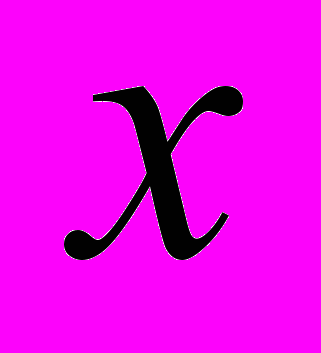. Например, стоимость продукции 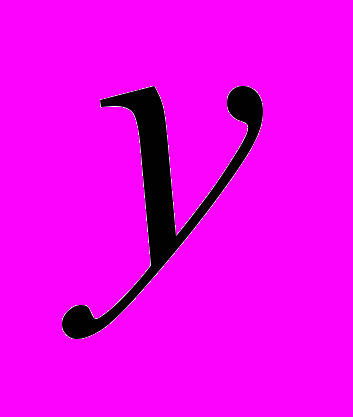от ее количества 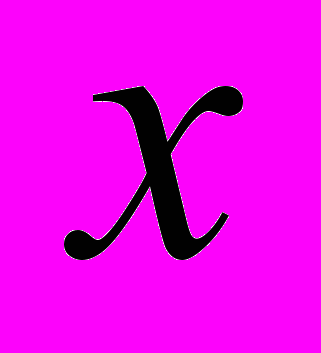, прибыль предприятия 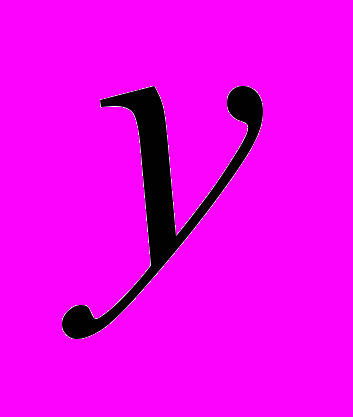от количества выпускаемой продукции 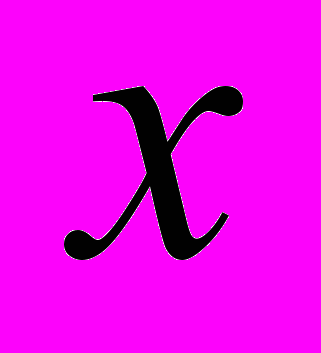. Числовое значение параметра
может быть задано, например, как стоимость единицы выпускаемой продукции. Если значение параметра не задано, то его можно найти по данным значениям фактора производства 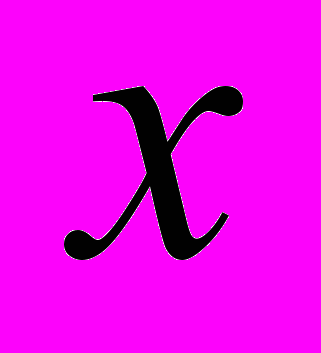и соответствующих результатов производства 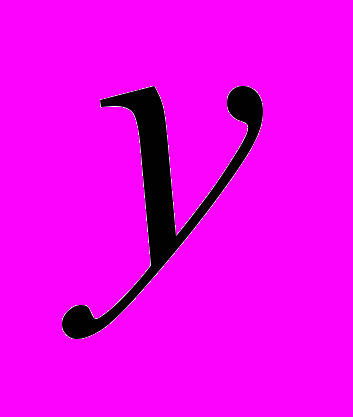.Определение параметров производственных функций часто называют оценкой параметров или параметризацией. В настоящее время для нахождения параметров производственных функций малых и средних предприятий используют специальные программные продуты для персонального компьютера и ЭВМ.
В случае, когда нет возможности использовать программные продукты для определения параметров производственных функций малых и средних предприятий, эти параметры можно найти следующими методами: методом контрольных точек; методом средних; методом сумм; методом наименьших квадратов [1].
Для определения параметров методом контрольных точек выбираем на корреляционном поле точки, число которых равно неизвестным параметрам в выбранной модели для производственной функции. Подставляя координаты этих точек в выбранное уравнение, получим систему уравнений. Из этой системы находим неизвестные параметры и получаем уравнение искомой зависимости.
В методе средних наблюдаемые значения разбивают на группы, число которых равно неизвестным параметрам в выбранной математической модели, и подставляем их средние значения в выбранное уравнение для производственной функции.
В методе сумм, зная суммы данных показателей, можно перейти к средним показателям, а затем выполнить расчеты с помощью метода средних, разбив данные показатели на нужное число групп.
Эти методы рекомендуется применять также на начальных стадиях получения производственных функций малых и средних предприятий.
В методе наименьших квадратов искомые параметры производственной функции должны обеспечивать минимум суммы квадратов между теоретическими и фактическими значениями результативного фактора. Этот метод используется с первой четверти девятнадцатого века и широко распространен в настоящее время в программных продуктах для персонального компьютера и ЭВМ.
Самыми доступными из программных продуктов являются статистический пакет «Stadia» [3] и табличный процессор Excel [2], содержащий пакет анализа, который предназначен для решения основных задач статистики, а также некоторое число статистических функций.
В пакете «Stadia» процедура простой регрессии (в блоке «Статистические методы», «Регрессивный анализ») предоставляет возможность строить наиболее употребительные регрессивные модели по статистическим данным. Если в предполагаемом списке моделей нет подходящей, то следует обратиться к разделу общей регрессии, где можно задать по формуле любую алгебраическую модель, а также получить уравнение множественной регрессии.
В ходе анализа можно получить следующие результаты: выбрать из нескольких математических моделей ту, которая с большей точностью описывает экспериментальную зависимость; построить прогноз на будущее на основе выбранной модели с 95 % доверительным интервалом; провести анализ регрессивных остатков.
Проведем в пакете «Stadia» оценку параметров линейной производственной функции
выручки от затрат на труд предприятия «Экотранс» г. Белгорода по квартальным данным за 2007-2009 годы приведенными в таблице.| Прибыль 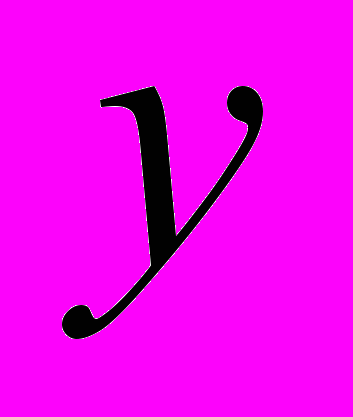 (тыс. руб.) | Затраты на труд 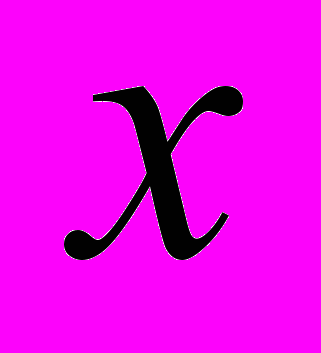( тыс. руб.) |
| 31972 | 10939,5 |
| 32290 | 11410,6 |
| 33698 | 13436,4 |
| 33568 | 13611,9 |
| 36098 | 15286,3 |
| 40724 | 16495,2 |
| 42081 | 19346,6 |
| 44174 | 18194,3 |
| 44237 | 17538,3 |
| 49300 | 19849,6 |
| 50701 | 20305,7 |
| 55338 | 19880,6 |
Корреляционное поле для этих данных имеет вид.
Для линейной зависимости выручки от затрат на труд предприятия «Экотранс» г. Белгорода по квартальным данным за 2007-2009годы получаем следующее уравнение производственной функции
, где 
теоретическое значение прибыли. В табличном процессоре MICROSOFT EXCEL в режиме «Регрессия» пакета анализа по этим данным получаем следующее уравнение производственной функции выручки от затрат на труд
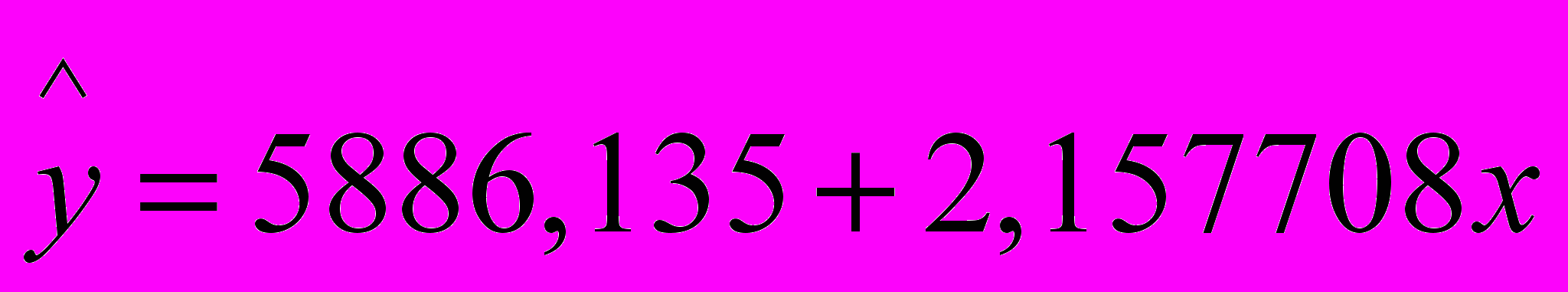.Итак, в настоящее время с широким распространением ПЭВМ имеется возможность использовать в практической деятельности малых и средних предприятий универсальные и специализированные статистические пакеты для оценки параметров производственных функций. В дальнейшем эти результаты используются для эконометрического и экономического анализа данного предприятия.
Статистические программные продукты делают методы оценки параметров производственных функций доступными и наглядными, не требуют выполнения вручную трудоемких расчетов. За исследователем остается постановка задачи, выбор метода, интерпретация и использование полученных результатов.
Список литературы
1. Гришин А.Ф., Кочерова Е.В. Статистические модели: построение, оценка, анализ: Учеб. пособие. – М.: Финансы и статистика, 2005. – 416 с.
2. Калинина В.Н. Математическая статистика: Учебник / Калинина В.Н., Панкин В.Ф. – М.: Высш. шк., 2001. – 336 с.
3. Кулаичев А.П. Полное собрание сочинений в трех томах. Том 1. Методы и средства анализа данных в среде Windows. STADIA / Изд. 3-е, перераб. и доп. – М: Информатика и компьютеры. 1999. – 341с., ил.
АНКЕТА
участника международной научно-практической интернет-конференции профессорско-преподавательского состава, аспирантов и студентов высших учебных заведений "Инновационные технологии: приоритетные направления развития"
12-14 апреля 2011 г.
| Фамилия | Москаленко |
| Имя | Николай |
| Отчество | Иванович |
| Место работы (учебы) | Белгородский университет потребительской кооперации |
| Должность | доцент кафедры естественнонаучных дисциплин |
| Ученое звание, ученая степень | кандидат физико - математических наук, доцент |
| Название доклада | Оценка параметров производственных функций малых и средних предприятий |
| Номер секции | №1 |
| Телефон | 8–906–566–72–69 |
| | |