Geum.ru

Передмова

Вид материалаДокументы

Содержание


5. Методичні вказівки до розв'язання задач
6. Інформаційно-методичне забезпечення
Подобный материал:
1   2   3

5. МЕТОДИЧНІ ВКАЗІВКИ ДО РОЗВ'ЯЗАННЯ ЗАДАЧ


Приклад 1

Таблиця розподілу робітників за виконанням норм виробітку

Групи за виконанням норм виробітку, %
Кількість робітників, чол.
Середина інтервалу, x
Кумулята, f
xf
Відхилення від середньої

1
2
3
4
5
6

До 100
12
97.5
12
1170
-12.3

100-105
20
102.5
32
2050
-7.3

105-110
80
107.5
112
8600
-2.3

110-115
46
112.5
158
5175
2.7

115-120
36
117.5
194
4230
7.7

120 та вище
6
122.5
200
735
12.7

Разом
200
x
X
21960
x


Так як дані згруповані, середнє розраховується за формулою середньої арифметичної зваженої:


.


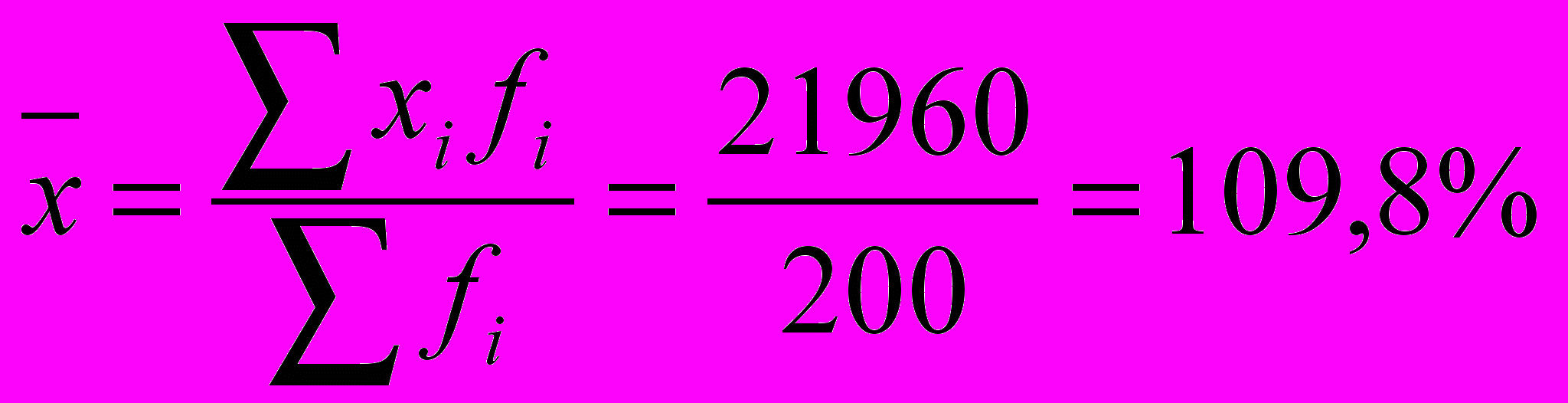Для розрахунку показників варіації побудуємо таблицю розрахунку показників варіації та форми розподілу



Групи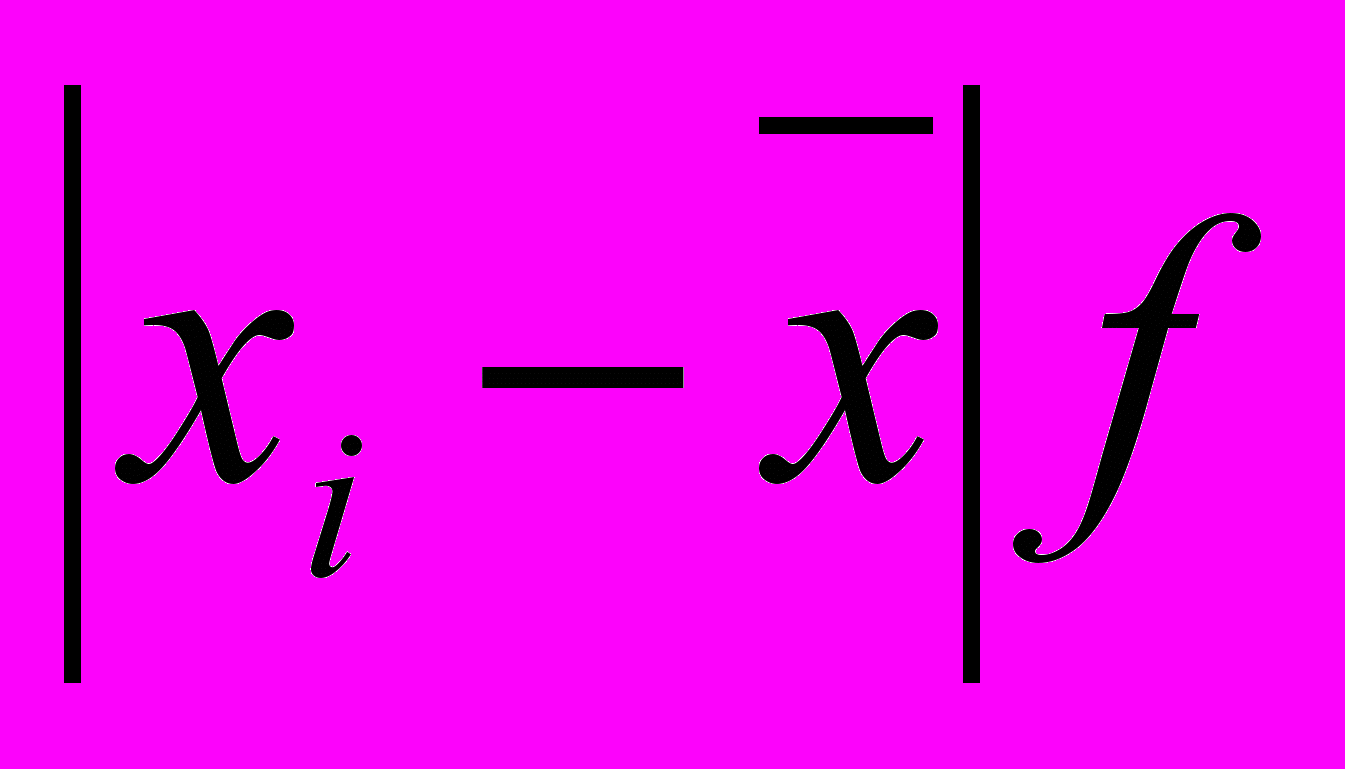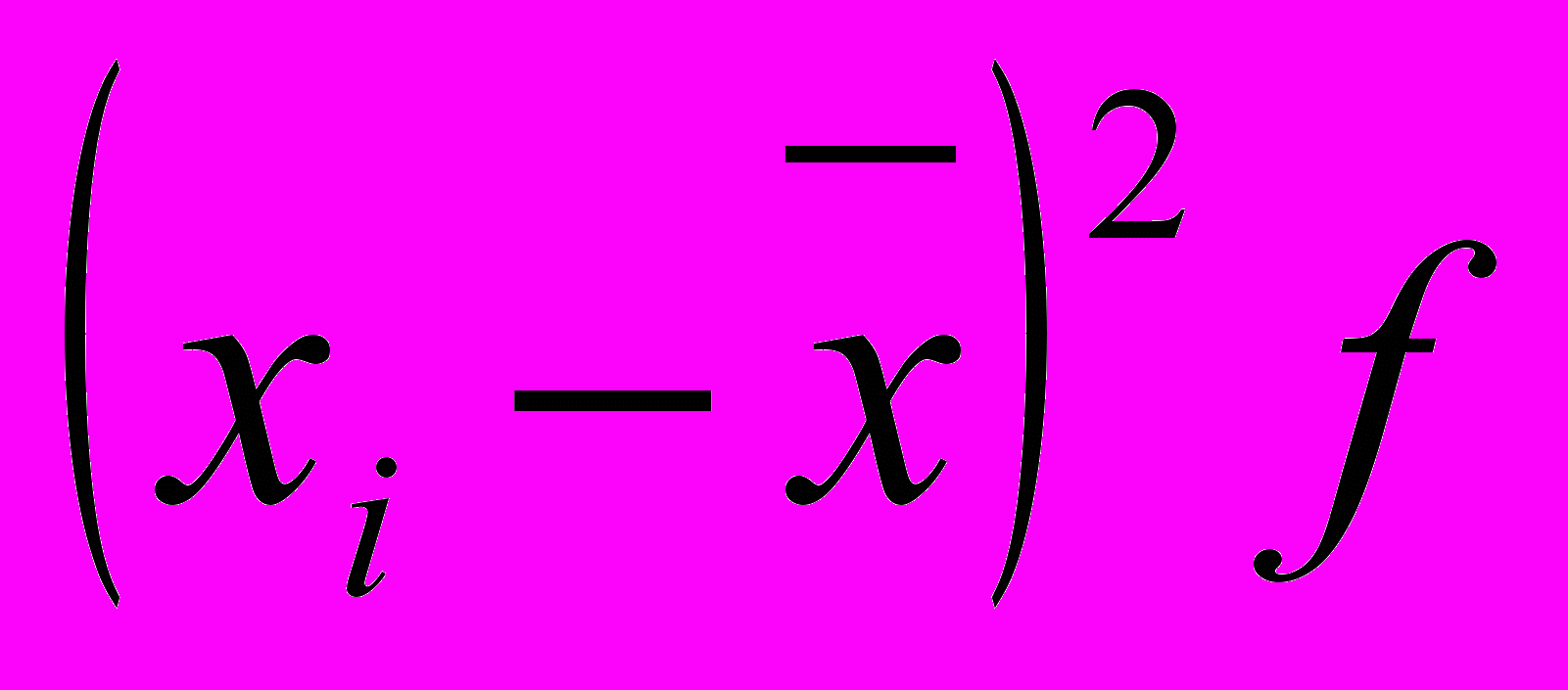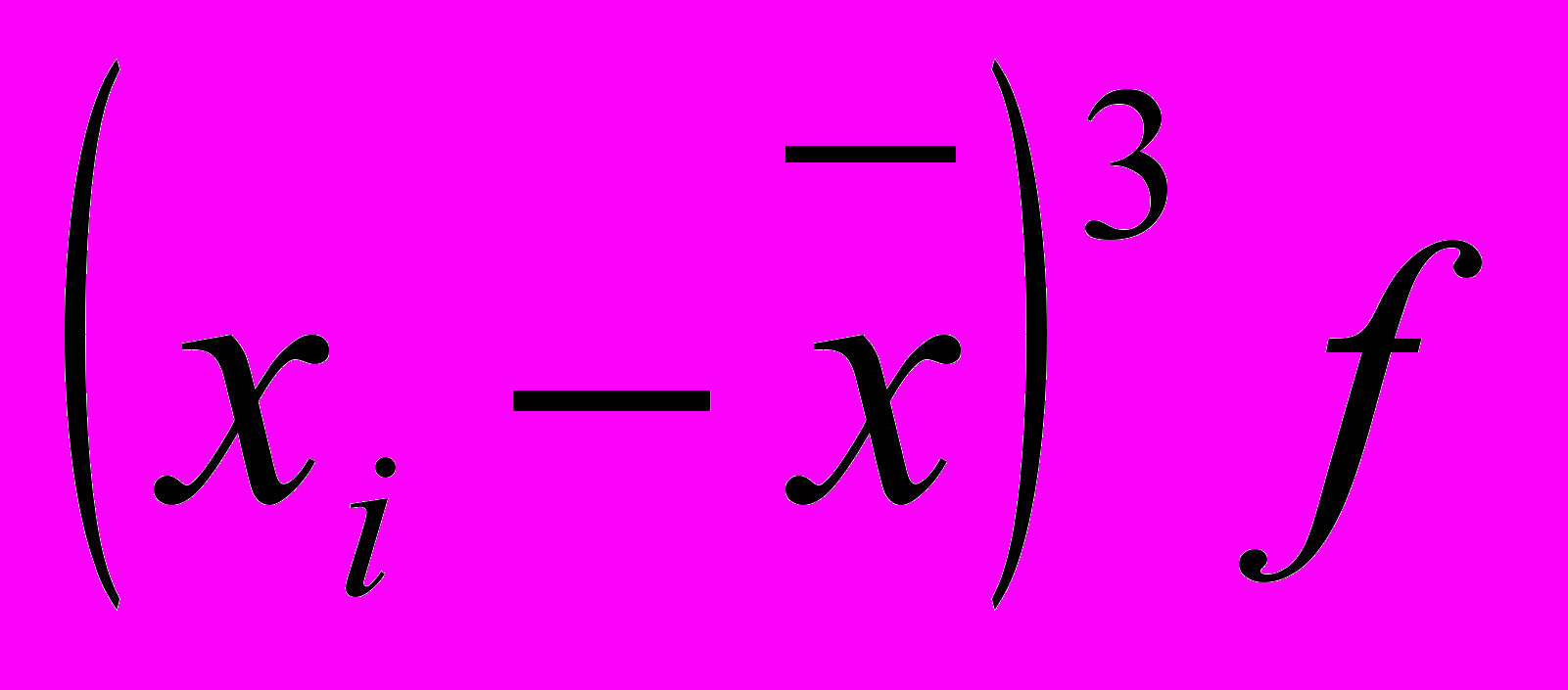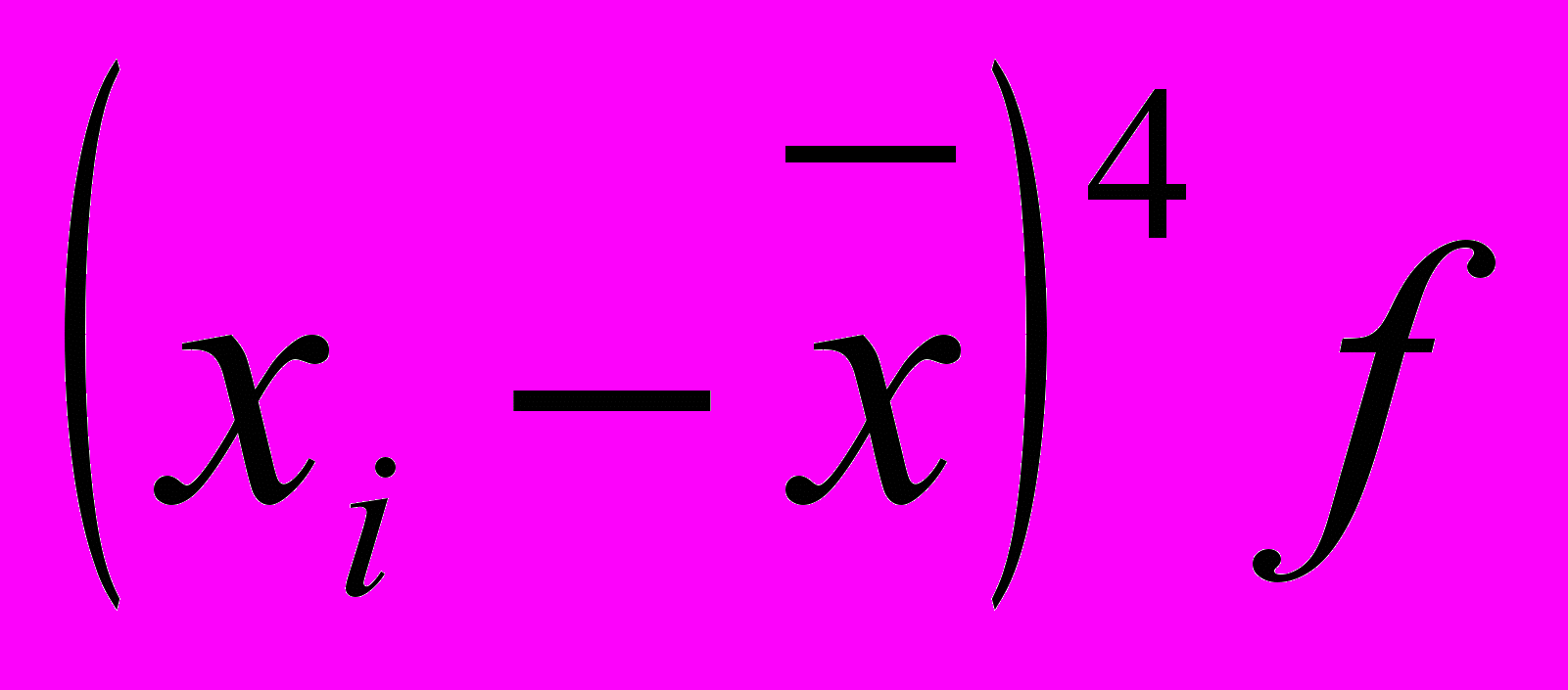








1
2
3
4

1
147.6
1815.48
-22330.4
274663.9

2
146.0
1065.80
-7780.3
56796.5

3
112.0
423.20
-973.4
2238.7

4
124.2
355.34
905.4
2444.6

5
277.2
2734.44
16435.2
126550.9

6
76.2
967.74
12290.3
156086.8

Разом
883.2
7362.00
-1453.2
618781.4


У таблиці в графах 1-2 наведені проміжні дані, які розраховані для зручності користування форму­лами. Використаємо їх для розрахунку середнього лінійного відхилення та дисперсії для згрупованих да­них:

.



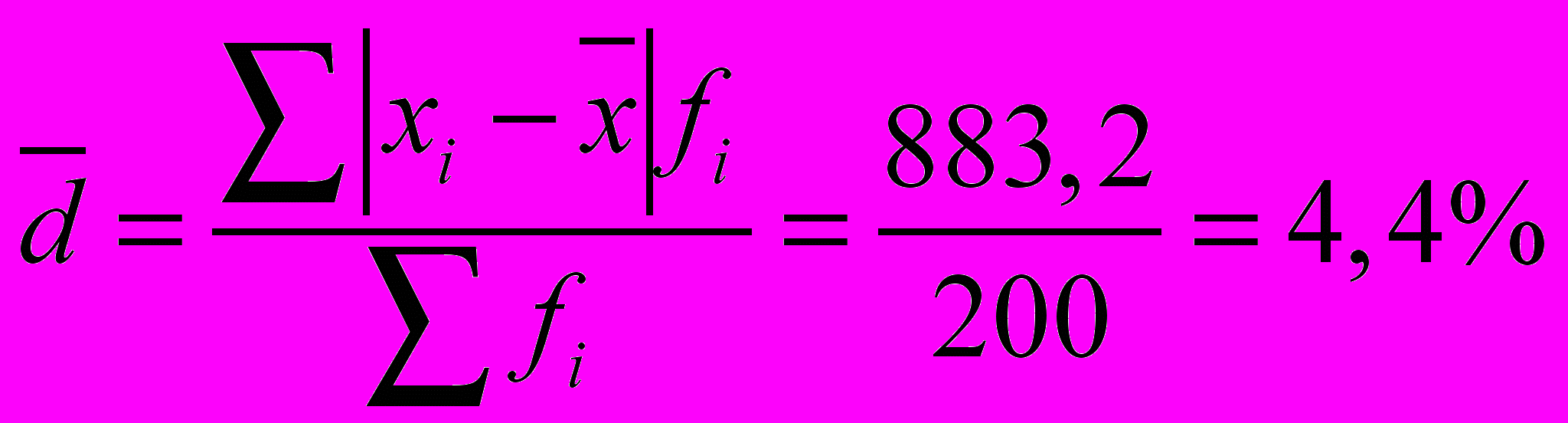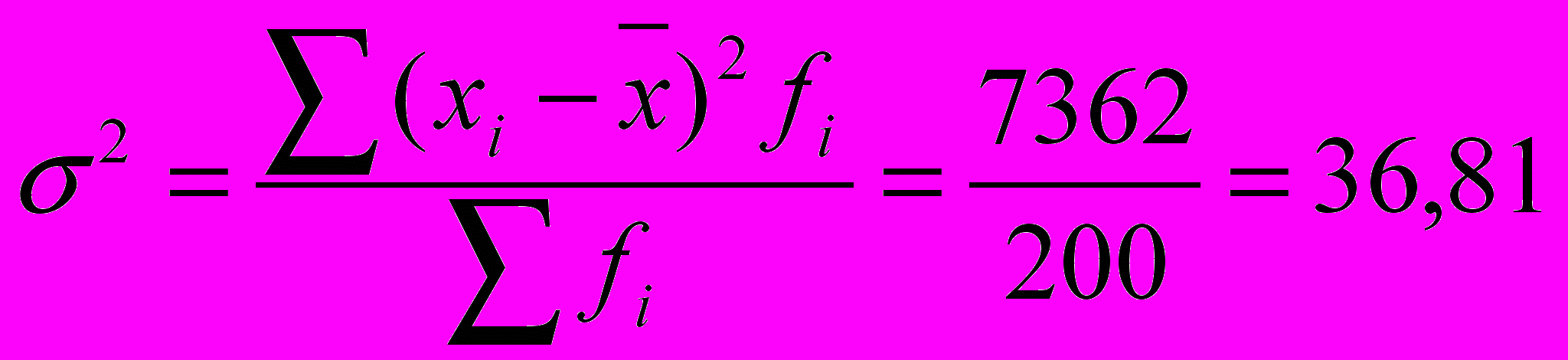
Середнє квадратичне відхилення:

.

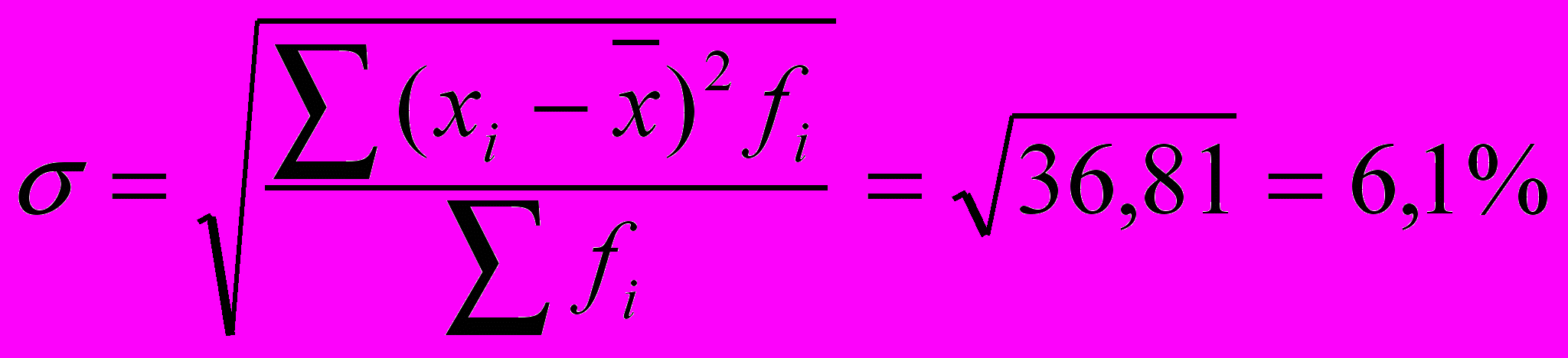Відносні характеристики варіації:

а) лінійний коефіцієнт варіації

,

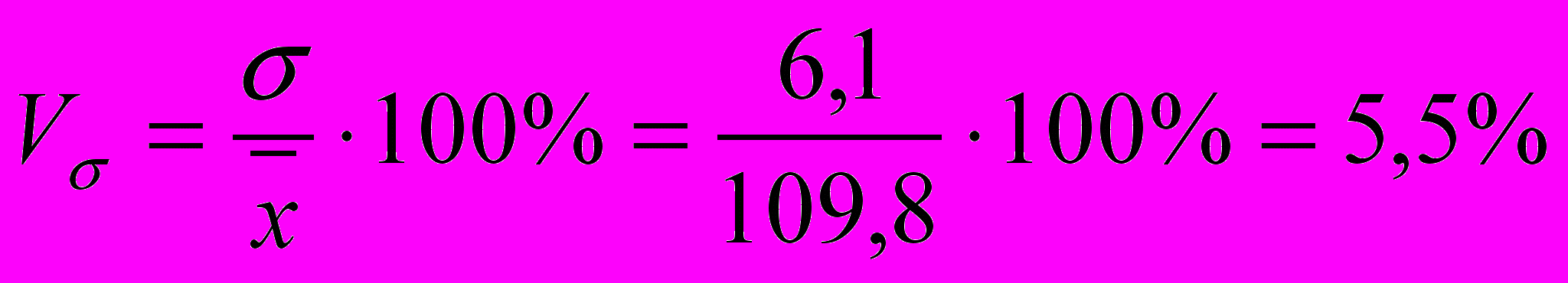або

,

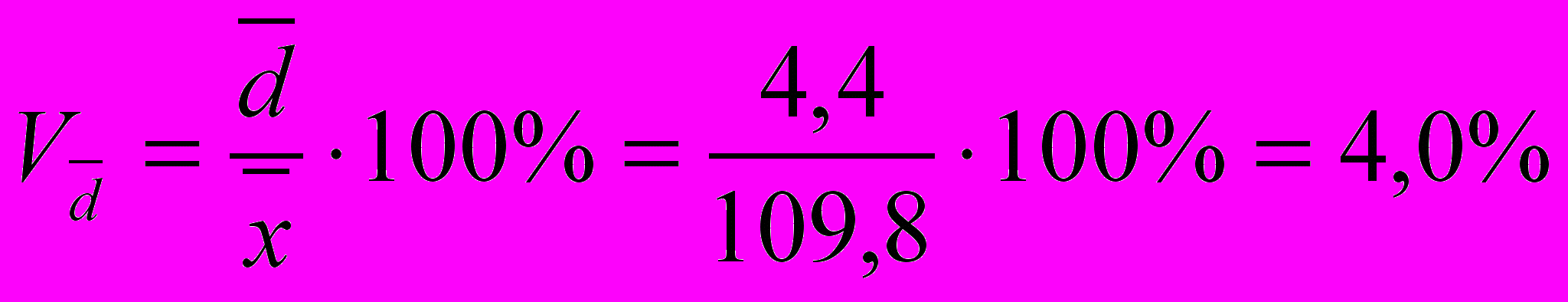Відносно низькі коефіцієнти варіації свідчать про однорідність сукупності робітників за виконанням норм виробітку.

Для характеристики форми розподілу використаємо коефіцієнт асиметрії та ексцесу через моменти третьо­го та четвертого порядку

,

.

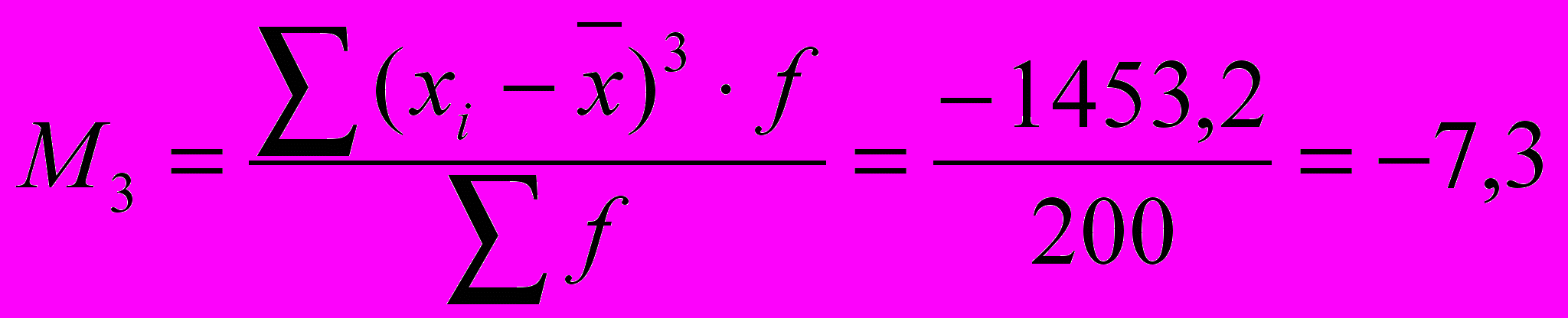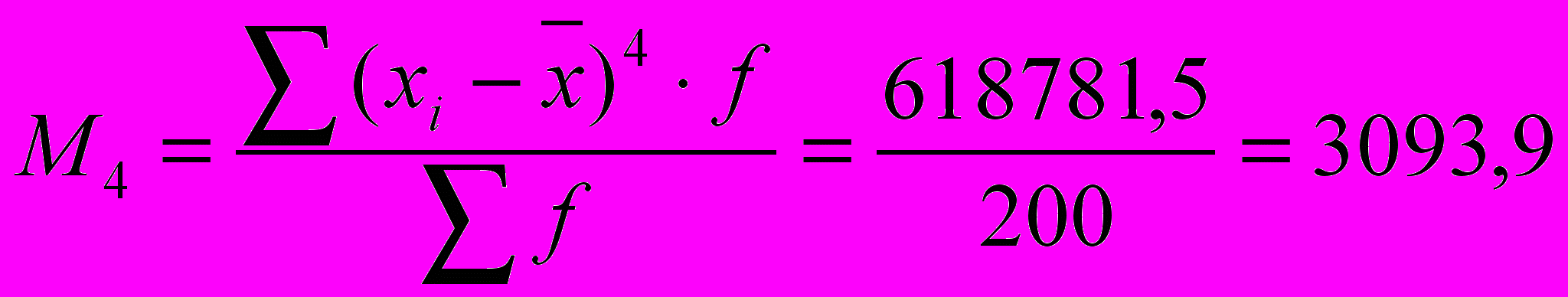Тоді

,

.

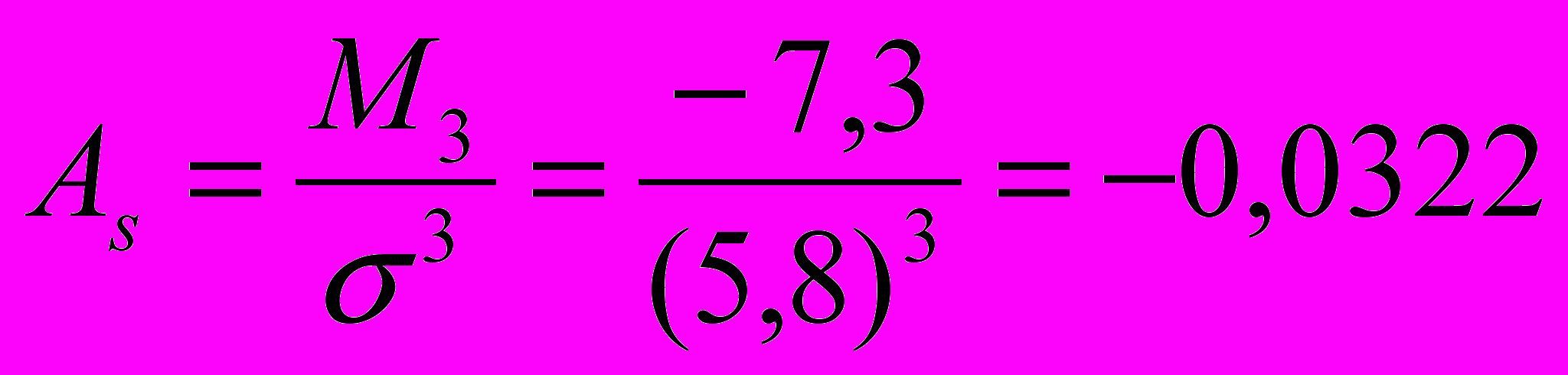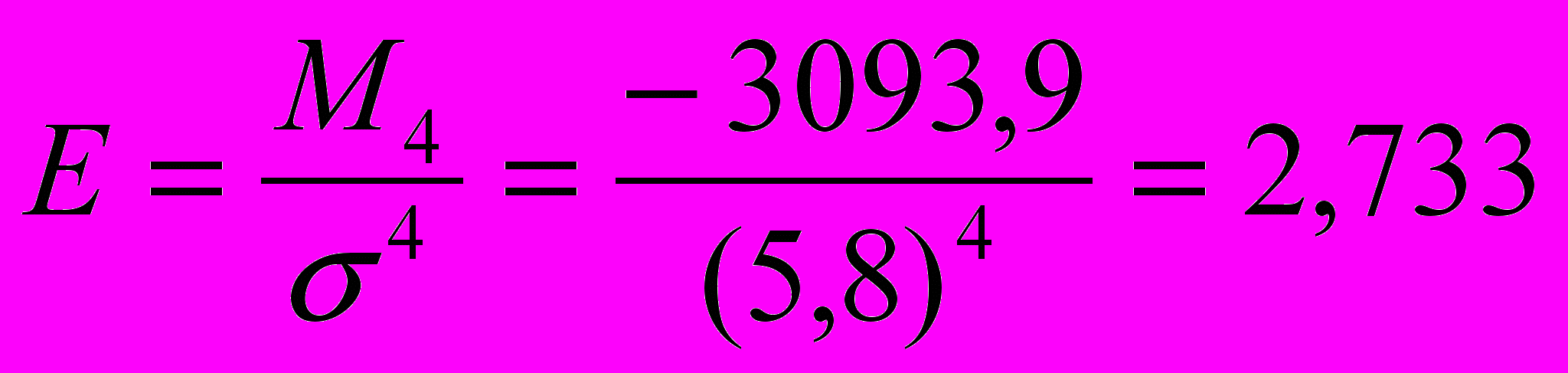Розраховані значення свідчать про те, що розподіл робітників за виконанням норм виробітку лівосторон­ній з невеликою плосковерхістю. Побудуємо графік розподілу:





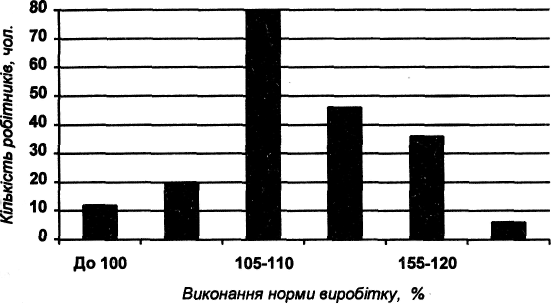
Приклад 2

Маємо такі дані про годинний виробіток деталей робітниками двох груп, які пройшли перепідготовку (N1) і не пройшли (N2), чисельністю 5 чол. кожна.


Таблиця — Годинний виробіток робітників, які пройшли і не пройшли перепідготовку

№ п/п


1
Годинний виробіток деталей, од.
Індивідуальне відхилення від загальної середньої
Квадрат індивідуального відхилення

група 1
група 2
група 1
група 2
група 1
група 2

2
3
4
5
6
7

1
40
62
-14
8
196
64

2
48
66
-6
12
36
144

3
43
60
-11
6
121
36

4
45
68
-9
14
81
196

5
44
64
-10
10
100
100

Разом
220
320
-50
50
534
540


Дисперсійний аналіз дає можливість визначити роль систематичної та випадкової варіації у загальній варіації і тим самим визначити роль фактора, покладеного в основу групування, в зміні результативної ознаки. Для цього використовують правило складання дисперсії, згідно з яким загальна дисперсія дорівнює сумі двох дисперсій: середньої із групових і міжгрупової:



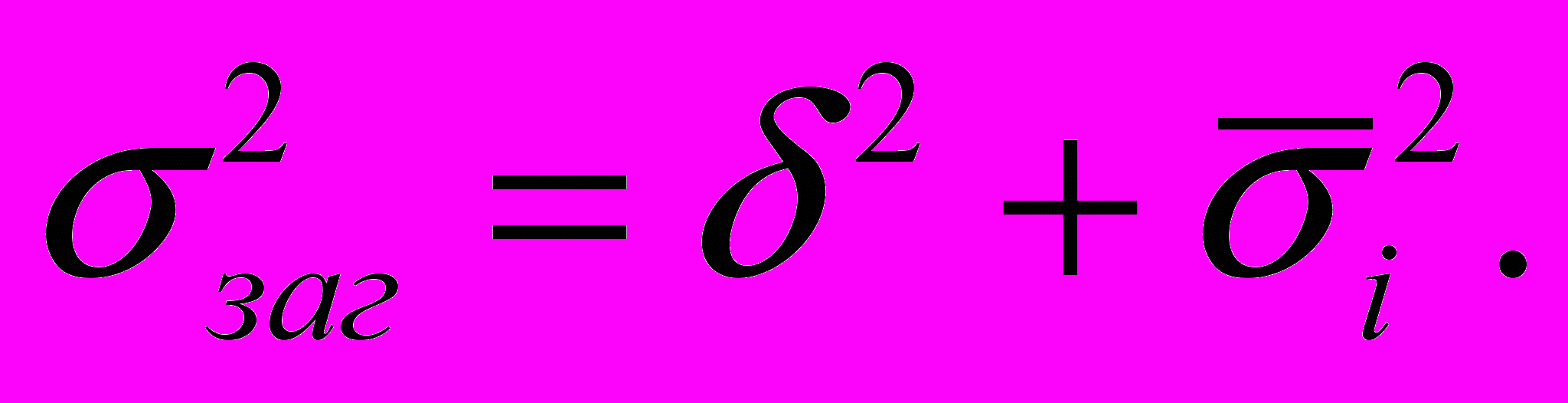
Тісноту зв'язку характеризує співставлення міжгрупової дисперсії із загальною. Це відношення на­зивається кореляційним відношенням:



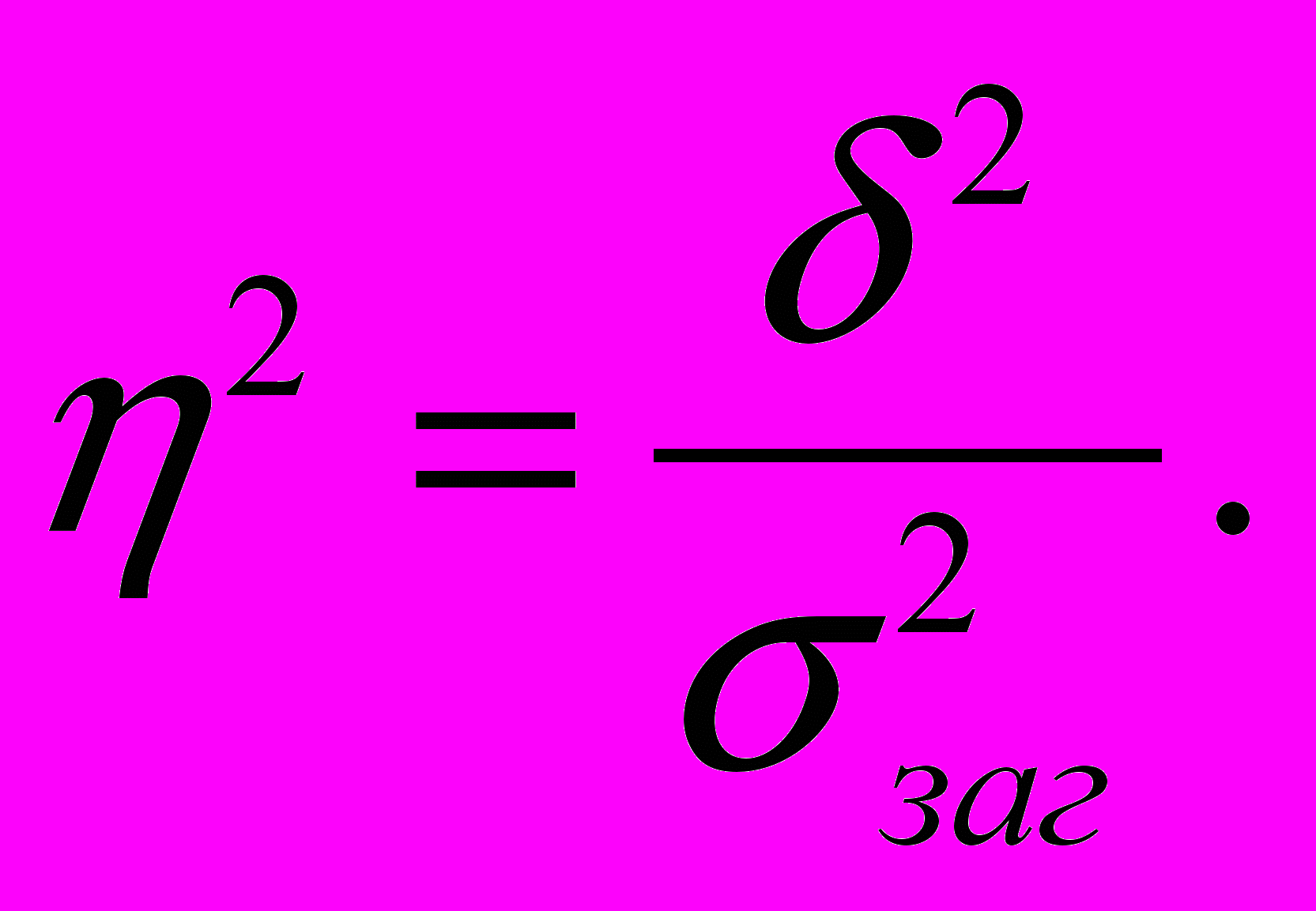
Обчислимо ці параметри для наведеного прикладу. Спочатку обчислимо групові та загальні середні.

Графи 2 таблиці є розрахунковими.

Загальна дисперсія, яка характеризує загальну варіацію під впливом усіх факторів, дорівнює



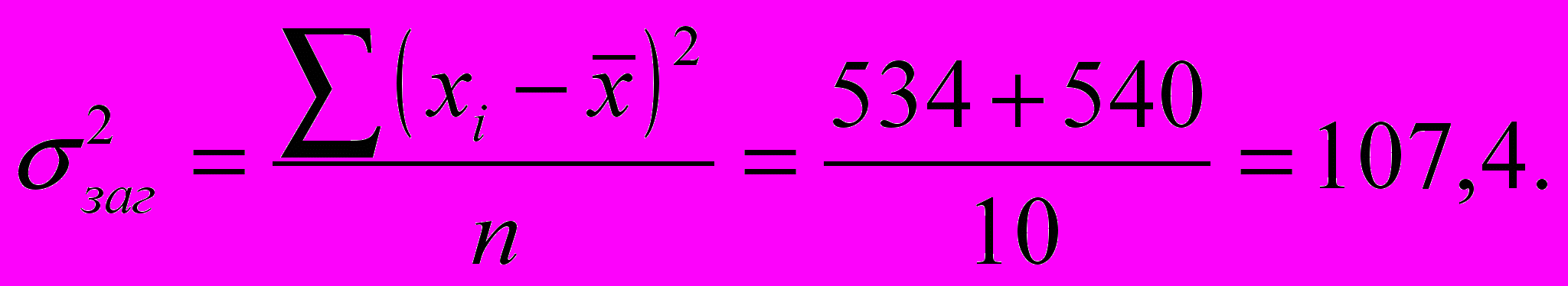
Загальна середня дорівнює



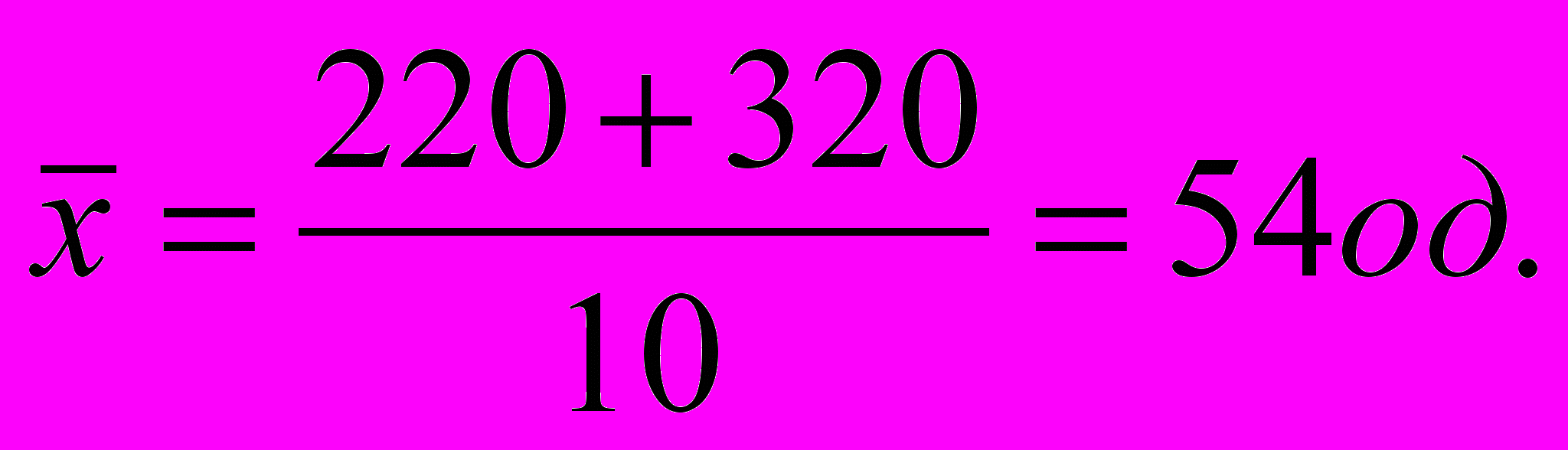
Міжгрупова дисперсія, яка характеризує факторну варіацію, тобто відмінності у виробітку, обумовлені тим, що частина робітників пройшла перепідготовку, становить:





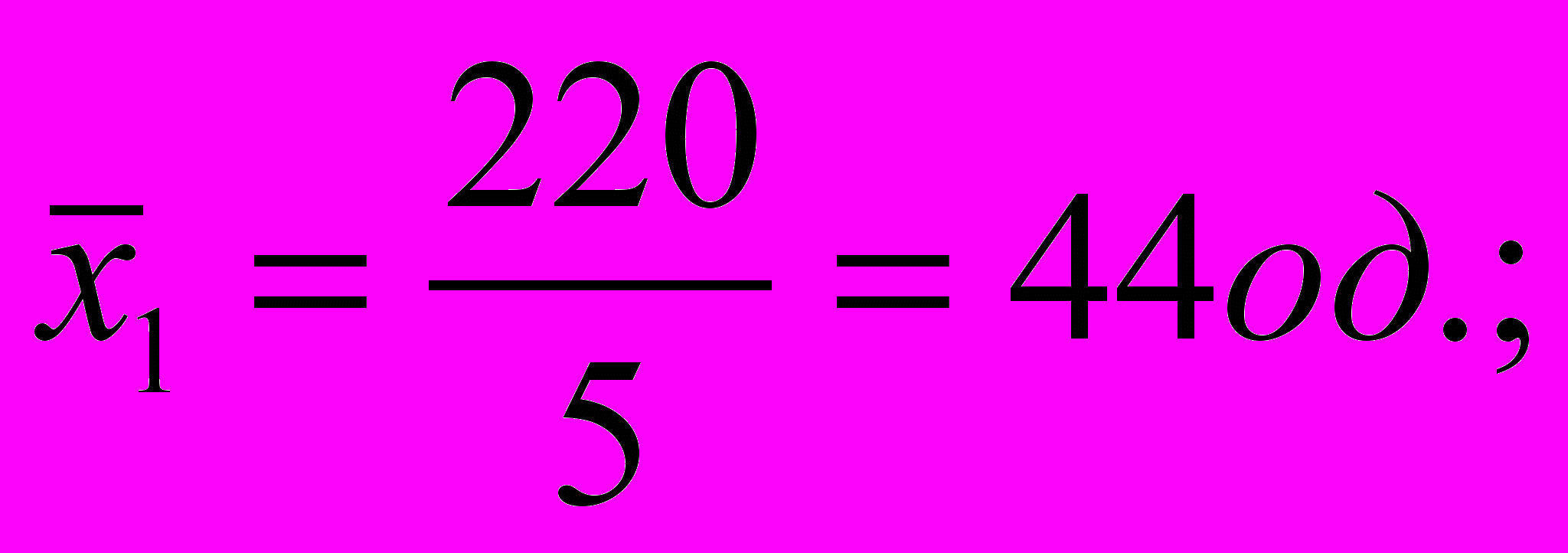
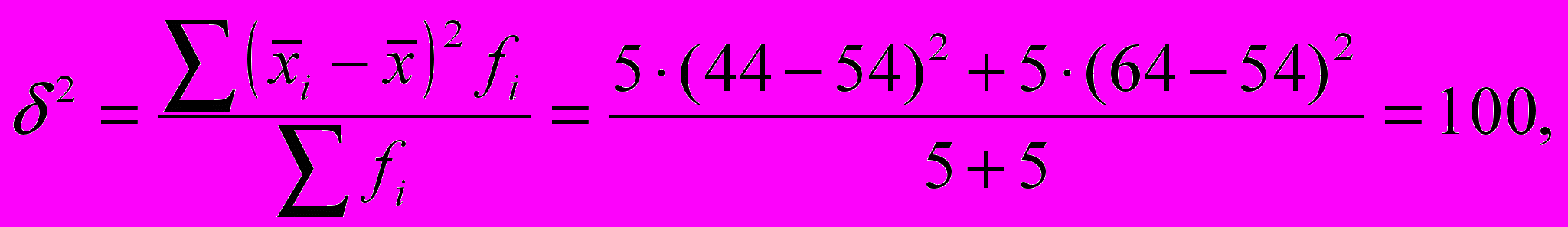
де 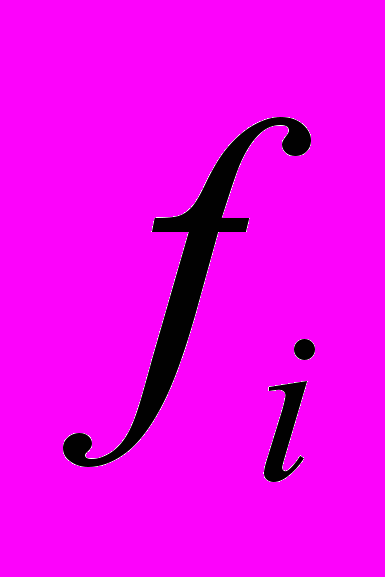– число одиниць у групі, i — число груп. Таким чином, кореляційне відношення становить

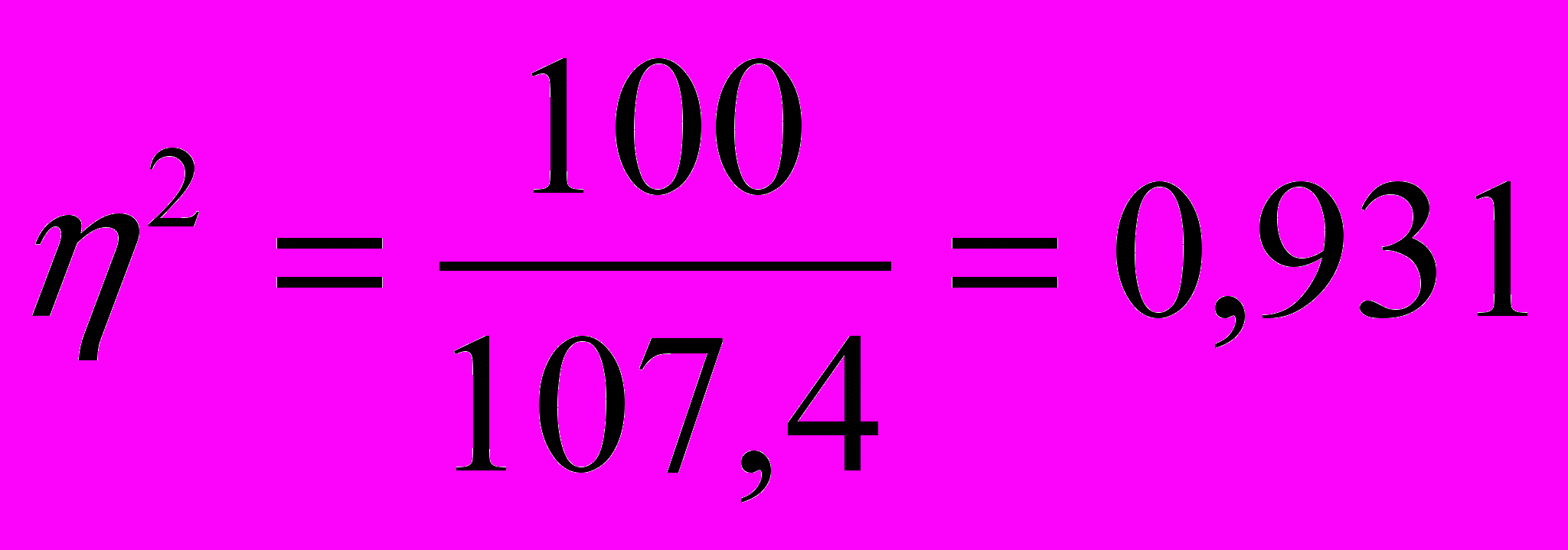(тобто 93,1%).

Це треба розуміти так, що 93,1 % всієї варіації обу­мовлено фактором, який покладено в основу групу­вання, і тільки 6,9 % варіації є результатом дії інших. Такими, наприклад, можуть бути вік робітника, його стать та ін.

Кореляційне відношення змінюється від 0 до 1. Коли міжгрупова дисперсія дорівнює нулю, що мож­ливо лише тоді, коли всі групові середні однакові, тобто коли кореляційний зв'язок між середніми відсутній. Причому міжгрупова дисперсія дорівнює загальній, а середня з групових – нулю. Це означає, що кожному значенню факторної ознаки відповідає єдине значення результативної ознаки, тобто зв'язок між ознаками функціональний.

Припустимо, що ми поділили робітників на дві групи за ознакою числа літер у прізвищі (парне чи не­парне) і обчислені групові середні відрізняються. Але в цьому випадку різниця є випадковістю.

Перевірку істотності (невипадковості) відхилень групових середніх здійснюють за допомогою стати­стичних критеріїв. У даному випадку можна викори­стати критерій Фішера, або порівняти фактичне значення 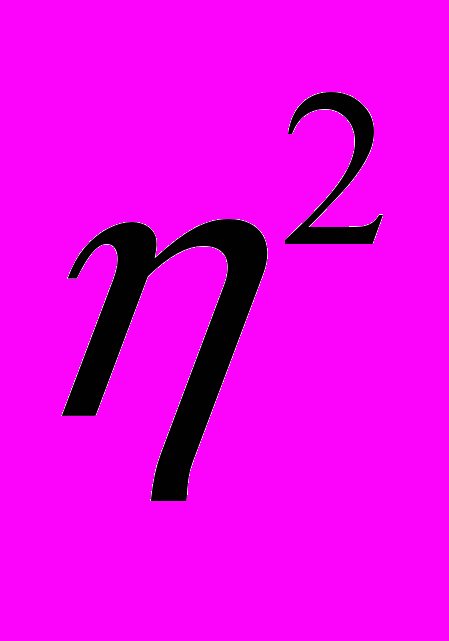з критичним (табличним).

У таблиці розподіл залежить від числа ступенів вільності факторної К1 та випадкової К2 дисперсій.



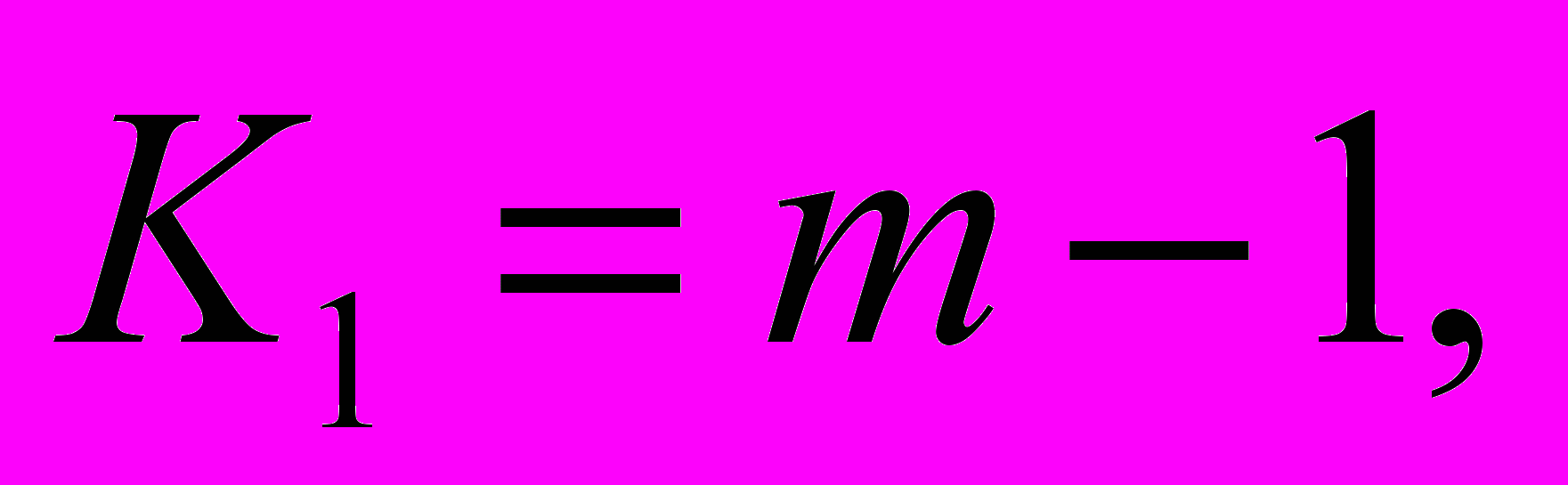
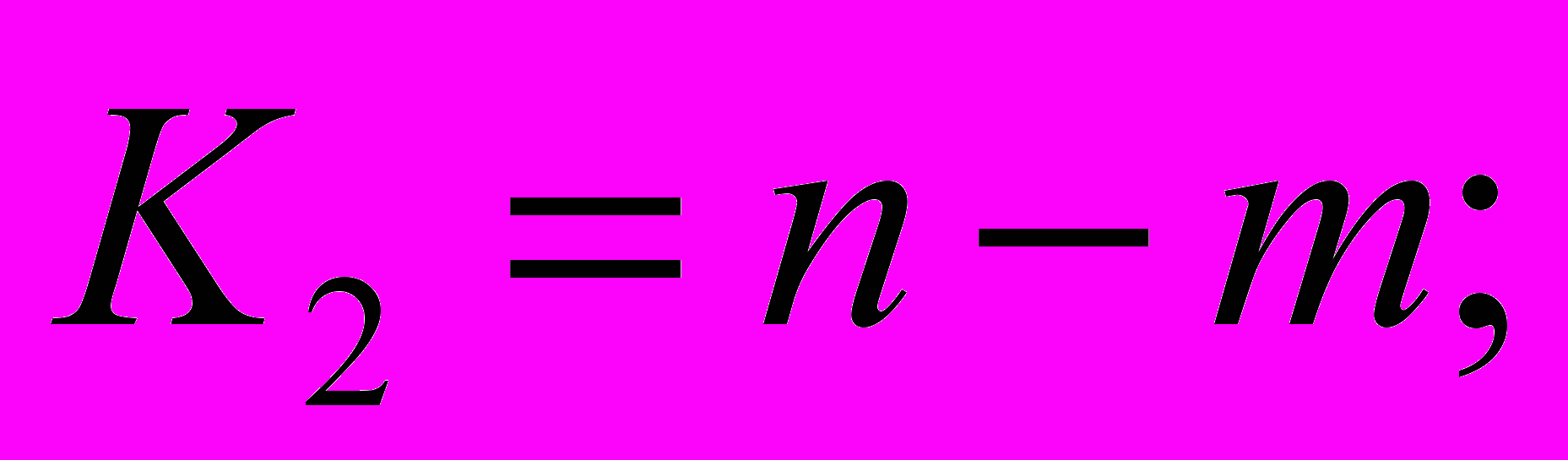
де т — число груп; п — загальний обсяг сукупності.

«Входами» в таблицю критичних значень є числа ступенів вільності К1, Кг та рівень значимості , який задається дослідником і характеризує, в якій мірі він ризикує помилитися в своєму припущенні (про «невипадковість»).


Для нашого прикладу



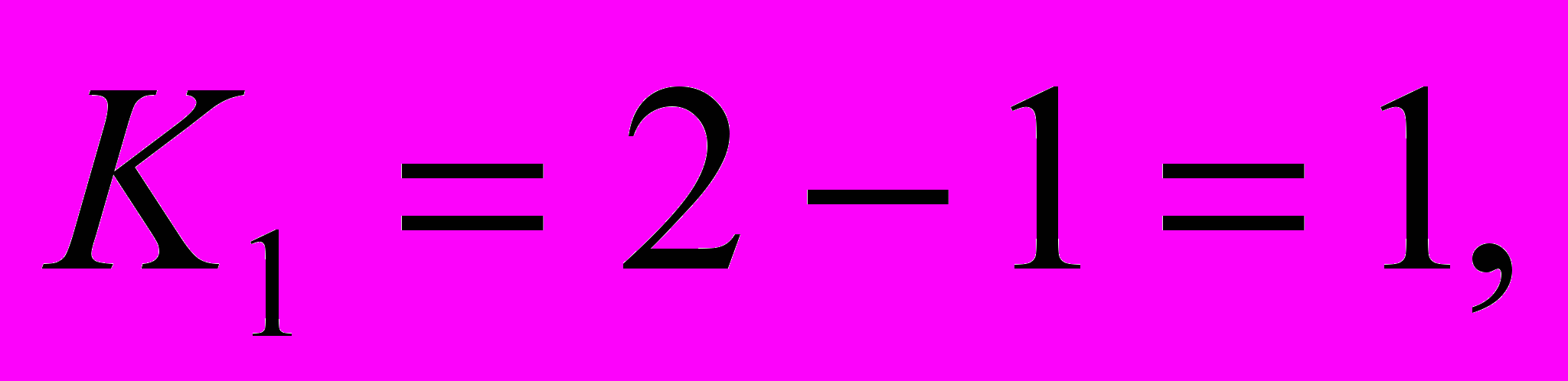
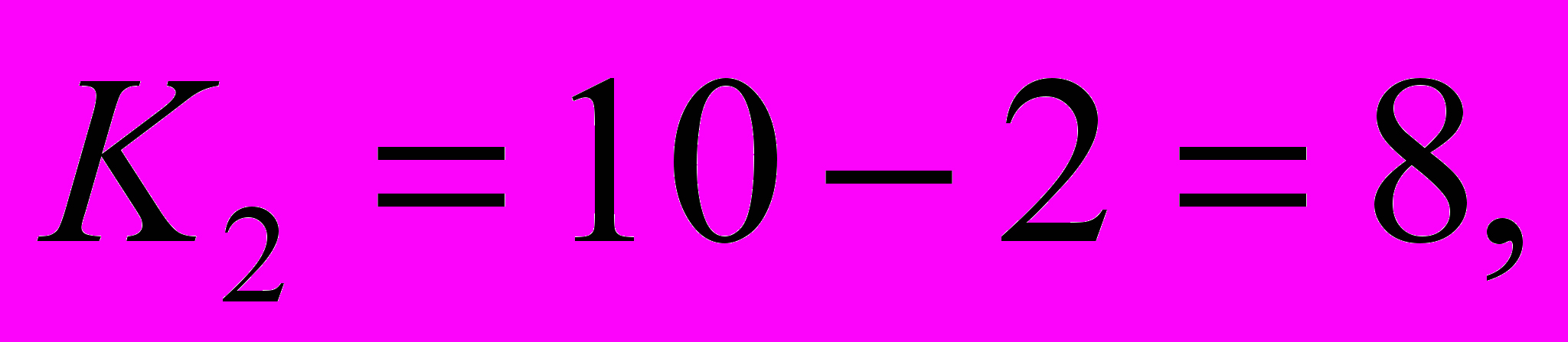
а  оберемо на рівні 5 %.

За таблицею критичних значень для рівня істотності  = 0,05 знаходимо .

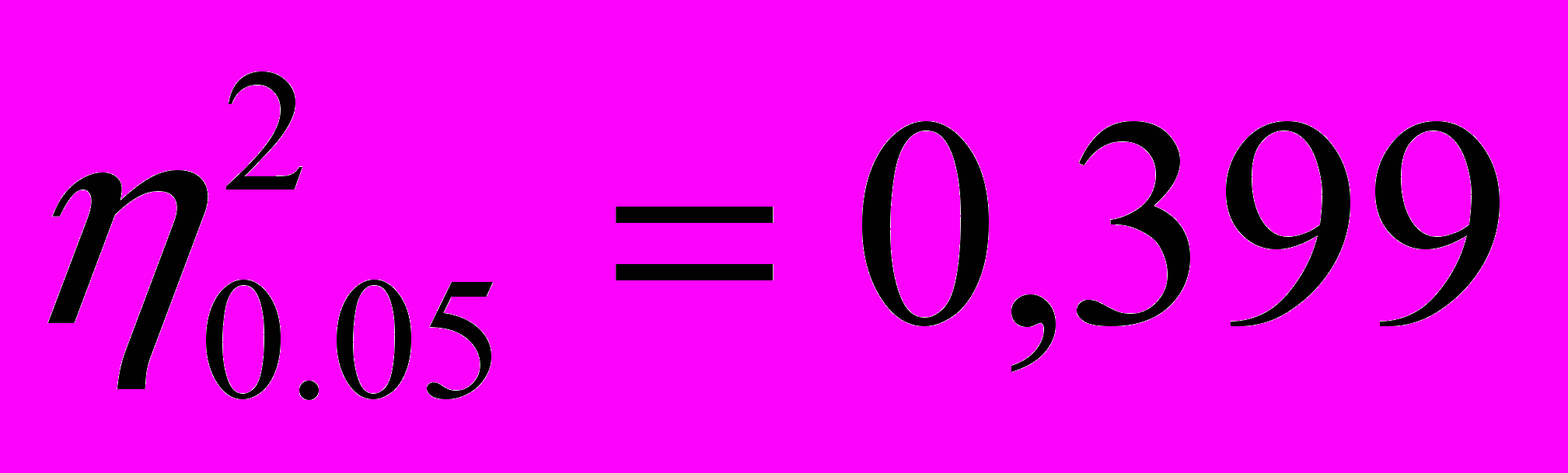Це означає, що тільки в 5 випадках із 100 може ви­падково виникнути кореляційне відношення, яке пе­ревищує значення 0,399. Тепер треба порівняти фак­тичне значення з критичним. Якщо воно більше кри­тичного, то зв'язок між факторною і результативною ознакою вважається істотним:



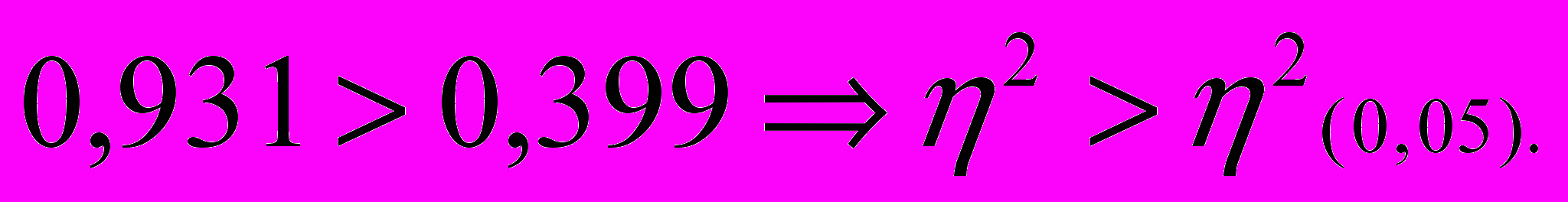
Тобто, зв'язок між фактом проходження робіт­ником перепідготовки та зростанням продуктивності праці слід вважати істотним.


Приклад 3

З отари овець загальною чисельністю 1000 голів (N) вибірковій контрольній стрижці було піддано 100 голів (n), середній настриг вовни при цьому становив 4,2 кг на одну вівцю при середньому квадратичному відхиленні 1,5 кг. Визначити межі, в яких знаходиться середній настриг вовни для усіх 1000 голів з імовірні­стю 0,954 (t = 2).

У даному разі маємо простий випадковий відбір, до того ж, зрозуміло, безповторний. Підставимо дані у відповідні формули:

,

.

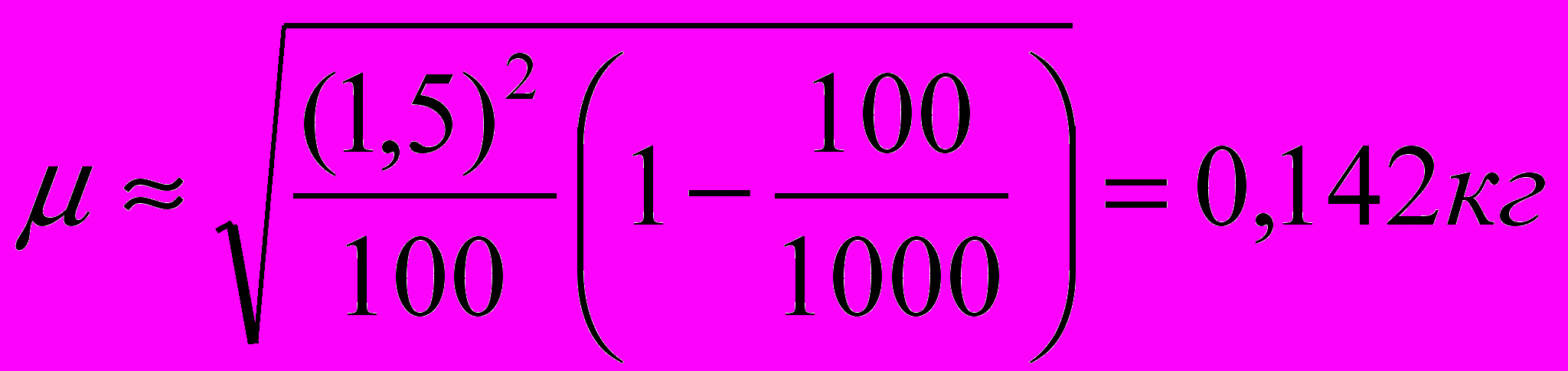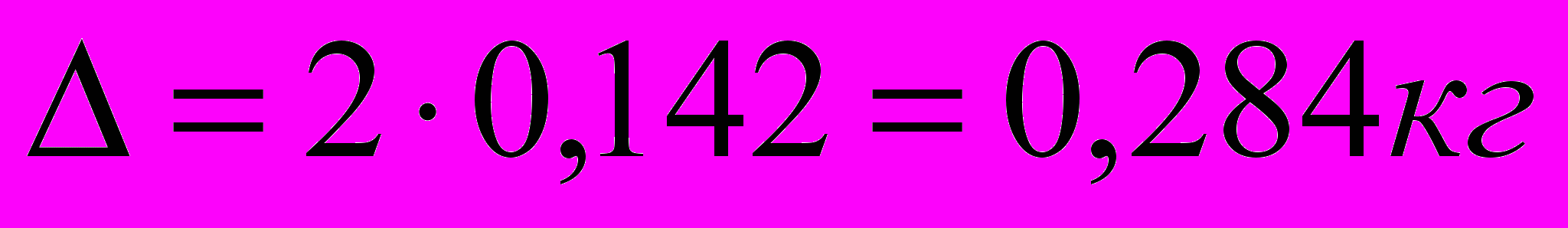Тоді одне із можливих значень, в межах яких може знаходитись середній настриг вовни, розраховуєтся за формулою

.

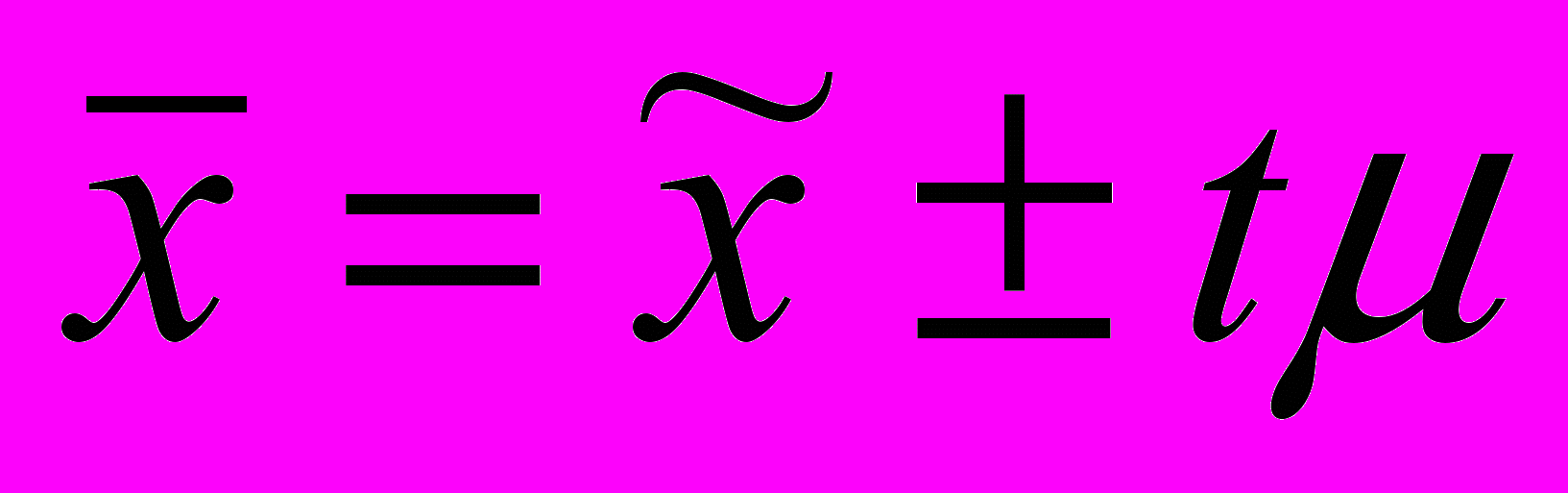У загальному вигляді це записується таким чином:

,

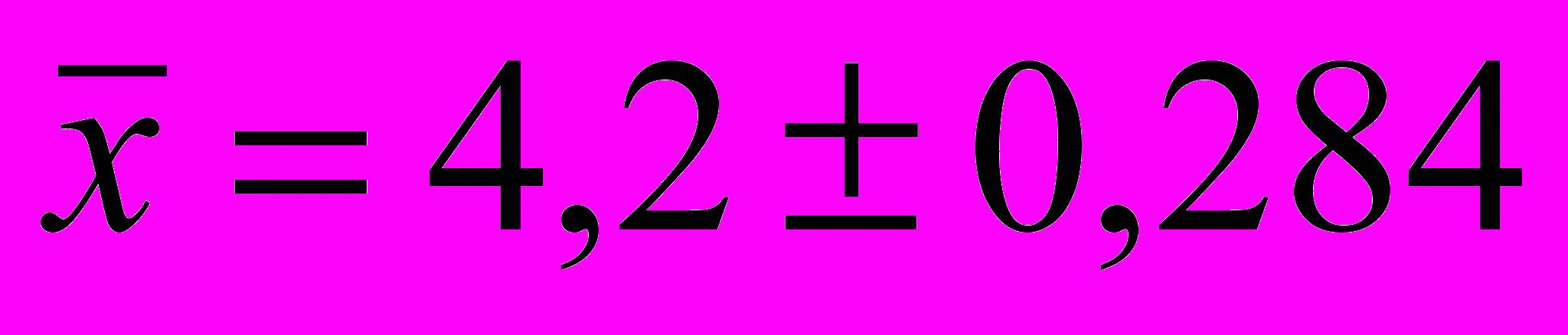що дорівнює:

.

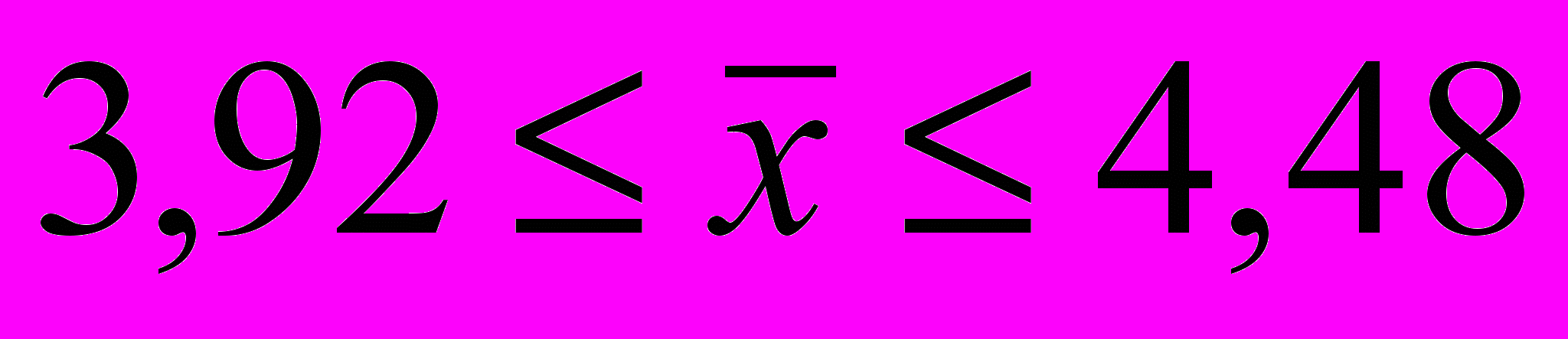Таким чином, на підставі проведеної вибірки га­рантуємо, що у 954 випадках із 1000 середній настриг вовни буде знаходитися в межах: від 3,9 до 4,4 кг на одну вівцю.

Приклад 4

Маємо такі дані:

Товарні

групи
Обсяг споживання у поточних цінах, грош. од.
Індекси цін ip
(p1q1)/ip

I квартал p0q0
II квартал p1q1






М'ясопродукти
320000
315000
0,90
350

Молоко про-дукти
28000
26530
0,95
27926

Хлібопродукти
32000
32817
0,98
33487

Разом
380000
374527
X
411413

Обчислити індекс рівня споживання продуктів харчування на душу населення, якщо відомо, що чисельність населення зросла на 4%.

Зрозуміло, що рівень споживання продуктів на душу населення ми обчислимо, якщо розділимо загальний обсяг споживання на чисельність населення:

;

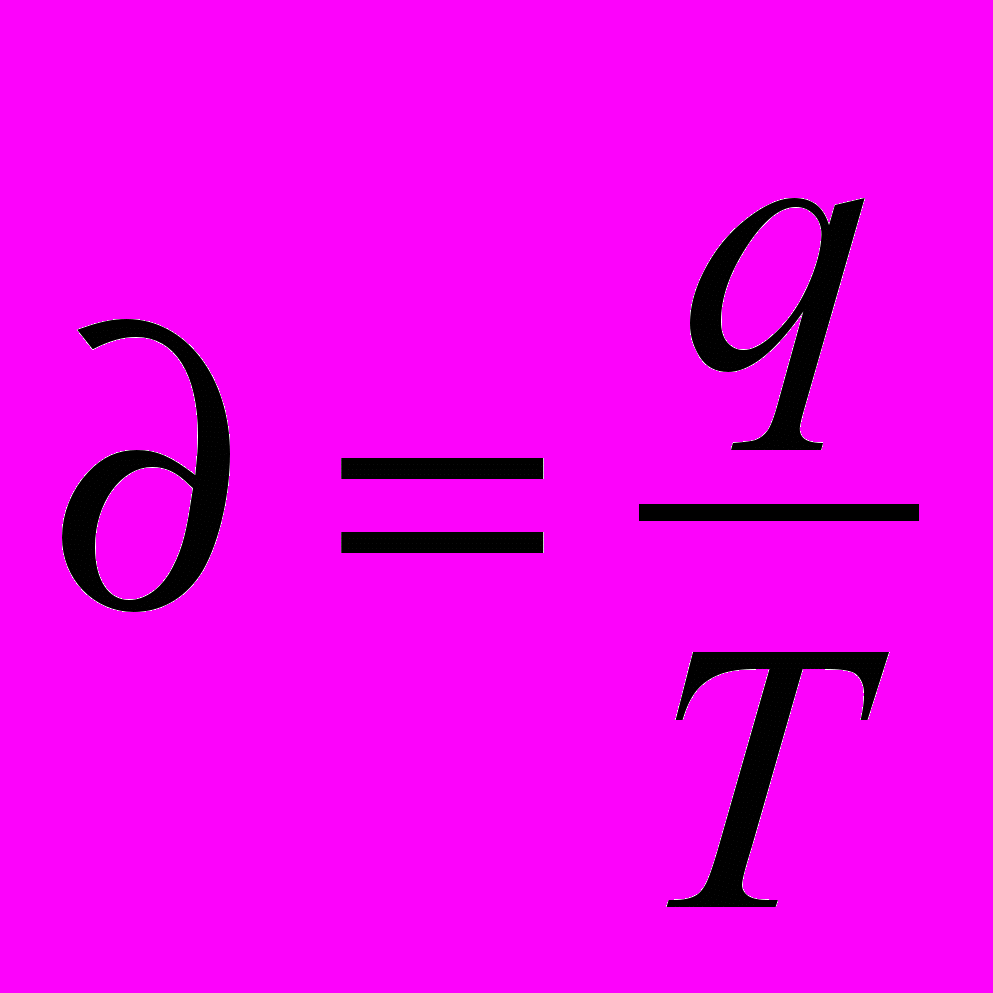таким чином

.

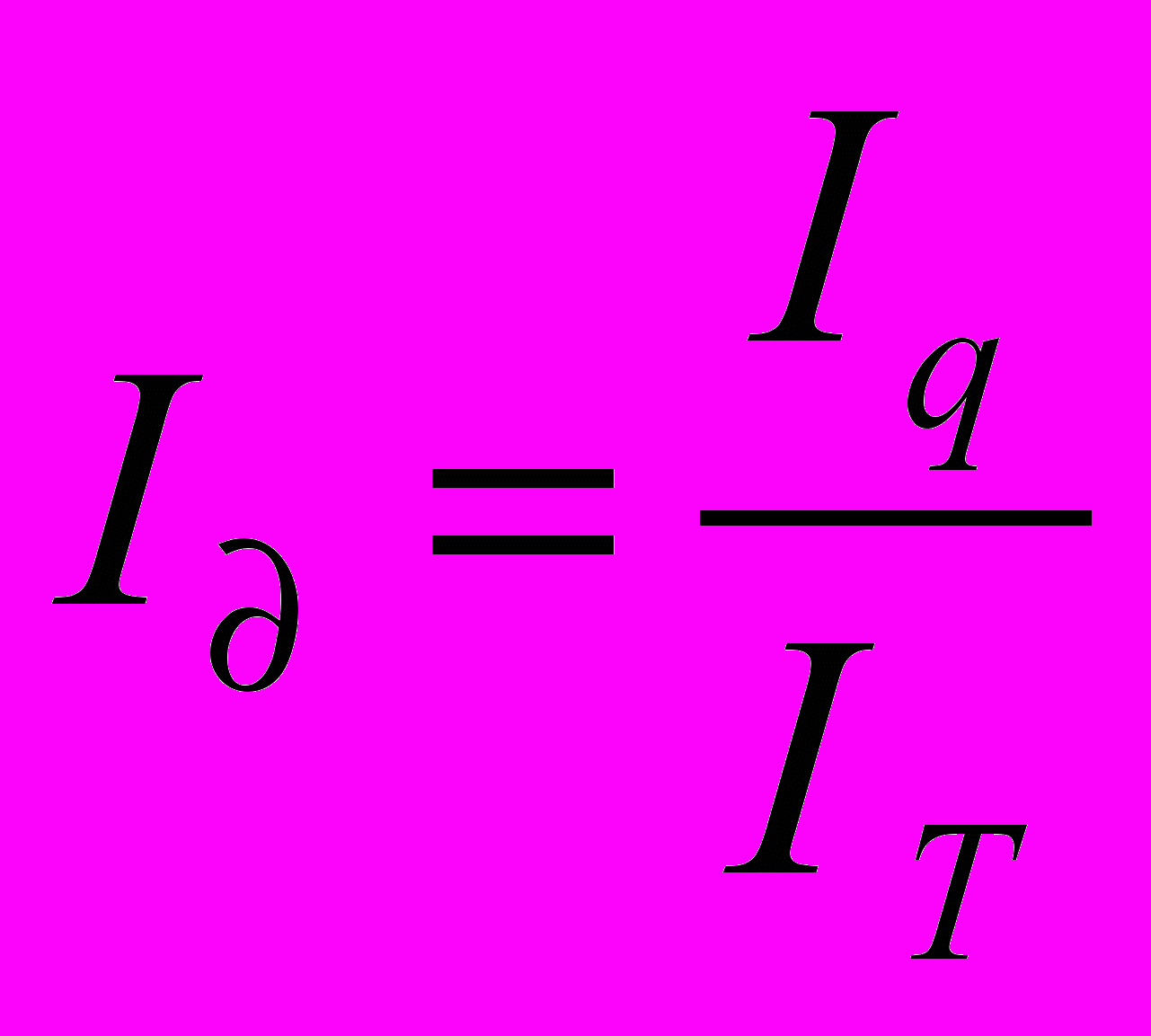Згідно з умовою задачі ІT = 1,04. Залишається обчислити Іq.

У звичайному вигляді він має форму (3).

Для зручності ми рекомендуємо приводити в графах таблиць умовні позначення. Ми бачимо, що в умові задачі наведені агрегати, тобто знаменник, ми вже маємо. Необхідний чисельник ми обчислимо, використавши індивідуальні індекси.

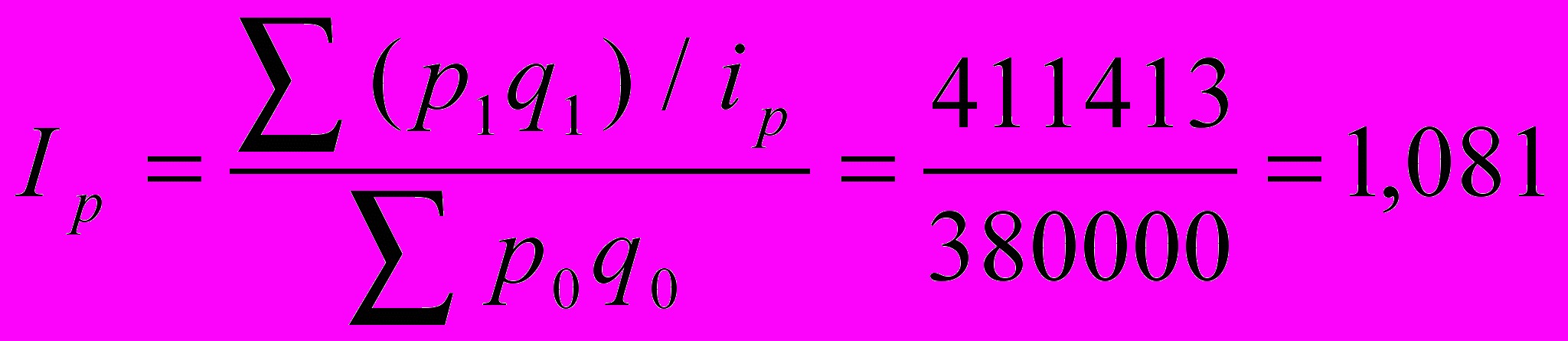(тобто 108,0%).

Звідки

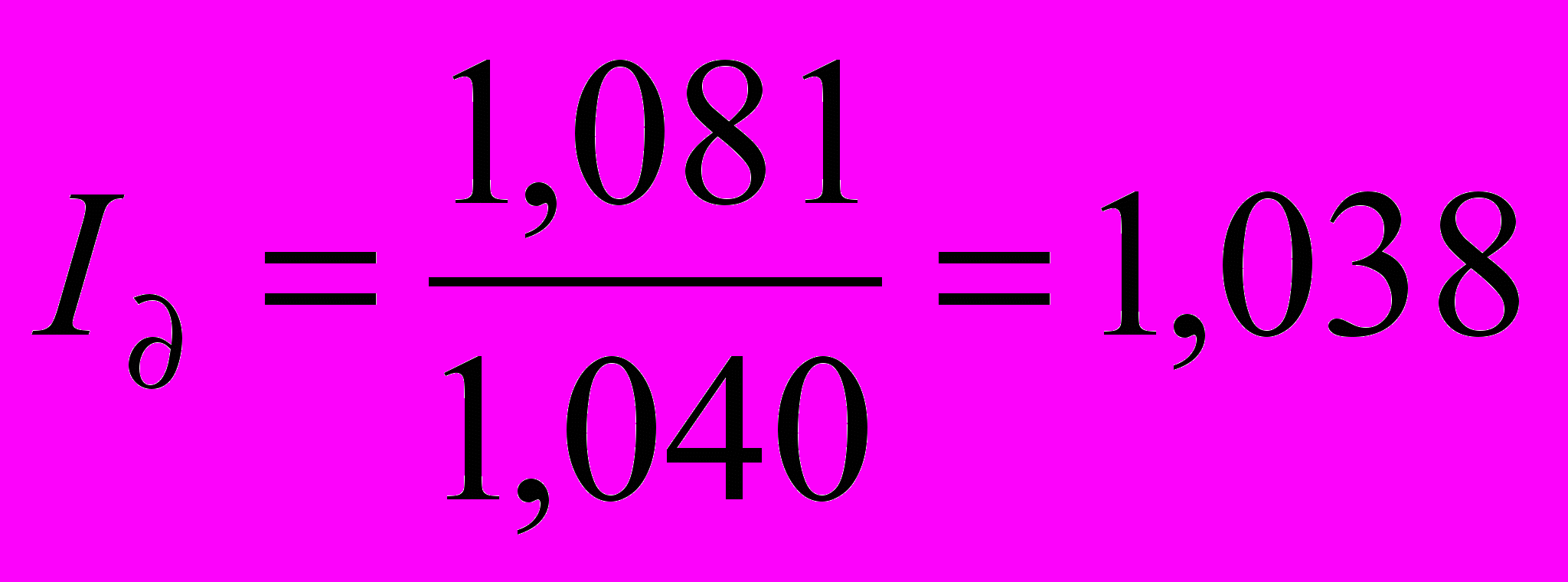(тобто 103,8%).

Отже, рівень споживання на душу населення збільшився на 3,8%.


6. ІНФОРМАЦІЙНО-МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ
      1. Аптон Г. Анализ таблиц сопряженности. — М.: Финансы и статистика, 1982. — 144с.
  1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. — М.: Изд-во ВЦАНСССР, 1983.
  2. Елисеева И.И., Юзбашев М.М. Общая теория статистики. — М.: Финансы и статистика, 2001. — 480с.

4. Єріна А.М., Кальян З.О. Теорія статистики: Практикум. — К.: Товариство “Знання”, КОО, 1997. — 325с.

5. Єріна А.М. Статистичне моделювання та прогнозування: Навч. Посібник. — К.: КНЕУ, 2001. — 170с.

6. Кимбл Г. Как правильно пользоваться статистикой. — М.: Финансы и статистика, 1982. — 296с.

7. Рунион Р. Справочник по непараметрической статистике. — М.: Финансы и статистика, 1982. — 200с.

8. Статистика — Под ред. А.В. Головача. — К.: Вищі школа, 2003.

9. Теория статистики: Учебник. Под ред. Р.А. Шмойловой. — М.: Финансы и статистика, 1998.

10. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке: Методы обработки данных. — М.: Мир, 1980. — 610с.

11. Вентцель Е.С. Теория вероятностей. — М.: Наука, 1968. — 576с.

12. Румшиский Л.З. Элементы теории вероятностей. — М.: Наука, 1976. — 240с.

13. Тернер Д. Вероятность, статистика и исследование операций. — М.: Статистика, 1976. — 432с.