4. статистичні показники
| Вид материала | Документы |
- І. Теоретична частина, 637.27kb.
- Тема Статистичні показники, 204.72kb.
- Перелік питань до заліку з дисципліни «Статистика фінансів», 17.59kb.
- Розділ: Різне Класифікація графіки, 96.86kb.
- Розроблена на основі реформованого податкового законодавства, відповідно до норм чинного, 82kb.
- Мета: навчитися аналізувати абсолютні та відносні статистичні показники побудова графіку, 167.44kb.
- Предмет, методи І завдання економічної статистики, 31.54kb.
- Програма дисципліни "Статистичні методи обробки інформації" Упорядник: проф. Сніжко, 77.9kb.
- План виступу директора Гадяцького науково методичного центру Смірнової Т. Ю. Вступ, 345.75kb.
- Реферат на тему: індекси, 49.38kb.
ТЕМА 4. СТАТИСТИЧНІ ПОКАЗНИКИ
1. Абсолютні показники.
2. Відносні величини в статистиці.
3. Середні величини.
4. Показники варіації.
Теорія статистичних показників в економічній науці та практиці має велике значення. Звітність підприємств та організацій, внутрішньо фірмове та стратегічне планування, дослідницька та аналітична робота, моделювання та прогнозування базуються на використанні різних систем економічних показників. Саме тому теорія статистичних показників займає одне з головних місць в теорії статистики.
Статистичний показник – це узагальнююча характеристика соціально-економічного явища та процесу, в якій поєднується якісна та кількісна визначеність останнього.
Якісний зміст показника залежить від суті явища (процесу) і знаходить своє відображення у назві (народжуваність, прибутковість тощо).
Кількісний бік явища представляють число та його вимірник.
Показники різноманітні за способом обчислення, ознакою часу.
За способом обчислення розрізняють первинні та похідні показники. Первинні показники визначаються шляхом зведення та групування даних і подаються у формі абсолютних величин. Похідні показники обчислюються на базі первинних показників і мають форму середніх та відносних величин.
За ознакою часу показники поділяються на інтервальні та моментні. Інтервальні показники характеризують явище за певний час (день, місяць, рік), наприклад, обсяг виробництва продукції, введення житла в дію, перевезення вантажів тощо. До моментних показників відносять показники, які характеризують явище на певний момент часу: протяжність нафтопроводів на кінець року, залишки обігових коштів на початок місяця, чисельність населення, наявність запасів матеріальних ресурсів тощо.
Всі показники, що використовують в статистиці, за формою виразу класифікують на абсолютні, відносні та середні.
1. Абсолютні показники.
Абсолютні показники характеризують фізичні розміри соціально-економічних явищ та процесів, що вивчаються, а саме їхню масу, площу, обсяг, довжину, а також можуть представляти обсяг сукупності. До абсолютних показників, наприклад, відносять площу території країни, обсяг промислового виробництва, експлуатаційну довжину залізничних шляхів, кількість підприємств галузі тощо.
За способом вираження абсолютні показники поділяються на індивідуальні та сумарні. Індивідуальні виражають розміри кількісних ознак окремих одиниць сукупності (обсяг продукції, виробленої певним робітником за місяць, чисельність робітників на окремих підприємствах). Вони отримуються безпосередньо під час статистичного спостереження. Сумарні показники характеризують підсумкове значення ознаки за певною частиною сукупності і отримуються в результаті підсумовування індивідуальних (обсяг виробленої цехом продукції за місяць, чисельність робітників на підприємствах галузі, регіону тощо).
Залежно від конкретної задачі дослідження та характеру явища використовують натуральні, трудові та вартісні (грошові) показники.
В міжнародній практиці використовують такі натуральні одиниці виміру, як тонни, кг, квадратні, кубічні та прості метри, км, милі, літри, штуки тощо. В групу натуральних також входять умовно-натуральні показники, які використовуються в тих випадках, коли якийсь продукт має декілька різновидів. Так, різні види органічного палива переводять в умовне паливо з теплотою згорання 29,3 мДж/кг (7000 ккал/кг), мило різних сортів – в умовне мило з 40%-вим вмістом жирних кислот, консервні банки різного обсягу – в умовні консервні банки обсягом 353,4 см3 тощо.
До трудових одиниць виміру, що дозволяють враховувати як загальні витрати на підприємстві, так і трудомісткість певних операцій технологічного процесу, відносяться людино-дні та людино-години.
В умовах ринкової економіки особливе значення мають вартісні одиниці виміру, які дозволяють дати грошову оцінку соціально-економічним об’єктам та явищам.
2. Відносні величини в статистиці.
В статистичній практиці для аналітичних цілей широко застосовують відносні показники.
Відносні величини характеризують співвідношення між кількісними характеристиками соціально-економічних явищ та процесів. Будь-яка відносна величина представляє собою дріб, чисельником якого є порівнянна величина, а знаменником – база порівняння. Відносна величина показує, у скільки разів порівнянна величина більша базисної, або яку частку вона становить відносно базисної, іноді – скільки одиниць однієї величини припадає на 1, на 100, на 1000, на 10000 і т.д. одиниць іншої. Відносні величини визначаються у формі коефіцієнтів, процентів, проміле, продециміле тощо.
За аналітичною функцією виділяють відносні величини інтенсивності, динаміки, порівняння, структури та координації.
Відносна величина інтенсивності (ВВІ) характеризує ступінь поширення явища, що вивчається, у певному середовищі:
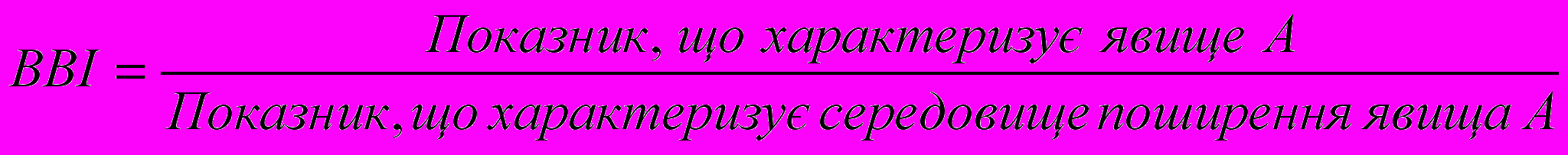 .
.Відносна величина інтенсивності розраховується в тих випадках, коли абсолютна величина є недостатньою для формування обґрунтованих висновків про масштаби явища, його розміри, насиченість, щільність (плотность) поширення.
Наприклад, показник рівня економічного розвитку країни – ВВП на душу населення, демографічні коефіцієнти (народжуваності, смертності) на 1000 чол. населення, забезпеченість лікарями на 10000 чол., захворюваність на 100000 чол., густота населення на 1 км2, для визначення забезпеченості населення легковими автомобілями розраховують число автомашин на 100 сімей.
Відносна величина динаміки (ВВД) характеризує напрямок та інтенсивність зміни явища у часі; розраховується співвідношенням значень показника за два періоди чи моменти часу.
 .
.Розрізняють відносні величини динаміки з постійною чи змінною базою порівняння. Якщо порівняння відбувається з одним і тим же базисним рівнем, наприклад, першим роком періоду, що вивчається, отримують базисні відносні величини динаміки. При розрахунку відносних показників динаміки зі змінною базою (ланцюгових показників) порівняння відбувається з попереднім рівнем, тобто база порівняння постійно змінюється.
Приклад. Виробництво цукру в Україні в січні –квітні 1996 р. характеризується наступними даними (табл.. 4.1.)
Таблиця 4.1.
| Місяць | Січень | Лютий | Березень | Квітень |
| Обсяг виробництва, тис. т | 108 | 138 | 131 | 206 |
Розрахуємо базисні та ланцюгові показники динаміки (табл. 4.2.):
| Змінна база порівняння (ланцюгові показники) | Постійна база порівняння (базисні показники) |
| 138/108*100%=127,8%, або 1,278 131/138*100%=94,9%, або 0,949 206/131*100%=157,3%, або 1,573 | 138/108*100%=127,8%, або 1,278 131/108*100%=121,3%, або 1,213 206/108*100%=190,7%, або 1,907 |
Базисні та ланцюгові відносні показники динаміки взаємопов’язані між собою наступним чином: добуток усіх ланцюгових відносних показників дорівнює відносному показнику з постійною базою за період, що вивчається (всі показники – у вигляді коефіцієнтів):
1,278*0,949*1,573=1,907, або 190,7%.
Таким чином, обсяг виробництва цукру за 4 місяці виріс у 1,907 рази (коефіцієнт росту, індекс росту), в процентному виразі - це 190,7% (темп росту). Інакше кажучи, за 4 місяці обсяг виробництва цукру збільшився на 90,7% (темп приросту).
В середньому кожного місяця обсяг виробництва зростав порівняно з попереднім місяцем в
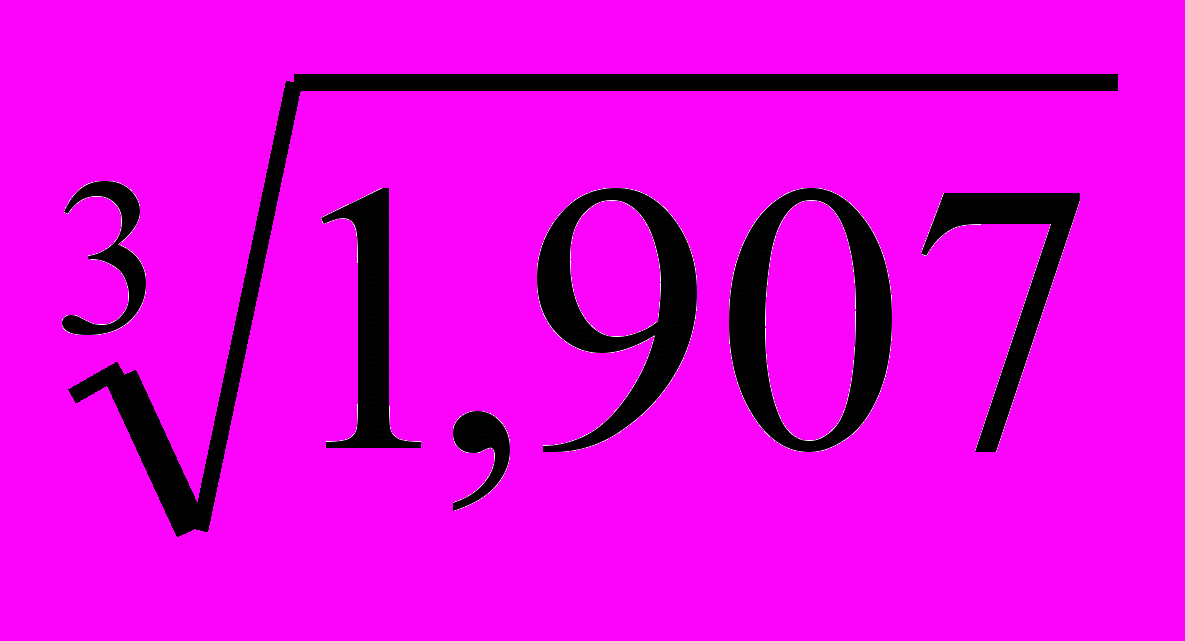 =1,24 рази (середньомісячний коефіцієнт росту або індекс росту), або на 24% (середньомісячний темп приросту).
=1,24 рази (середньомісячний коефіцієнт росту або індекс росту), або на 24% (середньомісячний темп приросту).Відносна величина порівняння (ВВП) представляє собою співвідношення одного й того ж абсолютного показника, що характеризує різні об’єкти (підприємства, фірми, райони, області, країни тощо):
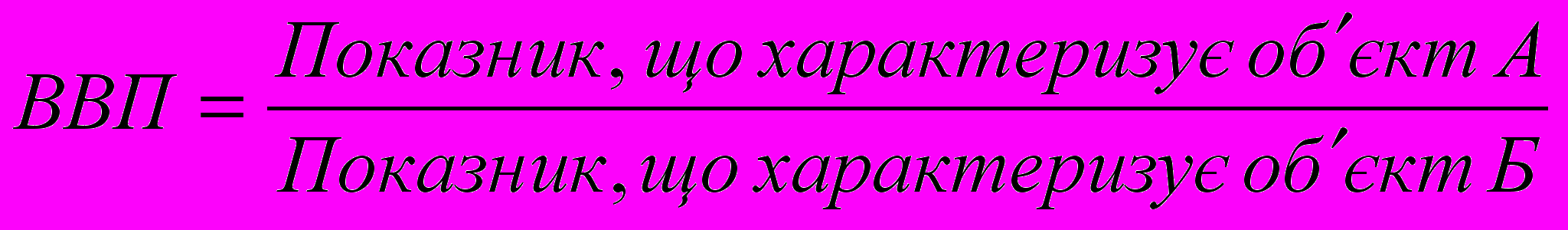 .
.Наприклад, у країні А ВВП на душу населення становить 3522 дол. США, в країні Б – 5280. Якщо прийняти за базу порівняння країну А, то можна сказати, що в країні Б ВВП на душу населення в 105 рази вищий (5280/3522=1,5). Якщо базою порівняння виступає країна Б, то у країні А ВВП на душу населення становить 2/3 рівня країни Б (3522/5280=0,67).
Базою порівняння може виступати еталонне значення показника (норматив, стандарт тощо). Відхилення відносної величини від еталону від 1 до 100% свідчить про порушення оптимального співвідношення. Наприклад, раціональна норма харчування дітей у віці 1 – 3 роки передбачає споживання 1540 ккал і 53 г білка. За даними обстеження домогосподарств регіону фактичне споживання становить 1370 ккал і 46 г білка, тобто фактичне споживання відхиляється від раціональної норми за калорійністю харчування на 11% (1370/1540=0,89), за білком – на 13% (46/53=0,87).
Відносна величина структури (ВВС) характеризує склад, структуру сукупності за тією чи іншою ознакою, обчислюється відношенням розміру складової частини до загального підсумку:
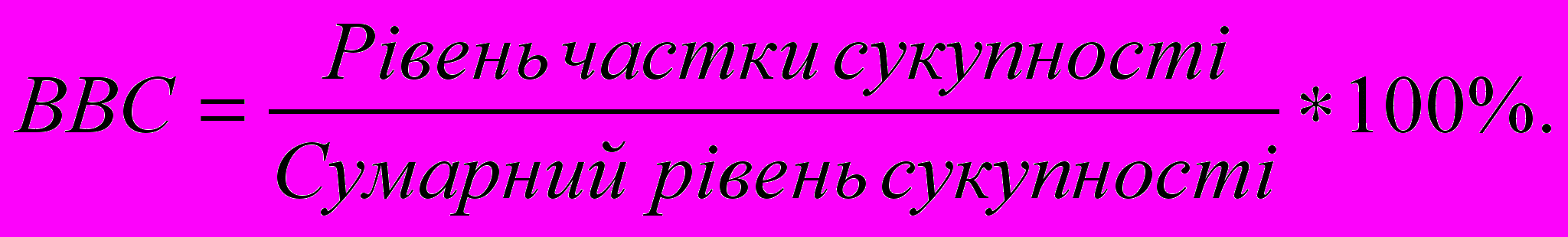
Відносні величини структури називають частками, сума їх становить 100%.
На використанні часток ґрунтується порівняльний аналіз складу різних за обсягом сукупностей, оцінка структурних зрушень у часі. Різницю між частками називають процентними пунктами.
Співвідношення між окремими складовими сукупності є відносними величинами координації. Вони показують скільки одиниць однієї частини сукупності припадає на 1 або 100 одиниць іншої, прийнятої за базу порівняння.
Наприклад, на початок року капітал фірми становив 400 млн. гр. од., з них власний капітал – 260 млн. гр. од., залучений – 140. Частка власного капіталу становить 260/400=0,65, частка залученого капіталу – 140/400=0,35. сума часток дорівнює 0,65+0,35=1. Співвідношення власного і залученого капіталу показує, що на 100 гр. од. Власного капіталу припадає 54 гр. од. залученого.
3. Середні величини.
Найбільш поширеною формою статистичних показників, що використовуються в соціально-економічних дослідженнях, є середня величина. Вона представляє собою узагальнюючу кількісну характеристику ознаки в статистичній сукупності. Показник в формі середньої величини відображає типові риси і надає узагальнюючу характеристику однотипних явищ за однією варіативною ознакою. Він відбиває рівень цієї ознаки, віднесений до одиниці сукупності.
У статистичній практиці середні величини поділяють на два великі класи:
- ступеневі середні;
- структурні середні.
До ступеневих середніх відносять такі найбільш відомі види як середня геометрична, середня арифметична та середня квадратична. Як структурні середні розглядаються мода і медіана.
Ступеневі середні в залежності від форми надання вихідних даних можуть бути простими або зваженими.
Проста середня величина розраховується за не згрупованими даними і має наступний загальний вигляд:
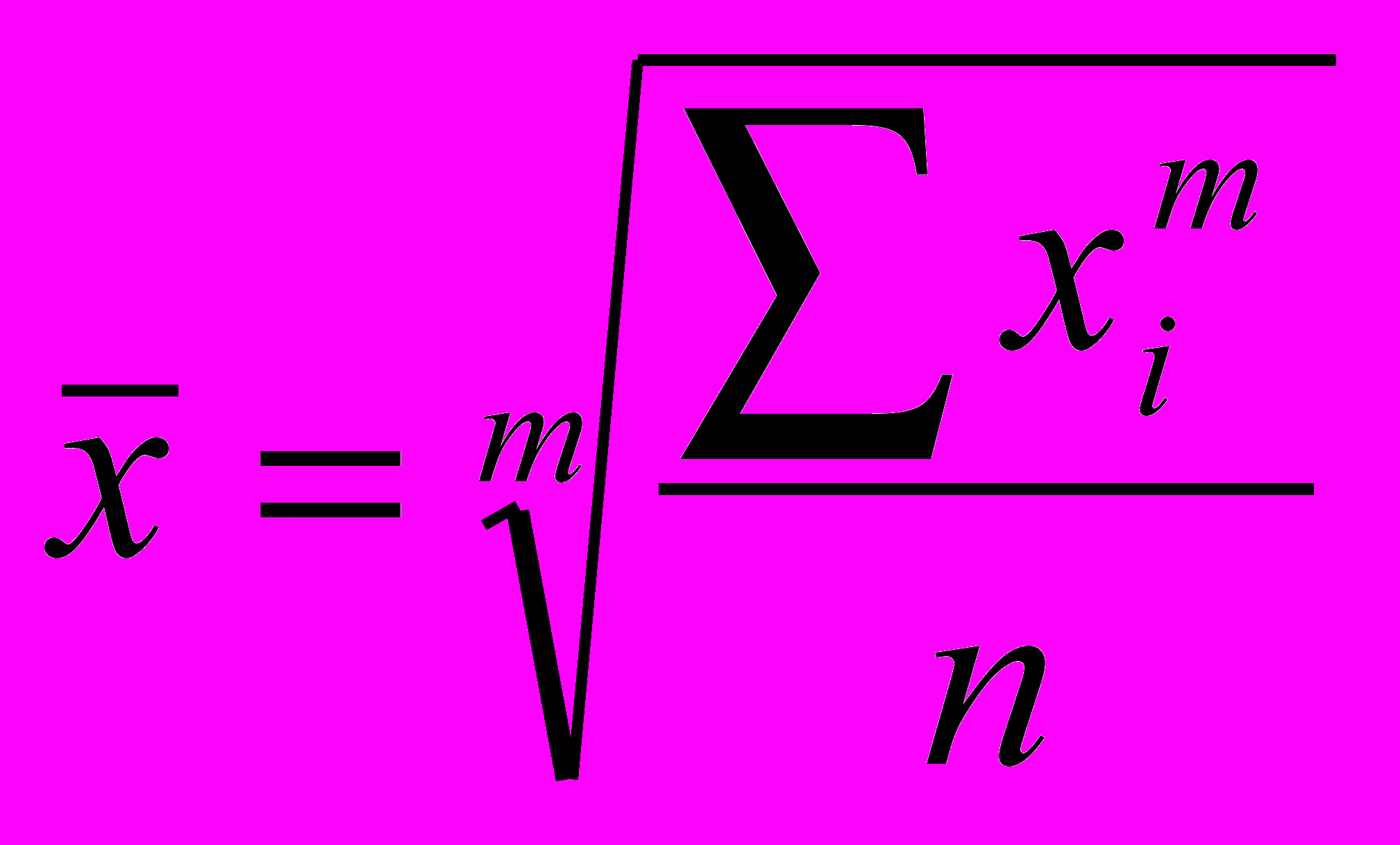 ,
,де xi – індивідуальне значення варіативної ознаки (варіанта);
m – показник ступеня середньої;
n – число варіант.
Зважена середня розраховується за згрупованими даними і має загальний вигляд:
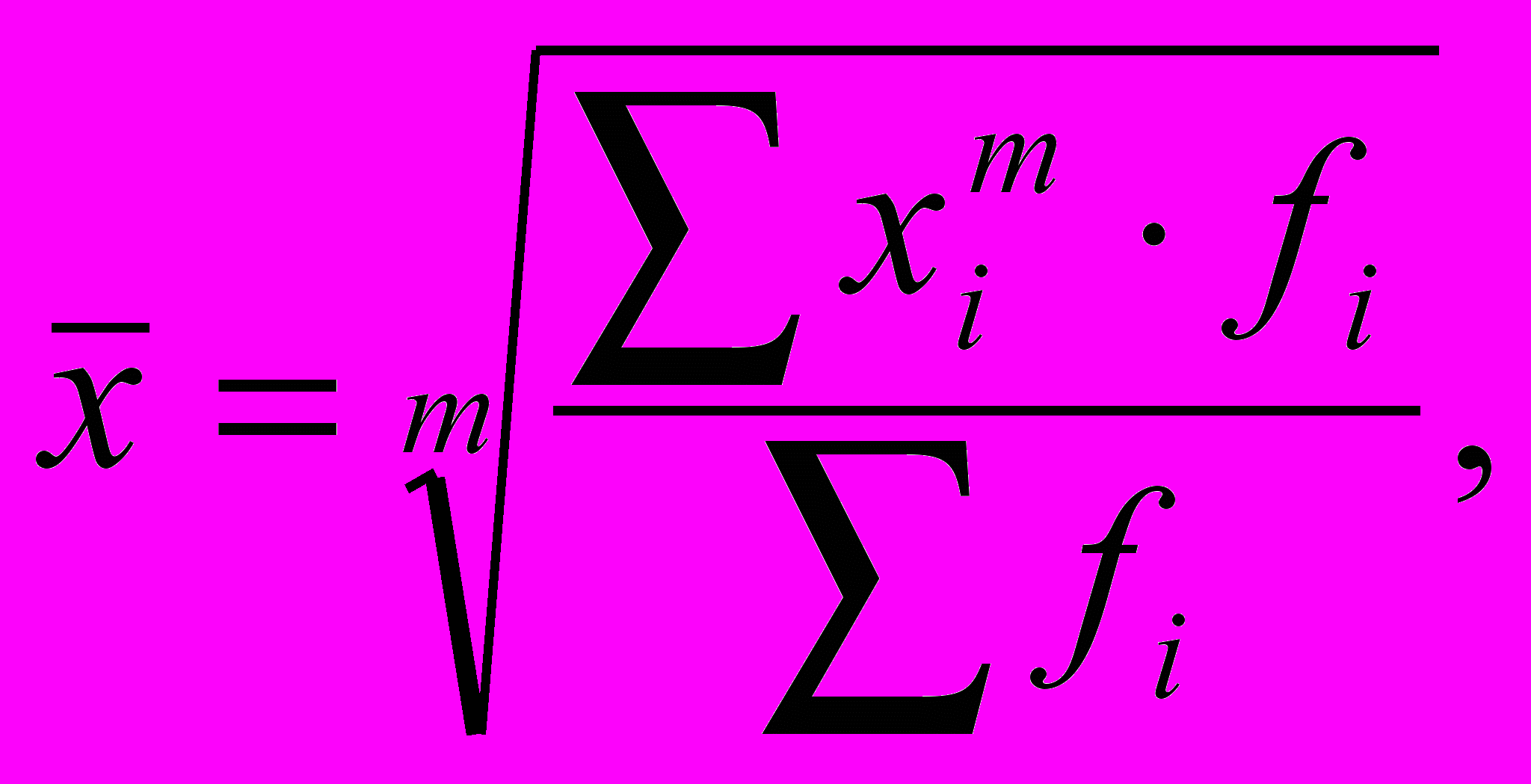
де xi – варіанта (значення) варіативної ознаки або серединне значення інтервалу, в якому вимірюється варіанта;
m – показник ступеня середньої;
fi – частота, яка показує скільки разів зустрічається і-те значення ознаки.
В залежності від того, яке значення приймає показник ступеня (m), розрізняють наступні види ступеневих середніх (табл. 4.3.).
Таблиця 4.3.
Види ступеневих середніх
| Вид ступеневої середньої | Показник ступеня | Формула розрахунку | |
| Проста | Зважена | ||
| Середня гармонійна | m= - 1 | 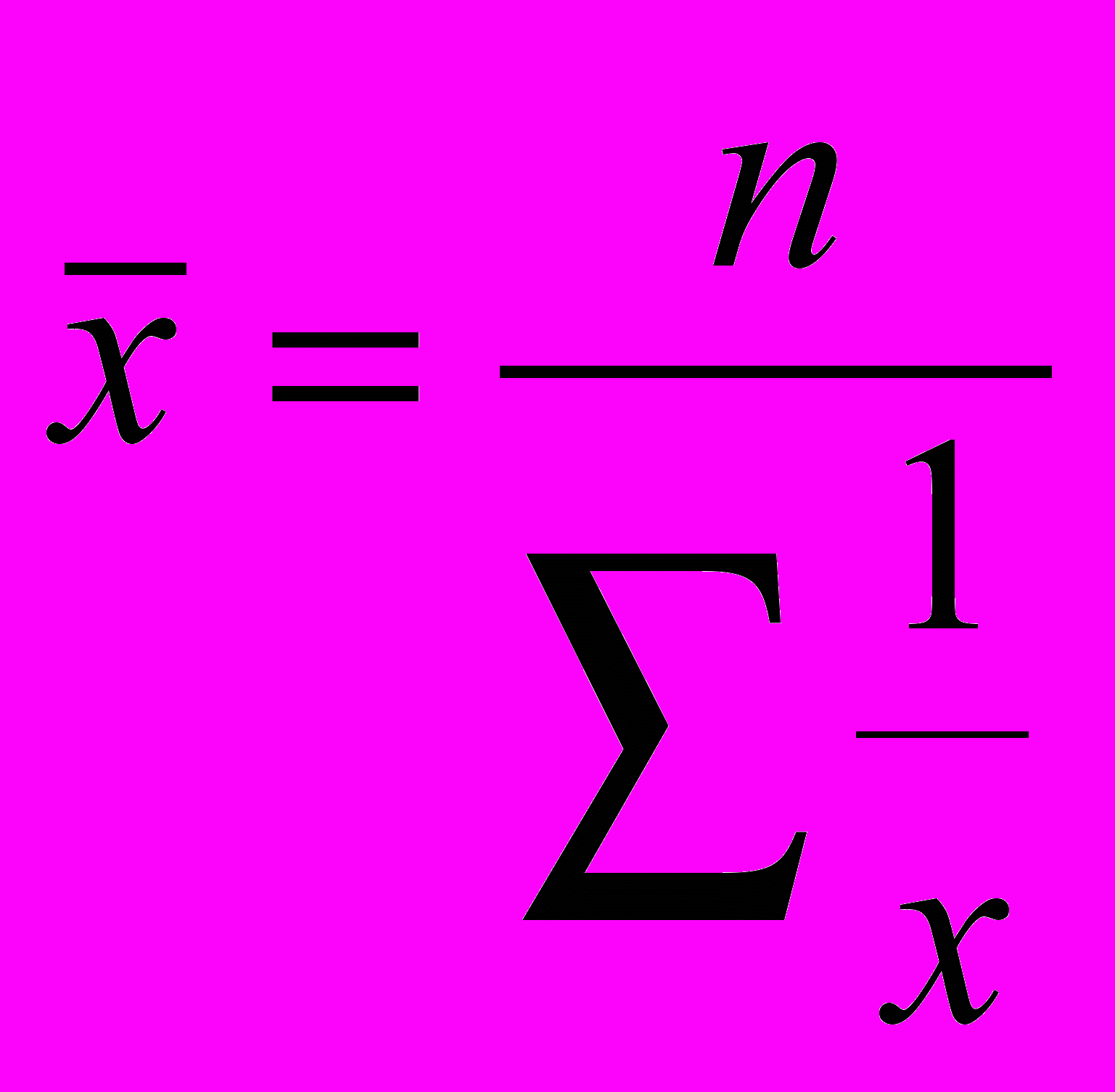 | 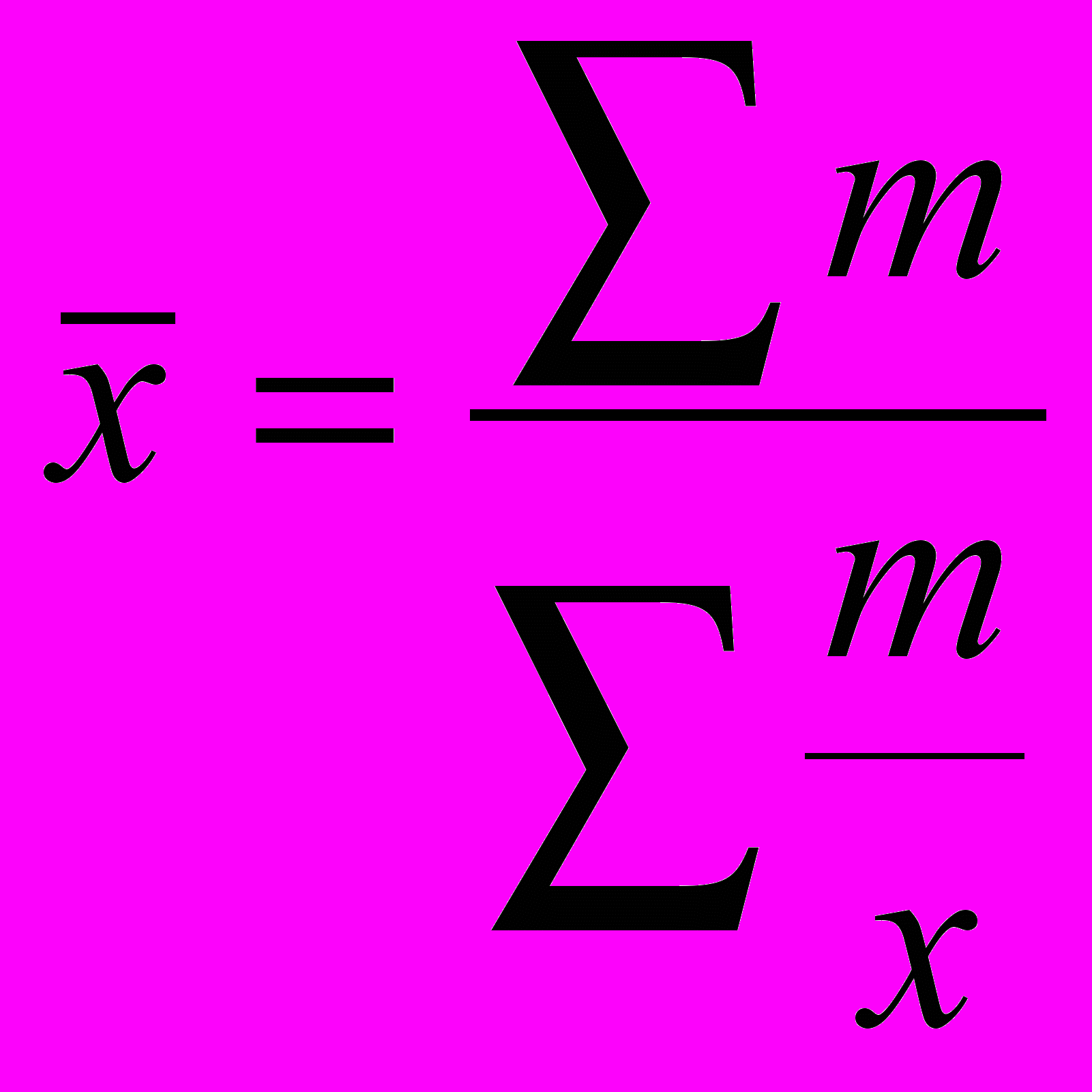 , m=xf , m=xf |
| Середня геометрична | m→0 | 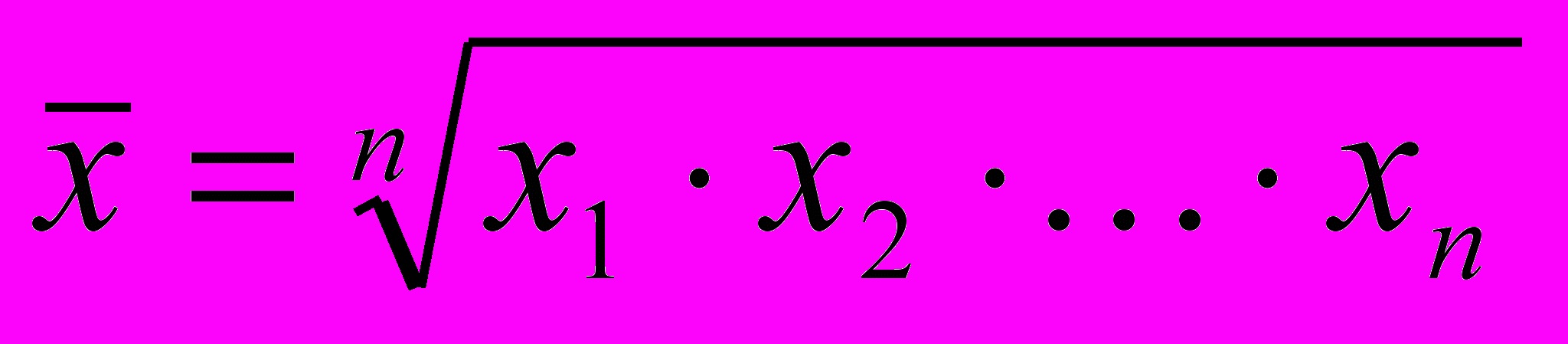 | 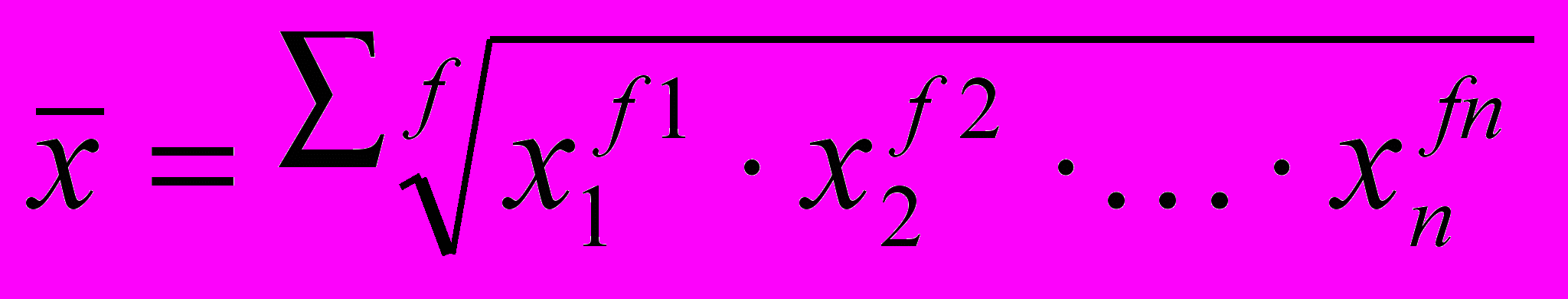 |
| Середня арифметична | m=1 | 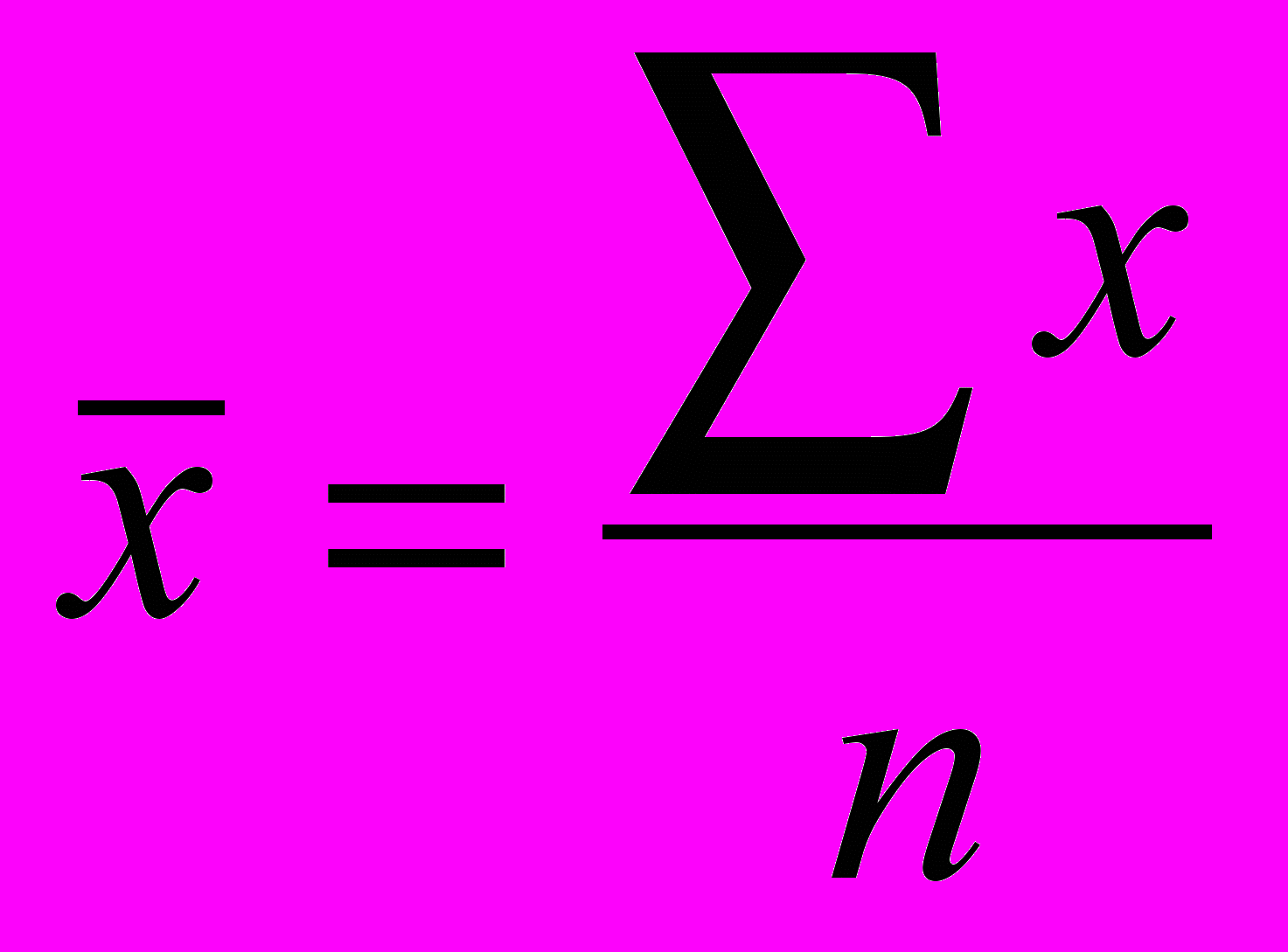 | 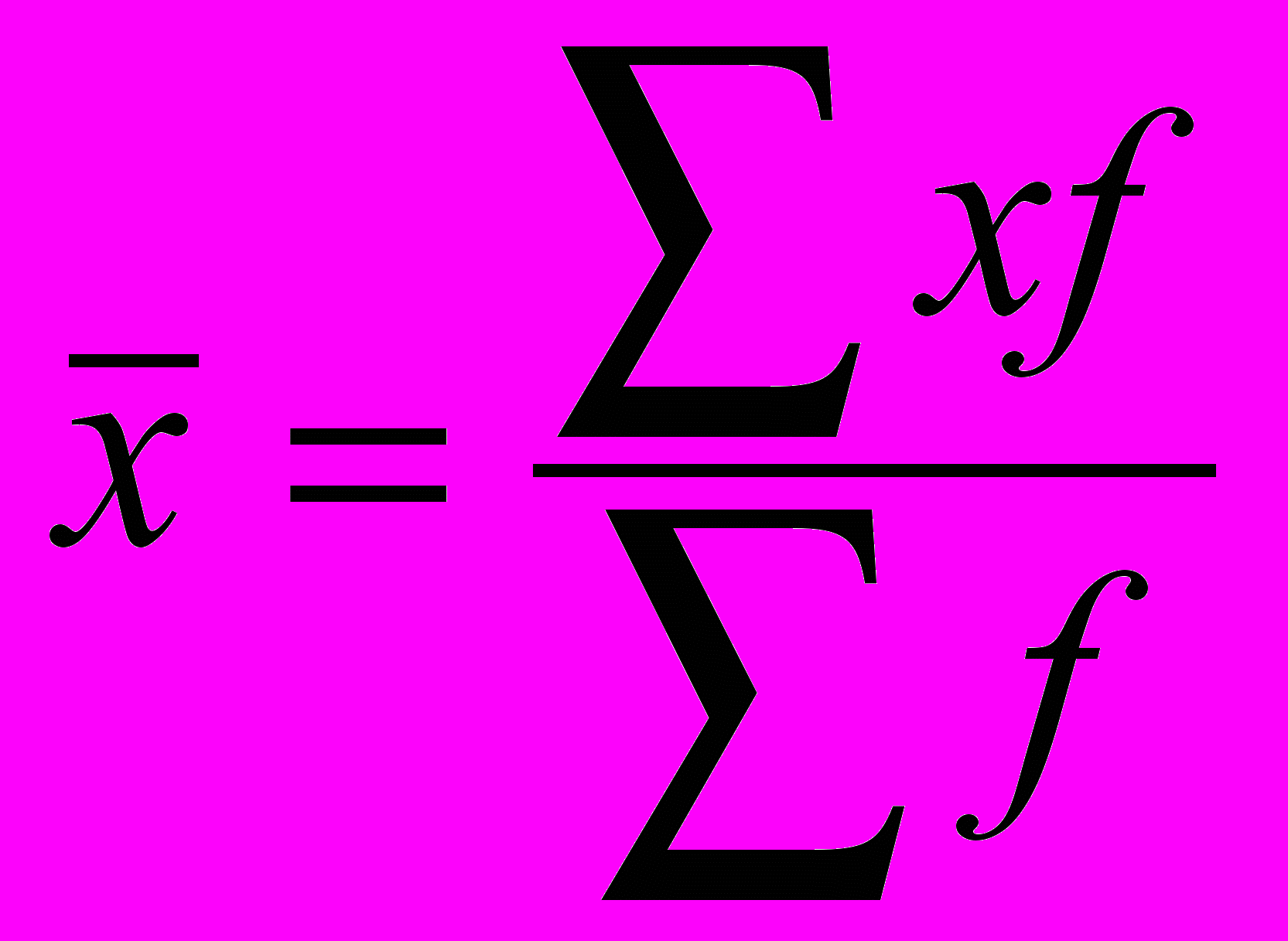 |
| Середня квадратична | m=2 | 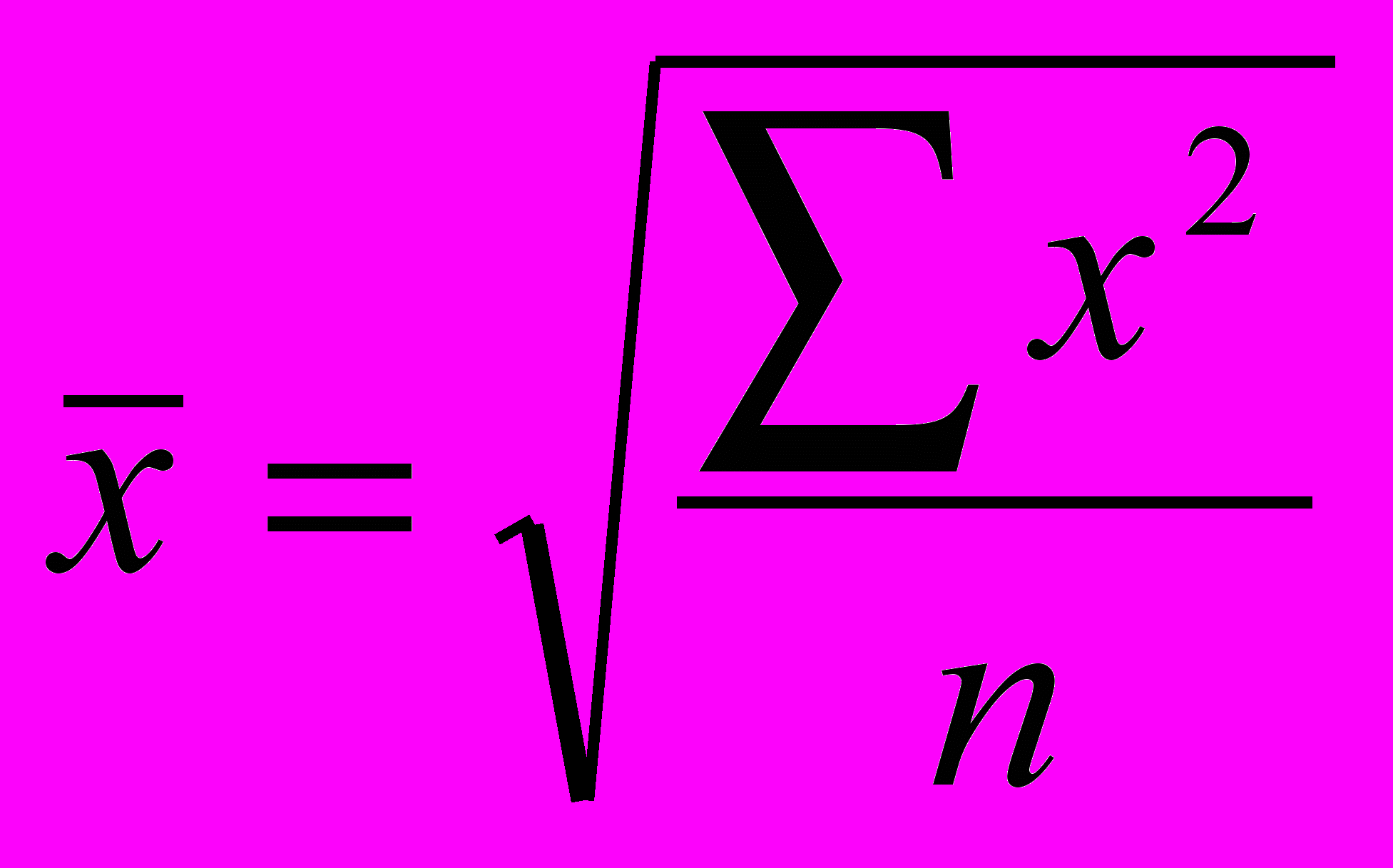 | 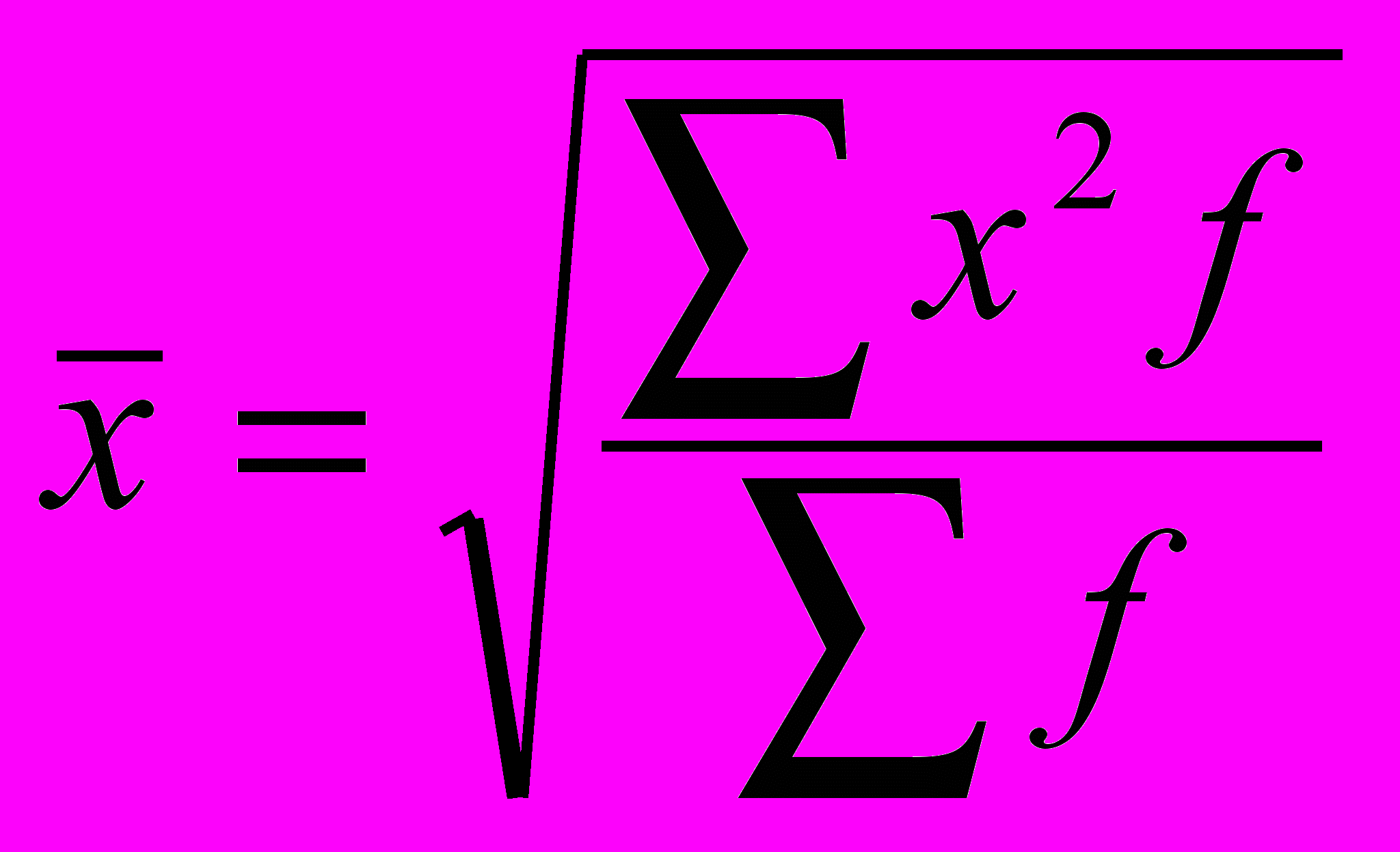 |
| Середня кубічна | m=3 | 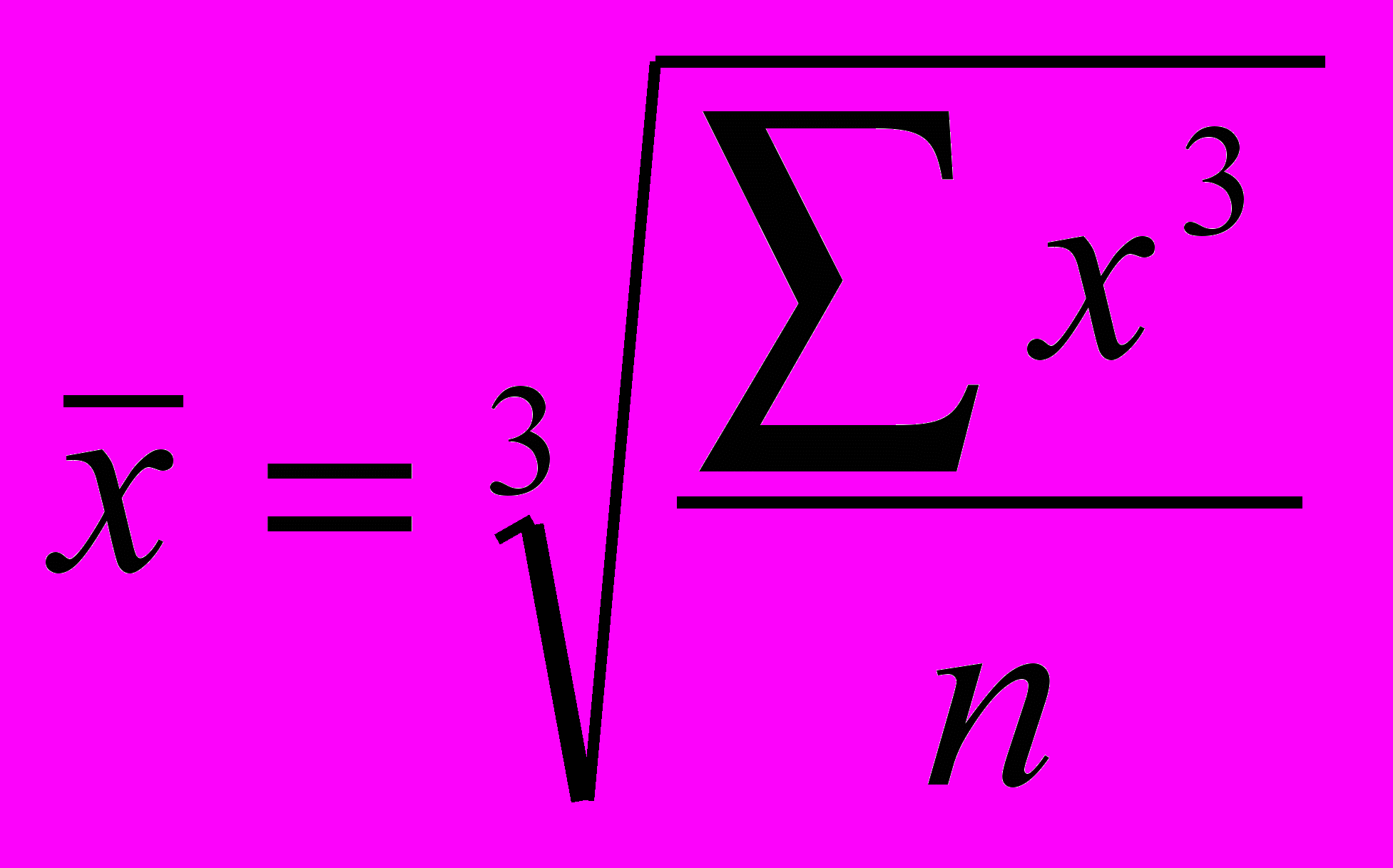 | 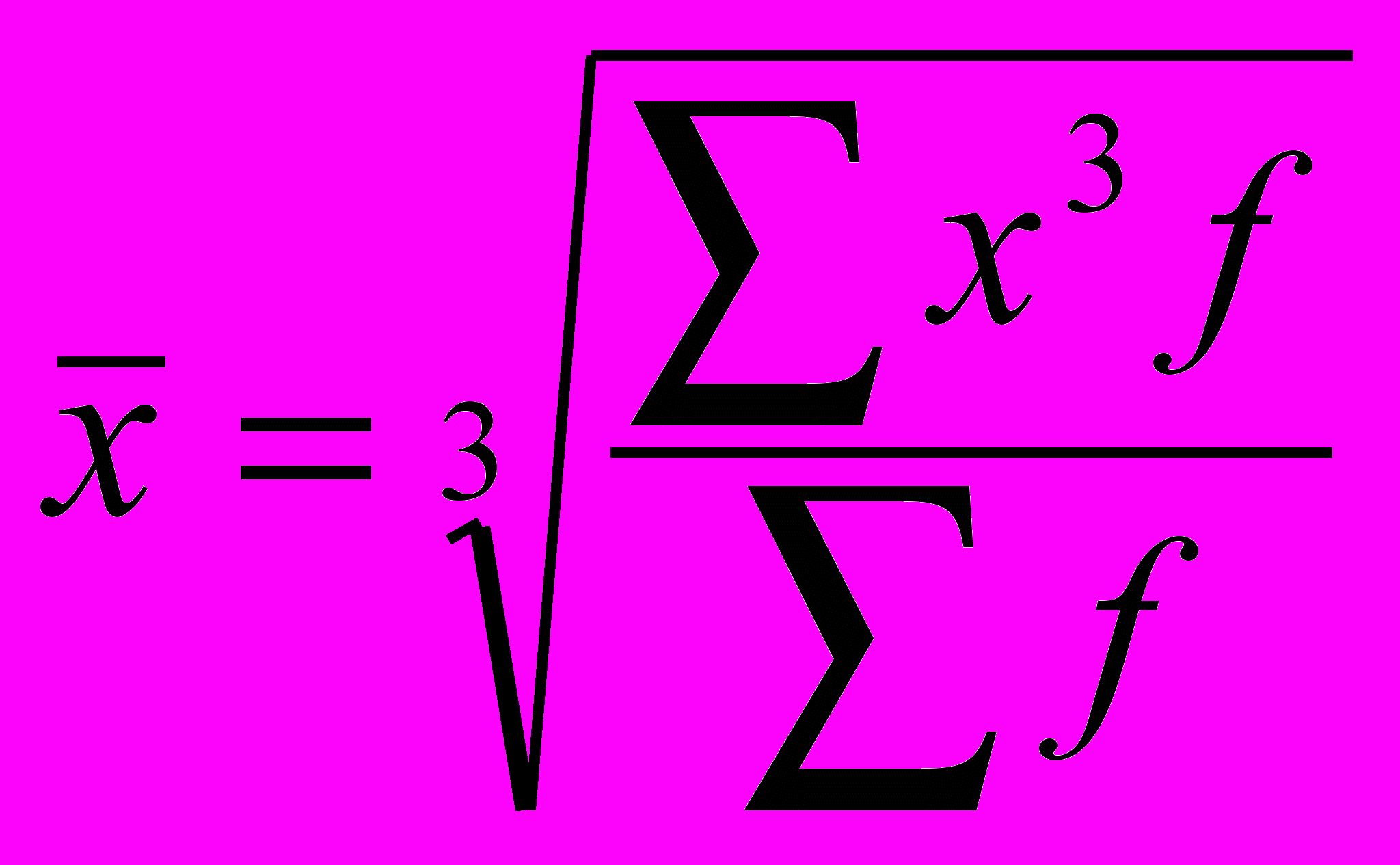 |
При вивченні закономірностей розподілу застосовують середню арифметичну, варіації – середню квадратичну, інтенсивності розвитку – середню геометричну. Різні види середніх, обчислені для одних і тих же даних, мають різну величину. Співвідношення між ними має наступний вигляд і називається правилом мажорантності середніх (тобто при збільшенні показника ступеня т збільшується і відповідна середня величина):
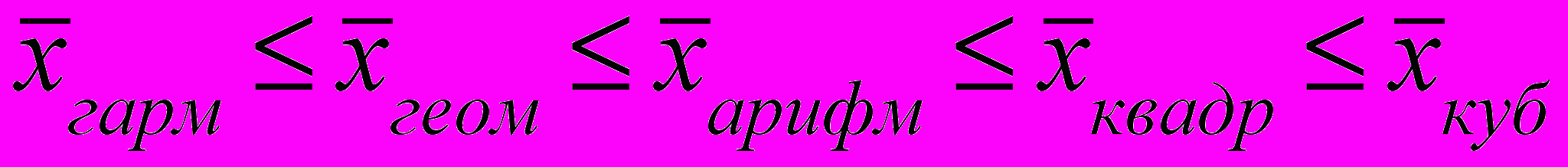 .
.В статистичній практиці частіше, ніж інші види середніх, використовують середню арифметичну та середню гармонійну.
Середня арифметична – одна з найбільш поширених, застосовується в тих випадках, коли обсяг варіативної ознаки для всієї сукупності є сумою індивідуальних значень її окремих елементів.
Приклад. Статутний фонд акціонерної компанії сформований 6 засновниками; розмір внеску кожного з них становить, грн.. грн.: 6; 10; 12; 9; 7; 4. Середній внесок одного засновника:
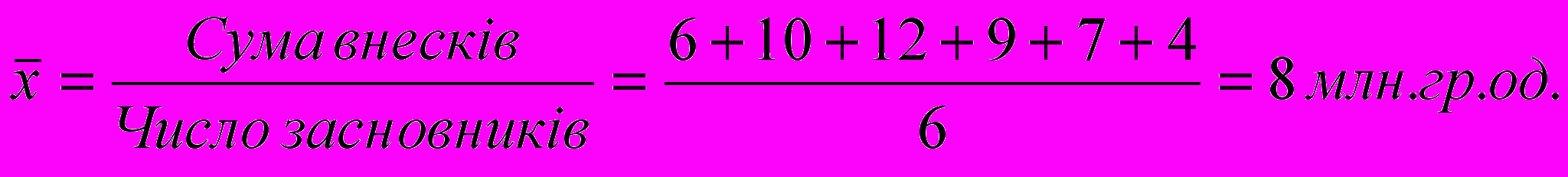
Так, за результатами складання іспиту студентами групи (табл. 4.4.)
Таблиця 4.4.
| Оцінка знань студентів, балів | xj | 5 | 4 | 3 | 2 | Разом |
| Кількість оцінок | fj | 8 | 12 | 6 | 4 | 30 |
| Питома вага оцінок, % | dj | 26,7 | 40,0 | 20,0 | 13,3 | 100 |
На основі частот:
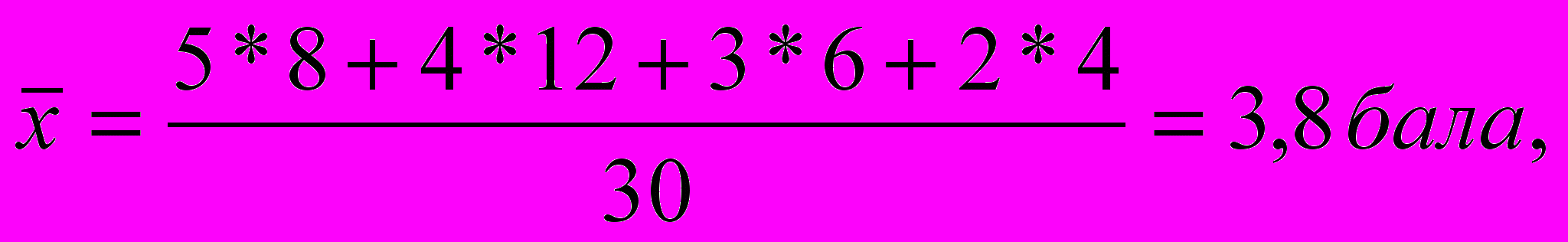
на основі часток:
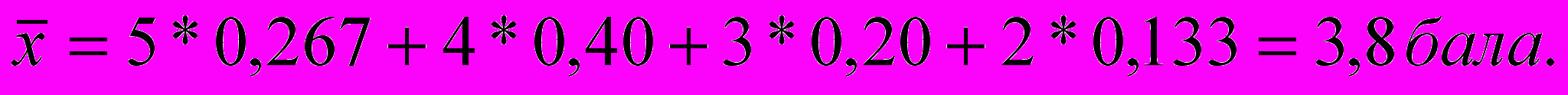
Середня хронологічна розраховується при аналізі показників, які задані дискретно, тобто у формі величин, що характеризують явище на пені моменти часу, певні дати.
Якщо показники характеризують аналізоване явище за період, розбитий на рівні проміжки часу, то середня величина у таких випадках визначається як середня хронологічна
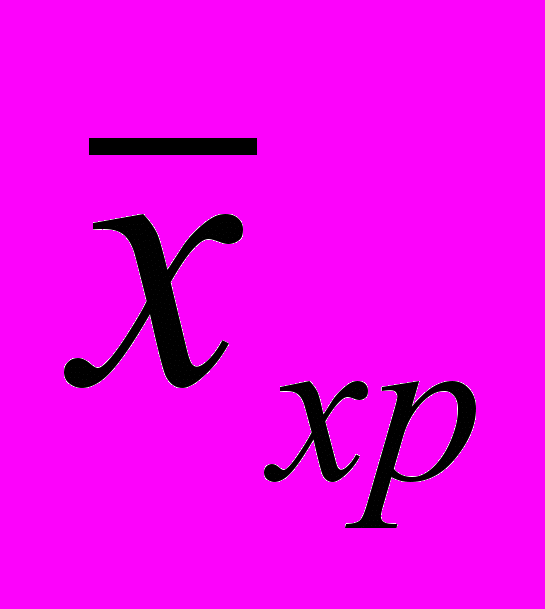 за формулою:
за формулою: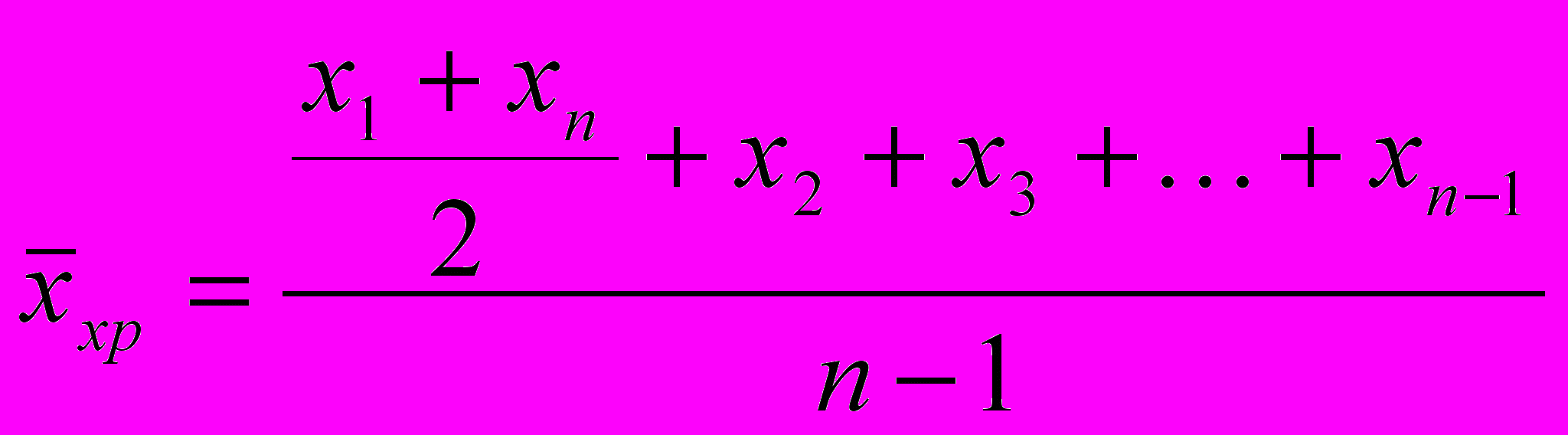 ,
,де п – число моментів.
Приклад. У комерційному банку сума кредиторської заборгованості на початок кожного кварталу становила, млн. гр. од.: 1.01. – 20; 1.04. – 26; 1.07. – 32; 1.10. – 29; 31.12. – 22. Середньоквартальна сума кредиторської заборгованості складає:
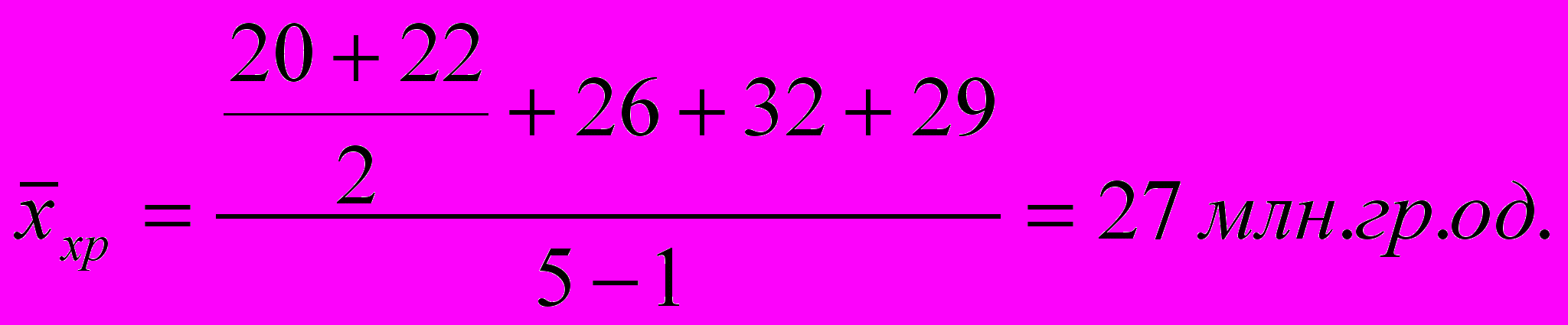
Середня гармонійна застосовується в тих випадках, коли нам не відомі самі варіанти, а відомі або їхні обернені числа (тоді використовується середня гармонійна проста), або добуток одиниць сукупності на значення ознаки (тобто m=x*f) (тоді використовують середню гармонійну зважену).
Середню гармонійну використовують, наприклад, для визначення середніх затрат праці, часу, матеріалів на одиницю продукції, на одну деталь за двома (трьома тощо) підприємствами, робітниками, які зайняти виготовленням одного й того ж виду продукції, однієї й тієї ж деталі.
Приклад. Маємо дані про витрати часу в годинах на виготовлення однієї деталі кожним з трьох робітників: ½, 1/3, 1/7. Треба обчислити середні витрати часу на виготовлення однієї деталі.
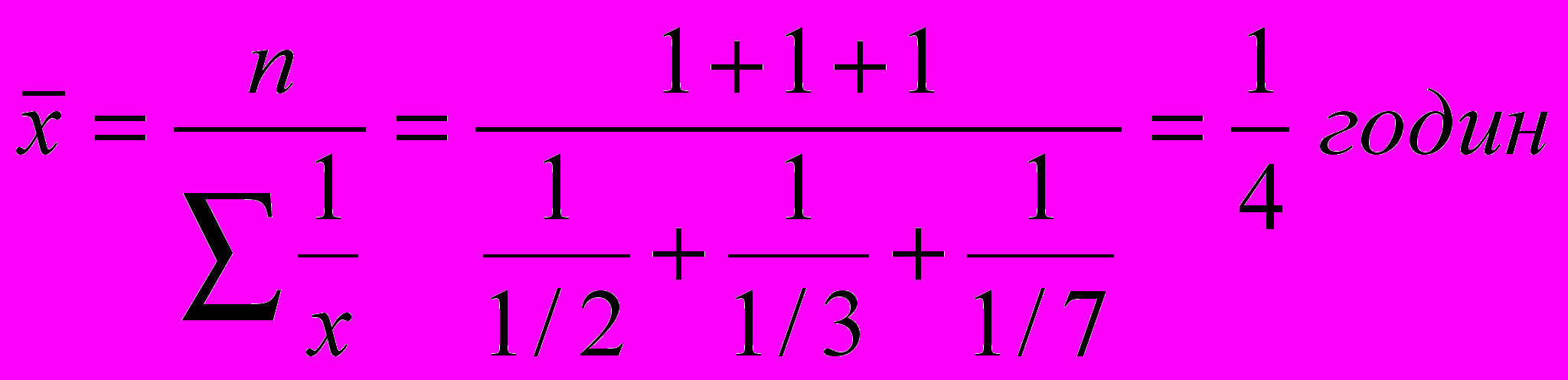
Приклад. Три промислових підприємства виробляють міксери. Собівартість виробництва міксера на 1-му підприємстві – 50 грн., на 2-му – 30 грн., на 3-му – 60 грн. визначити середню собівартість виробництва міксера за умови, що витрати на виробництво на 1-му підприємстві складають 600 грн., на 2-му – 660 грн., на 3-му – 900 грн.
Якби кожне з підприємств випускало б по одному міксеру, то можна було б застосувати формулу середньої арифметичної
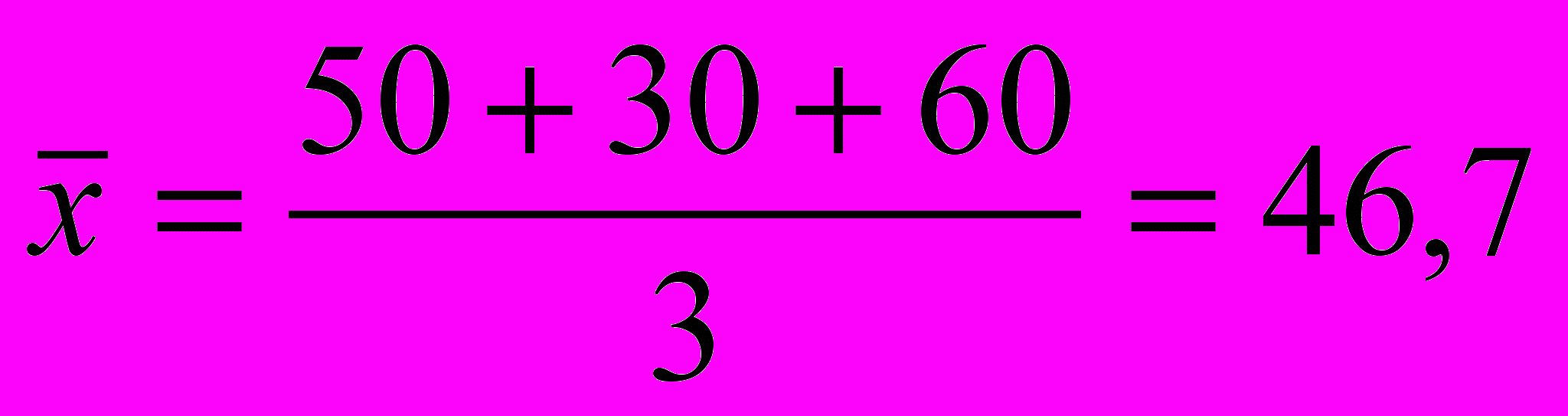 грн., але це не так, а тому:
грн., але це не так, а тому: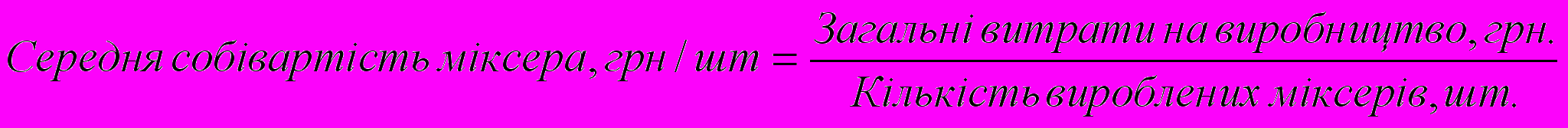
Використовуючи формулу середньої гармонійної зваженої, розрахуємо середню собівартість 1-го міксера:
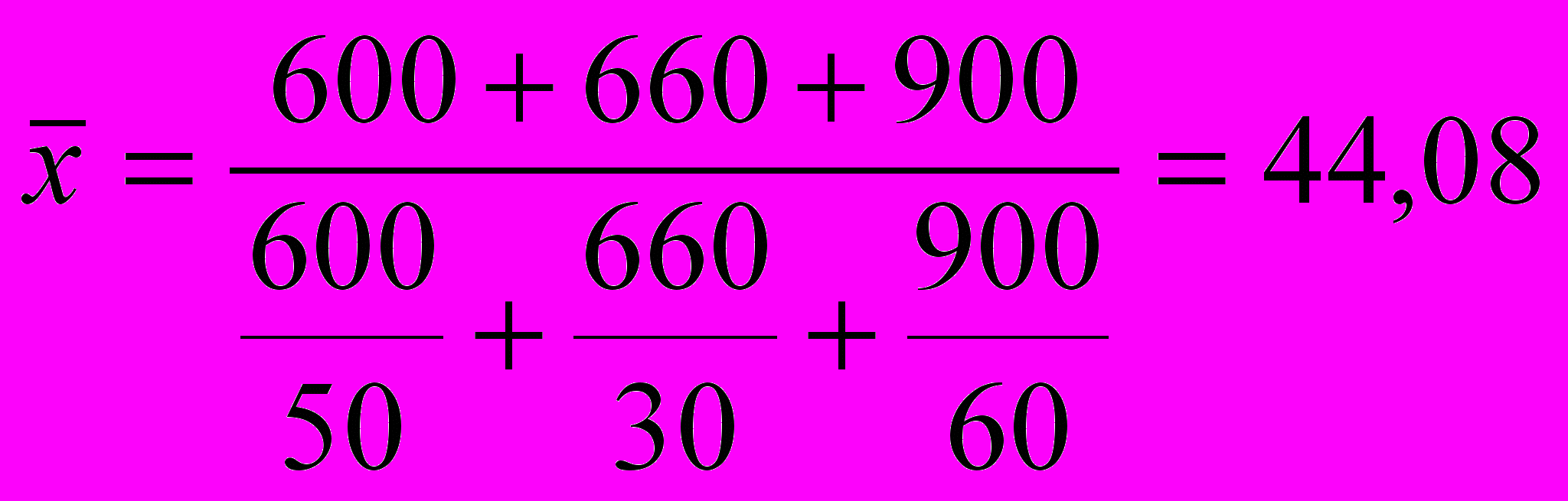 грн.
грн.Середня геометрична найчастіше використовується для розрахунку середнього значення за індивідуальними відносними показниками динаміки.
Середня геометрична визначається як добуток відносних величин динаміки хі, які є кратним співвідношенням і-го значення показника до попереднього (і-1). Формула середньої геометричної:
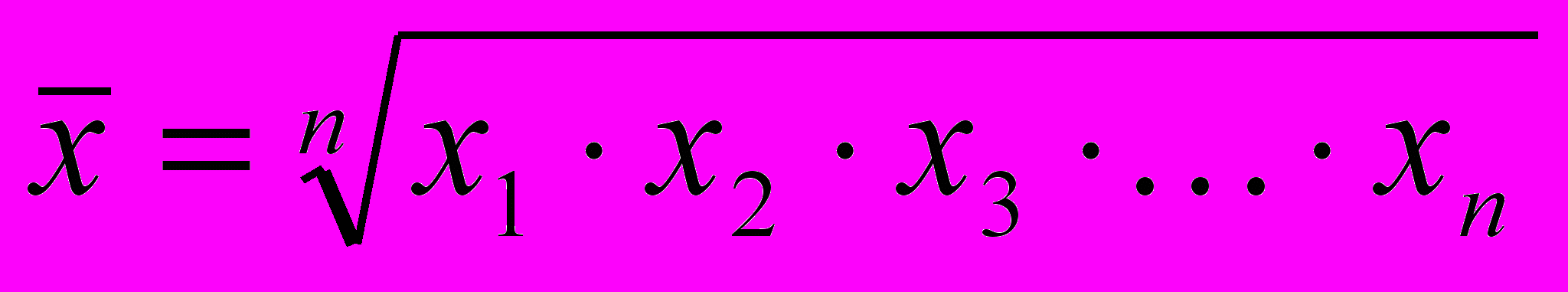 ,
,де п – число осереднюваних величин.
Приклад. Кількість зареєстрованих злочинів за чотири роки зросла у 1,57 рази, у тому числі за перший рік – у 1,08; за другий – у 1,1; за третій – у 1,18; за четвертий – у 1,12 рази. Середньорічний темп зростання кількості зареєстрованих злочинів становить:
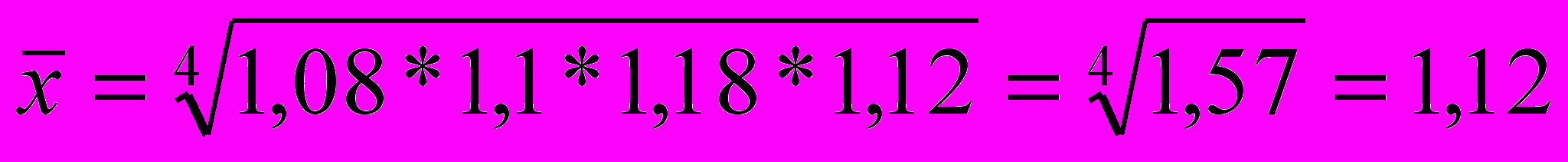 рази, тобто число зареєстрованих злочинів зростало щорічно у середньому на 12 %.
рази, тобто число зареєстрованих злочинів зростало щорічно у середньому на 12 %.Для осереднення ознак рангової шкали застосовують нормований середній бал. Спочатку слід ранжирувати значення ознаки в порядку зростання якості.
Нормований середній бал обчислюється за формулою:
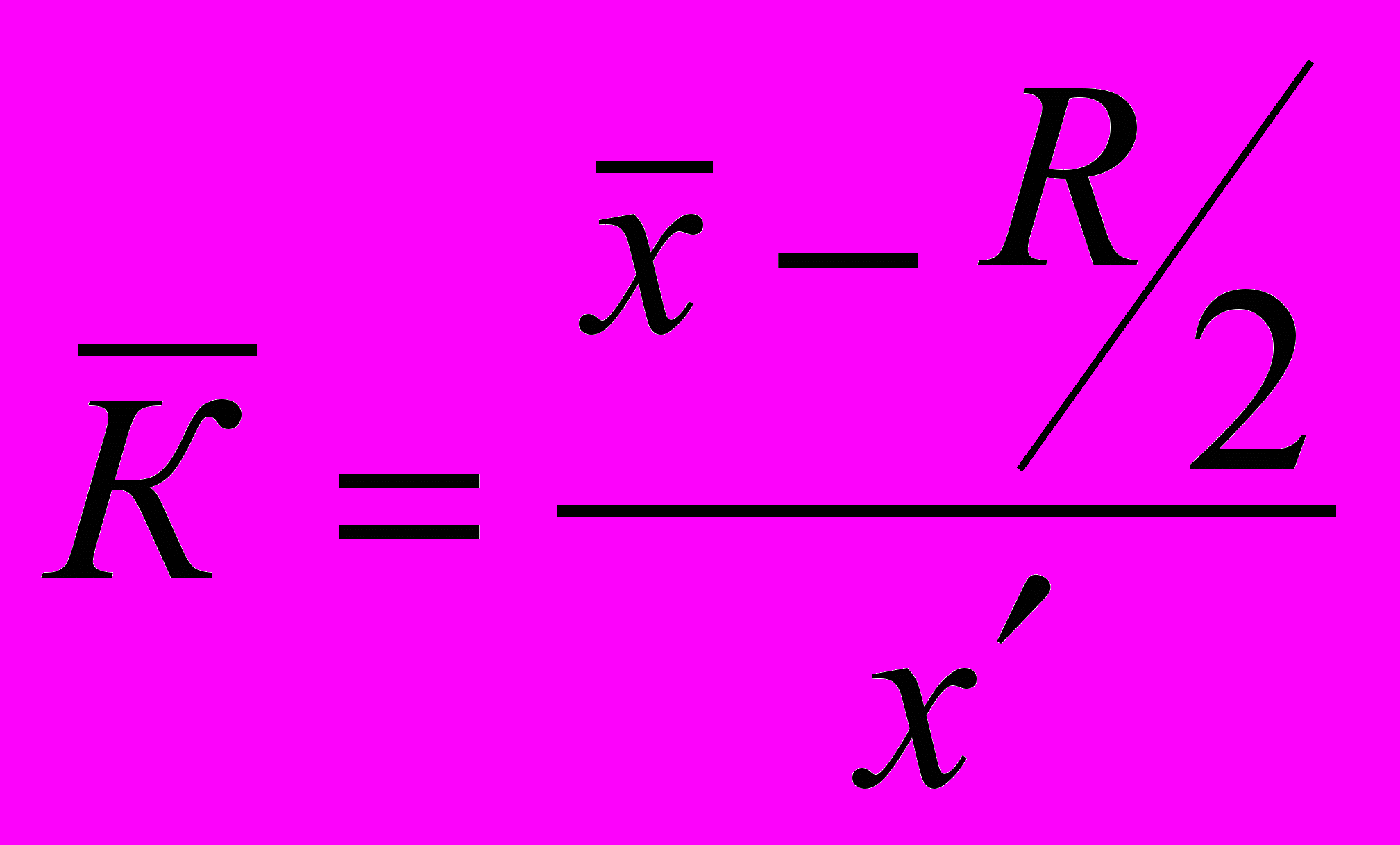 ,
,де
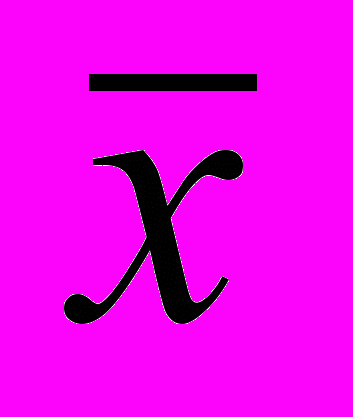 - середньозважений ранг відповідей (
- середньозважений ранг відповідей (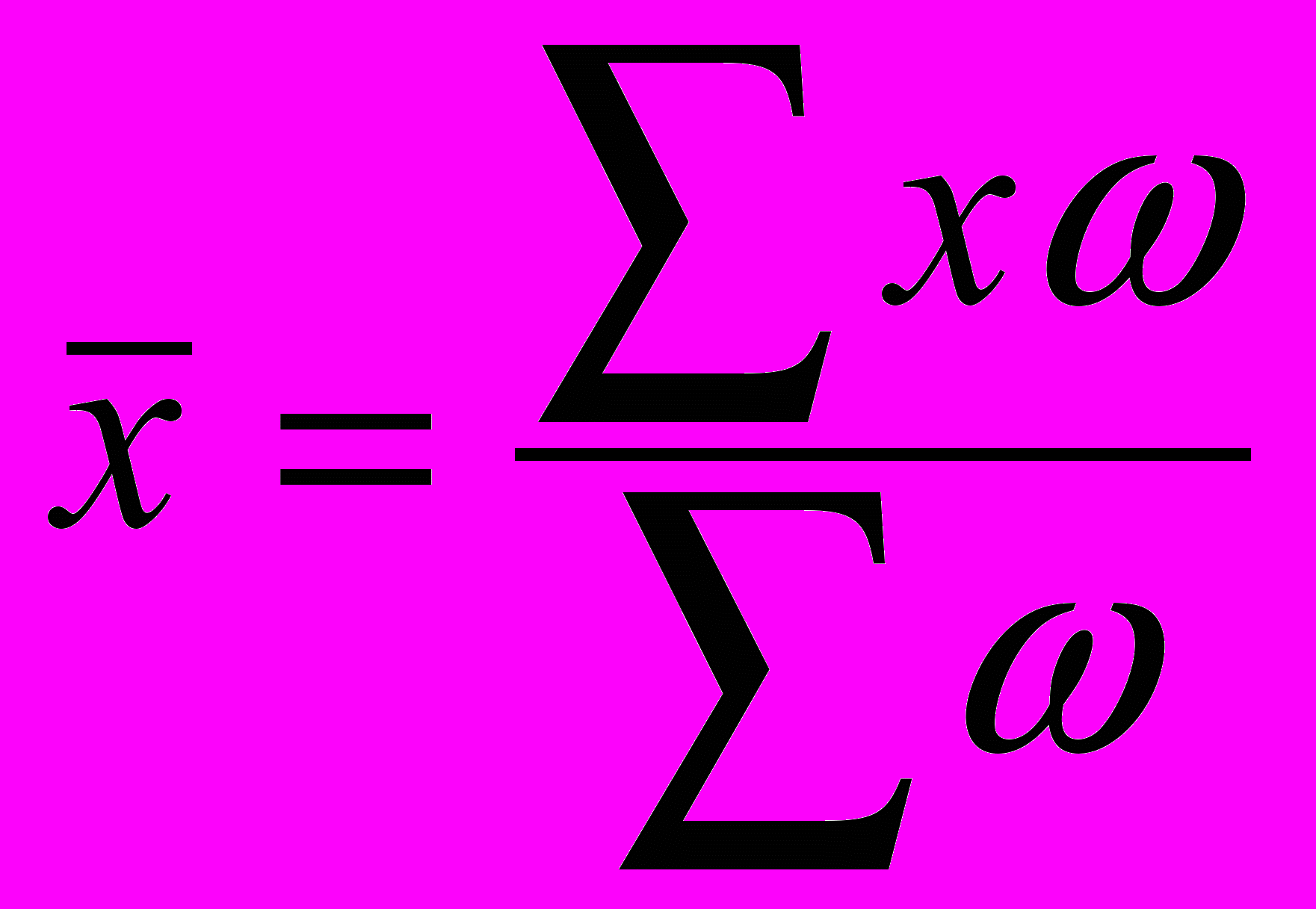 , де х – ранг,
, де х – ранг,  - частка відповідей, %);
- частка відповідей, %);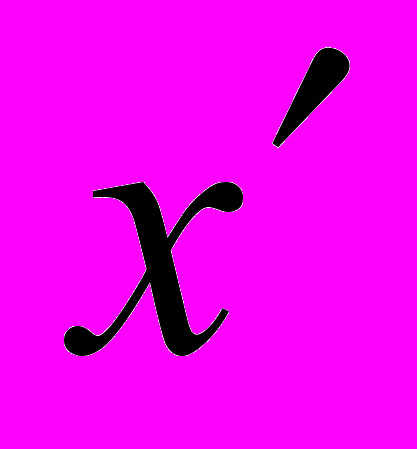 - середина шкали рангів (
- середина шкали рангів (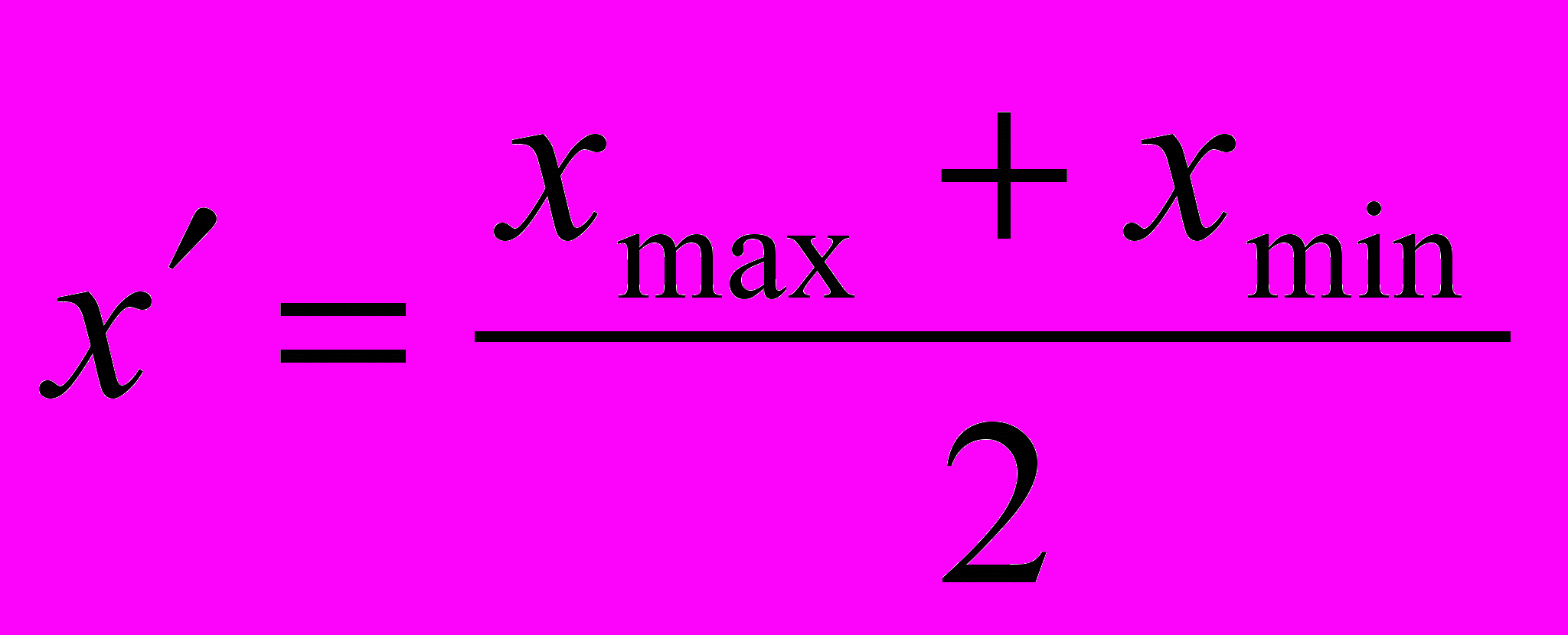 );
);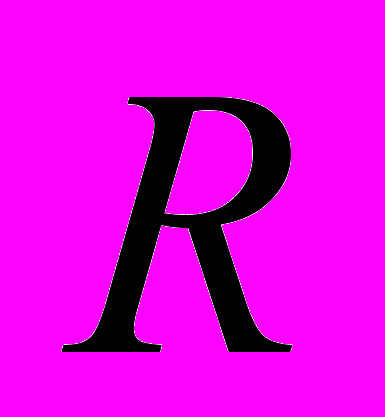 - розмах шкали рангів (
- розмах шкали рангів (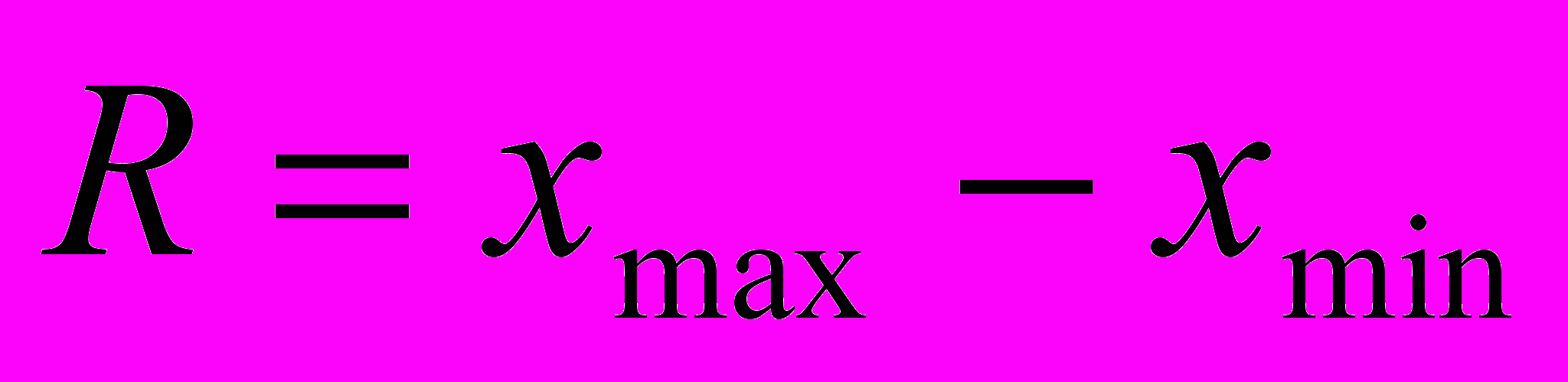 )
)Приклад. Визначити середній бал якості відеокліпів, що демонструвалися по телебаченню, використовуючи такі дані:
| Рівень якості відеокліпів | Кількість відповідей, % до підсумку,  | Ранг, х |
| Дуже висока Висока Середня Нижча за середню Низька | 6 10 43 25 16 | 5 4 3 2 1 |
| Разом | 100 | -- |
Рішення:
Нормований середній бал обчислюється за формулою:
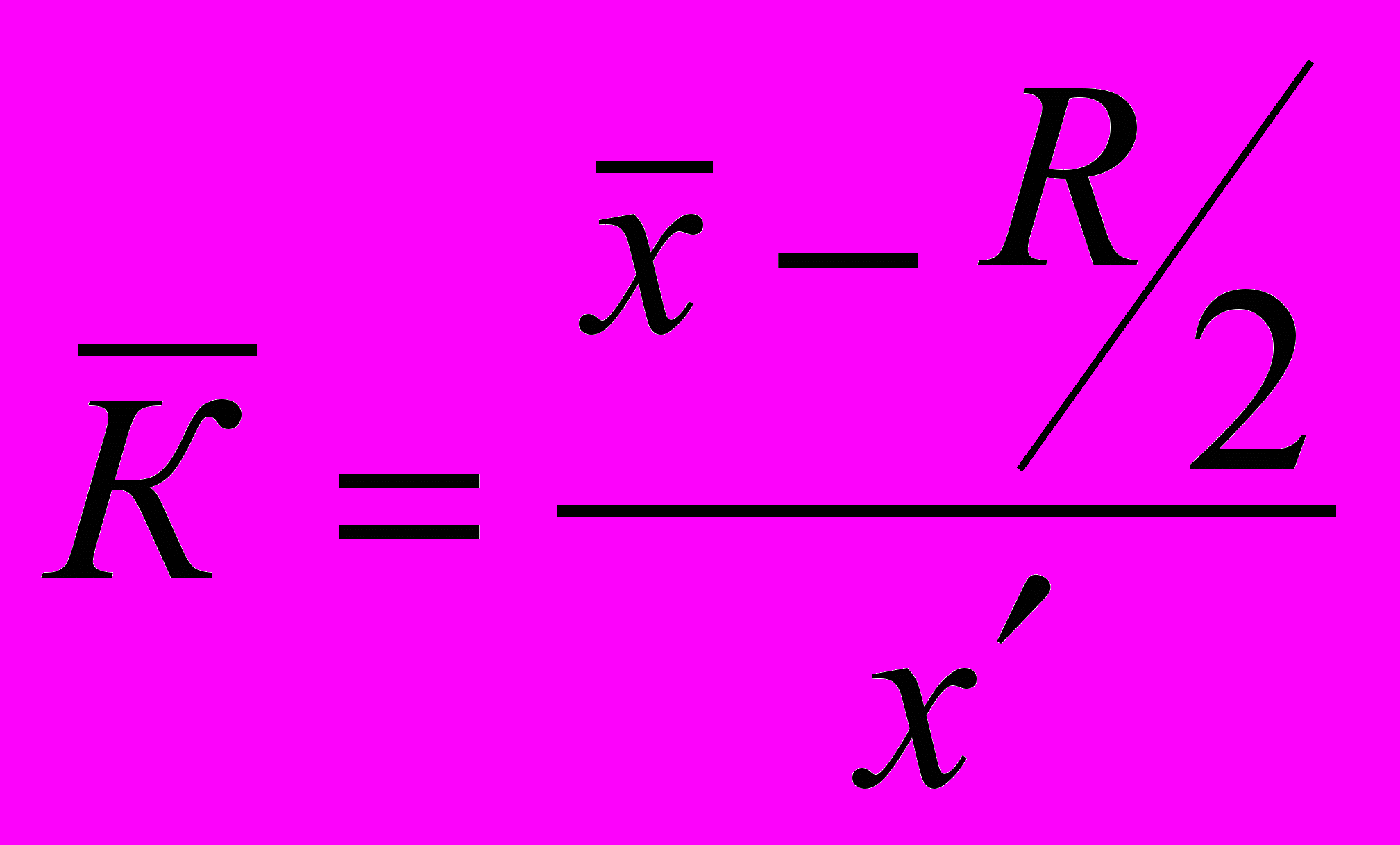 ,
,де
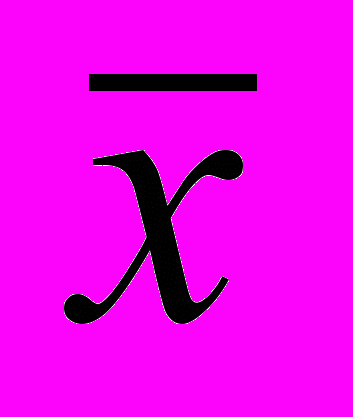 - середньозважений ранг відповідей:
- середньозважений ранг відповідей: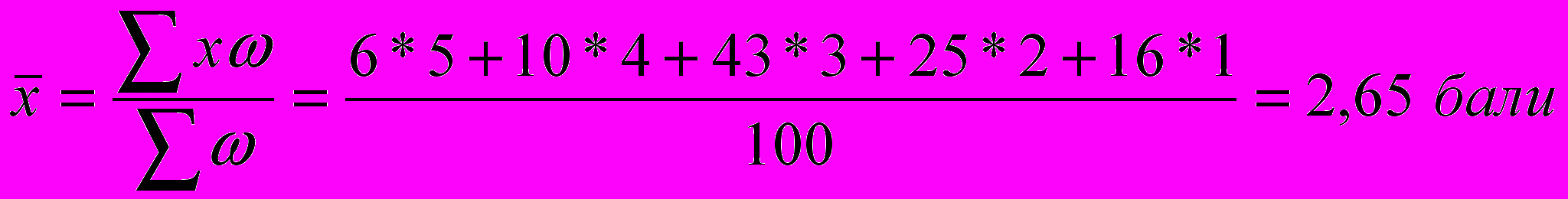 ;
;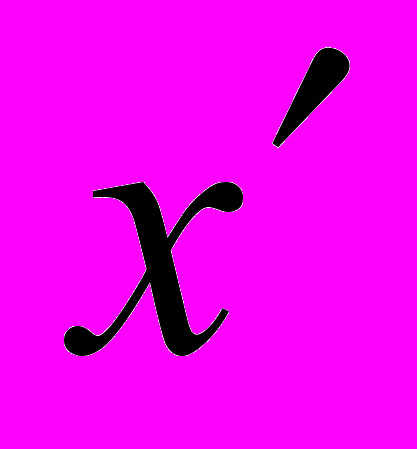 - середина шкали рангів:
- середина шкали рангів: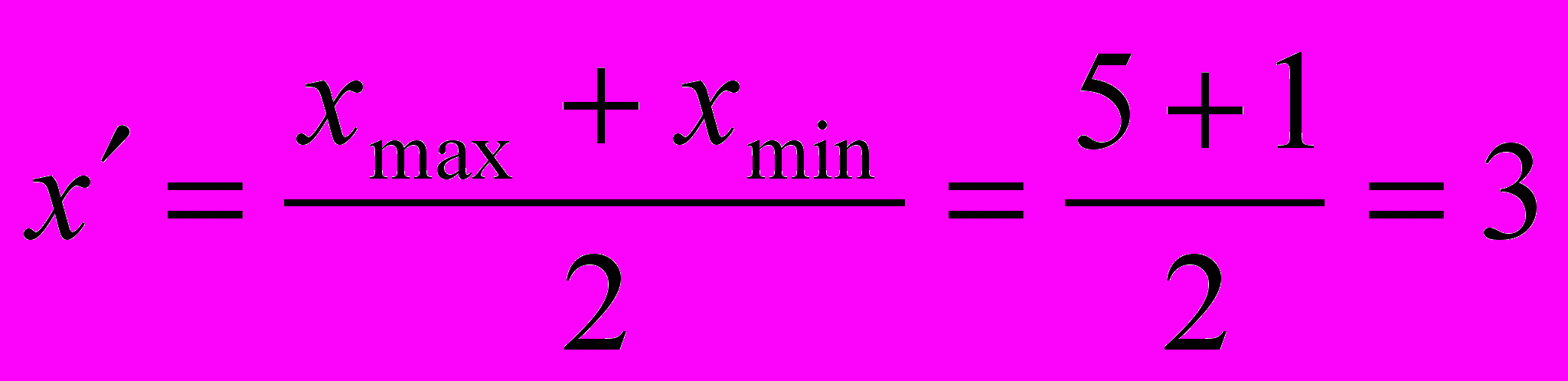 ;
;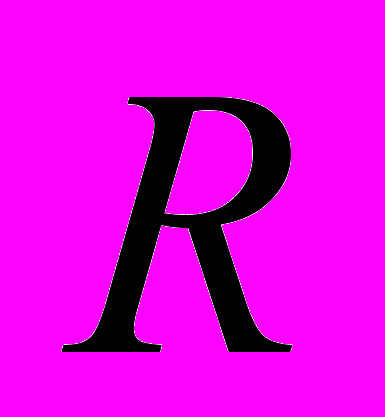 - розмах шкали рангів:
- розмах шкали рангів: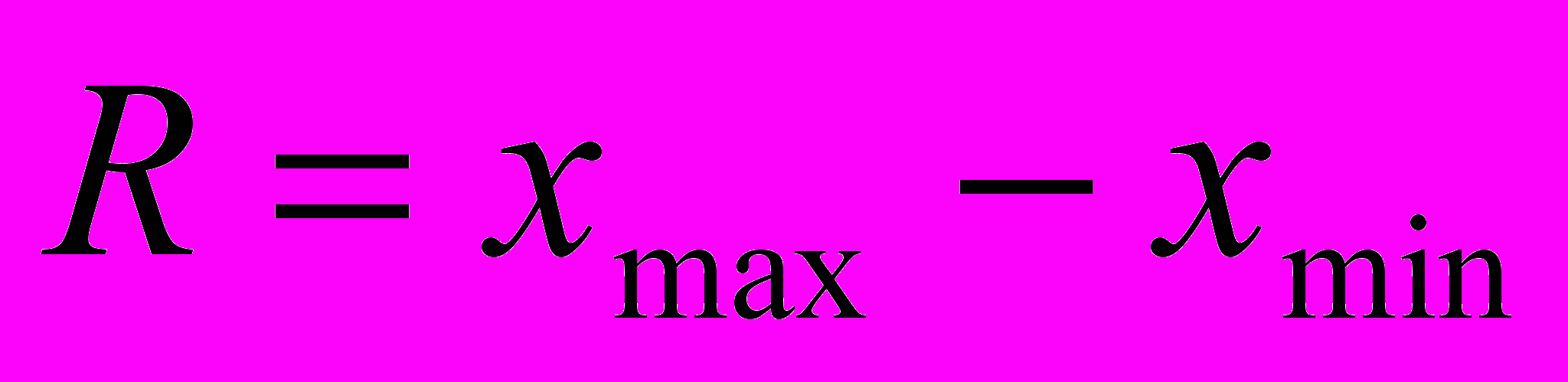 = 5-1= 4.
= 5-1= 4.Тож, нормований середній бал дорівнює:
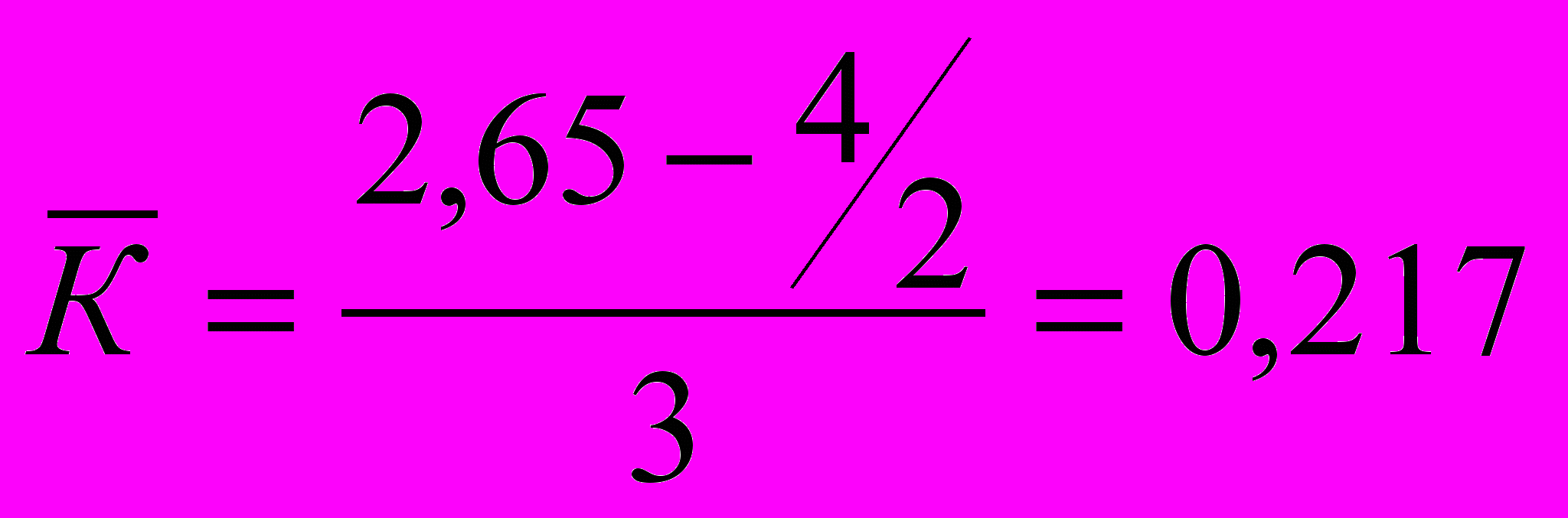 , або 21,7%
, або 21,7%Структурні середні. Особливий вид середніх величин – структурні середні – використовують для вивчення внутрішньої побудови рядів розподілу. Найчастіше використовують показники моди й медіани.
Мода (Мо) – це значення варіанти, яка найчастіше повторюється в ряді розподілу. У дискретному ряді моду легко відшукати візуально за максимальною частотою, або часткою. Наприклад, в результаті опитування населення щодо самовизначення матеріального стану за чотирма градаціями (добрий, задовільний, незадовільний, нестерпний) більшість респондентів визначили свій стан як незадовільний. Або у розподілі сучасних сімей за кількістю дітей найпоширенішими є малодітні сім’ї, що мають одну дитину. Зустрічаються ряди, що мають дві моди (бімодальний ряд) або декілька (полімодальний). Наприклад, на фондовому ринку однаково високим попитом користуються як найдешевші акції, так і дорогі. В інтервальному ряді легко відшукати модальний інтервал, а приблизне значення моди обчисляють за формулою:

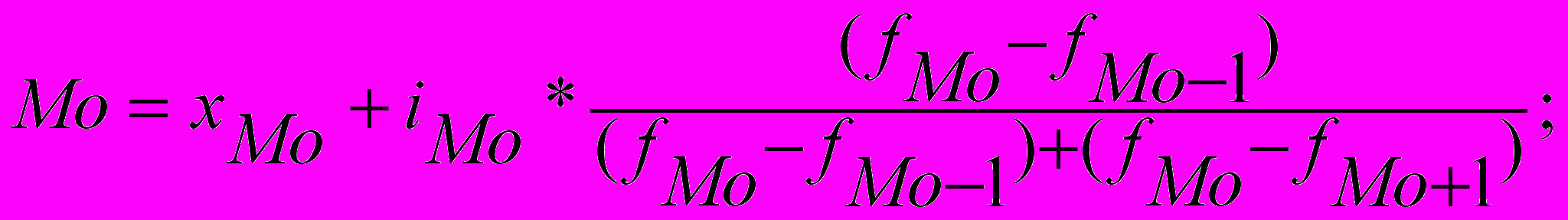
де хМо – нижня межа модального інтервалу;
іМо – велична (розмір) модального інтервалу;
fMo – частота модального інтервалу;
fMо-1 – частота передмодального інтервалу;
fMo+1 – частота післямодального інтервалу.
Медіана (Ме) – варіанта, яка припадає на середину упорядкованого ряду розподілу і ділить його на дві рівні за обсягом частини. Так, якщо в ряді розподілу робітників за віком Ме=34, то це означає, що половина з них менші за цей вік, половина – старші цього віку. У дискретному ряді для знаходження медіани обчислюють півсуму частот, і визначають значення ознаки, для якої накопичена частота (частка) дорівнює або перевищує половину обсягу сукупності. В інтервальному ряду в такий спосіб визначається медіанний інтервал, а значення медіани в інтервалі визначається за формулою:
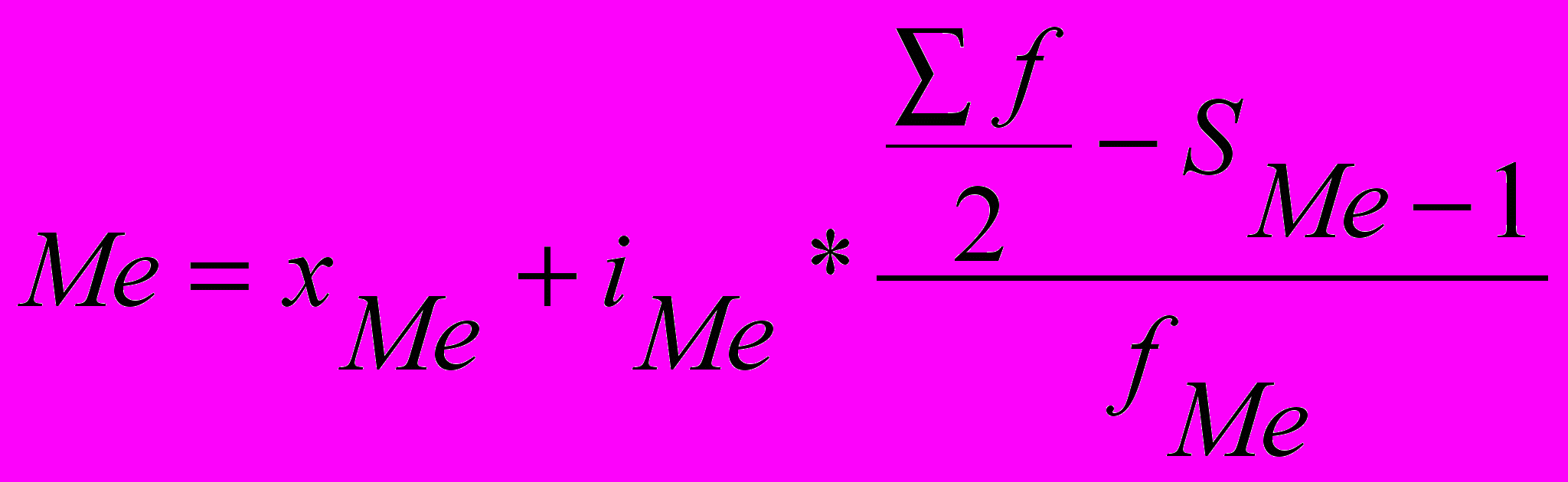 ;
;де xMe – нижня межа медіанного інтервалу;
iMe – величина (розмір) медіанного інтервалу;
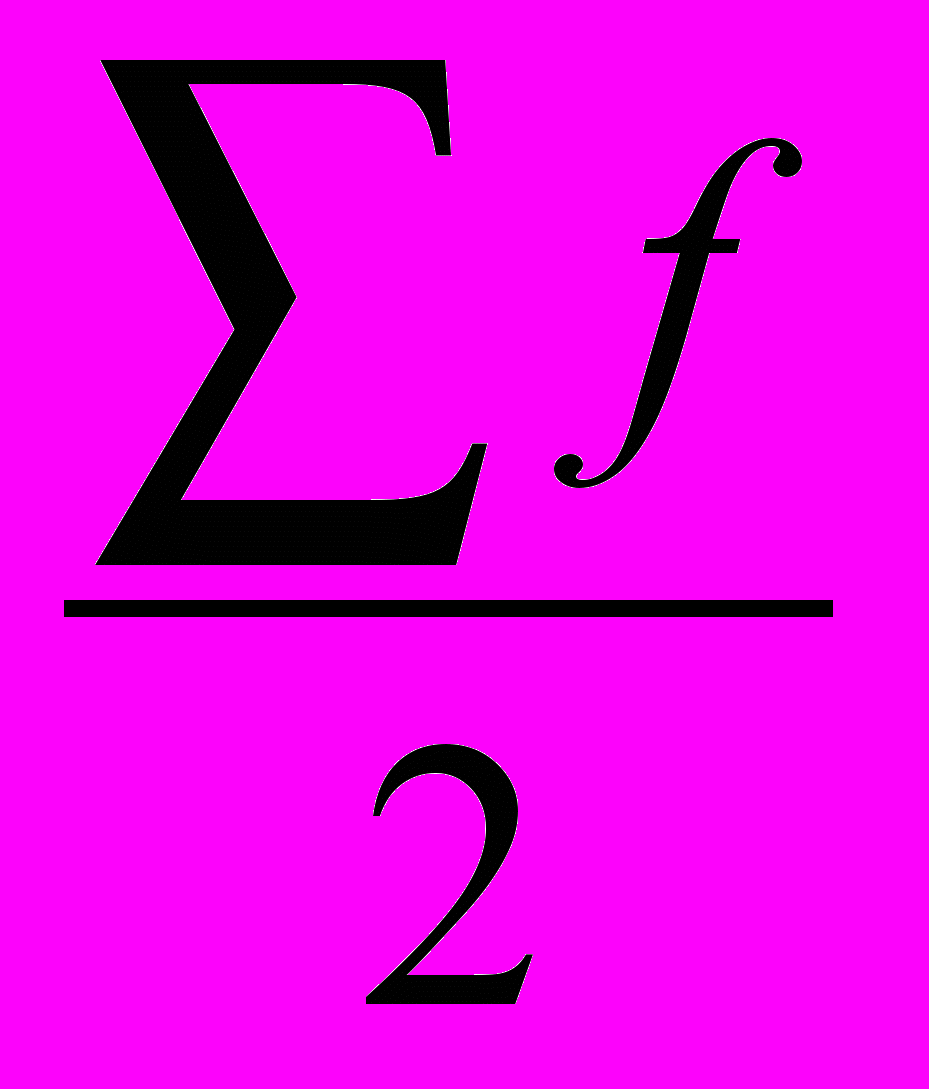 - півсума частот;
- півсума частот;SMe-1 – сума накопичених частот перед медіанного інтервалу;
fMe – частота медіанного інтервалу.
За даними таблиці 4.5.найбільшими попитом користуються акції з терміном обертання в інтервалі 4 – 6 місяців. Це модальний інтервал, ширина якого іМо=2, а нижня межа хМо=4, частота fMo=29, передмодальна частота fMo-1=13, а післямодальна частота fMo+1=22. Модальний термін обертання облігацій становить:

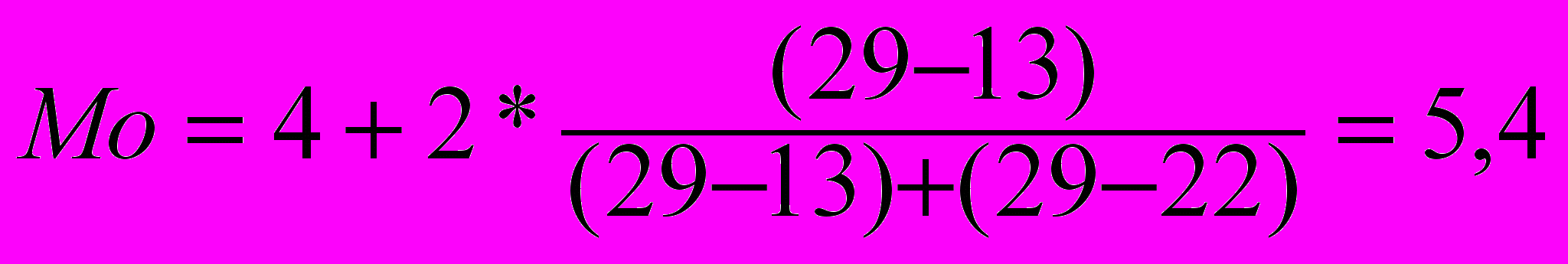 міс.
міс.Таблиця 4.5.
| Термін обертання, місяців, х | Кількість проданих держоблігацій, тис., fi | Накопичена сума частот, тис., 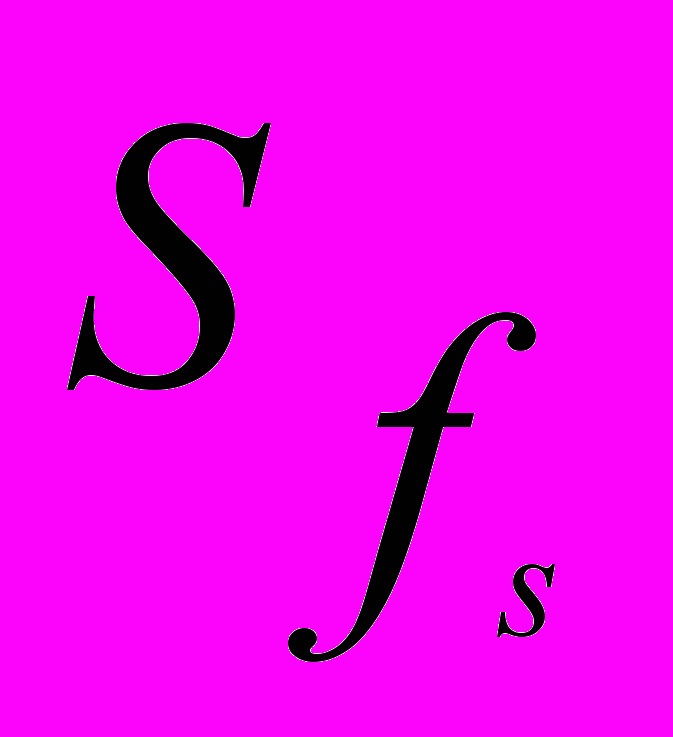 | хі | хіfi |
| До 2 2 – 4 4 – 6 6 – 8 8 – 10 10 і більше | 15 13 29 22 12 9 | 15 28 57 79 91 100 | 1 3 5 7 9 11 | 15 39 145 154 108 99 |
| Разом | 100 | Х | Х | 560 |
Сума накопичених частот
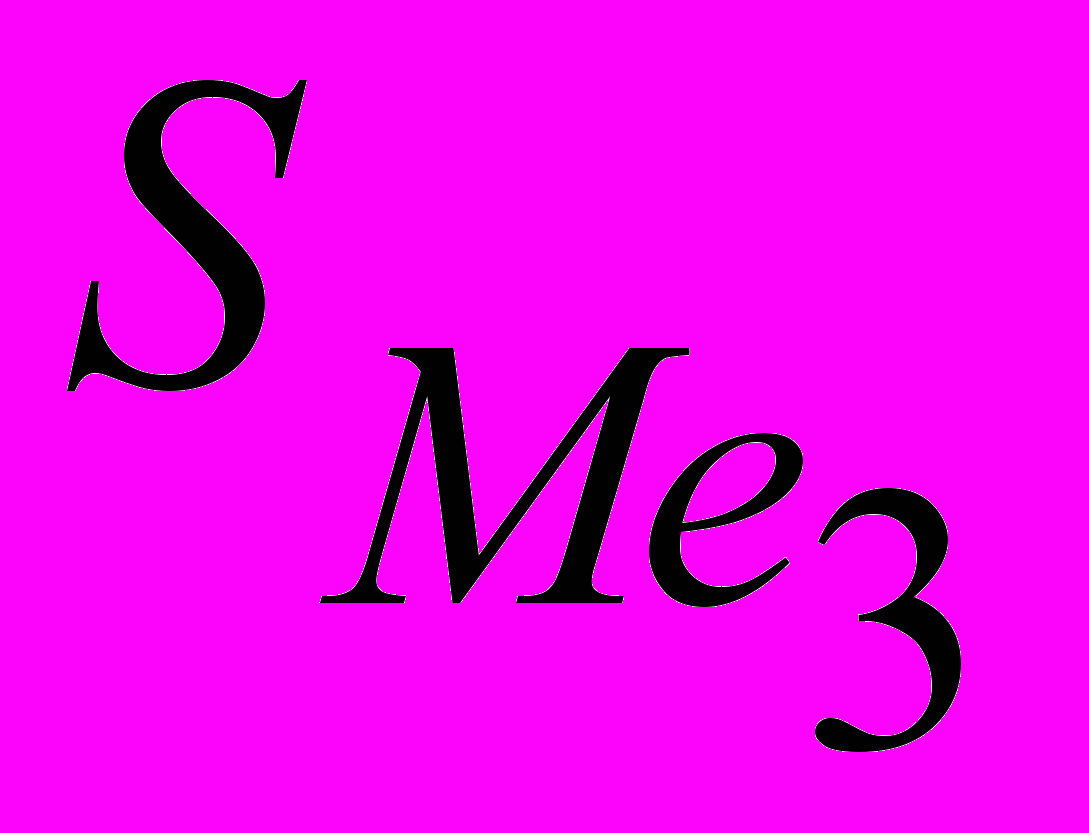 =57 визначає, що п’ятидесята з початку ряду облігація знаходитиметься в інтервалі 4 – 6 з частотою fMe=29. медіанний термін обертання проданих облігацій становить:
=57 визначає, що п’ятидесята з початку ряду облігація знаходитиметься в інтервалі 4 – 6 з частотою fMe=29. медіанний термін обертання проданих облігацій становить: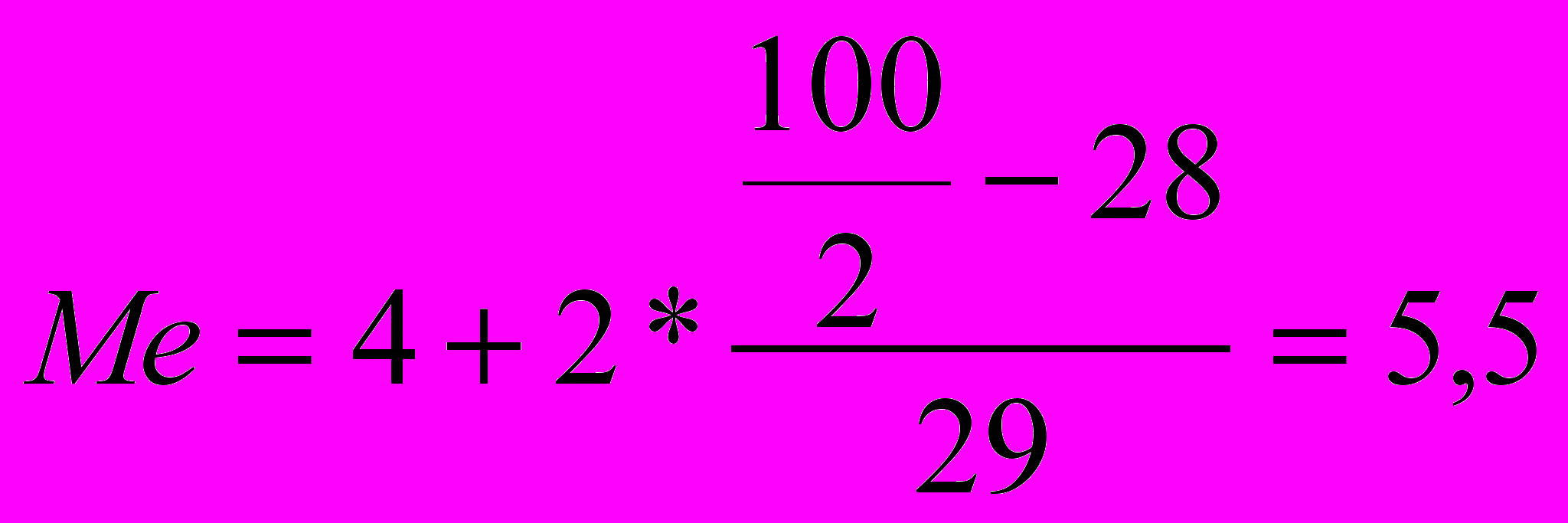 міс.
міс.Тож половина облігацій продавалися з терміном обертання менше, ніж півроку – 5,5 міс., а половина – більше 5,5 міс.
У симетричних рядах розподілу значення моди та медіани збігаються з середньою величиною (
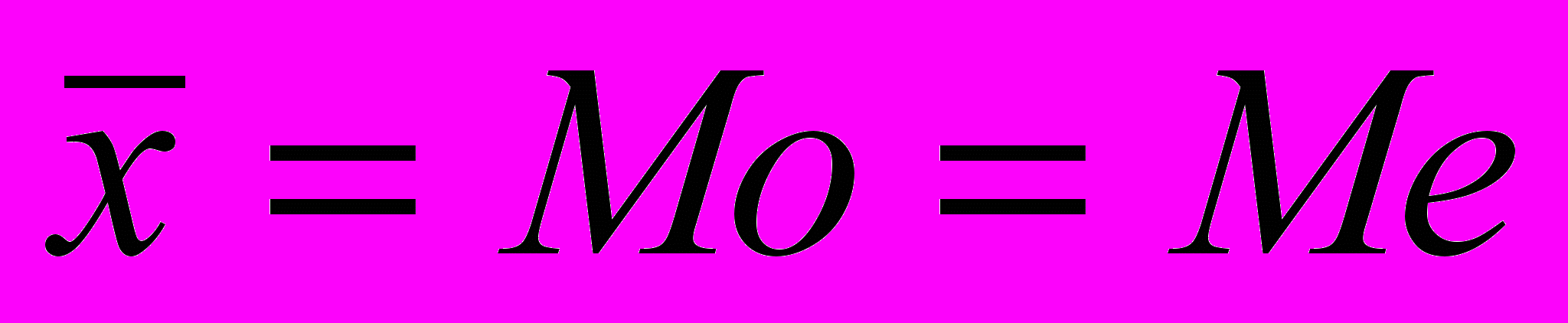 ).
).4. Показники варіації.
Варіація ознаки є властивістю статистичної сукупності і зумовлена дією безлічі взаємопов’язаних причин, серед яких є основні і другорядні. Основні формують центр розподілу, другорядні – варіацію ознаки, сукупна їх дія – форму розподілу.
Конкретні умови, в яких знаходиться кожний з об’єктів, що вивчається, а також особливості їхнього власного розвитку (соціальні, економічні тощо) виражаються відповідними числовими рівнями статистичних показників. Таким чином, варіація, тобто незбіг (несовпадение) рівнів одного й того ж показника у різних об’єктів, має об’єктивний характер і допомагає пізнати сутність явища, що вивчається.
Дослідження варіації в статистиці та соціально-економічних дослідженнях має велике значення, тому що величина варіації ознаки в статистичній сукупності характеризує її однорідність.
В статистичній практиці для вивчення та вимірювання варіації використовують різноманітні показники варіації в залежності від поставленого завдання. До них відносяться розмах варіації, середнє лінійне відхилення, середній квадрат відхилень (дисперсія), середнє квадратичне відхилення і коефіцієнт варіації.
Розмах варіації (R) є найпростішим вимірювачем варіації ознаки. Це різниця між найбільшим і найменшим значенням ознаки:
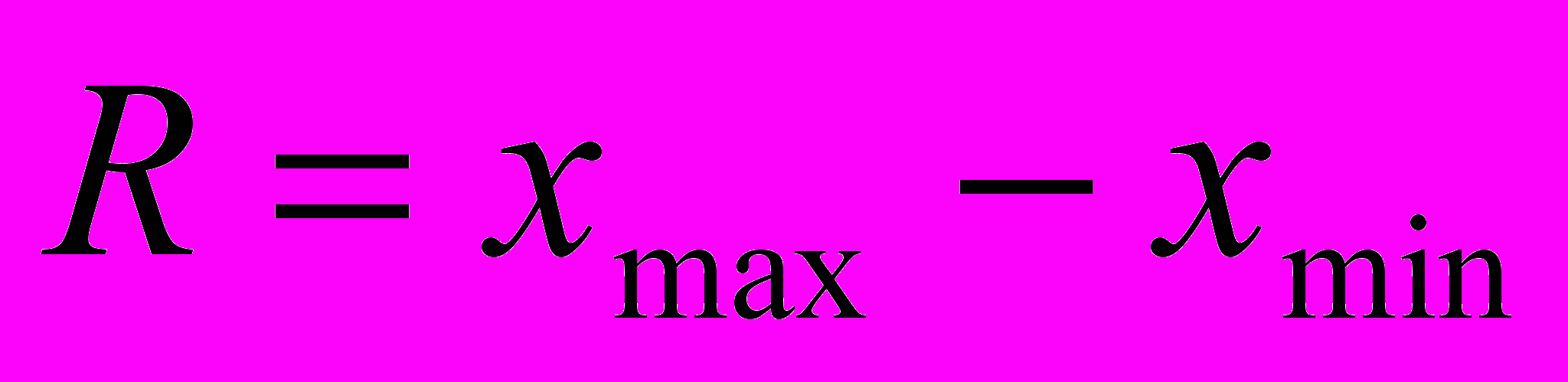 .
.Однак розмах варіації показує лише крайні значення ознаки. Повторюваність проміжних значень не враховується.
Середнє лінійне відхилення (
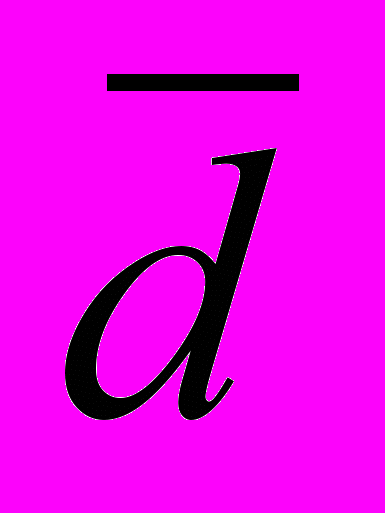 ) представляє собою середню величину із відхилень варіантів ознаки від їхньої середньої. Його можна розрахувати за формулою середньої арифметичної простої або зваженої в залежності від відсутності або наявності часток в ряду розподілу.
) представляє собою середню величину із відхилень варіантів ознаки від їхньої середньої. Його можна розрахувати за формулою середньої арифметичної простої або зваженої в залежності від відсутності або наявності часток в ряду розподілу.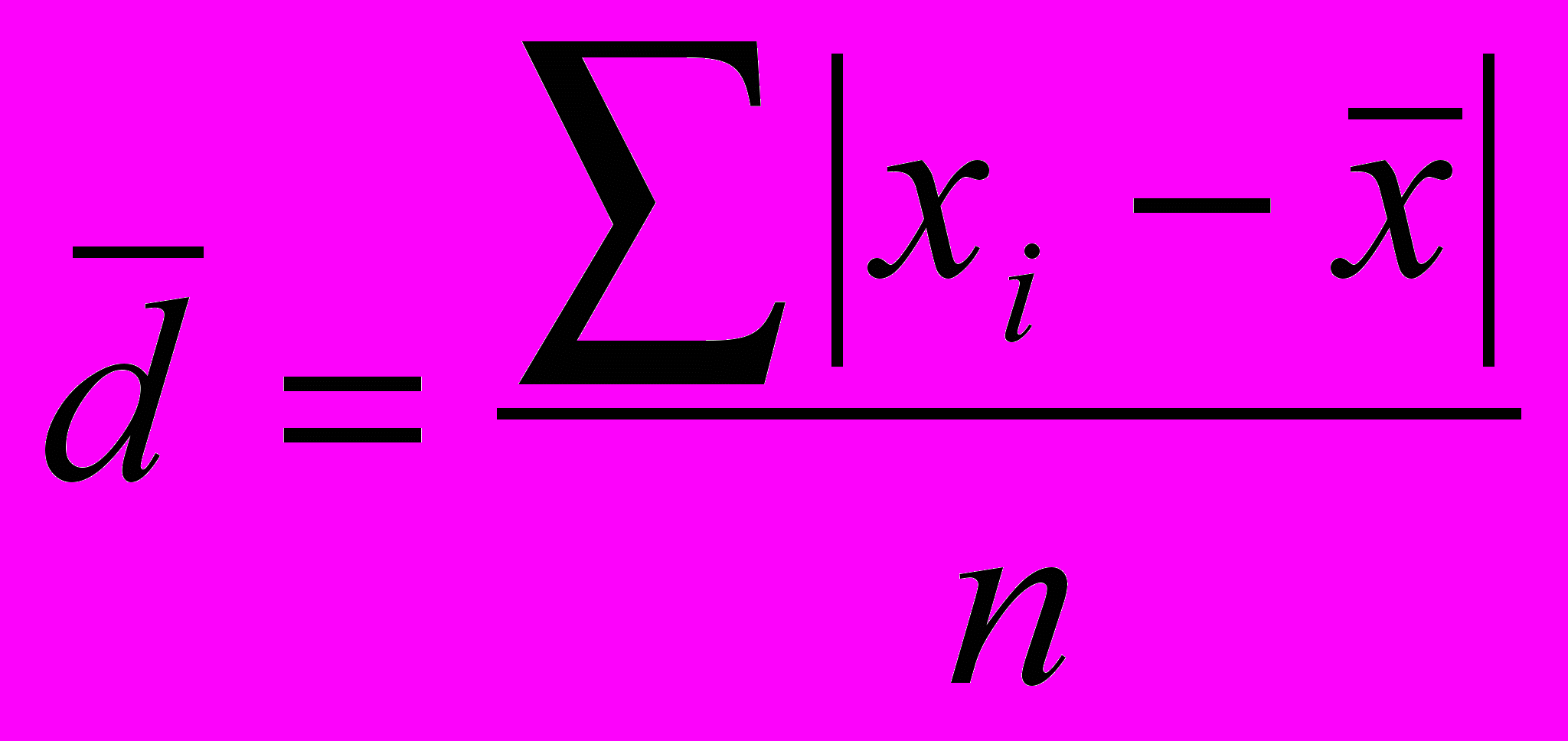 - просте середнє лінійне відхилення,
- просте середнє лінійне відхилення,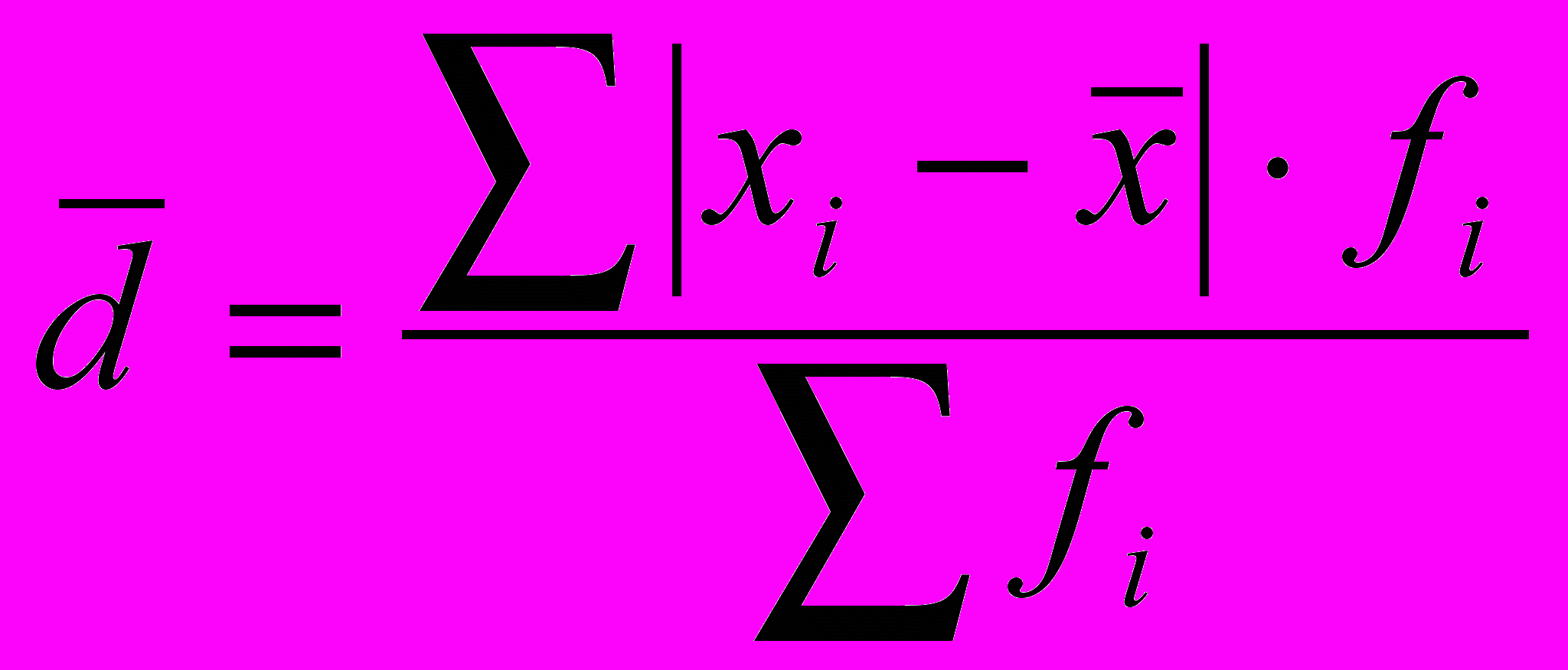 - зважене середнє лінійне відхилення,
- зважене середнє лінійне відхилення,де xs – і-тий варіант ознаки;
fs – питома вага і-того варіанту;
n – кількість варіантів;
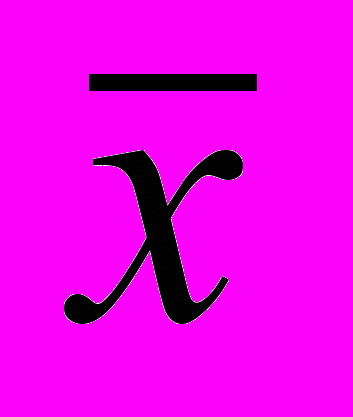 - середня арифметична величина.
- середня арифметична величина.Показник середнього лінійного відхилення знайшов широке застосування на практиці. За його допомогою аналізуються, наприклад, склад працюючих, ритмічність виробництва, рівномірність постачань матеріалів, розробляються системи матеріального стимулювання.
Треба пам’ятати, що алгебраїчна сума відхилень від середнього рівня дорівнює нулеві, тобто середнє значення відхилення для будь-якої випадкової величини прямує к нулю. Тому в статистичних наукових дослідженнях для виміру варіації частіше використовують показник дисперсії.
Приклад. На основі даних таблиці 4.6.розрахуємо середнє лінійне відхилення для дискретного ряду розподілу.
Таблиця 4.6.
Розподіл вчителів середніх шкіл району за стажем роботи
| Стаж роботи, років, хі | Кількість вчителів, в % до підсумку, fi | xifi | 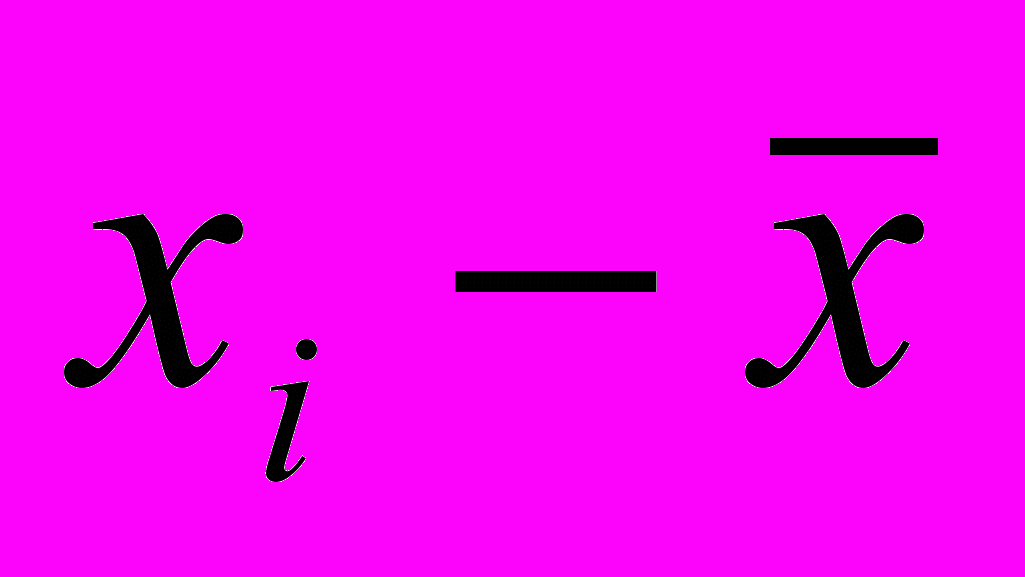 | 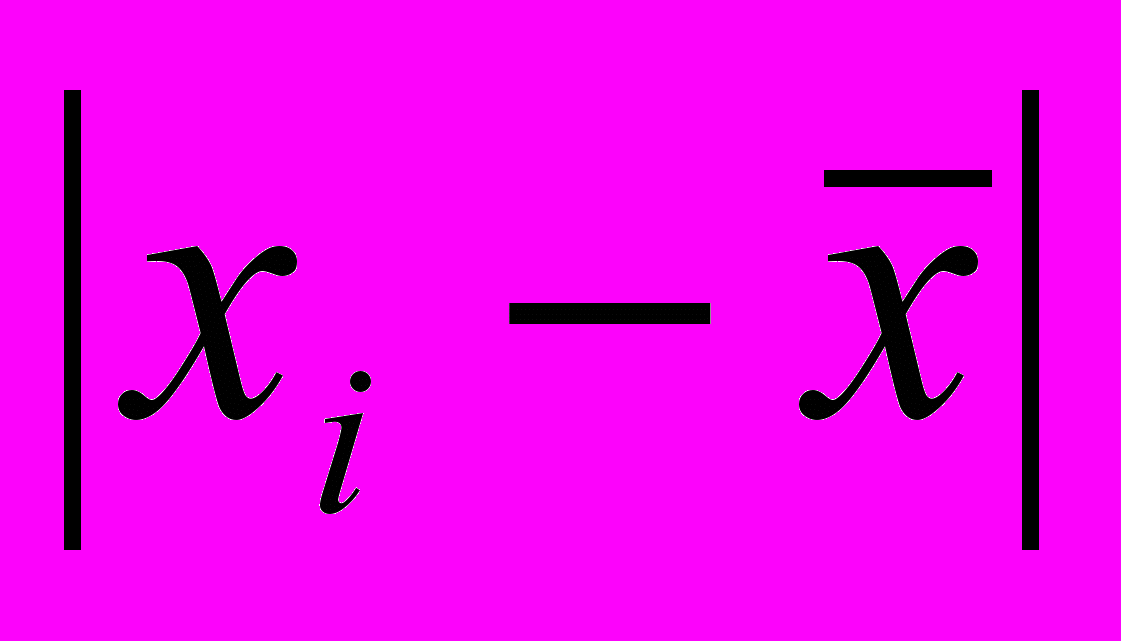 | 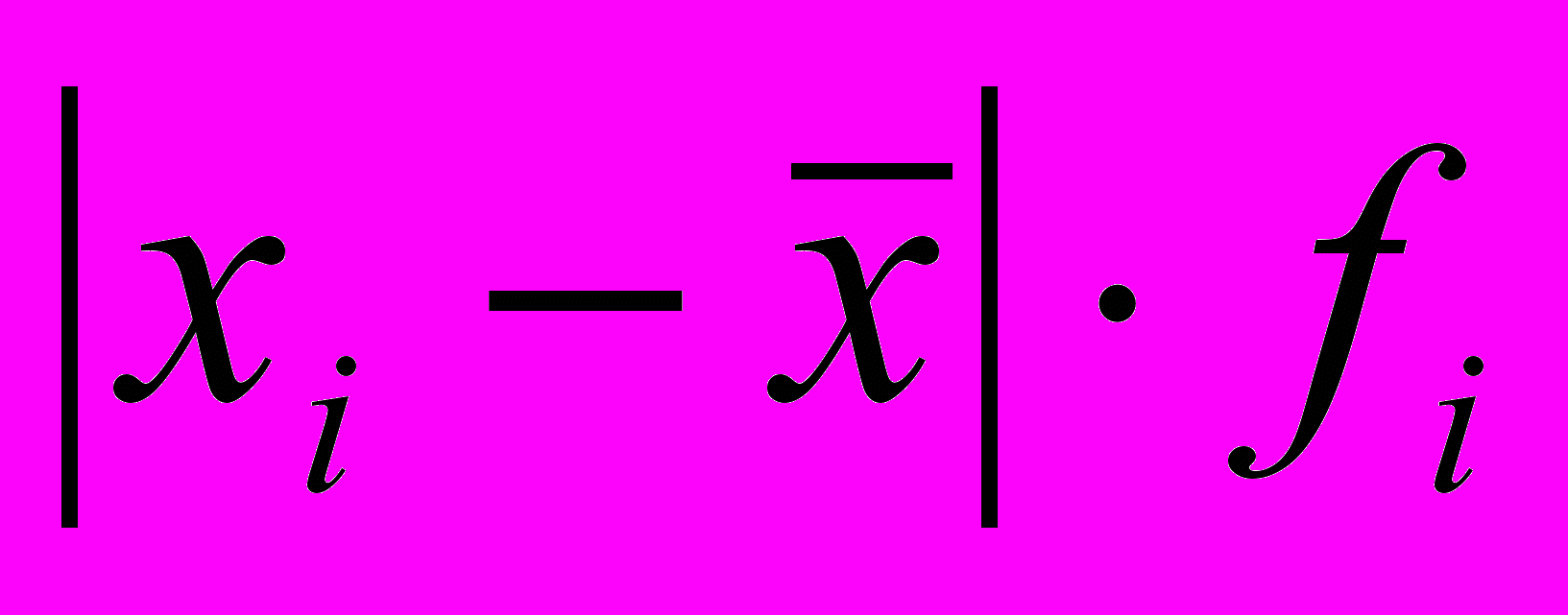 |
| А | 1 | 2 | 3 | 4 | 5 |
| 8 9 10 11 12 | 14 20 30 24 12 | 112 180 300 264 144 | -2 -1 0 1 2 | 2 1 0 1 2 | -28 -20 0 24 24 |
| Разом | 100 | 1000 | - | - | 96 |
Розмах варіації за стажем складає:
R=12 – 8 = 4 роки.
Допоміжні розрахунки наведені в графах 3 – 6 таблиці.
Середній стаж роботи визначимо за формулою середньозваженої арифметичної:
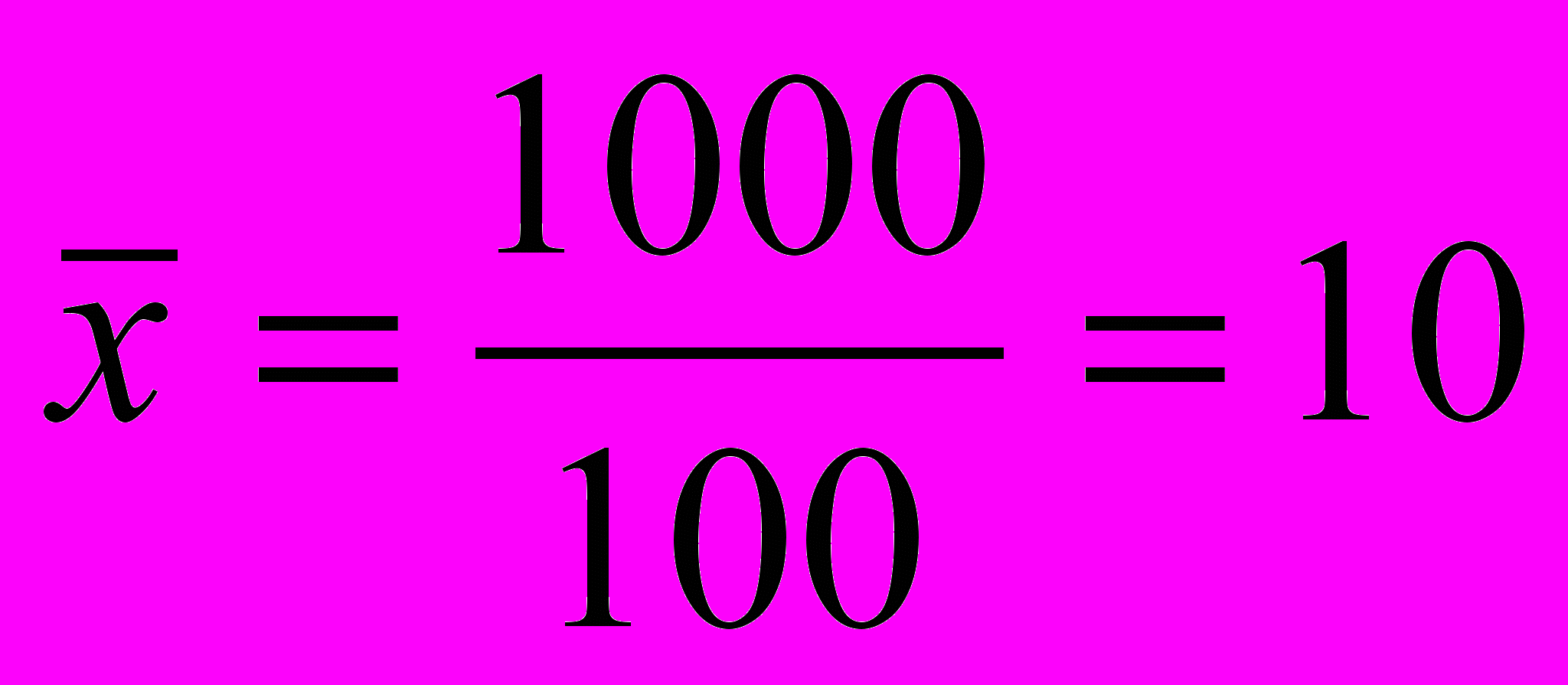 років.
років.Середнє лінійне відхилення стажу роботи вчителів середніх шкіл району складає:
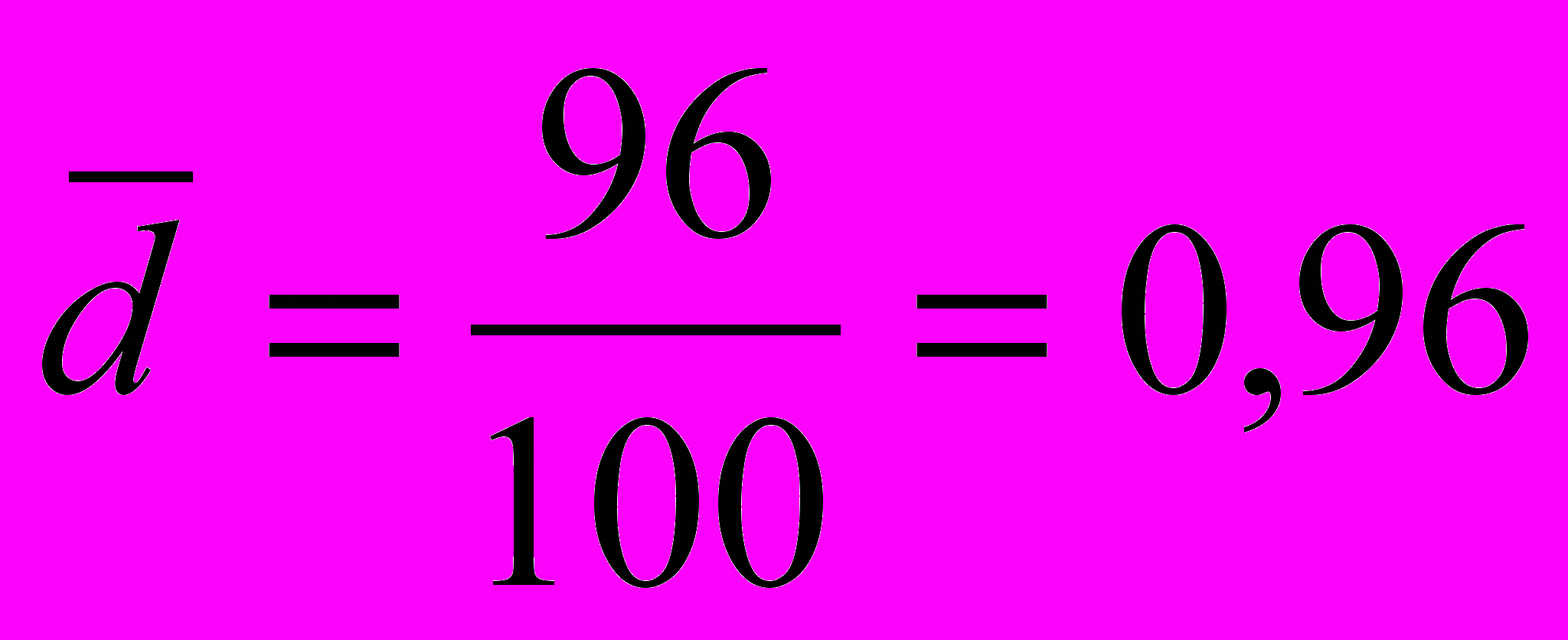 роки.
роки.Дисперсія(
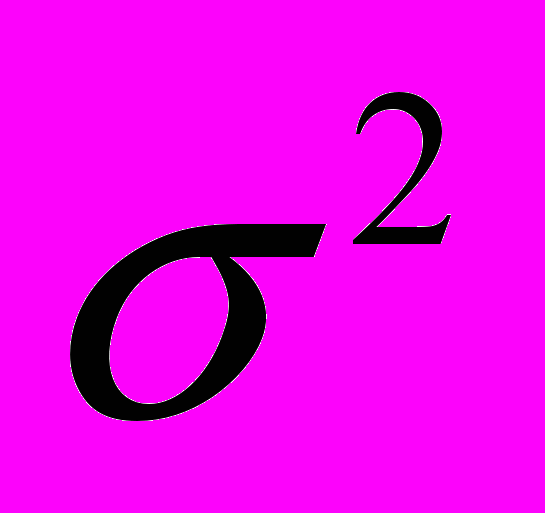 - сігма-квадрат) представляє собою середній квадрат відхилень індивідуальних значень ознаки від її середньої величини. Дисперсія розраховується за формулами простої середньої незваженої і зваженої відповідно:
- сігма-квадрат) представляє собою середній квадрат відхилень індивідуальних значень ознаки від її середньої величини. Дисперсія розраховується за формулами простої середньої незваженої і зваженої відповідно: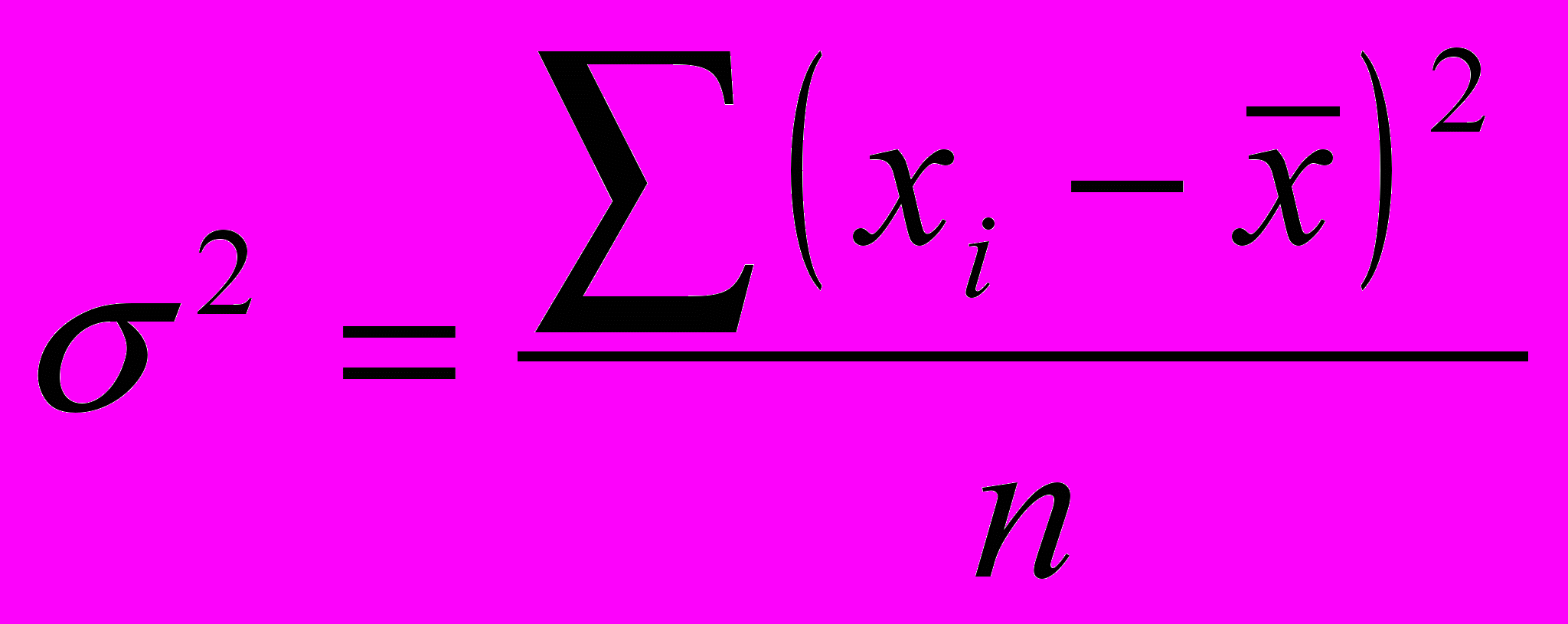 ;
;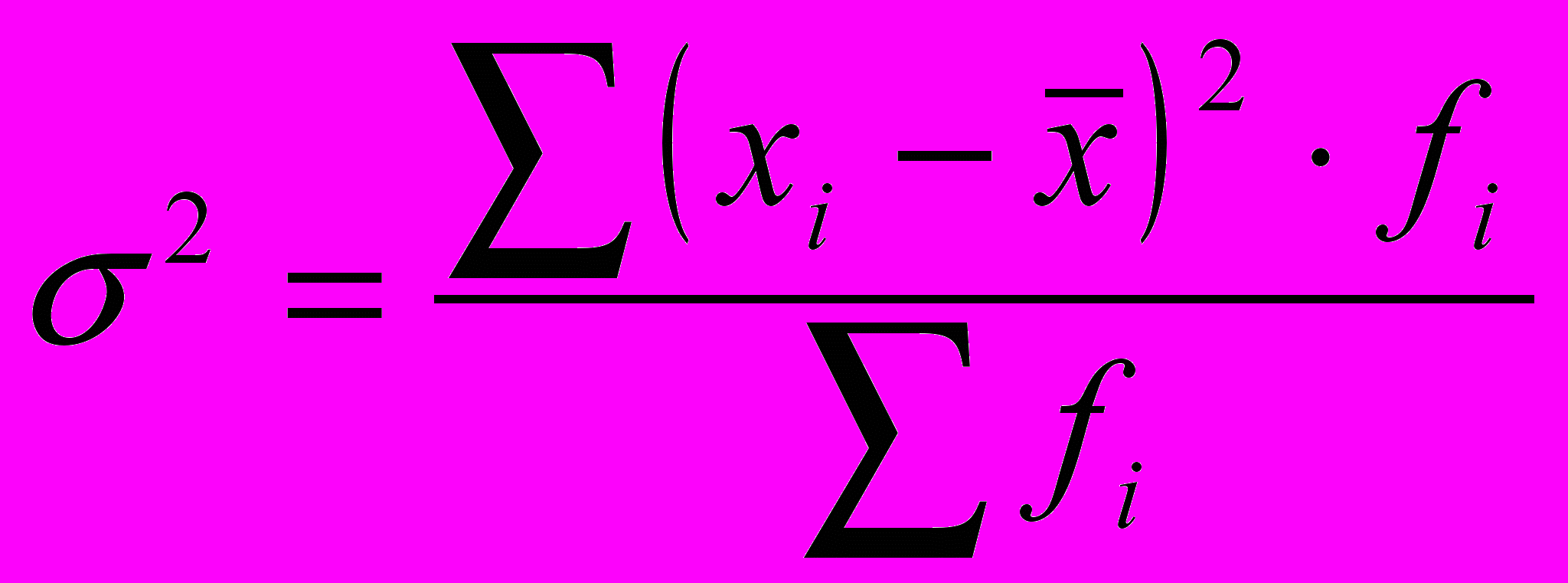 .
.На практиці застосовують більш просту формулу для розрахунку дисперсії:
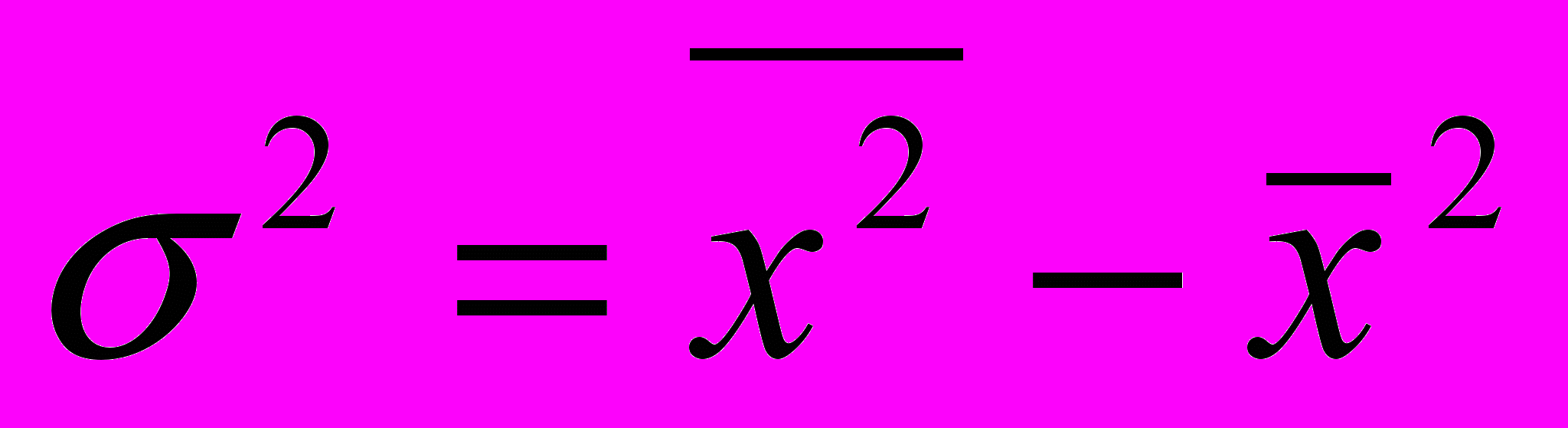 .
.Середнє квадратичне відхилення (σ) – це корінь другого ступеню із середнього квадрата відхилень певних значень ознаки від їх середньої:
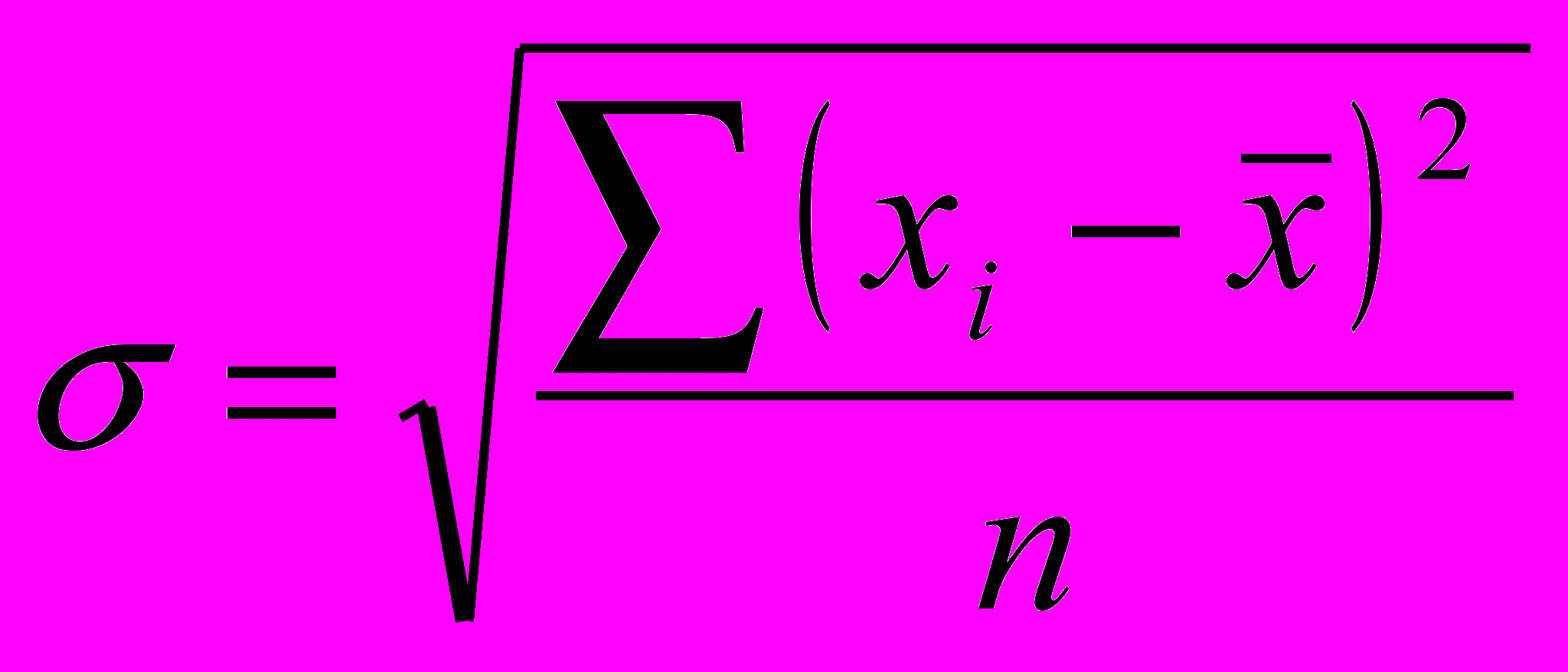 (для незгрупованих даних);
(для незгрупованих даних);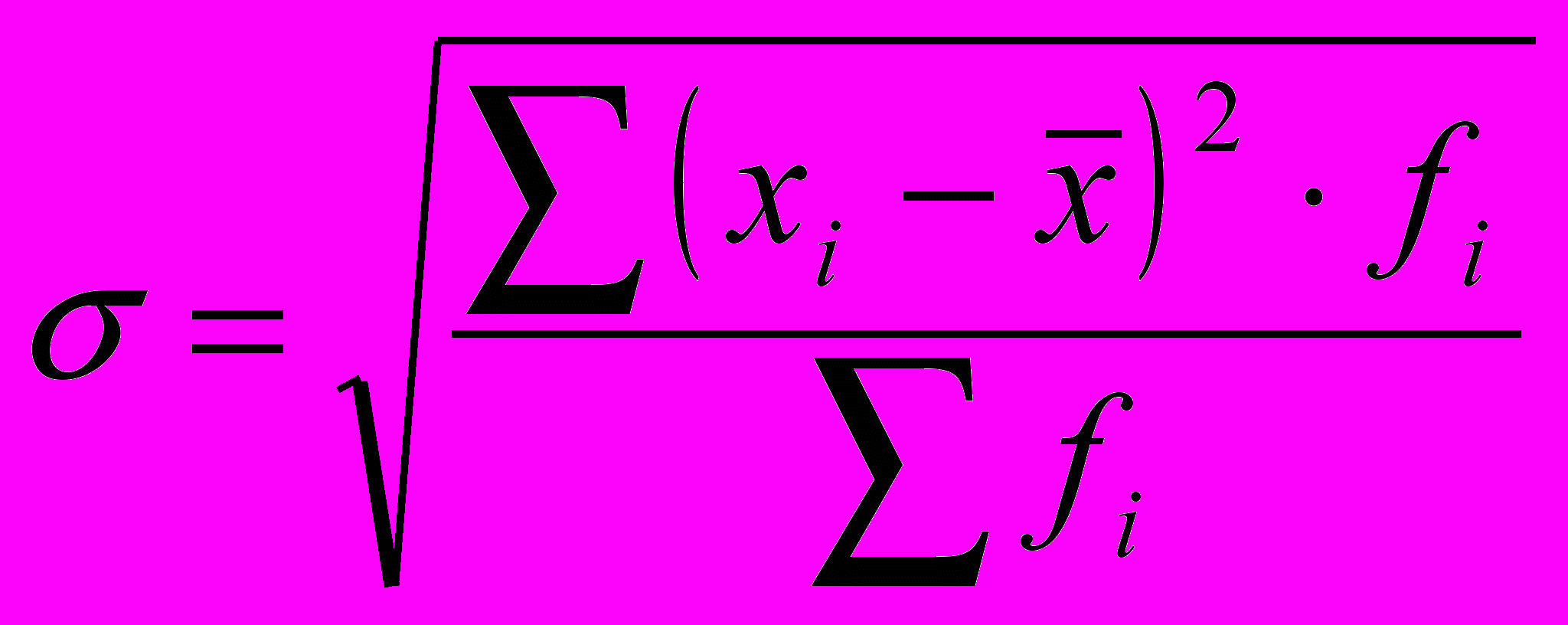 (для згрупованих даних).
(для згрупованих даних).Приклад. Розрахуємо дисперсію і середнє квадратичне відхилення для наступного ряду розподілу (табл..4.7.)
Таблиця 4.7.
Розподіл магазинів міста за товарообігом в ІІ кварталі 1998 року
| Групи магазинів за величиною товарообігу, тис. грн., | Число магазинів, fi | Середина інтервалу, т. грн., хі | xifi | 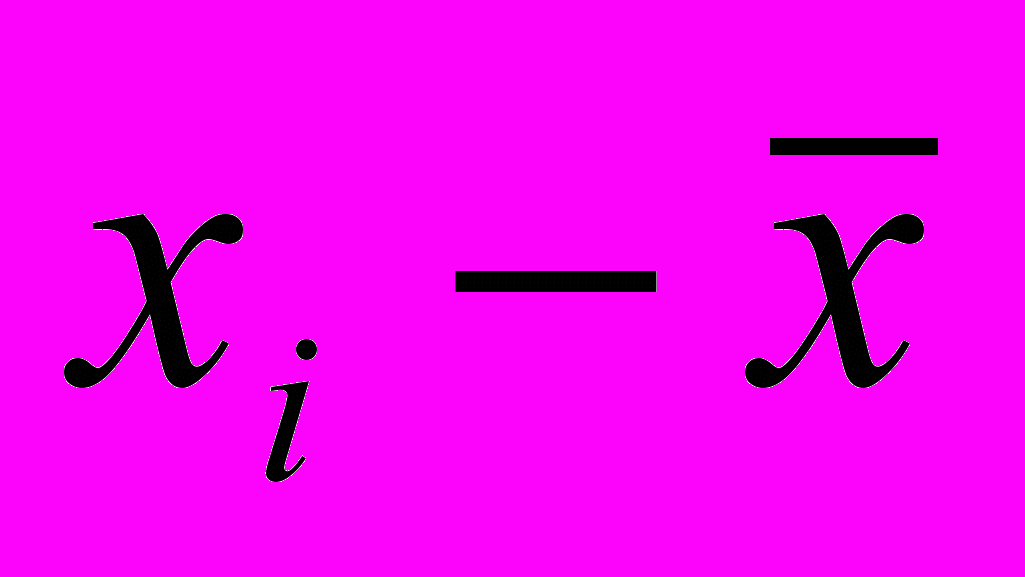 | 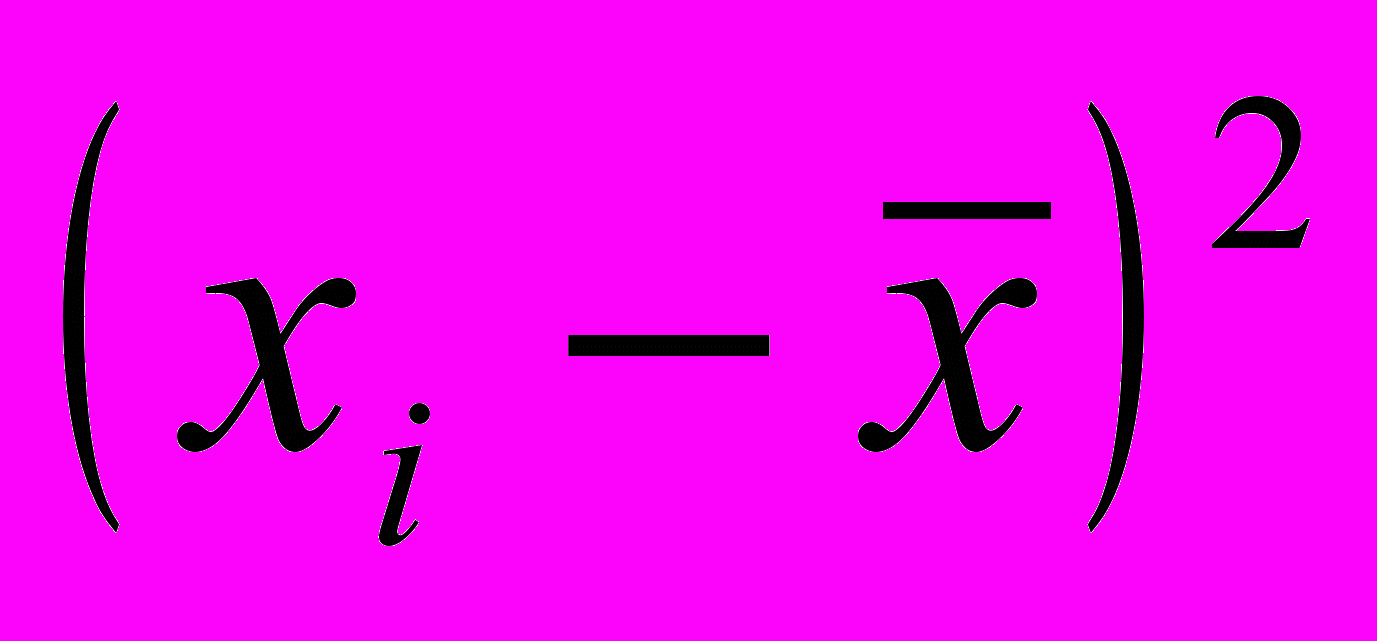 | 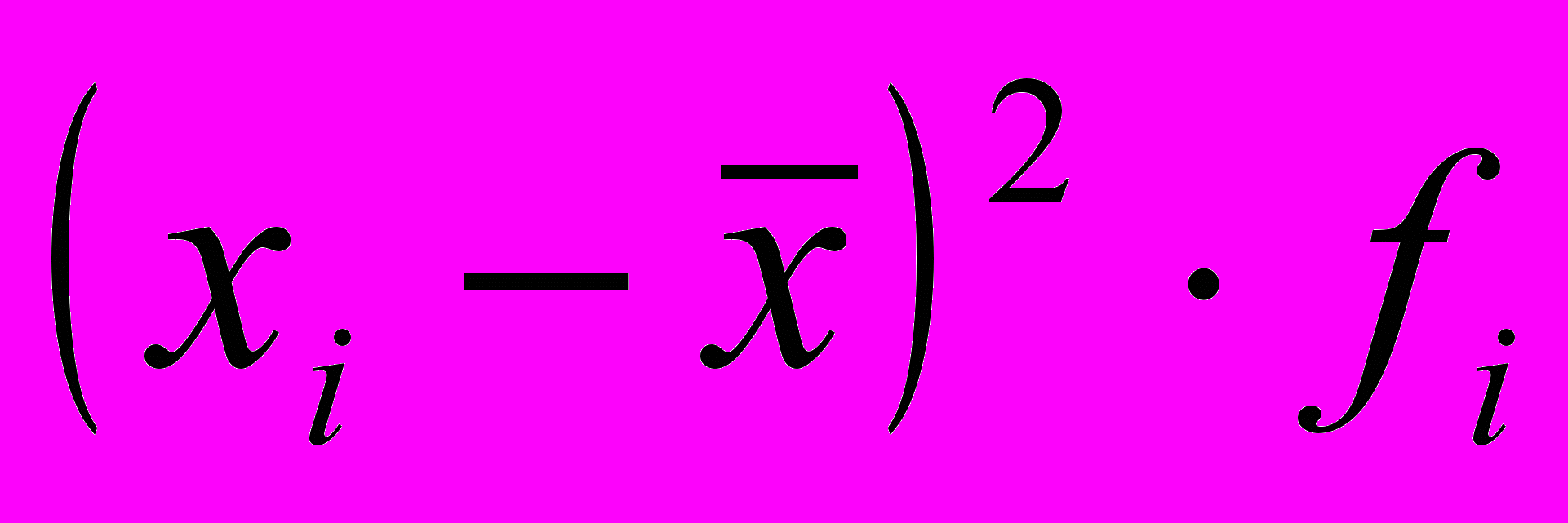 |
| А | 1 | 2 | 3 | 4 | 5 | 6 |
| 40-50 50-60 60-70 70-80 80-90 90-100 100-110 110-120 120-130 130-140 | 2 4 7 10 15 20 22 11 6 3 | 45 55 65 75 85 95 105 115 125 135 | 90 220 455 750 1285 1900 2310 1265 750 405 | -49,2 -39,2 -29,2 -19,2 -9,2 0,8 10,8 20,8 30,8 40,8 | 2420,64 1536,64 852,64 368,64 84,64 0,64 116,64 432,64 948,64 1664,64 | 4841,28 6146,56 5968,48 3686,40 1269,60 12,80 2566,08 4759,04 5691,84 4993,92 |
| Разом | 100 | - | 9420 | - | - | 39936,00 |
При розрахунку показників варіації за інтервальним рядом розподілу необхідно спочатку визначити середини інтервалів, а потім вже вести подальший розрахунок, розглядаючи ряд середин інтервалів як дискретний ряд розподілу.
Результати допоміжних розрахунків для визначення дисперсії та середнього квадратичного відхилення знаходяться в графах 2 – 6 таблиці 4.7.
Середній розмір товарообігу визначається за середньозваженою арифметичною і складає:
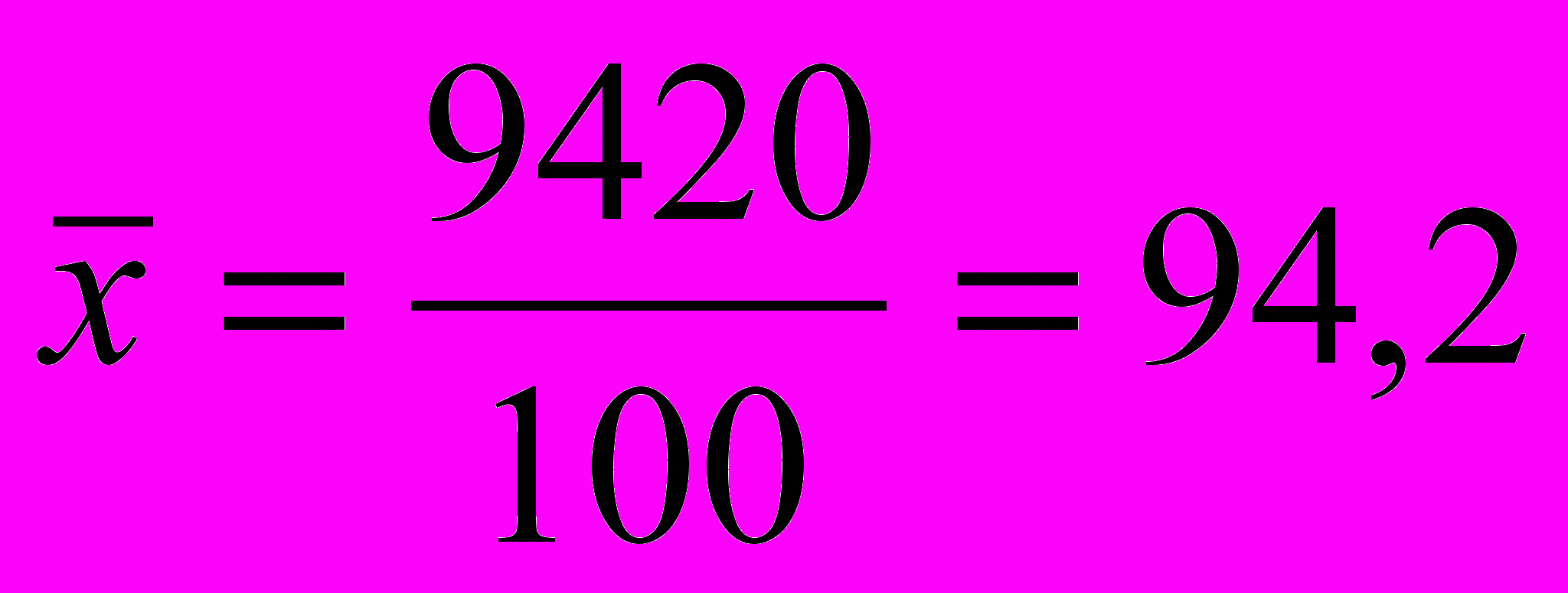 тис. грн.
тис. грн.Дисперсія товарообігу
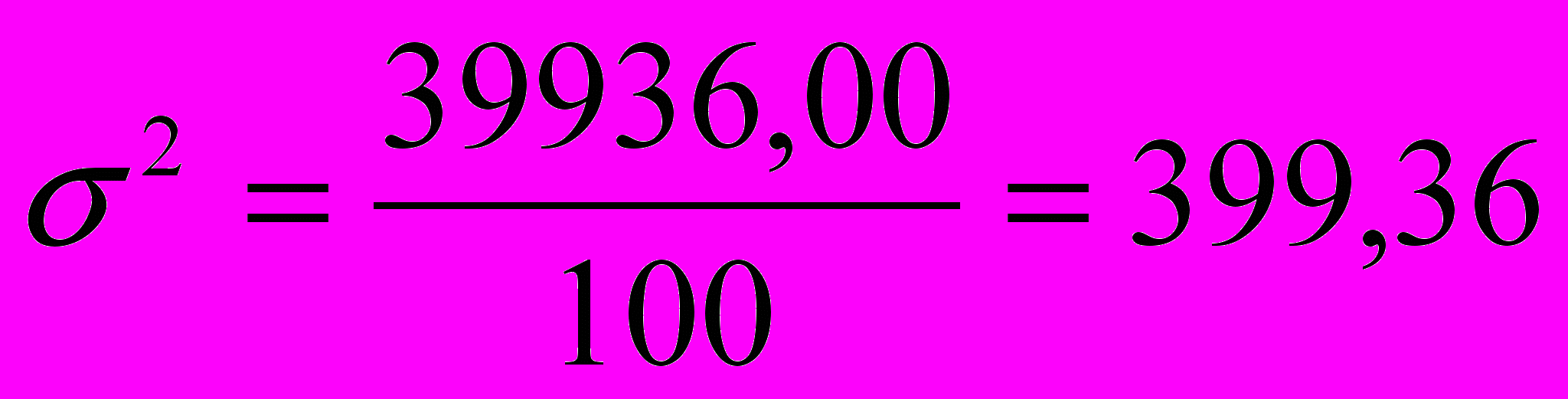 .
.Середнє квадратичне відхилення товарообігу визначається як квадратний корінь з дисперсії:
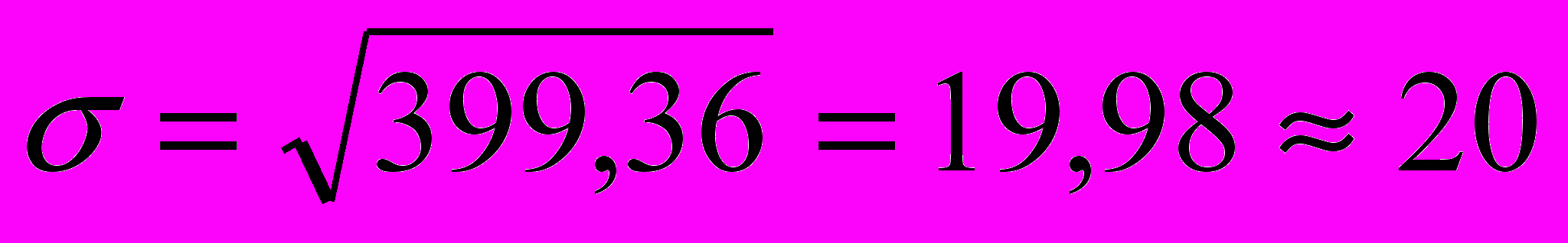 тис. грн.
тис. грн.Для порівняння варіації різних ознак або однієї ознаки в різних сукупностях використовують відносні показники варіації. Коефіцієнти варіації розраховуються як відношення абсолютних характеристик варіації (
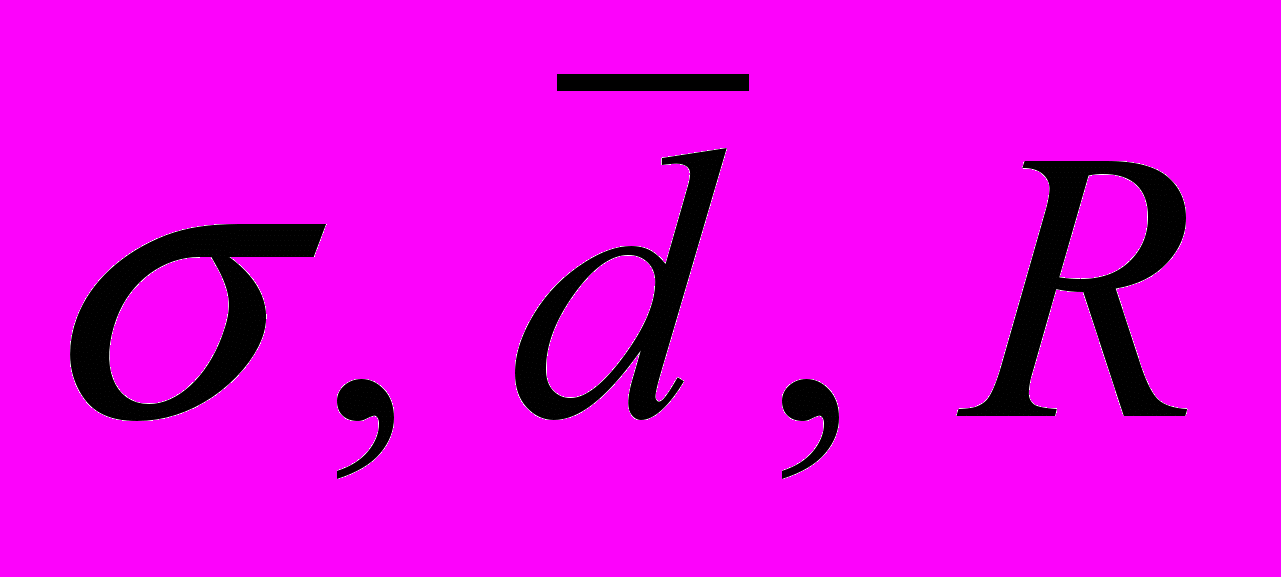 ) до центру розподілу і часто виражаються процентами. Отже:
) до центру розподілу і часто виражаються процентами. Отже:- Коефіцієнт осциляції:
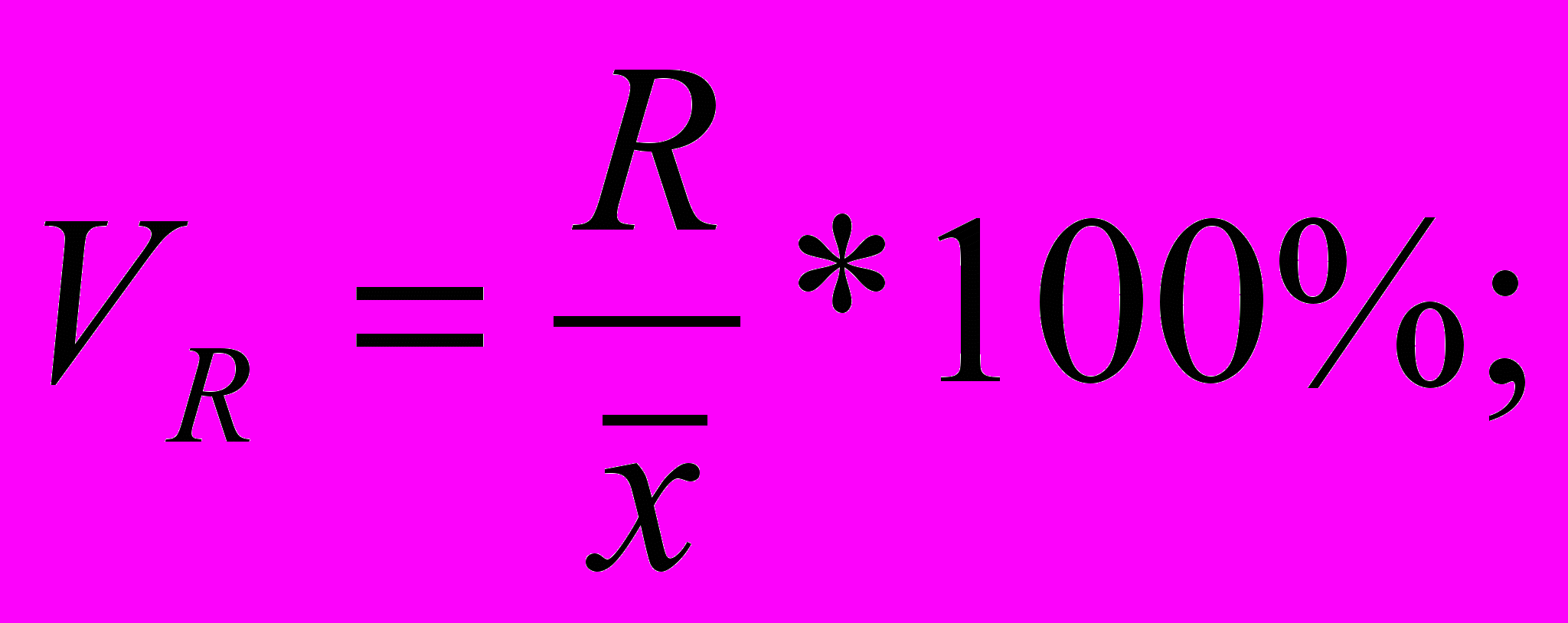
- Лінійний коефіцієнт варіації:
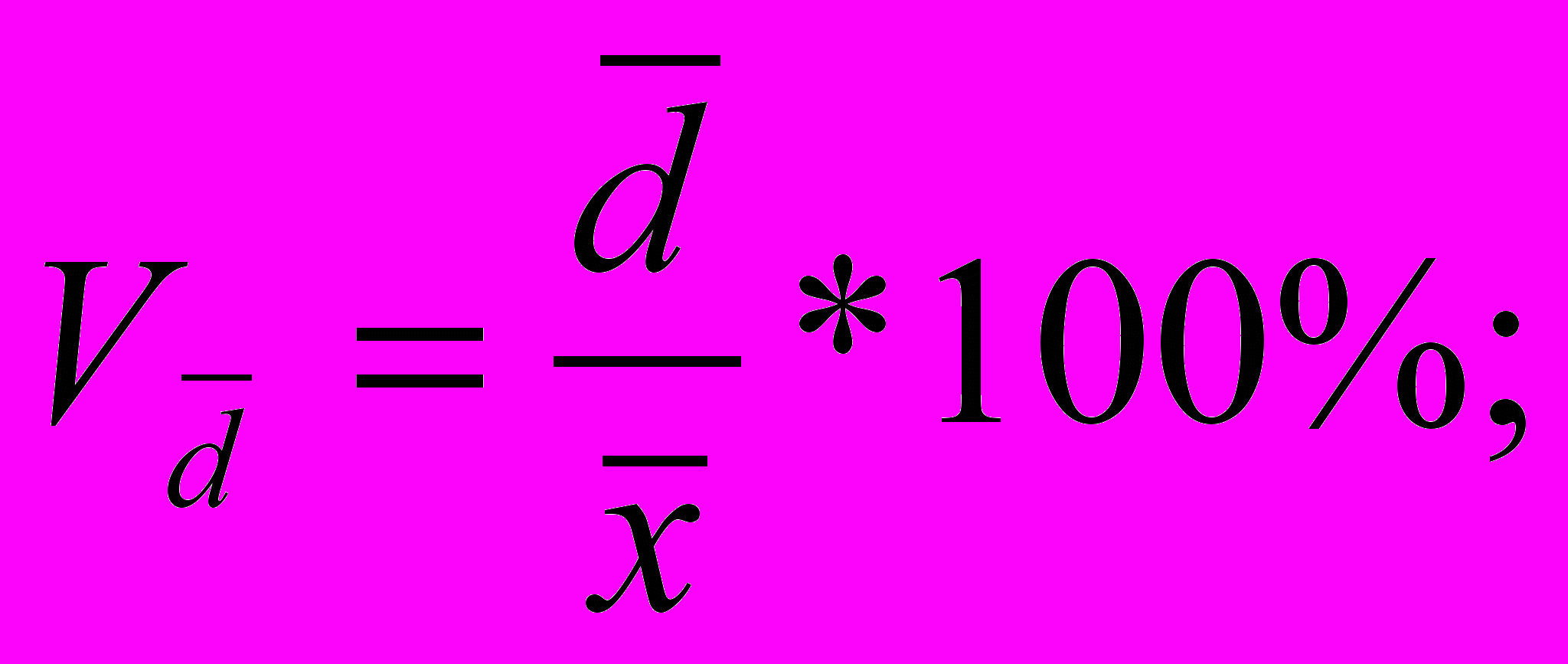
- Квадратичний коефіцієнт варіації:
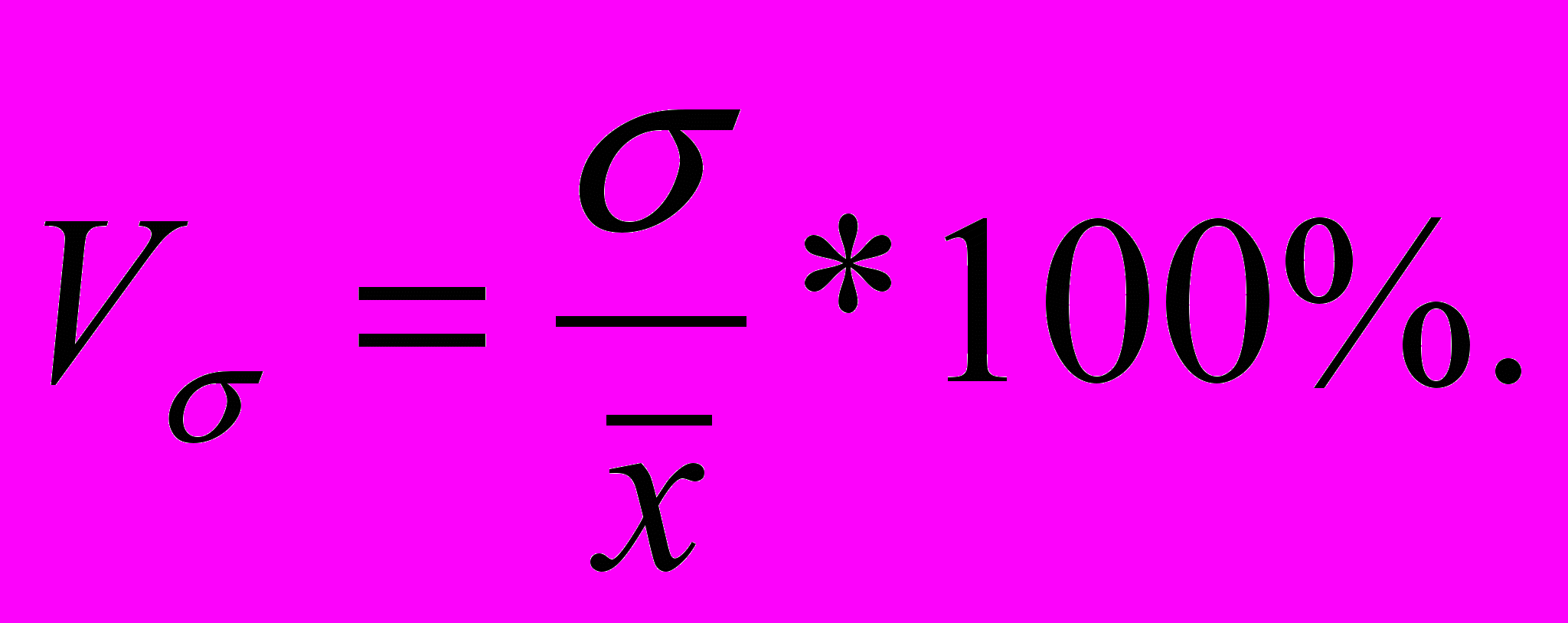
В статистиці сукупності, що мають коефіцієнт варіації (Vσ) більший 30-35%, вважаються неоднорідними.
Приклад. За даними вибіркових обстежень домогосподарств, середньодушові витрати на харчування становили 80 гр. од.; на придбання промислових товарів – 35; дисперсії відповідно – 256 та 196.
Порівняти ступінь варіації витрат домогосподарств на харчування та придбання промислових товарів можна за допомогою квадратичного коефіцієнта варіації:
витрати на харчування:
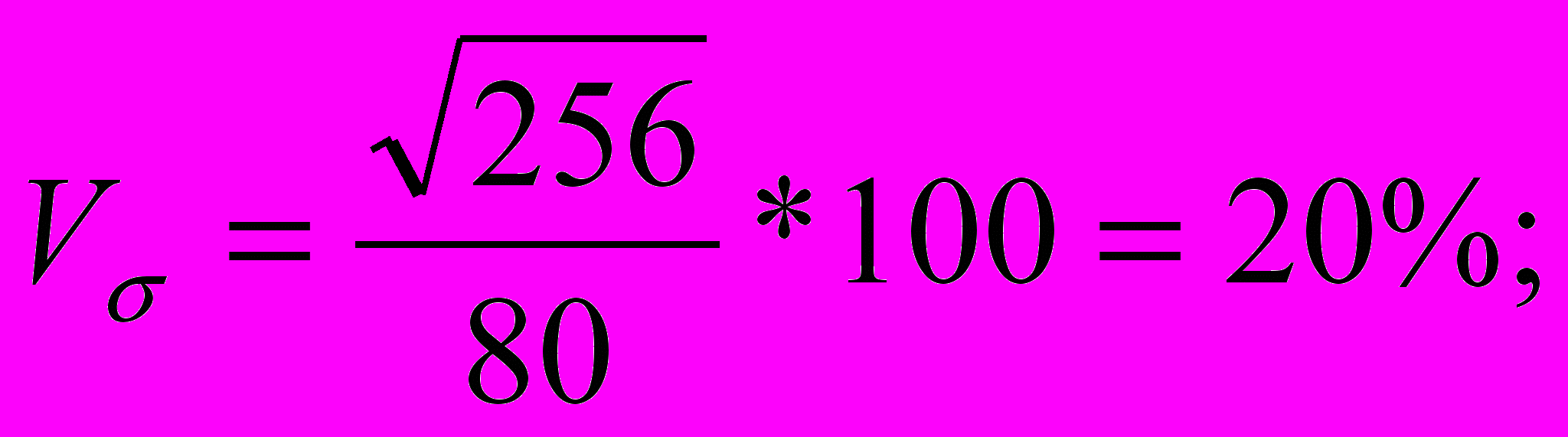
витрати на придбання промислових товарів:
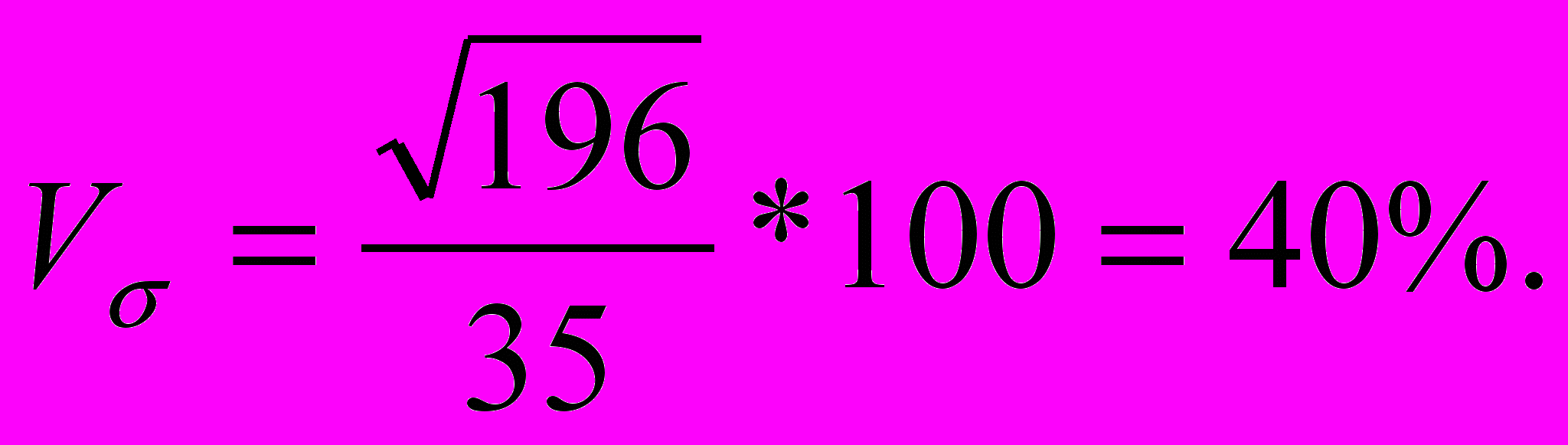
Отже, ступінь варіації витрат на придбання промислових товарів значно вищий.
