К дипломному проекту на тему

Вид материала

Подобный материал:

1 2 3 4 5 6

Рисунок 5 – логическая модель базы данных.

Проектирование программного обеспечения.

В данной дипломной работе при проектирование АС будет использоваться структурный подход к разработке системы. Диаграммы потоков данных вида IDEF0.

Структурное программирование — методология разработки программного обеспечения, в основе которой лежит представление программы в виде иерархической структуры блоков. Предложена в 70-х годах XX века Э. Дейкстрой, разработана и дополнена Н. Виртом.

В соответствии с данной методологией

1. Любая программа представляет собой структуру, построенную из трёх типов базовых конструкций:

* последовательное исполнение — однократное выполнение операций в том порядке, в котором они записаны в тексте программы;

* ветвление — однократное выполнение одной из двух или более операций, в зависимости от выполнения некоторого заданного условия;

* цикл — многократное исполнение одной и той же операции до тех пор, пока выполняется некоторое заданное условие (условие продолжения цикла).

В программе базовые конструкции могут быть вложены друг в друга произвольным образом, но никаких других средств управления последовательностью выполнения операций не предусматривается.

2. Повторяющиеся фрагменты программы (либо не повторяющиеся, но представляющие собой логически целостные вычислительные блоки) могут оформляться в виде т. н. подпрограмм (процедур или функций). В этом случае в тексте основной программы, вместо помещённого в подпрограмму фрагмента, вставляется инструкция вызова подпрограммы. При выполнении такой инструкции выполняется вызванная подпрограмма, после чего исполнение программы продолжается с инструкции, следующей за командой вызова подпрограммы.

3. Разработка программы ведётся пошагово, методом «сверху вниз».IDEF0 — Function Modeling — методология функционального моделирования и графическая нотация, предназначенная для формализации и описания бизнес-процессов. Отличительной особенностью IDEF0 является её акцент на соподчинённость объектов. В IDEF0 рассматривается логические отношения между работами, а не их временна́я последовательность (WorkFlow).

Так же отображаются все сигналы управления, которые на DFD (Диаграмме Потоков Данных) не отображались. Данная модель является одной из самых прогрессивных моделей и используется при организации бизнес-проектов и проектов, основанных на моделировании всех процессов как административных, так и организационных.

Современные CASE-средства охватывают обширную область поддержки многочисленных технологий проектирования ИС: от простых средств анализа и документирования до полномасштабных средств автоматизации, покрывающих весь жизненный цикл ПО. CASE-средства (от Computer Aided Software/System Engineering) позволяют проектировать любые системы на компьютере. Необходимый элемент системного и структурно-функционального анализа, CASE-средства позволяют моделировать бизнес-процессы, базы данных, компоненты программного обеспечения, деятельность и структуру организаций. Применимы практически во всех сферах деятельности. Результат применения CASE-средств - оптимизация систем, снижение расходов, повышение эффективности, снижение вероятности ошибок.

При выборе CASE – средств для разработки АС эксплуатация ВС был выбран как наиболее оптимальный инструмент визуального моделирования BPwin.

BPwin обладает удобным инструментом для навигации по уровням декомпозиции модели. BPwin - ведущий инструмент визуального моделирования бизнес-процессов. Дает возможность наглядно представить любую деятельность или структуру в виде модели, что позволит оптимизировать работу организации, проверить ее на соответствие стандартам ISO9000, спроектировать организационную структуру, снизить издержки, исключить ненужные операции, повысить гибкость и эффективность. Являясь стандартом де-факто, BPwin поддерживает сразу три нотации моделирования: IDEF0 (федеральный стандарт США), IDEF3 и DFD.

Для определения этапов разработки системы был использован ГОСТ 34.602-89 и ГОСТ 34.601-90.

Опишите каждую диаграмму

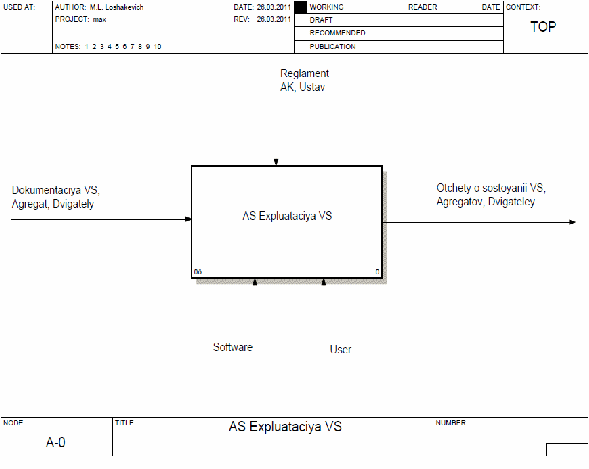
Рисунок 6 – функциональная автоматизированная система «Эксплуатация воздушных судов»

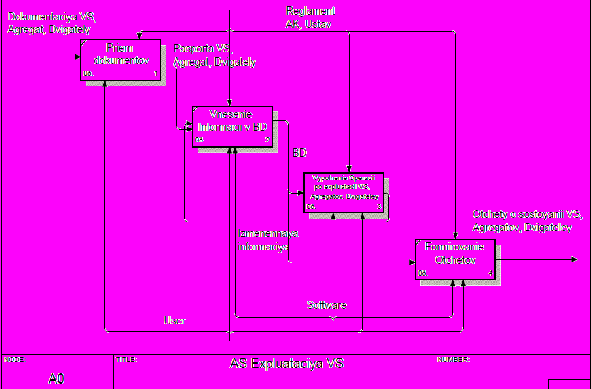
Рисунок 7 – Автоматизируемые функции. Добавьте диаграмму, описывающую формирование отчётов

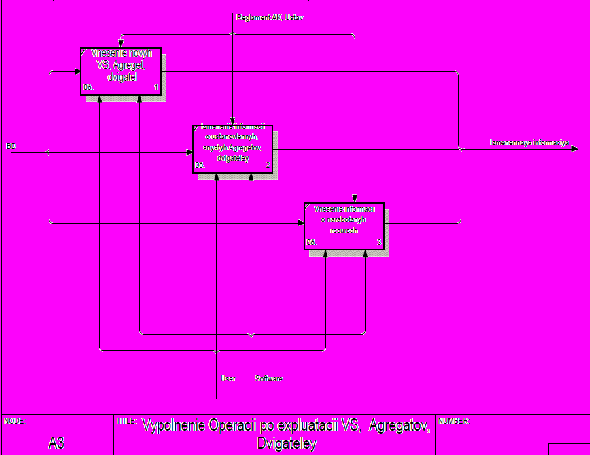
Рисунок 8 – Выполнение операций с данными. Не понятно, чем "Введение информации в БД" отличается от "Выполнения операций с данными". Судя по этой диаграмме, везде происходит ввод данных.

Расчет оптимизации парка ВС Добавьте входные и выходные данные, чтобы можно было выполнить оптимизацию. Добавьте оптимизацию и на диаграммы

Оптимизация это выбор наилучшего варианта из множества возможных [66, 68,136]. Если критерий выбора известен и вариантов немного, то решение может быть найдено путем перебора и сравнения всех вариантов. В нашем случае число возможных вариантов очень большое, что полный перебор практически невозможен. В этом случае приходится формулировать задачу на языке математики и применять специальные методы поиска оптимального решения, т.е. методы оптимизации [67].

Все задачи оптимизации делятся на два класса:

1) задачи математического программирования, или статические задачи [8, 57, 128];

2) задачи оптимального управления, или динамическими задачами.

Различие между этими классами состоит в том, что в задачи математического программирования необходимо найти оптимальное число, а в задаче оптимального управления оптимальную функцию. С формально-математической точки зрения, это различие существенно, но в нашем, прикладном случае это является условным, и этим различием мы пренебрегаем.

В нашем случае задача заключается в том, чтобы определить наиболее эффективные ВС, но необходимо учесть, что на выбор оптимальных вариантов воздушных судов большое влияние оказывает величина значений параметрического ряда, определить их оптимальное количество, обеспечивающие выполнение объемов пассажирских перевозок в установленные сроки, а также определить для каждого типа ВС наиболее рациональное распределение по маршрутам.

Решение вышеуказанной комплексной задачи должно дать ответ на следующие вопросы:

1) какие типы ВС необходимо применять для заданного объема пассажирских перевозок;

2) на каких маршрутах целесообразно использовать каждый тип ВС;

3) какое количество ВС необходимо иметь авиакомпании для выполнения пассажирских перевозок.

В рассматриваемой задаче предполагается, что все пассажирские перевозки выполняются в полном объеме, со 100 % загрузкой и с установленной регулярностью полетов. Предположим что, необходимо из определенного пункта «А» произвести воздушную перевозку по «n» маршрутам, в соответствии с рисунком 9.

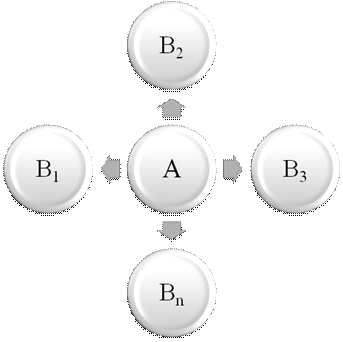
Рисунок 9 - Схема авиаперевозок.

Предполагаем, что обслуживают эти маршруты следующие типы воздушных судов 1,2,...M, где M - тип воздушного судна.

Предположим, что известно количество авиапассажиров, которых необходимо перевести по каждому маршруту за определенный промежуток времени, за неделю, за месяц и т.д.

Обозначим это количество перевозимых авиапассажиров как:

b1 - количество перевозимых авиапассажиров по 1-му маршруту;

b2 - количество перевозимых авиапассажиров по 2-му маршруту;

bn - количество перевозимых авиапассажиров по N-му маршруту.

Количество рейсов, совершаемых на 1-ом маршруте воздушными судами первого типа обозначим Х1,1.

Количество рейсов, совершаемых на 2-ом маршруте воздушными судами первого типа обозначим Х1,2.

Соответственно количество рейсов, совершаемых на I-ом маршруте воздушными судами J-ого типа, обозначим ХIJ,

где I=1,2,...N, J=1,2,...M.

Количество пассажиров, перевозимых за один рейс на I-ом маршруте воздушными судами J-ого типа, обозначим аIJ,

где I=1,2,...N, J=1,2,...M.

Расходы на один рейс на I-ом маршруте воздушного судна J-ого типа, обозначим сIJ,

где I=1,2,...N, J=1,2,...M.

Предположим, что каждый маршрут обслуживают воздушные суда всех марок 1,2,...M. Тогда для первого маршрута количество перевозимых пассажиров вычисляем по формуле

.

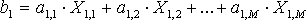(1)

Для второго маршрута количество перевозимых пассажиров вычисляем по формуле

.

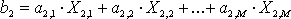(2)

Окончательно для всех маршрутов составляем систему ограничений-равенств

,

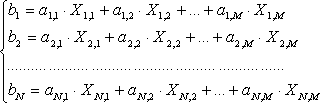(3)

где аIJ - известные величины,

;

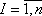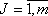bI - известные величины,

;

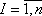ХIJ - неизвестные величины,

.

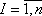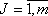Общую сумму расходов на все рейсы всех маршрутов вычисляем по формуле

.

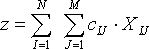(4)

Если необходимо минимизировать общую суммы расходов по формуле (4) при выполнении системы ограничений-равенств (3), то получаем задачу линейного программирования [13,70, 133].

Задача линейного программирования решается симплекс-методом, т.е. этим методом находят ХIJ, где

;

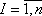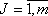После определения ХIJ, при

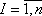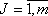, зная расстояние, скорость, возможно, определить оптимальный парк воздушных судов для узла перевозок «А».

Возможно, к системе ограничений-равенств добавить систему ограничений-равенств (неравенств) по количеству рейсов воздушного судна каждого типа, в результате получаем общее количество рейсов на всех маршрутах воздушных судов типа 1, известное значение, вычисляемое по формуле

.

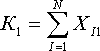(5)

Общее количество рейсов на всех маршрутах воздушных судов типа 2, известное значение, вычисляемое по формуле

.

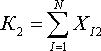(6)

Окончательно систему ограничений равенств по общему количеству рейсов на всех маршрутах для каждого типа воздушного судна вычисляем по формуле

,

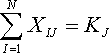(7)

где

.

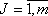Добавляя к системе ограничений (1) систему ограничений (7), возможно, минимизировать общую сумму расходов (4). В результате опять получаем задачу линейного программирования, которую решаем симплекс-методом. Для решения необходимо задать bI, aIJ, cIJ, KJ,

.

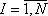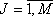Для определения рационального использования капиталовложений необходимо провести экономическое обоснование структуры гипотетического парка ВС по авиакомпаниям, их географическому расположению и в целом по стране.

Рост производительности и объем пассажирских перевозок должен опережать стоимость, что является условием эффективного использования каждого нового ВС.

Осталось спроектировать непосредственно ПО (описать модули, спроектировать интерфейс) и сделать руководство пользователя.

Экономико-математическая постановка задачи

Для выполнения объема пассажирских перевозок располагаем различными вариантами воздушных судов, т.е. проводим расчет и выбор всех имеющихся воздушных судов в данной авиакомпании на одном маршруте. В процессе решения задачи необходимо установить, сколько различных вариантов ВС и какие наиболее целесообразно использовать для выполнения работ по пассажирским перевозкам. При выборе варианта ВС и определения оптимального парка ВС необходимо описать все технические и экономические параметры существенные для данной задачи. В этом случае воспользуемся математическими расчетами, дополняющие мысленные представления управляемого процесса в виде таблиц и графических зависимостей. Использование математических методов при формировании представлений об авиакомпаниях как экономических объектах и процесса пассажирских перевозок в ходе экономического анализа, прогнозирования, планирования называют применением экономико-математических методов. Наиболее распространенная форма, основной инструментарий воплощения экономико-математических методов это экономико-математическое моделирование. Моделирование представляет воспроизведение образа реального объекта в виде его модели, а модель и есть образ реального объекта или процесса пассажирских перевозок в вещественной или описательной форме. Математическое моделирование опирается на математическое описание процесса пассажирских перевозок в виде формул, зависимостей с помощью математических символов, знаков. В связи с тем, что рассмотреть процесс пассажирских перевозок без экономической составляющей невозможно, то соответствующая модель называется экономико-математической. Система уравнений (4.2)-(4.8) образует экономико-математическую модель задачи [60].

Экономико-математическая модель представляет формализованное описание управляемого процесса пассажирских перевозок, включающее заранее заданные, известные параметры, показатели и искомые неизвестные величины, характеризующие вместе состояние объекта, его функционирование, объединенные между собой связями в виде математических зависимостей, соотношений. Вполне логично, что экономико-математическая как и любая другая модель, рассмотренная в третьей главе, не способна воплотить и отразить все свойства моделируемого процесса. Модель способна быть только аналогом моделируемой системы, отражающим основные, существенные свойства рассматриваемой системы. Главное требование, предъявляемое к экономико-математической модели, заключается в том, что она должна обладать адекватностью, т.е. соответствовать моделируемому объекту и процессу [126]. Источником информации при составлении экономико-математической модели являются отчеты авиакомпаний по итогам работы за год, следовательно, предложенная экономико-математическая модель в полном объеме обладает адекватностью. Большинство экономико-математических моделей носит дискретный и статичный характер, тогда как моделируемые процессы во многом непрерывны и динамичны. В связи, с чем различают:

1) дискретные модели, которые отражают состояние объекта в отдельные, фиксированные моменты времени, а непрерывные характеризуют непрерывное изменение показателей деятельности объекта во времени;

2) имитационные модели это экономико-математические модели, используемые в целях имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники;

3) факторные модели. В эту группу входят модели с экономическими факторами, от которых зависит состояние и изменение объекта, а также параметры, зависящие от этих показателей состояние объекта;

4) оптимизационные модели. Эти модели позволяют выбрать из всех возможных решений самый лучший, оптимальный вариант. В математическом смысле «оптимальность» понимается как достижение экстремума критерия оптимальности, называемой также целевой функцией. Если целевая функция, ограничения, связи между искомыми показателями выражены в виде линейных зависимостей, то оптимизационная модель сводится к задаче линейного математического программирования и сама модель также называется линейной;

5) детерминированные модели, модели в которых случайность, проявляющаяся в поведении объекта, в явной форме не учитывается;

6) стохастические модели, оперирующие методами теории случайных процессов, теории вероятности и математической статистики, но данный вопрос не входит в область наших исследований.

Динамичны и условия, в которых функционирует моделируемый процесс. За период, охватывающий отрезок времени между моделированием и реальным функционированием процесса, который должна предсказать модель, условия функционирования объекта, заложенные в модель, могут настолько измениться, что поведение процесса будет заведомо отличаться от предсказанного математической моделью. Отработанный, применяемый аппарат экономико-математического моделирования опирается в основном на использование детерминированных моделей. Также необходимо учитывать действие факторов случайности и неопределенности на управляемые экономические процессы и объекты, учет которых в экономико-математической модели затруднен.

Оптимальный парк воздушных судов гражданской авиации на основе параметрического ряда

Воздушное судно характеризуется большим количеством параметров - весовых, геометрических, аэродинамических, о чем уже упоминалось в третьей главе. При оптимизации парка ВС необходимо провести увязку параметров ВС с процессом пассажирских перевозок, чем эффективнее будет произведена увязка, тем экономически выгоднее окажется процесс.

Из вышесказанного следует, что для осуществления процесса пассажирских перевозок с минимальными затратами необходимо иметь ВС, которые возможно оценить, построив параметрический ряд, основанный на прогнозе развития отечественного и мирового самолетостроении.

Исходные данные для расчета параметрических рядов могут быть заданы на определенный, довольно длительный перспективный период, обусловленный планированием исходных показателей. Следовательно, для каждого следующего периода должны быть разработаны новые параметрические ряды применительно к условиям нового периода.

Решение задачи оптимизации перспективных параметрических рядов связано с рассмотрением сложной динамической стохастической системы. Сложность системы определяется большим количеством взаимосвязанных факторов в системе. Динамический характер данной системы заключается в том, что в течение перспективного периода, на который определяется параметрический ряд, происходит изменение объема пассажирских перевозок, условий их выполнения и следовательно, количества ВС в парке.

Однако возникают сложности учесть факторы, связанные с ВС, трудность получения необходимой информации, количественно характеризующей те или иные факторы. Все это говорит о необходимости на данном этапе рассматривать статическую задачу для определенного отрезка времени.

Составление параметрического ряда заключается в определении основных характеристик ВС, и с помощью математических методов определяется оптимальное ВС на каждом конкретном маршруте.

В работе был рассмотрен параметрический ряд двух авиакомпаний, с имеющимся парком ВС.

Выбор оптимального парка ВС с учетом тактико-технических характеристик, воздушного сообщения, количества пассажиров в ВС, количества рейсов в месяц и затраченных расходов на I-ом маршруте в месяц производим комплексно с помощью симплекс-метода. Информация, которую можно получить с помощью симплекс-метода, не ограничивается лишь оптимальными значениями переменных [20, 24, 45, 46, 130]. Симплекс-метод позволяет дать экономическую интерпретацию полученного решения и провести анализ модели на чувствительность. Анализ модели на чувствительность это процесс, реализуемый после того, как оптимальное решение получено. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели.

Процесс решения задачи линейного программирования симплекс-методом носит итерационный характер, т.е. однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор, пока не будет получено оптимальное решение. Процедуры, реализуемые в рамках симплекс-метода, естественно требуют применения персональных ЭВМ. В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при которой, начиная с некоторой исходной допустимой точки осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка (тип ВС на маршруте), соответствующая оптимальному решению.

Исходной точкой при определении оптимального парка ВС является начальное решение. От исходной точки осуществляется переход к следующей смежной точки. Выбор точки зависит от коэффициентов целевой функции, где коэффициент больше функция подлежит максимизации, что приводит к экстремальной точке. После чего указанный процесс повторяется, для выяснения существует ли другая экстремальная точка, соответствующая лучшему допустимому решению. В результате такой итеративный процесс позволяет найти оптимальное ВС для соответствующего маршрута.

Выбор каждой последующей экстремальной точки при использовании симплекс метода определяется следующими правилами:

1) каждая последующая точка должна быть смежной с предыдущей;

2) обратный переход к предшествующей экстремальной точке не может производиться.

Блок-схема симплекс-метода в первой канонической форме представлена в соответствии с рисунком 10.

Симплекс-алгоритм состоит из следующих этапов:

1) используя линейную модель стандартной формы, определяем начальное допустимое базисное решение путем приравнивания к нулю небазисных переменных;

2) из числа текущих небазисных (равных нулю) переменных выбирается включаемая в новый базис переменная, увеличение которой обеспечивает улучшение значения целевой функции. Если такой переменной нет, вычисления прекращаются, т.к. текущее базисное решение оптимально. В противном случае осуществляется переход к следующему этапу;

3) из числа переменных текущего базиса выбирается исключаемая переменная, которая должна принять нулевое значение (стать небазисной) при введении в состав базисных новой переменной;

4) находится новое базисное решение, соответствующее новым составам небазисных и базисных переменных. Осуществляется переход к этапу «2».

Схема алгоритма выбора оптимального парка ВС с помощью симплекс-метода представлена в соответствии с рисунком 11.

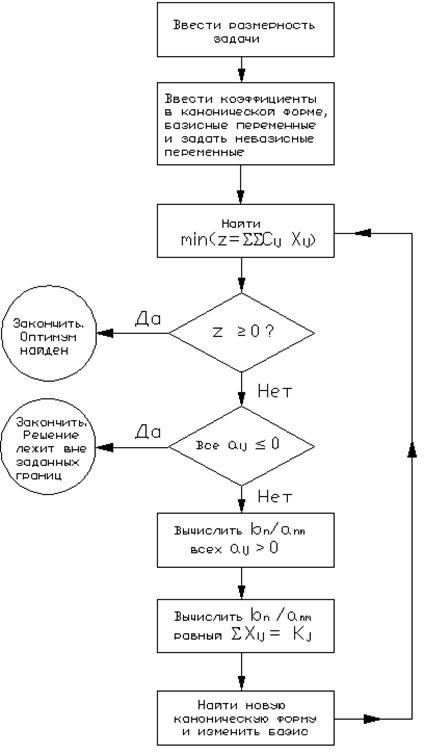
Рисунок 10 - Блок схема симплекс-метода

Из теоретических положений, лежащих в основе построения симплекс-метода, следует, что угловая точка полностью определяется базисным решением задачи линейного программирования. Условия оптимальности и допустимости симплекс-алгоритма обеспечивает переход от начальной допустимой точки (начального базисного решения) к смежной точке, соответствующей улучшенному значению целевой функции. Максимальное количество итераций, необходимых для получения оптимума (т.е. количество базисных решений), не превосходит , где N - число переменных, а M - число уравнений модели линейного программирования, представленной в стандартной форме.

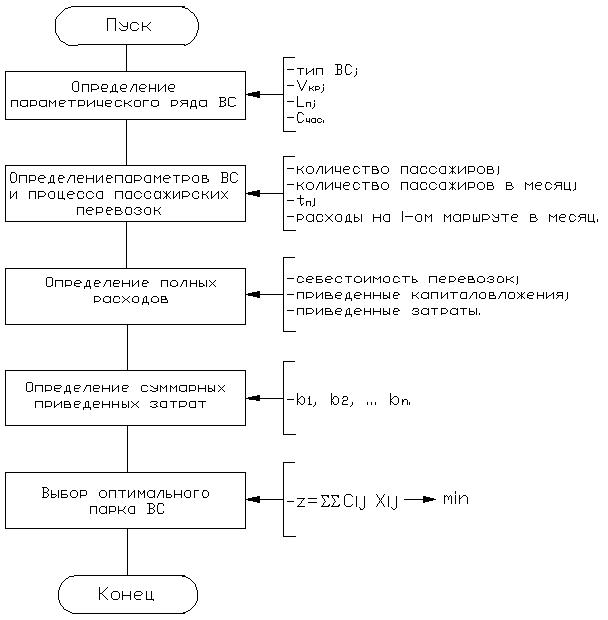
Рисунок 11 - Схема алгоритма выбора оптимального парка ВС.

На маршруте Тюмень-Москва-Тюмень общее количество перевезенных пассажиров за месяц равно b1=61488 человек.

Введем обозначение:

Х1 - количество рейсов в месяц воздушного судна Boeing 737-500 на маршруте Тюмень-Москва-Тюмень;

Х2 - количество рейсов в месяц воздушного судна Ту-134 на маршруте Тюмень-Москва-Тюмень;

Х3 - количество рейсов в месяц воздушного судна Ту-154 на маршруте Тюмень-Москва-Тюмень.

Количество перевозимых пассажиров за один рейс Тюмень-Москва-Тюмень составляет:

- воздушное судно Boeing 737-500 - 240 пассажиров;

- воздушное судно Ту-134 - 152 пассажира;

- воздушное судно Ту-154 - 340 пассажиров.

В результате линейное ограничение-равенство для маршрута Тюмень-Москва-Тюмень представлено в виде

.

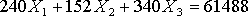(8)

Количество перевозимых пассажиров в месяц на маршруте Тюмень-Санкт-Петербург-Тюмень равно b2=11712 человек.

Введем обозначение:

Х4 - количество рейсов в месяц воздушного судна Boeing 737-500 на маршруте Тюмень-Санкт-Петербург-Тюмень;

Х5 - количество рейсов в месяц воздушного судна Ту-134 на маршруте Тюмень-Санкт-Петербург-Тюмень;

Х6 - количество рейсов в месяц воздушного судна Ту-154 на маршруте Тюмень-Санкт-Петербург-Тюмень.

В результате линейное ограничение-равенство для маршрута Тюмень-Санкт-Петербург-Тюмень представлено в виде

.

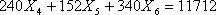(9)

Количество перевозимых пассажиров в месяц на маршруте Тюмень- Ростов-на-Дону- Тюмень равно b3=5856 человек.

Введем обозначение:

Х7 - количество рейсов в месяц воздушного судна Boeing 737-500 на маршруте Тюмень- Ростов-на-Дону- Тюмень;

Х8 - количество рейсов в месяц воздушного судна Ту-134 на маршруте Тюмень- Ростов-на-Дону- Тюмень;

Х9 - количество рейсов в месяц воздушного судна Ту-154 на маршруте Тюмень- Ростов-на-Дону- Тюмень.

В результате линейное ограничение-равенство для маршрута Тюмень- Ростов-на-Дону- Тюмень представлено в виде

.

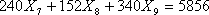(10)

Количество перевозимых пассажиров в месяц на маршруте Тюмень-Уфа-Тюмень равно b4=5856 человек.

Введем обозначение:

Х10 - количество рейсов в месяц воздушного судна Boeing 737-500 на маршруте Тюмень-Уфа-Тюмень;

Х11 - количество рейсов в месяц воздушного судна Ту-134 на маршруте Тюмень-Уфа-Тюмень;

Х12 - количество рейсов в месяц воздушного судна Ту-154 на маршруте Тюмень-Уфа-Тюмень.

В результате линейное ограничение-равенство для маршрута Тюмень-Уфа-Тюмень представлено в виде

.

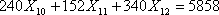(11)

Количество перевозимых пассажиров в месяц на маршруте Тюмень-Мюнхен-Тюмень равно b5=2928 человек.

Введем обозначение:

Х13 - количество рейсов в месяц воздушного судна Boeing 737-500 на маршруте Тюмень-Мюнхен-Тюмень;

Х14 - количество рейсов в месяц воздушного судна Ту-134 на маршруте Тюмень-Мюнхен-Тюмень;

Х15 - количество рейсов в месяц воздушного судна Ту-154 на маршруте Тюмень-Мюнхен-Тюмень.

В результате линейное ограничение-равенство для маршрута Тюмень-Мюнхен-Тюмень представлено в виде

.

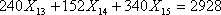(12)

Количество перевозимых пассажиров в месяц на маршруте Тюмень-Душанбе-Тюмень равно b6=11712 человек.

Введем обозначение:

Х16 - количество рейсов в месяц воздушного судна Boeing 737-500 на маршруте Тюмень-Душанбе-Тюмень;

Х17 - количество рейсов в месяц воздушного судна Ту-134 на маршруте Тюмень-Душанбе-Тюмень;

Х18 - количество рейсов в месяц воздушного судна Ту-154 на маршруте Тюмень-Душанбе-Тюмень.

В результате линейное ограничение-равенство для маршрута Тюмень-Душанбе-Тюмень в виде

.

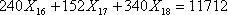(13)

Количество перевозимых пассажиров в месяц на маршруте Тюмень-Казань-Тюмень равно b7=8784 человек.

Введем обозначение:

Х19 - количество рейсов в месяц воздушного судна Boeing 737-500 на маршруте Тюмень-Казань-Тюмень;

Х20 - количество рейсов в месяц воздушного судна Ту-134 на маршруте Тюмень-Казань-Тюмень;

Х21 - количество рейсов в месяц воздушного судна Ту-154 на маршруте Тюмень-Казань-Тюмень.

В результате линейное ограничение-равенство для маршрута Тюмень-Казань-Тюмень представлено в виде

.

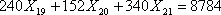(14)

Расчет коэффициентов в целевой функции, т.е. суммарные расходы на все рейсы всех маршрутов осуществляем из следующих соображений:

1) средняя вместимость воздушных судов:

- Boeing 737-500 - 120 мест;

- Ту-134 - 76 мест;

- Ту-154 - 170 мест;

2) если цена одного рейса Boeing 737-500 равна единице, то цену одного рейса самолета Ту-134, вычисляем по формуле

,

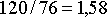(15)

;

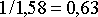(16)

3) цену одного рейса воздушного судна Ту-154, вычисляем по формуле

,

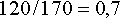(17)

.

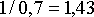(18)

С учетом введенных выше обозначений количества рейсов в месяц для рассматриваемых типов воздушных судов на всех маршрутах и с учетом цен одного рейса для каждого типа воздушного судна на рассматриваемых маршрутах, целевая функция суммарных расходов на все рейсы всех маршрутов ОАО «ЮТэйр», предлагается в виде

.

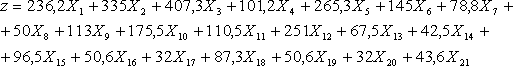(19)

В целевой функции (19) коэффициенты при неизвестных есть цены определенного типа воздушного судна на определенном маршруте.

Значение цен в целевой функции уменьшены в 105 раз, для реализации более точных расчетов. Соответственно для определения реального значения целевой функции ее расчетное значение необходимо умножить на 105.

Для целевой функции (19) система ограничений-равенств в соответствии с уравнениями (8)-(14), представлена в виде

.

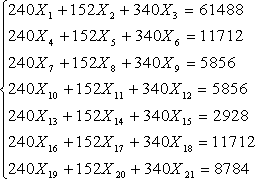(20)

При системе ограничений-равенств (20) и целевой функции - суммарные расходы по всем маршрутам, в соответствии с целевой функцией (19) необходимо найти такие значения неизвестных Х1, Х2, ...Х21, при которых значение целевой функции (19) будет минимальным. Это задача линейного программирования и как говорилось выше, решаем симплекс-методом. Минимальное значение целевой функции, в рублях, равно

.

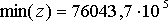(21)

На основании полученных результатов расчета можно сделать вывод:

1) на трех маршрутах, а именно Тюмень-Москва-Тюмень, Тюмень-с. Петербург-Тюмень и Тюмень- Ростов-на- Дону-Тюмень экономически эффективно использовать воздушное судно типа Б737-500;

2) на трех маршрутах, а именно Тюмень-Уфа -Тюмень, Тюмень-Душанбе-Тюмень и Тюмень-Мюнхен-Тюмень экономически эффективно использовать воздушное судно типа Ту134. Но в связи с тем, что на воздушных судах этого типа установлена устаревшая авионика, то в города Европейского Союза осуществляет полет воздушное судно типа Б737-500;

3) на маршруте Тюмень-Казань-Тюмень экономически эффективно использовать воздушное судно типа Ту154.

Графическое решение задачи по оптимизации парка воздушных судов для авиакомпании ОАО «ЮТэйр» по маршрутам, представлено в соответствии с рисунками 12-18.

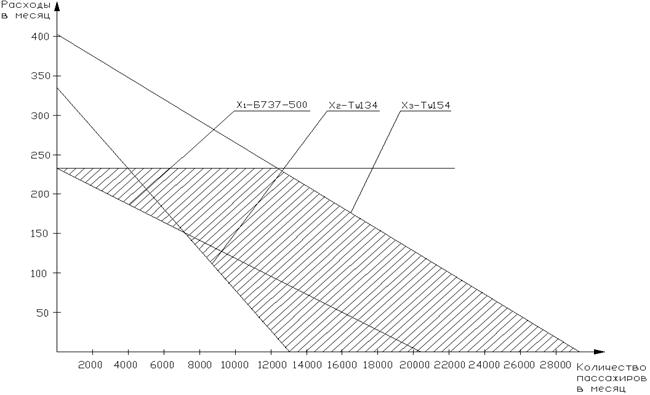
Рисунок 12 - Область допустимых решений маршрута Тюмень-Москва-Тюмень.

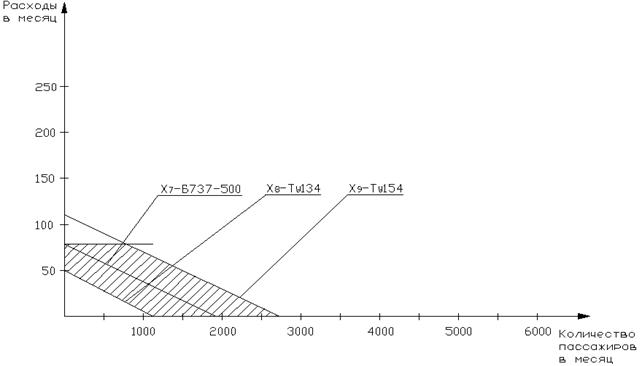
Рисунок 13 - Область допустимых решений маршрута Тюмень-с. Петербург-Тюмень

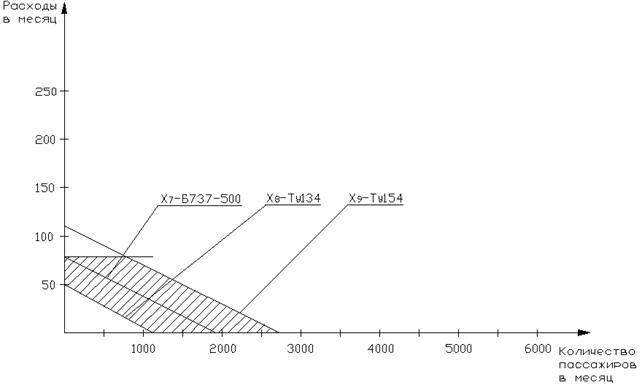
Рисунок 14 - Область допустимых решений маршрута Тюмень- Ростов-на- Дону-Тюмень

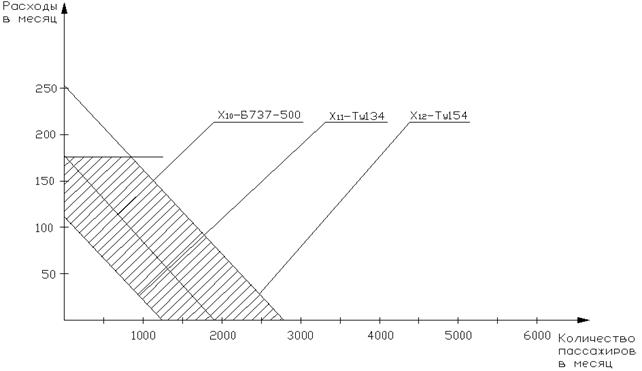
Рисунок 15 - Область допустимых решений маршрута Тюмень-Уфа -Тюмень

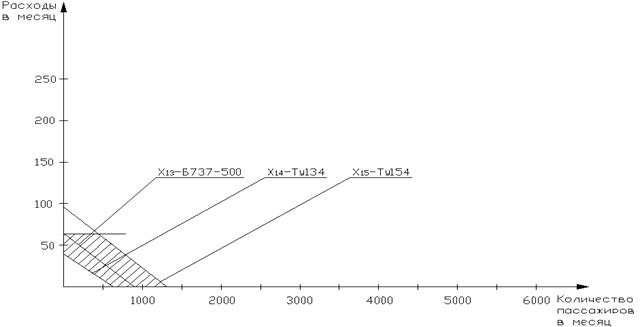
Рисунок 16 - Область допустимых решений маршрута Тюмень-Мюнхен-Тюмень

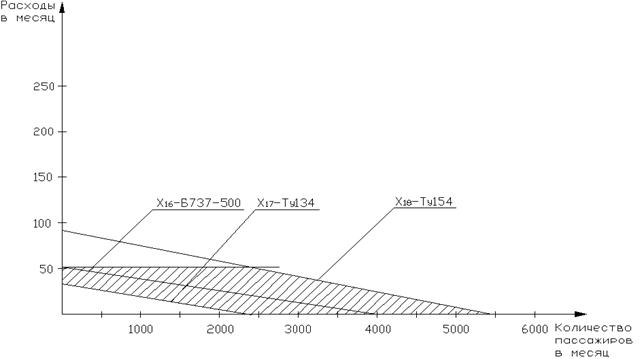
Рисунок 17 - Область допустимых решений маршрута Тюмень-Душанбе-Тюмень

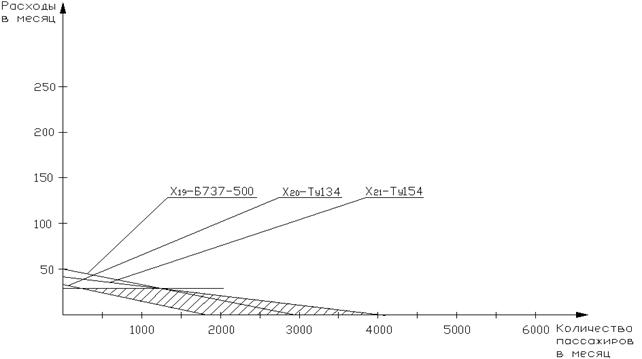
Рисунок 18 - Область допустимых решений маршрута

Тюмень-Казань- Тюмень

На графических зависимостях наглядно представлена оптимальная область использования каждого типа воздушного судна в зависимости от количества пассажиров и себестоимости полета с учетом введенных выше ограничений.

Расчет результирующих показателей экономической эффективности.

Внедрение современных информационных технологий - дело дорогостоящее. Однако пора повального увлечения информатизацией прошла, и сегодня ни один мыслящий руководитель не будет заниматься информатизацией своего производства без просчета прямых выгод от ее внедрения и эксплуатации, что невозможно без тщательного анализа и определения их экономической эффективности и целесообразности.

Экономическая эффективность капитальных вложений на разработку и внедрение автоматизированной системы предполагает сопоставление результатов автоматизации и затрат на неё. Для оценки эффективности инвестиционных проектов широко используется метод дисконтирования.

Метод дисконтирования рекомендован министерством финансов РФ для оценки эффективности инвестиционных проектов. Он базируется на дисконтных вычислениях по приведению доходов и расходов, связанных с реализацией системы, к некоторому моменту времени (к расчетному году).

Программу, как любое техническое решение необходимо рассматривать с экономической точки зрения экономической целесообразности и пользы. Целью технико-экономического обоснования разработки является количественное и качественное доказательство экономической целесообразности усовершенствования программы, а также определение организационно-экономических условий ее эффективного функционирования.

Эффективность программного модуля определяется его качеством и эффективностью процесса разработки и сопровождения. Качество программного изделия определяется тремя составляющими:

- с точки зрения специалиста-пользователя данного программного продукта;

- с позиции использования ресурсов и их оценки;

- по выполнению требований на программное изделие.

Программное изделие должно быть разработано так, чтобы оно выполняло свои функции без лишних затрат ресурсов (оперативной памяти ЭВМ, машинного времени, пропускной способности каналов передачи данных и др. – на стадии функционирования; время разработки и денежных ресурсов – на стадии использования программного изделия).

Содержание технико-экономического обоснования разработки программы заключается в следующем:

- расчет технико-экономических показателей и выбор базы сравнения;

- определение трудоемкости и стоимости программного обеспечения;

- расчет цены ПО;

- расчет капитальных и эксплуатационных затрат на разработку;

- определение показателей финансово-экономической эффективности.

В общем случае единовременные затраты на создание системы рассчитываются без НДС и определяются по формуле:

К_об = К_раз + К_прог + К_изг, (22)

где К_раз - затраты на проектирование (разработку) системы, тыс.р.; К_прог- затраты на программирование, тыс.р.; К_изг - затраты на изготовление, тыс.р.

Таблица 18 Данные для расчета единовременных затрат предприятия

1	Среднемесячный оклад разработчика, тыс.руб	Зо	24
2	Коэффициент доплат к ЗП, д.ед.	Кд	0,15
3	Районнный коэф., д.ед.	Кр	0,05
4	ЕСН, д.ед.	Кесн	0,24
5	Время разработки системы, мес или час	Траз	3,88
6	Время использования ПК для разработки, час	Тпрог	768
7	Коэф. Накладных расходов, д.ед	Кн.прог	0,02
8	Годовой фонд работы ПК, час	Тпол	12600
9	Годовой фонд оплаты труда персонала обслуживающего, руб.	ЗП	288
10	Норма амортизационных отчислений ПК, д.ед.	Нпк	0,12
11	Норма амортизационных отчислений Здания, д. ед.	Нзд	0,05
12	Стоимость ПК,т.руб.	Кпк	27
13	Коэф. Накладных расходов на экспл. ПК,д.ед.	Кнэкс	0,08
14	Потребляемая мощность ПК , кВт	N	0,4
15	Стоимость кВт/час, руб.	Ц	0,557
16	Коэф. Затрат на ремонт ПК (от стоимости), д.ед.	Ктр	0,08
17	Затраты на материалы для эксплуатации ПК, р	М	1370
18	Коэф затрат на содержание ПК, д.ед.		0,1
19	Коэф. Затрат на транспортировку разработанной системы, дед.	Ктрп	0,08
20	Коэф. Затрат на монтаж и наладку, д.ед	Коб	0
21	Коэф. Рентабельности предприятия разработчика, д.ед.	r	0,25
22	НДС, де.д.	НДС	0,18
23	Единовременные затраты на создание системы автоматизации , тыс. р.	К	56312,98
24	Монтаж установка запуск, д.ед.	Кмуз	0,1
25	Коэф. Накладных расходов, д.ед.	Кнраз	0,17
26	Коэф. Интенсивного использования мощности ПК	Км	0,2
27	Коэф. Перевода ед.времени	Кч	0,01
28	Коэф. Использования оборудования, д.ед.	Кинт i	1
29	Коэф. Накладных расходов, д.ед.	Кнризг	0,05
Единовременные затраты
Коб =	76972,472

Затраты на разработку можно представить в виде:

К_раз = З_о Т_раз (1+К_д)  (1+К_р)  (1+Кесн)  (1+К_н.раз) , (23)

где З_о - месячный оклад разработчика, р.;

Т_раз - трудоемкость разработки проекта и проектной документации, чмес.;

К_д, К_р - соответственно коэффициенты доплат к заработной плате и районный, доли ед.;

Ке_сн – Единый социальный налог, доли ед. ;

К_нраз- коэффициент накладных расходов, доли ед.

Расчет затрат на проектирование системы
Краз =	163,13143

Таблица 19 Данные для расчета трудоемкости разработки

	Стадии	Трудоемкость чел./мес.
1	изучение патентов	0,1
2	Изучение литературных источников	0,1
3	Разработка технического задания	0,2
4	Разработка эскизного проекта	0,24
5	Разработка технического проекта	0,24
6	Разработка рабочего проекта	1
7	Внедрение проекта	2
	Итого	3,88

Затраты на разработку программного обеспечения можно представить в виде:

К_прог=З_о Т_прог(1+К_д)(1+К_р)(1+К_сн)(1+К_н.прог) +С_мч Т_прогК_ч, (24)

где Зо - месячный оклад программиста, тыс.р;

Т_прог– трудоемкость создания программы, мес.;

К_{н.прогр} - коэффициент накладных расходов, доли ед. ;

C_мч - стоимость машино-часа ПК, р.;

К_ч - коэффициент перевода единиц времени.

Расчет затрат на разработку ПО
Кпрог =	28414,236

Таблица 20 Перечень материалов используемых при функционировании ПК

	Наименование	Кол-во в год	Цена за ед., руб.	Стоимость, руб.
1	Гибкие магнитные диски, шт.	1	50	50
2	Раправка картриджей	3	250	750
3	Бумага, пч	4	125	500
5	Салфетки для протирки техники, уп.	2	35	70
	Итого			1370

Таблица 21 Расчет затрат на разработку на изготовление

и отладку проектируемой системы

	Наименование	Кол-во, шт.	цена заед., руб.	сумма, руб
1	Рабочее место специалиста	1	45000	45000
	Итого			45000

Затраты на электроэнергию рассчитаем по формуле:

, (25)

где Ц_эл - стоимость одного кВтч электроэнергии, р.;

N_i - мощность i-го вида оборудования, Вт;

К_{инт i} - коэффициент интенсивного использования оборудования, доли ед.;

t_i - время использования i-го вида оборудования, час;

n - количество использованных приборов, шт.

Затраты на электроэнергию
Э =	561,456

Подставив данные, получим годовые затраты на электроэнергию действующего варианта системы.

Таблица 22 Затраты на энергию

	Наименование оборудования	Потребляемая мощность	Стоимость квт/час	Время использования	Затраты на энергию
1	АРМ	0,15	0,557	20	1,671
2	Сервер	0,6	0,557	168	56,1456
	Итого				57,8166

Затраты на ремонт рассчитываются по формуле:

, (26)

где К_тр- коэффициент, учитывающий годовые затраты на ремонт, доли ед. ;

К_обi - стоимость оборудования, используемого при проверке системы на работоспособность, р. ;

n - количество единиц оборудования, шт.;

Т_примi - время использования i-го вида оборудования, год.

Затраты на ремонт
Тр = 2,16

Затраты на амортизацию используемого при изготовлении и настройке оборудования рассчитываются по формуле:

А = К_обi  Н_аi Т_примi/100

где H_ai- норма амортизации i-го вида оборудования, %.

Затраты на амортизацию
А = 3,24

Таблица 23 Амортизация оборудования

	Наименование оборудования	Балансовая стоимость	Норма амортизации	Время использования	Затраты на объект
1	АРМ	20000	0,12	20	480
2	Сервер	75000	0,12	168	15120
	Итого				15600

Накладные расходы, связанные с изготовлением и отладкой проектируемой системы, рассчитаем по формуле:

Н_ризг = Т_м  З₀  (1 + К_д)  (1 + К_р)  К_нризг. (27)

Накладные расходы
Нрэкс =	27,8208

Таблица 24 Результирующая таблица

для расчетов по статьям калькуляции

	статьи затрат	Затраты на изготовление
1	материалы	0
2	покупные комплектующие изделия	0
3	Электроэнергия	57,8166
4	Производственная ЗП	18432
5	Доплата к ЗП с учетом районного коэф.	2903,04
6	ЕСН	5120,41
8	потери от брак	0
9	Накладные расходы	1112,832
10	Налоги входящие в себестоимость	0
11	Внепроизводственные расходы	0
	Итого	27626,0982

Для обоснования эффективности системы используем метод дисконтирования. В нашем случае единовременные затраты на создание системы осуществлены за 1 год.

Со 2 года расчетного периода внедрение автоматизированной системы обеспечит экономию времени сотрудников, экономию на заработной плате, так как позволит сократить численность персонала.

Годовые эксплуатационные затраты в условиях функционирования системы могут быть определены как сумма:

С = С_эл + С_зп + С_рем + С_а , (28)

где С_эл - затраты на электроэнергию, потребляемую системой, р.;

C_зп - зарплата обслуживающего персонала с начислениями, р.;

C_рем - затраты на ремонт, р.;

C_а - затраты на амортизацию, р.

Просчитаем затраты до внедрения и после внедрения системы в таблице 25.

Вариант 1 – до внедрения

Вариант 2 – после внедрения

Таблица 25

Показатель	ва-нт	Значение
Затраты на энергию Cэл	1	9357,6
	2	561,456
Затраты на ЗП Сзпп	1	1386
	2	332,64
Затраты на ремонт спр	1	0,06735
	2	0,027
Затраты на амортизацию Са	1	0,08082
	2	0,0324
Затраты на амортизацию помещения Сз	1	0
	2	0
итого С	1	10743,74817
	2	894,1554
		9849,59277

C_эл = N  Ц_эл  Т_зад  К_инт , (29)

C_зпп = 12  З₀₃  (1 + К_пр)  (1 + К_р)  (1 + К_есн).

C_пр = (К_обор  К_пр)/100 ,

C_а = (К_обор Н_а)/100 ,

По формуле рассчитываем затраты до внедрения и после внедрения системы. Расчет эксплуатационных затрат можно вести по изменяющимся статьям затрат. В результате чего мы определяем прибыль, обеспечиваемую внедрением системы.

Таблица 26 Изменение трудоемкости выполнения работ

Вид операций	До внедрения, в часах	После внедрения, в часах	Тариф, з/п, руб.	Итого (до), руб.	Итого (после), руб.
Работа специалиста лаборанта	96	48	300	28800	14400
Работа технолога	144	72	350	50400	25200

Расчет величины чистого дисконтированного дохода целесообразно представить в таблице 27.

Таблица 27

показатель	1	2	3	4	5	6
Единовременные затраты	76972
Экономия эксплутационных затрат		9073	9073	9073	9073	9073
Амортизационные отчисления		15394,49	15394,49	15394,49	15394,49	15394,49
Налог на имущество		1231,560	923,670	615,780	307,890	7,27
Налог на прибыль		0	0	0	0	0
чистый доход		39600	39600	39600	39600	39600
Коэф дисконтирования	1	0,909	0,826	0,751	0,683	0,621
Год ЧДД		36000,00	32727,27	29752,07	27047,33	24588,48
ЧДД	-76972	-40972,00	-8244,73	21507,34	48554,67	73143,16

На основании данных таблицы 27 определим срока окупаемости проекта. Срок окупаемости капитальных вложений в рассматриваемый проект составит 3 года.

Внедрение проекта рассматриваемого в дипломной работе при его внедрении в эксплуатацию в учреждении, приведет к снижению трудозатрат, а следовательно к экономии текущих затрат. А также повлияет на эффективность работы всего предприятия в целом, а значит, вложение инвестиций в разработку данного проекта является экономически целесообразным.

Blog

К дипломному проекту на тему