А. Н. Туполева Кафедра автоматизированных систем обработки информации и управления М. П. Шлеймович, М. В. Медведев Методическое руководство

Вид материала

Руководство

Подобный материал:

• А. Н. Туполева Кафедра автоматизированных систем обработки информации и управления, 97.34kb.
• Рабочая программа по дисциплине "Организация ЭВМ и систем" для специальности 230102, 93.42kb.
• Методические указания к курсовому проектированию по дисциплине проектирование автоматизированных, 1086.71kb.
• Рабочая программа По дисциплине «Надежность, эргономика и качество асоиу» По специальности, 197.76kb.
• Рабочая программа по дисциплине: Теория информации Для специальности: 230102 Автоматизированные, 90.58kb.
• Курса, 21.08kb.
• Рабочая программа дисциплины «Архитектура ЭВМ и вычислительных сетей» для специальности, 325.46kb.
• Реферат по дисциплине «Поиск и обработка экономической информации» на тему: «Автоматизированных, 153.2kb.
• Методические указания, контрольные задания и указания на курсовой проект по дисциплине, 410.04kb.
• Методическое руководство по дипломному проектированию, 662.78kb.

Министерство образования и науки Российской Федерации


Казанский государственный технический университет

имени А.Н. Туполева

____________________________________________

Кафедра автоматизированных систем обработки информации и управления


М. П. Шлеймович, М.В. Медведев


Методическое руководство

к лабораторной работе

по основам теории управления


«Качество управления в линейной системе автоматического управления»


КАЗАНЬ 2010

Качество управления в линейной системе автоматического управления

При исследовании систем автоматического управления необходимо решать задачу обеспечения требуемых показателей качества переходного процесса: быстродействия, колебательности, перерегулирования, характеризующих точность и плавность протекания переходного процесса.

Будем считать, что САУ описывается системой дифференциальных уравнений с постоянными коэффициентами.


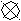
X(t)₁

ε(t)

Y(t)

-


W(t)




Рис.1.1.


1. Оценка качества регулирования в статическом режиме методом коэффициента ошибок.


Установившаяся ошибка регулирования САУ (1.1-1.4)

(s) = X(s) – Y(s)=X(s)-E(s)*W(s) (1.1)

ε(s)(1+W(s))=X(s) (1.2) ε(s)X(s)=ε(s)*(1+W(s))=X(s)) (1.3)

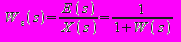(1.4)

Ошибку регулирования можно представить в виде ряда:

, (1.5)

где C₀ … C_m - коэффициенты ошибок, при этом:

С₀ = W_ε(0) - коэфф. статической и позиционной ошибки; (1.6)

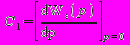- коэффициент скоростной ошибки; (1.7)

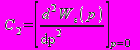коэфф. ошибки от ускорения; (1.8)

W_ε - передаточная функция замкнутой САУ.


2. Оценка качества управления в динамическом режиме по кривой переходного процесса.

Для получения оценок качества управления наиболее часто используют переходную характеристику (рис. 2.1).

К прямым оценкам качества относят:

1. длительность переходного процесса (время регулирования) t_р – минимальное время, по истечении которого выходная величина h(t) будет отклоняться от установившегося значения h_уст не более чем на допустимую погрешность ∆;
   
2. перерегулирование  - максимальное отклонение переходной характеристики h(t) от установившегося значения h_уст, выраженное в процентах:
   

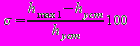, (2.1)

где h_max1 – значение первого максимума;

3. частоту колебаний ;
   
4. число колебаний за время регулирования n;
   
5. время достижения первого максимума t_max1;
   
6. время нарастания переходного процесса t_н – время, за которое переходная характеристика в первый раз достигает установившееся значение;
   
7. декремент затухания , равный отношению модулей двух смежных отклонений от установившегося значения:
   

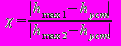. (2.2)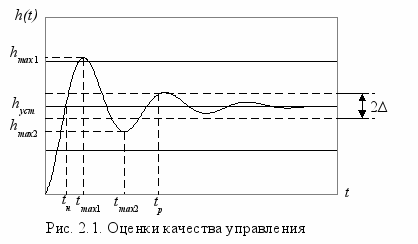




Пример 2.1. Построить временные характеристики системы с передаточной функцией (2.3).

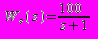, (2.3)

где 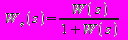(2.4)


1. 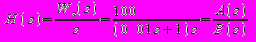. (2.5)

2. . (2.6)

3. 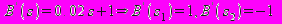. (2.7)

4. 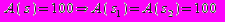. (2.8)

5. . (2.9)

6. 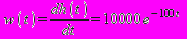. (2.10)

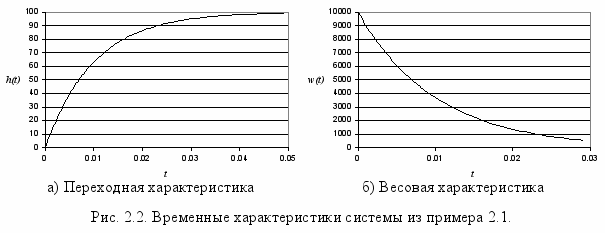Временные характеристики данной системы представлены на рис. 2.1.


Задание

Выполнить анализ качества управления в статистическом режиме методом коэффициента ошибок и в динамическом режиме по кривой переходного процесса.

Структура системы:

W(s) = 15s + 4 W(s) = 15/(10s + 3) W(s) = 15s + 7 W(s) = s + 21 W(s) = 7/(3s + 13) W(s) = 15s W(s) = 15s + 2 W(s) = 9s +14 W(s) = 15s/(3s + 1) W(s) = 8s/(2s + 3)

W(s) = 4s W(s) = 15(0.001s +1) W(s) = 1.7s + 0.1 W(s) = 0.1/(0.001s + 3) W(s) = 100(0.0001s + 1) W(s) = 100/(0.0001s + 1) W(s) = 13(0.01s + 5) W(s) = 13/(0.001s + 7) W(s) = 5s + 1 W(s) = 100/(5s + 1)

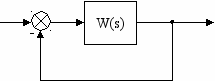
Примечание. При анализе качества управления методом коэффициентов ошибок считать, что на вход системы подается сигнал вида x(t) = at + b, a > 0, b > 0. Параметры сигнала задать самостоятельно. На одном графике отобразить исходный сигнал x(t) и ошибку (t).