Анализ результатов выполнения диагностической контрольной работы по алгебре в 9 классе (05. 04. 11)
| Вид материала | Учебник |
СодержаниеАнализ результатов выполнения заданий ДКР по I части Общие результаты выполнения ДКР Методические рекомендации |
- Анализ диагностической работы по информатике от 19. 04. 2012г. 19. 04. 2012 год, 24.31kb.
- Задания для выполнения контрольной работы студентами экономических специальностей заочного, 212.23kb.
- Общие методические указания по контрольным работам кэахд цель выполнения контрольной, 43.08kb.
- Методические указания к выполнению контрольной работы для студентов заочной формы обучения, 62.56kb.
- Варианты контрольной работы №1 по дисциплине «Оборудование ооп» Выбор варианта контрольной, 209.43kb.
- План работы: Анализ результатов контрольной работы; Изучение нового материала, 111.71kb.
- Методические рекомендации к выполнению контрольной работы для студентов заочной формы, 160.47kb.
- Методические указания к выполнению контрольной работы для студентов заочной формы обучения, 125.09kb.
- Общие методические указания по выполнению контрольной работы практика выполнения контрольной, 496.46kb.
- Методические рекомендации по выполнению контрольной работы Для выполнения данной контрольной, 113.09kb.
Анализ результатов выполнения диагностической контрольной работы по алгебре в 9 классе (05.04.11)
- Формат и особенности ДКР
- На выполнение работы отводилось 4 часа (240 минут).
- Для записи решений и ответов учащимся выдавались 4 бланка (1 бланк ответов АВ и 3 бланка ответов С).
- Работа состояла из двух частей. Первая часть содержала 18 заданий: А1 – А8 и С1 – С10. Вторая часть содержала 5 заданий: С11 – С15.
- При выполнении заданий первой части нужно было указывать только ответы. При этом:
- при выполнении заданий А1 – А8 ответы необходимо было занести в бланк ответов АВ под номером выполняемого задания. К каждому заданию А1 – А8 приведены 4 варианта ответа, из которых только один верный.
- при выполнении заданий С1 – С10 ответы необходимо занести в бланк ответов С без решения.
- время выполнения первой части ограничено - 90минут.
- По истечении 90 минут оба бланка изымались.
- Перерыв между I и II частями работы не делался.
- Вторую часть работы (задания С11 – С15) учащиеся выполняли на бланке ответов С. Это должен быть новый бланк. На этом бланке не могли быть написаны ответы к заданиям С1 – С10.
- При выполнении этой части работы в бланк ответов С нужно занести полное обоснованное решение.
- При выполнении заданий с развернутым решением (С9 – С13) все необходимые рисунки и чертежи выполнялись «от руки». Карандаш не использовался!
- Пользоваться калькуляторами и справочными таблицами не разрешалось.
-
Анализ результатов выполнения заданий ДКР по I части
Учебник
При выполнении заданий I части учащиеся должны были продемонстрировать определенную системность знаний и широту представлений. В ней проверялось не только владение базовыми алгоритмами, но и знание и понимание важнейших элементов содержания (понятий, их свойств, приемов решения задач и пр.), умение пользоваться различными математическими языками, умение применять знания к решению математических задач, не сводящихся к прямому применению алгоритмов, а также применение знаний в простейших практических ситуациях.
2.1. Содержание заданий. Результаты выполнения заданий
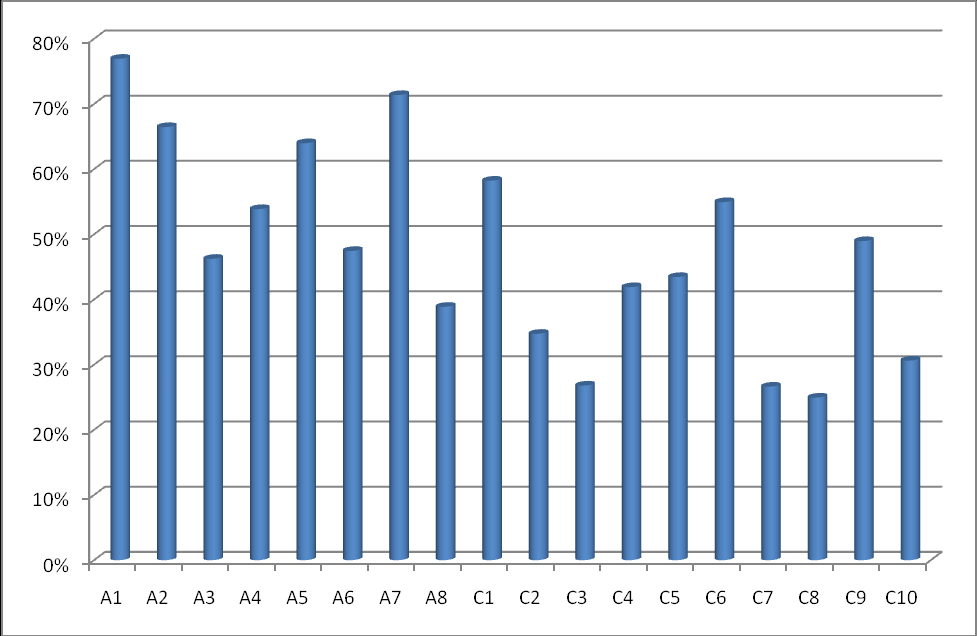
| | Обозначение задания в работе | Содержание задания | Процент правильных ответов |
| 1 | А1 | Деление чисел записанных в стандартном виде. Прикидка и оценка результатов вычислений. | 77% |
| 2 | С1 | Решение задачи на процентные отношения | 58% |
| 3 | С2 | Умножение одночленов. Преобразование выражений содержащих степени с натуральным показателем. | 35% |
| 4 | А2 | Выражение одной переменной величины через другую в указанной формуле. | 66% |
| 5 | С3 | Разложение квадратного трехчлена линейные множители на множители | 27% |
| 6 | С4 | Понятие об иррациональном числе | 42% |
| 7 | А3 | Свойства числовых неравенств | 46% |
| 8 | С5 | Чтение графиков реальной физической зависимости | 43% |
| 9 | С6 | Нахождение числа по его части | 55% |
| 10 | А4 | Решение квадратного неравенства | 54% |
| 11 | А5 | Условие принадлежности точки графику функции | 64% |
| 12 | А6 | Графическая интерпретация решения системы линейных неравенств. | 47% |
| 13 | А7 | Переход от словесной формулировки соотношения между величинами к алгебраической. Составление уравнения по условию задачи. | 71% |
| 14 | С7 | Использование графика квадратичной функции для решения неравенства | 27% |
| 15 | А8 | Использование графика арифметической прогрессии для определения ее членов. | 39% |
| 16 | С8 | Графическое решение системы нелинейных уравнений. | 25% |
| 17 | С9 | Определение вероятности события | 49% |
| 18 | С10 | Определение среднего результата измерений и медианы числового ряда | 31% |
2.2. Анализ неуспешных заданий
При выполнении заданий первой части работы, как и предыдущие годы, наибольшие затруднения у учащихся вызывают задания, решение которых требует применить умение пользоваться различными математическими языками, умение перейти от одного языка к другому, умение применять знания к решению математических задач, не сводящихся к прямому применению алгоритма. Т.е. те задачи, которые относятся к первой категории познавательной области: знание/понимание. В данной работе это прежде всего задания А3, А6,А8, С3,С7, С8.
Главная причина их неуспешного выполнения на наш взгляд , есть следствие методических «просчетов» учителя при организации учебного процесса на уроке. Основная цель урока математики – это не разучивание решений задач определенного типа, а работа по развитию мышления учащихся.
- Анализ результатов выполнения заданий ДКР по II части
3.1. Содержание заданий
| Порядковый номер задания | Обозначение задания в работе | Содержание задания |
| 19 | С11 | Преобразование числовых выражений содержащих иррациональные выражения в числителе и знаменателе дроби |
| 20 | С12 | Исследование наличия и количества корней линейного и квадратного уравнения |
| 21 | С13 | Построение графика дробно-рациональной функции. Использование графика функции для решения неравенства (графический способ) |
| 22 | С14 | Применение свойств делимости натуральных чисел для составления формулы общего члена арифметической прогрессии. Вычисление количества ее членов. |
| 23 | С15 | Решение текстовой задачи |
3.2. Результаты выполнения заданий
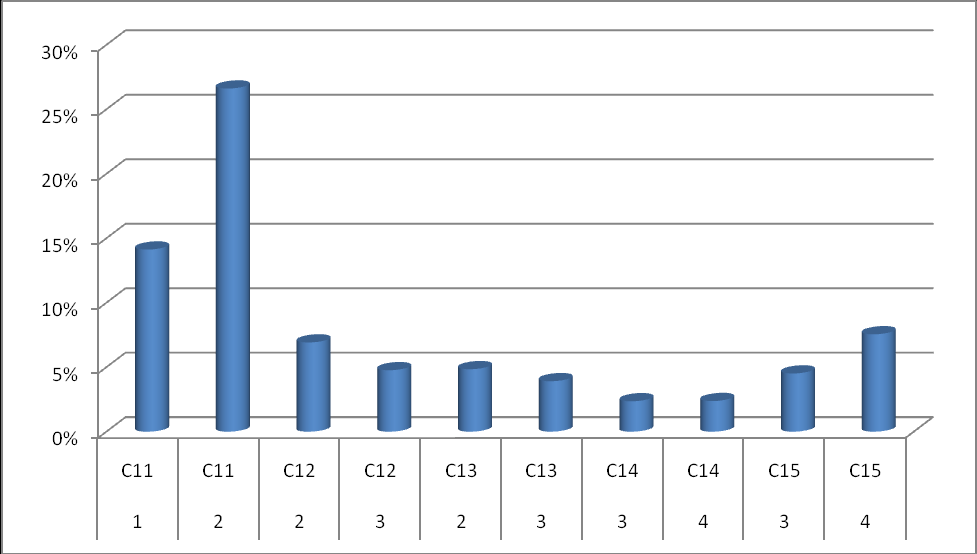
| Обозначение задания в работе | Баллы | Процент учащихся, получивших указанные баллы | |
| С11 | 1 | 14% | 41% |
| 2 | 27% | ||
| С12 | 2 | 7% | 12% |
| 3 | 5% | ||
| С13 | 2 | 5% | 9% |
| 3 | 4% | ||
| С14 | 3 | 2% | 4% |
| 4 | 2% | ||
| С15 | 3 | 5% | 13% |
3.3. Анализ выполнения II части
Задания этой части работы являются заданиями повышенного и высокого уровня сложности. Степень и качество выполнения заданий II части дают возможность дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленную часть выпускников, в частности, составляющих потенциал профильных классов. Следовательно, учитель не обязан добиваться умения их выполнять от каждого учащегося класса. Вместе с тем обращает на себя внимание тот факт, что учащиеся более или менее успешно справляются с «алгоритмической» частью этих заданий ( в том числе и учащиеся лицеев и классов с углубленным изучением математики) и весьма незначительная их часть может математически грамотно и ясно записать их решения, приводя при этом необходимые пояснения и обоснования (что является одним из важнейших критериев при оценке правильности выполнения заданий этой части работы). Это свидетельствует о том, что учителя в повседневной практике преподавания основное внимание уделяют овладению учащимися формально-оперативным алгебраическим аппаратом, пренебрегая при этом всеми другими аспектами обучения математики.
Как видно из приведенной выше таблицы и диаграммы, процент выполнения заданий этой части понижается пропорционально увеличению уровня сложности задания небольшое исключение составляет задание С15 – текстовая задача.
- Общие результаты выполнения ДКР
Таблица количества участников ДКР
| Район | Количество участников |
| Адмиралтейский | 429 |
| Василеостровский | 785 |
| Выборгский | 940 |
| Калининский | 1738 |
| Кировский | 1464 |
| Колпинский | 306 |
| Красногвардейский | 918 |
| Красносельский | 593 |
| Кронштадский | 318 |
| Курортный | 313 |
| Московский | 541 |
| Невский | 498 |
| Петроградский | 394 |
| Петродворцовый | 679 |
| Приморский | 866 |
| Пушкинский | 342 |
| Фрунзенский | 862 |
| Центральный | 483 |
| Итого | 12339 |
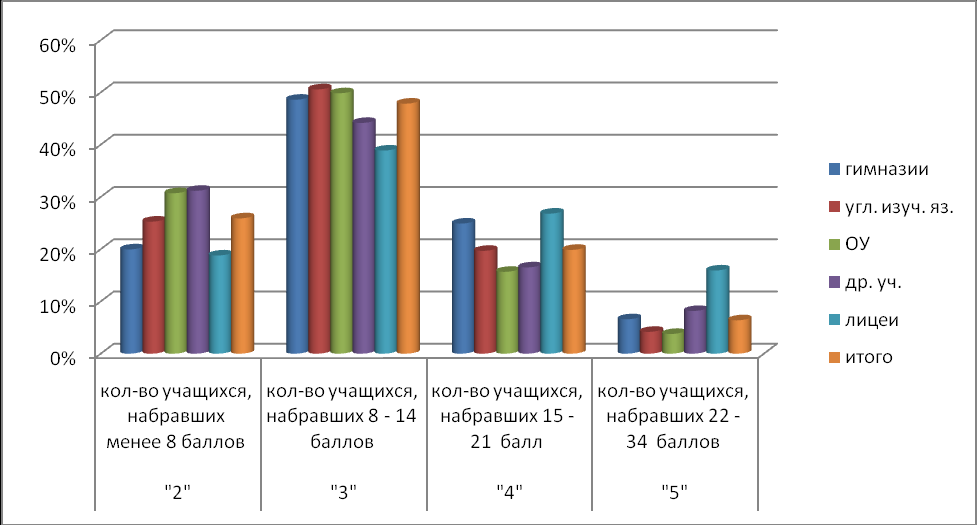
Результаты выполнения ДКР (в процентах) отражает приведенная ниже таблица.
| | гимназии | углубл | ОУ | др.уч. | лицеи | итого | |
| кол-во ОУ | 56 | 64 | 197 | 24 | 38 | 379 | |
| кол-во учащихся, выполнявших работу | 2325 | 2323 | 5305 | 539 | 1847 | 12339 | |
| | |||||||
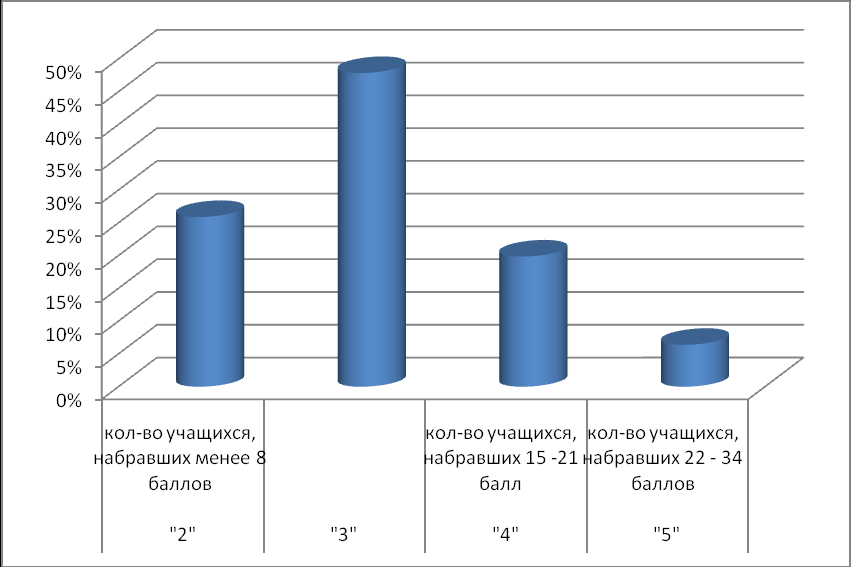
| % набравших менее 8 баллов | 20% | 25% | 31% | 31% | 19% | 26% | «2» |
| % набравших 8 - 14 баллов | 49% | 51% | 50% | 44% | 39% | 48% | «3» |
| % набравших 15 -21 балл | 25% | 20% | 16% | 17% | 27% | 20% | «4» |
| % набравших 22 - 34 баллов | 7% | 4% | 4% | 8% | 16% | 6% | «5» |
| Средний балл | 3,18 | 3,02 | 2,92 | 3,02 | 3,41 | 3,07 | |
Результаты выполнения ДКР 2011 вполне соответствуют их распределению по типам ОУ (а значит по уровню подготовки учащихся и их мотивации к обучению вообще и математике в частности).
- Методические рекомендации
До начала итоговой аттестации осталось не так много времени. На этом этапе следует заниматься не столько повторением «вообще», сколько сконцентрировать внимание на тех вопросах, которые вызывают наибольшие затруднения у учащихся. В этот период, как никогда, необходим дифференцированный подход.
При подготовке к выполнению I части работы особое внимание следует уделить формированию навыков самоконтроля, проверке ответа на правдоподобие, на критическую оценку результатов.
При подготовке к выполнению II части работы необходимо обращать внимание учащихся на точность и полноту приводимых обоснований.
В кодификаторе элементов содержания и требования к уровню подготовки обучающихся, освоивших основные общеобразовательные программы основного общего образования, для проведения в 2011 году государственной (итоговой) аттестации (в новой форме) по математике указано, что учащийся должен умет:
- моделировать практические ситуации и исследовать построенные модели с использованием аппарата алгебры.
- уметь перейти от словесной формулировки соотношений между величинами к алгебраической.
- проводить доказательные рассуждения при решении задач, выстраивать аргументацию при доказательстве, записывать математические рассуждения, доказательства.
Мы много говорим о необходимости развития у учащихся навыков устной и письменной математической речи, о необходимости формирования осознанности знаний учащихся, однако, никогда ранее при выполнении аттестационной работы эти умения и навыки никак не учитывались, не проверялись и не оценивались. Теперь же это один из важных критериев, который оказывает существенное влияние на итоговую оценку, определяющий уровень компетентности учащихся.
Немаловажную роль играет и психологическая подготовка учащихся, их собранность, настрой на успешное выполнение каждого из заданий работы. Не следует стремиться выполнить I часть работы за более короткое время. В первую очередь это касается «сильных» учащихся. Каким бы легким не казалось учащимся то или иное задание, к его выполнению следует относиться предельно серьезно. Именно поспешность наиболее часто приводит к появлению неточностей, описок и т.п., а значит, и к неверному ответу на вопрос задачи.
Старший преподаватель кафедры физико-математического образования СПбАППО, председатель предметной комиссии /Жигулев Л.А./
22.04.2010.
