1 Понятие структур данных и алгоритмов

Вид материала

Документы

Содержание 6.2.1. Основные определения 6.2.2. Логическое представление и изображение деревьев. Метод вложенных скобок

Подобный материал:

• Рабочей программы дисциплины Структуры и алгоритмы обработки данных по направлению, 21.62kb.
• А. М. Горького математико-механический факультет кафедра алгебры и геометрии Библиотека, 334.84kb.
• Д. С. Осипенко Понятие алгоритма. Примеры алгоритмов. Свойства алгоритмов. Способы, 96.46kb.
• Об использовании структур представления данных для решения возникающих задач; знать, 116.73kb.
• Программа дисциплины структуры и алгоритмы компьютерной обработки данных для специальности, 506.16kb.
• «Понятие об алгоритме. Примеры алгоритмов. Свойства алгоритмов. Типы алгоритмов, построение, 84.9kb.
• Утверждаю, 254.87kb.
• Язык описания алгоритмов начертательной геометрии adgl, 70.57kb.
• Программа дисциплины Математическое программирование Семестры, 10.84kb.
• Метод принятия решения в выборе варианта реализации алгоритмов при разнородных условиях, 70.86kb.

6.2. Деревья

6.2.1. Основные определения

Дерево - это граф, который характеризуется следующими свойствами:

• 1. Cуществует единственный элемент (узел или вершина), на который не ссылается никакой другой элемент - и который называется КОРНЕМ (рис. 6.8, 6.9 - A,G,M - корни).
  
• 2. Начиная с корня и следуя по определенной цепочке указателей, содержащихся в элементах, можно осуществить доступ к любому элементу структуры.
  
• 3. На каждый элемент, кроме корня, имеется единственная ссылка, т.е. каждый элемент адресуется единственным указателем.
  

Название "дерево" проистекает из логической эквивалентности древовидной структуры абстрактному дереву в теории графов. Линия связи между парой узлов дерева называется обычно ВЕТВЬЮ. Те узлы, которые не ссылаются ни на какие другие узлы дерева, называются ЛИСТЬЯМИ (или терминальными вершинами)(рис. 6.8, 6.9 - b,k,l,h - листья). Узел, не являющийся листом или корнем, считается промежуточным или узлом ветвления (нетерминальной или внутренней вершиной).

Для ориентированного графа число ребер, исходящих из некоторой начальной вершины V, называется ПОЛУСТЕПЕНЬЮ ИСХОДА этой вершины. Число ребер, для которых вершина V является конечной, называется ПОЛУСТЕПЕНЬЮ ЗАХОДА вершины V, а сумма полустепеней исхода и захода вершины V называется ПОЛНОЙ СТЕПЕНЬЮ этой вершины.







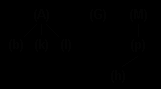
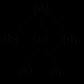
рис. 6.8. Дерево рис. 6.9. Лес

Ниже будет представлен важный класс орграфов - ориентированные деревья - и соответствующая им терминология. Деревья нужны для описания любой структуры с иерархией. Традиционные примеры таких структур: генеалогические деревья, десятичная классификация книг в библиотеках, иерархия должностей в организации, алгебраическое выражение, включающее операции, для которых предписаны определенные правила приоритета.

Ориентированное дерево - это такой ациклический орграф (ориентированный граф), у которого одна вершина, называемая корнем, имеет полустепень захода, равную 0, а остальные - полустепени захода, равные 1. Ориентированное дерево должно иметь по крайней мере одну вершину. Изолированная вершина также представляет собой ориентированное дерево.

Вершина ориентированного дерева, полустепень исхода которой равна нулю, называется КОНЦЕВОЙ (ВИСЯЧЕЙ) вершиной или ЛИСТОМ; все остальные вершины дерева называют вершинами ветвления. Длина пути от корня до некоторой вершины называется УРОВНЕМ (НОМЕРОМ ЯРУСА) этой вершины. Уровень корня ориентированного дерева равен нулю, а уровень любой другой вершины равен расстоянию (т.е. модулю разности номеров уровней вершин) между этой вершиной и корнем. Ориентированное дерево является ациклическим графом, все пути в нем элементарны.

Во многих приложениях относительный порядок следования вершин на каждом отдельном ярусе имеет определенное значение. При представлении дерева в ЭВМ такой порядок вводится автоматически, даже если он сам по себе произволен. Порядок следования вершин на некотором ярусе можно легко ввести, помечая одну вершину как первую, другую - как вторую и т.д. Вместо упорядочивания вершин можно задавать порядок на ребрах. Если в ориентированном дереве на каждом ярусе задан порядок следования вершин, то такое дерево называется УПОРЯДОЧЕННЫМ ДЕРЕВОМ.

Введем еще некоторые понятия, связанные с деревьями. На рис.6.10 показано дерево:

Узел X называется ПРЕДКОМ (или ОТЦОМ), а узлы Y и Z называются НАСЛЕДНИКАМИ (или СЫНОВЬЯМИ) их соответственно между собой называют БРАТЬЯМИ. Причем левый сын является старшим сыном, а правый - младшим. Число поддеревьев данной вершины называется СТЕПЕНЬЮ этой вершины. ( В данном примере X имеет 2 поддерева, следовательно СТЕПЕНЬ вершины X равна 2).



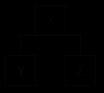
рис.6.10. Дерево

Если из дерева убрать корень и ребра, соединяющие корень с вершинами первого яруса, то получится некоторое множество несвязанных деревьев. Множество несвязанных деревьев называется ЛЕСОМ (рис. 6.9).

6.2.2. Логическое представление и изображение деревьев.

Имеется ряд способов графического изображения деревьев. Первый способ заключается в использовании для изображения поддеревьев известного метода диаграмм Венна, второй - метода вкладывающихся друг в друга скобок, третий способ - это способ, применяемый при составлении оглавлений книг. Последний способ, базирующийся на формате с нумерацией уровней, сходен с методами, используемыми в языках программирования. При применении этого формата каждой вершине приписывается числовой номер, который должен быть меньше номеров, приписанных корневым вершинам присоединенных к ней поддеревьев. Отметим, что корневые вершины всех поддереьев данной вершины должны иметь один и тот же номер.

МЕТОД ВЛОЖЕННЫХ СКОБОК

(V0(V1(V2(V5)(V6))(V3)(V4))(V7(V8)(V9(V10))))

Все эти представления демонстрируют одну и ту же структуру и поэтому эквивалентны. С помощью графа можно наглядно представить разветвляющиеся связи, которые по понятным причинам привели к общеупотребительному термину "дерево".



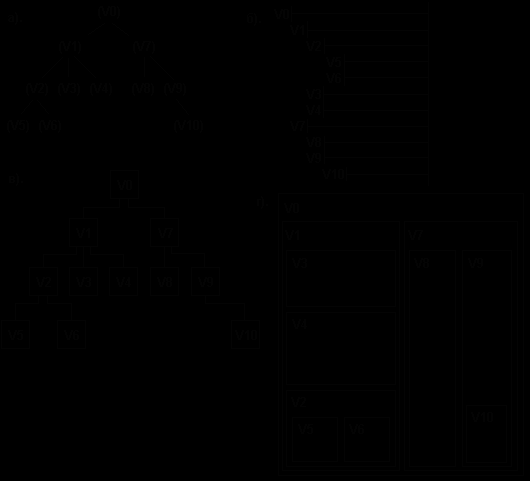
Рис.6.11. Представление дерева : а)- исходное дерево, б)- оглавление книг, в)- граф, г)- диаграмма Венна