Естествознание как комплекс наук о природе. Наука в постижении бытия

Вид материала

Документы

Содержание 1.4. Математика как специфический язык естествознания. 2.1. Познание как процесс отражения действительности 2.2. Формы познания, их соотношение. Рациональные формы 2.3. Достоверность научного знания и критерии его ограничения. Принцип фальсификации Общие модели развития науки. Роль научных революций в истории науки. Классификация моделей Прагматические модели Абстрактные модели Косвенное подобие Особенности моделей Основные типы моделей систем Если при исследовании системы не учитываются ее изменения во времени, то модель называется статической.

Подобный материал:

• Естествознание как комплекс наук о природе (естественных наук) Дифференциация наук, 216.86kb.
• 1. Понятие и определение иммунитета, 164.05kb.
• Лекция Естествознание – единая наука о природе. Основные этапы развития естествознания, 20.66kb.
• Концепция современного естествознания Глава 1: Предмет естествознания, 397.47kb.
• Программа курса «Методология и методика научного исследования» Специальность 080507, 44.29kb.
• Тематика семинарских занятий. Тема Естествознание и его место в культуре, 105.96kb.
• Программа предусматривает рассмотреть три аспекта бытия науки: • наука как познавательная, 195.42kb.
• Вопросы кандидатского экзамена по истории и философии науки, 168.1kb.
• Вопросы кандидатского экзамена по истории и философии науки, 136.8kb.
• Вопросы кандидатского экзамена по истории и философии науки, 252.02kb.

1.4. Математика как специфический язык естествознания.

Как бы то ни было, естествознание все шире использует математический аппарат для объяснения природных явлений. Можно выделить несколько направлений математизации естествознания:

• количественный анализ и количественная формулировка качественно установленных фактов, обобщений и законов конкретных наук;
  
• построение математических моделей (об этом несколько позже) и даже создание таких направлений, как математическая физика, математическая биология и т.д.;
  
• построение и анализ конкретных научных теорий, в частности их языка.
  

Рассмотрим математику как специфический язык науки, отличающийся от естественного языка, где, как правило, используют понятия, которые характеризуют определенные качества вещей и явлений (поэтому их часто называют качественными). Именно с этого начинается познание новых предметов и явлений. Следующий шаг в исследовании свойств предметов и явлений - образование сравнительных понятий, когда интенсивность какого-либо свойства отображается с помощью чисел. Наконец, когда интенсивность свойства или величины может быть измерена, т.е. представлена в виде отношения данной величины к однородной величине, взятой в качестве единицы измерения, тогда возникают количественные, или метрические, понятия. Прогресс в научном познании часто связан с введением именно количественных понятий и созданием количественного языка, которые и исторически, и логически возникают на основе языка качественных описаний. Количественный язык выступает как дальнейшее развитие, уточнение и дополнение обычного, естественного языка, опирающегося на качественные понятия. Таким образом, количественные и качественные методы исследования не исключают, а скорее дополняют друг друга. Известно, что количественные понятия и язык использовались задолго до того, как возникло экспериментальное естествознание. Однако только после появления последнего они начинают применяться вполне сознательно и систематически. Язык количественных понятий наряду с экспериментальным методом исследования впервые успешно использовал Г. Галилей.

Преимущества количественного языка математики в сравнении с естественным языком состоят в следующем:

• такой язык весьма краток и точен. Например, чтобы выразить интенсивность какого-либо свойства с помощью обычного языка, нужно несколько десятков прилагательных. Когда же для сравнения или измерения используются числа, процедура упрощается. Построив шкалу для сравнения или выбрав единицу измерения, можно все отношения между величинами перевести на точный язык чисел. С помощью математического языка (формул, уравнений, функций и других понятий) можно гораздо точнее и короче выразить количественные зависимости между самыми разнообразными свойствами и отношениями, характеризующими процессы, которые исследуются в естествознании. С этой целью используются методы математики, начиная от дифференциального и интегрального исчисления и кончая современным функциональным анализом;
  
• опираясь на крайне важные для познания законы науки, которые отображают существенные, повторяющиеся связи предметов и явлений, естествознание объясняет известные факты и предсказывает неизвестные. Здесь математический язык выполняет две функции: с помощью математического языка точно формулируются количественные закономерности, характеризующие исследуемые явления; точная формулировка законов и
  
• научных теорий на языке математики дает возможность при получении из них следствий применить богатый математический и логический аппарат.
  

Все это показывает, что в любом процессе научного познания существует тесная взаимосвязь между языком качественных описаний и количественным математическим языком. Эта взаимосвязь конкретно проявляется в сочетании и взаимодействии естественно-научных и математических методов исследования. Чем лучше мы знаем качественные особенности явлений, тем успешнее можем использовать для их анализа количественные математические методы исследования, а чем более совершенные количественные методы применяются для изучения явлений, тем полнее познаются их качественные особенности.           

2. Основы методологии науки.
   

2.1. Познание как процесс отражения действительности


Процесс отражения и воспроизведения действительности в мышлении субъекта, результатом которого является новое знание о мире, называется познанием. Непосредственные функции научного познания - описание, объяснение и предсказание процессов и явлений действительности, и это позволяет управлять поведением изучаемых объектов и создавать системы с заранее заданным поведением. Описание заключается в фиксировании результатов опыта (эксперимента или наблюдения) с помощью систем обозначения, принятых в науке. В процессе объяснения происходит раскрытие сути изучаемого объекта через постижение закона, которому подчиняется данный объект. Научное предвидение- это определение и описание на основе научных законов явлений природы и общества, которые не известны в данный момент, НО могут возникнуть или быть изучены в будущем. Важнейшей формой научного предвидения является прогнозирование - выработка суждений о состоянии какого-либо объекта или явления в будущем (например, прогноз погоды). Это вероятностное суждение о будущем строится на основе специальных научных исследований и возможно благодаря тому, что мир един, а деление на наблюдаемый и ненаблюдаемый, на изученный и неизученный мир происходит в процессе мышления. С возрастанием роли науки в жизни общества научное обоснование становится целесообразным и даже необходимым во многих сферах жизни общества, но заметим, что далеко не везде оно возможно и далеко не всегда уместно. Знания приобретаются человеком во всех формах его деятельности - в обыденной жизни, в политике, экономике, искусстве, инженерном деле, однако здесь получение знания не является главной целью. Так, искусство предназначено для создания эстетических ценностей, где на первый план выходит отношение художника к реальности, преломленной через его внутренний мир; экономические реформы оцениваются прежде всего с точки зрения их эффективности и практического результата; продуктом инженерной деятельности является проект, разработка новой технологии, изобретение, которые оцениваются с позиции их практической пользы, оптимального использования ресурсов, расширения возможностей преобразования реальности. Одна из конечных целей научного познания - быть воплощенным на практике, т.е. в целенаправленной деятельности людей по освоению и преобразованию действительности. Часто эта деятельность связана с развитием техники - совокупности искусственных органов, средств (прежде всего орудий труда), предназначенных для усиления и расширения возможностей человека по преобразованию природы и использования в этом процессе ее сил и закономерностей. Основное назначение техники - облегчение и повышение эффективности трудовых усилий человека, освобождение его от работы в опасных условиях, улучшение его жизни в целом.


2.2. Формы познания, их соотношение.


Познание действительности происходит в трех основных формах - чувственной, рациональной и иррациональной. Чувственное познание включает ощущение, восприятие и представление. С помощью ощущений в сознании человека происходит отражение отдельных свойств внешних предметов и внутренних

состояний организма при непосредственном воздействии материальных раздражителей. Восприятие отвечает за отражение в сознании человека внешних предметов и ориентации в окружающем мире. Представления- возникающие в сознании человека образы предметов и явлений внешнего мира или их свойств, которые человек когда-то воспринимал или ощущал.

Рациональные формы познания можно свести к понятиям, суждениям и умозаключениям. Понятия- это форма мышления, отражающая предметы в их существенных признаках. Формы мышления, в которых человек выражает вещь в ее связях и отношениях, называются суждением. Под умозаключением понимается такая форма мышления, посредством которой из одного или нескольких суждений выводится новое суждение.

Среди иррациональных форм познания особое значение для науки имеет интуиция - постижение истины путем непосредственного ее усмотрения без обоснования с помощью доказательства. Иными словами, интуиция может быть определена как субъективная способность выходить за пределы опыта путем мысленного <озарения> или обобщения в образной форме непознанных связей, закономерностей.

Еще на заре истории человечества существовало обыденно-практическое познание, поставлявшее элементарные сведения о природе, о самих людях, условиях их жизни, общении, социальных связях и т.п. Основой такого познания был опыт повседневной жизни, практики людей. При этом большое значение имело мифологическое познание. В рамках мифологии вырабатывались определенные знания о природе, космосе, о самих людях и т.д.

Мифология - основа художественно-образной формы познания, которая в дальнейшем получила развитое выражение в искусстве, хотя оно не решает познавательные задачи, но содержит в себе достаточно мощный познавательный потенциал. Одной из исторически первых форм познания является религиозное познание. Особенности его определяются Тем, что оно обусловлено непосредственной эмоциональной формой отношения людей к господствующим над ними земными силами (природными и социальными).


2.3. Достоверность научного знания и критерии его ограничения.


Важной проблемой является определение научности знания и отграничения его от других видов знания. Повторим, что понятие <истинное> не эквивалентно понятию <научное>. Существует совокупность критериев научности, используя которые можно отличить научное знание от ненаучного. Так, современные физики не обсуждают возможность построения вечного двигателя, а астрономы не относятся всерьез к работам по астрологии. Вместе с тем в теоретических журналах публикуется множество статей, где представлены научные гипотезы - предположительное суждение о связи явлений.

Методология науки для целей отграничения научного знания от ненаучного использует несколько принципов. Наиболее часто говорят о трех из них - рациональности, верификации и фальсификации. Принцип рациональности является основным средством обоснованности знания; он как бы ориентирует исследователя на определенные нормы и идеалы научности, а также эталоны знаний.

Согласно принципу верификации, некое понятие или суждение имеет значение, если оно сводимо к непосредственному опыту или высказыванию о нем, т.е. эмпирически проверяемо. Различают непосредственную верификацию, когда происходит прямая проверка утверждений, формулирующих данные наблюдения и эксперимента, икосвенную верификацию, когда устанавливаются логические отношения между косвенно верифицируемыми утверждениями. Использование принципа верификации дает возможность разделить научное и ненаучное знания, но он плохо справляется с поставленной перед ним задачей, если некоторая система представлений построена таким образом, что практически любой наблюдаемый факт можно объяснить в его пользу (религия, идеология, астрология и т.д.).

Принцип фальсификации предложил известный методолог науки XX в. К. Поппер; суть этого принципа в том, что критерием научного статуса теории является ее фальсифйци-руемость, или опровержимость, т.е. знание приобретает уровень научного только в том случае, если оно в принципе опровержимо. По представлениям Поппера, эксперименты, направленные на попытку опровергнуть некую теорию, наиболее эффективно подтверждают ее истинность и научность. Так, если все известные вам вороны имеют темный окрас, то направьте, следуя этому принципу, свои поиски не на отыскание еще одной темной вороны, а поищите среди них белую ворону. Важность принципа фальсификации обусловлена следующим. Несложно получить подтверждения, или верификации, почти для каждой теории, если искать только подтверждения. По мнению Поппера, каждая <хорошая> научная теория является некоторым запрещением - она <запрещает> появление определенных событий. Чем больше теория запрещает, тем она лучше. Теория, не опровержимая никаким мыслимым событием, является ненаучной; можно сказать, что неопровержимость представляет собой не достоинство теории, а ее порок. Каждая настоящая проверка теории является попыткой ее фальсифицировать (опровергнуть).

Зачастую ненаучное знание пытаются выдать за научное и представляют в наукообразной форме. Сегодня распространено мнение о том, что современная наука консервативна и ограниченна, поскольку не признает так называемые нетрадиционные, паранаучные концепции - астрологию, парапсихологию, уфологию и т.д. Эти концепции появились не в наше время, а сотни и тысячи лет назад, однако до сих пор соответствующие исследования не считаются научными, так как не дали достоверных, научно установленных фактов. А наука не может наделить статусом научности те исследования, которые не являются обоснованными. Широко известно высказывание по этому поводу Ф. Бэкона: <...правильно ответил тот, который, когда ему показали выставленное в храме изображение спасшихся от кораблекрушения принесением обета и при этом добивались ответа, признает ли теперь он могущество богов, спросил в свою очередь: <А где изображение тех, кто погиб после того, как принес обет?> Таково основание почти всех суеверий - в астрологии, в сновидениях, в поверьях, в предсказаниях и т.п. Люди, услаждающие себя подобного рода суетой, отмечают то событие, которое исполнилось, и без внимания проходят мимо того, которое обмануло, хотя последнее бывает гораздо чаще>. Эти паранаучные концепции не приняты научным сообществом, поскольку с точки зрения науки они не пополняют наше знание о действительности.

4. Общие модели развития науки. Роль научных революций в истории науки.
   

Понятие модели и моделирования

Одна из характерных особенностей современного естествознания - его модельный характер, т.е. все объекты, явления и процессы описываются с помощью моделей. В определенном смысле расширение границ естествознания можно представить как построение более подходящих и совершенных моделей природы. Модельный характер естествознания связан и с тем, что значимость того или иного факта можно определить, лишь опираясь на какую-либо модель.

Понятие модели стало пониматься широко лишь в XX в. Вначале модель стала осознаваться как нечто универсальное в научных дисциплинах информационного, кибернетического, системного направлений, а позднее эта идея распространилась на всю науку. При этом понятие абстрактной модели не сводится к математическим моделям, а относится к любым знаниям и представлениям о мире [18, 20, 22, 30, 33].

Под моделью будем понимать вещественный или мысленно представляемый аналог определенного оригинала, подобный ему в существенных для конкретного исследования чертах. По сути модель является неким <заместителем> оригинала в познании и практике. Основные функции моделей - фиксация знаний и получение информации. Они служат для хранения и расширения знания или, как иногда говорят, информации об оригинале, конструирования оригинала, преобразования и управления им.

Моделированием называется исследование каких-либо явлений, процессов или систем путем построения и изучения их моделей, а также использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.

Моделирование - одна из основных категорий теории познания. На идее моделирования по существу базируется любой метод научного исследования.

Моделирование является важным этапом целенаправленной деятельности, так как она ориентирована на реализацию образа желаемого будущего, т.е. модели состояния. Например, земледелец возделывает почву для того, чтобы произвести продукты питания; студент учится для того, чтобы приобрести профессию; ученые изучают природу для того, чтобы получить знания об окружающем мире. Любая деятельность осуществляется по определенному плану (алгоритму), который является образом будущей деятельности, т.е. ее моделью. При этом приходится оценивать текущий результат предыдущих действий и выбирать следующий шаг из многих возможных, в связи с чем необходимо сравнивать последствия всех возможных шагов, не выполняя их реально, другими словами, изучать их на модели. Кроме того, сама модель является целевым отображением, причем не самого по себе объекта-оригинала, а того, что в нем нас интересует, т.е. то, что соответствует поставленной цели. Поскольку модель - это целевое отображение, можно говорить о множественности моделей одного и того же объекта: для разных целей, как правило, требуются разные модели.

Классификация моделей

В зависимости от направленности моделирования (теоретическая или практическая) модели можно разделить на познавательные и прагматические [22]. Познавательные модели являются формой организации и представления знаний, средством соединения новых знаний с имеющимися. Поэтому при обнаружении расхождения между моделью и реальностью встает задача устранения этого расхождения путем изменения модели, так как познавательная деятельность ориентирована в основном на приближение модели к реальности, которую модель отображает. Примером здесь могут служить все усложняющиеся модели пространства и времени в естествознании.

Прагматические модели являются средством управления и средством организации практических действий, способом представления образцовых действий или их результата. При их использовании в случае обнаружения расхождений между моделью и реальностью усилия направляют на изменение реаль-

ности так, чтобы приблизить реальность к модели. Прагматические модели носят нормативный характер, выполняя функцию стандарта, образца, под которые <подгоняются> деятельность и ее результаты. Прагматические модели - это планы, алгоритмы и программы действий (например, по преобразованию ландшафта какой-либо территории) и т.д. Следовательно, познавательные модели стремятся отражать существующее, а прагматические - желаемое.

Модели также можно разделить на статические - модели конкретного состояния интересующего нас объекта - и динамические - когда возникает необходимость в отображении процесса изменений состояния. Например, в одних случаях нужны модели некоторого ландшафта в некоторый момент времени, а в других - модель сезонной смены его состояний; можно описать структуру кристалла алмаза, а можно рассмотреть процесс его формирования; можно характеризовать анатомию человеческого организма или построить модель его функционирования или развития.

Наибольшее распространение получила классификация моделей на абстрактные (мысленные, идеальные) и материальные (реальные, вещественные) в зависимости от способа их воплощения или реализации или на основании использования того или иного способа передачи информации, поскольку в распоряжении человека, создающего модель, имеются средства самого сознания и средства окружающего материального мира [30, 33].

Абстрактные модели - идеальные конструкции, построенные средствами мышления, сознания. Для человеческого мозга важную роль играют неязыковые формы мышления: эмоции, бессознательное, интуиция, озарение, образное мышление, подсознание и т.п. К абстрактным моделям относятся лингвистические конструкции - продукт мышления, готовый или почти готовый для передачи другим носителям языка. Естественные языки являются универсальным средством построения абстрактных моделей, поскольку на них можно говорить практически обо всем, и, кроме того, языковые модели обладают неоднозначностью. Многозначность слов (например, <мало>, <много>, <несколько>) наряду с многовариантностью их возможных соединений во фразы позволяет отобразить любую

ситуацию с достаточной для обычных практических целей точностью. Для ситуаций, когда приблизительность естественного языка становится недостатком, вырабатывается специфический язык. Например, у северных народов имеется несколько десятков разных слов, обозначающих снег в различных состояниях; языковые модели различных естественно-научных отраслей более точны и содержат больше информации, чем естественные языки. Новые знания аккумулируются в новых моделях, и если старых языковых средств для их построения не хватает, то возникают еще более специализированные языки. Одним из специальных и достаточно универсальных языков науки является математика.

В общем случае мысленные модели, используемые в естествознании, можно разделить на образные, образно-знаковые и знаковые модели. К образным моделям относятся неформализованные мысленные представления, гипотетические построения, разного рода модели-аналогии и прочие модельные представления; например, утверждая, что Земля похожа на шар, мы выстраиваем образную модель; в более сложном виде -это словесное описание некоторой гипотезы, теории, концепции или парадигмы. Образно-знаковые модели - разного рода схемы, графы, чертежи, графики - широко распространены в естествознании; так, в науках о Земле и астрономии большое значение имеет такой вид образно-знаковых моделей, как карты. Знаковыми моделями называют определенным образом интерпретированные системы. Наиболее важны в этой группе математические модели.

Материальные (реальные, вещественные) модели - некоторая материальная конструкция. Чтобы она могла быть отображением, т.е. замещала в каком-то отношении оригинал, между оригиналом и моделью должно быть установлено отношение схожести, подобия. В рамках материальных моделей по характеру подобия выделяют модели, построенные на принципе прямого и косвенного подобия; иногда выделяют модели условного подобия.

К построенным на основе прямого подобия относят пространственно и физически подобные модели. Пространственно подобные модели геометрически подобны оригиналу. Языком пространственно подобных моделей передаются наи-

более общие черты формы объекта и соотношения определенных его частей. Например, фотографии, макет рельефа местности, масштабированные модели самолетов или гидротехнических сооружений, макеты зданий, шаблоны и т.п. Физически подобные модели обладают механическим, динамическим, кинематическим и другими видами подобия с оригиналом. Эти модели широко применяются во многих отраслях естествознания. Так, с их помощью изучают на небольших лабораторных установках деформации, происходящие в земной коре, формирование долин крупных рек, влияние еще не построенных гидроэлектростанций на окружающую среду и т.д.

Прямое подобие (геометрически и физически подобные модели) связано с проблемой переноса результатов моделирования на оригинал. Например, при изучении поведения русла реки на уменьшенной модели часть условий эксперимента можно привести в соответствие с натурой, изменяя масштабы модели (скорость течения, глубина потока, морфология русла), а часть условий (вязкость и плотность воды, сила тяготения, определяющие свойства волн, и т.д.) не может быть масштабирована. Задачами пересчета данных модельного эксперимента на реальные условия занимается теория подобия, которая позволяет перейти с использованием коэффициентов подобия от оригинала к модели и наоборот.

Косвенное подобие между оригиналом и моделью - аналогия - проявляется в совпадении или достаточной близости их абстрактных моделей и используется в практике реального моделирования. Наиболее известна электромеханическая аналогия, основанная на том, что некоторые закономерности электрических и механических процессов описываются одинаковыми дифференциальными уравнениями, различающимися лишь физической интерпретацией переменных, входящих в эти уравнения. Поэтому можно не только заменить неудобное и громоздкое экспериментирование с механической конструкцией на простые опыты с электрической схемой, перепробовать множество вариантов, не переделывая конструкцию, но и проверить на модели варианты, в механике пока не осуществимые (например, с произвольным и непрерывным изменением масс, длин и т.д.). Роль моделей, обладающих косвенным подобием оригиналу, очень велика. Например, часы являются

аналогом времени; подопытные животные у медиков - аналоги человеческого организма; автопилот - аналог летчика; электрический ток в подходящих цепях может моделировать течение воды в водоносном горизонте или в русле реки, а также транспортные потоки, перенос информации в сетях связи и т.д.

Модели условного подобия основаны на том, что подобие оригиналу устанавливается в результате соглашения. К ним причисляют различные географические карты и планы (модели местности), рабочие чертежи (модели будущей продукции), разнообразные сигналы (модели сообщений), деньги (модель стоимости), удостоверения личности (официальная модель владельца) и т.д. Данные модели являются вещественной формой, в которой абстрактные модели могут передаваться от одного человека к другому, храниться до момента их использования на основе соглашения о том, какое именно состояние реального объекта ставится в соответствие конкретной абстрактной модели. Обычно эти соглашения формулируются в виде совокупности правил построения моделей условного подобия и правил пользования ими. (Заметим, что выше эти модели мы определяли как мысленные образно-знаковые. Это подчеркивает условность рассматриваемой классификации, а также широту охвата и многоплановость модельных представлений.)

Особенности моделей

Для того чтобы модель отвечала своему назначению, необходимо существование условий, обеспечивающих ее функционирование. Так, географическую карту можно понять, только зная значения тех условных обозначений, которые на нее нанесены; древнеегипетская клинопись не могла быть прочитана, пока не был найден камень, на котором текст был изображен и на забытом древнеегипетском языке, и на древнегреческом. Следовательно, для реализации своих модельных функций модель должна быть согласована со средой, в которой ей предстоит функционировать.

Главными различиями между моделью и действительностью являются конечность, упрощенность и приближенность мо-

дели [22]. Так, реальный мир бесконечен в своих проявлениях и связях. Однако бесконечный мир необходимо познавать конечными средствами, имеющимися в распоряжении человека. Это возможно именно в результате построения моделей. Так, А. Розенблют и Н. Винер отмечали, что частные модели являются единственным средством, выработанным наукой для понимания мира. Конечность мысленных моделей выражается в том, что они наделяются строго фиксированным количеством свойств. В вещественных моделях из множества свойств объекта-модели выбираются и используются лишь некоторые свойства, подобные свойствам объекта-оригинала.

Конечность моделей делает неизбежными их упрощенность и приближенность. Как правило, для достижения цели оказывается вполне достаточным неполное, упрощенное отображение действительности. Степень упрощения зависит от целей моделирования. Упрощение является важным средством для выявления главных эффектов в исследуемом явлении. Это видно на примере таких моделей, как идеальный газ, непоглощающее зеркало, абсолютно черное тело, математический маятник и т.д. Уровень упрощения обусловливается также возможностью оперирования с моделями. Так, одно дело проводить моделирование с использованием логарифмической линейки, а другое - с помощью компьютера. Более того, давно замечено, что из двух моделей, с одинаковой точностью описывающих некоторое явление, более простая будет и более успешной. Например, геоцентрическая модель Птолемея позволяла с достаточной точностью рассчитать движения планет, предсказать затмения Солнца, но требовала расчетов по очень громоздким формулам с переплетением многочисленных <циклов>. На смену геоцентрической системе пришла более простая и изящная гелиоцентрическая система Н. Коперника.

Приближенность моделей в отображении действительности также является неотъемлемым свойством модели. Так, абсолютно точной картой страны будет только сама эта страна, а абсолютно точной моделью атома может быть сам атом. Приемлемое различие определяется целью моделирования. Так, точность наручных часов обычно достаточна для повседневных целей и недостаточна для многих других целей, в том числе научных.

Модель, с помощью которой достигается поставленная цель, должна быть адекватна этой цели, т.е. требования полноты, точности и истинности должны выполняться не вообще, а лишь в той мере, которая достаточна для достижения цели. Например, геоцентрическая модель Птолемея была адекватной в смысле точности описания движения планет и не лишена истинности: относительно Земли Солнце и планеты действительно движутся; шаман, объясняющий свое успешное врачевание силами духов, предлагает адекватную, но ложную модель. В ряде случаев удается ввести меру адекватности модели, т.е. указать способ сравнения моделей по степени успешности достижения цели с их помощью. В таких случаях говорят об идентификации модели (о нахождении в заданном классе моделей наиболее адекватной), об исследовании чувствительности и устойчивости моделей (о зависимости меры адекватности модели от ее точности), об адаптации моделей (подстройке параметров модели с целью повышения адекватности) и т.п.

Заметим, что об истинности, правильности или ложности модели самой по себе говорить бессмысленно. Степень истинности выявляется лишь в практическом соотнесении модели с отображаемой ею натурой, причем изменение условий, в которых ведется сравнение, весьма значимо влияет на его результат и может привести к существованию двух противоречивых, но одинаково истинных моделей одного объекта. Примером этого могут являться волновая и корпускулярная модели света или электрона; эти модели различны, противоположны и истинны, но каждая в своих условиях.

Любая модель явно или неявно содержит условия своей истинности, и одна из опасностей практики моделирования состоит в применении модели без проверки выполнения этих условий. Например, при обработке экспериментальных данных часто употребляют статистические процедуры, не проверяя условий их применимости (скажем, нормальности или независимости). Когда это делается вынужденно (не всякое условие возможно проверить), к полученным результатам должно быть осторожное, условное отношение. Такие ситуации выдвинули перед исследователями проблему создания моделей, применимость которых сохраняется в некотором диапазоне условий.

Основные типы моделей систем

При изучении систем используют модели <черного>, <белого> и <серого> ящика. Систему представляют как <черный ящик>, если неизвестно внутреннее строение самой системы; ее поведение и функционирование изучается по входному и выходному сигналам. При изучении системы как <белого ящика>, наоборот, известны все элементы и их взаимосвязи. Систему рассматривают как <серый ящик>, когда что-то из внутреннего строения объекта известно, а что-то остается неизвестным, например модель состава системы с неизвестной структурой или, наоборот, модель структуры с неизвестным составом.

В рамках модели <черного ящика> внутреннее устройство системы изображают в виде непрозрачного ящика, выделенного из окружающей среды (рис. 4.1). Эта модель отражает два важных свойства системы - целостность и обособленность от среды [22]. Система не является полностью изолированной от среды, она связана со средой и с помощью этих связей взаимодействует с ней (входы и выходы системы). В модели <черного ящика> отсутствуют сведения о внутреннем содержании системы, а задаются, фиксируются и перечисляются только входные и выходные связи системы со средой. В одних случаях достаточно содержательного словесного описания входов и выходов; тогда модель <черного ящика> является просто их списком. В других случаях требуется количественное описание некоторых или всех входов и выходов с заданием двух множеств Хя У входных и выходных переменных.



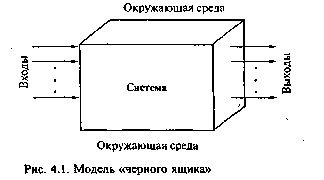
Модель <черного ящика> в ряде случаев является единственно применимой при изучении систем. Например, при исследовании психики человека или влияния лекарства на живой организм ученый лишен возможности вмешательства в систему иначе, как только через ее входы, и делает выводы лишь на основании наблюдения за ее выходами. Часто приходится ограничиваться моделью <черного ящика> в связи с отсутствием данных о внутреннем устройстве системы. Например, мы не знаем, как <устроен> электрон, но знаем, как он взаимодействует с электрическими и магнитными полями, с гравитационным полем. Это и есть описание электрона на уровне модели <черного ящика>.

Для решения вопросов, касающихся внутреннего устройства системы, недостаточно только модели <черного ящика> -необходимы более развитые модели. Например, любая система внутренне неоднородна, что позволяет различать составные части самой системы, причем некоторые части системы в свою очередь могут быть разбиты на составные части и т.д. Части системы, которые рассматриваются как неделимые, называют элементами, а части системы, состоящие более чем из одного элемента, - подсистемами. В результате получается модель состава системы, которая описывает, из каких подсистем и элементов состоит система (рис. 4.2) [22].

Для того чтобы составить представление о свойствах изучаемого объекта, часто бывает необходимо выявить определенные связи (отношения) между элементами. Совокупность связей элементов друг с другом, обеспечивающих целостность системы, называют ее структурой. Модель структуры в простейшем виде представляет собой список существенных для решения конкретной задачи отношений. Так, при расчете механизма не учитываются силы взаимного притяжения его деталей, хотя, согласно закону всемирного тяготения, такие силы объективно существуют; в то же время вес деталей (т.е. сила их притяжения к Земле) учитывается обязательно.

Поскольку все структурные схемы имеют много общего, возможно абстрагирование от их содержательной стороны и соответственно построение схем, в которых обозначены только элементы и связи между ними, а также (в случае необходимости) разница между элементами и между связями. Такая

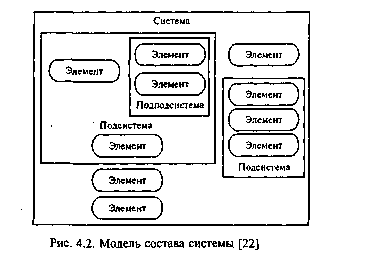
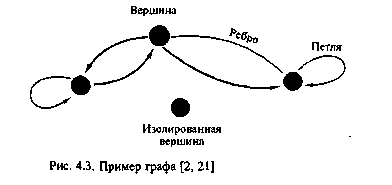
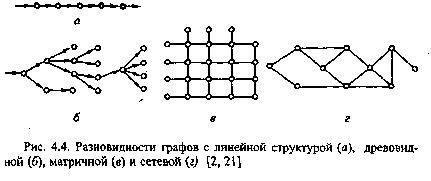
схема называется графом. Граф (рис. 4.3) состоит из обозначений элементов произвольной природы - вершин и обозначений связей между ними - ребер (дуг). Если необходимо отразить несимметричность некоторых связей, линию, изображающую ребро, снабжают стрелкой. Если направления связей не обозначаются, граф называют неориентированным, при наличии стрелок - ориентированным (полностью или частично). Любая пара вершин может быть соединена с любым количеством ребер; вершина может быть соединена сама с собой (тогда ребро называют петлей). Если в графе требуется отразить другие различия между элементами или связями, то либо приписывают разным ребрам различные веса (взвешенные графы), либо раскрашивают вершины или ребра (раскрашенные графы).

Графы могут изображать любые структуры, в том числе в различных областях естествознания. Так, при анализе природных систем часто используют линейные, древовидные (иерархические), матричные и сетевые структуры (рис. 4.4). Например, в виде древовидного графа можно изобразить речной бассейн и изучать соотношение притоков и главного русла.

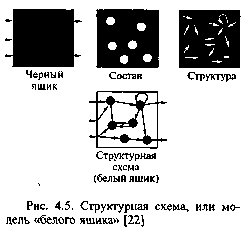
Если соединить модели <черного ящика>, состава и структуры, то образуется модель, которую часто называют <белый (прозрачный) ящик> (рис. 4.5). В <белом ящике> указываются все элементы системы, все связи между элементами внутри системы и связи определенных элементов с окружающей средой (входы и выходы системы). Такие модели часто называют структурными схемами системы.

Если при исследовании системы не учитываются ее изменения во времени, то модель называется статической. Чтобы понять и описать, как система работает (функционирует) и что



происходит с ней самой и с окружающей средой в ходе ее развития, нужны такие модели, которые отражают поведение систем, описывают происходящие с течением времени изменения, последовательность этапов, операций, действий, причинно-следственные связи. Модели, отображающие изменения в системах в течение времени, называются динамическими.

Разработано большое количество динамических моделей, описывающих процессы с различной степенью детальности: от самого общего понятия динамики, движения вообще, до формальных математических моделей конкретных процессов типа уравнений движения в механике или волновых уравнений в теории поля.

Обычно говорят о двух типах динамики системы: функционировании, т.е. устойчивой последовательности постоянно действующих процессов в системах, обеспечивающей сохранение того или иного характерного для значительного отрезка времени состояния этой системы, и развитии - необратимом, направленном, закономерном изменении системы, которое может привести к смене структуры системы. Типы динамических моделей такие же, как и статических, но элементы этих моделей имеют временной характер. Так, динамический вариант <черного ящика> содержит указания о начальном (<вход>) и конечном (<выход>) состояниях системы; модели состава соответствует перечень этапов в некоторой упорядоченной последовательности действий; динамический вариант <белого ящика> - подробное описание происходящего или планируемого процесса.