Мичио каку параллельные миры «сосриЯ» 2 0 0 8 Об устройстве мироздания, высших измерениях и булушем Космоса
| Вид материала | Документы |
СодержаниеПочему струны? Это единственный вид симметрии, которыйПозволяет менять местами все известные физикам субатомные части-цы. Загадка супергравитации |
- Мичио каку параллельные миры «софия» 2 0 0 8 Об устройстве мироздания, высших измерениях, 5404.28kb.
- Michio kaku parallel worlds, 5399.45kb.
- Параллельные миры, 862.52kb.
- Первая. Появление богини среди людей глава вторая, 5073.31kb.
- Питейная субстанция, 184.42kb.
- Строение мироздания , 814.95kb.
- «Удивительное путешествие в параллельные миры», 20.4kb.
- С. Э. Воронин Тайны мироздания в современной науке и религии, 1366.15kb.
- Параллельные миры, 127.57kb.
- «Химия космоса», 282.27kb.
Почему струны?
Хотя все предыдущие попытки построить единую теорию поля с
треском провалились, струнная теория до сих пор выдержала все
испытания. В сущности, ей нет равных. Существуют две причины, по
которым струнная теория преуспела там, где все остальные теории
потерпели поражение.
Во-первых, будучи основанной на протяженном предмете (стру-
не), струнная теория избегает многих отклонений, связанных с
точечными частицами. Как заметил Ньютон, гравитационное взаи-
модействие, окружающее точечную частицу, при приближении к ней
тановится бесконечным. (В знаменитом законе обратных квадратов
*1ыотона гравитационное взаимодействие увеличивается пропорци-
онально зависимости 1/г2, так что оно стремится к бесконечности,
когда мы приближаемся к точечной частице; то есть когда г стремит-
ся к нулю, гравитационное взаимодействие возрастает и стремится к
/0, что представляет собой бесконечность.)
. Даже в квантовой теории эта сила остается бесконечной, если мы
гриблизимся к квантовой точечной частице. За многие десятилетия
|>ейнман и другие ученые создали ряд хитрых правил, с помощью
соторых эти и многие другие противоречия можно было замести
юд ковер. Но для того, чтобы исключить все бесконечности в кван-
товой теории гравитации, недостаточно даже мешка ухищрений,
собранного Фейнманом. Проблема в том, что точечные частицы бес-
конечно малы, а это означает, что их силы и энергии потенциально
5есконечны.
i Но при внимательном рассмотрении струнной теории мы увидим,
гго есть два способа, при помощи которых мы можем избавиться от
»тих противоречий. Первый способ исходит из топологии струн, а
(гторой из-за своей симметрии называется суперсимметрией.
\ Топология струнной теории носит совершенно другой характер,
щем топология точечных частиц, а отсюда различны и возникающие
противоречия. (Грубо говоря, поскольку струна обладает конечной
длиной, это означает, что силы не стремятся к бесконечности при
приближении к струне. Рядом со струной силы возрастают про-
порционально зависимости 1 /L2, где L — это длина струны, соиз-
меримая с длинной Планка, порядка 10"33 см. Эта длина L позволяет
ртсечь все противоречия.) Поскольку струна не является точечной
яастицей, обладая определенным размером, можно показать, что
противоречия «размазаны» вдоль всей струны, и отсюда все физи-
ческие величины становятся конечными.
ч Хотя интуитивно кажется совершенно очевидным, что все про-
тиворечия струнной теории «размазаны» и потому конечны, точное
математическое выражение этого факта довольно сложно и пред-
ставлено «эллиптической модулярной функцией», одной из самых
странных функций математики. Ее история настолько захватывающа,
Что ей даже довелось играть ключевую роль в одном из голливудских
|фильмов. «Умница Уилл Хантинг» — это история о неотесанном
пареньке из рабочей семьи с окраин Кембриджа (его играл Мэтт
Дэймон), который демонстрировал потрясающие способности к
математике.
В сущности, фильм «Умница Уилл Хантинг» основан на жизни
Сринивазы Рамануджана, величайшего математического гения два-
дцатого столетия. Он вырос в бедности и изоляции от основных на-
учных достижений возле Мадраса в Индии на рубеже XIX и XX веков.
Поскольку юноша жил в условиях оторванности от научного мира,
ему пришлось до многого доходить самому, основываясь на европей-
ской математике XIX века. Его карьера была подобна взрыву сверхно-
вой, мимолетно осветившей небеса его математической гениальнос-
тью. Его смерть была трагична: он умер от туберкулеза в 1920 году в
возрасте 37 лет. Подобно Мэтту Дэймону из фильма «Умница Уилл
Хантинг», Рамануджан грезил математическими уравнениями, в
данном случае эллиптической модулярной функцией: написанная
для двадцати четырех измерений, она обладает причудливыми, но
красивыми математическими свойствами. Математики и по сей день
пытаются расшифровать «утерянные записи Рамануджана», обна-
руженные после его смерти. Оглядываясь на работу Рамануджана,
мы видим, что ее можно обобщить и свести к восьми измерениям, ко-
торые напрямую применимы к струнной теории. Физики добавляют
еще два измерения для построения физической теории. (Например,
создание поляризованных солнцезащитных очков основано на том
факте, что свет обладает двумя физическими поляризациями: он мо-
жет вибрировать влево-вправо или вверх-вниз. Но математическая
формулировка света в уравнениях Максвелла представлена четырьмя
компонентами. Две из этих четырех вибраций, в сущности, лишние.)
Если мы добавим еще два измерения к функциям Рамануджана, то
«волшебными числами» математики становятся 10 и 26, которые
являются «волшебными числами» и в струнной теории. Таким обра-
зом выходит, что в каком-то смысле Рамануджан занимался струнной
теорией еще до Первой мировой войны!
Сказочные свойства этих эллиптических модулярных функций
объясняют, почему теория должна существовать в десяти измере-
ниях. Только в таком количестве измерений будто по волшебству
исчезает большая часть противоречий, наводняющих все остальные
теории. Но сама по себе топология струн не обладает достаточной
«властью», чтобы исключить все эти противоречия. Остальные
противоречия струнной теории устраняются при помощи второй ее
характеристики — суперсимметрии.
Суперсимметрия
В струне заключены некоторые величайшие симметрии, извест-
ные науке. Обсуждая инфляционное расширение Вселенной и
Стандартную модель в главе 4, мы видели, что симметрия предостав-
ляет нам прекрасный способ организации субатомных частиц в при-
ятные и изящные модели. Три типа кварков могут быть организованы
согласно симметрии SU(3), которая позволяет кваркам меняться
между собой местами. В теории ТВО считается, что пять типов квар-
ков и лептонов могли бы быть организованы согласно симметрии
SU(5).
В струнной теории благодаря этим симметриям уходят оставши-
еся противоречия и аномалии. Поскольку симметрии представляют
собой одно из наиболее прекрасных и мощных средств, имеющихся
В нашем распоряжении, то вполне можно было бы ожидать, что
Теория Вселенной должна обладать наиболее изящной и мощной
симметрией, какая только известна науке. Логичной была бы сим-
метрия, которая позволила бы менять местами не только кварки,
йо и все частицы, которые можно встретить в природе. Это зна-
чит, что все уравнения должны оставаться неизменными, если мы
изменим положение всех частиц относительно друг друга. Такой
Подход в точности описывает симметрия суперструны, называемая
вуперсимметрией[12]. Это единственный вид симметрии, который
Позволяет менять местами все известные физикам субатомные части-
цы. Такая симметрия является идеальным претендентом на место
Симметрии, которая организует все частицы Вселенной в единое,
Изящное целое.
* Если рассматривать все взаимодействия и частицы Вселенной,
'Шо мы увидим, что, в зависимости от спина, все они делятся на две
Категории — «фермионы» и «бозоны». Они ведут себя как волчки,
которые могут вращаться с различными скоростями. К примеру,
спин фотона, частицы, являющейся носителем электромагнитного
взаимодействия, равен единице. Гравитон, частица гравитации,
имеет спин, равный двум. Все частицы, обладающие спином, выра-
жающимся целым числом, называют бозонами. Подобным образом,
частицы вещества описываются при помощи субатомных частиц,
спин которых выражается полуцелыми значениями — 1/2, 3/2, 5/2
и так далее. (Частицы с полуцелыми значениями спина называют
фермионами. К ним относятся электрон, нейтрино и кварки.) Таким
образом, суперсимметрия изящно выражает дуализм, возникающий
между бозонами и фермионами, между взаимодействиями и веще-
ством.
В теории, основанной на суперсимметрии, у каждой частицы есть
напарник: каждый фермион находится в паре с бозоном. Хотя мы ни-
когда не наблюдали этих суперсимметричных партнеров в природе,
физики окрестили партнера электрона «сэлектроном», который об-
ладает спином, равным нулю. (Физики добавляют «с» для описания
суперпартнера какой-либо частицы.) Слабые взаимодействия вклю-
чают в себя частицы, называемые лептонами: их суперпартнеров
называют слептонами. Подобным образом и у кварка может быть
партнер с нулевым спином, который называется скварком. В целом,
партнеры всех известных частиц (кварков, лептонов, гравитонов,
фотонов и так далее) называются счастицами, или суперчастицами.
Эти счастицы нам еще только предстоит обнаружить при помощи
ускорителей частиц (возможно, наше оборудование еще не достаточ-
но мощное, чтобы мы могли получить эти частицы).
Но поскольку все субатомные частицы являются либо ферми-
онами, либо бозонами, то в теории суперсимметрии содержится
потенциал объединения всех известных субатомных частиц одной
простой симметрией. Теперь у нас есть достаточно обширная сим-
метрия, которая включит в себя целую Вселенную.
Представьте себе снежинку. Пусть каждый из шести ее кончиков
представляет субатомную частицу, при этом бозоны расположены
через один и за каждым бозоном следует фермион. Красота этой
«суперснежинки» состоит в том, что при вращении она остается
неизменной. Таким образом, эта суперснежинка объединяет все
частицы и их счастицы. Поэтому, если мы попытаемся построить
гипотетическую единую теорию поля, в которой есть лишь шесть
кастиц, то вполне естественно, что лучшим претендентом на эту роль
явится суперснежинка.
Суперсимметрия помогает устранить все оставшиеся бесконеч-
ности, которые для других теорий оказывались роковыми. Ранее мы
уже упоминали о том, что большая часть отклонений устраняется
благодаря топологии струны — то есть, поскольку струна обладает
конечной длиной, силы не стремятся к бесконечности при прибли-
жении к самой струне. При рассмотрении оставшихся отклонений
мы видим, что они делятся на два типа, исходя из взаимодействий бо-
зонов и фермионов. Однако два типа действий, производимых этими
.частицами, всегда имеют противоположный знак, а потому действие
|фермиона всегда компенсируется действием бозона! Иными слова-
ми, поскольку действия бозона и фермиона всегда имеют противопо-
ложный знак, то оставшиеся в теории противоречия взаимоустраня-
юхся. Таким образом, суперсимметрия — это не просто витринное
крашение. Это не только симметрия, которая дарит эстетическое
удовольствие, — это неотъемлемый элемент для устранении откло-
нений в струнной теории.
Вспомним аналогию конструирования гладкой ракеты, в кото-
рой вибрации могут возрасти настолько, что в конечном счете у нее
оторвет крылья. Одним из решений этой проблемы является приме-
нение силы симметрии для корректировки конструкции крыльев —
таким образом, чтобы вибрации, возникающие в одном крыле,
компенсировали вибрации в другом. Когда одно крыло вибрирует по
часовой стрелке, второе крыло должно вибрировать против часовой
стрелки, что уравновешивает вибрацию первого крыла. Таким об-
разом, симметрия ракеты — казалось бы, всего лишь искусственный
художественный элемент — имеет ключевое значение в устранении
и балансировке нагрузок на крылья ракеты. Подобным образом и су-
персимметрия устраняет отклонения благодаря тому, что бозонная и
фермионная части полностью компенсируют действие друг друга.
(Суперсимметрия также решает ряд сложных технических
проблем13], фатальных для ТВО. Для устранения математических
противоречий в ТВО необходима суперсимметрия.)
Хотя суперсимметрия несет в себе очень мощную идею, в настоя-
щее время не существует никаких экспериментальных доказательств
ее истинности. Это может объясняться тем, что суперпартнеры из-
вестных нам электронов и протонов могут попросту обладать слиш-
ком большой массой, чтобы мы могли получить их на современных
ускорителях частиц. Однако существует очень даже привлекательное
доказательство существования суперсимметрии. Мы знаем, что три
квантовых взаимодействия различны по силе. В сущности, при малых
энергиях сильное взаимодействие в 30 раз сильнее слабого взаимо-
действия и в сотню раз сильнее электромагнетизма. Однако так было
не всегда. Мы предполагаем, что в момент Большого Взрыва все три
взаимодействия были равны по силе. Возвращаясь назад во времени,
физики могут вычислить силы трех взаимодействий в начале времен.
Анализируя Стандартную модель, физики обнаружили, что силы
трех взаимодействий, видимо, стремились к равенству в момент
Большого Взрыва. Но они не в точности равняются друг другу. Зато
когда мы добавляем суперсимметрию, то все три взаимодействия
в точности совпадают друг с другом по силе, а это именно то, что
предполагается в единой теории поля. И хотя этот факт не является
прямым доказательством в пользу суперсимметрии, он все же пока-
зывает, что суперсимметрия, по крайней мере, вписывается в рамки
известной физики.
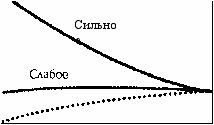
Сила
взаимодействий

[Вывод Стандартной модели
?Хотя в суперструнах в принципе не существует настраиваемых пара-
метров, струнная теория может предложить решения, удивительно
близкие к Стандартной модели с ее пестрым собранием причудливых
субатомных частиц и девятнадцатью «гуляющими» параметрами
(такими, как массы частиц и их силы взаимодействия). Кроме того, в
Стандартной модели существуют три идентичные (и лишние) копии
; всех кварков и лептонов, что кажется совершенно бесполезным.
[Ксчастью, струнная теория может без напряжения вывести многие
качественные характеристики Стандартной модели. В 1984 году
Филип Канделас из Техасского университета, Гари Хоровиц и Эндрю
Стромингер из Калифорнийского университета в Санта-Барбаре, а
[также Эдвард Виттен показали, что если свернуть шесть из десяти
[измерений струнной теории и при этом сохранить суперсимметрию
|в оставшихся четырех измерениях, то крошечный шестимерный мир
[можно описать при помощи того, что математики называют много-
образием Калаби-Яу. Взяв несколько примеров из пространств
Калаби-Яу, они показали, что симметрию струны можно свести к
теории, которая удивительно близка к Стандартной модели.
l Таким образом, струнная теория дает нам простой ответ на то,
[почему в Стандартной модели существуют три излишних поколе-
ния. В струнной теории количество поколений или излишеств в
кварковой модели связано с количеством «отверстий», которые
мы обнаруживаем в многообразии Калаби-Яу. (Например, возьмем
| пончик, велосипедную камеру и кофейную чашку — все они явля-
, ются поверхностями с одним отверстием. В оправе для очков два
отверстия. В пространствах Калаби-Яу может существовать про-
извольное количество отверстий.) Таким образом, просто выбрав
многообразие Калаби-Яу, в котором есть определенное количество
отверстий, мы можем построить Стандартную модель с различными
поколениями лишних кварков. (Поскольку мы никогда не видим
пространства Калаби-Яу из-за того, что оно очень маленькое, мы
также никогда не видим и того факта, что это пространство, подобно
пончику, пронизано отверстиями.) В течение многих лет группы
физиков пытались каталогизировать все возможные пространства
Калаби-Яу, осознавая тот факт, что топология этого шестимерного
пространства определяет кварки и лептоны нашей четырехмерной
Вселенной.
М-теория
Всеобщее увлечение струнной теорией, имевшее место в 1984 году,
не могло продолжаться вечно. К середине 1990-х годов триумфальное
шествие теории суперструн начало сбавлять темп. Легкие проблемы,
которые решала эта теория, были уже все выбраны, и остались только
сложные. Одной из таких проблем было открытие миллиардов реше-
ний струнных уравнений. При компактификации, или свертывании
пространства-времени различным образом, струнные решения
можно было записывать в любом измерении, а не только в четырех.
Каждое из миллиардов струнных решений соответствовало матема-
тически непротиворечивой Вселенной.
Физики внезапно начали тонуть в струнных решениях. Что при-
мечательно, многие из этих решений выглядели очень похожими
на нашу Вселенную. Выбрав подходящее пространство Калаби-Яу,
можно было относительно несложно воспроизвести многие из
существенных черт Стандартной модели с ее причудливым скопле-
нием кварков и лептонов, даже с ее любопытным набором поколе-
ний. Однако чрезвычайно сложной задачей (неразрешенной и по
сей день) было обнаружить первоначальную Стандартную модель
с определенными значениями ее девятнадцати параметров и тремя
излишними поколениями. (Ошеломляющее количество струнных
решений, вообще-то, приветствовалось физиками, которые поддер-
живали идею Мультивселенной, поскольку каждое решение пред-
ставляет полностью непротиворечивую параллельную вселенную.
Однако удручал тот факт, что физики испытывали сложности в обна-
ружении именно нашей Вселенной в этих джунглях вселенных.)
Одной из причин сложности этого предприятия является то, что в
конечном счете суперсимметрию все же нужно разрушить, посколь-
ку в нашем мире низких энергий мы этой симметрии не наблюдаем.
К примеру, мы не видим в природе сэлектрона — суперпартнера
электрона. Если оставить суперсимметрию нетронутой, то масса
каждой частицы должна быть эквивалентна массе ее суперчастицы.
• Физики считают, что суперсимметрия была нарушена, и результатом
этого является то, что массы суперчастиц огромны и, таким образом,
суперчастицы находятся вне пределов досягаемости современных
ускорителей частиц. Но в настоящее время никто еще не предложил
правдоподобного механизма для нарушения суперсимметрии.
Дэвид Гросс из Института теоретической физики Кавли в Санта-
< Барбаре заметил, что существуют миллионы и миллионы решений
; струнной теории в трех пространственных измерениях, что несколь-
ко смущает, поскольку нет способа, с помощью которого мы можем
выбирать среди них.
Были и другие вопросы, в частности то, что существовало пять
непротиворечивых струнных теорий. Было сложно представить, что
Вселенная могла позволять существование пяти отдельных единых
теорий поля. Эйнштейн считал, что у Бога не было выбора при соз-
: дании Вселенной, так почему же Бог должен был создать целых пять
вселенных?
Первоначальная теория, основанная на формуле Венециано,
описывает то, что называют суперструнной теорией типа I. В теории
типа I фигурируют как открытые струны (с двумя концами), так и
замкнутые струны (свернутые в окружность). Эту теорию очень
активно разрабатывали в начале 1970-х годов. (Используя струнную
теорию поля, Киккаве и мне удалось каталогизировать полный набор
струнных взаимодействий типа I. Мы показали, что струны типа I
требуют пять взаимодействий. Что касается замкнутых струн, то мы
показали, что там необходим только один член взаимодействия.)
Мы с Киккавой также показали, что возможно построение пол-
ностью непротиворечивых теорий только с замкнутыми струнами
(то есть похожими на петлю). Сегодня такие теории называются
струнными теориями типа II, где струны взаимодействуют путем
расщепления на две струны меньшего размера (этот процесс напо-
минает митоз в клетках).
Наиболее реалистичной струнной теорией считается теория гете-
ротических струн, сформулированная группой ученых из Принстона
(в том числе Дэвидом Гроссом, Эмилем Мартинеком, Райаном Ромом
и Джеффри Харви). Теория гетеротических струн может содержать в
себе группы симметрии, называемые Е(8)хЕ(8) или 0(32), которые
достаточно велики, чтобы включить в себя теории'ТВО. Теория гете-
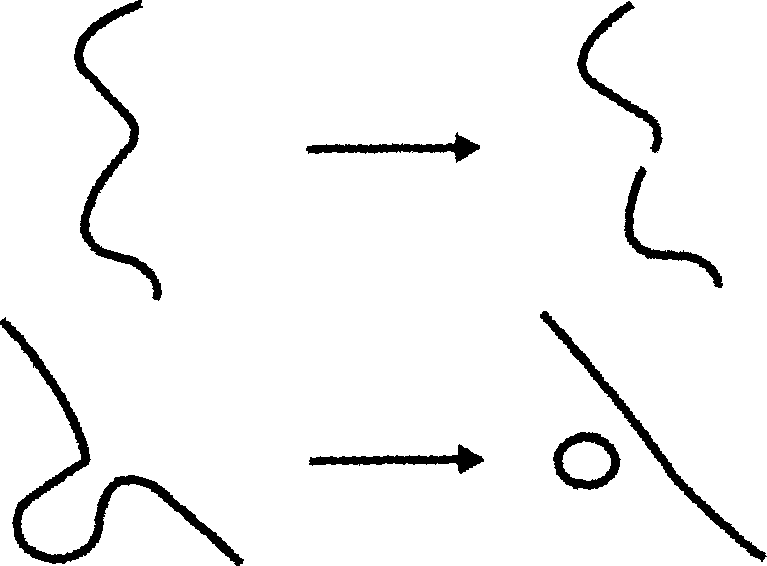
о — о
X
Взаимодействие струн типа I может проходить в пяти различных вариантах.
В ходе этих взаимодействий струны могут разрываться, соединяться
и расщепляться. Для замкнутых струн характерно лишь последнее
взаимодействие, которое напоминает процесс митоза в клетках.
ротических струн полностью основывается на замкнутых струнах.
В 1980-е и 1990-е годы, говоря о теории суперструн, ученые подра-
зумевали теорию гетеротических струн, поскольку она достаточно
богата, чтобы позволить анализировать внутри нее Стандартную мо-
дель и теории ТВО. Например, группу симметрии Е(8)хЕ(8) можно
■разбить до симметрии Е(8), а затем — Е(6), которая, в свою очередь,
■достаточно велика, чтобы включать симметрию SU(3)xSU(2)xU(l)
[«Стандартной модели.
Загадка супергравитации
Вдобавок к наличию пяти теорий суперструн существовал еще один
насущный вопрос, позабытый в погоне за решением струнной теории.
И976году три физика — Питер ван Ньювенхойзен, Серджо Феррара
и Дэниэл Фридман, в то время работавших в Государственном универ-
ситете Нью-Йорка в Стоуни-Брук, обнаружили, что первоначальная
теория гравитации Эйнштейна могла стать суперсимметричной, если
ввести в нее всего лишь одно новое поле, суперпартнер первоначаль-
ного гравитационного поля со спином 3/2 (названное гравитино, что
означает «маленький гравитон»). Эта новая теория получила назва-
ние теории супергравитации. В ее основе лежали точечные частицы,
а не струны. В отличие от теории суперструн, где существовала бес-
конечная последовательность нот и резонансов, в теории супергра-
витации было всего лишь две частицы. В 1979 году Юджин Креммер,
Джоэл Шерк и Бернар Джулия из французской Высшей технической
школы показали, что самая общая теория супергравитации может
1быть записана в одиннадцати измерениях. (При попытках записать
теорию супергравитации в двенадцати или тринадцати измерениях
возникали математические противоречия.) В конце 1970-х — начале
1980-х годов считалось, что теория супергравитации вполне могла бы
оказаться мифической единой теорией поля. Теория супергравита-
ции даже вдохновила Стивена Хокинга на слова о том, что виден не-
вдалеке «конец теоретической физики» (в ходе его инаутурационной
I лекции при занятии в Кембриджском университете той самой кафе-
I Дры математики, которую в свое время возглавлял сам Исаак Ньютон).
I Но супергравитация вскоре столкнулась с теми же проблемами, какие
{погубили и предыдущие теории. Хотя в теории супергравитации
[ было меньше противоречий, чем в обычной теории поля, но в ней не
(хватало завершенности и было полно потенциальных аномалий. Как
и все остальные теории поля (за исключением струнной теории), она
| рассыпалась на глазах у ученых.
Еще одной суперсимметричной теорией, которая может суще-
ствовать в одиннадцати измерениях, является теория супермембран.
Хотя струна обладает только одним измерением, определяющим ее
длину, у супермембраны может быть два или более измерений, по-
скольку она представляет собой поверхность. Что примечательно,
два типа мембран — двубранные и пятибранные — также оказывают-
ся непротиворечивыми в одиннадцати измерениях.
Однако и в теории супермембран не обошлось без проблем.
Супермембраны широко известны тем, что с ними очень сложно
работать, а их квантовые теории действительно расходятся. В то
время как скрипичные струны настолько просты, что еще греки-
пифагорейцы смогли выработать законы гармонии, работать с мем-
бранами настолько трудно, что даже сегодня ни у кого не возникло
удовлетворительной теории музыки, основанной на них. Кроме того,
было доказано, что эти мембраны неустойчивы и в конечном итоге
распадаются на точечные частицы.
Итак, к середине 1990-х годов у физиков было несколько загадок.
Почему существовало пять струнных теорий в десяти измерениях?
И почему в одиннадцати измерениях было две теории — супергра-
витации и супермембран? Более того, все они обладали суперсиммет-
рией.
