Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации

Вид материала

Документы

Содержание Визначення змінних величин. Визначення мети та побудову рівняння цільової функції моделі лінійного програмування. Визначення обмежувальних факторів та побудову їх рівняння. Види готової продукції Визначення обмежень та побудова їх рівняння. Виробнича потужність (час роботи обладнання) Матеріальні ресурси (основний інгредієнт) Обсяг реалізації (кількість одиниць реалізації) Умова позитивності змінних величин цільової функції Поиска решения

Подобный материал:

• Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации, 231.57kb.
• Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации, 357.62kb.
• Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации, 931.79kb.
• Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации, 265.79kb.
• Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации, 541.79kb.
• Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации, 329.51kb.
• Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации, 207.48kb.
• Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации, 938.89kb.
• Www mydisser com Заказ индивидуальных авторских работ, от контрольной до диссертации, 449.07kb.
• Diplomrus ru Заказ индивидуальных авторских работ, от контрольной до диссертации, 590.5kb.

Таким чином, з метою отримання 50 000 грн. прибутку хлібопекарне підприємство повинно забезпечити реалізацію хліба та хлібобулочних виробів встановленого асортименту у кількості 88 305 одиниць на суму 177 449,12 грн.

Показник запасу міцності, визначений у грошовому вимірнику при запланованому обсязі реалізації у розмірі 177 449,12 грн. свідчить, що Хлібокомбінат Бобринецького районного споживчого товариства може знижувати обсяг реалізації хліба та хлібобулочних виробів в межах 132 029,71 грн. (177 449,12 – 45 419,41) або 65 703 одиниць (88 305 – 22 602) без ризику зазнати збитки.

При цьому, значення коефіцієнту запасу міцності - 0,744 (65 703 / 88 305) - характеризує невисокий ступінь ризику підприємства отримати збитки у разі зменшення обсягу реалізації продукції і означає, що його можна знизити на 74,4 % перш, ніж буде досягнута критична точка беззбитковості підприємства.

Показник операційного важеля складає 1,3 (88 305 х 0,761 / 50 000) і свідчить про те, що при збільшенні обсягів реалізації хліба та хлібобулочних виробів Хлібокомбінату Бобринецького районного споживчого товариства вище точки беззбитковості на 1 %, прибуток підприємства зросте на 1,3 % і, навпаки, при скороченні обсягів реалізації прибуток зменшиться у тій же пропорції. Значення цього показника підтверджує наш попередній висновок про не високий ступінь підприємницького ризику і характеризується наявністю досить низького рівня постійних витрат підприємства та високого рівня змінних витрат на одиницю продукції.

Водночас, аналіз беззбитковості можна використати для моделювання майбутнього прибутку. Так, розрахунки доводять, що у разі забезпечення реалізації хліба та хлібобулочних виробів у розмірі 100 000 од. Хлібокомбінат Бобринецького районного споживчого товариства отримає прибуток у розмірі 58 900 грн. (100 000 х 0,761 – 17 200) при незмінній комбінації продажу.

Таким чином, аналіз беззбитковості підприємства виступає одним із ефективних методів аналізу релевантної інформації в процесі прийняття оперативних управлінських рішень, який дозволяє встановлювати ступінь взаємозв’язку між витратами, обсягом діяльності та прибутком підприємства, оптимізувати структуру витрат, асортимент, обсяги та ціну реалізації продукції, визначати рівень підприємницького ризику підприємства.

Водночас, слід враховувати, що не зважаючи на значущість та потужність цього інструменту управлінського обліку в основу аналізу беззбитковості підприємства покладено ряд обмежень та припущень, ігнорування яких може призвести до прийняття неадекватних управлінських рішень. Найважливішими з них є наступні:

1. Аналіз беззбитковості є доцільним лише в межах релевантного діапазону.
   
2. Поведінка загальних витрат та виручки від реалізації підприємства чітко визначена і є лінійною в межах релевантного діапазону.
   
3. Витрати підприємства можна досить точно розподілити на змінні та постійні. При цьому, постійні витрати залишаються незмінними, а змінні витрати змінюються прямо пропорційно до обсягу реалізації підприємства в межах релевантного діапазону.
   
4. На зміну загального рівня витрат та виручки від реалізації, підприємства релевантно впливає лише обсяг реалізації готової продукції. При цьому, всі інші показники: ціна реалізації, ціни і тарифи на основні матеріали і послуги, продуктивність праці робітників, рівень технології та організації виробництва залишаються незмінними.
   
5. Обсяг виробництва дорівнює обсягу реалізації підприємства або зміни початкових та кінцевих залишків готової продукції незначні.
   
6. Комбінація продажу є сталою. При її зміні необхідно уточнити значення середньозваженого маржинального доходу і решти показників, розрахованих на його основі [47, с. 199-201].
   

На наступному етапі аналізу взаємозв’язку витрат, обсягу діяльності та прибутку хлібопекарних підприємств, на нашу думку, необхідно застосовувати математичні методи моделювання його основних параметрів з метою оптимізації виробничої діяльності.

В процесі прийняття оперативних управлінських рішень щодо оптимізації виробничої діяльності підприємства широко застосовується метод лінійного програмування, який забезпечує розподіл обмежених ресурсів з метою досягнення оптимального кінцевого результату.

Лінійне програмування використовується для розв’язання багатьох екстремальних задач, рішення яких зводиться до визначення оптимальних значень (максимального або мінімального) деяких змінних величин функції за умови наявності альтернатив і обмежувальних факторів. Так, метою його застосування можуть бути максимізація обсягів діяльності, прибутку або маржинального доходу, а також мінімізація змінних, постійних чи загальних витрат підприємства тощо.

В загальному вигляді лінійне програмування представляє собою один із математичних методів, який використовується для оптимізації виробничої діяльності шляхом розв’язання серії лінійних рівнянь наявних обмежень. Однак, застосування його є можливим лише у тих випадках, коли фактори і змінні величини, що досліджуються, мають математичну визначеність і кількісну обмеженість, коли в результаті певної послідовності розрахунків відбувається взаємозамінність факторів, коли логіка у розрахунках суміщаються з логічно обгрунтованою сутністю явища.

Отже, характерною особливістю лінійного програмування є логічний аналіз і певний порядок, алгоритм розрахунків, що включає наступні стадії:

І. Побудова моделі лінійного програмування. Цей етап передбачає визначення мети та здійснення математичної формалізації задачі лінійного програмування, що заключається в ідентифікації відповідних змінних величин та мети, описанні цільової функції і обмежень на ресурси у формі лінійних співвідношень.

Основна процедура побудови моделі лінійного програмування є загальною для всього розмаїття задач і передбачає:

1. Визначення змінних величин. В моделі лінійного програмування змінними величинами виступають комбінації продажу продукції, кількість окремих виробів або кількість ресурсів, значення яких необхідно оптимізувати в межах наявних обмежень.
   
2. Визначення мети та побудову рівняння цільової функції моделі лінійного програмування. Рівняння цільової функції – це алгебраїчне зображення мети. В загальному вигляді модель цільової функції можна відтворити наступним чином:
   

Y = a₁x₁ + a₂x₂ + …… + a_nx_n ,

де a₁ , a₂, a_n - коефіцієнти;

x₁ , x₂ x_n - змінні величини.

Залежно від того, якою є кінцева мета моделі лінійного програмування, визначаються показники відповідних коефіцієнтів та змінних величин, наприклад:

- максимізація обсягів реалізації продукції підприємства


Y = a₁x₁ + a₂x₂ + …… + a_nx_n max ,

де a₁ , a₂, a_n - ціна реалізації окремих видів продукції;

x₁ , x₂ x_n - кількість реалізованих одиниць окремих видів продукції;

Y - загальний обсяг реалізації.

- максимізація маржинального доходу підприємства


Y = a₁x₁ + a₂x₂ + …… + a_nx_n max ,

де a₁ , a₂, a_n - маржинальний доход на одиницю продукції;

x₁ , x₂ x_n - кількість реалізованих одиниць окремих видів продукції;

Y - загальний маржинальний доход.

• максимізація прибутку підприємства:
  

Y = a₁x₁ + a₂x₂ + …… + a_nx_n max ,

де a₁ , a₂, a_n - прибуток на одиницю окремих видів продукції;

x₁ , x₂ x_n - кількість реалізованих одиниць окремих видів продукції;

Y - загальний прибуток.

• мінімізація змінних витрат підприємства:
  

Y = a₁x₁ + a₂x₂ + …… + a_nx_n mіn ,

де a₁ , a₂, a_n - змінні витрати на одиницю окремих видів продукції;

x₁ , x₂ x_n - кількість одиниць окремих видів продукції;

Y - загальні змінні витрати.

3. Визначення обмежувальних факторів та побудову їх рівняння. У якості обмежень можуть виступати виробничі, матеріальні та трудові ресурси підприємства, наявність підприємницького ризику, рівень попиту на продукцію, особливості оподаткування тощо. Обмеження оформлюються у вигляді рівняння. Рівняння обмеження – це алгебраїчне зображення одного з обмежувальних чинників, типу:
   

a₁₁x₁ + a ₁₂ x₂ + …… + a _1n x_n  в ₁,

де a₁₁ , a ₁₂ , a _1n - коефіцієнти;

x₁ , x₂ , x_n - змінні величини цільової функції;

в ₁ - значення обмежувального фактору.

Крім того, особливе значення має дотримання умови позитивності змінних величин. Тому, одним із обов’язкових рівнянь обмежень є наступне:


x₁ , x₂ , x_n  0,

де x₁ , x₂ , x_n - змінні величини цільової функції.

Таким чином, в узагальненому вигляді задачу лінійного програмування можна сформулювати наступним чином:

Максимізація:

Y = a₁x₁ + a₂x₂ + …… + a_nx_n max

в умовах системи лінійних обмежень:

a₁₁x₁ + a ₁₂ x₂ + …… + a _1n x_n  в ₁

a₂₁x₁ + a ₂₂ x₂ + …… + a _2n x_n  в ₂

……………………………………………

a_n1x₁ + a _m2 x₂ + …… + a _mn x_n  в _m

x₁ , x₂ , x_n  0

Мінімізація:

Y = a₁x₁ + a₂x₂ + …… + a_nx_n mіn

в умовах системи лінійних обмежень:

a₁₁x₁ + a ₁₂ x₂ + …… + a _1n x_n  в ₁

a₂₁x₁ + a ₂₂ x₂ + …… + a _2n x_n  в ₂

……………………………………………

a_n1x₁ + a _m2 x₂ + …… + a _mn x_n  в _m

x₁ , x₂ , x_n  0


ІІ. Розв’язання моделі лінійного програмування. При цьому, після формулювання задачі лінійного програмування розглядаються всі можливі варіанти рішень (сполучення змінних), серед яких обирається те, що дозволяє оптимізувати цільову функцію. На практиці моделі лінійного програмування розв’язуються переважно за допомогою відповідно пакету прикладних програм за умов наявності комп’ютерної техніки. При цьому, залежно від кількості змінних у рівнянні цільової функції, можуть бути застосовані різні методи рішення: при наявності лише двох змінних – графічний метод або метод розв’язання простої системи рівнянь; за умови наявності більше двох змінних – симплекс-метод.

Графічний метод розв’язання моделі лінійного програмування передбачає побудову графіку, в якому вісі координат відображають значення змінних величин, а в площину системи координат наносяться лінії наявних обмежень виробничих ресурсів, які дозволяють визначити зону можливих рішень (зона можливих рішень – це площина графіка лінійного програмування, окреслена лініями рівнянь наявних обмежень, точки якої задовольняють мету цільової функції та всі обмеження задачі).

Метод розв’язання простої системи рівнянь передбачає відповідне перетворення визначених рівнянь обмежень на просту систему рівнянь і визначення за допомогою існуючих математичних прийомів оптимального співвідношення змінних величин цільової функції.

Симплекс-метод – це метод матричної алгебри, який передбачає визначення оптимального значення цільової функції за допомогою відповідного алгоритму дій. Принцип, який лежить в основі симплекс-методу, досить простий – передбачається, що оптимальному рішенню відповідає одна із крайніх точок зони можливих рішень. Цей принцип і визначає відповідний алгоритм симплекс-методу, який у спрощеному вигляді може бути описаний наступним чином: за допомогою відповідних математичних прийомів проводиться оцінка значення цільової функції у всіх крайніх точках зони можливого рішення; при цьому, перехід від однієї крайньої точки до іншої здійснюється лише за умови поступового покращення значення цільової функції; якщо виявляється, що деяке базисне рішення покращити неможливо, то воно визнається оптимальним для задачі лінійного програмування.

ІІІ. Аналіз рішення моделі лінійного програмування. Цей етап передбачає обов’язкове визначення ступеня чутливості моделі лінійного програмування до зміни значень обмежувальних чинників (факторів). Існує три основних аналітичних аспекти рішення задачі лінійного програмування, які підлягають ретельному дослідженню:

• вплив додаткової кількості обмежених ресурсів;
  
• вплив додаткової кількості необмежених ресурсів;
  
• вплив змін в коефіцієнтах цільової функції [195].
  

Для демонстрації можливостей застосування методу лінійного програмування в процесі прийняття управлінських рішень щодо оптимізації виробничої діяльності підприємства використано дані про діяльність Хлібокомбінату Бобринецького районного споживчого товариства.

З метою визначення оптимального співвідношення обсягів реалізації обраних довільно окремих видів продукції у виробничій програмі хлібокомбінату, яке забезпечить отримання максимально можливого маржинального доходу підприємства, за даними таблиці 3.11 здійснено поетапну постановку та розв’язання моделі лінійного програмування.


Таблиця 3.11

Дані про діяльність Хлібокомбінату Бобринецького районного споживчого товариства для побудови моделі лінійного програмування

Види готової продукції	Маржина-льний дохід на одиницю продукції, грн.	Значення обмежувальних ресурсів
виробнича потужність на одиницю продукції, маш.-год.	борошно пшеничне в/г на одиницю продукції, кг.	критичний обсяг реалізації, од.
Хліб домашній подовий в/г 0,500 – х1	0,66	0,02	0,3655	1 808
Хліб Інгулець в/г 0,670 – х2	0,96	0,02	0,4898	7 911
Хліб степовий подовий І г 0,680 – х3	0,94	0,02	0,4996	5 425
Батон нарізний в/г 0,500 – х4	0,75	0,03	0,3685	1 356
Бублик з маком в/г 0,100 – х5	0,35	0,03	0,0725	1 130
Бублик з цукром в/г 0,100 – х6	0,35	0,03	0,0725	2 260
Зірочка з повидлом в/г 0,075 – х7	0,40	0,04	0,0396	2 712
Разом	х	20 000	30 500	22 602

Послідовність та порядок побудови і розв’язання моделі лінійного програмування відповідає наступним вищерозглянутим етапам:

1. Визначення змінних величин. У нашому випадку є 7 змінних величин, в якості яких виступає кількість одиниць реалізації окремих видів готової продукції хлібопекарного підприємства х₁ – х₇ (табл. 3.10).
   
2. Визначення мети та побудова цільової функції. Метою моделі лінійного програмування є максимізація маржинального доходу хлібокомбінату, алгебраїчне зображення якої має вигляд:
   

Y = 0,66х₁ +0,96х₂ + 0,94х₃ + 0,75х₄ +0,35х₅ + 0,35х₆ +0,40х₇ max,

де Y – загальний маржинальний доход підприємства;

х₁ – кількість одиниць реалізації хліба домашнього подового в/г 0,500;

х₂ – кількість одиниць реалізації хліба Інгулець в/г 0,670;

х₃ – кількість одиниць реалізації хліба степовий подовий І г 0,680;

х₄ – кількість одиниць реалізації батона нарізного в/г 0,500;

х₅ – кількість одиниць реалізації бублика з маком в/г 0,100;

х₆ – кількість одиниць реалізації бублика з цукром в/г 0,100;

х₇ – кількість одиниць реалізації зірочки з повидлом в/г 0,075.

3. Визначення обмежень та побудова їх рівняння. В нашому випадку реалізація хліба та хлібобулочних виробів хлібокомбінату обмежена виробничою потужністю підприємства – 20 000 маш.-год. на місяць, кількістю основного інгредієнту – борошна пшеничного вищого гатунку – 30 500 кг. на місяць та мінімальною кількістю одиниць реалізації, яка не повинна бути нижчою точки беззбитковості, з тим, щоб гарантувати отримання прибутку.
   

Виробнича потужність (час роботи обладнання):

Для виробництва хліба та хлібобулочних виробів необхідна певна кількість машино-годин роботи обладнання хлібокомбінату щоденно, показники якої в розрізі окремих видів продукції наведені в таблиці 3.11. Максимальний час роботи обладнання складає – 20 000 маш.-год. на місяць.

Отже, рівняння обмеження виробничої потужності має вигляд:

0,02х₁ + 0,02х₂ + 0,02х₃ + 0,03х₄ + 0,03х₅ + 0,03х₆ + 0,04х₇  20 000

Матеріальні ресурси (основний інгредієнт):

Виробництво хліба та хлібобулочних виробів потребує використання борошна пшеничного вищого гатунку. Видаток борошна на одиницю продукції обмежений технологічними нормами, наведеними в розрізі окремих видів хлібобулочних виробів в таблиці 3.11, і не повинний перевищувати 30 500 кг.

Отже, рівняння обмеження матеріальних ресурсів має вигляд:

0,3655х₁ + 0,4898х₂ + 0,4996х₃ + 0,3685х₄ + 0,0725х₅ + 0,0725х₆ +

0,0396х₇  30 500


Обсяг реалізації (кількість одиниць реалізації):

Обсяг реалізації окремих видів готової продукції хлібозаводу не повинний бути нижчим за точку беззбитковості (табл. 3.11).

Отже, рівняння обмеження обсягів реалізації мають вигляд:

х₁ ≥ 1 808;

х₂ ≥ 7 911;

х₃ ≥ 5 425;

х₄ ≥ 1 356;

х₅ ≥ 1 130;


х₆ ≥ 2 260;

х₇ ≥ 2 712.

Умова позитивності змінних величин цільової функції:

Необхідно передбачити, що хлібокомбінат не може виробляти готову продукцію у від’ємній кількості. Тому рівняння позитивності має вигляд:

х₁, х₂, х₃, х₄, х₅, х₆, х₇ ≥ 0

Таким чином, кінцева модель лінійного програмування хлібокомбінату Бобринецького районного споживчого товариства на предмет оптимізації його маржинального доходу має такий вигляд:

Y = 0,66х₁ + 0,96х₂ + 0,94х₃ + 0,75х₄ + 0,35х₅ + 0,35х₆ + 0,40х₇ max,

при обмеженнях:

• виробничої потужності:
  

0,02х₁ + 0,02х₂ + 0,02х₃ + 0,03х₄ + 0,03х₅ + 0,03х₆ + 0,04х₄  20 000;

• матеріальних ресурсів:
  

0,3655х₁ + 0,4898х₂ + 0,4996х₃ + 0,3685х₄ + 0,0725х₅ + 0,0725х₆ + 0,0396х₇  30 500;

• обсягів реалізації:
  

х₁ ≥ 1 808;

х₂ ≥ 7 911;

х₃ ≥ 5 425;

х₄ ≥ 1 356;

х₅ ≥ 1 130;

х₆ ≥ 2 260;

х₇ ≥ 2 712.

• умова позитивності:
  

х₁, х₂, х₃, х₄, х₅, х₆, х₇ ≥ 0

4. Рішення моделі лінійного програмування. Рішення задачі лінійного програмування з метою максимізації або мінімізації її цільової функції можна здійснювати з використанням стандартної програми EXCEL.
   

Для цього, спочатку необхідно сформувати умовні дані, ввівши у редакторі формул рівняння цільової функції та обмежень і залишивши вільними ячейки для показників обсягів реалізації окремих видів хлібобулочних виробів, які слід визначити (рис.3.4).




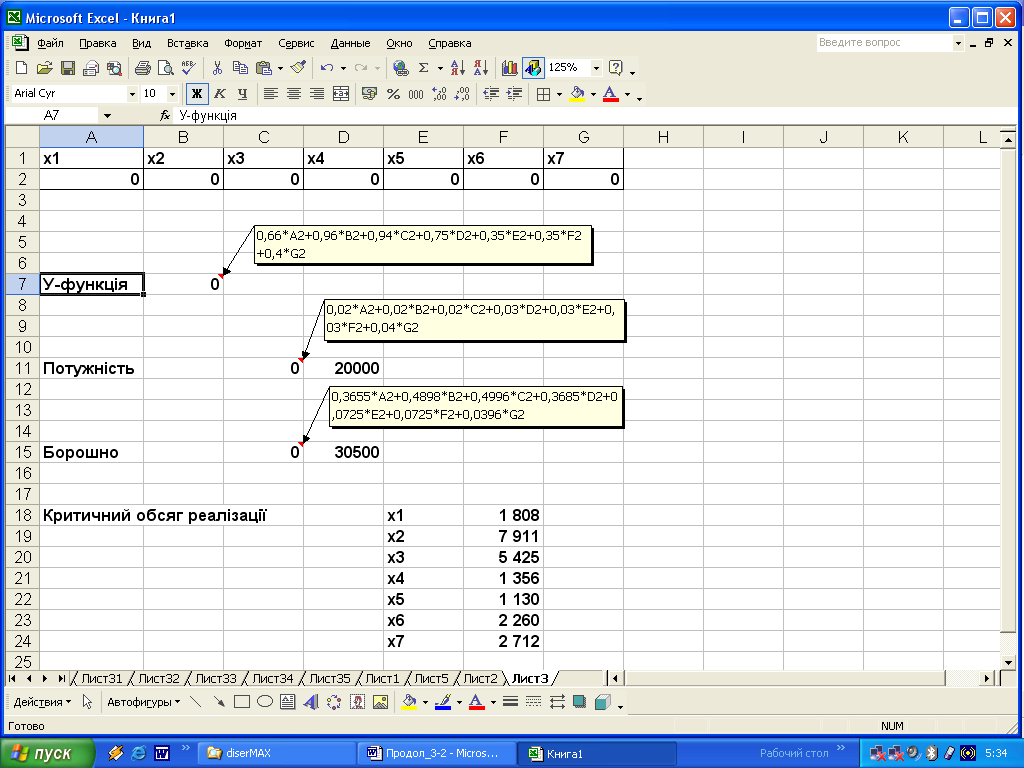
Рис. 3.4. Умовні дані для рішення задачі лінійного програмування на робочому аркуші EXCEL


Безпосереднє рішення задачі лінійного програмування відбувається через пункти головного меню Сервис – Поиск решения, у діалоговому вікні якого необхідно зазначити вхідну інформацію, зображену на робочому аркуші EXCEL (рис. 3.4). При цьому, кінцева мета моделі лінійного програмування відзначається прапорцем біля режиму Равной максимальному значению, а умова позитивності не вводиться окремими рівняннями обмеження, а відмічається прапорцем у групі опцій Параметры біля режиму Неотрицательные числа.

Після здійснення зазначених процедур діалогове вікно Поиска решения повинно мати вигляд, зображений на рис. 3.5.

Виконавши програму необхідно зберегти знайдене оптимальне рішення задачі лінійного програмування на робочому аркуші EXCEL, який тепер матиме вигляд, зображений на рис. 3.6.



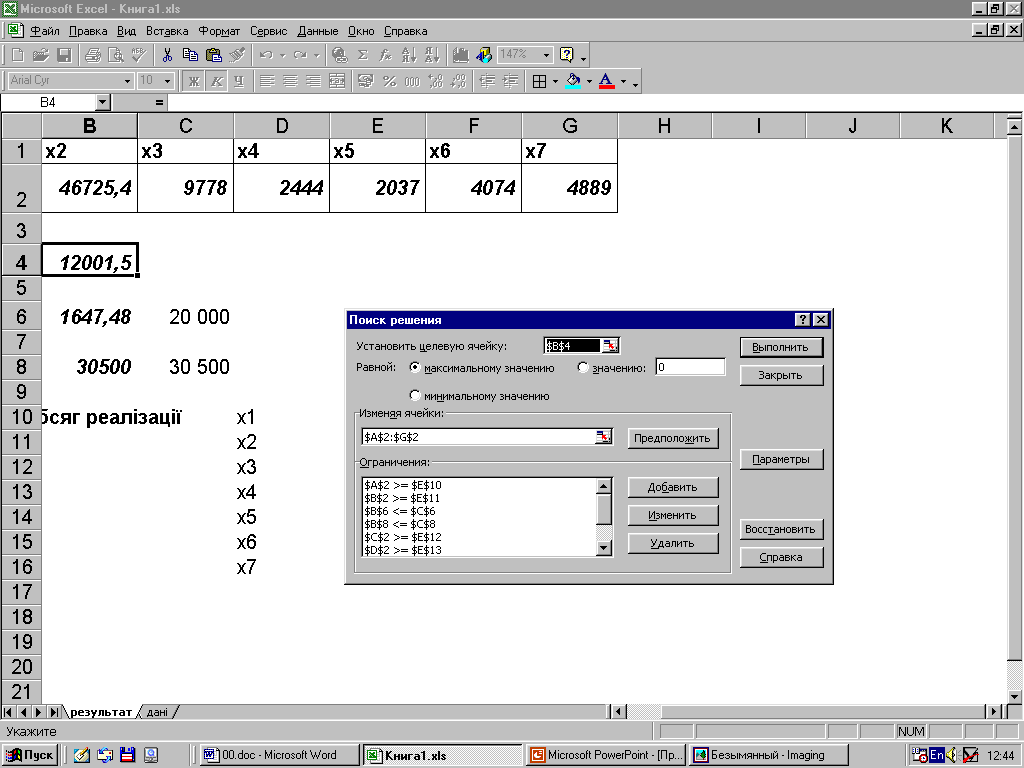
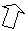
Рис. 3.5. Діалогове вікно Поиска решения


Проведені процедури дали змогу встановити показники змінних величин х₁=1808, х₂=14612, х₃=5425, х₄=1356, х₅=1130, х₆=2260, х₇=485518 і розрахувати максимальне значення цільової функції при реалізації відповідного співвідношення окремих видів хлібобулочних виробів:

Y = 0,66  1 808 + 0,96  14 612 + 0,94  5 425 + 0,75  1 356 +

0,35  1 130 + 0,35  2 260 + 0,40  485 518 = 216 731грн.

Таким чином, при реалізації хліба домашнього подового в/г вагою 0,500 кг. у кількості 1 808 од., хліба Інгулець в/г вагою 0,670 кг. обсягом 14 612 од., хліба степового подового І г вагою 0,680 кг. у кількості 5 425 од., батона нарізного кількістю 1 356 од., бублика з маком кількістю 1 130 од., бублика з цукром кількістю 2 260 од., зірочки з повидлом кількістю 485 518 од. на місяць за умов наявних обмежень виробничої потужності, матеріальних ресурсів та обсягів реалізації підприємства досягається максимальний показник маржинального доходу хлібокомбінату Бобринецького районного споживчого товариства у розмірі 216 731 грн. При цьому, матеріальні ресурси та виробничі потужності підприємства будуть задіяні на повну силу.




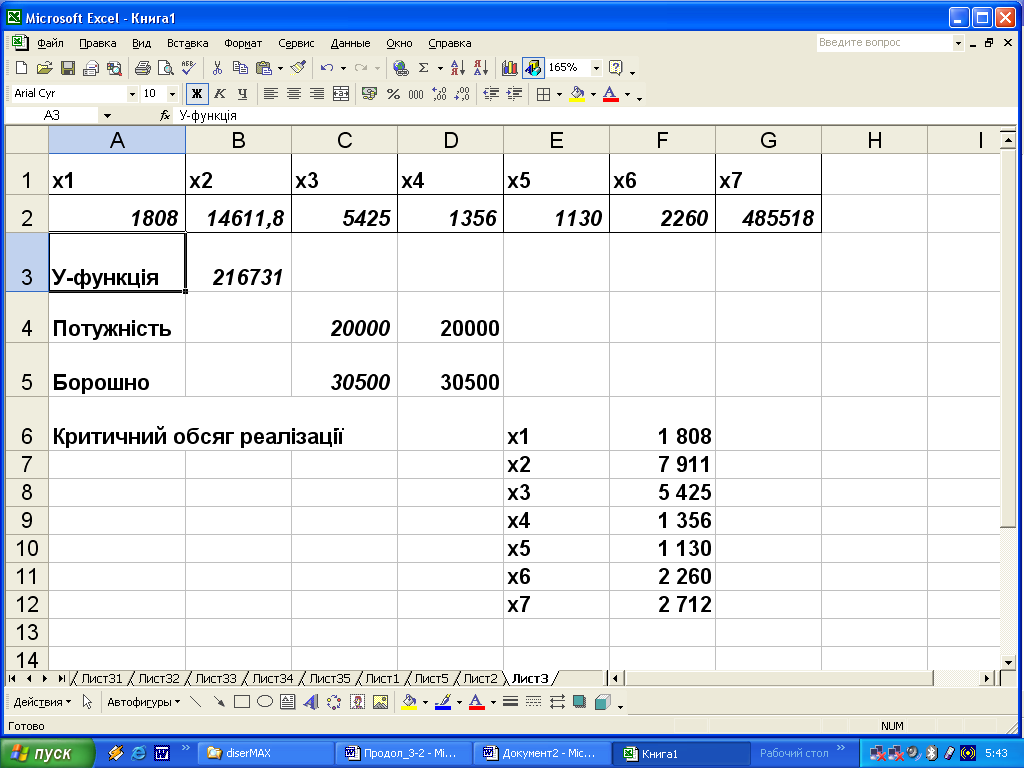
Рис. 3.6. Результати рішення задачі лінійного програмування на робочому аркуші EXCEL


За таких умов прибуток хлібопекарного підприємства, визначений як різниця між маржинальним доходом та постійними витратами, складе 199 531 грн. (216 731 – 17 200). При цьому звертає на себе увагу той факт, що п’ять із семи видів хліба та хлібобулочних виробів за наявних обмежувальних факторів мають реалізовуватися на рівні критичного обсягу беззбитковості тоді, як суттєво збільшити слід обсяги реалізації хліба Інгулець та зірочки з повидлом і це незважаючи на не найвищі показники маржинального доходу на одиницю продукції по даних видах виробів.

Отже необхідність застосування в обліково-аналітичній практиці вітчизняних підприємств лінійного програмування є очевидною. Оскільки інформація, отримана за його допомогою, може широко використовуватися у процесі прийняття оперативних управлінських рішень і забезпечення ефективної їх реалізації.


автор кандидат економічних наук

Ночовна Юлія Олександрівна