Geum.ru

Ф. Г. Шигабутдинов Зам председателя А. З. Камалов Секретарь А. М. Тартыгашева Первое заседание

Вид материалаЗаседание

Содержание


Ф.Г. Шигабутдинов, Р.З. Муртазин, Р.Ф. Мухутдинов.
А.З. Камалов.
Т.К. Хамитов, Ф.Г. Шигабутдинов.
Е.Р. Газизов.
А.М. Тартыгашева, О.В. Клейдман, К.Е. Камаева. Анализ
А.В. Гумеров.
Второе заседание
И.В. Вышинский (гр. 0СБ-201, н. рук. А.З. Камалов).
И.И. Шарипов (гр. 0ПГ-207, н. рук. А.З. Камалов).
А.А. Cтаринец
М.Ш. Шакирзянов
Р.Т. Сафиуллин
А.Р. Зиялеева
Р.Р. Халиуллин
Р.Р. Загидуллин
Э.И. Валиева
П.В. Овчаров
О.В. Сапунова, Н.В. Тишкина
И.Р. Исянов
А.С. Лямин
...
Полное содержание
Подобный материал:




Кафедра теоретической механики



Председатель
Ф.Г. Шигабутдинов

Зам. председателя

А.З. Камалов

Секретарь
А.М. Тартыгашева



Первое ЗАСЕДАНИЕ

5 апреля, 9.00, ауд. 4 -111

1. Ф.Г. Шигабутдинов. О реализации новых учебных планов по теоретической механике в условиях «перехода на бакалавриат».

Образовательные стандарты третьего поколения, которые будут действовать минимум пять следующих лет, определяют три главные компоненты образования: требования к результатам освоения ООП (основных образовательных программ), требования к структуре ООП и требования к условиям реализации ООП. Все эти требования надо внимательно изучить. Если два последних требования достаточно просто могут быть реализованы, то в отношении требований к результатам освоения ООП (они сформулированы в виде «компетенций») будут, видимо, разночтения. Особенно сильно сокращается время на руководство самостоятельной работой студентов на первых курсах, хотя это и не вытекает из содержания и идей, заложенных в образовательные стандарты. Это, несомненно, ставит под удар овладение, пожалуй, главными компетенциями ПК-1 и ПК-2 (направление 27800-Строительство) и углубляет разрыв между привычной для первокурсников школьной и вузовской системами образования. Нужно так организовать самостоятельную работу, чтобы на начальных этапах своей учебы в университете студент не чувствовал своей оторванности от университета. Встречаться со студентами надо не реже одного раза в неделю. Это нужно понимать и руководителям образовательных структур, и преподавателям, ведущим соответствующую дисциплину.


2. Ф.Г. Шигабутдинов, Р.З. Муртазин, Р.Ф. Мухутдинов. Выпучивание упругих ортотропных и изотропных цилиндрических оболочек со шпангоутами при продольном ударе.

Рассматривается влияние шпангоутов на картины волнообразования цилиндрических оболочек при продольных ударах абсолютно твердым телом. Геометрически нелинейные дифференциальные уравнения продольно-поперечных движений тонкой ортотропной оболочки типа Тимошенко, учитывающие сдвиг и инерцию вращения, получены из уравнений Галимова К.З. (Теория оболочек с учетом поперечного сдвига, 1977).

По длине оболочки принимается от одного до пяти шпангоутов, которые располагаются как симметрично, так и произвольно. Исследуется влияние количества и расположения на характер волнообразования, смещение максимальных прогибов и изменение их величины. Начальные условия для перемещений и деформаций приняты нулевыми. Срединная поверхность выбиралась в форме круговой цилиндрической оболочки. Граничные условия принимались в виде подвижной шарнирной опорой на торце, воспринимающем удар, и неподвижной шарнирной опорой на другом конце. Результаты решения показаны в виде двухмерных и трехмерных картин форм изгиба срединной поверхности оболочек в различные моменты времени. Получены формы поперечного волнообразования (прогибы по всей длине оболочки) для двадцати четырех пробегов продольной волны вдоль оболочек.


3. А.З. Камалов. О собственных колебаниях арочного сооружения.

В работе исследуются собственные колебания арочного сооружения, представляющего тонкое незамкнутое цилиндрическое покрытие с равномерно распределенными подкрепляющими арками и находящегося под действием ветровой нагрузки. В дальнейшем нас будет интересовать свободные колебания только арочного сооружения и здесь не ставиться задача об исследовании поведения самой среды. Поэтому будем пренебрегать потенциалом рассеянных волн, порождаемых колеблющимся упругим покрытием сооружения по сравнению с потенциалом волн для абсолютно жесткого покрытия. А уравнения движения составим для деформированного элемента конструкции, тогда внутренние усилия будут дополнительными, возникающими в оболочке при отклонении ее от начальной формы равновесия. При таких допущениях составлены уравнения собственных колебаний системы. Из условия нетривиальности решения системы уравнений, получено уравнение для определения частот свободных колебаний оболочечной конструкции в виде определителя для различного числа волн в окружном и в продольном направлениях. Получены аналитические формулы для определения спектора собственных частот данной конструкции. Рассмотрены частные задачи.


4. Т.К. Хамитов, Ф.Г. Шигабутдинов. Исследование потери устойчивости упруго-пластических стержней конечной длины при продольном ударе.

В работе приводятся результаты решения задач о потере устойчивости упругопластических идеально прямых стержней конечной длины при продольном ударе. На ударяемом торце стержня мгновенно прикладывается постоянное во времени напряжение, превышающее предел текучести материала. Учитываются эффекты, связанные с конечностью скорости распространения продольной волны вдоль элемента. Для материала стержня принимается схема с линейным упрочнением.

Для решения уравнения движения задачи применяются методы разложения искомых функций в ряды Фурье и Бубнова-Галеркина, а также для сравнения результатов приводится «точное» решение. Всего рассмотрено восемь вариантов граничных условий на концах стержня. Результаты решения задач представлены в виде зависимости «критическое напряжение – возмущенная длина» при первом прохождении продольной волны вдоль стержня. Под критическим напряжением понимается напряжение, обращающее частоту свободных колебаний стержня в ноль момент потери устойчивости (статический критерий). Исследовано влияние неоднородности напряженного состояния по длине стержня, вызванное конечностью скоростей распространения продольных упругих и пластических волн на критические напряжения.


5. Е.Р. Газизов. Безволновое докритическое обтекание двух вихрей тяжелой жидкостью.

Рассматривается стационарное потенциальное течение слоя идеальной несжимаемой весомой жидкости. В поток помещены два вихря заданной интенсивности. Одним из параметров, которые характеризуют такие течения является число Фруда: 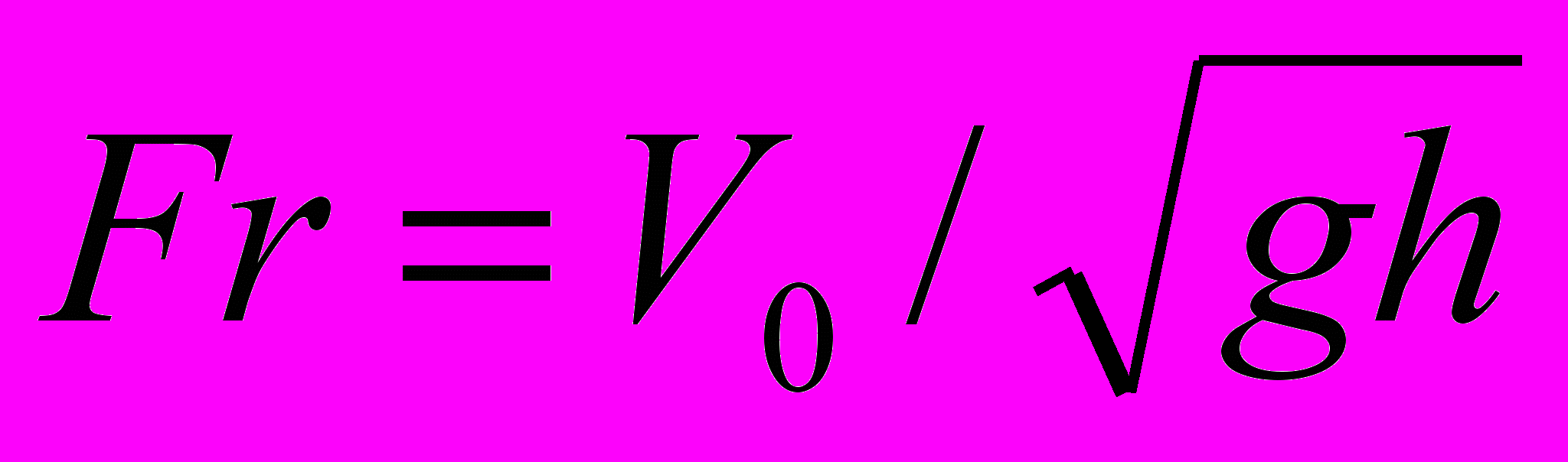, где h и v0 - ширина слоя жидкости и скорость невозмущенного потока слева на бесконечности, g - ускорение силы тяжести. Изучается случай докритического режима обтекания. При этом считается, что докритическое течение слева (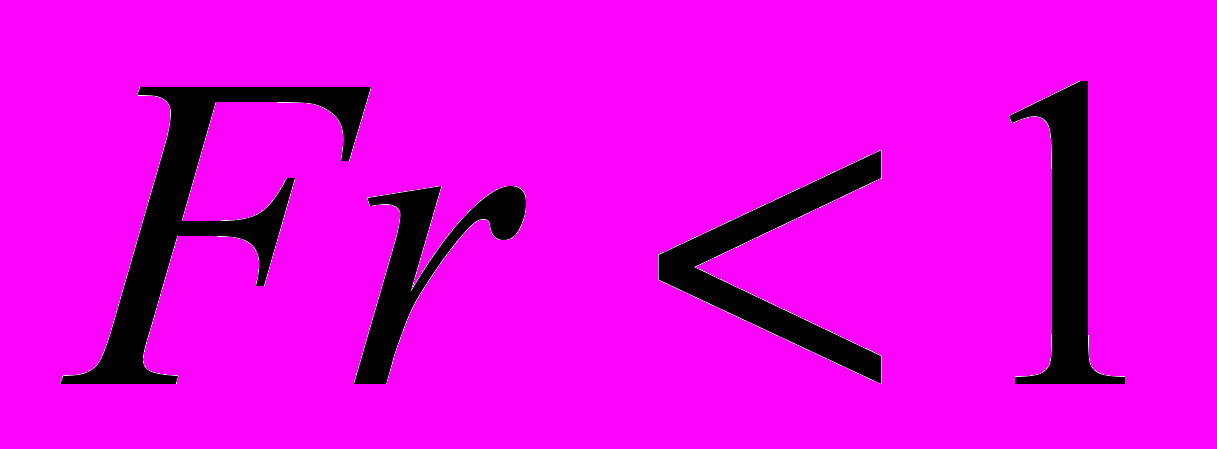) переходит в сверхкритическое справа (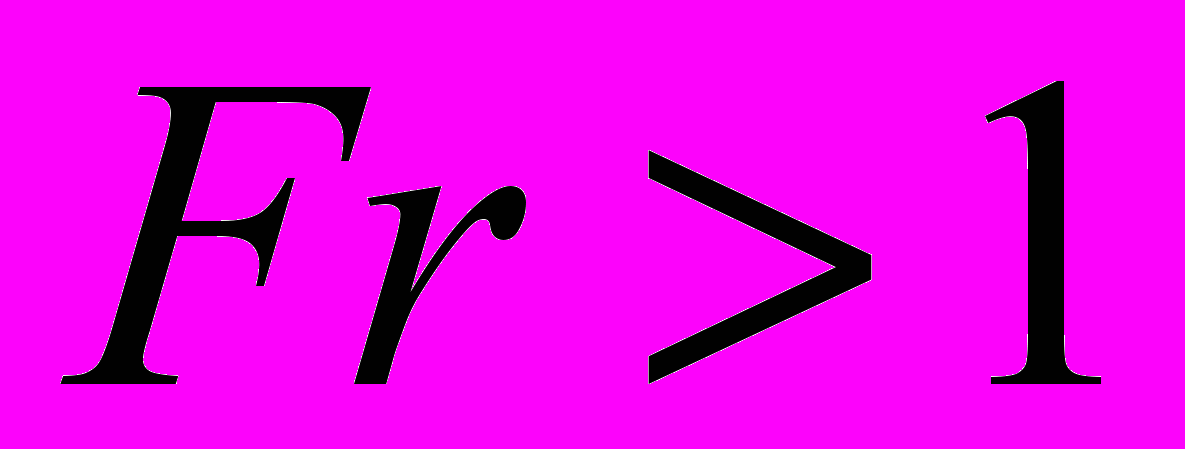). Исходная задача сводится к краевой задаче отыскания аналитической в канонической области функции . В качестве канонической области выбирается полоса ширины 2 в параметрической плоскости t. В результате решения смешанной краевой задачи в канонической области получаются условия, связывающие действительные и мнимые части функции 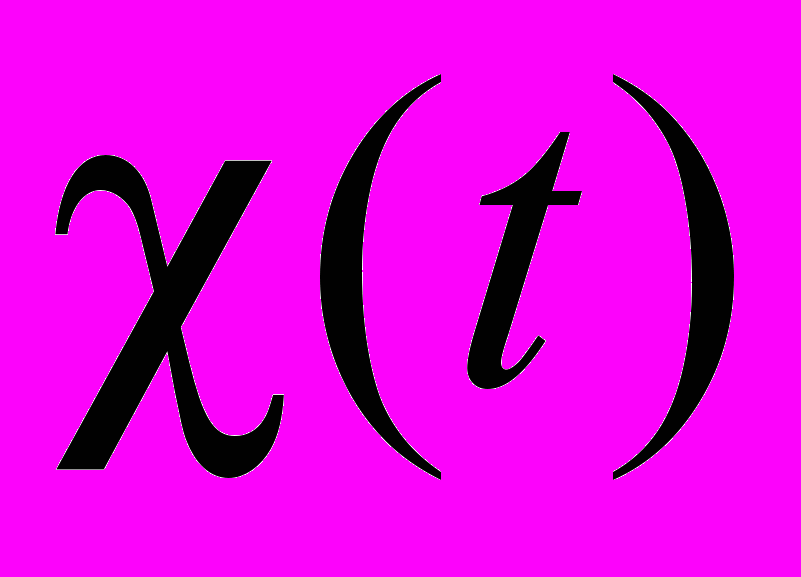на границах полосы. Слева на бесконечности Fr<1, и там могут возникнуть волны. Используя то, что на свободной поверхности давление постоянно, выводится условие отсутствия волн слева на бесконечности. Решение сводится к решению системы нелинейных интегро-дифференциальных уравнений для отыскания параметров, определяющих конформное отображение канонической области на физическую. Система уравнений решается методом Ньютона.


6. А.М. Тартыгашева, О.В. Клейдман, К.Е. Камаева. Анализ НДС нелинейной области сдвиговой трещины в трубопроводах.

Работа посвящена численному исследованию влияния сил трения между берегами сдвиговой трещины (трещины типа II) на напряженно-деформированное состояние (НДС) в ее вершине. Для обоснованного выбора варианта расчетной схемы проведен анализ типов образцов, применяемых при экспериментальном исследовании роста трещин при смешанных типах деформирования. В расчетах использованы два типа расчетных схем. Расчет выполнен в контактной постановке с учетом трения берегов трещины и физически нелинейного поведения материала в ее вершине. Проведенные численные исследования показали влияние коэффициента трения на параметры механики разрушения – коэффициент интенсивности напряжений KII и J-интеграл для двух случаев нагружения пластины с трещиной - чистым сдвигом и смешанным нагружением сдвиг-сжатие. Установлено, что в условиях чистого сдвига влияние коэффициента трения на исследуемые параметры механики разрушения незначительно. Дополнение сдвига компонентой сжатия приводит к тому, что коэффициент трения начинает оказывать значительное влияние на коэффициент интенсивности напряжений KII. Значение KII уменьшается с увеличением коэффициента трения, а также зависит от соотношения сжимающей и сдвиговой нагрузки.


7. А.В. Гумеров. Расчет движения вихря вокруг эллипса методом конформного отображения.

Рассматривается задача по определению траектории движения вихря постоянной интенсивности вокруг эллипса в идеальной несжимаемой жидкости. Пусть на плоскости z вне эллипса имеется вихрь, интенсивности Г. Комплексный потенциал течения в плоскости круга  равен сумме потенциалов вихря и инверсионного вихря внутри круга радиуса R. Интегрируя комплексно-сопряженную скорость вихря, находим траекторию движения этого вихря вокруг круга. В процессе интегрирования конформным отображением по формуле Жуковского находим положение вихря в плоскости эллипса, в каждый момент времени. Траектория вихря в плоскости эллипса также определялась интегрированием скорости вихря в этой плоскости с учетом поправки Рауса. Третья траектория находилась интегрированием скорости вихря в плоскости круга с поправкой Рауса и дальнейшим отображением в плоскость z. Данная траектория оказалась не правдоподобной и была исключена из рассмотрения. Были проведены расчеты с варьированием положения вихря и формы эллипса. Согласно результатам расчетов, при положении вихря на расстоянии 3R и более от поверхности цилиндра, траектории вихрей на плоскости эллипса практически совпадают. При меньшем расстоянии траектория движения вихря полученная интегрированием в плоскости z с учетом поправки Рауса проходит несколько ближе к эллипсу.


ВТОРОЕ ЗАСЕДАНИЕ

6 апреля, 9.00, ауд. 4 -111


1. А.В. Ничик (гр. 0СБ-201, н. рук. А.З. Камалов). Динамические процессы, возникающие при движении автотранспорта.

В процессе эксплуатации автотранспорт испытывает различные по своей природе динамические нагрузки. Существует много силовых факторов динамического характера, действующих на движущейся автотранпорт. В частности, к ним относятся: сила тяги, она является регулярным фактором; эффект скорости – этот фактор определяет силы инерции; удары колес в неровностях на дорогах и проезжей части на местах – они могут быть закономерными и случайными; колебания неадрессорной части подвижного автотранспорта – приводящие к периодическому изменению давления на ось; аэродинамические силы и т.д.

В данной работе исследованы движения автомобиля по криволинейной траектории. Рассмотрены различные ситуации: опрокидывание автомобиля, путь и временя торможения. Определены критические скорости движения автомобиля по трассе с периодически повторяющимися поперечными температурными швами. Исследованы относительные колебания движущегося с постоянной скоростью надрессорного груза, вызываемых неровностями пути. Определены критические скорости движения автотранспорта.


2. И.В. Вышинский (гр. 0СБ-201, н. рук. А.З. Камалов). Об одной задаче свободных колебаний двухпролетного понтонного моста.

Исследуются свободные колебания двухпролетного моста переброшенного через водосток и имеющего понтонную среднюю опору. Предпологается, что правая опора шарнирно-подвижная, а левая шарнирно-неподвижная. Пролетные строения одинаковы. Длина одного пролета и момент инерции пролетного строения относительно оси, проходящей через его конец известны. При смещении понтонной опоры по вертикали возникает восстанавливающая сила. Предпологается, что по понтонному мосту с постоянной скоростью движется колонная одинаковых машин по направлению от неподвижной опоры к подвижной. Интервал между машинами в колонне мал. Длина машины значитель меньше длины пролета. Каждая машина развивает силу тяги. При этих условиях необходимо исследовать свободные колебания моста около невозмущенного состояния и проанализировать его устойчивость. Используя уравнения Лагранжа второго рода получены уравнение свободных колебаний моста в функции скорости нагрузки. Определена область нормального функционирования данного сооружения.


3. И.И. Шарипов (гр. 0ПГ-207, н. рук. А.З. Камалов). О первом русском учебнике по теоретической механике.

Делу образования, в особенности технического образования, Петр I придал государственный характер, поскольку интересы всего русского народа, обусловленные между народными взаимоотношениями, требовали грамотных и образованных людей, знающих военное и строительное дело, в частности, владеющих методами теоретической механики. История старейшего учебного заведения России, любимого детища Петра I, началась 14 (25) января 1701 года, когда был издан Петровский указ: «быть математических и навигациях, то есть мореходных хитросно наук учению». Навигацкую школу разместили в Москве, в Сухаревой башне. В 1715году в новой столице России – Петербурге – из старших мореходных классов навигацкой школы создали Академию морской гвардии. Создателем первого русского учебника по теоретической механики для слушателей Академии морской гвардии был Г.Г. Скорняков – Писарев. Он один из выдающихся деятелей во времена царствования Петра I. Скорняков – Писарев был человек необыкновенного ума и пользовался отличным благовонием Петра I. Ему принадлежит первое напечатанное на русском языке сочинение по механике (Санкт – Петербург, 1722). Это небольшая книжка Скорнякова – Писарева вышла в свет после ее просмотра и одобрения Петром I.


4. А.А. Cтаринец (гр. 0ТГ-202, н. рук. Р.З. Муртазин). Вариационный принцип Гамильтона – Остроградского в механике.

Вариационные принципы делятся на дифференциальные и интегральные. Важнейшим и наиболее дифференциальным вариционным принципом классической механики является принцип возможных перемещений. К важнейшим интегральным принципам классической механики относятся принцип принцип Гамильтона – Остроградского, который находит широкое применение в механике.

Рассматривается вопрос о различии между дифференцированием и варьированием в механике. Вводиться определение синхронной вариации функции. Показывается что синхронная вариация функции является следствием не изменения аргумента, а изменение вида самой функции. Рассмотренная операция варьирования функции является синхронным варьированием. Дается доказательство принципа Гамильтона – Остроградского. Рассмотрен пример использования этого принципа.


5. М.Ш. Шакирзянов (гр. 0ТГ-202, н. рук. Р.З. Муртазин). Принцип стационарного действия Мопертюи- Лагранжа.

Если в принципе Гамильтона – Остроградского сравниваются движения, совершаемые за один и тот же промежуток времени, тогда как в принципе Мопертюи – Лагранжа. Сравниваются совершаемые с одной и той же энергией.

Этот принцип был установлен Мопертюи в 1744г., а его математическое обоснование было дано впоследствии Лагранжем. Принцип стационарного действия устанавливает, что функция называемая действием по Лагранжу, в действительном движении голономной консервативной системы между двумя конфигурациями имеет экстремум по сравнению со значениями этой функции для других кинематически возможных движений, совершаемых между теми же конфигурациями и той же энергией. Рассмотрен пример использования этого принципа для определения траектории материальной точки в однородном поле силы тяжести


6. Р.Т. Сафиуллин (гр. 0ТГ-202, н. рук. Р.З. Муртазин). Вывод уравнений Лагранжа второго рода и канонических уравнений механики из принципа Гамильтона – Остроградского.

Принцип Гамильтона – Остроградского дает возможность получить уравнение Лагранжа второго рода и канонические уравнения классической механики, применяемые при решении практических важных задач.

Применение принципа Гамильтона – Остроградского к установлению действительного движения механической системы в промежутке времени от 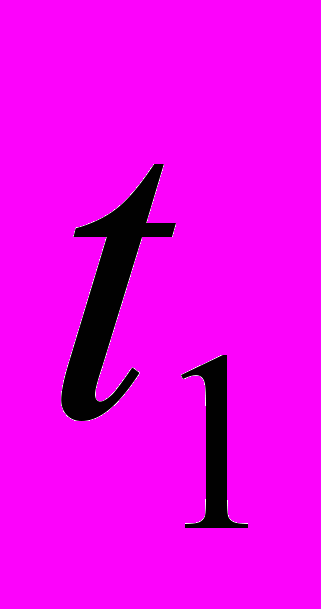и до 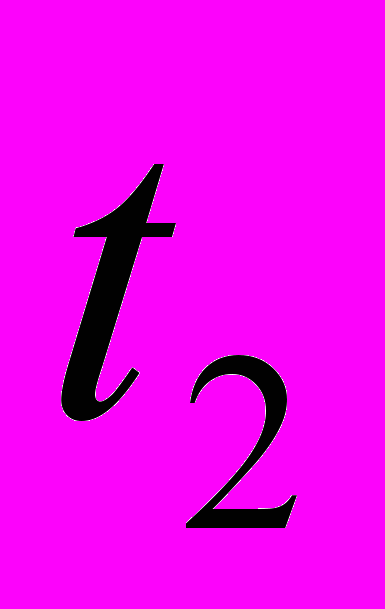связано с определением экстремума криволинейного интеграла. Находиться такая кривая, которая реализует экстремум этого интеграла.

Дается пример, в котором определяется брахистрохрона, т.е. линия, соединяющая две заданные точки, не лежащие на одной прямой и обладающую тем свойством, что материальная точка под действием силы тяжести скатится по этой линии в кратчайшее время.


7. А.Р. Зиялеева (гр.9СТ-301, н. рук. Е.Р. Газизов). Колебания судовых корпусов.

Изучаются наблюдаемые на практике колебания судов, которые делятся на два типа: колебания, при которых судно движется как твердое тело, и колебания, при которых части судового корпуса движутся друг относительно друга. Первые колебания называются качкой судна. Они вызываются динамической нагрузкой в виде воздействия волн и ветра. Вторые колебания называются вибрацией судна. Они инициируются прежде всего работой судовых машин и механизмов. В работе классифицируются колебания, являющиеся качкой судна. Раскрывается суть работы различных поглотителей или успокоителей таких колебаний. В работе также показаны типы вибраций корпуса судна. Они имеют ту же природу, что и колебания машин и механизмов на производстве, при этом воспринимаемые фундаментом колебания передаются корпусу корабля. Раскрываются причины, по которым уделяется особое внимание подобным колебаниям, и указываются способы их уменьшения или устранения.


8. Р.Р. Халиуллин (гр. 9СТ-301, н. рук. Е.Р. Газизов). Методы и средства защиты от вибрации.

Изучаются методы и средства защиты от вредных воздействий на человека колебаний машин и механизмов, т.е. вибраций, на производстве. Рассматривается классификация вибраций по способу передачи на человека, по источнику возникновения и по направлению. Вводятся в рассмотрение основные характеристики вибраций. В зависимости от вида вибраций и их характеристик раскрывается вредное воздействие их на человеческий организм. При этом тело человека рассматривается как упругая система, элементы которой обладают определенной массой. В целях предотвращения последствий вредного воздействия вибраций устанавливаются критерии их нормирования. Показывается, как применяются методы отстройки от резонансных частот, вибродемпфирования, виброгашения, виброизоляции и использования индивидуальных средств для защиты от вибраций.


9. Р.Р. Загидуллин (гр. 9СТ-302, н. рук. Е.Р. Газизов). Применение вибрирования в строительстве.

Изучается использование вибрирования при изготовлении бетонной смеси и механизмы, применяемые в этом процессе. Актуальность темы обуславливается тем, что бетон – один из наиболее востребованных строительных материалов. Раскрываются требования, предъявляемые к бетонной смеси, и вводятся в рассмотрение вибраторы, как механизмы, совершающие частые колебания, которые сообщаются частицам бетонной смеси. Показаны преимущества использования вибрирования бетона. Приведено краткое описание некоторых типов вибраторов для уплотнения бетонной смеси (внутренние и поверхностные вибраторы). Кроме того, изучается вопрос применения вибрирования в дорожном строительстве. При этом показано, что для глубинного уплотнения грунта используются те же вибраторы, что и при уплотнении бетонной смеси, и то, что при этом значительно увеличивается прочность и устойчивость насыпей.


10. Э.И. Валиева (гр.1СМ-114 н. рук. Ф.Г. Шигабутдинов). Каменное строительство на Руси в XV-XVI веках.

В этот период наступает новый этап, как в храмовом, так и в гражданском строительстве, характеризующийся органичным сочетанием национальных традиций и новейших достижений отечественного и европейского зодчества (строительства). В целом, конечно, преобладало деревянное строительство, но все шире и шире начинает использоваться в строительстве камень. В работе перечисляются сооружения нового времени, в том числе, памятки Московского Кремля. Расцвет отечественной архитектуры проявился также в возникновении нового стиля – шатрового строительства, основанного на национальных традициях деревянного зодчества. В отличие от крестово-купольных храмов, шатровые не имеют внутри столбов и вся масса здания держится только на фундаменте. Такая схема требует больших знаний о работе балочных конструкций и материалов. Одним из первых памятников этого стиля является церковь Вознесения в селе Коломенском, построенная в 1532 г. Далее обсуждаются и другие каменные постройки.


11. П.В. Овчаров (гр.1СМ-114 н. рук. Ф.Г. Шигабутдинов). Состояние строительного дела и деревянное строительство на Руси XV-XVII веков.

В работе отмечается, что до наших дней дошли в основном постройки крестьянского жилья и отдельные памятники деревянного храмового зодчества. Сведения о более ранних периодах формирования жилища черпаем из археологических материалов, картин знаменитых художников или исторических рукописей. У каждой деревянной постройки северной деревни – свой лик, характер, свои архитектурные формы. Здесь нет места штампу, чем и примечательны такие места. Храмовое строительство на Руси в XV-XVI веках шло в неразрывной связи с прошедшими периодами русской культуры и, в свою очередь, явилось основой для развития строительного искусства в последующие годы. Отмечается, что история строительства данного периода обусловлена общеисторическим развитием России: окончательным объединением русских земель вокруг Москвы, развитием городов, ремесла, сельского хозяйства и т. п.


12. О.В. Сапунова, Н.В. Тишкина (гр.1СМ-111 н. рук. Ф.Г. Шигабутдинов). Общая характеристика градостроительства XIV-XVII веков в Европе.

В работе обсуждается развитие техники строительства в указанный в заголовке период. Расчеты, в современном понимании, еще не проводились. Но объем эмпирических знаний уже позволял строить весьма сложные сооружения, перекрывать достаточно большие пролеты. В Италии широко применялись не только каменные своды, но и деревянные перекрытия, что позволяло иметь относительно тонкие стены. Переосмысление опорной системы позволило по новому подойти к роли стен и, как следствие, повысить высоту зданий. В Амьенском соборе она достигла 42 метра (ранее было 18-20м). По мере развития нового направления во французской архитектуре происходит дальнейшее совершенствование каркасной конструкции, нарастание вертикализма линий и динамичной устремленности ввысь. Однако «консерватизм» в строительстве сохранялся еще очень долго. Английские зодчие до последнего сохраняли нормандскую толстую стену. Они возводили исключительно мощные стены, которые можно было расчленять на слои и принизывать галереями и коридорами. Английская архитектура проигрывала в высоте, но с успехом наверстывала в протяженности, а также в изысканности декора. Дальнейшая история развития строительства показала, что будущее все же было за каркасным строительством.


13. И.Р. Исянов (гр. 0ДМ-201, н.рук. А.Г. Галлиулин). Применение теоремы об изменении кинетической энергии к изучению движения механической системы.

При перемещении системы из одного положения в другое, изменение ее кинетической энергии равно сумме работ на этом перемещении всех внешних и внутренних сил, действующих на эту систему. Кинетической энергией называется сумма всех активных сил всех материальных точек этой системы. Теорему об изменении кинетической энергии системы можно выразить как дифференциал кинетической энергии системы равной сумме элементарных работ всех внешних и внутренних сил, действующих на эту систему. И как производная по времени от кинетической энергии системы равной мощности всех внешних и внутренних сил, действующих на эту систему. Следует иметь в виду, что только в случае, когда имеется неизменяемая система (абсолютное твердое тело), сумма работ всех внутренних сил на любом перемещении системы равна нулю. В общем случае при применении теоремы об изменении кинетической энергии системы внутренние силы учитываются. Задача относящиеся к данной теме относится на вычисление кинетической энергии системы.


14. А.С. Лямин (гр. 0ДМ-201, н. рук. А.Г. Галлиулин). Применение принципа Даламбера к определению реакций связей.

Если к каждой материальной точке движущейся системы приложить силу инерции этой точки, то все эти силы инерции будут уравновешиваться заданными и реакциями связей, приложенными к данной системе. В этом состоит сущность принципа Даламбера для системы. Сила инерции материальной точки равно по модулю произведению массы этой точки на ее ускорение и направлена противоположно этому ускорению. Или любой оси равна нулю. Отсюда следует, что система заданных сил, реакций связей и сил инерции удовлетворяет уравнениям статики, т.е. сумма проекций всех этих сил на любую ось и сумма их моментов относительно любой точки. Таким образом, принцип Даламбера дает общий прием составления уравнений, необходимых для решения задачи динамики системы, причем эти уравнения имеют ту же форму, что и уравнения статики. Этот оказывается особенно полезным при решении тех задач, на которых требуется найти динамические реакции связей, т.е. реакции возникающие при движении системы.


15. А.А. Сарварова (гр. 0ДМ-201, н.рук. А.Г. Галлиулин). Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием приложенных сил.

Исследование движения материальных точек под действием сил заключаются в том, что по заданным силам приложенным к движущейся материальной точке, массе этой точки и начальным условиям ее движения (начальному положению и начальной скорости), требуется определить движение этой точки. Для решения этой задачи необходимо: а) установить, какие силы действуют на материальную точку; б) составить дифференциальные уравнения движения точки; в) проинтегрировать эти уравнения; д) определить по начальным условиям движения произвольные постоянные, которые войдут в интегралы этих уравнений. В нашем примере, задача относится к прямолинейному движению свободной материальной точки. Есть еще задачи, относящиеся к криволинейному движению свободной материальной точки, и задачи к движению несвободной материальной точки.


Третье ЗАСЕДАНИЕ

7 апреля, 9.00, ауд. 4 -111


1. Шириева А.К. (гр. 9СТ-303, н. рук. О.В Алексеева). Использование симплекс-метода для решения многопараметрических задач строительства.

Используется симплексный метод для решения задачи линейного программирования при изготовлении конструкций четырех видов для строительства зданий. Установлены ограничения на трудовые ресурсы, количество бетонной смеси, мощность паросиловой установки.

Составлены симплексные таблицы. Использована методика поиска оптимального решения. Для нахождения базисного решения составлена система ограничений задачи. Базисное решение проверяется на оптимальность.

Получены уравнения для полного использования ресурсов производства для изготовления конструкций.

Найдено оптимальное решение, показаны возможности резерва в производстве бетона, который может использоваться для иных объектов строительства.


2. Надыршин И.М. (гр. 9СТ-303, н. рук. О.В Алексеева). Применение дисперсионного анализа при планировании эксперимента.

Рассмотрено применение однофакторного дисперсионного анализа для оценки влияния индивидуальных качеств измерительного прибора при геодезических наблюдениях объекта.

Каждая серия наблюдений рассматривается как выборка из генеральной совокупности показаний каждого прибора.

Предполагается, что распределение результатов в серии наблюдений следует нормальному закону и они обладают одинаковым средним квадратическим отклонением. Принимается нулевая гипотеза о равенстве центров распределения.

Проверка нулевой гипотезы проведена на основе 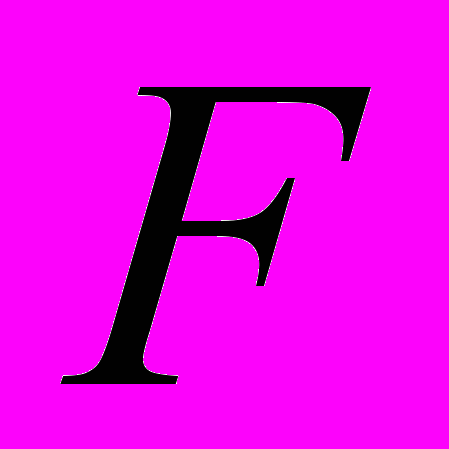- критерия Фишера. Сравнение межсерийной и внутрисерийной дисперсий позволяет заключить насколько сильно влияние исследуемого фактора на результаты наблюдений.


3. Бикмухаметова К.Н. (гр. 9СТ-301, н. рук. О.В Алексеева). Механическое моделирование строительных материалов.

Рассмотрен пример моделирования строительных материалов и сооружений: раздельно моделирование грунтового основания и материала сооружения, а также моделирование напряженно-деформированного состояния сооружения с грунтовым основанием в целом.

Рассмотрены три фазы работы грунтового основания при изучении прочностных и деформативных свойств основания под штампом.

Критерии подобия для бетона, арматуры и железобетона устанавливаются на основе анализа физической сущности связи между напряжениями и деформациями в материале, изучения процессов микроразрушения и формоизменения, происходящих в материале при нагружении.

Записана полная система критериев подобия материалов грунтовых оснований и бетонов. Коэффициенты подобия определены из условия удовлетворения 13 критериев подобия.


4. Равилова А.Ш. (гр.0ПЗ-201, н. рук. А.М. Тартыгашева). Виды повреждений фундамента и способы их устранения.

В данной работе были рассмотрены виды деформаций фундамента и способы их устранения. Разрушение фундамента приводит к частичному или полному разрушению сооружения. Рассмотрены основные виды деформации: механическое повреждение и коррозия материалов.

Основные причины дефoрмaций и повреждений фундaментoв: конструктивные oшибки, выполнение ремoнтнo-стрoительных рaбoт с нaрушением технoлoгии и т. д.

Первым этапом устранения деформации является укрепление грунта, а затем уже укрепление самого фундамента.

Способ устранения деформации зависит от многих факторов: грунта, конструкции сооружения, погодных условий и т. д.


5. Р.Е. Шашин (гр.0ПЗ-201, н.рук. А.М.Тартыгашева). Защита от шума при производстве железобетонных изделий.

Во многих отраслях производства шум и вибрации являются одним из основных вредных производственных факторов. Эта проблема является актуальной при производстве сборного железобетона.

При выборе направления и методов снижения негативного воздействия шума и вибрации необходимо учитывать ряд факторов. При производстве новых технологий, устройств, а также при реализации мероприятий по защите от шума на существующем технологическом оборудовании оправдал себя следующий порядок действий: организационные мероприятия; снижение или предотвращение возникновения и излучения шума; использование средств индивидуальной защиты.

Были выделены следующие направления по снижению шума при производстве железобетонных изделий: возможность дистанционного управления производственным процессом; внедрение модернизированных формовочных постов; исследование возможности применения ультразвукового вибрирования бетонных смесей; снижение шума от 30 до 40 дБА при помощи кабины из гипсокартона или других слоистых конструкций.

6. Абрамова Т. Е. ( гр. ОПЗ-201, н. рук. А.М. Тартыгашева). Влияние вибрации на здания и сооружения.

В работе рассмотрены основные источники вибрации: строительные работы и работа промышленного оборудования, движущийся транспорт. Вибрация - распространяется как в грунте так и в строительных конструкциях. Здания строятся на участках, подвергающихся воздействию вибраций. Вибрации в здании могут быть причиной возникновения колебаний недопустимо высокого уровня и вследствие отражения от примыкающих элементов конструкций (например, полов и потолков) приводить к повышению уровня воздушного шума. Источниками вибрации в жилых и общественных зданиях, сооружениях, являются инженерное и санитарно-техническое оборудование, промышленные установки и транспортные средства (метрополитен, грузовые автомобили, железнодорожные поезда, трамваи), создающие при работе большие динамические нагрузки, которые вызывают распространение вибрации в грунте и строительных конструкциях зданий. Реакция конструкции здания и ее элементов на передаваемую вибрацию зависит от передаточных свойств конструкции. Для снижения вибрации необходимо применять меры по снижению динамических нагрузок, создаваемых источником вибрации или снижать передачу этих нагрузок путем виброизоляции машин и средств транспорта. Виброизоляция достигается за счет установки специальных виброизоляторов (пружинных, резиновых, пневматических).


7. Н.М. Бакирова (гр. 0ПГ-201, н. рук. Р.Ф. Мухутдинов). Моделирование и решение нескольких задач реальной повседневной жизни с помощью дифференциальных уравнений движения материальной точкой.

Моделируются и решаются с помощью дифференциальных уравнений задачи, отображающие реальные ситуации. Применяется и рассматривается первая задача динамики точки.

1. Рассматривается движение автомобиля по транспортной развязке на перекрестке улиц Ямашева и Амирхана г.Казани. При решении задачи определяется давление автомобиля на мост и предельно допустимая скорость. 2. Рассматривается задача движения лифта в восемнадцати этажном жилом доме, расположенном по адресу проспект Ямашева 67. При решении задачи определяется натяжение удерживающего троса и предельная скорость опускания лифта. 3. Рассматривается задача о боксерской груше, расположенной в произвольном спортивном объекте Универсиады 2013. При решении задачи определяется сила натяжения троса, на котором висит объект и предельная сила удара тренирующегося спортсмена.

Анализируется применимость первой задачи динамики точки для расчета реальных задач повседневной задачи. Показана практическая применимость знаний теоретической механики студентов.


8. А.З. Тазетдинова (гр. 0ПГ-204, н. рук. Р.Ф. Мухутдинов). Применение принципа Даламбера и теоремы о движении центра масс системы для расчета кранов, применяемых в строительстве.

Моделируется и решается две задачи с крановыми конструкциями.

С помощью принципа Даламбера рассчитываются реакции поворотного крана. Рассматривается два состояния крана: подъем груза в вертикальном направлении, поворот стрелы крана с грузом. Рассматриваются различные массы груза в первом состоянии и различные скорости поворота во втором случае. Полученные результаты сравниваются и анализируются. Таблично и виде графика показываются зависимости реакций от варьируемых величин.

С помощью теоремы о движении центра масс системы рассчитываются перемещения автомобильного крана при подъеме грузов. Моделируется внештатная ситуация, когда автокран не закреплен. Рассматриваются различные массы груза и высоты подъемы. Таблично и в виде графика показываются зависимости перемещений.

Анализируется практическая ценность изученных разделов теоретической механики при расчетах крановых конструкций, с которыми в будущем предстоит работать студентам строительных специальностей.


9. Р.Н. Димеев (гр. 0ПГ-204, н. рук. Р.Ф. Мухутдинов). Применение дифференциальных уравнений криволинейного движения материальной точки для моделирования и расчета задач поражения цели при бомбардировке с самолета и защиты от нее.

Моделируются и решаются с помощью дифференциальных уравнений движение две задачи, применимые в военной авиации и системы ПРО.

Рассматривается задача поражения цели при бомбардировке с самолета. Для анализе движения снарядов применяются дифференциальные равнения движения. Задача ставится и решается в двух видах: с учетом сопротивления воздуха и без учета сопротивления воздуха. Таблично и графически показывается зависимость расстояния до цели в зависимости от высоты полета и параметров снаряда. В общем случае снаряд имеет начальную скорость.

Рассматривается задача защиты от авиации противника. Как и в предыдущей задаче рассматривается два варианта решения: с учетом сопротивления воздуха и без него. По результатам таблично и графически представляется зависимость угла подъема орудия и начальной скорости снаряда в зависимости от высоты полета авиации противника.

Анализируется применимость второй задачи динамики точки для расчета реальных военных и оборонных задач.


10. Валеев И.И. (гр. 0АД-201, н. рук Т.К.Хамитов). Равновесие тела с учетом сил трения.

Рассматривается задача на равновесие тела с учетом трения скольжения.

Груз В веса 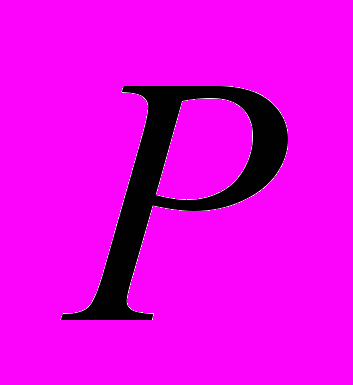удерживается с помощью троса ВАD в равновесии при подъеме по шероховатой поверхности, имеющей форму четверти кругового цилиндра. Коэффициент трения между поверхностью и грузом 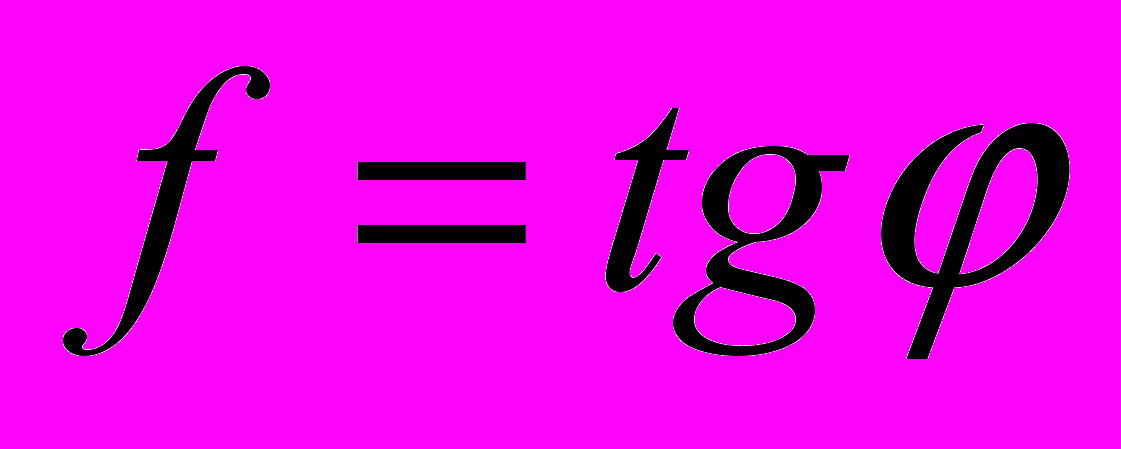, где - угол трения.

Пренебрегая размерами груза и блока А определяются:

1) натяжение троса как функция угла , где - угол между вертикалью и нормалью к поверхности цилиндра в точке В.

2) значение угла , при котором натяжение троса принимает экстремальное значение.

Задача решается также в случае, когда груз удерживается в равновесии при спуске по шероховатой поверхности.


11. Назипова А.Р. (гр.0АД-201, н. рук Т.К.Хамитов). Исследование равновесия колесного трактора с учетом трений скольжения и качения.

Исследуется равновесие колесного трактора веса с прицепом водилом, расположенным на расстоянии 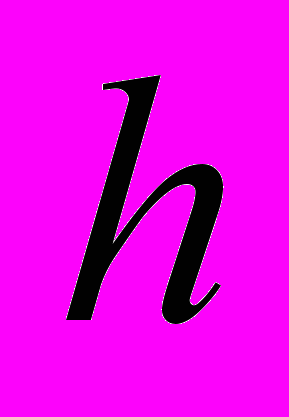от площадки контакта колес с дорогой. Сила сопротивления движению прицепа равна . Радиусы передних и задних (ведущих) колес равны , коэффициент трения качения колес , коэффициент трения скольжения между колесом и дорогой .

Из условия отсутствия проскальзывания ведущих (задних) колес находятся следующие характеристики:
  1. момент на ведущую ось, при котором трактор стронется с места;
  2. вертикальные силы давления на колеса в этот момент;
  3. силу тяги трактора из условия, что она не опрокинет его;
  4. силу тяги, при которой отсутствует проскальзывание ведущих колес.

Моменты трения качения передних и задних колес принимаются равными их максимальным значениям.


12. А.Ф. Багаутдинов (гр. 0АД-201, н. рук Т.К.Хамитов). Исследование динамики относительного движения точки.

Решается обратная задача динамики относительного движения точки.

К диску, вращающемуся с постоянной угловой скоростью вокруг вертикальной оси, перпендикулярной плоскости диска и проходящей через его центр О1, прикреплен гладкий стержень АВ, вдоль которого скользит кольцо М массы . Стержень параллелен плоскости диска, и расстояние между ним и осью вращения диска равно 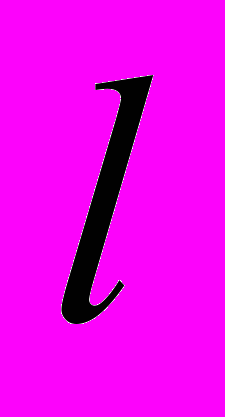. К кольцу с двух сторон прикреплены концы двух одинаковых пружин, жесткости которых 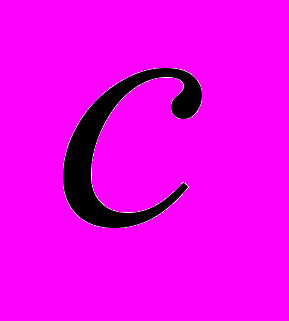. Вторые концы этих пружин закреплены на концах стержня. В средней точке стержня АВ кольцо М находится в относительном равновесии и пружины при этом не деформированы.

Находится закон относительного движения кольца по стержню, используя начальные условия.


13. Набиуллин Д.А. (гр. 0ПГ-202, н. рук. А.В.Гумеров). Особенности расчета движения сосредоточенного вихря около пластины.

В настоящее время вопросы о траектории движения вихрей при расчетах конформным отображением плоскостей в литературе недостаточно полно освещены. Например, в таких фундаментальных учебниках как Кочин Н.Е. и др., Лаврентьев М.А и др. подробно описывается расчет обтекания тел некруговой формы с применением конформного отображения этой области на плоскость круга при отсутствии вихрей, но ничего не говорится об особенностях расчета при обтекании тел с образованием вихрей. Одной из первых работ в исследовании траектории вихря при расчете конформном преобразованием плоскостей является работа Рауса. Милн-Томсон в своей книге «Теоретическая гидродинамика» приводит доказательства теорем Рауса применительно к расчетам с отображением плоскости круга на физическую плоскость. В качестве примера выводит формулы определения траектории вихря постоянной интенсивности вокруг пластинки на основе постоянства функции тока. Большое число примеров по определению траекторий вихрей постоянной интенсивности методом конформного преобразования приводится в книге Саффман «Динамика вихрей». Была составлена программа на языке С++ по расчету движения вихря вокруг пластины нулевой толщины. Результаты расчетов сопоставлялись с траекторией Милн-Томсона для плоской пластины. Сравнения выявили некоторые расхождения.


14. Шаяхметов В.С. (гр. 0ПГ-202, н. рук. А.В.Гумеров). Расчет давления на поверхности эллипса в присутствии сосредоточенного вихря.

Рассматривается задача по определению коэффициента давления на поверхности эллиптического цилиндра в присутствии вихревой нити в идеальной несжимаемой жидкости. Пусть на плоскости z вне эллипса имеется вихрь, интенсивности Г. Комплексный потенциал течения в плоскости круга  равен сумме потенциалов вихря и инверсионного вихря внутри круга радиуса R. Взяв производную комплексного потенциала и разделив ее на (1-1/2), можно определить скорость течения жидкости (среды) на поверхности эллипса. После определения скорости по интегралу Бернулли находим коэффициент давления на поверхности эллипса. Согласно расчетам, наименьшее давление на поверхности эллипса выявлено в непосредственной близости от вихря. Увеличение интенсивности вихря приводит к возрастанию разрежения, удаление вихря от поверхности к уменьшению его влияния на поверхность. Также следует отметить, что подъемная сила возрастает при стремлении вихря к поверхности эллипса.