Ф. Г. Шигабутдинов Зам председателя А. З. Камалов Секретарь А. М. Тартыгашева Первое заседание
| Вид материала | Заседание |
- Ф. Г. Шигабутдинов Зам председателя А. З. Камалов Секретарь А. М. Тартыгашева Первое, 261.12kb.
- У. Г. Зиннуров Зам председателя канд экон наук, доц. З. Ж. Гумерова Секретарь ст преп., 124.72kb.
- Программа и тезисы докладов Конгресса-2010 санкт-петербург, 240.76kb.
- Н. А. Шишков (зам председателя), 1974.79kb.
- Н. А. Шишков (зам председателя), 1980.47kb.
- Программа четырнадцатой конференции молодых ученых-химиков нижегородской области (17-19, 125.08kb.
- Академики в п. Волгин (председатель),, 12468.59kb.
- Семенов Сергей Максимович, канд техн наук, зав кафедрой информационных систем и компьютерных, 157.7kb.
- А. Ф. Андреев ифп, председатель > В. Г. Каменский ифп, зам председателя > Е. Г. Николаев, 390.61kb.
- И. П. Павлова (наб. Макарова, 6) >10. 30 Открытие конференции 11. 45 Первое пленарное, 519.2kb.
Кафедра теоретической механики
| Председатель | Ф.Г. Шигабутдинов |
| Зам. председателя | А.З. Камалов |
| Секретарь | А.М. Тартыгашева |
Первое ЗАСЕДАНИЕ
7 апреля, 9.00, ауд. 4 -111
1. Ф.Г. Шигабутдинов. Видео курс лекций по статике.
В докладе демонстрируется видео курс по статике для студентов инженерных вузов. Курс представлен на 9 DVD дисках и может быть просмотрен на персональных компьютерах и на бытовых видеопроигрывателях. Изложение ведется в реальном времени, запись производилась в аудиториях для лекционных занятий. Материал адресован лицам обучающимся по заочной форме обучения, получающим второе высшее образование, отставшим по уважительным причинам, лицам изучающим курс самостоятельно. Материал разбит не по номерам лекций (было прочитано 9 лекций), а по темам, что при необходимости позволяет дополнять курс новым темами или не изучать отдельные темы. На дисках приводятся методические рекомендации по изучению материала, теоретическое изложение дополнено рассмотрением задач, способствующим успешному выполнению контрольных и расчетно–графических работ. По мнению автора найдено оптимальное соотношение между объемом изложенного материала и временем необходимым для его первичного просмотра. Видео курс поддерживается учебным пособием автора на бумажном носителе.
2. Ф.Г. Шигабутдинов, А.Ф. Шигабутдинов. К вопросу о подготовке специалистов корпоративных научно-исследовательских центров.
Развитие отечественной экономики по инновационному пути предполагает уход от сырьевой зависимости, повышение в структуре национальной экономики доли перерабатывающей промышленности с внедрением новых инновационных технологий, повышение качества производимых товаров и услуг. В России имеются важные предпосылки для модернизации и развития экономики по инновационному пути. Представляется очень важным активно использовать имеющиеся ресурсы и, не ломая сложившуюся систему функционирования производства, последовательно наращивать инновационный потенциал отечественной экономики. В современной конкурентной мировой экономике компании стремятся иметь собственные, ориентированные на решение технологических проблем, корпоративные научные центры. Продукцией таких центров являются новые технологии, которые внедряются на предприятии, а затем, как правило, продаются другим организациям. Это значительно повышает прибыль современных высокотехнологичных компаний, она слагается не только от продажи продукции, производимой предприятием, но и от реализации интеллектуальной собственности компании, исключительной задачей научного центра является также содействие руководству компании в формировании стратегического плана ее развития. Персонал научных центров состоит из специалистов различного профиля. Поэтому, техническое перевооружение страны, ориентированное на производство конкурентоспособной на мировом рынке продукции, потребует резкого увеличения инвестиций в подготовку персонала научных центров. Потребует формирование системы профессионального образования, обладающей высоким научно-техническим потенциалом, фундаментальностью, универсальностью и межотраслевым характером, учитывающей последние достижения национальной и мировой науки.
3. Ф.Г. Шигабутдинов, А.Ф. Шигабутдинов. Формирование системы подготовки специалистов корпоративных научно-исследовательских центров как фактор инновационного развития отраслевой экономики.
Инновационный путь предполагает развитие, основанное в первую очередь на знаниях, современных технологиях и инновационных процессах. К примеру, нефтехимические процессы настолько наукоемкий продукт, что даже крупнейшие мировые корпорации не в состоянии финансировать собственную разработку всех используемых в производстве технологий и значительная часть нефтехимических технологий крупными компаниями закупается с рынка. Однако, успешное развитие крупного предприятия нефтехимической отрасли будет малоэффективным без систематического взаимодействия с прикладной наукой. Современные научные центры крупных мировых промышленных компаний (корпоративные научные центры) имеют исчерпывающее техническое оснащение и большую испытательную базу. Научные центры компаний включают специалистов различного профиля, в том числе специалистов академической науки, технологов, конструкторов оборудования, материаловедов, прочнистов и т.д. Подготовка этих высококвалифицированных специалистов требует особого подхода с учетом лучших традиций отечественного и мирового опыта фундаментального и профессионального образования. Наиболее ценным в образовании специалиста научного центра предприятия становятся его умение и способность самостоятельно работать, учиться и переучиваться.
4. Р.З. Муртазин, Ф.Г. Шигабутдинов. Уравнения движения оболочек переменной толщины применительно к задачам удара.
В предыдущем выступлении авторов были доложены дифференциальные уравнения движения тонких пологих оболочек вращения переменной толщины с учетом поперечного сдвига и инерции вращения. Предполагалось их использование в задачах удара с учетом конечности скорости распространения возмущений. В качестве поверхности приведения использована была серединная поверхность.
Однако, одним из способов изготовления оболочек является намотка нитей на оправку. При этом при наличии переменности толщины, случайной или выполненной по конструктивным соображениям, серединная поверхность уже не является поверхностью симметрии тела оболочки. В предполагаемом докладе выведенные ранее уравнения обобщаются на случай произвольной поверхности приведения, в том числе и внутреннюю.
Уравнения записаны в общем случае в тензорном виде. В физических составляющих уравнения представлены для урезанного эллипсоида, цилиндра, урезанного конуса.
5. А.З. Камалов. О некоторых проблемах контроля самостоятельной работы студентов по кинематике.
Устный опрос студентов по теоретическому материалу в начале практических занятий, как правило, не дает истинной картины подготовленности студентов к практическим занятиям. Поскольку преподаватель в начале занятия успевает опросить максимум двух – трех студентов. Чтобы контроль был эффективным, студент должен знать, что он на каждом занятии будет опрошен и получит соответствующую оценку. Оперативно это можно реализовать только при помощи тестирования. В рекомендуемом вопроснике по кинематике приведены 93 вопроса. С использованием их, составлены 125 тестов, каждый из которых содержит по 6 вопросов. На каждый вопрос даются четыре ответа, два из них верные и два не верные. Вопросник по кинематике предназначен для оперативного контроля текущей работы студентов при ежемесячной аттестации, а также при оценке остаточных знаний студентов по кинематике.
6. А.З. Камалов. О вынужденных колебаниях арочного сооружения под действием ветровой нагрузки.
Исследуются вынужденные колебания арочного сооружения с полуцилиндрическим покрытием с равномерно распределенными подкрепляющими арками, находящегося под действием ветровой нагрузки. Считается, что ветровая нагрузка на подкрепляющие арки передается через цилиндрическое покрытие соединяющее их. Предполагается, что движение воздуха ламинарное и при решении задач вынужденных колебаний арочного сооружения под действием возмущенной среды вводиться сумма двух потенциалов. Один из них определяется как потенциал волн для абсолютно жесткого покрытия, возбуждаемых источником, второй – как потенциал рассеянных волн, порождаемых колеблющимся упругим покрытием. При указанных допущениях и предложениях исследованы колебания арочного сооружения. В частности, получены амплитуды вынужденных колебаний, критические значения скорости ветра.
7. О.В. Алексеева. О методике контроля текущей успеваемости студентов очной формы обучения.
Предложена методика контроля текущей успеваемости студентов, имеющая целью повышение успеваемости студентов очной формы обучения.
Разработаны формы аттестационных ведомостей для фиксирования преподавателями кафедр состояния текущей успеваемости студентов, которое на данный момент времени должно выполняться в соответствии с учебными семестровыми планами и фактического состояния, а также формы сводных аттестационных ведомостей для оформления их деканатами.
Обсуждается периодичность проведения контроля текущей успеваемости студентов в течении семестра, оптимальное для последующей работы деканата с отстающими студентами на строительно-технологическом факультете.
Проведен анализ использования методики на строительно - технологическом факультете.
8. Р.Ф. Мухутдинов. Исследование сходимости конечно-разностной схемы осесимметричного выпучивания цилиндрических оболочек переменной толщины при продольном ударе.
Рассматривается осесимметричное движения цилиндрических изотропных и ортотропных оболочек переменной и постоянной толщины при продольных ударах абсолютно твердым телом. Геометрически нелинейные дифференциальные уравнения движений тонкой оболочки типа Тимошенко, учитывающие сдвиг и инерцию вращения, получены из уравнений Галимова К.З. (Теория оболочек с учетом поперечного сдвига, 1977). Начальные условия соответствуют условиям удара телом по оболочке. Граничные условия принимались в виде комбинаций жесткого защемления и шарнирного опирания.
Изучаются и сравниваются различные варианты пространственной и временной сетки шагов метода конечных разностей по явной схеме, примененного к решению системы дифференциальных уравнений движения. Получены формы поперечного волнообразования (прогибы по всей длине оболочки) для девяти и более пробегов продольной волны вдоль оболочек, для исследования возможностей построенного алгоритма и программ. Результаты для сравнения представлены графически, в виде наглядных трехмерных графиков, в качестве осей координат выбрана продольная координата оболочки и время.
9. Ф.Г. Шигабутдинов, Р.З. Муртазин, Р.Ф. Мухутдинов. Влияние ортотропии на выпучивание упругих цилиндрических оболочек с постоянной и переменной толщиной при продольном ударе.
Рассматриваются осесимметричные и неосесимметричные продольно-поперечные движения цилиндрических ортотропных оболочек переменной и постоянной толщины при продольных ударах абсолютно твердым телом. Геометрически нелинейные дифференциальные уравнения продольно-поперечных движений тонкой ортотропной оболочки типа Тимошенко, учитывающие сдвиг и инерцию вращения, получены из уравнений Галимова К.З. (Теория оболочек с учетом поперечного сдвига, 1977).
Исследуются различные варианты соотношения модулей упругости оболочек. Начальные условия для перемещений и деформаций приняты нулевыми. Срединная поверхность выбиралась в форме круговой цилиндрической оболочки. Граничные условия принимались в виде подвижной шарнирной опорой на торце, воспринимающем удар, и неподвижной шарнирной опорой на другом конце. Для решения дифференциальных уравнений использовался метод конечных разностей по явной схеме. Результаты решения показаны в виде трехмерных форм изгиба срединной поверхности оболочек в различные моменты времени. Получены формы поперечного волнообразования (прогибы по всей длине оболочки) для девяти пробегов продольной волны вдоль оболочек.
10. Е.Р. Газизов. Обтекание вихрей тяжелой жидкостью.
Изучается стационарное потенциальное обтекание вихрей идеальной несжимаемой весомой жидкостью. При этом сначала в поток помещается вихрь заданной интенсивности
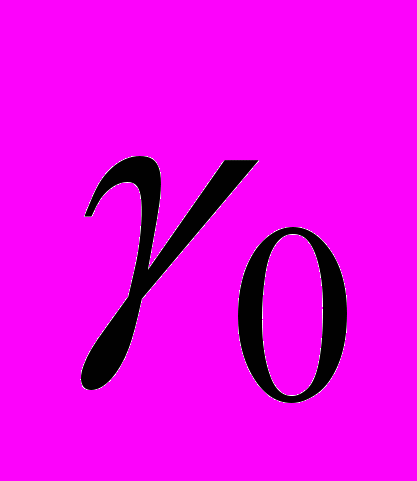. После прохождения этого вихря на поверхности возникают волны. Требуется решить задачу помещения в жидкость второго вихря интенсивности 
таким образом, чтобы справа на бесконечности волны отсутствовали. Ищется конформное отображение канонической области 
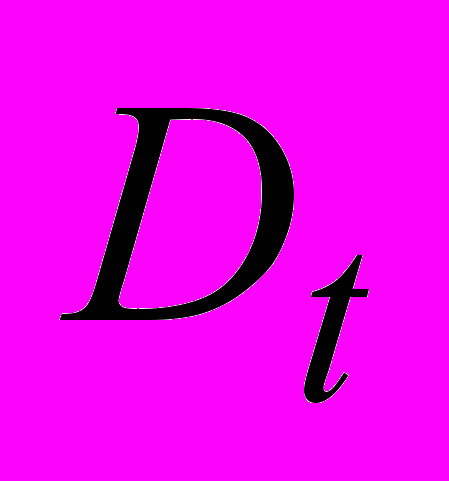в параметрической плоскости 
на физическую область течения 
. В качестве канонической области выбирается полоса ширины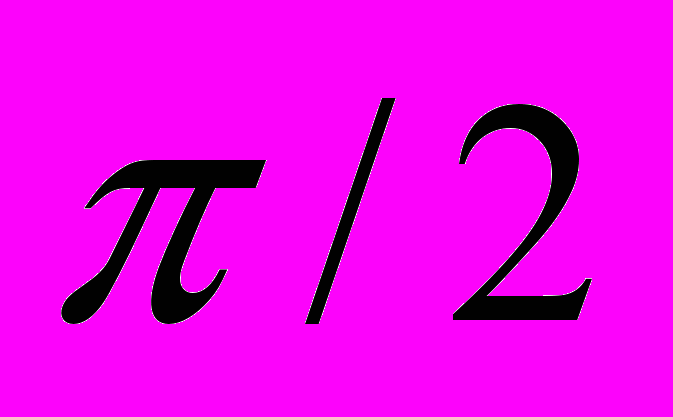 
. Нахождение конформного отображения сводится к краевой задаче отыскания аналитической и канонической области 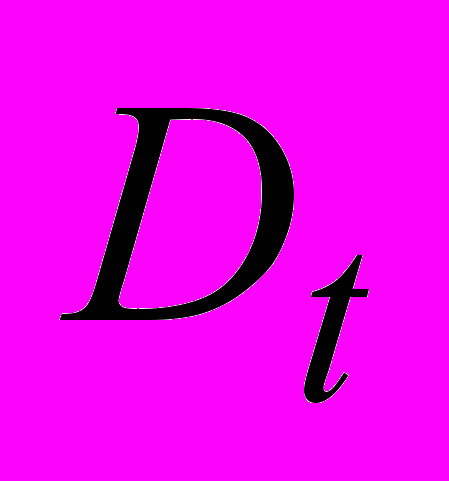функции 
, где 
- глубина невозмущенного уровня свободной поверхности слева на бесконечности. После этого решение задачи сводится к решению системы нелинейных интегро-дифференциальных уравнений для отыскания параметров, определяющих конформное отображение канонической области на физическую. Система уравнений после дискретизации решается методом Ньютона. 11. А.М. Тартыгашева, В.Н. Шлянников, Н.В. Бойченко. Нелинейные эффекты стеснения во взаимоперпендикулярных плоскостях при двухосном нагружении.
В настоящее время уже не вызывает сомнений необходимость систематических исследований эффектов стеснения в общей трехмерной постановке для установления различий между проявлением стеснения во взаимоперпендикулярных плоскостях. В данной работе численно в трехмерной постановке проведен анализ напряженно-деформированного состояния (НДС) круговой области, содержащей прямолинейную трещину. Установлена необходимость учета толщины тела при анализе эффектов стеснения. Необходимо отметить принципиальное отличие распределений эффективного напряжения на свободной поверхности образца и в срединной поверхности. Распределения эффективного напряжения в случае плоской деформации по характеру и по значениям аналогичны распределениям в плоскости симметрии трехмерного тела, а именно, в этих случаях отсутствует зависимость эффективного напряжения от времени ползучести при всех рассмотренных вариантах нагружения.
12. Т.К. Хамитов. Выпучивание упругопластических стержней при продольном ударе.
Рассматривается задача о выпучивании упругопластических полубесконечных стержней при продольном ударе, когда нагрузка на ударяемом торце мгновенно достигает своего максимального значения и остается постоянной. Для материала стержня принимается схема с линейным упрочнением. Предполагается, что потеря устойчивости происходит при первом прохождении волны сжатия вдоль стержня. Уравнение продольных движений считается решенным. Для решения уравнения поперечных колебаний применяется метод Бубнова-Галеркина. Как и в упругой задаче, в качестве функций прогибов используются стержневые функции из решения аналогичной статической задачи устойчивости. Рассмотрены четыре варианта граничных условий на ударяемом торце.
Критические нагрузки (напряжения) получены из равенства нулю усеченного определителя бесконечной системы однородных алгебраических уравнений относительно коэффициентов разложения функции прогиба в ряд Фурье. Аналитически доказывается сходимость бесконечных определителей. В качестве примеров рассматривались стальные и дюралюминиевые стержни. Вычисления проводились для различных значений касательного модуля. Результаты решения задач представлены в виде графиков и таблиц.
13. А.В. Гумеров Численные расчеты плоскопараллельного отрывного обтекания тел методом дискретных вихрей
В рамках исследования ветровых воздействий на сооружения, рассматривается нестационарная задача отрывного обтекания тел произвольной формы невязкой несжимаемой средой. Численная реализация задачи базируется на использовании метода дискретных вихрей. На поверхности обтекаемого тела располагается вихревая сетка. Посредине этих вихрей размещаются контрольные точки, в которых выполняются граничные условия о непроницаемости тела. След за обтекаемым телом моделируется свободными дискретными вихрями, движущимися вместе с потоком. Циркуляции свободных вихрей определяются завихренностью в точке отрыва и остаются неизменными по времени. Таким образом, математическое моделирование обтекания тел данным методом заключается в определении значений циркуляций вихрей, расположенных на контуре, с учетом интенсивностей свободных вихрей в следе. По циркуляциям этих вихрей может быть рассчитана величина скорости и давление в любой точке плоскости течения вне обтекаемого тела и непосредственно на его поверхности.
Второе заседание
8апреля 14.00, ауд. 4-111
1. А.А. Загайнова (гр. 29-202 н. рук. Ф.Г. Шигабутдинов). Исследование относительного движения точки.
В работе исследуются движение сложного кривошипно шатунного механизма в случае, когда одно звено механизма совершает прямолинейное движение. Сложность механизма заключается в том, что в его структуре содержатся два ползуна, один из которых совершает сложное движение по подвижной направляющей. Плоскости соприкосновения ползунов с их направляющими предполагаются идеально гладкими. Неподвижная направляющая сохраняет свое положение в пространстве, подвижная направляющая выполнена в виде гладкой рейки с прямой осью. Такое движение можно рассматривать исходя из теории относительного движения точки при плоско – параллельном движении всего механизма.
Определяются кинематические характеристики ползуна. Математическим аппаратом при решении задачи являются векторная алгебра и аналитические представление полученных уравнений. Результаты решения доводятся до числа.
2. А.А. Шайбаков (гр. 29-202 н. рук. Ф.Г. Шигабутдинов). Исследование кинематических характеристик составной плоской конструкции, одно из звеньев которой движется поступательно.
Задача исследуется с использованием теории плоско-параллельного движения твердого тела или системы твердых тел и теории относительного движения точки. Конструкция механизма включает два абсолютно твердых тела. Одно из них имеет неподвижную точку, выполненную в виде цилиндрического шарнира, может вращаться относительно этой точки. Само тело изготовлено из двух стержней, жестко скрепленных между собой под прямым углом. Второе тело, совершающее поступательное движение в направляющей, опирается одним концом на абсолютно гладкую поверхность одного из стержней первого тела. Соединение стержня с ползуном тоже происходит по абсолютно гладким поверхностям. В задаче задано движение тела, совершающего поступательное движение. Определяются кинематические характеристики точек вращающегося тела в различных положениях. Задача решается в общем виде. Математическим аппаратом для решения задачи выбрана векторная алгебра.
3. Н.А. Ефимова (гр. 29-201 н. рук. Ф.Г. Шигабутдинов). Исследование равновесия клина с учетом трения.
Исследуется равновесие клина, сжатого силой между двумя подвижными телами. Исследуется условие предельного равновесия. Силы трения в технике имеет и положительное, и отрицательное значение. С одной стороны они препятствуют движению, а с другой без наличия сил трения движение было бы невозможно. В докладе представлено исследование равновесия механической системы с учетом сил трения: между двумя телами, лежащими на шероховатой поверхности, вставлен клин с шероховатыми боковыми плоскостями. Клин вдавливается между этими телами силой, увеличивающейся во времени до тех пор, пока одно из тел не начнет движение. Требуется определить силу трения в предельном состоянии равновесия, действующую на тело, оставшееся неподвижным. Поставленную проблему удается решить анализируя состояние предельных равновесий тел, входящих в механическую систему. Решение производится при различных значениях геометрических характеристик тел, механических характеристик явления. Решение доведено до числа, сделаны выводы.
4. А.А. Курзякова (гр. 29-201 н. рук. Ф.Г. Шигабутдинов). Равновесие кривошипно-ползунного механизма с учетом и без учета трения между ползуном и направляющей.
Исследуется равновесие кривошипно ползунного механизма под действием двух сил с учетом и без учета сил трения в «трущихся элементах». К маховику, жестко соединенному с кривошипом кривошипно – шатунного механизма, подвешен груз. Нить, на котором весит груз, намотана на маховик без проскальзывания и считается нерастяжимой. Груз может привести механизм в движение, если не приложить силу, сопротивляющуюся движению к ползуну. Ползун может совершать прямолинейные поступательные движения вдоль вертикальной оси механизма. В докладе исследуется вопрос о силе, которую надо приложить к ползуну, чтобы механизм оказался в равновесии. Явление моделируется в двух случаях когда ползун может скользить в абсолютно гладких направляющих, и когда в ползуне возникает силы сопротивления – трения с заданным коэффициентом. Решение проводится в двух случаях, результаты сравниваются, даются практические рекомендации по подбору активной силы, приложенной к ползуну.
5. А.Р. Бикмухаметов (гр. 03-208 н. рук. А.З. Камалов). О некоторых ошибках в математических рассуждениях.
Математика представляет собой научную основу и является мощным инструментом современных фундаментальных и технических дисциплин. Именно, поэтому во все времена математические дисциплины подвергались различным реформам в системе образования.
В данной работе излагаются высказывания некоторых известных ученых – математиков, касающиеся реформ в системе образования. Рассматриваются примеры ложных рассуждений и анализ этих примеров. Далее приводятся примеры, иллюстрирующие характерные ошибки при математических рассуждениях. Предложены задачи на нахождение ошибок в этих математических рассуждениях.
При подборе предложенных задач главное внимание было обращено на уяснение сути и характерных ошибок при математических рассуждениях.
6. Н.Ш. Зиганшина (гр. 03-208 н. рук. А.З. Камалов). О достижениях механики античного периода.
Понимание основ любой науки, в том числе и теоретической механики, невозможно без знания истории ее возникновения.
Механика является одной из древнейших наук, возникновение и развитие которой обусловлено потребностями практики. Именно поэтому, развитие механики тесно связано с развитием земледелия, с ростом городов, возведением крупных построек.
В данной работе рассматривается история классической механики и обзор развития механики в античности, в частности, зарождение механики у древних греков. Показывается роль в развитии механики таких великих ученых мировой науки как Левкиппа, Демокрита, Эпикура, Марка Поллиона Витруля, Герона, Паппа, Платона, Аристотеля, Архимеда, Птоломея и др. Отмечается что после распада Римской империи была полностью утрачена теоретическая основа и возобладала только ремесленная.
7. А.Ф. Минсагиров (гр. 03-208 н. рук. А.З. Камалов). Жизнь Исаака Ньютона и его научное наследие.
Для творческой деятельности полезен жизненный опыт выдающихся представителей прошлых поколений. В данной работе исследуется жизнь И.Ньютона и его научное наследие. Приводятся интересные факты из жизни великого ученого и обзор его фундаментальных трудов «Математические начала натуральной философии», «Оптика», основные законы классической механики, дифференциальное и интегральное исчисления, закон всемирного тяготения. Отмечается, что им созданы основы небесной механики, открыта дисперсия света, построен зеркальный телескоп.
В знаменитом сочинении «Математические начала натуральной философии», изданном в 1687г., И. Ньютон в систематическом виде изложил основные законы классической механики. Эти законы, установленные на основании наблюдений и опытов И. Ньютона и его предшественников, являются объективными законами природы.
8. А.Р. Хатимов (гр. 03-201 н. рук. А.В. Гумеров). Возможные причины колебания волгоградского моста
Волгоградский мост — один из ключевых объектов программы комплексного развития Волгоградского транспортного узла, а также один из крупнейших объектов транспортной инфраструктуры российского значения. Колебания волгоградского моста, амплитуда которых составляла до 1 метра, вызвали удивление многих экспертов в области мостостроения. Впервые в мире это произошло с балочным мостом, а не с висячим. Висячие и вантовые мосты очень чувствительны к ветровым нагрузкам. Обычно, когда их проектируют, создают макеты и потом продувают в аэродинамической трубе, чтобы определить ветровые нагрузки. Балочные — самый простой вид мостов. Основная отличительная особенность балочной системы состоит в том, что с пролётных строений на опоры передаются только вертикальные нагрузки, а горизонтальные отсутствуют. А волгоградский мост балочный, такие ветровые нагрузки для них, по-видимому, не учитывались. К балочным мостам обычно относились спокойно – не было прецедентов, чтобы они от ветровой нагрузки могли разрушаться. Следует еще учитывать, что конструкция современных мостов стала облегченной. Раньше вес полезной нагрузки составлял около 20%, а оставшиеся 80% – мост нес сам себя. В современных мостах получается примерно 50 на 50. Мосты стали легче, ветровая нагрузка для них стала опаснее.
9. А.Р. Ювакаева, А.Р. Садыкова (гр. 03-201 н. рук. А.В. Гумеров). Методы моделирования обтекания сооружений ветровым потоком.
На сегодняшний день существуют два основных метода численного решения дифференциальных уравнений механики жидкости и газа – сеточные (эйлеровы) и бессеточные (лагранжевы). Эйлеровы методы основаны на решении уравнений движения на разного рода сетках (конечно-разностых, конечно-элементных или конечно-объемных) невязкой жидкости или вязкой жидкости. Лагранжевы методы основываются на предположении о потенциальном характере течения вне обтекаемой поверхности. Для его решения обтекаемая поверхность и ее след заменяется некоторым распределением элементарных особенностей с потенциалом известного вида. Потенциалы особенностей удовлетворяют уравнению Лапласа. Задача сводится к удовлетворению граничных условий и отысканию интенсивностей вихрей. Достоинством сеточных методов является их строгая математическая обоснованность, контролируемая погрешность. Расчеты на мелкой сетке ведут к большим вычислительным затратам. Из недостатков влияние положения границ расчетной области и характера граничных условий, необходимость построения расчетной сетки. При использовании лагранжевых методов поле течения определяется на самой поверхности и в следе. Автоматическое удовлетворение условиям на бесконечности, снимает проблему с влиянием положения границ и характера граничных условий. Недостатки – невозможность явного учета вязкости, наличие ряда свободных параметров.
10. М.М. Исламов (гр. 03-201 н. рук. А.В. Гумеров). Исследование устойчивости несимметричного развития вихрей за круговым цилиндром.
Рассматривается поперечное отрывное обтекание кругового цилиндра несжимаемой невязкой жидкостью. Скорости движения вихрей равны местной скорости жидкости. Интенсивности развивающихся вихрей пропорциональны квадрату скорости течения вблизи точки отрыва потока от цилиндра. Несимметричность вводится скачкообразным смещением первого вихря на малую величину в заданном направлении. Пусть в некоторый момент времени t симметрично развивающаяся пара вихрей имеет интенсивности Г и занимает положения
и 
, где i – мнимая единица. В этот момент первый вихрь получает малое возмущение 
и оказывается в отклоненном от симметричного положении 
, где p – малая величина, (
). Требуется исследовать характер дальнейшего изменения возмущения . Для этого необходимо определить знаки производных 
и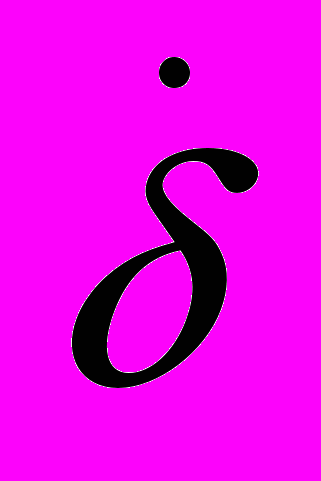 
в равенстве 
, где 
– комплексная скорость течения в точке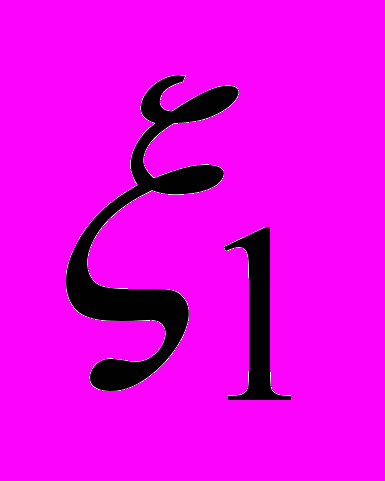 
. Разложив 
в ряд Тейлора по степеням p и оставив в разложениях только линейные составляющие относительно p, и выделив действительные мнимые части, получим систему уравнений 
, 
. Варьируя значения 
и 
при различных 
и 
можно определить знак функции А и В. Расчеты показали, что практически весь вихревой след находится в области неустойчивости. 11. Е.Г. Ванюкова (гр. 07-201 н. рук. Р.З. Муртазин). Определение положений равновесия консервативной механической системы.
Согласно принципу возможных перемещений необходимым и достаточным условием равновесия механической системы является равенство нулю суммы элементарных работ всех активных сил (и сил трения, если они совершают работу) на любом возможном перемещении системы. Это условие записывается в обобщенных координатах.
Доказывается, что консервативная механическая система находиться в равновесии в тех положениях, для которых потенциальная энергия системы имеет экстремум (в частности, минимум или максимум).
Дается определение возможных перемещений, способы вычисления возможных работ. В данной работе для конкретного примера из строительной практики определяются положения равновесия консервативной механической системы с одной степенью свободы.
12. Л.Г. Хисамиева (гр. 07-201 н. рук. Р.З. Муртазин). Устойчивость состояния равновесия консервативной механической системы.
Состояние равновесия механической системы может быть устойчивым, неустойчивым и безразличным. Состояние равновесия называется устойчивым, если эта система, выведенная из положения равновесия, совершает колебания около этого положения. Весьма актуальной является задача об определении устойчивости заданных состояний равновесия механической системы. Критерий устойчивости для систем с голономными и стационарными связями, находящихся в консервативном силовом поле, устанавливается в зависимости от потенциальной энергии этих систем.
Проводится исследование устойчивости положений равновесия консервативной механической системы по теореме Лагранжа – Дирихле.
Критерий Лагранжа – Дирихле является достаточным условием устойчивости состояния равновесия системы в поле консервативных сил. Оценить состояние равновесия консервативной системы можно на основании специальных теорем А.М. Ляпунова.
13. И.В. Васильев (гр. 07-201 н. рук. Р.З. Муртазин). Применение общего уравнения динамики и уравнений Лагранжа второго рода к исследованию движения механической системы с двумя степенями свободы.
Исследуется движение механической системы с двумя степенями свободы. Уравнения Лагранжа второго рода дают единый и при том достаточно простой метод решения задач динамики. Важное преимущество этих уравнений состоит в том, что их вид и число не зависят ни от количества тел, входящих в рассматриваемую систему ни от того, как эти тела движутся.
Определяется число уравнений Лагранжа второго рода числом степеней свободы системы и позволяют из строительной практики заранее исключить из рассмотрения все неизвестные реакции связей. Уравнения Лагранжа второго рода являются дифференциальными уравнениями движения механической системы в обобщенных координатах.
На конкретном примере (если связи идеальные) рассматривается применение общего уравнения динамики и уравнений Лагранжа второго рода к исследованию движения консервативной механической системы.
14. И.Л. Владимиров (гр. 2911-201 н. рук. А.Г. Галиуллин). Применение общего уравнения динамики к исследованию движения механической системы с одной степенью свободы.
В данной работе определяются ускорения грузов механической системы и натяжения в ветвях нитей, применением общих уравнений динамики. Т.е. при движении системы с идеальными голономными удерживающими связями сумма элементарных работ активных сил и сил инерции равна нулю на всяком возможном перемещении системы из любого ее положения. Принцип возможных перемещений дает универсальный аппарат для решения задач о равновесии. Принцип Даламбера, являясь основой метода кинетостатики, позволяет задачи о движении тел представить в виде задач о равновесии. Сочетание этих двух наиболее общих принципов приводит к другим общим принципам. Их прямое объединение (принцип Даламбера – Лагранжа) дает общее уравнение динамики. Уравнения выражающее этот принцип, позволяет составить дифференциальные уравнения движения механической системы. Если при этом система представляет собой совокупность каких-нибудь твердых тел, то для составления уравнений нужно к действующим на каждое тело активным силам прибавить приложенную в любом центре силу, равную главному вектору сил инерции, и пару с моментом, равным главному моменту сил инерции относительно этого центра, а затем применить принцип возможных перемещений.
15. А. Г. Мингазова (гр. 2911-201 н. рук. А.Г. Галиуллин). Применение принципа возможных перемещений к определению реакций опор составной конструкции.
В данной работе применяя принцип возможных перемещений, определяются реакций опор составной конструкции. Если на систему материальных точек наложены те или иные связи, то для такой системы не всякое перемещение оказывается возможным. Возможным перемещением данной системы называется совокупность любых бесконечно малых перемещений материальных точек этой системы, допускаемых в данный момент наложенными на систему связями. Для определения сил реакций связей, мысленно отбросив эту связь, заменяется ее действие реакцией этой связи, считавшимся активной силой. Затем составляется уравнение работ, выражающих принцип возможных перемещений. После определения сил реакций связей, производится проверка правильности решения задачи. Для чего составляются уравнения равновесия систем сил, полученных в разделе статики курса Теоретической механики в зависимости от того, где они находятся, на прямой, в плоскости и в пространстве. При правильности решения задачи, во всех уравнениях должны получатся нули.
16. Р.Ф. Рахматуллина (гр. 2911-201 н. рук. А.Г. Галиуллин). Применение уравнений Лагранжа второго рода к исследованию движения механической системы с двумя степенями свободы.
Уравнения Лагранжа второго рода представляют собой систему обыкновенных дифференциальных уравнений второго порядка относительно неизвестных функций q. Для того чтобы составить эти уравнения, кинетическую энергию Т системы необходимо выразить через обобщенные координаты q и обобщенные скорости. Чтобы найти обобщенную силу Q, соответствующую обобщенной координате q, нужно данной механической системе сообщить такое возможное перемещение, при котором изменяется только одна координата q, а все остальные обобщенные координаты остаются неизменными. Затем составляется сумма элементарных работ всех заданных сил на этом перемещении и разделить эту сумму на возможное перемещение обобщенных координат. Интегрируя систему уравнений Лагранжа, находятся обобщенные координаты q как функции времени t произвольных постоянных С определяемых начальными условиями движения системы.
17. В.Р. Ермилев (гр. 10-202 н. рук. А.Г. Галиуллин). Исследование плоского движения твердого тела.
Рассматривается пример, при приложении некоторых усилий к твердому телу, исследуется некоторые кинематические характеристики вращательного движения. Из кинематики известно, что при плоскопараллельном движении положение твердого тела определяется тремя параметрами: двумя координатами какой – нибудь точки этого тела и углом его поворота вокруг оси, проходящей через эту точку и перпендикулярной к той неподвижной плоскости, параллельно которой движется данное тело. Если движение твердого тела является несвободным, то в правые части уравнений войдут еще неизвестные реакции связей. Для их определения надо будет составить дополнительные уравнения, отражающие те условия, которые налагаются на движение тела связями.
Суть задачи заключается в том, что, если тело движется параллельно данной неподвижной плоскости, то его кинетическая энергия равна сумме кинетических энергии центра тяжести в предположении, что в нем сосредоточена вся масса тела, и кинетической энергии тела в его вращательном движении вокруг оси, проходящей через центр тяжести и перпендикулярной к данной неподвижной плоскости.
18. А.М. Садыков (гр. 10-203 н. рук. А.Г. Галиуллин). Исследование вращательного движения твердого тела вокруг неподвижной оси.
Рассматривается пример, при приложении некоторых усилий к твердому телу, исследуется некоторые кинематические характеристики вращательного движения твердого тела. Согласно принципу Даламбера, заданные силы, реакции закрепленных точек и сил инерции всех материальных частиц данного тела уравновешиваются. Поэтому составляются шесть известных из статики уравнений равновесия сил, приложенных к твердому тел; для этого приравниваются нулю сумма проекций всех этих сил на каждую из трех координатных осей и сумма их моментов относительно каждой из этих осей. При некотором их преобразовании, получается дифференциальное уравнение второго порядка , которое и является дифференциальным уравнением вращательного движения твердого тела вокруг неподвижной оси. Решая для данного примера эту дифференциальную уравнению, решая его получим необходимые кинематические характеристики вращательного движения твердого тела.
19. Э.А. Хадеев (гр. 06-201 н. рук. А.Г. Галиуллин). Применение теории об изменении кинетического момента к определению угловой скорости твердого тела.
Главный момент количеств движения всех материальных точек системы относительно данного центра или данной оси называется кинетическим моментом системы относительно этого центра или этой оси. Следовательно имеем кинетические моменты относительно трех координатных осей в пространстве. Взяв производные по времени от кинетических моментов получаются главные моменты всех внешних сил относительно заданных координатных осей. Исследуя эти полученные уравнения, преобразуя их получим дифференциальное уравнения вращательного движения твердого тела. Решая дифференциальную уравнению, решая его получим необходимые кинематические характеристики вращательного движения. Теоремой моментов пользуются для изучения вращательного движения тел. Закон сохранения момента количеств движения позволяет по величине или по скорости перемещения одной части системы определить изменение угловой скорости другой ее части. При этом из рассмотрения исключаются все наперед неизвестные внутренние силы, а также внешние силы, пересекающие ось вращения или ей параллельные.
Третье заседание
9 апреля 9.00, ауд. 4-111
1. Л.М. Гумерова (гр. 14-201 н. рук. А.М. Тартыгашева). Сложное движение точки на примере задачи о движении обода колеса.
В данной работе освещены вопросы сложения скоростей и ускорений при сложном движении точки. Приведена общая постановка задачи о сложном движении твердого тела.
Найден радиус кривизны траектории точки обода колеса катящегося без скольжения по прямолинейному рельсу при известных скорости и ускорений центра колеса. Построен годограф вектора скорости точки обода колеса радиуса а, при этом скорость и ускорение центра колеса заданы. При решении за полюс была принята точка контакта обода колеса и рельса. Скорость точки обода колеса прямопорциональна скорости центра колеса, а ускорение обода колеса прямопорциональна квадрату скорости центра колеса и обратно пропорциональна радиусу колеса.
Получено правило сложения угловых ускорений твердого тела методом сложного движения точки. Вычислены скорость и ускорение образующих конуса, который катиться без скольжения по плоскости при известной скорости центра основания конуса.
2. А.А. Строкина (гр. 14-201 н. рук. А.М. Тартыгашева). Плоскопараллельное движение точки.
В данной работе приводятся основные выкладки о плоскопараллельном движении твердого тела. Подробно доказаны теоремы Эйлера и Шаля. Рассмотрена задача о приведении векторов к простейшему виду. Решена задача определения оси винта при сложном движении точки по винтовой линии, сопровождающий трехгранник совершает два движения: поступательное и вращательное. В результате установлено. Скорость произвольной точки тела, связанного с естественным трехгранником, равна моменту кинематического винта относительно этой точки. Данное движение определяется винтом. Показана возможность применения теории винтов в кинематике.
Приведено подробное доказательство теоремы Моцци для общего случая перемещения твердого тела. Рассмотрен вопрос об определении мгновенного центра скоростей эпициклических или планетарных передачах.
3. А.Н. Садыкова (гр. 14-201 н. рук. А.М. Тартыгашева). Сферическое движение твердого тела.
В первой части работы кратко изложена теория о сферическом движении твердого тела: углы Эйлера, теорема Эйлера – Даламбера и т.д.
Во второй части работы решена задача с использованием уравнений движения свободного твердого тела.
Поставлена задача об исскуственной горизонтальной площадке на качающемся корабле. Созданной с помощью карданова подвеса. Определена ориентация внутреннего кольца подвеса относительно корабля, т.е. определены соответствующие направляющие косинусы. При этом ось вращения внешнего кольца параллельна продольной оси корабля; угол поворота внешнего кольца обозначается через
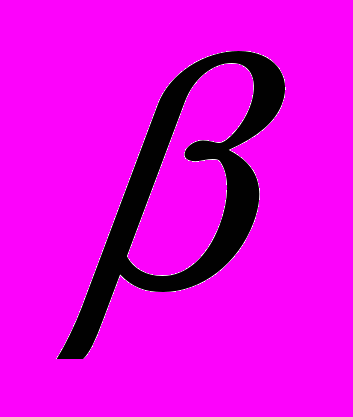(угол бортовой качки). Угол поворота внутренней рамки обозначается через 
. Результат представлен в виде таблицы зависимости между координатами x, y, z, связанными с внутренним кольцом и 
, 
и 
, связанными с кораблем.4. Д.Р. Халилова (гр. 14-201 н. рук. А.М. Тартыгашева). Способы задания движения точки в различных системах координат.
В работе показано три способа задания движения векторный, координатный и естественный. Выведены формулы связывающие данные виды движения. Рассмотрена задача о построении естественного трехгранника.
Определена траектория движения электрона в постоянном магнитном поле, а также закон движения электрона по винтовой линии.
При решении задачи варьирировались параметры а, k, и v, зависящие от напряженности магнитного поля, массы, заряда и скорости электрона.
В результате установлено, что электрон в постоянном магнитном поле движется по винтовой линии, с шагом винта, зависящем от
и 
. Движение электрон начинает из положения 
по закону 
.5. Т.Ш. Ганиуллина (гр. 14-201 н. рук. А.М. Тартыгашева). Сравнение уравнений движения в классической и классической статистической механике.
В первой части рассказано в процессе получения приближенных численных решений уравнений о движении и о необходимости получать точное решение на основе других математических методов.
Вторая часть посвящена нахождению уравнений движения на простом механическом примере. Интересными являются примеры показывающие уравнения движения в классической и классической статистической механике.
Выведено уравнение Лиувилля описывающее эволюцию во времени функции распределения гамильтоновой системы в фазовом пространстве. Проиллюстрировано нахождение траектории множества точек в фазовом пространстве. Множество траекторий растягивается в одной координате
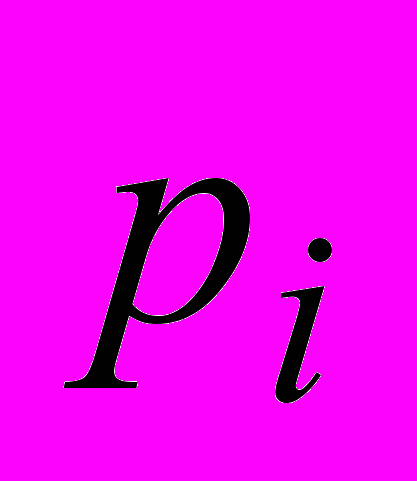но сжимается по другой 
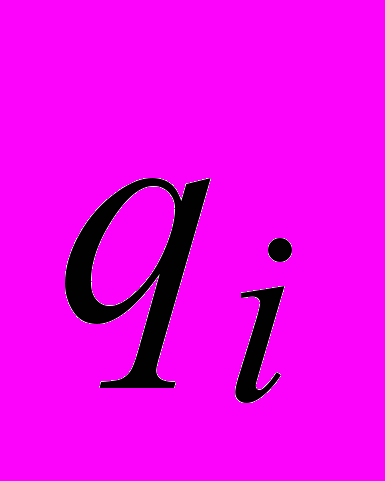, т.о. произведение 
остается константой.Для сравнения приведены уравнения Бололюбова, Больцмана и Власова.
6 . А.П. Хмелева (гр. 10-302 н. рук. А.Ф. Шигабутдинов). Расчет механической системы с одной степенью свободы на вынужденные колебания.
В работе исследуются вынужденные колебания механической системы с одной степенью свободы. Механическая система состоит из катка, который при колебаниях может совершать и плоскопараллельное движение и двух элементов прикрепленных к катку. Один из них упругий элемент, а второй элемент вводит в систему вязкое трение. На систему в процессе движения действует вынуждающая сила, изменяющаяся при периодическому закону.
Исследования движения основано на решении уравнения Лагранжа второго рода, которое предварительно в работе выводится. Определяются кинематические характеристики отдельных точек механической системы при колебаниях и анализируется сопротивление в демпфере и его влияние на колебания. Решение задачи доведено до числа при конкретных значениях механических характеристик системы.
7 . Е.Н. Льдокова (гр. 10-302 н. рук. А.Ф. Шигабутдинов). Определение динамических характеристик механической системы с одной степенью свободы.
Рассматриваются механические колебания механической системы
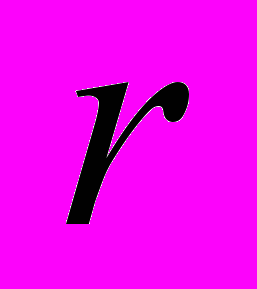с одной степенью свободы при наличии вынуждающих сил. Система состоит из трех абсолютно твердых тел и двух элементов 
– элемента с вязким трением и упругого элемента. Тела системы выполнены в виде диска совершающего вращательные колебания; рейки, совершающей поступательное движение и стержня, совершающего вращательное движение. Диск и стержень связаны с упругой связью, а рейка с вязкой связью. Вынуждающие силы изменяются по периодическому закону. Колебания исследуются с использованием уравнения Лагранжа второго рода, которое получено в работе. Это уравнение с математической стороны является дифференциальным уравнением второго порядка с постоянными коэффициентами этого уравнения являются некоторый константы , зависящие от механических характеристик системы. Исследуются решение уравнения колебаний в зависимости от механических характеристик системы. Решение доведено до числа.8 . Е.А. Медведев (гр. 10-301 н. рук. А.Ф. Шигабутдинов). Исследование свободных и вынужденных колебаний механической системы с одной степенью свободы.
В работе сравниваются свободные и вынужденные колебания механической системы с одной степенью свободы. В отличие от прямолинейных колебаний можно получить из второго закона Ньютона, здесь используются уравнения Лагранжа второго рода. Эти уравнения получены в работе с учетом механических характеристик системы. Система состоит из плоского диска, скрепленного с двумя гибкими связями и стержня, на который наложена вязкая связь. Стержень может совершать только вращательные движения относительно одного из своих концов, а диск «обкатывается» по заданной криволинейной траектории, совершая плоскопараллельное движение. Определяются параметры колебаний и кинематические характеристики отдельных точек механической системы. Исследуется влияние вязкой связи на колебания. Определяются условия при которых рассматриваемые колебания становятся близки. Решение доведено до числа.
9. А.В. Зубарева (гр. 06-301 н. рук. Е.Р. Газизов). Укладка бетона вибрированием.
Приводятся общие сведения о бетонах и их классификация по плотности, по видам применяемого вяжущего вещества, по структуре и назначению. Рассматриваются основные свойства бетона, такие как прочность при сжатии, водонепроницаемость, огнестойкость, коррозиестойкость. Раскрывается процесс приготовления (сосредоточенного в основном на автоматизированных бетонных заводах и в бетоносмесительных узлах предприятий), транспортирования и укладки бетона в конструкции, таким образом, чтобы были обеспечены монолитность бетонной кладки, проектные физико–механические показатели и однородность бетона, его сцепление с арматурой и полное заполнение (без пустот) пространства возводимой конструкции.
Описываются различные виды вибраторов для уплотнения бетонной смеси, используемые на строительных площадках и на заводах сборочного железобетона.
10. О.С. Олудина (гр. 06-301 н. рук. Е.Р. Газизов). Усталость элементов конструкций и машин.
Рассматривается изменение механических и физических свойств материалов под длительным действием циклически изменяющихся во времени напряжений и деформаций. Исследуется состояние материалов при усталостном процессе. Анализируется изменение состояния материалов, протекающие по стадиям, и их зависимость от исходных свойств, вида напряженного состояния, истории нагружения и влияния среды. Раскрывается метод наблюдения за возникновением и подрастанием трещин, который позволяет указать на недочеты или ошибки проекта, правил изготовления и эксплуатации изделий. Обосновывается возможность включения некоторой части процесса развития трещин в срок службы изделия. Проводится анализ поля напряжений у трещины с учетом остаточных напряжений, возникающих вследствие пластической деформации материала, технических факторов перераспределения остаточных сварочных напряжений при подрастании трещины.
11 . Басов А.С. (гр. 06-301 н. рук. Е.Р. Газизов). Производство работ по вибрационному погружению труб и свай.
Описывается история внедрения вибрационной техники и технологии в фундаментостроении. Раскрывается суть вибрационного метода погружения свай и труб, его преимущества в сравнении с традиционными методами. Описываются требования, предъявляемые к вибрационной технике и технологии производства работ, в связи с необходимостью генерирования минимального уровня колебаний при использовании вибрационного метода. Приводятся примеры различных машин для вибрационного погружения свай, шпунта, труб и оболочек, различающихся по динамическому воздействию на вибропогружатели и вибрационно-ударные погружатели и по схеме устройства на вибропогружатели простейшего типа и с подрессорной пригрузкой. Рассматриваются проблемы, возникающие при вибрационном методе погружения свай и труб. Описывается такие метод, основанный на комбинированном воздействии вибрации (или вибрации с ударом) и статического пригруза.
12 . И.В. Потапова (гр. 06-303 н. рук. Е.Р. Газизов). Оценка качества железобетонных элементов неразрушающими методами.
Рассматриваются неразрушающие методы контроля качества бетона, которые позволяют определить прочность не только поверхности, но и глубинных слоев бетона, выявлять внутренние дефекты в изделии, возникающие в процессе производства и эксплуатации.
Описываются механические методы, при которых поверхности изделия подвергаются механическому воздействию и прочность бетона определяют по сопротивлению, которое образец оказывает этому воздействию. При этом рассматривается группа методов, основанная на измерении твердости бетона, осуществляемая путем вдавливания в его поверхность штампа определенной формы, и группа методов основанных на принципе упругого отскока. Также рассматриваются физические методы, которые позволяют оценить прочность бетона по скорости и затуханию звукового импульса, по частоте собственных колебаний и других подобных характеристиках.
13 . И.И. Мингазов (гр. 06-303 н. рук. Е.Р. Газизов). Испытание конструкций динамической нагрузкой.
Классифицируются нагрузки, быстро изменяющие свою величину, направление или место приложения на конструкции. Описывается проведение испытаний натурных сооружений динамической эксплутационной нагрузкой и испытание конструкций и сооружений искусственно создаваемой вибрационной нагрузкой.
Рассматриваются задачи, решаемые в ходе вибрационных испытаний. Описывается расчет конструкций на вибрационную нагрузку с целью определения величины динамических перемещений и деформаций и последующей проверки соблюдения условий нормальной эксплуатации. Описывается расчет частоты свободных колебаний, который позволяет решить вопрос о допустимости установки на исследуемом объекте какого-либо агрегата, создающего при его движении возмущающую нагрузку с определенной частотой, или же выяснить, какой агрегат из ранее установленных создает резонанас, и найти возможные пути ликвидации этого явления. Приводятся способы снижения уровня вибрационной конструкции.
Олимпиада по теоретической механике
Состоится 11 апреля 2011г в 9 часов 30 минут, ауд. 2-402. Участвуют студенты, посещавшие заседания кружка по теоретической механике (75 человек) КГАСУ и все желающие. Приглашаются команды других вузов г. Казани. Призовыми считаются первые шесть мест, отдельно подводятся итоги по факультетам.
Зав.кафедрой __________________________________________