Интеллектуальные системы принципы конструирования интеллектуальных систем

Вид материала

Документы

Содержание Шагом ДСМ-рассуждения будем называть однократное применение п.п.в.-1 (индукции) или п.п.в.-2 (аналогии). 2. Тактом Первым Этапом (Этап I) Условием стабилизации

Подобный материал:

• Аннотация программы учебной дисциплины «Интеллектуальные системы», 915.14kb.
• Аннотация учебной программы дисциплины «Интеллектуальные системы», 1141.83kb.
• Аннотация учебной программы дисциплины «Интеллектуальные системы», 781.23kb.
• Аннотация учебной программы дисциплины «Интеллектуальные системы», 759.09kb.
• Рабочей программы дисциплины Интеллектуальные системы управления инфокоммуникациями, 21.49kb.
• Лекция №10: «Интеллектуальные системы принятия решений и управления в условиях конфликта», 581.94kb.
• Рабочая программа учебной дисциплины интеллектуальные системы Наименование дисциплины, 175.19kb.
• Системы искусственного интеллекта и нейронные сети, 208.41kb.
• О. Ю. Якубовская 2011 г. Дисциплина: Операционные системы (2 часть из 2) Специальность:, 45.21kb.
• А. М. Иванов Научно-информационный материал «Методические материалы к практическим, 91.96kb.

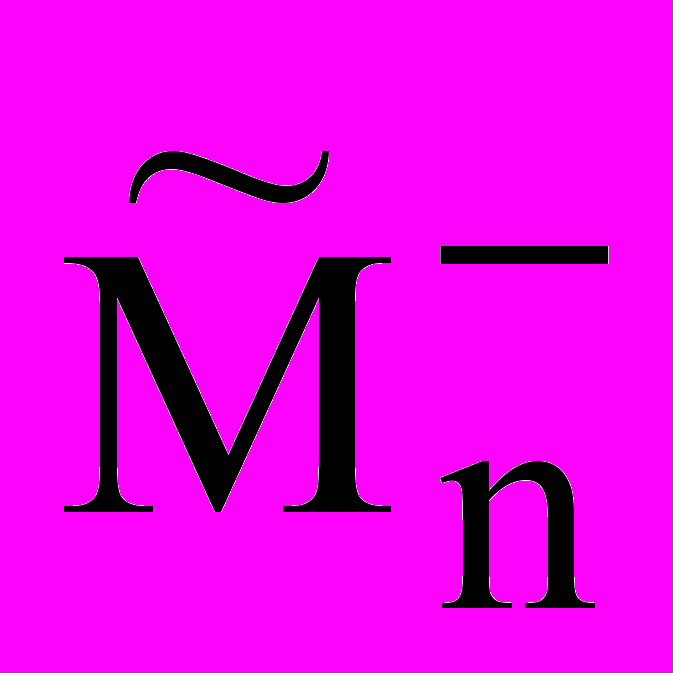⇌k(V,W, k). Заметим, что предикаты M_n⁺(V, W) и M_n^(V, W) зависят от параметра n, выражающего число применений правил правдоподобного вывода к БФ, изменяющих ее состояние.

Пусть С - значение V, а Q – значение W, тогда правила правдоподобного вывода (п.п.в.-1 для индукции) формулируются следующим образом:

(I)⁺ Если M_n⁺(С, Q) истинно и M_n^(С, Q) ложно, то высказывание «С есть причина Q» имеет истинностное значение 1, n+1;

(I)^ Если M_n⁺(С, Q) ложно и M_n^(С, Q) истинно, то высказывание «С есть причина Q» имеет истинностное значение 1, n+1;

(I)⁰ Если M_n⁺(С, Q) истинно и M_n^(С, Q) истинно, то высказывание «С есть причина Q» имеет истинностное значение 0, n+1

(I)^ Если M_n⁺(С, Q) ложно и M_n^(С, Q) ложно, то высказывание «С есть причина Q» имеет оценку (, n+1).

Выразим теперь эти правила правдоподобного вывода (п.п.в.-1) формально:

(I)⁺ ,

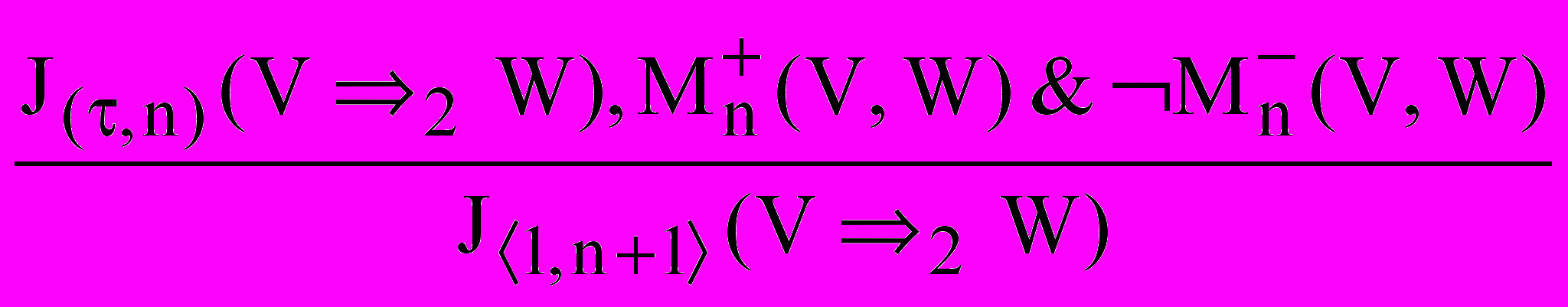(I)^ ,

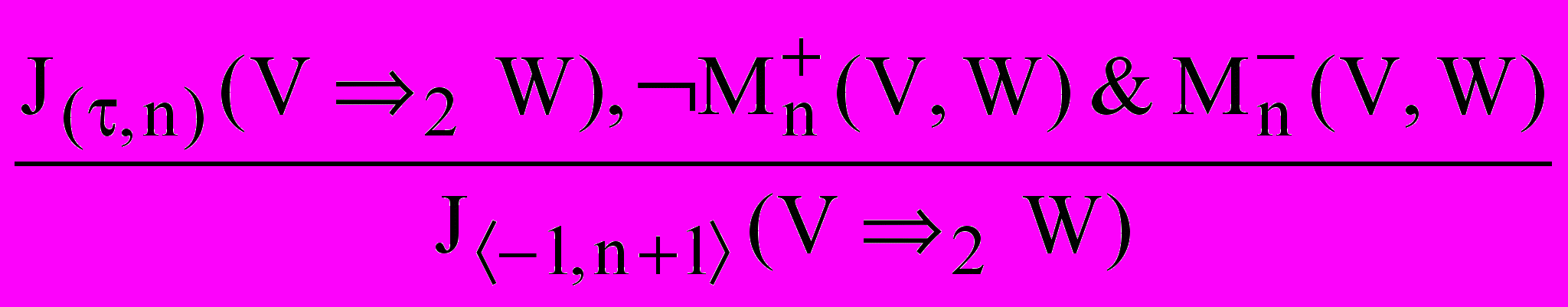(I)⁰ ,

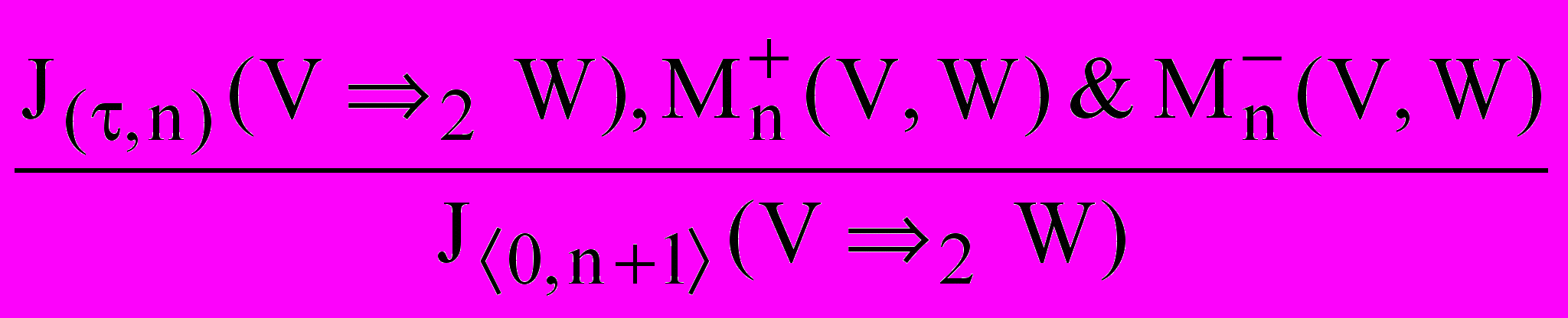(I)^ .

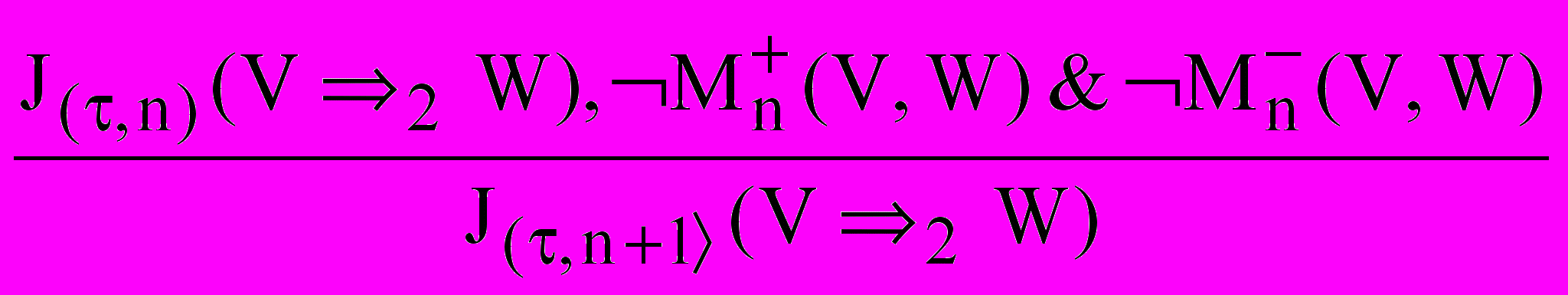П.п.в.-1 являются семейством правил, т.к. (I)^ зависят от параметра n, выражающего степень правдоподобия как истинностных значений =, n, где =1, 0, так и множества истинностных значений (, n).

Порождаемый предикат V₂W (подобъект V есть причина наличия (отсутствия) эффекта W) является результатом извлечения из БФ сходства соответствующих примеров (ЭУ и СФ), выражающего зависимость причинно-следственного типа (ЭЗ и УИ). Предикат V₂W есть результат индуктивного обобщения посредством сравнения рассматриваемых примеров из БФ.

Начальное состояние БФ может быть представлено следующим образом:

БФ= БФ⁺БФ^БФ^, где

БФ⁺={X,Y|J_1,0(X₁Y)},

БФ^={X,Y|J_1,0(X₁Y)},

а БФ^={X,Y|J_(,0)(X₁Y)},

где X,Y - упорядоченная пара объект, эффект;

БФ^, где {+, , }, есть множества пар X,Y таких, что выполняются J_1,0(X₁Y), J_1,0(X₁Y) и J_(,0)(X₁Y), соответственно¹³.

Формулируемые ниже правила правдоподобного вывода по аналогии – п.п.в.-2 – используются для уменьшения неопределенности фактов из БФ^. П.п.в.-2 используют результаты применения п.п.в.-1 (индукции) – гипотезы вида J_{, n}(C₂Q), где {1,1, 0}, а n1.

П.п.в.-2 формулируются посредством предикатов аналогии П_n⁺(V,W), П_n^(V,W), П_n⁰(V, W) и П_n^(V,W). П_n⁺(V,W) и П_n^(V,W) определяются, соответственно, посредством параметрических предикатов 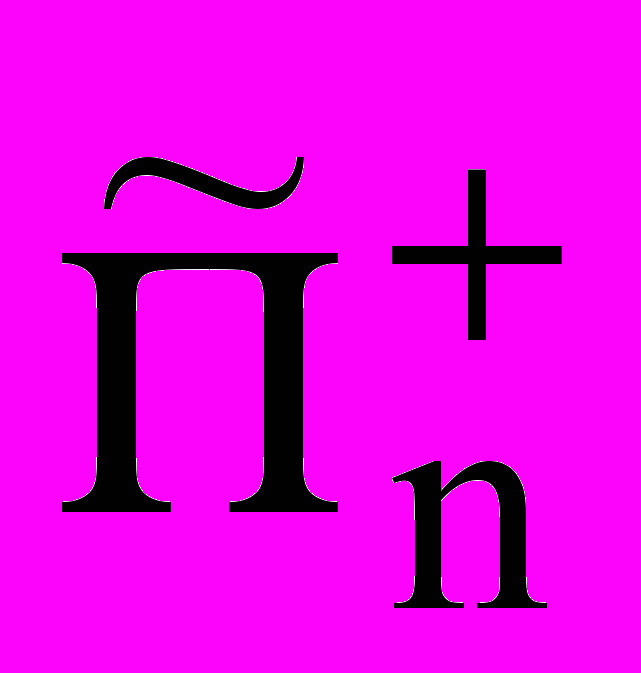(V,W,k) и 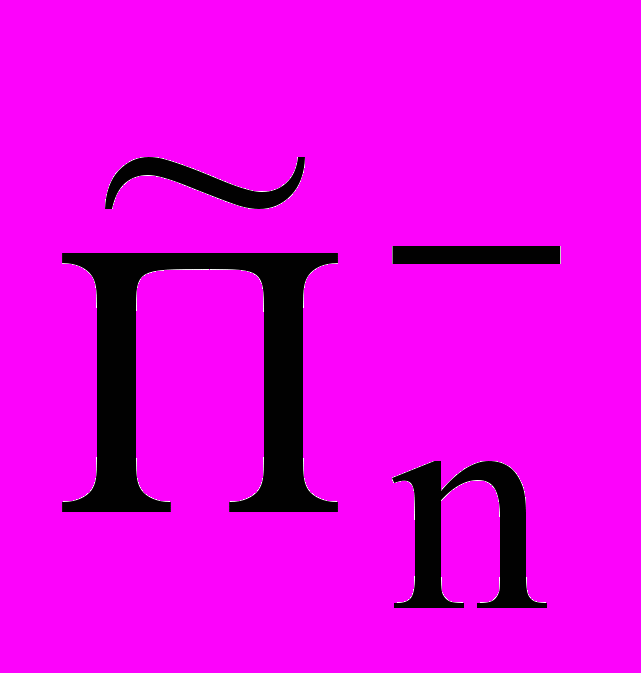(V,W,k), где k – параметр, выражающий число порожденных гипотез, представленных формулами J_(1,n)(X_i₂Y_i) и J_(1,n)(X_i₂Y_i) для 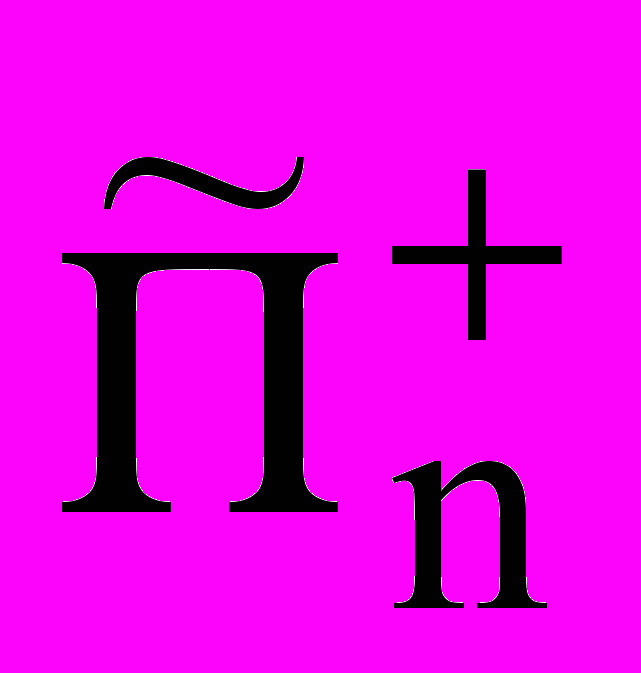и 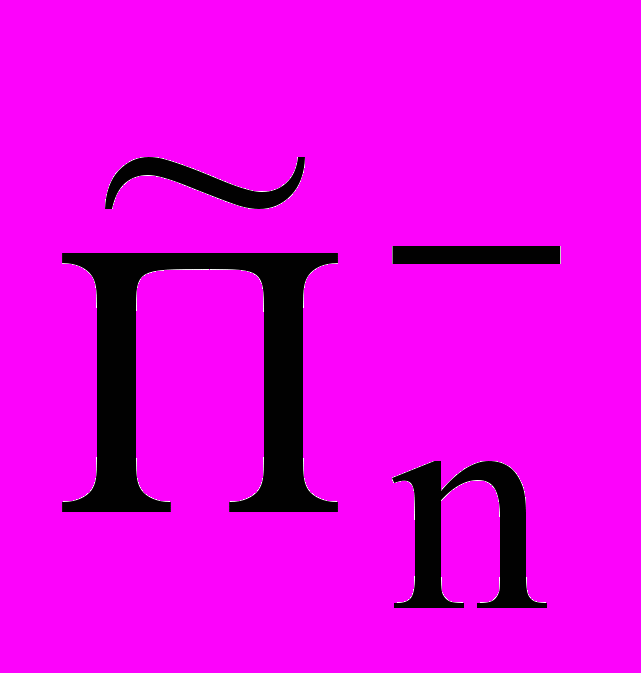, соответственно, где i=1, …, k.

Результатом применения п.п.в.-2 являются гипотезы о наличии (отсутствии) изучаемого эффекта у соответствующих объектов, относительно которых имелась оценка «неопределенно». Таким образом, п.п.в.-2 порождают предсказания вида J_{, n+1}(C₁Q), где {1,1, 0}, или J_{, n+1}(C₁Q), а n – число шагов, за которое были получены гипотезы о () – причинах, используемые в предикатах П_n⁺(V,W) и П_n^(V,W) (гипотезы с истинностными значениями 0, n используются в предикате П_n⁰(V,W)).

Предикат 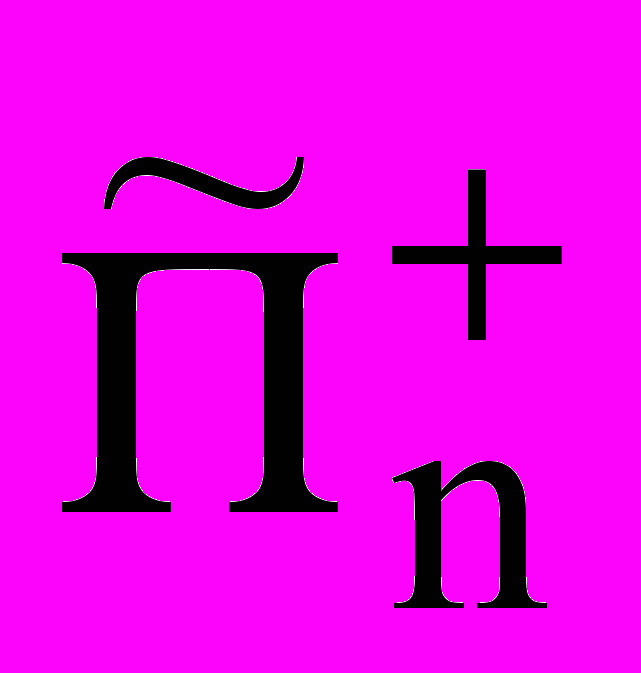(V,W,k) выражает условие такое, что объект V содержит позитивные причины Х₁, …,Х_k для множеств свойств Y₁, …,Y_k, соответственно, а множество свойств W, представляющее изучаемый эффект, покрывается множествами Y₁, …,Y_k (k – параметр). Это условие выразимо формулой

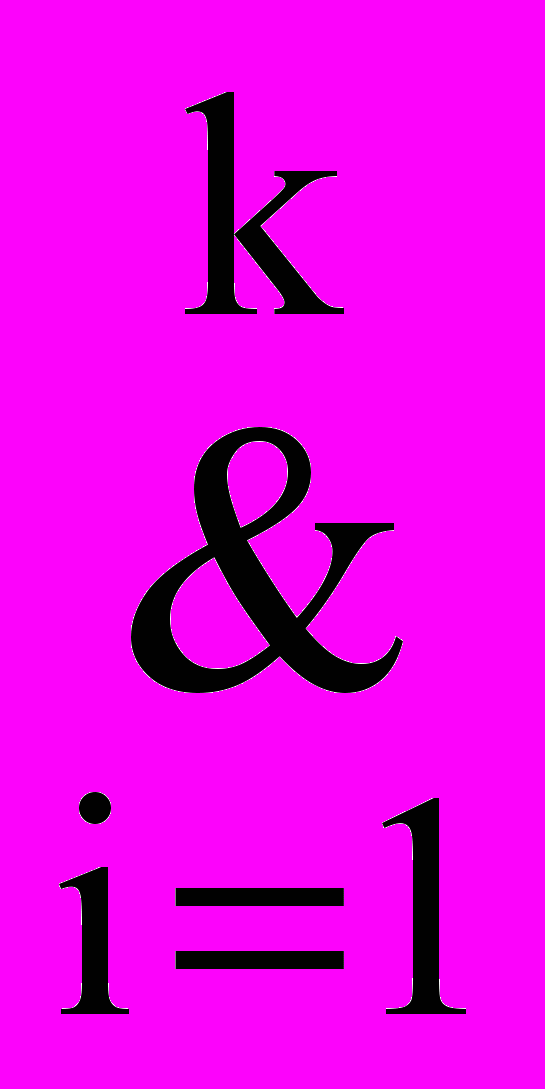(X_i (J_(1,n)(X_i₂Y_i)&(X_iV)&(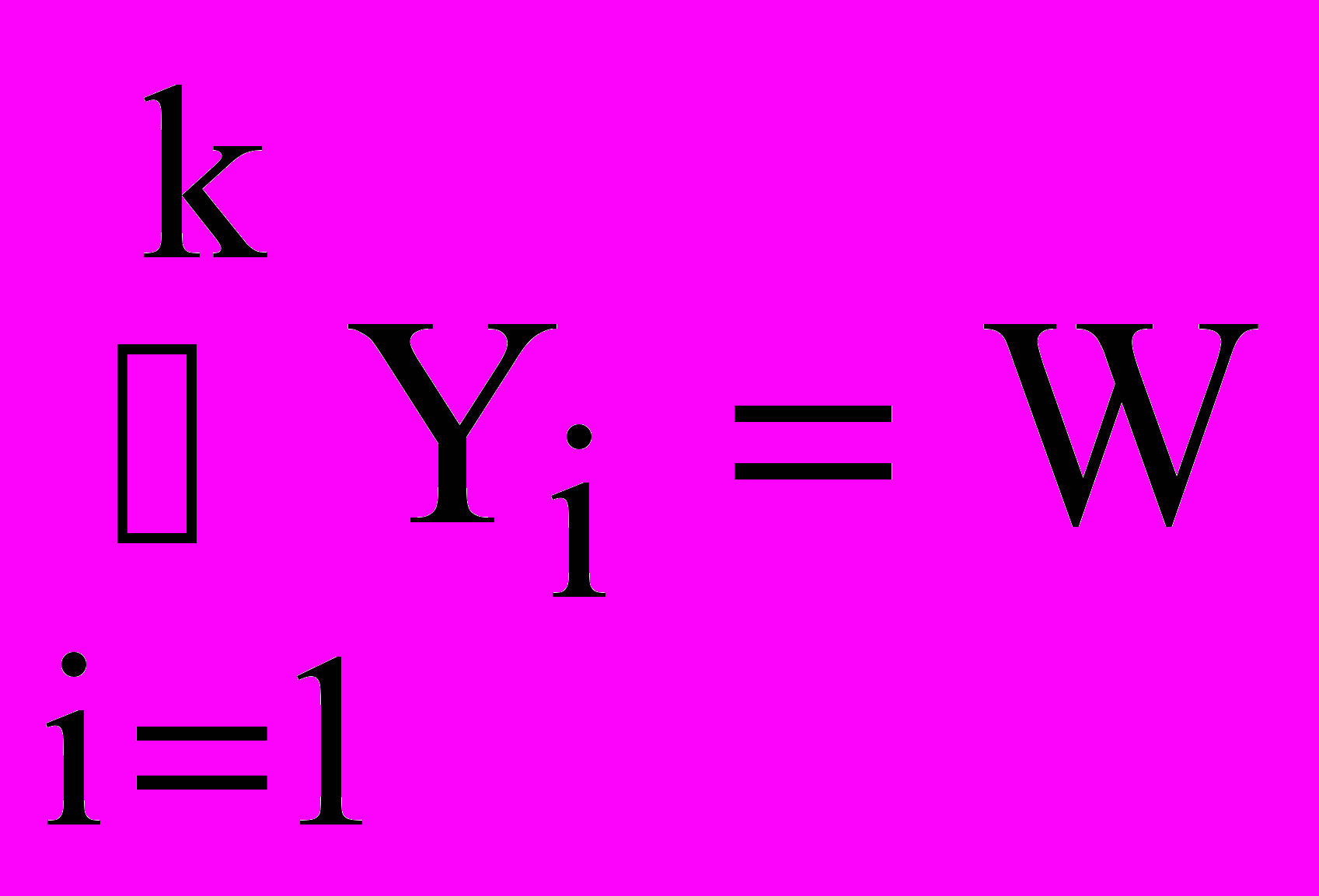)).(1)

Вторым условием, содержащимся в П_n⁺(V,W), является условие исчерпываемости всех причин, вынуждающих наличие множества свойств таких, что они включаются в V. Это условие выразимо формулой

Y(X(J_(1,n)(X₂Y&(XV))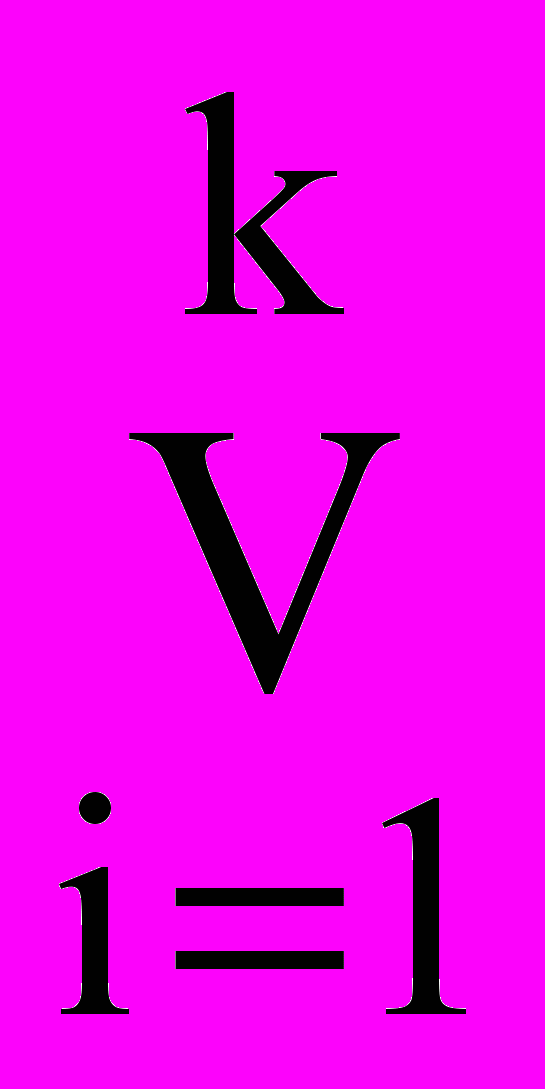((Y=Y_i))). (2)

Третьим условием, содержащимся в П_n⁺(V,W), является условие, утверждающее, что V не содержит ни отрицательных причин Z, ни Z таких, что J_(0,n)(Z₂U) Z для любого непустого подмножества свойств U множества W.

Это условие выразимо формулой

U((UW)(U))Z((J_(1,n)(Z₂U)  J_{(0, n)}(Z₂U))&(ZV)). (3)

П_n^(V,W) определяется аналогично с заменой в (1) и (2) J_{(1, n)} на J_(1,n) и с заменой в (3) J_(1,n) на J_(1,n).

Определение предиката П_n⁺(V,W) образовано конъюнкцией условий (1), (2) и (3) и применением кванторов существования к переменным Y₁, …,Y_k: Y₁, …, Y_k((1)&(2)&(3))¹⁴.

Предикаты П_n⁰(V,W) и П_n^(V,W) определяются следующим образом:

П_n⁰(V,W)⇌X₁Y₁X₂Y₂(J_(1,n)(X₁₂Y₁)& J_(1,n)(X₂₂Y₂)&(Y₁Y₂)&(X₁Y₁)&(X₂ Y₂) & (Y₁ W)&(Y₂W))XY(J_{(0, n)}(X₂Y)) & (XV)(YW)),

П_n^(V,W)⇌П_n⁺(V,W)П_n^(V,W) П_n⁰(V,W)

Из определений П_n⁺(V,W), П_n^(V,W) и П_n⁰(V,W) следуют утверждения (а) и (в):

(а) VW(П_n⁺(V,W)П_n^(V,W)),

(в) VW(П_n^ (V,W)П_n⁰(V,W)), где {+, }.

Аналогично п.п.в.-1 формулируются п.п.в.-2 (правила вывода для аналогии):

(II)⁺ ,

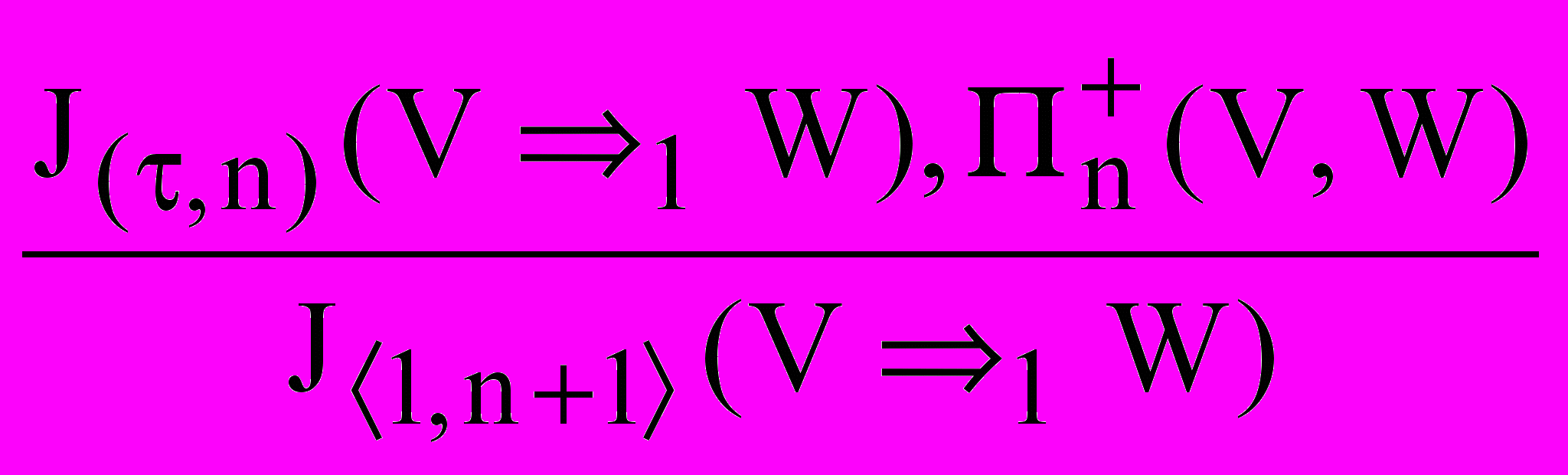(II)^ ,

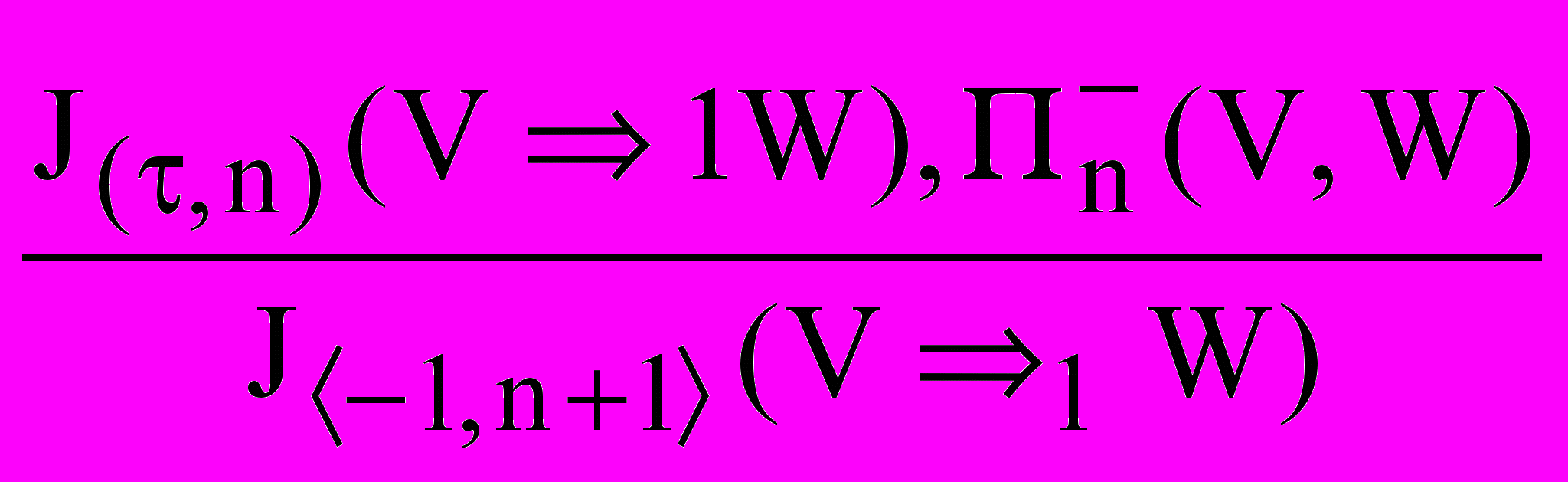(II)⁰ ,

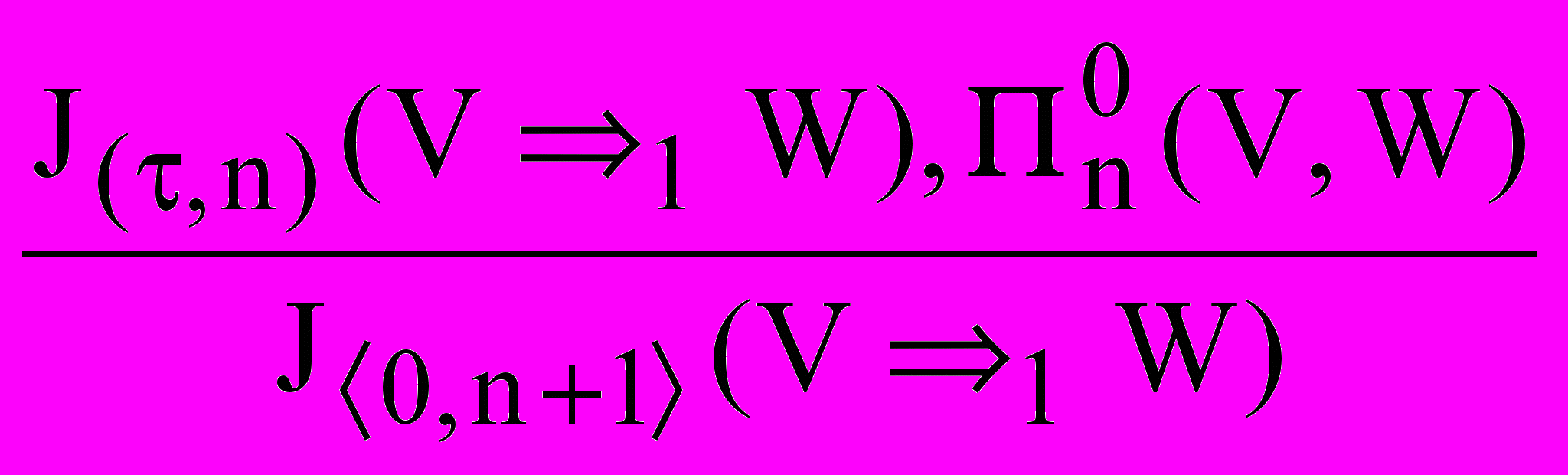(II)^

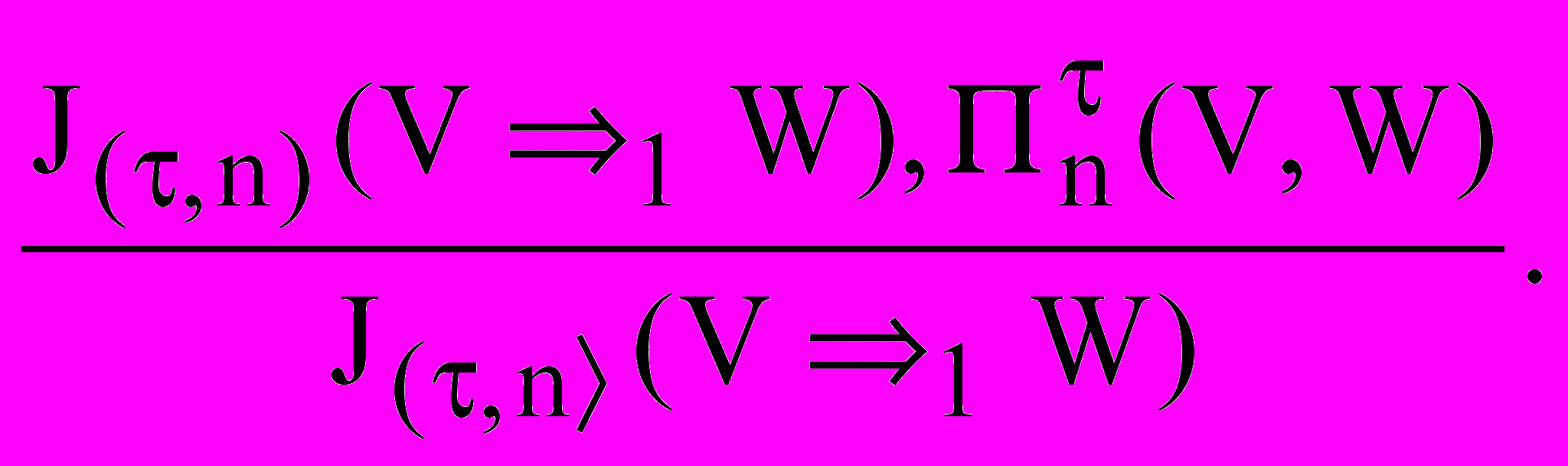
Из определений предикатов П_n⁺(V,W), П_n^(V,W) и П_n⁰(V,W) следует, что они представляют формализацию выводов по аналогии. В самом деле, П_n^(V,W) содержат в качестве подформул формулы J_(,n)(Х₂Y), где {1,1}, а n0. Эти подформулы получены в результате применения п.п.в.-1 (индукции) к БФ (и ее расширениям посредством п.п.в.-2). Но J_(,n)(Х₂Y) является сходством фактов или гипотез J_,i(V_j₁W_j), где i n, а потому результат п.п.в.-2, которым является J_{, n}(V₁W) сходен с J_,i(V_j₁W_j), что соответствует структуре вывода по аналогии [7].

Рассмотрим теперь строение ДСМ-рассуждений¹⁵.

1. Шагом ДСМ-рассуждения будем называть однократное применение п.п.в.-1 (индукции) или п.п.в.-2 (аналогии).

2. Тактом ДСМ-рассуждения будем называть упорядоченное последовательное применение п.п.в.-1 и п.п.в.-2 (т.е. двух шагов).

3. Первым Этапом (Этап I) ДСМ-рассуждения будем называть последовательное применение тактов (п.п.в.-1 п.п.в.-2)₁ (п.п.в.-1 п.п.в.-2)₂…( п.п.в.-1 п.п.в.-2)_n1 (п.п.в.-1 п.п.в.-2)_n такое, что множество порожденных гипотез на такте n совпадает с множеством гипотез на такте n1, где n – номер первого такого совпадения. Такт n будем называть тактом стабилизации первого этапа ДСМ-рассуждения.

Таким образом, Этап I осуществляет итерацию тактов «индукция – аналогия» до стабилизации порождения гипотез.

Охарактеризуем теперь применение ДСМ-рассуждений к БФ и начальному состоянию БЗ, содержащей правило вывода Г, аксиомы булевской структуры данных и аксиомы каузальной полноты, являющиеся основанием для принятия гипотез посредством абдукции [7]. Применение п.п.в.-1 к БФ и последующее применение п.п.в.-2 на этапе I порождает расширение – БФ₁, определяемое ниже.

Для характеризации этапа I введем следующие определения:

БФ₀=БФ, БФ=БФ⁺БФ^БФ^,

где БФ^={X,Y| J_{, 0}(X₁Y)} {1,1, 0}, а БФ^={X,Y | J_{(, 0)}(X₁Y)};

БФ₁⁺={V,W| J_{1, 2}(V₁W)},

БФ₂⁺={V,W| J_{1, 4}(V₁W)},

БФ₃⁺={V,W| J_{1, 6}(V₁W)},

∶

БФ_n⁺={V,W| J_{1, 2n}(V₁W)}.

Аналогично определяются БФ_n^ и БФ_n⁰, а БФ_n^={V,W| J_{(, 2n)}(V₁W)}.

_n^=БФ₀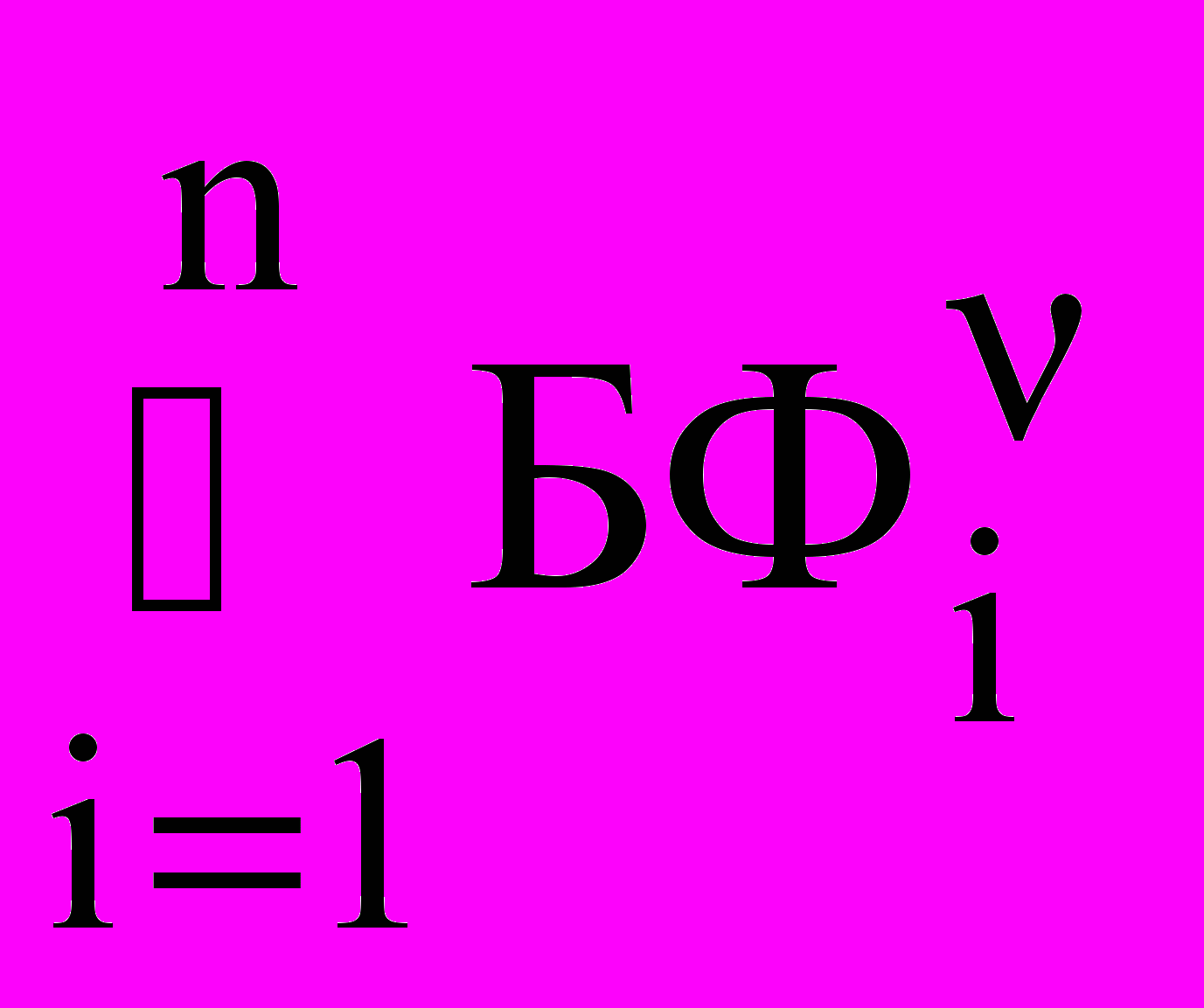^(), {1,1, 0, },

_n=_n⁺_n^_n⁰ _n^, где 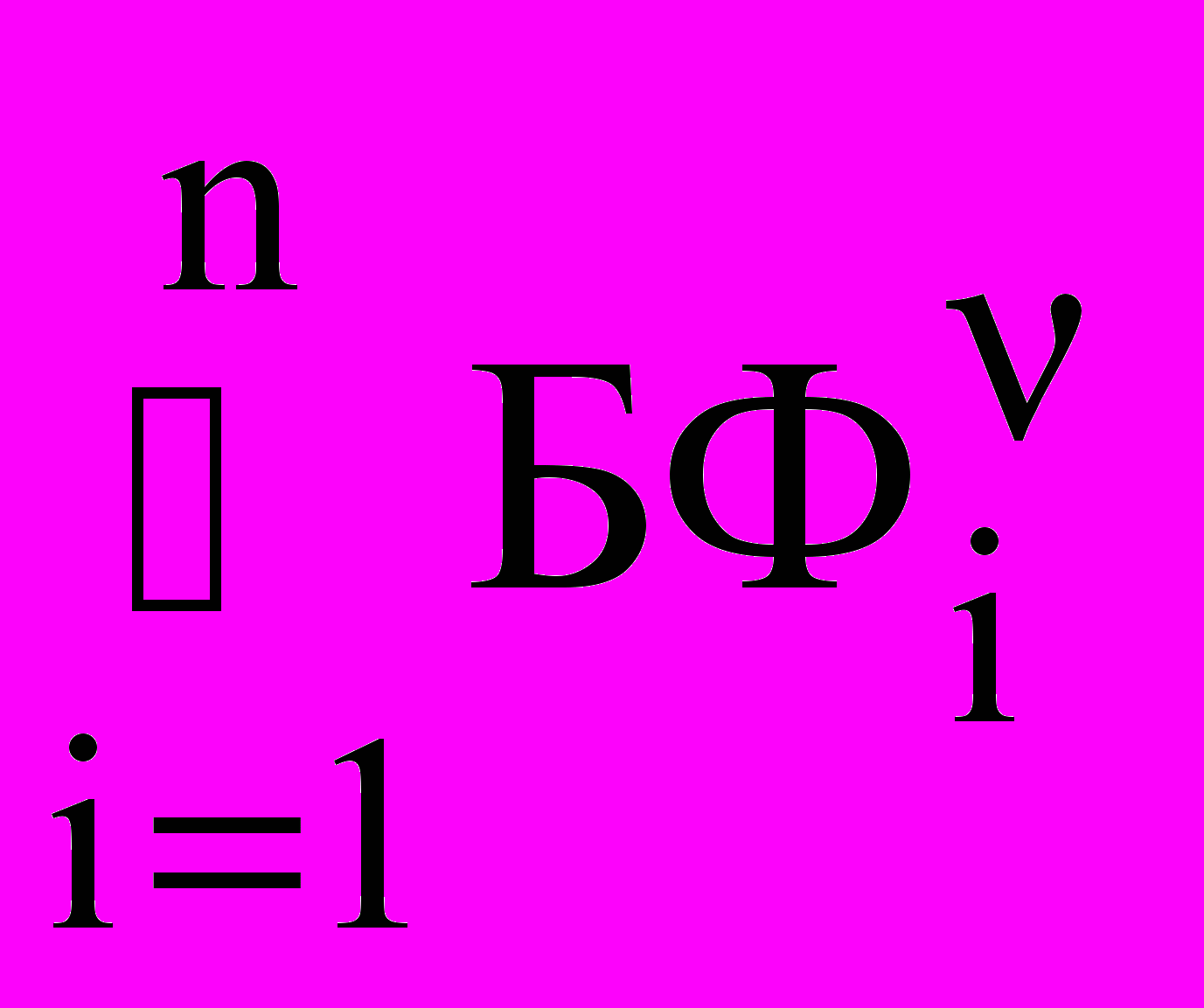, i0 – часть базы знаний, порожденная ДСМ-рассуждением за n тактов. Очевидно, что

{V,W| J_{, 2n}(V₁W)}= {V,W| П^_2n1(V,W) & J_(,2n1) (V₁W)}, где {+,, 0}; а

{V,W| J_{(, 2n)}(V₁W)}= {V,W| П^_2n1(V,W)& J_(,2n1) (V₁W)}.

Очевидно, что

БФ_n⁺={V,W| П⁺_2n1(V,W)&J_(,2n1) (X₁Y)}.

Таким образом,

БФ₁^={V,W| П₁^(V,W)&J_(,1) (V₁W)},

БФ₂^={V,W| П₃^(V,W)&J_(,3) (V₁W)},

БФ₃^={V,W| П₅^(V,W)&J_(,5) (V₁W)},

.

.

.

БФ_n ^={V,W| П^_2n1(V,W)&J_(,2n1) (V₁W)}, где {+,, 0, }.

Заметим, что БФ есть база фактов, в которой факты представлены формулами J_{, 0} (C₁Q) и J_(,0)(C₁Q); однако БФ_i ^, где {1,1, 0, }, i=1, 2, … являются фрагментами базы знаний, так как они порождены ДСМ-рассуждением, включающим на последнем шаге п.п.в.-2.

Другими фрагментами базы знаний являются БЗ_n^, порожденные ДСМ-рассуждениями, последним шагом которых являются п.п.в.-1.

БЗ₀={V,W| J_{(, 0)}(V₂W)},

БЗ₁^={V,W| J_(,1) (V₂W)},

БЗ₂^={V,W| J_(,3) (V₂W)},

БЗ₃^={V,W| J_(,5) (V₂W)},

.

.

.

БЗ_n ^={V,W| J_(,2n1) (V₂W)},

где {1,1, 0}, n1.

Соответственно,

БЗ_n ^={V,W| J_(,2n1) (V₂W)}, где n1.

Очевидно, что

БЗ_n ⁺={V,W|М⁺_2n2(V,W)&М^_2n2(V,W)& J_(,2n2) (V₂W)}, где n2.

Аналогично определяются БЗ_n ^ для = 1, 0,  для М⁺_2n2(V,W)& М^_2n2(V,W), М⁺_2n2(V,W)& М^_2n2(V,W) и М⁺_2n2(V,W) &М^_2n2(V,W), соответственно.

Определим также БЗ_n, _n^ и _n, где

БЗ_n= БЗ_n⁺ БЗ_n^ БЗ_n⁰  БЗ_n^,

_n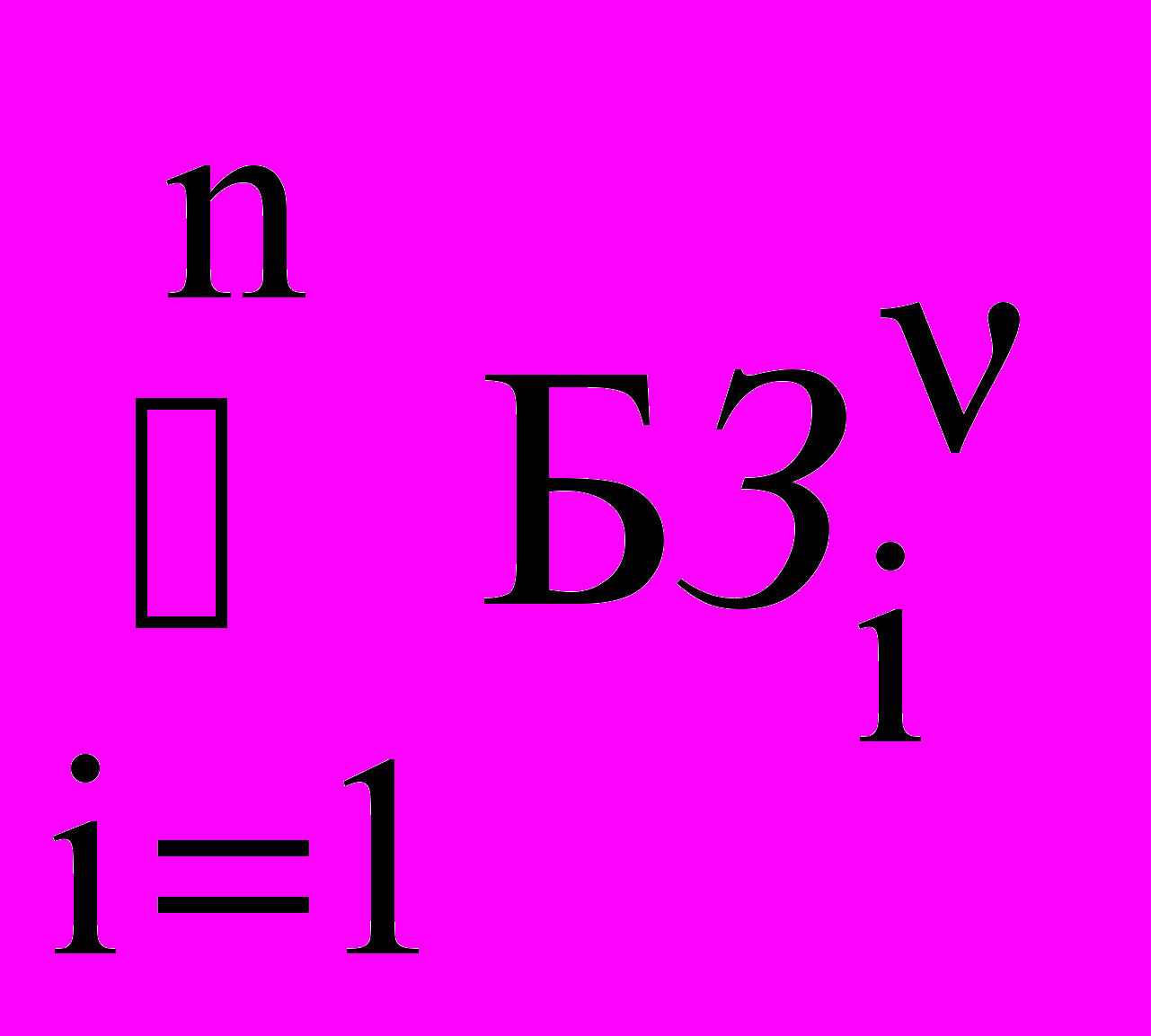^=, {1,1, 0, },

_n= БЗ₀ _n⁺ _n^  _n⁰ _n^, где n1.

Базисом ДСМ-рассуждения является пара БФ₀, БЗ₀, n- м тактом – пара _n, _n+1, где БЗ₀={V,W| J_{(, 0)}(V₂W)}.

Условием стабилизации (окончанием Этапа I) ДСМ-рассуждения является равенство _n=_n+2.

Определим отношение вложения ⊑ для _m и _m:

_m ⊑_m+2 ⇌(⁺_m  ⁺_m+2) & (^_m^_m+2) & (_m⁰⁰_m+2) & (^_m+2 ^_m),

_m⊑_m+2⇌