Г. В. Алексеев, д-р физ мат
| Вид материала | Документы |
- В. А. Каймин Информатика Учебник, 2601.27kb.
- В. А. Каймин Информатика Учебник, 2601.15kb.
- В. А. Каймин Информатика Учебник, 2602.83kb.
- Председатель чл кор. Ран, д-р физ мат наук, проф. В. Д. Мазуров Секретарь аспирант, 410.25kb.
- Владимир Галатенко доктор физ мат наук, зав, 956.79kb.
- Лекции по математике выпуск, 812.39kb.
- Электронный маркетинг, 4818.36kb.
- Авторы программы и лекторы: доктор физ мат наук, профессор Д. А. Таюрский (Dmitrii., 162.8kb.
- Удк 533. 59 Применение высокодозовой ионной имплантации для упрочнения волочильного, 39.73kb.
- Канд физ-мат, 787.32kb.
Г. В. Алексеев, д-р физ.-мат. наук
Ин-т прикладной математики ДВО РАН
(Россия, 690041, Владивосток, ул. Радио, 7,
тел.(4232) 311397, Е-mail: alekseev@iam.dvo.ru)
Д. А. Терешко, к-т физ.-мат. наук
Ин-т прикладной математики ДВО РАН
(Россия, 690041, Владивосток, ул. Радио, 7,
тел.(4232) 312631, Е-mail: ter@iam.dvo.ru)
Теоретическое и численное исследование обратных задач переноса примеси в вязкой жидкости
Аннотация. Данная работа посвящена теоретическому и численному исследованию обратных задач для стационарной модели тепломассопереноса в вязкой жидкости. Сформулированы теоремы, устанавливающие достаточные условия существования и локальной единственности исходной краевой задачи, а также разрешимость, справедливость принципа множителей Лагранжа и локальную единственность для экстремальной задачи. На основе результатов теоретического исследования предлагается алгоритм численного решения обратных задач, обсуждаются результаты вычислительных экспериментов.
1. Введение. В последнее время уделяется большое внимание обратным задачам для моделей тепломассопереноса в вязкой несжимаемой жидкости. В этих задачах неизвестные плотности граничных либо распределенных источников, коэффициенты дифференциальных уравнений модели или граничных условий восстанавливаются по дополнительной информации о решении исходной краевой задачи. Важно отметить, что обратные задачи могут быть сведены к соответствующим экстремальным задачам при помощи выбора подходящего минимизируемого функционала качества, адекватно описывающего рассматриваемую обратную задачу. В результате этого обратные задачи и задачи управления могут быть исследованы с помощью единого подхода, основанного на теории оптимального управления в гильбертовых пространствах (см. [1]).
Пусть Ω – ограниченная область в пространстве Rm, m=2, 3 с липшицевой границей . Рассмотрим краевую задачу для стационарных уравнений Обербека-Буссинеска
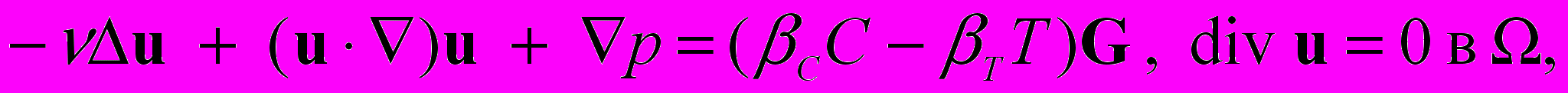
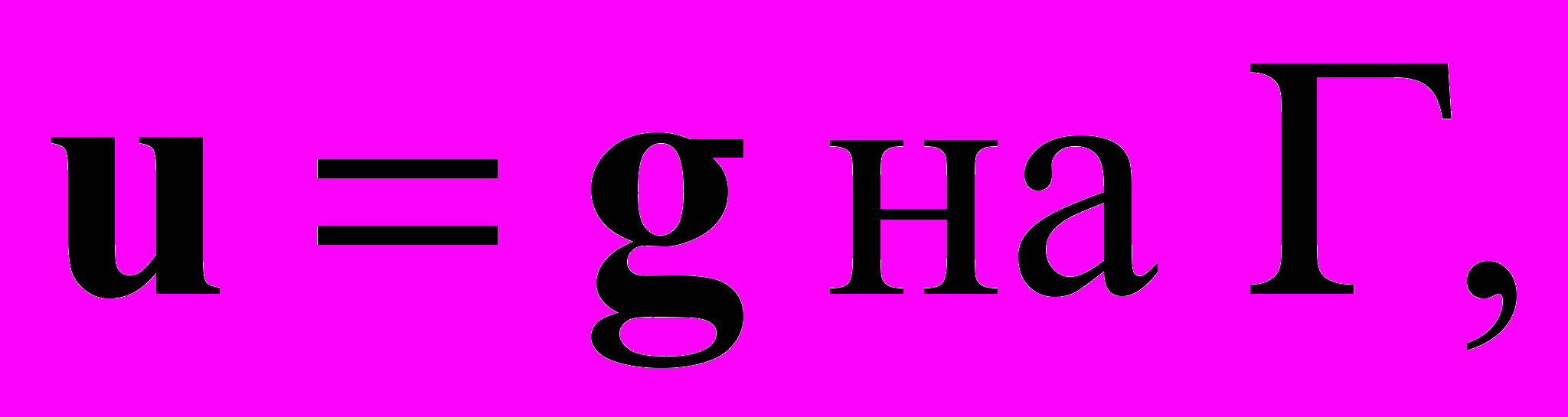 (1)
(1)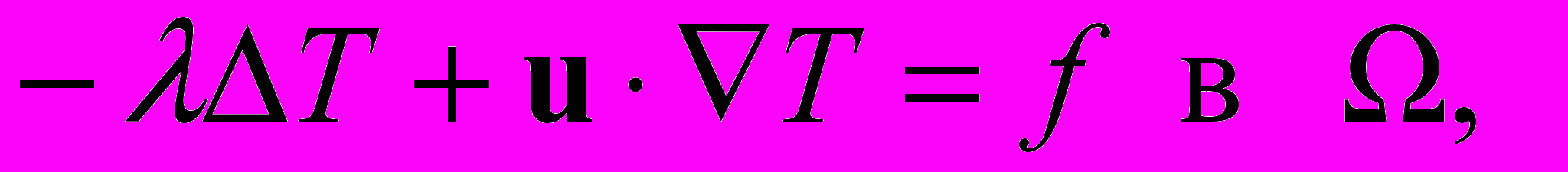
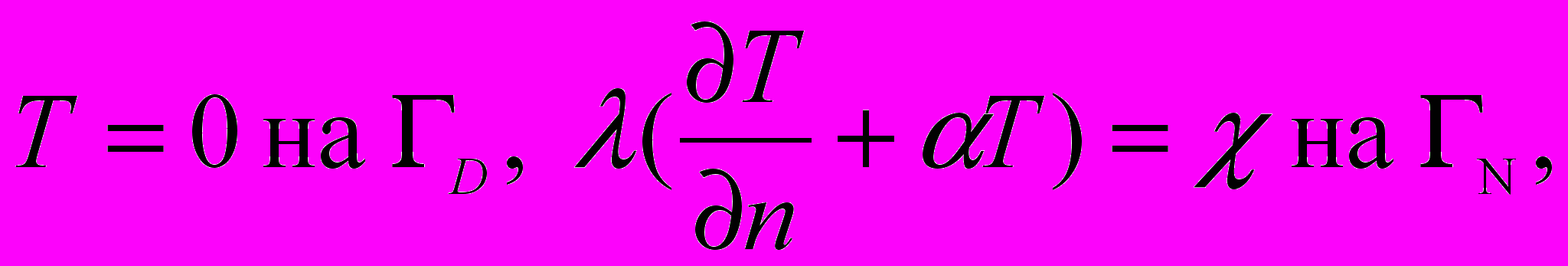 (2)
(2)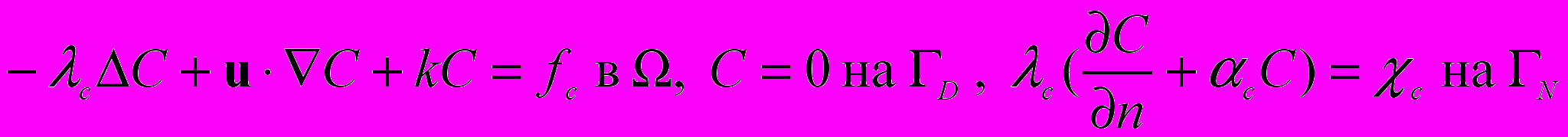 , (3)
, (3)описывающую стационарное течение вязкой несжимаемой теплопроводной жидкости в области Ω. Здесь u, p, T и C – скорость, давление, температура и концентрация загрязняющего вещества, – коэффициент кинематической вязкости, G – вектор ускорения свободного падения, T и C – объемные коэффициенты теплового и массового расширения, – коэффициент температуропроводности, с – коэффициент диффузии, g – заданная вектор-функция на границе , , с, , с – некоторые функции на части N=\D границы , n – единичный вектор внешней нормали. Постоянная плотность выбрана равной 1.
В частном случае, когда C=0, задача (1)-(3) разбивается на две задачи: задачу (1), (2) для уравнений тепловой конвекции в приближении Обербека-Буссинеска и линейную краевую задачу (3) (при заданной скорости u), описывающую распространение пассивной примеси. Экстремальные задачи для модели (1), (2) изучались разными авторами (см., например, [2-6]). В другом частном случае, когда T=0, задача (1)-(3) распадается на задачу (1), (3) для модели переноса вещества и линейную задачу конвекции-диффузии (2) для температуры T. Экстремальные задачи для (1), (3) рассматривались в [7-9]. Упомянем также работы [10,11], в которых были рассмотрены обратные задачи восстановления неизвестных плотностей тепла и вещества для общей модели (1)-(3).
Будем предполагать, что выполняются следующие условия:
- Ω – ограниченная область в R3 с липшицевой границей ΓC0,1, состоящей из n связных компонент Г(i), i=1,2,…,n; открытые участки ГD и ГN границы Г удовлетворяют условиям ΓDC0,1, meas ΓD>0, ΓNC0,1,
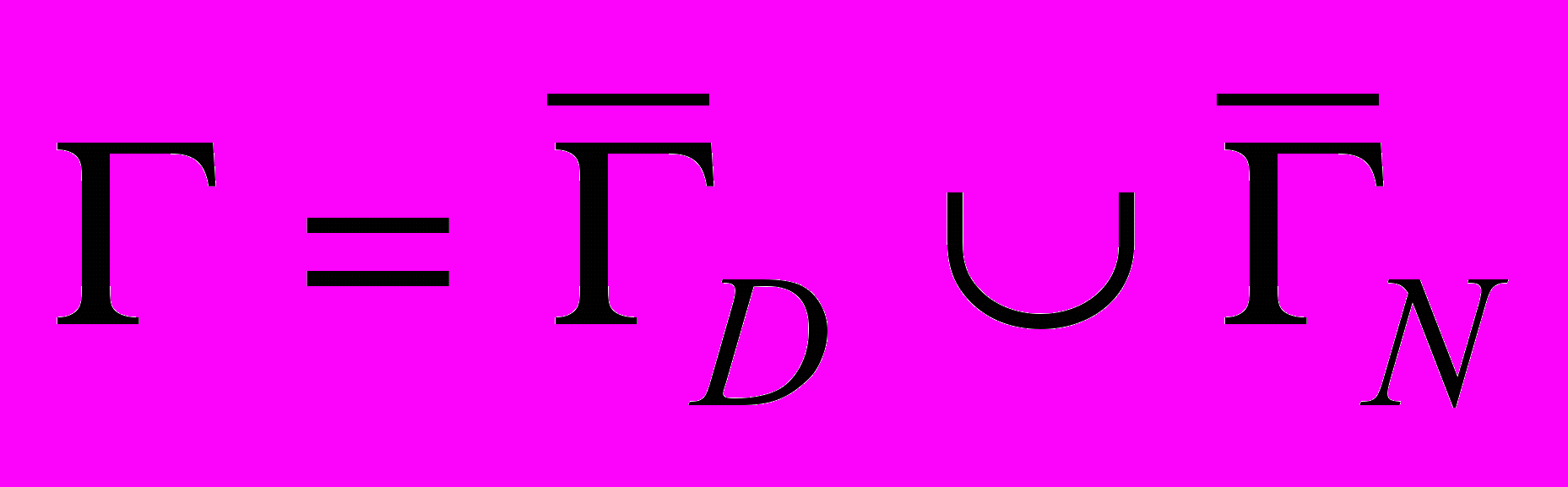 ;
;
- gH1/2(Γ), fL2(Ω), fcL2(Ω).
Ниже мы будем использовать пространства Соболева Hs(D), где sR, а в качестве D может выступать область Ω или ее подмножество Q либо граница Γ или некоторая ее часть с положительной мерой. В частности, нам потребуются функциональные пространства H1(Ω), H1(Ω), L2(Ω), H1/2(), H1/2(D) и их подпространства
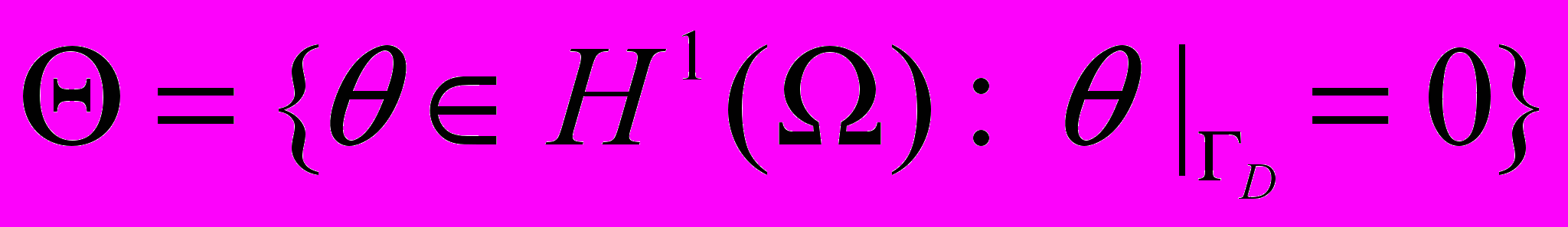 ,
, 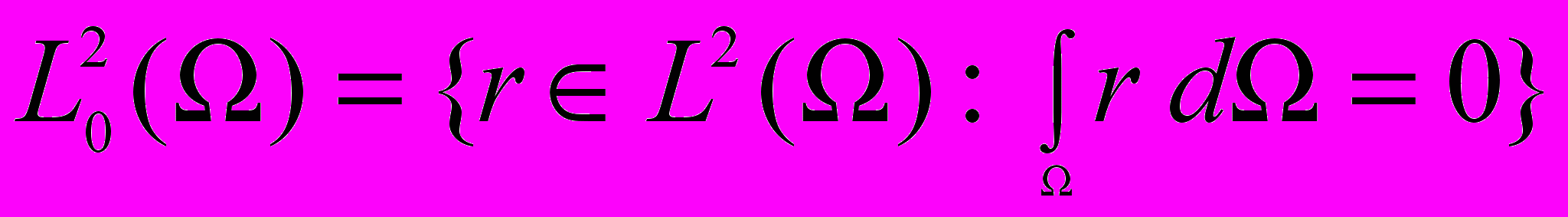 ,
, 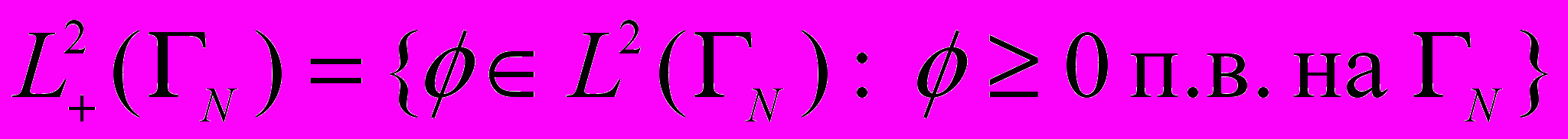 ,
, 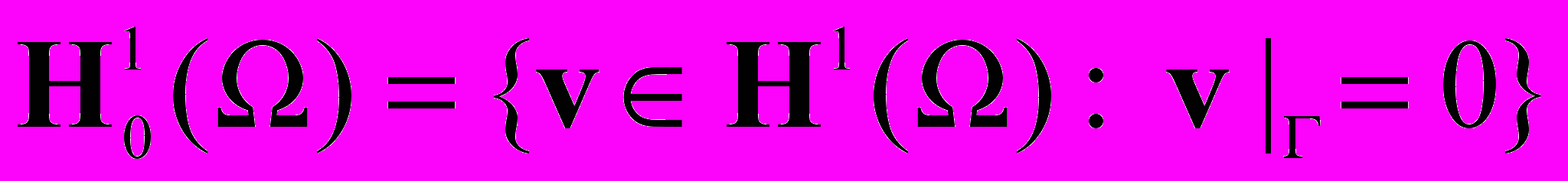 ,
, .
.Скалярные произведения и нормы в L2(Ω) или L2(N) обозначаются через
 , || || или
, || || или 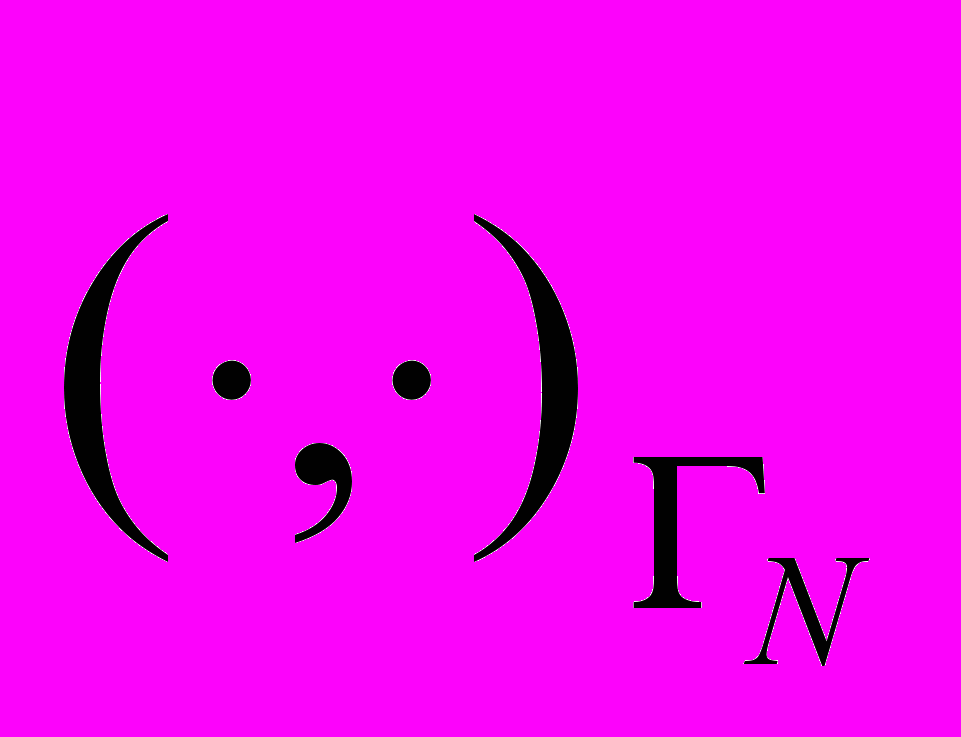 ,
, 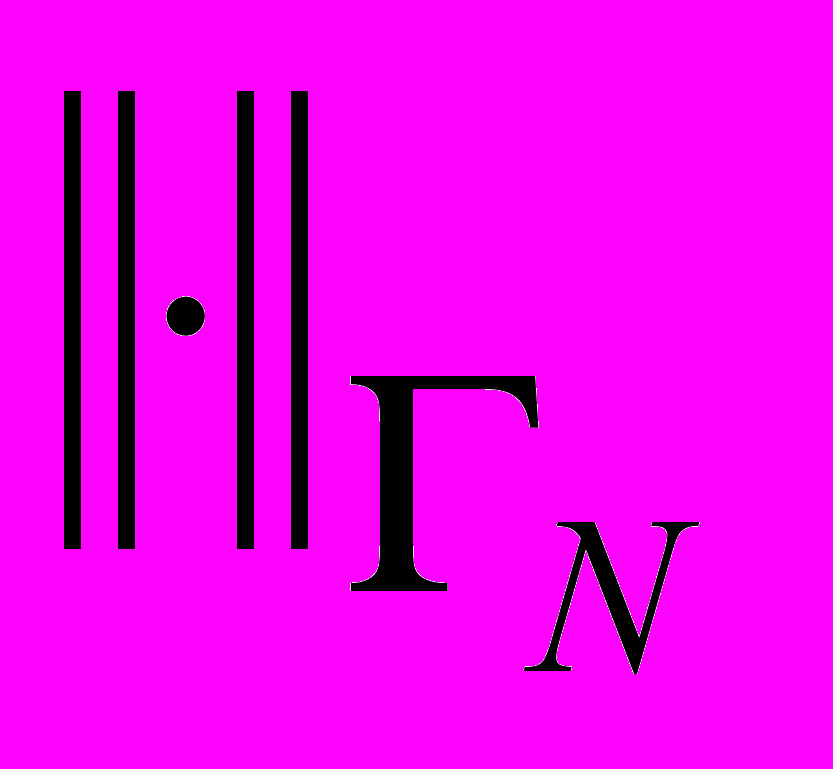 . Норму в H1(Ω) обозначаем || ||1.
. Норму в H1(Ω) обозначаем || ||1. Справедлива следующая вспомогательная лемма (см. [1]):
Лемма 1. При выполнении условия (i) существуют такие константы i>0, i>0 и 1, что
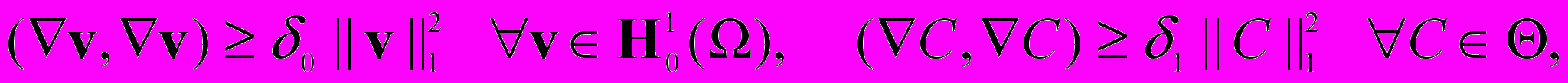
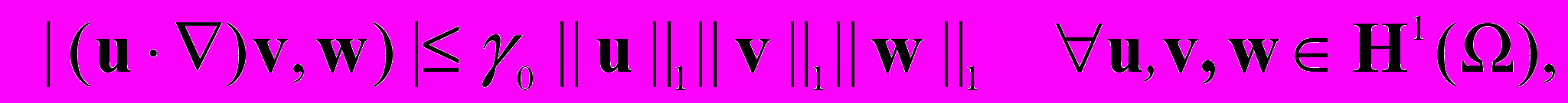
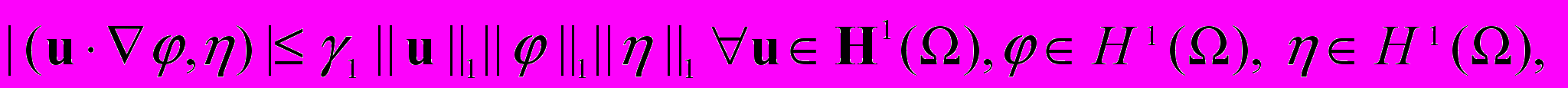
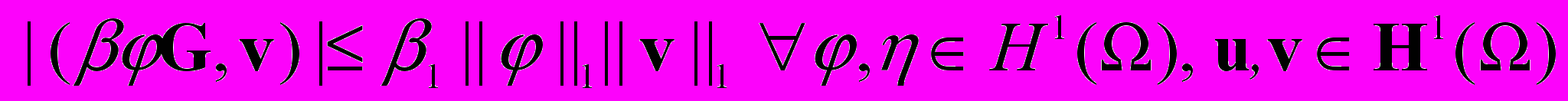 ,
,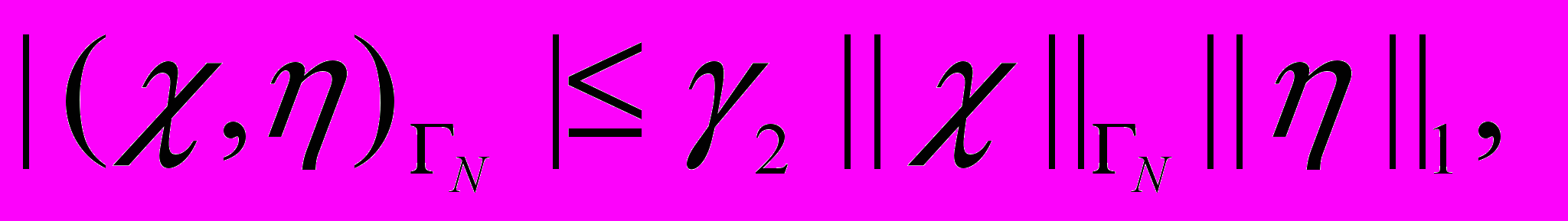
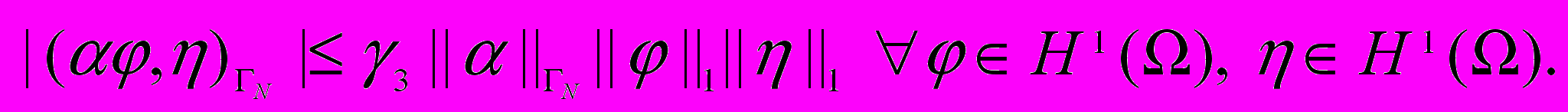
2. Теоретический анализ экстремальных задач. Рассмотрим краевую задачу (1), (3) при T=0. Ниже на нее будем ссылаться для краткости как на задачу 1. Будем предполагать, что функции αc и c в граничном условии для C неизвестны вместе с решением (u,p,C). Такая ситуация может наблюдаться в случае, когда область Ω имеет границу Γ, состоящую из внешней компоненты ΓD, на которой задано условие Дирихле, и внутренней компоненты ΓN. Естественно предположить, что значения концентрации C на внешней границе ΓD и в малой подобласти Q, лежащей в окрестности ΓD, могут быть измерены. В то же время внутренняя граница ΓN может оказаться недоступной для измерений. Поэтому параметры αc и c, которые относятся к внутренней границе, неизвестны. В этой ситуации возникает задача идентификации, в которой необходимо найти решение (u,p,C) задачи (1), (3) при T=0 вместе с парой (αc,c), используя измеренные значения поля концентрации Cd в некоторой области Q. Аналогичные примеры возникают в задачах для модели теплопереноса (1), (2).
Для решения задачи идентификации применим метод оптимизации. Это означает, что мы будем искать неизвестные функции (u,p,С,αс,с) с помощью минимизации некоторого функционала качества
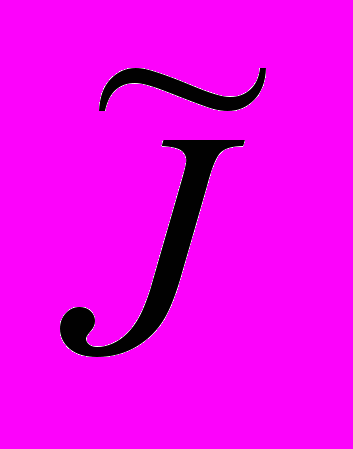 . В качестве
. В качестве 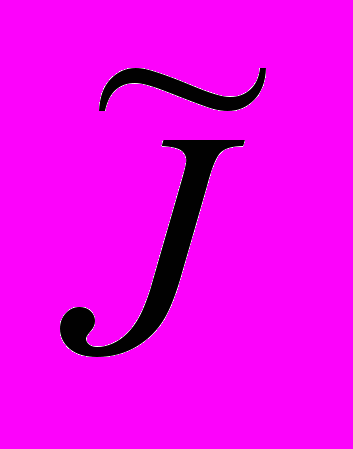 будем рассматривать функционалы
будем рассматривать функционалы ,
, 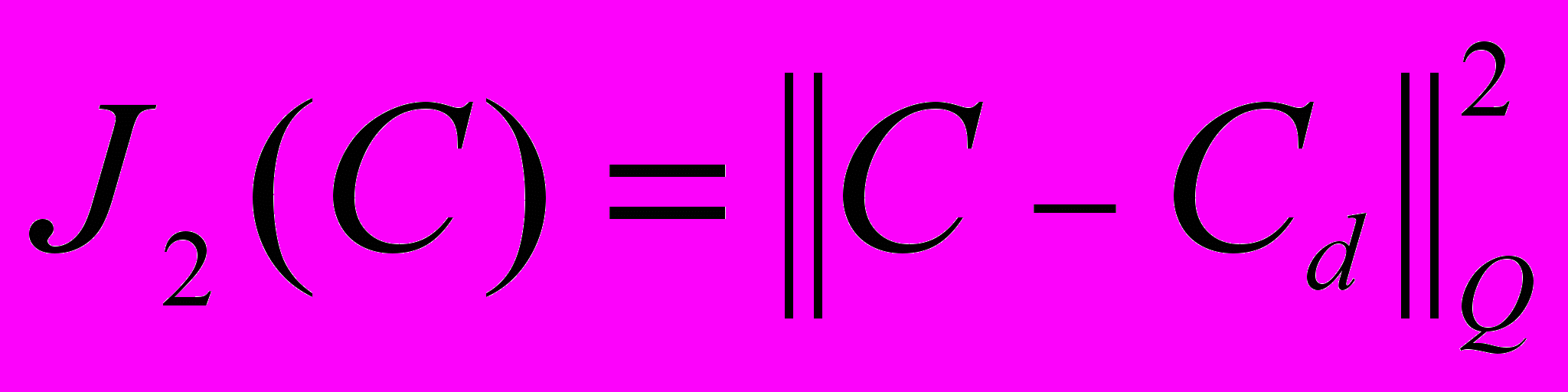 ,
,где функции ζd L2(Q) и Cd L2(Q) моделируют измеренное поле завихренности и концентрации в Q. Разобьем все данные задачи 1 на две группы: группу управлений, содержащую функции αc и c, и группу фиксированных данных, содержащую функции (f,g,k,fc). Полагая u=(αc,c), u0=(f,g,k,fc), x=(u,p,C),
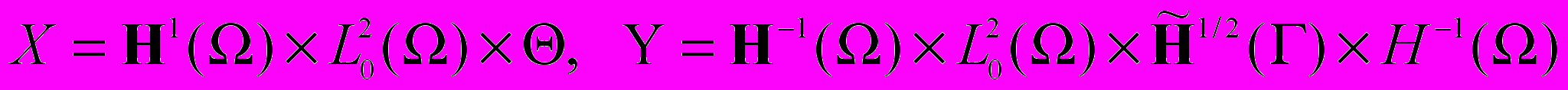 ,
,введем оператор F=(F1,F2,F3,F4):XKY, действующий по формулам
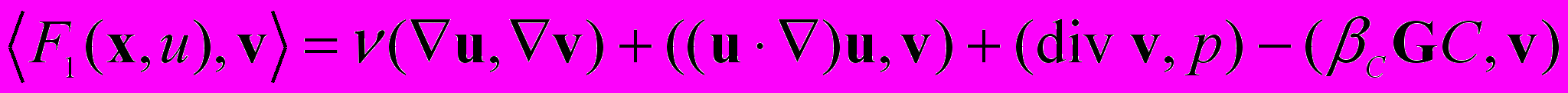 ,
, 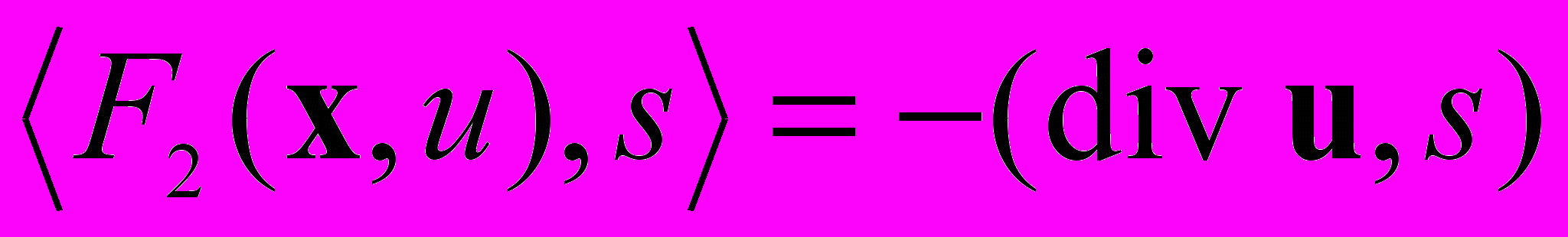 ,
, 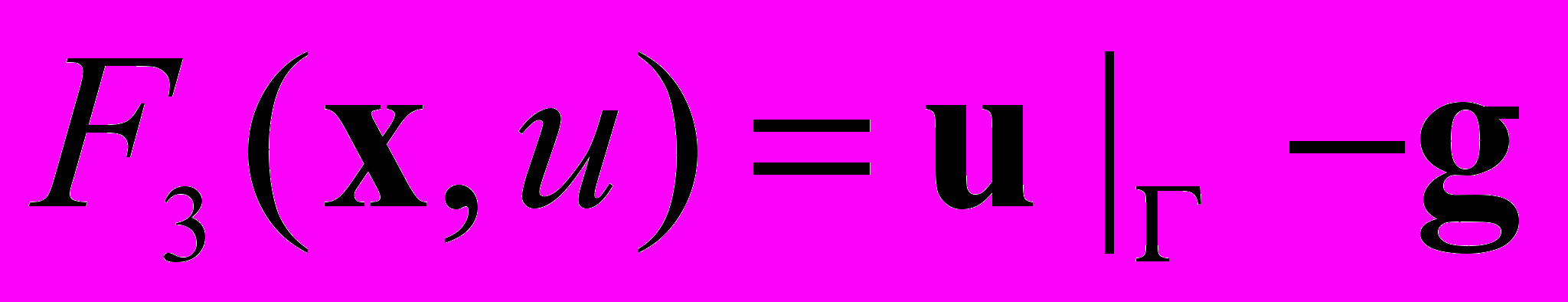 ,
, 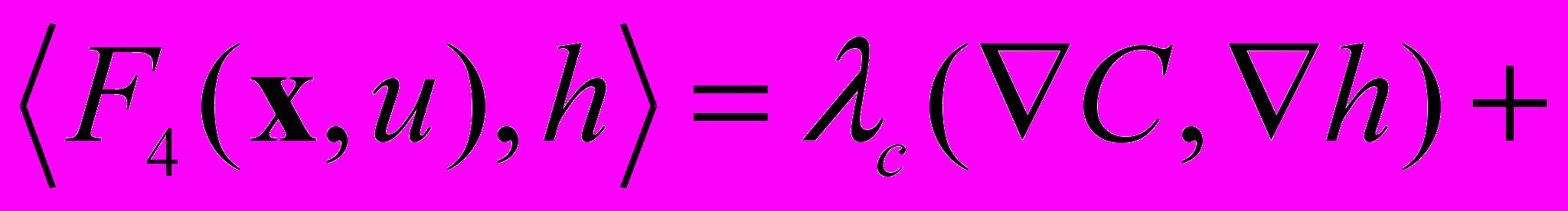
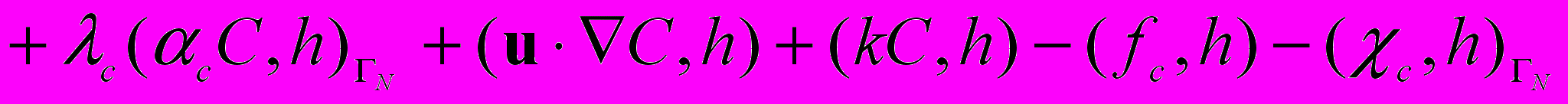 .
.Умножим первое уравнение в (1) на функцию
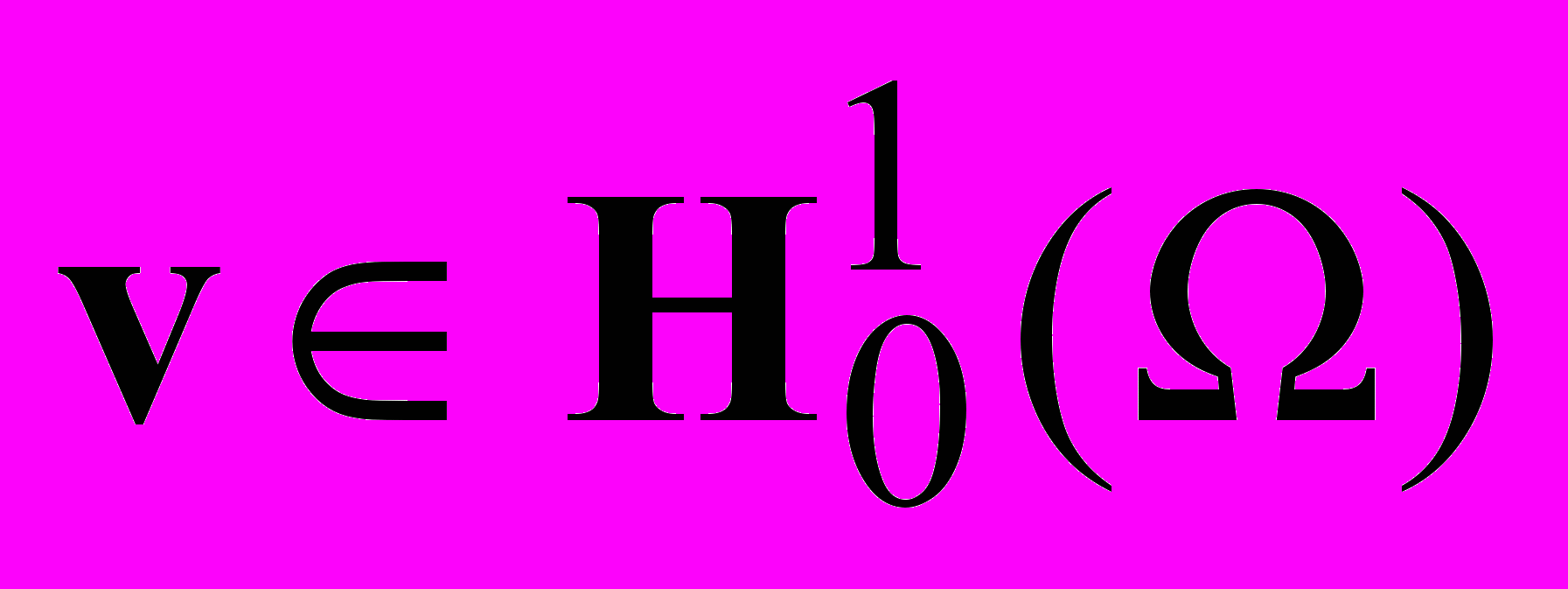 , уравнение в (2) на функцию hΘ и проинтегрируем полученные соотношения по Ω. Применяя формулы Грина, мы получаем слабую формулировку задачи 1. Она заключается в нахождении тройки (u,p,С) X из операторного уравнения
, уравнение в (2) на функцию hΘ и проинтегрируем полученные соотношения по Ω. Применяя формулы Грина, мы получаем слабую формулировку задачи 1. Она заключается в нахождении тройки (u,p,С) X из операторного уравнения F(x,u) = F(u,p,C,αc,c) = 0.
Ниже будем предполагать, что управления αc и c изменяются на множествах
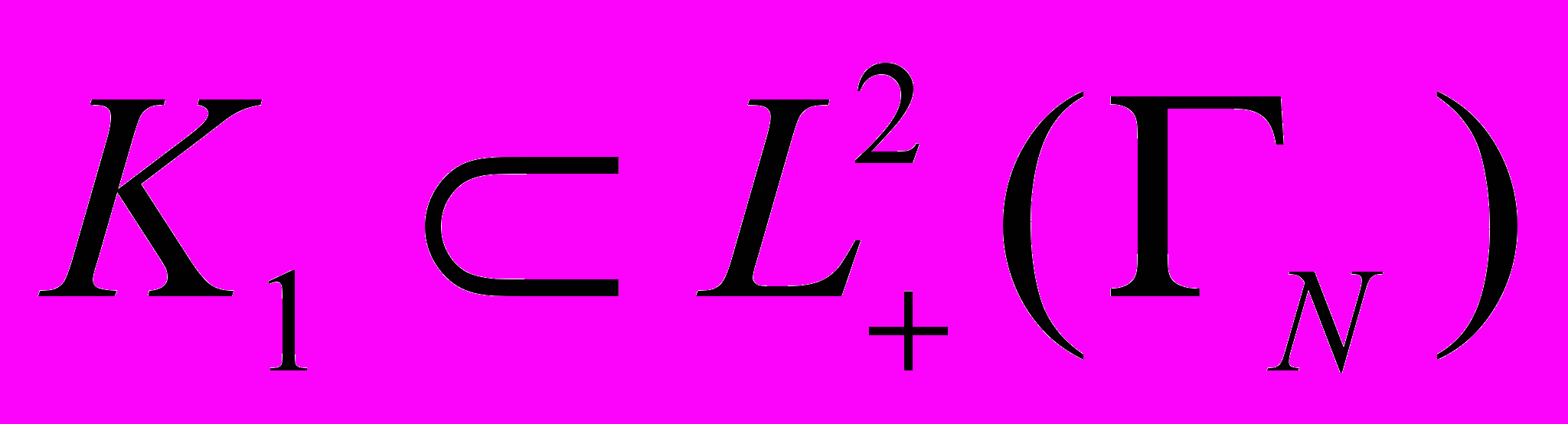 и K2 L2(N). Через 0, 1 и 2 обозначим неотрицательные константы. Более точно, предположим, что выполняются следующие условия:
и K2 L2(N). Через 0, 1 и 2 обозначим неотрицательные константы. Более точно, предположим, что выполняются следующие условия:(j)
 и K2 L2(N) – непустые замкнутые выпуклые множества; 0>0, l 0 и Kl – ограниченное множество либо l > 0, l=1,2.
и K2 L2(N) – непустые замкнутые выпуклые множества; 0>0, l 0 и Kl – ограниченное множество либо l > 0, l=1,2. Сформулируем следующую задачу условной минимизации:
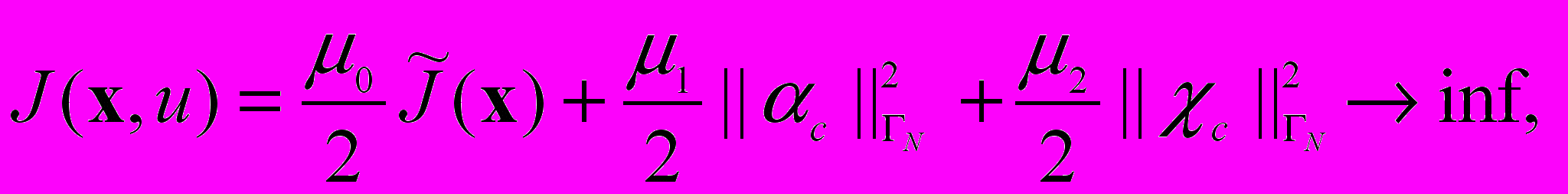
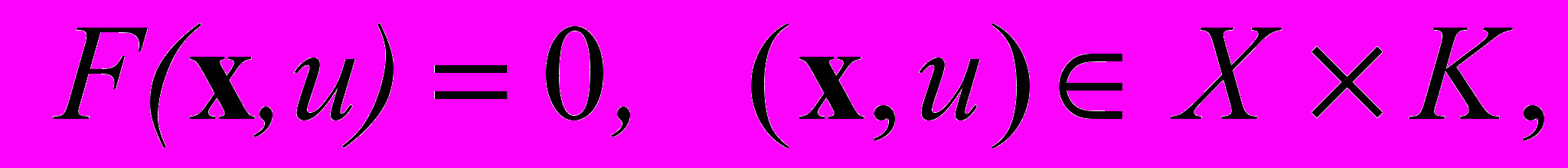 (4)
(4)где K=K1K2.
Следующие теоремы устанавливают достаточные условия существования и локальной единственности решения задачи 1, а также разрешимость, справедливость принципа множителей Лагранжа и локальную единственность для экстремальной задачи (4). Их доказательства можно найти в [1,4,9].
Теорема 1. При выполнении условий (i), (ii) задача 1 для любой пары (αc,c)K имеет слабое решение (u,p,C), удовлетворяющее оценкам
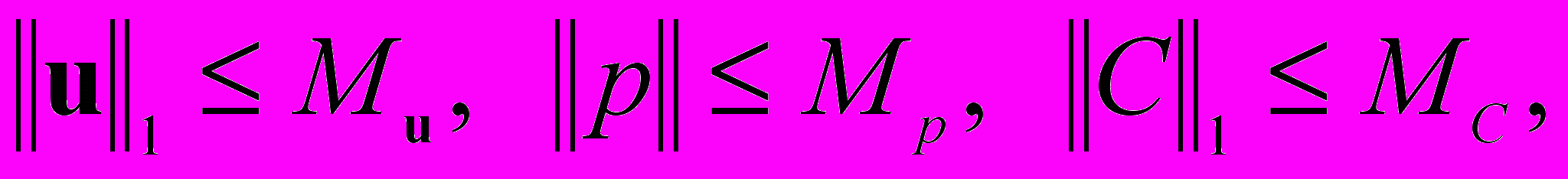
где Mu(u0,u), Mp(u0,u) и MC(u0,u) – непрерывные неубывающие функции норм функций f, g, fc, αc и c. Если, кроме того, f, g, fc и c являются малыми в том смысле, что e+a<1, где
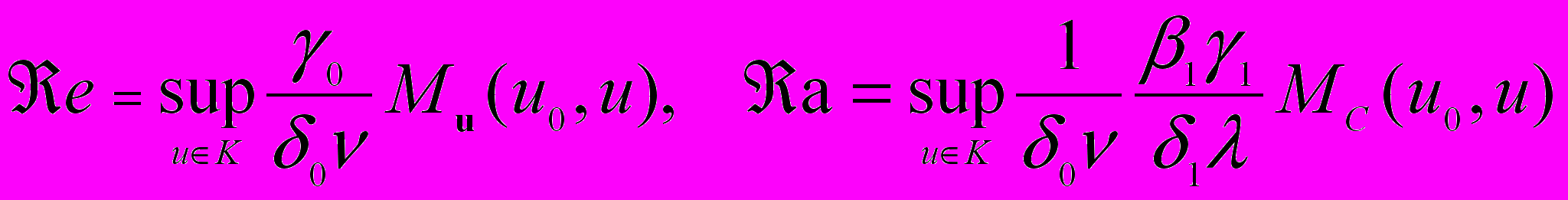 ,
,то слабое решение задачи 1 единственно для любого элемента uK.
Теорема 2. Пусть выполняются условия (i), (ii), (j). Тогда существует, по крайней мере, одно решение задачи (4).
Теорема 3. Пусть при выполнении условий (i), (ii), (j) элемент
 является точкой локального минимума в задаче (4). Тогда существует ненулевой множитель Лагранжа
является точкой локального минимума в задаче (4). Тогда существует ненулевой множитель Лагранжа  такой, что выполняется уравнение Эйлера-Лагранжа
такой, что выполняется уравнение Эйлера-Лагранжа 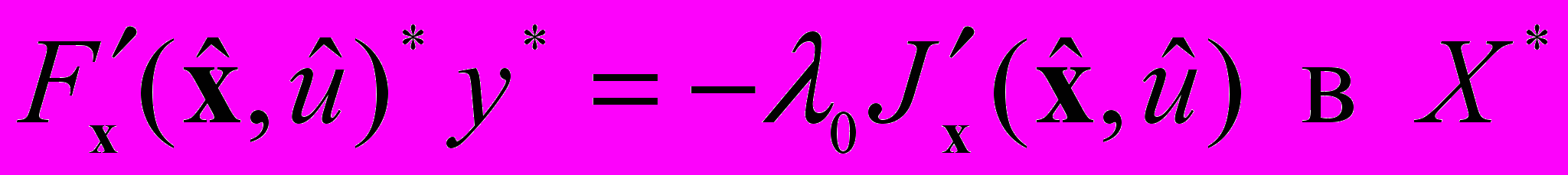
для сопряженного состояния y* и справедлив принцип минимума, который эквивалентен неравенству
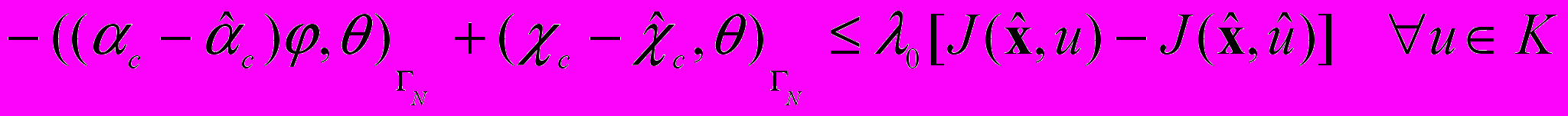 (5).
(5).Теорема 4. Пусть в условиях теоремы 3 e + a < 1/2, μ0 >0 и выполняются следующие неравенства:
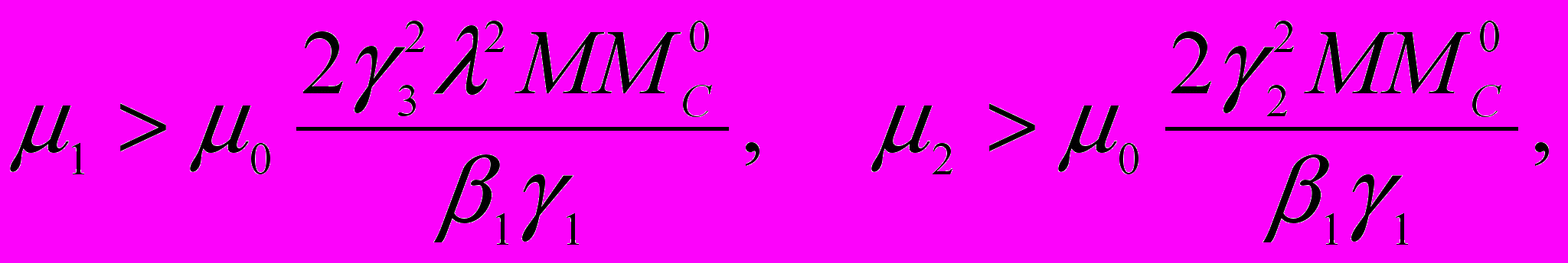
где
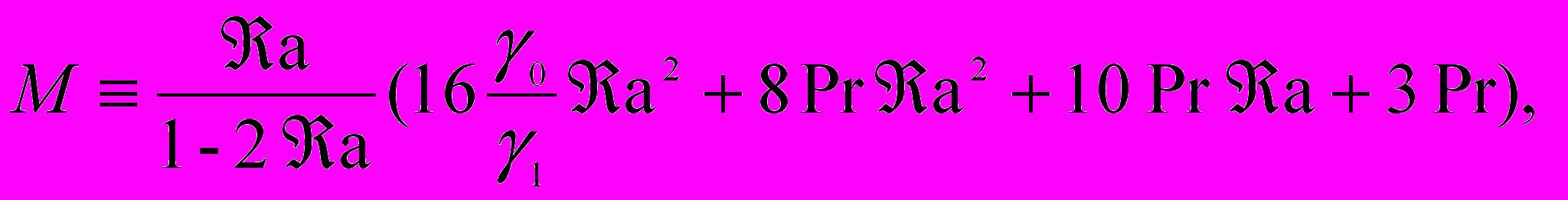
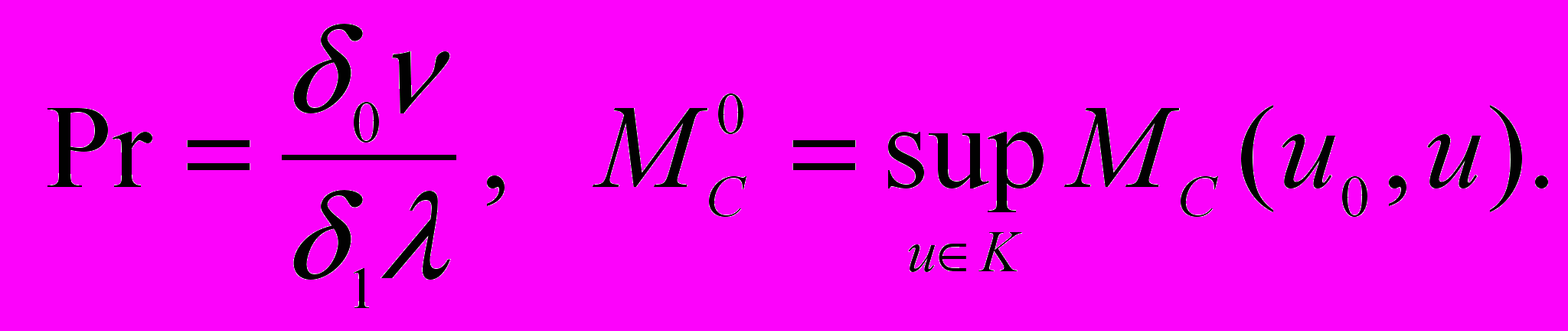
Тогда решение (u,p,C,c,c) задачи (4) при
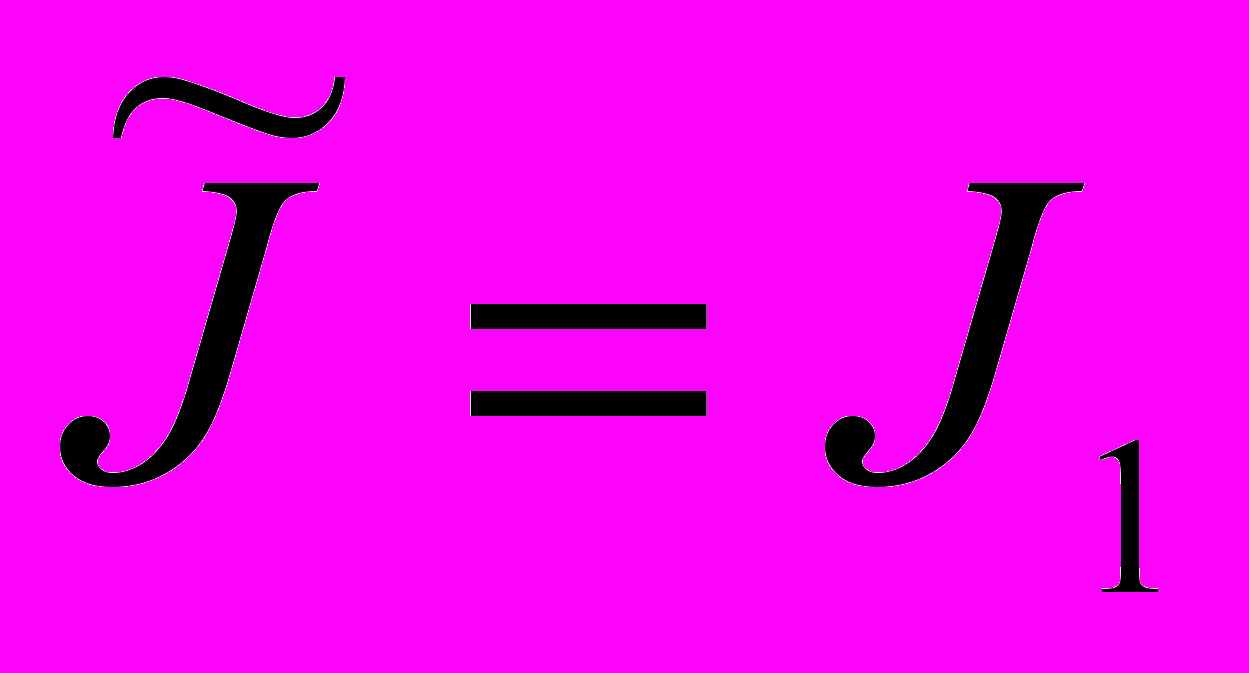 единственно.
единственно.По аналогичной схеме формулируются экстремальные задачи для модели (1), (2) при C=0. Более подробно об этом можно прочитать в работах [1-7].
3. Численный анализ. Рассмотрим сначала экстремальную задачу для уравнений (1), (3) при T =0. В качестве единственного управления будем использовать функцию c на части ГN границы Г. При этом будем считать, что множество управлений K совпадает со всем пространством L2(ГN) и 2>0. Тогда минимум функционала будет достигаться во внутренней точке множества K и принцип минимума (5) можно заменить следующим тождеством:
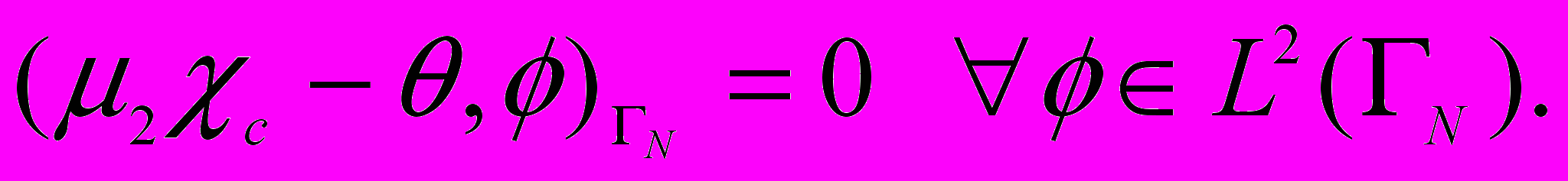
Выразив отсюда c по формуле c = /2, мы можем исключить управление из системы оптимальности. Полученные соотношения, содержащие в качестве неизвестных величин основное состояние (u,p,C) и сопряженное состояние (,,), для краткости будем записывать в виде операторного уравнения (u,p,C,,,)=0. Здесь – некоторый нелинейный оператор, определяемый введенным выше оператором F. Для численного его решения предлагается итерационный алгоритм, основанный на методе Ньютона. Он состоит из следующих этапов:
0. Выбираем начальное приближение u0, p0, C0, 0, 0, 0. Полагаем n=0.
1. Вычисляем
 как решение линейного операторного уравнения
как решение линейного операторного уравнения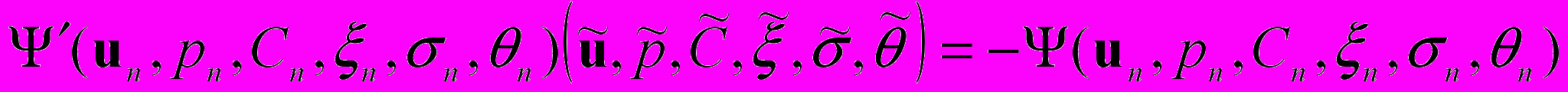 . (6)
. (6)2. Пересчитываем значения искомых величин по формулам
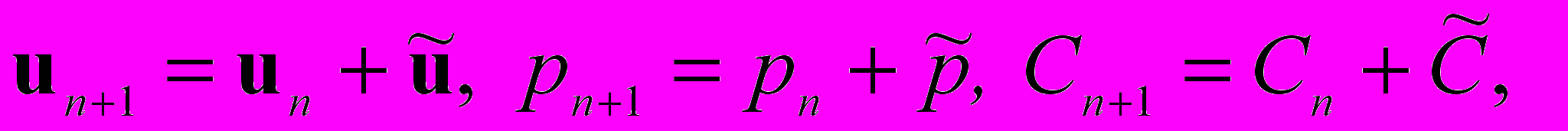

3. Проверяем условие выхода из цикла. Если оно не выполняется, то увеличиваем номер шага n на 1 и переходим к этапу 1.
Использование метода Ньютона связано с нелинейностью оператора . В проведенных вычислительных экспериментах роль условия выхода из цикла играло неравенство
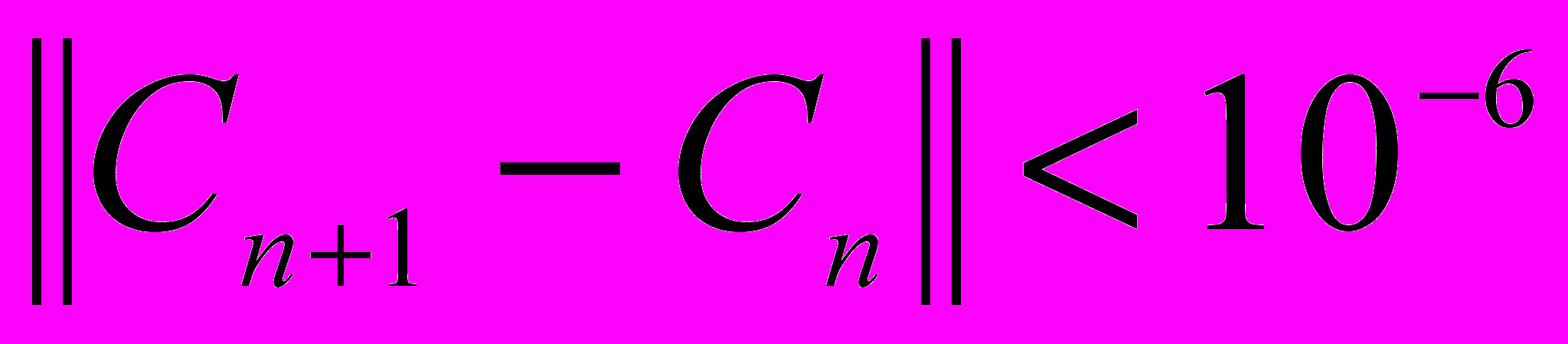 . Операторное уравнение (6) в подробной записи представляет собой краевую задачу для системы линейных уравнений в частных производных. Для ее решения используется метод конечных элементов.
. Операторное уравнение (6) в подробной записи представляет собой краевую задачу для системы линейных уравнений в частных производных. Для ее решения используется метод конечных элементов.Рассмотрим задачу условной минимизации для уравнений (1), (3) при Т=0, заключающуюся в нахождении неизвестной плотности c граничного источника загрязнения (играющей роль единственного управления) из условия минимума функционала
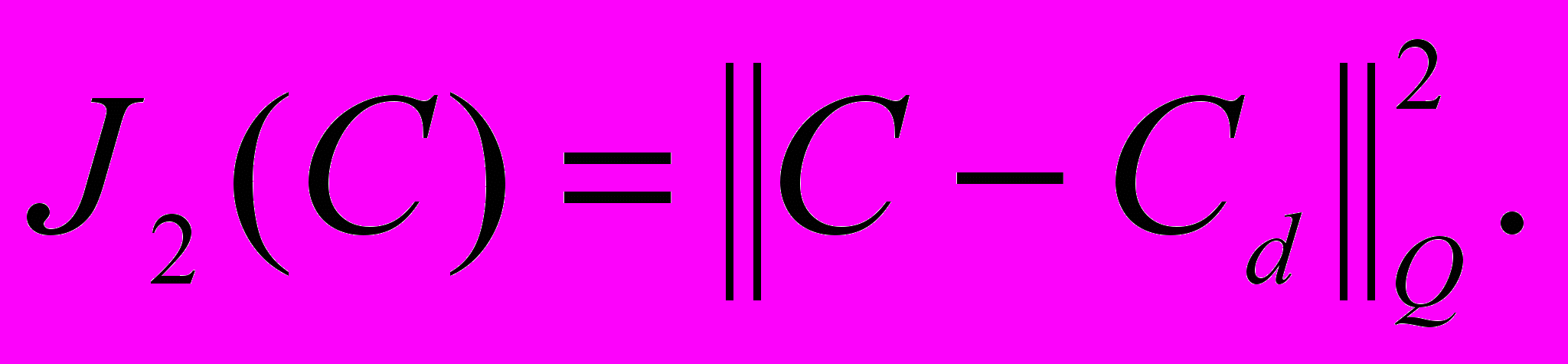 Здесь Cd – измеренное в некоторой подобласти Q поле концентрации примеси. В вычислительных экспериментах в качестве функции Сd использовалось решение краевой задачи (1), (3) для некоторой функции cd, заданной на части ГN границы Г. При этом моделировался процесс переноса загрязнения вязкой несжимаемой жидкостью в канале
Здесь Cd – измеренное в некоторой подобласти Q поле концентрации примеси. В вычислительных экспериментах в качестве функции Сd использовалось решение краевой задачи (1), (3) для некоторой функции cd, заданной на части ГN границы Г. При этом моделировался процесс переноса загрязнения вязкой несжимаемой жидкостью в канале 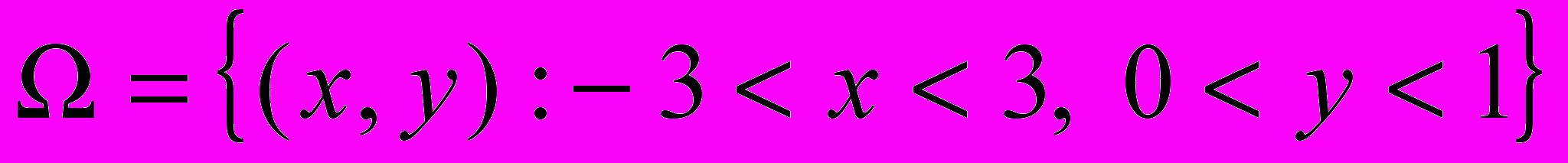 . Множество наблюдений Q располагалось ниже по течению в правой части области Ω и требовалось восстановить граничную функцию c на верхней стенке канала. На рис. 1а представлены графики исходной функции cd и полученного решения c на верхней границе области течения для случая, когда множество Q занимает ровно половину области Ω. Легко заметить, что на правой половине графики практически совпадают. Так как в данном случае информация о поле концентрации Сd в левой половине не задана, то функция c при
. Множество наблюдений Q располагалось ниже по течению в правой части области Ω и требовалось восстановить граничную функцию c на верхней стенке канала. На рис. 1а представлены графики исходной функции cd и полученного решения c на верхней границе области течения для случая, когда множество Q занимает ровно половину области Ω. Легко заметить, что на правой половине графики практически совпадают. Так как в данном случае информация о поле концентрации Сd в левой половине не задана, то функция c при 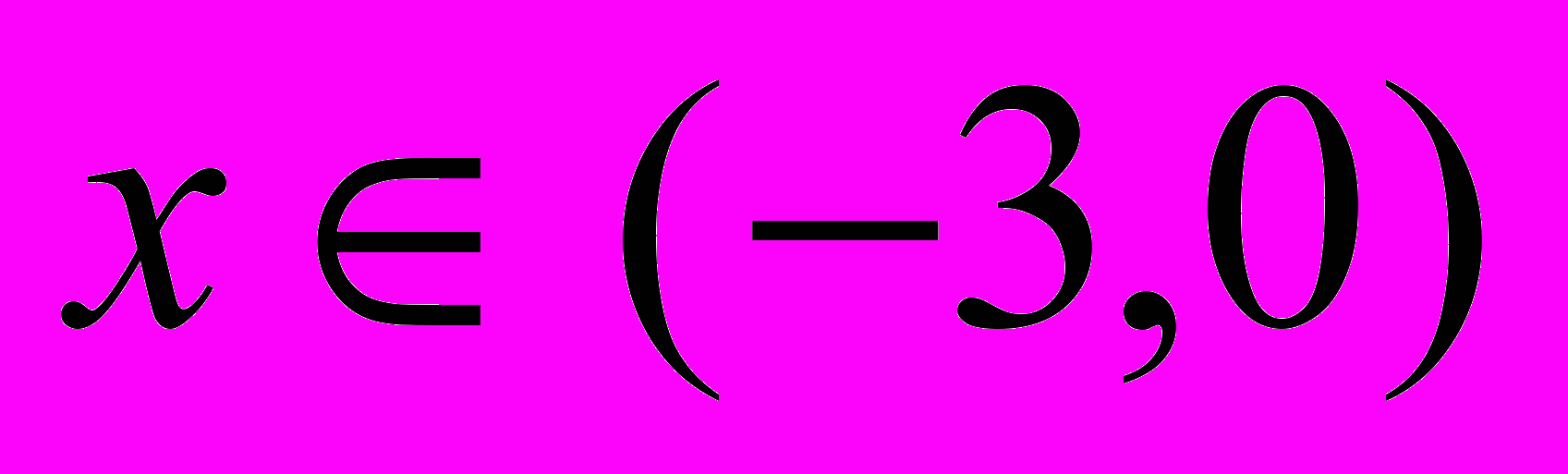 определяется не очень точно. Если множество Q совпадает со всей областью Ω, то такое хорошее восстановление граничного управления наблюдается на всей области определения функции c.
определяется не очень точно. Если множество Q совпадает со всей областью Ω, то такое хорошее восстановление граничного управления наблюдается на всей области определения функции c.

а б
Рис. 1. Зависимость точности восстановления от размера множества Q
Для оценки точности решения экстремальной задачи используются следующие две относительные погрешности:
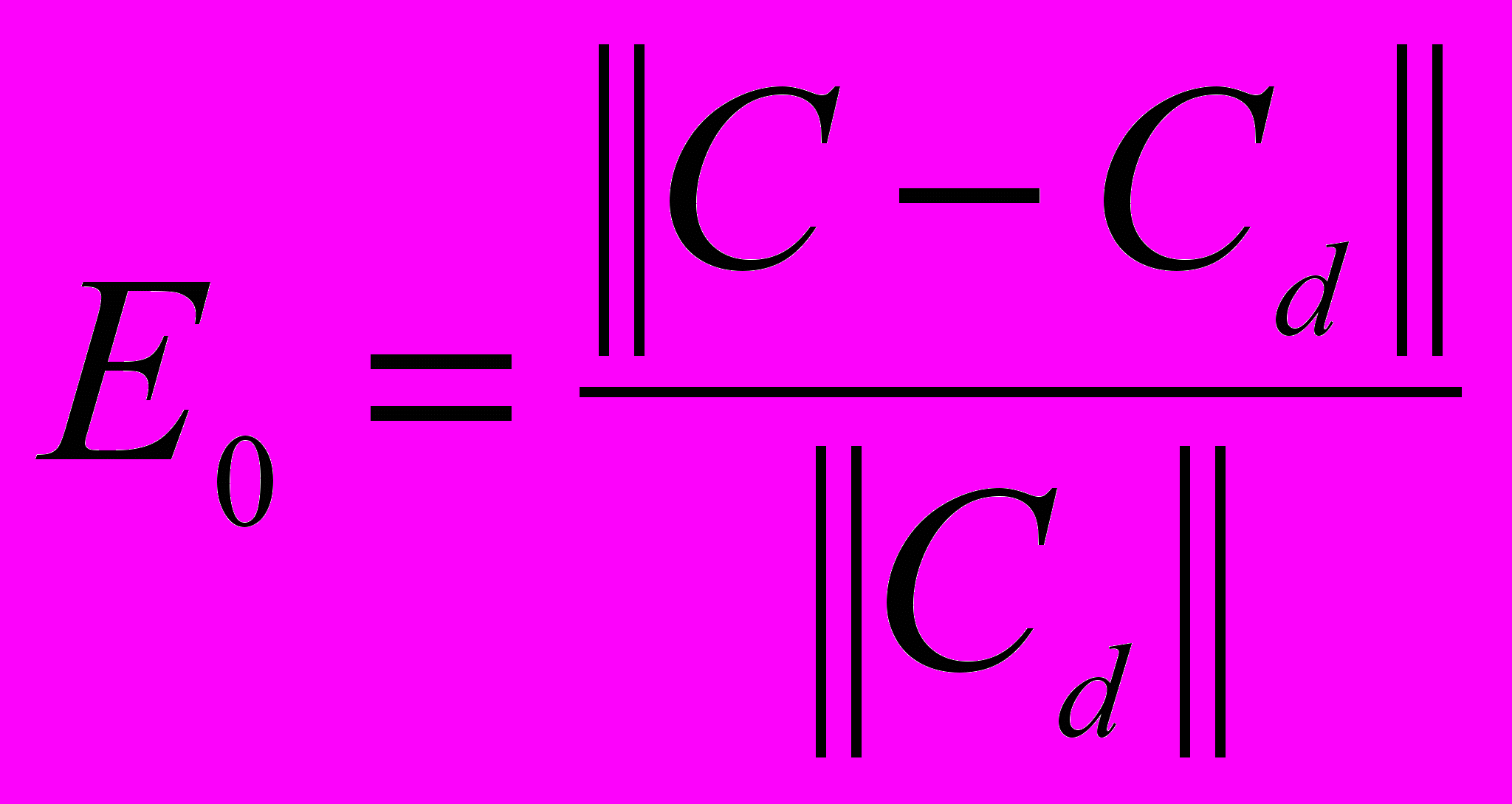 ,
, 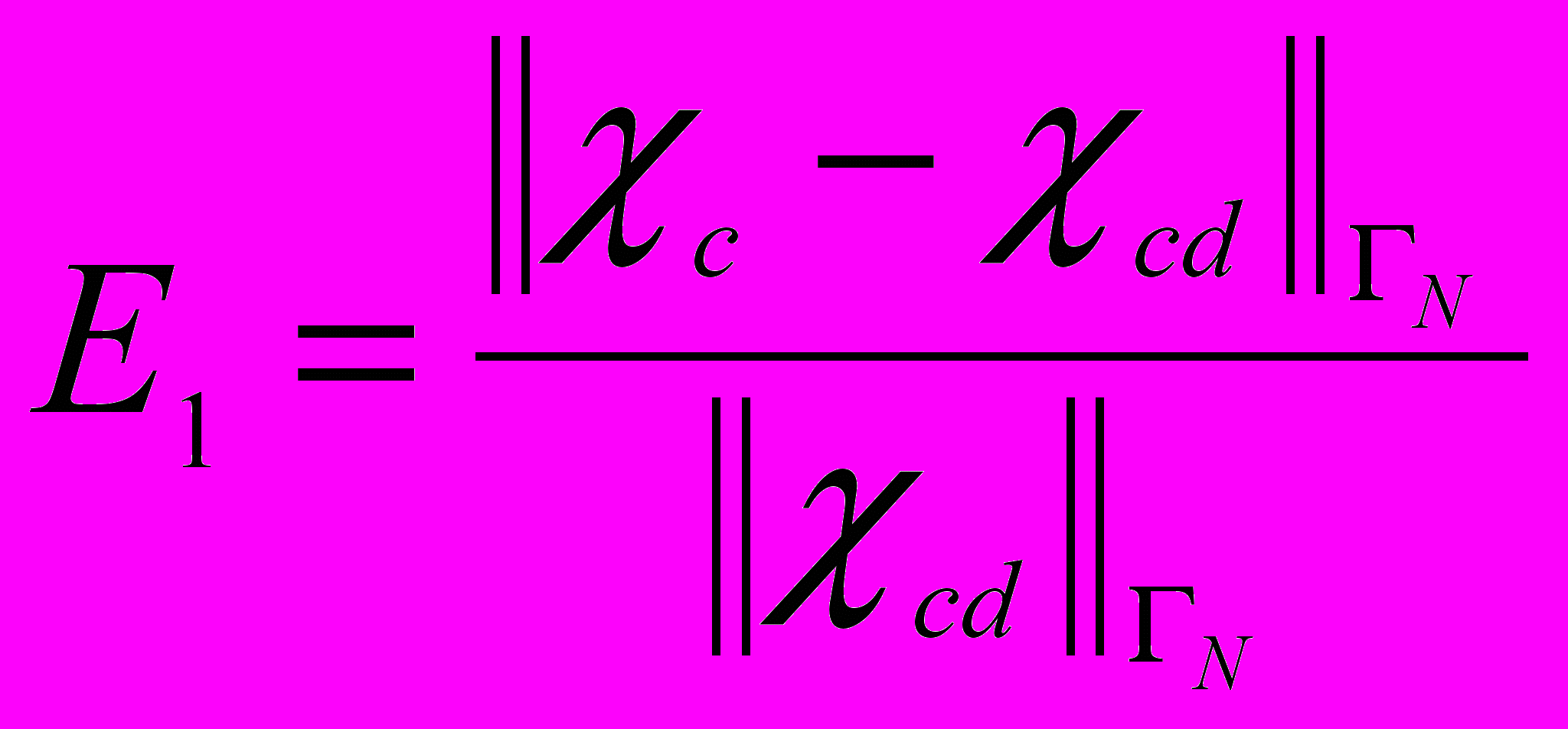 .
.Зависимости этих величин от относительного размера множества Q представлены на рис. 1б. Хорошо видно, что с увеличением размера подобласти Q относительные ошибки уменьшаются. Если множество наблюдений Q занимает половину области Ω, то относительная ошибка для концентрации составляет примерно 3%. В случае, когда множество Q совпадает со всей областью Ω, величина E0 принимает значение порядка 10-6. Более подробное обсуждение результатов вычислительных экспериментов можно найти в [1].
Работа поддержана грантом Президента РФ (проект НШ-2810.2008.1) и грантами ДВО РАН (проекты 06-I-П22-086, 06-II-СО-03-010, 06-III-А-03-072).
Список литературы
1. Алексеев Г.В., Терешко Д.А. Анализ и оптимизация в гидродинамике вязкой жидкости. – Владивосток: Дальнаука, 2008. 320 с.
2. Gunzburger M.D., Hou L., Svobodny T.P. The approximation of boundary control problems for fluid flows with an application to control by heating and cooling // Comput. Fluids. 1993. V. 22. P. 239-251.
3. Ito K., Ravindran S.S. Optimal control of thermally convected fluid flows // SIAM J. Sci. Comput. 1998. V. 19, № 6. P. 1847-1869.
4. Алексеев Г.В. Разрешимость стационарных задач граничного управления для уравнений тепловой конвекции // Сиб. мат. журн. 1998. Т. 39, № 5. C. 982-998.
5. Lee H.-C., Imanuvilov O.Y. Analysis of optimal control problems for the 2-D stationary Boussinesq equations // J. Math. Anal. Appl. 2000. V. 242. P. 191-211.
6. Алексеев Г.В. Обратные экстремальные задачи для стационарных уравнений тепловой конвекции // Вестник НГУ, Серия: матем., мех. информ. 2006. Т. 6, вып. 2. С. 6-32.
7. Capatina A., Stavre R. A control problem in bioconvective flow // J. Math. Kyoto Univ. 1998. V. 37, № 4. P. 585-595.
8. Алексеев Г.В. Обратные экстремальные задачи для стационарных уравнений теории массопереноса // Журн. вычисл. матем. и матем. физ. 2002. Т. 42, № 3. С. 380-394.
9. Алексеев Г.В., Соболева О.В., Терешко Д.А. Задачи идентификации для стационарной модели массопереноса // Прикл. мех. техн. физ. 2008. Т. 49, № 4. С. 24-35.
10. Алексеев Г.В. Разрешимость обратных экстремальных задач для стационарных уравнений тепломассопереноса // Сиб. мат. журн. 2001. Т. 42, № 5. С. 971-991.
11. Алексеев Г.В. Коэффициентные обратные экстремальные задачи для стационарных уравнений тепломассопереноса // Журн. вычисл. матем. и матем. физ. 2007. Т. 47, № 6. С. 1055-1076.
