Степанец Владимир Яковлевич доцент Кожич Павел Павлович Минск 2008 г. Оглавление Оглавление 2 Список обозначений ко всей выпускной работе 3 реферат

Вид материала

Реферат

Содержание Глава 4. Основные результаты и их обсуждение. 23 Действующий личный сайт 27 Список обозначений ко всей выпускной работе Глава 1. Обзор Macromedia Flash. Глава 2. Методика исследований. Первый этап Второй этап Метод использования путевых координат Метод кодирования весов ячеек по модулю 3 Метод разметки ДРП по Акерсу Метод уменьшения поля поиска Метод двойного распространения. Метод с использованием быстрого алгоритма трассировки лаби­ринтов Глава 3. Описание алгоритма с мгновенным нахождением пути минимальной длины с заданными координатами на Macromedia Flash Глава 4. Основные результаты и их обсуждение. Список литературы к реферату Интернет ресурсы в предметной области исследования. Действующий личный сайт kypa.narod.ru Презентация магистерской диссертации. Referat.ppt Список литературы к выпускной работе.

Подобный материал:

• Забрейко Петр Петрович доцент Кожич Павел Павлович Минск 2007 г. Оглавление Оглавление, 254.67kb.
• Кожич Павел Павлович, доцент Запрудский Сергей Николаевич Минск 2010 г. Оглавление, 202.51kb.
• Сидорская Ирина Владимировна старший преподаватель Кожич Павел Павлович Минск 2010, 900.44kb.
• Кожич Павел Павлович, профессор Воробьев Василий Петрович Минск 2010 г. Оглавление, 247.09kb.
• Коледа Виктор Антонович, ст преподаватель Пол Кожич Минск 2010 г. Оглавление Оглавление, 340.48kb.
• Краснопрошин Виктор Владимирович ст преподаватель Кожич Павел Павлович Минск 2008, 166.87kb.
• Козик Любовь Антоновна, ассистент Позняков Андрей Михайлович Минск 2008 оглавление, 293.15kb.
• Кожич Павел Павлович Минск 2010 г Оглавление Оглавление 2 Применение информационных, 302.47kb.
• Громко Николай Иванович Минск, 2008 оглавление список обозначений ко всей выпускной, 267.64kb.
• Винарский Владимир Афанасьевич ассистент Шешко Сергей Михайлович Минск 2008 г. Оглавление, 156.88kb.

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ


Выпускная работа по
«Основам информационных технологий»

на тему

«Информационные технологии в

дистанционном обучении.»


Магистрант кафедры математической электроники

Егельский Павел Анатольевич

Руководители:

доцент физ-мат наук

Степанец Владимир Яковлевич

доцент Кожич Павел Павлович


Минск – 2008 г.

Оглавление

Список обозначений ко всей выпускной работе

IT – информационные технологии

ДРП – дискретное рабочее пространство

Реферат «Информационные технологии в дистанционном обучении.»

Введение.

Стремительное развитие IT уже подготовило основу для устранения естественного разрыва между фундаментальными знаниями и их применением на практике.

Современные IT все шире внедряются не только в жизнь людей в целом, но и в сферу науки, обеспечивая принципиально новый уровень получения обобщения знаний, их распространения и использования.

В результате применения новых технологий легко достигаются следующие цели:

- увеличивается понимание материала (благодаря, различным методам его представления);

- увеличивается число рассматриваемых задач (благодаря сокращению числа рутинных преобразований);

- исследуются более сложные модели, так как громоздкие вычисления переданы соответствующим компьютерным системам исследуемой области;

- больше внимания уделяется качественным аспектам;

- исчезает страх при работе с громоздкими выкладками и приобретается уверенность в символьных вычислениях;

- прививается вкус к анализу результатов;

- вырабатываются устойчивые практические навыки проведения математических рассуждений.

Очевидно важное место IT (в частности, систем компьютерной математики) и их развития в свете дистанционных методов обучения, которые являются одним из наиболее быстро развивающихся направлений системы образования. Это качественно новый прогрессивный вид обучения, базирующийся на современных IT и использующий современные средства коммуникаций (телевидение, видео и аудио средства обучения, компьютерные глобальные и локальные сети).

Иногда изучение учебных материалов не дает полное представление того, как на самом деле осуществляется тот или иной метод на практике, для этого нужно вводить в наше образование такие электронные учебные пособия, которые простой студент, мог бы открыть и на практическом примере увидеть, как данный метод выглядит наяву, в этом нам и помогают IT.

Так как применение средств автоматизации является необходимым условием создания аппаратно-программных систем обработки информации, курс «САПР» уже давно включен в качестве основной дисциплины в учебные программы подготовки всего спектра специалистов для электроники. При этом изучение существующих методов и алгоритмов автоматизированного проектирования с одной стороны является залогом их дальнейшего грамотного и эффективного использования, а с другой является необходимой основой дальнейшего совершенствования этих средств.

С другой стороны повышение качественных показателей изучения средств САПР тесно связано с созданием и использованием современных средств и методов обучения. Так на настоящий момент разработано огромное число методов и алгоритмов автоматизированного проектирования, описанных в различных монографиях, учебных пособиях, журнальных статьях и материалах конференций, доступ к которым по тем или иным причинам во многих случаях затруднен. Уже в силу этого, простая систематизация этой информации, ее перевод в электронный вид и размещение на соответствующем доступном учебном сервере позволит существенно повысить качественные показатели подготовки специалистов.

В данной работе будут рассмотрены применение IT для разработки электронного пособия по разделу конструирования систем, а именно трассировки соединений, ведь она является одной из наиболее сложных задач проектирования топологических чертежей СБИС, а затем рассмотрены разработки Macromedia Flash приложений и в дальнейшем введение этого пособия в наше образование.

Глава 1. Обзор Macromedia Flash.

Для разработки электронного пособия по курсу САПР была использована технология Macromedia Flash MX. Она обладает всеми возможностями, которые можно найти в других технологиях создания графических изображений, мультимедийных презентаций и фильмов, обладая в отличие от них простыми и удобными инструментами разработки. Иными словами Macromedia Flash MX является наиболее удачным сочетанием изобразительных возможностей графики, инструментальных средств работы с ней и механизма включения результата в Web-страницы.

Кроме того, использование в Macromedia Flash MX векторной графики в формате Shockwave Flash (SWF) позволяет радикально сократить объем данных, описывающих движущееся изображение. В файле хранятся только первоначальное изображение и уравнение траектории, а все промежуточные кадры рассчитываются в момент воспроизведения. Этим Macromedia Flash существенно отличается от обычных компьютерных видео-роликов, в которых последовательно сменяют друг друга десятки кадров в секунду. Для хранения и передачи таких видеозаписей требуются огромные объемы памяти и сверхскоростные каналы связи.

Дополнительным преимуществом формата SWF является его переносимость. Это означает, что этот формат данных может использоваться на любой аппаратно-программной платформе. И еще одной особенностью Macromedia Flash является то, что созданные изображения могут быть легко дополнены интерактивными элементами и звуковым сопровождением.

Все выше сказанное сделало средства Macromedia Flash наиболее распространенным на настоящий момент инструментом для разработки средств дистанционного обучения.

Глава 2. Методика исследований.

2.1. Теоретические выкладки.

Метод точной трассировки с распространением по сетке

Метод точной трассировки с распространением по сетке, называемый также методом трассировки лабиринтов, - это в сущности общее наименование группы методов, объединяемых использова­нием алгоритма поиска самого короткого пути в графе, широко извест­ного в области исследования операций и теории сетей.

Основным алгоритмом, используемым в рассматриваемом методе, является алгоритм Ли. Интуитивно его можно уподо­бить процессу распространения волн от бросаемых в воду камешков.

Этот алгоритм может использоваться как на этапе проведения глобальной трассировки, так и на этапе выполнения точной трассировки. В последнем случае поиск маршрутов выполняется на так называемом решетчатом графе (рис. 1.9).

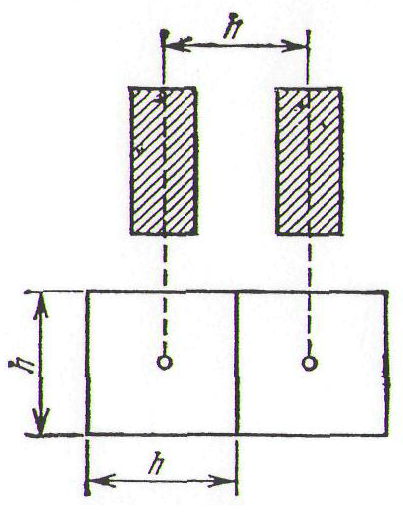
Для выполнения волнового алгоритма все свободное для трассировки соединений пространство кристалла СБИС разбивается на элементарные ячейки. Размеры ячеек и их количество определяются площадью поля, до­пустимой плотностью расположения выводов элементов и проводников. Выбранная система ячеек определяет среду, в которой осуществляется построение соединений. В простейшем случае ячейка представляет собой квад­рат со стороной h, равной расстоянию между средними линиями двух соседних печатных проводников (рис. 1.12).

Если размеры поля по горизонтали и вертикали со­ответственно 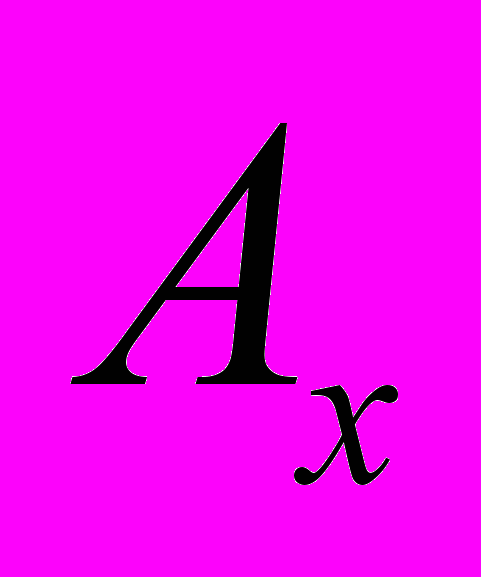и 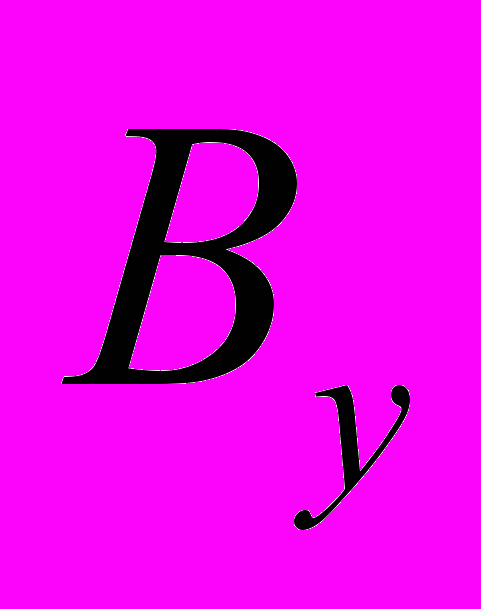, то получим дискретное рабочее поле (ДРП) с 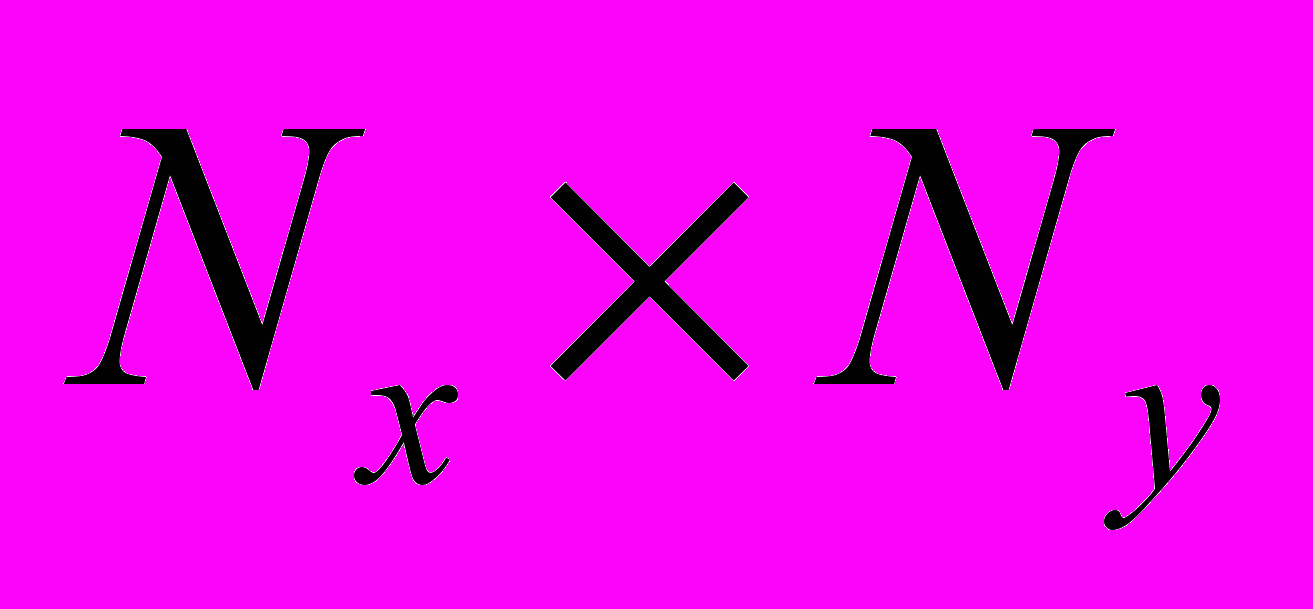ячейками:

, ,

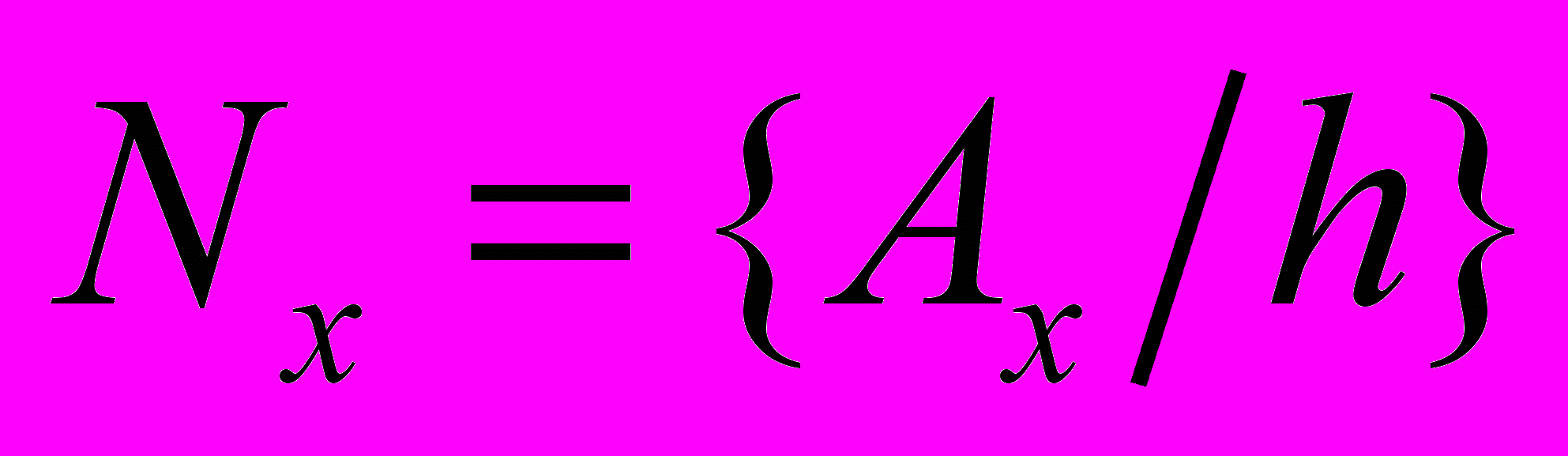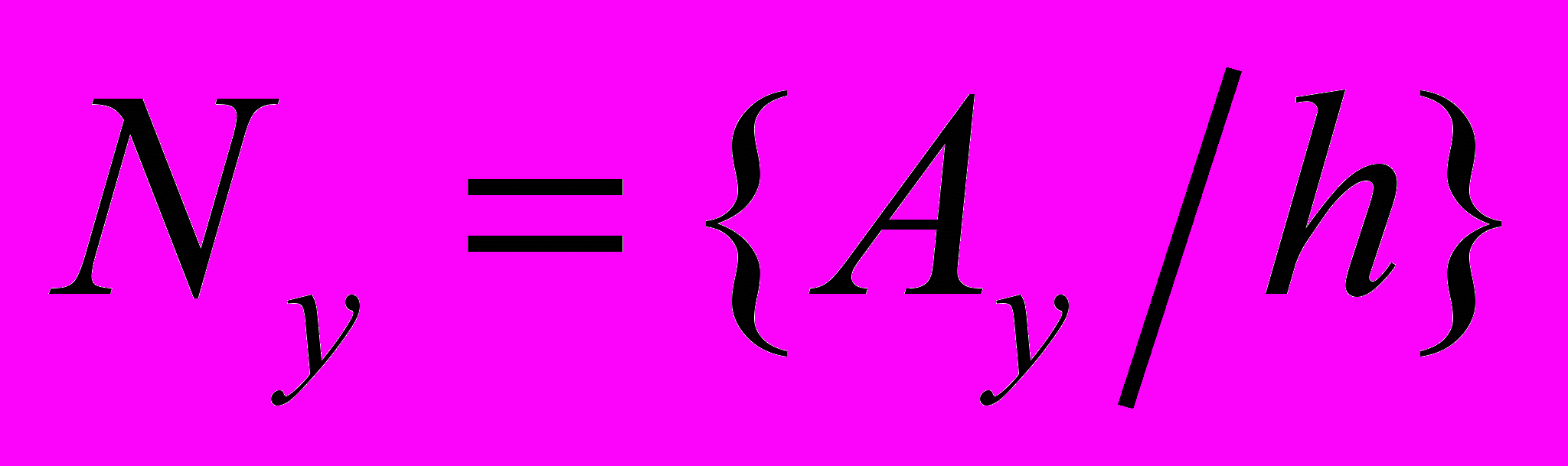где - символы ближайшего большего целого.

В данном ДРП (рис. 1.14) определяется множество

занятых ячеек, соответствующие зонам, запрещенным для проведения соединений: вы­воды элементов, технологические области, ранее проведенные со­единения и т. д. По мере прове­дения соединений множества за­нятых и свободных ячеек изменя­ются.


Рис. 1.12. Ячейки коммутационного поля.
Основу всех модификаций ал­горитма Ли составляет процеду­ра построения оптимального в за­данном смысле пути между дву­мя известными ячейками ДРП. Процедура состоит из двух эта­пов: поиска пути и проведения пути.

Первый этап

Распространение волны на ДРП

В программе Macromedia Flash: на первом этапе из одной из заданных ячеек ДРП - источника моделируем распространение числовой вол­ны до тех пор, пока ее фронт не достигнет второй отме­ченной ячейки ДРП - цели, либо наступает момент, ког­да в очередной фронт нельзя включить ни одну новую незанятую ячейку ДРП. В первом случае искомый путь существует, во втором - нет.

Чтобы иметь возможность следить за прохождением фронта волны, его фрагментам на каждом этапе присваивают некоторые веса:

,

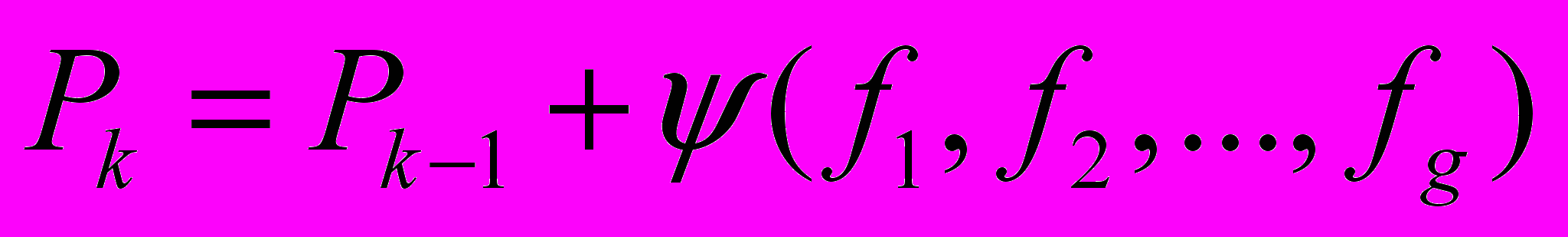где 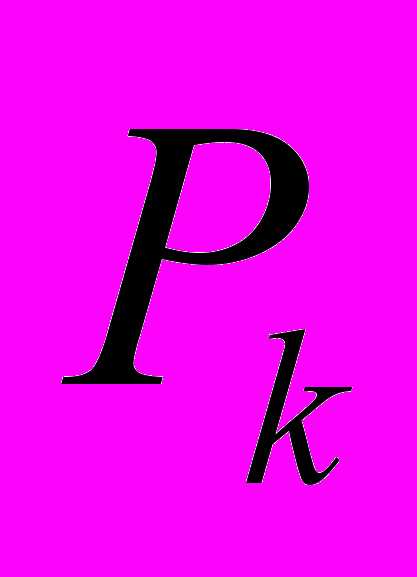и 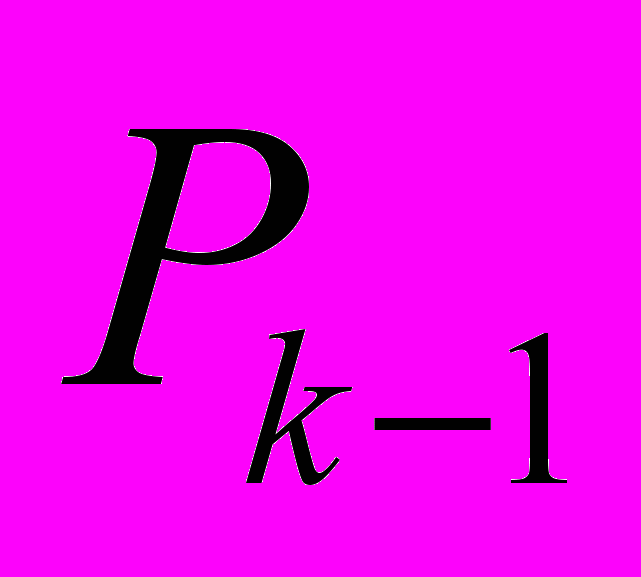- веса ячеек k-го и 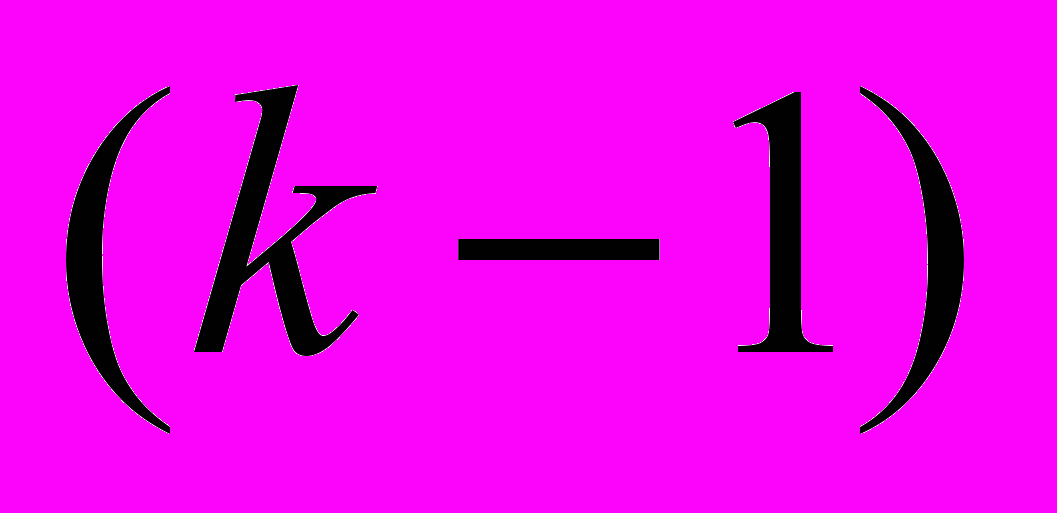-го фронтов; 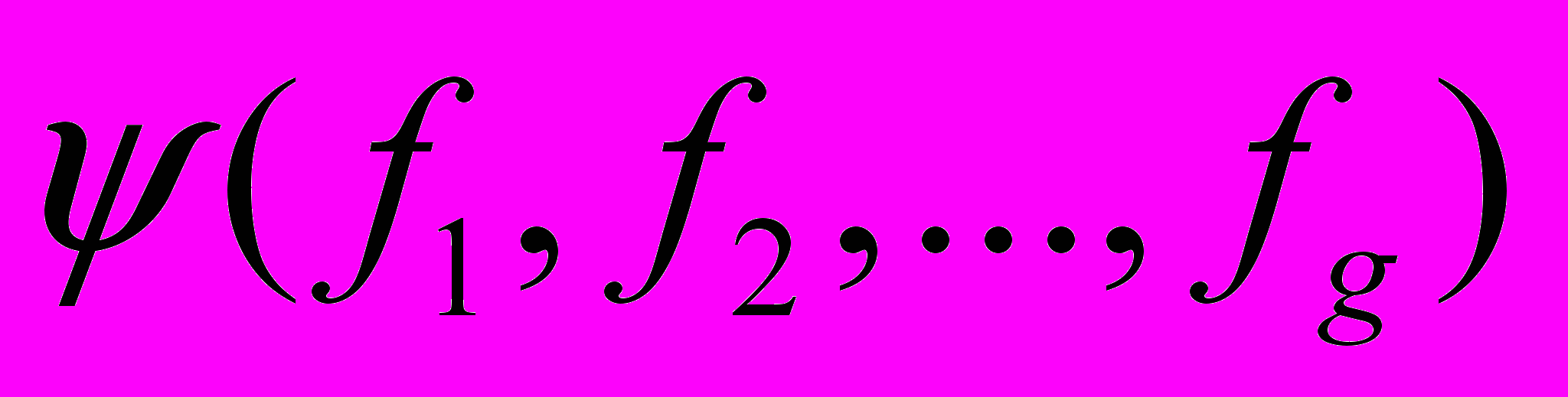- весовая функция, являющаяся показателем качества проведения пути, каждый параметр которой 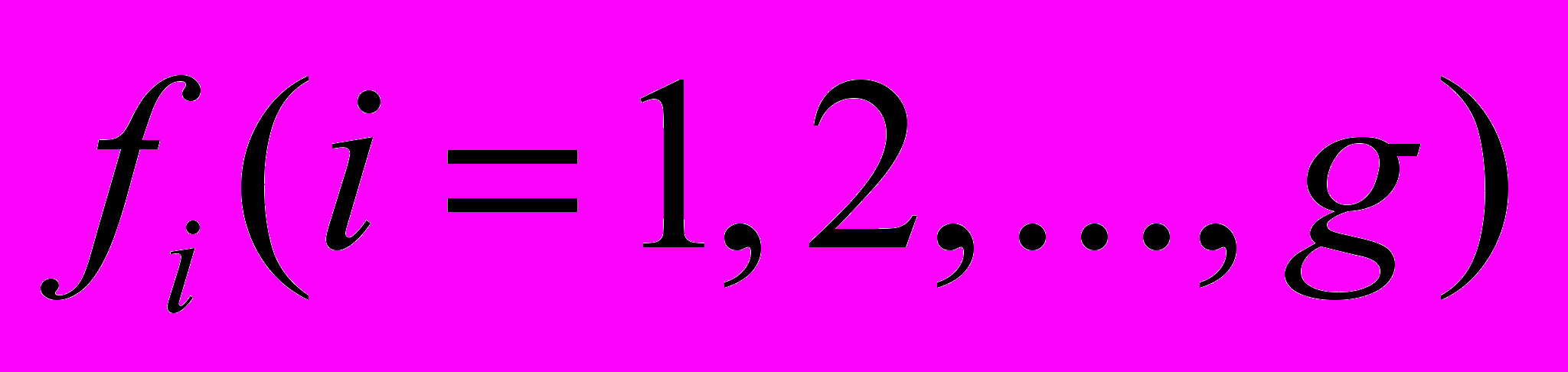характеризует путь с точ­ки зрения одного из критериев качества (длины пути, числа пересе­чений и т. п.). На 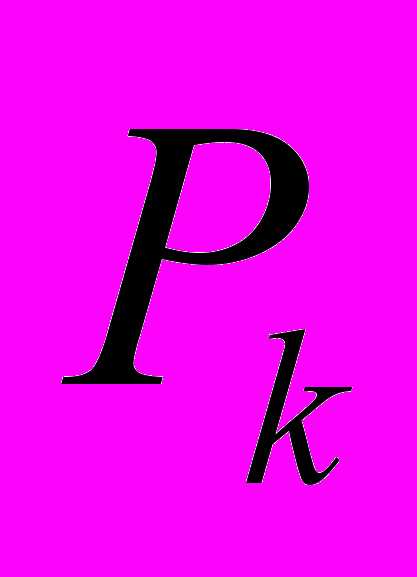накладывают одно ограничение - веса ячеек предыдущих фронтов не должны быть больше весов ячеек последую­щих фронтов. Фронт распространяется только на соседние ячейки. Соседние ячейки (рис. 1.13) могут быть определены списком:

.

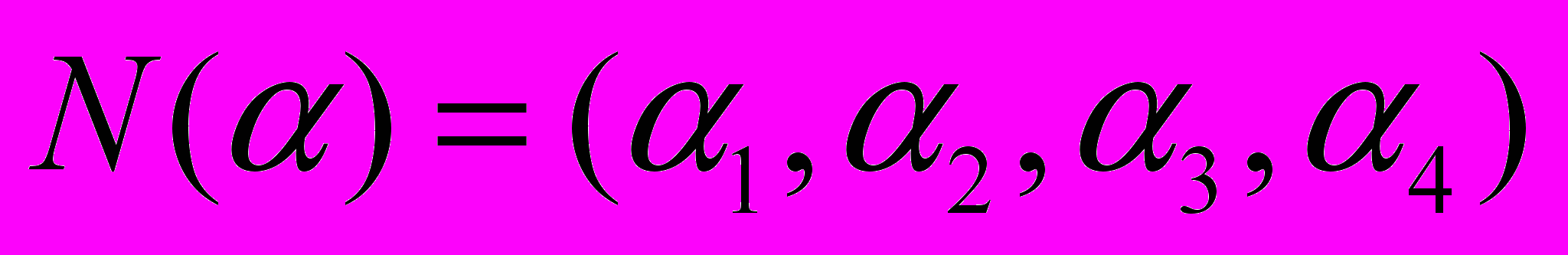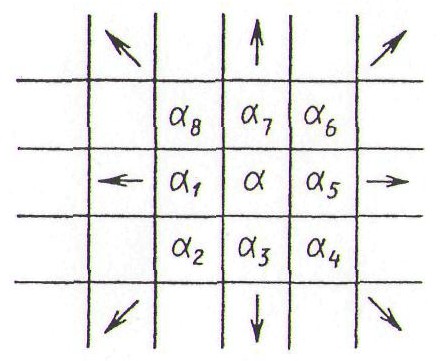
Возможно и другое определение списка (рис. 1.13, б):

.

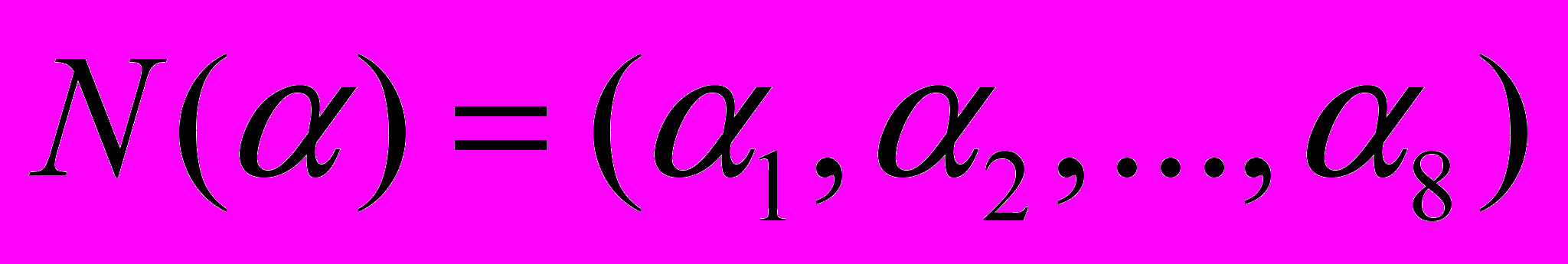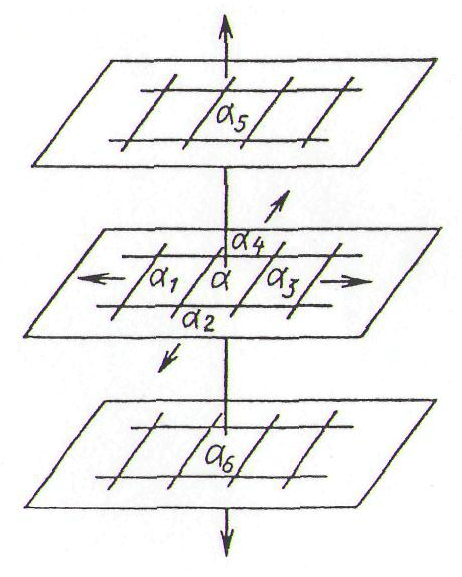
Трехмерный случай с 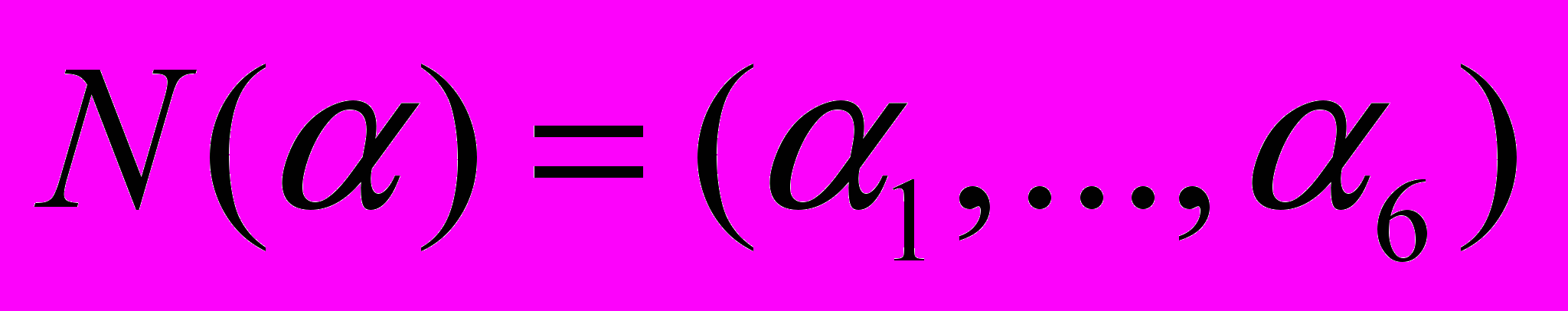представлен на рис. 1.13, в. Два последних списка применяют реже первого. Отличие между ними состоит в том, что в первом случае для проводника допустимы только горизонтальные направления, а во втором – еще и диагональные.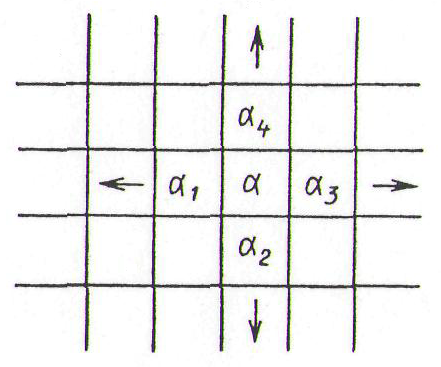







а)



в)


б)

Рис. 1.13. Множество соседних с ячеек ДРП: а – при использовании четырех направлений; б – при использовании восьми направлений; в – при использовании шести направлений (трехмерный случай).


Из ранее сказанного следует, что все условия, которые необходимо выполнить при про­ведении соединения, в том числе и условия оптимально­сти, должны быть заложены в правила движения волны, т. е. в правила построения ее очередного фронта.

Второй этап

Проведение пути

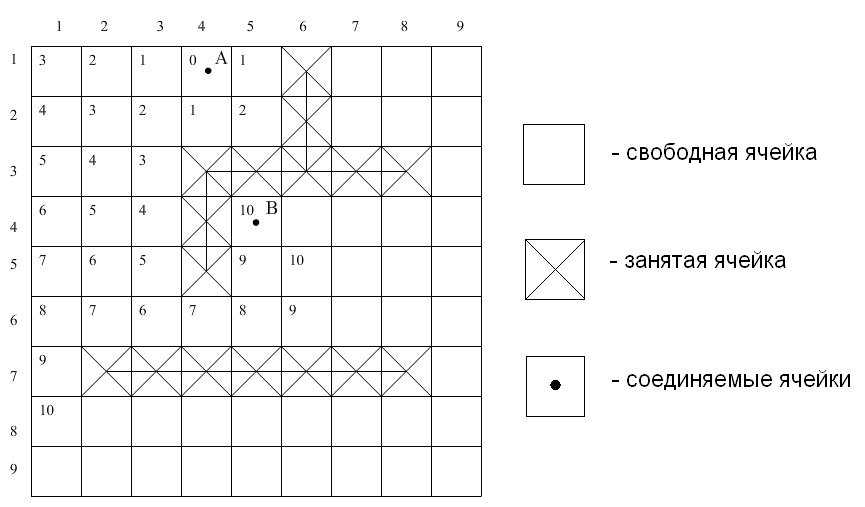
В программе Macromedia Flash: на втором этапе алгоритма осуществляется проведе­ние пути. Проведение пути бывает прямым и обратным. Для прямого проведения следует, начиная от ячейки-источника, двигаться по направле­нию распространения волны, переходя последовательно от ячейки с меньшим весом к соседней ячейке с боль­шим весом, до тех пор, пока не будет достигнута ячейка-цель. В обратном проведении пути следует, начинать от ячейки-цели и двигаться в направлении, противоположном направле­нию распространения волны, переходя последовательно от ячейки с большим весом к соседней ячейке с мень­шим весом, до тех пор, пока не будет достигнута ячейка-источник. Ячейки ДРП, выделенные в ходе указанного процесса, и определяют искомое оптимальное соедине­ние. В общем случае их несколько.



а)


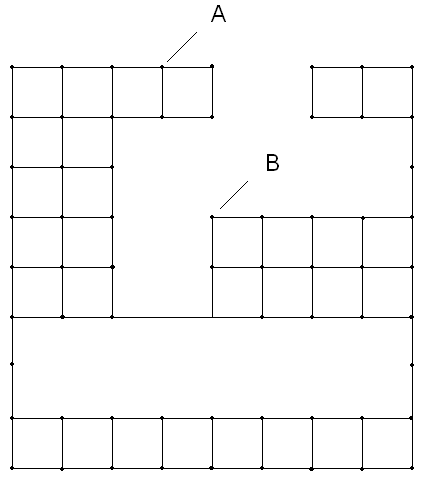
в)



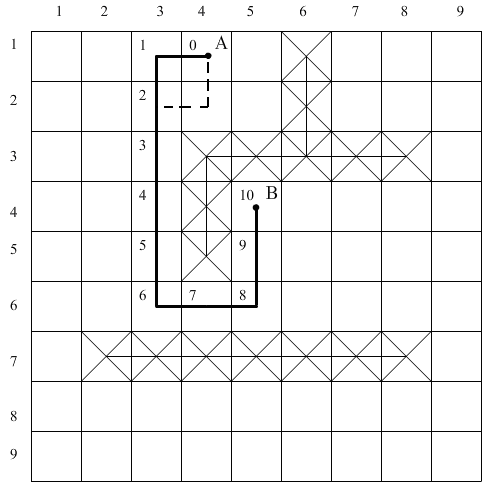
б)

Рис. 1.14. Распространение волны на ДРП (а), решетчатый граф, соответствующий ДРП (б), построенная цепь (в), пунктиром показан другой эквивалентный путь.


Алгоритм Ли имеет следующие особенности:

1. если между точками A и B, путь существует, то его всегда можно найти;
   
2. из множества возможных путей можно определить кратчайший при заданном отношении занятости ячеек ДРП;
   
3. реализация алгоритма проста, но требуются значительные ресурсы памяти;
   
4. специфика расположения элементов и особенности конструкции учитываются выбором отношения занятости, не требуя модификации алгоритма.
   

В рассмотренном варианте реализации алгоритма, когда, каждая ячейка ДРП может иметь одно из двух состояний: пустая (свободная), занятая или содержать весовую отметку 1, 2, 3, ... , L, где L - максимальная длина пути в ДРП. Поэтому для описания состояния одной ячейки требуется 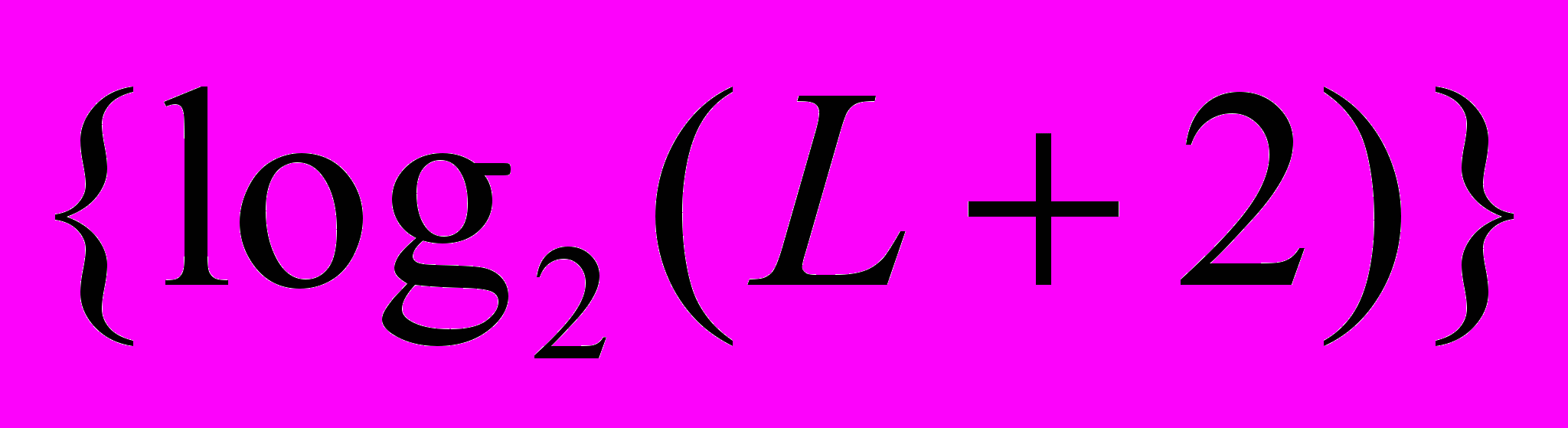разрядов.

Метод использования путевых координат

Уменьшение объема требуемой памяти может быть достигнуто модификацией основного алгоритма, один из которых и есть метод использования путевых координат.

В этом методе изменяется этап распространения волны. Путевой координатой ячейки 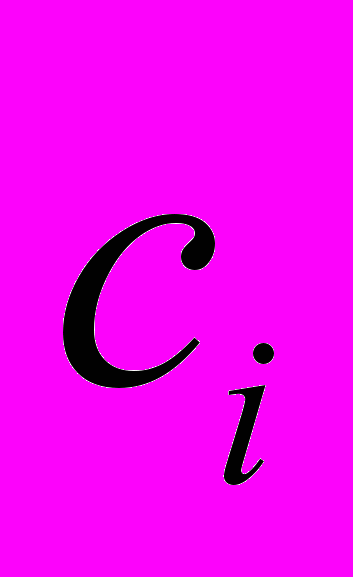фронта 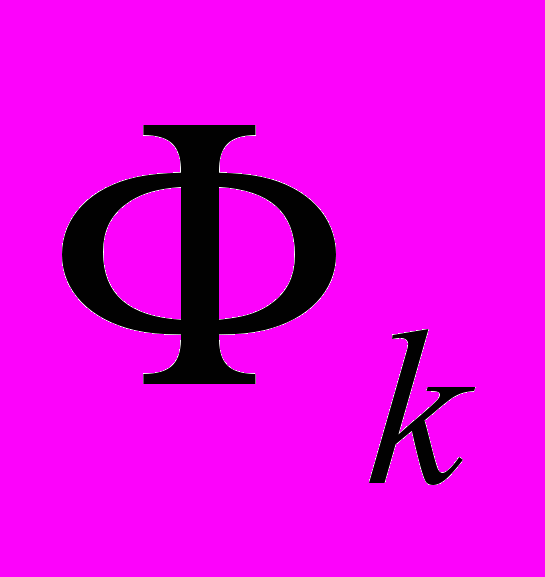будем называть ту соседнюю с ней ячейку фронта 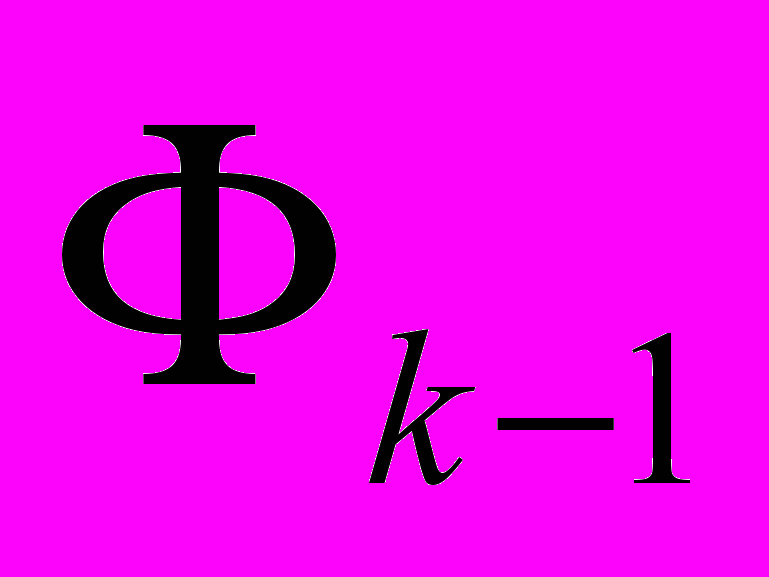, от ко­торой 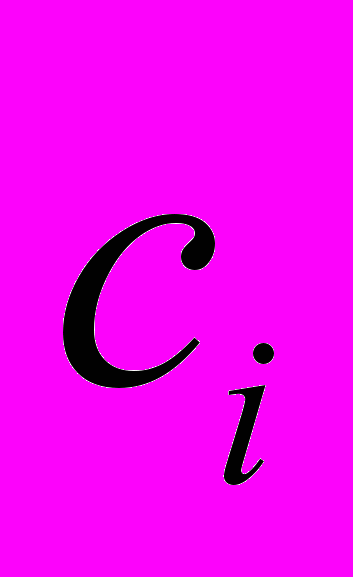получает свой вес. Для рассматриваемой окре­стности соседства имеем четыре возможных путевых ко­ординаты ячейки 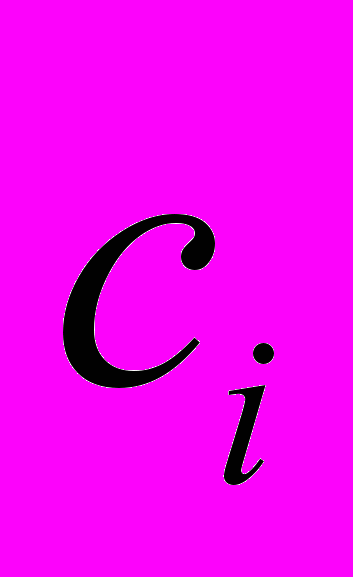: 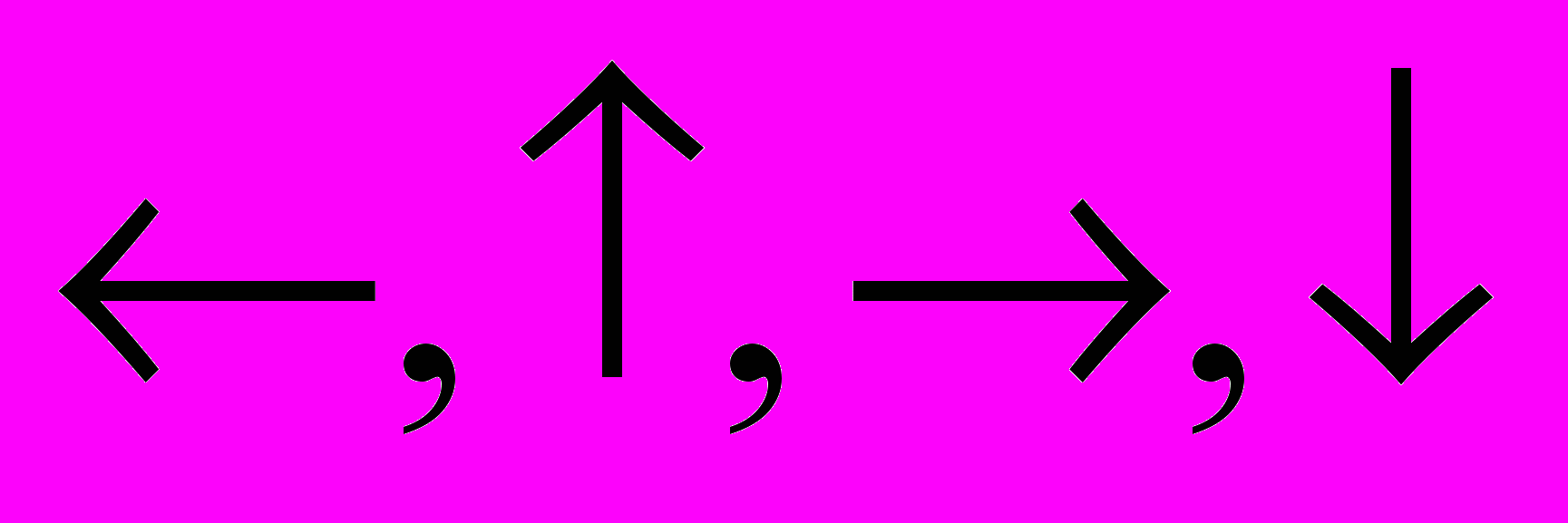. Использование путевых координат при распространении волны позволяет исклю­чить вычисление и хранение весов ячеек ДРП (рис. 1.15, а). Назначение путевой координаты ячейке 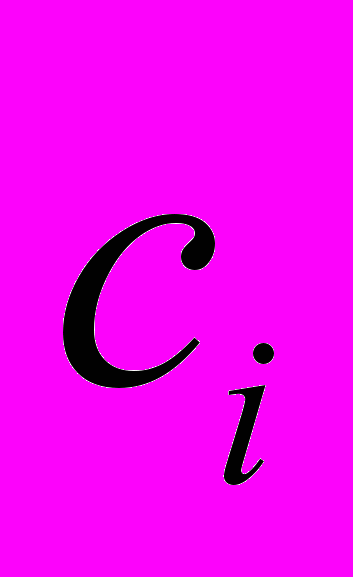в слу­чае, если имеется несколько соседних ячеек фронта 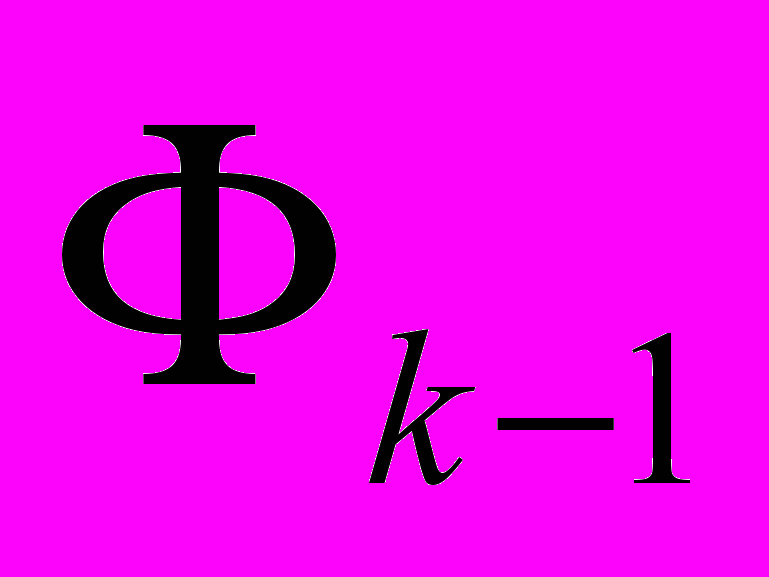, производится согласно выбранному правилу прио­ритетов. Например: 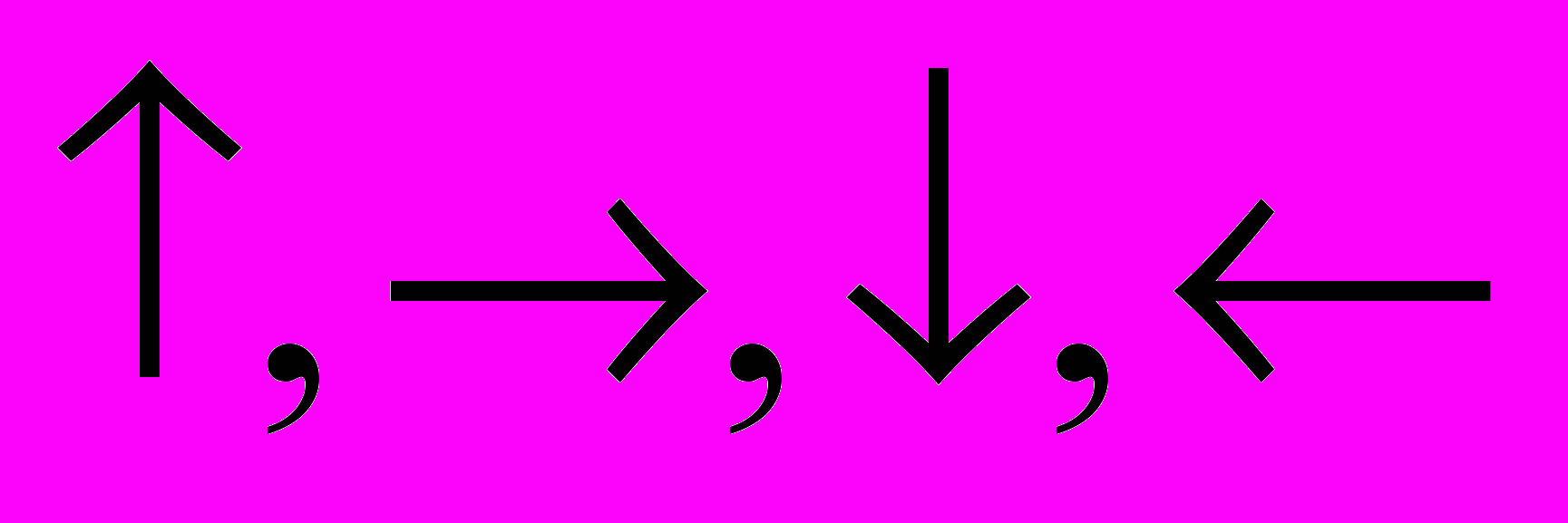. Этап проведения пути состоит в отслеживании путевых координат в размеченном ДРП, начиная от ячейки-цели (рис. 1.15). В ме­тоде путевых координат ячейка ДРП может быть в од­ном из следующих состояний: пустая, занятая или содер­жать путевую координату 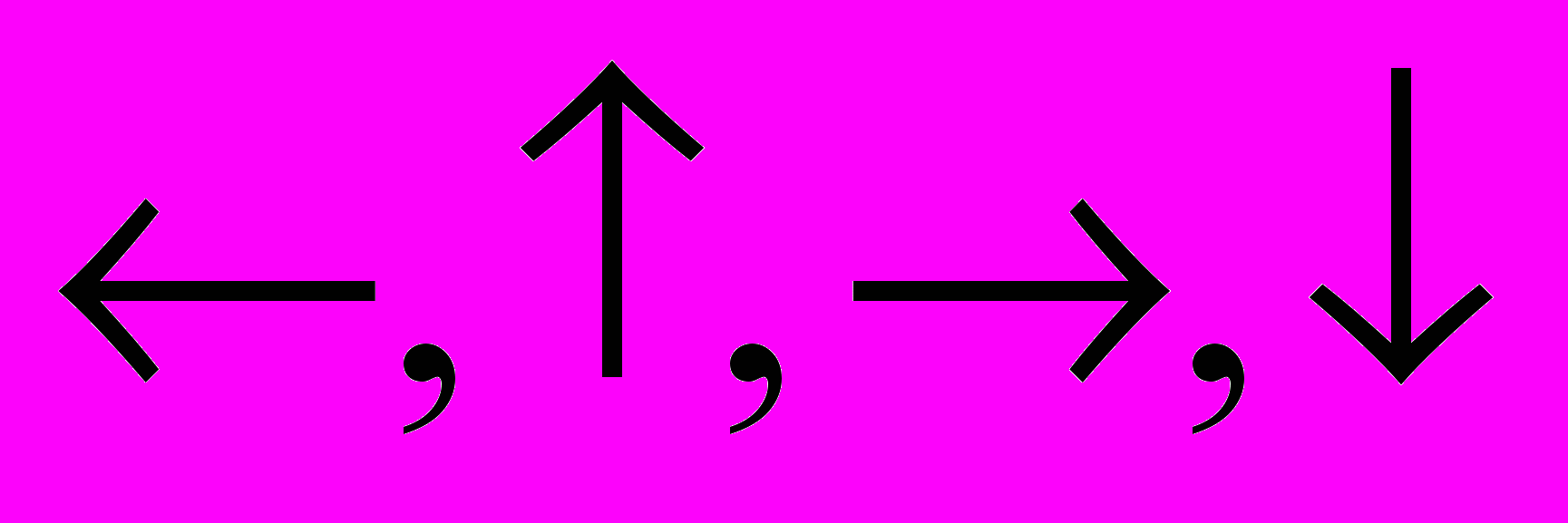. Таким образом, требуемое число разрядов памяти на одну ячейку ДРП составляет .



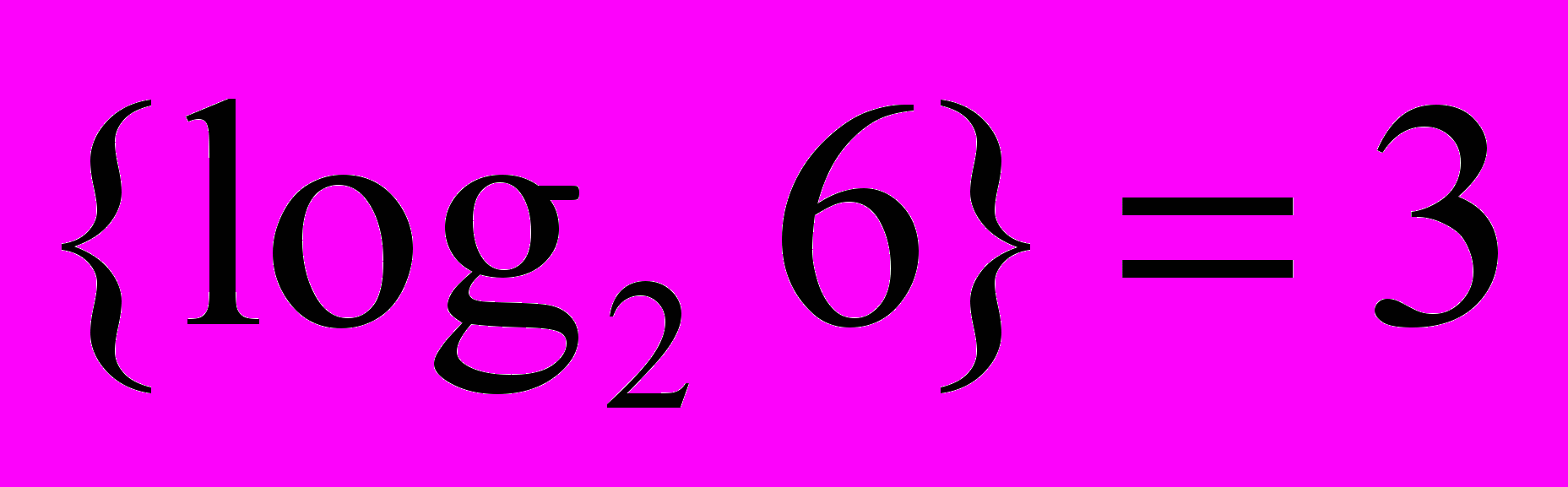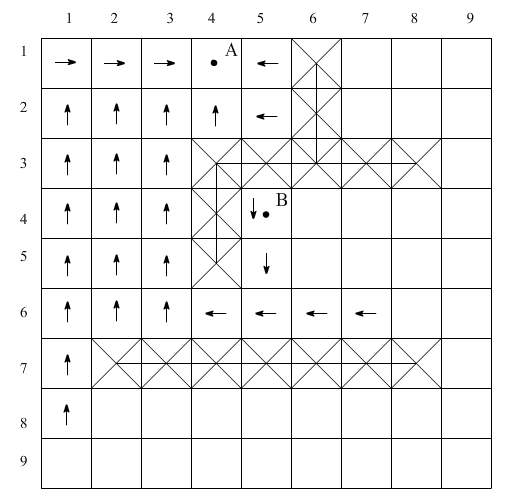
а)

б)



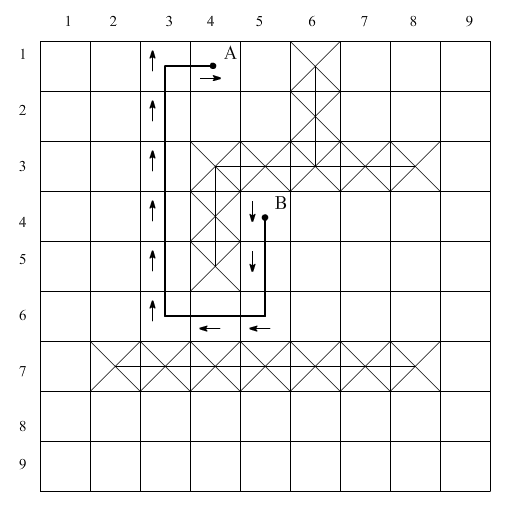
Рис. 1.15. Использование путевых координат: а – распространение волны, б – проведение пути.

Метод кодирования весов ячеек по модулю 3

К аналогичному сокращению объема информации приводит метод кодирования весов ячеек по модулю 3. Поскольку в окрестности данной ячейки с весом k могут находиться лишь ячейки с весом k-1 или k+1, то ячей­кам ДРП, включаемым в очередной фронт 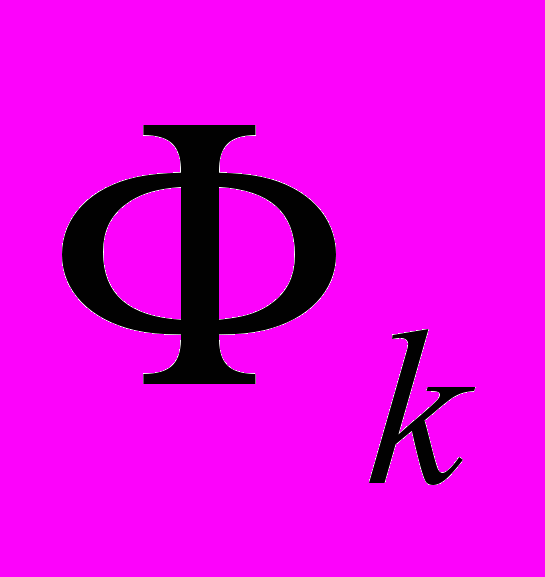, возможно, приписывать не само значение веса k, а отметку 1, 2 или 3, сравнимую с k по модулю 3 (рис. 1.16, а). В этом случае для кодирования состояния одной ячейки ДРП требуется 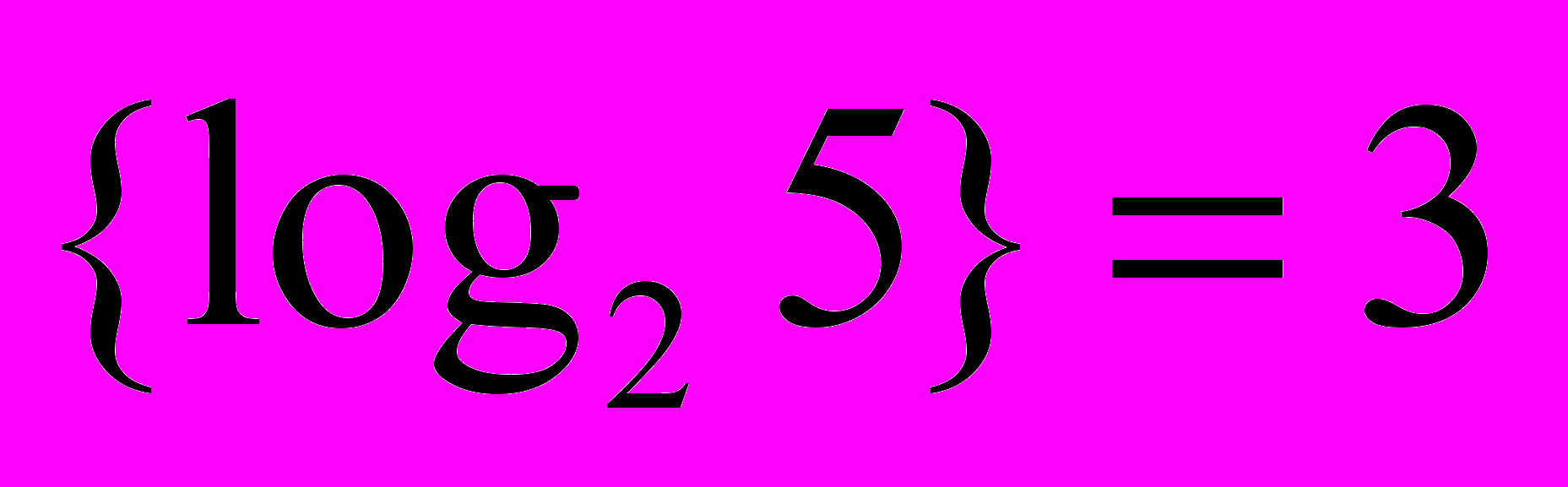двоичного разряда.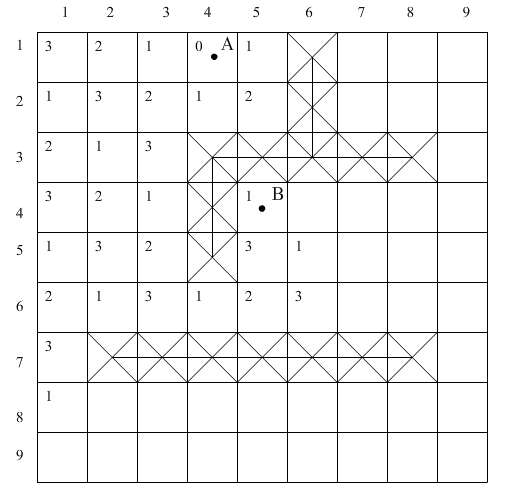



а)



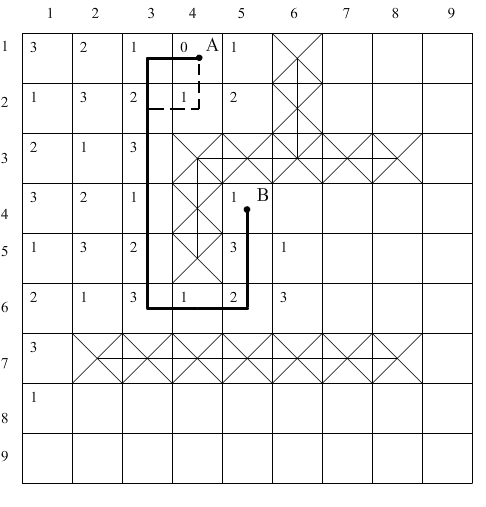
б)

Рис. 1.16. Кодирование весов ячеек по модулю: а – распространение волны, б – проведение пути.

Метод разметки ДРП по Акерсу

Наиболее экономичный способ кодирования состоя­ний ячеек ДРП предложен Акерсом. При распро­странении волны ячейки ДРП получают отметки в соот­ветствии с базовой последовательностью 1, 1, 2, 2, 1, 1, 2, 2, …. Данная последовательность характерна тем, что в ней любой член имеет разных соседей слева и справа. Вначале все незанятые ячейки, соседние с ячей­кой-источником, помечаются 1, затем все ячейки фронта 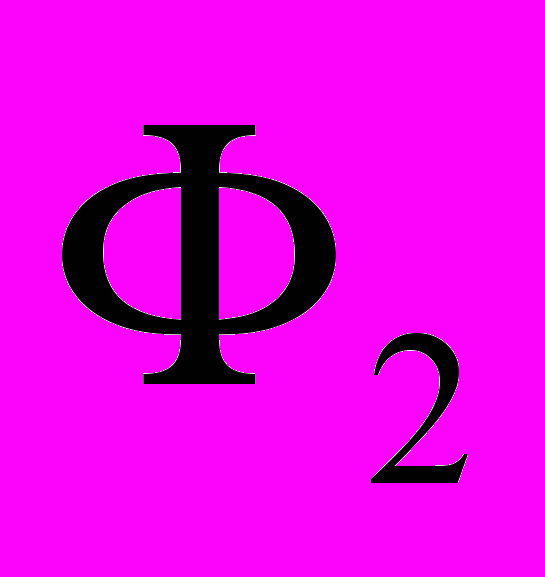помечаются также 1. Далее отметка 2 присваивается ячейкам фронта 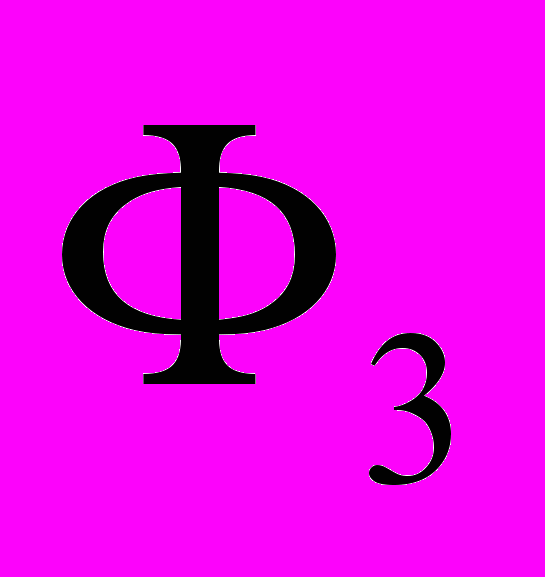и т. д. (рис. 1.17). Для построения пути в общем случае необходимо найти необходимую подпоследовательность отметок базовой последователь­ности. Это легко может быть сделано по отметке ячейки-цели и отметке соседней с ней ячейки. В нашем случае это сама базовая последовательность 1, 1, 2, 2, 1, 1, 2, .... На основании этой последовательности выделяет­ся искомый путь в ДРП. В неопределенных ситуациях, так же как и в основной схеме алгоритма, должно быть использовано некоторое правило приоритетов.

В методе Акерса ячейка ДРП может находиться в следующих состояниях: пустая, занятая, иметь отметку 1 или 2. Таким образом, на каждую ячейку ДРП необ­ходимо всего два двоичных разряда памяти.



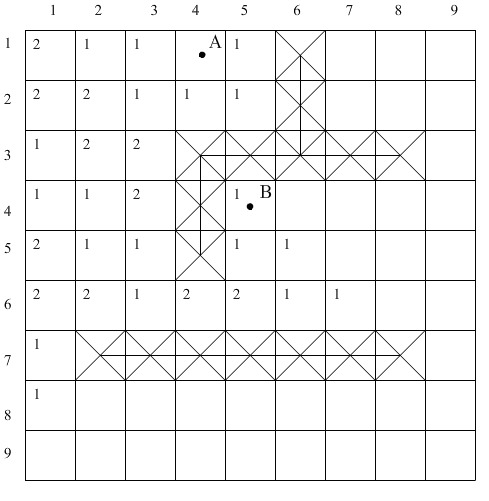
а)



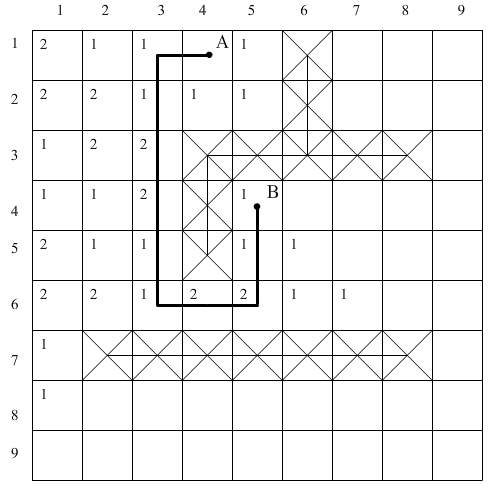
б)

Рис. 1.17. Разметка ДРП по Акерсу: а – распространение волны, б – проведение пути.

Метод уменьшения поля поиска

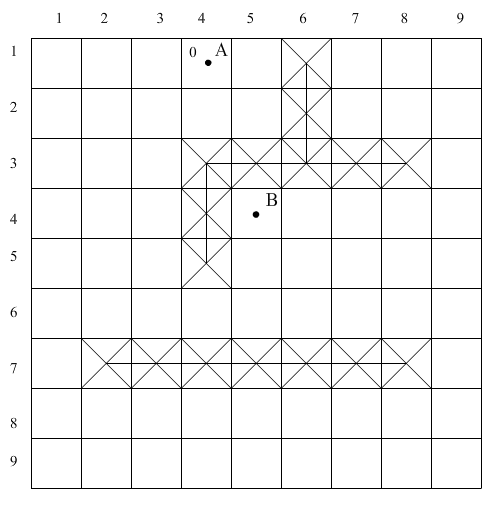
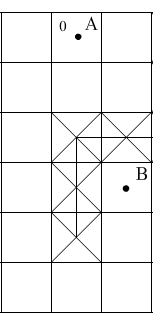
Еще одним фактором, оказывающим влияние на объем памяти при использовании алгоритма Ли, является количество узлов сетки, образующих фронт волны. Если объем памяти ограничен, то в этом случае целесообразно использовать моди­фицированный метод уменьшения поля поиска, согласно которому при любом расшире­нии фронта волны будет запоминаться информация только о строго определенном количестве узлов сетки (рис. 1.18). В данном случае нахождение самого короткого маршрута не гарантируется и смысл обработки несколько теряется. Вместе с тем сохраняется справедливость утверждения: «Если маршрут существует, то он обязательно будет найден».



а)



б)

Рис. 1.18 Уменьшение поля поиска: а – ДРП, б – уменьшенный объем поля поиска.

Метод двойного распространения.

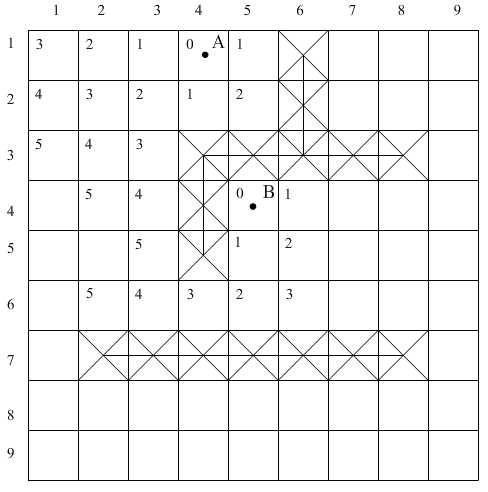
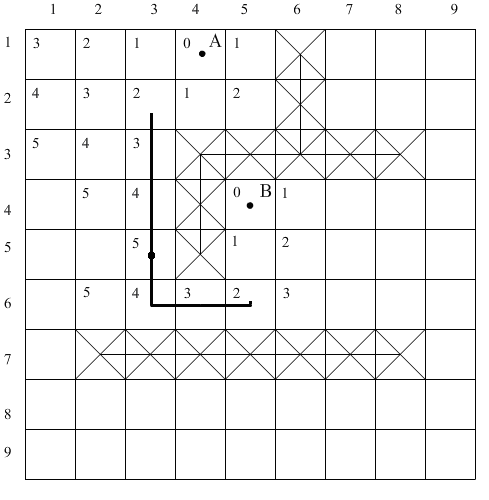
Если из двух исходных точек (А и В), как из центров, распространяются два фронта, то поле поиска, осуществляемого до момента столкновения двух этих волн, приблизительно в два раза уже, чем при наличии только одной исходной точки (рис. 1.19).

Приоритеты направлений в отношении перемещения к целевой точке. При условии, что положение целевой точки за­ранее известно, метки присваиваются в соответствии со следую­щей последовательностью приоритетов.



а)



б)

Рис. 1.19 Двойное распространение: а – распространение волны, б – проведение пути.

Метод с использованием быстрого алгоритма трассировки лаби­ринтов

Особенностью данного метода поиска является очень высо­кая скорость перемещения в направлении к целевой точке, и поэтому его эффективность в случае сложных лабиринтообразных структур оказывается весьма низкой. Тем не менее число ячеек, задействованных при поиске, в данном случае обычно меньше, чём при использовании алгоритма Ли, а скорость до­стижения целевой точки выше. Метод трассировки с рас­пространением по сетке, представляющий собой модифициро­ванный алгоритм Ли, иногда также называют быстрым мето­дом трассировки лабиринтов или методом поиска в глубину.

Правила построения данного метода.

Приоритеты направлений в отношении перемещения к целевой точке. При условии, что положение целевой точки за­ранее известно, метки присваиваются в соответствии со следую­щей последовательностью приоритетов.

1. Предпочтительно перемещение в сторону точки В.
   
2. Если имеется степень свободы, предпочтительно пере­мещение по прежнему направлению.
   
3. Если перемещение по прежнему направлению невоз­можно, следует вернуться в узел сетки, последним получившим новую метку.
   
4. Если движение в направлении точки В невозможно, то, допустив возможность перемещения в направлении от точки В, следует перемещаться с последовательностью приоритетов 2, 3.
   

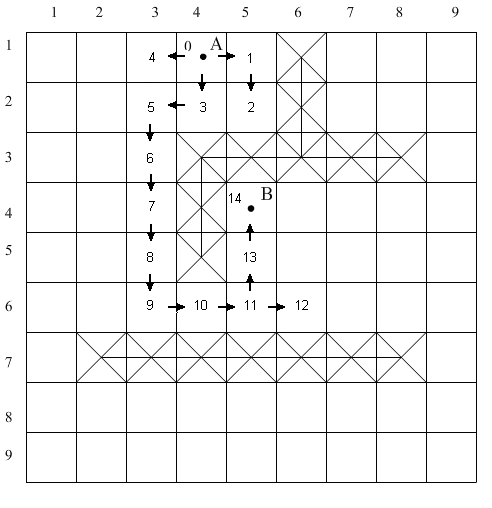
Рис. 1.20. Поиск с использованием быстрого алгоритма трассировки лаби­ринтов.

Глава 3. Описание алгоритма с мгновенным нахождением пути минимальной длины с заданными координатами на Macromedia Flash

На рисунке 1.25 показано как выглядит основное поле программы на начальном этапе.



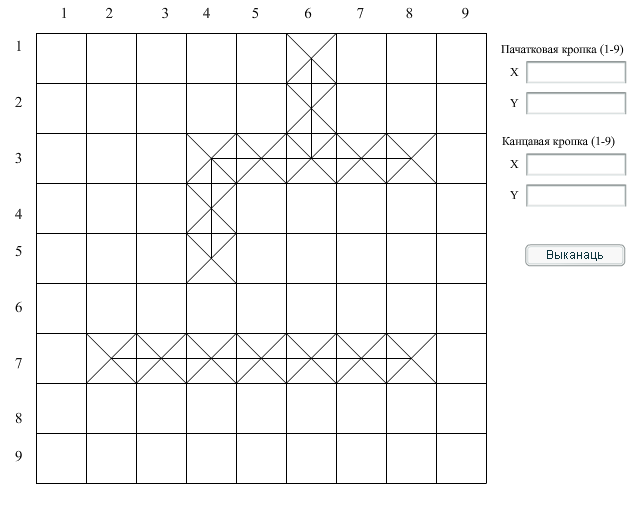
Рис.1.25. Нахождение пути минимальной длины с заданными координатами


В данной программе вводятся нужные координаты начальной точки, а затем конечной точки. После нажатия на кнопку выполнить, программа автоматически по алгоритму Ли находит путь минимальной длины и выводит его на экран.





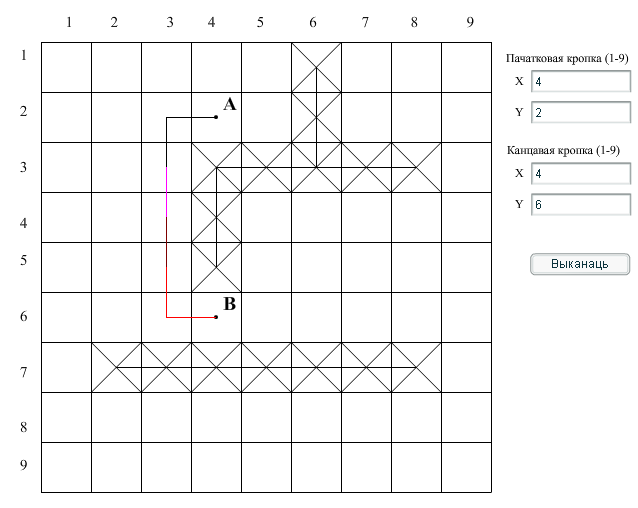
Рис.1.26. Примеры алгоритма нахождение пути минимальной длины с заданными координатами


Код на Macromedia Flash, который налагается на кнопку: выполнить:


on(click)

{

//trace("pressed "+_root.Ax.text);

//var i=98;

//i=i+Number(_root.Ax.text);

//trace(i);

_root.A1._visible=true;

_root.A1._x=75+50*(Number(_root.Ax.text)-1);

_root.A1._y=75+50*(Number(_root.Ay.text)-1);

_root.B1._visible=true;

_root.B1._x=75+50*(Number(_root.Bx.text)-1);

_root.B1._y=75+50*(Number(_root.By.text)-1);

//trace(Bx.Text);

coordX=_root.B1._x;

coordY=_root.B1._y;

step=0;

dir=0;

val=89;

Table = new Array(9);

for (i=0;i<9;i++)

{

Table[i]=new Array(9);

}

for (i=0;i<9;i++)

for (j=0;j<9;j++)

Table[i][j]=98;


Table[0][5]=99;

Table[1][5]=99;

Table[2][3]=99; Table[2][4]=99; Table[2][5]=99; Table[2][6]=99; Table[2][7]=99;

Table[3][3]=99;

Table[4][3]=99;

for (i=1;i<6;i++)

{ Table[6][i]=99; }

//trace("hello");


function Proverka(value1:Number):Number

{

//trace(value1);

i,j;

prov=true;

while (prov == true) {

for (i=0; i<9; i++) {

for (j=0; j<9; j++) {

if (Table[i][j] == value1) {

prov=Ustanovka (i,j,value1);

}

}

}

value1++;

if (value1 == 90) {

prov=false;

}

}

return 0;

}


function Ustanovka(i:Number, j:Number, value1:Number):Boolean

{

back;

//trace("i="+i+" j="+j+ " value1="+value1);

if ((i-1>=0) && (Table[i-1][j] == 98)) {

Table[i-1][j]=value1+1;

back=true;

}

if ((i+1<9) && (Table[i+1][j] == 98)) {

Table[i+1][j]=value1+1;

back=true;

}

if ((j-1>=0) && (Table[i][j-1] == 98)) {

Table[i][j-1]=value1+1;

back=true;

}

if ((j+1<9) && (Table[i][j+1] == 98)) {

Table[i][j+1]=value1+1;

back=true;

}

return true;

}

function Back(i:Number, j:Number):Number

{

back=false;

step++;

k=0;

//trace("Back: i="+i+" j="+j+ " A="+Table[i][j]+" step="+step);

if (Table[i][j] == 0)

{

dir=5;

return 1;

}

else {

if (dir != 5)

{

if ((i-1>=0) && (Table[i-1][j]
{

val=Table[i-1][j];

dir=1;

back=true;

//trace("dir1");

switch (step)

{

case 1: _root.Lv1._visible=true;

_root.Lv1._x=coordX;_root.Lv1._y=coordY;

coordY=coordY-50;//trace(coordY);

break;


case 2: _root.Lv2._visible=true;

_root.Lv2._x=coordX;_root.Lv2._y=coordY;

coordY=coordY-50;//trace(coordY);

break;


case 3: _root.Lv3._visible=true;

_root.Lv3._x=coordX;_root.Lv3._y=coordY;

coordY=coordY-50;//trace(coordY);

break;


case 4: _root.Lv4._visible=true;

_root.Lv4._x=coordX;_root.Lv4._y=coordY;

coordY=coordY-50;

break;

case 5: _root.Lv5._visible=true;

_root.Lv5._x=coordX;_root.Lv5._y=coordY;

coordY=coordY-50;

break;

case 6: _root.Lv6._visible=true;

_root.Lv6._x=coordX;_root.Lv6._y=coordY;

coordY=coordY-50;

break;

case 7: _root.Lv7._visible=true;

_root.Lv7._x=coordX;_root.Lv7._y=coordY;

coordY=coordY-50;

break;

case 8: _root.Lv8._visible=true;

_root.Lv8._x=coordX;_root.Lv8._y=coordY;

coordY=coordY-50;

break;

case 9: _root.Lv9._visible=true;

_root.Lv9._x=coordX;_root.Lv9._y=coordY;

coordY=coordY-50;

break;

}

}

if ((i+1<9) && (Table[i+1][j]
val=Table[i+1][j];

dir=2;

//trace("dir2");

back=true;

switch (step)

{

case 1: _root.Lv1._visible=true;

_root.Lv1._x=coordX;_root.Lv1._y=coordY+100;

coordY=coordY+100;break;


case 2: _root.Lv2._visible=true;

_root.Lv2._x=coordX;_root.Lv2._y=coordY+100;

coordY=coordY+100;break;


case 3: _root.Lv3._visible=true;

_root.Lv3._x=coordX;_root.Lv3._y=coordY+100;

coordY=coordY+100;break;


case 4: _root.Lv4._visible=true;

_root.Lv4._x=coordX;_root.Lv4._y=coordY+100;

coordY=coordY+100;break;

case 5: _root.Lv5._visible=true;

_root.Lv5._x=coordX;_root.Lv5._y=coordY+100;

coordY=coordY+100;break;

case 6: _root.Lv6._visible=true;

_root.Lv6._x=coordX;_root.Lv6._y=coordY+100;

coordY=coordY+100;break;

case 7: _root.Lv7._visible=true;

_root.Lv7._x=coordX;_root.Lv7._y=coordY+100;

coordY=coordY+100;break;

case 8: _root.Lv8._visible=true;

_root.Lv8._x=coordX;_root.Lv8._y=coordY+100;

coordY=coordY+100;break;

case 9: _root.Lv9._visible=true;

_root.Lv9._x=coordX;_root.Lv9._y=coordY+100;

coordY=coordY+100;break;

}

}

if ((j-1>=0) && (Table[i][j-1]
val=Table[i][j-1];

dir=3;

back=true;

//trace("dir3");

switch (step)

{

case 1: _root.Lh1._visible=true;

_root.Lh1._x=coordX-50;_root.Lh1._y=coordY;

coordX=coordX-50;break;


case 2: _root.Lh2._visible=true;

_root.Lh2._x=coordX-50;_root.Lh2._y=coordY;

coordX=coordX-50;break;


case 3: _root.Lh3._visible=true;

_root.Lh3._x=coordX-50;_root.Lh3._y=coordY;

coordX=coordX-50;break;


case 4: _root.Lh4._visible=true;

_root.Lh4._x=coordX-50;_root.Lh4._y=coordY;

coordX=coordX-50;break;

case 5: _root.Lh5._visible=true;

_root.Lh5._x=coordX-50;_root.Lh5._y=coordY;

coordX=coordX-50;break;

case 6: _root.Lh6._visible=true;

_root.Lh6._x=coordX-50;_root.Lh6._y=coordY;

coordX=coordX-50;break;

case 7: _root.Lh7._visible=true;

_root.Lh7._x=coordX-50;_root.Lh7._y=coordY;

coordX=coordX-50;break;

case 8: _root.Lh8._visible=true;

_root.Lh8._x=coordX-50;_root.Lh8._y=coordY;

coordX=coordX-50;break;

case 9: _root.Lh9._visible=true;

_root.Lh9._x=coordX-50;_root.Lh9._y=coordY;

coordX=coordX-50;break;

}

}

if ((j+1<9) && (Table[i][j+1]
val=Table[i][j+1];

dir=4;

//trace("dir4");

back=true;

switch (step)

{

case 1: _root.Lh1._visible=true;

_root.Lh1._x=coordX;_root.Lh1._y=coordY;

coordX=coordX+50;break;


case 2: _root.Lh2._visible=true;

_root.Lh2._x=coordX;_root.Lh2._y=coordY;

coordX=coordX+50;break;


case 3: _root.Lh3._visible=true;

_root.Lh3._x=coordX;_root.Lh3._y=coordY;

coordX=coordX+50;break;


case 4: _root.Lh4._visible=true;

//trace("coordX="+coordX+" coordY="+coordY);

_root.Lh4._x=coordX;_root.Lh4._y=coordY;

coordX=coordX+50;break;

case 5: _root.Lh5._visible=true;

_root.Lh5._x=coordX;_root.Lh5._y=coordY;

coordX=coordX+50;break;

case 6: _root.Lh6._visible=true;

_root.Lh6._x=coordX;_root.Lh6._y=coordY;

coordX=coordX+50;break;

case 7: _root.Lh7._visible=true;

_root.Lh7._x=coordX;_root.Lh7._y=coordY;

coordX=coordX+50;break;

case 8: _root.Lh8._visible=true;

_root.Lh8._x=coordX;_root.Lh8._y=coordY;

coordX=coordX+50;break;

case 9: _root.Lh9._visible=true;

_root.Lh9._x=coordX;_root.Lh9._y=coordY;

coordX=coordX+50;break;

}

}

//trace("dir="+dir);

switch (dir)

{

case 5:break;

case 1:Back(i-1,j);break;

case 2:Back(i+1,j);break;

case 3:Back(i,j-1);break;

case 4:Back(i,j+1);break;

}

}

}

return 0;

}

x1=Number(_root.Ax.text)-1;

y1=Number(_root.Ay.text)-1;

n=y1;m=x1;

Table[n][m]=0;

Proverka(0);

x2=Number(_root.By.text)-1;

y2=Number(_root.Bx.text)-1

Table[x2][y2]=90;


Back(x2,y2);


stop();


}

Глава 4. Основные результаты и их обсуждение.

В настоящее время одно из инноваций — это использование дистанционных методов обучения, которое является одним из наиболее быстро развивающихся направлений системы образования. Это качественно новый прогрессивный вид обучения, базирующийся на современных информационных технологиях и использующий современные средства коммуникаций (телевидение, видео и аудио средства обучения, компьютерные глобальные и локальные сети). Разработка Macromedia Flash приложений позволит ввести такой вид обучения и на нашем факультете или поможет студентам 3-го и 4-го курса лучше разобраться в предоставленной программе обучения.

В качестве наглядного примера разработано Macromedia Flash приложение, в котором показаны различные методы трассировки, и с помощью Macromedia Flash приложения непонятный материал превращается в более понятным для понимания студентов на расстоянии.

Также были выявлены и проиллюстрированы основные преимущества и недостатки, их различия, каждого метода в отдельности. Считаю Macromedia Flash наиболее удобной программой для представления сложного математического и не только математического материала.

Заключение.

Таким образом, видно, что при использовании IT дистанционное обучение становится намного проще.

В данной работе были написаы и рассмотрены Macromedia Flash приложения:

- распространение волны на ДРП и проведение пути,

- метод использования путевых координат,

- метод кодирования весов ячеек по модулю 3,

- метод разметки ДРП по Акерсу,

- метод уменьшения поля поиска,

- метод двойного распространения,

- Метод с использованием быстрого алгоритма трассировки лабиринто

проанализирована эффективность их применения в конструировании систем,

- был детально описан пример алгоритма нахождения пути минимальной длины с заданными координатами на Macromedia Flash

Список литературы к реферату

1. Норенков И.П. Основы автоматизированного проектирования. — М.: МГТУ им. Н.Э.Баумана, 2002.

2. Рейнхард Р., Даут С. Macromedia Flash 8. Библия пользователя.

3. Норенков И.П., Кузьмик П.К. Информационная поддержка наукоемких изделий. — М.: МГТУ им. Н.Э.Баумана, 2002.

4. Норенков И.П., Трудоношин В.А. Телекоммуникационные технологии и сети. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2000.

5. Степанец В.Я., Cистемы автоматизированного проектирования: Учебное пособие для отделения математической электроники, 2007.(расположен на сервере ММФ БГУ)

Предметный указатель к реферату.

Macromedia Flash 5

Метод двойного распространения. 15

Метод использования путевых координат 11

Метод кодирования весов ячеек по модулю 3 12

Метод разметки ДРП по Акерсу 13

Метод с использованием быстрого алгоритма трассировки лабиринтов 16

Метод точной трассировки с распространением по сетке 6

Метод уменьшения поля поиска 14

Описание алгоритма с мгновенным нахождением пути минимальной длины с заданными координатами 17

Проведение пути 9

Распространение волны на ДРП 7

Интернет ресурсы в предметной области исследования.

1. ссылка скрыта - Электронная библиотека мехмата МГУ. Содержит множество книг по физике, математике, информатике. Книги доступны для скачивания в форматах pdf и djvu, необходимо только зарегестрироваться.
   
2. ссылка скрыта - Электронная библиотека мехмата БГУ.
   
3. ссылка скрыта - Образовательный математический сайт.
   
4. ссылка скрыта - Математический сайт, содержащий большое количество курсов лекцийи другой литературы.
   
5. ссылка скрыта - Электронный каталог новейших технологических продуктов.
   
6. ссылка скрыта - Электронная энциклопедия.
   
7. ссылка скрыта - Одна из последних разработок Google, позволяющая искать точную библиографическую информацию для научных книг и статей.
   
8. ссылка скрыта -коллекция математический программ, статей и баз данных.
   

Действующий личный сайт

ссылка скрыта

Граф научных интересов

Магистранта Егельского П. А. механико-математического факультета

Специальность математическая электроника.

Смежные специальности 01.01.07 – Вычислительная математика 1. Теория приближенных методов и численных алгоритмов решения задач алгебры, дифференциальных и интегральных уравнений, задач дискретной математики, экстремальных задач, задач управления, некорректных задач других задач линейного, нелинейного и стохастического анализа. 2. Теория и методы параллельных вычислений. 01.01.02 – Дифференциальные уравнения Обоснование численных методов решения дифференциальных, интегральных, интегро-дифференциальных, функционально-дифференциальных и дифференциально-операторных уравнений.

Основная специальность 01.01.01 – математическая электроника 1.САПР. 2. Технология электроники

Сопутствующие специальности 01.01.03 – математическая физика; Физические задачи, приводящие к дифференциальным уравнениям в частных производных Обыкновенные дифференциальные уравнения. Решение линейных уравнений и систем произвольного порядка с постоянными коэффициентами. 01.01.06 – Математическая логика, алгебра и теория чисел 1. Аналитическая, алгебраическая и геометрическая теории чисел; диофантовы уравнения и приближения. 2. Логические и логико-математические языки, логические системы и логико-математические теории, теории моделей, алгоритмическая разрешимость логических и логико-математических теорий, теории множеств.

Презентация магистерской диссертации.

Referat.ppt

Список литературы к выпускной работе.

1. Норенков И.П. Основы автоматизированного проектирования. — М.: МГТУ им. Н.Э.Баумана, 2002.
   
2. Рейнхард Р., Даут С. Macromedia Flash 8. Библия пользователя.
   
3. Норенков И.П., Кузьмик П.К. Информационная поддержка наукоемких изделий. — М.: МГТУ им. Н.Э.Баумана, 2002.
   
4. Норенков И.П., Трудоношин В.А. Телекоммуникационные технологии и сети. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2000.
   
5. Степанец В.Я., Егельский П.А., Гинтовт А.Ю. Cистемы автоматизированного проектирования: Учебное пособие для отделения математической электроники, 2007.(расположен на сервере ММФ БГУ)