Diskrētā matemātika Discrete mathematics Дискретная математика
| Вид материала | Документы |
СодержаниеНавыки и компетенции Введение. Моделирование. Псевдокод. Темы курса 5. Дискретная математика. Теоретический минимум. Студент (ФИО, группа) 6. Экзамеиационные вопросы |
- Джеймс А. Дискретная математика и комбинаторика [Текст] / Джеймс А. Андерсон, 42.79kb.
- Темы курсовой работы по дисциплине "дискретная математика" (Приложение к рабочей программе, 128.96kb.
- Рабочая программа дисциплины (модуля) Дискретная математика, 101.32kb.
- Рабочая программа учебной дисциплины «Дискретная математика» Направление подготовки, 139.29kb.
- Примерная программа наименование дисциплины «Дискретная математика» Рекомендуется для, 135.29kb.
- Аннотация программы учебной дисциплины «Дискретная математика и математическая логика, 55.65kb.
- Методические указания к выполнению курсовой работы по дисциплине " Дискретная математика", 254.75kb.
- Mathematics and the search for knowledge morris kline, 498.28kb.
- Учебная программа для специальности: (рабочий вариант) 1-310301-02 Математика (научно-педагогическая, 120.64kb.
- Календарный план учебных занятий по обязательной дисциплине «Дискретная математика, 109.62kb.
| 8. | MA0303 | Дискретная математика |
1. Описание курса
Diskrētā matemātika |
| Discrete mathematics |
Дискретная математика |
| 1. | Уровень учебного курса: | B, NT | ||
| 2. | Кредитные пункты: | 2 | ||
| 3. | Автор курса: | Доцент, Dr.Sc.Ing В. Гераськов | ||
| 4. | Testing form | Экзамен | ||
| 5. | Preliminary courses | Высшая математика, Линейная алгебра | ||
| 6. | Annotation | Цели и задачи курса:
Навыки и компетенции:
| ||
| 7. | Код курса | MA 0303 | | |
8. Содержание курса:
| | Темы |
| 1. | Введение. Моделирование. Псевдокод. |
| 2. | Логика и доказательство. Высказывания и логика. Предикаты и кванторы. Методы доказательств. Математическая индукция. Корректность алгоритмов. |
| 3. | Теория множеств. Множества и операции над ними. Алгебра множеств. |
| 4. | Aлгоритмы. Целые числа. Матрицы. Сложность алгоритмов. Приложения теории чисел. Матрицы. |
| 5. | Отношения. Бинарные отношения. Свойства отношений. Отношения эквивалентности и частичного порядка. |
| 6. | Функции. Обратные отношения и композиция отношений. Обратные функции и композиция функций. Принцип Дирихле. |
| 7. | Комбинаторика. Правила суммы и произведения. Комбинаторные формулы. Бином Ньютона. Эффективность алгоритмов. |
| 8. | Графы. Графы и терминология. Эйлеровы и гамильтоновы графы. Планарные графы. Деревья. |
| 9. | Ориентированные графы. Пути в орграфах. Проблема кратчайшего пути в графе. |
| 10. | Булева алгебра. Булевы функции. Карта Карно. Логические схемы. Минимизация логических схем. |
| 11. | Вычислительные модели. Языки и грамматики. Конечные автоматы. Машина Тьюринга. |
| 12. | Теория кодирования. Генератор матриц. Коды Хемминга. |
| 9. | Требования к слушателям: | Для получения полного объема кредитных пунктов необходимы:
|
| 10. | Литература |
|
2. Методический план
| | Темы курса | Литература, источники учебной информации |
| 1. | Введение. Моделирование. Псевдокод. | [2] гл.1 |
| 2. | Логика и доказательство. Высказывания и логика. Предикаты и кванторы. | [2] гл.2 [14] es.com/rbjpub/logic/ |
| 3. | Методы доказательств. Математическая индукция. Корректность алгоритмов. | [2] гл.2 [14] csusb.edu/notes/rel/ |
| 4. | Теория множеств. Множества и операции над ними. Алгебра множеств. | [2] гл.3 [14] csusb.edu/notes/sets/ |
| 5. | Aлгоритмы. Целые числа. Матрицы. Сложность алгоритмов. | [4] гл.3, 4, 5 s.dcs.st-and.ac.uk/~history/Mathematicians/html |
| 6. | Приложения теории чисел. Матрицы. | [4] гл..3, 4,7, 22he-knot.com/blue/chinese.php |
| 7. | Отношения. Бинарные отношения. Свойства отношений. Отношения эквивалентности и частичного порядка. | [2] гл.4 [14] csusb.edu/notes/rel/rel. |
| 8. | Функции. Обратные отношения и композиция отношений. Функции. Обратные функции и композиция функций. Принцип Дирихле. | [2] гл.5 [14] csusb.edu/notes/proofsl |
| 9. | Комбинаторика. Правила суммы и произведения. Комбинаторные формулы. Бином Ньютона. Эффективность алгоритмов. | [2] гл.6 [14] be/~ping1339/tel.htm |
| 10. | Графы. Графы и терминология. Эйлеровы и гамильтоновы графы. Планарные графы. Деревья. | [2] гл.7 [14] du/~cpmawata/peterse/ |
| 11. | Ориентированные графы. Пути в орграфах. Проблема кратчайшего пути в графе. | [2] гл.8 [14] nysb.edu/~algorith/files |
| 12. | Булева алгебра. Булевы функции. Карта Карно. Логические схемы. Минимизация логических схем. | [2] гл.9 eecs.berkeley.edu/~cs150/sp97/ |
| 13. | Вычислительные модели. Языки и грамматики. Конечные автоматы. | [4] гл.17, [5] ch.10 [14] w.unibe.ch/studenten/l |
| 14. | Теория кодирования. Генератор матриц. Коды Хемминга. | [4] гл.18 [14] nb.ca/tervo/ee4253/ |
- Методические рекомендации
- Подготовить и защитить реферат (темы рефератов см. ниже)
- Выполнить домашнее задание и контрольную работу.
- Ответить на вопросы теоретического минимума.
- Выполненные работы присылать на электронный адрес: vgeraskov@yahoo.com
- Заключительная аттестация: согласно организационному плану института и графику сессии.
- Контрольные задания
Темы рефератов:
- Приложения теории чисел
- Рекурсивные функции и алгоритмы.
- Машина Тьюринга.
- Минимизация логических схем.
- Алгоритмы поиска кратчайшего пути в графе
Тест
| 1 | Пусть 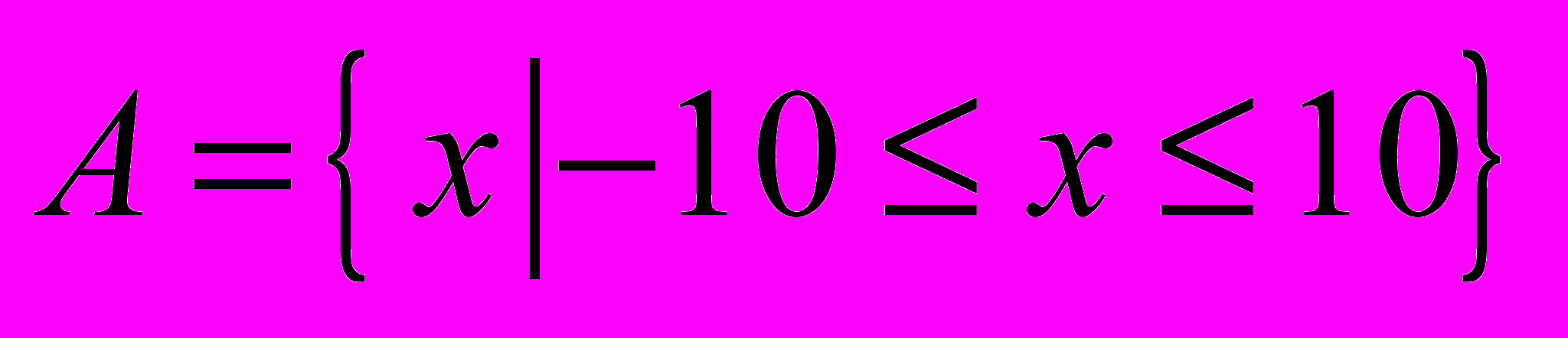 , , 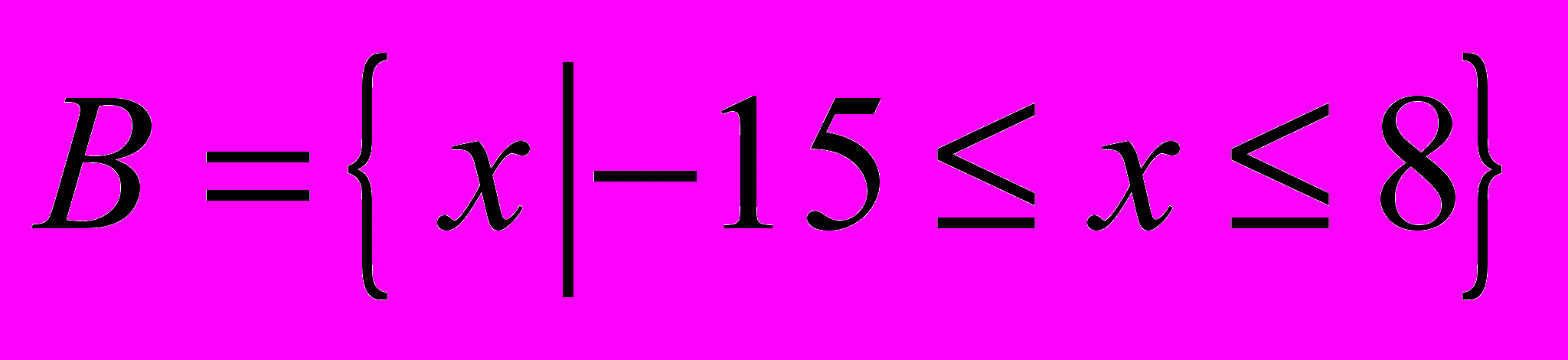 , , 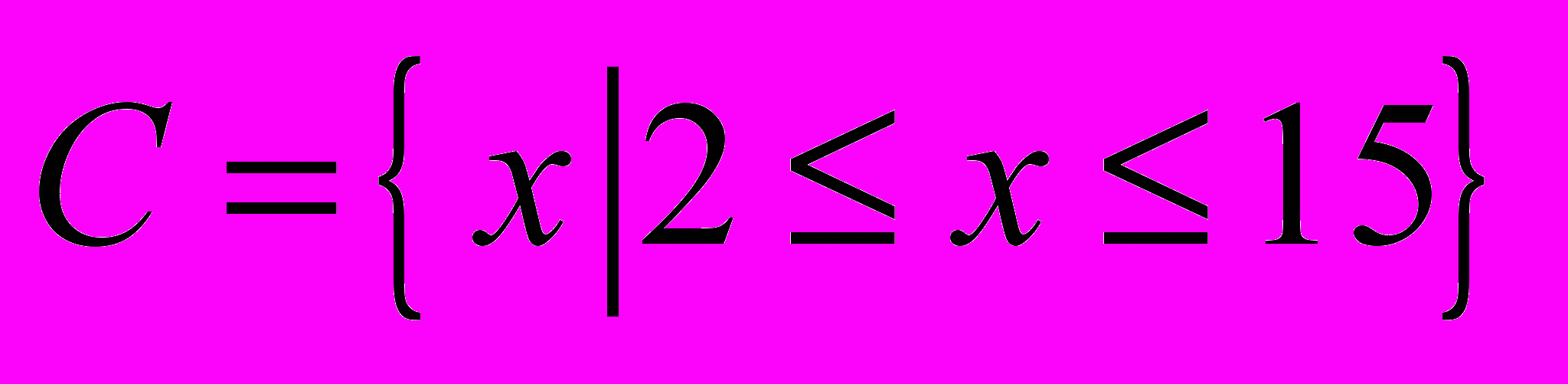 и универсальное множество U = Z, где Z-множество целых чисел. Найти каждое из следующих множеств: и универсальное множество U = Z, где Z-множество целых чисел. Найти каждое из следующих множеств:a) 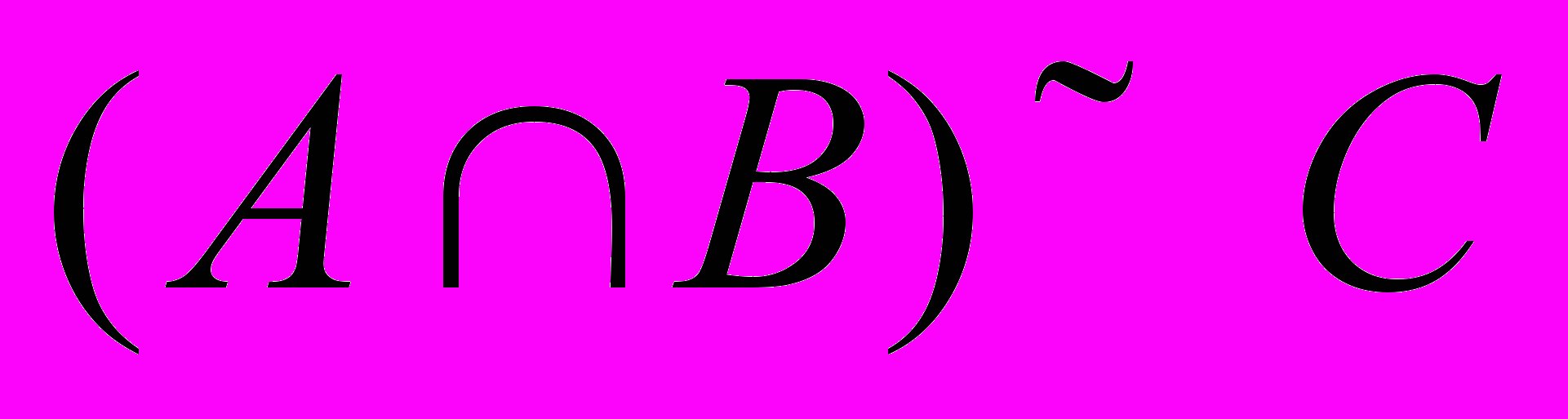 b) b) 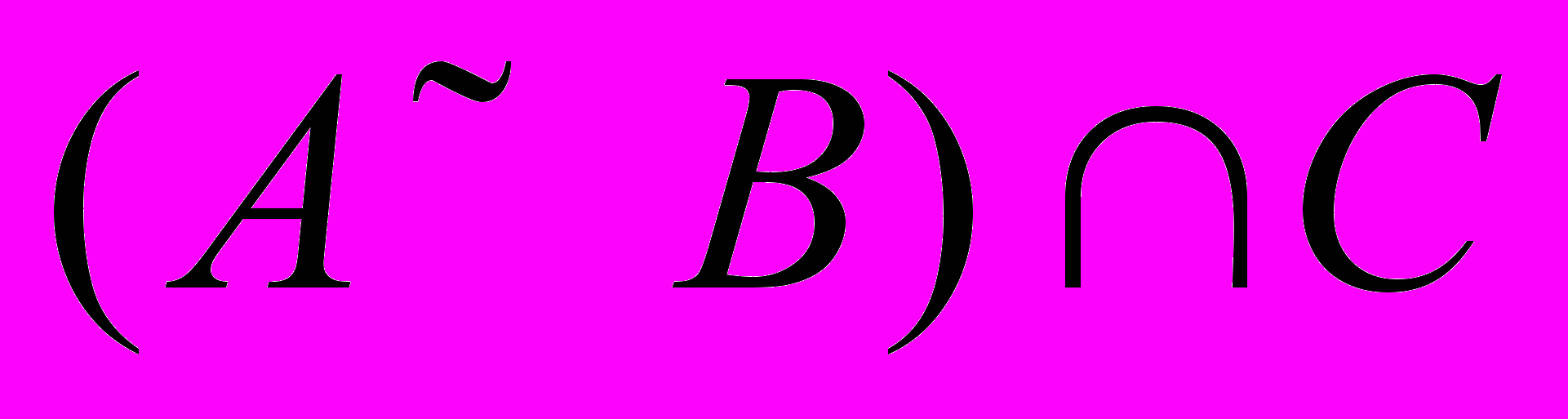 c) c) 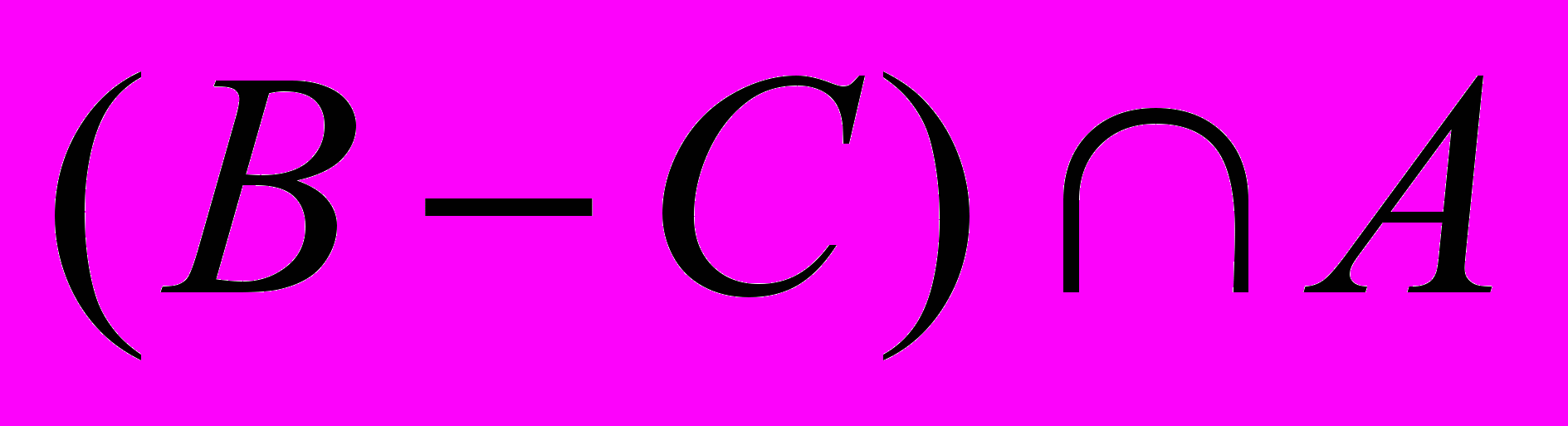 d) d) 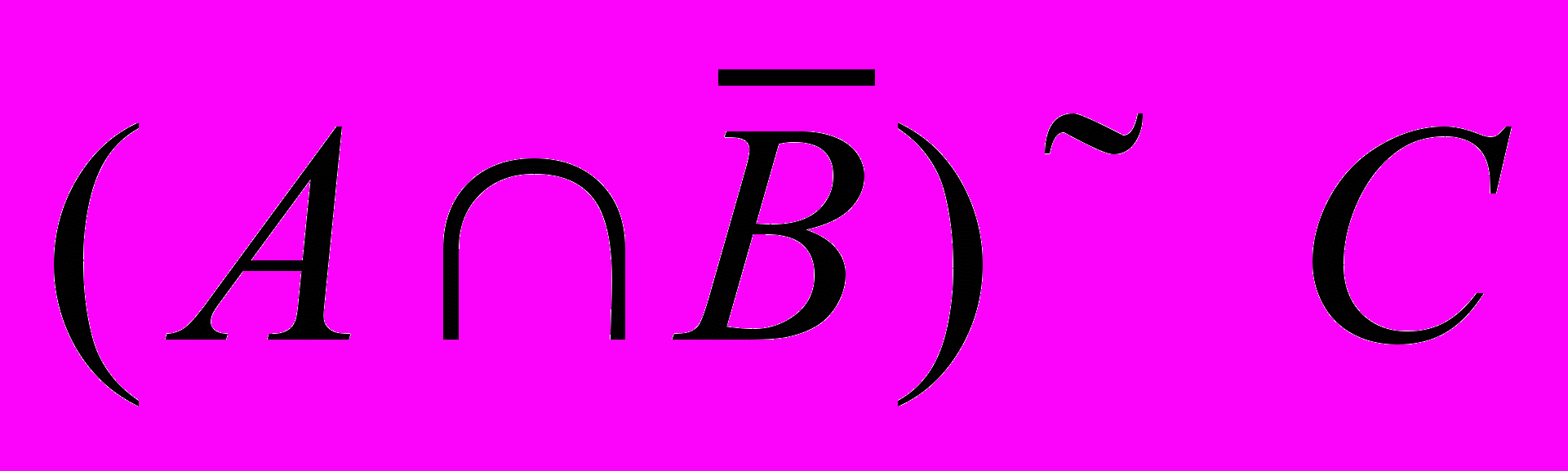 |
| 2 | С помощью алгоритма Евклида найти наибольший общий делитель gcd(2468, 8642) |
| 3 | Докажите методом математической индукции высказывание: 1 + 5 + 9+…+ (4n — 3= n(2n — 1) для всех натуральных чисел n. |
| 4 | a) Преобразовать десятичное число 3275 в двоичное и шестнадцатеричное; b) преобразовать шестнадцатеричное число EB7C516 в восьмеричное и десятичное. |
| 5 | Покажите, что высказывание 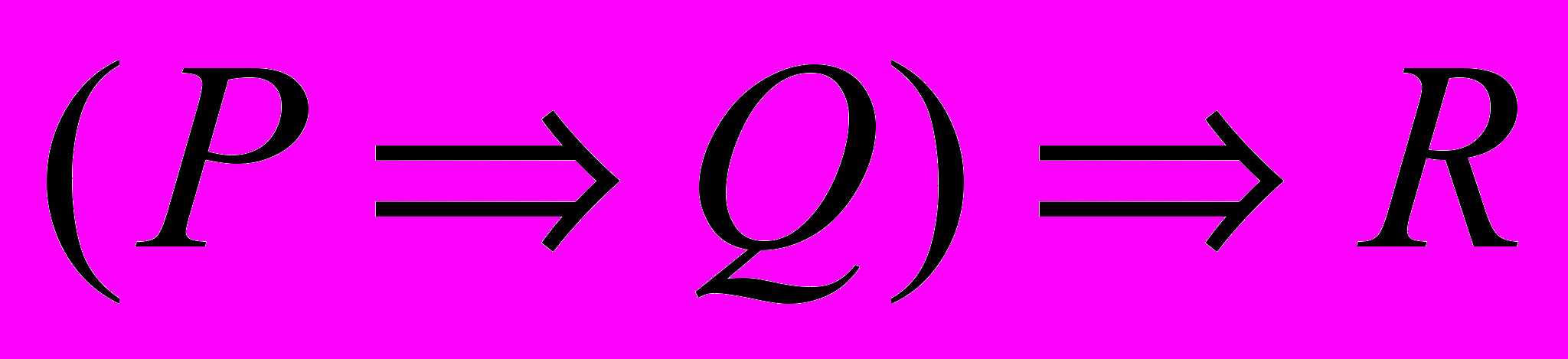 логически эквивалентно высказыванию логически эквивалентно высказыванию 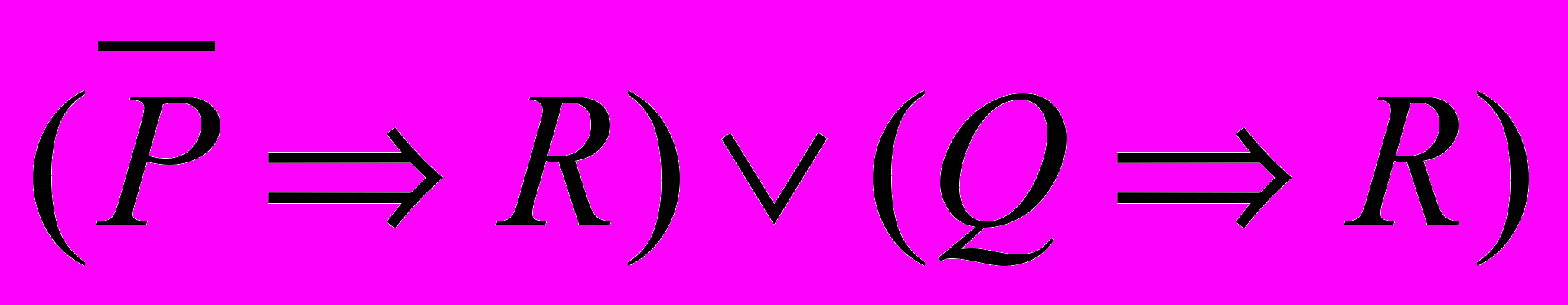 |
| 6 | Пароль, открываюш;ий доступ к компьютеру, состоит из шести символов. Первые два из них — строчные буквы латинского алфавита (всего 26 букв), а оставшиеся четыре могут быть как цифрами, так и строчными буквами. Сколько можно придумать различных паролей? |
| 7 | Нарисуйте граф, чья матрица смежности имеет вид:  |
| 8 | Нарисуйте диаграмму Хассе для частично упорядоченного множества {1, 2, 3, 5, 6, 10, 15, 30} с отношением «х делит у»; |
| 9 | Заполните таблицу истинности булева выражения 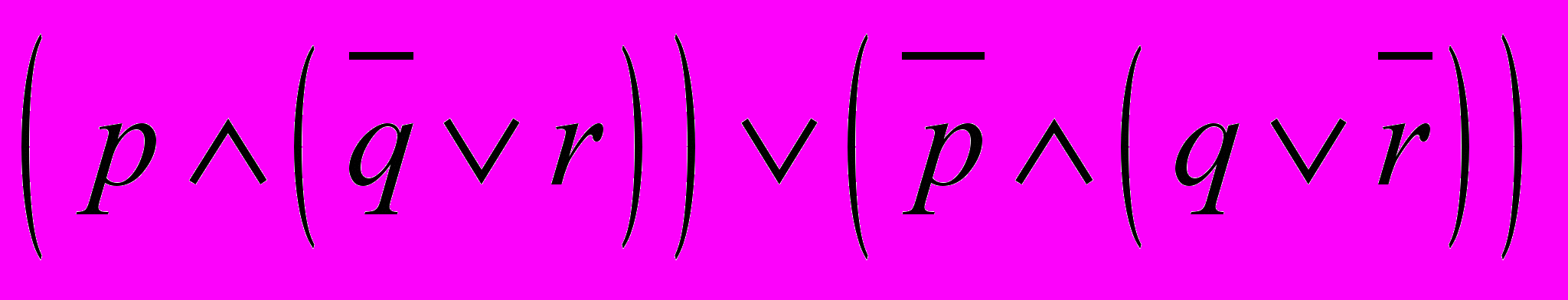 и найдите его дизъюнктивную нормальную форму. и найдите его дизъюнктивную нормальную форму. |
| 10 | Запишите выражение 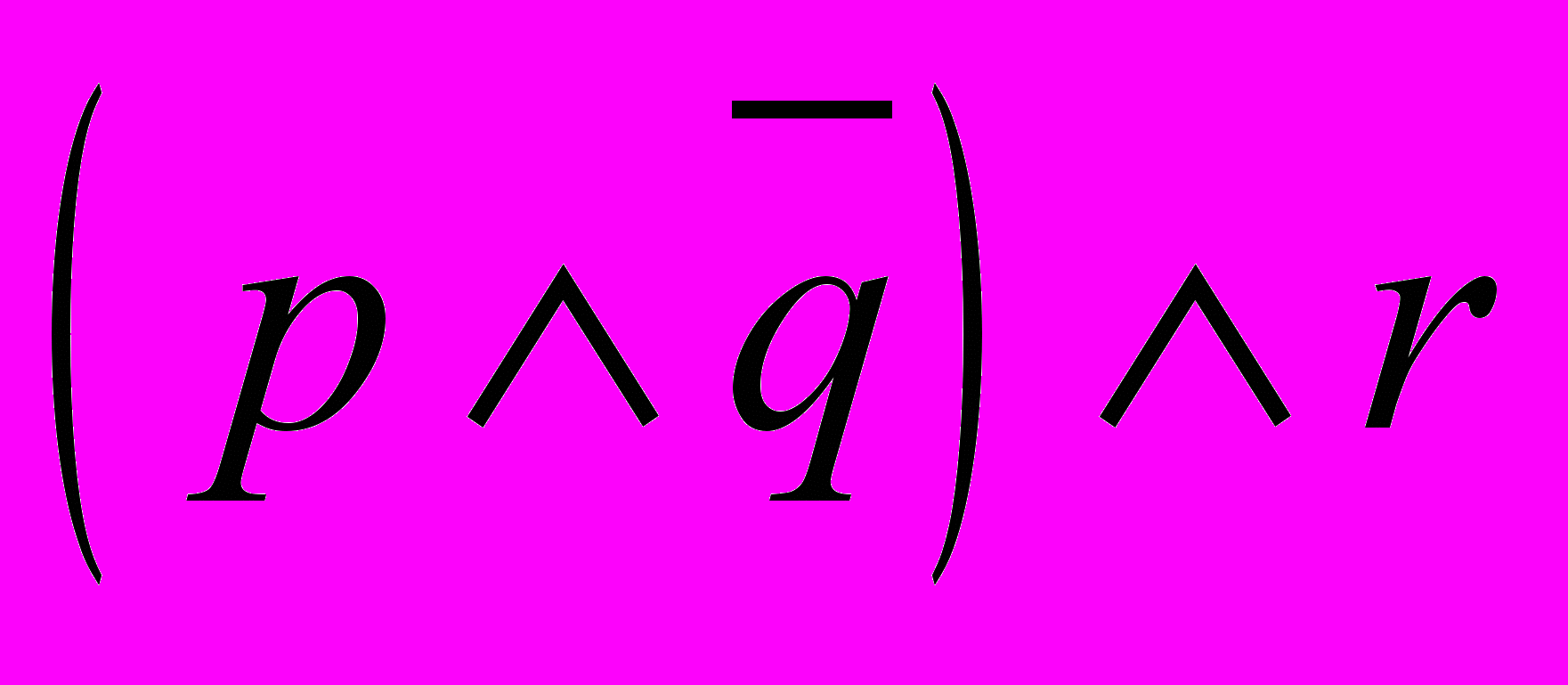 , используя только операции , используя только операции 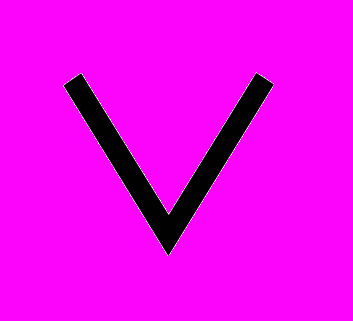 и и  . . |
Домашнее задание
- Матрица смежности орграфа G имеет вид
-
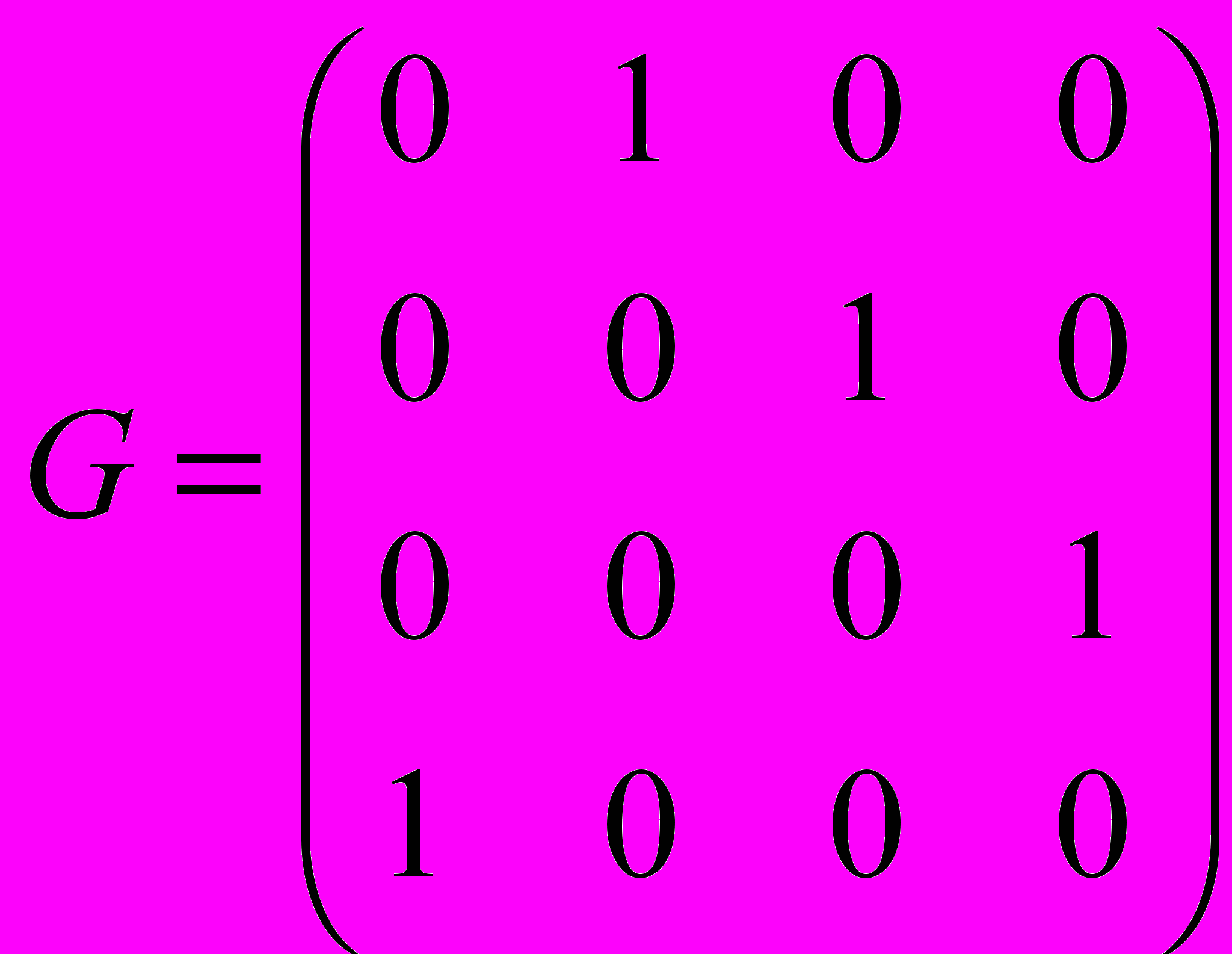
Найдите матрицу достижимости М* этого орграфа.
2 С помощью алгоритма Дейкстры найдите кратчайший путь от вершины A до всех остальных вершин в графе
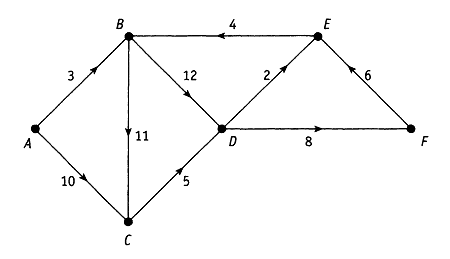
- В таблице приведены расстояния (в км) между шестью городами (A, B, C, D, E и F):
| | A | B | C | D | E | F |
| A | - | 78 | 56 | 73 | 71 | 114 |
| B | 78 | - | 132 | 121 | 135 | 96 |
| C | 56 | 132 | - | 135 | 85 | 154 |
| D | 73 | 121 | 64 | - | 144 | 116 |
| E | 71 | 135 | 85 | 144 | - | 185 |
| F | 114 | 96 | 154 | 116 | 185 | - |
Используя алгоритм поиска минимального остовного дерева, найдите кабельную сеть минимальной общей длины, связывающую все шесть городов.
5. Дискретная математика. Теоретический минимум.
Дать краткое пояснение или определение всем ниже перечисленным терминам (рекомендуется перекопировать таблицу теоретического минимума в отдельный файл, увеличить ячейки правого столбца для записи краткой информации необходимого, на ваш взгляд, содержания/объема.
(заполнить правую сторону, подготовить в виде отдельного документа, распечатать и подписать)
| | Студент (ФИО, группа) | |
| | Учебный предмет | Дискретная математика |
| | Высказывания, предикаты, кванторы | |
| | Методы доказательства | |
| | Математическая индукция | |
| | Множества и подмножества | |
| | Операции с множествами | |
| | Бинарные отношения | |
| | Свойства отношений | |
| | Функции | |
| | Принцип Дирихле | |
| | Основные принципы (правила) комбинаторики | |
| | Сочетания, размещения, перестановки | |
| | Бином Ньютона | |
| | Граф, ориентированный граф | |
| | Маршрут, цикл, дерево | |
| | Эйлеровы и гамильтоновы графы | |
| | Матрица смежности графа | |
| | Задача коммивояжера | |
| | Кратчайший путь в ориентированном графе | |
| | Будевы функции | |
| | Карта Карно | |
| | Логические схемы | |
| | Языки и грамматики | |
| | Конечные автоматы | |
| | Машина Тьюринга | |
| | Codes, Hamming codes | |
| | Числа Фибоначи | |
| | Алгоритмы | |
| | Сложность алгоритмов | |
| | Алгоритм Евклида | |
| | Закон больших чисел | |
6. Экзамеиационные вопросы
Пример экзаменационного билета
| 1 | Составить таблицу истинности булева выражения: 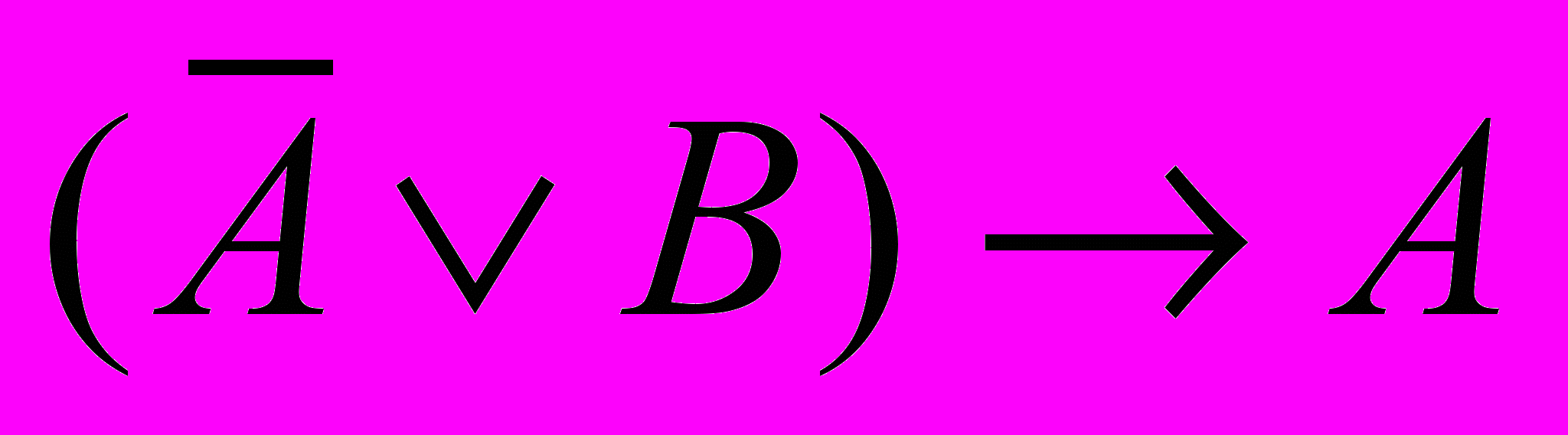 |
| 2 | Изобразить множества, используя диаграммы Венна: 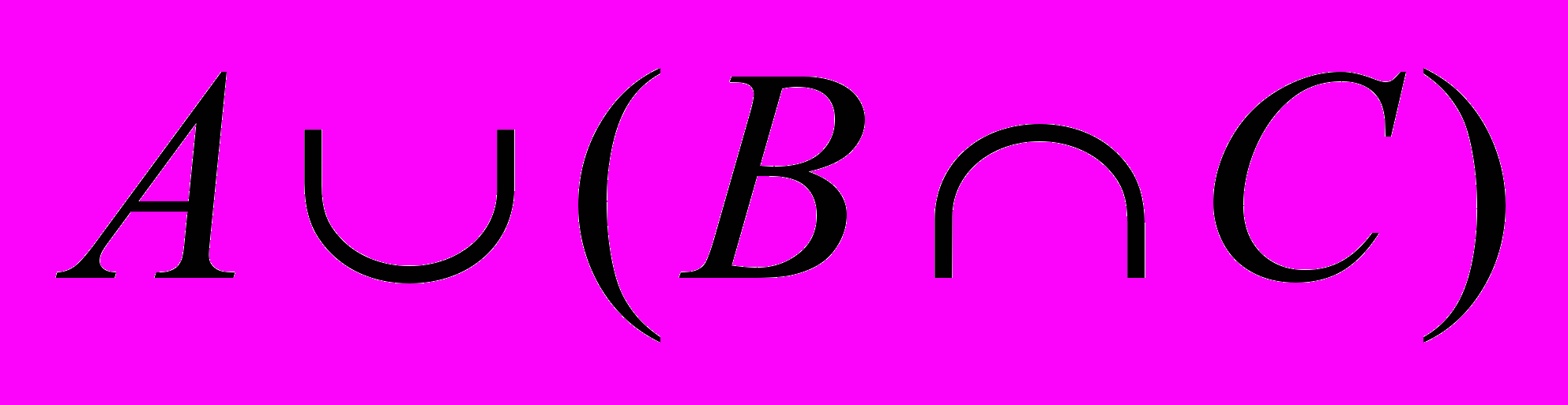 |
| 3 | Пусть 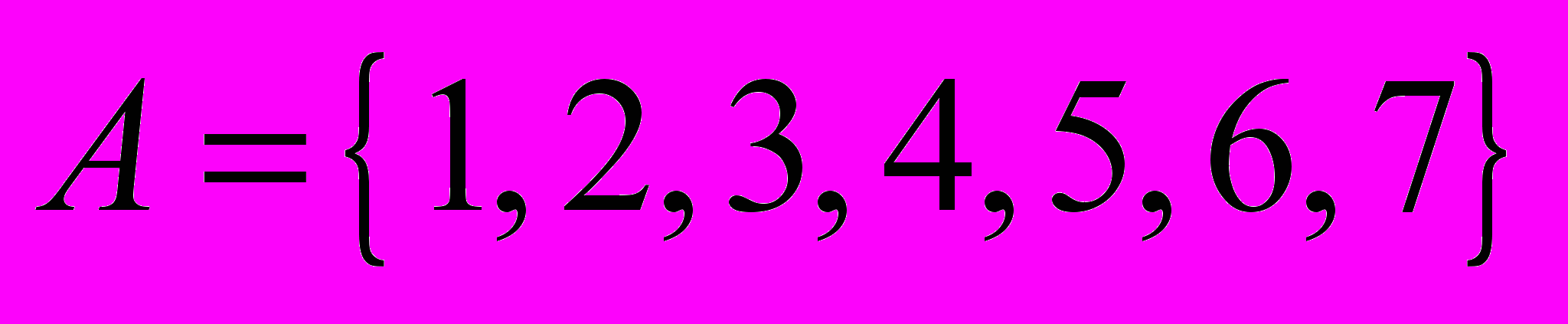 , , 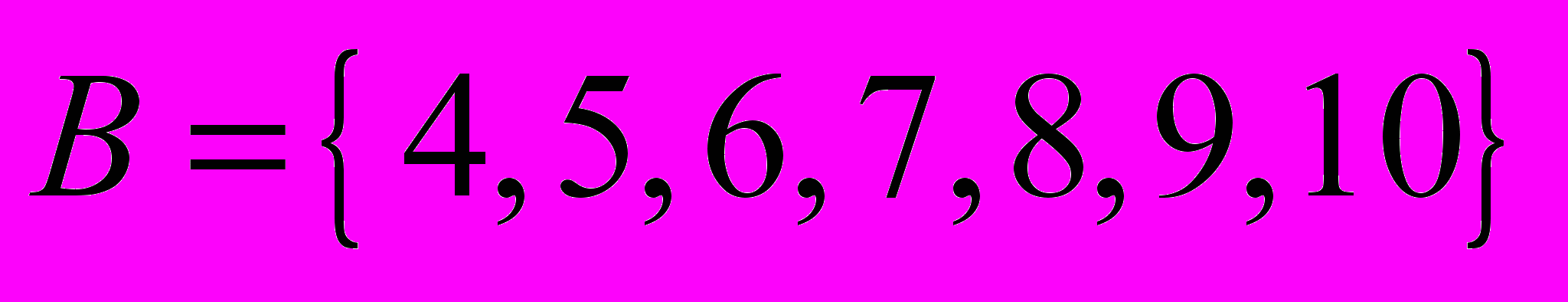 , , 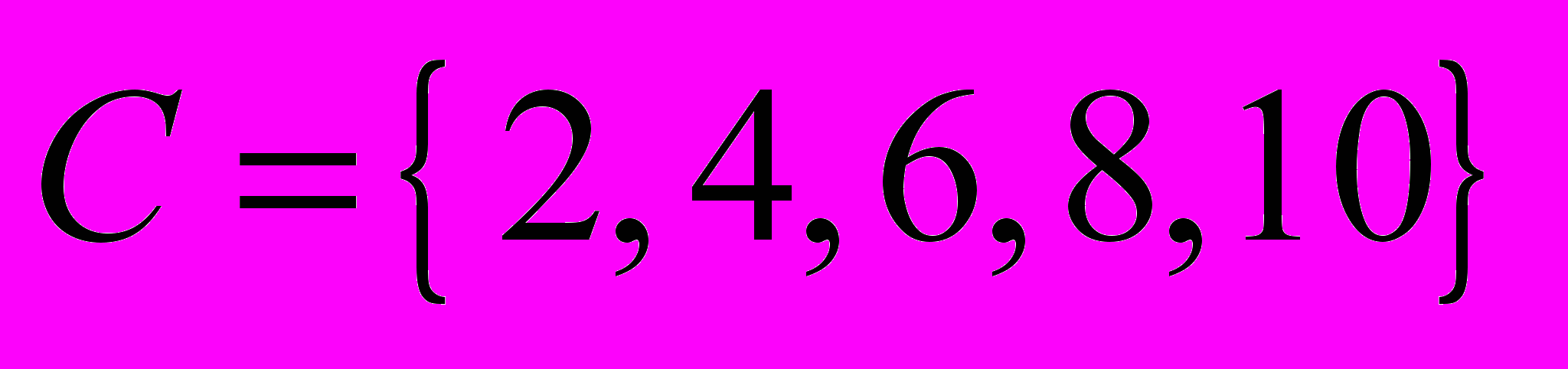 , а универсальное множество , а универсальное множество 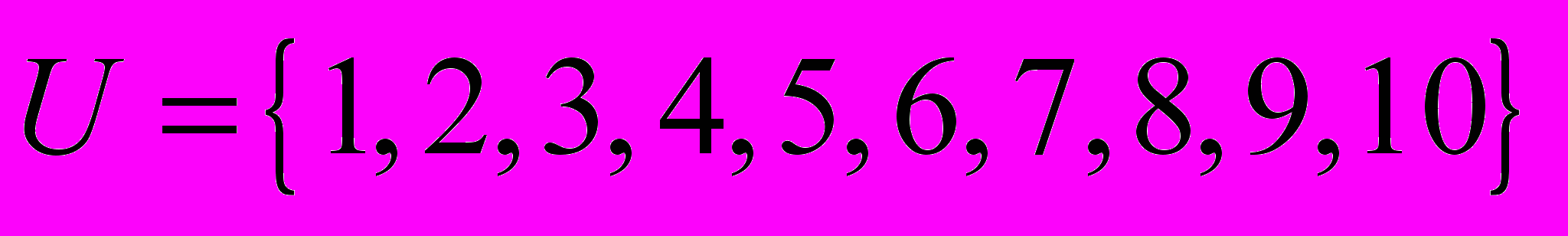 . Найти множество: . Найти множество: 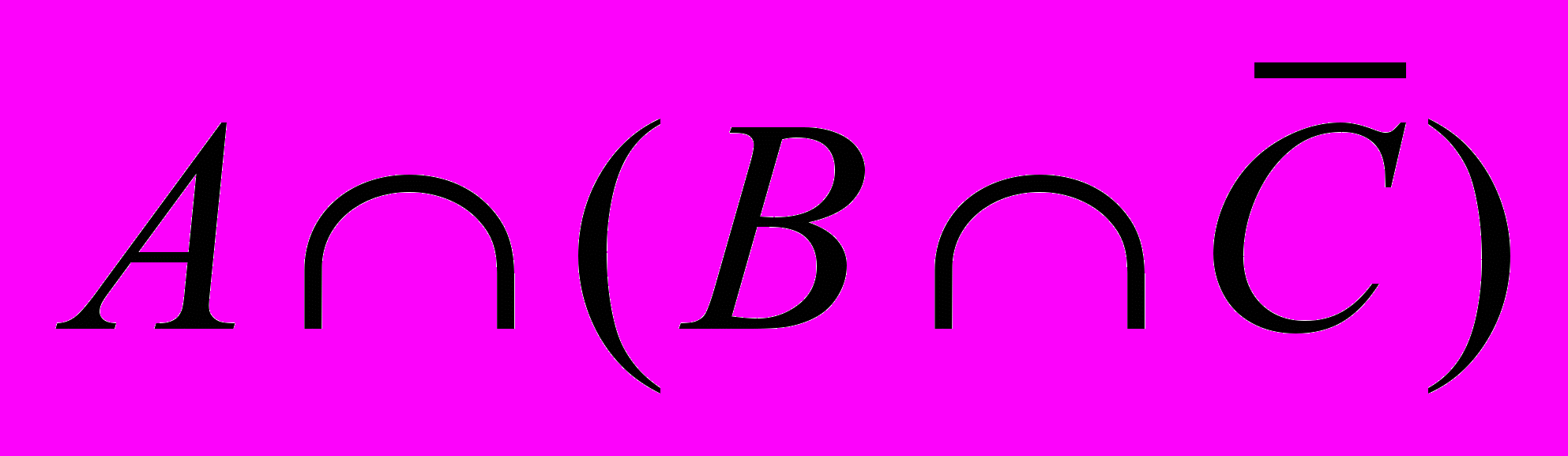 |
| 4 | Преобразовать шестнадцатеричное число 2С4B в двоичное, восьмеричное и десятичное. |
| 5 | Изобразить граф с матрицей смежности:  |
| 6 | Используя алгоритм Евклида, найти наибольший общий делитель чисел 621 и 437 ( gcd(621, 437)) |
| 7 | Сколько 8 битных чисел содержат 3 нуля и 5 единиц? |
| 8 | Методом математической индукции доказать, что: 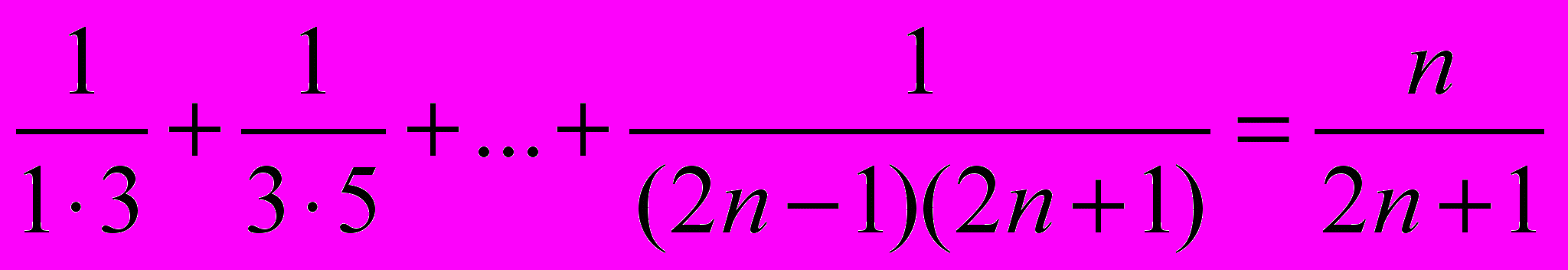 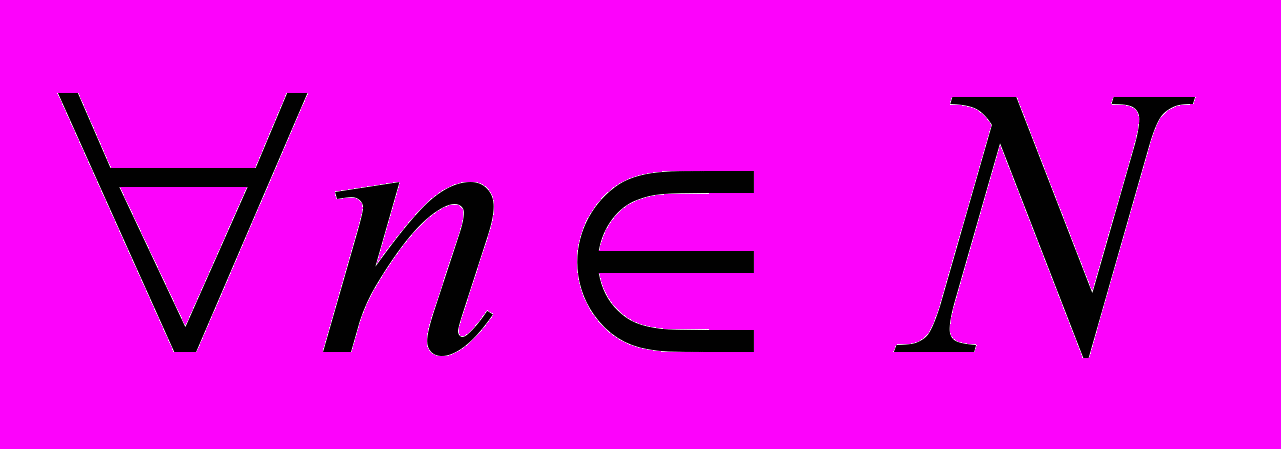 |
| 9 | Показать, что булева функция  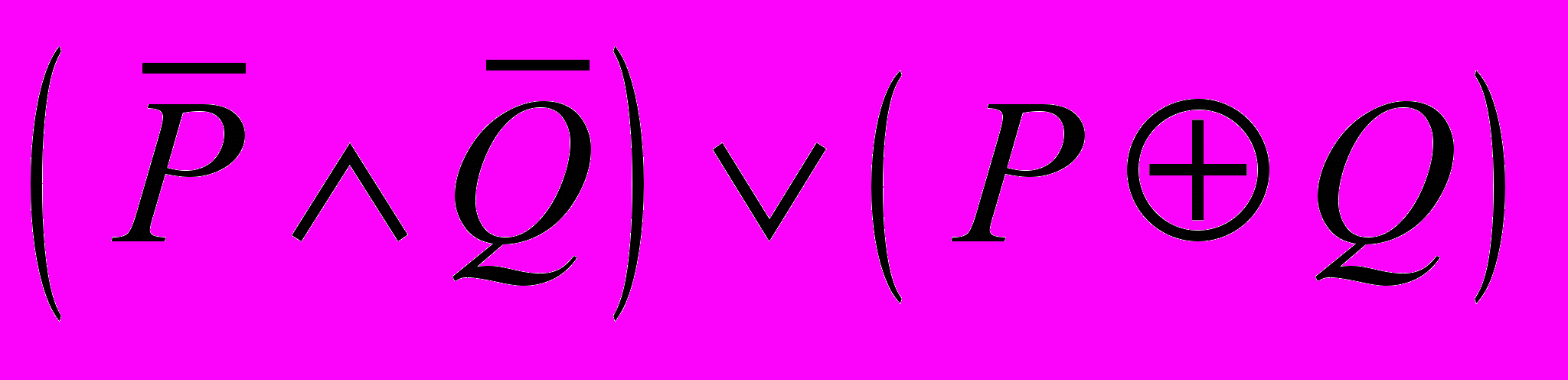 может быть реализована логической схемой, содержащей только два элемента (AND и NOT): может быть реализована логической схемой, содержащей только два элемента (AND и NOT):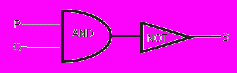  |
| 10 | Пусть  . .В каждом случае найти |S|. (a) |A| = 3 and |B| = 3 (b) |A| = 3 and |B| = 5 (c) |A| = m and |B| = n |
Координатор курса:
Доцент, Dr.Sc.Ing В.Гераськов
