Прочность и устойчивость тонкостенных систем с конструктивными особенностями 05. 23. 17- строительная механика

Вид материала

Автореферат

Содержание Актуальность темы. Целью работы Научная новизна работы Основные научные положения, выносимые на защиту Практическая ценность работы Обоснованность и достоверность полученных результатов Личный вклад диссертанта Реализация результатов работы Апробация работы. Полнота опубликованных работ. Структура и объем диссертации. Основная часть В первом разделе Во втором разделе В третьем разделе Список опубликованных работ по теме диссертации Жұмыстың мақсаты. Зерттеу нысаны. Жұмыстың ғылыми жаңалығы Негізгі ғылыми тұжырым ... Полное содержание

Подобный материал:

• «Строительная механика и металлические конструкции», 76.69kb.
• Расписание утверждаю, 64.12kb.
• Устойчивость и управление в нестационарных системах, 23.13kb.
• Программа подраздела «История механики», 75.11kb.
• Лекция 23. Отладка и обработка исключительных ситуаций Корректность и устойчивость., 391.81kb.
• Министерство образования и науки Республики Казахстан, 25731.2kb.
• Колонна отпарная, прочность, устойчивость, теплообменник, насос, 10.38kb.
• Лекция №2, 129.67kb.
• В. О. Веретьева Л. М. Воропай, научный кандидат химических наук, доцент, 67.88kb.
• Строительная механика Общая трудоемкость дисциплины, 24.92kb.

УДК 624.04: 624.075 На правах рукописи

СЫДЫКОВА ДАМЕЛЬКАН КАКЕНОВНА

Прочность и устойчивость тонкостенных систем

с конструктивными особенностями


05.23.17- строительная механика


Автореферат

диссертации на соискание ученой степени

кандидата технических наук


Республика Казахстан

Алматы, 2010


Работа выполнена в Казахской головной архитектурно- строительной академии (КазГАСА)


Научный руководитель доктор технических наук Достанова С.Х.


Официальные оппоненты доктор технических наук

Боженов А. Ш.

кандидат технических наук

Лапин В.А.


Ведущая организация Казахский Национальный технический университет им. К.И.Сатпаева


Защита состоится 29 ноября 2010г. в 14⁰⁰ часов на заседании диссертационного совета Д14.50.04. при Международной образовательной корпорации на базе Казахской головной архитектурно-строительной академии (КазГАСА) по адресу: 050043, Республика Казахстан, г.Алматы, ул. К.Рыскулбекова, 28, Зал Ученого Совета.

Тел.: +(727)229-46-11, факс: (727)220-59-79, е-mail: kazgasa@itte.kz


С диссертацией можно ознакомиться в библиотеке Казахской головной архитектурно-строительной академии по адресу: 050043 г.Алматы, ул. К.Рыскулбекова,28.


Автореферат разослан «26» октября 2010г.


Ученый секретарь

диссертационного совета Д14.50.04

доктор технических наук Д.М. Байтурсунов

ВВЕДЕНИЕ


Общая характеристика работы. Основу исследований составляют теоретический анализ теории устойчивости и прочности тонкостенных систем и выбор метода решения, основанного на вариационном принципе с использованием дискретизации и разделения крутильных деформаций на чисто крутильные и крутильно - изгибные. Особое внимание уделено разработке приближенных методов определения критических нагрузок, соответствующих потере устойчивости тонкостенных конструкций, основанных на вариационном принципе Лагранжа - Кастильяно.

Актуальность темы. Широкое применение тонкостенных конструкций, элементами которых являются гибкие стержни, балки, пластинки и оболочки различных очертаний, требует совершенствования теории и методов их расчета. Очень важным этапом в этом звене является правильный выбор расчетной модели, учитывающей особенности работы конструкции и дающей результаты, которые близки к реальной работе системы

Строительство новых сложных конструкций выдвигает множество проблем, одним из решений которых является вопросы уменьшения веса, т.е. оптимизации массы и стоимости системы, увеличение надежности и безопасности, что приводят к необходимости расширения теоретических и экспериментальных исследований в области прочности и устойчивости.

При проектировании современных элементов конструкций и сооружений важным этапом является расчет на прочность. Однако в практической работе при проведении расчетов на прочность тонкостенных систем конструктору и инженеру предлагаются громоздкие расчеты, связанные с решением неоднородных дифференциальных уравнений, которые приводят к большому объему вычислений и часто теряется при этом точность и ясность расчета.

Подробный и глубокий анализ теоретических предпосылок, на которых основана современная методика расчета тонкостенных конструкций, позволяет вскрыть противоречия в современной концепции прочности, устойчивости и динамики тонкостенных конструкций.

В данной работе используется новый теоретический подход к расчету тонкостенных систем: для стержней – использование принципа разделения крутильных деформаций на чисто крутильные и крутильно - изгибные; для плит и оболочек - метод дискретизации с учетом реактивных усилий по линии контакта отдельных элементов в виде нелинейных функций, новые модели в задачах устойчивости, которые позволяют решать задачи прочности и устойчивости более точно и без громоздких вычислений по сравнению с классическими методами.

Тема диссертации актуальна и способствует созданию эффективных конструкций и сооружений. Работа выполнена в соответствии с научными программами научно-исследовательских работ КазГАСА.

Целью работы является исследование прочности и устойчивости тонкостенных систем с конструктивными особенностями и приложение новых теоретических и практических подходов к расчету инженерных задач.

Для достижения этой цели в работе поставлены следующие задачи:

- разработать модели тонкостенного стержня, плит и цилиндрической оболочки с конструктивными особенностями;

-на основе вариационного метода уточнить уравнения равновесия и разработать методику инженерного расчета тонкостенных конструкций с использованием метода разделения крутильных деформаций;

- выполнить расчеты на прочность тонкостенного стержня открытого профиля, плит и пологой цилиндрической оболочки по разработанной методике;

- определить критические нагрузки для тонкостенных стержней по предлагаемой методике;

- оценить и сравнить результаты расчетов для тонкостенных конструкций по предлагаемой методике с классической теорией В.З.Власова.

Научная новизна работы

- предложен новый подход к расчету тонкостенных стержней путем разделения углов закручивания на чисто крутильные и крутильно-изгибные;

- предложен новый подход к расчету плит и цилиндрических оболочек путем дискретизации системы на отдельные полосы в двух направлениях с учетом их взаимосвязей с помощью нелинейных функций;

- определено напряженное состояние в тонкостенном стержне с учетом разделения углов закручивания и сделаны сравнения с известными классическими решениями;

- исследовано напряженно-деформированное состояние железобетонных пологой оболочки и плит с конструктивными особенностями по данной методике и даны сравнения с классическими решениями;

- разработаны математические модели для расчета тонкостенных стержней на устойчивость;

- на основании предложенной методики выполнены расчеты на устойчивость тонкостенного стержня при центральном сжатии и чистом кручении, сделаны сравнения с имеющимися данными расчета по теории Власова.

Основные научные положения, выносимые на защиту

-новые расчетные модели напряженно-деформированного состояния тонкостенных стержней, плит и тонких пологих оболочек;

- новые расчетные модели для исследования потери устойчивости тонкостенных стержней;

- результаты расчета на прочность тонкостенных стержней, плит и пологих оболочек по предлагаемой методике, оценка и сравнение результатов с известными решениями;

- результаты расчета на устойчивость тонкостенного стержня при центральном сжатии и изгибе по данной методике;

- алгоритмы для численных расчетов тонкостенных конструкций на прочность и устойчивость по предлагаемой методике.


Практическая ценность работы

Полученные результаты расчетов можно использовать при проектировании тонкостенных конструкций, показаны преимущества предлагаемой методики с двухсторонней оценкой по сравнению с существующей концепцией прочности упругих систем и вариационными принципами механики. Предлагаемая методика дает уточненные результаты в сравнении с классическими подходами по теории В.З.Власова, проверена экспериментально другими авторами. Разработаны упрощенные алгоритмы для инженерных расчетов на прочность тонкостенных стержней, плит и оболочек без громоздких вычислений, связанных с решением дифференциальных уравнений четвертого порядка. Разработан алгоритм для определения критических нагрузок при изгибе и кручении тонкостенного стержня.

Обоснованность и достоверность полученных результатов подтверждается тем, что они были получены на основе классических понятий и принципов механики, современных теоретических достижений механики деформируемого твердого тела, строительной механики, прикладных методов математического анализа, моделирования и сопоставления полученных решений с известными решениями.

Личный вклад диссертанта состоит в непосредственном выполнении исследований по всем частям и звеньям диссертации, а именно, в сборе, систематизации и обработке литературных материалов по особенностям работы тонкостенных конструкций, разработке алгоритмов расчета на прочность и устойчивость, реализации многовариантных численных расчетов, анализе и рекомендаций для инженерных расчетов.

Реализация результатов работы

Теоретические основы работы внедрены в учебный процесс Казахской академии транспорта и коммуникаций для студентов, аспирантов, магистрантов, а также внедрены в учебный процесс Казахской Головной архитектурно-строительной академии.

Основные результаты включены в отчеты:

- по теме 737 (грант, от 20.07.02) /Прогнозирование приоритетов развития: строительной науки, технологий, конструкций, зданий и сооружений, конкурентно способных в условиях рыночных отношений/;

- по теме 420 (грант, от 20.02.03г.) /Прогнозирование приоритетов развития: строительной науки, технологий, конструкций, зданий и сооружений, конкурентно способных в условиях рыночных отношений/.

Апробация работы. Основные научные положения и результаты работы докладывались и обсуждались на республиканских и международных научных конференциях: «Транспорт Евразии: Взгляд в ХХ1 век» (Алматы, 16-17 октября, 2002г.), «Вопросы прикладной физики и математики», ( Алматы, 29-30 апреля, 2003г.), «Теория функций, функциональный анализ и их приложения» (Семипалатинск , 1-4 июля 2003г.), «Инновационные технологии в области информатики, математики и физики» (Алматы, 11 мая 2006 г.), «Актуальные проблемы естественно-научных дисциплин» (Алматы, 29 ноября 2007г.), «Современные концепции естествознания и информационных технологий », (Алматы, 22 января 2009г.), «Механика и строительство транспортных сооружений» (Алматы, 26-27- января 2010г.).

Полнота опубликованных работ. Основные результаты теоретических исследований, полученные в работе, и составляющие содержание диссертации освещены в 16 научных трудах.

Структура и объем диссертации. Диссертационная работа состоит из введения, трех разделов, заключения, списка использованных источников из 102 наименований. Общий объем диссертации - 98 страниц, включая 20 рисунков и 25 таблиц.


ОСНОВНАЯ ЧАСТЬ


Во введении обосновывается актуальность темы, сформулированы цель и применяемые методы исследований, показана новизна и научные положения, выносимые на защиту, практическая ценность диссертационной работы, обоснованность и достоверность полученных результатов, апробации практических результатов.

В первом разделе приводится обзор современного состояния исследований прочности и устойчивости тонкостенных конструкций. Большую роль в развитии теории и методов расчета конструкций сыграли И.Г.Бубнов, С.П.Тимошенко, Б.Г.Галеркин, П.Ф.Папкович, А.Н.Крылов, В.З. Власов и другие.

Всесторонний анализ современной теории прочности и устойчивости тонкостенных конструкций с точки зрения линейной и нелинейной строительной механики изложены в трудах следующих ученых: В.В. Новожилов, Х. М. Муштари, К.З. Галимов, Е.Л. Бернштейн, А.С. Вольмир, Я.Г. Пановко, В.Г.Пискунов, В.В.Пикуль, и других. Необходимо отметить труды по устойчивости тонкостенных стержней и оболочек таких ученых, как А. Л. Гольденвейзер, Ю.Н.Работнов, Н.К.Снитко, В.В.Болотин, А.Р.Ржаницын, И.И.Гольденблат и др.

Разработками теоретических и экспериментальных методов расчета тонкостенных конструкций (элементами которых являются стержни, балки, пластинки, оболочки) при исследовании их прочности занимались: G. Hermann, С.А.Амбарцумян, Н.А. Алумяэ, Н.Я.Амиро и др. В развитие строительной механики тонкостенных конструкций внесли определенный вклад казахстанские ученые: Ж.С. Ержанов, Т.Ж.Жунусов, Ш.М.Айталиев, Е.Т. Божанов, А.А.Кусаинов, А.Ш.Баженов, С.К.Ельмуратов и др.

Предложенная В.З.Власовым теория стержней открытого профиля построена на следующих геометрических гипотезах:

а) тонкостенный стержень открытого профиля рассматривается как оболочка, обладающая в плоскости поперечного сечения жестким (недеформируемым) профилем;

б) деформация сдвига срединной поверхности, характеризующаяся изменением прямого угла, между координатными линиями (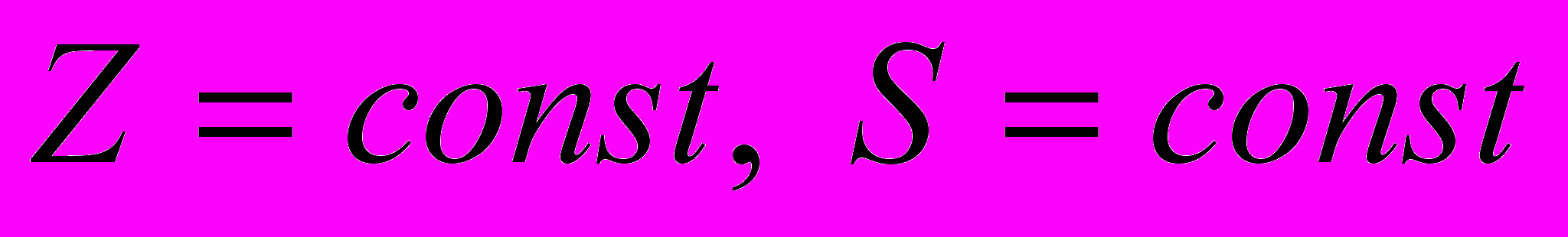) принимается равной нулю.

Как известно, вариационные принципы механики деформируемого твердого тела являются основополагающими, т.к. в них включены все внешние и внутренние силовые факторы, действующие на систему извне и внутри. Согласно этим принципам из всевозможных равновесных состояний при заданных воздействиях система принимает такое состояние, которое соответствует минимуму полной энергии системы. Многие уравнения равновесия для бесконечно малого элемента системы при внешних воздействиях получены на основании вариационного принципа Лагранжа – Кастильяно, и это говорит об их правильности и достоверности. Доказано, что все уравнения и решения для линейных задач механики деформируемого твердого тела (решения сопротивления материалов) полностью соответствуют вариационным принципам. В работе А.П.Лещенко «Фундаментальная строительная механика упругих систем» доказано, что некоторые известные уравнения равновесия для плоских задач теории упругости не полностью удовлетворяют вариационным принципам, т.е. имеются противоречия, которые можно устранить только путем использования основных принципов механики. Для тонкостенных стержней, которые имеют двоякую природу, а именно одновременно их рассматривают как простой стержень и как оболочку, экспериментально доказано, что имеются некоторые расхождения с теоретическими результатами. В.З.Власов рассматривал тонкостенный стержень как длинную цилиндрическую или призматическую оболочку, воспринимающую в каждой точке срединной поверхности как тангенциальные (нормальные и сдвигающие) усилия, так и моменты (крутящие - в поперечных сечениях и изгибающие - в продольных).

В данной работе на основании вариационного принципа используется новый подход к расчету тонкостенных конструкций, который заключается в следующем: используется принцип разделения полных крутильных деформаций для тонкостенного стержня на чисто крутильные и крутильно – изгибные. Это обосновано тем, что внешний силовой фактор - бимомент в классической теории В.З.Власова относится к внутренним усилиям и не участвует в работе внешних сил системы. На самом деле полный угол закручивания для тонкостенного стержня суммируется из углов закручивания, соответствующих чистому изгибу и изгибно-крутильной деформации, поэтому работа внешних крутящих сил при закручивании состоит из двух слагаемых: одно относится к работе части крутящего момента на чисто крутильных деформациях, второе к работе крутящего момента на крутильно- изгибных деформациях, последнее включает работу бимомента. Этот учет корректирует уравнения равновесия для тонкостенного стержня, выведенные В.З.Власовым. В дальнейшем в данной работе учитывается это противоречие и разработаны модели для тонкостенных конструкций в расчетах на прочность и устойчивость. Полученные модели позволяют решать задачи прочности и устойчивости более точно и с меньшим объемом вычислений по сравнению с классическими методами.

В данной работе использованы следующие наиболее распространенные модели для расчета на прочность тонкостенных стержней:

1.Модель тонкостенного стержня по теории В.З.Власова

Поведение тонкостенных стержней при изгибе в двух направлениях и кручении описывается системой трех дифференциальных уравнений, составленных для недеформированного состояния:

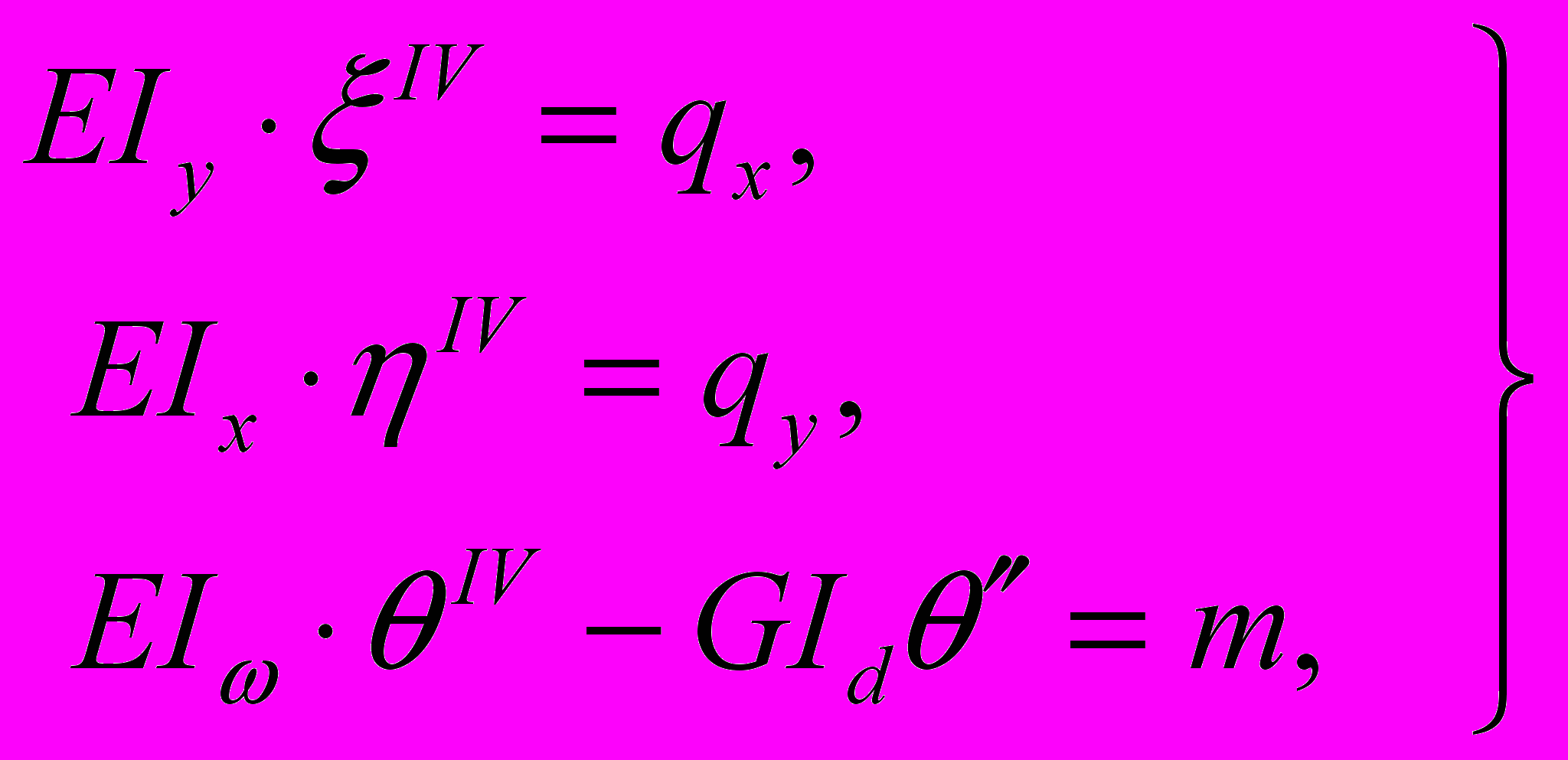(1)

где первые два уравнения – это уравнения изгиба стержня, как балки, в направлении осей х и у, а третье – уравнение стесненного кручения тонкостенного стержня; 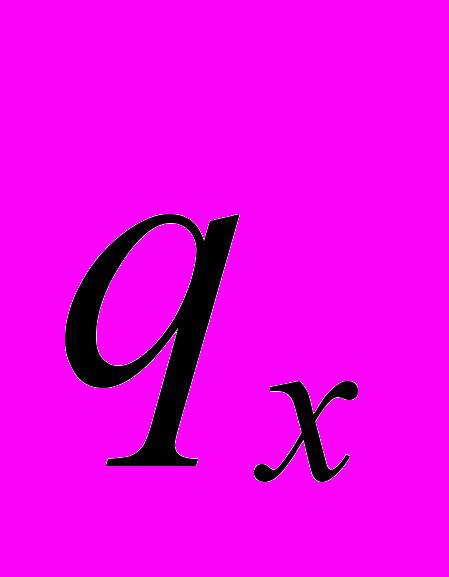и 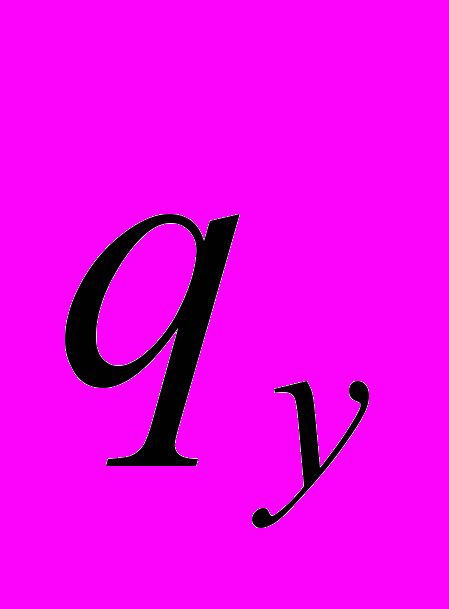- интенсивности погонных поперечных нагрузок; 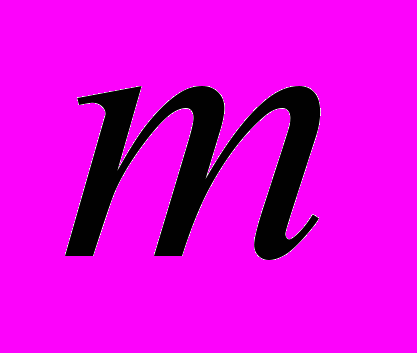- интенсивность внешнего крутящего момента, определяемого относительно центра изгиба, EI_х, EI_у - жесткости на изгиб в двух плоскостях, EI_ω - изгибно-крутильная жесткость, ζ – перемещение вдоль оси х, η – перемещение вдоль оси у, θ – полный угол закручивания.

2.Уточненная модель с учетом деформируемости контура

Если рассмотреть равновесие бесконечно малой полоски длинной 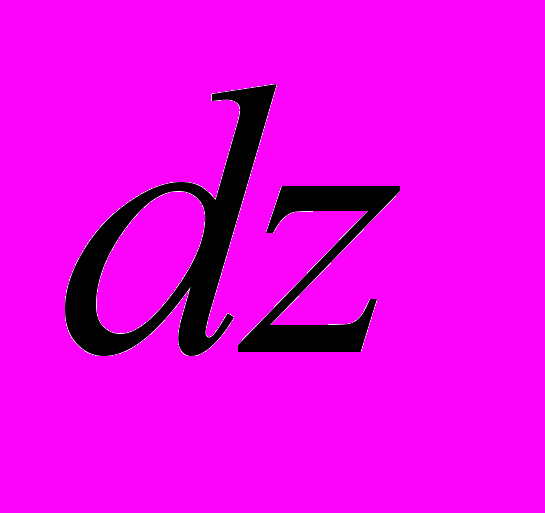тонкостенного стержня в деформированном состоянии, то уравнения (1) приобретают следующий вид:

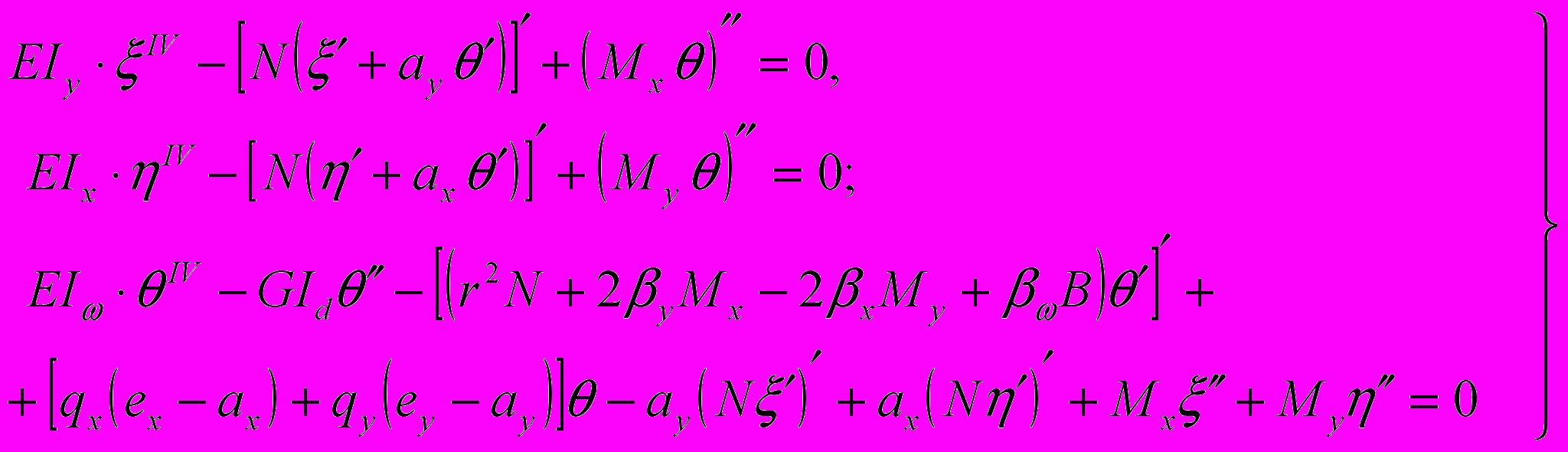(2)

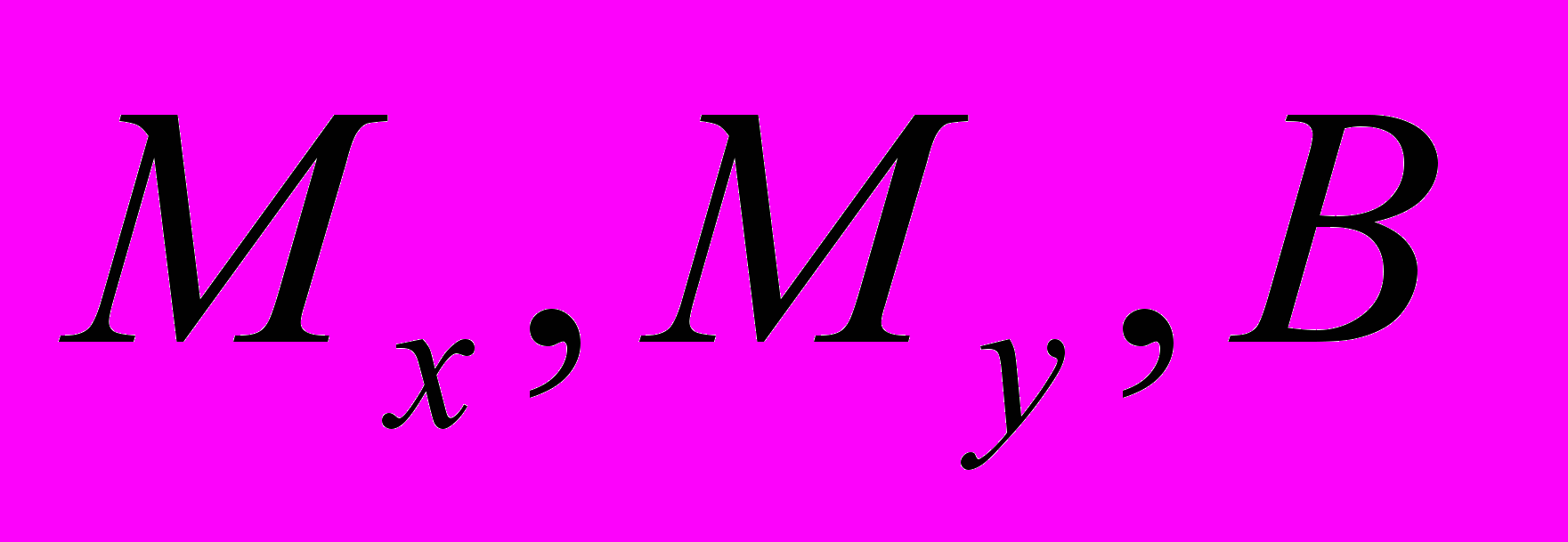здесь - продольная сила; - соответственно изгибающие моменты относительно осе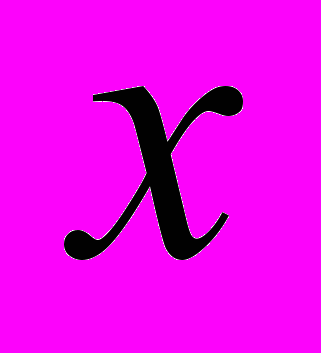й и 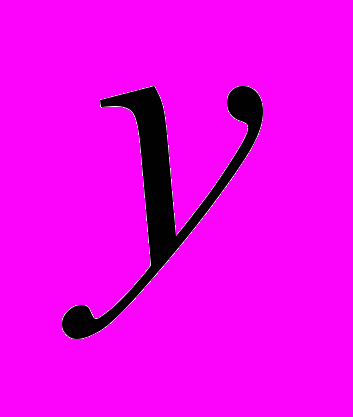и бимомент; 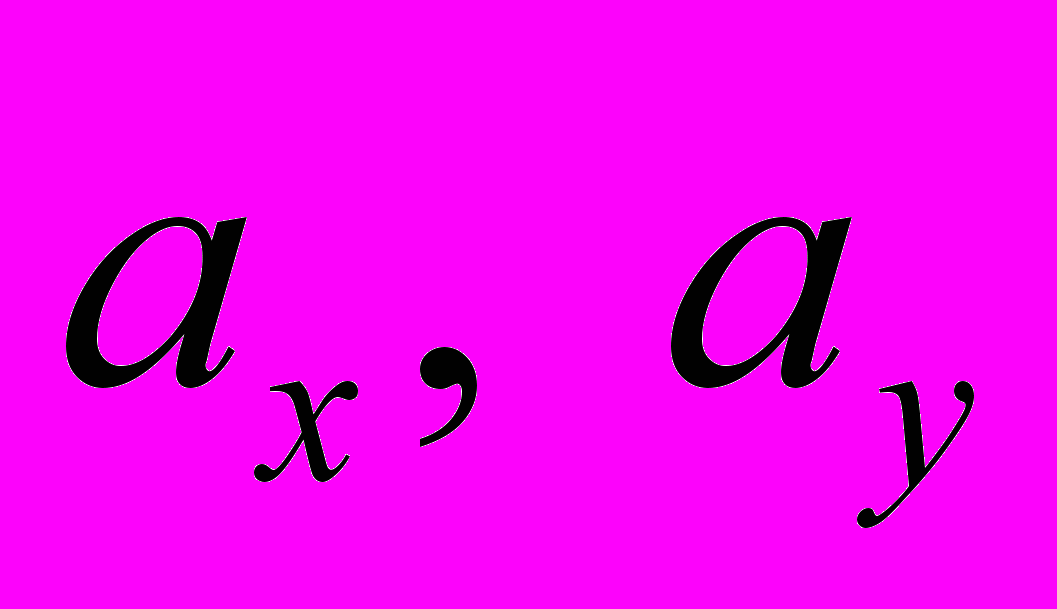- координаты центра изгиба; 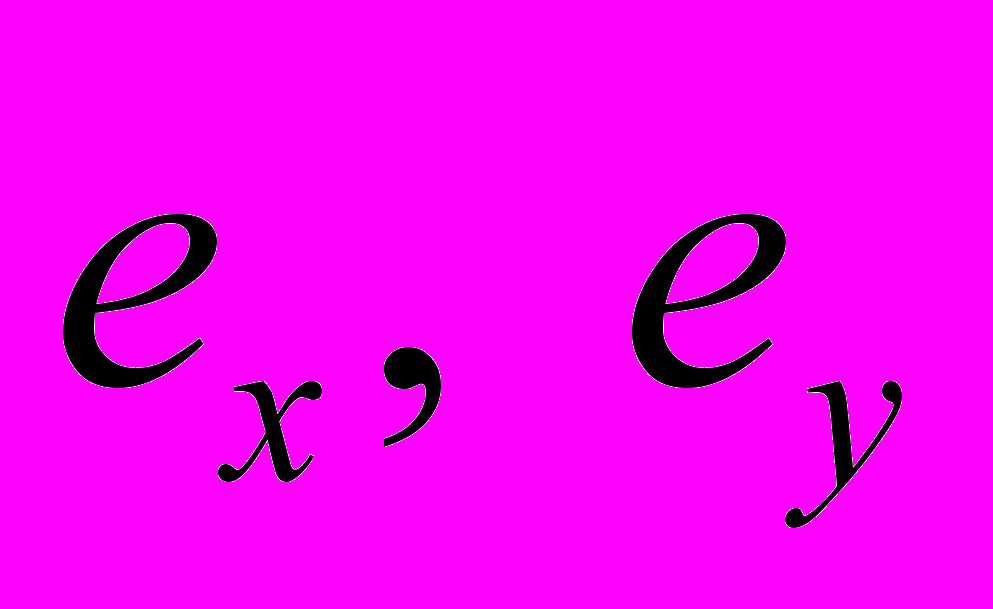- координаты точки приложения заданной погонной нагрузки в плоскости поперечного сечения; 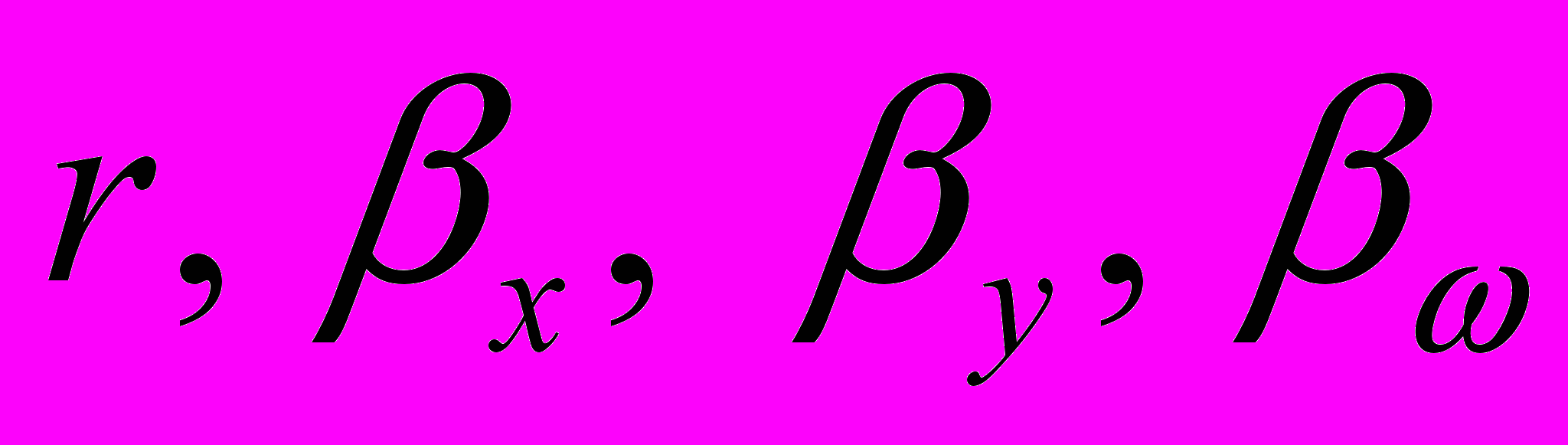-геометрические характеристики, определяемые по следующим формам:

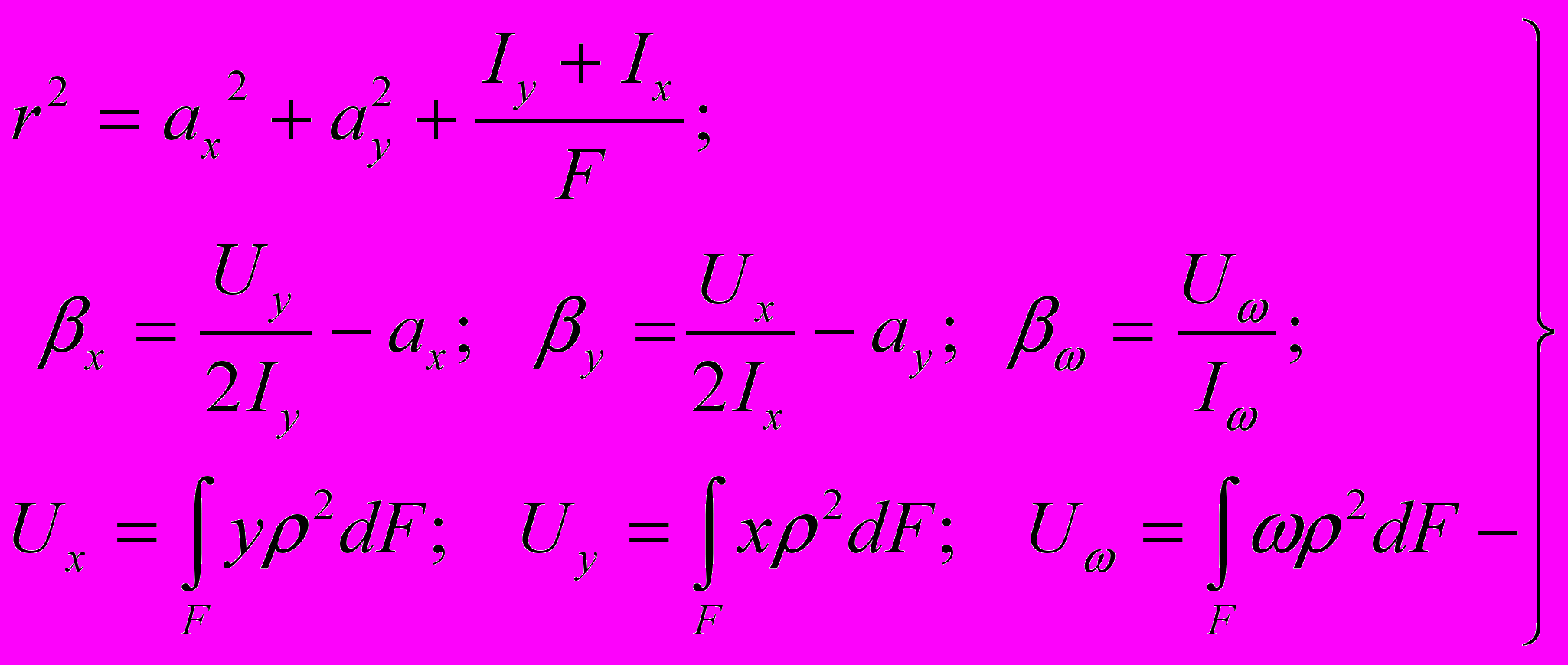(3)

где U_x, U_y, U_ω -полярно осевые и секториально-полярный моменты инерции;

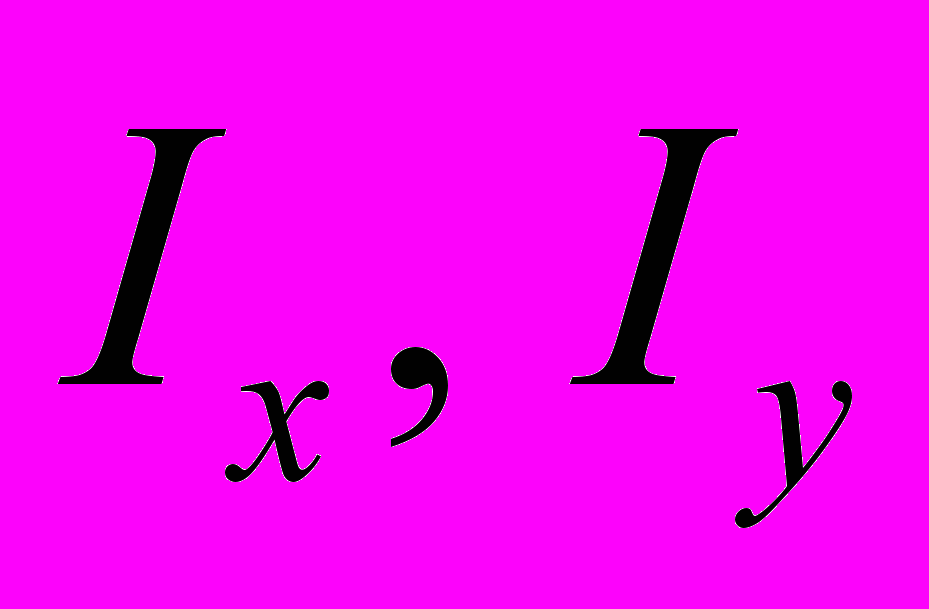- осевые моменты инерции; 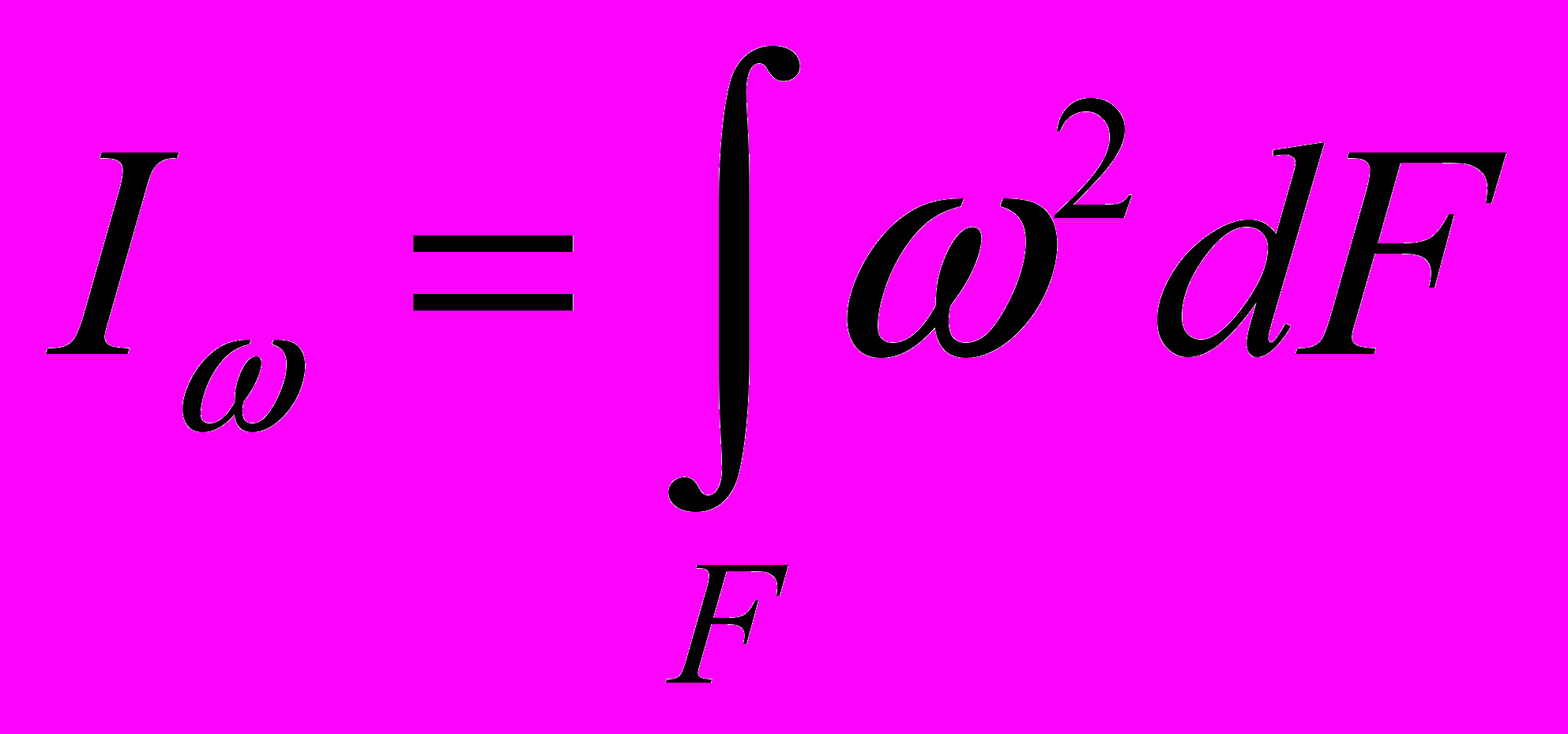- секториальный момент инерции; 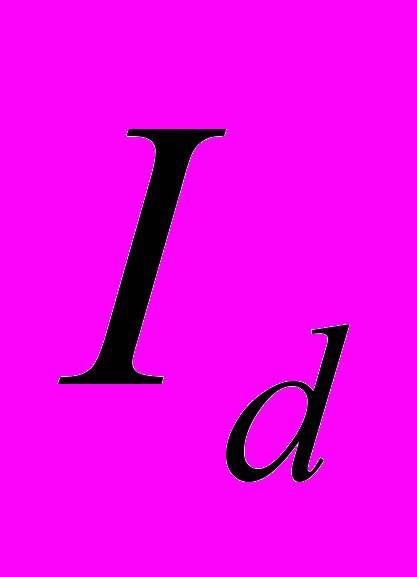- момент инерции чистого кручения.

Уравнения (2) являются наиболее общими уравнениями устойчивости тонкостенного стержня.

3.Модель тонкостенного стержня по А.П. Лещенко

На основе вариационного метода А.П. Лещенко получена новая система дифференциальных уравнений прочности тонкостенных стержней


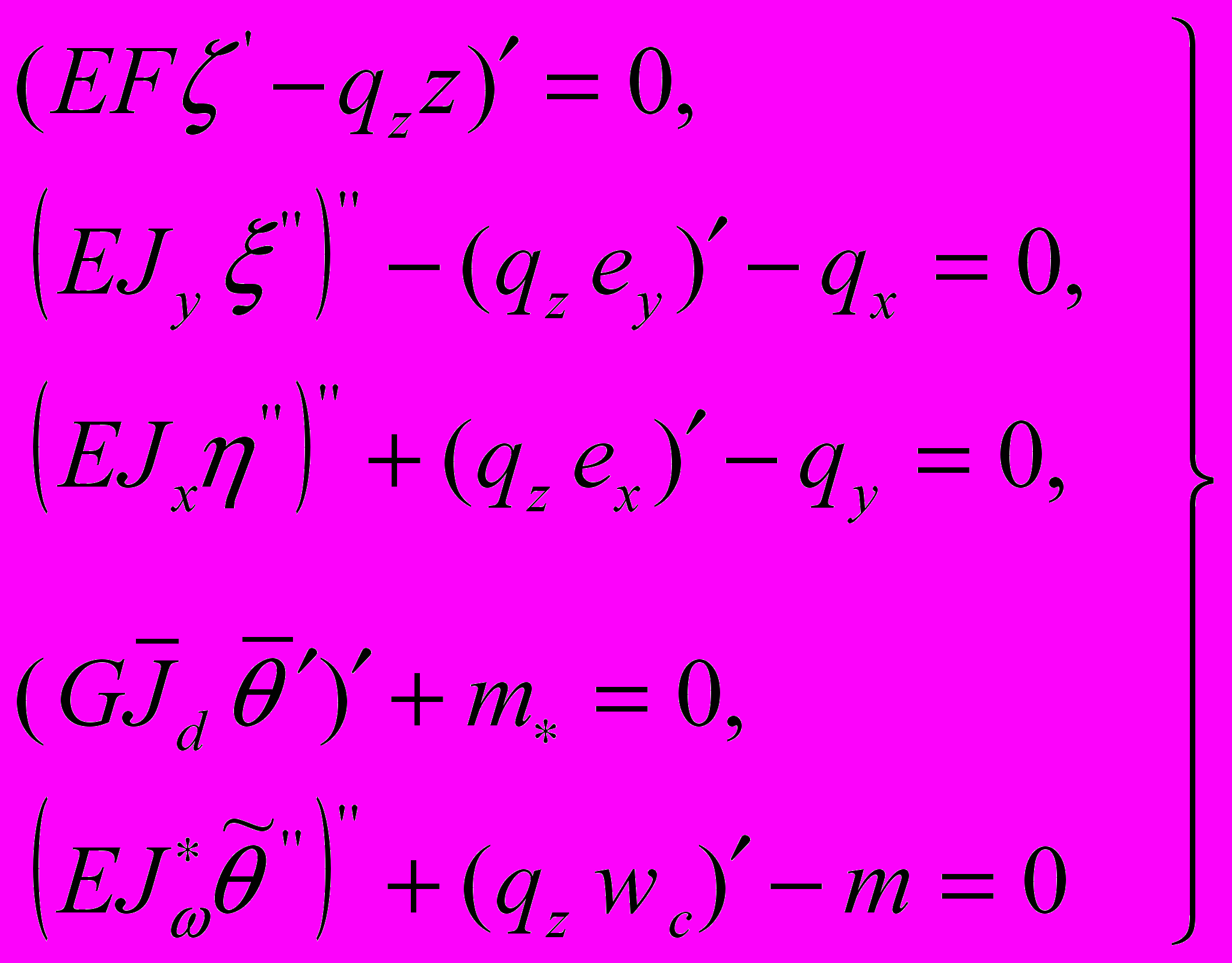(4)

Обозначения такие же, как в уравнении (2), отличием является разделение полного угла закручивания θ. Система дифференциальных уравнений (4) выведена в предположении, что угол закручивания тонкостенной конструкции состоит из суммы двух углов закручивания – угла кручения относительно центра чистого кручения 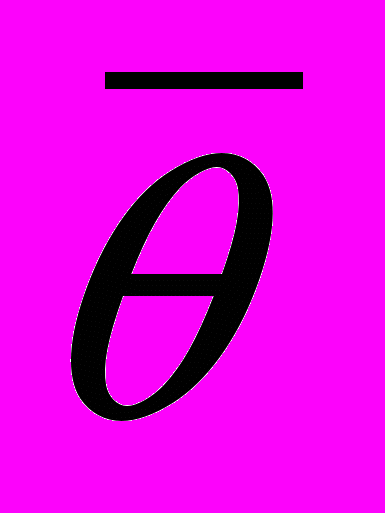и угла кручения относительно центра свободного кручения 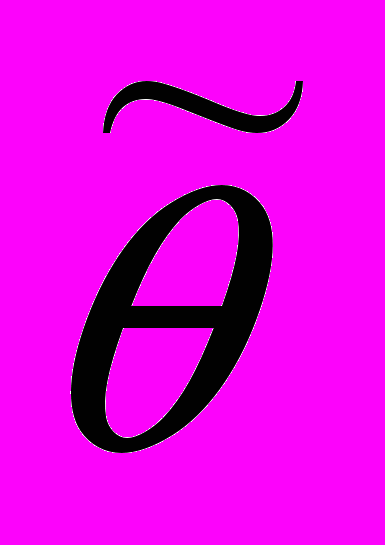, m – интенсивность крутящего момента относительно центра изгиба, m_*- интенсивность крутящего момента относительно центра тяжести сечения.

Модели жестких и гибких пластин, используемые в данной диссертации:

1. Техническая теория изгиба пластин основана на гипотезах Кирхгофа и предполагает отсутствие усилий в срединной плоскости, т.е. мембранные усилия равны нулю:

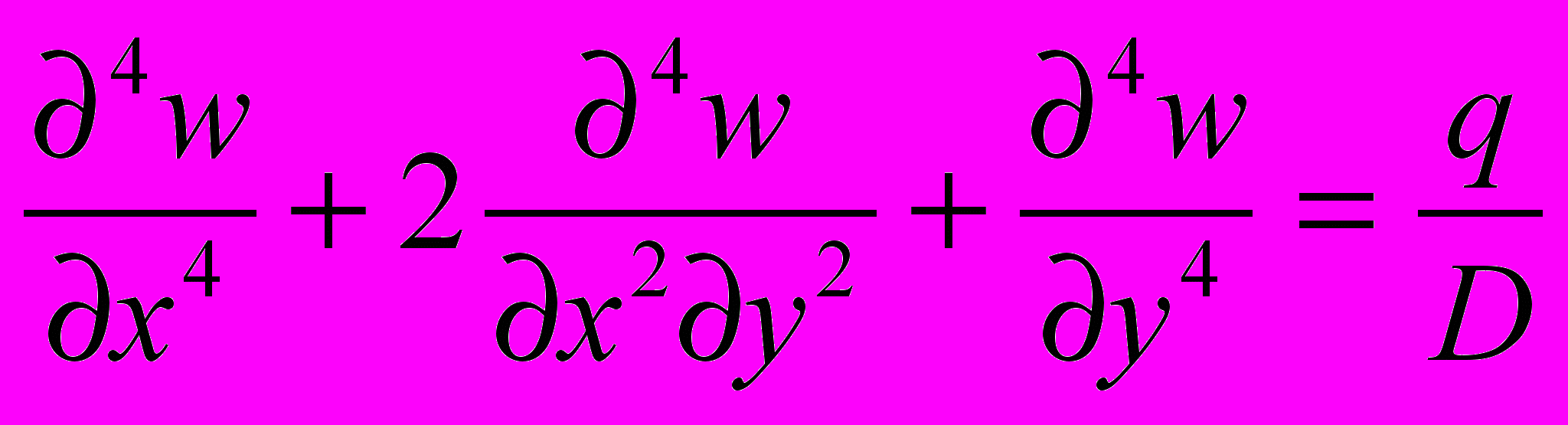(5)


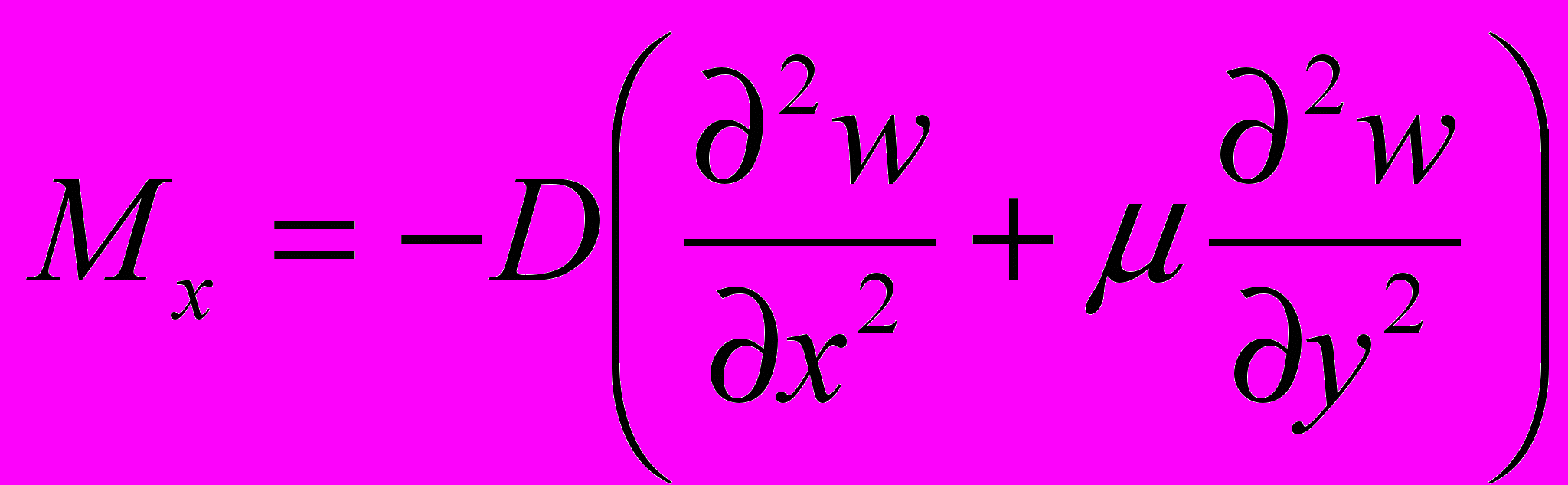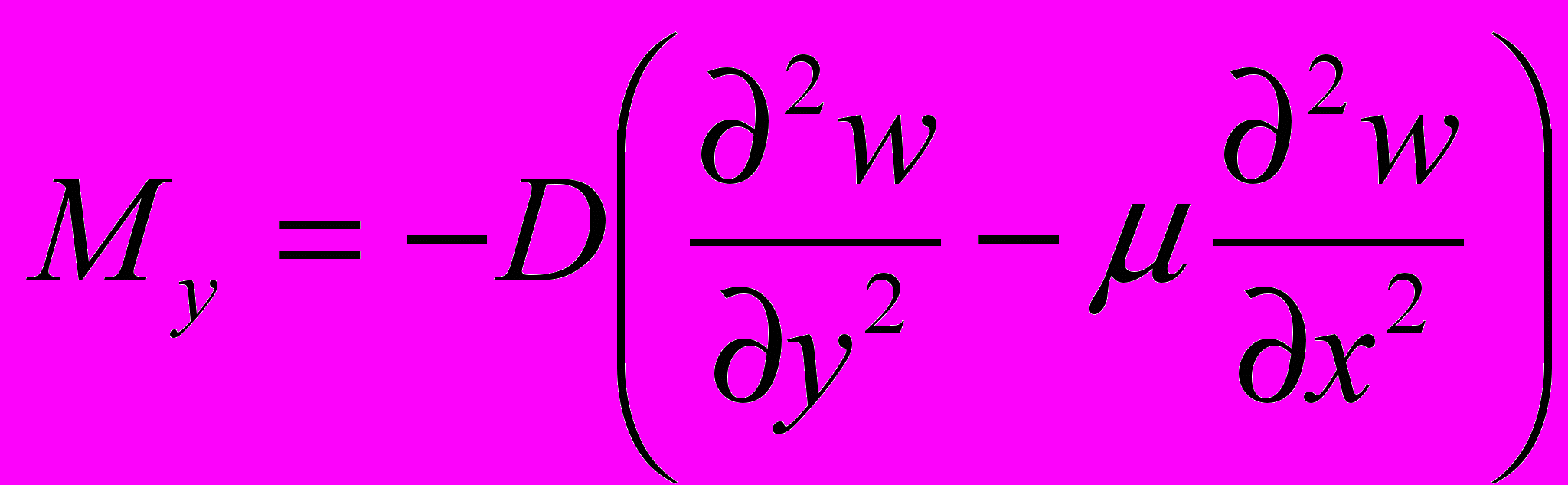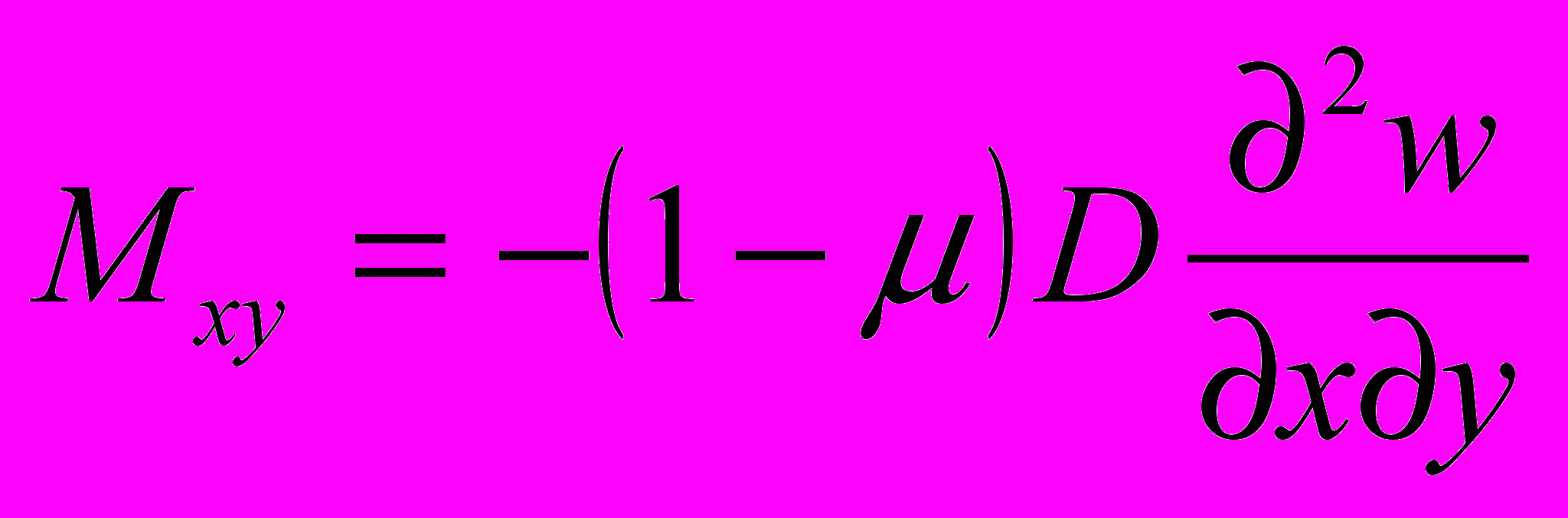, , (6)

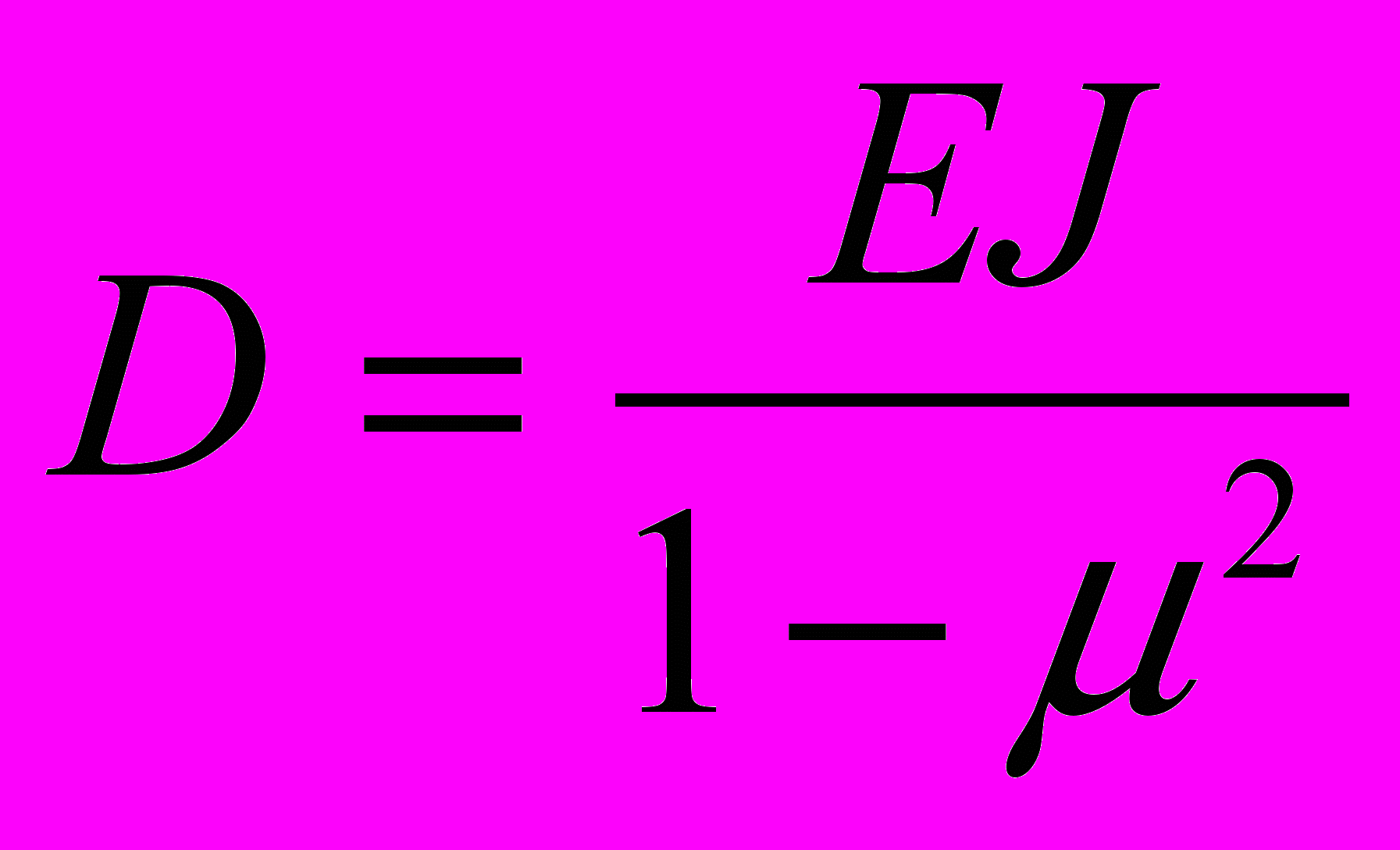, где w – прогиб пластины, q, - нормальная к срединной плоскости пластины нагрузка, μ- коэффициент Пуассона.

2. Уточненная теория изгиба пластин. Если по верхней и нижней поверхности пластины действуют касательные напряжения, то уравнения (6) можно учесть при изгибе через пары сил, равные произведению касательного усилия на плечо, равное половине толщины пластины. Эти уравнения учитывают контакт между слоями пластины или плиты с основанием. На основании технической теории в качестве исходных уравнений принимаем следующие:

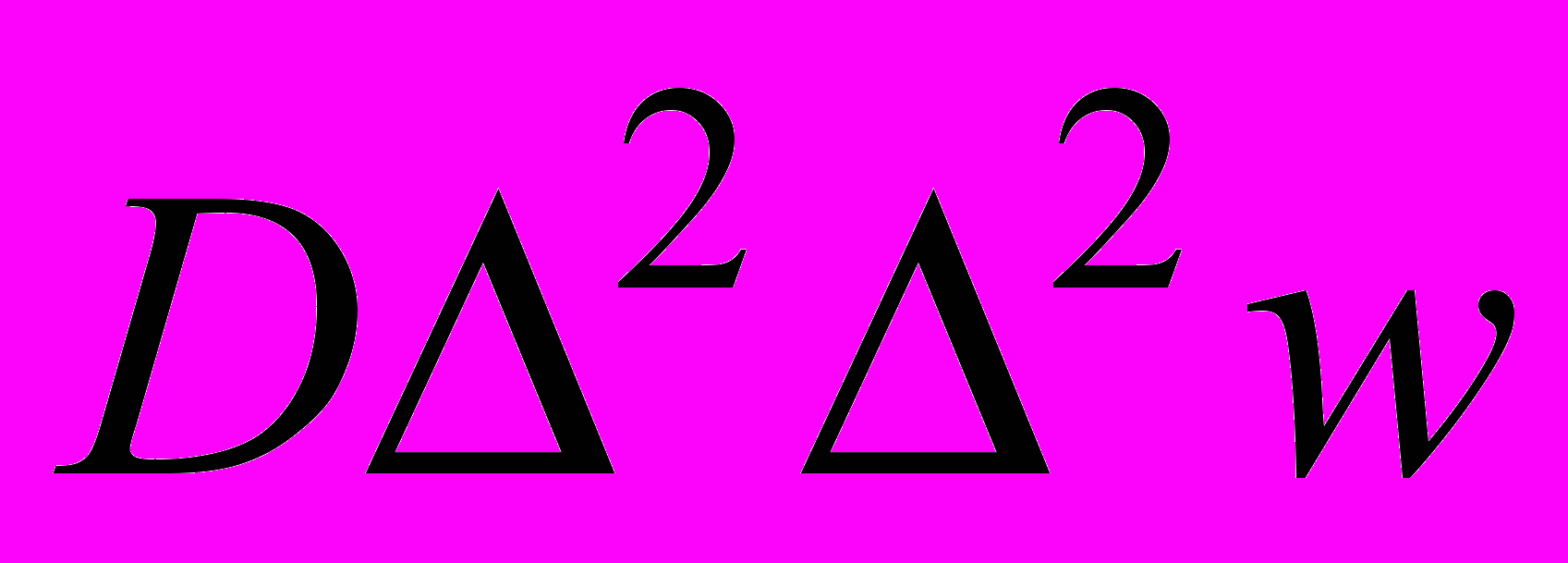-(P₃+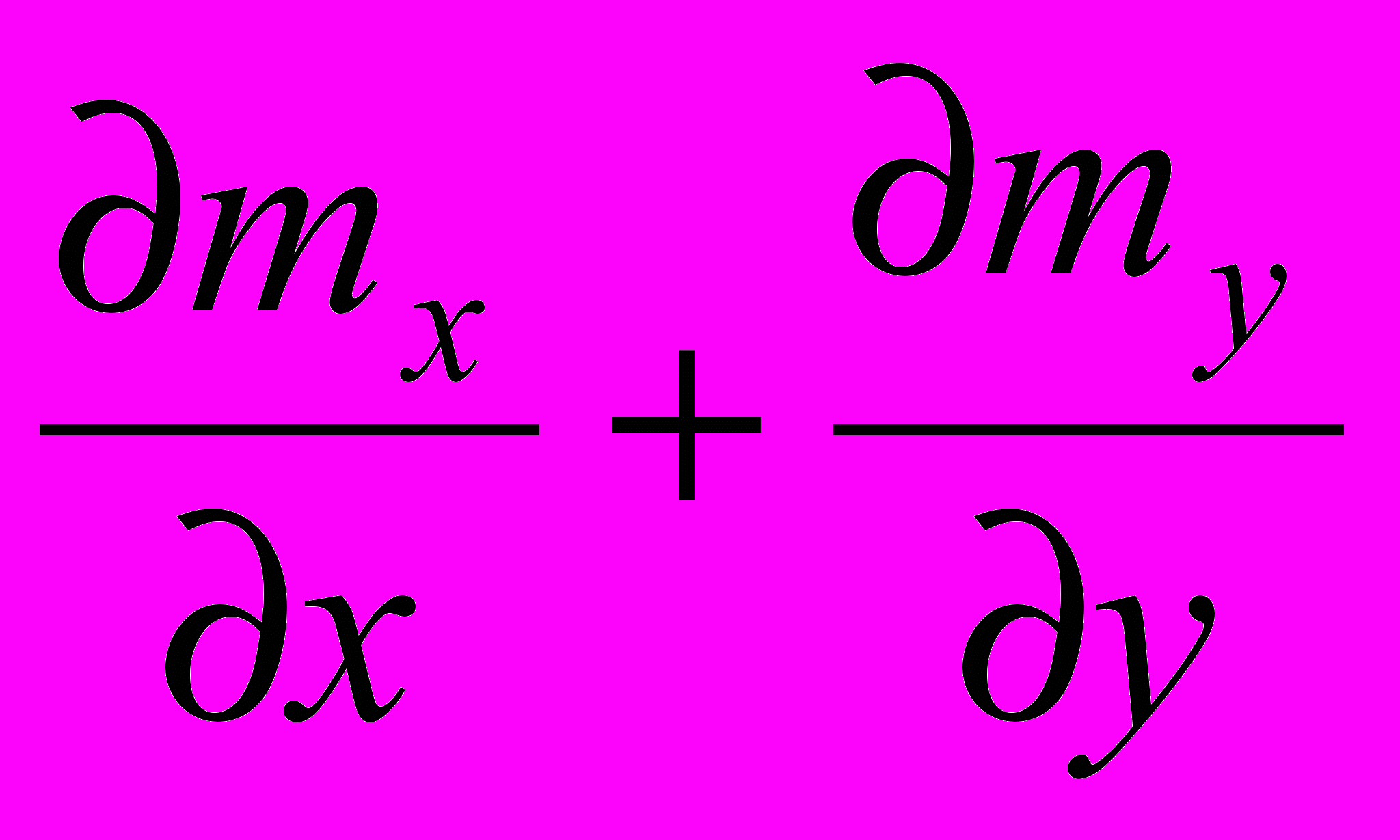) =0, (7)

где - нормальные перемещения, 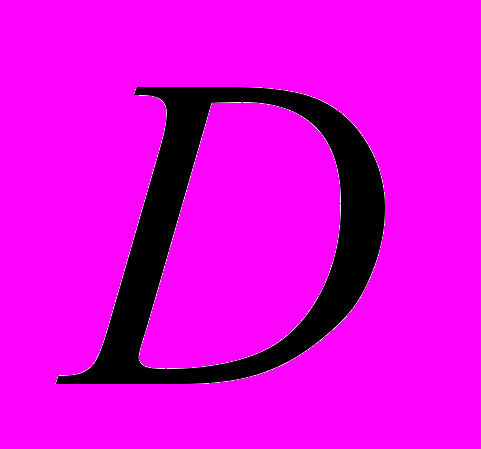- цилиндрическая жесткость, Е – модуль упругости оболочки, 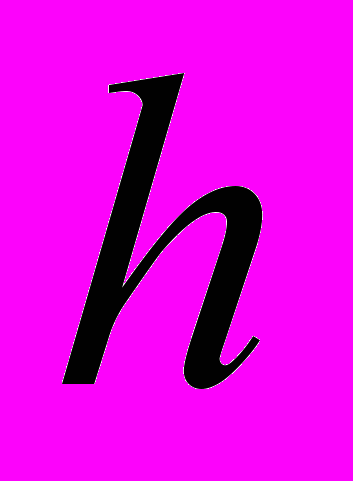- толщина оболочки, m_{x ,}m_y – внешние погонные моменты, создаваемые касательными напряжениями на поверхности.

3. Теория гибких пластин

При малых толщинах пластины, когда ее прогибы от поперечной нагрузки превышают 1/4 - 1/5 толщины, техническая теория дает искаженные результаты, и пластина должна рассматриваться как гибкая. Теория гибких пластин основывается на учете наряду с поперечным изгибом также и деформирования пластин в своей плоскости. Уравнения колебаний гибкой пластины в прямоугольной системе координат имеют вид:


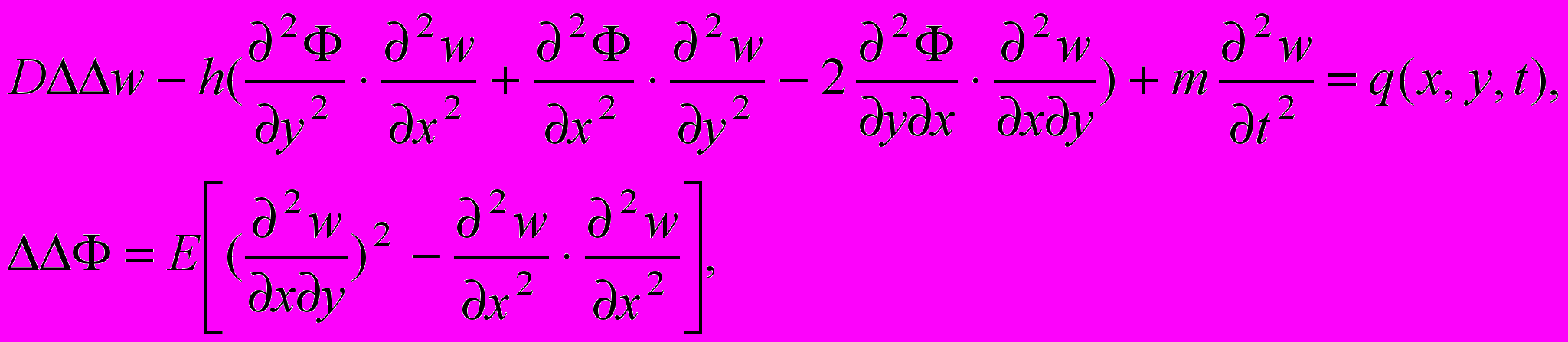(9)

где Ф – функция напряжений, связанная с напряжениями в срединной поверхности пластины дифференциальными зависимостями.

В (9) w – прогиб, Е- модуль упругости, h - толщина, q – интенсивность нормальной нагрузки, m – интенсивность внешнего изгибающего момента. Эти уравнения называются нелинейными уравнениями Кармана.

4. Модель пластины по А.П. Лещенко

А.П. Лещенко рассматривает плиту как совокупность отдельных тонкостенных полос - балок в двух направлениях, связанных между собой уравнениями совместности деформаций в точках контакта. Для этого плита разбивается на ряд полос в направлении осей Oz и Oy и рассматривается напряженно-деформированное состояние наиболее нагруженной полосы под действием факторов, учитывающих ее работу в теле плиты.

Воздействие плиты на полосу заменяется внешней нагрузкой подпора, распределенной по параболическому закону. Нагрузка подпора представляется в виде:

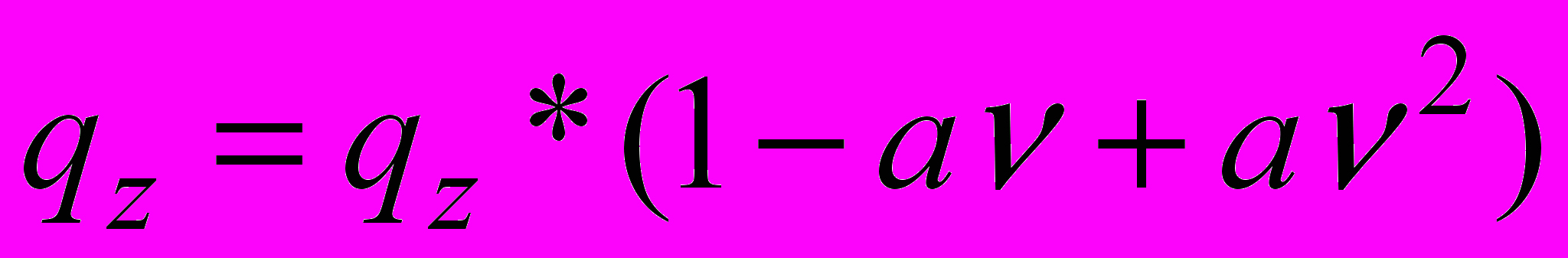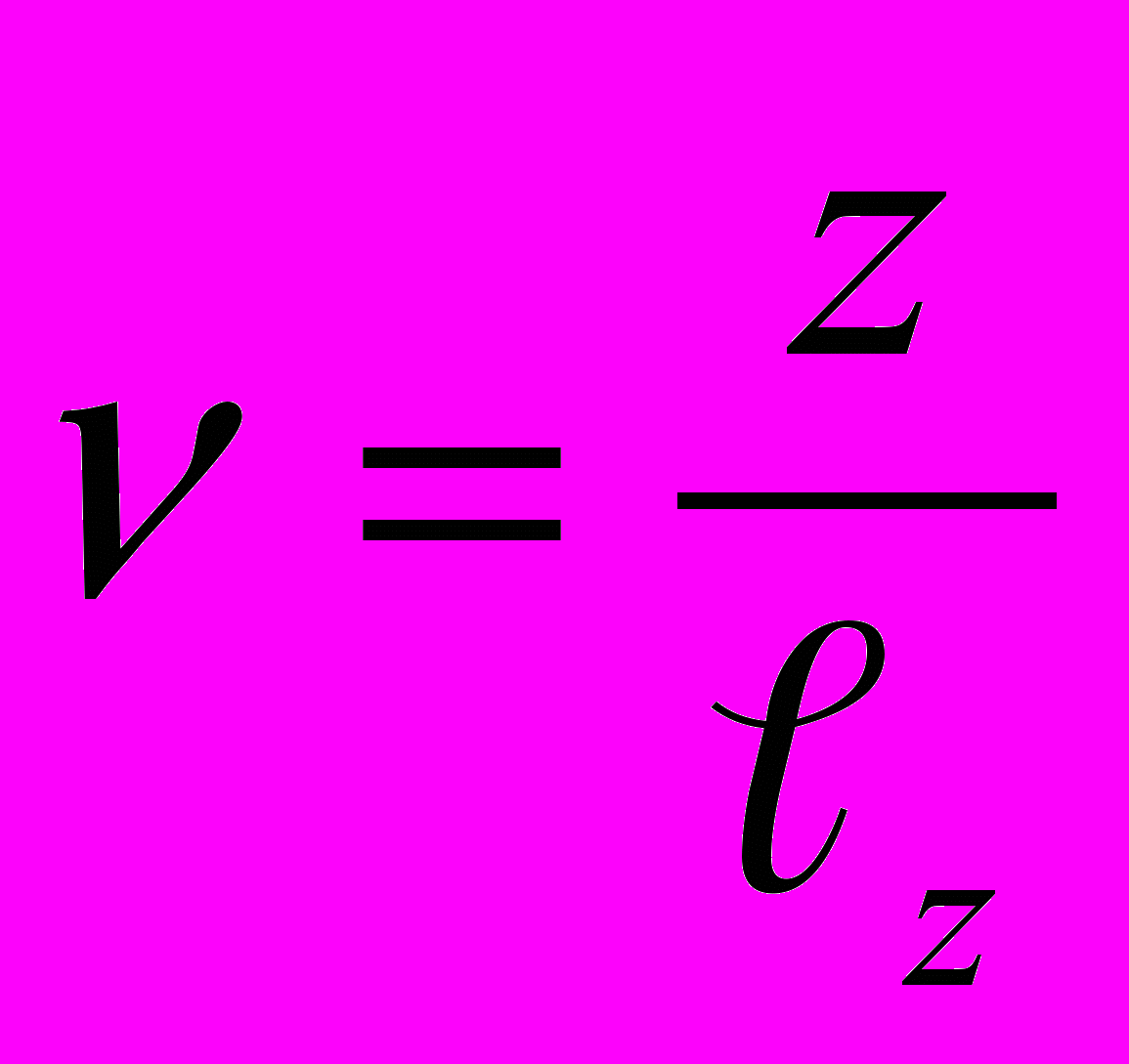, где (10)

В (10) величина «α» - неизвестный коэффициент, подлежащий определению.

Величина подпора определяется из условия равновесия вырезанной из плиты полосы- балки. Аналогично, рассматривается полоса в другом направлении, величина подпора в ней также представляется в виде уравнения (10), только с другим коэффициентом β. Последовательно рассматривая каждую полосу в двух направлениях, определяется напряженно-деформированное состояние плиты в целом. Расчет ведется от наиболее загруженного участка к менее загруженным, используя дельта функции и функции Хевисайда для сосредоточенных сил и разрывных параметров системы..

Основные модели для пологих оболочек, используемые в данной работе:

1. Теория пологих оболочек

Практические расчеты оболочек чаще всего связаны с нормальной составляющей внешней нагрузки Р₃ (собственный вес, полезная нагрузка, снег, и т.п.)_, поэтому, если положить Р₁=Р₂=0, то после преобразований получаем следующие основные уравнения теории пологих оболочек:

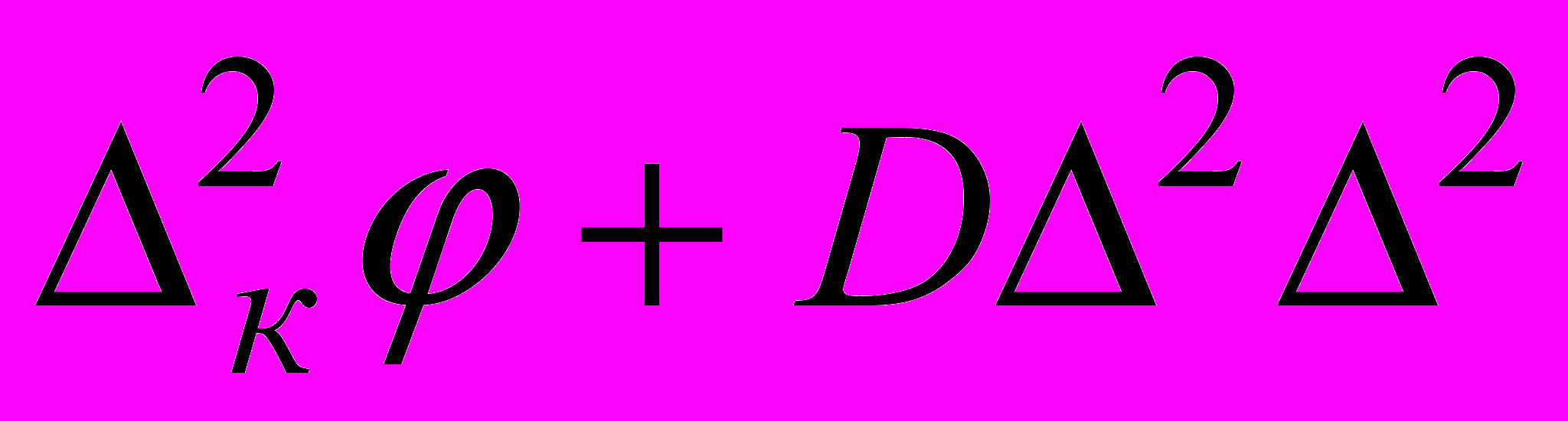w-(P₃ +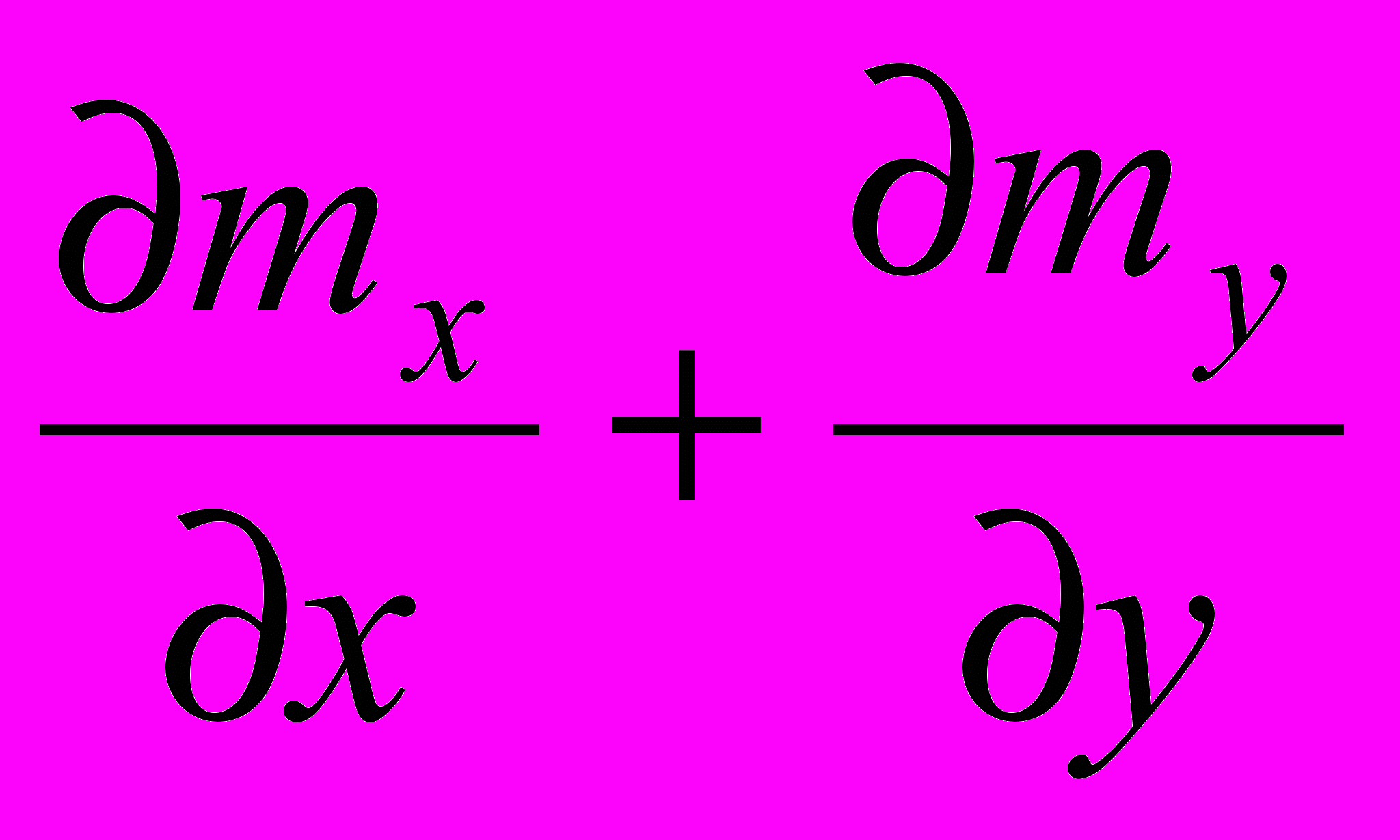) =0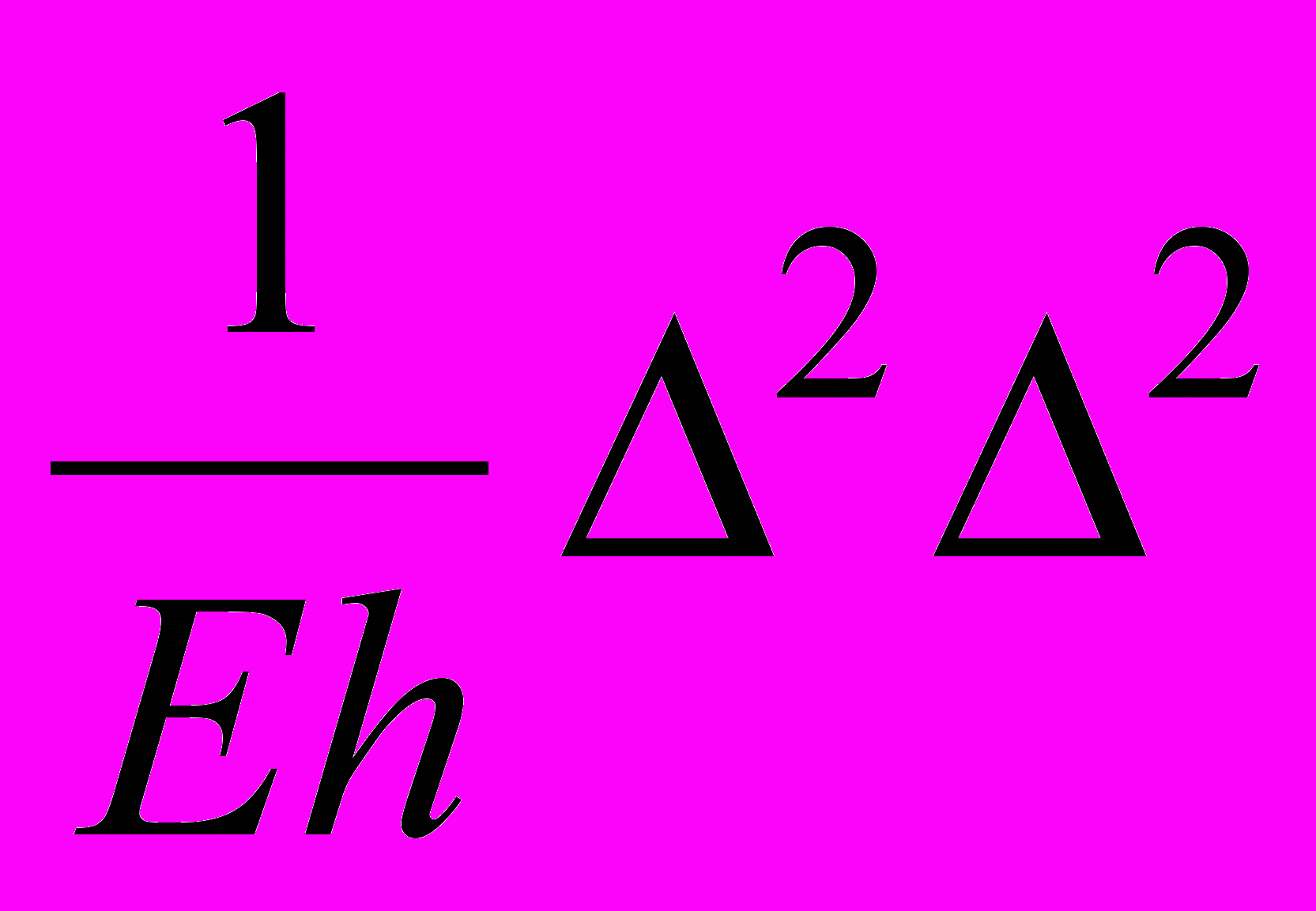

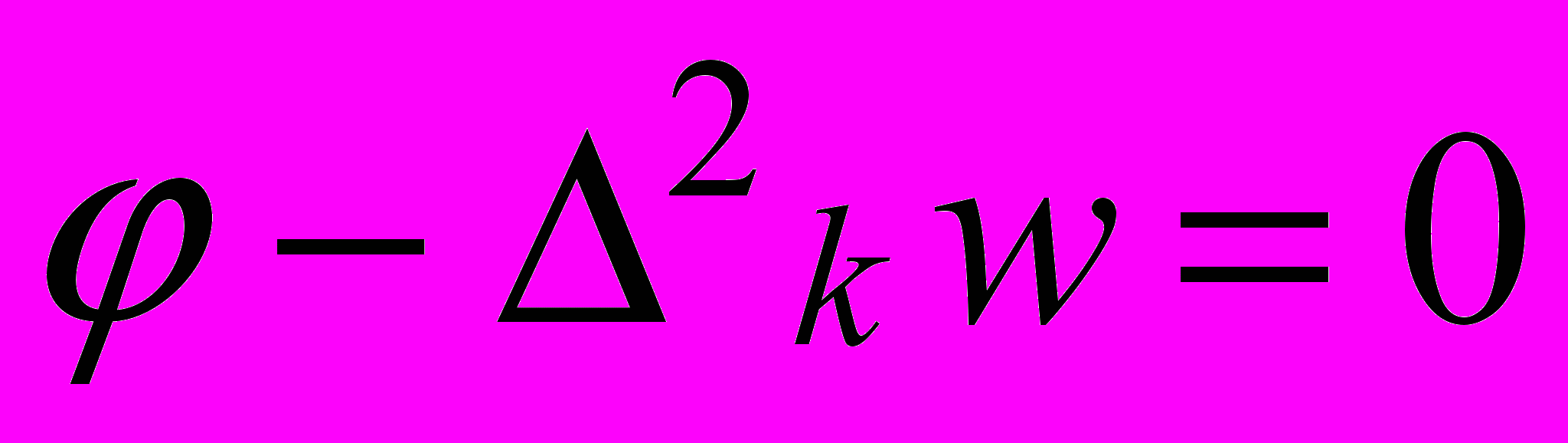, (11)

где 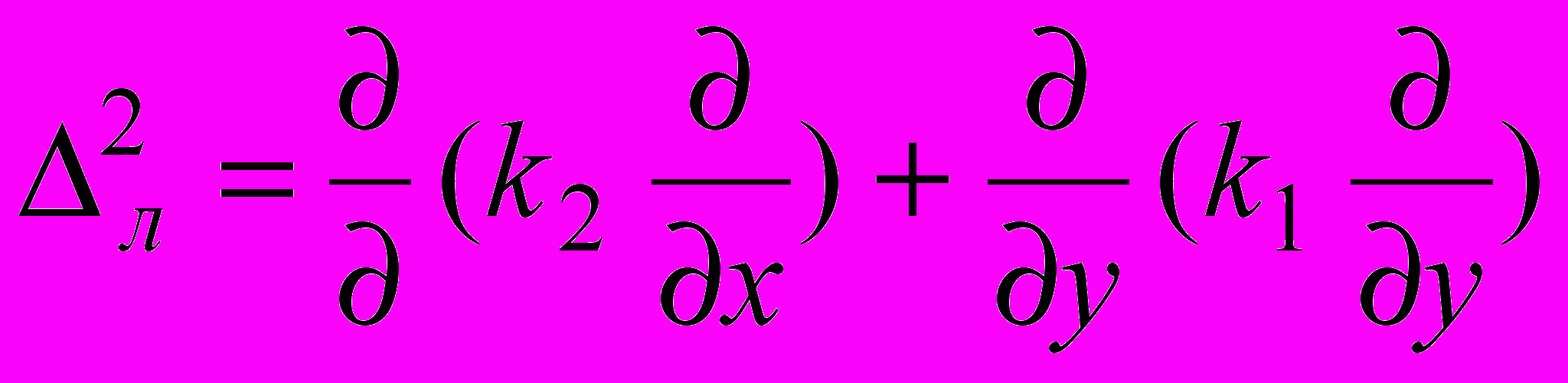, k₁, k₂ - главные кривизны оболочки. Если k₁, k₂ представляют собой постоянные величины, тогда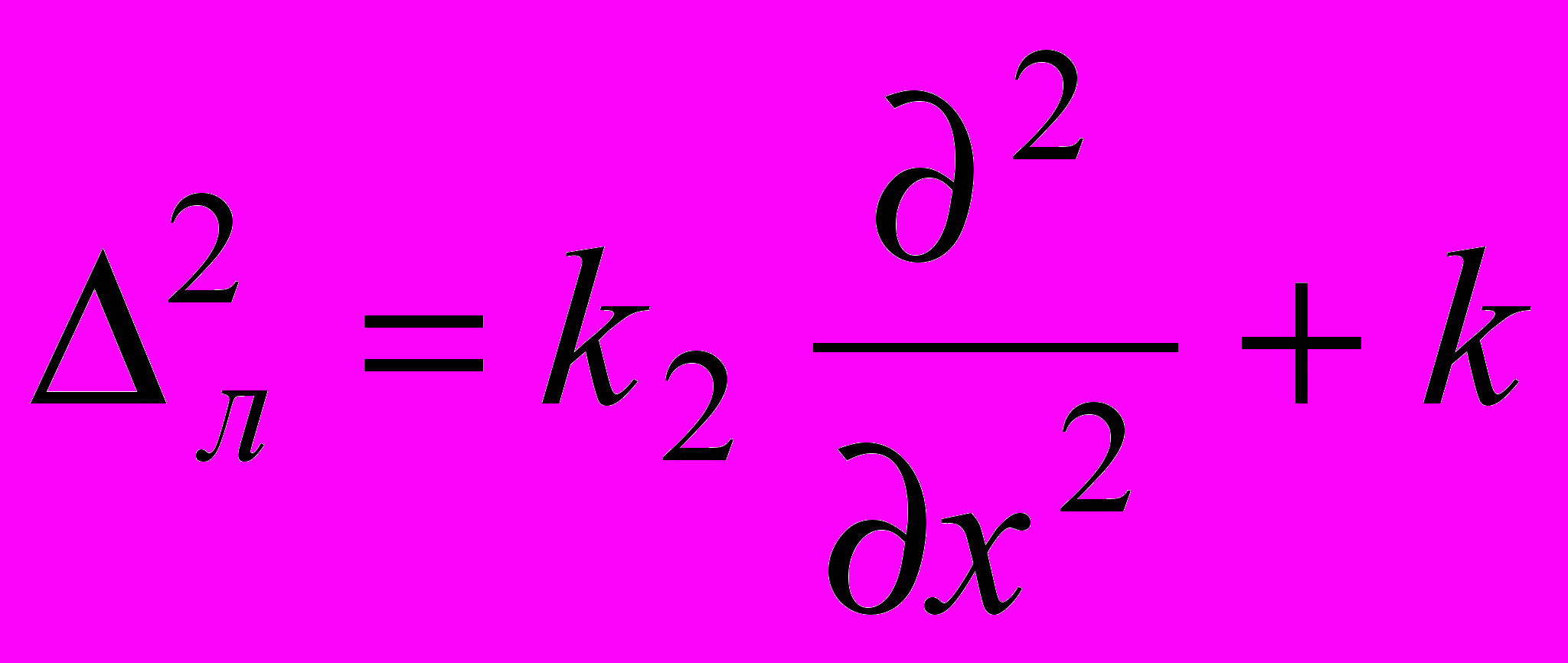

.

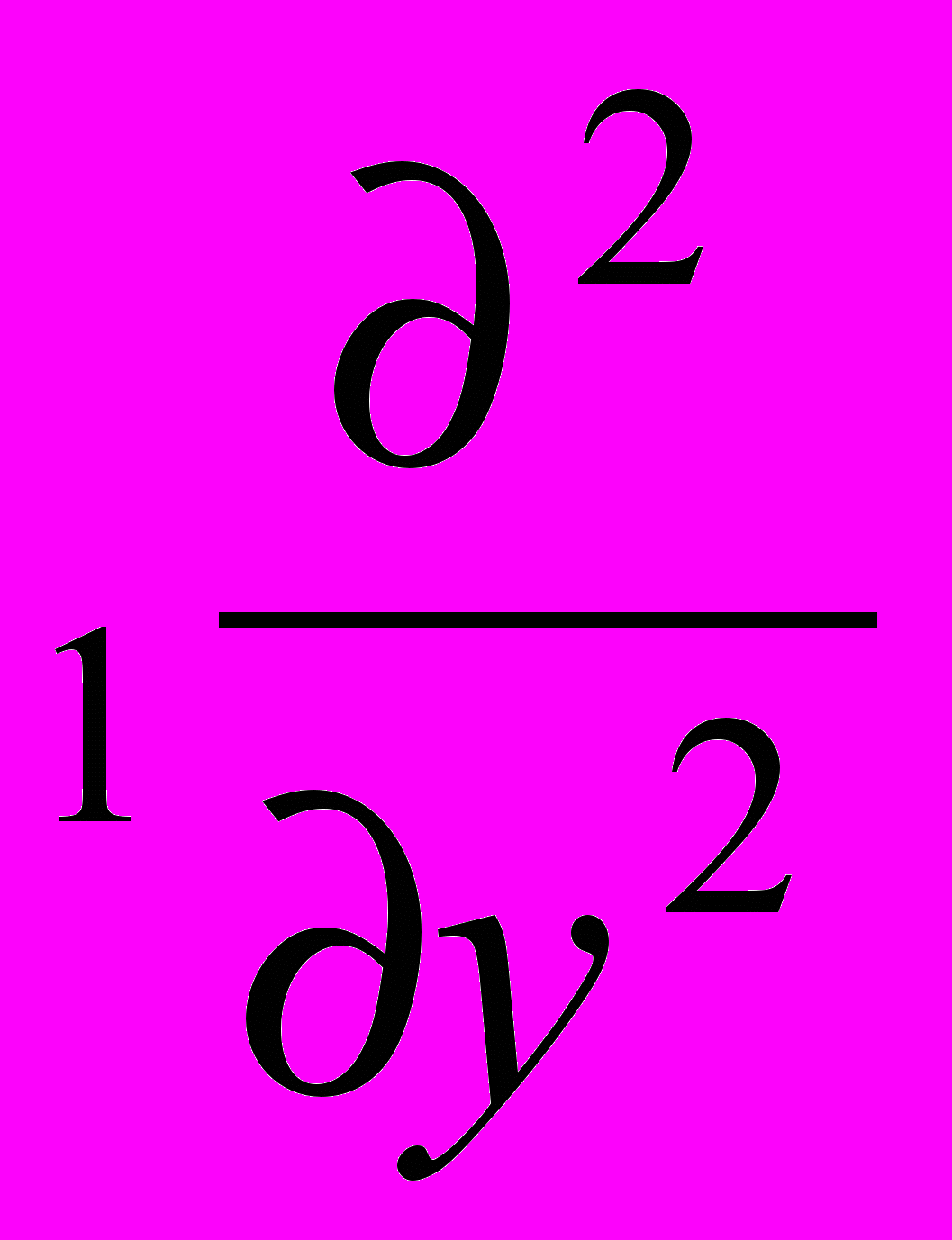Внутренние усилия определяются дифференциальными зависимостями

через функции напряжения и прогиба. Если одна из кривизны равна нулю, то оболочка преобразовывается в цилиндрическую поверхность.

2. Приближенные уравнения Донелла-Власова

Используя функции  и w для пологой оболочки с постоянными жесткостями на растяжение, изгиб и с постоянным коэффициентом Пуассона можно получить следующие разрешающие уравнения относительно неизвестных  и w:





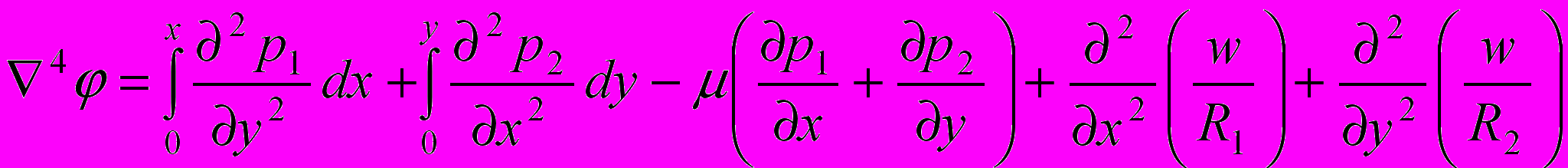
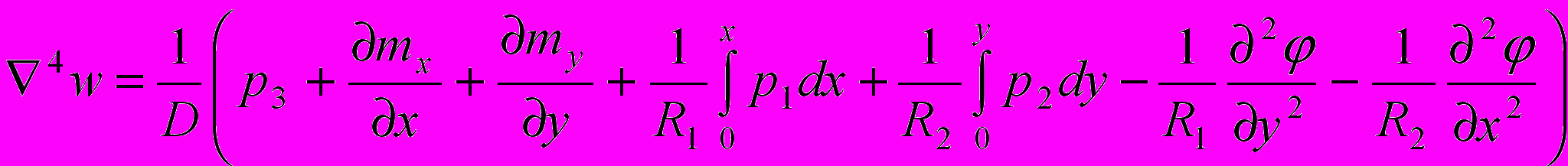
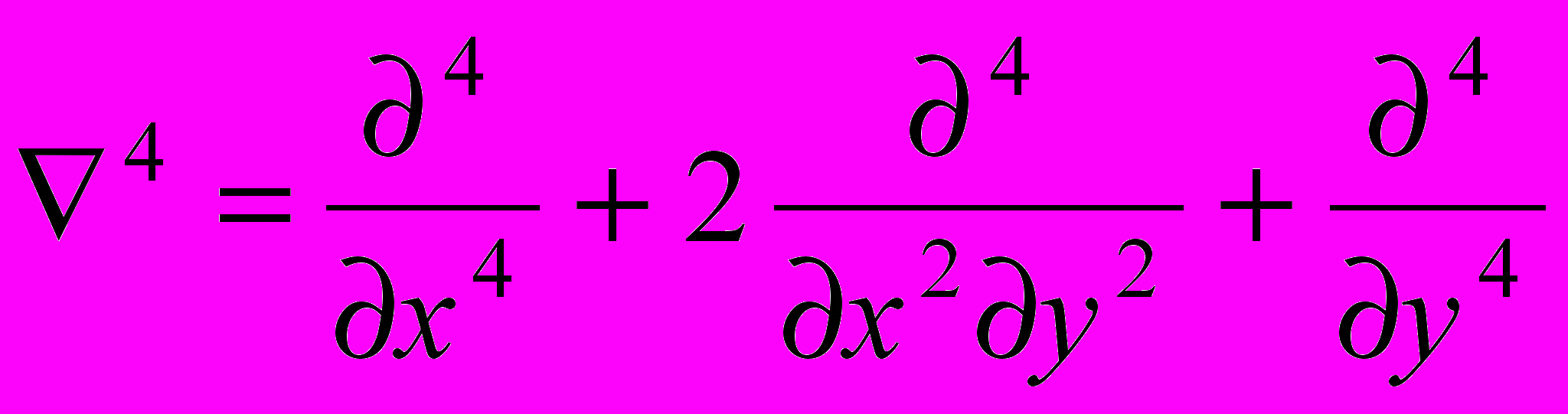(12)


В (12) w - прогибы оболочки, т.е. перемещения по нормали к срединной поверхности оболочки; р₁ , р_2, р₃ – внешняя нагрузка в направлении координатных осей х,у,z; R₁ , R₂ - радиусы кривизны оболочки в двух направлениях, D – цилиндрическая жесткости на изгиб; m_х , m_у – интенсивность внешних распределенных изгибающих моментов;

μ – коэффициент Пуассона.

Полагая одну кривизну, равной нулю, получаем основные уравнения для цилиндрической оболочки. Если две кривизны равны нулю, то получаем уравнения для пластины. По аналогии с гибкими пластинами можно представить нелинейные уравнения пологих оболочек.

3. Модель оболочки по А.П.Лещенко
   

Цилиндрическую оболочку А.П. Лещенко рассматривает как совокупность отдельных прямолинейных тонкостенных полос - балок в продольном направлении и криволинейных полос в окружном направлении, связанные между собой уравнениями совместности деформаций в точках контакта. Для этого оболочка разбивается на ряд прямолинейных и криволинейных полос в продольном и тангенциальном направлениях и рассматривается напряженно-деформированное состояние наиболее нагруженной полосы под действием факторов, учитывающих ее работу в теле оболочки. Воздействие оболочки на полосу заменяется внешней нагрузкой подпора, распределенной по параболическому закону, аналогично (10). Величина подпора определяется из условия равновесия вырезанной из оболочки полосы - балки или криволинейного элемента. Последовательно рассматривая каждую полосу в двух направлениях, определяется напряженно-деформированное состояние оболочки в целом. Расчет ведется от наиболее загруженного участка к менее загруженным, используя дельта функции и функции Хевисайда для сосредоточенных сил и разрывных параметров системы..

Во втором разделе приведены расчеты тонкостенного стержня по методу А.П.Лещенко для 2-х задач: 1. изгиб с кручением двутавровой балки под действием силы, приложенной в середине пролета;

2. металлическая балка -образного сечения при одновременном действии поперечной и внецентренно приложенной сил.

Рассмотрена модель А.П. Лещенко с учетом деформируемости контура, сделан расчет и проведено сравнение с решением по теории В.З.Власова.

Нормальные и касательные напряжения определяются по следующим формулам:

,

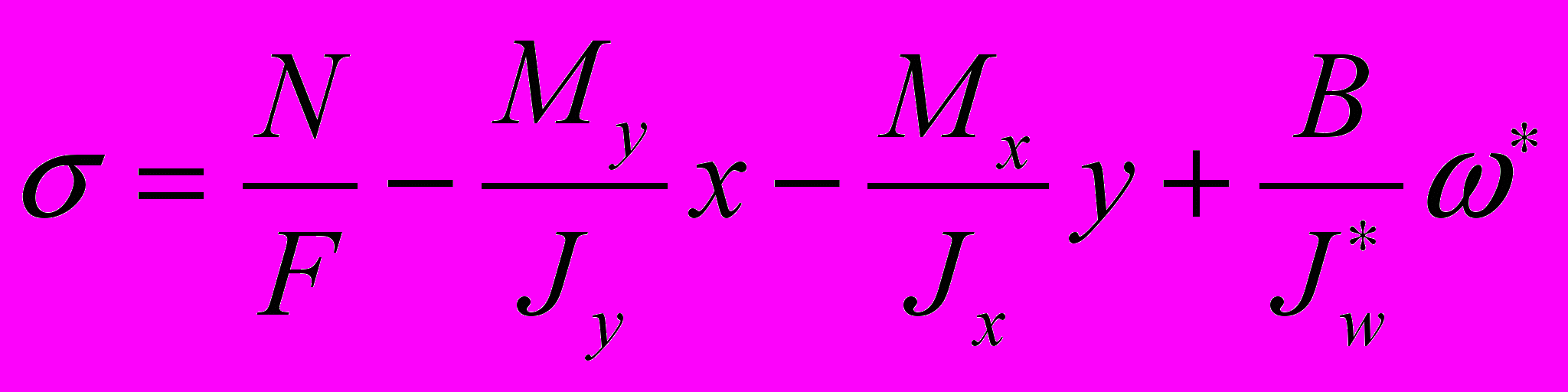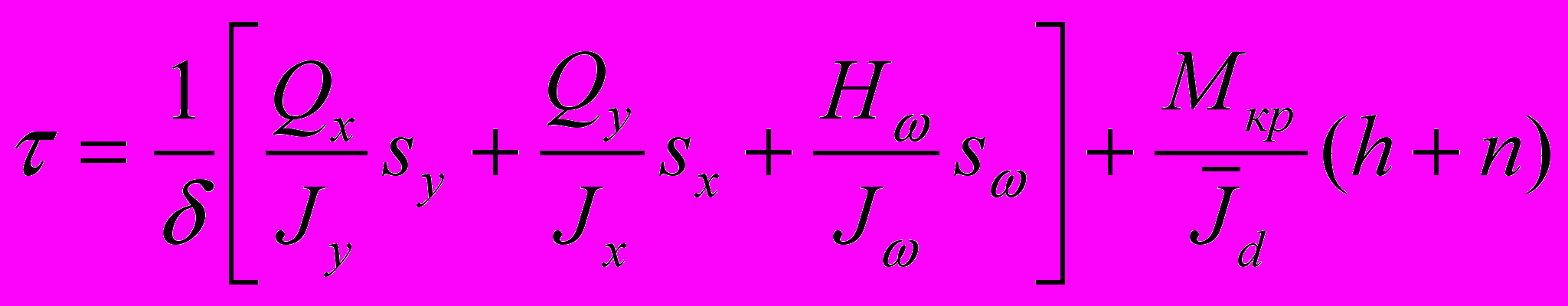, (13)


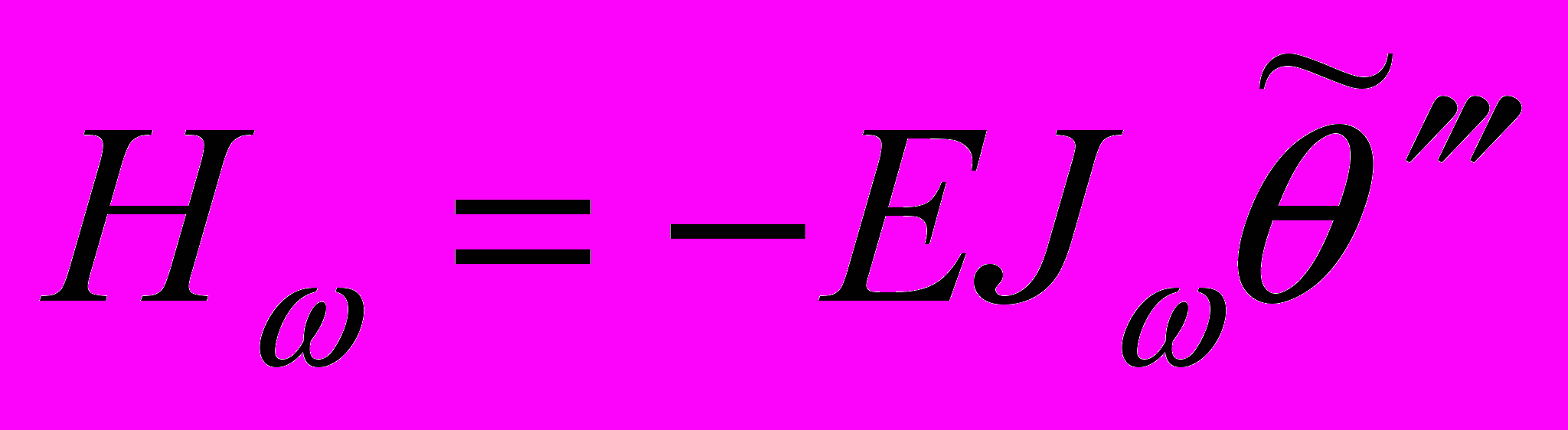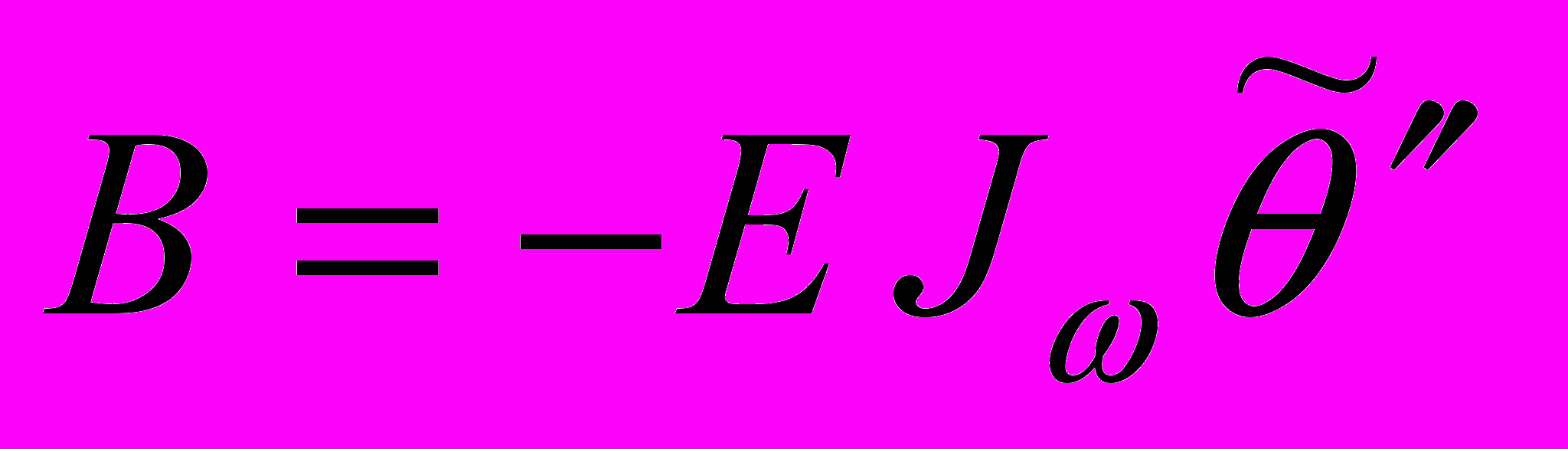где , и - бимомент

В таблице 1 приведены значения максимальных нормальных и касательных напряжений для случая - образного сечения. Рассмотрены расчеты на прочность железобетонной плиты и пологой цилиндрической оболочки в упругой стадии работы. Оболочка подкреплена ребрами в продольном направлении, сделаны расчеты при различных отношениях стрелы подъема к толщине, для плит рассматриваются перекрестные ребра в двух направлениях. Количество полос варьируется, достаточно хорошая сходимость для выбранных систем обеспечивается при делении оболочки в продольном направлении на 8 элементов, в тангенциальном на 4, для плит общее количество полос равно 10.


Таблица 1- Значения максимальных нормальных и касательных напряжений

Макс. напряжения	Данная методика [кг/см2]	Теория Власова [кг/см2]	Расхождения в %
σ	1423	1510	5,6
τ	76,7	82,2	6,8

Для оболочки рассматриваются два случая загружения (Рисунок 1):

а) б)








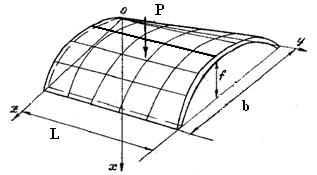
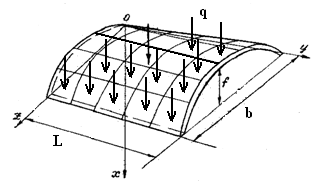
Рисунок 1- Схемы загружения пологой цилиндрической оболочки

В качестве внешней нормальной нагрузки q, действующей на оболочку, рассматривается его собственный вес.

Рассматриваются различные варианты закрепления оболочки по краям:

1) 4 края шарнирно опертые, т.е. прогибы и изгибающие моменты по краям равны нулю.

2) Два края защемлены (z=0,z=b); два другие края вдоль оси z шарнирно опертые.

3) Все края защемлены.

Задача о прочности тонкой, пологой цилиндрической оболочки, шарнирно – опертой по контуру и загруженной равномерно распределенной нагрузкой q была решена по аналогичной методике. В силу симметрии системы для численного расчета зафиксированы следующие точки в срединной поверхности (Рисунок 2).




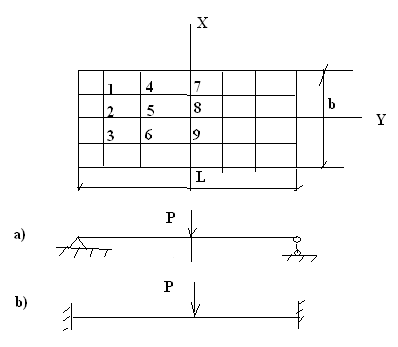
Рисунок 2- Срединная плоскость, a) шарнирное

опирание, b)заделка с двух сторон


Аналогично рассматривается пластина для двух случаев нагружения (Рисунок 3):

а) б)






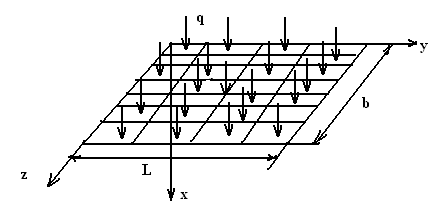
Рисунок 3- Схема загружения плит


Рассмотрены различные варианты закрепления плиты.

В таблицах 2-6 представлены некоторые результаты расчета. В таблице 2 представлены усилия в гладкой цилиндрической панели, шарнирно опертой по всем краям при действии сосредоточенной силы


Таблица 2 - Усилия в гладкой цилиндрической панели, шарнирно опертой по всем краям при действии сосредоточенной силы

№ точки	w10-2 [м]	Мх103[кгм]	Му103 [кгм]	Q1 [кг]	Q2 [кг]
1	0,12	0,010	0,058	10,85	8,14
2	0,16	0,013	0,112	16,77	2,11
3	0,11	0,010	0,056	10,85	-8,14
4	0,29	0,097	0,131	15,00	23,43
5	0,19	0,11	0,250	37,23	4,33
6	0,215	0,097	0,131	5,67	-23,43
7	0,28	0,333	0,123	4,87	41,7
8	0,32	0,46	0,58	2,45	2,11
9	0,28	0,22	0,123	4,87	41,7

При наличии 1 го центрального ребра в направлении оси у и 1-го центрального ребра в кольцевом направлении значения прогибов и внутренних усилий уменьшаются. Их значения представлены в таблице 3.

Таблица 3- Усилия в ребристой цилиндрической панели, шарнирно опертой по всем краям

№ точки	w10-2 [м]	Мх103[кгм]	Му103 [кгм]	Q1 [кг]	Q2 [кг]
1	0,11	0,009	0,055	10,45	8,12
2	0,14	0,013	0,11	16,17	2,00
3	0,11	0,011	0,053	10,28	-8,01
4	0,25	0,094	0,126	14,00	23,13
5	0,17	0,10	0,243	47,23	4,13
6	0,19	0,095	0,128	3,67	-22,43
7	0,24	0,32	0,118	2,87	38,7
8	0,30	0,44	0,550	1,23	1,11
9	0,26	0,20	0,115	2,55	31,7

В таблице 4 представлены значения перемещений, изгибающих моментов, поперечных сил в двух направлениях для гладкой плиты, шарнирно опертой по всем краям.


Таблица 4 -Усилия в гладкой плите, шарнирно опертой по всем краям

№ точки	w10-2 [м]	Мх103[кгм]	Му103 [кгм]	Q1 [кг]	Q2 [кг]
1	0,32	0,03	0,175	32,56	24,42
2	0,48	0,04	0,30	50,32	0
3	0,32	0,03	0,175	32,56	-24,42
4	0,89	0,19	0,32	45,14	70,30
5	0,58	0,3	0,75	111,0	0,0
6	0,64	0,19	0,32	45,14	-70,3
7	0,85	0,65	0,37	0	125,0
8	0,93	1,32	1,75	0	0
9	0,85	0,65	0,37	0	-125,0

Для случая равномерно распределенной нагрузки в таблице 5 показаны значения максимальных прогибов, соответствующих точке в середине пролета оболочки для различных значений отношения высоты подъема к толщине оболочки при различных значениях жесткости ребра (I_p –момент инерции сечения ребра) для случая шарнирного опирания оболочки по всем краям. Сделаны многовариантные расчеты для других случаев опирания.

Таблица 5- Значения прогибов w 10^-2 [м] для центральной точки оболочки

Ip 10- 4 [м4]	f/h=1		f/h=5
	По данной работе	По теории Власова	По данной работе	По теории Власова
0(гладкая оболочка)	3,5	4,02	0,61	0,70
1,33	1,6	2,56	0,55	0,63
6,66	0,48	0,55	0,32	0,36
13,3	0,27	0,31	0,22	0,25

В таблице 6 приведены значения максимальных нормальных напряжений для оболочки шарнирно опертой по всем краям, как менее жесткой в сравнении со случаем жесткого защемления.


Таблица 6 - Значения максимальных нормальных напряжений σ [кг/см²] для центральной точки оболочки

Ip 10- 4 [м4]	f/h=1		f/h=5
	По данной работе	По теории Власова	По данной работе	По теории Власова
0 (гладкая оболочка)	61,66	69,49	12,33	13.98
1,33	-48,23	-53,05	-0,24	-0,28
6,66	-51,66	-58,58	-20,66	-24,43
13,3	-53,87	-61,60	-24,50	-28,46
15,00	-56,17	-63,45	-28,75	-31,72

Из таблицы 6 видно, что в гладкой оболочке в центре возникают растягивающие усилия, которые в дальнейшем воспринимаются арматурой; при наличии одного ребра в центре возникают сжимающие напряжения, удовлетворяющие условию прочности для железобетона; относительно деформации из таблиц 3-5 видно, что наибольшие прогибы возникают в гладкой оболочке; с увеличением высоты подъема прогибы резко уменьшаются; с увеличением жесткости ребра напряжения уменьшаются как по данной методике, так и по теории В.З.Власова. Усиление граничных условий приводит к уменьшению напряжений и деформации в оболочке.

Аналогичные выводы и анализы сделаны для железобетонной плиты.

В третьем разделе рассматривается устойчивость тонкостенных стержней. Используя модель А.П.Лещенко с учетом деформируемости контура сечения, рассмотрены следующие задачи (Рисунок 4-7):

1. Внецентренно сжатый стержень (Рисунок 4); 2. Потеря устойчивости, связанная с появлением кручения и изгибом в другой плоскости (Рисунок 5); 3. Действие поперечной нагрузки с эксцентриситетом (Рисунок 6); 4. Потеря устойчивости при чистом изгибе (Рисунок 7).




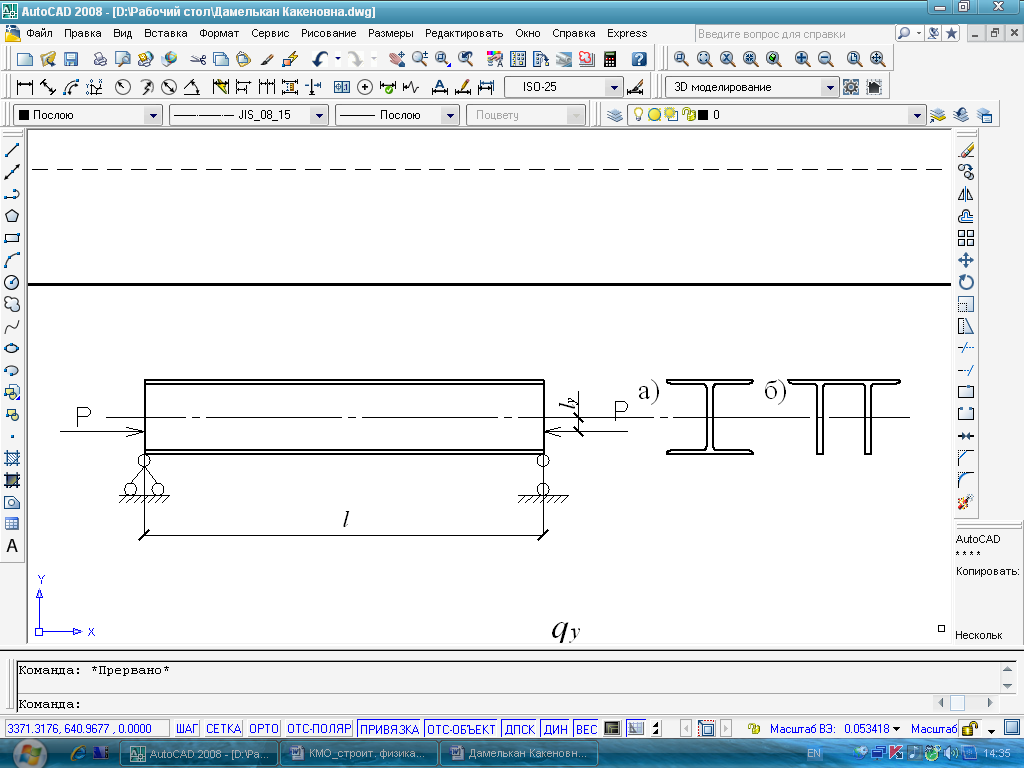
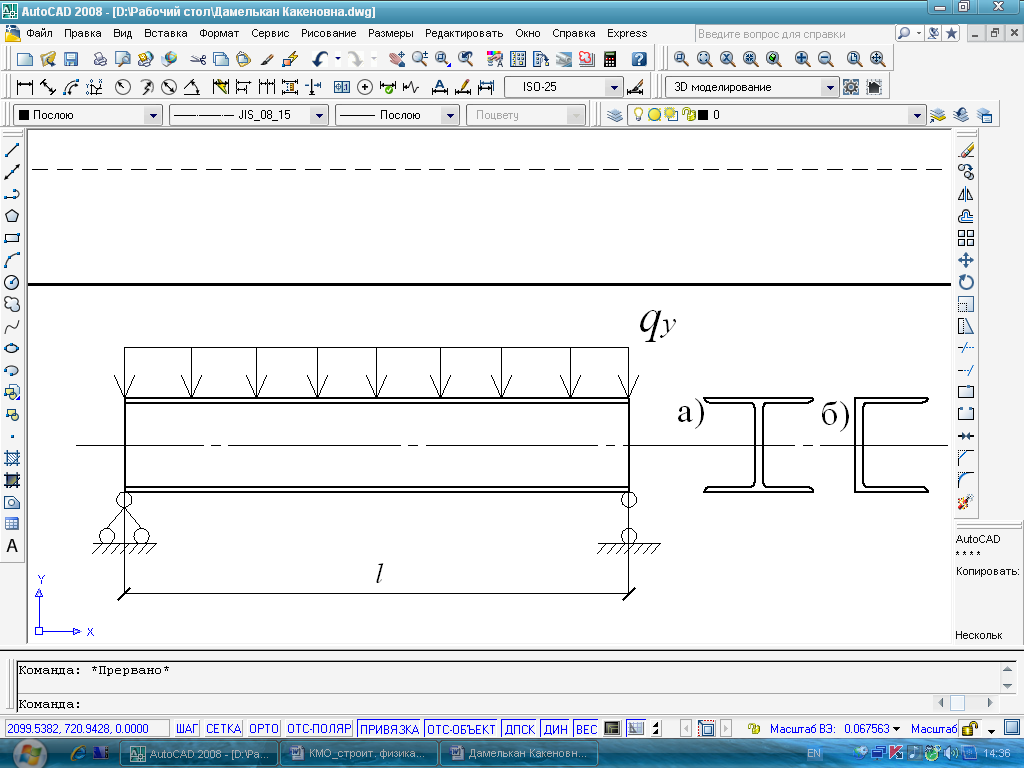
Рисунок 4 - Внецентренно сжатый стержень Рисунок 5 -Потеря устойчивости, связанная с появлением кручения и изгибом в другой плоскости



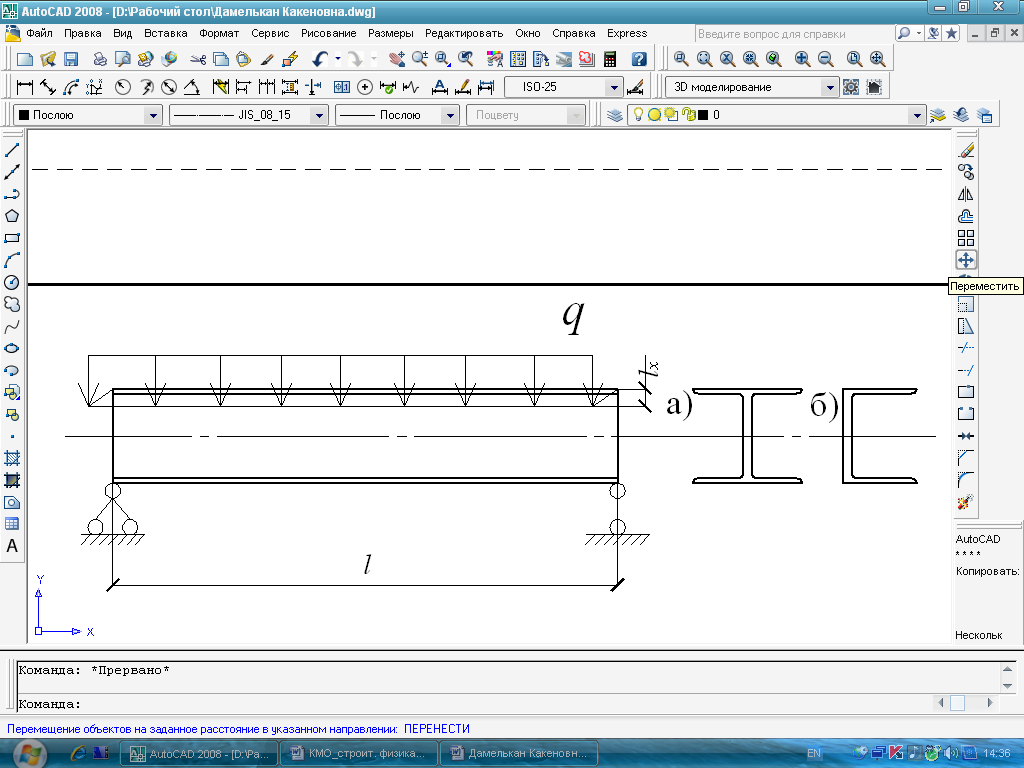
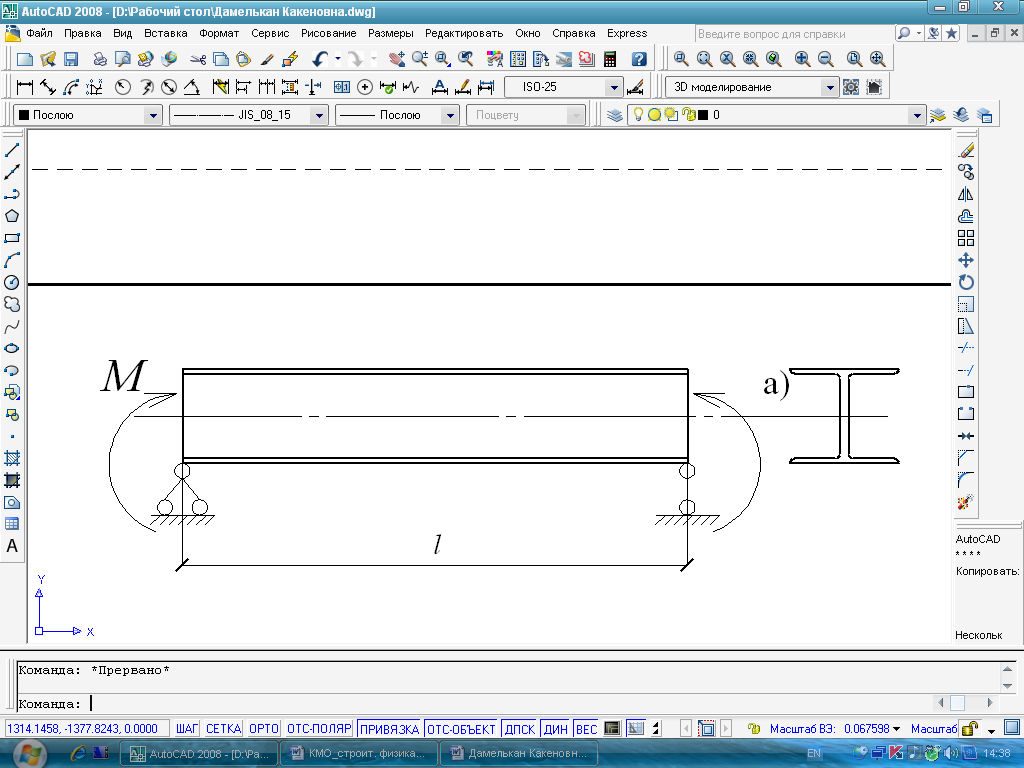
Рисунок 6 - Действие поперечной нагрузки Рисунок 7- Потеря устойчивости при чистом с эксцентриситетом изгибе

Для выбранных моделей составлены основные уравнения.

Приведен пример по расчету центрально сжатого стержня, шарнирно опертого по двум краям (Рисунок 4), величина эксцентриситета е_у =0:

С учетом разделения полных углов закручивания, основные уравнения имеют вид:

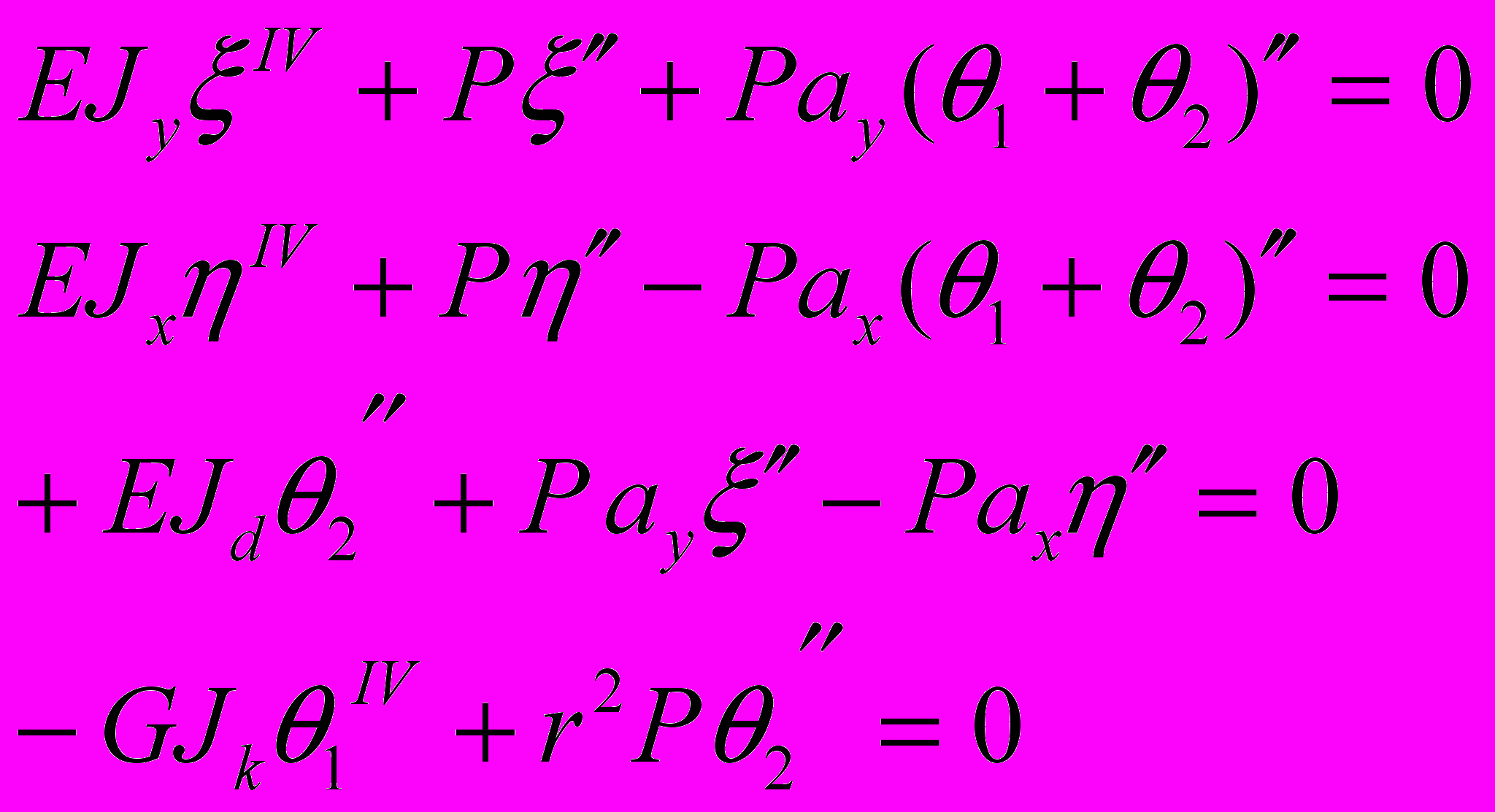(14)

Решение уравнений (14) ищется в виде синусоидальных функций, которые удовлетворяют граничным условиям.

После их подстановки в (14), получаем систему 4 линейных однородных уравнений 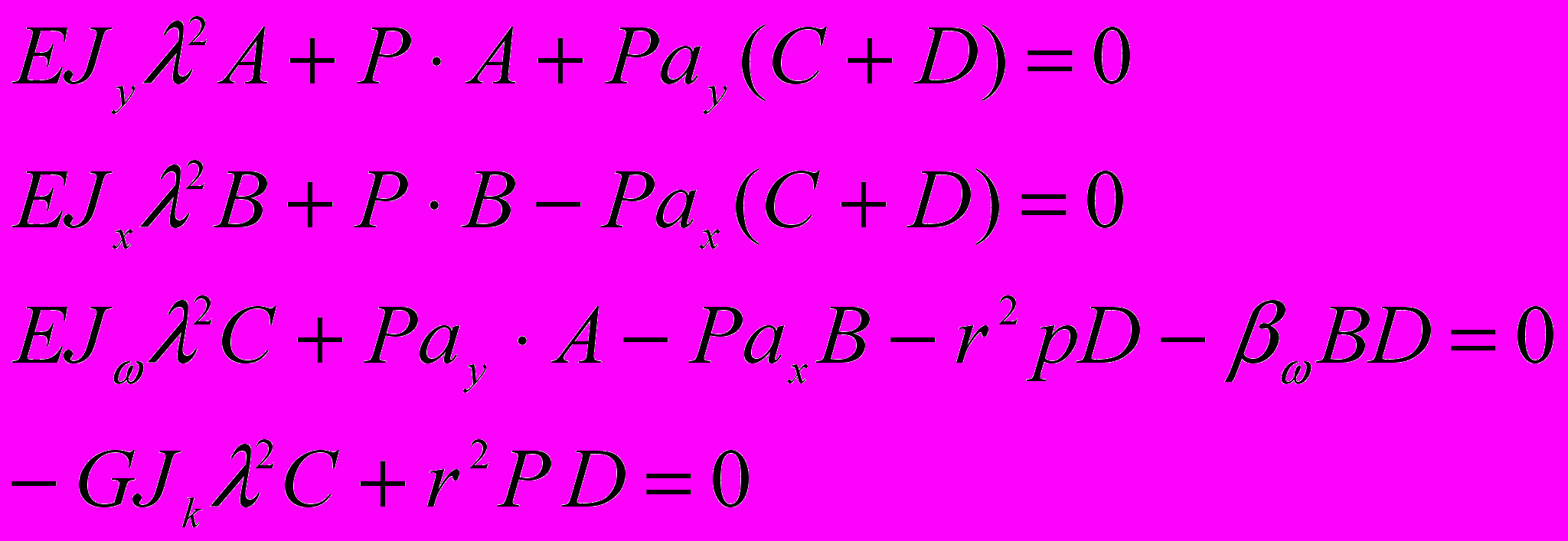(15):

(15)

Приравнивая определитель (15) к нулю, получаем уравнение устойчивости, из которого можно определить критические нагрузки, соответствующие крутильно-изгибным формам потери устойчивости. Раскрыв определитель, получаем нелинейное алгебраическое уравнение 4 порядка (уравнение Декарта-Эйлера) относительно неизвестной величины критической нагрузки, которое можно привести к уравнению Кардано, решение которого известно. В таблице 6 приведены значения критических сил и напряжений для центрально сжатого стержня. Приведены сравнения с другими решениями.


Таблица 6- Значения критических сил и напряжений для центрально сжатого стержня

Критические силы и напряжения	По данному методу	По теории В.З.Власова	Критические нагрузки по Эйлеру	Расхождение в % с теор. В.З.Власова
Ркр [т]	42,8	47,6	86,3	10,1
σкр [кг/см2]	856	950	1726	9,89

ЗАКЛЮЧЕНИЕ


По результатам исследований сделаны следующие выводы:

1. Сделан анализ теории и методов расчета тонкостенных стержней. Выявлены противоречия в основных дифференциальных уравнениях равновесия, которые не в полной мере соответствуют основным принципам строительной механики.

2. Разработаны модели тонкостенных элементов конструкций, основанные на принципе разделения полных крутильных деформаций на чисто крутильные и крутильно-изгибные. Используя вариационный метод, составлены уравнения равновесия и уравнения устойчивости для тонкостенного стержня с учетом деформируемости контура.

3. Выполнены расчеты на прочность тонкостенных стержней по предложенной модели, проведены сравнения полученных результатов с решениями по теории Власова, полученные результаты выявили уменьшение нормальных и касательных напряжений в пределах от 6% до 15%.

4. Многовариантные расчеты на прочность ребристых плит и пологих цилиндрических оболочек по данной методике и сравнения полученных результатов с классическими решениями, показали снижение напряжений и деформаций в пределах от 5% до 13%. Увеличение жесткости системы за счет конструктивных особенностей оболочки снижают нормальные напряжения до 13%, а касательные напряжения на 6,5%. В плите это влияние усиливается, нормальные напряжения уменьшаются до 15%, касательные – до 8%.

5. Расчеты на устойчивость тонкостенных стержней показали, что использование данной методики расчета привели к увеличению значений критических нагрузок на 10%. В результате несущая способность таких стержней увеличивается на 10% и позволяет системе сохранить устойчивые равновесные формы деформирования.

6. Предложенная методика расчета тонкостенных конструкций с учетом разделения углов поворота на чисто крутильные и крутильно-изгибные подтверждается экспериментальными данными. Расчет позволяет сэкономить расход материала и тем самым снизить себестоимость таких конструкций. Учитывая простоту и ясность предлагаемой методики, рекомендуется ее использовать в инженерных расчетах тонкостенных конструкций зданий и сооружений.


СПИСОК ОПУБЛИКОВАННЫХ РАБОТ ПО ТЕМЕ ДИССЕРТАЦИИ

1. Божанов Е.Т., Секеев К.М., Сыдыкова Д.К Концептуальная модель расчета на прочность тонкой пологой цилиндрической оболочки шарнирно опертая по контуру и загруженная равномерно распределенной нагрузкой // Вестник КазАТК. - Алматы, 2002. - № 6. - С. 78-82.
   
2. Божанов Е.Т., Секеев К.М., Сыдыкова Д.К. Концептуальная модель расчета на прочность тонкой пологой цилиндрической оболочки шарнирно опертая по контуру и загруженная в центре сосредоточенной нагрузкой // Вестник КазГАСА. - Алматы, 2003. - № 6. - С. 56-58.
   
3. Божанов Е.Т., Секеев К.М., Сыдыкова Д.К. Анализ концепции упругой системы пластин и пологих цилиндрических оболочек // Транспорт Евразии: Взгляд в XXI век: материалы II Международной научно-практической конференции. – Алматы: КазАТК им. М.Тынышпаева, 2003. - С. 265-271.
   
4. Божанов Е.Т., Сыдыкова Д.К. Качественный метод решения некоторых уравнений устойчивости стержней // Вестник Каз ГАСА. - Алматы, 2003. - № 8. - С. 85-87.
   
5. Божанов Е.Т., Сыдыкова Д.К. Общие сведения о рамно-балочных мостах и описание их конструкций // Вопросы прикладной физики и математики: материалы Международной научно-практической конференции. - Алматы, 2003. - С. 155-158.
   
6. Сыдыкова Д.К Расчет на устойчивость пролетного строения рамно-балочного моста // Вопросы прикладной физики и математики: материалы Международной научно-практической конференции. - Алматы, 2003. - С. 158-166.
   
7. Божанов Е.Т., Секеев К.М., Сыдыкова Д.К. Решение качественным методом дифференциальных уравнений свободных колебаний стержня // Теория функций, функциональный анализ и их приложения: материалы Международной научно-практической конференции. - Семипалатинск, 2003. -С. 192-193.
   
8. Божанов Е.Т., Сыдыкова Д.К. Методика решения дифференциального уравнения устойчивости тонкостенных стержней с изменяемой по длине жесткостью // Вестник КазНУ им. Аль-Фараби. - Алматы, 2004. - № 4(43). -С. 89-95.
   
9. Секеев К.М., Сыдыкова Д.К. Методика расчета изгиба с кручением двутавровой балки с силой, приложенной в середине пролета // Вестник КазНУ им. Аль-Фараби. - Алматы, 2004. - № 2(41). - С. 138-145.
   
10. Божанов Е.Т., Сыдыкова Д.К. Решение качественным методом дифференциальных свободных колебаний стержня // Вестник КазНУ. - Алматы, 2005. - С. 67-69.
    
11. Сыдыкова Д.К., Секеев К.М., Толганбаев А.Ж. Один алгоритм для определения внешних силовых факторов и деформации при изгибе и кручении тонкостенного стержня// Инновационные технологии в области информатики, математики и физики: сборник материалов Республиканской межвузовской научно-методической конференции. - Алматы, 2006. - С. 85-91.
    
12. Сыдыкова Д.К., Секеев К.М., Толганбаев А.Ж. Расчет на изгиб с кручением двутавра нагруженной силой в середине пролета // Актуальные проблемы естественно-научных дисциплин: сборник материалов Международной научно-методической конференции. - Алматы, 2008. – С. 43-47.
    
13. Толганбаев А.Ж., Секеев К.М., Сыдыкова Д.К. Расчет тонкостенных стержней основанное на принципе раздельного угла кручения // Вестник КазГАСА. - Алматы, 2008. - № 5. - С.53-56.
    
14. Толганбаев А.Ж., Секеев К.М., Сыдыкова Д.К. Колебание цилиндрического стержня, подверженного осевому напряжению// Современные концепции естествознания и информационных технологий: сборник материалов Международной научно-методической конференции. - Алматы, 2009. - С. 25-30.
    
15. Достанова С.Х., Сыдыкова Д.К. К теории устойчивости тонкостенных конструкций // Теоретические и экспериментальные исследования строительных конструкций: материалы Международной научно-методической конференции. - Алматы, 2009. - С. 21-23.
    
16. Достанова С.Х., Слымбаева А.К., Сыдыкова Д.К. Обобщенная модель для расчета слоистых пластин при изгибе // Механика и строительство транспортных сооружений: труды Международной научно-практической конференции, посвящ. 75-летию Заслуженного деятеля науки и техники Казахстана, Академика НАН РК, доктора технических наук, профессора Айталиева Ш.М. - Алматы, 2010. – С. 230-234.
    

Сыдыкова Дамелькан Какенқызы


Конструктивті ерекшеліктері бар жұқа қабырғалы жүйелердің

беріктігі және тұрақтылығы


05.23.17. – Құрылыс механикасы


Түйін


Мәселенің өзектілігі. Жұқа қабырғалы конструкциялардың қолдануының элементтері болып табылатын иілгіш стержіндер, арқалықтар, тақталар және әртүрлі қабықтар теорияларын және есептеу әдістерін жетілдіруді талап етеді. Бұл буында өте маңыздысы конструкция жұмысының ерекшелігін ескеретін және нәтиже беретін есептеу моделінің дұрыс таңдалуында. Сондықтан осы жұмыста жұқа қабырғалы жүйелердің беріктігі мен тұрақтылығын зерттеу мақсаты заманауи құрылыс үшін өзекті болып табылады. Бұл тиімді конструкциялар мен ғимараттарды жобалауға мүмкіндік береді.

Жұмыстың мақсаты. Конструктивті ерекшеліктері бар жұқа қабырғалы жүйелердің беріктігі мен тұрақтылығын зерттеу мен инженерлік есептерді жаңа теориялық және практикалық тұрғыда қарастыру.

Мақсатқа жету үшін келесі мәселелер қарастырылды:

- тақталардың, цилиндрлік қабықшалардың модельдері ұсынылған;

- вариациялық әдіс негізінде тепе-теңдік теңдеулері анықталған және бұрамалы деформацияларды бөлу әдісін қолданып жұқа қабырғалы конструкциялардың инженерлік есебінің әдістемесі ұсынылды;

- жұқа қабырғалы стержіннің дифференциалдық теңдеулерінің жуықталған шешімдерінің әдістемесі ұсынылды;

- ашық профильді жұқа қабырғалы стержіннің беріктігінің есебі ұсынылды;

- ұсынылған әдістеме бойынша жұқа қабырғалы стержіндері үшін критикалық жүктемелерге анықтама беру.

Зерттеу нысаны. Құрылыс конструкцияларында және ғимараттарда өте жиі қолданылатын тақталар, стержіңдер, кабықтар.

Зерттеу әдістері. Жұқа қабырғалы конструкциялар есебі үшін В.З. Власов және А.П. Лещенколардың классикалық әдістері қолданылды.

Жұмыстың ғылыми жаңалығы

Жұмыстың теориялық негізі Қазақ көлік және коммуникация академиясының студенттеріне, аспиранттарына, магистранттарына арналған және Қазақ бас сәулет-құрылыс академиясының оқу процесстеріне енгізілді.

Алынған есептеу нәтижелерін жұқа қабырғалы конструкцияларды жобалау үшін қолдануға болады, көрсетілген әдістің механиканың вариациялық әдісімен серпімді жүйенің беріктігімен салыстырғанда нәтижелеу екенін көрсетеді, бұл В.З. Власовтың теориясы бойынша классикалық нақтыланған, нәтижелер салыстырылған, басқа авторлар жағынан да эксперименталды тексерілген.




Негізгі ғылыми тұжырым

- жұқа қабырғалы стержіндердің кернеулі-деформацияланған күйі мен тақталардың жаңа есептеу моделі;

- жұқа қабырғалы стержіндердің тұрақтылығын жоғалтуын зерттеу үшін жаңа есептеу моделі;

- бағалау және белгілі шешімдер нәтижесімен салыстыру, ұсынылған әдіс бойынша жұқа қабырғалы стержіндердың беріктігінің , тақталардың есептеу нәтижелері;

- центрлік сығу және таза айналдыру кезіндегі осы әдіс бойынша жұқа қабырғалы стержіндер үшін тұрақтылықтылығына арналған есептеу нәтижелері;

- ұсынылған әдіс бойынша жұқа қабырғалы конструкциялардың беріктігі мен тұрақтылығының сандық есебінің алгоритмі.

Қорытынды. Жұқа қабырғалы стержіндердің, тақталардың, цилиндрлік қабықшалардың жаңа модельдері ұсынылған және осы жүйелердің сандық есептері көрсетілген.

Жұмыс нәтижелерін жүзеге асыру. Келтірілген есептеу әдісі мен модельдер жұқа қабырғалы конструкциялардың теориялық және практикалық есебін жетілдіруіне себеп болады, бұл материалдың шығынын үнемдейді.





SUMMARY


SYDYKOVA DAMELIKAN KAKENOVNA


Strength and stability thin-walled systems with constructive particularity


05.23.17- Building mechanics


Urgency of the problem. Broad using thin-walled design, which element are flexible rods, beams, plates and shells of the different contours, requires the improvements to theories and methods of their calculation. Very important stage in this section is a right choice to accounting model, taking into account particularities of the work to designs and giving results, which close to real functioning the system. So problem of the study to stability and strength thin-walled systems in given work actual and promotes creation efficient design and buildings.

The purpose of the work is a study to strength and stability thin-walled systems with constructive particularity and exhibit new theoretical and practical approach to calculation of the engineering task.

The object of the study is thin-walled rod, plates and sloping shell with constructive particularity.

Methods of the research. The classical models V.Z.Vlasov and model A.P.Leschenko and numerical method of mechanical engineering.

Scientific novelty of the work

- is offered new approach to calculation thin-walled rod by division corner of twist on purely twist and twist-bending;

- is offered new approach to calculation plates and cylindrical shells by discrete the system on separate strips in two directions with provision for their intercontacts by means of nonlinear function;

- is determined tense condition in thin-walled rod with provision for division corner of twist and are made comparisons with the known classical decisions;

- explored tense-deformed condition of the reinforced -concrete sloping shell and plates with constructive particularity on given to methods and are given comparisons with classical decisions;

- is designed mathematical models for calculation thin-walled rod on stability;

- on the grounds of offered method’s are executed calculations on stability thin-walled rod under central compression and clean torsion, are made comparisons with calculation results on theories V.Z.Vlasova.

Scientific and practical value

The Theoretical bases of the work are introduced in scholastic process of the Kazakh academy of the transport and communication for student, graduate student, megastars, as well as are introduced in scholastic process Kazakh main architectural-building academy. The got results calculation possible to use when designing thin-walled design, are shown advantage of the proposed methods with two-way estimation in contrast with existing concept to strength of the elastic systems and variation principle mechanical engineers. Proposed methods give more accurate result in comparison with classical approach on theories V.Z.Vlasova.

The main scientific achievements:

- a new accounting models tense-deformed conditions thin- rod, plate and thin sloping shell;

- a new accounting models for study of the loss to stability thin-walled rod;

- a results of the calculation on toughness тонкостенных rod, captive and пологих shell on proposed to methods;

- a results of the calculation on stability thin-walled rod under central compression on given to methods.

The conclusions. The designed model thin-walled element design, founded on principle of division full twisting deformation on purely twisting and torsion-bending. The executed calculations on strength and stability thin-walled rod, plate and sloping shell on offered to models.

Efficiency or value of the work. The present method of the calculation and models promote the development and improvement building mechanical engineers, and promotes creation efficient design and buildings. The calculation allows economizing of the material and reducing the prime cost such design.

СЫДЫКОВА ДАМЕЛЬКАН КАКЕНОВНА

Прочность и устойчивость тонкостенных систем

с конструктивными особенностями


05.23.17- строительная механика


Автореферат

диссертации на соискание ученой степени

кандидата технических наук


Подписано в печать 10.10.2010г.

Формат 60-84 1/16. Бумага офсетная

Заказ № _____ Объем 1.0 п.л. Тираж 100 экз.


Издательский дом «Строительство и архитектура»

Казахская головная архитектурно-строительная академия

050043, Республика Казахстан, г.Алматы, ул. К.Рыскулбекова, 28.

Тел.: +(727)229-46-11