Програма співбесіди з інформатики для абітурієнтів, що вступають на механіко-математичний факультет

Вид материала

Содержание

Подобный материал:

МІНІСТЕРСВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

МИКОЛАЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ІМЕНІ В.О. СУХОМЛИНСЬКОГО

МЕХАНІКО-МАТЕМАТИЧНИЙ ФАКУЛЬТЕТ

КАФЕДРА інформатики

“ЗАТВЕРДЖУЮ”

Ректор ________________В.Д.Будак

“ 22 ” ЛЮТОГО 2012 Р.

ПРОГРАМА СПІВБЕСІДИ

З ІНФОРМАТИКИ

Для абітурієнтів, що вступають

на механіко-математичний факультет

за освітньо-кваліфікаційним рівнем «магістр»

на денну форму навчання.

Спеціальність: 8.04030201 Інформатика.

Миколаїв 2012

Розробник: доц. Тихонова Т.В.

Затверджено на засіданні кафедри інформатики

Протокол № 11 від 19 січня 2012 р.

Затверджено на засіданні Вченої ради механіко-математичного факультету

Протокол № 5 від 25 січня 2012 р.

Прийом на навчання за освітньо-кваліфікаційним рівнем “магістр” здійснюється на конкурсній основі за результатами вступних випробувань.

Особи, які здобули освітньо-кваліфікаційний рівень “бакалавр” та «спеціаліст» за відповідною спеціальністю беруть участь у конкурсі за результатами фахових вступних випробувань.

Вступники проходять співбесіду в обсязі діючих програм освітньо-кваліфікаційного рівня – “бакалавр”.

1.Програма

Питання з курсу «Програмування»

Cтруктурне програмування: принципи, основні алгоритмічні структури.
Мова структурного програмування. Алфавіт, лексеми. Основні поняття мови: оператори, ідентифікатори, числа, рядки, константи. Приклади.
Стандартні типи даних мови програмування. Набір функцій i операцій, введених для кожного із стандартних типів. Пріоритет операцій. Приклади.
Оператори керування ходом виконання програми. Оператори переходу, умовні, варіанту, оператори циклів. Приклади.
Підпрограми у мові програмування. Види параметрів. Стандартні підпрограми. Локальні та глобальні змінні. Рекурсивні підпрограми. Приклади.
Організація даних в мові програмування. Масиви, рядки, структури (записи). Опис і ініціалізація.
Вказівники. Динамічні структури даних (списки, стеки, черги).
Обробка файлів даних у мові програмування.
Об’єктно-орієнтоване програмування: основні принципи, поняття класу та об’єкту. Визначення класу в С++. Призначення і використання конструкторів і деструкторів класу в С++.
Призначення і використання перевантаження функцій і операцій в С++.
.Успадкування класів в С++. Приховування атрибутів і операцій. Ініціалізація базових класів.
Призначення і реалізація поліморфізму і віртуальних функцій в С++.

Питання з курсу «Бази даних та інформаційні системи»

Поняття інформаційної системи. Класифікація інформаційних систем.
Поняття БД, СУБД. Типи БД. Переваги та недоліки кожного типу.
Реляційне моделювання. Модель ”сутність-зв’язок”. Види зв’язків.
Мова запитів SQL.

Питання з курсу «Програмне забезпечення ЕОМ».

Класифікація ПЗ ЕОМ: системне, службове, прикладне ПЗ.
Поняття операційної системи. Класифікація ОС, склад ОС. Поняття інтерфейсу користувача. Поняття файлової системи.
Системи обробки текстової інформації: класифікація, функціональні можливості. Режими роботи текстового процесора.
Системи мультимедіа: класифікація, функціональні можливості. Формати аудіо-, відео-файлів.
Системи комп’ютерної графіки: класифікація. Поняття растрової та векторної графіки. Формати графічних файлів. Основні режими роботи графічного редактору.

Питання з курсу «Комп’ютерні мережі».

Поняття про глобальну та локальну комп’ютерні мережі. Апаратне й програмне забезпечення мереж. Топологія комп’ютерних мереж.
Призначення й структура мережі Інтернет. Протоколи Інтернету. Адресація в Інтернеті, поняття IP-адреси, доменного імені та URL-адреси.
Засоби пошуку інформації в Інтернеті. Принципи функціонування веб-каталогів та пошукових систем. Стратегії пошуку інформації.
Поняття гіпертекстового документа, гіперпосилання, веб-сторінки та веб-сайту. Мови розробки електронних ресурсів мережі Інтернет.
Модель протоколів ISO OSI за рівнями ієрархії, що використовується в комп'ютерних мережах.

Питання з курсу «Архітектура ЕОМ».

Подання інформації в ЕОМ. Форми подання чисел в ЕОМ.
Кодування алфавітно-цифрової інформації.
Мікропроцесори: структура, основні функції, типи та характеристики мікропроцесорів.
Пам`ять ЕОМ. Внутрішня та зовнішня пам`ять комп`ютера. Ієрархічна організація пам'яті.
Типи запам'ятовуючих пристроїв. Способи організації доступу до даних.
Системні інтерфейси і інтерфейси вводу-виводу. Пристрої вводу-виводу інформації.

Питання з курсу «Математичний аналіз».

Множина дійсних чисел та її основні властивості. Теореми про існування точної верхньої і нижньої граней множини. Числова послідовність, границя числової послідовності. Границя суми, добутку, частки. Існування границі послідовності 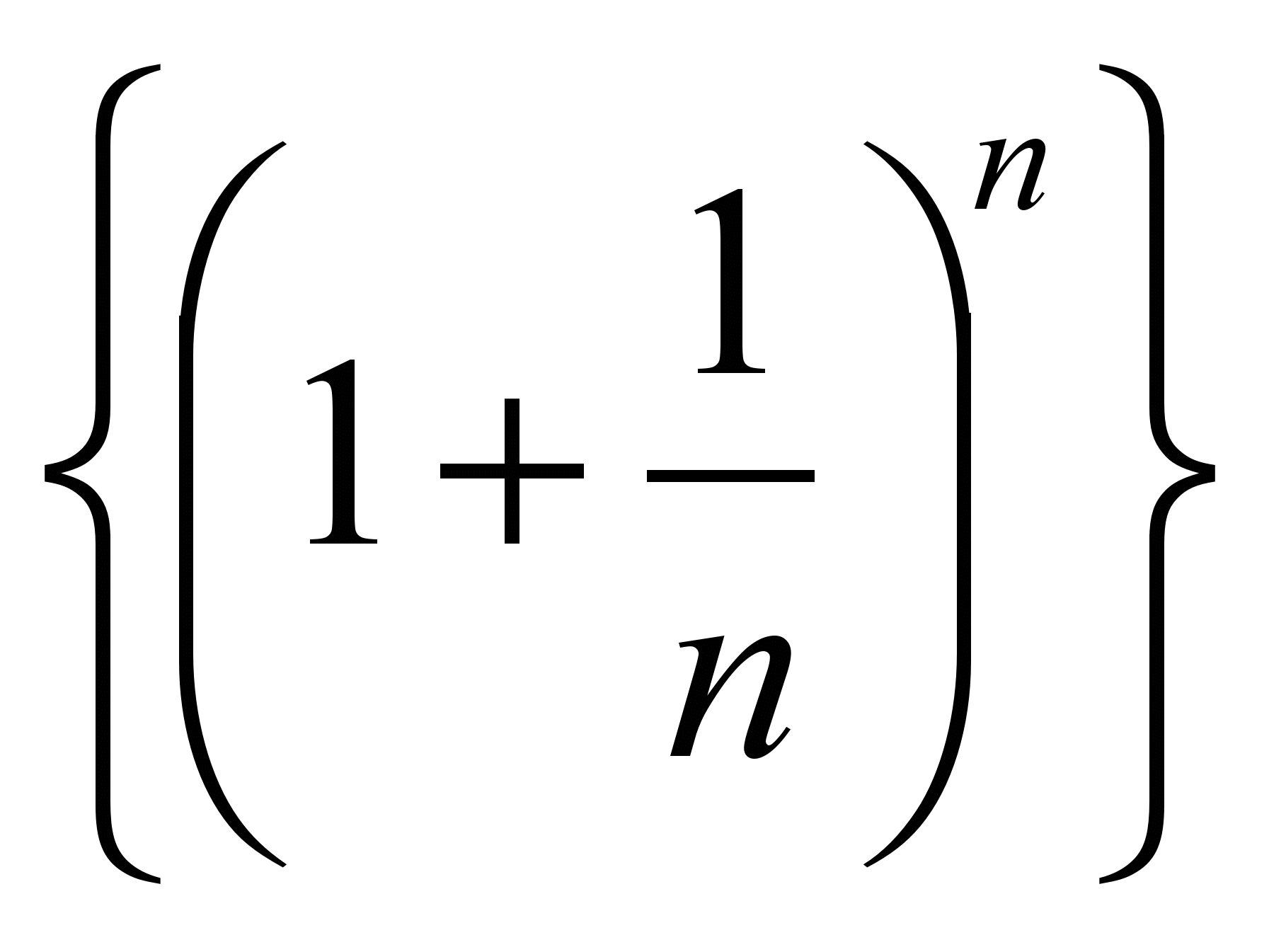. Критерій Коші.
Відображення множини (функції). Способи задання функції. Границя функції, її основні властивості. Перша і друга важливі границі.
Диференційованість функції однієї змінної. Похідна. Таблиця похідних. Похідна суми, добутку, частки, похідна оберненої функції, похідна складної функції.
Екстремум функції однієї змінної. Необхідна і достатня умови екстремуму. Точки перегину. Асимптоти графіка функції. Схема дослідження і побудови графіка функції.
Означений інтеграл. Необхідна і достатня умови інтегрованості функції. Інтегрованість неперервної функції. Властивості означеного інтеграла.
Застосування означеного інтеграла до обчислення довжини дуги, об’єму тіла обертання, площі поверхні обертання. Застосування означеного інтеграла в механіці.
Розвиток поняття інтеграла. Подвійні, потрійні і криволінійні інтеграли та їх застосування до обчислення площ, об’ємів, площ поверхонь, мас, центра маси, моментів інерції, роботи силового поля. Зв’язок між ними.
Числові ряди. Геометричний ряд. Гармонічний ряд. Достатні ознаки збіжності рядів з додатними членами: Даламбера, Коші, інтегральна. Знакозмінні ряди. Теорема Лейбніца. Абсолютно і умовно збіжні ряди і їх властивості.
Частинні похідні функції декількох змінних. Диференційованість і диференціал. Достатня умова екстремуму функцій двох змінних.
Поняття степеневого ряду з дійсними членами. Інтервал збіжності. Обчислення радіуса збіжності за формулами Коші-Адамара і Даламбера. Розклад в степеневий ряд деяких основних елементарних функцій.

Питання з курсу «Алгебра та геометрія».

Поле комплексних чисел. Геометричне зображення комплексних чисел. Операції над комплексними числами в алгебраїчній формі. Тригонометрична форма комплексного числа.
Розв’язування систем лінійних рівнянь методом Гауса. Критерії сумісності та визначеності систем лінійних рівнянь.
Матриці. Дії над матрицями. Умови існування оберненої матриці. Способи обчислення оберненої матриці.
Векторний простір (означення, приклади, властивості). Базис і розмірність скінченновимірного простору.
. Скалярний, векторний і мішаний добуток двох векторів, його властивості і застосування. добуток двох векторів, його властивості і застосування.
Пряма лінія на площині. Способи задання та рівняння. Взаємне розташування прямих на площині.
Криві другого порядку. Канонічні рівняння, властивості.
Пряма лінія і площина в просторі. Способи задання та рівняння. Відстань від точки до прямої на площині і в просторі.

Питання з курсу «Дискретна математика».

Множини, операції з ними та властивості операцій. Декартів добуток. Потужність множин. Теореми про потужність перетину та об’єднання двох та більше множин. Діаграми Ейлера–Венна.
Елементи комбінаторики. Факторіал. Перестановки, розміщення та комбінації з повторенням та без. Біном Ньютона, трикутник Паскаля. Властивості біноміальних коефіцієнтів. Формула п-го доданку розкладу біному.
Натуральні числа. Індукція і дедукція. Аксіоми Пеано. Метод математичної індукції. Числові функції Ціла, дробова частина числа, застосування. Кількість дільників та сума дільників натурального числа. Функція Ейлера.
Графи та способи їх визначення. Лема про рукостискання. Матриці суміжності та інцидентності. Шлях в графі. Ейлерові, напівейлерові графи та їх критерій. Гамільтонові графи. Дерева та ліси. Планарні графи. Загальні метричні параметри.

Питання з курсу «Методи оптимізації та дослідження операцій».

Симплекс-метод розв’язання задач лінійного програмування. Метод штучного базису.
Методи розв’язання транспортних задач.
Градієнтні методи розв’язання задач нелінійного програмування.
Матричні ігри. Методи розв’язання матричних ігор.

Питання з курсу «Чисельні методи».

Методи наближеного розв’язання алгебраїчних і трансцендентних рівнянь.
Методи наближеного розв’язання систем лінійних алгебраїчних рівнянь.
Методи наближеного обчислення визначених інтегралів.
Методи наближеного інтегрування диференціальних рівнянь.

2.Критерії оцінювання

Оцінка “відмінно” (180-200 балів) ставиться, якщо студент:

показав повне знання фактичного матеріалу;
повністю і строго довів всі твердження питань білету;
вільно володіє понятійним і термінологічним апаратом;
показав вміння розв’язувати навчальні задачі.

Оцінка “добре” (150-179 балів) ставиться, якщо студент показав:

показав повне знання фактичного матеріалу, але з деякими неточностями;
повністю довів всі твердження питань білету, але з деякими неточностями;
в цілому володіє понятійним і термінологічним апаратом;
показав вміння розв’язувати навчальні задачі.

Оцінка “задовільно” (124-149 балів) ставиться, якщо студент показав:

неповне знання фактичного матеріалу;
задовільне володіння базовою термінологією;
вміє пояснити способи розв’язування навчальних задач зі сторонньою допомогою.

Оцінка “незадовільно” (100-123 бали) ставиться за умови, що студент:

має уяву щодо змісту фактичного матеріалу, але відповідь не наповнюється реальним змістом;
не володіє понятійним і термінологічним апаратом;
не може пояснити способи розв’язування навчальних задач навіть зі сторонньою допомогою.

3.Література

Програмування

Архангельский А.Я. Программирование в С++Builder 5..- М.: ЗАО"Изд-во БИНОМ", 2000.- 1152с.
Архангельский А.Я. Программирование в С++Builder 6.- М.: Бином, 2002.- 1152с.
Архангельский А.Я. Программирование Delphi 6.- М.: БИНОМ, 2003.- 1119с.
Р. Вайнер, Л. Пинсон. С++ изнутри. - Киев: НПИФ "ДиаСофт", 1993.
Х.М.Дейтел, П.Дж.Дейтел. Как программировать на С++.М.:Бином.1998.
Лафоре Р. Объектно-ориентированное программирование в C++.- СПб: Питер, 2003.- 928с.
И.Пол. Объектно-ориентированное программирование с использованием С++. - Киев: НПИФ "ДиаСофт", 1995.
Г. Шилдт. Самоучитель С++. BHV-Санкт-Петербург. 1997.
Фаронов В.В. TurboPascal 7.0. Начальный курс. -М.: Колидж,1997.
Турбо Pascal 7.0 – К.: Издательская группа BHV, 2002 – 496 с.
А. Епашненков, В. Епашненков Программирование в среде Turbo Pascal 7/0/ - М.: «Диалог-Мифи», 1993. – 288 с.

Бази даних та інформаційні системи

Дейт К. Введение в системы баз данных. “Диалектика”. 1988, 1999.
Мартин Дж. Организация баз данных в вычислительных системах. Мир. 1980.
Ульман Дж. Основы системы баз данных. Финансы и статистика. 1983.
Дрибас В.П. Реляционные модели баз данных. Изд-во БГУ. Минск. 1982.
Системы управления базами данных и знаний, под ред. А.Н.Наумова. Финансы и статистика. 1991.
Чери С., Готлоб Г., Танке Л. Логическое программирование и базы данных. Мир. 1992.
Калиниченко Л.А., Рывкин В.М. Машины баз данных и знаний. Наука. 1990.
Кокорева Л.В., Перевозчикова О.Л., Ющенко Е.Л. Диалоговые системы и представление знаний. Наук. думка. К. 1992. 448с.
Т.Конноли, К.Бегг, А.Страчан. Базы Вільям. Проектирование, реализация и сопровождение. Вільям и практика. Вільямс.2000.

Програмне забезпечення ЕОМ

Глобальна мережа Інтернет / Федько В.В., Плоткін В.І. – Харків: Веста: Ранок, 2003. – 96 с.
Информатика: практикум по технологии работы на компьютере / Н.В.Макаровой. – М.: Финансы и статистика, 2001. – 256 с.
Информатика: Учебник / Макаровой Н.В. – М.: Финансы и статистика, 2001. – 768 с.
Лупан І. Комп’ютер та лабораторні роботи з інформатики // Інформатика (ПВ). – 2002. - №3. – С. 3, №4. – С. 5.
Ляхович В.Ф. Основы информатики. - Ростов н/Д: Феникс, 2001.- 608 с.
Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика: учеб. пособие для студ. пед. вузов. – М., 1999. – 816 с.
Рамський Ю.С., Рибко Г.Ю. Проектування й опрацювання баз даних: Посібник для вчителів. – Тернопіль: Богдан, 2005. – 116 с.
Руденко В.Д., Макарчук О.М., Патланжоглу М.О. Практичний курс інформатики / Мадзігона В.М.- К.: Фенікс, 2000.
Тхір І.Л. та ін. Посібник користувача ПК. – 1998
Фігурнов В.Є. IBM PC для пользователя. Краткий курс. – 1999
Шафрин Ю.А. Информационные технологии: В 2 ч. Ч. 2: Офисная технология и информационные системы. – М.: ЛБЗ, 2000. – 336 с.

Комп’ютерні мережі

Андерсон Кристо, Минаси Марк Локальные сети. – К.: ВЕК. – 1999.
Бройдо В.Л. Вычислительные системы, сети и телекоммуникации. – СПб.: Питер. – 2002.
Габассов Ю.Ф. Internet 2000. – СПб.:BHV. – 1999.
Кент Питер. Internet: следующий шаг. – М.: Компьютер. – 1996.
Компьютерные сети. – М.: Microsoft Press. – 1996.
Кулаков Ю.А., Луцкий Г.М. Компьютерные сети. – К.: Юниор. – 1998.
Олифер В.Г., Олифер Н.А. Компьютерные сети. Принципы, технологии, протоколы. Учебник для вузов. – СПб: Питар. – 2000.

Архітектура ЕОМ

Столлингс В. Структурная организация и архитектура компьютерных систем. Вильямс, 2002. – 896 с.
Хамахер К., Враженич З., Заки С. Организация ЭВМ. –Питер, 2003. –843 с.
Таненбаум Э. Архитектура компьютера. –Питер, 2003. –698 с.

Математичний аналіз

Давидов М.О. Курс математичного аналізу. Частина 1. Функції однієї змінної. – К.: “Вища школа”, 1990. –383 с.
Давидов М.О. Курс математичного аналізу. Частина 2. Функції багатьох змінних і диференціальні рівняння. – К.: “Вища школа”, 1991. –366 с.
Давидов М.О. Курс математичного аналізу. Частина 3. Елементи теорії функцій і функціонального аналізу. – К.: “Вища школа”, 1979. – 384 с.
Шкіль М.І. Математичний аналіз. Частина I. – К.: “Вища школа”, 1994. – 423 с.
Шкіль М.І. Математичний аналіз. Частина II. – К.: “Вища школа”, 1995.
Берман Г.Н. Сборник задач по курсу математического анализа. – М.: “Наука”, 1972. – 416 с.

Алгебра

Завало С.Т., Костарчук В.Н. та інші. Алгебра і теорія чисел. 1ч. – К.: Вища школа, 1979.
Завало С.Т., Костарчук В.Н. та інші. Алгебра і теорія чисел. 2ч. – К.: Вища школа, 1980.
Завало С.Т. та інші. Алгебра і теорія чисел. Практикум. 1ч. – К.: Вища школа, 1984.
Завало С.Т. та інші. Алгебра і теорія чисел. Практикум. 2ч. – К.: Вища школа, 1986.
Бородін О.І. Теорія чисел. – К.: «Вища школа», 1970. – 275 стор.
Бухштаб А.А. Теория чисел. – М.: «Просвещение», 1966. – 384 стр.

Геометрія

Атанасян Л.С. Аналитическая геометрия. Ч.І. Аналитическая геометрия на плоскости. – М.:Просвещение, 1967.
Атанасян Л.С., Базылев В.Т. Геометрия.Ч.І. Учебное пособие для студентов физ.-мат.фак.пед.ин-тов.-М.:Просвещение, 1986.- 336с.
Базылев В.Т., Дуничев К.И. Сборник задач по геометри: Учеб.пособие для студентов физ.-мат.фак.пед.ин-тов.-М.:Просвещение, 1980.
Клетенник Д.В. Сборник задач по аналитичекой геометрии.-М.:Наука, 1967.-256с.
Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии.-М.: Физматгиз., 1962.-296с.

Дискретна математика

Акимов О.Е. Дискретная математика. Логика, группы, графы. -М.: Лаборатория Базовых Знаний, 2003. – 376 с.
Бондаренко М.Ф., Білоус Н.В., Руткас А.Г. Комп’ютерна дискретна математика. – Харків: «Компанія СМІТ», 2004. – 480 с.
Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. – М.: Физматлит, 2004. – 416 с.
Горбатов В.А. Основы дискретной математики. - М.: Высш. шк., 1986. – 312 с.
Капітонова Ю.В., Кривий С.Л., Летичевський О.А. Основи дискретної математики. – К.:Наукова думка, 2002. – 578 с.
Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. - М.: Энергоатомиздат, 1988. – 480 с.

Чисельні методи

Гаврилюк І.П., Макаров В.Л. Методи обчислень: Підручник: У 2ч. – К.: Вища шк., 1995. – Ч.2., 431 с.
Гаврилюк І.П., Макаров В.Л. Методи обчислень: Підручник: У 2ч. – К.: Вища шк., 1995. – Ч.1., 367 с.
Гаврилюк І.П., Макаров В.Л. Методи обчислень: Підручник: У 2ч. – К.: Вища шк., 1995. – Ч.2., 431 с.
Боглаев Ю.П. Вычислительная математика и программирование. -М.: Высшая школа, 1990.
Шуп Т. Прикладные численные методы в физике и технике. - М.: Высшая школа 1990.
Воробьева Г.Н. , Данилова А.Н. Практикум по вычислительной математике. -М. : Высшая школа, 1990, 208.
Демидович Б.П. , Марон И.А. Основы вычислительной математики. -М. : Наука, 1970.

Методи оптимізації та дослідження операцій

Акулич И.Л. Математическое программирование в примерах и задачах. Учебное пособие для студентов экономических специальностей вузов. М.: Высшая школа, 1986. -319 с.
Ашманов С.А., Тимохов В.В. Сборник задач по оптимизации. — М.: Наука, 1984. — 251 с.
Карманов В.Г. Математическое программирование. — М.: Наука, 1981. — 387 с.
Кузнецов А.В., Сакович В.А., Холод Н.И. и др. Сборник задач и упражнений по высшей математике: Математическое программирование. Минск: Вышэйшая школа, 1995. -382 с.