Раскраски § 53. Правильная раскраска

Вид материала

Документы

Содержание Граф, дополнительный к совершенному графу, также является совершенным. G верно утверж­дение 2). Нужно доказать, что для любого порожденно­го подграфа G' А независимо, то и равенство (3) доказано. Пусть G G — тершенный граф, для каждой клики В Граф G является совершенным тогда и только тогда, когда ни он, ни его дополнение G не содержат порожденных подграфов вида G S — одно из его минимальных по включе­нию разделяющих множеств вершин, G G не будет полным, то из теоремы 62.1 вытекает, что в G G — триангулированный граф поряд­ка п G не имеет порожденных подграфов вида 2К

Подобный материал:

• Библиотека Гумер психология, 518.71kb.
• Природный календарь рыболова, 117.39kb.
• Сказка о принцессе Смешанное Число. Давным-давно в математическом царстве, арифметическом, 21.17kb.
• Бытие – не-бытие александр Н. Павлов Россия, Санкт-Петербург Июнь 08, 2011, 43.62kb.
• Семейные традиции воспитания в императорских семьях, 91.6kb.
• Isbn 978-5-7262-1376 нейроинформатика 2011, 164.77kb.
• Вышлю почтой из Николаева в любой город Украины. Возможен обмен на диски, которых нет, 222.99kb.
• Недостатки молодого учителя в общении с учащимися и способы их преодоления, 133.12kb.
• Геннадий Дмитриевич Бердышев Теория и практика голодания ради здоровья и долголетия, 6337.41kb.
• И. а. Остренин Научный руководитель В. Г. Когденко,, 27.15kb.

§ 61. Совершенные графы

Как отмечалось выше, хроматическое число и плот­ность любого графа удовлетворяют очевидному неравен­ству χ(G)≥φ(G). При этом, как свидетельствует теоре­ма 54.5, разность χ(G) - φ(G) может быть как угодно велика. В этом параграфе изучаются графы, обладающие тем свойством, что хроматическое число и плотность не только самого графа, но и каждого его порожденного подграфа, равны.

Граф называется совершенным, если

χ(H )= φ(H) (1)

для любого его порожденного подграфа H.

Из этого определения непосредственно вытекает, что всякий порожденный подграф любого совершенного гра­фа является совершенным.

Очевидно, что все полные и пустые графы совершенны. Примером совершенного графа может служить также каждый двудольный граф поскольку для любого его под­графа H либо χ(H )=φ(H)=2 (если H непустой), либо χ(H )=φ(H)=1 (при пустом H).

Совершенные графы введены К. Бержем в I960 году. Интерес к этим графам связан прежде всего с двумя обстоятельствами. Во-первых, многие трудно разрешимые в общем случае задачи теории графов успешно решают­ся для совершенных графов. Во-вторых, ряд широко известных классов графов содержится в классе совершенных. Таковы, например, все двудольные, пороговые, расщепляемые и триангулированные (см. § 62) графы. Исследования, посвященные совершенным графам и, в частности, связанной с ними гипотезе Бержа, речь о которой пойдет ниже, во многом определяют лицо современной теории графов.

Теорема 61.1. Граф, дополнительный к совершенному графу, также является совершенным.

Эту теорему в виде гипотезы сформулировал К. Берж 1961 г. Позже ее независимо доказали Д. Р. Фалкерон (1971 г.) и Л. Ловас (1972 г.). Ниже приводится доказательство Л. Ловаса.

Лемма 61.2. Следующие два утверждения равносильны:

1. граф G является совершенным;
   
2. в
   любом непустом порожденном подграфе G' графа G есть такое независимое множество вершин А, что
   

Пусть G — совершенный граф, G' — его непустой порожденный подграф. Тогда χ(G') = φ(G'). Следовательно, существует правильная φ(G')-раскраска графа G'. если А — какой-либо цветной класс при этой раскраске, то множество А независимо и χ(G'— A) ≤φ(G')— 1. Из последнего неравенства вытекает (2), поскольку φ(H) ≤ χ(H) для любого графа H.

П
усть теперь для некоторого графа G верно утверж­дение 2). Нужно доказать, что для любого порожденно­го подграфа G' графа G выполняется неравенство

И
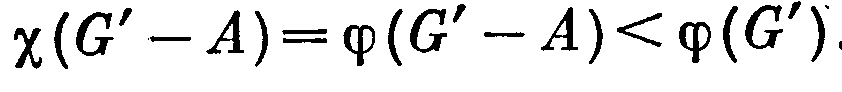
з неравенства (3) следует равенство плотности и хро­матического числа, ибо противоположное неравенство всегда верно. Воспользуемся индукцией по \G’\. Если G' — пустой граф, то (3) тривиально. Пусть G' непуст, \G'\ =k > 1 и для каждого порожденного подграфа мень­шего чем k порядка верно неравенство, аналогичное не­равенству (3). Для независимого множества А вершин графа G', удовлетворяющего неравенству (2), имеем по индуктивному предположению:

Н
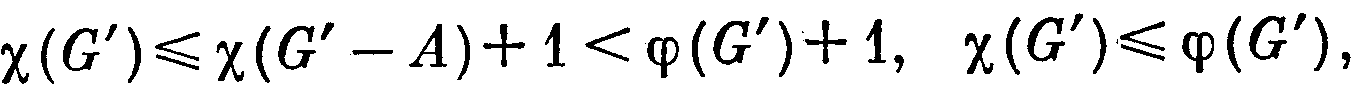
о так как множество А независимо, то

и равенство (3) доказано.

Пусть G и H — произвольные графы. Будем считать их множества вершин не пересекающимися и следующим образом определим новый граф F. Отметим произвольную вершину v графа G и положим VF = (VG U VH)\v. Вер­шины а и b графа F будем считать смежными, если вы­полняется одно из следующих трех условий:

1. ab € EG,
   
2. аb€ЕН,
   
3. a € VG, b €VH, av €EG или b € VG, a €VH, bv € EG.
   

Скажем, что граф F получается из графа G в резуль­тате замены вершины v графом Я.

Лемма 61.3. Граф, полученный из совершенного графа в результате замены вершин совершенными гра­фами, также является совершенным.

Очевидно, что достаточно рассмотреть лишь одну замену вершины. Пусть G и H — совершенные графы, a F получается из G в результате замены вершины v гра­фом Я. Учитывая лемму 61.2, достаточно показать, что в любом порожденном подграфе F' графа F есть незави­симое множество вершин А, пересекающееся с каждой наибольшей кликой графа F'. Вначале пусть F' = F. За­фиксируем какую-либо правильную φ(G)-раскраску гра­фа G. Пусть В — цветной класс, содержащий вершину v. Выберем в графе Н такое независимое множество вершин С, что φ(H - С) < φ(С). Теперь покажем, что множество (BUC)\v = А удовлетворяет нужным условиям. В самом деле, В независимо в G, С независимо в Н. Если же b € B \ v, c € C, то вершины b и v не смежны в G, а потому b и с не смежны в F. Итак, А — независимое множество вершин графа F.

Остается показать, что А пересекается с каждой наи­большей кликой графа F. Пусть К — одна из таких клик, L = К ∩ VH. Если L ≠ 0, то L содержит какую-либо наибольшую клику D графа H, поскольку любая вершина рафа G — v либо смежна в F с каждой вершиной графа H, либо ни с одной из них. Так как D∩C ≠ 0, то К ∩ А ≠ 0. Если же L = 0, то K€VG\v, φ(F)=\K\ ≤ φ(G — v) ≤ φ(G). Но очевидно, что φ(G) ≤ φF). Следовательно, \K\ = φ(G), клика К пересекается с каждым цветным классом любой правильной φ(G)-раскраски графа G, К∩(B\v)≠0, значит, К ∩ А ≠ 0. Доказано, то в графе F есть независимое множество вершин, юторое пересекается с каждой наибольшей кликой того графа.

Теперь заметим, что аналогичное свойство имеет любой порожденный подграф F' графа F, поскольку F' либо получается из некоторого порожденного подграфа G' графа G в результате замены вершины v порожденным подграфом Н' графа Н, либо является порожденным подграфом графа G.

Лемма 61.4. В любом совершенном графе G есть лика, пересекающая каждое наибольшее независимое ножество вершин графа G.


Проведем доказательство от противного. Пусть G — тершенный граф, для каждой клики В которого суще-гвует такое наибольшее независимое множество вершин , что В∩А=¢. Пусть, далее, В₁, ..., В_г — список всех клик графа G, А_i — наибольшее независимое множество вершин, такое что А_i ∩ В_i≠ 0 (i=1,r). Для произвольной вершины v графа G обозначим через w(u) число всех ножеств А_i, содержащих эту вершину. Заменив в G каждую вершину v полным графом K_w(v), получим граф G', который по лемме 61.3 окажется совершенным. Оценим число φ(С). Очевидно, что всякая клика графа G' есть объединение клик графов, заменивших в G вершины какой-либо клики. Поэтому


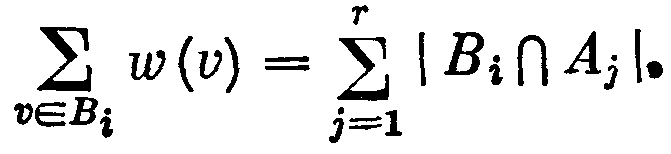
Поскольку каждое из множеств А_i вносит единицу в те и только те из чисел w{v), для которых v € Aj, то

Н
о очевидно, что


Следовательно,


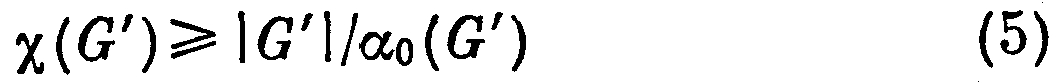
Далее,

(теорема 54.7). Построим последовательность, выписав поочередно все элементы множества А1, все элементы множества А2, ..., все элементы множества Аr .Пусть l — длина этой последовательности. Очевидно, что



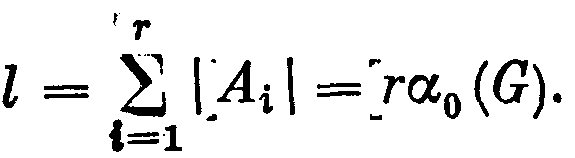
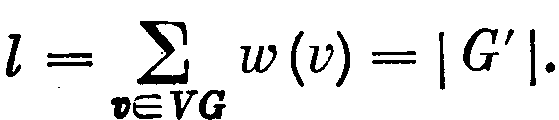
С другой стороны, каждая вершина v графа G фигури­рует в этой последовательности ровно w(v) раз, поэтому

Наконец, очевидно, ao(G') = ao(G).

Н
еравенство (5) теперь принимает вид

Но φ(G') = χ(G'), что противоречит совокупности нера­венств (4) и (6). Полученное противоречие и доказыва­ет лемму.

Доказательство теоремы 61.1. Пусть G — совершенный граф, Н —_непустой порожденный подграф дополнительного графа G’. Тогда Н’ — порожденный под­граф графа G. Согласно лемме 61.4 в графе Н’ есть кли­ка В, пересекающаяся с каждым наибольшим независи­мым подмножеством вершин. В графе Н множество В не­зависимо и пересекается с каждой наибольшей кликой. Следовательно, в силу леммы 61.2 граф G’ является со­вершенным.

Напомним читателю, что c(G) означает число кликового покрытия графа G. Очевидно, что αо(G) = φ(G’), c(G) = χ(G), поэтому из теоремы 61.1 вытекает

Следствие 61.5. Граф является совершенным тог­да и только тогда, когда ао(Н) = с(Н) для любого его по­рожденного подграфа Н.

Приведем без доказательства теорему, характеризую­щую совершенные графы в терминах многогранников. С каждой бинарной матрицей А без нулевых столбцов можно связать два многогранника: многогранник Р(А) ={х: Ax ≤ 1, х ≥ 0}, введенный в § 28, и многогранник Р_с (А) — выпуклую оболочку множества целых точек мно­гогранника Р(А). Очевидно, что Р_С(А) € Р(А).

Теорема 61.6. (В. Хватал, 1975 г.). Пусть А — матрица клик графа G. Тогда для того, чтобы граф G был совершенным, необходимо и достаточно выполнение равенства Р_С(А) = Р(А).

Легко видеть, что условием, необходимым для того, чтобы граф был совершенным, является отсутствие в нем порожденных простых циклов нечетной длины l ≥ 5. В самом деле, если С — такой цикл, то φ(С) = 2 < χ(С) = 3. Из теоремы 61.1 вытекает, что таких циклов нe должен содержать и граф, дополнительный к совер­шенному. В 1962 году К. Берж высказал предположение, то эти два условия не только необходимы, но и достаточны для того, чтобы граф был совершенным.

Сильная гипотеза Берж а. Граф G является совершенным тогда и только тогда, когда ни он, ни его дополнение G не содержат порожденных подграфов вида G_2h+hk>2.

Эта гипотеза, не доказанная и не опровергнутая до зго времени, инициировала исследование совершенных эафов и привела ко многим интересным результатам.


§ 62. Триангулированные графы

Граф G называется триангулированным (или хордальным), если ни один из его порожденных подграфов не яляется простым циклом длины l ≥ 4. Это означает, что триангулированном графе для любого его простого цикла длины l ≥ 4 есть ребро, соединяющее две несоседние вершины этого цикла. Такое ребро называется хордой.

На рис. 62.1 изображены два графа G и Н, из которыx G является триангулированным, а Н не является.

Очевидйо, что граф является триангулированным, если все его компоненты — триангулированные графы. Следую­щая характеризация связных триангулированных гра­фов принадлежит Г. Дираку. В ней используется поня­тие разделяющего множества вершин. Множество S вер­шин графа G называется разделяющим множеством вер­шин, если граф G — S имеет больше компонент, чем граф G. Если при этом Gi(i=1,i) —компо­ненты графа G—S,то
порожденные подграфы G (VGi U S) называются ча­стями графа G относительно S.

Теорема 62.1. Связ­ный граф является триангулированным тогда и только тогда, когда любое его разделяющее множество вершин, минимальное относительно включения, есть клика.

Необходимость. Пусть G — триангулированный связный граф, S — одно из его минимальных по включе­нию разделяющих множеств вершин, G₁ ,..., G_p — компо­ненты графа G — S, v — некоторая вершина, принадлежа­щая множеству S. Тогда для любого индекса i = 1, р вер­шина v смежна с некоторой вершиной графа G_i , иначе множество S\v было бы также разделяющим.

Пусть v₁ и v₂ — две произвольные вершины из S, a L1=( v₁, и₁, и₂, ..., и₁, v₂), L₂ = (v₁ , w₁, w₂, ..., w_t, v₂) — такие цепи минимальной длины, что (и₁, и₂, ..., и_i) — цепь графа G₁, a ( w₁, w₂, ..., w_t)—цепь графа G₂. По­скольку граф G является триангулированным, то цикл С = L₁ U L₂ имеет хорду. Так как длины цепей L₁ и L₂ минимальны, то эта хорда не может иметь ни один из следующих видов: v_iu_j1, v_iw_k1 , u_j1u_j2 , w_k1w_k2,,(i=1, 2, j1=1,l , j2=1,l, k1=1,t, k2=1,t) А так как вершины графов G₁ и G₂ друг с другом не смежны, то она также не может иметь вид u_iw_k (j=1,l, k=1,t). Таким обра­зом, эта хорда совпадает с v₁v₂ и, следовательно, верши­ны v₁ и v₂ смежны. Тем самым доказано, что множество S является кликой.

Достаточность. Пусть в графе G любое мини­мальное разделяющее множество вершин является кли­кой. Рассмотрим произвольный простой цикл С графа G

д
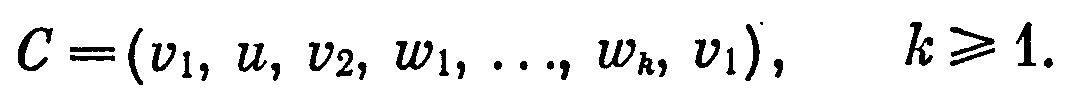
лины, большей трех:

Любой минимальный (v₁, v₂)-сепаратор S (см. § 35) дол­жен содержать вершину и и хотя бы одну из вершин w_i.Так как G (S) — полный граф, то для этой вершины w_i,-ребро uw_i является хордой цикла С.

Теорема 62.2. Каждый триангулированный граф является совершенным.


Доказательство теоремы основано на следующей лемме.

Лемма 62.3. Пусть S — разделяющее множество вер­шин графа G, являющееся кликой. Тогда если каждая часть графа G относительно S — совершенный граф, то и сам граф G — также совершенный.

• Пусть G' — произвольный порожденный подграф графа G, φ(G)=φ, S’ = S∩VG'. Если S^r = VG'_; то G'-полный и потому совершенный граф. Если S' ≠ VG' и граф G' — S' связен, то G' — порожденный подграф не­которой части графа G относительно множества S. По­скольку всякая такая часть совершенна, то и G' — совершенный граф. Остается случай, когда множество S' явля­ется разделяющим для графа G'. Если G’₁ ..., G’_p —части графа G' относительно S’ то любая из них является порожденным подграфом некоторого совершенного гра­фа — соответствующей части графа G относительно множества S. Поэтому она сама — совершенный граф. Сле­довательно, χ(G'i) = φ(G'i) ≤ φ. Вершины графа G', невходящие в S' и принадлежащие различным частям G',не смежны. Поэтому, раскрасив φ цветами вершины каждого из графов Gi так, чтобы любая вершина из множе­ства S' имела при всех этих раскрасках один и тот же цвет, получим правильную φ-раскраску графа G'. Следовательно, χ(G') =φ =φ(G').
  
• Доказательство теоремы 62.2. Воспользу­емся индукцией по числу вершин графа. Для графов по­рядка п ≥ 3 утверждение очевидно. Пусть G — триангулированный граф, \G\ — п>3, и пусть теорема верна для графов с меньшим числом вершин.
  

Полный граф является совершенным. Если же граф G не будет полным, то из теоремы 62.1 вытекает, что в G существует разделяющее множество вершин S, являющее­ся кликой. По индуктивному предположению все части графа G относительно S — совершенные графы. Но тогда по предыдущей лемме и сам граф G является совер­шенным. <

Следующая теорема проливает свет на строение три­ангулированных графов и окажется полезной в даль­нейшем.

Вершина графа называется симплициалъной, если ее окружение — клика.

Теорема 62.4. Любой триангулированный граф имеет симплициалъную вершину. Более того, если этот граф отличен от полного, то в нем есть по меньшей мере две несмежные симплициалъные вершины.

Утверждение теоремы очевидно для полных гра­фов и легко проверяемо для графов, имеющих не более трех вершин. Пусть G — триангулированный граф поряд­ка п > 3, отличный от полного, и пусть теорема верна для графов, порядки которых меньше чем п. Пусть, да­лее, и и v — две несмежные вершины графа G и S — ми­нимальный (и, v) -сепаратор. Обозначим через G_u и G_v части графа G относительно S, содержащие, соответствен­но, вершины и и v. Покажем, что графы G_u и G_v имеют симплициальные вершины, не принадлежащие множест­ву S. Если G_u — полный граф, то симплициальной явля­ется любая его вершина. В противном случае по индук­тивному предположению граф G_u имеет две симплициальные вершины. Поскольку по теореме 62.1 граф G(S) — полный, то хотя бы одна из них не принадлежит S. Аналогично показывается существование симплициальной вершины, не принадлежащей множеству S, в графе G_v. Очевидно, что эти две симплициальные вершины не смежны.

Легко показать, что триангулированным является вся­кий расщепляемый граф. Связь между классами триан­гулированных и расщепляемых графов устанавливается следующей теоремой, полученной С. Фолдесом и П. Хам-мером в 1977 году и содержащей характеризацию рас­щепляемых графов в терминах запрещенных порожден­ных подграфов.


Теорема 62.5. Для графа G следующие утвержде­ния эквивалентны:

1. граф G расщепляем;
   
2. оба графа G и G’ являются триангулированными,
   
3. граф G не содержит порожденных подграфов вида 2К.2, С4 и С5.
   

> 1)=>2). Пусть G — расщепляемый граф. Тогда, по определению, существует разбиение A U В = VG на клику 4 и независимое множество В. Пусть в G есть порожден­ный простой цикл С_p длины р. По меньшей мере одна из двух соседних вершин этого цикла должна быть в А. Но з А любые две вершины смежны, поэтому р ≤ 3. Тем замым доказано, что любой расщепляемый граф является триангулированным. Поскольку дополнительный к рас­цепляемому граф также расщепляем, то истинность импликации 1)=>2) доказана.

Импликация 2)=>) очевидна, поскольку порожден­ный подграф триангулированного графа также должен быть триангулированным, а графы 2К₂, С4 и С5 или их дополнения не такие.

Остается доказать истинность импликации 3)=>1). Пусть граф G не имеет порожденных подграфов вида 2К₂, С4 и С5. Среди всех наибольших клик графа G выберем гакую клику А, чтобы граф G — А имел наименьшее число ребер, и положим В = VG\A. Докажем, что либо В = ¢ (и тогда граф G расщепляем, поскольку он полный), либо В — независимое множество. Пусть, напротив, существует ребро ху, оба конца которого х и у принадлежат множеству В. Каждая из вершин х и у не смежна хотя бы с одной вершиной из клики А, поскольку последняя максимальна. Если бы каждая вершина, входящая в А, кроме некоторой вершины z, была смежна и с х, и с у, то множество (A\ z) U x U у было бы кликой, что противоречит выбору клики А. Следовательно, в А существуют две не­совпадающие вершины и и v такие, что хи ¢ EG и yи ¢ EG.

Так как граф G не имеет порожденных подграфов 2К₂ и С₄,то из двух возможных ребер xv и уи ровно одно действительно есть в G. Пусть, например, xv ¢ EG, уu €EG.

Если |A|>2, то рассмотрим произвольную вершину v € A\(u\v). Пусть вначале yw ¢ EG. Тогда, если хw ¢ EG, то G(x, у, v, w) = 2K₂. Если же xw € EG, то G(х, у, и, w) = C₄. Следовательно, yw €EG и, таким образом, у смежна с каждой вершиной из множества A\v. Поэтому множество A'=A\v U y является наибольшей кликой. Если же вершины w не существует, т. е. |A| =2, то множество А' также является наибольшей кликой.

С
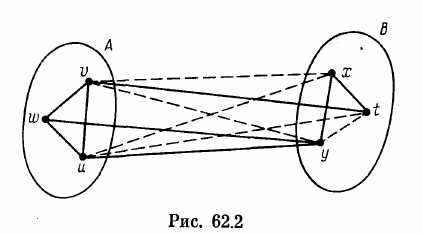
другой стороны, \E(G-A')\>\E{G-A)\, xy€EG, xu¢EG. Поэтому в VG\A существует такая вершина t,что t≠y, tv € EG, ty ¢ EG. Тогда в G должно быть ребро xt, иначе G(t, x, у, v) = 2K₂. Аналогично tu ¢ EG, иначе G (t, х, у, и) = С₄ (см. рис. 62.2, на котором отсутствующие ребра обозначены пунктиром). Но тогда G(t, х, у, и, v) = С5, что противоречит условию. Получен­ное противоречие доказывает, что множество В независи­мо и, следовательно, G — расщепляемый граф.

Как показывают примеры, граф, дополнительный к триангулированному, не обязательно сам является триан­гулированным (например, граф 2К2 = С₄ не является три­ангулированным). Следовательно, класс всех расщепля­емых графов уже класса триангулированных графов.