Раскраски § 53. Правильная раскраска

Вид материала

Документы

Содержание 2 получается из графа G в результате слияния вершин и и v, то f(G,t) = f(G Хроматическая функция любого графа G равна симме хроматических функций некоторого числа полных графов, порядки которых не больше G — дерево порядка п. G ребра, инцидент­ные одной вершине, имеют различные цвета, то χ'(G) ≥ Δ(G). G — двудольный граф с минимальным числом ребер, для которого χ'(G) = ΔA(G)+ G и рассмотрим разбиение множества ребер на цветные классы: Очевидно, что граф G G. Достаточно доказать, что любой полный подграф графа G

Подобный материал:

• Библиотека Гумер психология, 518.71kb.
• Природный календарь рыболова, 117.39kb.
• Сказка о принцессе Смешанное Число. Давным-давно в математическом царстве, арифметическом, 21.17kb.
• Бытие – не-бытие александр Н. Павлов Россия, Санкт-Петербург Июнь 08, 2011, 43.62kb.
• Семейные традиции воспитания в императорских семьях, 91.6kb.
• Isbn 978-5-7262-1376 нейроинформатика 2011, 164.77kb.
• Вышлю почтой из Николаева в любой город Украины. Возможен обмен на диски, которых нет, 222.99kb.
• Недостатки молодого учителя в общении с учащимися и способы их преодоления, 133.12kb.
• Геннадий Дмитриевич Бердышев Теория и практика голодания ради здоровья и долголетия, 6337.41kb.
• И. а. Остренин Научный руководитель В. Г. Когденко,, 27.15kb.

§ 55. Хроматический полином

Поскольку t-раскраской графа G является произволь­ное отображение вида VG->{1, 2, ..., n}, то число по­парно различных t-раскрасок этого графа равно числу всех таких отображений, т. е. tⁿ, где n=\VG\. Но если ограничиться только правильными раскрасками, то вопрос о числе различных среди них становится сложным. Ко­личество попарно различных правильных t-раскрасок графа G называется хроматической функцией графа G и обозначается через f(G, t).

Очевидно, что наименьшее из чисел t, для которых f(G, t)≠0, есть χ (G).

Для некоторых графов хроматическая функция опре­деляется совсем легко. Например, f (О„, t) = tⁿ, так как цвета всех вершин пустого графа можно выбирать неза­висимо друг от друга. При правильной раскраске пол­ного графа К_п первая вершина может иметь любой из t заданных цветов, а для окраски каждой из последующих вершин разрешается использовать н
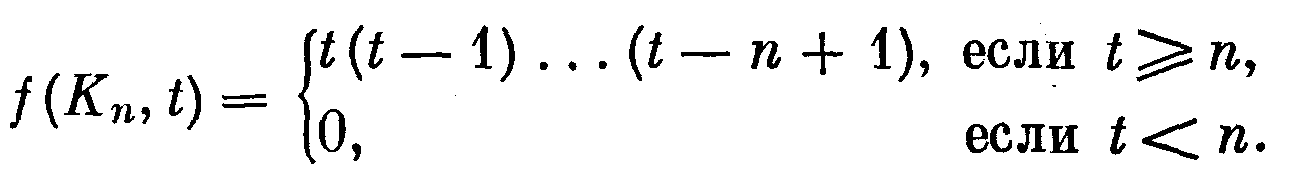
а один цвет меньше, чем для предыдущей. Поэтому f(K_n, t) = t(t—l).... ,(t—n+ 1). Итак, имеем

В общем случае, как отмечалось выше, вычисление хроматической функции сопряжено с большими трудно­стями. Приведем несколько утверждений, позволяющих упрощать ее вычисление.

У
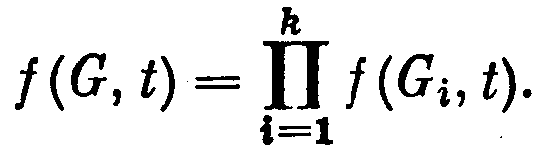
тверждение 55.1. Если G = G1 U G2 U ... U G_k — дизъюнктное объединение графов, то

Это утверждение вытекает из того, что раскраска каждой из компонент G_t может выбираться незави­симо.

У
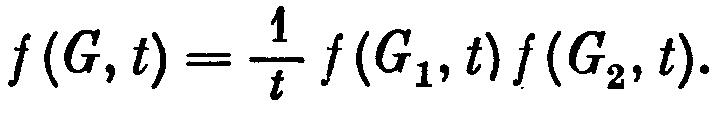
тверждение 55.2. Если G = Gi U G₂ и графы G1 и G₂ имеют только одну общую вершину, то

Фиксируем какую-либо правильную раскраску ƒ1 графа G1. Для продолжения ее до правильной раскраски графа G нужно взять такую правильную раскраску f₂ графа G₂, при которой цвет f₁(v) вершины v, общей для графов G1 и G₂, равен цвету f₂(v). Поскольку число правильных t-раскрасок графа G₂, при которых цвет вер­шины v фиксирован, не зависит от этого цвета, то для выбора раскраски f₂ имеется f(G₂, t)/t возможностей, откуда и следует равенство (1).

Утверждение 55.3. Пусть и и v — две несмежные вершины графа G. Если G1 = G + uv, a G ₂ получается из графа G в результате слияния вершин и и v, то f(G,t) = f(G₁ t) + f(G₂,t).

Число правильных t-раскрасок графа G, при кото­рых цвета вершин и и v различны, не изменится, если к G присоединить ребро uv. Следовательно, это число равно f(G1, t). Аналогично, число правильных f-раскрасок графа G, при которых цвета вершин и и v совпада­ют, равно f{G₂, t). Складывая эти два числа, получим число всех правильных f-раскрасок графа G, т. е. f(Gj).

Предыдущее утверждение позволяет свести вычисле­ние функции f (G, t) произвольного графа G к вычисле­нию хроматических функций графов с большим числом ребер или с меньшим числом вершин, и следовательно, в конце концов,— хроматических функций полных гра­фов. К сожалению, число этих графов может оказаться катастрофически большим.

Очевидно

Следствие 55.4. Хроматическая функция любого графа G равна симме хроматических функций некоторого числа полных графов, порядки которых не больше, чем \G\.

Поскольку f(K_n, t) — полином от t, то верно

Следствие 55.5. Хроматическая функция f(G, t) любого графа является полиномом от t.

Поэтому хроматическую функцию f(G, t) обычно на­зывают хроматическим полиномом графа G.

Н
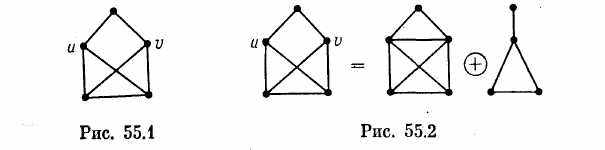
айдем с помощью утверждения 55.3 хроматический полином графа G, изображенного на рис. 55.1. При этом

в
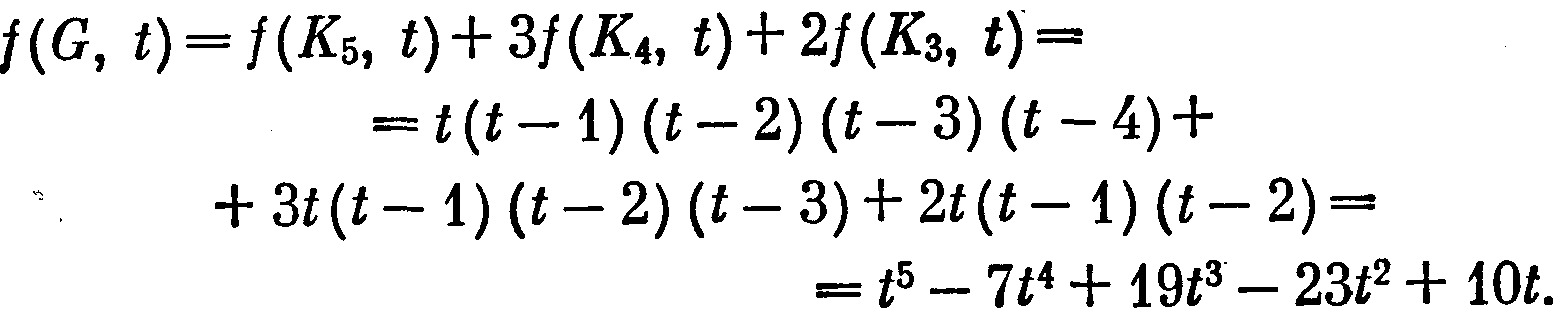
место f(G, t) = f(G₁ t) + f(G₂, t) будем писать G = G1 + G2 или рисовать соответствующие графы. На пер­вом шаге получим ситуацию, представленную на рис. 55.2. Далее см. рис. 55.3. Итак,


Используя утверждение 55.3, можно уточнить вид хроматического полинома. Следующую теорему предла­гаем доказать самостоятельно.

Рис. 55.3

Т
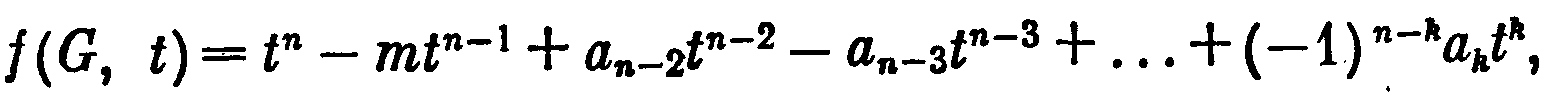
еорема 55.6. Хроматический полином любого (п, т)-графа G, содержащего ровно k связных компо­нент, имеет вид

где а_{ —целые неотрицательные числа.

Несомненный интерес представляет следующий во­прос, ответ па который пока не получен: каким условиям должен удовлетворять полином, чтобы он был хромати­ческим полиномом некоторого графа? Любопытно было бы найти условия, при которых хроматические полино­мы графов совпадают. Примерами таких графов являют­ся деревья, которые можно определить в терминах хро­матических полиномов.

Т
еорема 55.7. Граф G порядка п является деревом тогда и только тогда, когда


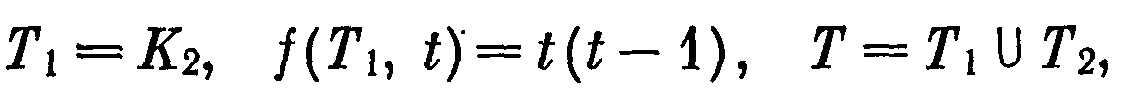
Докажем только необходимость условия теоремы, а достаточность оставим читателю в качестве упражне­ния. Пусть G — дерево порядка п. Воспользуемся индук­цией по п. При п =1 имеем G = K1, f (G, t) = t, при n = 2 — G = K₂, f (G, t) = t(t — 1). Следовательно, при п = 1,2 равенство (2) верно. Предположим теперь, что это равенство верно для любого дерева G порядка m, 2 ≤ m < п, и рассмотрим дерево Т порядка п. Если и — концевая, a v — смежная с ней вершины дерева Т, Т1 = T (u , v), Т₂ = Т - и,то


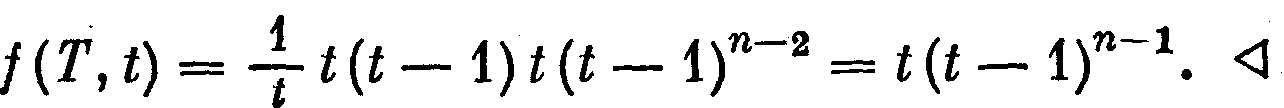
и по индуктивному предположению f(T₂, t) = t (t — l) ^n-2. Применяя затем утверждение 57.2, получаем

§ 56. Раскраска ребер

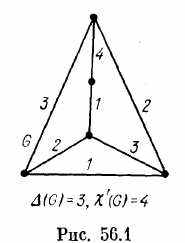Реберной k-раскраской графа G называется функция φ, ставящая в соответствие каждому его ребру е число φ (е) из множества (1, 2, ..., к). Если φ — реберная рас­краска и ф(е) = с, то говорят, что ребро е окрашено в цвет с. Множество всех ребер, окрашенных в фиксиро­ванный цвет, называют реберным цветным классом. Ре­берная раскраска называется правильной, если смежные ребра имеют разные цвета. Граф, допускающий правиль­ную реберную k-раскраску, называется реберно k-раскрашиваемым. Минимальное число k, при котором граф G является реберно k-раскрашиваемым, называется хрома­тическим индексом (хроматическим классом, реберным хроматическим числом) графа G и обозначается через χ‘(G).Если χ '(G) = k, то граф G называется реберно k-хроматическим.

Поскольку ребра любого графа G смежны тогда, когда смежны соответствующие вершины реберного графа L(G), то χ'(G) можно определить как хроматическое число графа L(G),т. е. χ'(G) = χ(L(G)).

При правильной реберной раскраске каждое множе­ство ребер одного цвета является паросочетанием. По­этому число χ'(G) можно рассматри­вать как наименьшее число паросочетаний, на которые разбивается множе­ство ребер графа G.

Поскольку при любой правильной раскраске графа G ребра, инцидент­ные одной вершине, имеют различные цвета, то χ'(G) ≥ Δ(G). Легко приве­сти примеры, когда χ'(G)> Δ(G) (см. рис. 56.1).

С
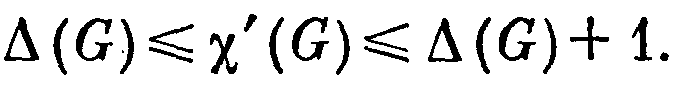
ледующая теорема, принадлежа­щая В. Г. Визингу (1964 г.), дает поразительно точные оценки хроматического индекса графа.

Теорема 56.1. Для любого графа G верны не­равенства

Как отмечалось выше, левое из этих неравенств очевидно, остается доказать правое. Оно верно для К₂. Предположим, что в общей ситуации правое неравенство не выполняется. Среди всех графов, ему не удовлетво­ряющих, выберем граф G с минимальным числом ребер. П
усть е1 € EG, Н = G — е1. Имеем

Пусть Δ = Δ(G). Зафиксируем правильную раскраску φ’: ЕН -> {1, 2, ..., Δ + 1} ребер графа H и скажем, что цвет q € {1, 2, ..., Δ + 1} отсутствует в вершине v € VH, если φ(е) ≠ q для любого ребра е, инцидентного верши­не v. Так как число возможных цветов больше чем Δ, то в каждой вершине отсутствует хотя бы один цвет.

Пусть е1 = ху1, a s и t1 — цвета, отсутствующие в вер­шине х и в вершине у1 соответственно. Исходя из пары у1, t1, построим индуктивно две последовательности —

вершин у1, у2,…, уk и цветов t1, t2, ..., t_h,— удовлетво­ряющие следующим трем условиям:

1. xy_i = e_i € EG ( i=1,k);
   
2. цвет ti отсутствует в вершине y_i(i = i,k);
   
3. φ(e_i+1) = ti (i = 2, k-1).
   

Пусть последовательности у1, ..., у_i и t1, ...., ti уже по­строены. Если существует такое ребро е = ху € ЕН, ин­цидентное вершине x , что у € (у1, ..., уi), φ(е) = t_i, то полагаем уi+1 = y и берем в качестве t_i+1 один из цветов, отсутствующих в вершине у. Если же описанного ребра е не существует, то полагаем k = i. Нужные последова­тельности построены.

Далее возможны две ситуации.

1. Не существует ребра ху € ЕН, для которого φ(xy) = t_h. Переопределим функцию φ, положив φ(е_{) = ti(i = 1, k) и оставив значения на других ребрах неизмен­ными. Получена правильная раскраска φ: EG -> {1, 2, .., Δ + 1} ребер графа G.
   
2. Существует ребро ху € ЕН, для которого φ(ху) = t_k. Тогда это ребро совпадает с каким-либо из e_i (i = 2, к). Пусть, скажем, ху = еj. Снова переопределим функцию φ, полагая φ(ei) = ti (i=1,j —1). Ребро еj пока не окрашено, значения функции φ на всех остальных ребрах не меняются.
   

Рассмотрим остовный подграф F графа G, ребрами которого служат все ребра графа G, имеющие цвет s или t_k. Очевидно, что степень каждой вершины графа F не более двух, и потому каждая его связная компонента является либо простой цепью, либо простым циклом, либо К1. Степени вершин х, y_j, и y_k в F не более едини­цы, следовательно, эти три вершины не могут входить в одну компоненту. Рассмотрим отдельно два случая.

а) Вершины х и y_j, находятся в разных компонентах графа F. В этом случае в компоненте, содержащей вер­шину y_j, переставим цвета s и t_k, т. е. положим φ(е) = s,
если было φ(е) = t_k, и наоборот. Тогда цвет s будет отсутствовать и в вершине x, и в вершине y_j, что позволит положить φ(е) = s. Вновь получается правильная
(Δ + 1)-раскраска ребер графа G.

б) Вершины х и y_h находятся в разных компонентах графа F. Положим φ(е_i) = t_i {i = j, k — i), а ребро е_к оставим пока не окрашенным. Это действие не затраги­вает ребер графа F. Переставим теперь цвета s и t_h в компоненте графа F, содержащей вершину y_h. Теперь цвет s отсутствует и в вершине x, и в вершине у_к. По­лагаем далее φ(е_k) = s.Построена правильная (Δ + 1)-раскраска ребер графа G.

Итак, в любой ситуации строится правильная (Δ + 1)-раскраска ребер графа G, что противоречит не­равенству (1). Это противоречие и доказывает теорему.

В частности, теорема Визинга свидетельствует о том, что теорема 54.5 о существовании графов без треуголь­ников с произвольно большим хроматическим числом пе­рестает быть верной в классе реберных графов, где хро­матическое число и плотность графа различаются не бо­лее чем на 1. Тем не менее даже в этом случае, т. е. в узком классе реберных графов, хроматическое число определяется сложно: несмотря на то, что величина χ'(G) может принимать только два значения — Δ(G) или Δ(G)+1 — ее определение является весьма трудной задачей.

Найдем хроматический индекс для некоторых клас­сов графов.

Т
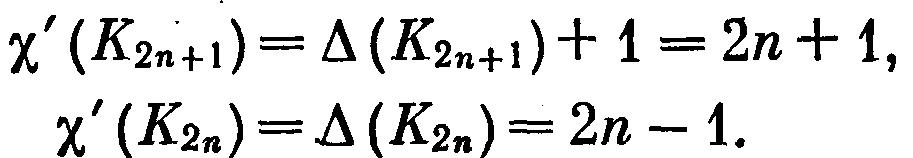
еорема 56.2. Справедливы равенства

Д
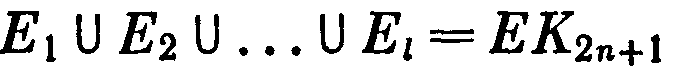
окажем первое равенство. Пусть

—
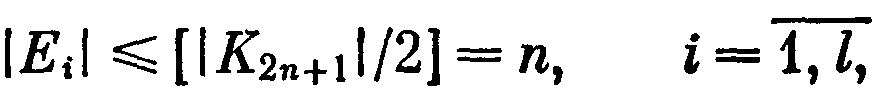
разбиение множества ЕК_2n+1 на цветные классы. Так как ребра одного класса не смежны, то

о
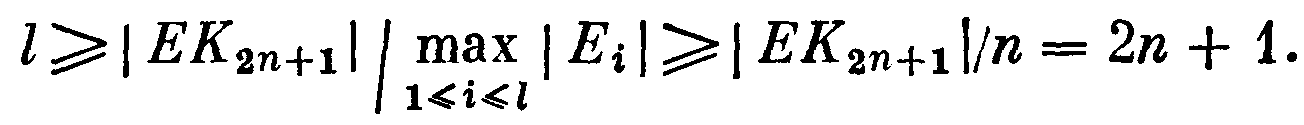
ткуда получаем

Из теоремы 56.1 теперь следует, что χ'(К_2n+1)=l=2n+1.

Перейдем ко второму соотношению. Пусть v — про­извольная вершина графа К_2n - Рассмотрим граф G = К_2n — v = K_2n-1. По доказанному выше ребра графа G можно раскрасить 2п — 1 цветами. Так как степень лю­бой вершины и графа G равна 2n — 2, то некоторый цвет не будет представлен в вершине и. С другой стороны, множество всех ребер цвета c_i образует паросочетание в графе G. Поэтому вследствие нечетности \VG\ найдется такая вершина и_i, что цвет c_i, будет отсутствовать в и_i Отсюда следует, что цвета, отсутствующие в вершинах графа G, попарно различны. Для получения требуемой раскраски ребер графа К_2п нужно приписать каждому ребру vи_i цвет, не представленный в вершине и_i.

Теорема 56.3 (Д. Кёниг, 1931). Для любого дву­дольного графа G верно равенство χ' (G) = Δ (G).

Пусть, напротив, утверждение теоремы неверно, и G — двудольный граф с минимальным числом ребер, для которого χ'(G) = ΔA(G)+ 1. Тогда для любого ребра ее EG справедливо равенство χ'(G - е) = Δ(G — e) ≤ Δ(G). Зафиксируем ребро e = uv € EG и правильную реберную Δ(G)-раскраску φ графа G — e и обозначим че­рез М_w множество цветов, отсутствующих в некоторой вершине w. Очевидно, что М_и≠ ¢, M_v ≠ ¢. Если М_и ∩ M_v ≠ ¢, то ребро е можно окрасить в цвет, принадле­жащий этому пересечению. Поэтому М_и ∩ M_v ≠ ¢. Пусть s € M_u, t € M_v. Рассмотрим цепь L, начинающуюся в вер­шине v, ребра которой попеременно окрашены в цвета s и t и которая имеет наибольшую длину среди таких цепей. Вершина и не входит в L, иначе (v, и)-подцепь цепи L вместе с ребром е образовала бы в графе G цикл нечетной длины, что невозможно в двудольном графе. Переставив цвета s и t в цепи L, можно затем окрасить ребро е в цвет s, что противоречит исходному предполо­жению.

Типичная ситуация отражается следующей теоремой, приводимой без доказательства (см. обзор [21]).

Теорема 56.4. Для почти каждого графа G верно равенство

χ’(G) = Δ(G).

§ 57. Связь матроидных разложений графов с раскрасками

Отметим простые связи, существующие между матро-идными разложениями графов и раскрасками. Напомним, что матроидным разложением графа G называется пред­ставление его в виде объединения

G = G₁ U G₂ U ... U G_μ

М-графов, т. е. графов, все связные компоненты которых суть полные графы; минимальное число μ компонент в матроидных разложениях графа G — матроидное чис­ло μ(G).

З
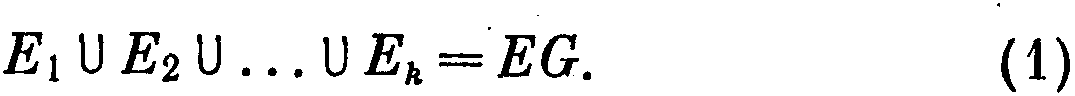
афиксируем правильную раскраску ребер графа G и рассмотрим разбиение множества ребер на цветные классы:

Очевидно, что граф G_i для которого VG_i = VG, EG_i = E_i, является M-графом, и

G = G₁ U G₂ U ... U G_k (2)

— матроидное разложение. Итак, разбиение на цветные классы (1) определяет матроидное разложение (2) гра­фа G. Тем самым доказано

Утверждение 57.1. Для любого графа G верно неравенство

μ(G)<χ’(G)

Учитывая это неравенство и теорему 56.3, получаем

Утверждение 57.2. Если граф G не содержит тре­угольников, то

μ(G)<χ’(G)

Для любого двудольного графа G верно равенство

μ(G) = Δ(G).

Если граф G не содержит треугольников, то его реберный граф L(G) и граф клик Q(G) могут разли­чаться только изолированными вершинами. Следователь­но, если χq(G)—хроматическое число графа Q(G), то χq(G) = χ’(G), так что для графа G без треугольников μ(G)=χq(G) = χ’(G). Применяя теорему 56.3, получим второе равенство.

Для матроидного числа произвольного графа хрома­тическое число его графа клик является верхней грани­цей. А именно, верно

У
тверждение 57.3. Для любого графа G справед­ливо неравенство

Подграф, порожденный в G объединением клик, входящих в один цветной класс при правильной вершин­ной раскраске графа клик Q(G), является M-графом, по­скольку все его связные компоненты — полные графы. Следовательно, если

V₁U V₂ U...U V_k = VQ(G)

— разбиение на цветные классы множества вершин гра­фа клик, a Gi получается из порожденного подграфа G(V_i) в результате присоединения всех вершин из VG\ V_i как изолированных, то G = G₁ U G₂ U ... U G_k — матроидное разложение. Тем самым неравенство (3) доказано.

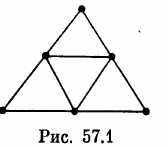
В качестве иллюстрации рассмотрим граф G, изобра­женный на рис. 57.1; для него Q(G) = K₄, χ q(G) = χ’(G)=4, μ(G)=3.

Утверждение 57.4. Для произвольного графа G равенства μ(G) = 2 и χq(G) = 2 равносильны.

Если χq(G) = 2, то μ(G) ≤ 2. Но при μ(G) =1 ни­какие две максимальные клики графа G не пересекают­ся, и потому Q(G)—пустой граф, χq(G) =1. Итак, при χ(G) = 2и μ(G) = 2.

О
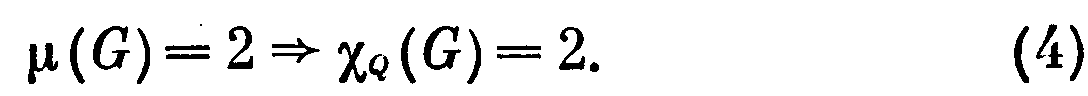
стается доказать истинность импликации

Доказательство основано на следующей очевидной комбинаторной лемме.

Лемма 57.5. Пусть S — конечное множество, каждо­му из элементов которого приписан один из двух фикси­рованных цветов или оба эти цвета. Если для любой пары элементов множества S существует общий приписанный им цвет, то тогда и все элементы множества имеют об­щий приписанный им цвет.

Пусть теперь

G = G₁ U G₂ (5)

— матроидное разложение графа G. Достаточно доказать, что любой полный подграф графа G целиком содержится в каком-либо из G_i; если это так, то разложение (5) определяет правиль­ную 2-раскраску графа клик и истин­ность импликации (4) доказана.

Каждому из ребер графа G следую­щим образом припишем один из цве­тов {1, 2} или оба эти цвета. Именно, всем ребрам графа G_i (i = l, 2) при­писывается цвет i. Пусть теперь Q — клика графа G, e_ue₂ € EG(Q).

Если ребра е₁ и е₂ смежны, то в порожденном под­графе G(Q) существует третье ребро е, смежное с ними обоими. Какие-то два из этой тройки ребер имеют общий цвет, поскольку цветов только два. Но концы этих трех ребер вместе входят в одну из связных компонент гра­фа Gi, являющихся полными графами, следовательно, а третье ребро имеет тот же цвет. Итак, для любой пары смежных ребер графа G(Q) существует общий приписан­ный им цвет.

Если же ребра е₁ = u₁v₁ и е₂ = u₂v₂ не смежны, то в графе G(Q) есть еще четыре ребра е₃ = u₁u₂, е₄ = v₁v₂, е₅ = u₁v₂, е₆= v₁u₂. Для каждой пары смежных из этих ребер существует общий цвет, откуда очевидно вытека­ет, что существует цвет, общий для ребер е₁ и е₂.

Доказано, что любые два ребра графа G(Q) имеют общий цвет. В силу леммы 57.5 существует общий цвет, например 1, приписанный всем ребрам графа G(Q). По­следнее означает, что G(Q) содержится в одной из ком­понент графа G₁.

Из утверждения 57.4 вытекает

Следствие 57.6. Если χ(G) = 3, то и μ(G) = 3.