Биографические сведения

АРИСТОТЕЛЬ (348-322 гг до н. э.) - основоположник логики. Написал книги «Категории», «Первая аналитика», «Вторая аналитика». (Исследовал различные формы рассуждений, ввел понятие силлогизма.)

А

ристотель родился в горо­де Стагира на фракийском по­бережье полуострова Хальки-дика. Его отец был врачом и другом македонского царя Аминта II. Аристотель рос и учился вместе с сыном Амин­та — будущим царем Филип­пом II Македонским, и на про­тяжении всей жизни его судьба была тесно связана с македон­ским царским домом. В воз­расте 18 лет Аристотель отпра­вился в Афины к великому мыслителю Платону и провел в его школе около 20 лет. Он был самым выдающимся из учеников Платона, глубоко ус­воившим его знания и идеи, но далеко не всегда согласным со своим учителем. В 343 г. до н. э. царь Филипп приглашает друга своей юности, ставшего тем временем величайшим ученым, быть наставником своего сына Александра. Когда через не­сколько лет Александр сам ста­новится царем, знаменитым Александром Македонским, Аристотель возвращается в Афины и собирает вокруг себя учащуюся молодежь, которой читает курсы различных наук. В 323 г. до н. э. умер Александр Македонский, и в Афинах по­бедила антимакедонская пар­тия. Аристотель, как друг и учи­тель Александра, должен был покинуть Афины. Год спустя он умер на острове Евбея.

Г. В. ЛЕЙБНИЦ (1646-1716)

Г

отфрид Вильгельм Лейб­ниц родился в г. Лейпциге (Саксония). Его отец был про­фессором этики, а дед — про­фессором права Лейпцигского университета. Обширная до­машняя библиотека позволила способному юноше параллель­но с гимназическим образова­нием получить глубокие позна­ния как в классической, так и современной науке. В 1661 г. Лейбниц становится студен­том и изучает философию, юриспруденцию и математику в университетах Лейпцига, Иены и Альтдорфа. В 1666 г. он защищает сразу две диссер­тации на звание доцента — по юриспруденции и математике. Затем Лейбниц служит при дворах немецких князей в качестве юриста, находится на дипломатической работе. С 1676 г. и до самой смерти Лейбниц состоял советником и библиотекарем при дворе ганноверского герцога. На протяжении этих 40 лет Лейб­ниц вел научные исследова­ния, публиковал научные тру­ды, поддерживал переписку со всеми ведущими учеными эпохи.

Лейбниц был универсальным ученым, внесшим суще­ственный клад в философию, юриспруденцию,

историю, физику и математику. Он яв­ляется одним из создателей дифференциального и инте­грального исчислений, комби­наторики, теории определите­лей. Значительна и научно-ор­ганизаторская деятельность Лейбница — он был одним из основателей Прусской акаде­мии наук в Берлине. Вклад в логику - предложил использовать в логике математическую символику и впервые высказал мысль о возможности применения в ней двоичной системы счисления.


ДЖ. БУЛЬ (1815-1864)

Д

жордж Буль родился в Линкольне (Англия) в семье мелкого торговца. Материаль­ное положение его родителей было тяжелым, поэтому Джордж смог закончить толь­ко начальную школу для детей бедняков; в других учебных за­ведениях он не учился. Этим, может быть, отчасти и объяс­няется, что, не связанный тра­дициями, он пошел в науке своим оригинальным путем. Мальчиком Буль самостоя­тельно изучил латынь, древне­греческий, немецкий и фран­цузский языки, прочел основ­ные философские трактаты. С ранних лет начался трудовой путь Буля — он искал работу, дающую какой-то заработок и в то же время оставляющую возможности для дальнейшего самообразования. После многих неудачных попыток Булю удалось открыть маленькую элементарную школу, в кото­рой он преподавал сам. Школьные учебники по мате­матике привели его в ужас сво­ей нестрогостью и нелогично­стью. Буль вынужден был об­ратиться к сочинениям клас­сиков науки и самостоятельно проштудировать обширные труды Лапласа и Лагранжа.

В связи с этими занятиями у него появились первые само­стоятельные идеи. Результаты своих исследований Буль со­общал в письмах профессо­рам математики (Д. Грегори, А. де Моргану) знаменитого Кембриджского университета и вскоре получил известность как оригинально мыслящий математик. В 1849 г. в г. Корк (Ирландия) открылось новое высшее учебное заведение — Куинз колледж. По рекомен­дации коллег-математиков Буль получил здесь профессу­ру, которую сохранил до своей смерти в 1864 г. Только здесь он имел возможность не толь­ко обеспечить старость роди­телей, но и спокойно, без мыс­лей о хлебе насущном, зани­маться наукой. Здесь же он же­нился на дочери профессора греческого языка Мери Эве­рест, которая не только много помогала Булю в работе, но и оставила после его смерти ин­тересные воспоминания о сво­ем муже; она стала матерью че­тырех дочерей Буля, одна из которых — Этель Лилиан Буль, в замужестве Войнич, — автор популярного в нашей стране романа «Овод».

Вклад в логику - 1847 г. – Джордж Буль в работе «Математический анализ логики» изложил основы булевой алгебры. Разработал алфавит, орфографию и грамматику.


К. ШЕННОН

К

лод Эльвуд Шеннон окончил в середине 30-х гг. Мичиганский университет, защитив там два диплома бака­лавра — по электротехнике и по математике. Получив рабо­ту в Массачусетском техноло­гическом институте, он, желая подработать, выполнял обя­занности оператора «диффе­ренциального анализатора» — механического вычислитель­ного устройства, решающего сложные дифференциальные уравнения. Главный недоста­ток этого механизма состоял в том, что расчеты проводились в десятичной системе счисления; чтобы поставить машине задачу, оператор, пачкаясь в машинном масле, несколько дней вручную подбирал поло­жения шестереночных пере­дач. Шеннон решил усовер­шенствовать «дифференциаль­ный анализатор», заменив шестеренки и валики электри­ческими схемами. В своей док­торской диссертации, опубли­кованной в 1938 г., Шеннон изложил свои идеи о примене­нии алгебры логики в электри­ческих цепях. Данная работа считается поворотным пунк­том в развитии вычислитель­ной техники. 1938 г. – американский математик и инженер Клод Шеннон связал Булеву алгебру (аппарат математической логики), двоичную систему кодирования и релейно-контактные переключательные схемы, заложив основы будущих ЭВМ.

ТЕМА «АЛГЕБРА ВЫСКАЗЫВАНИЙ. ОСНОВНЫЕ ОПЕРАЦИИ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ»

1. Что такое логика? Формальная логика. Математическая логика.

2. Этапы развития логики.

3. Применение математической логики.

4. Алгебра высказываний. Простые и сложные высказывания.

5. Основные операции алгебры высказываний.


1. Что такое логика? Формальная логика. Математическая логика.

LOGOS (греч.)- слово, понятие, рассуждение, разум. Слово «логика» обозначает совокупность правил, которым подчиняется процесс мышления. Основными формами абстрактного мышления являются: понятия, суждения, умозаключения. Понятие - форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов. (трапеция, дом) Суждение - мысль, в которой что-либо утверждается или отрицается о предметах. (Весна наступила, и грачи прилетели) Умозаключение - прием мышления, посредством которого из исходного знания получается новое знание. (Все металлы - простые вещества). Логика (формальная) - наука о законах и формах правильного мышления. Математическая логика - изучает логические связи и отношения, лежащие в основе логического (дедуктивного) вывода.


2. Этапы развития логики.

I. АРИСТОТЕЛЬ (384-322 гг. до н.э.) - ОСНОВОПОЛОЖНИК ЛОГИКИ

Силлогизм - рассуждение, в котором из заданных двух суждений выводится третье.

1. Все млекопитающие имеют скелет. Все киты - млекопитающие. Следовательно, все киты имеют скелет.

2. Все квадраты - ромбы. Все ромбы - параллелеграммы. Следовательно, все квадраты - параллелограммы.

Аристотель выделил все правильные формы силлогизмов, которые можно составить из рассуждений вида:

«Все А суть В»; «Некоторые А суть В»; «Все А не суть В»; «Некоторые А не суть В»

Логика, основанная на теории силлогизмов называется классической.

II. Декарт Рене (1596-1650, фр. философ, математик). Рекомендовал в логике использовать математические методы.

III. Лейбниц Г.В. (1646-1716, нем. ученый и математик) - gредложил использовать в логике математическую символику и впервые высказал мысль о возможности применения в ней двоичной системы счисления.

IV. Джордж Буль (1815-1864, анл.) - основоположник мат. логики. 1847 г. – Джордж Буль в работе «Математический анализ логики» изложил основы булевой алгебры. Разработал алфавит, орфографию и грамматику.

V. ВКЛАД В СТАНОВЛЕНИЕ И РАЗВИТИЕ МАТ. ЛОГИКИ: Аугустус де Морган (1806 - 1871); Уильям Стенли Джевонс (1835 - 1882); Платон Сергеевич Порецкий (1846-1907); Чарлз Сандерс Пирс (1839-1914)


4. Алгебра высказываний. Простые и сложные высказывания.

Алгебра высказываний - раздел математической логики, изучающий высказывания и логические операции над ними.

Высказывание - это повествовательное предложение, о котором можно сказать, что оно истинно или ложно.

Высказываниями не являются: 1) восклицательные и вопросительные предложения. 2) определения.

3) предложения типа: «он сероглаз»; «x²-4x+3=0».

Высказывание, которое можно разложить на части, будем называть сложным, а неразложимое далее высказывание - простым.

Логическая операция	Обозначения	Эквивалент в русском языке
Инверсия (логическое отрицание)	НЕ, NOT, 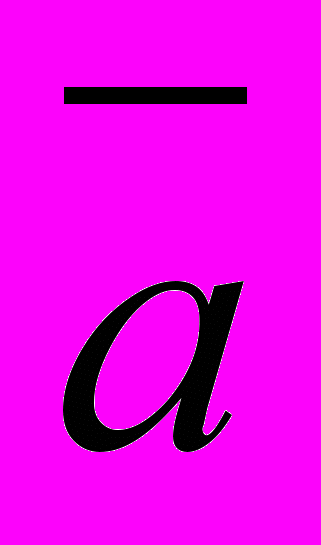,	не; неверно, что ...
Конъюнкция (логическое умножение)	И, AND, , &, • , 	И А НО
Дизъюнкция (логическое сложение)	ИЛИ, OR, , +, , 	Или; Либо…, либо … Или…, или…
Импликация (логическое следование)	, , 	если ..., то ...; из ... следует ...; ... достаточно для ...; для ... , необходимо ...
Эквиваленция (логическое равенство)	, , , 	... если и только если ...; ... тогда и только тогда, когда ...; … в том и только в том случае, когда ...; необходимо и достаточно

Домашнее задание.

1. Выучить конспект. Подготовиться к тестированию.
   
2. Знать ответы на вопросы: основные формы абстрактного мышления, что изучает формальная логика; что изучает математическая логика; изложите основные этапы развития логики; области применения математической логики; что такое высказывание; какие высказывания бывают; какие высказывания называются простыми, а какие – сложными; что не является высказыванием; основные логические операции и их свойства; приоритет логических операций.