Эварист Галуа (биографические сведения)
| Вид материала | Документы |
- Дальма А. Эварист Галуа, революционер и математик: Пер с франц. 2-е изд, 683.55kb.
- Урок-обсуждение тема: «Житие Аввакума, им самим написанное», 96.84kb.
- Муниципальное общеобразовательное учреждение, 663.62kb.
- Урок по теме «Жизнь и творчество Владимира Маяковского», 15.69kb.
- Урока: Михаил Юрьевич Лермонтов. Судьба поэта, 182.07kb.
- Биографические кризисы личности, 360.86kb.
- Тема Содержание, 64.24kb.
- Введение 2 Биографические сведения. 2 Теория и практика., 152.5kb.
- Биографические сведения, 75.08kb.
- Краткие биографические сведения о руководителях Криволапов Александр Наумович, 37.41kb.
Зарождение теории Галуа (XIX век)
Эварист Галуа (биографические сведения)
Эварист Галуа родился 26 октября 1811г. в небольшом французском городке Бур-ля-Рен в десяти километрах от Парижа. До 12 лет Галуа обучался под руководством матери. В октябре 1823г. Эварист был принят в Королевский колледж Луи-ле-Гран в Париже (сегодня лицей Луи-ле-Гран). Первые три года он считался одним из лучших учеников и с удовольствием занимался языками, литературой, историей. В октябре 1926г. Галуа начал заниматься в старшем классе колледжа – классе риторики, однако у него появились признаки утомления, и по рекомендации директора в январе 1927г. он вернулся на повторный курс. Там он вновь без труда стал одним из первых учеников, и в это же время Галуа начинает всерьез интересоваться математикой. По правилам колледжа учащиеся, питавшие интерес к точным наукам, могли в последние два года обучения заниматься математикой в подготовительном математическом классе. После подготовительного класса ученик мог пройти годичный основной и годичный специальный математические классы. Галуа воспользовался этим правилом: вернувшись на повторный курс, он одновременно поступил в подготовительный математический класс. Почти сразу же обнаружились его феноменальные математические способности. Он без труда одолел книгу Лежандра «Основы геометрии» и взялся за изучение сочинений Лагранжа «Решение численных уравнений», «Теория аналитических функций», «Лекции по теории функций».
Осенью 1827г. Галуа возвращается в класс риторики и продолжает занятия в подготовительном математическом классе. Он знакомиться с трудами Гаусса и Абеля. Без посторонней помощи он готовится к экзаменам в Политехническую школу.
Однако попытка поступить в Политехническую школу окончилась неудачей. Ему пришлось вернуться в колледж. К счастью, он перескочил через основной и оказался в специальном математическом классе, где работал Луи-Поль Ришар, блестящий преподаватель, оценивший способности Галуа. Под руководством Ришара Галуа написал свою первую научную работу «Доказательство одной теоремы о периодических непрерывных дробях», опубликованную в марте 1829г. в «Анналах математики». В это же время под влиянием работ Лагранжа Галуа начинает заниматься проблемой разрешимости алгебраических уравнений в радикалах. Первые результаты появились у него еще весной 1829г. Галуа направил их в Академию наук. Рассмотреть его работу взялся Коши, но, увы. По окончании учебного года Галуа вновь сделал попытку поступить в Политехническую школу и вновь провалился. По совету Ришара Галуа поступил в Приготовительную школу. 20 февраля 1830г. Эварист Галуа стал ее студентом.
Первый год обучения в Приготовительной школе оказался самым успешным в жизни Галуа. Здесь он познакомился с Огюстом Шевалье, и это знакомство быстро переросло в крепкую дружбу. Галуа увлеченно занимался математикой, написал три научных работы и представил их на конкурс в Академию. Однако рукопись Галуа попала в руки секретаря Академии Фурье, который вскоре после этого умер. Галуа сохранил копию и даже опубликовал свои работы в апрельском и июньском номерах «Бюллетеня математических наук», Галуа тут же кинулся «переделывать общество» и включился в политическую борьбу. Отдав свои симпатии республиканцам, Галуа вступил в Общество друзей народа, активно участвовал в работе революционных кружков. После восстановления монархии осенью 1830г. Галуа выступает в печати с резкой критикой двурушнического поведения в июльские дни директора Приготовительной школы Гиньо. Как следствие, его исключают из школы. Но математика уже отошла на второй план – все силы Галуа отданы революции. И тем не менее он нашел силы и время, чтобы еще раз послать свои работы на конкурс в Академию. Работы попали в руки Лакруа и Пуассону, которые в итоге сообщили, что не могут оценить рукопись положительно.
В июне 1831г. Галуа предстал перед судом по обвинению в попытке спровоцировать покушение на короля, был оправдан, но попал под надзор тайной полиции. 14 июля 1831г. Галуа принял участие в демонстрации, за что был задержан и оказался в тюрьме Сент-Пелажи. Здесь он отредактировал свое основное математическое сочинение «Мемуар об условиях разрешимости уравнений в радикалах». 29 апреля 1832г. кончился срок его заключения. Утром 30 мая какой-то прохожий нашел его тяжело раненым после дуэли на пистолетах на берегу пруда Глясьер в пригороде Парижа. Утром следующего дня Галуа скончался. Перед дуэлью он написал ряд писем, в том числе своему другу Шевалье и завещал ему все свои рукописи.
Эварист Галуа (биографические сведения) 1
2
При жизни Галуа практически не публиковался. Среди нескольких заметок и статей, выход в печать которых он успел застать, наиболее замечательна статья «Из теории чисел»1. В этой статье Галуа рассматривает полиномиальные сравнения вида
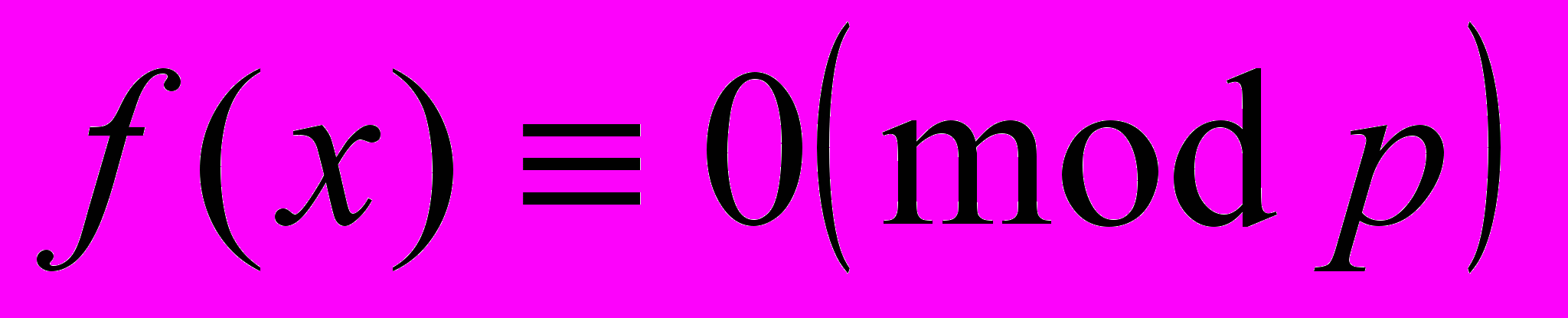 , не имеющие целых корней. Он рассматривает весьма полезную конструкцию присоединения к полю корня неприводимого уравнения, явно выделяя требование неприводимости и проводя аналогию с присоединением
, не имеющие целых корней. Он рассматривает весьма полезную конструкцию присоединения к полю корня неприводимого уравнения, явно выделяя требование неприводимости и проводя аналогию с присоединением 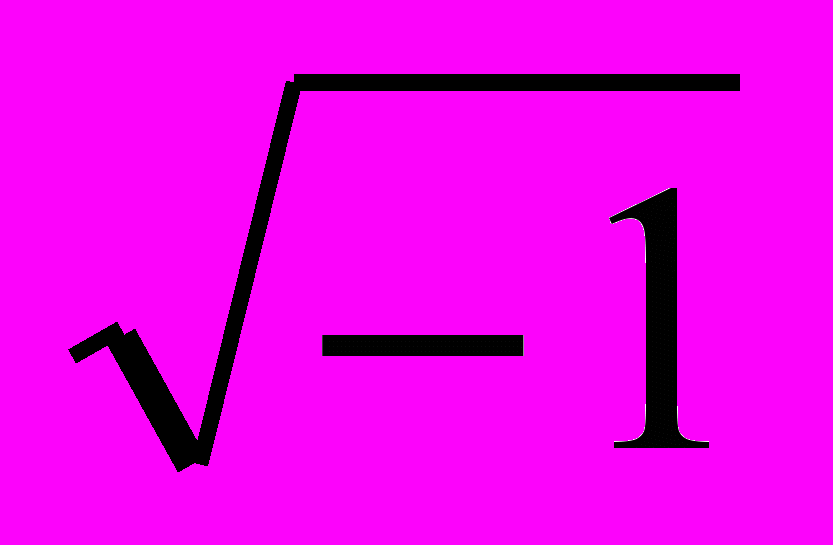 в анализе, и доказывает ряд теорем о конечных полях.
в анализе, и доказывает ряд теорем о конечных полях. Галуа завещал свои рукописи своему другу Огюсту Шевалье, в том числе свою основную работу «Мемуар об условиях разрешимости уравнений в радикалах». В последнем письме он пишет: «Я в своей жизни часто отваживался высказывать утверждения, в которых не был уверен; но все, что я написал здесь, у меня в голове скоро год, и слишком в моих интересах не ошибаться, чтобы меня можно было заподозрить в том, что я высказываю теоремы, полным доказательством которых не обладаю. Ты публично попросишь Якоби или Гаусса высказать их мнение не об истинности, а о важности этих теорем. После этого, надеюсь, найдутся люди, которые с пользой для себя расшифруют всю эту путаницу». Это письмо было опубликовано в 1832г. в «Энциклопедическом обозрении». Рукописи Шевалье получил от семьи Галуа. Неизвестно, какие усилия были приложены Шевалье и братом Галуа Альфредом, чтобы его работы были напечатаны. Альфреду повезло дожить до того времени, когда его брат стал знаменитым. Пытаясь привлечь внимание е работам брата, он встречался со многими математиками. Сохранилась копия письма от Альфреда к Якоби и переписанные Шевалье работы Галуа. Безусловно, трагедией для математики оказалась неполнота работы Галуа на момент его смерти, мало кому была охота разбираться в чужих набросках и вникать в их смысл, слишком больших усилий это требовало. Неизвестно, каким образом работы Галуа в конце концов попали в руки Лиувилля. К счастью, он честно попытался в них разобраться и самую важную часть опубликовал, сделав труды Галуа доступными широким математическим кругам.2 («Журнал чистой и прикладной математики», 1846г.). В отдельном издании в 1897г. работы Галуа занимают всего лишь 60 страниц формата А7 (одна восьмая листа).
В 1862г., Бурнем и Азра были опубликованы отрывки из ранних работ Галуа3. Они включают в себя школьные работы, спасенные Ришаром и заботливо сохраненные Эрмитом для потомства. Один фрагмент из публикации 1828г. показывает, что Галуа, как и Абель в свое время, на первых порах считал, что может решить уравнение пятой степени.
В 1870г., почти сорок лет после смерти Галуа, Камилль Жордан написал книгу «Алгебраические уравнения и теория подстановок». В предисловии говорится, что эта книга - лишь комментарий к работе Галуа. Именно этот труд привлек внимание математического мира к работам Галуа, потому что впервые открытия Галуа предстали перед читателями не в разрозненном виде, а в систематическом изложении, понятном для всех. В предисловии к своей книге Жордан пишет: «Галуа было суждено дать четкое обоснование теории разрешимости уравнений. […] Коренных идей три… идея приводимости, появившаяся уже в трудах Гаусса и Абеля, идея переходности, высказанная Коши, и, наконец, различие между простыми и сложными группами. Последней, наиболее важной из трех, мы обязаны Галуа». С момента выхода этой книги теория Галуа стала элементом математического образования и фундаментом для новых математических исследований.
Однако в работах Галуа содержалось нечто большее, чем удалось расшифровать его последователям. Галуа оставил туманную запись о связях между алгебраическими уравнениями и трансцендентными функциям и сделал таинственный намек на «теорию неоднозначности»4. Вполне возможно, это касалось многозначности трансцендентных функций, и, скорее всего, все то, что хотел сказать Галуа, было впоследствии сказано Риманом. Что же касается трансцендентных функций, в 1858г. Эрмит успешно завершил одно из исследований Галуа в решении уравнений пятой степени с помощью эллиптических модулярных функций, а в 1870г. Жордан выступил с теорией групп, управляющей поведением таких функций. Однако возможно, что Галуа имел в виду нечто большее.
В 1906 и 1097 годах Жюль Таннери опубликовал большую часть из оставшихся посмертных рукописей Галуа. С научной точки зрения они не имели особенного значения по сравнению с теми, которые еще в 1846г. опубликовал Лиувилль. 5
Эварист Галуа (биографические сведения) 1
2
Проблема разрешимости алгебраических уравнений в радикалах имеет долгую историю. Еще древние вавилоняне открыли способ решения уравнений второй степени
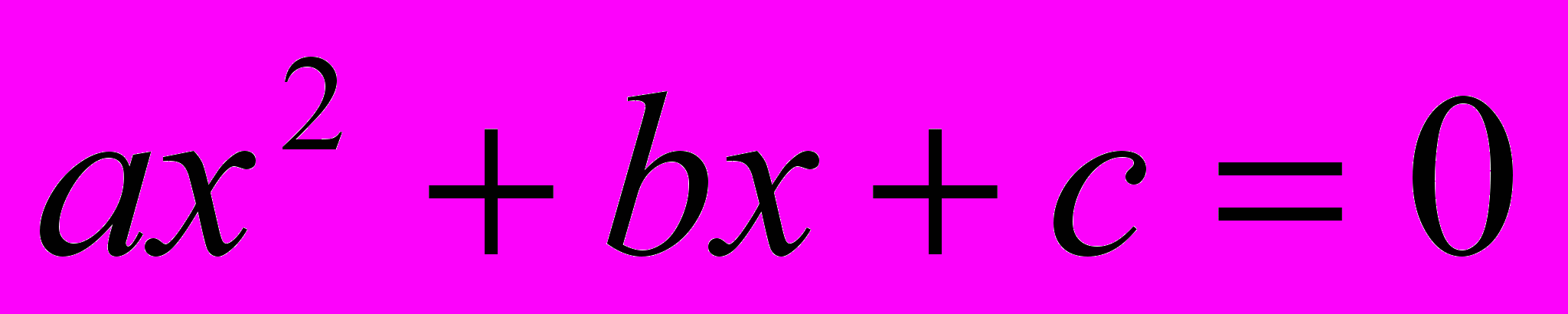 . Его корни находятся по формуле, известной сегодня каждому школьнику:
. Его корни находятся по формуле, известной сегодня каждому школьнику: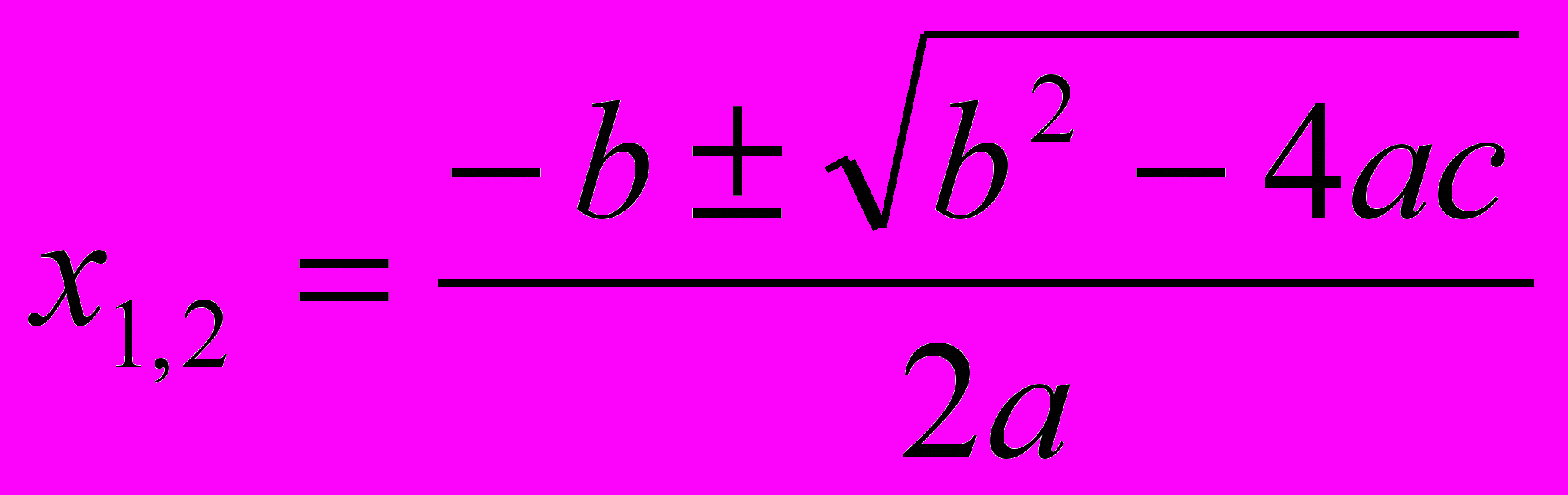
Заметим, что в это уравнение входят четыре арифметических действия над коэффициентами и квадратный радикал. В начале XVI века Сципионе дель Ферро и Николо Фонтана, более известный под именем Тарталья, получили формулу для корней кубического уравнения вида6
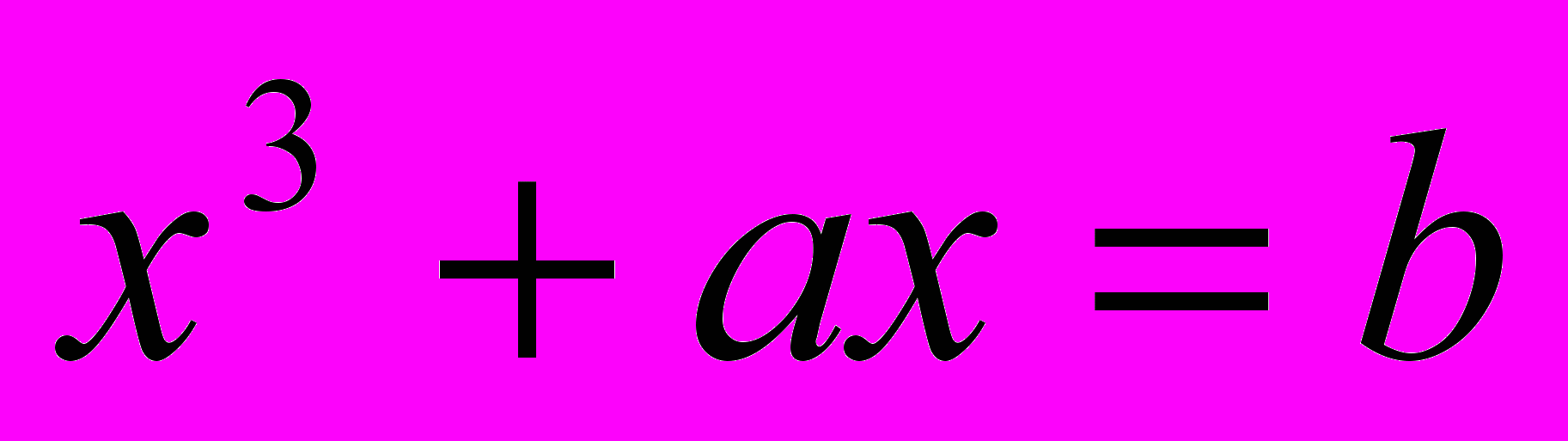 .
. 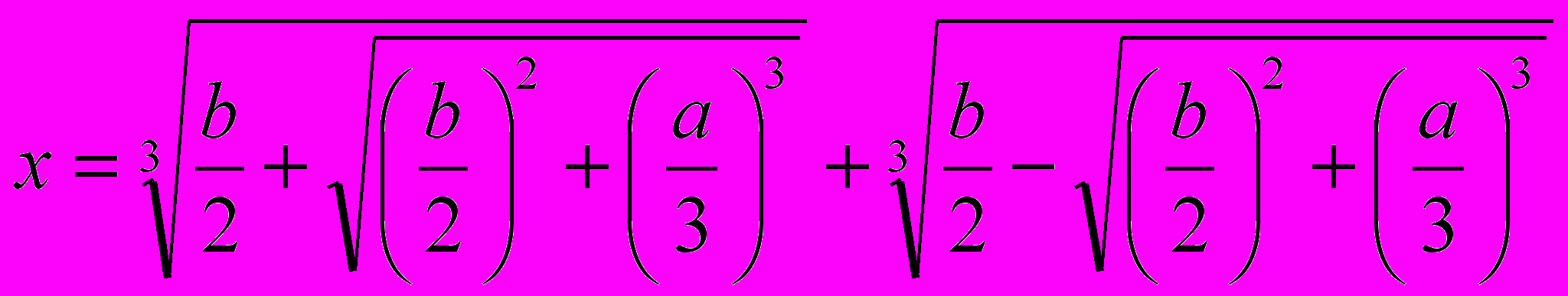
Как мы видим, в нее входят четыре арифметических действия, квадратный и кубический радикалы. Несколько позже Лодовико Феррари открыл формулу для корней четвертой степени, в которую входили радикалы самое большее четвертой степени. И естественно было бы ожидать, что корни алгебраического уравнения степени
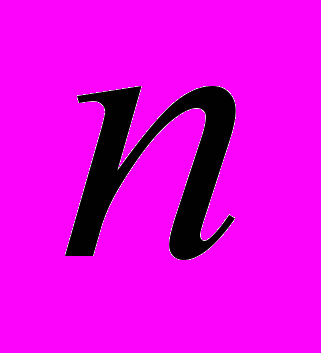
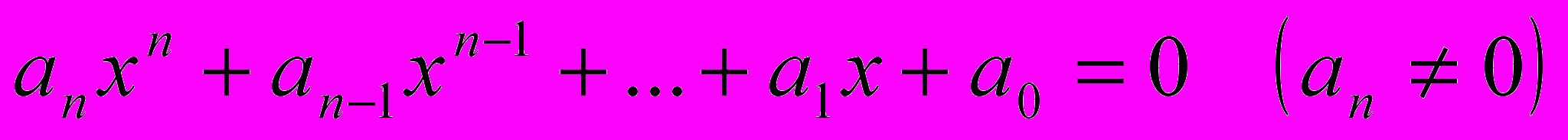
должны выражаться через радикалы самое большее
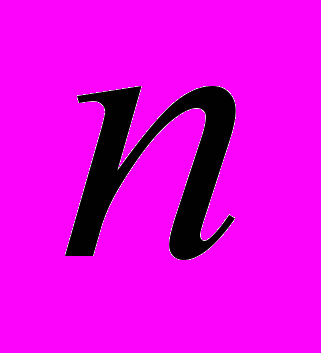 -ой степени. Однако усилия, прикладываемые многими выдающимися математиками на протяжении многих веков в поисках заветной формулы, оказались напрасными. Даже для уравнений пятой степени формулу получить не удалось. В конце концов, математики стали подозревать, что формул для уравнений степени
-ой степени. Однако усилия, прикладываемые многими выдающимися математиками на протяжении многих веков в поисках заветной формулы, оказались напрасными. Даже для уравнений пятой степени формулу получить не удалось. В конце концов, математики стали подозревать, что формул для уравнений степени 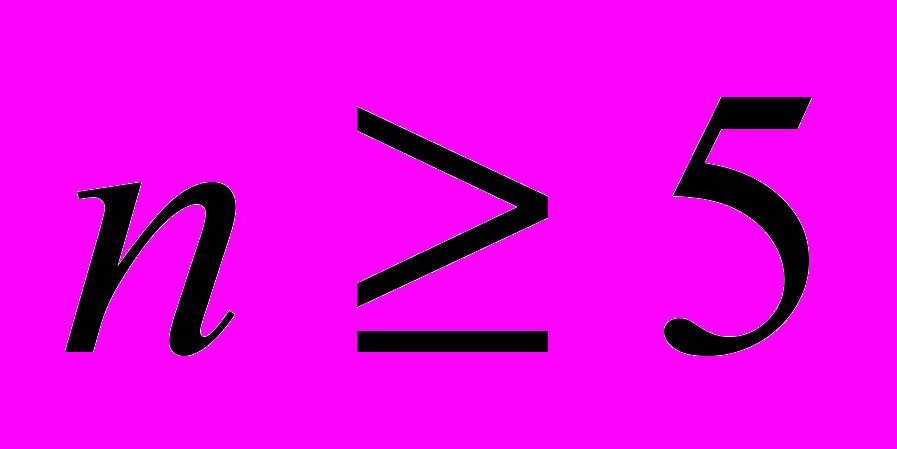 просто не существует, и пытаться доказать это.
просто не существует, и пытаться доказать это. Важный шаг в исследовании алгебраических уравнений был сделан Лагранжем, открывшим, что решение уравнений в радикалах тесно связано с перестановками их корней. Еще в 1321г. Леви Бен Гершон нашел, что существует
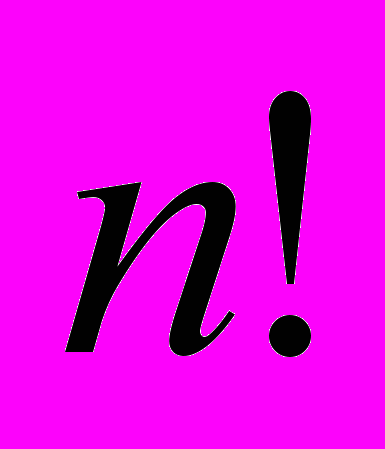 перестановок
перестановок 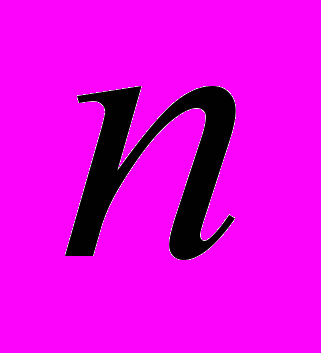 предметов. Эти перестановки – обратимые функции, которые образуют группу
предметов. Эти перестановки – обратимые функции, которые образуют группу 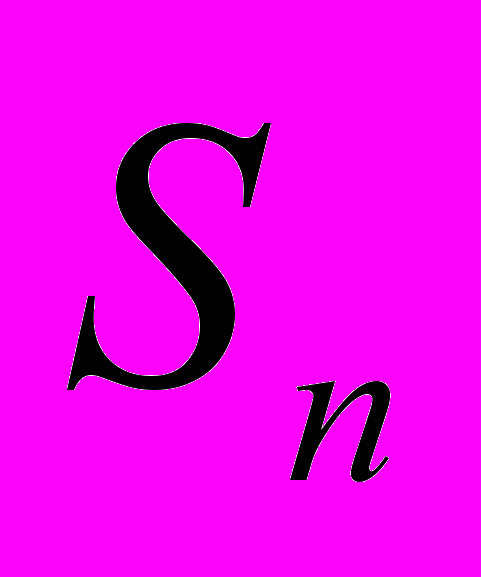 , хотя их поведение в процессе композиции не рассматривалось до XVIII века. Именно когда Вандермонд и Лагранж независимо друг от друга в 1770-1771г. применили идею перестановки к корням полиноминальных уравнений, были открыты первые теоретико-групповые свойства перестановок. Одновременно они открыли ключ к пониманию решения уравнения в радикалах. В 1771г. Лагранж публикует в Мемуарах Берлинской Академии свои "Рассуждения об алгебраическом решении уравнений», в котором делает критический пересмотр всех решений уравнений 3-ей и 4-ой степени и замечает, что все они в сущности основаны на следующем принципе.
, хотя их поведение в процессе композиции не рассматривалось до XVIII века. Именно когда Вандермонд и Лагранж независимо друг от друга в 1770-1771г. применили идею перестановки к корням полиноминальных уравнений, были открыты первые теоретико-групповые свойства перестановок. Одновременно они открыли ключ к пониманию решения уравнения в радикалах. В 1771г. Лагранж публикует в Мемуарах Берлинской Академии свои "Рассуждения об алгебраическом решении уравнений», в котором делает критический пересмотр всех решений уравнений 3-ей и 4-ой степени и замечает, что все они в сущности основаны на следующем принципе.Если уравнение
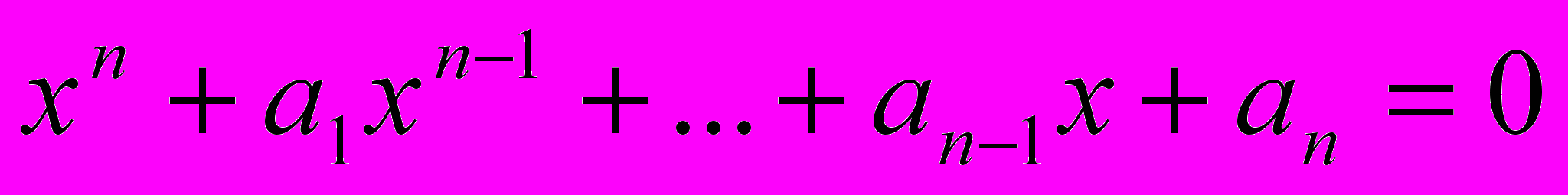 имеет корни
имеет корни 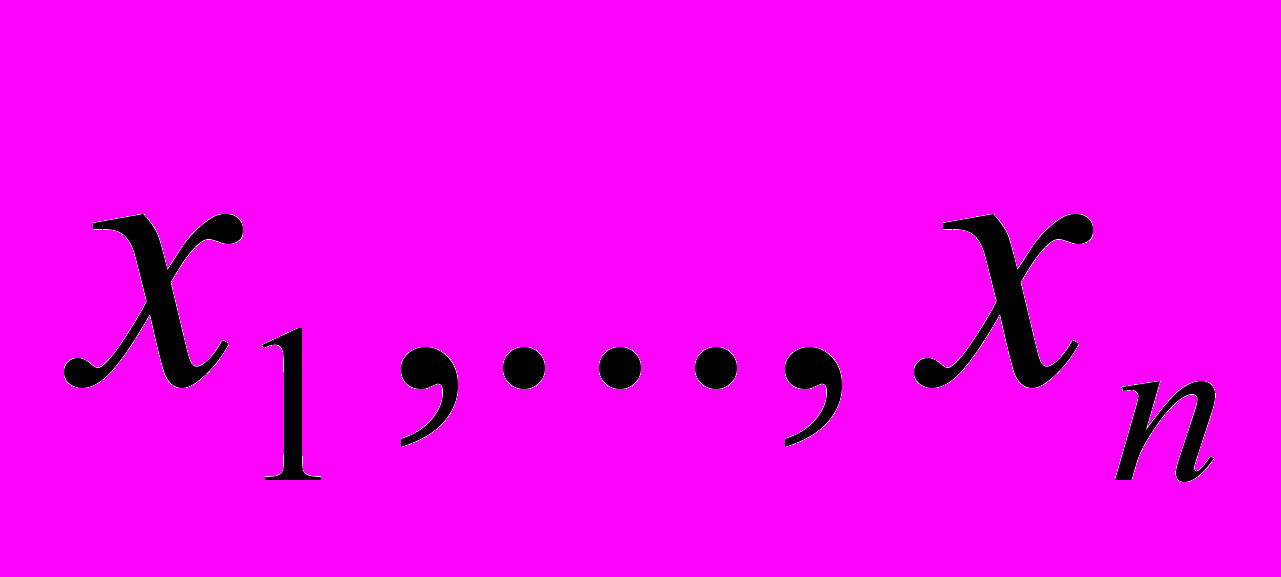 , то
, то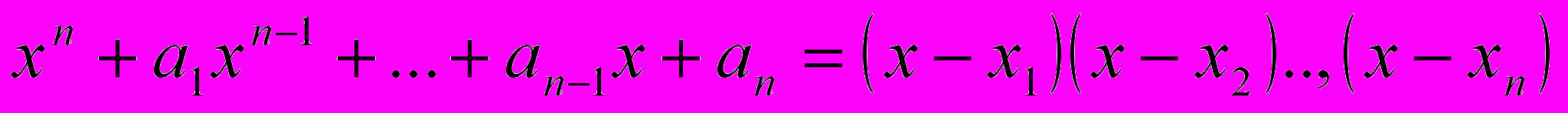 ,
,поэтому если перемножить правую часть и сравнить коэффициенты, мы найдем, что
 есть некоторые функции от корней. Более того, эти функции симметричны, т.е. неизменяемы при перестановке
есть некоторые функции от корней. Более того, эти функции симметричны, т.е. неизменяемы при перестановке 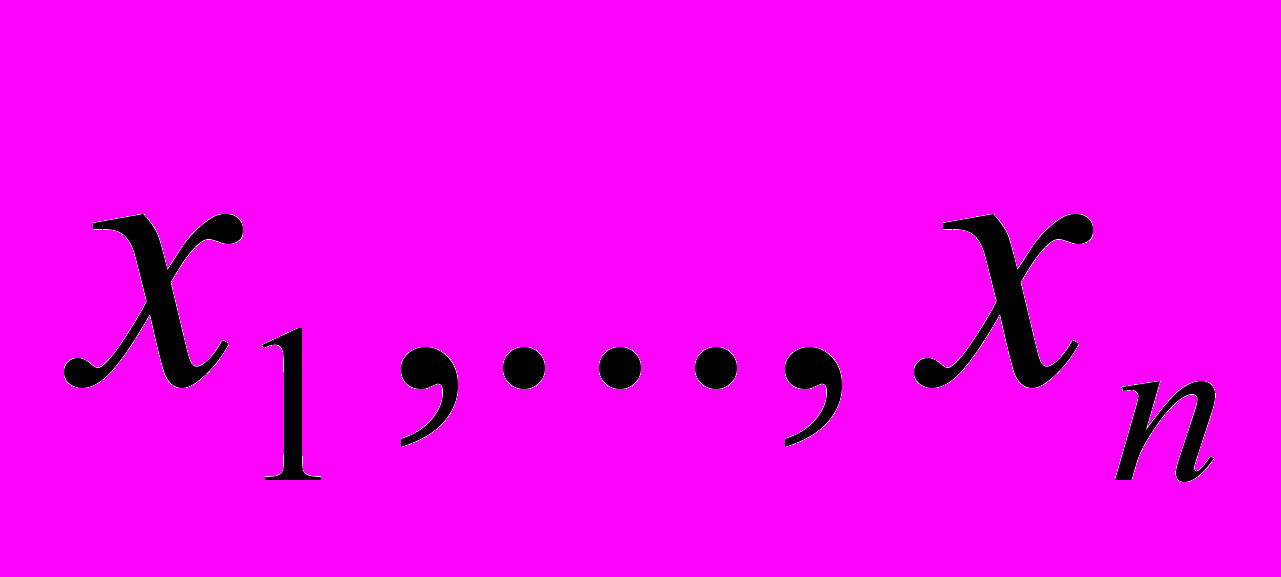 . Следовательно, любая рациональная функция от
. Следовательно, любая рациональная функция от 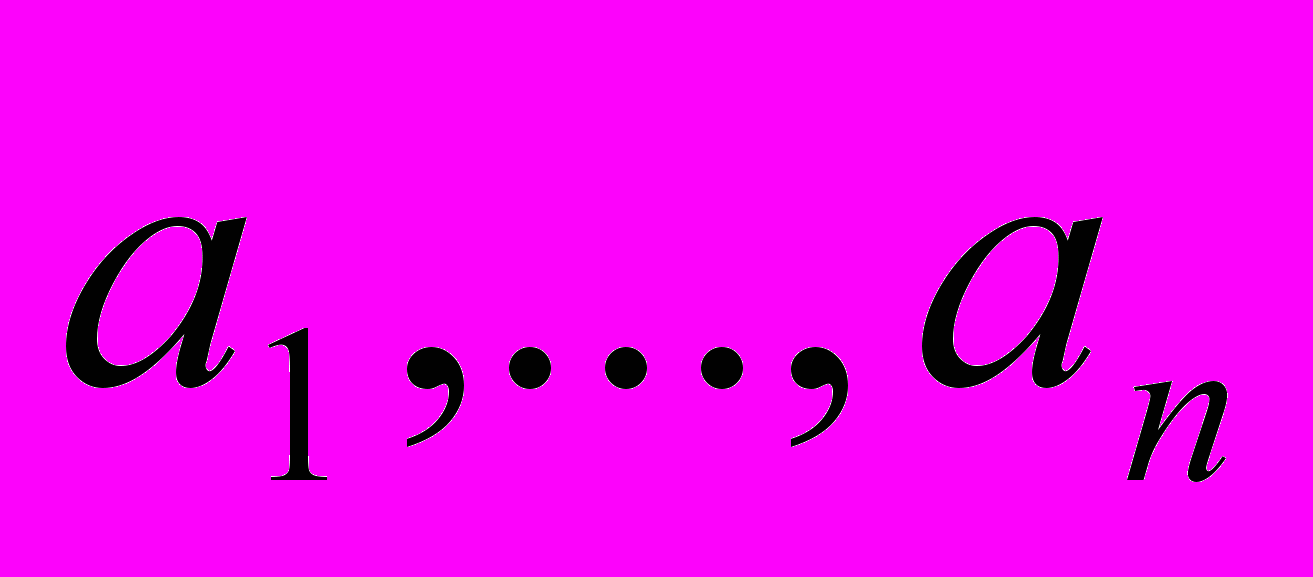 симметрична как функция от
симметрична как функция от 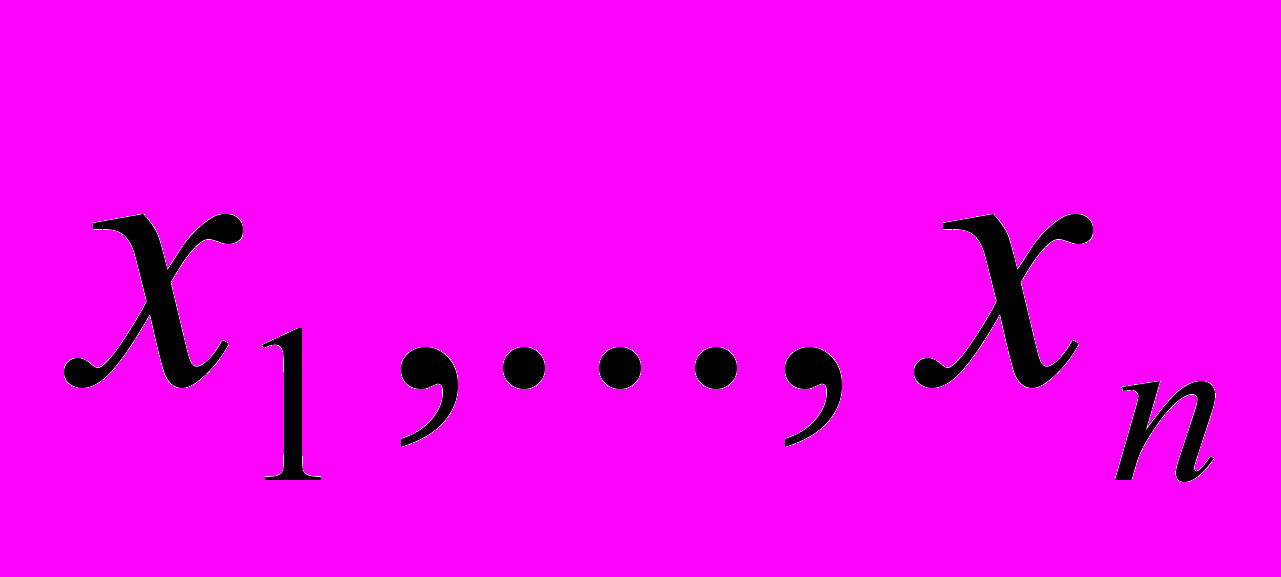 . Радикалы же уменьшают симметрию. Вандермонд и Лагранж нашли, что они могут объяснить предшествующие решения кубических и квадратных уравнений на основе уменьшения симметрии в соответствующих группах подстановок
. Радикалы же уменьшают симметрию. Вандермонд и Лагранж нашли, что они могут объяснить предшествующие решения кубических и квадратных уравнений на основе уменьшения симметрии в соответствующих группах подстановок 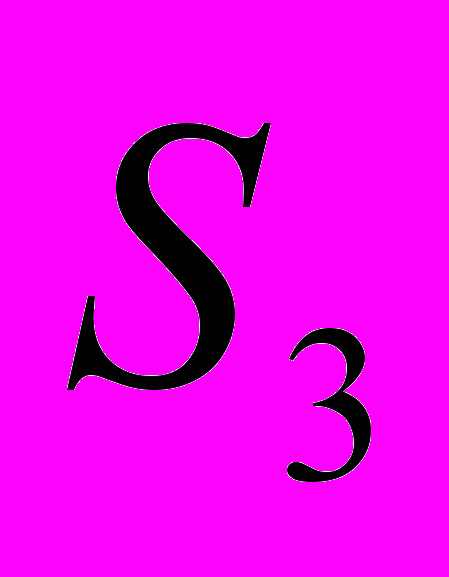 и
и 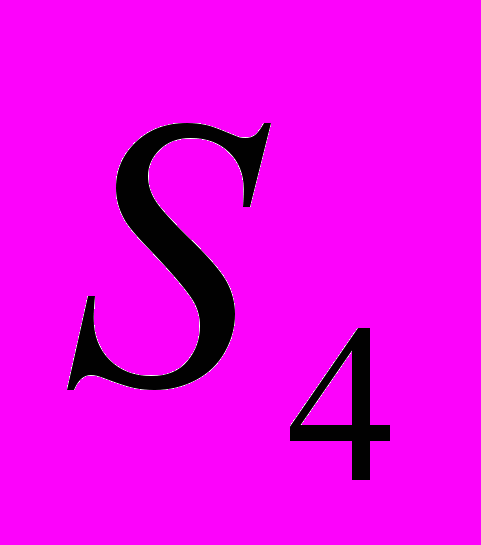 .
.Идея Лагранжа, названная им «истинной философией решения уравнений», была существенно дополнена и развита норвежским математиком Н.Х.Абелем7. В 1824г. в возрасте 22-х лет Абель доказал, что не существует формул, которые бы решали в радикалах алгебраическое уравнение степени
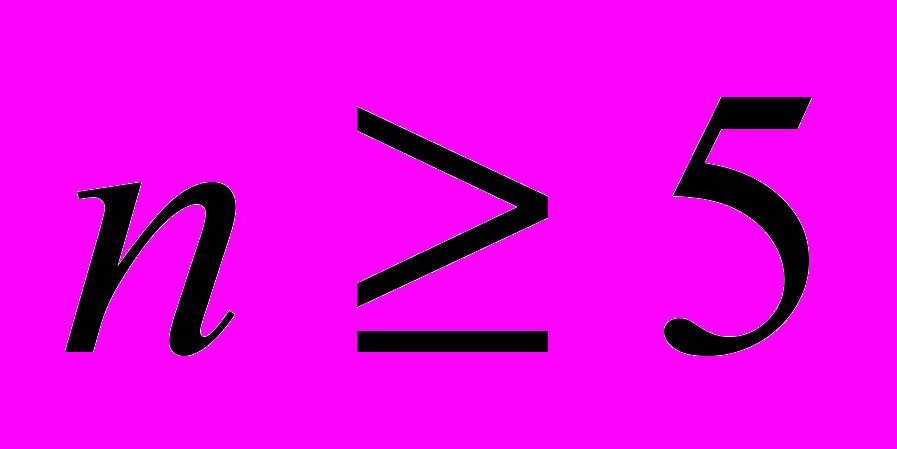 общего вида. Однако Абель не имел достаточно твердого понимания зависимости между радикалами и перестановками, чтобы оперировать произвольными уравнениями. Он не осознавал понятия группы, поэтому мы можем интерпретировать его результаты в теоретико-групповых терминах лишь ретроспективно.
общего вида. Однако Абель не имел достаточно твердого понимания зависимости между радикалами и перестановками, чтобы оперировать произвольными уравнениями. Он не осознавал понятия группы, поэтому мы можем интерпретировать его результаты в теоретико-групповых терминах лишь ретроспективно. Естественно, после работ Абеля встал вопрос о нахождении необходимого и достаточного условия, которое по коэффициентам
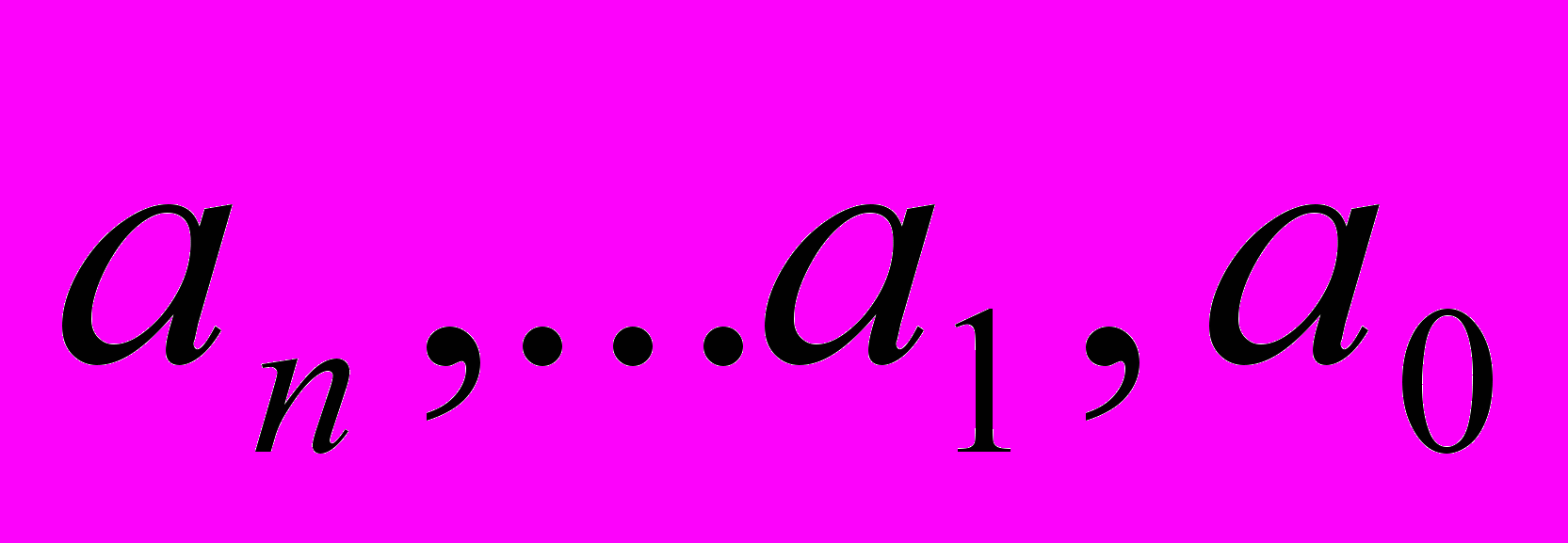 любого уравнения позволяло бы судить, решается ли оно в радикалах или нет. В течение 1829-1831гг. Галуа полностью решил эту труднейшую задачу.
любого уравнения позволяло бы судить, решается ли оно в радикалах или нет. В течение 1829-1831гг. Галуа полностью решил эту труднейшую задачу. Но прежде чем перейти непосредственно к достижениям Галуа, нельзя не остановиться на работах еще одного математика, чьи результаты Галуа активно использовал. Речь идет об «Арифметических исследованиях» Гаусса. Эта книга замечательно постоянным и широким применением общих алгебраических идей. Здесь Гаусс впервые определяет сравнения – первый в истории пример фактор-кольца, и доказывает, что мультипликативная группа поля вычетов по простому модулю
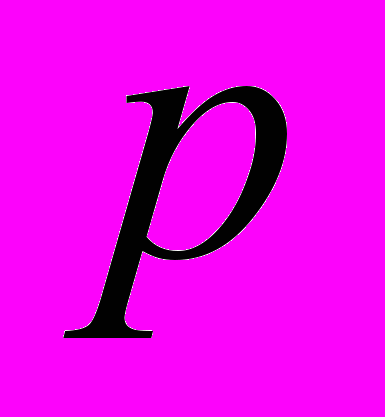 циклическая. Когда Галуа стал строить теорию конечных полей, он сразу же воспользовался тем, что доказательство Гаусса легко переносилось на случай произвольного конечного поля.
циклическая. Когда Галуа стал строить теорию конечных полей, он сразу же воспользовался тем, что доказательство Гаусса легко переносилось на случай произвольного конечного поля. Идеи Галуа были не понятны его современникам и считаются нелегкими для изучения и сейчас. Вот что пишет Феликс Клейн по этому поводу: «Я хотел бы обратить внимание на ту странную роль, которую теория Галуа как учебная дисциплина играет в наших университетах. Она является у нас причиной разногласий, одинаково прискорбных как для обучающих, так и для обучаемых. Дело заключается в том, что, с одной стороны, преподаватели, воодушевленные гениальностью открытия и важностью и глубиной его результатов, с особенной охотой читают лекции по теории Галуа; с другой стороны для понимания ее средним начинающим студентом именно эта область представляет собой непомерные трудности. В большинстве случаев это приводит к тому, что усилия преподавателей, затраченные с большим энтузиазмом и радостью, за редкими исключениями проходят мимо большинства слушателей, не встречая с их стороны никакого понимания». В то же время формулировка основной теоремы Галуа вовсе не сложна, при условии понимания нескольких базовых понятий.
Во-первых, Галуа с самого начала замечает, что следует различать отдельные случаи по степеням общности, с которой задано рассматриваемое уравнение. Между двумя крайними случаями - коэффициенты
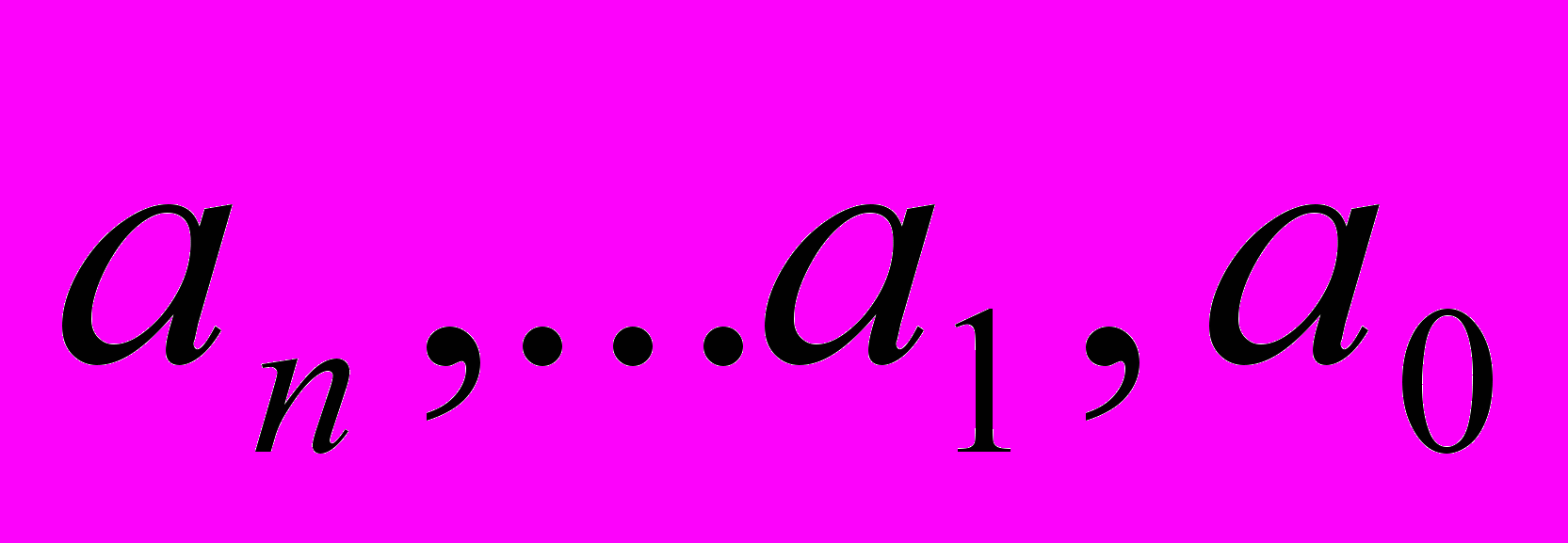 абсолютно произвольные переменные величины или же коэффициенты
абсолютно произвольные переменные величины или же коэффициенты 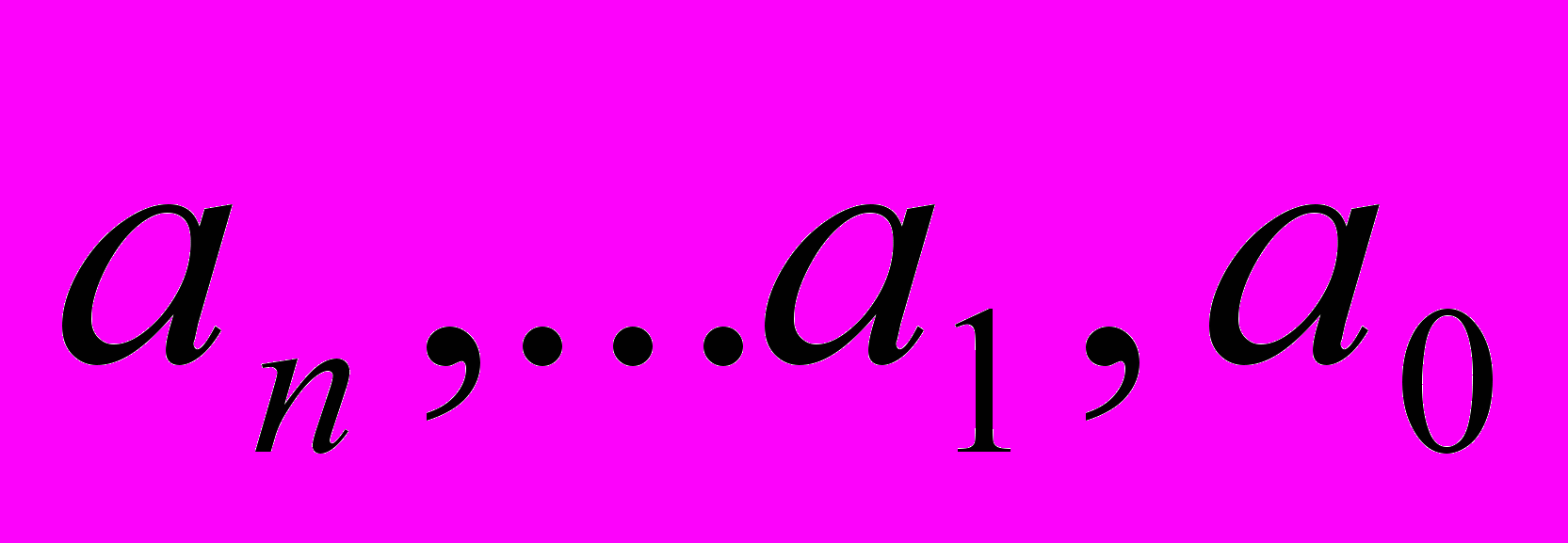 конкретные целые числа – лежит множество промежуточных возможностей. Первый важный поворот, который Галуа совершает в идейном плане, заключается в том, что он с самого начала требует точного определения того, что будет рассматриваться в качестве «рационального» и создает понятие «области рациональности». Название это возникло позже, а само понятие встречается, независимо от Галуа, и у Абеля. Также Галуа дал очень четкое определение принадлежности некоторой величины к полю, порожденному данными величинами, и неприводимого над полем многочлена. Понятие и само слово «группа» тоже впервые встречается именно у Галуа. Вместе с ним – и понятие нормальной подгруппы, которое, наконец, открывает секрет разрешимости в радикалах. Подгруппа
конкретные целые числа – лежит множество промежуточных возможностей. Первый важный поворот, который Галуа совершает в идейном плане, заключается в том, что он с самого начала требует точного определения того, что будет рассматриваться в качестве «рационального» и создает понятие «области рациональности». Название это возникло позже, а само понятие встречается, независимо от Галуа, и у Абеля. Также Галуа дал очень четкое определение принадлежности некоторой величины к полю, порожденному данными величинами, и неприводимого над полем многочлена. Понятие и само слово «группа» тоже впервые встречается именно у Галуа. Вместе с ним – и понятие нормальной подгруппы, которое, наконец, открывает секрет разрешимости в радикалах. Подгруппа  группы
группы 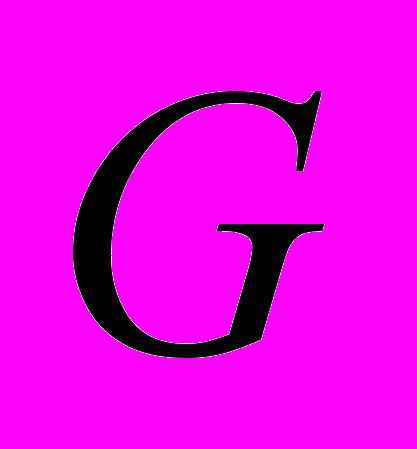 называется нормальной, если
называется нормальной, если 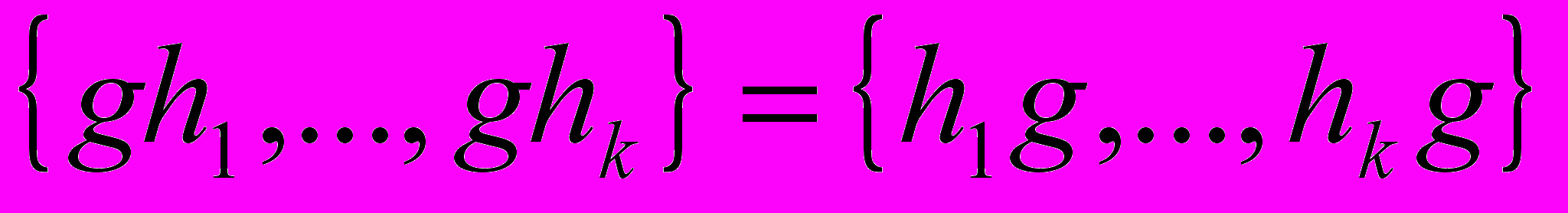
для каждого
 . Галуа показал, что всякое уравнение имеет группу
. Галуа показал, что всякое уравнение имеет группу 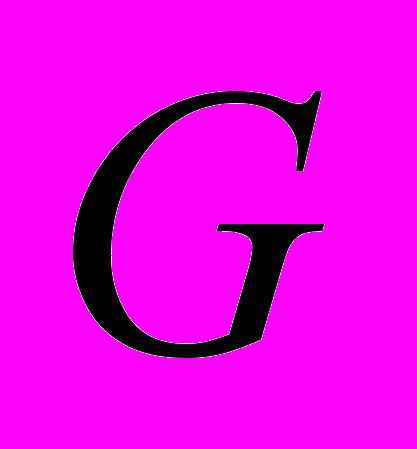 , состоящую из перестановок корней8, которые оставляют рациональные функции корней неизменными, и что уменьшение симметрии, сопровождаемое введением радикала, соответствует образованию нормальной подгруппы. Тогда решение в радикалах возможно только тогда, когда группу
, состоящую из перестановок корней8, которые оставляют рациональные функции корней неизменными, и что уменьшение симметрии, сопровождаемое введением радикала, соответствует образованию нормальной подгруппы. Тогда решение в радикалах возможно только тогда, когда группу 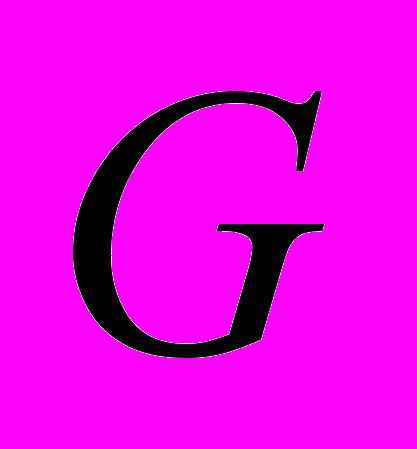 можно привести к тождественной перестановке цепочкой нормальных подгрупп, вложенных некоторым образом. Говоря современными терминами, группа
можно привести к тождественной перестановке цепочкой нормальных подгрупп, вложенных некоторым образом. Говоря современными терминами, группа 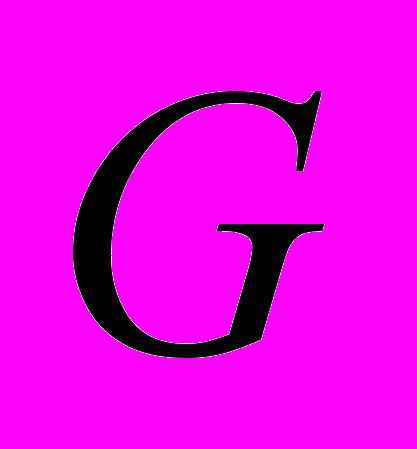 должна быть разрешима. Если мы имеем общее уравнение степени
должна быть разрешима. Если мы имеем общее уравнение степени 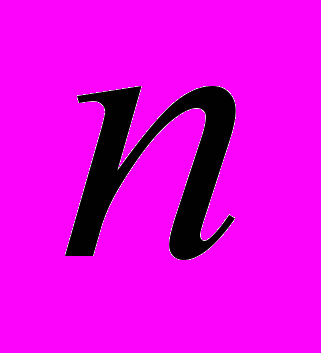 , то
, то 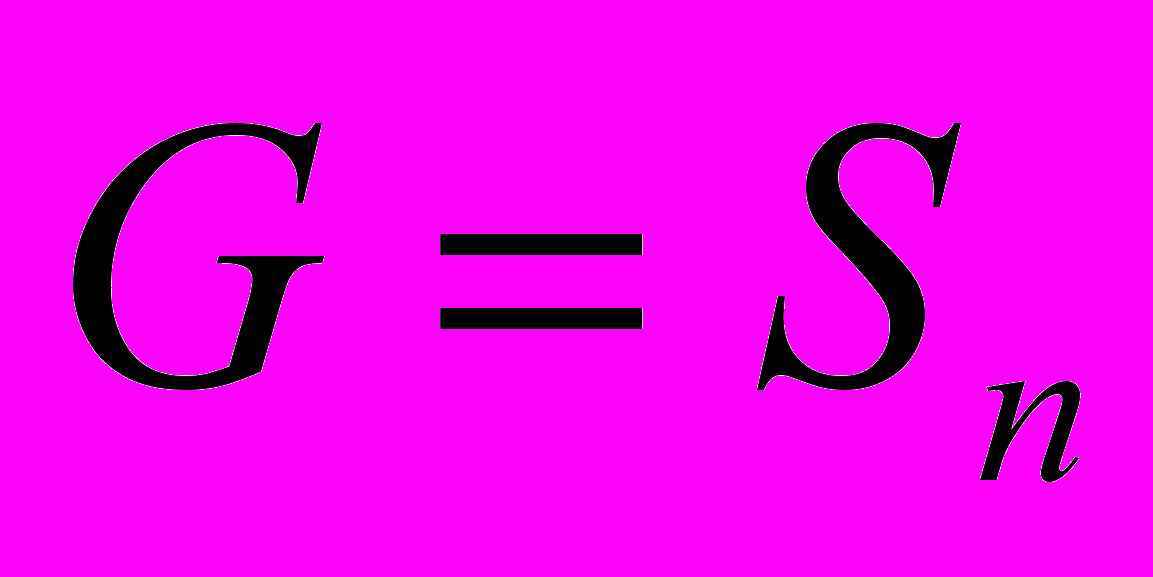 . Основная теорема теории Галуа формулируется следующим образом9 10:
. Основная теорема теории Галуа формулируется следующим образом9 10:Уравнение
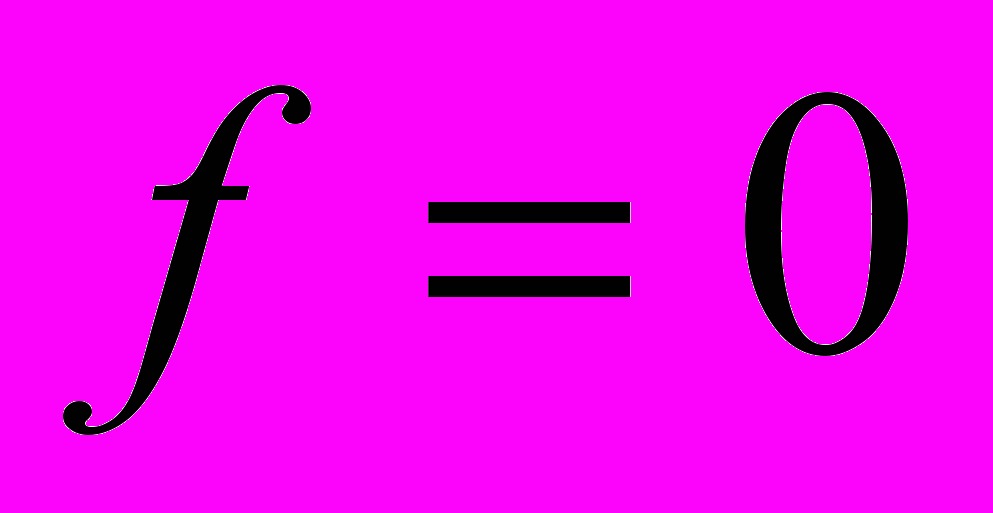 разрешимо в радикалах тогда и только тогда, когда разрешима его группа Галуа
разрешимо в радикалах тогда и только тогда, когда разрешима его группа Галуа 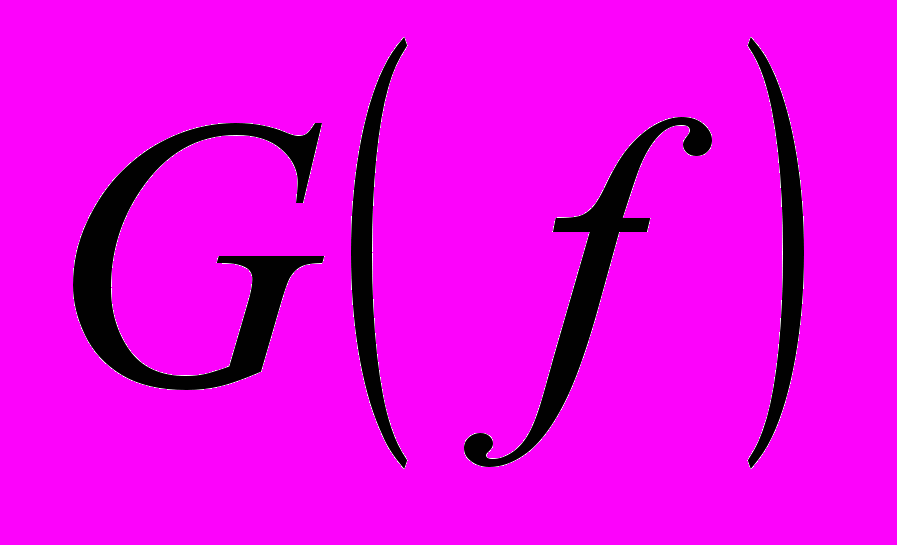 .
.В теореме Галуа ценно то, что группу
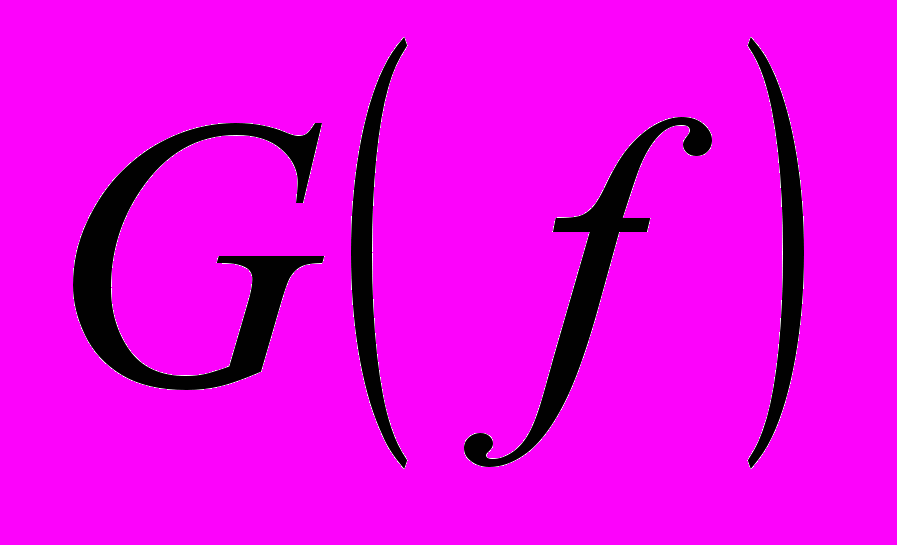 , как правило, можно вычислять, не зная корней уравнения
, как правило, можно вычислять, не зная корней уравнения 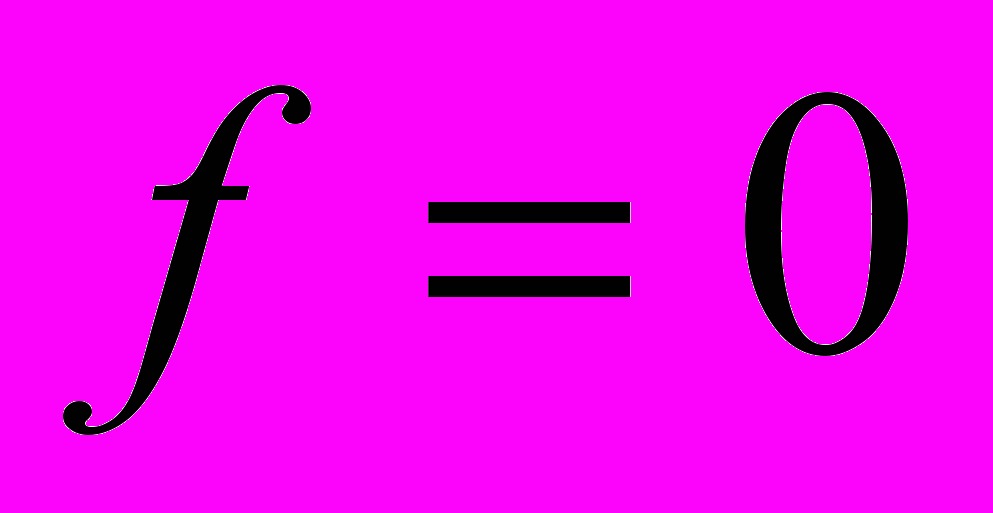 , только по его коэффициентам.
, только по его коэффициентам. Таким образом, эта теорема дает нам некий общий критерий разрешимости уравнений с использованием резольвент, а также указывает путь к их разысканию. Но тут сразу же встает целый ряд дальнейших проблем: найти все уравнения
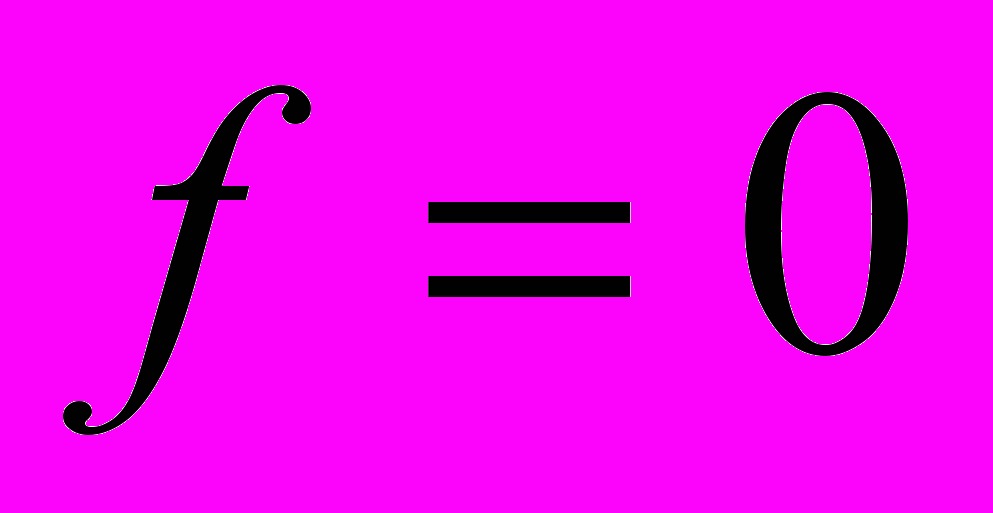 степени
степени 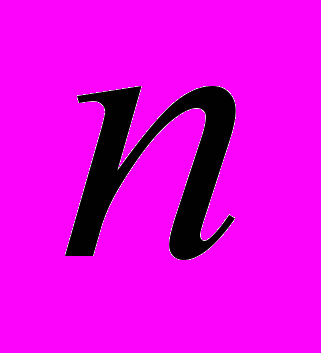 , имеющие при данной области рациональности определенную, наперед заданную группу подстановок; исследовать вопрос о том, сводимы ли друг к другу два уравнения такого рода, и если да, то какими средствами, и т.д. Все вместе это составляет огромную совокупность проблем, многие из которых не решены и сегодня.
, имеющие при данной области рациональности определенную, наперед заданную группу подстановок; исследовать вопрос о том, сводимы ли друг к другу два уравнения такого рода, и если да, то какими средствами, и т.д. Все вместе это составляет огромную совокупность проблем, многие из которых не решены и сегодня. Эварист Галуа (биографические сведения) 1
2
В конце XIX века идеи Галуа стали общеизвестными среди математиков. Влияние их неизменно возрастало. В очерке «Влияние Галуа на развитие математики», написанном в 1984г., Софус Ли назвал имена четырех наиболее значительных математиков XIX века: Гаусс, Коши, Абель и Галуа. Он пишет: «Видя, как плодотворны оказались идеи Галуа в стольких областях анализа, геометрии и даже механики, можно смело надеяться, что они окажут равное влияние и на математическую физику».
История собственно теории групп начинается с середины XIX века, после опубликования работ Галуа. Конечно, некоторые теоретико-групповые рассуждения встречаются уже в работах Эйлера и Ферма, а Лагранж и Вандермонд ввели в математику первый групповой объект – подстановки, но до Галуа теория групп находилась в зачаточном состоянии. Именно публикация в 1846г. его работ стала поворотным пунктом в теории групп. В них впервые было продемонстрировано, что решение старинного, важного вопроса о разрешимости уравнений может быть сведено к исследованию нового объекта – групп. Впервые группы выступают не как вспомогательный инструмент рассуждения, а как основной объект исследования. Большое значение имело использование Галуа таких сложных понятий, как простая группа, нормальная подгруппа, разрешимая группа. Будучи автором этих понятий, Галуа давал витиеватые и нечеткие определения, однако его примечания к собственным же теоремам показывают, сколь глубоким было у него понимание сущности этих объектов. И вскоре после выхода работ Галуа началось систематическое развитие теории групп. Но прежде чем перейти к более подробному рассмотрению вопроса дальнейшего развития теории групп, следует остановиться на одном важном моменте. Работы Галуа оказали неявное, но очень мощное влияние на переход от алгебры как науки об уравнениях к алгебре как науке о структурах. Методы Галуа привели последующих математиков к очень широкому взгляду на понятие закона композиции, хотя сам он не слишком глубоко развивал эти идеи. После того как алгебраисты английской школы в середине XIX века выделили абстрактное понятие закона композиции, тотчас была расширена сама область алгебры вследствие появления множества новых математических объектов. Буль построил алгебру логики, Гамильтон – алгебру векторов, кватернионов и общих гиперкомплексных систем. Работы Галуа пусть и не содержали непосредственного указания на такое развитие алгебры, однако та свобода, с которой Галуа оперировал абстрактными понятиями группы, нормальной подгруппы и т.д., безусловно, подтолкнули его преемников пересмотреть предмет изучения алгебры. Еще Серре говорит, что «алгебра есть, собственно говоря, анализ уравнений». И уже после 1850г., новые алгебраические изыскания все более и более группируются вокруг проблемы, которая сейчас считается основной в алгебре, - проблемы изучения алгебраических структур.
Что касается теории групп, то она первоначально развивается как теория конечных групп подстановок. Первое определение и первые исследования абстрактных групп были опубликованы Артуром Кэли в 1854г. Это была работа в двух частях «О группах, зависящих от символического уравнения
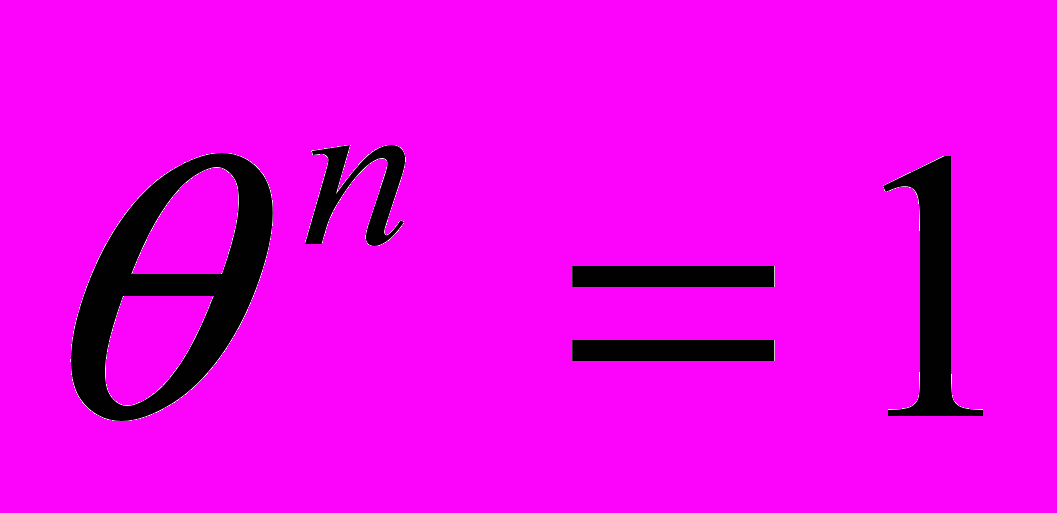 ». В этой работе Кэли определяет группу как множество символов с заданным законом композиции, который удовлетворяет условиям ассоциативности, существования единицы и однозначной разрешимости уравнений
». В этой работе Кэли определяет группу как множество символов с заданным законом композиции, который удовлетворяет условиям ассоциативности, существования единицы и однозначной разрешимости уравнений 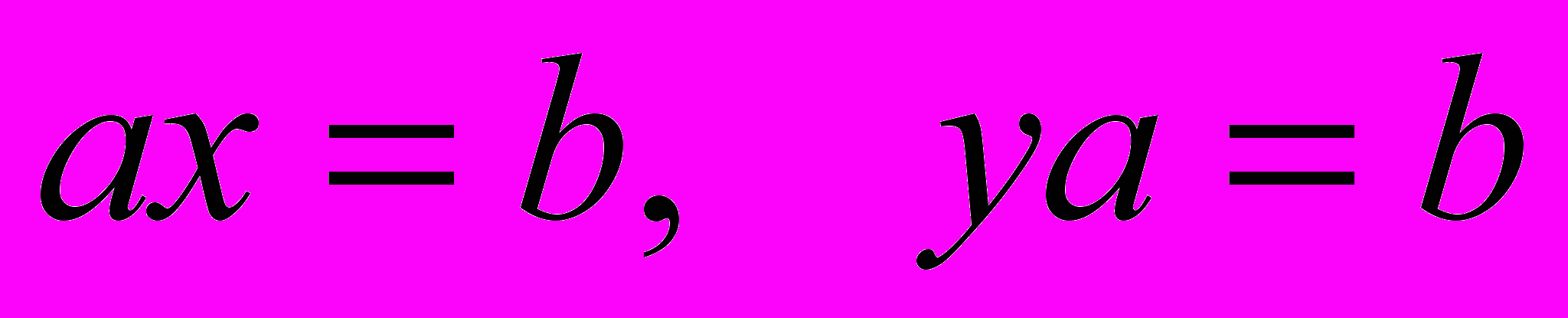 для любых
для любых 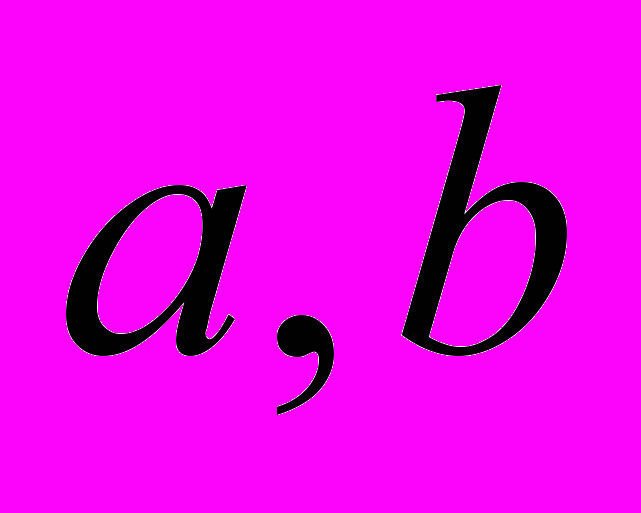 . Кэли указывает, что элементами группы могут быть подстановки, а могут быть и элементы другой природы, например, кватернионы. Закон композиции Кэли задает в виде «таблицы умножения», и до сих пор такой способ задания действия иногда называют «квадратом Кэли». В 1859г. Кэли опубликовал третью часть своей работы, в ней он доказывает, что все группы простого порядка циклические, а также находит всевозможные группы порядка восемь. Само название «группа» взято Кэли в память Галуа. Эти работы Кэли не сразу получили широкую известность, но потом стали примером определения группы и пересказываются почти во всех учебниках.
. Кэли указывает, что элементами группы могут быть подстановки, а могут быть и элементы другой природы, например, кватернионы. Закон композиции Кэли задает в виде «таблицы умножения», и до сих пор такой способ задания действия иногда называют «квадратом Кэли». В 1859г. Кэли опубликовал третью часть своей работы, в ней он доказывает, что все группы простого порядка циклические, а также находит всевозможные группы порядка восемь. Само название «группа» взято Кэли в память Галуа. Эти работы Кэли не сразу получили широкую известность, но потом стали примером определения группы и пересказываются почти во всех учебниках. Кроме работ Кэли, развитие теории групп в самой середине XIX века состояло в разнообразных исследованиях групп подстановок и в освоении наследия Галуа. В частности, большую работу проделал Серре, который включал в свои лекции по алгебре в Сорбонне все большие и большие части теории Галуа.
Дальнейшие крупные открытия в теории групп связаны с именем воспитанника и профессора Политехнической школы Жордана. В сочинениях11 Жордана есть уже явное выделение нормальных подгрупп, понятие простой группы, изложение доказанной им в 1869г. теоремы Жордана, обстоятельное исследование кратно-транзитивных групп. В этом сочинении впервые появляется понятие гомоморфизма (точнее, эпиморфизма) под названием l’isomorphisme mériédrique. Также Жордан ввел фундаментальное понятие представления одной группы другой и понятие факторгруппы. Кроме того, Жордан впервые рассматривает матричные группы с элементами из конечного поля, ставшие в XX веке предметом обстоятельных исследований, и дает богатый материал для исследования типов разрешимых групп. При изложении теории Галуа Жордан использует уже современный способ сопоставления уравнению не некоторого множества перестановок корней, а группы подстановок, и критерий разрешимости в радикалах у него выражается в разрешимости его группы Галуа. Кроме того книга Жордана дает немало приложений теории групп к другим областям математики, например, к алгебраическим функциям (группы монодромии), к эллиптическим и модулярным функциям. Наконец, к Жордану восходит и первое исследование бесконечных групп, которое несколько лет спустя было расширено в двух различных направлениях, Ли – с одной стороны, Клейном и Пуанкаре – с другой. Трактат Жордана стал на некоторое время учебником как по теории групп, так и по теории Галуа. Выход его знаменует окончание периода рождения теории групп.
Дальнейшее развитие идей Галуа связано с именами Клейна и Ли. Занимаясь в Париже под руководством Жордана, эти два математика пришли к мысли о группах совершенно другой природы, непрерывных группах. Ли положил начало их общей теории и приложил их к дифференциальным уравнениям, руководясь теми же принципами, которые лежат в основе приложения конечных групп к алгебраическим уравнениям, составляющего сущность теории Галуа. При этом интегрируемые системы дифференциальных уравнений соответствуют так называемым интегрируемым группам, структура которых аналогична структуре разрешимых конечных групп.
Клейн положил непрерывные группы с основу классификации различных геометрий: элементарной, проективной, шаровой и т.п. Этим он указал в математике место геометрии, задачи которой были сведены методами аналитической геометрии к задачам анализа, и привел «чисто геометрические» вопросы к изучению свойств непрерывных групп.
Еще одно приложение теории Галуа, на котором нельзя не остановиться, - это построения с помощью циркуля и линейки. Как оказалось, идея приложения групп к уравнениям имеет настолько всеобщий характер, что сфера ее применения не могла ограничиться сравнительно узким вопросом о разрешимости уравнений в радикалах. Поэтому вскоре оказалось, что методы Галуа могут быть применены и к другим вопросам, которые приводятся к алгебраическим уравнениям. Например, вопросы о построениях при помощи циркуля и линейки приводятся к вопросу, может ли заданное уравнение быть решено при помощи извлечения квадратных корней, и потому могут быть решены с помощью теории Галуа. Таким путем была доказана невозможность деления произвольного угла посредством циркуля и линейки на нечетное число частей, и тем самым обнаружилась бесплодность многочисленных попыток решить древнюю задачу «трисекции угла». Этому красивому приложению М.М.Постников посвятил целую главу в своем учебнике «Теория Галуа» (1963г.), изложив решения задач об удвоении куба, трех биссектрисах, построении правильного
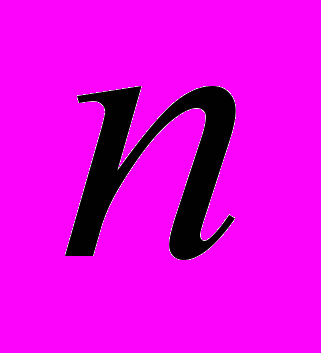 -угольника, квадратуре круга и луночках Гиппократа.
-угольника, квадратуре круга и луночках Гиппократа. Но особенно глубокие приложения теории Галуа допускает теория чисел. Вопрос об арифметической природе корней уравнения, как выяснилось, тесно связан со структурой его группы Галуа. Первый результат этого направления, который был предугадан Кронекером и строго доказан Вебером, звучит так: корни всякого уравнения с абелевой группой Галуа в поле рациональных чисел, как области рациональности, рационально выражаются через некоторые корни из единицы. В настоящее время существует около десяти различных доказательств этой теоремы. Кронекер занялся дальнейшим вопросом об уравнениях с абелевой группой в области рациональности, образованной мнимыми корнями квадратного уравнения. Оказалось, что такого рода величины получаются как значения эллиптических функций, допускающих так называемое комплексное умножение. Кронекер предположил, что эти значения дадут корни всех возможных абелевых уравнений в рассматриваемой области рациональности. Это предположение в общем случае удалось доказать Р.Фуэтету. Исследуя арифметические законы комплексного умножения, Фуэтет пришел к общим законам, имеющим место для уравнений, абелевых в произвольной области рациональности. Эти законы позволяют рассматривать поля корней таких уравнений, как обобщение, т.н. поля классов, и связывают степени этих уравнений с числом идеальных классов в рассматриваемой области рациональности. Здесь вскрывается глубокая связь между теорией Галуа и теорией идеалов, которые являются основным инструментом в теории алгебраических чисел. В тесной связи с упомянутыми законами стоит закон, открытый Дедекиндом, Фробениусом и Гурвицем, который в наиболее элементарном случае может быть сформулирован следующим образом:
Дан полином
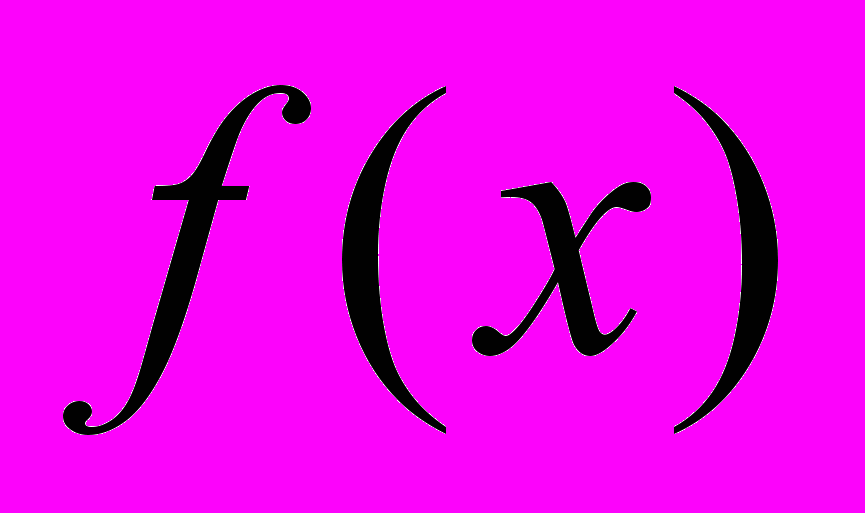 . Рассматривая его по модулю некоторого простого числа
. Рассматривая его по модулю некоторого простого числа 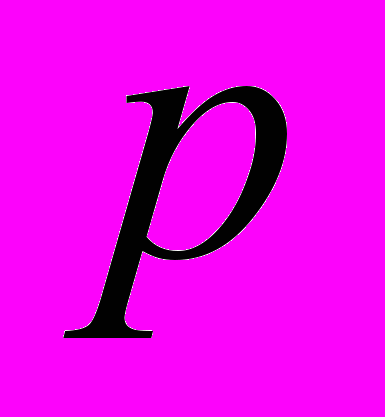 , разложим его на неприводимые множители:
, разложим его на неприводимые множители: 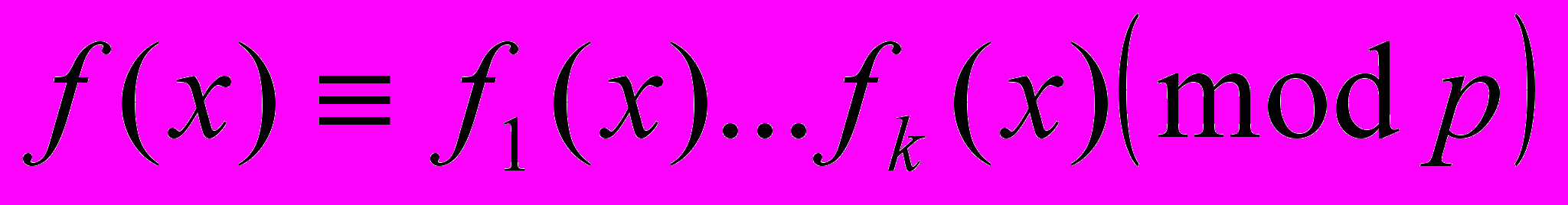 , где
, где 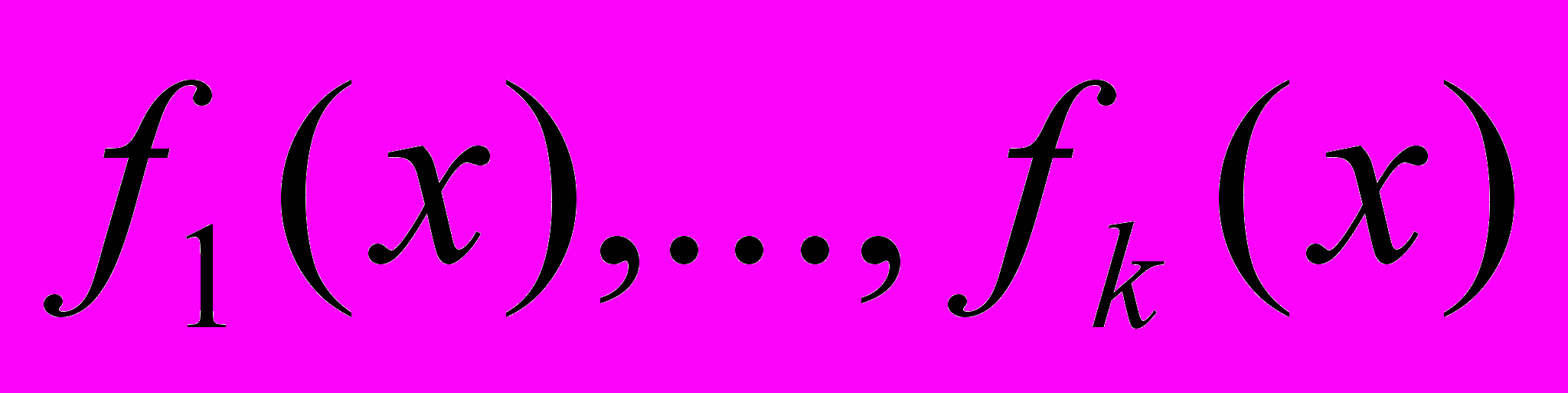 - неприводимые по модулю
- неприводимые по модулю 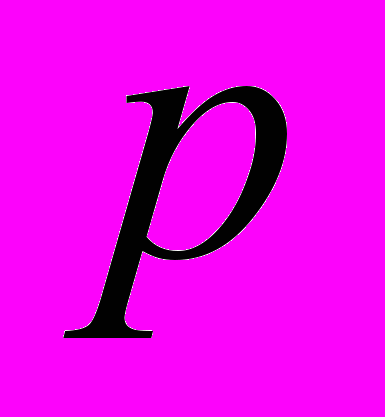 полиномы степеней
полиномы степеней 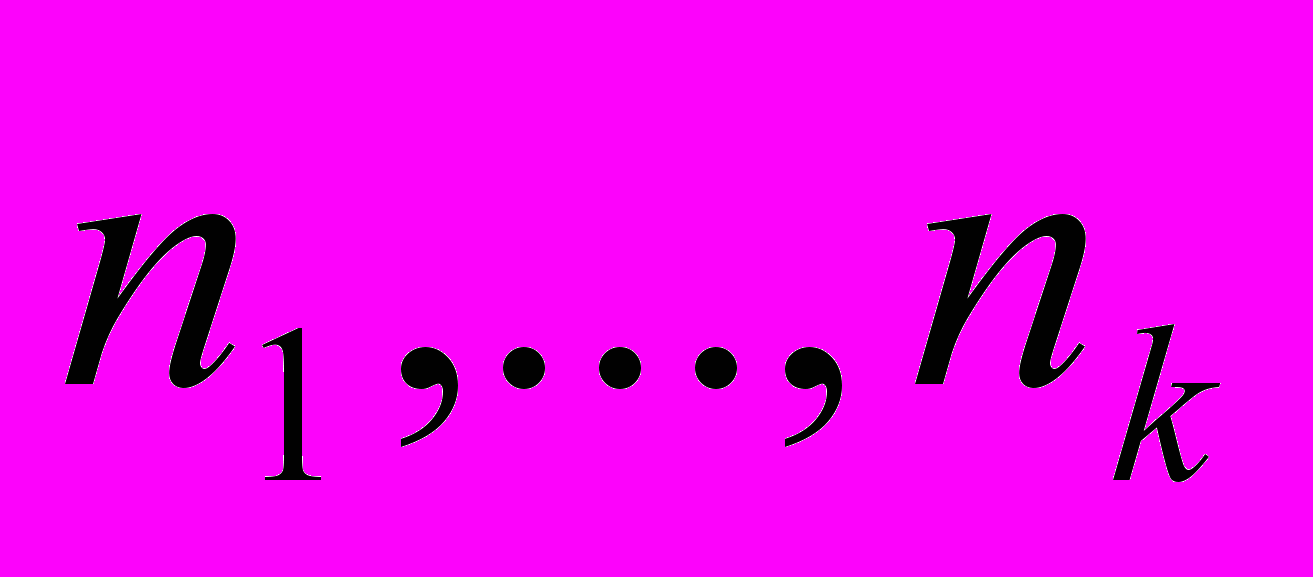 . Тогда группа Галуа этого уравнения содержит подстановку, состоящую из циклов порядков
. Тогда группа Галуа этого уравнения содержит подстановку, состоящую из циклов порядков 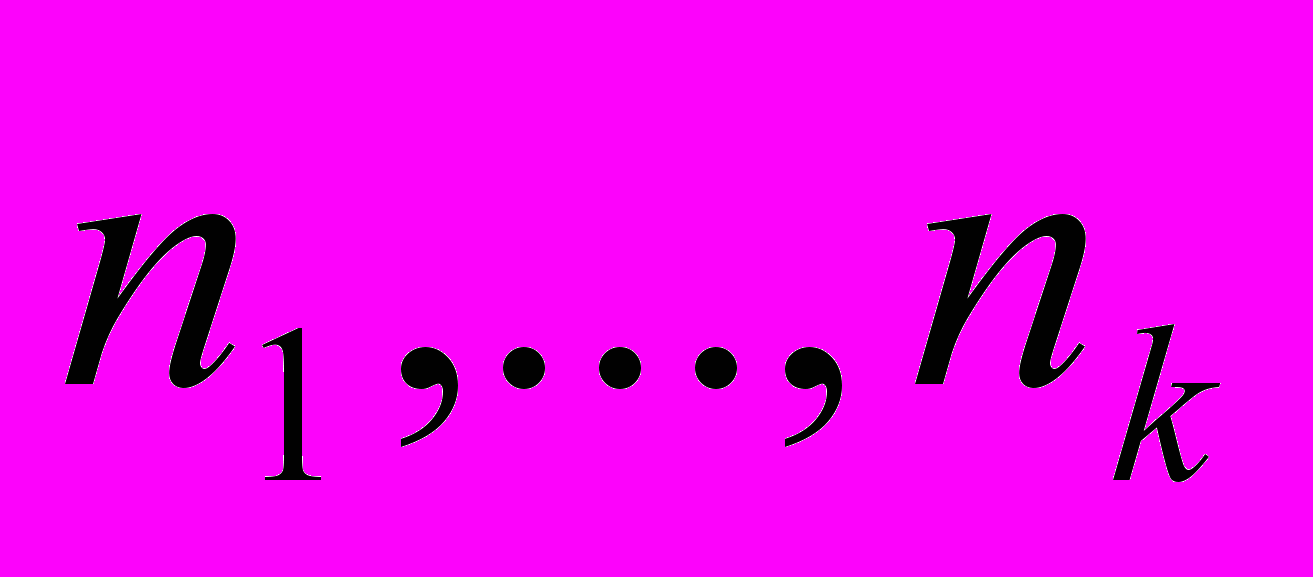 . Обратно, если группа Галуа уравнения
. Обратно, если группа Галуа уравнения 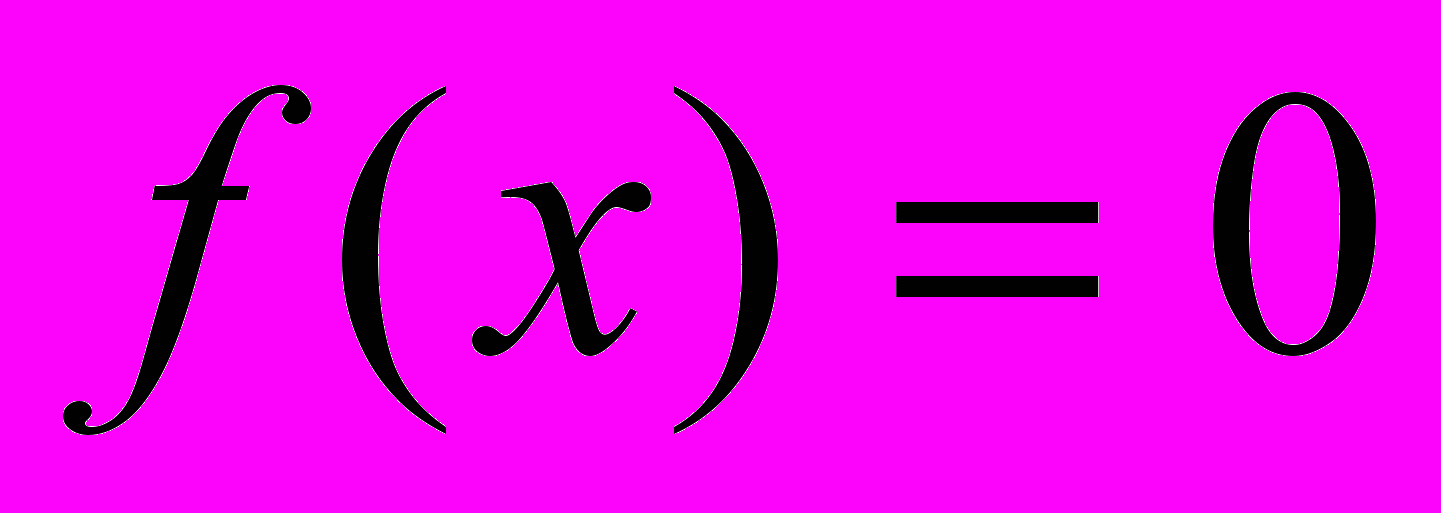 содержит подстановку, состоящую из циклов порядков
содержит подстановку, состоящую из циклов порядков 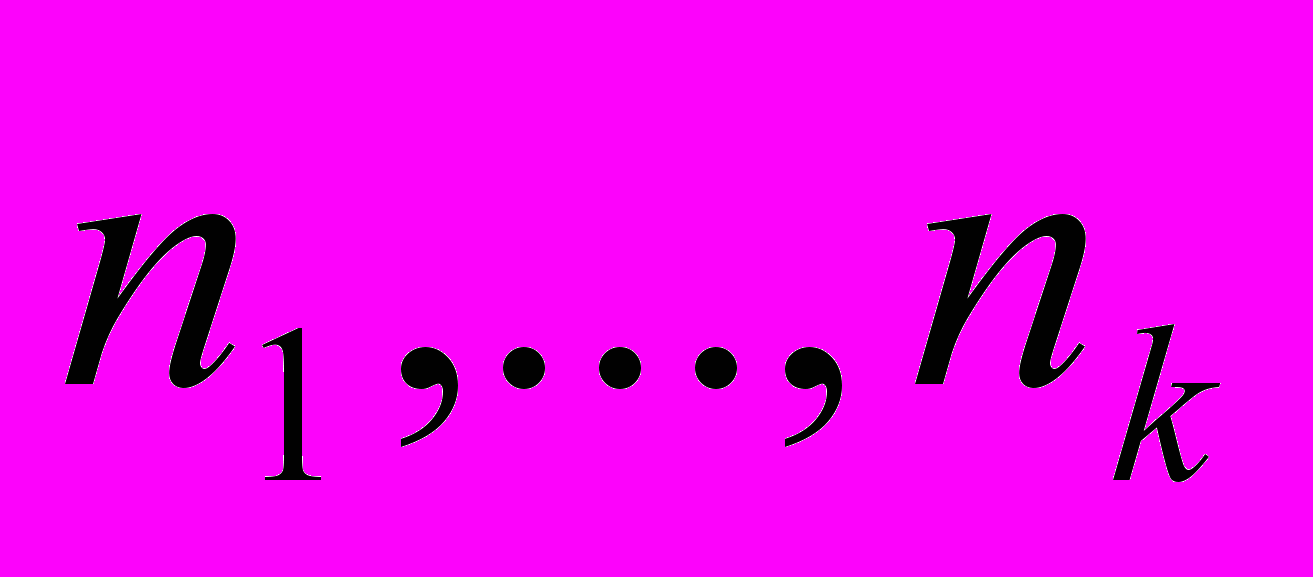 , то существует бесчисленное множество таких простых чисел, для которых имеет место разложение
, то существует бесчисленное множество таких простых чисел, для которых имеет место разложение 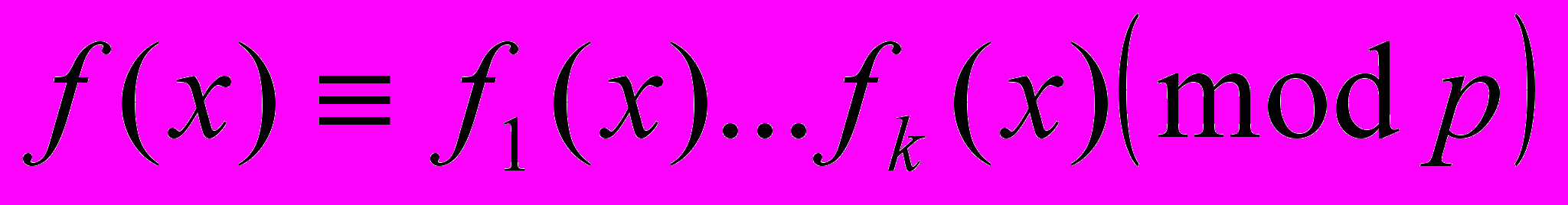 .
. Кроме своих приложений в теории алгебраических чисел, эта теорема позволяет устанавливать общие критерии для нахождения группы отдельных классов уравнений, а также устанавливать тождество двух заданных полей.
Нельзя не сказать о необычайном успехе, который выпал с конца XIX века на детище Галуа – идею группы – в анализе, геометрии, механике и теоретической физике. Конец XIX - начало XX вв. как раз и характеризуются вторжением понятия группы и родственных с ней алгебраических понятий (операторы, кольцо, идеал, модуль) в те разделы математики, в первую очередь алгебры, которые казались до этого очень удаленными от сферы господства этих понятий. Расширение исследований было подготовлено теми новыми точками зрения на алгебру как на теоретико-множественную, аксиоматическую науку, которые были подготовлены еще Галуа и разрабатывались в немецкой школе в конце XIX века под руководством Дирихле, Куммера, Кронекера, Дедекинда, Гильберта, а позже, в 20-х гг. XX века под руководством Эмми Нетер и Э.Артина. Один за другим появляются новые абстрактные понятия, которые формируют облик современной алгебры. Последователи Гаусса разрабатывают понятие поля (впоследствии теория Галуа была переписана в терминах полей и их расширений), Дедекинд вводит понятие идеала, тела и, совместно с Кронекером, модуля. Несколько позже Гильберт вводит понятие кольца. Благодаря теории Галуа был получен принцип классификации иррациональностей, и это дало новый виток развития теории алгебраических полей. В первую очередь это заслуга Дедекинда, который изложил в новых терминах и существенно развил в стройную систему теорию расширений полей. Он также впервые рассматривал группу Галуа как группу автоморфизмов исследуемого расширения, а не только как группу перестановок корней уравнения. Дедекинд доказал для числовых полей фундаментальную теорему о линейной независимости автоморфизмов, а также существование у поля Галуа нормального базиса. Наконец, он попытался разобраться с проблемой расширений бесконечного порядка, применив к ним теорию Галуа, однако вскоре показал, что сделать это невозможно. Он даже пробовал рассмотреть группу Галуа как топологическую группу, но окончательно эта идея была воплощена в жизнь Круллем в 1928г., когда последний развил теорию расширений Галуа бесконечного порядка.
Работа по аксиоматизации алгебры, начатая в последние годы XIX века Дедекиндом и Гильбертом, была с большим успехом продолжена Эрнстом Штейницем, затем алгебраистами школы Артина и Эмми Нетер. Трактат Ван-дер-Вардена12, опубликованный в 1930г., впервые собрал эти работы в единое целое, открыв пути и служа проводником для многочисленных исследований по абстрактной алгебре. Забегая вперед, отметим, что московская математика благодаря развитию своих старых теоретико-множественных традиций оказалась наиболее подготовленной к восприятию идей абстрактной алгебры.
1 Sur la théorie des nombres.-Bull.sci.math.,1830.
2 Journ. math. pures appl., т.11, стр.381 и далее.
3 R.Bourgne and J.P.Azra. Ecrits et mémoires mathématiques d’Evariste Galois: Edition critique intégrale de ses manuscripts et publications. Gauthier-Villard & Cie, Imprimeur-Editeur-Libraire, Paris, 1862.
4 «ambiguité des fonctions» (двусмысленность функций)
5 Что касается биографии Галуа, первым серьезным исследователем жизни и творчества Галуа был П.Дюпюи. В 1896г. он опубликовал биографию Галуа в журнале «Annales de l’Ecole Normale Supérieure». В 1889г. появился немецкий перевод этой работы. На русском же эта статья увидела свет только в 1936г. в качестве приложения к сочинениям Галуа под редакцией Н.Г.Чеботарева. Кроме того, в 1948г. в Нью-Йорке вышла романтизированная биография Эвариста Галуа «Избранник богов», написанная Леопольдом Инфельдом. На русском языке эта книга была напечатана в 1958г. в серии «Жизнь замечательных людей» (перевод М.Кана).
6 По другим сведениям это было сделано Кардано.
7 Забавное совпадение: Абель, как и Галуа, посылал свои работы в Париж в Академию наук, и она тоже затерялась, но не окончательно: уже после смерти Абелю была присуждена большая премия Парижской академии наук.
8 Сегодня эта группа носит название группы Галуа.
9 Сам Галуа сформулировал эту теорему только для случая простой степени уравнения, и звучи она следующим образом: «Для того чтобы неприводимое уравнение простой степени разрешалось в радикалах, необходимо и достаточно, чтобы все функции, инвариантные относительно подстановок
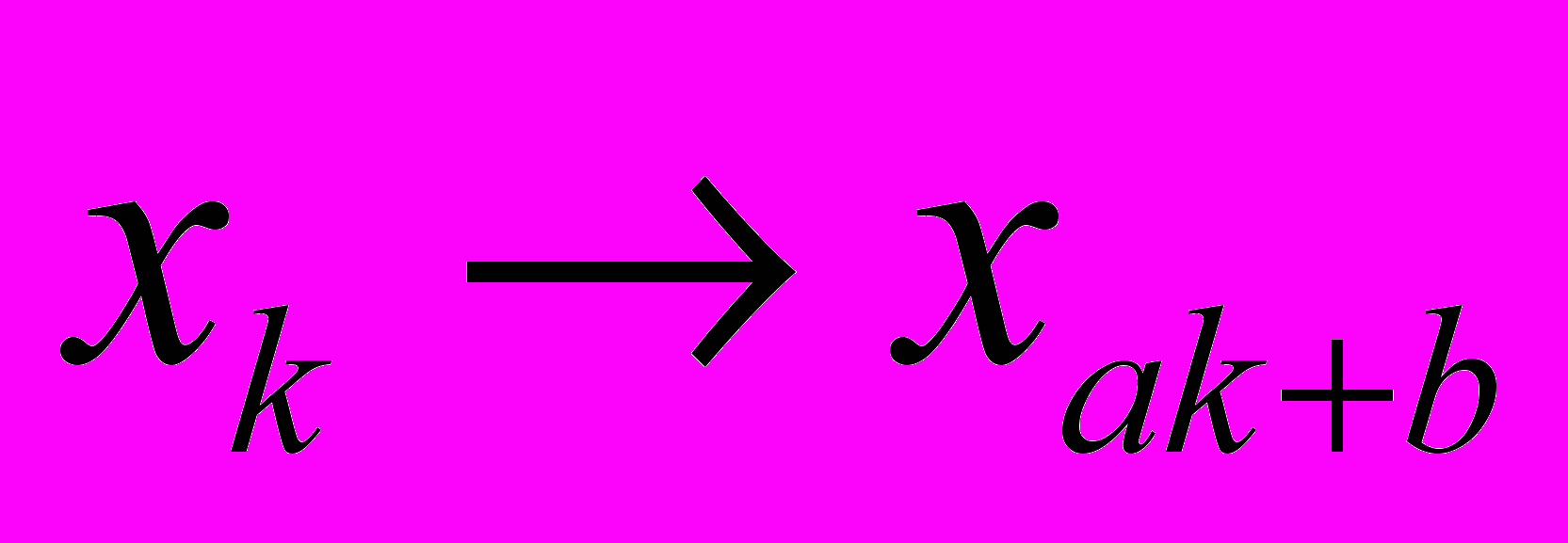 , были рационально известны».
, были рационально известны». 10 В современных учебниках по алгебре эта теорема формулируется в терминах теории расширения полей и звучит так: «Пусть
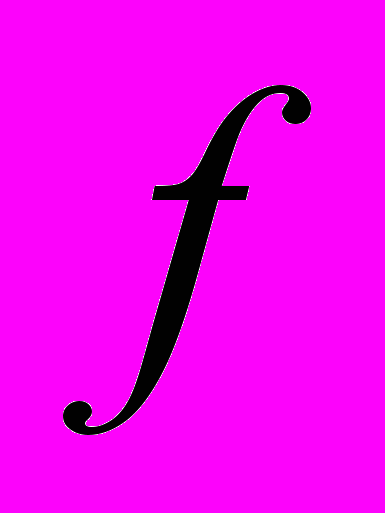 - неприводимый многочлен над полем
- неприводимый многочлен над полем 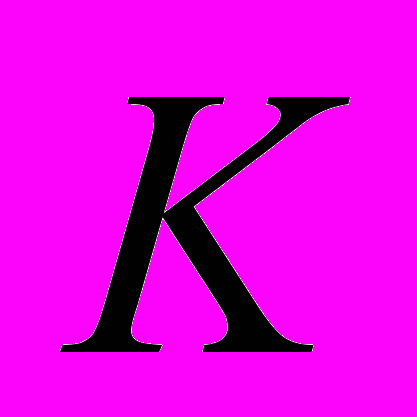 нулевой характеристики и
нулевой характеристики и 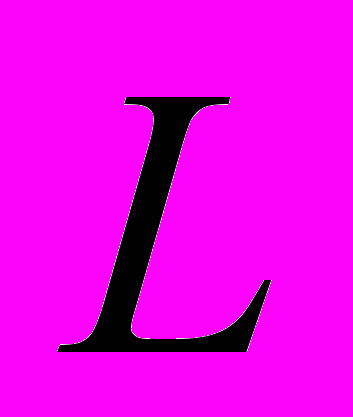 - его поле разложения над
- его поле разложения над 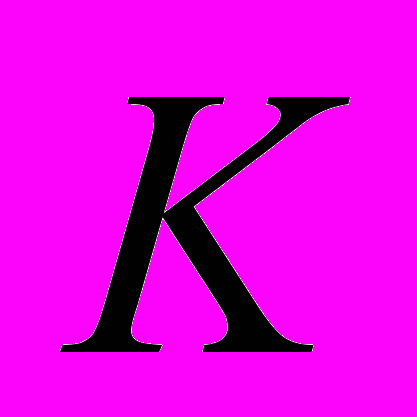 . Уравнение
. Уравнение  разрешимо в радикалах над полем
разрешимо в радикалах над полем 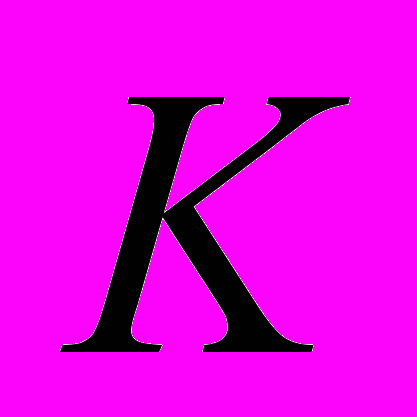 тогда и только тогда, когда группа
тогда и только тогда, когда группа 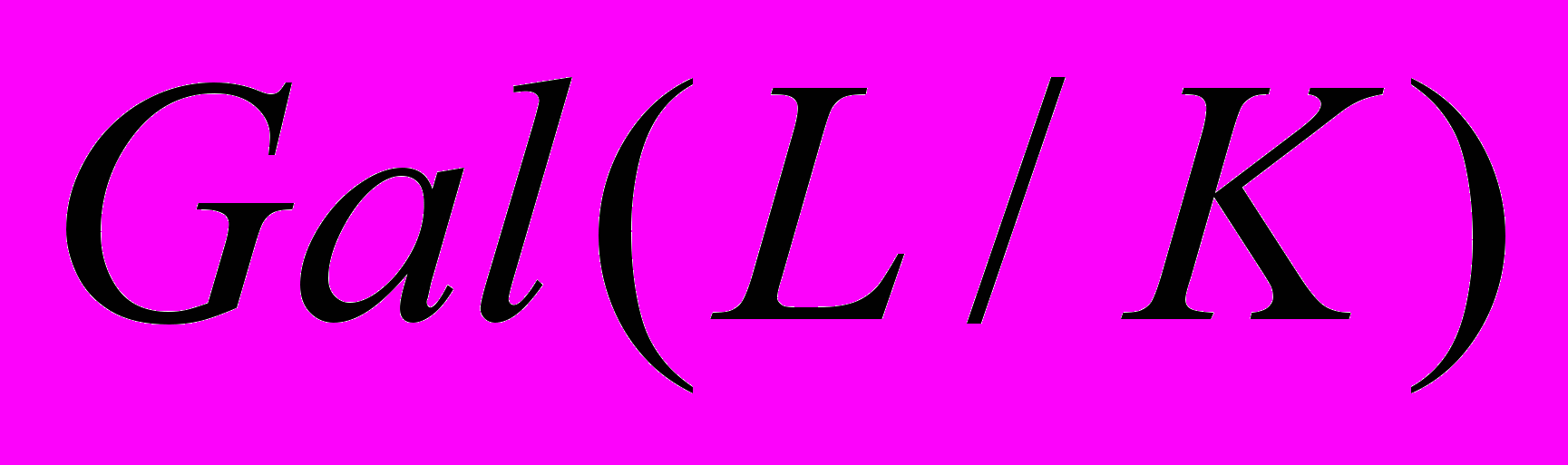 разрешима.»
разрешима.»11 Commentaires sur la mémoire de Galois. – C. r. Acad. csi. Paris, 1865. Commentaires sur Galois. – Math. Ann., 1869. Traité des substirutions et des équations algébriques. – Paris, 1870.
12 Van der Varden B.L. Moderne Algebra. 1re éd., 2 vol., Berlin (Springler), 1930-1931.
