Img src= 359419 html m1532edd0
| Вид материала | Документы |
- Img src= 311719 html 4cdda47f, 87.51kb.
- Img src= 331834 html 7dc629e6, 104.38kb.
- Img src= 244017 html 2e262098, 1013.21kb.
- Img src= 156052 html 7edceb3c, 198.88kb.
- Img src= 312803 html m4ce06215, 1582.25kb.
- Img src= 5485 html 5f4eb1a9, 235.78kb.
- Img src= 315193 html m4ee46b8b, 375.66kb.
- Img src= 327455 html 2e262098, 2244.44kb.
- Img src= 296920 html m6d569a14, 1406.01kb.
- Img src= 164872 html 3d8d891d, 230.67kb.



Историческая справка
Логика - одна из древнейших наук. Ее основателем считается величайший древнегреческий философ Аристотель, который первым систематизировал формы и правила мышления, обстоятельно исследовал категории "понятие" и "суждение", подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.
Античную логику, основанную Аристотелем, принято называть формальной. Это название происходит от основного принципа такой логики как науки, который гласит, что правильность рассуждения определяется только его логической формой или структурой и не зависит от конкретного содержания входящих в него высказываний. В современной логике этот принцип не всегда выдерживается.
Идею о возможности математизации логики высказал еще в XVII веке Г.В.Лейбниц. Он пытался создать универсальный язык, с помощью которого каждому понятию и высказыванию можно было бы дать числовую характеристику и установить такие правила оперирования с этими числами, которые позволили бы сразу определить, истинно данное высказывание или ложно. То есть споры между людьми можно было бы разрешать посредством вычислений. Идея Лейбница оказалось ложной, так как невозможно (не найдены способы) свести человеческое мышление к некоторому математическому исчислению.
Однако, подлинный прогресс этой науки был достигнут в середине XIX века прежде всего благодаря трудам Дж.Буля "Математический анализ логики". Он перенес на логику законы и правила алгебраических действий, ввёл логические операции, предложил способ записи высказываний в символической форме. В трудах Дж.Буля и Д.Моргана математическая логика оформилась как своеобразная алгебра - алгебра логики (или алгебра высказываний).
В развитии математической логики приняли участие многие выдающиеся математики и логики конца XIX и XX веков, в том числе К.Гедель (австр.), Д.Гильберт (нем.), С.Клини (амер.), Э.Пост (амер.), А.Тьюринг (анг.), А.Чёрч (амер.), А.Н.Колмогоров, П.С.Новиков, А.А.Марков и многие другие.
Современная математизированная формальная логика представляет собой обширную научную область, которая находит широкое применение как внутри математики (исследование оснований математики), так и вне ее (синтез и анализ автоматических устройств, теоретическая кибернетика, в частности, искусственный интеллект).
| Алгебра логики (алгебра высказываний) - раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов. |
Таким образом, объектами изучения алгебры логики являются высказывания.
Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно оно или ложно.
Обозначать высказывания будем большими буквами. Если высказывание А истинное, то будем писать "А = 1" и говорить: "А - истинно". Если высказывание Х ложно, то будем писать "Х = 0" и говорить "Х ложно".
ПРИМЕРЫ
А = "Солнце светит для всех." = 1 - истинное высказывание
В = "Все ученики любят информатику" = 0 - ложное высказывание
С = "Некоторые из учеников любят информатику." = 1
Д = "А ты любишь информатику?" - не высказывание, т.к. не является повествовательным предложением
Е = "Посмотри в окно." - не высказывание, т.к. является побудительным предложением
Ж = "Х * Х < 0" = 0 - ложное высказывание, т.к. какое бы Х мы не взяли произведение Х*Х будет неотрицательным
З = "2 * Х - 5 > 0" - не высказывание, т.к. для некоторых значений Х это выражение будет верным, а для других - нет.
И = "Крокодилы летают очень низко" - высказывание.
Последний пример показывает, что высказывания не обязательно должны быть истинными с точки зрения здравого смысла. Вопрос о том, летают или не летают крокодилы, могут волновать зоологов, но никак не логиков, так как им этот потрясающий факт безразличен. Логическая наука интересуется весьма своеобразно понимаемой истинностью или ложностью высказываний: под логическим высказыванием понимается определенное утверждение, которое может быть доказано или опровергнуто.
В алгебре логики над высказываниями можно производить различные операции (как и в алгебре действительных чисел определены операции сложения, деления, возведения в степень над числами). Мы рассмотрим только некоторые, наиболее важные из них.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
1. ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ)
| Образуется из простого высказывания с помощью добавления частицы НЕ к сказуемому или использованием оборота речи "НЕВЕРНО, ЧТО ...". |
Инверсия обозначается: не А ; А ;
 ; NOT A (в данном пособии - А)
; NOT A (в данном пособии - А) Операцию инверсии можно графически проиллюстрировать с помощью теории множеств и диаграмм Эйлера-Венна. В теории множеств логическому отрицанию соответствует операция дополнения к множеству.
| Таблица истинности
| Дополнение к множеству  | А - множество отличников  - множество не отличников - множество не отличников |
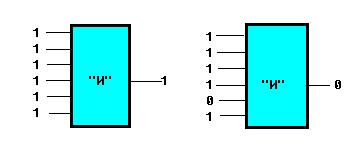
2. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЪЮНКЦИЯ)
| Образуется соединением двух высказываний в одно с помощью союза "И". | |||||||||||||||||||
| | Таблица истинности
| Пересечение множеств 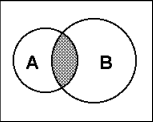 | А - множество отличников в классе В - множество спортсменов в классе А В - множество отличников, занимающихся спортом | | |||||||||||||||
3. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ)
| Образуется соединением двух высказываний в одно с помощью союза ИЛИ | |||||||||||||||||||
| | Таблица истинности
| Объединение множеств | А - множество отличников в классе В - множество спортсменов в классе А В - множество учеников класса, которые являются отличниками или спортсменами | | |||||||||||||||
4. ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ (ИМПЛИКАЦИЯ)
| Образуется соединением двух высказываний в одно с помощью оборота речи "ЕСЛИ ..., ТО... " |
Импликация обозначается: А В; А В
Говорят: "Если А, то В", "А имплицирует В", "А влечет В", "В следует из А".
ПРИМЕР: Пусть даны высказывания А = "На улице дождь", В = "Асфальт мокрый".
А импликация В = “Если на улице дождь, то асфальт мокрый”
| Таблица истинности
| |
5. ЛОГИЧЕСКОЕ РАВЕНСТВО (ЭКВИВАЛЕНТНОСТЬ)
| Образуется соединением двух высказываний в одно при помощи оборота речи "... ТОГДА И ТОЛЬКО ТОГДА, КОГДА ...". |
ПРИМЕРЫ
“Угол называется прямым тогда и только тогда, когда он равен 900”
Эквивалентность обозначается: А = В; А В ; А ~ В
| Таблица истинности
| Эквивалентность множеств |
СЛОЖНОЕ ВЫСКАЗЫВАНИЕ
| Если несколько простых высказываний объединены в одно с помощью логических операций, то такое высказывание называется сложным. |
ПРИМЕРЫ:
| Сложное высказывание | Составляющие простые высказывания | Форма сложного высказывания |
| Е = Идёт дождь, а у меня нет зонта | А=Идёт дождь В = У меня есть зонт | Е = А В |
| Е = Когда живётся весело, то и работа спорится | А = Живётся весело В = Работа спорится | Е = А В |
| Е = Идёт налево - песнь заводит, направо - сказку говорит | А = Идёт налево В = Идёт направо С = Песнь заводит D = Сказку говорит | E=(A C)V(B D) |
Мы всегда исходим из того, что для любого простого высказывания определено (известно), является ли оно истинным или ложным. По форме сложного высказывания и по таблицам истинности входящих в него логических операций всегда можно определить, истинное оно или ложное.
Реальную задачу, как правило, мы получаем в виде текста на естественном языке. И прежде, чем приступить к ее решению, мы должны выделить простые высказывания, отношения (связи) между ними и перевести их на язык формул (формализовать условие задачи, определить форму). Разберём примеры формализации сложных высказываний.
Определить форму сложного высказывания
- Е = " Ваш приезд не является ни необходимым, ни желательным"
Составляющие высказывания:
А = " Ваш приезд необходим ";
В = " Ваш приезд желателен "
E= A B
- Е = " Поиски врага длились уже три часа, но результатов не было, притаившийся враг ничем себя не выдавал"
Составляющие высказывания:
А = "Поиски врага длились три часа"
В = "Врага нашли (результат есть)"
С = "Враг себя выдал".
E= C A B
- E = " Если вчера было пасмурно, то сегодня ярко светит солнце"
А = "Вчера было пасмурно";
В = "Сегодня ярко светит сонце"
Е = А B
- Е = "И добродетель стать пороком может, когда ее неправильно приложат" (В. Шекспир)
А = "Добродетель неправильно приложат"
В = "Добродетель стать пороком может"
Е = А В
По форме высказывания получить фразу на естественном языке
- Е = (А В) (C D)
где А = "Человек с детства давал нервам властвовать над собой"
В = "Человек в юности давал нервам властвовать над собой"
С = "Нервы привыкнут раздражаться"
D = "Нервы будут послушны"
Ответ: Е = "Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться и будут ему послушны" (К.Д. Ушинский)
- Е = (В С) A
где А = "Некто является врачом"
В = "Больной поговорил с врачом"
С = "Больному стало легче"
Ответ: Е = "Если больному после разговора с врачом не становится легче, то это не врач" (В.М. Бехтерев)
ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Вычисление значений логических выражений выполняется в определенном порядке, согласно их приоритету:
- инверсия
- конъюнкция
- дизъюнкция
- импликация и эквивалентность
Операции одного приоритета выполняются слева направо. Для изменения порядка дейcтвий используются скобки.
ПРИМЕР 1: А V (B C) D = A
Порядок выполнения:
- А - инверсия
- В С - импликация
- (В С) D - конъюнкция
- А V (B C) D - дизъюнкция
- А V (B C) D = A - эквивалентность
ПРИМЕР 2: A V B C D = A
Порядок выполнения:
- А - инверсия
- С D - конъюнкция
- A V B - дизъюнкция
- (A V B) (С D) - импликация
- (A V B С D) = А - эквивалентность
ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ СЛОЖНЫХ ВЫСКАЗЫВАНИЙ
Значение сложного высказывания определяется по таблице истинности.
Посмотрим, может ли сама форма высказывания “сказать” нам, истинно ли высказывание или ложно. Для этого рассмотрим пример.
ПРИМЕР 1. В классе оказалось разбито стекло. Учитель объясняет директору: “Это сделал Коля или Саша. Но Саша этого не делал, так как в это время сдавал мне зачёт. Следовательно, это сделал Коля”.
- Формализуем данное сложное высказывание. Для этого выделим составляющие простые высказывания и определим их количество (n).
К = Это сделал Коля
С = Это сделал Саша
n = 2
- Определим форму высказывания E = (K V C) C K
- Определим количество строк и столбцов в таблице истинности. Так как каждое из высказываний может принимать всего два значения (0 или 1), то всего разных комбинаций 2n. Число строк в таблице равно 2n плюс две строки на заголовок. Число столбцов в таблице равно сумме числа простых высказываний (n) и числа логических операций, входящих в сложное высказывание.
В нашем примере:
число строк равно 22 + 2 = 6,
число столбцов 2 + 4 = 6
- Рисуем таблицу:
1
2
3
4
5
6
K
C
C
2
K V C
1 V 2
(K V C) C
4 3
(K V C) C K
5 3
0
0
0
1
1
0
1
1
- Заполняем таблицу последовательно по столбцам (3, 4, 5, 6) в соответствии с определениями логических операций.
| 1 | 2 | 3 | 4 | 5 | 6 |
| K | C | 2 | 1 V 2 | 4 3 | 5 3 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
ВЫВОД: мы получили в 6 столбце все единицы. Это означает, что для любых значений простых высказываний К и С значение сложного высказывания всегда истинно. То есть сама форма показала, что учитель рассуждал логически правильно.
Примечание: конечно, это логическое высказывание нельзя считать доказательством вины Коли. Коля будет виновен, только если истинно высказывание KЪC. Учитель это высказывание никак не обосновал, а просто предложил принять на веру.
ПРИМЕР 2. Построим таблицу истинности для высказывания
E = (A V B) C
В высказывание Е входят три переменные: А, В, С ( n=3 ) и четыре логические операции: инверсия В, инверсия С, дизъюнкция, импликация.
Таблица истинности будет состоять из 23 + 2 (заголовок) = 8 +2 = 10 строк и 3 + 4 = 7 столбцов
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| A | B | C | B 2 | C 3 | A V B 1 V 4 | A V B C 6 5 |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
АЛГОРИТМ ЗАПОЛНЕНИЯ ТАБЛИЦЫ ИСТИННОСТИ
(На примере n = 3)
Пусть сложное высказывание состоит из n простых . Тогда число строк в таблице истинности 2n (так как каждое высказывание может принимать лишь два значения - 0 или 1). Число столбцов в таблице равно сумме числа переменных и числа различных логических операций, входящих в высказывание.
Имеем 23 = 8 строк.
| В столбце А чередуем 4 нуля и 4 единицы. В столбце В чередуем 2 нуля и 2 единицы. В столбце С чередуем 1 ноль и 1 единицу. |
Таким образом, все возможные варианты учтены и никакие два не совпадают. Фактически такое заполнение столбцов соответствует двоичной записи чисел от 0 до 7. Столбцы с 4-го по 7-й заполняются в соответствии с таблицами истинности соответствующих логических операций, причём при заполнении каждого столбца операции выполняются над значениями одного или двух столбцов, указанных в строке заголовка таблицы.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| A | B | C | B 2 | C 3 | A V B 1 V 4 | A V B C 6 5 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 |
Если в формулу входят 4 переменные, то таблица истинности для этой формулы, включающая все возможные комбинации истинности или ложности ее переменных в таблице, будет состоять из 24 = 16 строк; при 5 переменных в таблице имеем 25 = 32 строки; при n переменных - 2n строк.
Для любого сложного высказывания можно построить его таблицу истинности. Это следует из того, что число входящих в него переменных конечно и каждое из них может принимать всего два значения. Заметим, что для всех натуральных чисел, например, такую таблицу построить нельзя.
ТОЖДЕСТВЕННО ИСТИННЫЕ И ТОЖДЕСТВЕННО ЛОЖНЫЕ ВЫСКАЗЫВАНИЯ
| Если сложное высказывание истинно для всех значений входящих в него переменных, то такое высказывание называется ТОЖДЕСТВЕННО ИСТИННЫМ или тавтологией (обозначается константой 1). |
НАПРИМЕР высказывание: "Демократ - это человек, исповедующий демократические убеждения" - всегда истинно, то есть является тавтологией.
Все математические, физические и др. законы являются тавтологиями. Например: (а+b)2 = a2 + 2ab + b2
Прогноз погоды на завтра может быть, например, таким: "Дождь будет или дождя не будет". Такое предсказание будет всегда истинным, хотя вряд ли кого устроит. Его математическая запись:
А V А = 1
(по закону исключенного третьего всегда должно быть истинным либо суждение, либо его отрицание).
Проверить, является ли сложное высказывание тождественно истинным, можно по таблице истинности.
Этот пример показывает, что эффективность средств математической логики видна тогда, когда трудно установить, вытекает ли какое-либо следствие из данных посылок или нет.
| Если сложное высказывание ложно при всех значениях входящих в него переменных, то такое высказывание называется ТОЖДЕСТВЕННО ЛОЖНЫМ ( обозначается константой 0 ). |
НАПРИМЕР, высказывание: "Сегодня среда, а это - второй день недели" является тождественно ложным. Тождественно ложным является и следующее высказывание: "Компьютер включен и компьютер не включен (выключен)". Математическая запись его такова:
A A = 0
(по закону противоречия: не могут быть одновременно истинны утверждение и его отрицание.)
| Если значения сложных высказываний совпадают при всех возможных значениях входящих в них переменных ,то такие высказывания называют РАВНОСИЛЬНЫМИ, ТОЖДЕСТВЕННЫМИ, ЭКВИВАЛЕНТНЫМИ |
В качестве примера рассмотрим два высказывания:
X = "Не может быть,что Матроскин выиграл приз и отказался от него"
X = ( A B )
Y = "Или Матроскин не отказался от приза или не выиграл его"
( Y = A V B )
Чтобы доказать равносильность (эквивалентность) X = Y, достаточно построить таблицу истинности сложного высказывания. Построим её.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| A | B | 1 | 2 | 1 2 | 5 | 3 V 4 | 6 = 7 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
Вывод о равносильности можно сделать по следующим признакам:
- Так как значения сложных высказываний X (столбик 5) и Y (столбик 6) совпадают для всех возможных значений входящих в них переменных, то по определению Х равносильно Y.
- Так как 7 столбец (раскрытие операции эквивалентности) содержит одни единицы, то тем самым доказано, что X = Y - есть тавтология.
