Казанцева Елена Аркадьевна Методист: Авдеев Виталий Владимирович Тема урок
| Вид материала | Урок |
СодержаниеИЛИ Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией Операции импликации и эквиваленции. |
- Казанцева Ольга Петровна с. Имисское 2006 г Тема урок, 50.25kb.
- Козлова Елена Викторовна Тема урок, 75.95kb.
- Сидорова Валентина Аркадьевна, учитель русского языка и литературы с. Лешуконское Тема, 57.13kb.
- Котова Елена Викторовна 4 класс III четверть урок, 99.38kb.
- Сидоркова Елена Аркадьевна, Курасова Елена Владимировна, Шуленина Ольга Владимировна, 498.52kb.
- Елена Абрамова Кризис разного возраста, 318.53kb.
- Подготовили Новикова Елена Адольфовна, учитель начальных классов; Давыдова Елена Егоровна,, 108.71kb.
- Голощапова Елена Геннадьевна, преподаватель русского языка и литературы Тема урок, 83.16kb.
- Голощапова Елена Геннадьевна, преподаватель русского языка и литературы Тема урок, 90.99kb.
- Заступник голови комісії, проректор з навчально-методичної роботи Сумського оіппо,, 191.86kb.
Конспект урока по информатике
Автор конспекта урока: Пуспешев ВладимирАлексадрович
Учитель: Казанцева Елена Аркадьевна
Методист: Авдеев Виталий Владимирович
Тема урока: Алгебра высказываний
Тип урока: Повторение, изучение нового материала
Возраст учащихся: класс
Задачи урока:
- Обучающая – формирование у учащихся понимания алгебраических высказываний и таблице вероятности
- Развивающая – развивать умение качественно оценивать поставленную задачу для правильного выбора способа решения задачи; развивать самостоятельность; логическое мышления учащихся.
- Воспитательная – формировать интерес к предмету, навыки контроля и самоконтроля; чувство ответственности, деловые качества учащихся.
После изучения темы ученики должны:
Знать:
Уметь:
План урока:
- Организационный момент
- Актуализация знаний
- Изучение нового материала
- Закрепление материала
- Подведение итогов
Средства обучения:
И Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением
Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцие логического умножения или конъюнкцией.
и обозначается знаком умножения " *" (может также обозначаться знаками
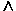 или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" — ложны.
или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" — ложны. Образуем составное высказывание С, которое получится в результате конъюнкции двух простых высказываний. С= АВ
Истинность такого высказывания задается специальной таблицей, таблицей истинности логического умножения.
| А | В | АВ |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
ИЛИ Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением
Объединение двух (или нескольких) высказываний с помощью союза «или» называется операцией логического сложения или дизъюнкцией.
и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание "10 не делится на 2 или 5 не больше 3" ложно, а высказывания "10 делится на 2 или 5 больше 3", "10 делится на 2 или 5 не больше 3", "10 не делится на 2 или 5 больше 3" — истинны.
Образуем составное высказывание С, которое получится в результате дизъюнкции двух простых высказываний. С=АvВ
Истинность такого высказывания задается специальной таблицей, таблицей истинности логического сложения.
| А | В | АvВ |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания(инверсия) ("не"), затем конъюнкция(*) ("и"), после конъюнкции — дизъюнкция(+) ("или").
Задание:
Сравнить два логических высказывания с помощью таблице истенности. АВ и АvВ
Операции импликации и эквиваленции.
Л
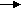 огическая операция импликации «если А то В», обозначается А В и задается следующей таблицей истинности.
огическая операция импликации «если А то В», обозначается А В и задается следующей таблицей истинности.| А | В | А 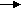 В В |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическая операция эквивалентности «А тогда В и только тогда», обозначается А~В и задается следующей таблицей истинности
| А | В | А~ В |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Задание:
1
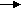 Докажите, что операция импликации А В равносильна логическому выражению АvВ
Докажите, что операция импликации А В равносильна логическому выражению АvВ2 Докажите, что операция эквиволентности А~ В равносильна логическому высказыванию (АВ) v(АВ)
3 Докажите, что логическое высказывание АВ равносильно логическому высказыванию АvВ
