Ii. Множественное рождение частиц в адрон-ядерных взаимодействиях

Вид материала

Документы

Подобный материал:

• Школа современной астрофизики, Пущино, 7-9 и 13-14 (или 10-11) июля 2008, 31.32kb.
• Лекция 19. Интерфейсы. Множественное наследование Интерфейсы как частный случай класса., 433.86kb.
• Исследования деления ядер урана и плутония при низких энергиях возбуждения. 01. 04., 549.02kb.
• 1. формирование сигнала в счетчике с вакумным фэу, 60.02kb.
• Возможность объяснения низкотемпературных ядерных реакций, исходя из логнормального, 455.14kb.
• Барионы и мезоны. Метастабильные адроны и резонансы. Странные и очарованные адроны., 22.91kb.
• Обнаружение эффекта подавления выходов заряженных адронов с большими поперечными импульсами, 1409.46kb.
• Обнаружение эффекта подавления выходов заряженных адронов с большими поперечными импульсами, 1409.48kb.
• Программа Государственного экзамена по подготовке магистра по направлению «Физика ядра, 32.88kb.
• Бакалов Валерий Пантелеевич. Основы теории цепей: учебник, 143.88kb.

Кривая с перегибом (точкой симметрии) имеется в области малых углов. Эти события, по-видимому, относятся к адрон-ядерным взаимодействиям, причем, с тяжелым ядром (Ag или Br) в эмульсии. Для этих взаимодействий характерна очень узкая струя первичного NN взаимодействия, энергия которого тогда оценивается 10⁴ ГэВ, и широкий конус ливневых частиц уже вторичного взаимодействия частиц, рожденных в этом NN взаимодействии, провзаимодействовавших с ядерным веществом при выходе из ядра.

Последнее, 7-е событие таблицы 2 вообще не имеет симметричной части и, по сути, является «двухфайербольным» событием 71, которые интенсивно начали в это время изучаться. Кластеризация частиц оказалась тесно связанной с угловыми корреляциями, которые изучались автором уже на эмульсиях, облученных на ускорителях, и будут рассмотрены отдельно.


§ 2 Рождение некоторых типов частиц в опытах на ускорителях


С появлением пучков ускоренных частиц до энергий, при которых уже начинается процесс множественного рождения (Дубна, протоны 9 ГэВ), и почти одновременно с разработкой и промышленным производством в СССР бесподложечных ядерных фотоэмульсий НИКФИ БР-2, регистрирующих следы частиц с минимальной ионизирующей способностью, начались исследования рождения частиц определенных типов, которые легко выделялись в эмульсии. Сюда относятся работы 78-80 по изучению гиперфрагментов, рожденных протонами с энергией 9 ГэВ и ^--мезонами с энергией 4.5 ГэВ, а также образование медленных -мезонов пучком ^--мезонов с энергией 3.8 ГэВ.

Гиперфрагменты, открытые М. Данишем и Е. Пневским в ядерных фотоэмульсиях 81, представлялись удобным объектом исследования рождения странных частиц (⁰), застревающих в ядре, замещая в нем обычный нуклон, и затем покидающим ядро-мишень в составе одного из фрагментов. Идентификация гиперфрагмента в событии упрощается тем обстоятельством, что чаще всего распад ⁰-частицы с испусканием -мезона или без него («безмезонные распады»), происходит уже после остановки фрагмента с ⁰-частицей внутри его в ядерной фотоэмульсии. Возникают связанные звезды, хорошо выделяющиеся в эмульсии. Таким образом, изучение гиперядер в фотоэмульсии оказывается связанным и с процессом множественного рождения частиц, т. к. ⁰-частицы не могут рождаться в NN взаимодействиях по одиночке, и с процессом испускания фрагментов в адрон-ядерном взаимодействии. Изучение поведения ⁰-частицы в ядре и до сих пор остается актуальным. До сих пор гиперфрагменты являются единственным примером связи странных частиц в ядерном веществе.

Определение сечения образования гиперфрагментов протонами с энергией 9 ГэВ в работе 78 дало величину, равную 0.20.1 мбн. по общему числу зарегистрированных гиперядер 20 шт. Все они образуются в звездах со средним числом медленных частиц n_h=14.01.4. Это дает основание считать, что гиперядра образуются при взаимодействии быстрого протона с тяжелым ядром в эмульсии (Ag, Br). Угловое распределение гиперфрагментов в лабораторной системе имеет четко выраженный избыток частиц в передней полусфере. Отношение «вперед-назад» равно 2.3, что хорошо согласуется с данными обзора 82.

Безмезонные распады гиперфрагментов исследованы в работах 79, 80. В отличие от мезонных распадов, их идентификация более трудна. В этом случае вторичные частицы уносят энергию около 140 МэВ. Но при этом имеется возможность получить сведения о характере ^оN взаимодействия. Согласно работе 83, при взаимодействии ^о-частицы с нуклоном, отношение канала, идущего через взаимодействие ее с нейтроном к каналу, идущему через взаимодействие с протоном (R=N/P) должно быть меньше или равно единице. В эксперименте 79 это отношение равно 1.25. Отсюда сделан вывод, что некоторая доля безмезонных распадов гиперфрагментов может идти через виртуальное ^о-состояние.

В работе 80 анализируются продукты распадов гиперфрагментов с использованием методов идентификации, описанных в главе I. Наличие двух быстрых нуклонов в одном событии соответствует предложенной в 83 схеме распада гиперфрагмента в результате реакции
^о+Nn+N. (30)

Другим «меченым» адроном, изученным в процессе множественного рождения является медленный -мезон, рождающийся при взаимодействии ^--мезонов с энергией 3.8 ГэВ с ядрами в фотоэмульсии 84. Интерес к рождению медленных -мезонов в то время возник еще и в связи с открытием резонансов. Было высказано предположение, что эти мезоны могут быть следствием распада пионных резонансов 85. В работе 84 изучались энергетические и угловые распределения -мезонов с энергией до 40 МэВ. Идентификация ⁺-мезонов производилась по их характерному ⁺-⁺-е⁺ распаду, а ^--мезонов по расщеплениям ядер эмульсии вызванных их захватом.

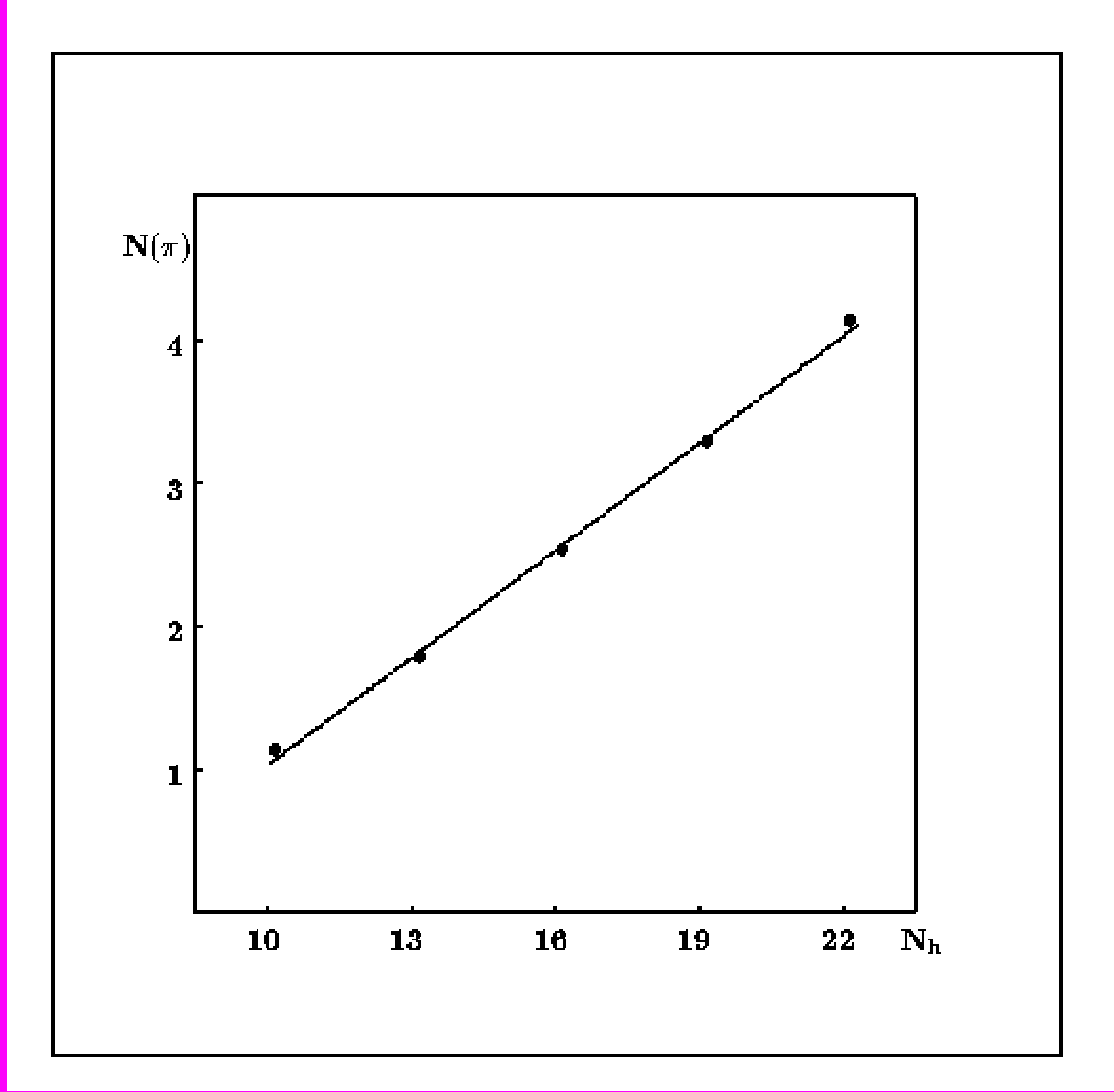
Всего исследовано 213 остановок -мезонов в эмульсии, 151 из них является ^--мезоном и 63 события являются ⁺. В 120 случаях рождение этих частиц происходит при расщеплении первичной частицей тяжелого ядра в эмульсии (n_h>8). Между степенью разрушения ядра и вероятностью испускания медленного -мезона установлена линейная зависимость (см. рис.7).

Рис. 7

Зависимость относительного числа N () медленных -мезонов на событие от числа N_h лучей в звезде в событиях, вызванных взаимодействием ^--мезонов с энергией 3.8 ГэВ с ядрами в фотоэмульсии.


В пределах ошибок не обнаружено различия угловых и энергетических спектров медленных -мезонов при расщеплении легких и тяжелых ядер в фотоэмульсии.

Анализируя данные о «подбарьерных» ⁺-мезонах работ 84,85, в которых изучалась вероятность их появления в pN и -N взаимодействиях,

можно заключить, что гипотеза рождения медленных ⁺-мезонов через пионные резонансы опровергается и фактом большой их вероятности рождения при взаимодействии -частиц с ядрами меди при энергии 390 МэВ 86, когда известные пионные резонансы рождаться не могли из-за малости энергии.

Развитие методов идентификации частиц и новая техника в виде микроскопов МИРЭ-1 и МИГЭ-1 позволили подойти к идентификации и других быстрых частиц, рождающихся при взаимодействии ^--мезонов с импульсом 7.2 ГэВ/с с ядрами в фотоэмульсии 87,88. Анализировались события с двумя 87, с тремя и четырьмя 88 частицами, ионизация которых была <1.5 от минимальной. По измерениям многократного рассеяния и ионизации идентифицированы -, K-мезоны, протоны, -гипероны и дейтоны. В изученном классе взаимодействий ^--мезонов с тяжелыми ядрами эмульсии сечение образования K⁺-мезонов в звездах с двумя релятивистскими частицами оказалось равным 9.94.7 мбн. Эта величина согласуется с расчетами по модели ядерного каскада с учетом выхода K-мезонов 89.

В работе 87 определены средние величины поперечных импульсов -мезонов, K-мезонов и протонов. В таблице 3 приведены средние значения самих импульсов частиц и средние величины P_ в сравнении с работой 90.

Все экспериментальные данные о множественном рождении частиц, полученные на первом этапе исследования этого явления в работах 76, 78-80, 84, 87, 88 оказались в русле современных представлений и были развиты в последующих работах при энергиях протонов 200 и 400 ГэВ.


Таблица 3.

Средние величины Р импульсов рожденных частиц и их Р_ (МэВ/с), в сравнении с работой [90].

частицы	импульсы	данные [87]	данные [90]
  K K p p	р р р р р р	72573 186100 78778 212100 1970390 400100	20016 22014 31034

§ 3 Угловые распределения и корреляции вторичных частиц
в адрон-адронных и адрон-ядерных взаимодействиях
при энергиях 200 и 400 ГэВ


Новый этап исследования процесса множественного рождения частиц начался с облучения эмульсионных камер выведенными пучками протонов 200 и 400 ГэВ и ^--мезонов 200 ГэВ в FNAL (США) в начале 70-х годов сотрудничеством многих лабораторий СССР (Алма-Ата, Гатчина, Дубна, Ленинград, Москва, Ташкент), а также Польши, Монголии, Чехословакии, Венгрии, Румынии. Обработка данных велась по Протоколу, обязательному для всех членов Сотрудничества. Создание банка событий обычно велось в Дубне, Гатчине, Ленинграде и Ташкенте. Таким образом, создавался уникальный экспериментальный материал, далеко превосходящий аналогичные данные отдельных Лабораторий, не входящих в Сотрудничество. В данной диссертации рассмотрены только те работы, которые выполнены автором и опубликованые в свое время от имени Сотрудничества, и работы автора на материале Сотрудничества, который получен с его участием, но опубликованные уже фактически после окончания Сотрудничества. Таким образом, здесь излагаются далеко не все работы различных Сотрудничеств, в которых автор принимал участие.

Угловые распределения ливневых частиц обсуждаются в терминах быстрот Y или квазибыстрот

=-ln tg (/2), (31)
где  это полярный (пространственный) угол между вектором импульса частицы p и импульсом p_о первичного адрона. Это определение  совпадает с определением быстроты

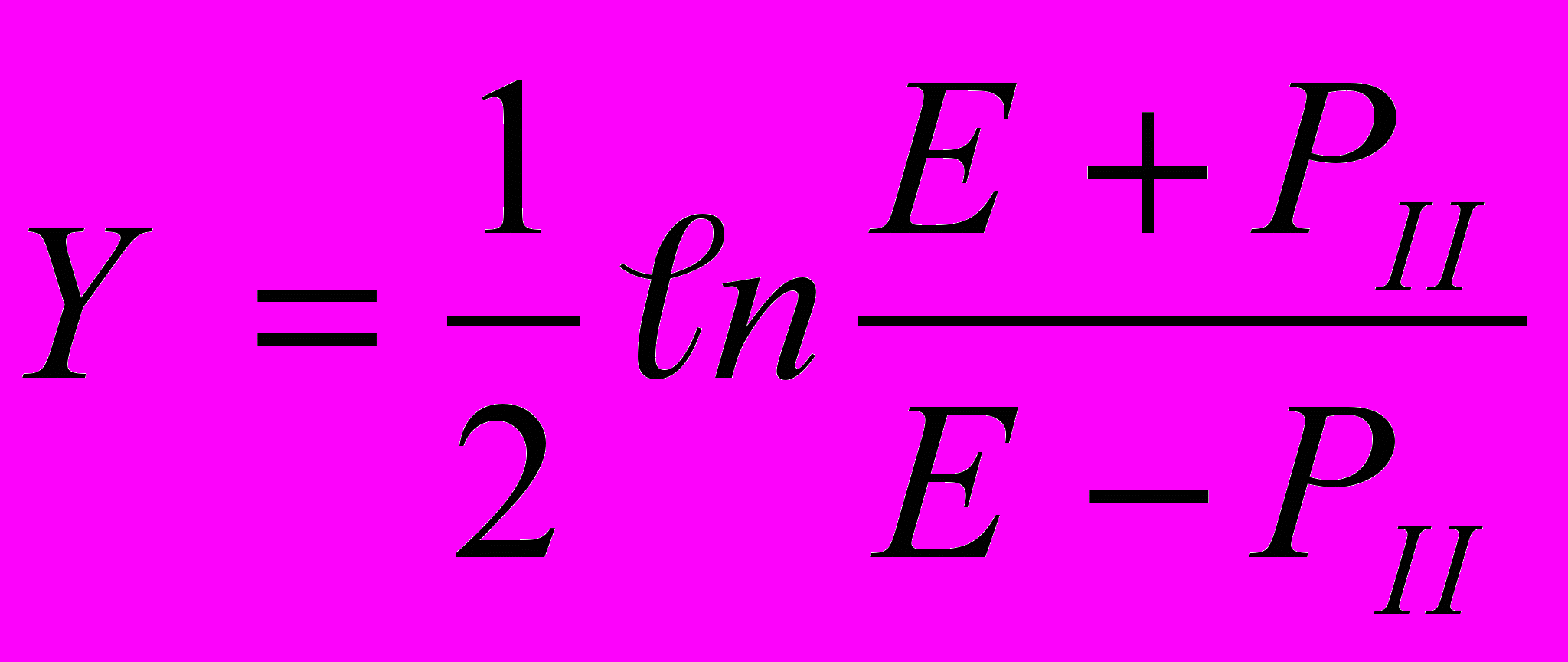(32)

для вторичной частицы в приближении, что для нее выполняются соотношения p/Е1, а Sin²>>m²/p². Оказалось, что распределения по  и по Y практически совпадают и т. о, только измеряя угол , мы получаем важную физическую информацию.

Квазибыстроты (как и быстроты) аддитивны 38, так что переход от распределения по  в лабораторной системе по (31), к распределению в системе центра масс, движущейся в лабораторной системе со скоростью _с, осуществляется просто сдвигом шкалы  на величину

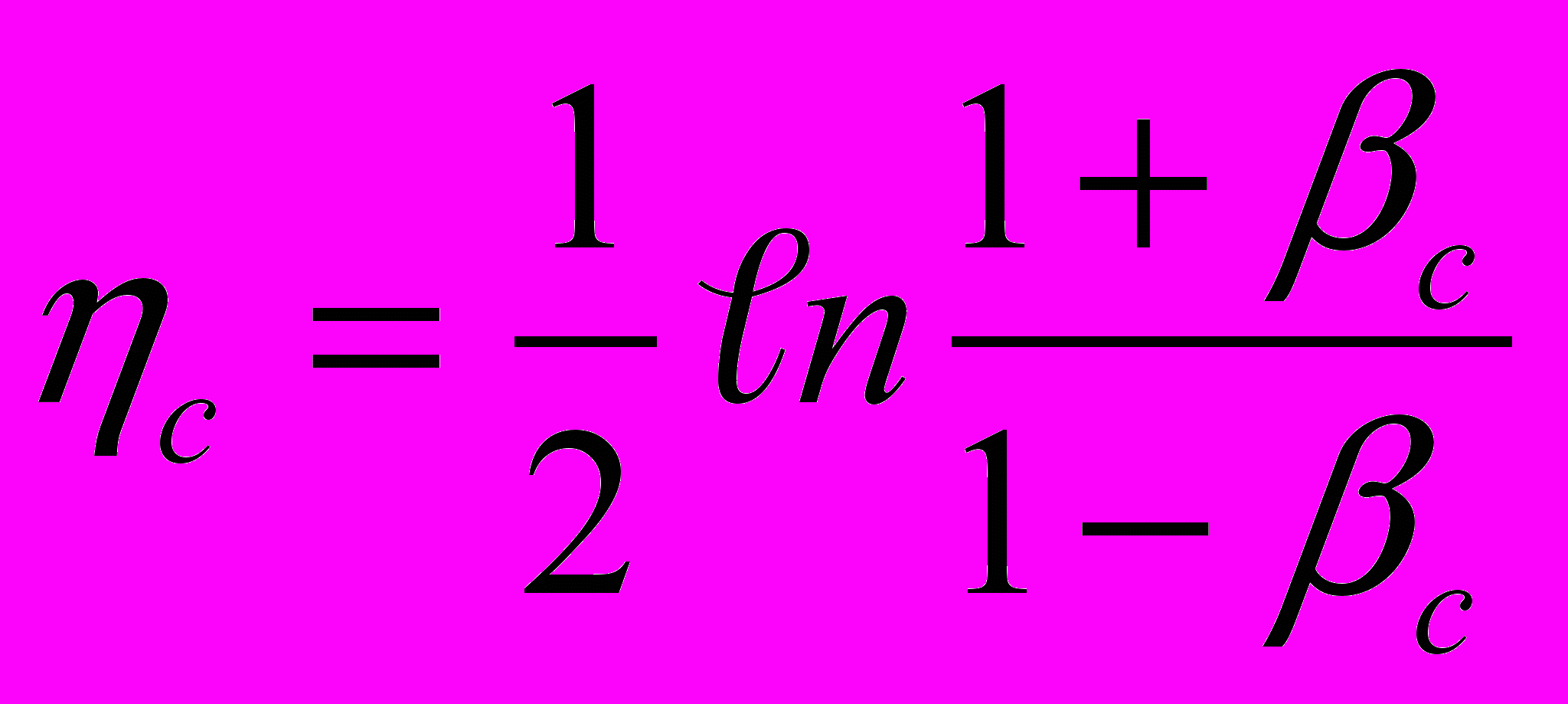. (33)

Для рр взаимодействий с энергией 200 ГэВ _с3.0.

В работах 41, 91 исследованы угловые распределения вторичных частиц в pN-взаимодействиях при импульсе 200 ГэВ/с и начато изучение корреляции в пространстве квазибыстрот. Сотрудничеством Алма-Ата - Ленинград - Москва - Ташкент на 3303 м следов первичных частиц из 9339 неупругих взаимодействий выделено 1620 взаимодействий, удовлетворявших критериям отбора неупругих квазинуклонных взаимодействий 34. Точность оценки угла =0 в этой работе была 0.3 мрд.

Распределение по квазибыстроте для групп событий с четным и нечетным числом вторичных релятивистских частиц в событии приведено на рис. 8. В таблице 4 приведены характеристики суммарных ливней при различных множественностях вторичных частиц. В последней строке приведены данные после исключения в событии одной «лидирующей» частицы с углом <0.5^о (если она есть). Угловое распределение качественно согласуется с термодинамической моделью 92, за исключением области больших квазибыстот в эксперименте. Попытка описания рождения частиц по обычному фазовому объему привела к резкому противоречию с экспериментом. В эксперименте распределение по квазибыстроте значительно шире.

Далее в 41 проведен статистический анализ однородности набора средних значений квазибыстрот _n,i в отдельных ливнях при фиксированной множественности n с использованием дисперсионного анализа 52. Нулевая гипотеза, состоящая в том, что все средние значения _n,i в событии для всех событий с данной множественностью n являются оценками одного и того же среднего суммарной выборки не отвергается.

Но гипотеза однородности выборки дисперсий распределения квазибыстрот в индивидуальных ливнях отвергается дисперсионным анализом уверенно. Распределение по квазибыстроте в каждом событии не является выборкой из суммарного ливня при данной множественности n. Это является указанием на эффекты кластеризации частиц при их множественном рождении в pN-взаимодействиях при энергии 200 ГэВ.


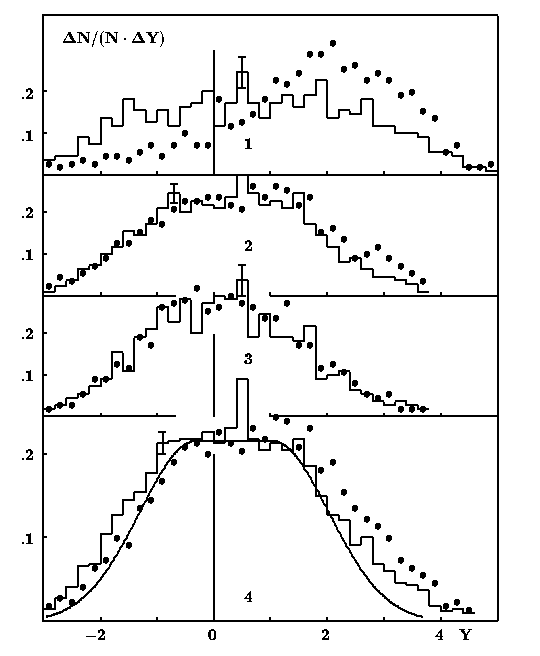Рис. 8

Распределения вторичных релятивистских частиц по квазибыстроте Y=-ln (tg /2) в рр (гистограммы) и pn взаимодействиях протонов с импульсом 200 ГэВ/с (черные точки). Для разных групп множественностей: 1 – рр с n_S=2, 4, 6, pn c n_S=1, 3, 5; 2 - рр с n_S=8, 10, 12, pn c n_S=7,9,11; 3 - рр с n_S>12, pn c n_S>11; 4 – все n_S четные (гистограмма), все n_S нечетные (точки). Плавная кривая внизу соответствует ожидаемому распределению в рр взаимодействиях по термодинамической модели [92]. Эксперимент [41].


Таблица 4.

Некоторые характеристики суммарных ливней в pN взаимодействиях в эмульсии при энергии 200 ГэВ/с.

тип. выбор.	число соб.	число след.	
все нечет. все чет. все соб. все без лидир.	990 630 1620 1514	6178 5208 11386 10352	3.761.56 3.431.53 3.611.55 3.341.33

В партонной модели Фейнмана 74 предполагается, что вероятность отсутствия партонов на интервале быстрот у ведет себя как
ехр (-A_ny), где A_n зависит от квантовых чисел «переносимых» указанным интервалом. Поэтому, получив экспериментальные величины квазибыстрот  в событиях с множественностью n были исследованы распределения быстротных интервалов =_i-_i+1 для вариационного ряда ₁>₂>...>_n в событии. Простейшая мультипериферическая модель предсказывает, что =(n-1)/Y, где Y=2_c, должно быть равно A_n. Экспериментальные интегральные распределения величин (>y) (вероятность наблюдения  больше данного), для всех множественностей действительно хорошо описываются экспонентой (см. рис. 9 и таб. 5) . в последнем столбце указано 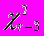, где r-3 число степеней свободы для r точек. Гипотеза экспоненциального распределения разностей квазибыстот в эксперименте не отвергается ни при каких множественностях, но и согласия с простым фазовым объемом или мультипериферической моделью нет. Все A_n больше ожидаемых величин . А это означает, что в эксперименте чаще рождаются частицы с малыми разностями быстрот.

Более детальное исследование различных областей по квазибыстроте , несколько условно разделенных на три части: 1 - область фрагментации мишени с <2.0; 2 - область пионизации с 2.0<<4.5 и область 3 - фрагментация первичной частицы с >4.5 выявило различие между ними.

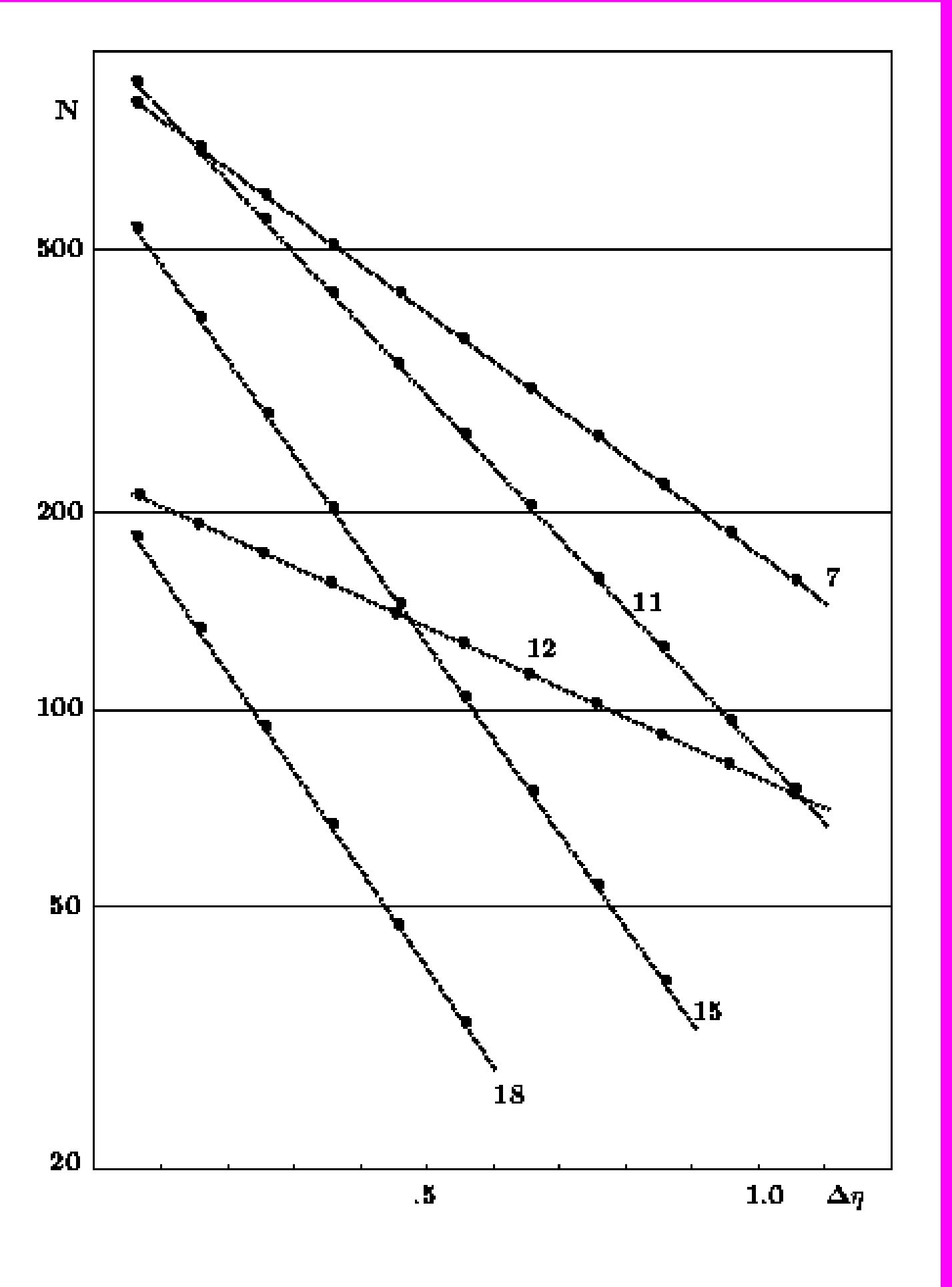Рис. 9

Распределение пар следов в одном событии с разностью квазибыстрот >. Числа у прямых (7, 11, 12, 15, 18) означают множественность ливневых частиц в событиях, для которых получена данная зависимость. Протоны с импульсом 200 ГэВ/с, эксперимент [41].

Таблица 5.

Параметр A_n в экспоненциальном распределении разностей квазибыстрот в событиях с разной множественностью ливневых частиц n_s в pN взаимодействиях при импульсе 200 ГэВ/с (работа [41]).

ns	число точек r	An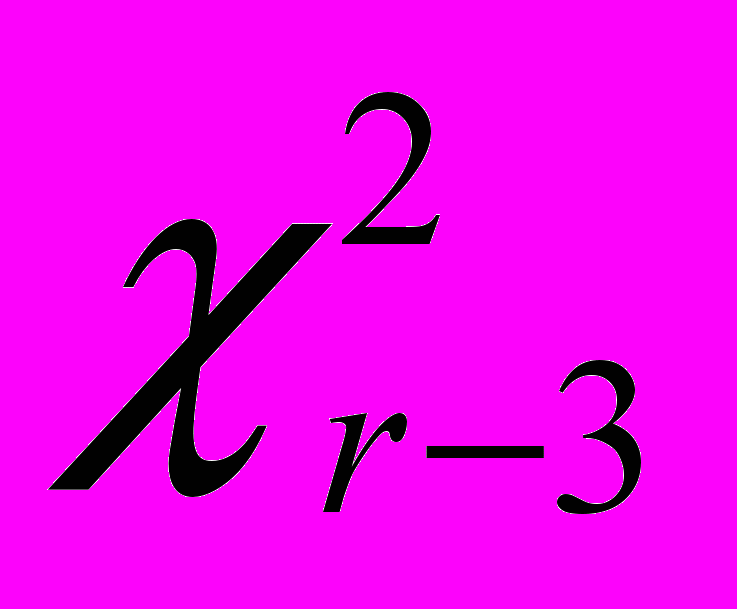
4 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20	10 18 11 10 12 11 11 11 11 11 10 9 6 6 5 4	1.0450.094 1.1400.033 1.5440.051 1.640.06 1.830.05 1.750.05 2.310.06 2.440.06 2.630.08 2.900.09 3.310.1 3.400.1 3.780.23 3.540.28 4.180.34 4.930.56	0.41 2.52 0.68 1.32 1.58 1.05 2.08 1.44 5.33 2.31 2.32 3.31 0.11 1.63 0.62 0.66

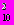
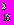Рис. 10 показывает, что в то время, как для обеих областей фрагментации 1 и 3 распределения величин  в них хорошо описываются экспонентами с А₁=1.6110.003 (=1.3) и А₃=1.8940.004 (=7.9), то для области пионизации такое описание оказывается плохим

(А₂=2.930.02, 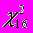=126.3). В этом случае распределение по  может быть хорошо описано зависимостью вида

f()=exp(-A+B()²) (34)

c А=2.880.06 и В=0.850.08 с 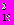=7.8.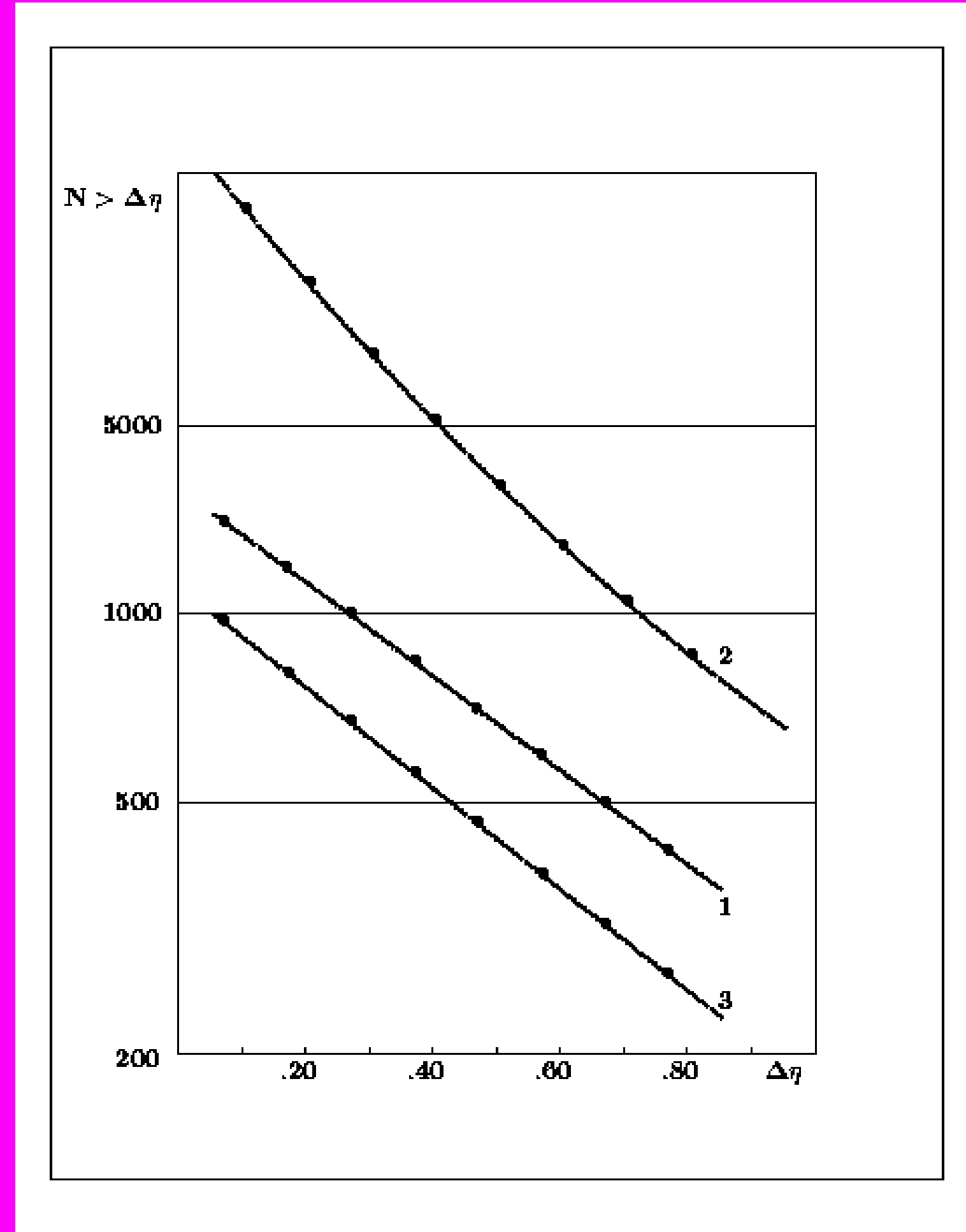


Рис. 10.

Интегральное распределение пар следов в pN взаимодействиях 200 ГэВ/с 41] с разностью квазибыстрот больше данной  для разных интервалов квазибыстрот. 1 – область фрагментации мишени (<2.0); 2 – область пионизации ( от 2.0 до 4.5); область фрагментации первичной частицы (>4,5).


Это отступление от линейного закона распределения разностей быстрот в области пионизации может рассматриваться как указание на наличие дальних корреляций в пространстве быстрот.

Таким образом, возникла проблема более детального изучения корреляции частиц при множественном рождении. Этот вопрос и будет рассмотрен в следующем параграфе.


§ 4 Корреляции вторичных частиц при множественном рождении в адрон-адронных, адрон-ядерных и ядерно-ядерных
взаимодействиях


Идея использования в физике высоких энергий аппарата корреляционных функций, до это развитого в классической статистической физике 93, была предложена Вильсоном и Мюллером в 1970 г. 94, 95. Физический смысл корреляционной функции состоит в определении вероятности нахождения некоторых объектов (молекул) в теории жидкостей или реальных газов, частиц при множественном рождении, в элементе фазового объема, в то время, как в нем уже находится по меньшей мере еще один такой (или другой) объект.

Если перейти к множественному рождению n частиц при взаимодействии частиц а и b друг с другом при энергии в их системе центра масс 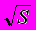, то сечение его в общем виде можно записать как произведение квадрата матричного элемента М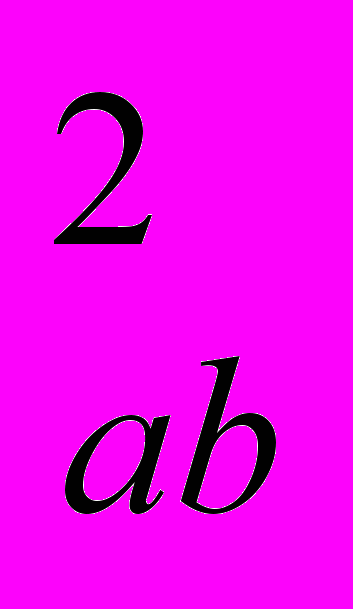(s) на элемент фазового объема

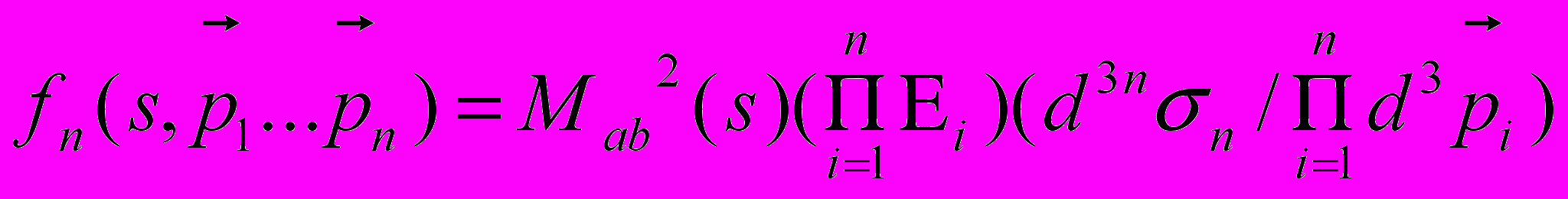. (35)

Плотность многочастичного распределения будет

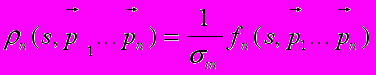. (36)

Если объектами, о которых говорилось при общем определении корреляционной функции, будут любые две из n частиц конечного состояния реакции

a+bc₁+c₂+все остальные n-2 частицы, (37)
то двухчастичная корреляционная функция будет определена как

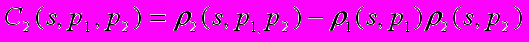. (38)

Смысл ее состоит в том, что она является мерой влияния частицы с₁ с импульсом 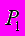, на вероятность того, что другая частица с₂ имеет импульс 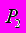при любом распределении по импульсам других n-2 частиц реакции (37). Обобщение (38) на 3-х, 4-х и т. д. частичные корреляции тривиально, однако в основном в множественном рождении частиц исследуются двухчастичные корреляции.

Определение двухчастичной корреляционной функции как меры влияния между состояниями двух частиц отличается от определения парного коэффициента корреляции обычного статистического анализа, являющегося мерой корреляции 30. Полностью проинтегрированная величина С₂ (s) не равна единице. Для тождественных частиц, а именно этот случай и рассматривается далее и чаще всего,

С₂ (s)=D-n² , (39)

где D=n²-n² дисперсия распределения по множественности частиц n при данной величине 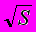частиц a и b 96. Таким образом, при отсутствии корреляции между частицами с₁ и с₂ все элементы матрицы C₂(s) не могут быть равны нулю. Чтобы отличить меру зависимости между частицами с₁ и с₂, определяемую через C₂(s), от корреляций определяемых в статистическом анализе, факт неравенства нулю матричного элемента 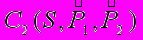стали объяснять «псевдокорреляциями» 97.

Различные модели дают разные зависимости полностью интегрированной корреляционной функции С₂(S) от S 96. Но в чисто практическом плане, естественно, желательно иметь дело с таким определением корреляционой функции, в которой при отсутствии динамических корреляций все матричные элементы ее были бы равны нулю. Такое исключение тривиальных кинематических корреляций было сделано в работе 98 для двухчастичных корреляций в области быстрот у₁ и у₂. Если между статистической зависимостью и корреляцией не делать различия, то можно определить величину

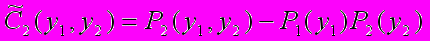, (40)
которая представляет собой разность вероятности совместного наблюдения величин у₁ и у₂ в некотором интервале быстрот и произведения вероятности безусловного их наблюдения в этом же интервале. Эту величину и следует принять за меру взаимной зависимости величин у₁ и у₂. Естественно, что при отсутствии корреляций

.

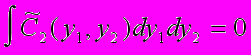Для МНИ все элементы матрицы 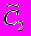(у₁, у₂) равны нулю. Никаких «псевдокорреляций» нет.

В работе 98 показано, что прежнее определение двухчастичной корреляционной функции просто связано с ее новым определением и

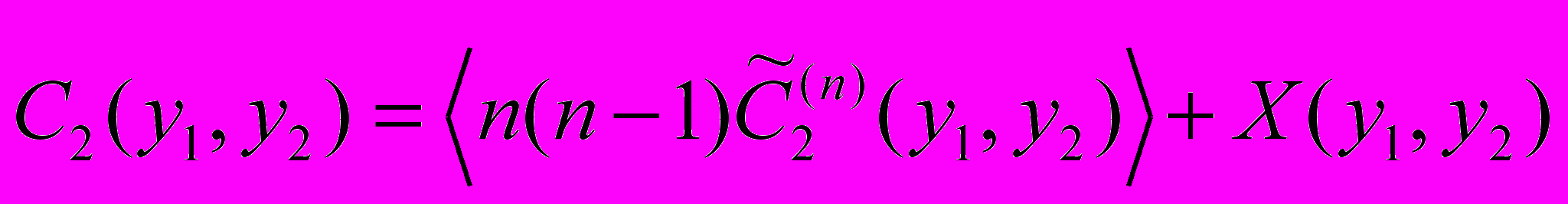. (41)

Здесь 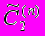(у₁, у₂) есть величина (40), определенная для фиксированного числа частиц n, а все первое слагаемое равно

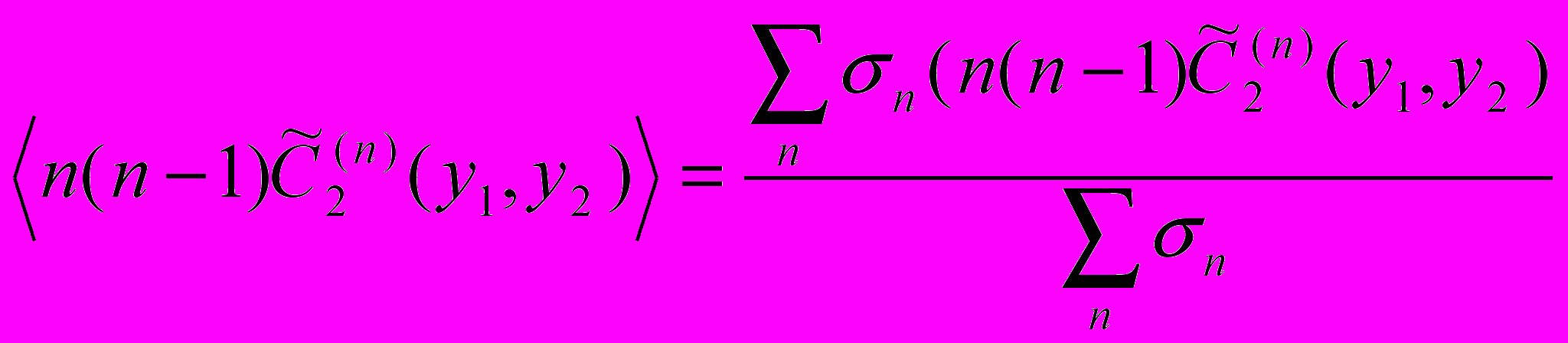. (42)

Именно в этом слагаемом и содержатся корреляции, если они есть, а второе слагаемое

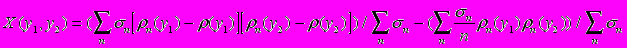(43)

от корреляций не зависит и содержит только комбинации одночастичных плотностей, определяемых как

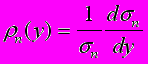. (44)

Это второе слагаемое дает основной вклад в величину матричного элемента (41), и поэтому как только мы добиваемся согласия одночастичных распределений  (у) и распределения по множественности, значения С₂(у₁,у₂) модели и эксперимента оказываются близкими друг другу.

При практическом осуществлении процедура вычисления величин матричных элементов С₂ в экспериментальной выборке событий выглядит просто. Весь интервал возможных значений быстрот в данном эксперименте делим на m равных интервалов Y. В pN взаимодействиях, при Y=0.5 получим, что m=12, так как Y_max6.0. Одночастичные плотности (44) есть просто эмпирическая вероятность значения быстрот Y попасть в соответствующий интервал Y для всего набора событий с данной множественностью n частиц в событии. Для оценки С₂(у₁, у₂) каждому из n значений Y в событии присваивается имя у₁, а затем всем остальным n-1 величинам в этом событии присваивается имя у₂, и подсчитывается число их одновременных с у₁ попаданий в определенный интервал Y. Общее число «испытаний» будет равно n(n-1).

Квадратная матрица размером mm будет симметричной. Линии равных величин С₂ на ней иногда представляют в виде контура, но чаще всего рассматривают только ее диагональные элементы, т. е. вероятность попадания у₁ и у₂ в один и тот же интервал быстрот Y от минимального Y_min+Y до максимального Y_max-Y.

Результаты, полученные при использовании стандартного метода корреляционных функций в анализе множественного рождения частиц в pN и pA 200 и 400 ГэВ 99, а также N и А взаимодействий 200 ГэВ в эмульсии оказались примерно одинаковыми 100. Рассмотрим, например, pN и pA взаимодействия при энергии 400 ГэВ. Общие характеристики этих взаимодействий изучались в работах 101, 102. Распределение по множественности отобранных 534 рр и 530 pn событии приведено на рис. 11. При изучении двухчастичных корреляций события когерентного рождения в pn взаимодействиях не учитывались. Распределение диагональных элементов с₂(₂=₁) для pN и рА взаимодействии приведено на рис. 12. И в том, и другом случае расчетные точки по МНИ лежат чуть ниже экспериментальных точек. Хорошо видны «псевдокорреляции». В МНИ вообще нет никаких корреляций в обычном их понимании, тем не менее в области пионизации (=0) величина С₂(₂=₁) явно отличается от нуля.

Абсолютная величина «псевдокорреляций» в рА взаимодействиях существенно больше, чем в pN взаимодействиях. Это может быть связано с более сложным характером рА взаимодействия, большим числом элементарных pN взаимодействий, как-то связанных друг с другом, большей неоднородностью распределения по множественности. Качественно имеется согласие с предсказаниями партонно-каскадной модели hA взаимодействий при учет конечности энергии частиц, участвующих во внутриядерных взаимодействиях 103.




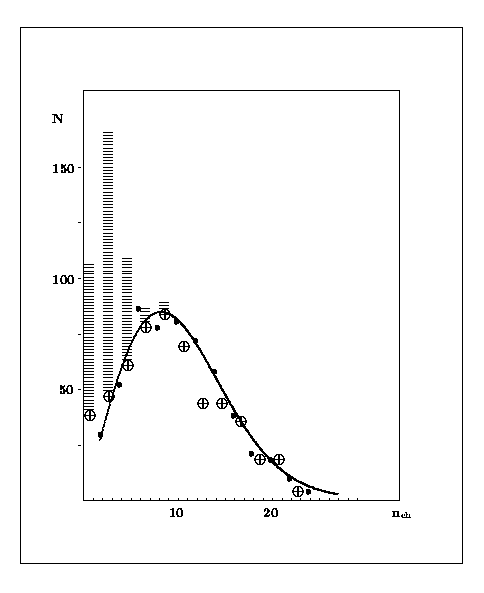
Рис. 11.

Распределение квазинуклонных событий по числу заряженных частиц n_ch при взаимодействии протонов с импульсом 400 ГэВ/с со свободными и связанными нуклонами в фотоэмульсии 161]. Обозначения: черные точки – рр взаимодействия, кружочки с крестиками – pn взаимодействия, над ними столбики из коротких горизонтальных линий – это когерентные взаимодействия типа рАрА+2 (см. 102]).



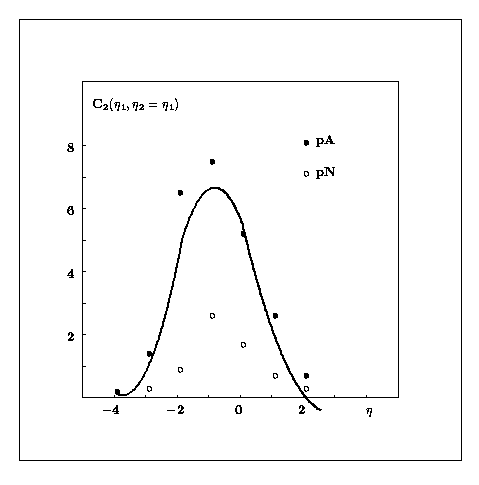Рис. 12

Распределение величин диагональных элементов корреляционной матрицы С₂ в зависимости от квазибыстроты  для pN и рА взаимодействий при импульсе протонов 400 ГэВ/с 99]. Плавная кривая - расчет в МНИ для рА взаимодействий. Рис. 13 показывает, что при этом распределение по  в расчете и эксперименте практически совпадают. Это свидетельствует о том, что хотя факт существования двухчастичных корреляций в pN и рА взаимодействий при энергиях 200-400 ГэВ установлен надежно, природа их остается не выясненной. Наиболее реальной причиной ближних корреляций рожденных частиц, по-видимому, является происхождение их от распада резонансов.


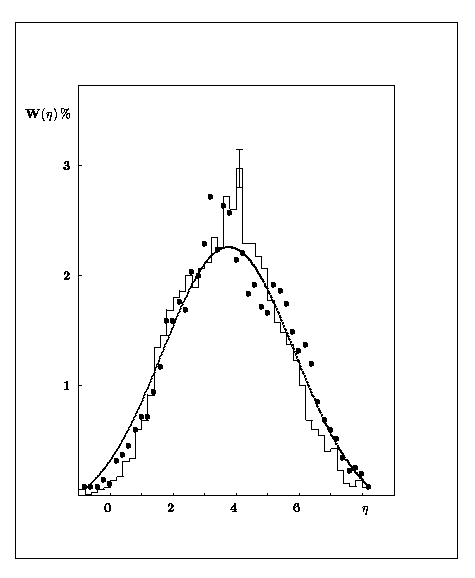Рис. 13

Распределение ливневых частиц по квазибыстроте  в рN взаимодействиях 400 ГэВ/с. Гистограмма – эксперимент 101], черные точки – расчет по ЦФО с учетом рождения резонансов 47]. Плавная кривая – нормальное распределение с дисперсией и средним оцененным по экспериментальной выборке.

Рассмотрим теперь нетрадиционные методы исследования корреляций вторичных частиц, использованные при анализе актов множественного рождения частиц в фотоэмульсии. Развитие этих методов связано прежде всего с некоторым разочарованием в надеждах на скорый и простой способ получения информации о динамике множественного рождения стандартным методом корреляционных функций.

Одним из таких методов является метод быстротных интервалов (МБИ), обоснованный в работе 104 и предложенный для использования при поиске кластеров 105. Основные результаты применения МБИ содержатся в работах 106-110.

Быстротный интервал К_i определяется как разность двух упорядоченных по возрастанию n величин быстрот, принадлежащих одному событию, если между ними находится К-1 значение быстроты,
т. е.

К_i=у_i+k-y_i (45)
при К=1, 2...n-1, i=1,2...n-K.

В работах 104, 106 авторы исходили из предположения о равномерной плотности частиц по быстроте, предполагая справедливость представлений простой мультипериферической кинематики 111. Действительно, в этой модели коэффициент корреляции между соседними частицами при К=1 достигает величины 0.25, но быстро стремится к нулю при увеличении расстояния между частицами по быстроте.

В кинематически допустимой области быстрот, только в сравнительно небольшой при энергиях 200-400 ГэВ области пионизации, гипотеза равномерного распределения по быстроте может быть справедливой. Именно там, как было показано, есть основания предполагать наличие корреляции (см. рис. 10). Таким образом, сделав довольно сильное предположение о распределении по квазибыстроте, авторы работы 104 нашли, что экспериментальное распределение К в pN взаимодействиях в эмульсии с ним расходиться при всех К.

Отсюда делается вывод о существовании многочастичных корреляции, т.к. расхождение наблюдается и при К>1.

Но корреляции быстрот через К=3 или К=5 частиц означало бы только наличие дальних, а не многочастичных корреляций. Очевидно, что МБИ вообще к корреляциям отношения не имеет, т. к. не содержит наблюдений совместного распределения частиц, таких, как ₂ (у₁, у₂) в определении С₂ (у₁, у₂). Расстояние между i-ой и i+k-ой величинами быстрот определяется функцией распределения быстрот. Собственно, это и было использовано в методе оценки параметра распределения малых углов фрагментов относительно неизвестного направления вектора р_о по наблюдениям углов _i,j между всеми фрагментами.

Экспериментальные данные работы [98] в виде ленты dst были обработаны в Гатчине, и из них были извлечены распределения по быстротным интервалам при К=1, 3, 5 для событий с множественностями n=8, 10, 12. Эти распределения в виде гистограмм изображены на рис. 14. Точками на этом же рисунке изображено их распределение, рассчитанное по МНИ со средними  и дисперсиями 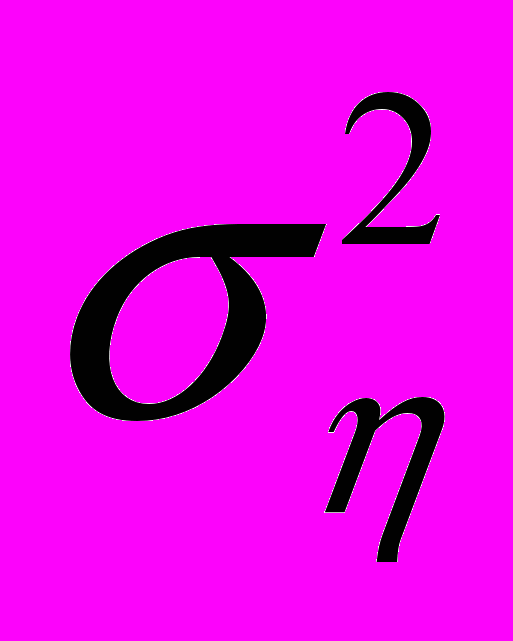, равными их экспериментальным величинам. Как видно, никакого расхождения эксперимента с МНИ не наблюдается. Да и не должно наблюдаться, хотя ближние корреляции быстрот в эксперименте существуют. Это сравнение данных о корреляциях в фотоэмульсии и в водородной пузырьковой камере весьма поучительно.