Geum.ru

Возможность объяснения низкотемпературных ядерных реакций, исходя из логнормального распределения частиц по энергиям

Вид материалаДокументы

Содержание


Раздел 3. Генерация изотопов в атмосферных разрядах
Подобный материал:


Возможность объяснения низкотемпературных ядерных реакций,

исходя из логнормального распределения частиц по энергиям.


Карасев Б.В.

Философское общество РФ


Раздел 1. Некоторые исторические моменты,

связанные с публикацией исследований автора


В журнале Физической химии (ЖФХ) автор опубликовал серию работ с эмпирическими обоснованиями критики распределения Максвелла[1,2]. Этот подход автор решил применить к объяснению данных по аномально большим выходам нейтронов, полученных в работах института им. Курчатова при исследовании высоковольтных разрядов в дейтерии. Однако, уже подготовленная к печати в кратких сообщениях ЖФХ( т.е., по существу, прошедшая рецензию статья) не пошла в печать. Ответ редакции гласил, что редакция ЖФХ не берется за рецензию, т.к. статья не соответствует профилю журнала (16.10.1981г., зав.ред. Масленникова). Попытки опубликовать работу не имели успеха до 1989г., когда автором был сделан доклад на Всесоюзном симпозиуме»Изотопы в гидросфере», в котором излагались результаты этого исследования с привлечением материалов по выходам нейтронов из разрядов в молниях. Кроме того, нами приводились результаты по генерации нейтронов при высоких давлениях в разрядах, что было несовместимо с механизмами ускорения реагирующих частиц.. Это сообщение вышло в свет даже несколько ранее того , как развернулась общеизвестная дискуссия по «холодному термояду» в марте 1989 г. . Однако , за это время в «Коллоидном журнале» был опубликован доклад о наблюдаемых выходах нейтронов в процессах разрушения кристаллов льда дейтерия при механических воздействиях. [3]. . Примечательно, что при пропускании разрядов через дейтерированные материалы при высоких давлениях были обнаружены высокие выходы нейтронов, что свидетельствует в пользу моделей, не использующих механизм ускорения частиц[4]. Деталями попыток пробить идею в печать заинтересовалась редакция РИА Новости, где история вопроса нашла сочувственное отражение [5].

По мнению рецензента А.Г. Липсона первым указал на применимость логнормального распределения для объяснения эффектов холодного синтеза в твердых телах В.А. Филимонов в 1991г. Восстанавливая последовательность событий в ряду сообщений о причинах наблюдаемых процессов ХЯС, можно представить и точку зрения В.А. Филимонова, который предложил модель синергетической активации ( СА) ХЯС, основанную на предположении о высокой степени неравновесности систем, при которой осуществляется квази-степенное распределение флуктуаций энергии между атомами системы, отличающееся от экспоненциального, постулируемого, современной теорией. Многостадийное возбуждение атомов в основном состоянии по В.А. Филимонову реализуется на фронтах ударных волн, волн детонации, при фазовых переходах в области расслоения фаз и т.д.[6]

С нашей точки зрения причина протекания ядерных реакций при низких температурах, неоднократно наблюдавшихся многими исследователями, вызвана однотипными причинами и имеет общие корни, приводящие к необходимости изменения модельного подхода к формированию функции распределения по энергиям, которая может быть аппроксимирована логнормальным законом [7,8].Модель уравновешенного состояния, предлагающая объяснение распределения по энергиям была опубликована еще в 1970 г. В популярном изложении возможных практических приложений предлагаемого статистического подхода обсуждались вопросы замены распределения Максвелла логнормальным распределением[9]. Открывается возможность использования низкотемпературных ядерных реакций для извлечения энергии из конденсированных сред, опираясь на ядерные процессы, протекающие на « хвостах»( фронтах) распределений.

Модель ускорительного механизма генерации нейтронов в разрядах в дейтерии, которые исследовались в первых отечественных экспериментах, была предложена также Б.А. Трубниковым [10]. После известной дискуссии по причинам протекания ядерных реакций при низких температурах были опубликованы эксперименты по ускорению кластеров дейтериевой воды до 300 кэВ, в которых были обнаружены аномально высокие сечения ядерных реакций с образованием протонов, намного порядков превышающие ожидаемые для рассматриваемых моделей[11]. Для этих экспериментов предложена модель коллективного ускорения [12]. В трудах конференций по проблеме ХЯС публиковались результаты, полученные Ромодановым В.А. и Скуратником Я.Б.[13], в которых наблюдались аномально высокие выходы трития в разрядах дейтерия. Предполагается, что возможной причиной выделения избыточного «дарового» тепла при работе роторных генераторов являются ядерные низкотемпературные реакции[14].

При проведении разрядов в дейтерии (напряжение - 38 В, ток 3А, время 10 мин) нами обнаружена генерация в дейтериевой воде трития , вдвое превышающая фоновые его значения в исходном дейтерии. Результаты были доложены в 2005 г.на конференции в Дагомысе.

Логнормальное распределение частиц по энергиям дает возможность оценивать результаты термоядерных процессов, протекающих в конденсированных средах при относительно низких температурах, рассчитывать эффективность реализации подобных модельных схем проведения процессов и их тепловые выходы. Поэтому представляется, что публикация наших ранних расчетов может содействовать конструкции реальных рабочих моделей. Тексты сообщений приводятся ниже во втором и третьем разделах работы, причем в начале второго раздела приводится фрагмент копии первоначальной статьи, принятой первоначально в Журнале Физической химии.

Раздел 2




Логнормальный закон распределения частиц по энергиям применен для расчетов термоядерных реакций в плазме. Он удовлетворительно описывает выходы нейтронов в плазме разряда при температурах 36-178 эв.

В работах [7,15,16,] автором показано, что логнормальный закон распределения при ряде достаточно общих условий может рассматриваться как равновесный закон распределения. Логнормальная функция обладает повышенными вероятностями появления частиц высоких энергий по сравнению с максвелловским законом распределения. Это свойство должно проявляться в различных процессах.

За последнее время в литературе все чаще обсуждаются данные о присутствии в низкотемпературной плазме частиц с повышенной энергией(«убегающие» электроны, рентгеновское излучение, аномально высокая по сравнению с распределением Больцмана заселенность высокоэнергетических уровней, сложные кривые распределения скоростей и энергий частиц, которые аппроксимируются двумя равновесными спектрами), что проявляется при исследовании плазмы различными методами: оптической спектрометрии[17], рентгеновской спектрометрии [18,19], при изучении потоков нейтронов [20] и т.д. Обычно для объяснения этих явлений выдвигаются различные механизмы [17,18,19,20,21,22,].

Интересно сравнить эмпирические данные , на которые опираются эти работы, с выводами предлагаемой теории. К сожалению, в литературе часто приводится материал в виде графиков и рисунков, которые плохо поддаются математической обработке. Поэтому наиболее показательно обсуждение данных, которые принципиально противоречат общепринятой теории.

В качестве примера рассмотрим эксперименты с высокотемпературной плазмой. Как известно [24,25], уже при относительно низких расчетных температурах в плазме отмечено появление нейтронного излучения и жесткого рентгеновского излучения, которые не могут быть объяснены на основе современной равновесной теории. Так, по [25] необходимо предположить присутствие в плазме с температурой в сотни электрон-вольт значительного количества частиц с энергией в 50 и более килоэлектроновольт, что, по мнению автора, полностью исключает тепловой механизм их генерации. Авторы работы [26] считают, что при повышении тока с 500 до 600 килоампер в их опытах при тепловом механизме генерации выход нейтронов должен был возрасти по крайней мере на порядок, однако он возрос приблизительно в 3,5 раза при увеличении тока в 1,3 раза.

Сделаем попытку объяснить отмеченные явления на базе логнормального закона распределения частиц по энергиям. Выведем некоторые соотношения ,необходимые для расчетов. Скорость относительного движения частиц g не зависит от вида функции распределения по скоростям. Она в 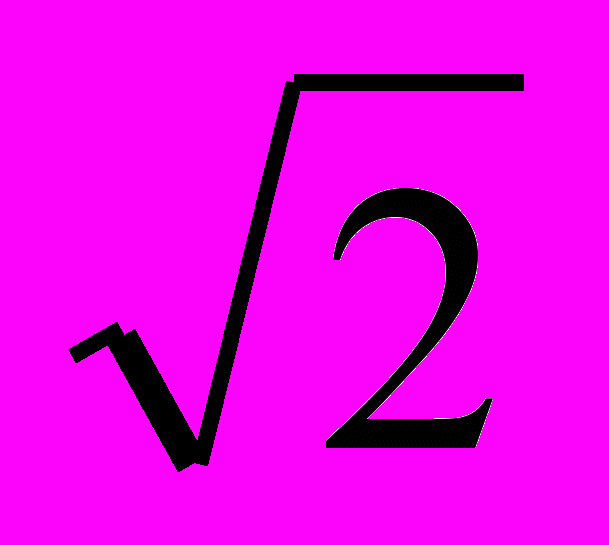раза больше средней скорости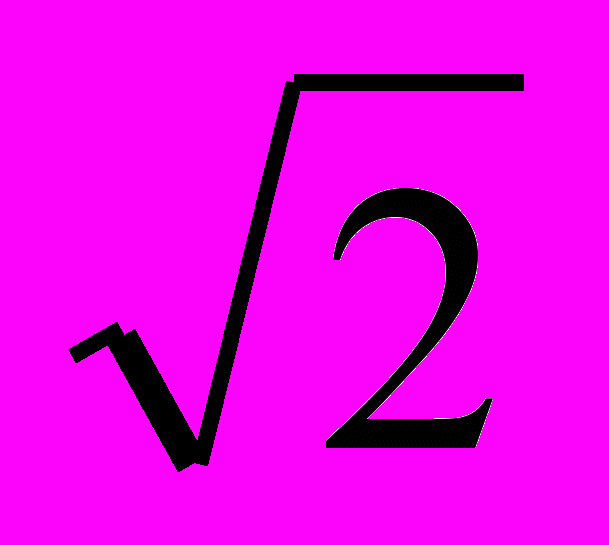 частицы, если частицы одинаковы по массе g= [27]. Соответственно средняя энергия относительного движения вдвое превышает среднюю энергию частиц. В работе [16] было показано, что для логнормального закона квадратичное логарифмическое отклонение закона распределения по энергиям в два раза больше логарифмического квадратичного отклонения закона распределения по скоростям SlnE2Slnv и на основании расчетов составляет Slnv0,4-0,48.

Если частицы статистически независимы, то функция распределения для двух сталкивающихся частиц равна произведению функций распределения:

f1,2 =f1 f2. При логнормальном законе распределения f 1,2 –логнормальна, а логарифмическая дисперсия f 1,2 , согласно свойствам логнормальной функции, равна сумме логарифмических дисперсий: S21,2=S21+S2 Функция f1,2 записывается:

f 1,2 = ( 2) -1/2( S1,2 E)-1 exp{( (lnE-)2/2 S2 1,2} (1)

Выход термоядерной реакции R(число актов в единицу времени) равен:

R= n2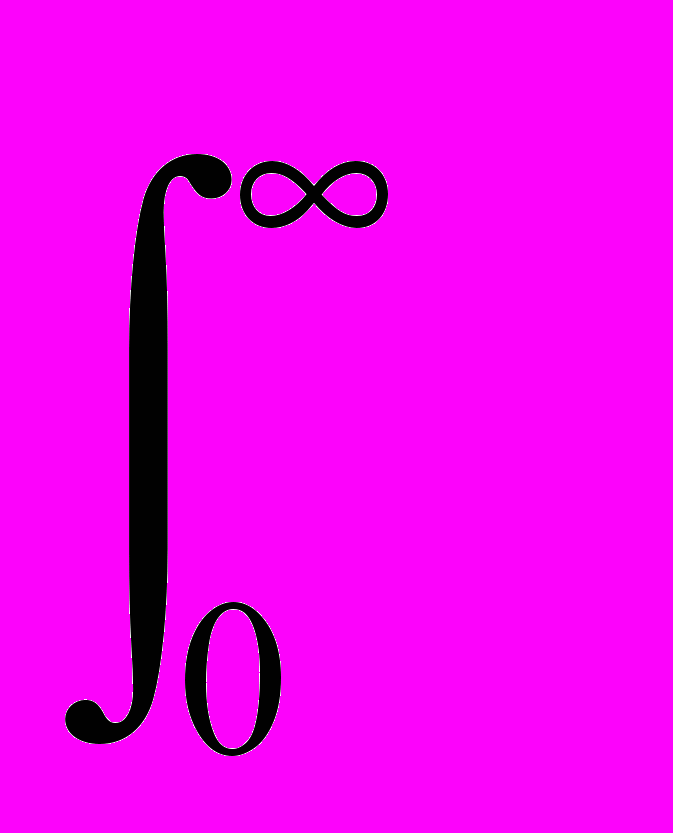f 1,2 vdv , (2)

где n- плотность частиц в 1 см3; - сечение реакции; v-cкорость.

Рассмотрим термоядерные реакции в дейтериевой плазме, где происходят следующие процессы:

D + D =H3 +p (3)

D + D = He3 +n (4)

Cогласно (3) и (4) выход R,рассчитанный по (2), необходимо удвоить.

Сечение реакции связано с энергией зависимостью [28]:

 =140/ Е(кэВ) ехр { - 44,4/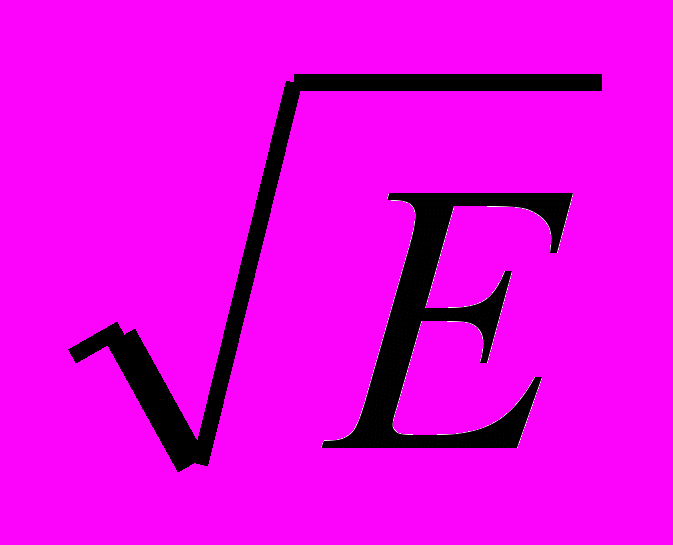} 10-24 cм2 (5)

В работе С.М. Осовца [29] рассматриваются условия, при которых наблюдается появление нейтронного и рентгеновского излучений в дейтериевом разряде согласно данным работы [30]. При токе I =150 ка, плотности дейтерия Т= 1018ат/см и температуре плазмы 36 эв наблюдались выходы нейтронов 108 нейтронов за импульс. Температура оценивалась по формуле:

Т=I2 1016/N 6,4 эв (6)

С.М. Осовец приходит к выводу, что нужно предположить присутствие в плазме частиц с энергией от 20 до 1000 кэв, что исключает тепловой механизм ускорения при максвелловском законе распределения частиц по скоростям и приводит к необходимости поисков новых механизмов ускорения частиц.

Применим логнормальный закон (1). Пусть Slnv =0,42, тогда SlnE=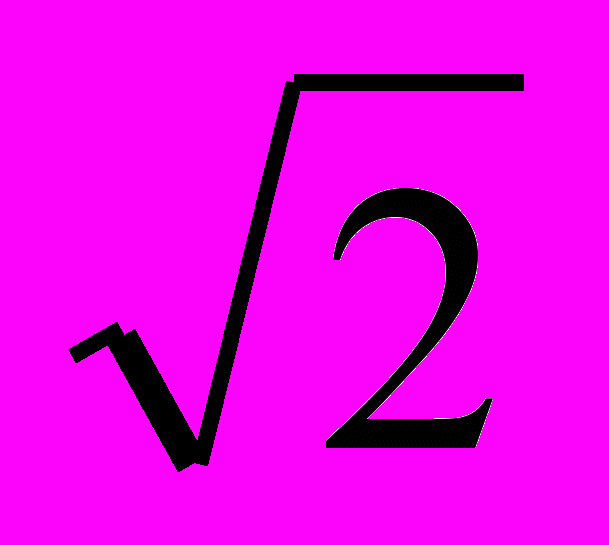(2Slnv)=1,188, =2 3/2T=108 эв. Из свойств логнормального закона следует, что = ln - S2/2. При длине разрядной трубки 1 м и радиусе жгута плазмы в момент выделения нейтронов r =2см плотность плазмы составляет 8 10 16 ат./см3 ,а объем реакционной полости 1,3 103/см3.

Интеграл в выражении (2) рассчитывался приближенным методом для интервалов энергий 4-5,5-10,10-20, 30-40,50-100, 100-200, 200-1000 кэв. Общий выход нейтронов определялся по формуле :

R=n21i <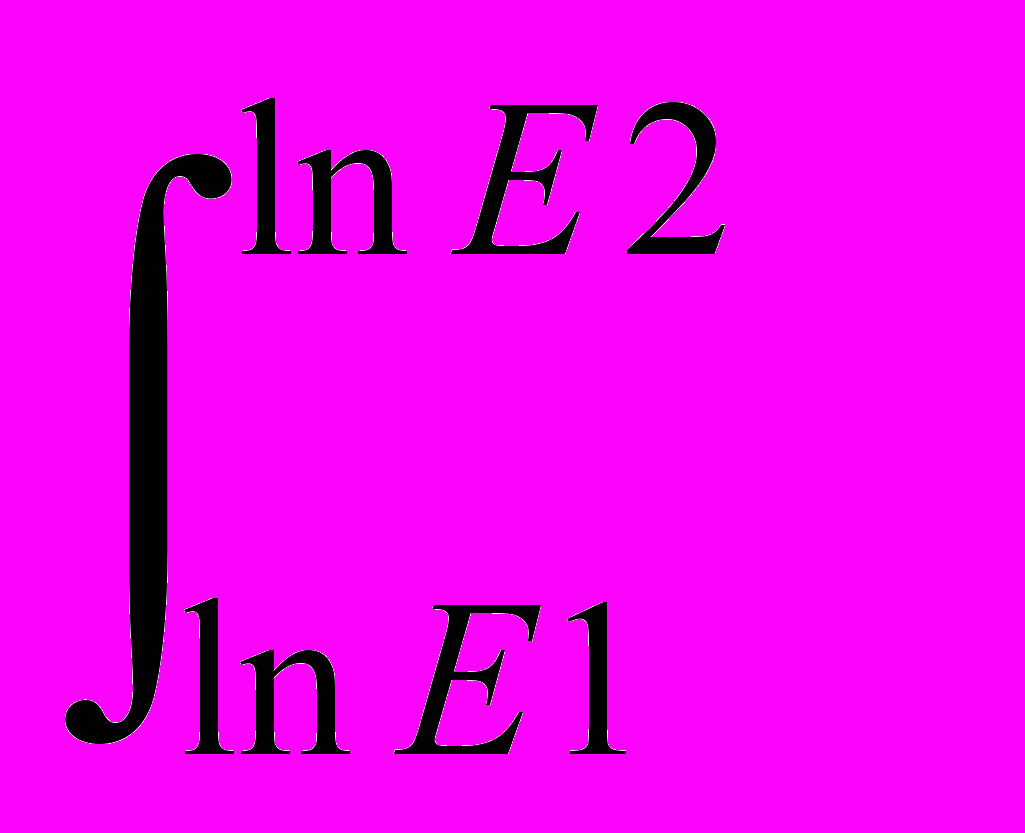> f1,2 dE, (7)

где i-число интервалов, <> и - средние значения для интервала.

Значения сечений реакций брались из таблицы, приводимой в работе [29].

Интересно отметить, что для логнормальной функции вероятности появления частиц с энергией выше 4 кэв относительно велики и составляют 10-4.

Расчетный выход нейтронов для S1.2=1,188 составляет R1,2 1012 нейтронов, а для S=1,36 (Slnv=0,48) R= 1,4 1013 n/cек. Последняя величина полностью объясняет наблюдаемый выход нейтронов, даже если время протекания реакции в разряде составляет 2с, как это было определено в экспериментах с иными параметрами плазмы[29]. Согласно сведениям , приводимым в работе [30], время протекания ядерной реакции, совпадающее со вторым сжатием плазменного шнура, составляет несколько десятков микросекунд, что полностью объясняет наблюдаемый выход и при S12=1,188. Другой критерий, который может быть использован для определения механизма процесса – зависимость выхода от температуры. Из рис.7а работы [30] находим , что при 117б5 ка отношение выходов нейтронов к выходу при 150 кА составляет о,13. Расчетное отношение по формуле (2) с использованием изложенного метода равно 0,14, что находится в прекрасном согласии с экспериментом. В работе [30] также приводятся данные по изменению выхода с изменением силы тока, протекающего через разряд. При давлении 0,01 мм.рт.ст. плотности 2,2 1018 ат/см и токе 500кА температура плазмы по формуле (6) составляет 178 эВ. Увеличение тока в 1,3 раза приводит к увеличению экспериментального выхода в 3,5 раза. Расчет по приведенному выше методу с применением логнормальной функции дает увеличение выхода в 5,5 раза, превышающего начальный. С учетом большого разброса экспериментальных выходов нейтронов эти соотношения также находятся в удовлетворительном согласии. Таким образом, тепловой механизм генерации нейтронов может быть объяснен на базе логнормального распределения частиц по энергиям. Находит объяснение и появление в экспериментах рентгеновских квантов с энергией до 300-400 кэВ. Одновременно объясняются высокоэнергетические «хвосты» распределений электронов и ионов, обнаруженные во многих экспериментах. Выгорание частиц может приводить к различным температурным зависимостям «хвостовых «распределений. Вычисления показывают, что при высоких температурах( 10-20 кэВ) выход реакции с применением логнормального закона приближается к выходу с использованием закона Максвелла, однако при этих температурах высокоэнергетические частицы создают ряд препятствий для проведения процесса управляемого синтеза, которые сейчас широко обсуждаются в печати.



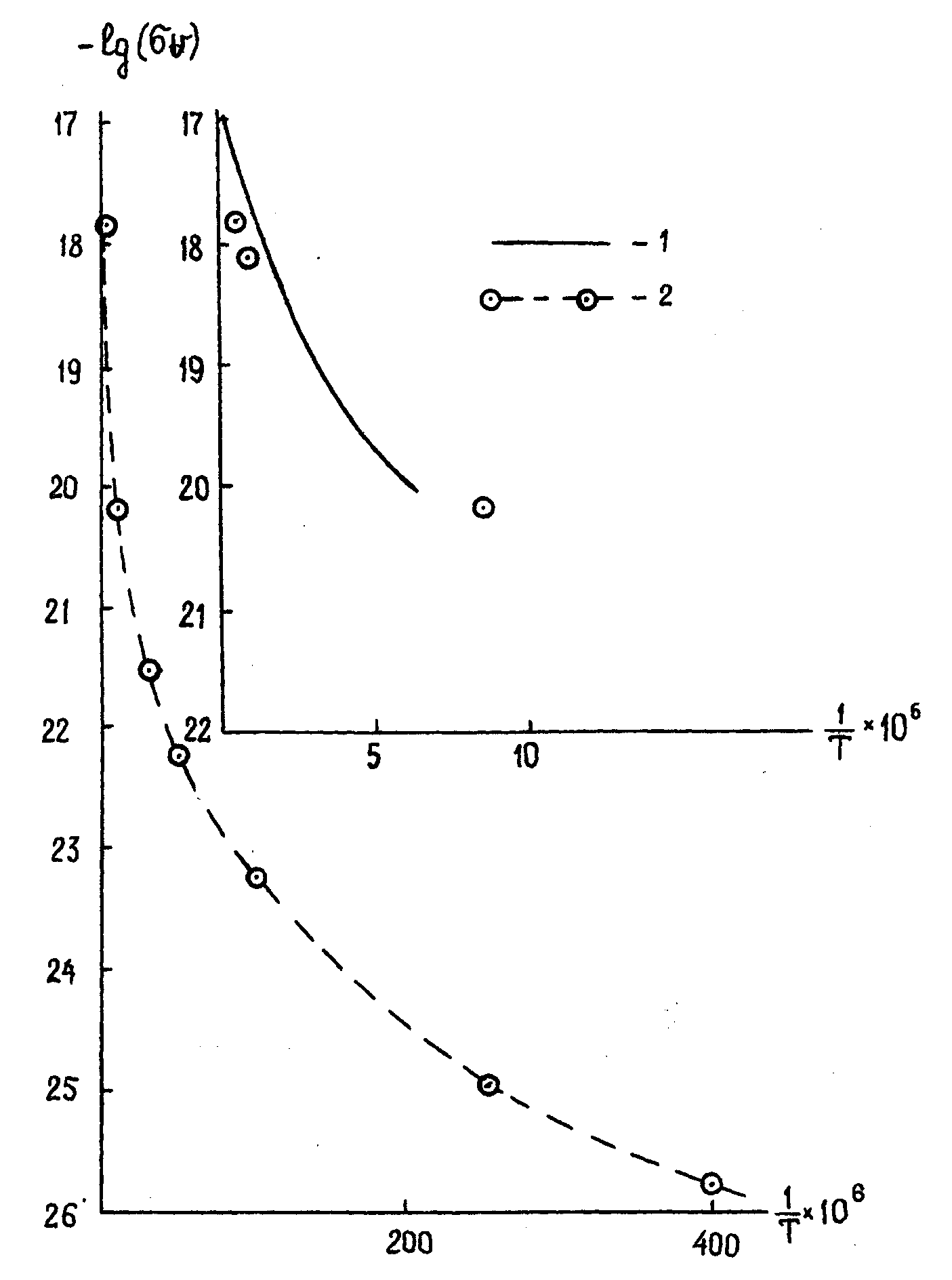
Рис.1 Зависимость логарифма произведения v от обратной температуры для реакции в дейтериевой плазме.

1. Максвелловский закон

2. Логнормальная функция.

На рис.1 представлены зависимости логарифма произведения v от обратной температуры для реакций в дейтериевой плазме. При высоких температурах ход кривой, рассчитанный на основе логнормального распределения, близок к ходу кривой на основе закона Максвелла. При низких температурах обнаруживаются резкие отклонения от аррениусовской зависимости. Подобные эффекты обнаружены за последнее время и при изучении химических реакций [32], делаются попытки их объяснения на основе туннельных механизмов. Возможно, что применение логнормального распределения частиц по энергиям позволит подойти к объяснению наблюдаемых эффектов. Предлагаемый подход может быть применен и к расчетам других реакций, таких, например, как скорость выделения нейтрино в ядерных реакциях на Солнце и т.д.


Раздел 3. Генерация изотопов в атмосферных разрядах

и логнормальное распределение частиц по энергиям.

В процессе развития разрядов молний в атмосфере возможно появление частиц высоких энергий ( например, электронов с энергией до 150 эВ). При моделировании разрядов в лабораторных условиях наблюдалось возникновение нейтронов по реакциям D(d,n) 3He, D(d,p) T ,D(T,n), 12C(d,n) 13N,( S.G. Stepanakis и др.1972). Возможно протекание и других ядерных реакций 12C(d,n) 13N, 14N(d,n) 150. Опираясь на результаты этих экспериментов была рассчитана ( L.M. Libby, H.R. Lukens,1973) генерация нейтронов в атмосферных разрядах, которая предположительно достигает 2-6 10-2/см2 сек (около 1015-1016 нейтронов на разряд), что составляет 1% от потока нейтронов, возникающих в атмосфере Земли при бомбардировке ее космическими частицами. Дополнительная компонента нейтронного излучения может варьировать во времени, что должно учитываться при расчетах содержания радиоуглерода, рождающегося в атмосфере по реакции 14N(n,p) 14 C. Разряды атмосферного электричества вблизи древесной растительности могут производить нейтроны, вызывающие ядерные реакции в древесине, в частности, образование радиоуглерода, который по химическим свойствам отличается от углерода древесины и может быть идентифицирован. В первых экспериментах (R.L. Fleicher, 1975) не удалось обнаружить нейтронных потоков от разрядов молний. Указывалось на то

Обстоятельство (R. L. Fleicher и др.1975), что механизм ускорения ионов, который, как предполагается, приводит к возникновению нейтронов в экспериментах, возможен только в среде с малой плотностью частиц и не может проявляться при атмосферном давлении и в конденсированных средах. В новых исследованиях ( G.N. Shah и др., 1985) экспериментально обнаружены нейтроны, продуцируемые атмосферными разрядами, однако природа их возникновения ( те термоядерные или тепловые процессы) требует дальнейшего исследования. Проблема механизма генерации нейтронов широко обсуждается при анализе экспериментов по управляемым термоядерным реакциям. Высокоэнергетические компоненты( нейтронное излучение, рентгеновские кванты , электроны и ионы высоких энергий) наблюдались уже в первых опытах с плазмой относительно низкой температурой. В многочисленных и разнообразных последующих экспериментах обнаружено появление высокоэнергетических частиц и излучения, для объяснения происхождения которых выдвинуты двухтемпературные модели. Предложены различные механизмы происхождения предполагаемых высокотемпературных компонент, с которыми связано нейтронное излучение.

Автором выдвигается механизм, основанный на представлении о логнормальном распределении частиц по энергиям как равновесном распределении. Логнормальное распределение может быть выведено как равновесное при условии сохранения логарифмической дисперсии. Принцип сохранения логарифмической дисперсии широко наблюдается в природе. Анализ процесса бинарного множественного соударения частиц идеального газа приводит к выводу о сохранении логарифмической дисперсии в этом процессе (теоретическое значение квадратичного логарифмического отклонения ln=1). Возможность логнормального распределения по энергиям вытекает из гауссовского вида функции распределения энтропии. На отклонения от максвелловского распределения частиц по энергиям обращалось внимание в литературе (T.M. Miller, 1974). Экспериментальные данные по распределению частиц Н2, Ne, Ar, N2 в этих опытах, как можно показать, лучше описываются на базе логнормальной функции. Логнормальная функция обладает повышенными вероятностями , по сравнению с максвелловской, появления частиц высоких энергий, что объясняет наблюдаемые закономерности распределения частиц в плазме. Обработка автором данных по распределению электронов по энергиям в низкотемпературной плазме и дейтронов в разряде «плазменного фокуса» показывает удовлетворительное согласие с логнормальным распределением ( ln=0,85-0,9). Рассчитанные значения выходов нейтронов для газовых разрядов в дейтерии удовлетворительно согласуются с экспериментом. Ход кривой зависимости скорости ядерной реакции в дейтерии от средней энергии частиц при малых и средних энергиях на порядки превышает соответствующие данные для больцмановского распределения. Наклоны температурного хода кривых удовлетворительно согласуются для данных по пинчам ( Б.А. Трубников,1984, в этом случае предполагался ускорительный механизм), а также по разрядам «плазменного фокуса» ( С.Ю. Лукьянов,1975) и теоретическим расчетам на базе логнормального распределения. Полученные результаты дают основание для применения логнормальной функции к расчету генерации изотопов в газовых разрядах. Они могут быть использованы для оценки скоростей диссипации изотопов из атмосфер планет, скоростей изотопного обмена и т.д. Наблюдаемые эффекты протекания ядерных реакций при разрушении твердых тел ( Дерягин и др.,1986) также могут найти объяснение на базе логнормальной функции распределения частиц по энергиям.


Литература

1..Карасев Б.В. Ж.физ.химии, 53,1976.1979.

2. .Карасев Б.В. Логнормальный закон распределения и сохранение логарифмической дисперсии// Журн. физ. химии.1980 Т.53.№12. С.3032-3037.

.3 Дерягин Б.В., Клюев В.А., Липсон А.Г., Топоров Ю.П. О возможности ядерных реакций при разрушении твердых тел.// Коллоидный журнал.1986.Т.48,№1. Стр.12-14.

4.Stepanakis S.J, Levin L.S., Hoshel D., Vitkovsky J.M., Young F.//Phys. Rev. Lett. 1972. V.29. №9. P.568.

5.. Карасев Б.В. Аналогичный случай. Страдания по холодному термояду.// Мир непознанного. РИА. Новости.1988.№ 2( 98). С.2-3.

6. Филимонов В.А. Верификация модели синергетической активации холодного ядерного синтеза//Холодный ядерный синтез.1994.М.: Межотраслевой научно-технический центр венчурных нетрадиционных технологий. С.66-70.

7.Карасев Б.В. Статистический подход к изучению природы и некоторые закономерности распределения вещества Земли// Пути познания Земли. М.: Наука.1970(1971). С131-132.

8. Карасев Б.В. Логарифмически –нормальная функция распределения и некоторые проблемы холодного термоядерного синтеза// Холодный ядерный синтез (ХЯС). Дагомыс-Сочи.19-26 мая.1996.1997. М. Эрзион С.229-237.

9. Соркин Э. Такие неслучайные логарифмы.// Техника и наука №2, 1979. С.24-26.

10.Трубников Б.А. О механизме рождения нейтронов в перетяжках плазменных полей// Письма в ЖЭ ТФ. 1984.Т.42. Вып.8 С.317-319.

11..Benkler R.J., Fridlander C., Feideman L. Cluster- impact Fusion// Phys. Rev. Lett.1989.V/63.№12..P.1292.

12. Великодный В.Ю., Битюрин , В.А. Кластерный синтез легких ядер. D+D.//Холодная трансмутация ядер. Дагомыс-Сочи.2001. 2002.Мю; Росс. АН С.131-140.

13. Ромоданов В.А., Савин В.И., Скуратник Я.Б., Элкснин В.В. Воспроизводимость генерации трития из ядерных реакций в конденсированных средах.// Холодный ядерный синтехз.1994. М.: МИТЦ ВЕНТ С.100-114.

14. Фоминский Л.П. Роторные генераторы дарового тепла. Сделай сам.2003. Черкассы. «Око-Плюс». Росс. АН Естественных наук.

15.Б.В. Карасев, Ж.физ. Химии,53,1976,1979.

16..2.Б.В. Карасев,54,3032,1980.

17.Б.П. Лавров, В.Н.Островский, В. И. Устимов, Ж.Т.Ф.,50,2072, 1980.

18.Ю.В. Есипчук , П.Е. Ковров, Препринт ИАЭ-3032, М.,1980.

19.В.В. Александров, Н.Г. Ковальский, В.Т. Силин,ЖЭТФ,1979,850, 1980.

20. С.А. Экдал. Приборы для научных исследований, №8, 3, 1979.

21. Т.А. Горбушина, Л.М. Дегтярев, Р.З. Сагдеев, В.Д. Шапиро, В.И. Шевченко, препринт И. П. М. АН СССР, №17, М.,1978.

22. В. Е. Захаров, ЖЭТФ , 62, 1745, 1972.

23. В.Н. Мельник, В.А. Кац, В. М. Конторович, ЖЭТФ. 78, 966, 1980.

24. И.В. Курчатов, Атомная энергия, №8, 65, 1956.

25. С.Ю. Лукьянов, Горячая плазма и управляемый синтез, «Наука», М., 1975,

408 с.

26..В. С. Комельков, Т.М. Морозова, Ю.В. Скворцов., в кн. Физика плазмы и проблема управляемых термоядерных реакций, Т.2, АН СССР, 1958, с. 170.

27. В.Ф. Ноздрев, А.А. Сенкевич, Курс статистической физики, « Высшая школа», М. 1965, 288 с.

28. В.И. Коган в кн. Физика плазмы и проблема управляемых термоядерных реакций, т.2 АН СССР, 1958, с.109.

29. С.М. Осовец, в кн. Физика плазмы и проблема управляемых термоядерных реакций, т.2, АН СССР,1958, С.165.

30. Н.А. Борзунов, Д. В. Орлинский, в кн. Физика плазмы и проблема управляемых термоядерных реакций, т.2, АН СССР, 1958,с.150.

31. И.В. Курчатов, Атомная энергия, 3, 65, 1956.

32. В.И. Гольданский, Успехи химии, 44, № 12, 2121, 1975.

33. Карасев Б.В.Изотопы в гидросфере. Каунас.1989. С.158-159.Подписано к печати 10 марта 1989 г.