Содержит проколотую окрестность т

Вид материала

Лекция

Содержание A - число или символ. 7. Предел сложной функции

Подобный материал:

• Отчет содержит 47 страниц печатного текста. Содержит базу данных литературных источников., 670.96kb.
• Société à responsabilité limitée. Paris, 6087.11kb.
• План занятий по курсу методы математического моделирования поток Умнова А. Е. 2011/2012, 145.73kb.
• Чарльз форт. 1001 забытое чудо. Книга проклятых, 4184.19kb.
• Чарльз форт. 1001 забытое чудо. Книга проклятых, 4191.7kb.
• Чарльз форт. 1001 забытое чудо. Книга проклятых, 4299.35kb.
• Пособие содержит теоретические сведения по русскому языку и разнообразные упражнения, 6272.93kb.
• 29 самых полезных продуктов на планете, 301.11kb.
• Школьный этап всероссийской олимпиады школьников по экономике, 47.21kb.
• Отчет представлен на 42 страницах; содержит 4 раздела (раздел 2 содержит 5 пунктов);, 20.7kb.

Лекция 8

4. Критерий Коши существования предела функции

Пусть D область определения функции f содержит проколотую окрестность т. x₀

Условие Коши: >0x,xD:|f(x)-f(x)|<

Т. (Критерий Коши) Для существования конечного предела

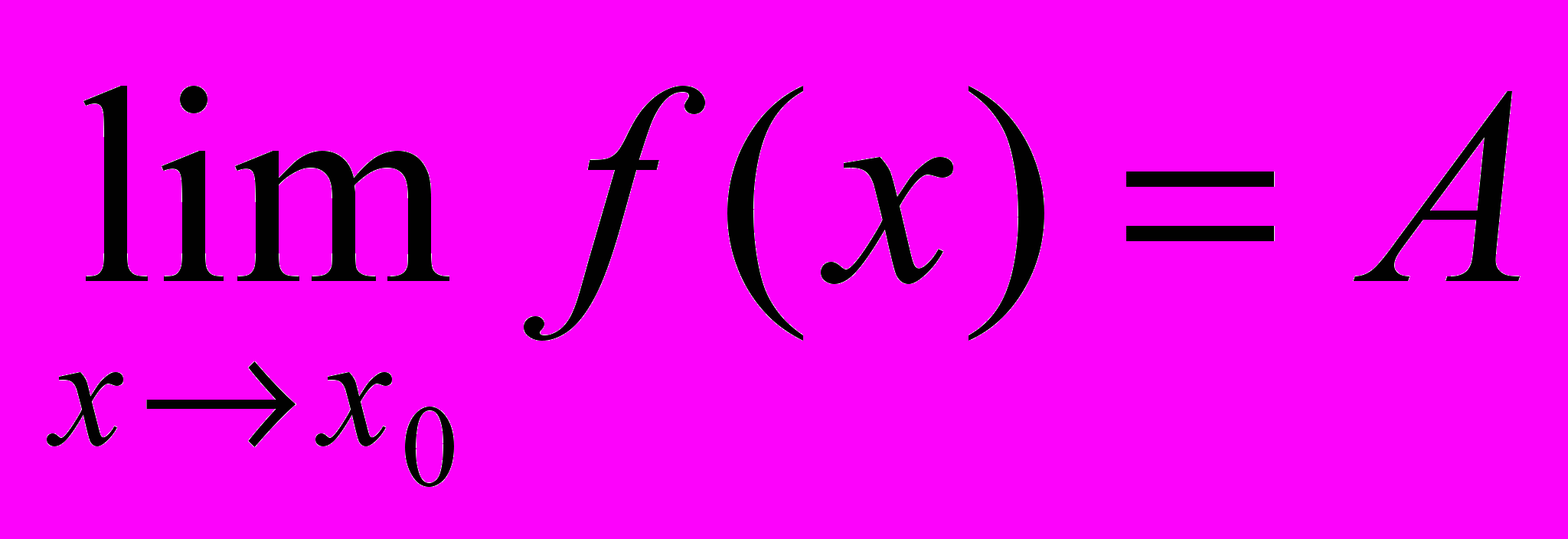
x₀ число или символ н. и д., чтобы f удовлетворяла условию Коши в окрестности точки x₀.

Необходимость. >0,/2 xD:|f(x)-A|</2. Для x,xD получим требуемое неравенство |f(x)-f(x)|<|f(x)-A|+|f(x)-A|/2+/2=.

Достаточность. Пусть {x_n} последовательность типа Гейне. Тогда {f(x_n)}

будет удовлетворять условию Коши для последовательностей, поэтому существует некоторый предел 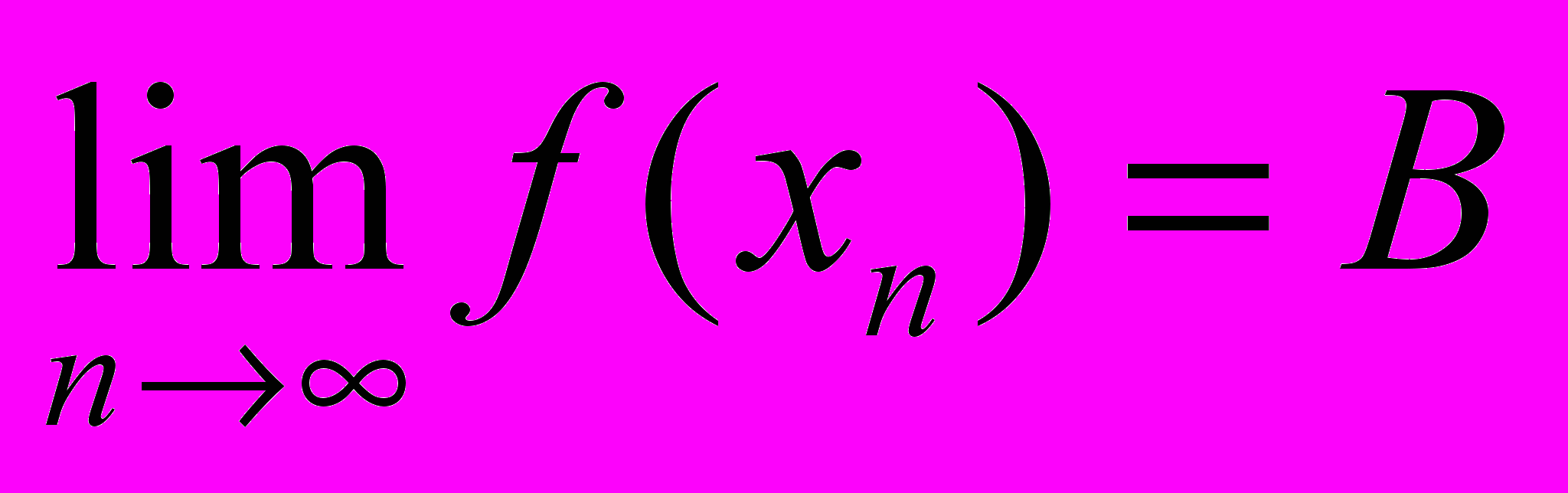. Докажем, что для любой другой последовательности типа Гейне {y_n} как в Гейне предел будет также равен B. Составим последовательность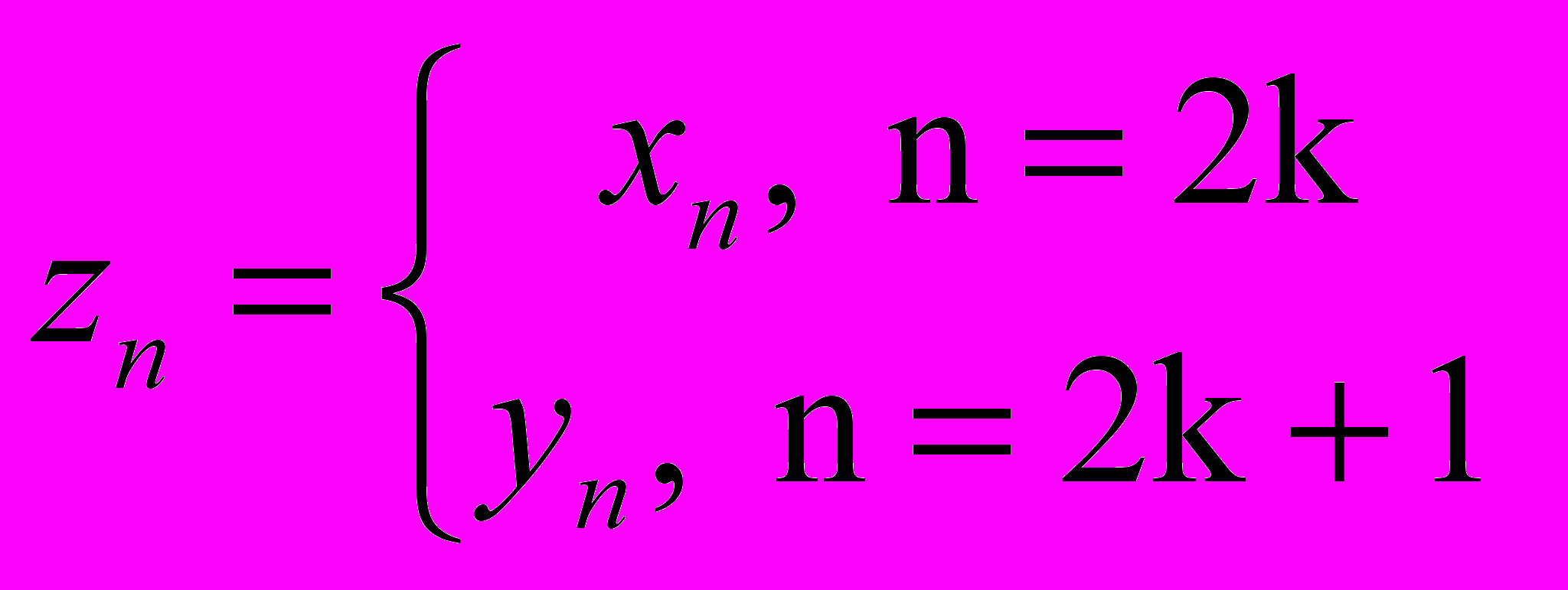



Эта последовательность будет последовательностью типа Гейне и, как уже доказано, предел 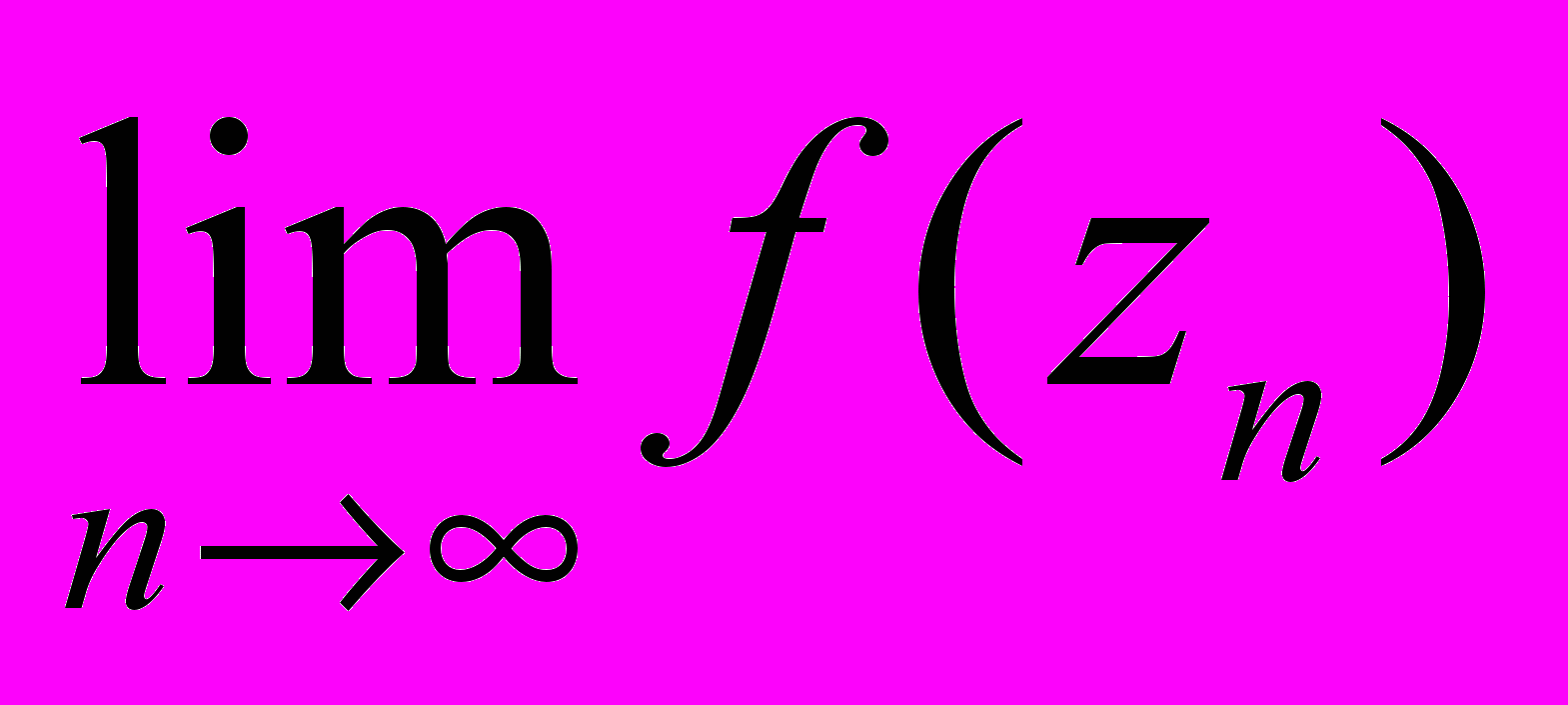должен существовать. Тогда все частичные пределы должны совпадать, в частности, =.

Сформулируем условие Коши для других случаев

Односторонние пределы: >0>0x,x(a,a+)D:|f(x)-f(x)|<

Условие Коши для +. f определена в окрестности +

>0bx,x(b,+)D:|f(x)-f(x)|<

5. Локальная ограниченность функции, имеющей конечный предел

Область определения D функции f содержит некоторую

Функция f локально ограничена в точке x₀, если она ограничена в некоторой окрестности этой точки M>0xU(x₀)D:|f(x)|M.

Теорема. Функция f имеющая конечный предел в окрестности точки x₀ локально ограничена в точке x₀.

Доказательство: =1,M=max{|A-1|,|A+1|,f(x₀)} или M=max{|A-1|,|A+1|}

Замечание. Теорема верна и в случае

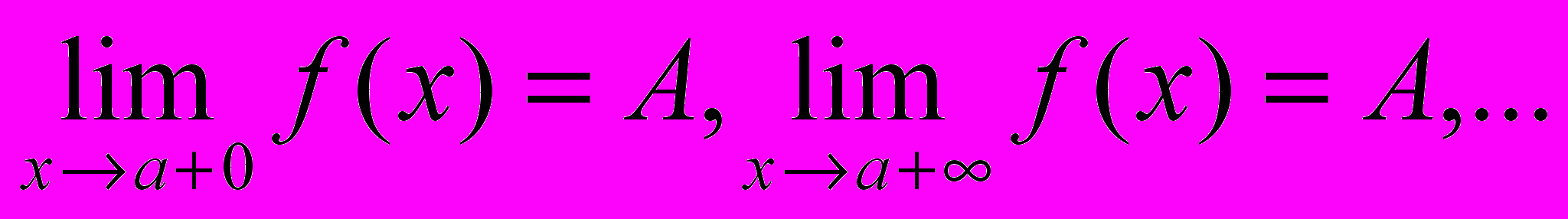
6. Сохранение знака функции, имеющей ненулевой предел в точке

Область определения X функции f содержит некоторую

Теорема.

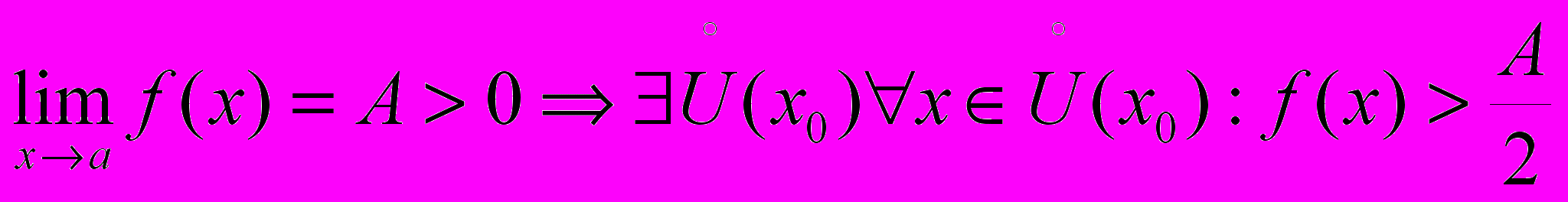
( f(x) сохраняет знак A в некоторой окрестности точки x₀)

Замечание 1.

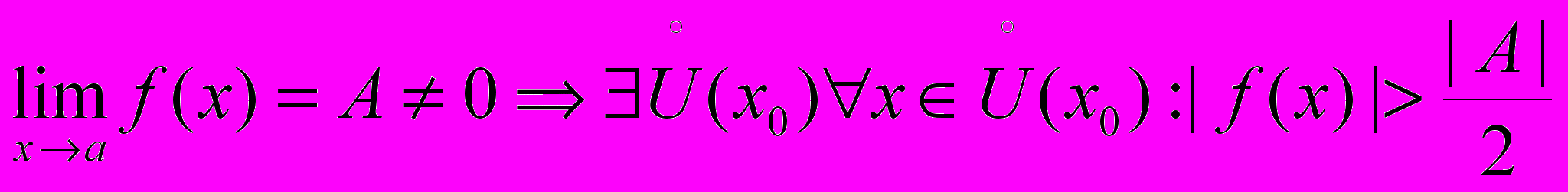
Замечание 2. Теорема верна и в случае

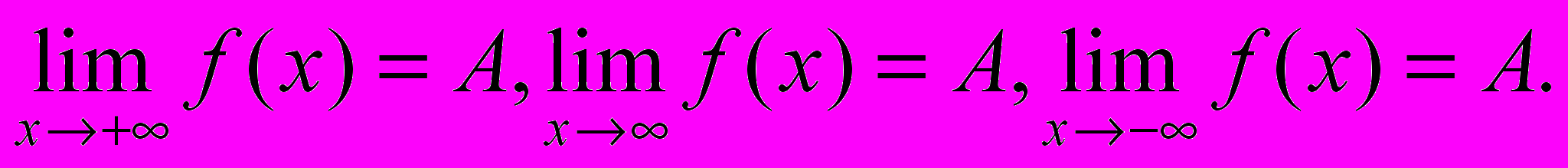
A - число или символ.

7. Предел сложной функции

f(x) определена на X, g(t) определена на T , область значений GX. Рассматривается функция F(t)=f(g(t)),tT.

Теорема. Пусть g определена на G=(,) или на (,)\{t₀},t₀ (,). f определена на (a,b) за исключением быть может точки x₀(a,b),tG:g(t)x₀, если tt₀. 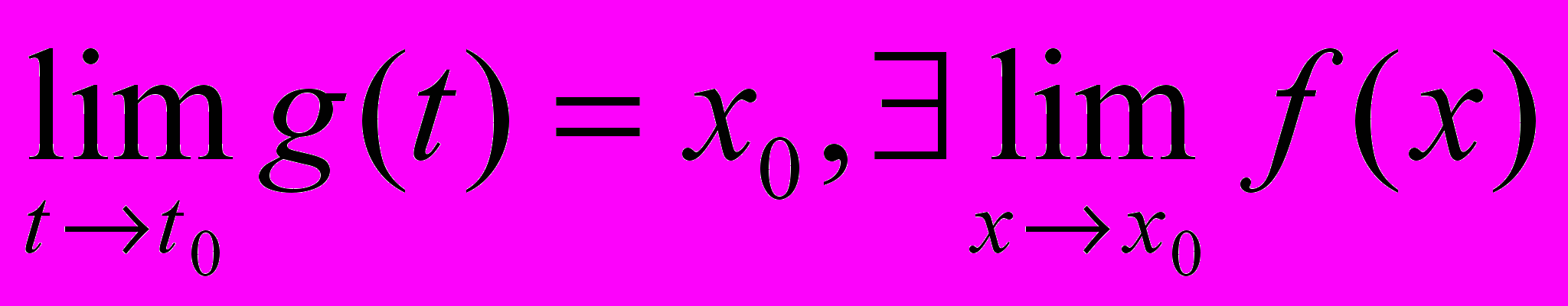. Тогда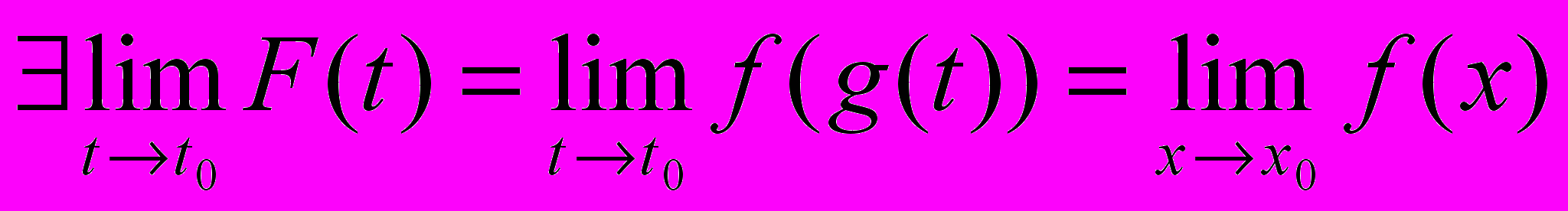

Доказательство: Пусть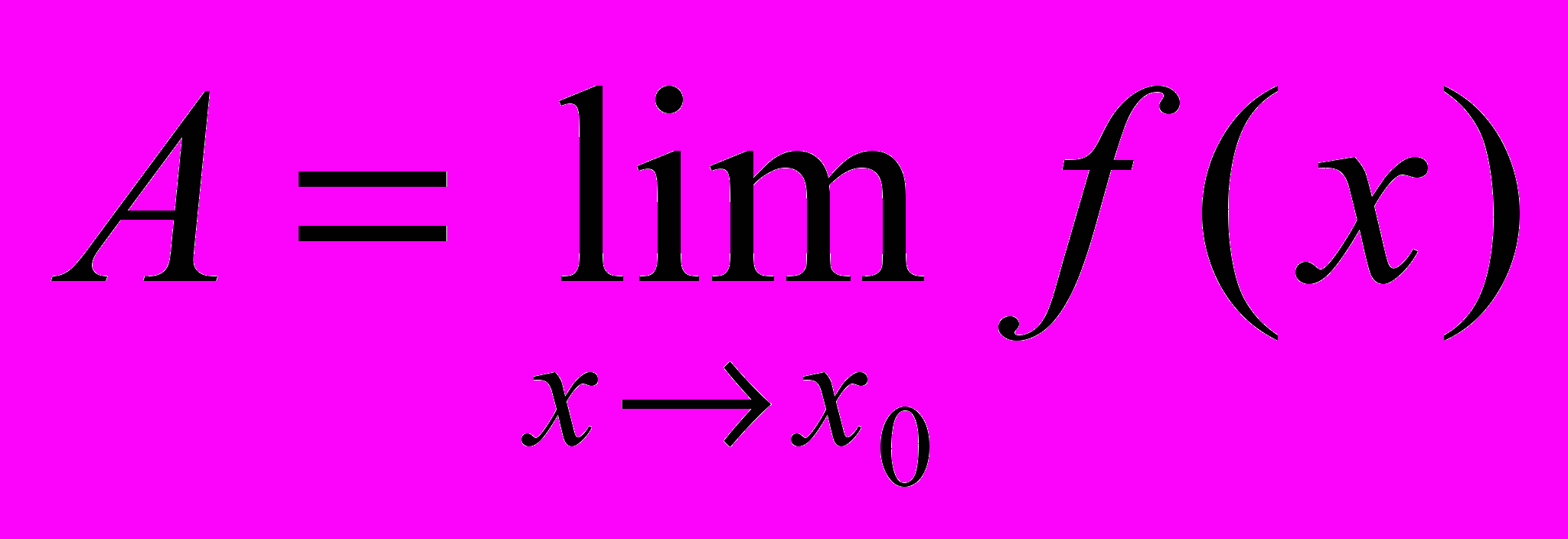. Возьмем >0>0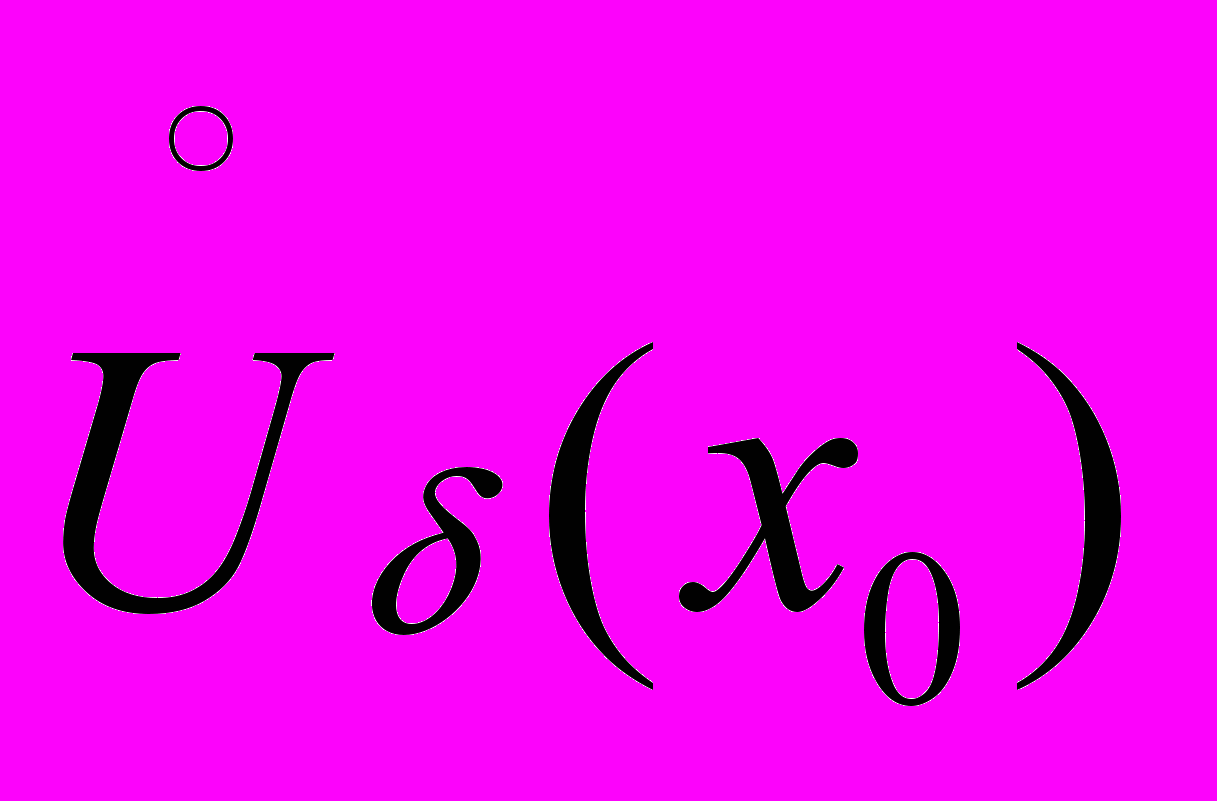x:f(x) , далее >0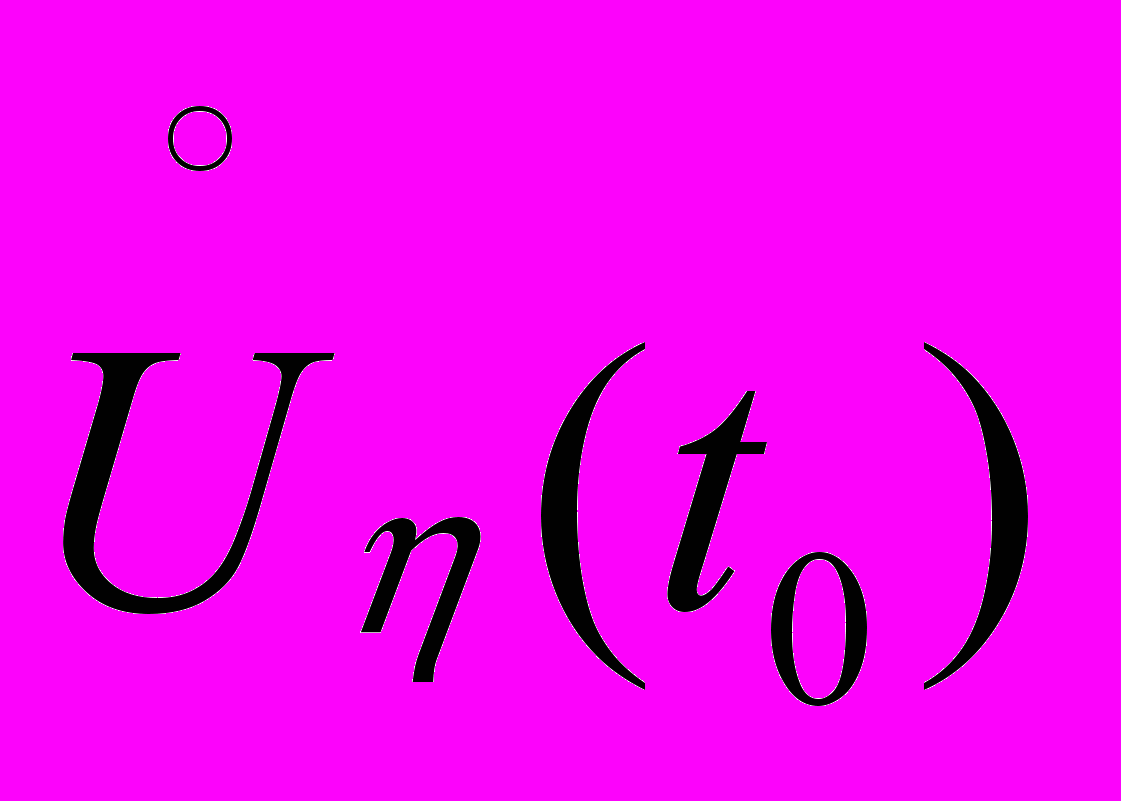t:g(t) 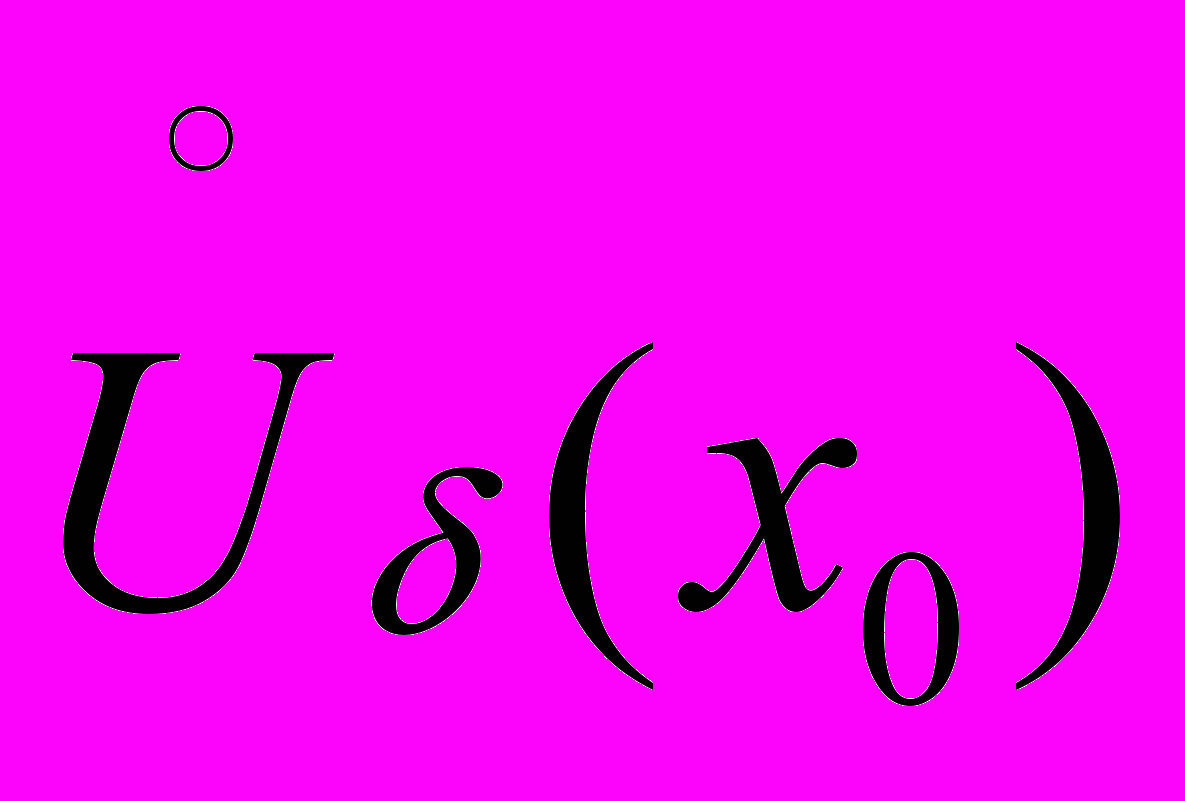,tt₀g(t)x₀. таким образом,

t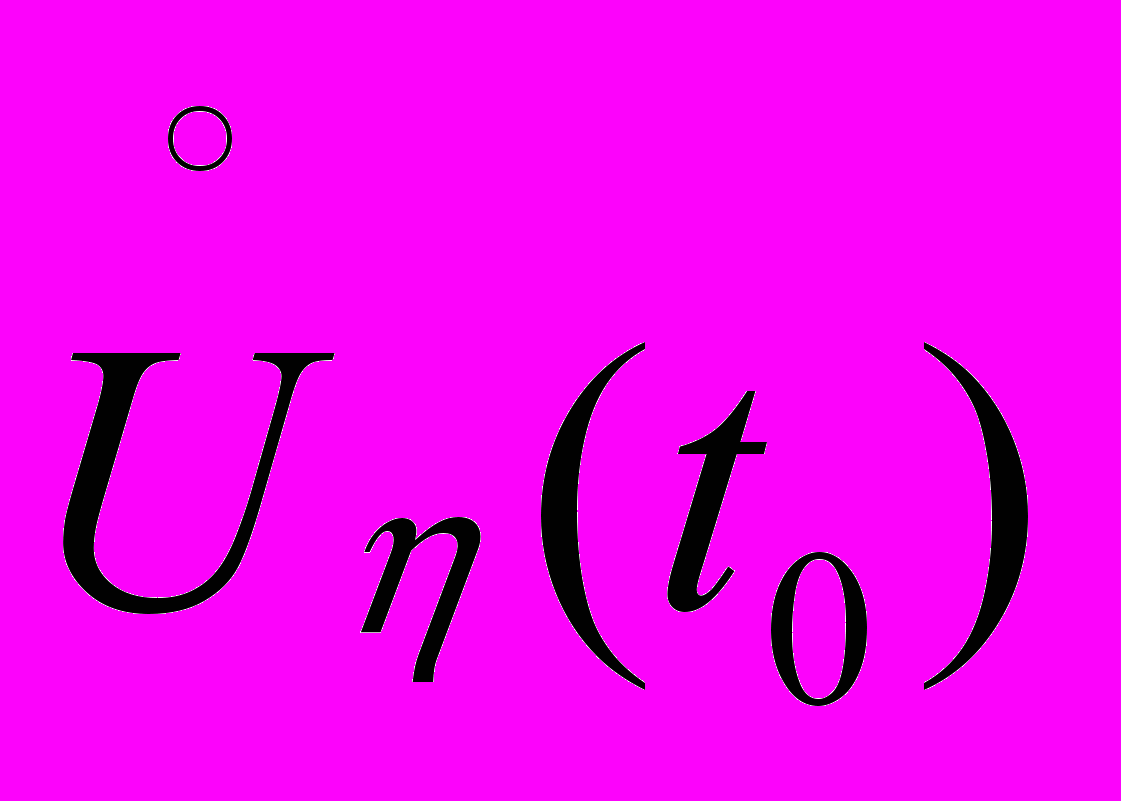 f[g(t)]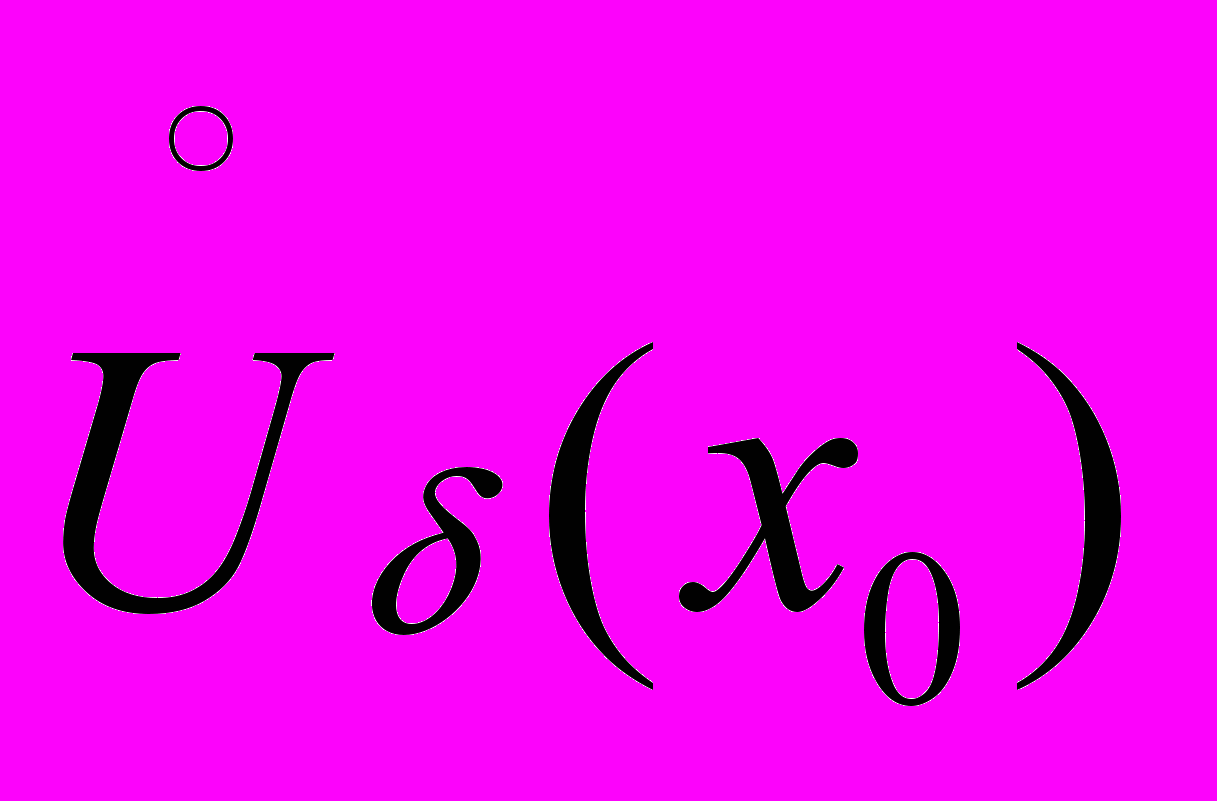

§3 Свойства пределов

1.Переход к пределу в неравенствах

Т. Если f(x)g(x) определены на (a,b) за исключением быть может x₀(a,b) и , А и B числа, то AB.

Замечание. Аналогично для случая f(x)