Стоты и интервалов времени, а также хранение и воспроизведение их единиц лежат в основе многочисленных измерительных задач, решаемых в совре­менной радиотехнике

Вид материала

Документы

Содержание Метод усреднения Нониусный метод

Подобный материал:

• Ния психоактивных веществ в организованных кол­лективах несовершеннолетних представляют, 4059.42kb.
• Учебно-методический комплекс дисциплины для студентов, обучающихся по специальности, 895.28kb.
• Учебно-методический комплекс дисциплины для студентов, обучающихся по специальности, 839.21kb.
• Российской Федерации, 71.43kb.
• Содержание Введение, 61.73kb.
• Хранение документов оперативное хранение документов, 1011.51kb.
• Школьные сми как фактор развития толерантности личности, 180.39kb.
• Оценка конкурентоспособности компаний быковская Т. Г. Красноярский государственный, 203.52kb.
• Программа курса (специальность Экология) физика, 79.76kb.
• Тема Власть, ее происхождение и виды Тема Политическая система, ее структура и функции, 1052.9kb.

Метод усреднения. Если нужно измерить периодически повторяющийся интервал ∆Т_х, то его длительность уве­личивают в n раз с помощью делителя частоты (умножителя периода) с коэффициентом деления n = 10^k, где k = 1, 2, ..., 5. Временной селектор открывается на интервал вре­мени ∆Т_х, и на электронный счетчик проходит N меток времени, приходящихся на n измеряемых интервалов. Относительная погрешность измерения при усреднении



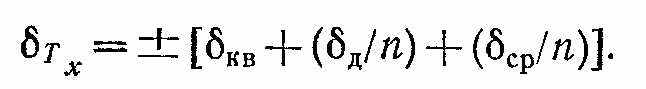
Если нужно измерить не периодический, но повторя­ющийся интервал времени, длительность которого сравнима с длительностью меток времени ∆Т_х≈Т_кв, то число меток N суммируется в течение некоторого числа n = 10^k из­меряемых интервалов; число n задается с помощью пере­счетной схемы. В результате получается следующее ра­венство: NT_кв = n∆Т_х, откуда искомый интервал ∆Т_х = (N/n) T_кв. Относительная погрешность в этом случае



Нониусный метод. При измерении коротких (десятки наносекунд) однократных импульсов погрешность дискрет­ности становится недопустимо большой. Нониусный метод позволяет значительно уменьшить ее при сравнительно невысоком быстродействии. Структурная схема измерения (рис. а) работает следующим образом.

В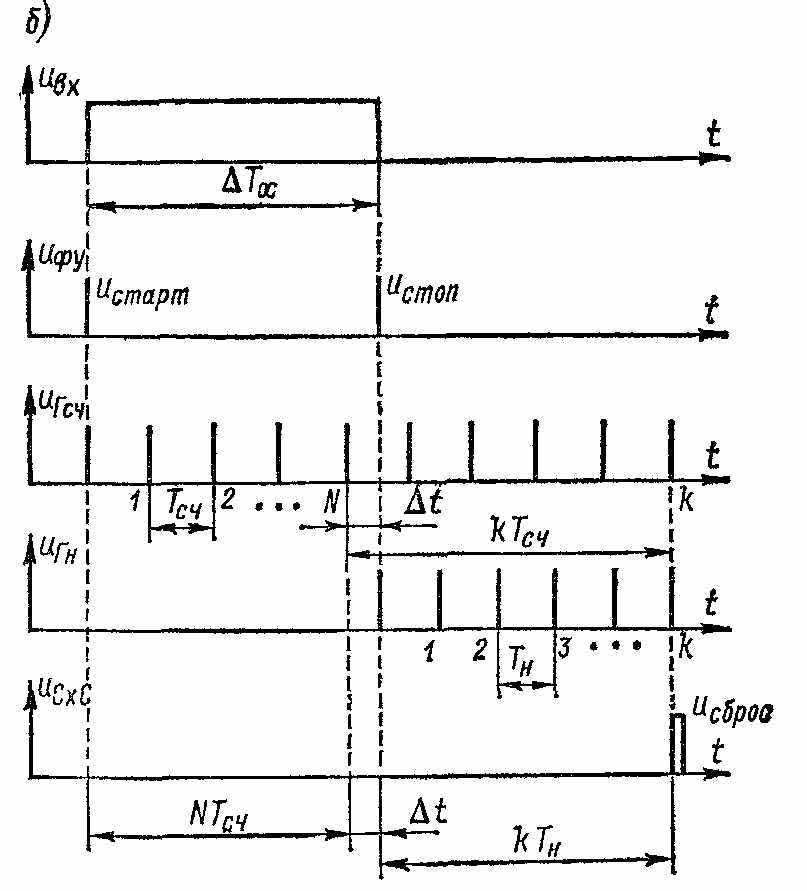ходное напряжение u_вх сигнала, длительность которого ∆Т_х нужно измерить, поступает на формирующее устрой­ство ФУ, с помощью которого вырабатываются два импульса u_старт и u_стоп, соответствующие началу и концу измеряемого интервала времени (рис. б). Стартовый импульс запускает генератор счетных импульсов Гсч с периодом по­вторения T_сч и одновременно с помощью триггера Т_г1 открывает временной селектор ВС₁; на электронный счетчик ЭСч₁ поступают счетные импульсы. Стоповый импульс закрывает Т_г1 и BC₁, ЭСч₁ фиксирует целое число счетных импульсов N, и измеряемый интервал можно записать в виде

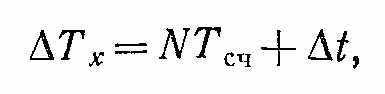(-14)

где ∆t— погрешность дискретности.

Для уменьшения этой погрешности используется гене­ратор нониусных импульсов Г_н, период следования которых Т_н меньше периода счетных импульсов: Т_н = (n-1) Т_сч/n, где n - некоторое число, обычно 10 или 100. Разность дли­тельностей импульсов Т_сч-Т_н=Т_сч/n называется шагом но­ниуса. Генератор нониусных импульсов запускается стоповым импульсом; последний с помощью триггера Т_г2 открывает временной селектор ВС₂, и на счетчик ЭСч₂ проходят но-ниусные импульсы. Временное расстояние между счетными и нониусными импульсами с каждым периодом уменьшается, и в момент их совпадения (перекрытия) схема сравнения СхС вырабатывает импульс сброса, приводящий всю схему в исходное состояние.

Погрешность дискретности можно выразить через число импульсов, счетных и нониусных, выработанных генерато­рами с момента прекращения счета N до момента совпадения импульсов k (cм. временную диаграмму):



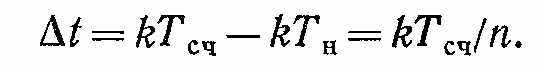
Следовательно, согласно формуле (-14), измеренный интервал времени



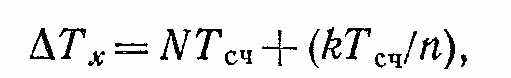
где первое слагаемое равно целому числу периодов счетных импульсов, а второе — числу шагов нониуса.

Дешифраторы и цифровой индикатор обеспечивают фиксирование числа N в старших разрядах, а числа k — в младших.

Погрешность измерения определяется длительностью и формой счетных и нониусных импульсов, нестабильностью генераторов и неполным совпадением k-тых импульсов. Погрешность дискретности ∆t зависит в основном от длитель­ности импульсов. В частности, при длительности импуль­сов прямоугольной формы τ = Т_сч/2n погрешность дискрет­ности распределена по равновероятному закону в пределах от минус Тсч/2n до Т_сч/2n и среднеквадратическое отклонение результата измерений составит

.


Контрольные вопросы.


1. Перечислите основные методы измерения частоты

2. Какова основная область применения резонансного метода измерения частоты? Принципы работы. Проходные и поглощающие частотомеры (волномеры).

3. Какие основные ограничения присущи методу измерения частоты при помощи заряда-разряда конденсатора?

4. В чем заключается принцип работы гетеродинного частотомера?

5. Объясните временные диаграммы, соответствующие режиму измерения часто­ты цифровым прибором.

6. Объясните временные диаграммы, соответствующие режиму измерения вре­менных интервалов цифровым прибором.

7. Как влияет погрешность дискретности на результат при измерении высоких и низких частот цифровым прибором?

8. Что такое кратковременная стабильность частоты и на что она может влиять в радиолокации?

9. Что такое долговременная стабильность частоты и на что она может влиять в радиолокации?