Видавництво Київського національного економічного університету імені Вадима Гетьмана

Вид материала

Документы

Подобный материал:

• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 80.2kb.
• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 57.56kb.
• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 31.21kb.
• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 39.46kb.
• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 66.88kb.
• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 118.45kb.
• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 81.58kb.
• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 63.61kb.
• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 79.13kb.
• Видавництво Київського національного економічного університету імені Вадима Гетьмана, 54.74kb.

К. Г. Валєєв, І. А. Джалладова

Математика на вступних випробуваннях

Навч. посіб. — К.: КНЕУ, 2006. — 400 с. Тв.обкл.

Гриф надано Міністерством освіти і науки України
Лист № 1.4/18-Г-578 від 27.07.06

Ціна: 35,80 грн.


ISВN 966–574–901–3


Посібник містить теоретичний матеріал і задачі з математики. Теоретичний матеріал включає викладання найбільш складних питань шкільного курсу арифметики, алгебри та елементарних функцій геометрії. Значна частина задач пропонувалась на вступних іспитах в різні вузи. Посібник містить багато авторських задач. Та задач по програмі вступних іспитів.

Посібник призначений для слухачів ПВ, вчителів математики, а також для тих, то готується до вступних випробувань у вузи, в тому числі самостійно. Також може бути корисним для всіх, то бажає в короткий термін систематизувати свої знання по математиці.


ЗМІСТ


Вступ 3


РОЗДІЛ 1. Множини чисел 5

1.1. Натуральні числа 5

1.2. Цілі числа 8

1.3. Ділення з остачею 10

1.4. Подільність натуральних чисел 11

1.5. Раціональні числа. Арифметичні дії над раціональними
числами 15

1.6. Відношення та пропорції 17

1.7. Десяткові дроби 19

1.8. Відсотки 21

1.9. Нескінченні десяткові дроби. Періодичні десяткові дроби 24

1.10. Поняття про ірраціональні числа. Дійсні числа. 27

1.11. Модуль дійсного числа та його властивості 30

РОЗДІЛ 2. Алгебраїчні вирази та їх перетворення 31

2.1. Основні поняття та формули 31

2.2. Ділення многочленів 32

2.3. Корінь n-го степеня з дійного числа. Арифметичний корінь
n-го степеня. Правила дій над коренями 38

2.4. Степінь з раціональним показником 43

2.5. Перетворення числових та алгебраїчних виразів 44

РОЗДІЛ 3. Радикали. Узагальнення поняття показника 56

3.1. Властивості степенів і коренів 56

3.2. Дії з радикалами 58

3.3. Обчислення ірраціональних виразів 63

3.4. Оцінки для радикалів 67

РОЗДІЛ 4. Алгебраїчні рівняння 72

4.1. Загальні відомості про рівняння 72

4.2. Рівняння першого степеня з одним невідомим 73

4.3. Рівняння другого степеня з одним невідомим 78

4.4. Задачі, які розв’язуються з використанням властивостей дискримінанта 81

4.5. Застосування формул Вієта 83

4.6. Розміщення корнів квадратного рівняння 87

4.7. Алгебраїчні рівняння вищих степенів та їх властивості 93

4.8. Розкладання многочлена на множники 94

4.9. Рівняння, що зводяться до квадратних рівнянь 102

4.10. Метод Кардано розв’язування кубічного рівняння 117

РОЗДІЛ 5. Ірраціональні рівняння 119

5.1. Основні поняття 119

5.2. Однорідні ірраціональні рівняння 131

5.3. Рівняння з кубічними ірраціональностями 132

5.4. Розв’язування складних ірраціональних рівнянь 134

5.5. Рівняння з модулями 138

5.6. Системи ірраціональних рівнянь 141

РОЗДІЛ 6. Тригонометричні вирази та їх перетворення 149

6.1. Відношення сторін трикутника 149

6.2. Означення і графіки тригонометричних функцій 151

6.3. Основні тригонометричні тотожності 158

6.4. Формули додавання кутів 159

6.5. Формули зведення 162

6.6. Перетворення добутків на суми 163

6.7. Формули додавання функцій 164

6.8. Подання тригонометричних функцій через тангенс половин-
ного кута 165

РОЗДІЛ 7. Тригонометричні рівняння 178

7.1. Обернені функції 178

7.2. Графік і властивості функції 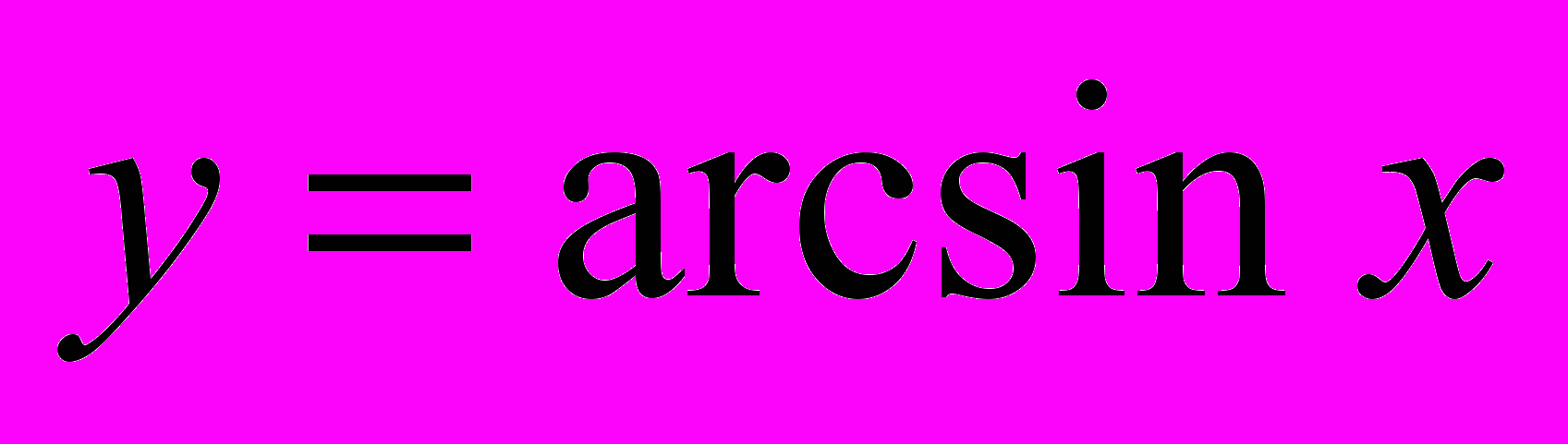179

7.3. Графік і властивості функції 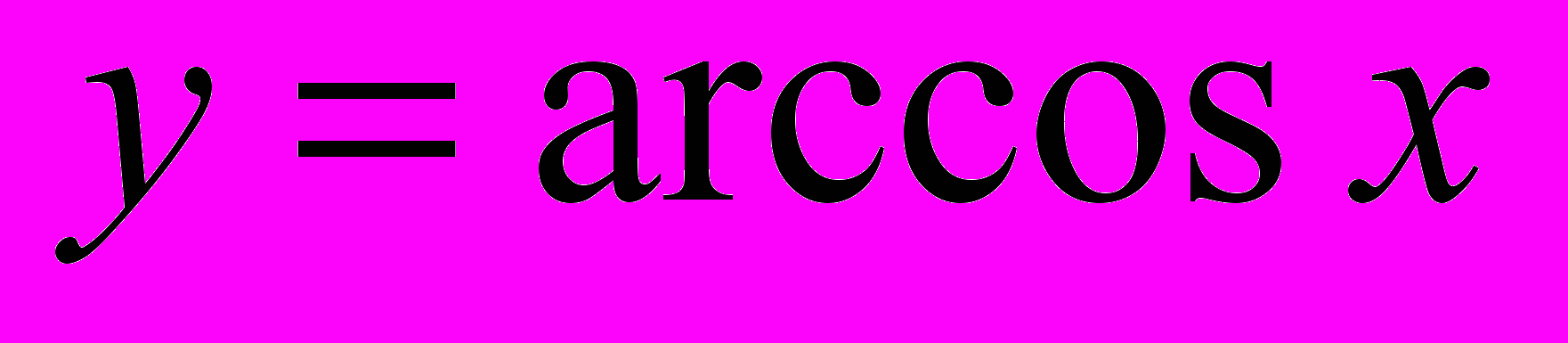181

7.4. Графік і властивості функції 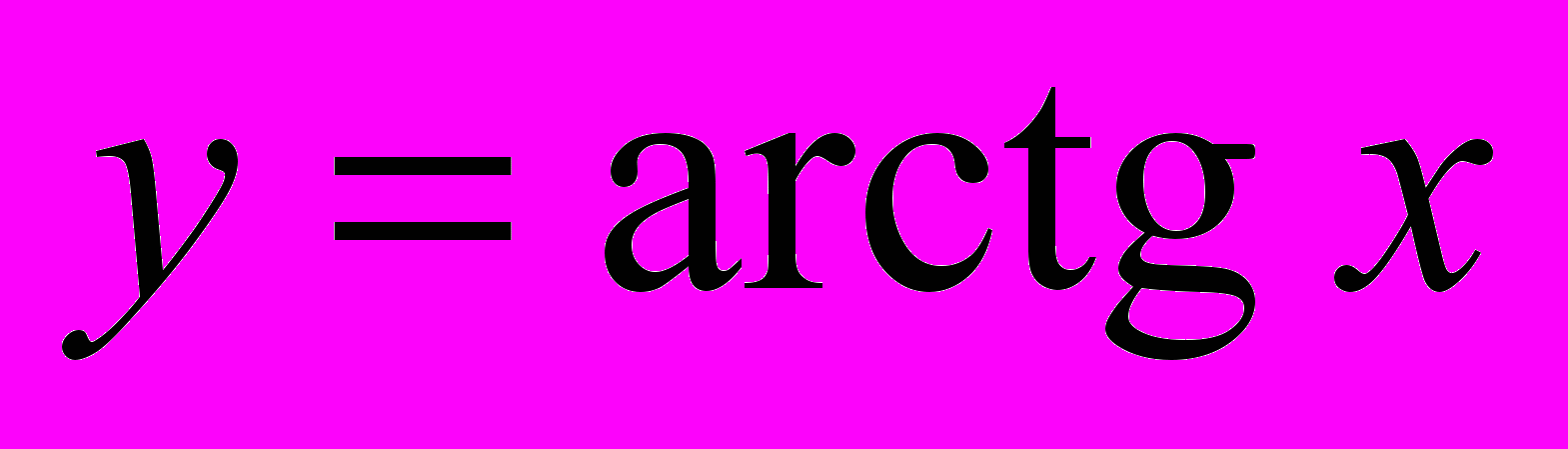183

7.5. Графік і властивості функції 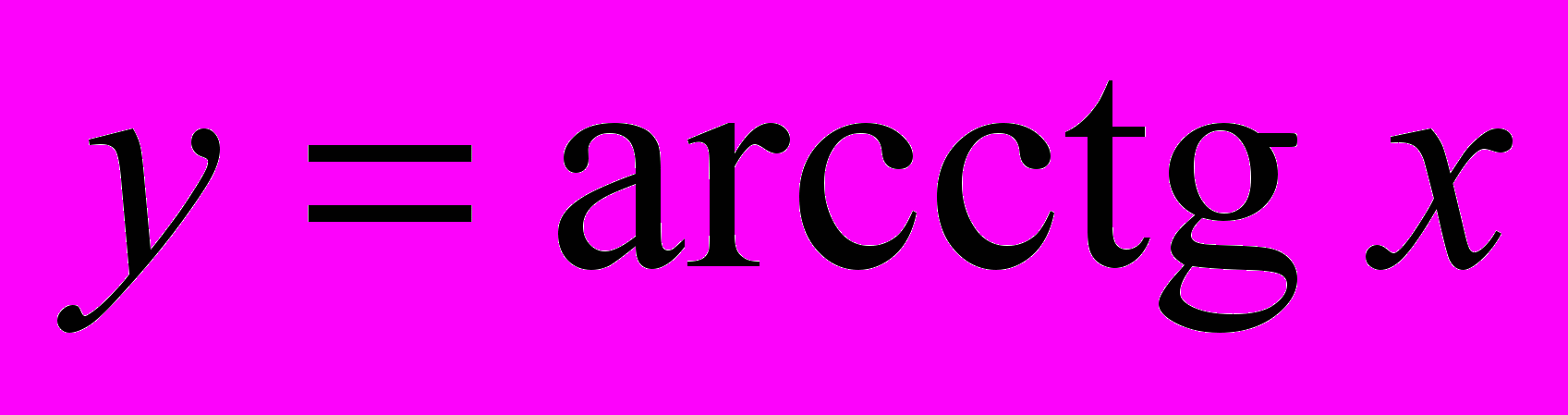185

7.6. Рівняння з оберненими тригонометричними функціями 189

7.7. Основні найпростіші тригонометричні рівняння 192

7.8. Лінійне рівняння 195

7.9. Метод зведення тригонометричного рівняння до алгебраїч-
ного 197

7.10. Однорідне тригонометричне рівняння 197

7.11. Метод розкладання тригонометричного рівняння
на множники 198

7.12. Перетворення добутків на суми, а сум на добутки 202

7.13. Методи розв’язування, що ґрунтуються на обмеженості
функцій 203

7.14. Системи тригонометричних рівнянь 204

РОЗДІЛ 8. Показникові та логарифмічні рівняння 215

8.1. Показникова функція 215

8.2. Логарифмічна функція 216

8.3. Перетворення логарифмічних виразів 217

8.4. Способи розв’язування логарифмічних рівнянь 219

8.5. Способи розв’язування показникових рівнянь 222

8.6. Показниково-степеневі рівняння 225

8.7. Системи показникових і логарифмічних рівнянь 226

РОЗДІЛ 9. Нерівності та методи їх розв’язування 232

9.1. Основні поняття 232

9.2. Нерівності першого степеня з одним невідомим 232

9.3. Квадратні нерівності 233

9.4. Метод інтервалів 234

9.5. Ірраціональні нерівності 236

9.6. Показникові нерівності 239

9.7. Логарифмічні нерівності 241

9.8. Система нерівностей 243

9.9. Тригонометричні нерівності 244

9.10. Алгебраїчні нерівності 249

РОЗДІЛ 10. Системи алгебраїчних рівнянь 256

10.1. Система лінійних алгебраїчних рівнянь 256

10.2. Система двох рівнянь із двома невідомими 259

РОЗДІЛ 11. Основи геометрїї 286

11. 1. Основні поняття планіметрії 286

11.2. Основні поняття стереометрії 304

11.3. Основи векторної алгебри 318

РОЗДІЛ 12. Основи комбінаторики і теорії імовірностей 328

12.1. Елементи комбінаторики 328

12.2. Випадкові події, імовірність подій 332

12.3. Теорема додавання ймовірностей 335

12.4. Теореми множення ймовірностей 338

12.5. Формула повної ймовірності. Формула Баєса 339

12.6. Повторення випробувань. Формула Бернуллі 342

12.7. Змішані задачі 342

РОЗДІЛ 13. Функції та їхні графіки 344

13.1. З історії поняття функції 344

13.2. Числова функція 346

13.3. Графік функції 347

13.4. Перетворення графіків 347

13.5. Відображення 354

13.6. Парні і непарні функції. Періодичність тригонометричних
функцій 357

13.7. Періодичні функції 360

13.8. Зростання й спадання функцій 365

13.9. Екстремуми 365

РОЗДІЛ 14. Похідна та її застосування 369

14.1. Відомості з історії 369

14.2. Поняття похідної 371

14.3. Похідні основних елементарних функцій 373

14.4. Правила диференціювання 373

14.5. Похідна оберненої функції 375

14.6. Похідна складеної функції 375

14.7. Логарифмічне диференціювання 377

14.8. Похідні вищих порядків 378

14.9. Правила знаходження похідних n-го порядку 379

14.10. Механічний зміст похідної 380

14.11. Рівняння дотичної та нормалі до кривої 381

14.12. Дослідження функцій 383

14.13. Ознака зростання і спадання функції 387

14.14. Критичні точки функції, максимуми і мінімуми 388


Література 393