Загальна програма з математики для підготовки до тестування на 2-ий курс радіофізичного факультету Алгебра та основи аналізу

Вид материала

Документы

Содержание Розв’язування рівнянь, нерівностей, систем рівнянь та нерівностей Функції. (лінійна)

Подобный материал:

• Робоча програма з курсу " Загальна теорія політики " для студентів факультету політико-інформаційного, 724.65kb.
• Програма навчальної дисципліни основи культурології галузь знань 0201 культура напряму, 503.8kb.
• Робоча навчальна програма дисципліни "Загальна теорія держави І права" Для спеціальностей, 321.84kb.
• Робоча програма навчальної дисципліни «Історія культурології» напряму підготовки культура, 676.38kb.
• Програма зовнішнього незалежного оцінювання з математики Мета зовнішнього незалежного, 149kb.
• Навчальна програма дисципліни „ культурологія для студентів факультету соціології спеціальність, 290.09kb.
• Програма навчальної дисципліни історія української культури напряму підготовки 040102, 264.69kb.
• Робоча програма навчальної дисципліни хемометричні методи аналізу даних напряму підготовки, 113.56kb.
• Програма вступних випробувань з дисципліни «Основи економіки» для абітурієнтів напряму, 87.66kb.
• Робоча програма затверджена на засіданні кафедри філософії Протокол №14 від "24" червня, 1203.01kb.

Загальна програма з математики для підготовки до тестування на 2-ий курс радіофізичного факультету


Алгебра та основи аналізу

1. Дійсні числа: поняття, геометричне зображення, основні властивості чисел, наслідки, числова пряма. Формули скороченого множення. Властивості нерівностей. Абсолютна величина (модуль) дійсного числа: означення, геометричний зміст, властивості. Рівняння та нерівності з модулем.
   
2. Сиепінь числа : ціла степінь; корінь з дійсного числа, арифметичне значення кореня; довільна раціональна степень додатного дійсного числа, їх властивості.
   
3. Комплексні числа: поняття; алгебраїчна, тригонометрична, показникова форми; геометричне зображення; дії над комплексними числами; формули Муавра та Ейлера.
   
4. Функція: загальне поняття та властивості ( область визначення, область значень, парність-непарність, періодичність, неперервність, зростання-спадання); способи задання функції; графік. Обернена функція та її графік.
   
5. Розв’язування рівнянь, нерівностей, систем рівнянь та нерівностей: основні поняття, геометричний смисл їх розв’язків; рівносильні перетворення; системи лінійних рівнянь та нерівностей.
   
6. Функції. 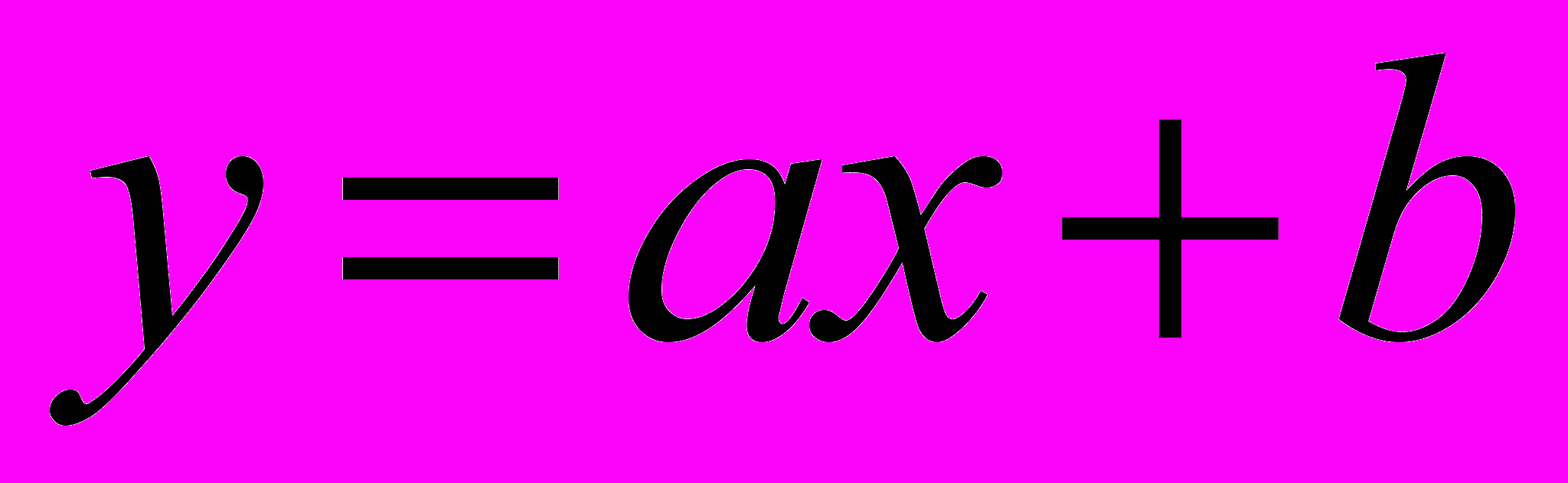(лінійна): властивості, графік, геометричний смисл коефецієнтів і .
   
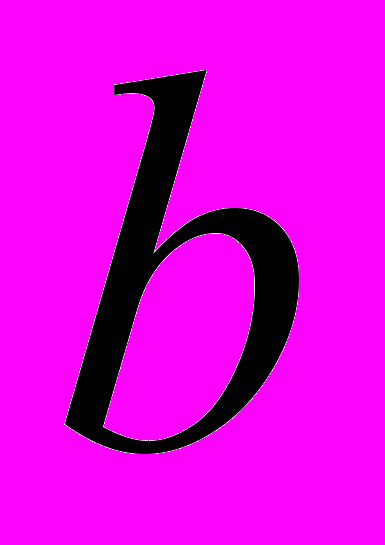7. Функція 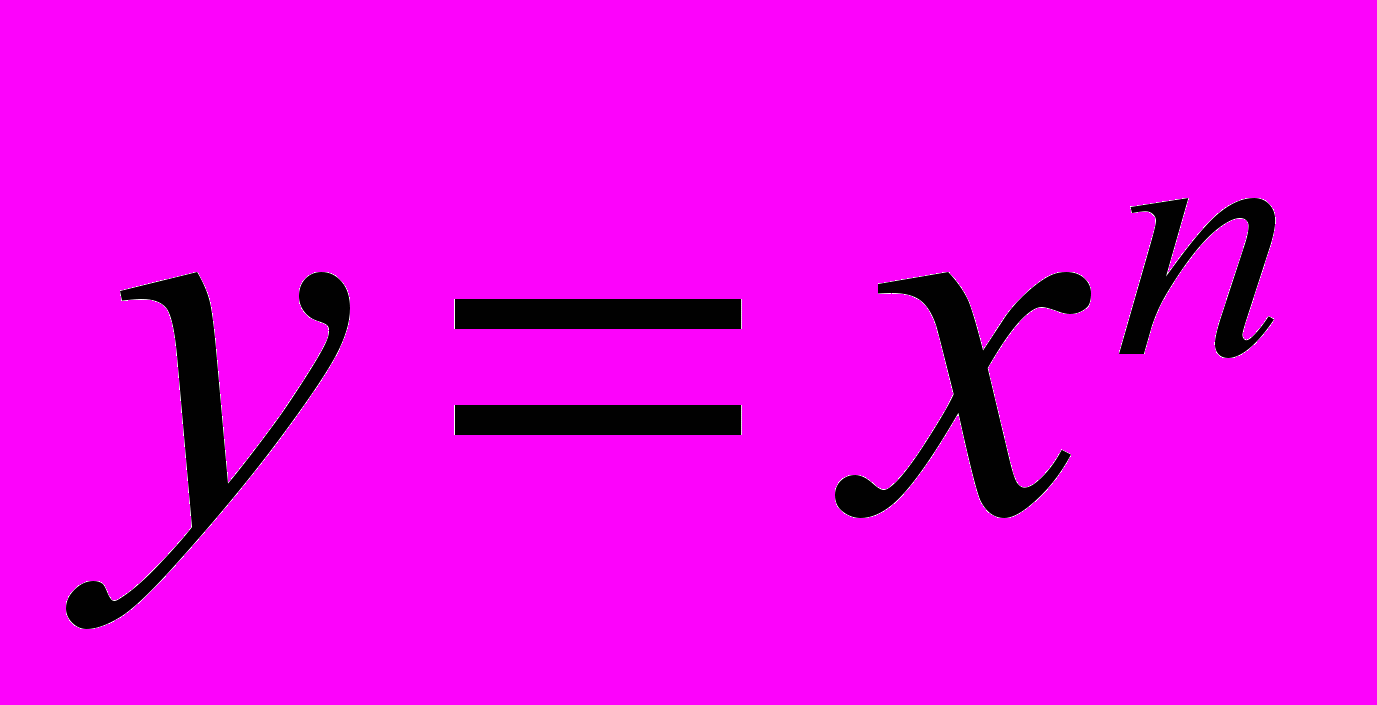(степенева): властивості та графіки найпростіших степеневих функцій .
   
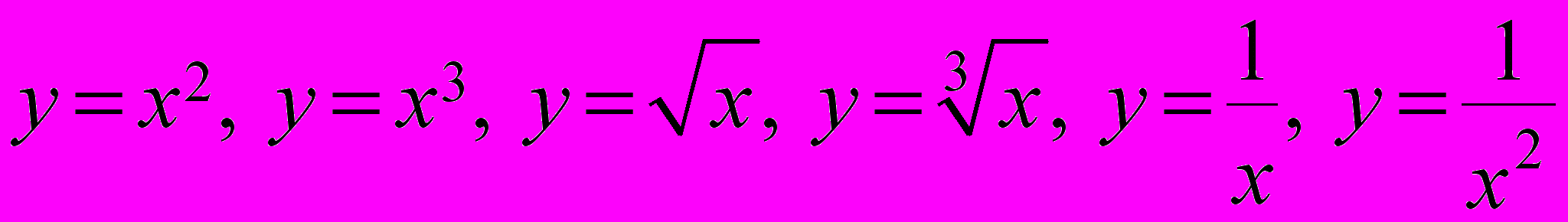8. Функція 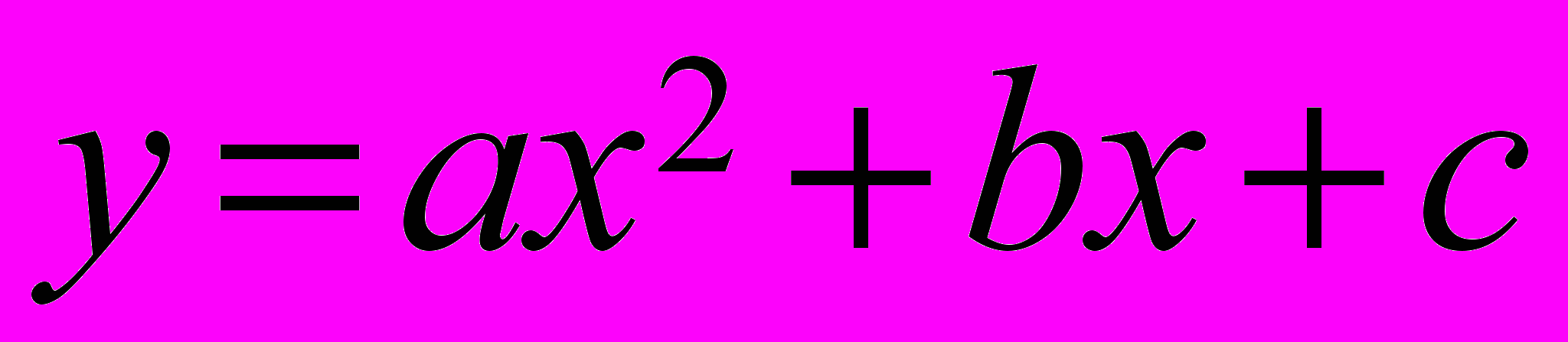: властивості, графік; квадратні рівняння, нерівності і такі, що до них зводяться. Теорема Вієта.
   
9. Показникова функція 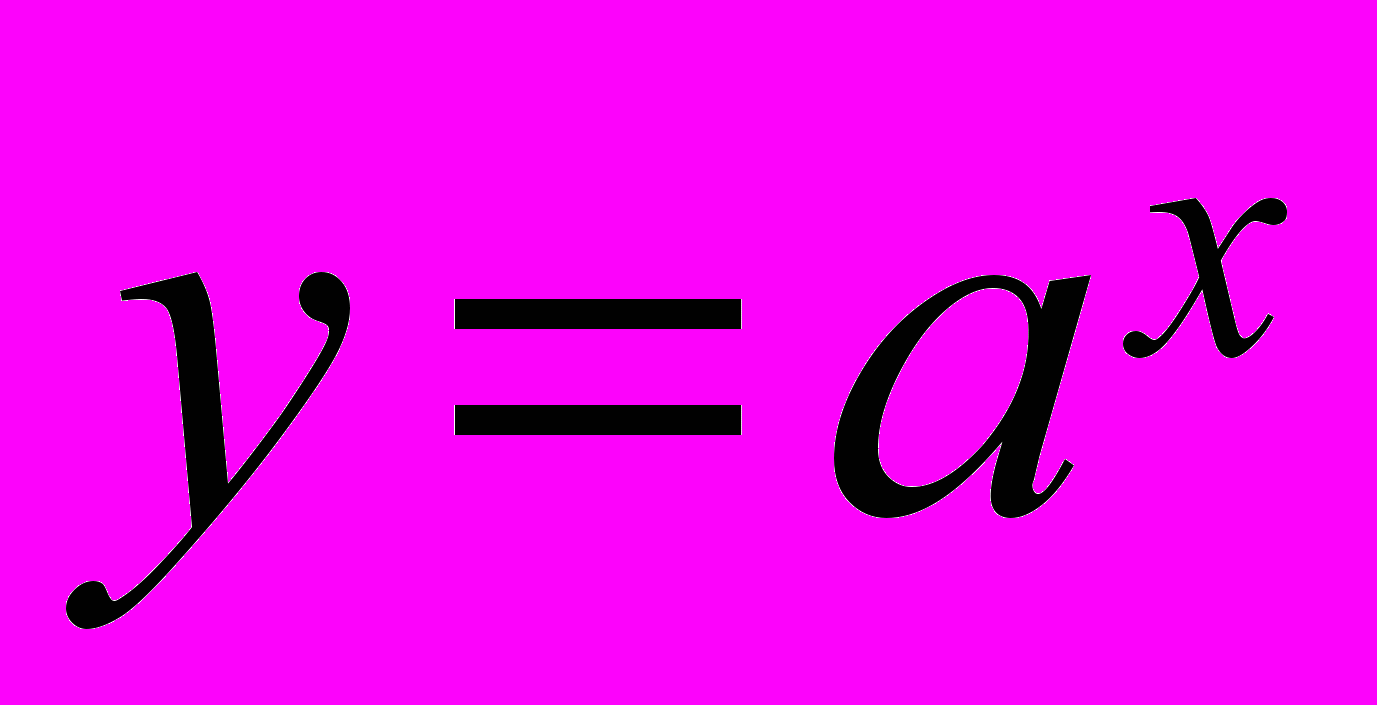та обернена до неї 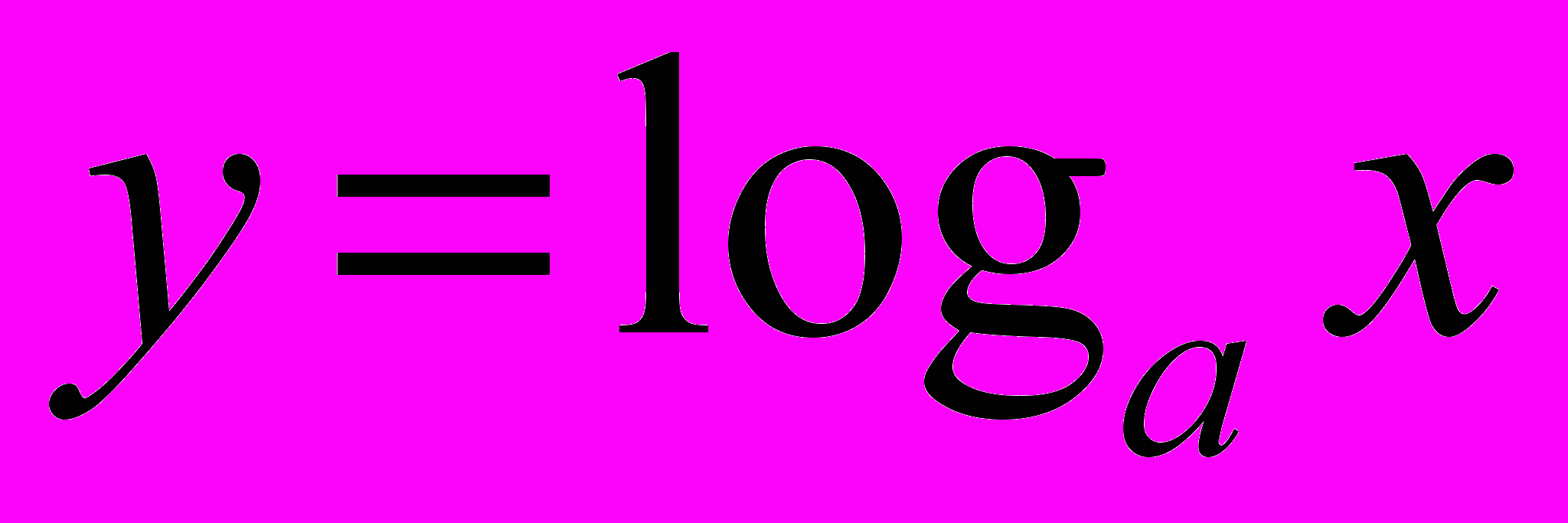: означення, властивості, графік, показникові та логарифмічні рівняння та нерівності.
   
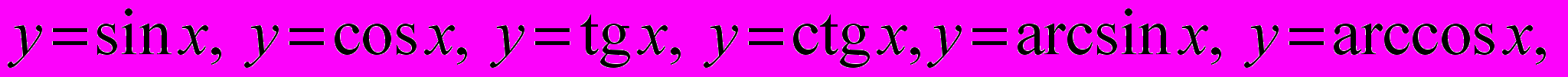
10. Тригонометричні та обернені тригонометричні функції 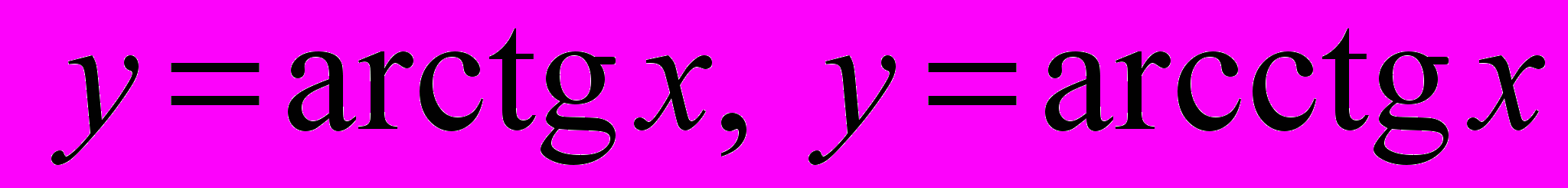: озачення, властивості, графіки; основні тригонометричні формули ; тригонометричні рівняння та нерівності.
    
11. Елементарні перетворення графіків функцій:
    

.

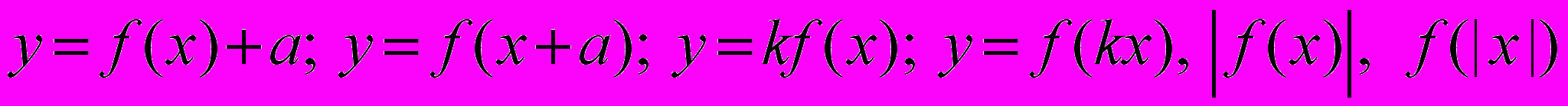12. Арифметична та геометрична прогресії: поняття, властивості, формули суми n членів прогресії. Нескінченно спадна геометрична прогресія: поняття, властивості, сума.
    
13. Похідна функції: означення, геометричний та фізичний смисл; таблиця похідних основних елементарних функцій, правила диференціювання, застосування до дослідження функцій.
    
14. Інтеграл: первісна та невизначений інтеграл; таблиця основних інтегралів, основні методи інтегрування. Визначений інтеграл: формула Ньютона-Лейбница; основні методи обчислення; застосування до обчислень площ та обє’мів.
    

Геометрія

1. Основи векторної алгебри: вектори і основні операції над ними; координати вектора в прямокутній декартовій системі координат, скалярний добуток векорів та його обчислення.
   
2. Аналітична геометрія на площині: пряма, парабола, коло, еліпс, гіпербола, основні рівняння.
   
3. Аналітична геометрія у просторі: рівняння площини.
   
4. Найпростіші плоскі та просторові фігури: прямокутник, трикутник, паралелограм, трапеція, круг, круговий сектор, паралелепіпед, піраміда, циліндр, конус, куля. Основні властивості та формули обчислення площ плоских та об’ємів просторових фігур.