Моделирование дифракционного распространения волн и структура поля радиоволн увч и свч на нерегулярных трассах

Вид материала

Автореферат

Содержание Ведущая организация Общая характеристика работы Научная новизна Практическая значимость На защиту выносятся следующие положения Апробация работы Личный вклад автора Объем и структура работы Содержание работы Первая глава Во второй главе Пятая глава U0 - поле, которое создает источник в точке В В шестой главе Основные результаты диссертации опубликованы в следующих работах

Подобный материал:

• Дисциплина «Электродинамика и распространение радиоволн» (ЭДи ррв) является одной, 170.21kb.
• Курс «Физические основы свч-электроники» Направления: «Техническая физика», «Электроника, 15.06kb.
• 15 січня 2009 р, 49.14kb.
• Направление – радиотехника профиль Радиоэлектронные системы Радиотехника, 22.68kb.
• Программа учебной дисциплины сд. Р. 05 «Распространение радиоволн» Специальности 071500,, 77.47kb.
• Тематический план лекций, 10.12kb.
• Самостоятельная работа 8-9 «Механические волны. Звук», 18.09kb.
• Дифракция, 95.57kb.
• Тема электромагнитные волны, 17.86kb.
• Программа учебной дисциплины «Распространение электромагнитных волн в плазме» Специальности, 82.76kb.

На правах рукописи


Дагуров Павел Николаевич


МОДЕЛИРОВАНИЕ ДИФРАКЦИОННОГО РАСПРОСТРАНЕНИЯ ВОЛН И СТРУКТУРА ПОЛЯ РАДИОВОЛН УВЧ И СВЧ НА НЕРЕГУЛЯРНЫХ ТРАССАХ


Специальность 01.04.03 - радиофизика


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

доктора физико-математических наук


Иркутск – 2010

Работа выполнена в Отделе физических проблем при Президиуме Бурятского научного центра Сибирского отделения РАН.


Официальные оппоненты:

доктор технических наук, профессор

Кашкин Валентин Борисович


доктор физико-математических наук, профессор

Тинин Михаил Валентинович


доктор физико-математических наук, профессор

Якубов Владимир Петрович


Ведущая организация:

Учреждение Российской академии наук

Институт радиотехники и электроники им. В.А. Котельникова РАН


Защита состоится 4 марта 2010 г. в 10⁰⁰ часов на заседании диссертационного совета Д 212.074.04 при Иркутском государственном университете по адресу: 664003, г. Иркутск, бульвар Гагарина, 20.


С диссертацией можно ознакомиться в Научной библиотеке Иркутского государственного университета.

Автореферат разослан «__» __________ 2009 г.


Ученый секретарь диссертационного

совета Д 212.074.04,

кандидат физико-математических наук,

доцент Б.В. Мангазеев

Общая характеристика работы


Актуальность проблемы. Непрерывное развитие радиоэлектронных средств различного назначения вызывает необходимость дальнейшего развития классического направления в радиофизике – распространения радиоволн вдоль земной поверхности. Это обусловлено тем, что качественные показатели сигнала и необходимые параметры аппаратуры в значительной степени определяются трактом распространения. Поэтому задача возможно более точного прогнозирования условий распространения, удовлетворяющего современному развитию радиоэлектроники, является актуальной. Проблема распространения радиоволн вдоль земной поверхности привлекала внимание многих выдающихся ученых. Большой вклад в ее решение внесли А. Зоммерфельд, Г. Вейль, П. Ван-дер-Поль, М.В. Шулейкин, Б.А. Введенский, В.А. Фок, Е.Л. Фейнберг и другие исследователи. Полученные ими фундаментальные результаты в основном относятся к распространению радиоволн вдоль регулярных поверхностей, таких как плоскость и сфера.

На загоризонтных трассах длиной до 100 – 150 км, а в гористой местности и на трассах большей протяженности доминирующим механизмом распространения радиоволн является дифракция. Практическое значение изучения закономерностей распространения на дифракционных трассах обусловлено потребностями частотно-территориального планирования как традиционных радиосистем различного назначения и проблемами электромагнитной совместимости между ними, так и быстрым развитием сотовой связи и систем беспроводного доступа. Актуальность проблемы также обусловлена появившимися в последнее время предложениями по использованию дифракционного механизма распространения для радиолиний, антенны которых устанавливаются в теневой зоне относительно друг друга. Это значительно упрощает выбор местоположения станций и позволяет избежать сооружения высоких и дорогих антенных опор. Возможность такого построения радиолиний обусловлена фундаментальным по своему значению переходом от аналоговой способа передачи информации к цифровым системам передачи связи, который позволяет существенно (на десятки децибел) уменьшить требуемый энергетический потенциал.

Реальные приземные трассы распространения являются в той или иной степени нерегулярными, т. е. имеющими неровности рельефа произвольной формы и различных масштабов. При расчете таких трасс возникает необходимость учета дифракции и рассеяния радиоволн на этих неровностях. Влияние нерегулярности рельефа наиболее выражено в условиях холмистой или гористой местности, когда препятствия рельефа зачастую можно аппроксимировать клиновидными препятствиями. При этом оказывается, что большое влияние на дифракционное поле (в отличие от трасс прямой видимости) наряду, естественно, с продольным профилем трассы распространения, оказывают и поперечные неровности рельефа. Такими поперечными неровностями могут служить и дифракционные экраны, с помощью которых можно регулировать дифракционное поле, усиливая или ослабляя его.

Целью диссертационной работы является разработка моделей дифракции радиоволн, учитывающих особенности геометрии препятствий рельефа и экспериментальное исследование пространственно-временной структуры поля УКВ на дифракционных трассах. Для достижения поставленной цели решались следующие основные задачи:

1. Разработка двумерных моделей распространения радиоволн на дифракционных трассах и трехмерных моделей распространения, учитывающих поперечную форму препятствий.
   
2. Развитие теории граничной дифракционной волны и обобщение ее на задачу многократной дифракции на нескольких последовательно расположенных экранах с произвольной формой краев.
   
3. Экспериментальное исследование распространения радиоволн на дифракционных трассах с клиновидными препятствиями для изучения пространственно-временной структуры поля УКВ, искажений диаграмм направленности антенн, поляризационных зависимостей сигнала.
   
4. Разработка методов регулирования электромагнитных полей с помощью дифракционных экранов и нового подхода к решению классических задач дифракции на ленте и щели.
   
5. Экспериментальное исследование эффективности применения дифракционных экранов в качестве пассивных ретрансляторов и ослабляющих элементов.
   

Научная новизна работы состоит в следующем:

1. Получено решение задачи многократной дифракции Френеля-Кирхгофа на N непрозрачных полуплоскостях при произвольной ориентации их краев. Показано, что путем преобразования систем локальных координат 2N-кратный дифракционный интеграл сводится к N-кратному интегралу. Предложен метод расчета поля на приземных трассах, аппроксимируемых последовательностью кусочно-плоских и кусочно-однородных участков с клиновидными препятствиями, с помощью параболического уравнения.
   
2. Проведен анализ влияния рефракционных свойств тропосферы и слоистых неоднородностей на поле на трассе с клиновидным препятствием. Показано, что это влияние уменьшается с увеличением высоты препятствия. Установлены значения интенсивности тропосферных слоев, вызывающих интерференционные флуктуации уровня поля.
   
3. Предложена и разработана модель многолучевого дифракционного распространения радиоволн, учитывающая поперечный профиль препятствия. Показано, что она удовлетворительно описывает экспериментальные зависимости. Исследовано влияние направленности антенн на дифракцию волн на неровном крае препятствия. Теоретически и экспериментально показано сглаживание интерференционной картины при уменьшении ширины диаграммы направленности.
   
4. Выполнено обобщение теории граничной дифракционной волны на многократную дифракцию волн на последовательно расположенных отверстиях (экранах).
   
5. Проведены исследования пространственно- временной структуры поля УКВ на дифракционных трассах. Установлена связь временных флуктуаций сигнала с особенностями пространственной структуры дифракционного поля естественных экранирующих препятствий. Обнаружено существование устойчивых в среднем пространственных экстремумов дифракционного сигнала. Экспериментально показано влияние многолучевости дифракционного поля на форму диаграмм направленности антенн в тени препятствий. Исследованы характеристики деполяризации сигнала на дифракционных трассах.
   
6. Выявлены особенности пассивной ретрансляции радиоволн с учетом влияния дифракционного поля прямого прохождения. Разработаны метод регулирования дифракционного поля прямого прохождения и метод уменьшения замираний поля на трассах с пассивными ретрансляторами. Разработан теоретически и подтвержден экспериментально метод уменьшения флуктуаций на открытых трассах с помощью последовательных дифракционных экранов.
   
7. Проведено обобщение классической задачи дифракции волн на проводящей ленте (щели) на случай произвольной ширины ленты и при малых углах скольжения падающей волны. Решение задачи основано на рассмотрении механизмов двукратной дифракции Френеля-Кирхгофа с учетом отражений от ленты и поляризации волны. Показано, что результирующее поле представляет собой сумму геометрооптической волны, волн однократной дифракции и волн, испытавших двукратное рассеяние на краях ленты. Получено простое выражение в элементарных функциях для ослабления поля при скользящем падении.
   

Практическая значимость

Результаты работы имеют практическое значение для проектирования систем радиосвязи и решения проблем электромагнитной совместимости в дифракционной области. Разработанные модели дифракционного поля позволяют уточнить методики расчета уровней сигнала в теневой зоне препятствий. Полученные экспериментальные результаты являются существенным вкладом в имеющиеся знания о механизмах дифракционного распространения. Метод обобщенной граничной волны при многократной дифракции за счет уменьшения размерности дифракционного интеграла с 2N до N существенно уменьшает вычислительные затраты при численном решении дифракционных задач радиофизики, оптики и акустики. Метод решения задачи дифракции электромагнитных волн на ленте и щели может послужить основой для разработки эффективных методов расчета поля от поверхностей конечных размеров при скользящем падении волны. Метод увеличения уровня поля внедрен на интервале радиорелейной линии. Результаты работы, связанные с дифракцией на ленте и теорией граничной дифракционной волны реализованы в учебном процессе в Бурятском госуниверситете.

На защиту выносятся следующие положения:

1. Обобщенная модель последовательной дифракции радиоволн на N полуплоскостях, учитывающая случай произвольно ориентированных краев полуплоскостей, путем преобразования локальных систем координат и применения многомерного метода стационарной фазы сводится к модели, использующей параллельные края. При этом 2N-кратный дифракционный интеграл преобразуется в N-кратный интеграл. Взаимный наклон краев приводит к явлениям фокусировки и дефокусировки дифракционного поля.
   
2. Трехмерная модель дифракционного распространения УКВ, учитывающая поперечную к направлению распространения форму гребней клиновидных препятствий, позволяет прогнозировать неоднородность пространственной структуры дифракционного поля поперек линии трассы.
   
3. Предложенный вывод поля граничной волны в области дифракции Френеля позволяет уточнить формирование граничной дифракционной волны. Введение амплитуды рассеяния волны элементом края и ее применение для расчета многократного рассеяния на элементах краев последовательно расположенных экранов (отверстий) дает метод расчета обобщенной граничной волны многократной дифракции. Полученное решение уменьшает размерность дифракционного интеграла в два раза и существенно сокращает время вычислений при расчете полей многократных дифракционных интегралов (при сравнимой точности вычислений на 2-3 порядка при двукратной дифракции).
   
4. Дифракционное поле СВЧ и УВЧ в тени препятствий рельефа имеет мелкомасштабные пространственные неоднородности с периодами в единицы – десятки метров и амплитудой колебаний до 10 - 20 дБ. Временные флуктуации сигнала в теневой зоне зависят от особенностей пространственной структуры поля. Неоднородная пространственная структура дифракционного поля приводит к искажениям диаграмм направленности и нерегулярной деполяризации поля.
   
5. Учет дифракционного поля препятствия позволяет оптимизировать ретрансляцию радиоволн с помощью дифракционных экранов, обеспечивающих увеличение уровня сигнала. Разработанный метод уменьшения отражений от земной поверхности с помощью последовательно расположенных экранов позволил уменьшить флуктуации сигнала на плоской трассе на 20 дБ.
   
6. Метод решения задачи дифракции на проводящей ленте и щели в проводящем экране, основанный на учете двукратной дифракции Френеля-Кирхгофа и векторного характера электромагнитной волны, в отличие от известных методов применим при произвольной ширине ленты и малых углах скольжения. Полученное решение представляет собой сумму геометрооптической волны, волн однократной дифракции и волны двукратной дифракции, удовлетворяет принципу взаимности и выражается через обычный и обобщенный интегралы Френеля.
   

Апробация работы

Основные результаты диссертационной работы были представлены на XII Всесоюзной конференции по распространению радиоволн, Томск, 1978, XIII Всесоюзной конференции по распространению радиоволн, Горький, 1981, межведомственном совещания «Ультракороткие волны и электромагнитная совместимость», Улан-Удэ, 1983, XIV Всесоюзной конференции по распространению радиоволн, 1984, XV Всесоюзной конференции по распространению радиоволн, 1987, Девятом международном Вроцлавском симпозиуме по электромагнитной совместимости, Вроцлав, 1988, International Symposium on Radio Propagation, Beijing, China, 1988, International. Symposium on Antennas and Propagation (ISAP^’ 89), Tokyo, Japan, 1989, XV Всесоюзной конференции по распространению радиоволн, Харьков, 1990, Всесоюзном совещании по приземному распространению радиоволн и электромагнитной совместимости, Улан-Удэ, 1990, XVII конференции по распространению радиоволн, Ульяновск, 1993, IV Международной научно-технической конференции «Распространение и дифракция волн в неоднородных средах», Москва,1994, URSI Commision F Trienal Open Symposium, Ahmedabad, India, 1995, XVIII Всероссийской конференции по распространению радиоволн, Санкт-Петербург, 1996, Российской научно-технической конференции по распространению и дифракции волн, Улан-Удэ, 1996, 8^th URSI Commision F Trienal Open Symposium, Aveiro, Portugal, 1998, XIX Всероссийской конференции по распространению радиоволн. Казань, 1999, International Symposium on Antennas and Propagation (ISAP2000), Fukuoka, Japan, XX Всероссийской конференции по распространению радиоволн, Нижний Новгород, 2002, IGARSS Anchorage, USA, 2004. 21-ой Всероссийской конференции по распространению радиоволн. Йошкар-Ола, 2005, ClimDiff Cleveland, USA,2005, International Seminar «Days on Diffraction’2006»: St. Petersburg, 2006, XIV International Symposium "Atmospheric and Ocean Optics. Atmospheric Physics":Tomsk, 2007, XXII Всероссийской конференции по распространению радиоволн, Ростов-на-Дону. 2008.

Публикации

По теме диссертации опубликовано 52 работы, из них 14 статей в рецензируемых журналах из перечня ВАК и 1 изобретение.

Личный вклад автора

Публикации, составляющие основу диссертационной работы, выполнены большей частью в соавторстве. Работа [1] выполнена под руководством Н.Б. Чимитдоржиева, работа [2] под руководством В.Г. Ямпольского. В большинстве других публикаций вклад автора являлся определяющим, ему принадлежат постановка задач исследования, выбор методов решения, непосредственное участие в теоретических и экспериментальных исследованиях, анализ результатов. Автор являлся научным консультантом диссертационной работы А.С. Заяханова и научным руководителем диссертационной работы А.В. Дмитриева.

Объем и структура работы

Диссертация изложена на 265 страницах машинописного текста, иллюстрируется 96 рисунками и графиками, состоит из введения, 6 глав, заключения, приложения и списка литературы из 188 наименований.


СОДЕРЖАНИЕ РАБОТЫ


Во введении обоснована актуальность темы, поставлены цель и задачи исследования, изложены новые научные результаты, полученные в работе и положения, выносимые на защиту; излагается структура и краткое содержание работы.

Первая глава посвящена разработке двумерных моделей дифракции волн.

В
первом параграфе главы рассмотрены методы решения задач распространения радиоволн вдоль земной поверхности. Показано, что простым и эффективным способом решения эти задач при наличии выраженных препятствий рельефа являются методы теории дифракции Френеля-Кирхгофа.

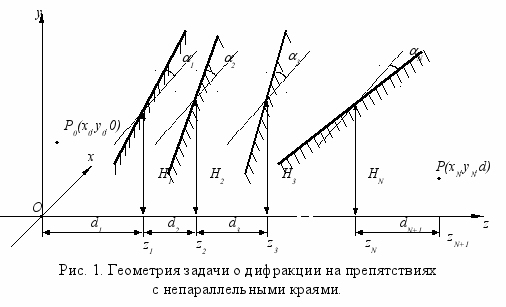
Во втором параграфе решается обобщенная задача дифракции на N непрозрачных полуплоскостях (рис. 1), когда их края ориентированы произвольным образом относительно друг друга. В результате последовательного применения принципа Гюйгенса-Френеля дифракционное поле в точке наблюдения записывается в виде многократного интеграла Релея-Зоммерфельда. В полученном 2N-кратном интеграле проводится преобразование локальных систем координат, связанных с каждым препятствием. Это преобразование позволяет устранить зависимость пределов интегрирования от поперечных координат, что дает возможность вычислить N-мерный интеграл по данным переменным в явном виде с помощью многомерного метода стационарной фазы. Далее, после преобразований, основанных на свойствах матриц, исходный интеграл для дифракционного поля сводится к N-кратному интегралу, характерному для дифракции на последовательно расположенных препятствиях с параллельными краями

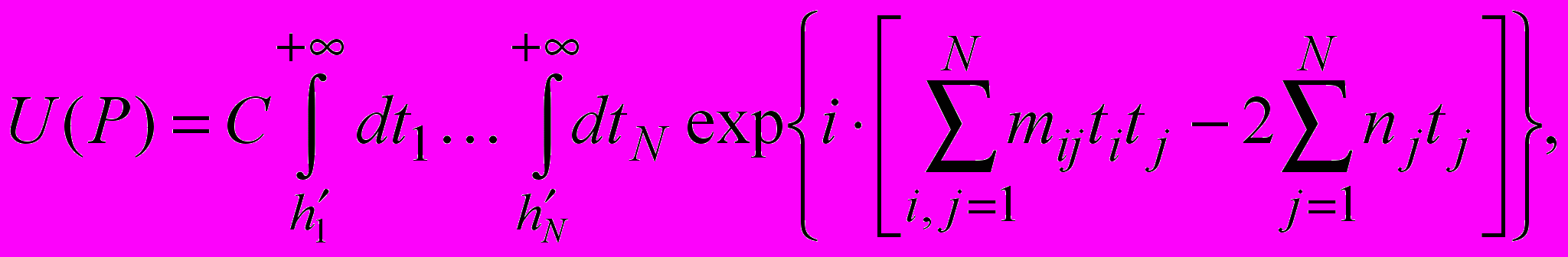(1)

Полученное выражение анализируется для случая двух препятствий. В этом случае поле можно вычислить с помощью однократного интеграла – обобщенного интеграла Френеля. Результаты численных расчетов на примере двух препятствий показывают, что для небольших закрытий (углов дифракции) зависимость от угла наклона краев выражена слабо, однако с увеличением закрытия данная зависимость резко возрастает. Установлено, что края полуплоскостей, перпендикулярные друг другу, не взаимодействуют между собой, а множитель ослабления поля в этом случае равен произведению множителей ослабления на одиночных препятствиях. При касательном распространении через две полуплоскости, края которых наклонены по отношению к горизонтали на углы α₁, α₂, для множителя ослабления получено следующее простое выражение

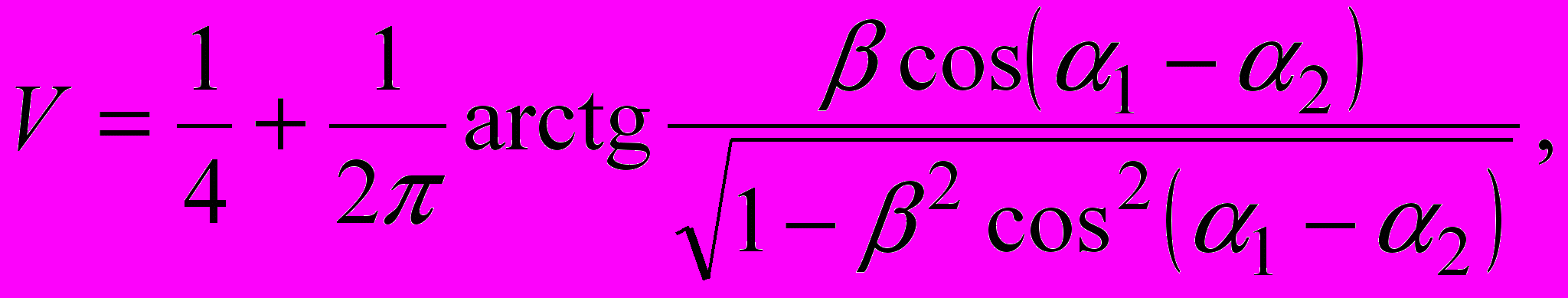(2)

где параметр β связан с расстояниями от источника до первого препятствия d₁, от первого препятствия до второго d₂ и расстоянием и от второго препятствия до точки наблюдения d₃ соотношением



На рис. 2 для примера показаны рассчитанные по этой формуле зависимости множителя ослабления от угла взаимной ориентации препятствий __ для различных значений  Из приведенных кривых следует, что наиболее заметно поле изменяется при близко расположенных друг к другу препятствий (большие ) и слабо зависит от  при разнесенных препятствиях (малые ).



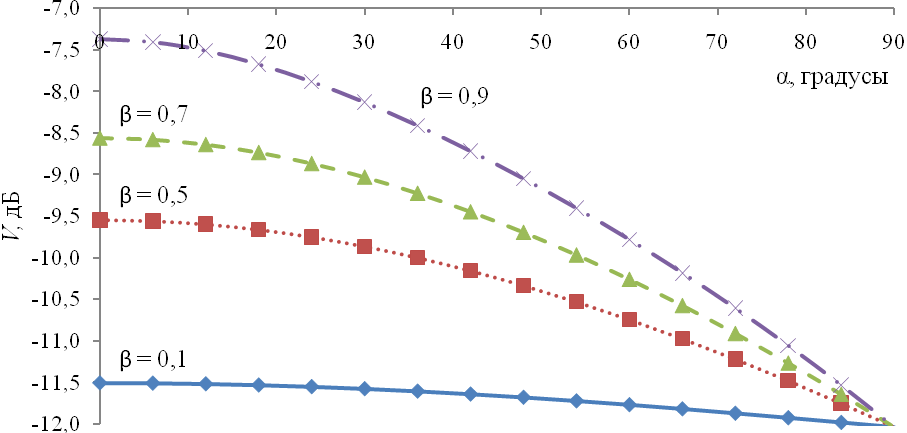
Рис. 2. Зависимость множителя ослабления от угла взаимной ориентации

Третий параграф главы посвящен рассмотрению методов вычисления многократных дифракционных интегралов типа (1). Сделан вывод, что лучшим методом вычисления, как по скорости расчёта, так и по получаемой точности результатов является метод Монте-Карло. Отмечается также, что данный метод является универсальным и пригоден для вычисления многократных интегралов, возникающих в задачах распространения радиоволн над земной поверхностью. В связи с этим в данной работе численные расчеты, связанные с вычислением многократных дифракционных интегралов, проводились методом Монте-Карло.

В четвертом параграфе главы рассматривается применение теории дифракции Френеля–Кирхгофа и метода параболического уравнения для прогнозирования поля на кусочно-плоских и кусочно-однородных трассах с клиновидными препятствиями. Модель трассы показана на рис. 3.

Для поля в точке В получено

, (3)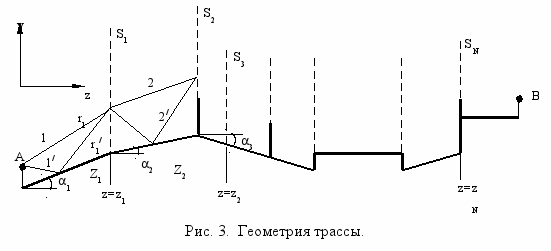


где поле U₁ на S₁, как это показано на рис. 3, является результатом интерференции прямого луча 1 и отраженного луча 1^/

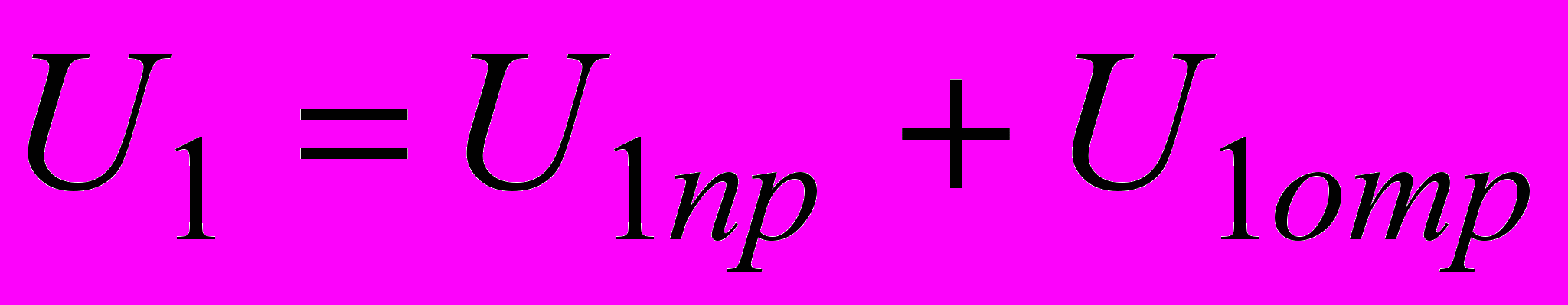, (4)

где

, .

Для коэффициента отражения f₁ при вертикальной поляризации используем следующее выражение, справедливое при произвольной высоте

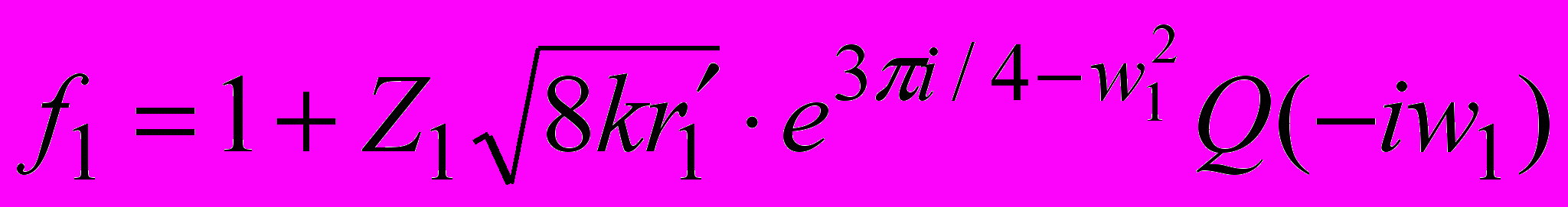, (5)

где - численное расстояние, ₁ – угол скольжения, , Z₁ - импеданс земной поверхности на первом участке.

В качестве функции Грина G_j будет выступать поле, которое точечный источник, расположенный в текущей точке плоскости S_j создал бы в текущей плоскости S_j+1 (в точке В при j = N)

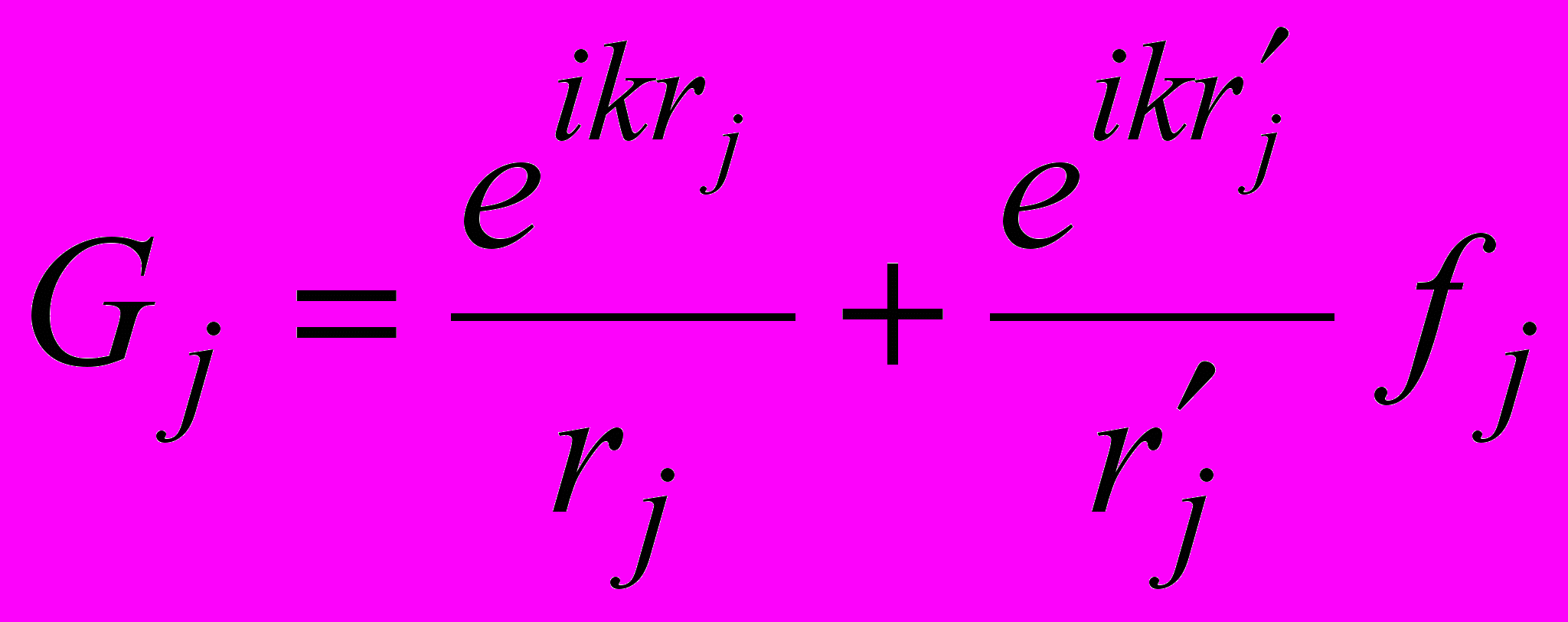, (6)

где - коэффициент отражения на j-ом участке, 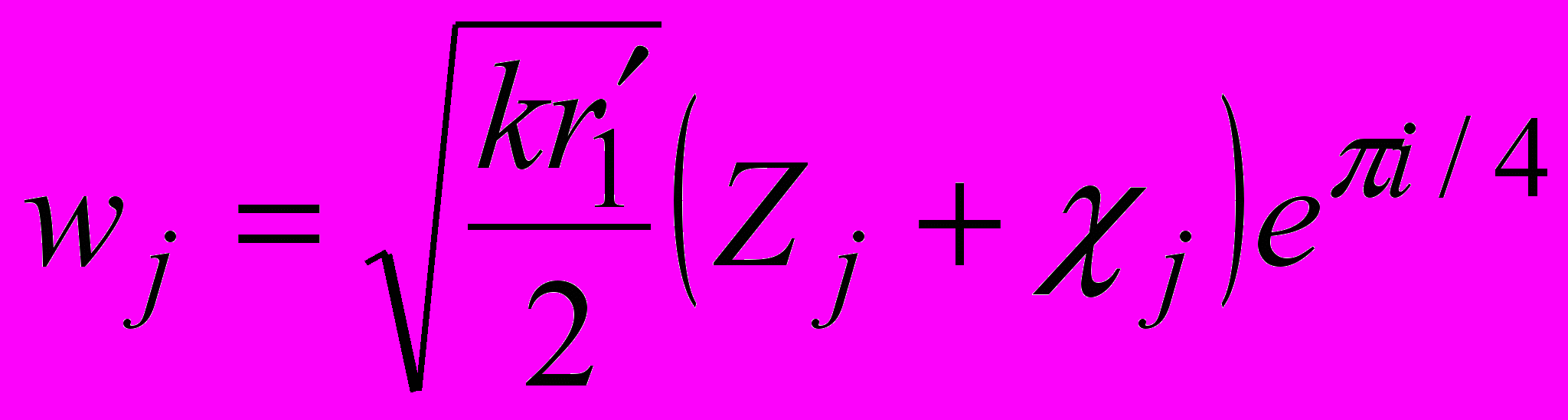- численное расстояние на j-ом участке, _j – соответствующий угол скольжения, Z_j - импеданс земной поверхности на j-ом участке,

В результате выражение (3) примет вид

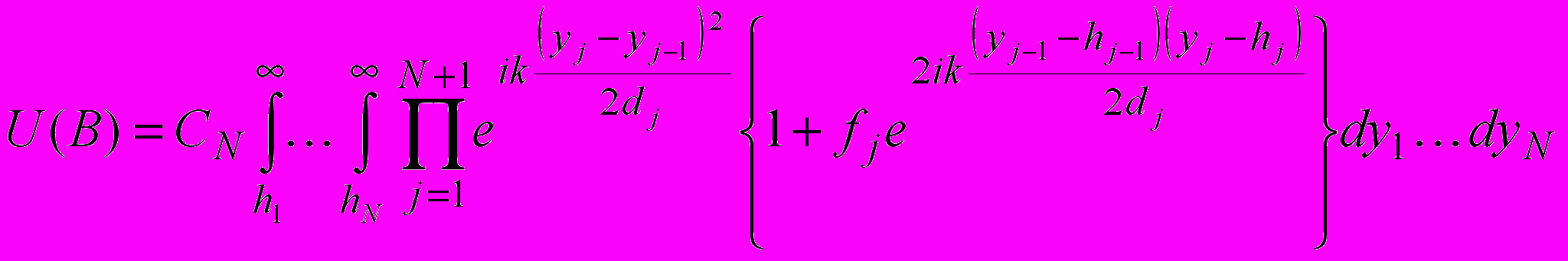, (7)

где

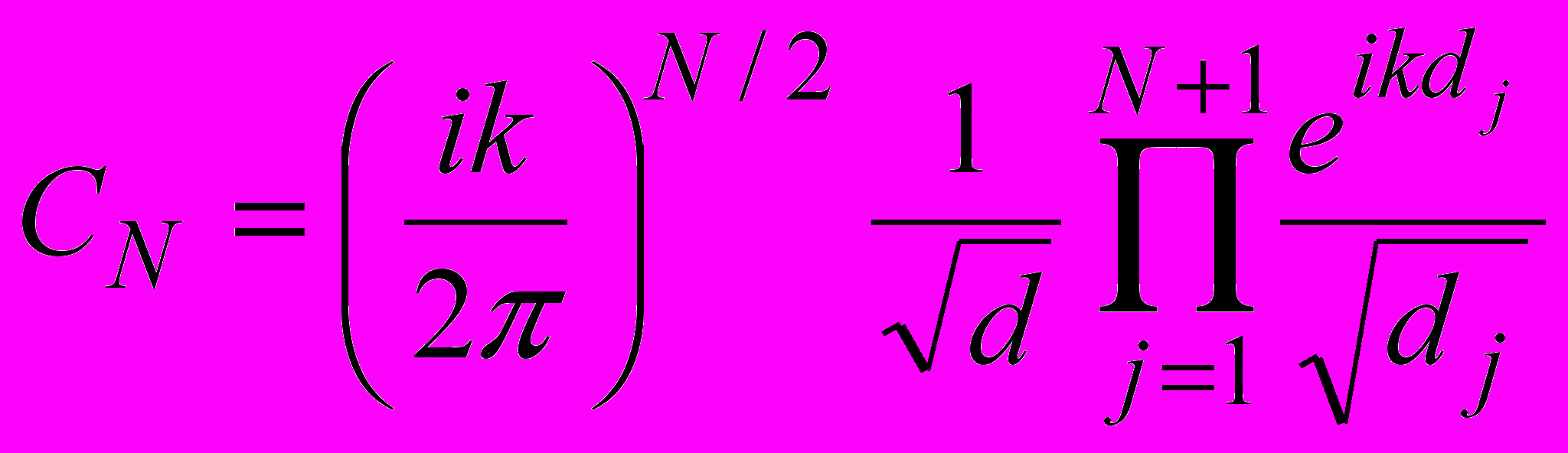, а .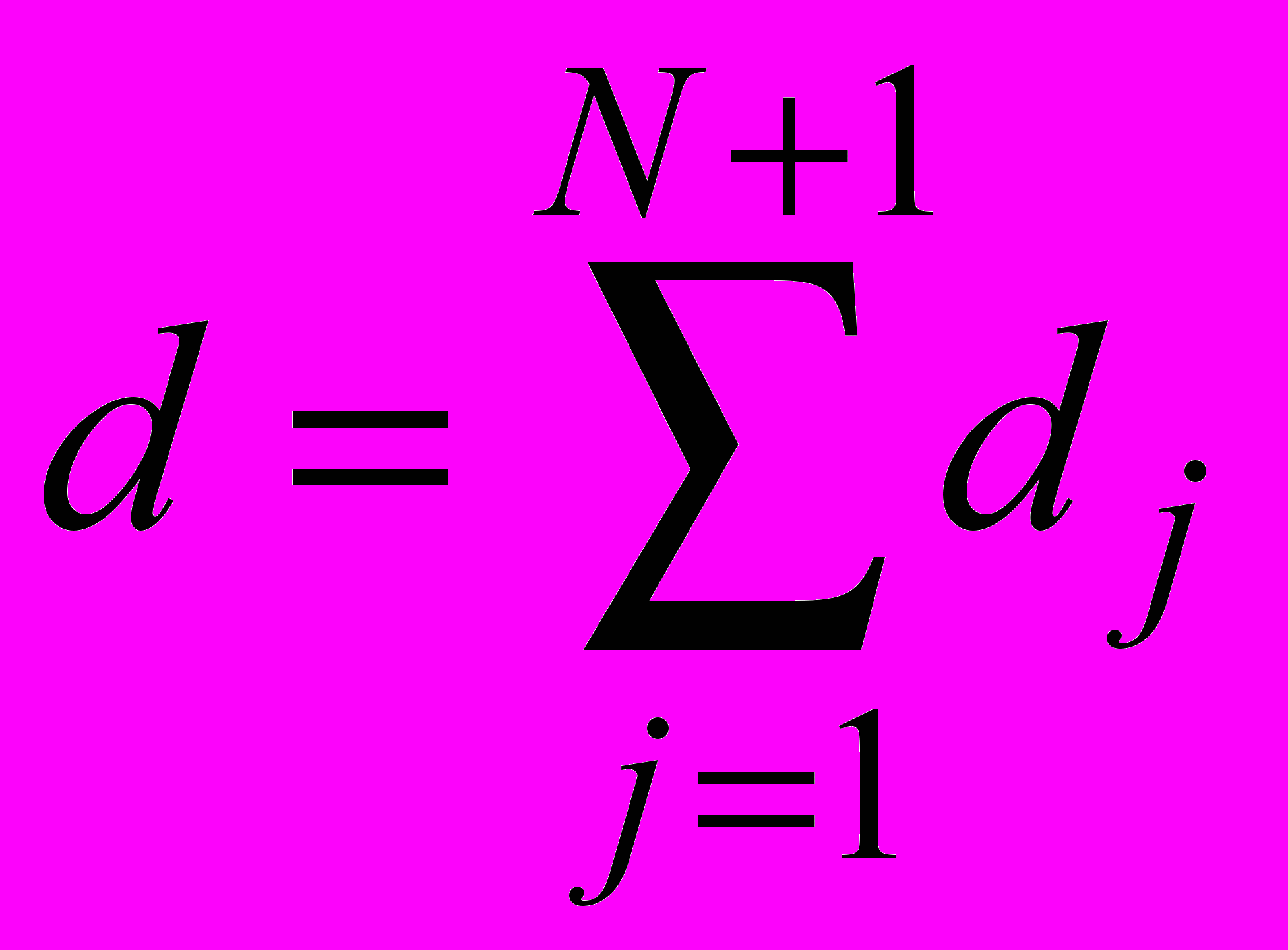

Выражение (7), таким образом, описывает поле на кусочно-плоской и кусочно-однородной трассе. Если выполнить умножения в интеграле (7), он распадается на сумму 2N+1 интегралов, представляющих собой гюйгенсовские волны, испытавшие различное число отражений от подстилающей поверхности - от отсутствия отражений до N отражений. Можно сказать, что выражение (8) представляет собой обобщенную 2N+1 – лучевую трактовку процесса распространения по аналогии с известной 4-х лучевой трактовкой дифракции на одиночном клиновидном препятствии, расположенном на земной поверхности. Интеграл (7) можно вычислить только численными методами и, очевидно, при этом нет необходимости проводить умножение, тем более при увеличении числа участков быстро увеличивается число членов в сумме. Этот интеграл аналогичен интегралу (1) и для его вычисления можно использовать метод Монте-Карло.

Метод параболического уравнения (МПУ) является эффективным методом решения задач распространения волн, нашедшим применение в различных областях физики. В последние годы он нашел широкое применение, в основном за рубежом, для расчета поля радиоволн в неоднородной атмосфере и трасс с нерегулярным рельефом. Рассмотрим применение МПУ к расчету поля на кусочно-плоской и кусочно-однородной трассе и сравненим решения с результатом, полученным с помощью метода Френеля-Кирхгофа. Полагаем далее, что множитель ослабления V в малоугловом приближении на каждом из участков удовлетворяет параболическому уравнению


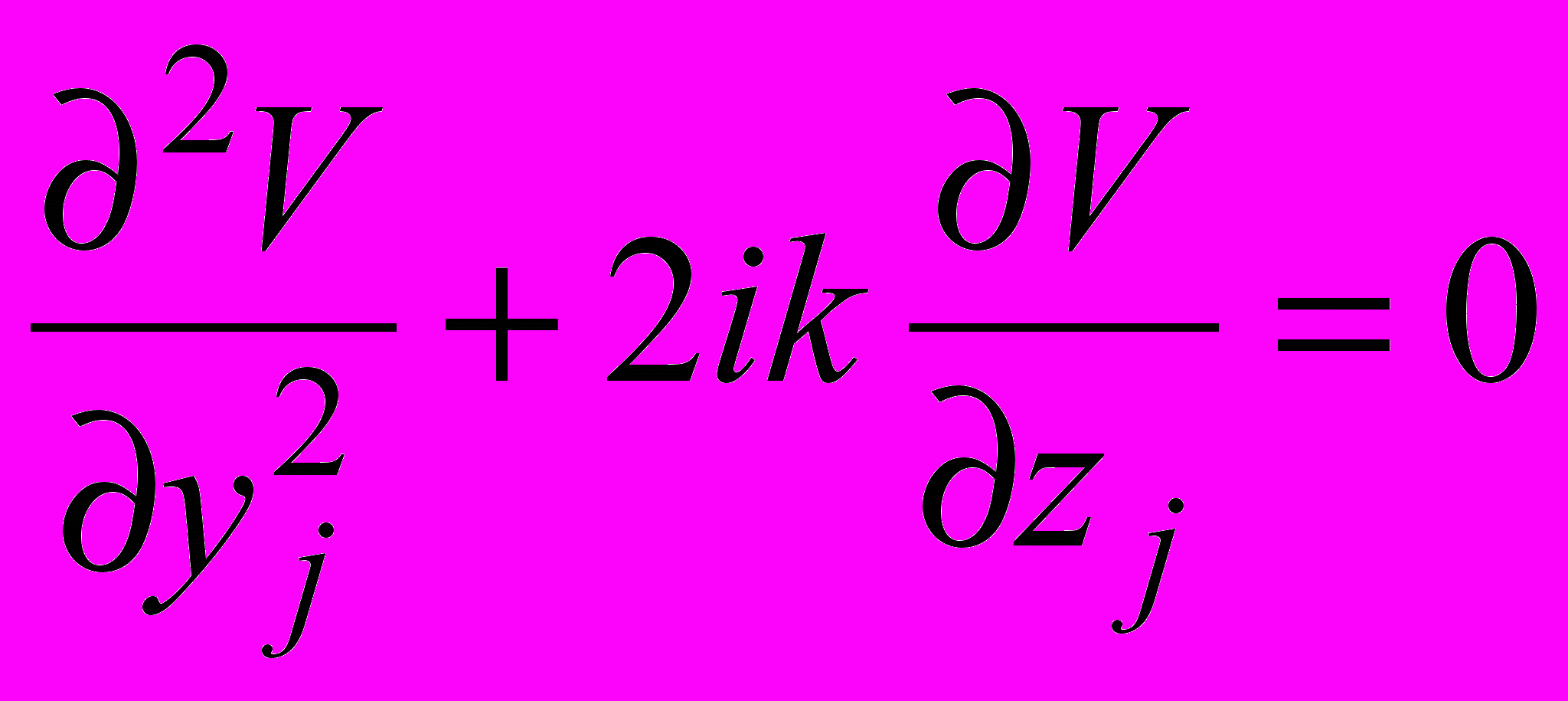, (8)

и импедансному граничному условию

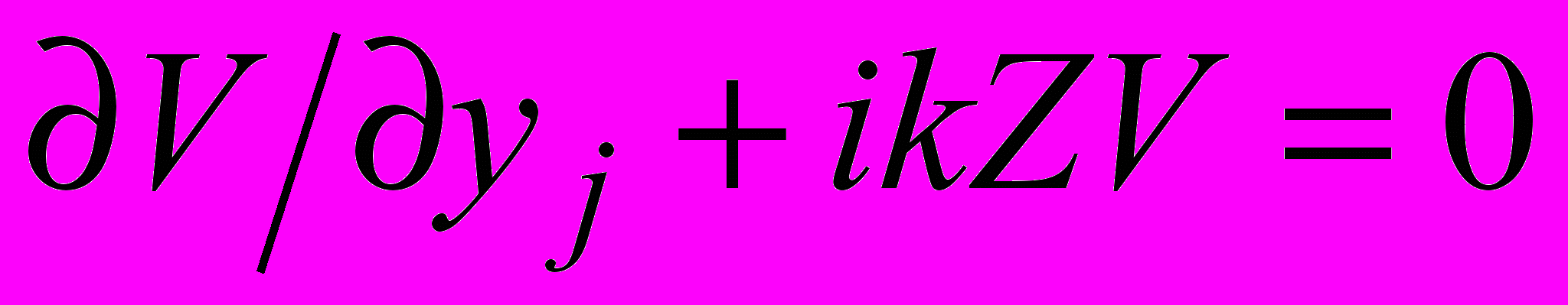, при y=0, (9)

где y_j z_j, – местные декартовы координаты на j-ом участке; точка (0, 0) совпадает с началом участка, а ось z_j лежит на j-ой границе раздела, геометрической или электрической.

Пусть решением уравнения (8) над первым участком является функция V₁(y₁, z₁). Пренебрегаем рассеянием от излома и в качестве начального распределения функции f(y₂)=V₂(0,y₂) на втором участке при y₂  0 можно взять распределение функции V₁(x₁, y₁).на оси y₂, а начальное распределение для y₂ 0 найти из соотношения:

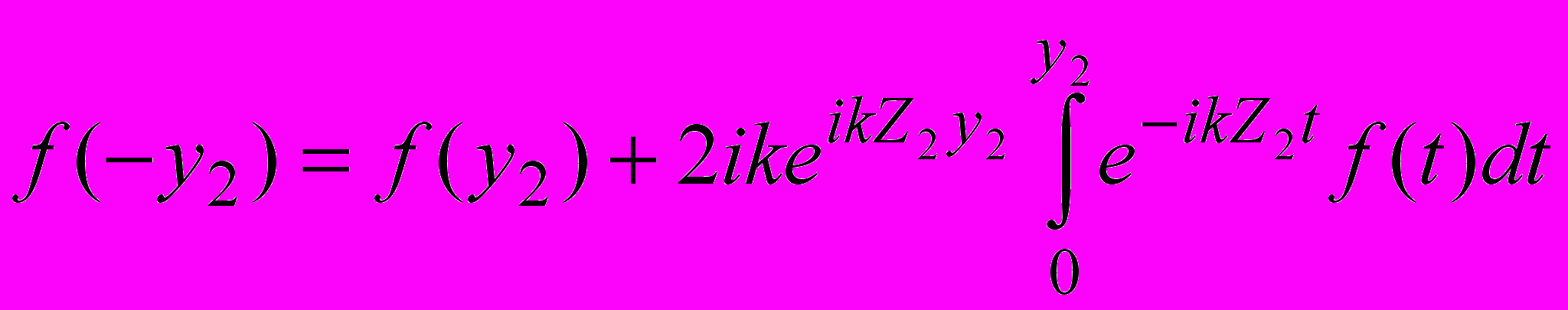(10)

Множитель ослабления на втором участке имеет вид:

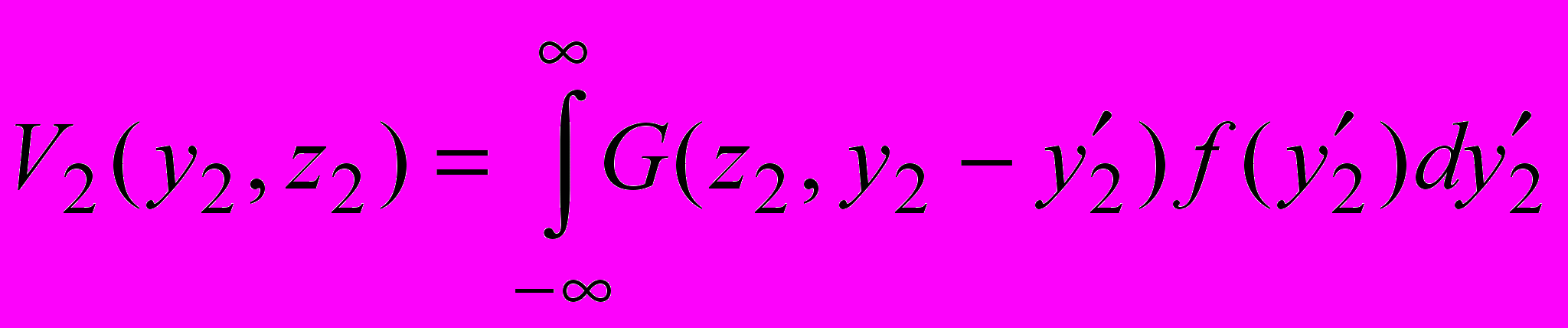, (11)

где .

В качестве функции f(y₂)=V₂(0,y₂)=V₁(x₁(y₂),y₁(y₂))=V₁(y₂) возьмем нормальную функцию ослабления для поднятого источника. Тогда

(12)

Продолжая эту процедуру, получим поле над N-ым участком в виде суммы многократных интегралов, которая эквивалентна формуле, основанной на теории дифракции Кирхгофа-Френеля.

В пятом параграфе главы рассмотрена задача дифракции волн на прямоугольном импедансном выступе и прохождение радиоволн через ограниченный лесной массив. Рассматривается модель распространения радиоволн на смешанной трассе, учитывающая лучи, распространяющиеся через лес. Впервые рассмотрен механизм распространения посредством боковой волны от гюйгенсовских источников. Приводятся результаты экспериментальных исследований распространения радиоволн через ограниченный лесной массив на длине волны 0,5 м. Геометрия модели показана на рис. 4, где изображены все возможные пути распространения.

_{Н
а рис. 5 приведены расчетные и экспериментальные зависимости}




Рис. 5. Зависимости уровня поля от расстояния. Высота передатчика 16 м. Горизонтальная поляризация.


В шестом параграфе рассмотрено влияние тропосферы на дифракционное поле клиновидного препятствия. Анализируется влияние тропосферной рефракции в приближении эквивалентного радиуса Земли. Показано, что рефракционные колебания уровня уменьшаются с увеличением высоты препятствия (угла дифракции). Здесь же решается задача о дифракции на клиновидном препятствии, над которым расположен отражающий тропосферный слой (рис. 6). Для решения задачи использован метод геометрической теории дифракции (ГТД). На рис. 6 показаны геометрооптические и дифракционные лучи, возникающие в данной задаче. Результирующее поле в точке, согласно ГТД имеет вид:

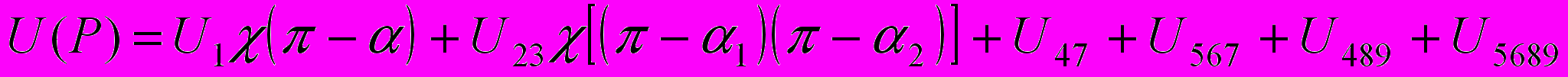, (13)

где 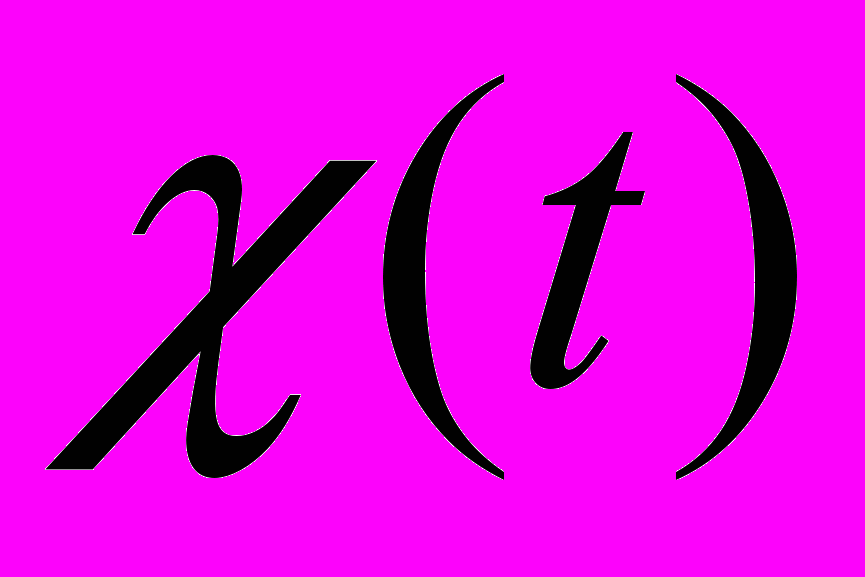– единичная функция Хевисайда, индексы показывают последовательный путь лучей.

В работе получены явные выражения для полей, входящих в формулу (13). Сравнение расчетных результатов с экспериментальными данными, полученными при модельных измерениях, показывает их хорошее соответствие.




Рис. 6. Геометрия задачи

Во второй главе рассмотрена трехмерная дифракция Френеля-Киргофа на клиновидных препятствиях, имеющих неровные края произвольной формы.

В первом параграфе рассмотрена дифракция сферической волны. Край препятствия аппроксимируется кусочно-линейной функцией (рис. 7), вписанной в реальную кривую края препятствия, полученную из фактических данных (из топографических карт или другими способами). Очевидно, при надлежащем выборе отрезков ломаной можно достаточно хорошо аппроксимировать любой неровный край. Аргументом в пользу такого выбора является также то обстоятельство, что края гребней реальных препятствий часто близки именно к ломаным линиям.

Установлен критерий неровности препятствия 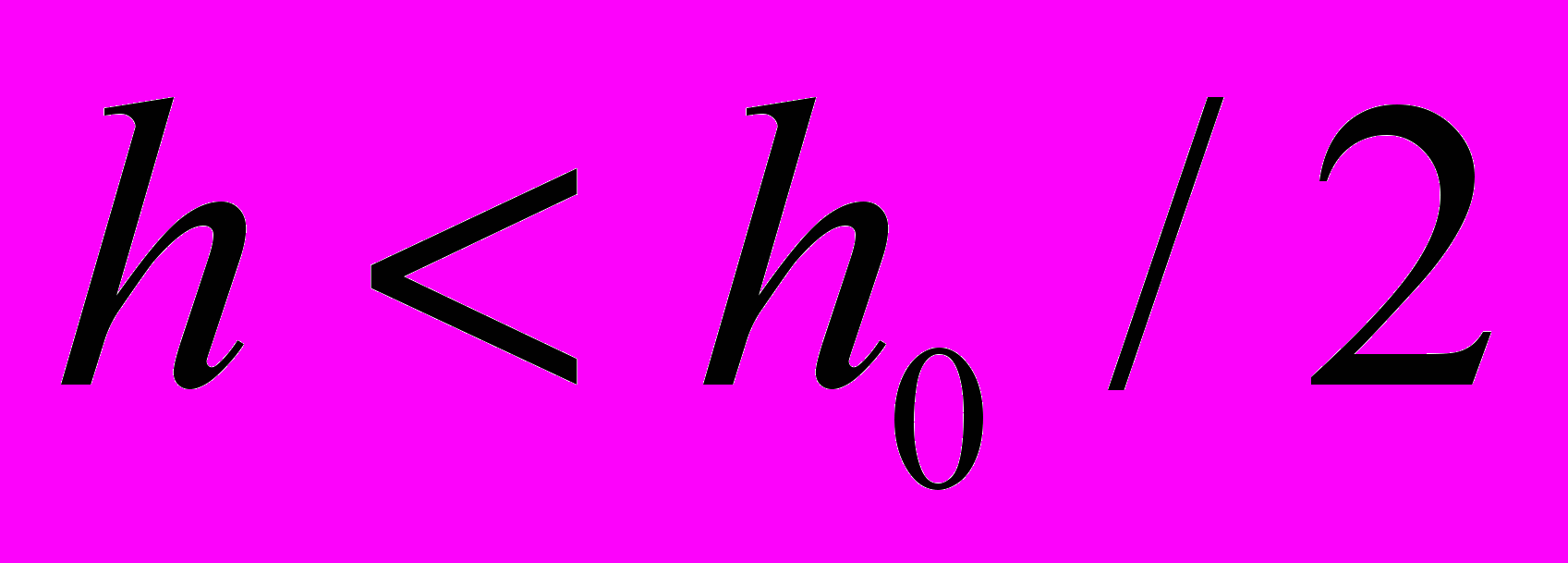,где h – размер неровностей, — размер зоны Френеля над гребнем препятствия.

Рис. 7. Аппроксимация гребня препятствия



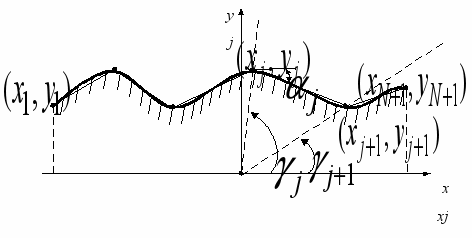
Получено следующее выражение для множителя ослабления поля, рассеянного отрезком

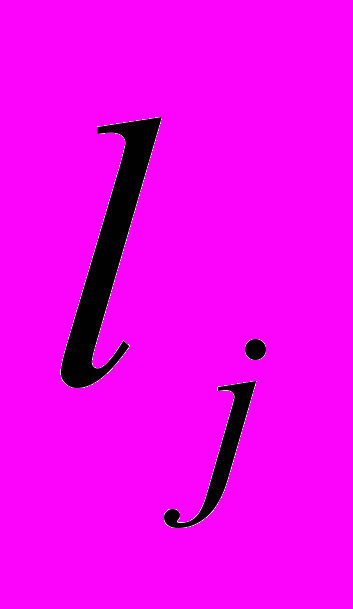
, (14)

где



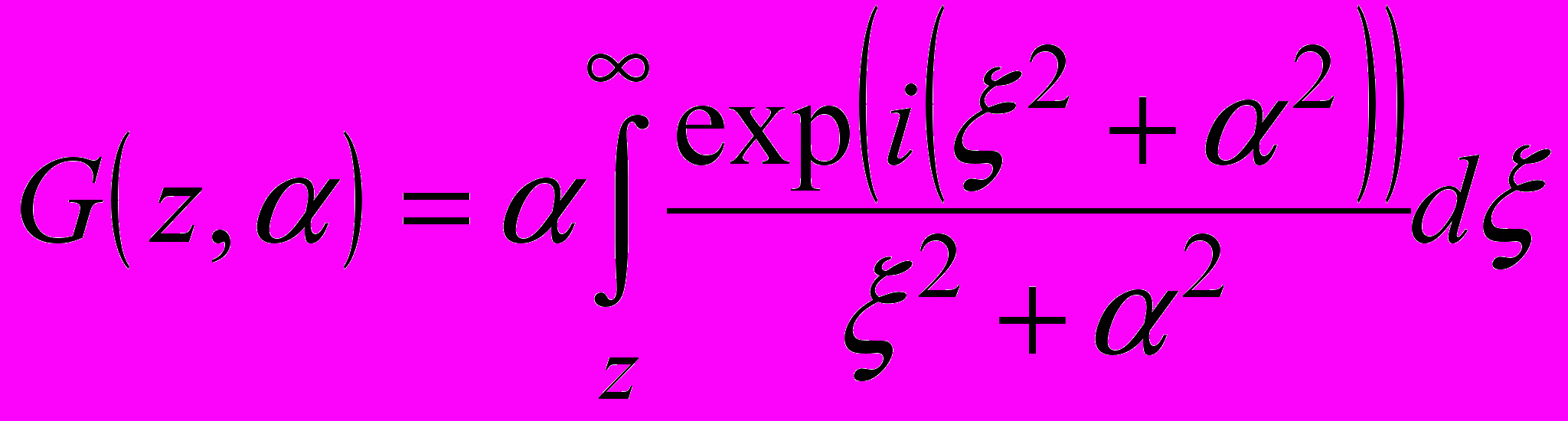
— обобщенный интеграл Френеля

Множитель ослабления V результирующего многолучевого поля за неровным препятствием получен как результат суммирования краевых волн, рассеянных всеми отрезками

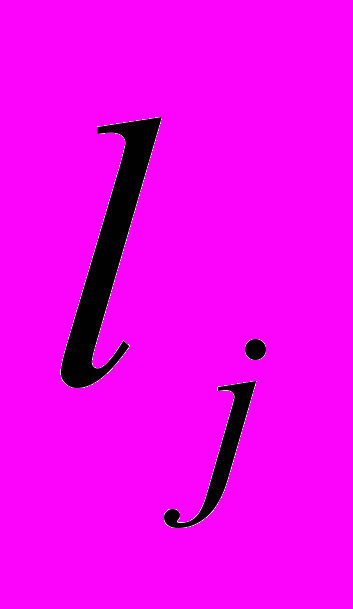
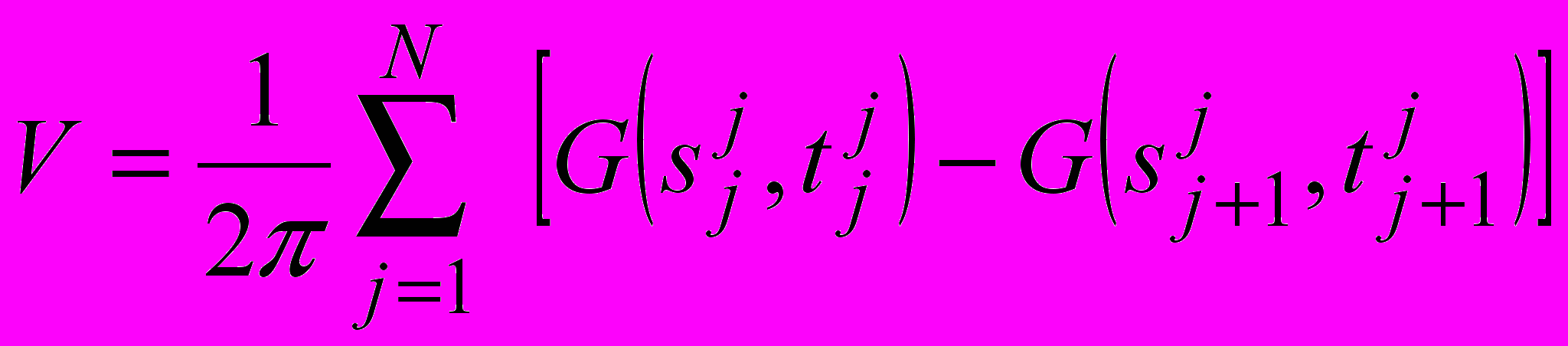(15)

Во втором параграфе главы оценивается влияние диаграммы направленности антенн в рамках предложенной выше модели многолучевого дифракционного распространения УКВ, основанной на аппроксимации гребня естественного препятствия кусочно-линейным краем. Геометрия задачи показана на рис 8.

Диаграмма направленности антенн представлялась в виде ряда по гауссовым функциям. Результирующее выражение имеет вид



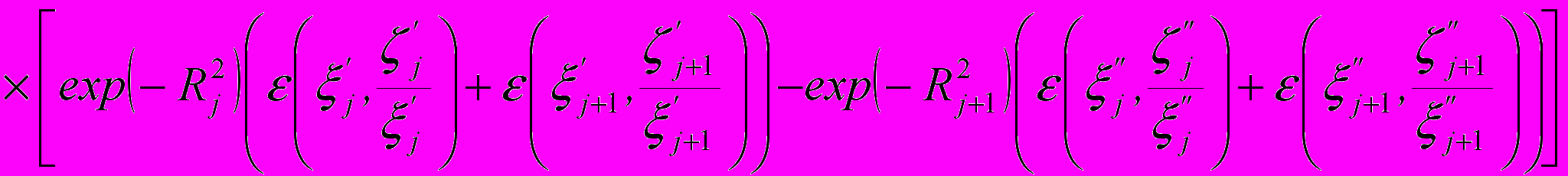(15)

где . – двумерный интеграл вероятностей.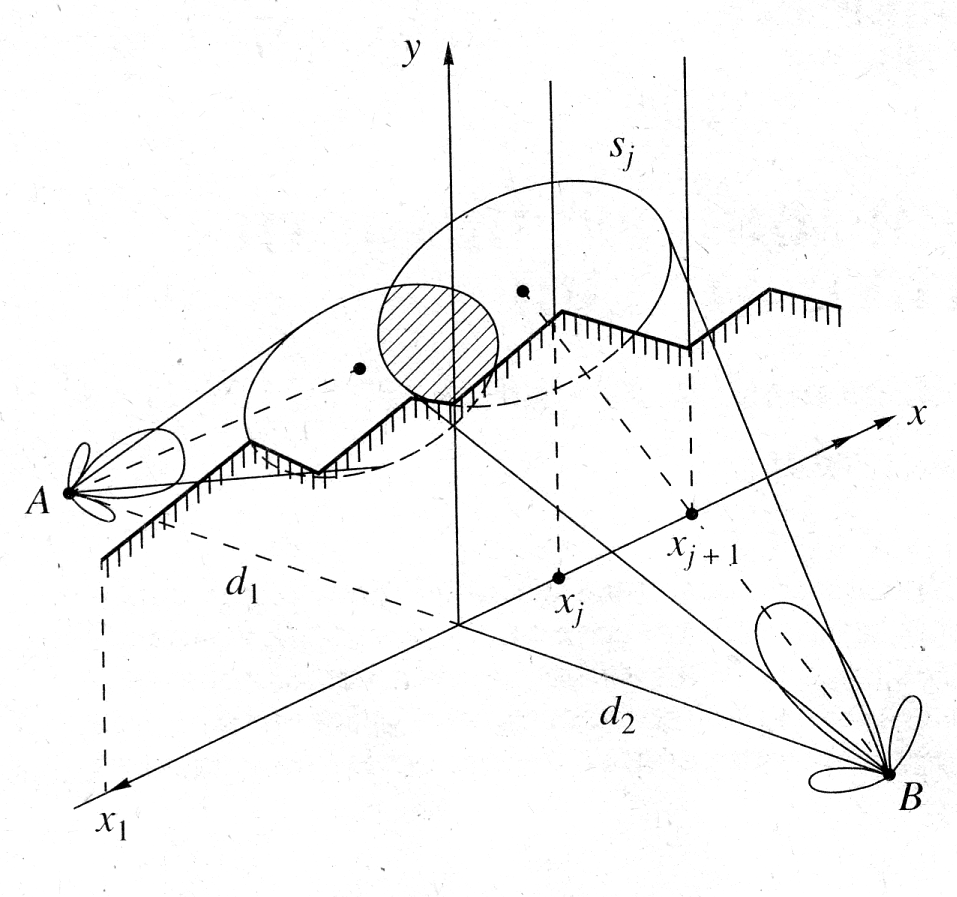



Рис. 8. Геометрия задачи о дифракции направленного излучения


Результаты сравнения расчетных и экспериментальных зависимостей приведены в главе 4.

Третья глава посвящена развитию теории граничных дифракционных волн в теории дифракции Френеля-Кирхгофа на классический случай однократной дифракции и многократной дифракции волн на нескольких последовательно расположенных препятствиях.


В первом параграфе главы приводится общие сведения о граничной волне и краткий обзор работ по этой проблеме.

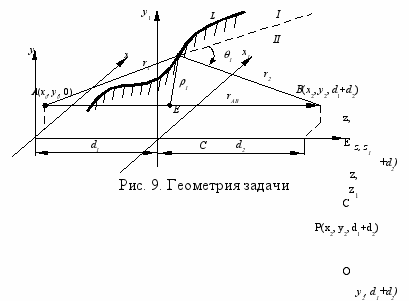
Во втором параграфе предложен новый, физически наглядный вывод выражения для граничной волны Юнга-Магги-Рубиновича в зоне дифракции Френеля. Предполагается, что край препятствия L может быть описан произвольной кусочно-гладкой функцией, имеющей кусочно-непрерывную первую производную. На рис. 9 показана геометрия задачи.

В приближении Френеля получено поле, рассеянное элементарным участком края (источником Юнга), при падении на край сферической волны

(16)

_{и, соответственно, поле всех гюйгенсовских источников}


(17)

где U₀ - поле, которое создает источник в точке наблюдения в отсутствии препятствия, , если между источником и точкой наблюдения есть прямая видимость и в противном случае.

Получено выражение для поля в случае края, заданного параметрическими уравнениями x = (t), y = y(t) (), которое имеет вид

. (18)

Приведены примеры применения полученного выражения для экранов с различной формой края и их сравнение с известными результатами.

В следующем, третьем параграфе впервые проведено обобщение понятия граничной дифракционной волны на случай многократной дифракции на нескольких препятствиях с произвольной формой краев. С этой целью вводится понятие амплитуды рассеяния dD_j на элементе края dl_j. Записывая волну, рассеянную на элементе первого препятствия в виде



где - падающая на край сферическая волна, из выражения (18) получим


(19)

После последовательного повторения процедуры для элемента края каждого препятствия получено выражение для поля многократной дифракции. Результирующее поле многократной дифракции имеет вид суммы геометрооптической волны и обобщенной граничной дифракционной волны U_g, которая в свою очередь является суммой граничных дифракционных волн различной кратности

(20)

Каждый член в сумме (7) описывает граничную дифракционную волну соответствующей кратности. Например, третий член в (7) дает волну, рассеянную последовательно всеми элементами dl_m, dl_n, dl_p при последовательном выполнении условий прямой видимости между источником А и элементом dl_m, элементами dl_m и dl_n, элементами dl_n и dl_p, элементом dl_p и точкой наблюдения В.

(21)

где выражения типа r_Aj и r_jl означают расстояния от точки А до элемента dl_j и от элемента dl_j до элемента dl_l, соответственно; обозначение представляет коэффициент дифракции на элементе dl_j при распространении сферической волны от точки А до точки В, а dD_mnp – коэффициент дифракции на элементе dl_n при распространении от элемента dl_m до элемента dl_p.

;

.

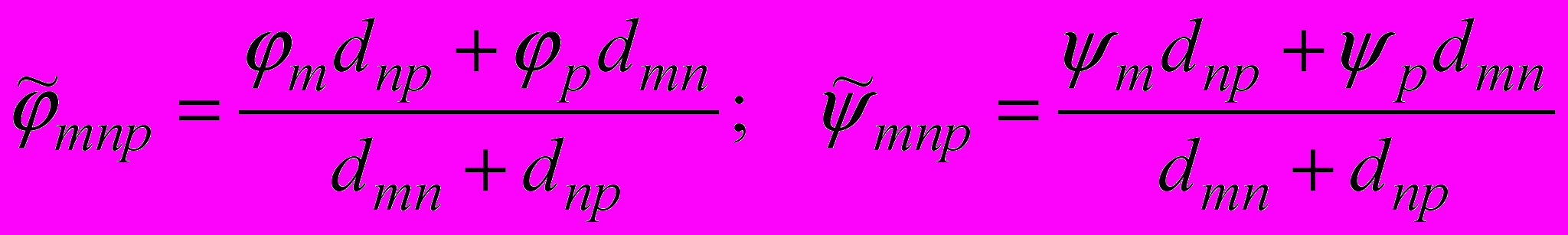Здесь d_ij означает расстояние по оси z между i-ым и j-ым препятствиями (экранами). Множитель ε_mnp в (8) описывает выполнение условия прямой видимости между соответствующими точками и элементами, он равен единице, когда эти условия выполняются и нулю в случае их невыполнения. Приведены условия отсутствия экранирования луча, распространяющегося между двумя точками, которые могут находиться как на краях препятствий, так и представлять собой месторасположение приёмника или передатчика. На рис. 10 в качестве примера показан процесс распространения волн для случая двух отверстий. Так, отрезок АВ показывает распространение прямой волны, ломаные Аdl₁B и Аdl₂B показывают путь, проходимый волнами, однократно дифрагировавшими на крае первого и второго отверстий соответственно, а ломаная Аdl₁dl₂B – показывает распространение волны, последовательно дифрагировавшей на каждом крае.



Рис. 10. Распространение граничных волн различной кратности для случая двух отверстий.

Таким образом, дифракционное поле за препятствиями имеет вид суммы многократных криволинейных интегралов с максимальной кратностью равной числу препятствий. Данный подход позволяет в два раза снизить кратность дифракционного интеграла по сравнению с интегралом, получаемым обычным применением теории Френеля-Кирхгофа.

В четвертом параграфе главы рассмотрен случай, когда край каждого препятствия аппроксимируется кусочно-линейной функцией, описывающей его реальный профиль. Число звеньев кусочно-линейной функции необходимо выбирать таким образом, чтобы обеспечить необходимую точность расчета. Получено выражение для амплитуды рассеяния в этом случае. Полное поле в точке наблюдения определяется суммой полей, переизлученных каждым отрезком каждого края. В предельном случае, когда края вырождаются в прямые линии, получается решение задачи, рассмотренное в предыдущей главе. Последнее более удобно для асимптотической оценки при больших закрытиях, так как пределы интегрирования по всем переменным являются бесконечными и применение метода стационарной фазы в этом случае не вызывает затруднений.

Рассмотрены частные случаи применения общей формулы к задачам дифракции на одном и двух препятствиях с кусочно-линейной границей. В случае одного препятствия формула совпадает с выражением, полученным ранее с помощью формулы Френеля-Кирхгофа.

В пятом параграфе приведены результаты экспериментальных исследований и сравнение с расчетных и измеренных зависимостей. Проведённые экспериментальные исследования на частоте 30 ГГц (l=0,01м) на системе из двух последовательно расположенных круговых и эллиптических отверстий в непрозрачных экранах (рис. 11, 12) подтверждают справедливость предложенного метода. Численное моделирование с помощью метода Монте-Карло показывает, что данный метод обеспечивает многократный выигрыш по времени вычислений по сравнению с методом интегрирования по апертурам.

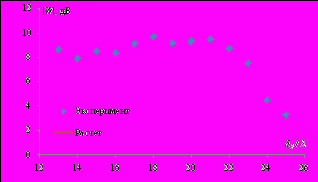Рис. 11. Зависимость множителя прохождения от расстояния между двумя круговыми отверстиями. d1=9,3l; R1= R2=2,5l.

Рис. 12. Зависимость множителя прохождения за двумя эллиптическими отверстиями поперёк направления распространения. d1=10l, d2=8l, d3=10l. A1=A2=4l, B1=B2=2l.