Моделирование дифракционного распространения волн и структура поля радиоволн увч и свч на нерегулярных трассах

Вид материала

Подобный материал:

1 2 3

В четвертой главе представлены результаты экспериментального исследования пространственно-временной структуры поля УКВ на дифракционных трассах протяженностью 5 – 113 км на длинах волн от 8 см до 74 см. На ряде трасс были проведены исследования искажений диаграмм направленности и поляризационные зависимости сигнала.

В первом параграфе главы рассмотрена пространственная структура поля. Пространственные флуктуации поля носит различный характер в зависимости от конкретной трассы и частоты излучения. На рис. 13 приведены примеры пространственного распределения относительных уровней поля на длине волны 11 см. Здесь же показаны продольные профили трасс. Кривые получены при непрерывном перемещении приемной антенны в горизонтальной плоскости перпендикулярно линии трассы (поперечные разрезы) при горизонтальной поляризации.

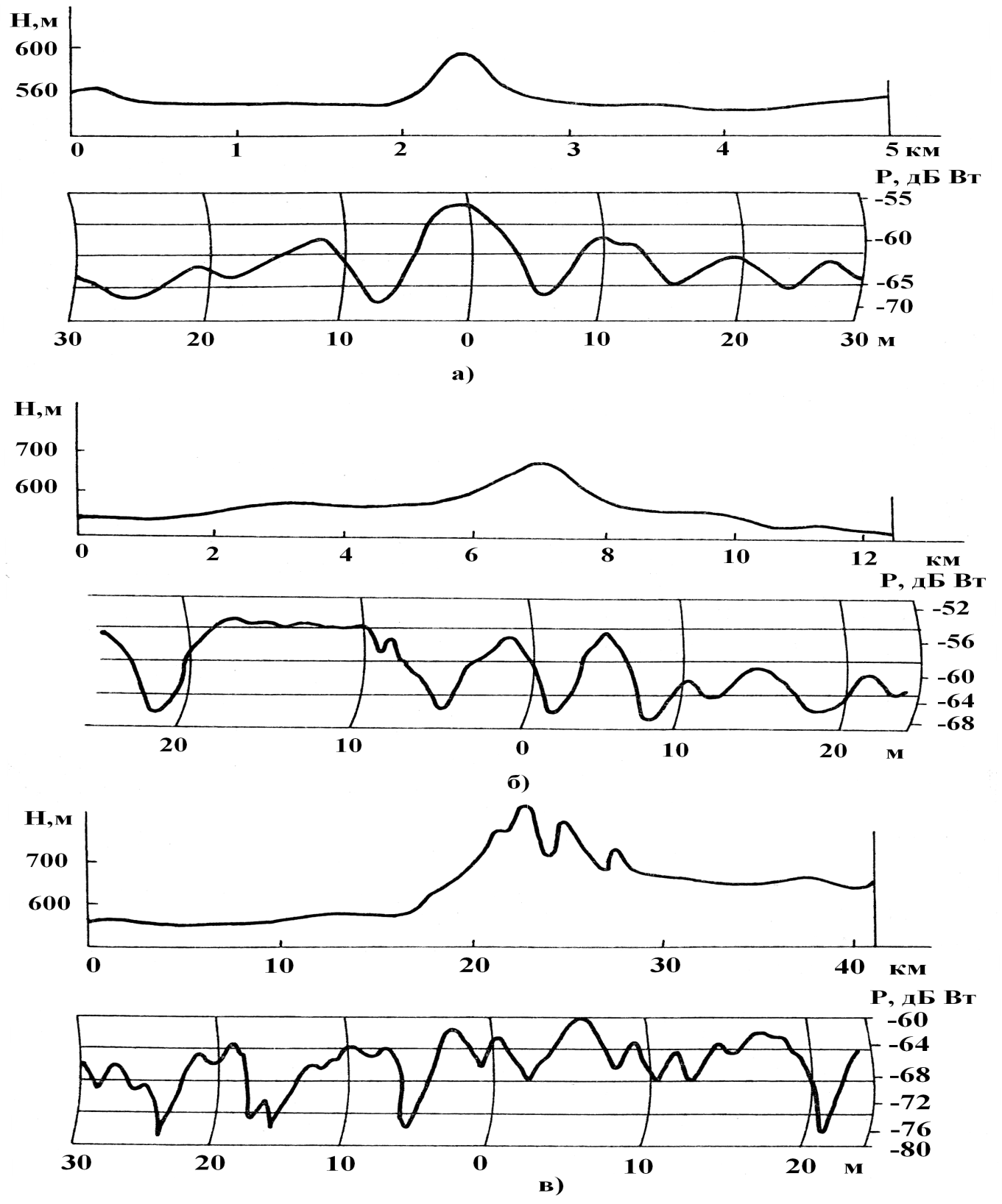
Рис. 13. Пространственная структура дифракционного поля на различных трассах

Р

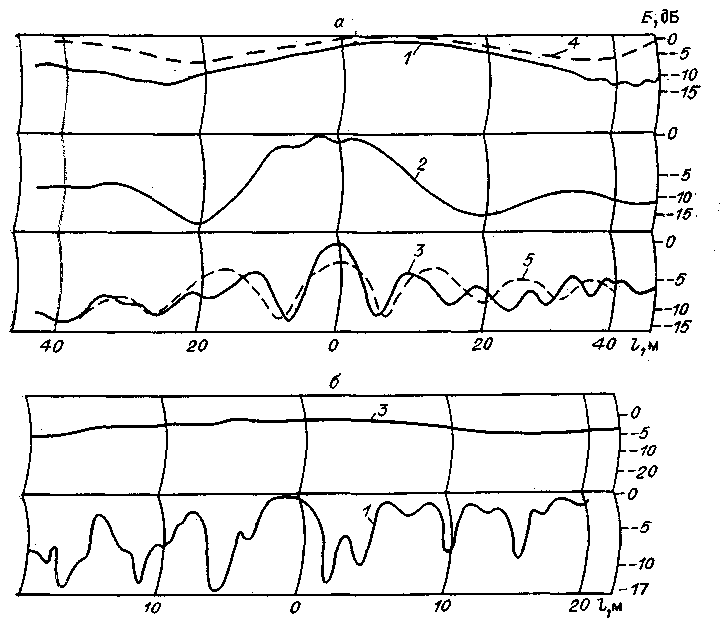
ис. 14. Примеры частотной зависимости пространственной структуры.

1 — λ = 11 см; 2 — λ = 44 см; 3 — λ = 74 см; 4, 5 — расчетные зависимости.

Из рис. 14 видно, что пространственная структура поля в теневой зоне существенно зависит от длины волны, причем влияние длины волны на формирование пространственного распределения поля в тени препятствия неоднозначно. Если на трассе 1 изменение несущей частоты сигнала вызывает только изменение квазипериодов пространственных флуктуации при увеличении или уменьшении их глубины, то на трассе 2 (профиль – рис. 13б) как следует из рис. 14б увеличение длины волны от 11 до 74 см приводит практически к полному исчезновению пространственной неоднородности поля.

На рис. 15 также показаны расчетные зависимости полученные с помощью результатов главы 3, которые показывают хорошее соответствие между ними и экспериментальных данными. Качественное соответствие расчетных и экспериментальных результатов видно также из рис. 15.

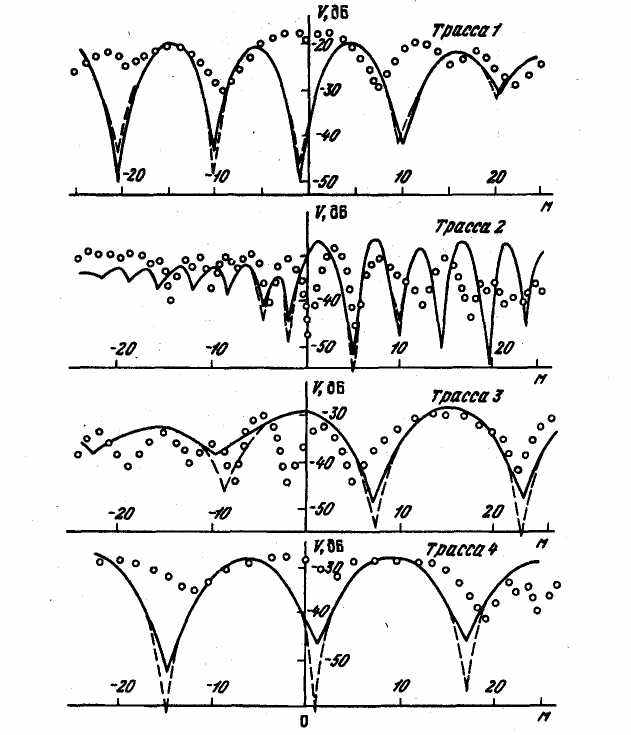
Рис. 15. Пространственная структура поля поперек трассы распространения

(λ = 11 см, кружки — эксперимент, сплошные линии — расчет, штриховые кривые — расчет по асимптотической формуле)

Во втором параграфе главы исследуются временные флуктуации уровня дифракционного поля. Пространственная картина дифракционного поля в тени естественных препятствий подвержена временным флуктуациям, причем изменяются не только уровни сигналов, но в общем случае и расположение максимумов и минимумов поля в пространстве.

На рис. 16 показан профиль двухвершинной трассы и обозначены точки, в которых проводились исследования, а на рис 17 приведены кривые устойчивости сигнала, полученные на этой трассе на волне с длиной 11 см. На данной трассе были обнаружены ранее неизвестные особенности в поведении дифракционного сигнала. Во-первых, было выявлено, что устойчивость сигнала на двухвершинной трассе А₀А₅ оказалась существенно выше, чем на одновершинной трассе А₀А₄, что позволяет говорить о некотором стабилизирующем действии второго препятствия А₄. Во – вторых, измерения на трассе А₀А₂ показали, что в точках пространственной структуры, где отмечается максимум и минимум уровня поля, разнесенных всего на 2 м наблюдается различное поведение сигнала.

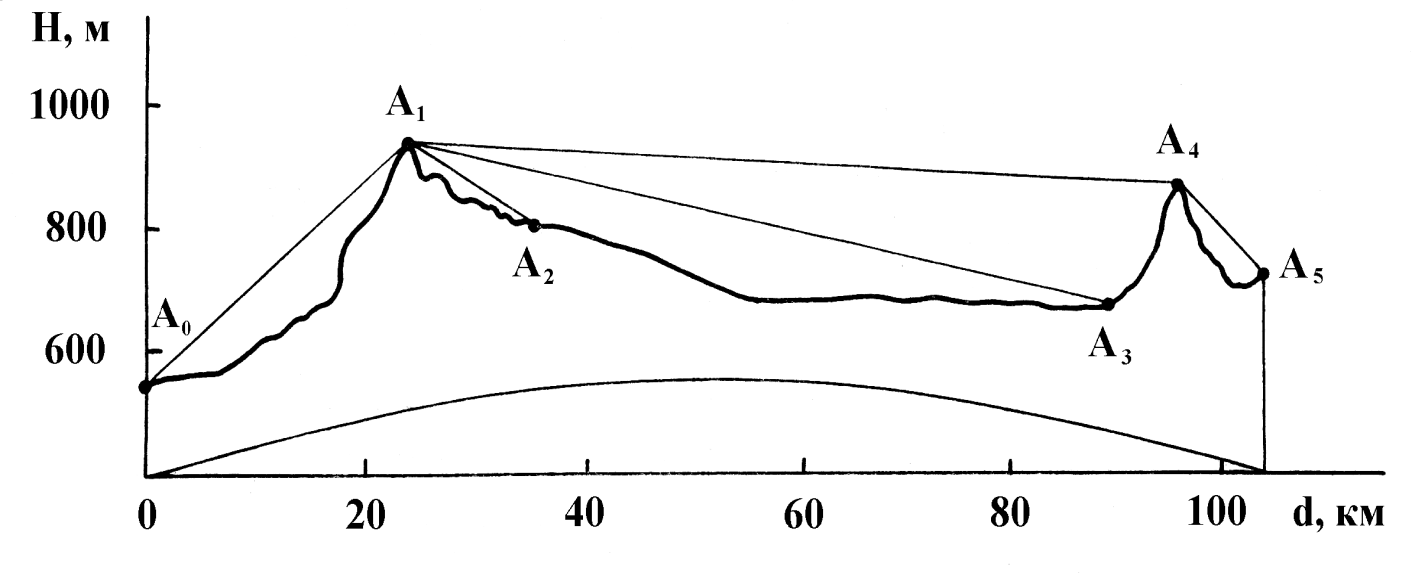
Рис. 16. Профиль двухвершинной трассы

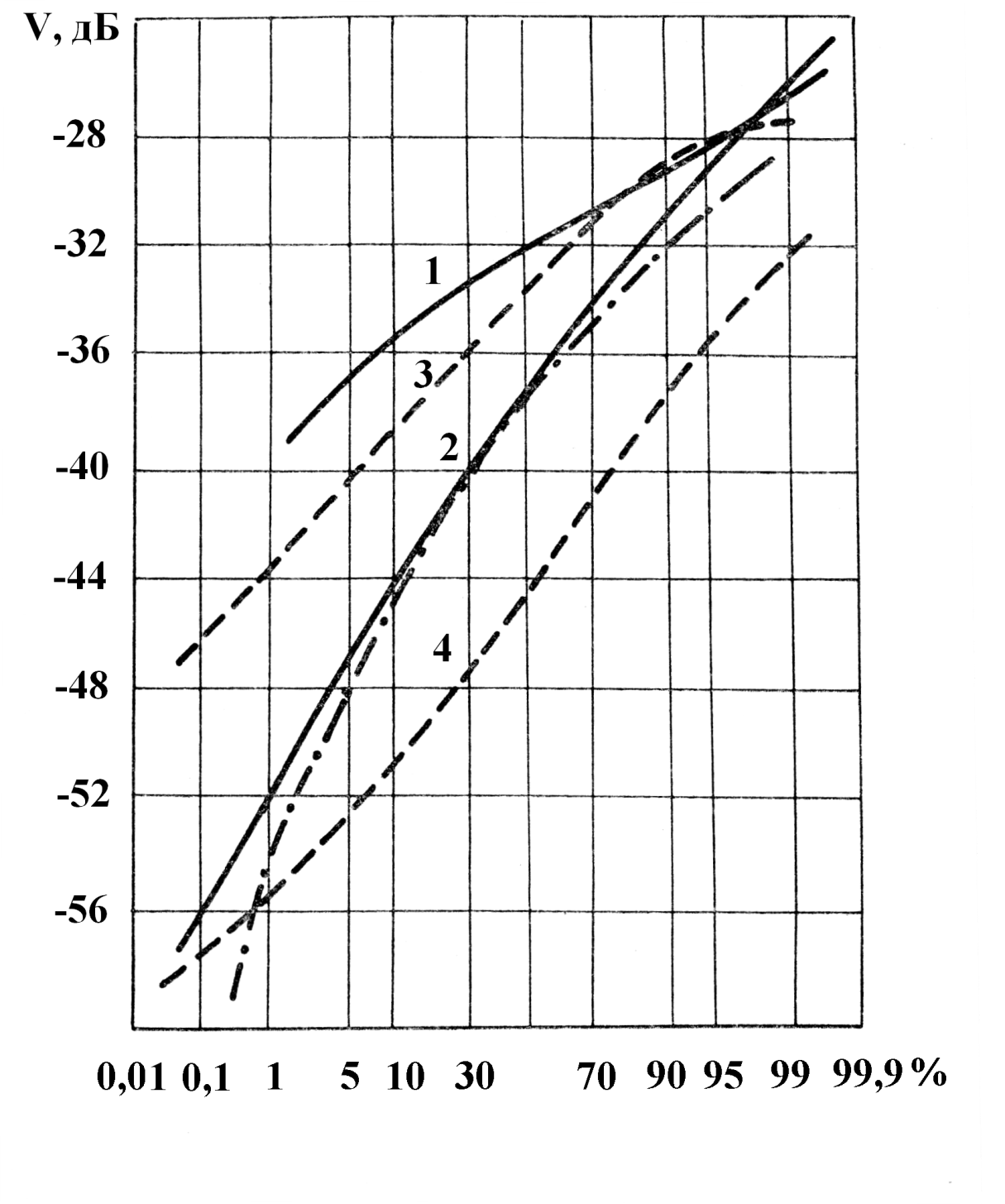
Рис. 17. Статистические распределения среднеминутных значений множителя ослабления поля на одновершинных участках трассы А₀А₅.

1 — А₁А₅, 523 ч записи; 2 — А₀А₄, 248 ч; 3 — А₀А₂ (в максимуме); 4 — А₀А₂ (в минимуме); 5 — закон Рэлея.

В параграфе 2 также приведены результаты исследований устойчивости сигнала на слабозакрытой трассе на длине волны 8 см, которые показали, что в этом случае на рапространение оказывает заметное влияние отражение от слоистых неоднородностей.

В третьем параграфе главы приведены результаты искажений диаграмм направленности антенн на дифракционных трассах. Измерения диаграмм направленности антенн в тени препятствий показывают сложную зависимость формы диаграммы от поперечного профиля препятствий и местоположения антенны. На рис. 18 для примера показаны диаграммы направленности, полученные на различных трассах в различных точках пространственной структуры поля. За нулевое направление принято истинное направление на излучатель.

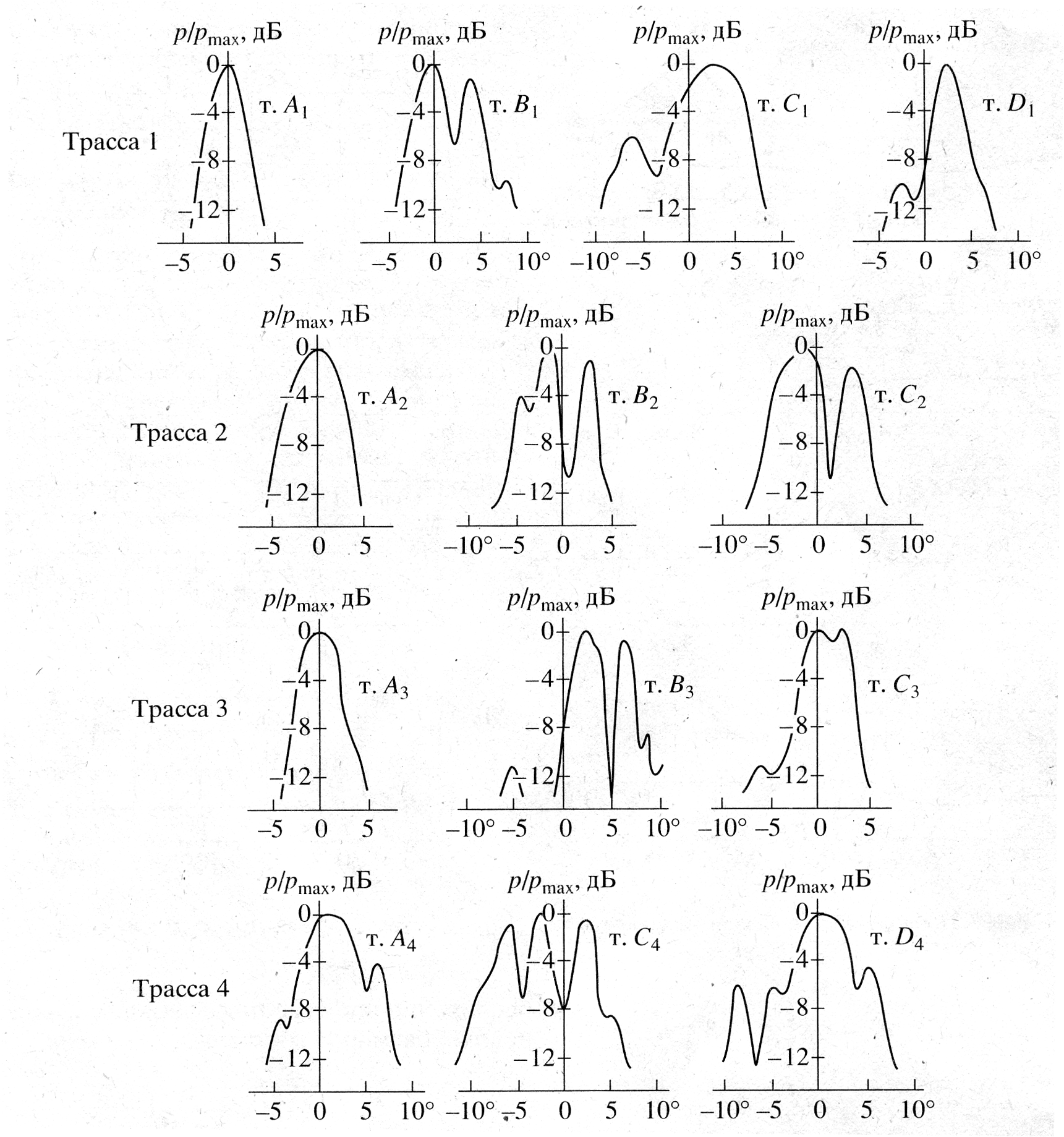
Рис. 18. Диаграммы направленности приемной антенны в различных точках пространственной структуры поля, λ = 11 см.

На рис. 19 показано сравнение расчетных и измеренных диаграмм направленности антенн, когда на трассе наблюдаются два выраженных луча.

Р

ис. 19. Расчетные и экспериментальные диаграммы направленности приемных антенн на трассе 9 в максимуме (кривые 1, 3) и минимуме (2, 4) поперечного разреза дифракционного поля. 1, 2 — расчет; 3, 4 — эксперимент.

В четвертом параграфе главы рассмотрены поляризационные зависимости сигнала. Измерения проводились на трассах небольшой протяженности от 5 км до 18 км с препятствиями рельефа в виде гор и холмов на волне длиной 11 см. Показано, на закрытых приземных трассах может наблюдаться значительная деполяризация как горизонтально и вертикально поляризованного сигнала. Обнаружено, что характер поляризационных зависимостей в значительной степени определяется особенностями препятствия.

Пятая глава посвящена изучению дифракционных экранов (дифракторов), с помощью которых можно регулировать дифракционное поле, а также новому подходу к решению классических задач дифракции на ленте и щели.

В первом параграфе анализируются условия ретрансляции и подавления сигнала, исходя из общей формулы для результирующего поля

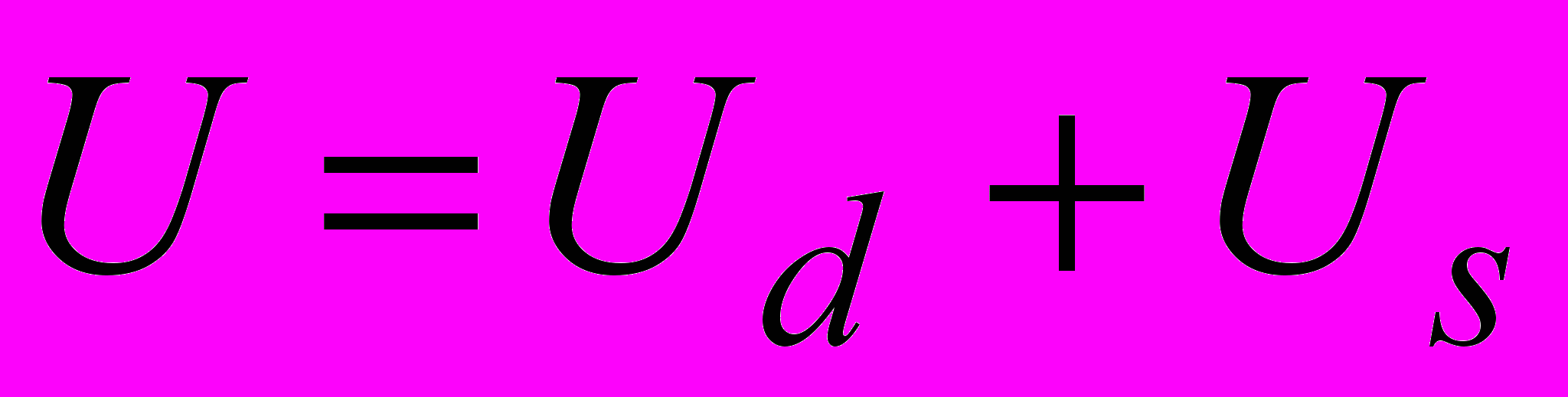, (22)

где U_d - дифракционное поле прямого прохождения, U_s - поле, рассеянное экраном.

Н

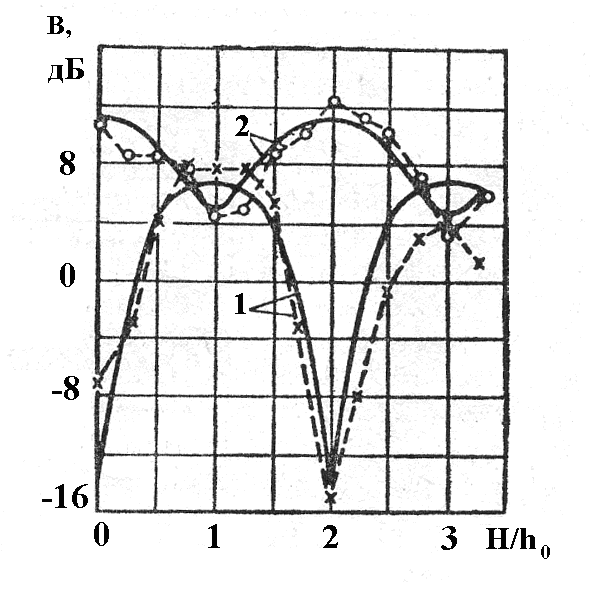
а рис. 20 приведены экспериментальные зависимости относительного изменения поля B на дифракционной трассе при установке дифрактора на

Рис. 20. Зависимости уровня поля на трассе с дифрактором от относительной величины зазора. Кружки, крестики – эксперимент, сплошные кривые – теория.

гребне экранирующего препятствия. Здесь же сплошными кривыми представлены расчетные зависимости. Как видно из рисунка, кривые хорошо согласуются между собой.

Второй параграф главы посвящен разработке метода уменьшения отражений от земной поверхности с помощью последовательных дифракционных экранов. Получены формулы, позволяющие рассчитывать коэффициент отражения от земной поверхности с установленными на ней экранами в зависимости от их геометрических характеристик и места их раположения.

Третий параграф главы посвящен новому подходу в рамках теории Френеля-Кирхгофа к задаче дифракции электромагнитных волн на идеально проводящих ленте и щели, которую обычно относят к числу так называемых эталонных задач теории дифракции. При скользящем распространении лента не создает тени и при обычном подходе волна не «видит» ее.

Суть предлагаемого метода состоит в введении двух дополнительных плоскостей S₁ и S₂(рис. 21), проходящих через образующие ленты и параллельных друг другу. Согласно принципу Гюйгенса-Френеля поле в точке В определяется суммарным воздействием всех гюйгенсовых источников на S₂. В свою очередь поле в текущей точке P₂ плоскости S₂ равно сумме полей всех гюйгенсовых источников на плоскости S₁ с учетом влияния ленты. Для учета этого влияния используется принцип зеркального изображения, согласно которому вводится зеркальное изображение P₁^*источника P₁.

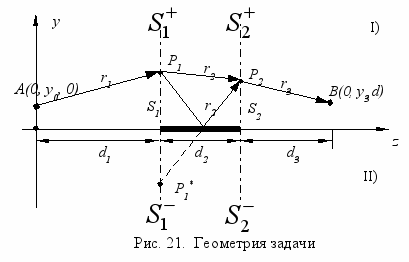
Записывая интеграл Кирхгофа отдельно для части пространства над и под лентой и используя приближение Френеля, получаем выражение для дифракционного поля в приемной точке В. Последнее, после интегрирования по поперечным координатам и ряда упрощений, приводит к следующему выражению

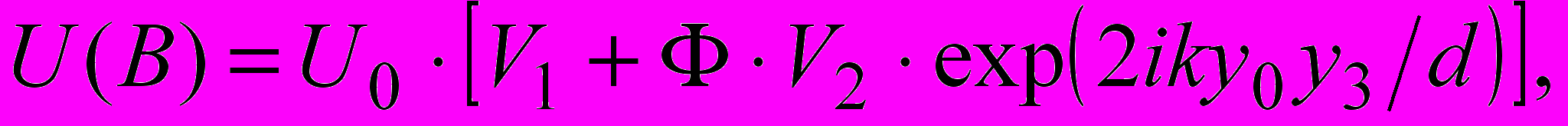(23)

где U₀ - поле, которое создает источник в точке В в отсутствии ленты, Ф - коэффициент отражения. Коэффициент отражения для идеально проводящей ленты может принимать два значения: Ф = -1, когда падающая волна поляризована параллельно краям ленты (горизонтальная поляризация), и Ф = 1 в противоположном случае (вертикальная поляризация). Слагаемые V₁ и V₂ входящие в формулу выражаются через комбинацию обычных и обобщенных интегралов Френеля, причем слагаемое V₁ описывает волны, приходящие в точку В без отражения, а V₂ – описывают отраженные от ленты волны. Показано, что результирующее поле в итоге имеет вид суммы геометрооптической волны, волн однократной и двукратной дифракции. Полученное выражение является равномерным относительно угла падения и удовлетворяет принципу взаимности.

На основании формулы (23) получено выражение, описывающее дифракционное поле при скользящем падении волн на ленту. Как и следовало ожидать при поляризации, перпендикулярной плоскости ленты, U(B) = U₀, т.е. волна не «замечает» ленту . Для поляризации, параллельной краям ленты получено следующее простое выражение

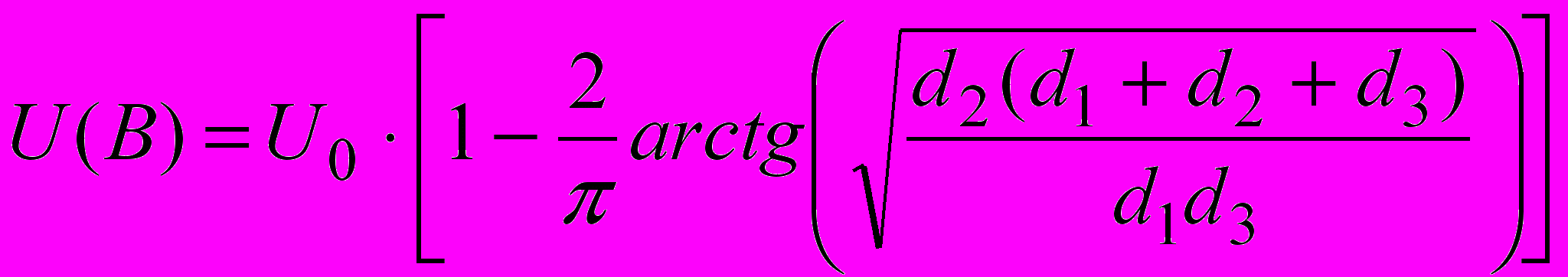. (24)

Оказывается, что выражение (24) правильно описывает поле как при ширине ленты, стремящейся к нулю (т.е. при d₂=0), так и в случае, когда лента занимает все пространство между источником и точкой наблюдения, тогда как теория предполагает, что ширина ленты и расстояния от источника и приемника до краев ленты много больше длины волны.

П

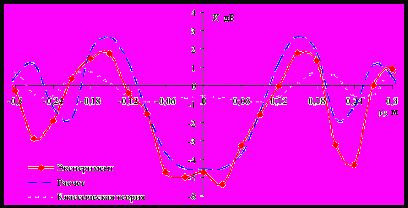
риведены результаты численного моделирования дифракции волн на ленте при различной поляризации падающего излучения и различных положениях источника. Представлены результаты экспериментов и их сравнение с результатами численных расчетов по полученным формулам. На рис. 22 представлены результаты измерений на волне длиной 0,03м для ленты шириной 0,085м. Из них следует, что расчет, основанный на предложенной модификации теории, удовлетворительно согласуется с экспериментом.

Рис. 22. Сравнение расчетных и экспериментальных результатов.

Ширина ленты 0,085м, угол скольжения: 5⁰.

В следующем параграфе рассмотренный выше подход применен к решению задачи дифракции электромагнитных волн на щели. Рассмотрен общий случай, когда образующие щель полуплоскости не лежат в одной плоскости. Получено решение, аналогичное решению (23) для ленты, которое также записывается в виде комбинации обычных и обобщенных интегралов Френеля и описывает различные типы волн, приходящих в точку наблюдения. Приведены результаты численных расчетов.

В шестой главе приведены результаты экспериментов с дифракционными экранами, полученные на различных радиолиниях.

Первый параграф главы посвящен экспериментальному изучению возможности увеличения уровня поля на трассе с пассивным ретранслятором путем регулирования дифракционного поля. Эксперимент проводился на пролете радиорелейной линии, который представляет собой дифракционную трассу с одним клиновидным препятствием. Поэтому над препятствием был установлен пассивный ретранслятор кольцеобразной формы. Экранирующее препятствие, на котором установлен ретранслятор, представляет собой холм с острым и ровным клиновидным гребнем, однако ретранслятор был спроектирован по методике, которая не учитывает дифракционное поле препятствия.

Поэтому с целью увеличения уровня поля на радиорелейном интервале были проведены эксперименты с экраном, регулирующим поле U_s по отношению к полю U_d. Длина экрана равнялась 40 м, что соответствует параметру u = 1,4.

Эксперименты заключались в изучении зависимости уровня поля от высоты экрана. На рис. 23 приведены зависимости выигрыша В относительно поля без экрана от высоты прямоугольного экрана h для разных антенн и на разных частотах. Из представленных данных видно, что регулирующий экран существенно увеличивает уровень поля пассивного ретранслятора.

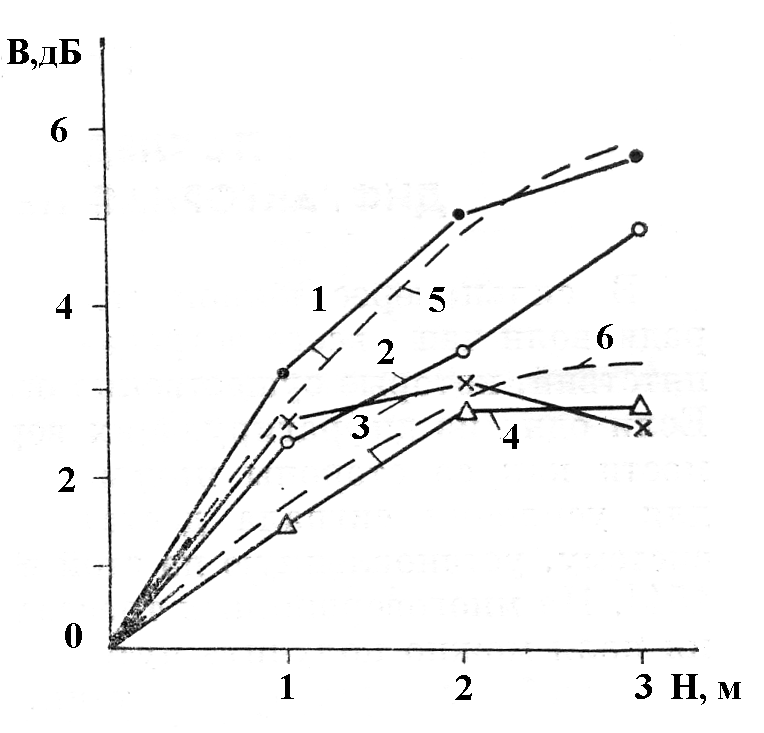
Рис. 23. Выигрыш в уровне сигнала в зависимости от высоты регулирующего экрана 1, 2 – нижняя антенна, 3, 4 – верхняя антенна; 1, 3 – f=3772,5 МГц, 2, 4 - f=3716,5 МГц; 5, 6 – расчетные зависимости.

Во втором параграфе главы приведены результаты экспериментального исследования особенностей распространения радиоволн с длиной λ = 8 см на протяженной трассе с пассивным ретранслятором и выявления физических механизмов, вызывающих замирания, на пересеченной трассе длиной 113 км. Приводятся кривые устойчивости, суточные зависимости сигнала, анализируется влияние регулирующего экрана.

Третий параграф главы посвящен экспериментальному исследованию метода уменьшения интерференционных замираний с помощью последовательных дифракционных экранов. Данный эксперимент был проведен на интервале радиорелейной линии прямой видимости длиной 44 км. Длина волны составляла 7,8 см. Земная поверхность в области формирования отраженного луча является ровной, что приводит к существованию интенсивного отраженного луча и глубоким замираниям. Для уменьшения отражательной способности земной поверхности на нее было установлено два последовательно расположенных экрана,.

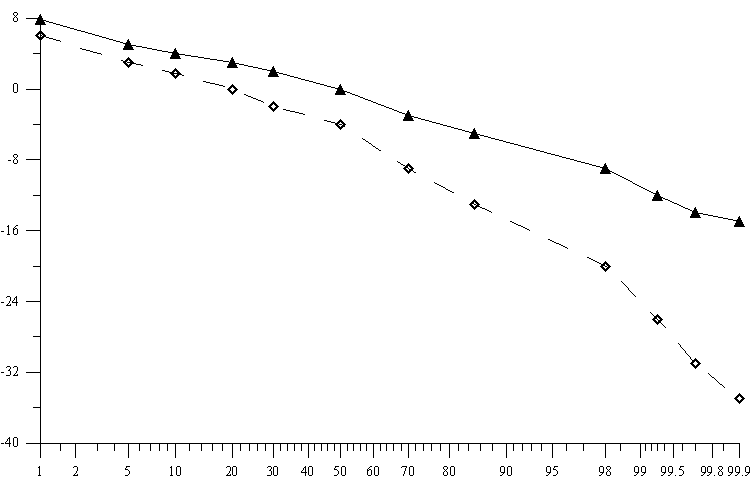
После установки экранов характер флуктуаций сигнала качественно изменился. Глубокие замирания, сопровождавшие процесс распространения радиоволн на этой трассе в разные периоды суток, практически исчезли. Это подтверждает и количественный анализ. На рис. 24. показаны интегральные кривые распределения множителя ослабления (кривые устойчивости, по оси абсцисс отложен процент времени, в течение которого множитель ослабления превышал значения, отложенные по оси ординат), которые свидетельствуют о высокой эффективности предложенного метода. Уменьшилась не только глубина флуктуаций с -35 дБ до -15 дБ, но и увеличился медианный уровень сигнала с -4 дБ, до 0 дБ.

2

1

f = 3828.5 МГц

Рис. 24. Кривые устойчивости сигнала до установки экранов и после установки экранов.

В Приложениях приведены свойства функций, связанных с обобщенным интегралом Френеля и акты внедрения.

Основные результаты и выводы

Обобщенная задача последовательной дифракции Френеля-Кирхгофа на N полуплоскостях при произвольно ориентированных краях путем преобразования локальных систем координат и применения многомерного метода стационарной фазы сведена к задаче с параллельными краями, при этом 2N-кратный дифракционный интеграл преобразован в N-кратный интеграл. Взаимный наклон краев приводит к явлениям фокусировки и дефокусировки дифракционного поля.
Предложено обобщение модели кусочно-плоской и кусочно-однородной трассы путем введения клиновидных препятствий, аппроксимируемых поглощающими полуплоскостями, и разработан способ расчета поля на таких трассах, основанный на методе параболического уравнения.
Проведен учет влияния неоднородности тропосферы на поле клиновидного препятствия. Показано, что по мере увеличения закрытия (угла дифракции) влияние тропосферной рефракции уменьшается. На основе геометрической теории дифракции разработана модель дифракции на клиновидном препятствии при наличии слоя над ним. Она позволяет рассчитывать характеристики сигнала при совместном действии двух механизмов распространения: дифракции на гребне препятствия и отражения от тропосферных слоев. Установлено, что при интенсивности слоя (скачке диэлектрической проницаемости), меньшей, чем 10^-6 влиянием слоя можно пренебречь.
При дифракции волны на полубесконечном импедансном слое предложен возможный механизм формирования результирующего поля в виде боковой волны от гюйгенсовских источников.
Разработаны трехмерные модели дифракционного распространения УКВ, учитывающие поперечную к направлению распространения форму гребней клиновидных препятствий и позволяющие прогнозировать пространственную структуру дифракционного поля
Предложен вывод поля граничной волны в области дифракции Френеля, имеющий ясный физический смысл и позволяющий наглядно представить формирование граничной дифракционной волны. С помощью введенной амплитуды рассеяния волны элементом края и её обобщения на последовательное многократное рассеяние на элементах краев последовательно расположенных экранов (отверстий) построена теория обобщенной граничной волны многократной дифракции. Полученный дифракционный интеграл имеет размерность в два раза меньшую, чем апертурный интеграл Френеля-Кирхгофа. На примере расчета поля двукратной дифракции показано, что полученное решение сокращает вычислительные затраты на 2-3 порядка при сравнимой точности.
Установлено, что пространственная структура поля УВЧ - СВЧ на дифракционных трассах является неоднородной с масштабами неоднородностей единицы – десятки метров и размахом колебаний, достигающим значений 10 - 20 дБ. Выявлено, что временные флуктуации сигнала в теневой зоне препятствий зависят от особенностей пространственной структуры дифракционного поля. Обнаружено, что на дифракционной трассе возможно существование сравнительно устойчивых во времени максимумов и минимумов уровня поля, расположенных вблизи друг друга.
Экспериментально установлено, что на дифракционных трассах наблюдаются искажения диаграмм направленности антенн. Эти искажения проявляются в расширении диаграмм направленности и расщеплении основного лепестка. Обнаружено, что характер деполяризации сигнала определяется локальными особенностями трассы распространения
Показано, что учет дифракционного поля препятствия позволяет оптимизировать пассивную ретрансляцию радиоволн с помощью дифракционных экранов. Экспериментально показано, что метод уменьшения отражений от земной поверхности с помощью последовательно расположенных экранов позволяет существенно уменьшить флуктуации сигнала на плоских трассах радиолиний. На исследованной трассе уменьшение глубины флуктуаций составило 20 дБ.
Предложен метод решения задачи дифракции на проводящей ленте и щели в проводящем экране, основанный на учете двукратной дифракции Френеля-Кирхгофа, который применим при произвольной ширине ленты и малых углах скольжения. Полученное решение представляет собой сумму геометрооптической волны, волн однократной дифракции и волны двукратной дифракции, удовлетворяет принципу взаимности и выражается через известные специальные функции теории дифракции.

Основные результаты диссертации опубликованы в следующих работах:

Статьи в журналах из перечня ВАК

Чимитдоржиев Н.Б., Дагуров П.Н., Дарижапов Д.Д., Ломухин Ю.Л., Цыбиков А.Е. Последовательная дифракторная ретрансляция радиоволн // Электросвязь. 1977. № 2. С. 63-68.
Дагуров П.Н., Кузьмин И.В,. Локшин В.Л, Спивак Н.Н., Чимитдоржиев Н.Б.,. Шамшин В.А,. Ямпольский В.Г. Устойчивость связи на радиорелейной линии с длинными пролетами // Электросвязь. 1979. № 5. С. 40-47.
Дагуров П.Н., Цыбиков А. Е., Чимитдоржиев Н.Б О дифракционном распространении сантиметровых волн // Изв. Вузов. Радиофизика. 1984. Т. 27. № 2. С. 163-173.
Дагуров П.Н.,Чимитдоржиев Н.Б. Дифракторная ретрансляция радиоволн на пересеченных трассах // Радиотехника. 1985. № 3. С. 73-74.
Дагуров П.Н., Заяханов А.С., Цыбиков А. Е., Чимитдоржиев Н.Б. Пространственно-временные флуктуации диаграммы направленности антенн при дифракционном распространении // Изв. Вузов. Радиофизика. 1985. Т. 28. № 10. С. 1218-1226.
Дагуров П.Н., Ломухин Ю.Л., Чимитдоржиев Н.Б. Ослабление бокового излучения антенн с помощью проводящих пластин. // Радиотехника. 1988. № 6. C.70-71.
Дагуров П.Н., Заяханов А.С., Цыбиков А. Е., Чимитдоржиев Н.Б. Исследование искажений поляризационных параметров дифракционного поля сантиметровых волн // Электросвязь. 1988. № 12. С. 49-52.
Дагуров П.Н., Заяханов А.С., Цыбиков А. Е., Чимитдоржиев Н.Б. Флуктуации направления главного максимума диаграммы направленности передающей антенны на закрытых приземных трассах // Радиотехника. 1989. № 3. С. 62-63.
Дагуров П.Н., Заяханов А.С., Чимитдоржиев Н.Б. Модель многолучевого дифракционного распространения УКВ // Радиотехника и электроника. 1994. Т.39. № 2. С. 199-207.
Дагуров П.Н., Заяханов А.С., Цыбиков А. Е. Влияние дифракционной многолучёвости на характеристики антенн // Радиотехника и электроника. 1998. Т. 43. № 12. С. 1477-1485.
Дагуров П.Н., Дмитриев А.В. Применение метода Кирхгофа к задаче дифракции волн на ленте при малых углах скольжения // Письма в ЖТФ. 2005. Т.31. Вып. 19. C. 22-27.
Дагуров П.Н., Дмитриев А.В. Многократная дифракция Френеля-Кирхгофа на полуплоскостях с произвольно ориентированными краями // Электромагнитные волны и электронные системы. 2008. № 6. С. 4-11.
Дагуров П.Н., Дмитриев А.В. О граничной дифракционной волне в теории Френеля-Кирхгофа. Письма в ЖТФ. 2009. Т. 35. Вып. 10. С. 49-57.
Дагуров П.Н., Дмитриев А.В. Граничные дифракционные волны при многократной дифракции Френеля-Кирхгофа. Оптика и спектроскопия. 2009. Т.107. № 8. С.306-311.

Blog

Моделирование дифракционного распространения волн и структура поля радиоволн увч и свч на нерегулярных трассах