Ю. В. Козырь Цель настоящей статьи ознакомление заинтересованных лиц с нюансами оценивания ставки дисконтирования. Часть материала этой статьи публиковалась ранее автором на сайте Appraiser ru и в книга

Вид материала

Книга

Содержание 2. Альтернативные способы оценки ставки дисконтирования Рыночная экстракция: общий случай Рыночная экстракция: частный случай 1 Рыночная экстракция: частный случай 2 В - выручка страховой компании от страхования данного актива, m 3. Особенности воздействия инфляции на ставку дисконтирования 4. Особенности соотнесения разнобазовых ставок дисконтирования D — амортизационные начисления. Пусть для примера известно, что мультипликатор P 5. Соответствие валюты выражения денежных потоков валюте выражения ставки дисконтирования

Подобный материал:

• Учет рисков и определение ставки дисконтирования, 238.44kb.
• О предоставлении в налоговые органы документов, используемых при учете организаций, 32.71kb.
• Конференция 'Роль аналитика в управлении предприятием' Критерии выбора ставки дисконтирования, 130.93kb.
• Всоответствии с пунктом 2 статьи 13, пунктами 1, 4 статьи 14, пунктом 1 статьи 16,, 174.1kb.
• Комментарий Сары Мэйо («Левый Авангард», 48/2003) Дата размещения материала на сайте:, 2448.02kb.
• Встатье систематизирована информация об основных командах в Linux, 138.28kb.
• Какая ставка налогообложения применяется при выплате физическому лицу – нерезиденту, 17.25kb.
• Цель настоящей статьи упорядочить возможные способы введения категорий пространства, 167.22kb.
• Приказ от 2 июня 2005 г. N 444 о полномочиях должностных лиц мвд россии по составлению, 328.01kb.
• Ьской области, повышения эффективности государственного управления, в соответствии, 90.03kb.

Аспекты оценивания и корректировки ставки дисконтирования


Ю.В. Козырь


Цель настоящей статьи – ознакомление заинтересованных лиц с нюансами оценивания ставки дисконтирования. Часть материала этой статьи публиковалась ранее автором на сайте Appraiser.ru и в книгах «Стоимость компании: оценка и управленческие решения», «Оценка и управление стоимостью компании», другая часть – один из представленных здесь методов рыночной экстракции, учет инфляции и циклов финансирования, - публикуется впервые.


1. Оценка среднерыночной доходности


Рассмотрим сначала способы определения среднерыночной доходности фондового рынка (параметр r_m в модели САРМ).

Прямой способ определения среднерыночной доходности заключается в сравнении изменения фондового индекса за несколько периодов с учетом среднерыночной нормы дивидендной доходности при приведении этой величины к годовому интервалу:


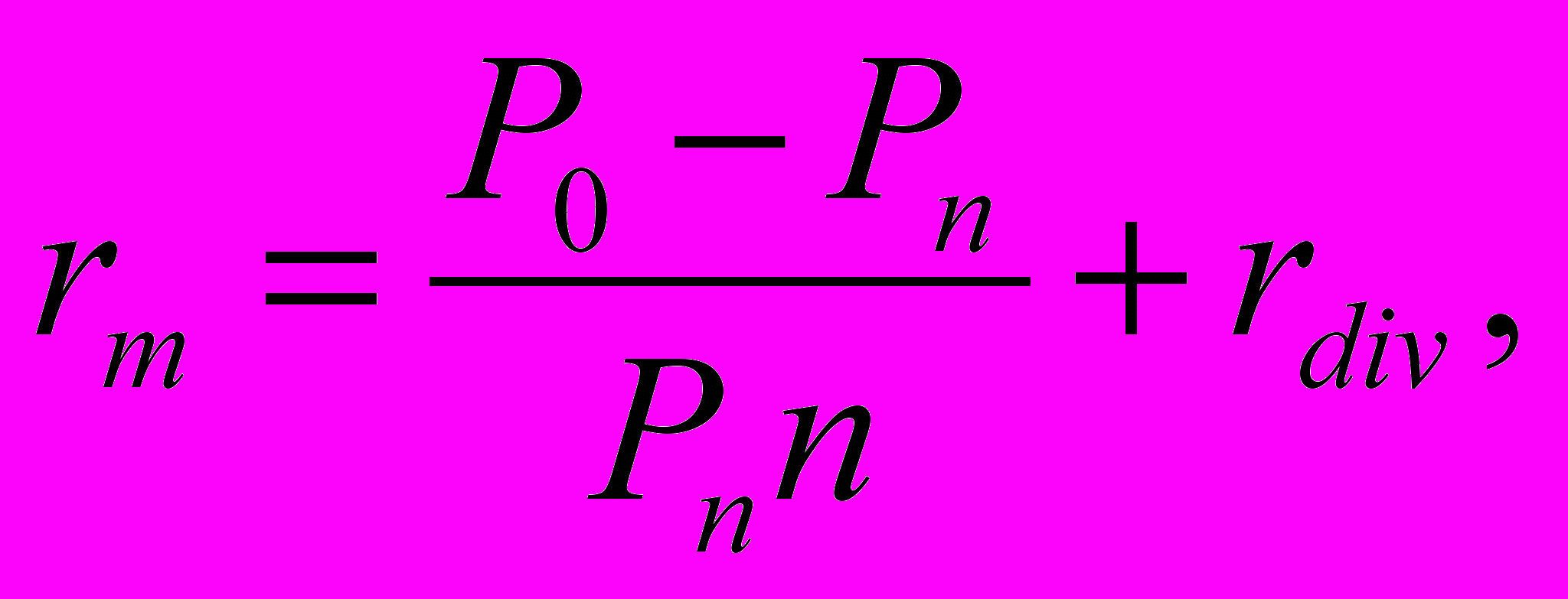(1.1)


где P₀ – текущее значение фондового индекса (РТС, ММВБ),

P_n - значение фондового индекса периодов назад,

n - число периодов интервала, в котором определяется среднерыночная доходность,

r_div - среднерыночная дивидендная доходность (отношение выплаченных за год дивидендов к цене приобретения акции).

Косвенный способ определения среднерыночной доходности заключается в использовании следующего выражения:

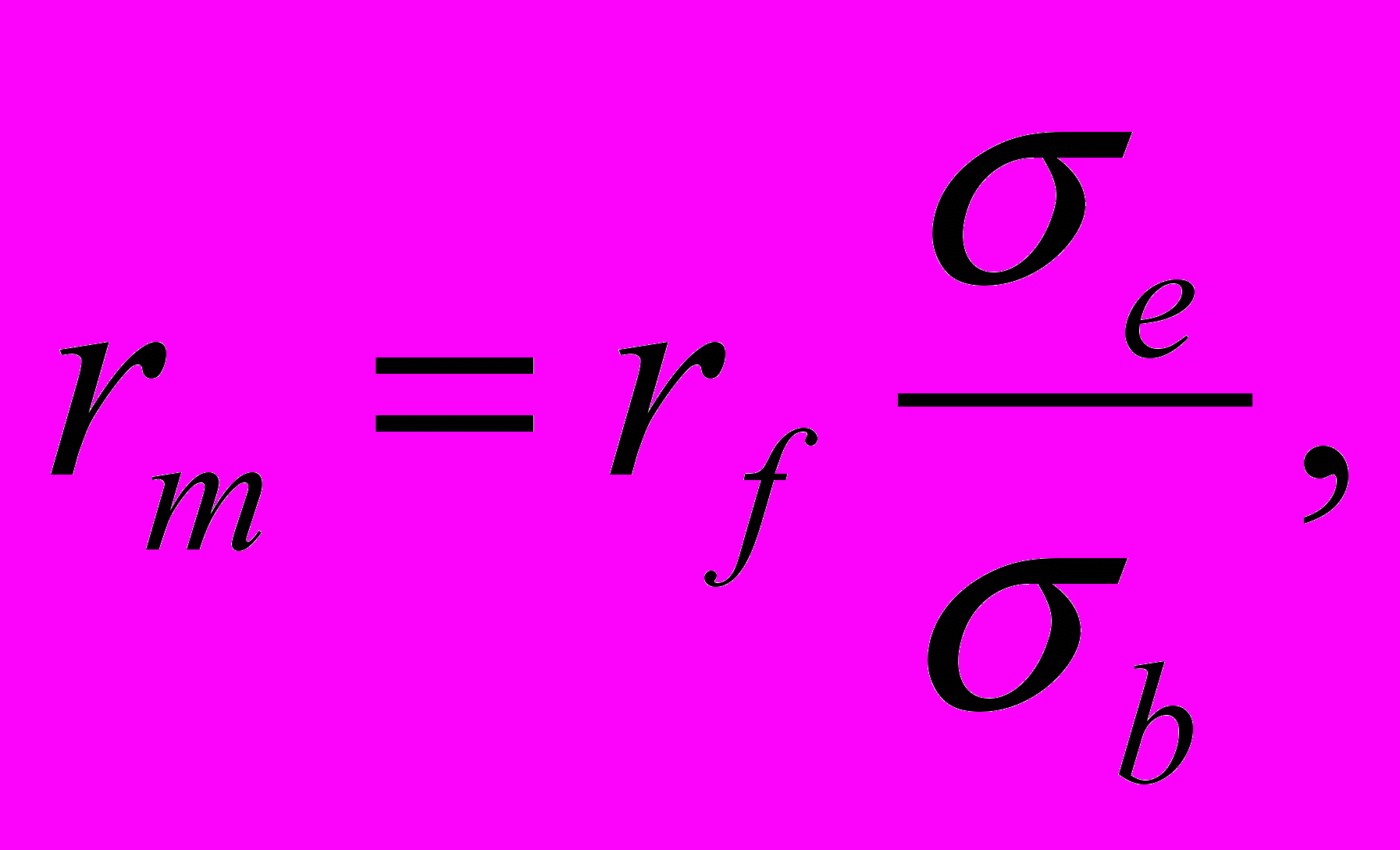(1.2)

где r_m — среднерыночная доходность акций;

r_f — безрисковый уровень доходности (доходность по правительственным облигациям);

_e — стандартное отклонение доходности российского рынка акций;

_b — стандартное отклонение доходности российского рынка облигаций.

По оценкам автора, отношение _e/_b по итогам 2004 г. для российского рынка составило 4,2, а значение r_m – 27-30% (при этом прямая оценка одной лишь курсовой разницы, т.е. без учета дивидендной доходности, дает значение порядка 23% - это значение основано на данных почти 10-летнего периода с 1995 по 2005 гг.).

2. Альтернативные способы оценки ставки дисконтирования


Как заметили авторы бестселлера «Принципы корпоративных финансов» Ричард Брейли и Стюарт Майерс, рынок зачастую сам подает сигналы, и нужно только суметь заметить и расшифровать их. Воспользуемся этим замечанием и попробуем «выпытать» у рынка информацию о ставке дисконтирования. Ниже представлено несколько подобных возможностей.


Рыночная экстракция: общий случай

Пусть имеется компания П₁ с денежными потоками 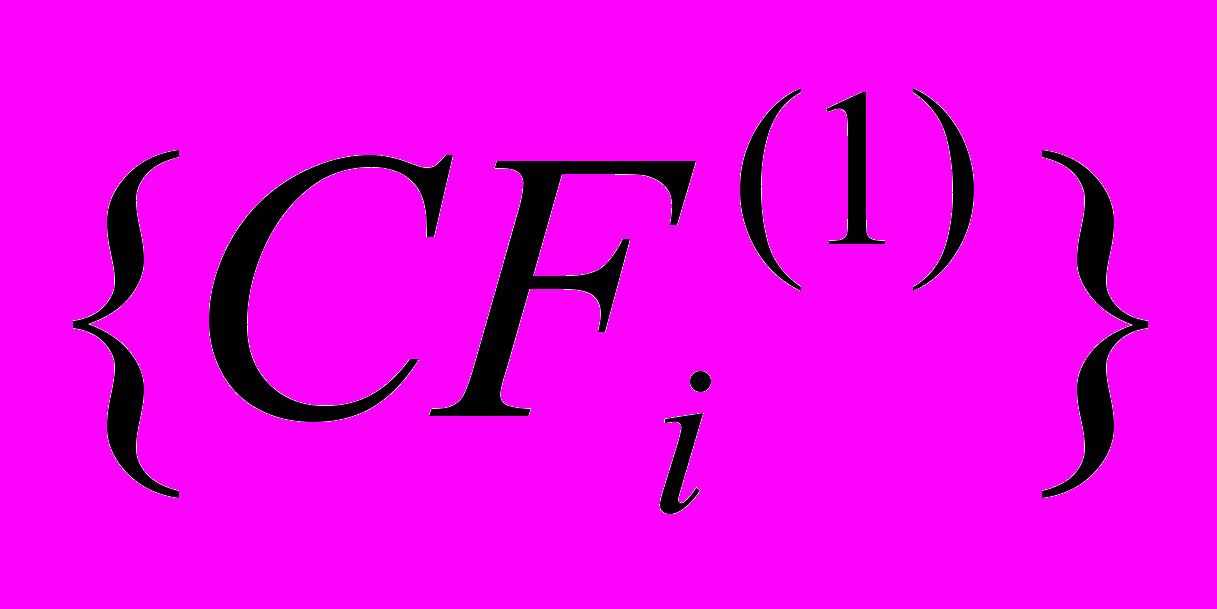, i = 1, …, N и прогнозируемым темпом роста денежных потоков в постпрогнозный период (начиная с (n + 1)-го года g_n1. Пусть для этой компании мы нашли близкую по некоторым параметрам компанию-аналог П₂, работающую в этой же отрасли. Известно, что рыночная стоимость акционерного капитала этой компании составляет P₂, его денежные потоки за сопоставимые периоды времени — 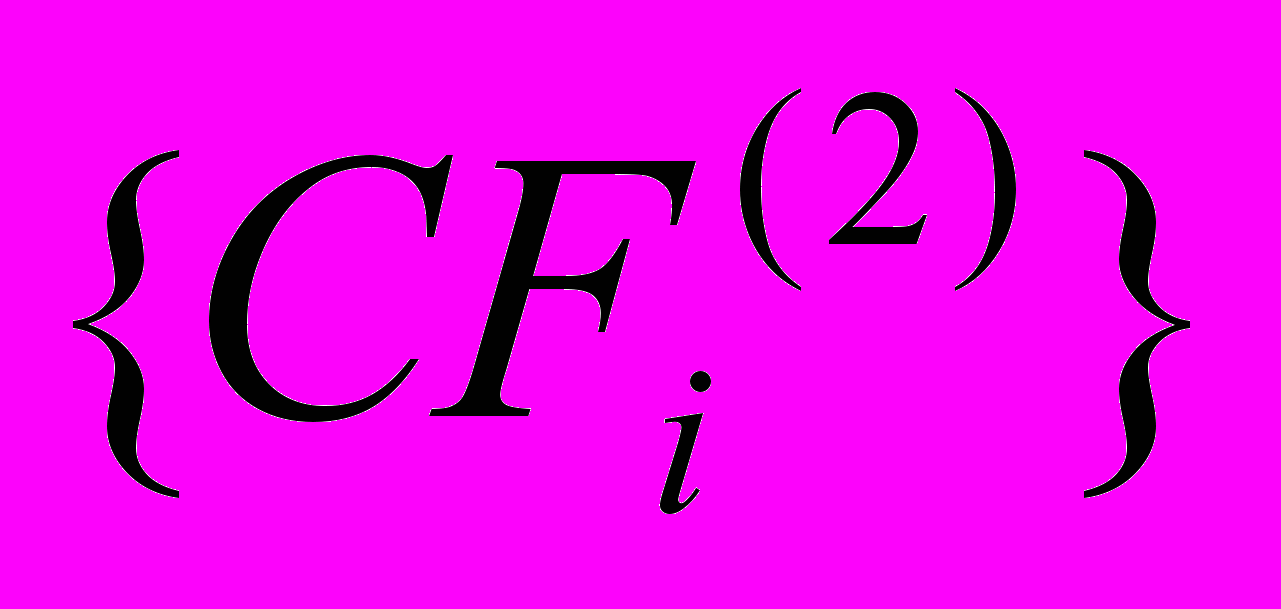, i = 1, …, N, а темп роста денежных потоков в тот же постпрогнозный период — g_n2.

Идея предложенного подхода заключается в нижеследующей двухшаговой процедуре.

Шаг 1. Определяют ставку дисконтирования d = d_a, ставящую в соответствие рыночную стоимость P₂ акционерного капитала компании-аналога П₂ с величинами его денежных потоков 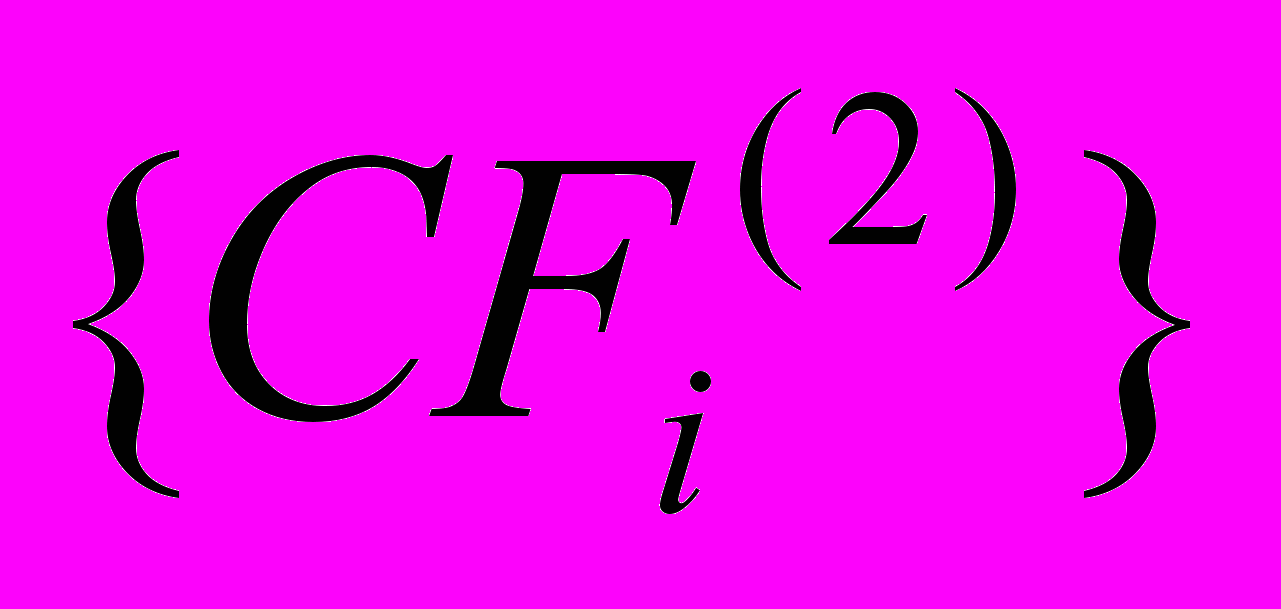, i = 1, …, N. Это делают, решая численными методами уравнение

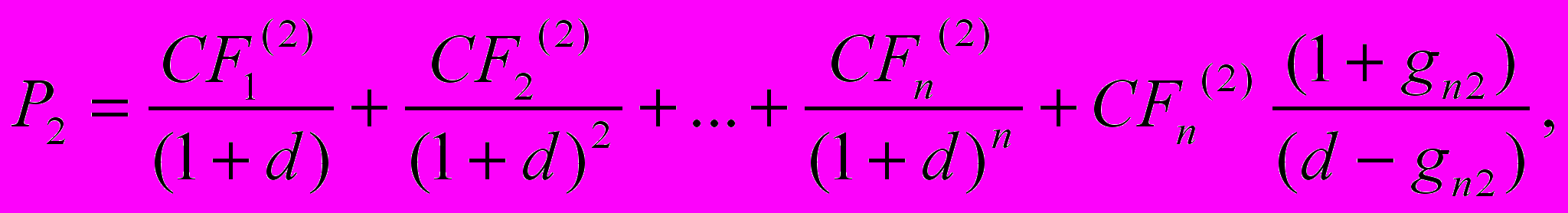(2.1)

где индекс (2) означает принадлежность к компании-аналогу П₂.

Шаг 2. Полученное из уравнения (2.1) для ставки дисконтирования d значение d_a корректируют на предмет различия в заемном капитале сравниваемых компаний и других специфических факторов.

Более подробно применение описанного выше подхода, называемого иногда методом рыночной экстракции, рассмотрим на следующем примере-задаче.

Пусть имеется некий объект оценки, который, как ожидается, будет ежегодно генерировать потоки, возрастающие на g_o = 7%. Продолжительность такой генерации потоков составит, как ожидается, t_o = 15 лет, после чего объект будет изношен на 100% и его остаточная стоимость будет равна нулю. Величина потока в текущем периоде CF_o равна 1 млн. руб.

Необходимо:

1. определить стоимость этого объекта.
   
2. для выполнения п.1 определить ставку дисконтирования r.
   

Предположим, после обработки рыночной информации оценщик определил следующие параметры наиболее типичного объекта-аналога:

• стоимость P_a = 10 млн. руб.;
  
• нормализованная величина денежных потоков текущего периода CF_a = 1 млн. руб./год;
  
• оставшийся срок жизни объекта-аналога t_a = 20 лет;
  
• ожидаемый темп роста денежных потоков g_a = 5%/год;
  
• остаточная стоимость объекта по истечении 20 лет равна нулю.
  

Решение.

Начнем решение со второго пункта задания – определения ставки дисконтирования. Согласно модели дисконтированных денежных потоков с постоянным ростом стоимость объекта-аналога определяется следующим образом:


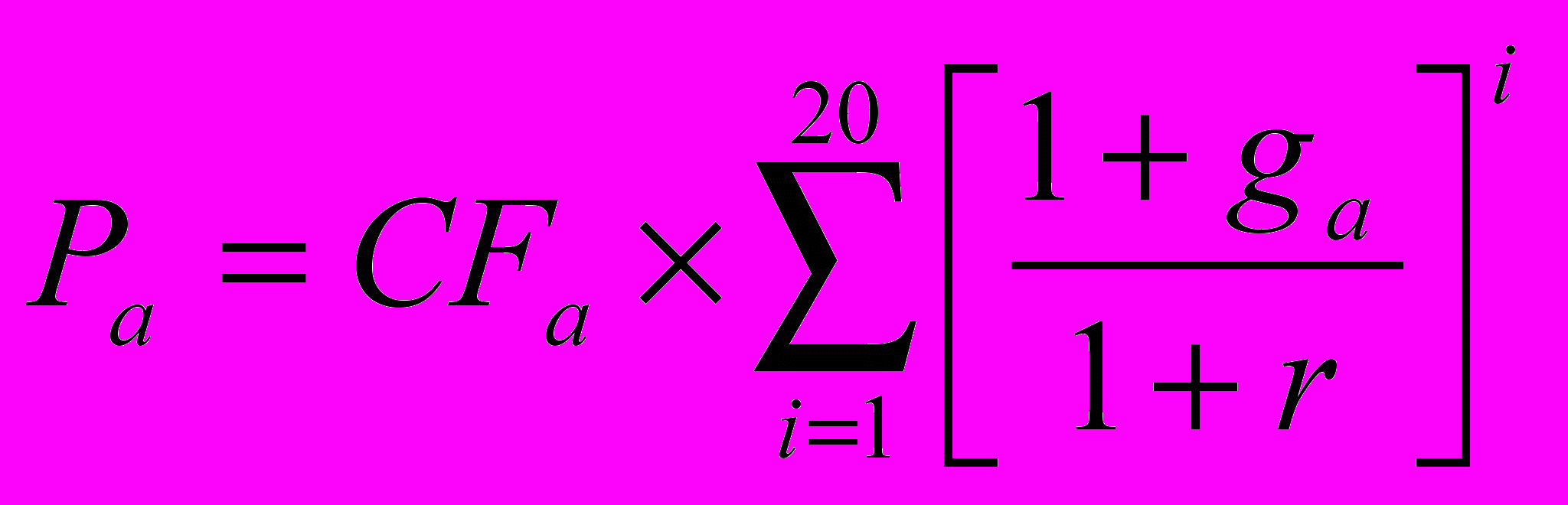. (2.2)


Введем обозначение:


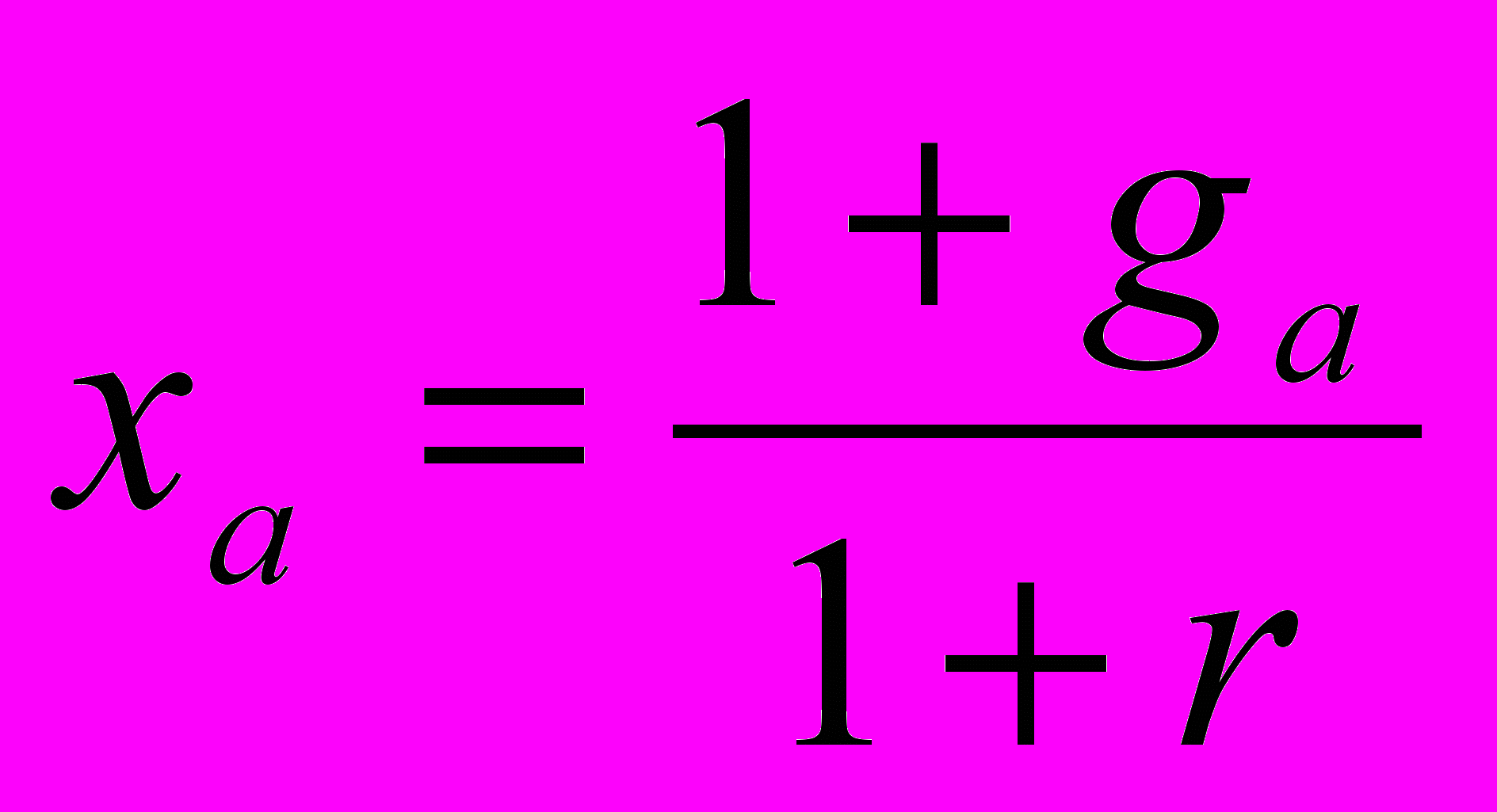. (2.3)


Из (2.3), зная x_a, можно найти ставку дисконтирования:


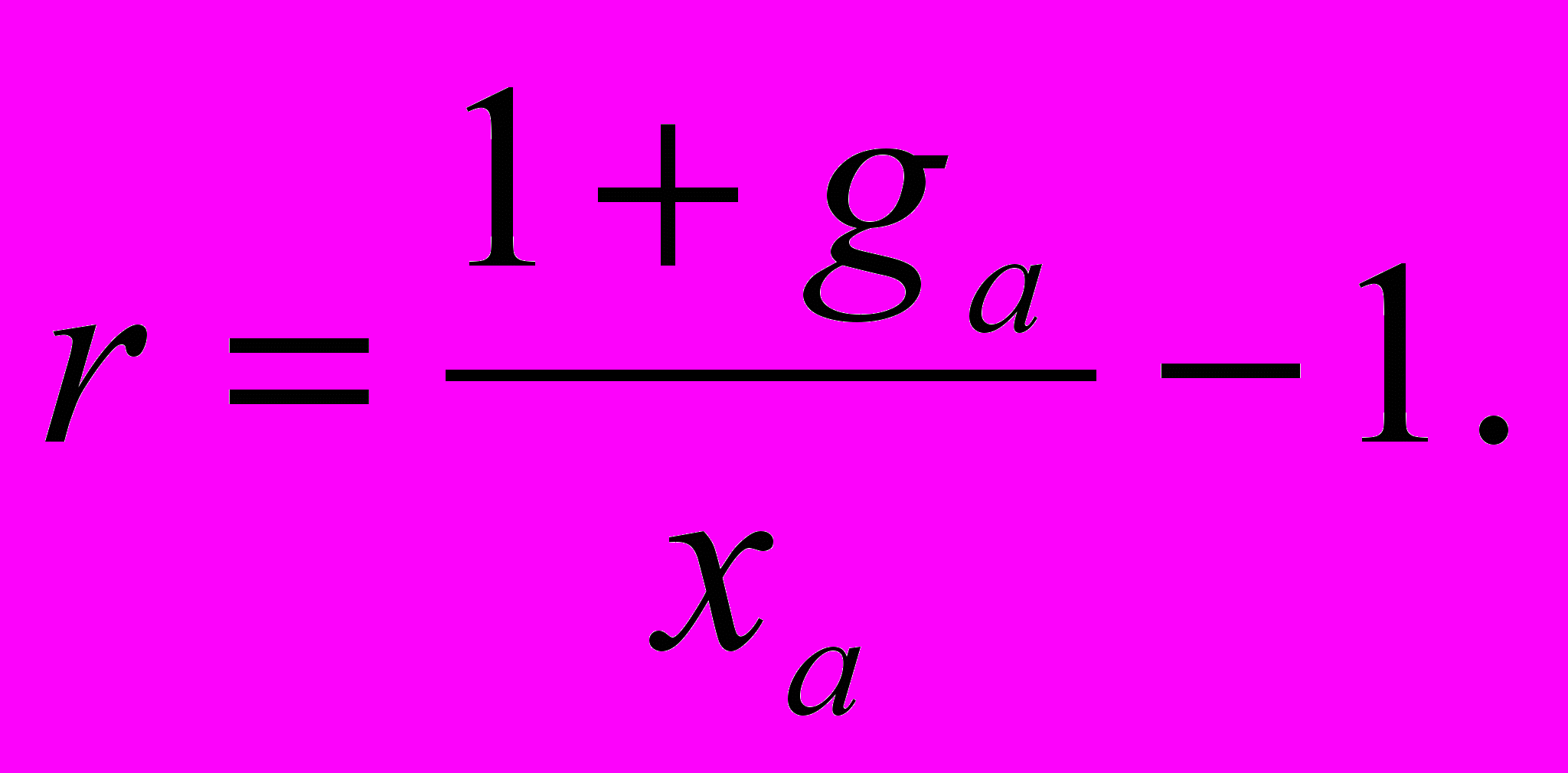(2.4)


Из выражений (2.2) и (2.3) следует:


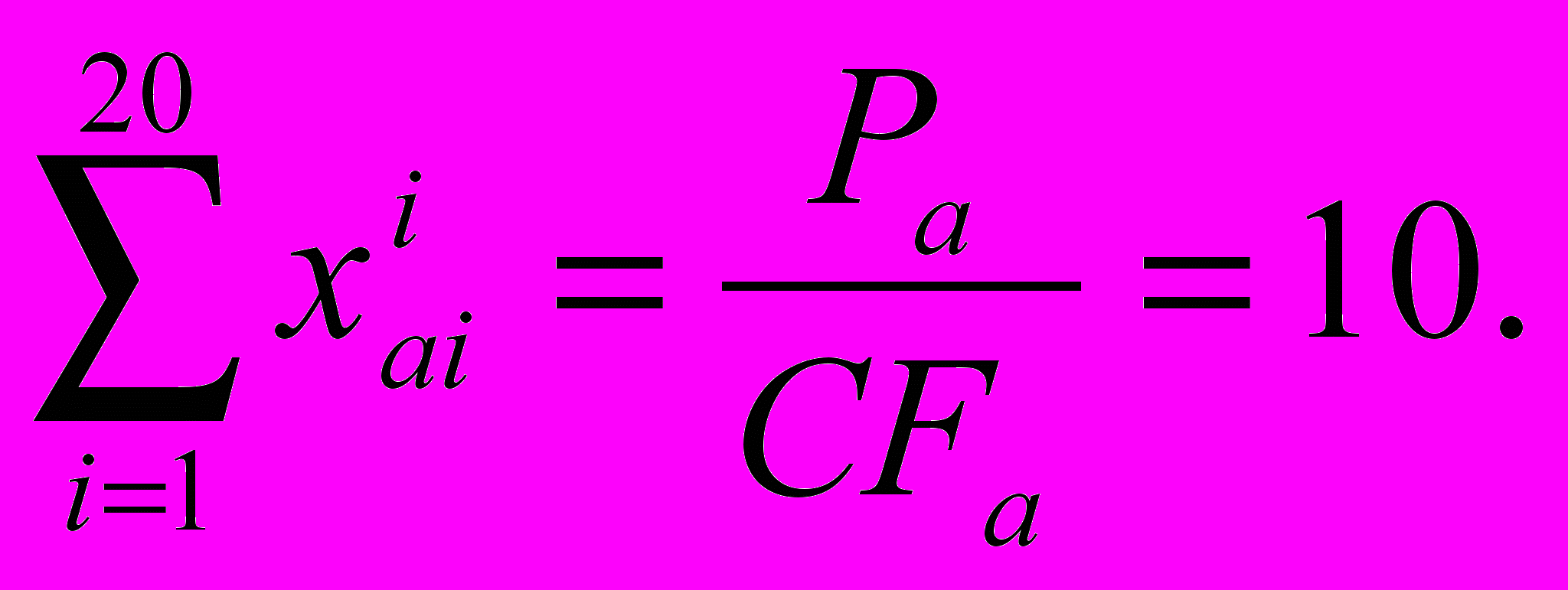(2.5)


В то же время известно, что сумма первых n членов геометрической прогрессии, коей является левая часть в (2.5) при x_a < 1 [параметры этой геометрической прогрессии следующие: первый член = {(1+ g_a)/(1 + r)}²⁰, q = 1/x_a] равна


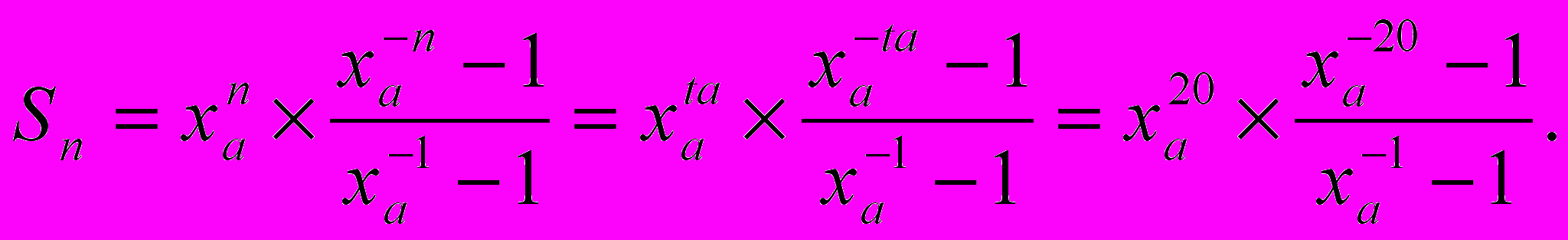(2.6)


В случае если x_a > 1 сумма первых n членов этой геометрической прогрессии определяется другим выражением:


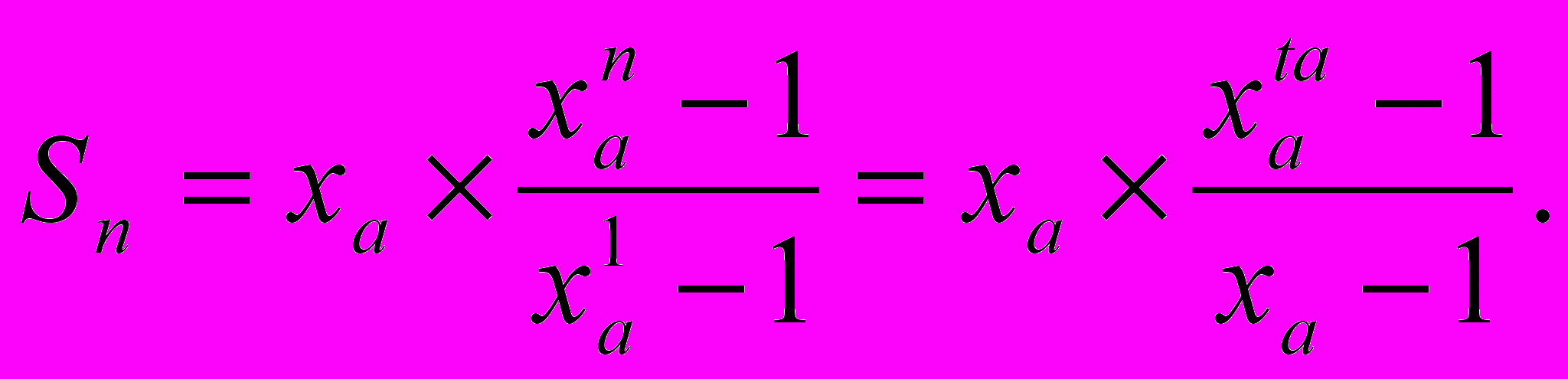(2.6-2)


И наконец, если x_a = 1, сумма первых n членов этой суммы равна nx_a.

Процедура нахождения x_a заключается в итеративном поиске такого значения, при котором сумма геометрической прогрессии, определяемая выражением (2.6), равнялась бы значению суммы прогрессии, определяемой выражением (2.5). Осуществим такие итерации.

Итерация 1. Пусть x_a = 0,7. Тогда согласно выражению (2.6)




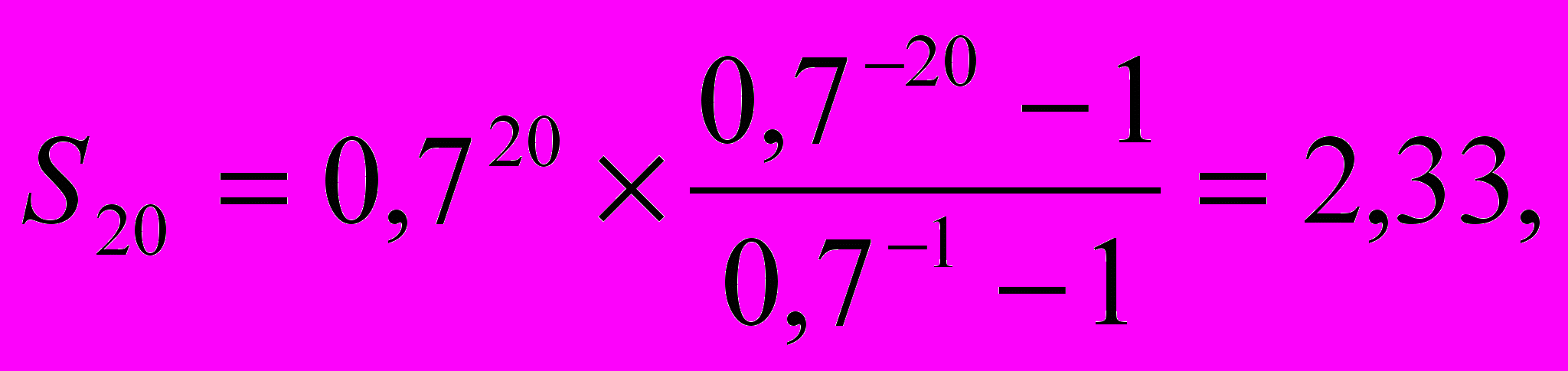
что ниже 10. Значит, надо сделать следующую итерацию, изменив значение x_a.

Итерация 2. Пусть x_a = 0,9. Тогда согласно выражению (2.6)




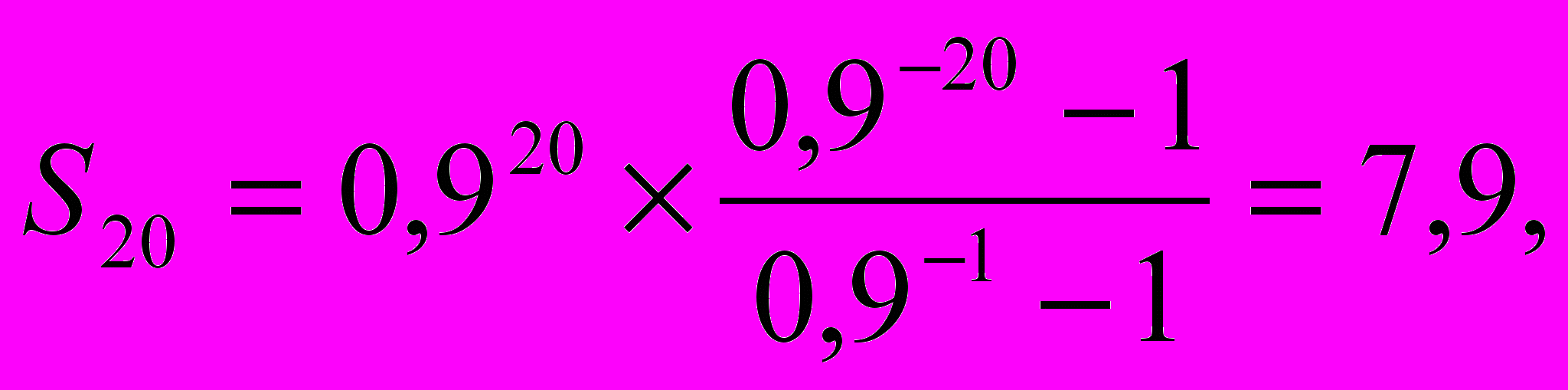
что хоть и выше предыдущего значения итерации, но опять ниже 10. Значит, надо вновь изменить значение x_a в сторону увеличения. Однако, поскольку значения x_a не могут превышать единицу, в следующей итерации прирост значения x_a должен быть незначительным.

Итерация 3. Пусть x_a = 0,95. Тогда согласно выражению (2.6)




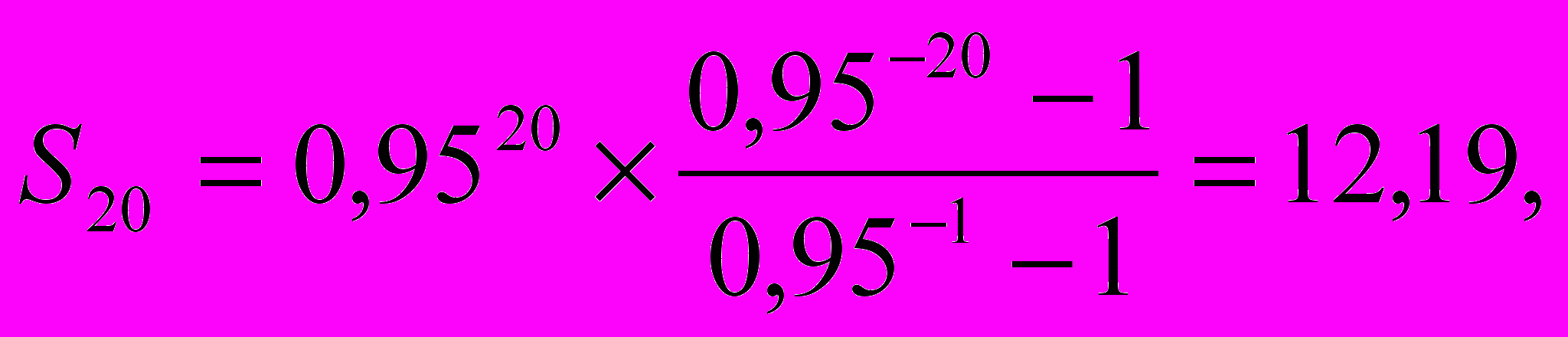
что выше 10. Следовательно, в следующей итерации необходимо понизить значение x_a.

Итерация 4. Пусть x_a = 0,925. Тогда согласно выражению (2.6)




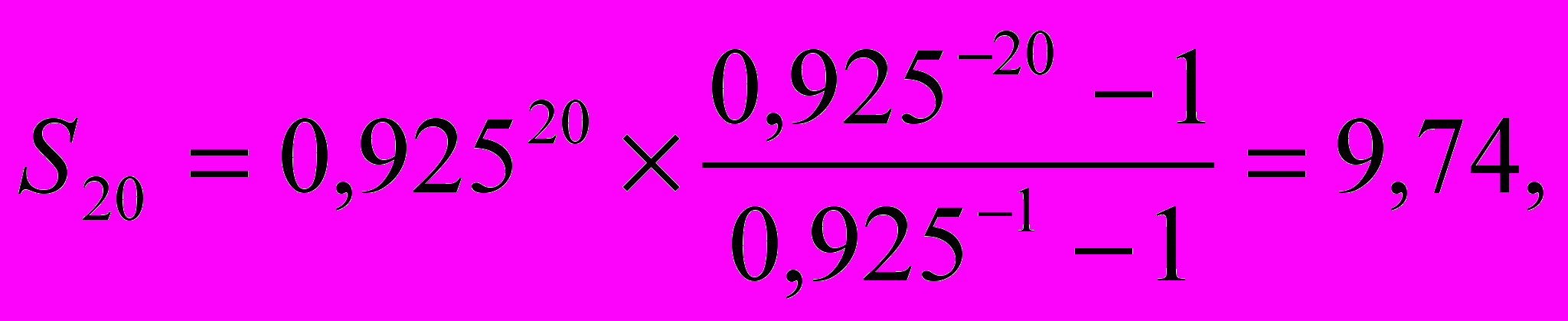
что ниже 10. Продолжив этот процесс, получим достаточно хорошее приближение значения x_a = 0,928, дающее сумму прогрессии равную 9,997. Приняв это значение за искомое, определим согласно выражению (2.4) значение ставки дисконтирования:




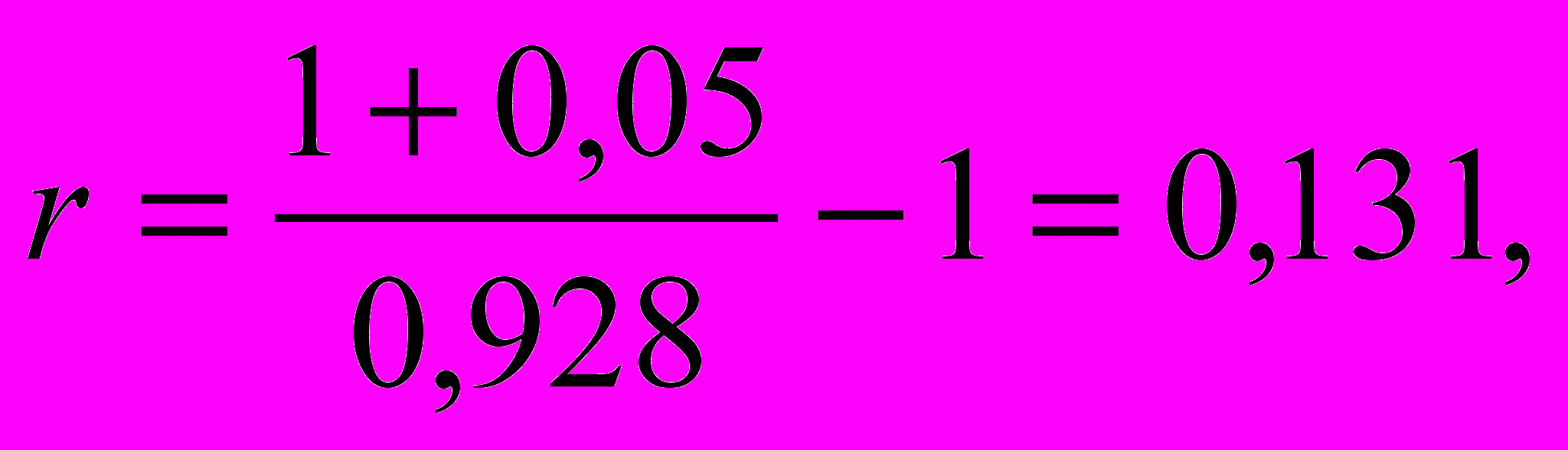
то есть 13,1%.

Теперь, определив значение ставки дисконтирования, найдем стоимость оцениваемого объекта:


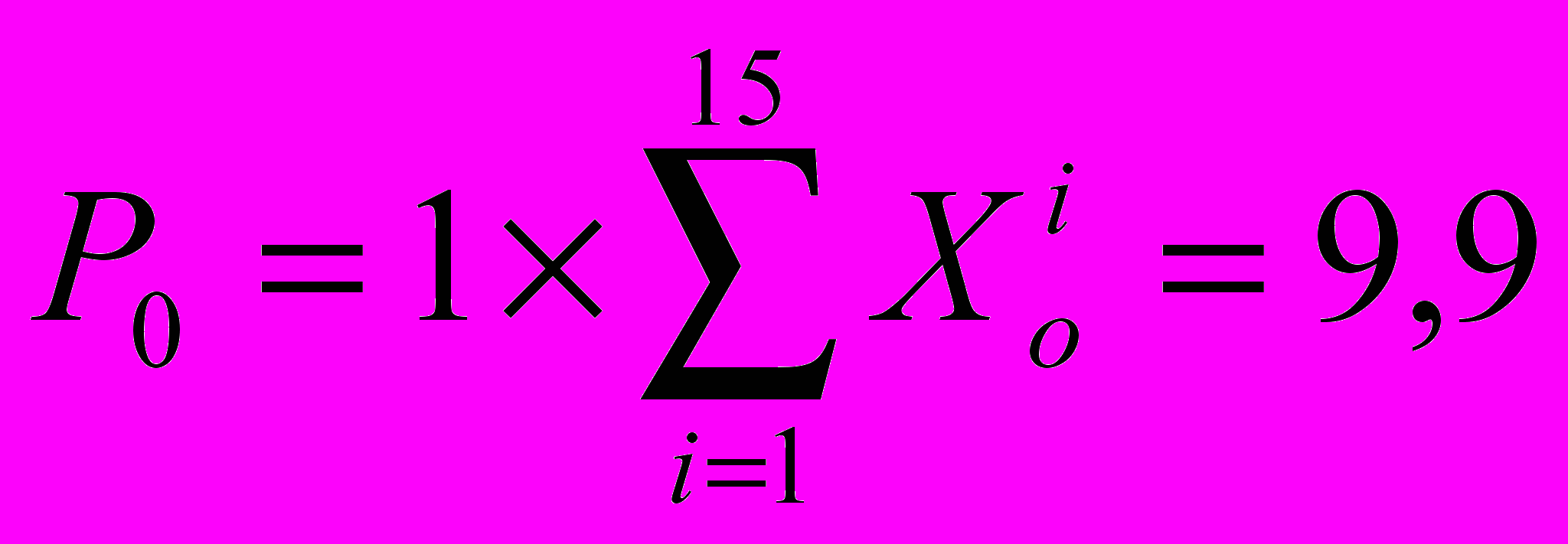млн. руб. (2.7)


(здесь X_o = (1 + 0,07)/(1 + 0,131) = 0,946)


Рыночная экстракция: частный случай 1


В некоторых случаях в определении ставки дисконтирования может помочь информация о рынке и условиях ведения бизнеса теми или иными инвесторами. Для иллюстрации таких возможностей предлагается к рассмотрению следующий пример.

Предположим, оценщику стало известно, что производитель самолетов продает каждый самолет по цене 30 млн. долл. при их себестоимости 20 млн. долл. Однако при покупке сразу двух самолетов производитель предоставляет скидку на второй самолет в размере 3 млн. долл., или 10 % (т.е. цена второго самолета составляет 27 млн долл., а цена двух самолетов — 57 млн долл.). Известно также, что в среднем один самолет продается через каждые 6 месяцев, причем первый из них продается сразу после изготовления. Предположим, что оба самолета произведены в одно и то же время. Предположим также, что у производителя имеется избыточный складской запас, т.е. на момент продажи имелось не менее двух готовых самолетов. Дополнительно известно, что издержки хранения изготовленного и не проданного самолета составляют величину С_хр, определяемую следующим образом:


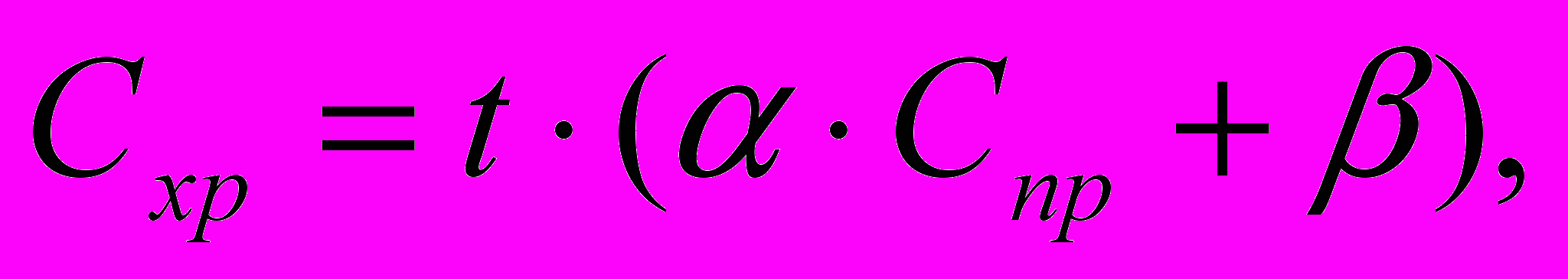(2.8)

где t — продолжительность хранения изделия на заводе с момента производства до продажи (по условию примера t = 0,5 года);

С_пр — себестоимость производства изделия (С_пр = 20 млн. долл.);

 — износ изделия в единицу времени (потеря стоимости, обусловленная моральным устареванием, порчей из-за вредного воздействия внешней среды и т.п.; при нормативном сроке эксплуатации самолетов данной серии (в нормо-часах) эквивалентном 25…30 лет,  = 0,04);

 — расходы завода направленные на хранение готовой продукции в единицу времени ( = 12000 долл. в год),

С_хр — издержки хранения готовой продукции (для вышеприведенных условий С_хр = 409500 долл.).

Таким образом, при сравнении двух вариантов продажи самолетов необходимо учитывать не только ускорение оборачиваемости активов при продаже большего количества изделий одновременно, но и издержки хранения готовой продукции. Если предположить, что производитель при назначении скидки руководствуется принципом одинаковой полезности «последовательного» и «параллельного» вариантов продажи (т.е. он выбирает скидку так, чтобы одновременная продажа двух изделий была для него также выгодна, как и продажа одного самолета раз в полгода), то должно выполняться равенство



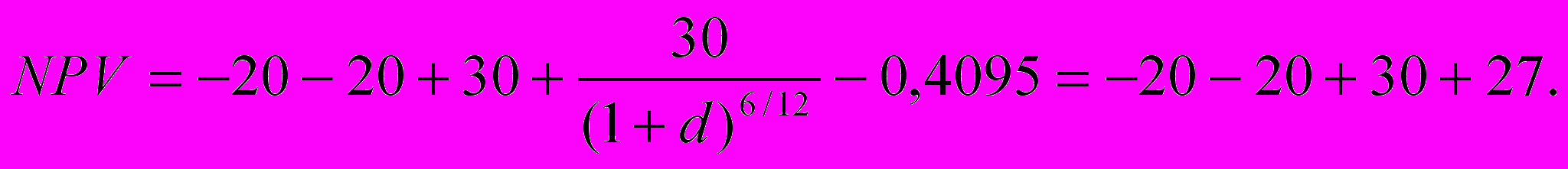
Решение этого уравнения относительно d дает значение ставки дисконтирования 19,8 %.

В общем случае при указанных выше предположениях и предоставлении скидки лишь для второго изделия, а также в предположении о том, что первое изделие реализуется сразу же после изготовления, ставку дисконтирования можно определять согласно формуле

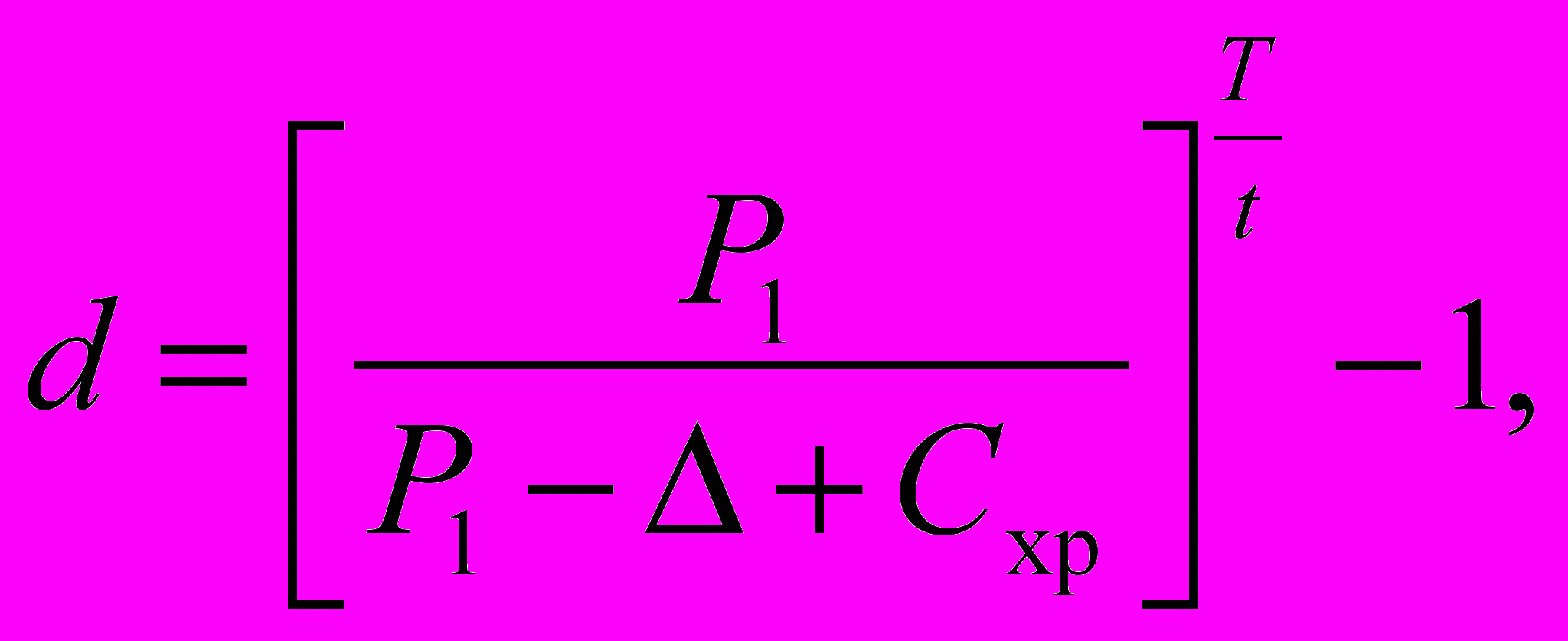(2.9)


где Р₁ — цена продажи одного изделия;

— размер скидки для второй единицы изделия;

C_хр — издержки хранения изделия за время t;

t — средний или ожидаемый период разделяющий продажи в «последовательном» режиме, доли года;

T — интервал времени, к которому привязана ставка дисконтирования, лет.


Рыночная экстракция: частный случай 2


Пусть оценивается некоторый доходоприносящий актив, застрахованный страховой компанией. Зная размер страховой премии по застрахованному активу, можно попытаться косвенно оценить вероятность наступления страхового случая, и через эту вероятность получить оценку ставки дисконтирования. Покажем идею применения этого метода.

Выручка страховой компании формируется на основе собранных страховых премий:


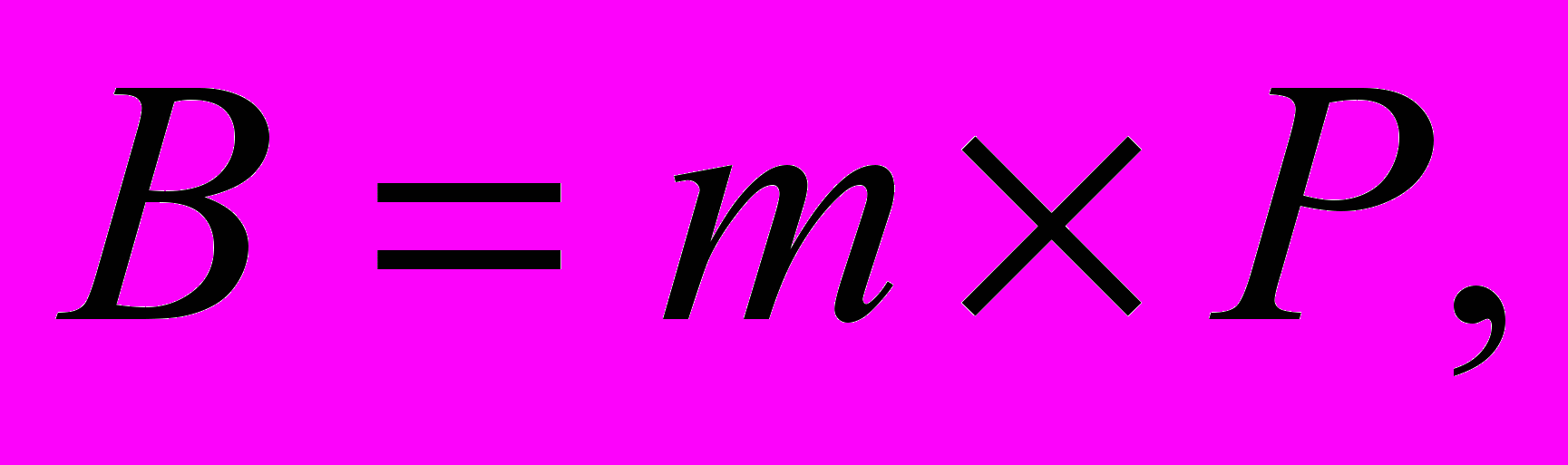(2.10)


где В - выручка страховой компании от страхования данного актива,

m - размер страховой премии – относительный тариф, рассчитываемый как доля от суммы страховой ответственности (страхового покрытия),

P – размер страховой ответственности страховой компании по застрахованному активу.

В то же время выручка страховой компании должна планироваться таким образом, чтобы она покрывала сумму страховых выплат за период (СтВ), накладные расходы компании (НР), и при этом еще оставалась прибыль (Пр):


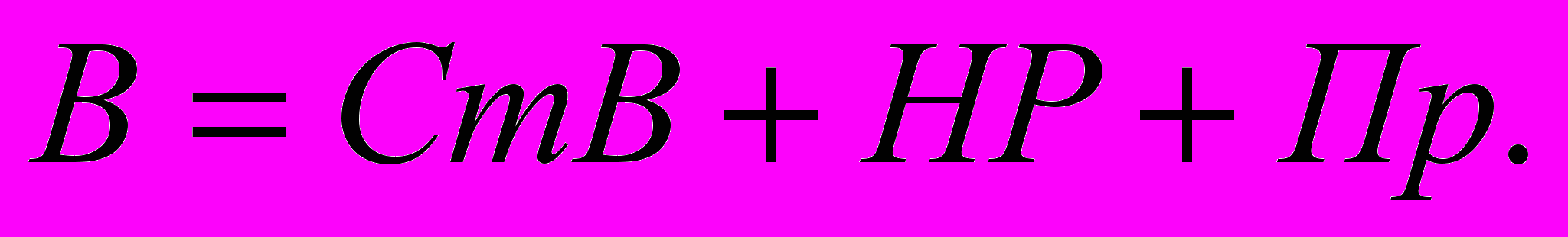(2.11)


Размер страховых выплат (СтВ) планируется исходя из статистических данных о вероятности наступления страховых случаев за период (год):


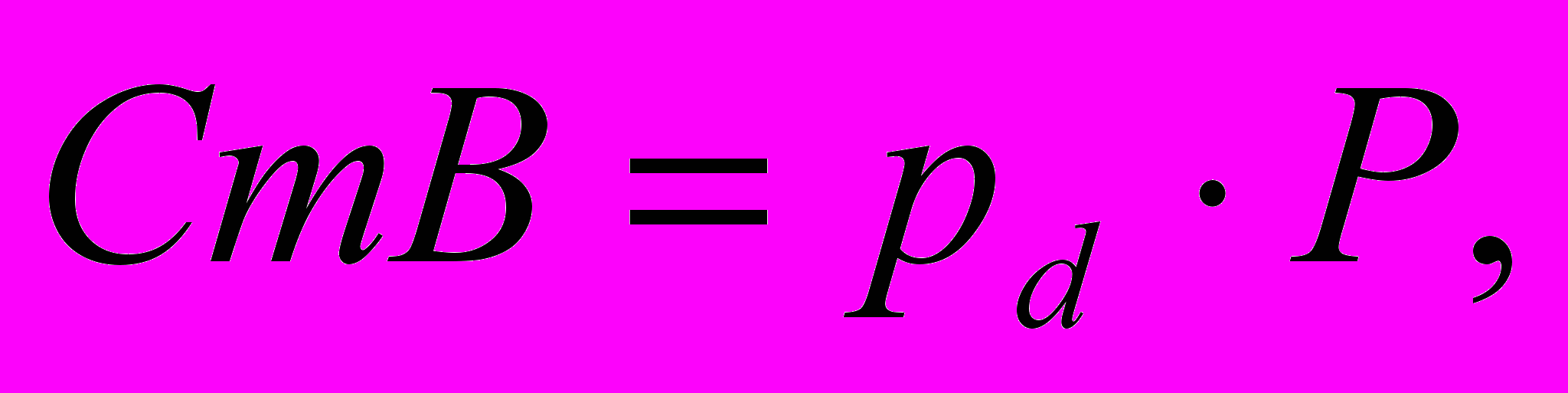(2.12)


где p_d – вероятность наступления страхового случая за год.

Из последнего выражения следует:





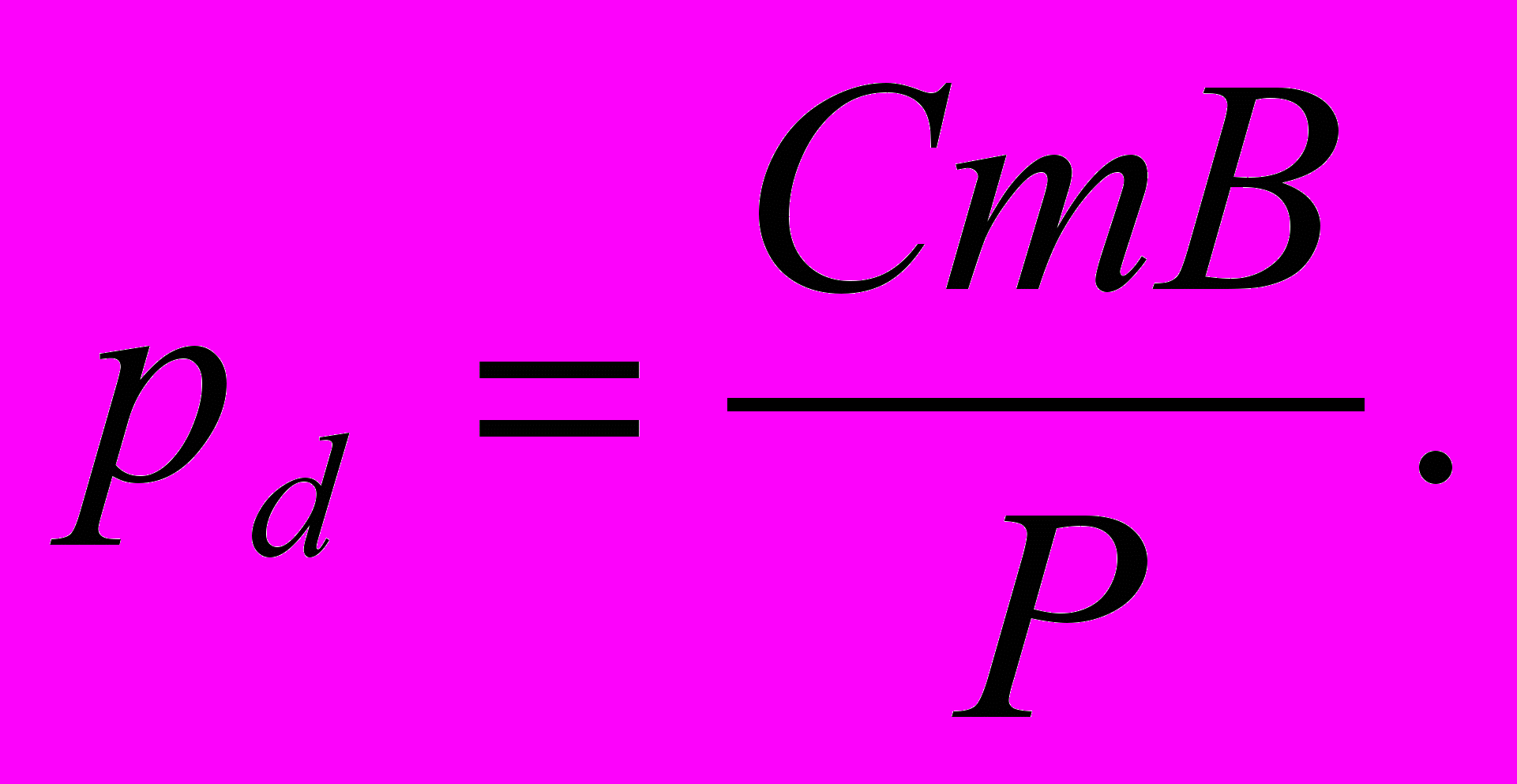
Подставляя в это выражение значение для Р, полученное из выражения (2.10) (Р = В/m), получим:


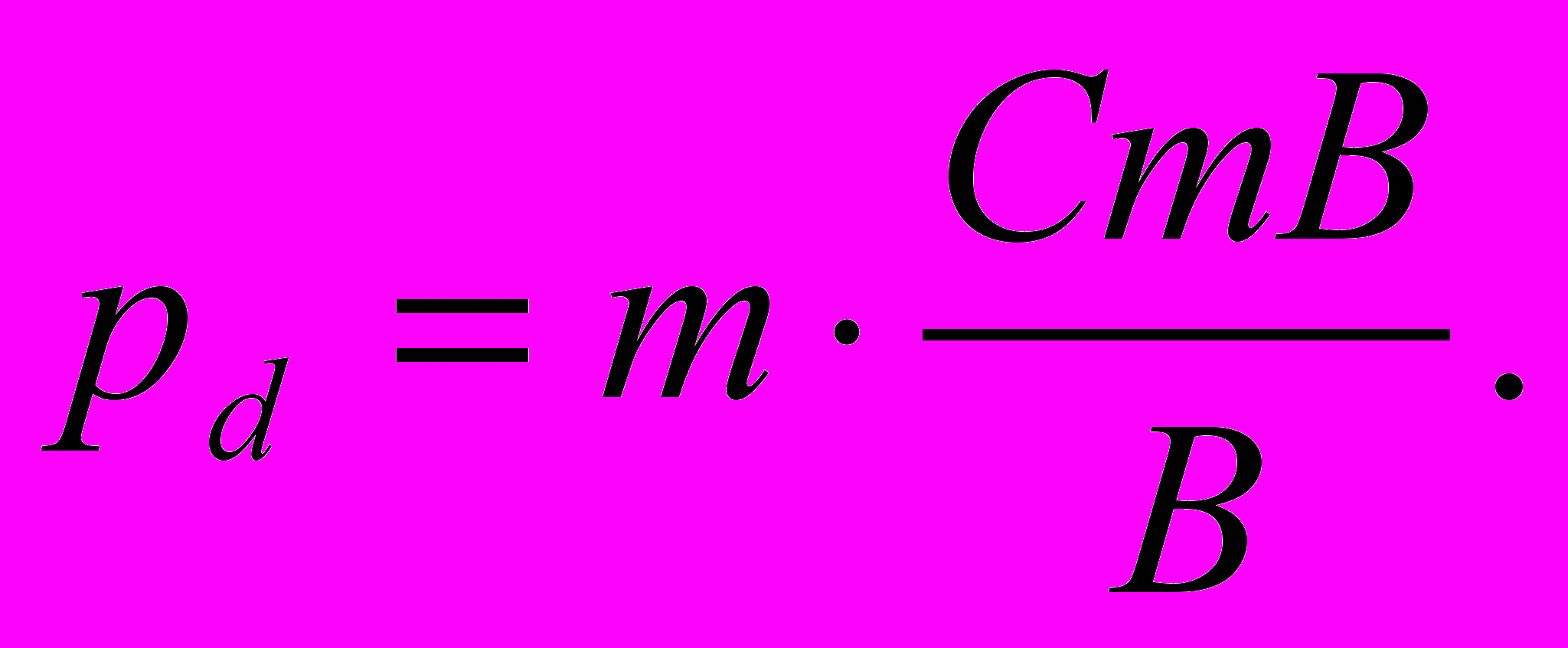(2.13)


Зная вероятность наступления страхового случая («дефолта» актива), можно оценить премию за риск для ставки дисконтирования оцениваемого доходоприносящего актива:





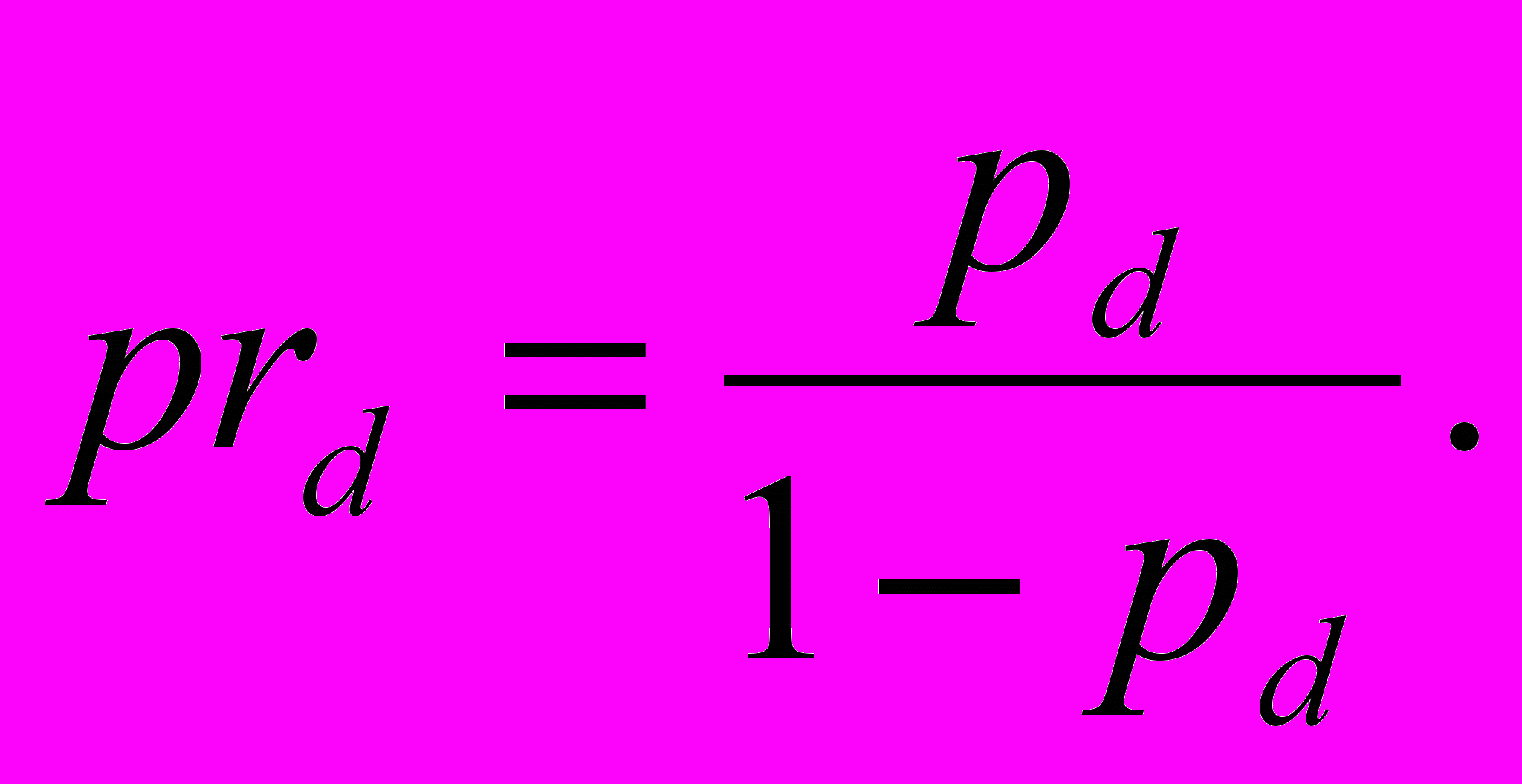
Примечание. В рамках настоящего примера для простоты рассмотрения неявно предполагалось, что компания осуществляет страхование однотипных объектов.


3. Особенности воздействия инфляции на ставку дисконтирования


Известно, что зависимость номинальной процентной ставки от значений реальной ставки и уровня инфляции описывается выражением И. Фишера:


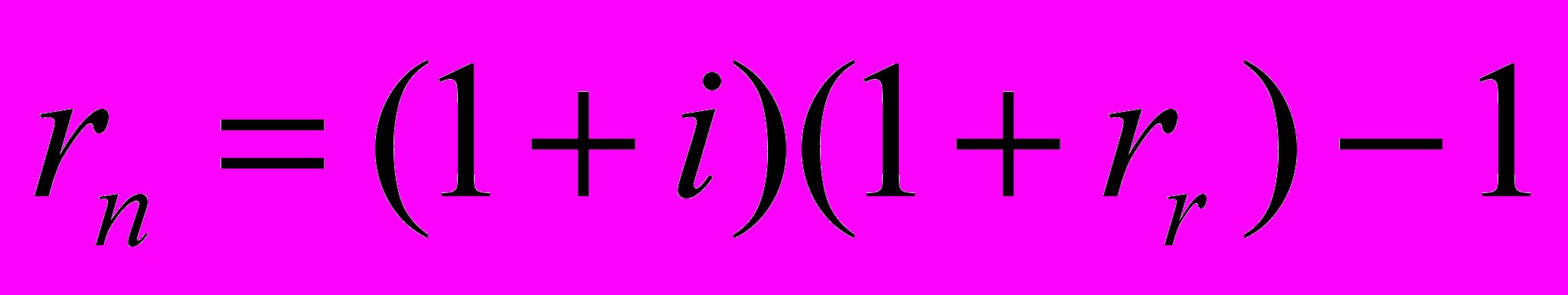, (3.1)


где r_n – значение номинальной процентной ставки,

i - уровень инфляции,

r_r - значение реальной процентной ставки.

В реальности наиболее целесообразным периодом дисконтирования является продолжительность цикла финансирования оцениваемой компании.

Рассмотрим схематично процесс осуществления корректировок. Предположим, значение ставки дисконтирования получено методом рыночной экстракции:


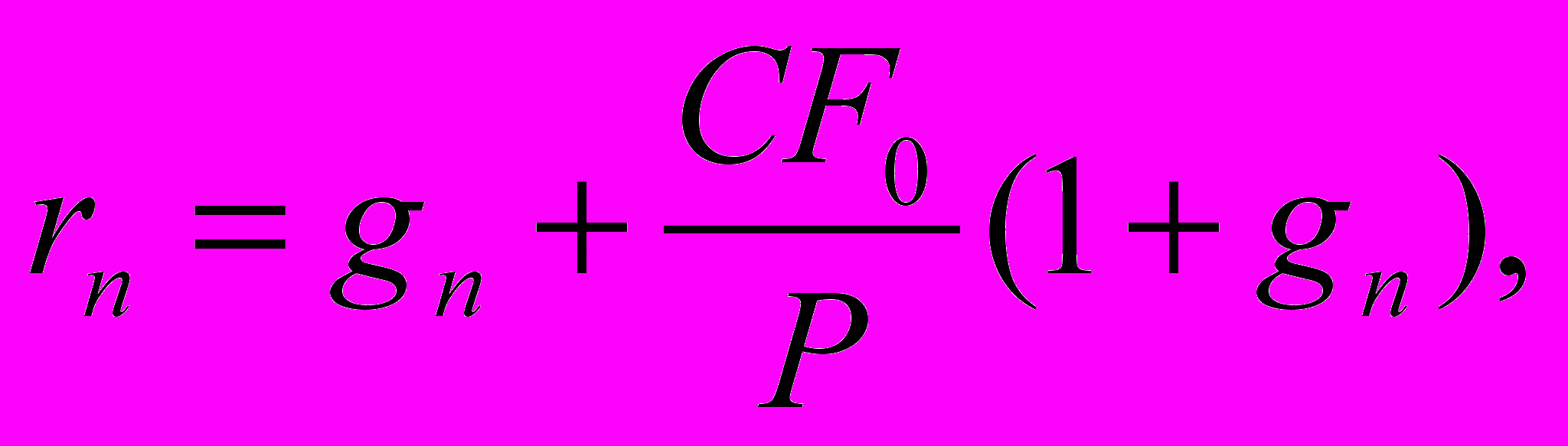(3.2)


где g_n – ожидаемый номинальный темп роста денежных потоков в год,

CF₀ - значение денежного потока за последний ретроспективный период- год,

P - стоимость актива, вытекающая из цен сделок с аналогичными объектами.

Следует однако учесть, что в реальности обычно потоки поступают в течение каждого финансового цикла, каждый из которых может быть меньше или больше календарного года, ввиду чего в расчетах следует учесть данный фактор. Сделать это можно несколькими способами.

1. Значения денежного потока и темпа роста берутся не в годовом исчислении, а в «циклическом», т.е. значения CF₀ и g берутся за период равный продолжительности финансового цикла. В результате этого адаптированные для вычислений номинальной ставки дисконтирования параметры выражения (3.2) трансформируются в следующие:
   

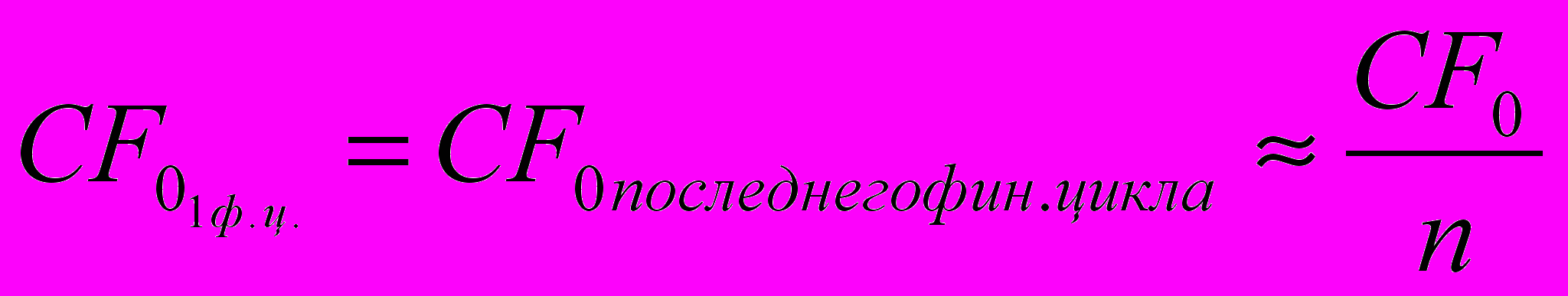, (3.3)


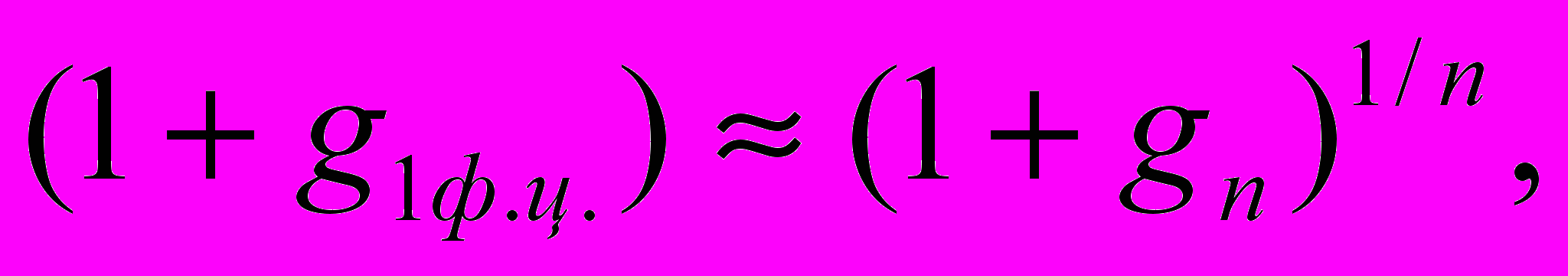(3.4)

где n – число циклов финансирования в году,

а само значение номинальной ставки дисконтирования для одного финансового цикла равно:


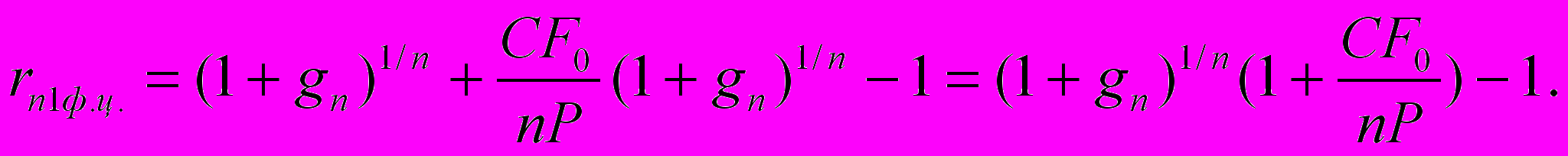(3.5)


Дальнейшие процедуры дисконтирования осуществляются посредством подстановки в числовой ряд дисконтируемых денежных потоков параметров полученных в выражениях (3.3)-(3.5), при этом при неизменности фактической длины прогнозного периода число членов расчетного числового ряда изменится в n раз.

2. С другой стороны, известно, что коммерческая деятельность компаний внутренне защищена от воздействия инфляции: при росте цен на входящее сырье обычно адекватно повышаются цены на готовую продукцию¹, поэтому воздействие инфляции осуществляется лишь в течение одного цикла финансирования. Принимая это во внимание, выражение (3.1) можно переписать в следующей уточненной форме:
   

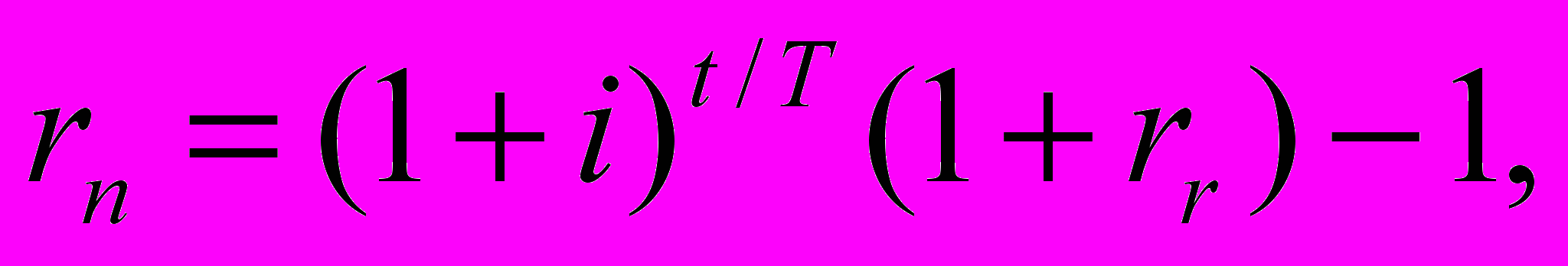(3.6)


где t – продолжительность цикла финансирования оцениваемого предприятия,

T - период времени соответствующий одному календарному году.

Для изучения возможностей использования выражения (3.6) рассмотрим две ситуации.

0. 1. Пусть для компании-аналога 1 известна номинальная ставка дисконтирования r_n1 и продолжительность финансового цикла – t_ф.ц.1. Чему равна ставка дисконтирования оцениваемой компании r_n0, если инфляция равна i, а продолжительность ее финансового цикла – t_ф.ц.0? Для ответа на этот вопрос распишем выражения для обеих ставок дисконтирования – известной r_n1 и неизвестной r_n0:
   

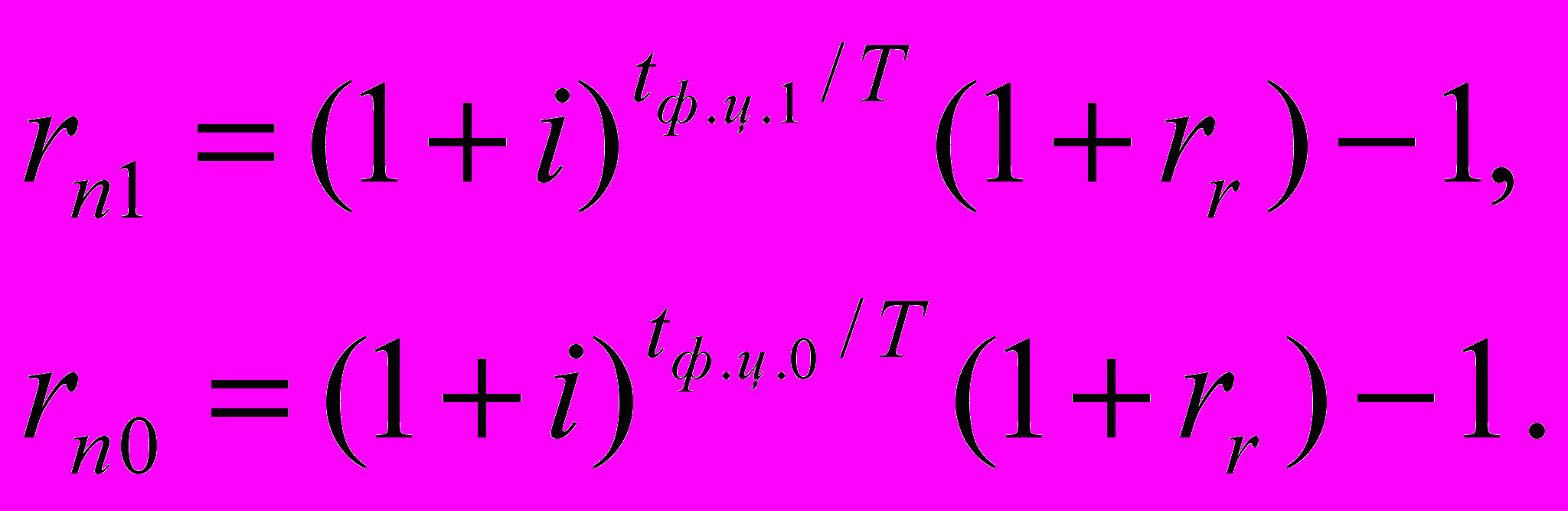
После несложных преобразований получим следующее выражение для значения искомой ставки:


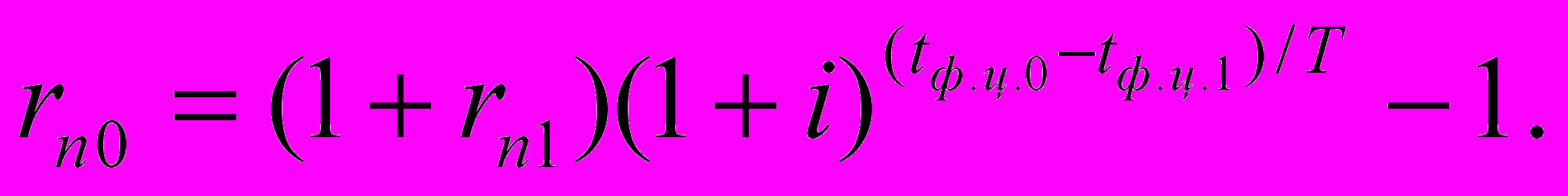(3.7)


Приведем пример с использованием выражения (3.7).

Пусть i = 12%, r_n1 = 20%, t_ф.ц.1 = 12 мес., t_ф.ц.0 = 6 мес.. Тогда

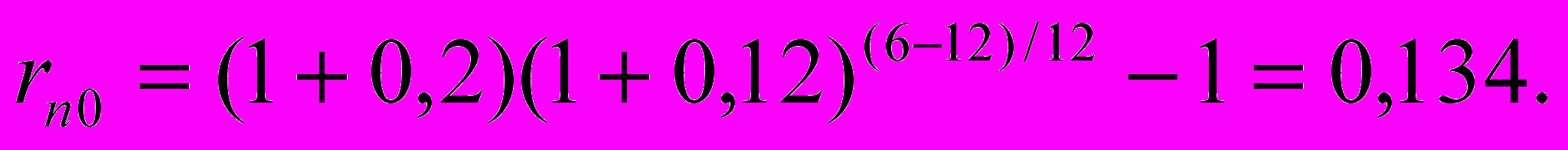
0. 2. Пусть было известно значение r_n при i = i₀ и продолжительности цикла финансирования t_ф.ц. Также известно, что в следующем периоде уровень инфляции станет равным i₁. Как изменится при этом ставка дисконтирования r_n при неизменности остальных параметров? Осуществив несложные манипуляции, получим следующее выражение для ответа на поставленный вопрос:
   

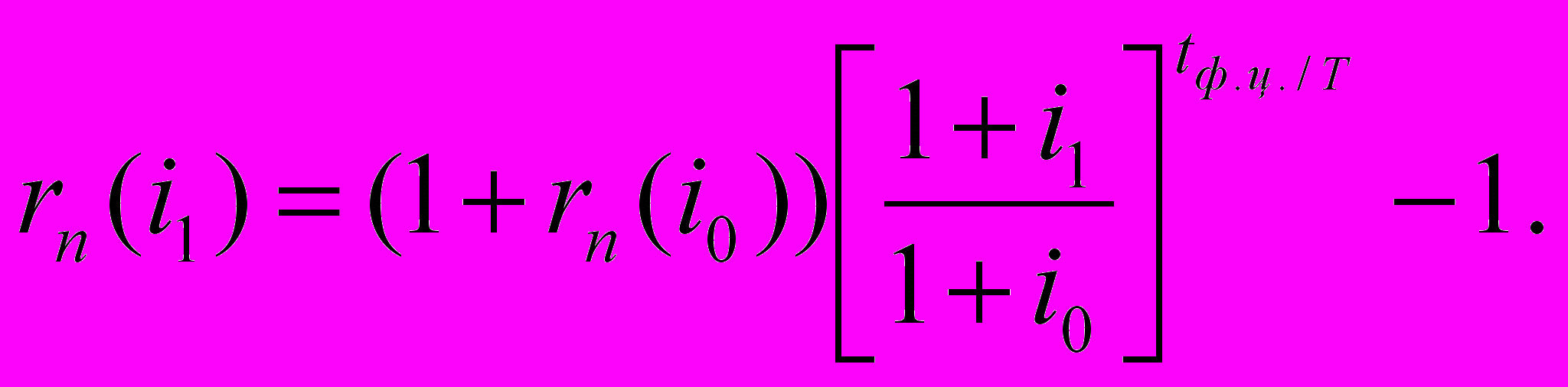(3.8)


Приведем пример с использованием выражения (3.8).

Пусть i₀ = 24%, i₁ = 12%, r_n(i₀) = 20%, t_ф.ц./T = 1/12. Тогда





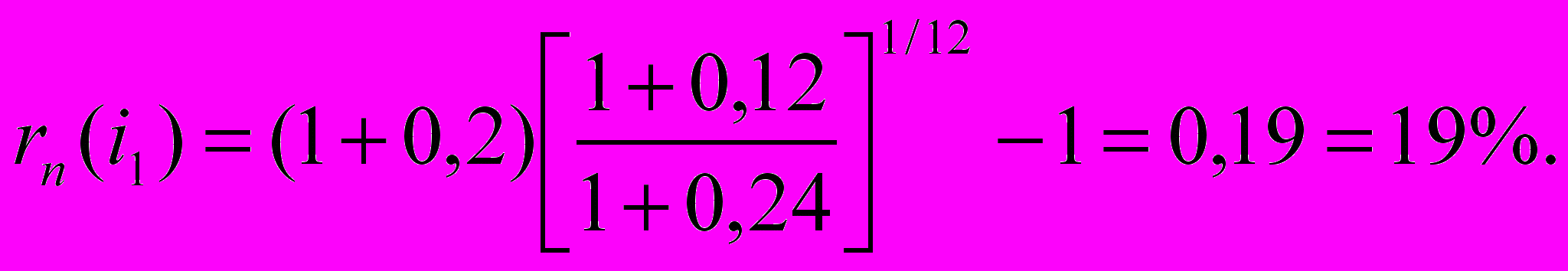
4. Особенности соотнесения разнобазовых ставок дисконтирования


Следует отметить, что иногда (например, в процессе принятия решений по венчурным инвестициям или в ряде случаев сделок по слияниям-поглощениям) ставка дисконтирования определяется самим инвестором посредством «назначения» ее желаемого уровня. Исходя из этого, рассчитывают приемлемый для инвестора уровень уплачиваемой цены, при котором достигается необходимый уровень доходности от сделки.

В то же время в оценочной литературе часто указывается на то, что каждому типу денежного потока должна соответствовать определенная ставка дисконтирования или ставка капитализации. Нередко при оценке компаний используется мультипликатор «Цена/Доход», размерность которого представляет собой «1 / Ставка капитализации дохода». При этом нередко возникает ситуация, когда для группы сопоставимых компаний-аналогов известен мультипликатор, основанный на одной базе дохода, а для оцениваемой компании известна другая база дохода. В таких случаях необходимо скорректировать базу дохода оцениваемой компании, приведя ее к базе известных компаний-аналогов, либо скорректировать мультипликатор (ставку капитализации) к базе оцениваемой компании. В качестве примера приведем выражения, которые можно использовать для корректировок ставок капитализации:

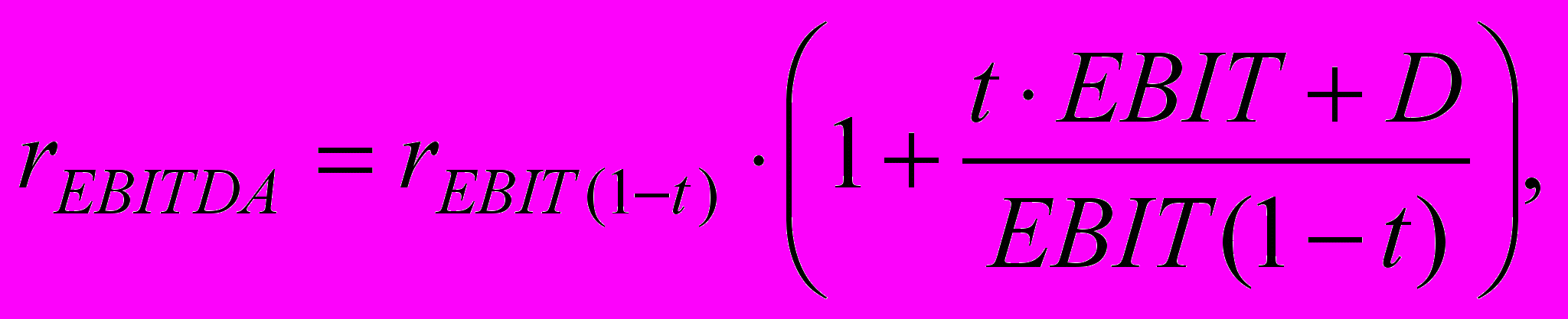(4.1)

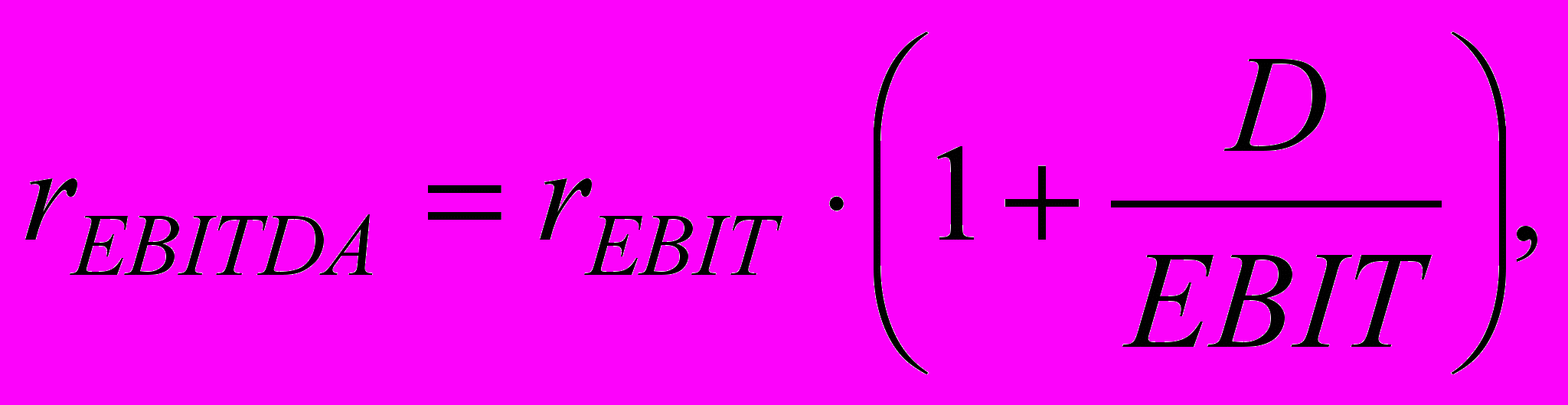(4.2)

где — ставка капитализации, используемая для прибыли до вычета процентов, налогов и амортизации;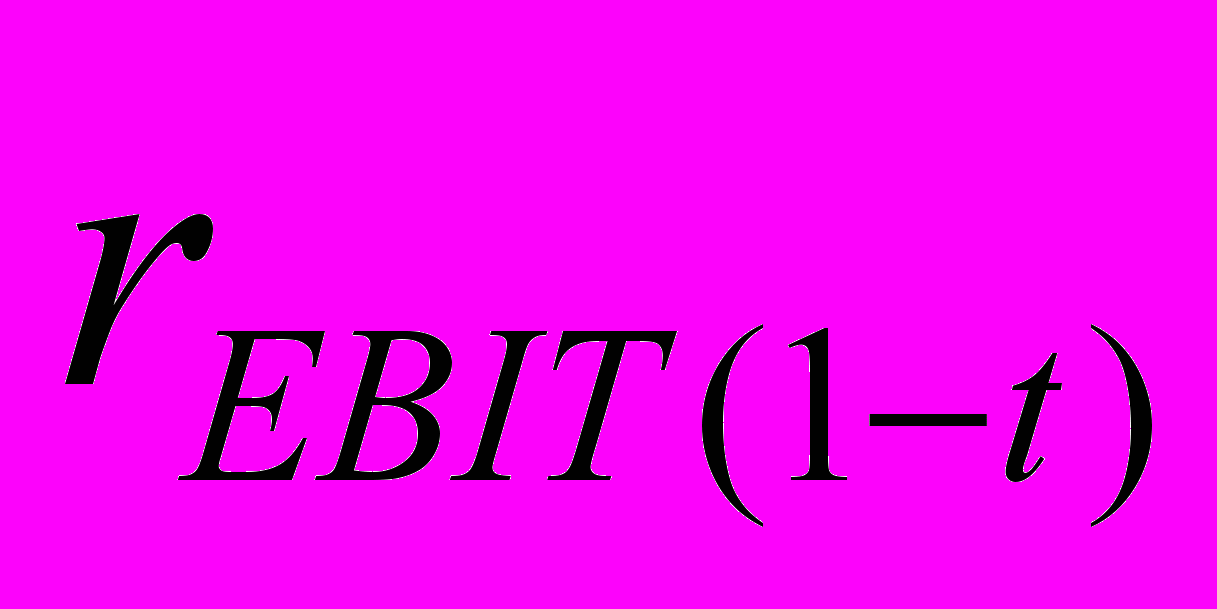

— ставка капитализации, используемая для прибыли до вычета процентов;

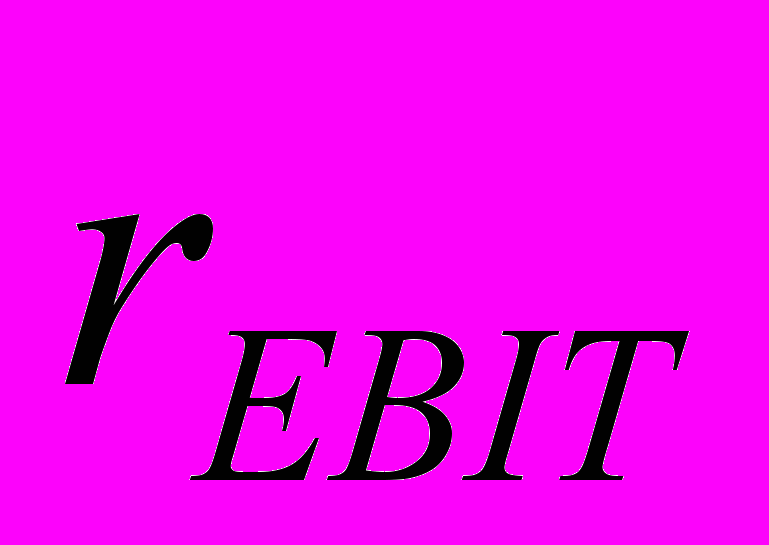— ставка капитализации, используемая для прибыли до вычета процентов и налогов;

t — эффективная ставка налога на прибыль;

EBIT — прибыль до вычета процентов и налога;

D — амортизационные начисления.

Пусть для примера известно, что мультипликатор P/EBIT = 7 (что при нулевых темпах роста эквивалентно ставке капитализации операционной прибыли 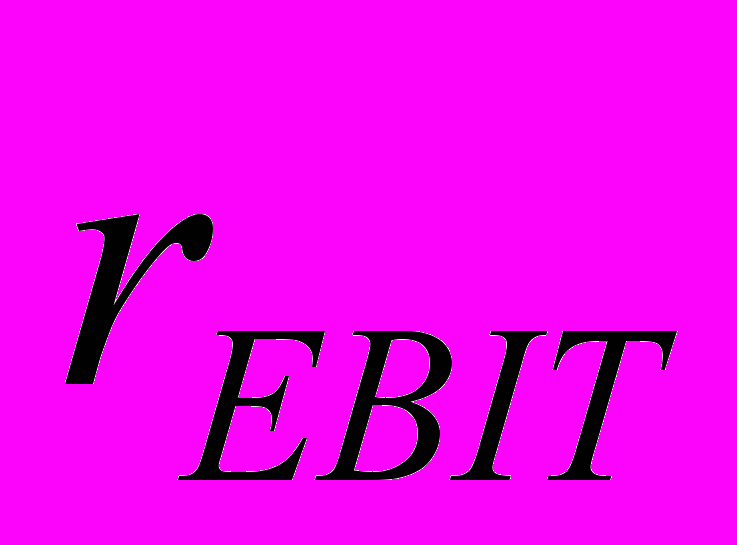= 1/7 = 0,143), EBIT = 200 и D = 80. Тогда ставка капитализации прибыли до вычета амортизации составит: 0,143(1 + 80/200) = 0,20.


5. Соответствие валюты выражения денежных потоков валюте выражения ставки дисконтирования


Еще один момент, на который хотелось бы обратить внимание читателя, заключается в соответствии валюты ожидаемых денежных потоков (и их темпа роста в постпрогнозном периоде) валюте ставки дисконтирования. Довольно распространенной ошибкой является оценка будущих денежных потоков российских компаний в долларах США при ориентации на рублевые процентные ставки или ставки доллара (инфляцию) в США. Чаще всего в расчетах используют неочищенные от инфляции номинальные денежные потоки соответствующих периодов и номинальную ставку дисконтирования. Совместное использование этих параметров является вполне корректным, однако необходимо помнить о том, что на темп роста денежных потоков в постпрогнозном периоде инфляция оказывает самое непосредственное влияние. Поэтому, если оценщик использует стандартное допущение о том, что темп роста денежных потоков пропорционален уровню цен, при «зашитой» в ставке дисконтирования инфляции порядка 10…15 % выбор темпа роста менее 10…15 % будет однозначно приводить к занижению стоимости объекта оценки (исключение составляют потоки компаний или проектов дегенеративного типа, у которых сокращается производство продукции в натуральном выражении). Если допустить, что для двух валют соблюдается паритет покупательской способности, то при переводе потоков с одной валюты a на другую валюту b трансформация ставки дисконтирования должна осуществляться следующим образом:

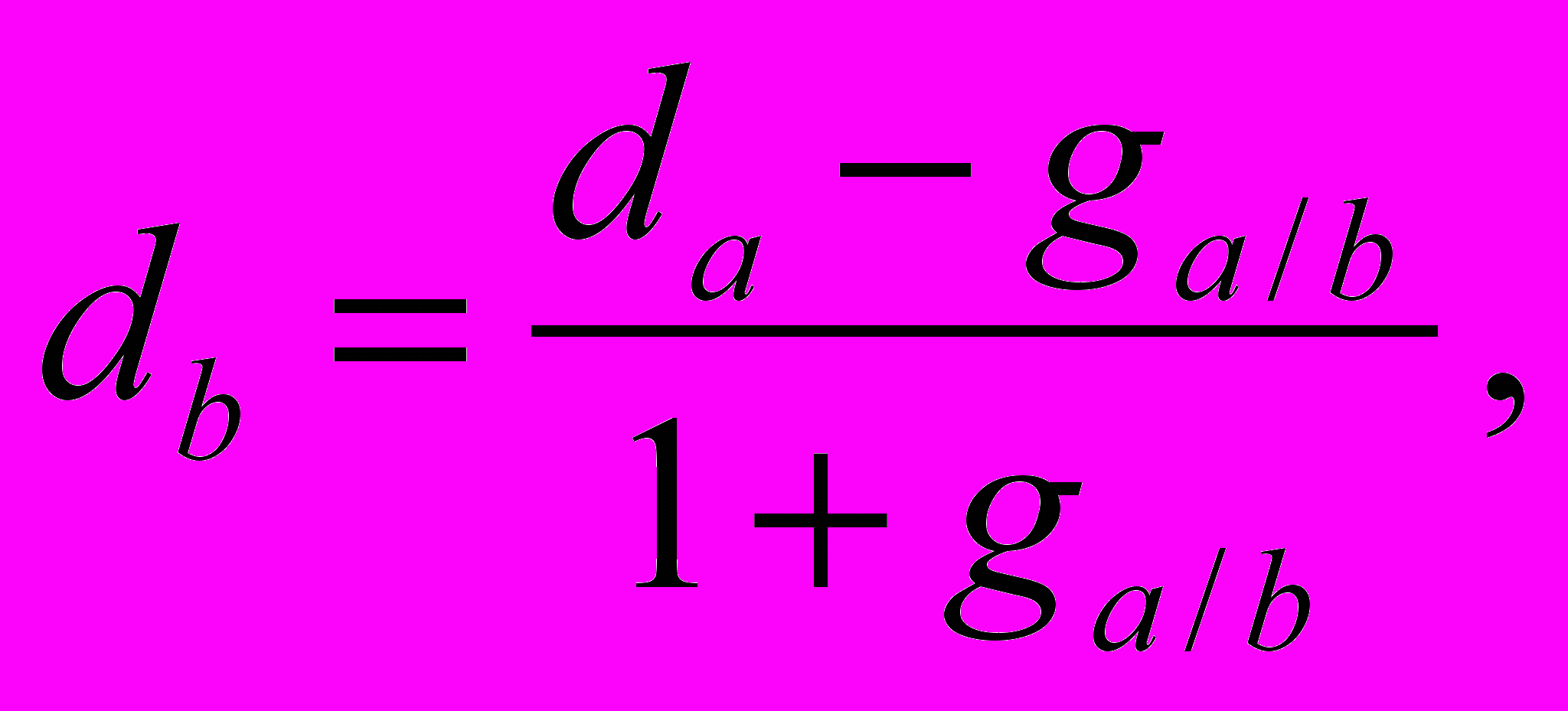(5.1)

Где d_b — ставка дисконтирования выраженная в «сильной» валюте b;

d_a — ставка дисконтирования выраженная в «слабой» валюте a;

g_a/b — темп снижения курса «слабой» валюты a относительно курса «сильной» валюты b.

Отметим, что выражение (5.1) верно лишь в случае, когда темп изменения сравниваемых валют пропорционален разности инфляции в соответствующих странах. Для демонстрации использования формулы (5.1) предположим, что объем выпуска оцениваемой российской компании останется неизменным в натуральном выражении, текущий курс рубля к доллару равен 30 руб./долл., а темп снижения рубля к доллару примерно совпадает с уровнем российской инфляции (10 %) и таковой принят в качестве темпа роста в постпрогнозном периоде (высоковато, конечно, но ведь это пример). Также предположим, что ставка дисконтирования денежных потоков выраженных в рублях составляет 20 %. Тогда, если оценщик пожелает по каким-либо причинам (например, для иностранных партнеров) использовать денежные потоки номинированные в долларах, в качестве ставки дисконтирования он должен использовать следующее значение:

d_$ = (0,2 – 0,1)/(1 + 0,1) = 0,1/1,1 = 0,09.

Предположим теперь, что данная компания генерирует 100 тыс. долл. в год свободных денежных средств, или 3 млн. руб. Тогда стоимость компании составит:

в рублевом эквиваленте: 3(1 + 0,1)/(0,2 – 0,1) = 33 млн. руб.;

в долларовом эквиваленте: 100/0,0909 = 1,10 млн. долл.

Как видно, полученные результаты — 33 млн. руб. и 1,1 млн. долл., — представляют собой одну и ту же стоимость (с учетом текущего курса доллара получим: 33 млн. руб./ 30 руб./долл. = 1,1 млн. долл.).

В настоящее время формула (5.1) неприменима для перевода рублевых ставок в долларовые, поскольку, во-первых, инфляция доллара в РФ превышает инфляцию рубля; во-вторых, при росте курса рубля относительно доллара инфляция в России все еще остается более высокой, чем в США (что обусловлено, прежде всего, политическими решениями Российского Правительства во второй половине 1998 г., приведшими к установлению более слабого курса рубля по сравнению с его сравнительной покупательной способностью).

В общем случае (т.е. когда темпы роста разновалютных потоков пропорциональны соответствующему темпу инфляции и отличны от нуля) трансформация ставки дисконтирования, выраженной в одной валюте, в ставку дисконтирования, выраженную в другой валюте, может осуществляться следующим образом:

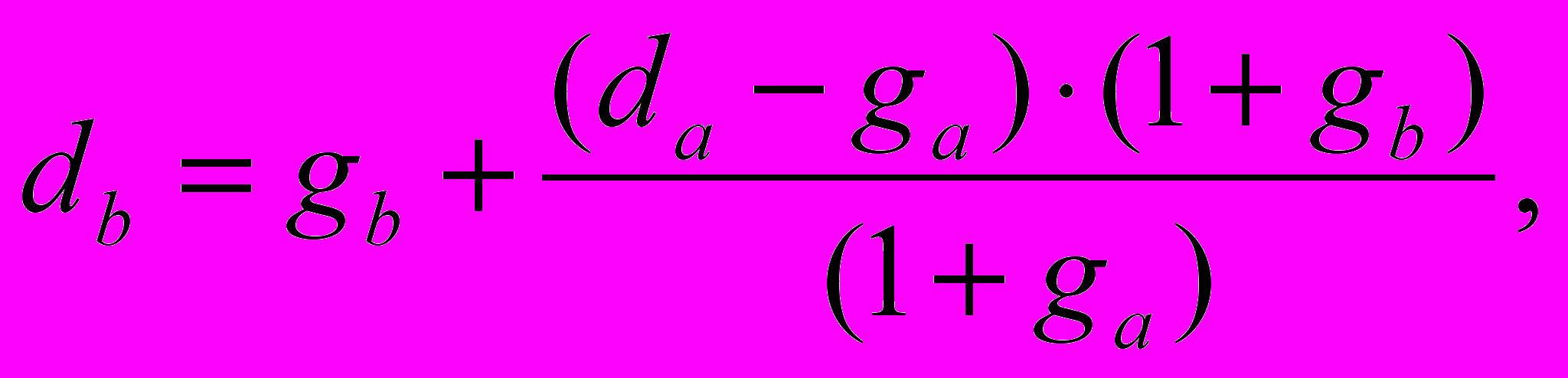(5.2)

где d_b — неизвестная ставка дисконтирования для валюты b;

d_a — известное значение ставки дисконтирования для потоков, выраженных в валюте a;

g_b — ожидаемый темп роста денежных потоков, выраженных в валюте b;

g_a — ожидаемый темп роста денежных потоков, выраженных в валюте a.

Рассмотрим другой пример с использованием выражения (5.2). Пусть известно, что потоки компании генерируются в России, где уровень инфляции (рубля) примерно равен 10%, и известно, что ставка дисконтирования рублевых потоков компании равна 20%. Также известно, что Правительство полно решимости укреплять не только реальный, но и номинальный курс рубля, и это номинальное укрепление на ближайший год составит 5%. Требуется оценить долларовую ставку дисконтирования (при этом пренебречь рассмотренным выше эффектом воздействия продолжительности финансового цикла на номинальную ставку дисконтирования). Из условия примера следует, что номинальный темп снижения курса доллара в России составит:





Подставляя это значение в (5.2), получим:





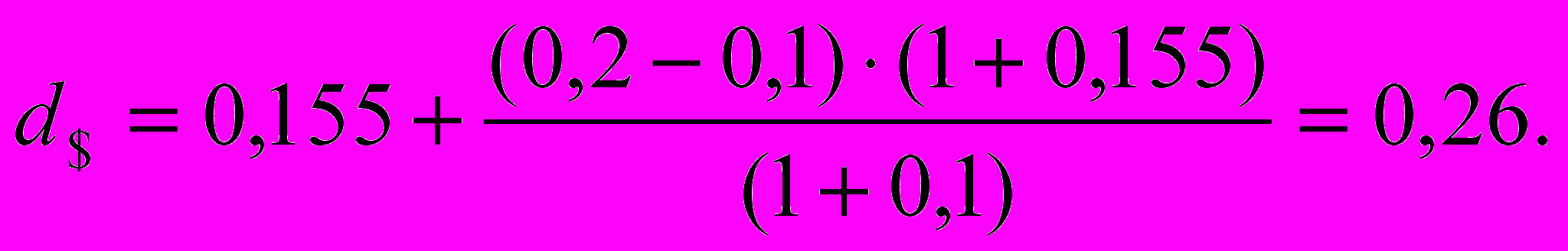
Как видно, полученное значение долларовой ставки дисконтирования (26%) превышает в данном случае значение рублевой ставки, что обусловлено снижением курса доллара относительно рубля и, как следствие, более высокую инфляцию доллара в России (по сравнению с инфляцией рубля). Отметим, что подобная ситуация (когда при меньшей инфляции доллара в США по сравнению с инфляцией рубля в России курс рубля укрепляется по отношению к доллару) объясняется превалированием фактора паритета покупательной способности над фактором процентного дифференциала. Такая ситуация возникла как следствие положительного торгового баланса России вообще (при хронически отрицательном торговом балансе США), и положительного сальдо в торговле РФ с США, в частности.


В заключение остается добавить, что затронутая тема слишком широка и многообразна, вследствие чего невозможно в рамках одной статьи (и даже нескольких) отразить все связанные с ней факторы, аспекты и нюансы…