Лекция 5 Замечание Если {[a n,b n ]} система вложенных стягивающихся к нулю отрезков и с[a

Вид материала

Лекция

Подобный материал:

• Вопросы вступительных экзамен по специальности в магистратуру, 59.93kb.
• Календарный план лекций по курсу «математический анализ» Для специальности «Математика», 39.98kb.
• Изменчивость и устойчивость александр Н. Павлов, 345.14kb.
• Лекция 15. Определённый интеграл, 71.1kb.
• Решение квадратных уравнений, 230.02kb.
• Лекция 2 Экономическая система, как объект кибернетики, 70.17kb.
• Введение «Стремиться к нулю» – тема Всемирного дня борьбы со спидом в 2011г, 431.1kb.
• Лекция n 11, 759.84kb.
• Физический диктант «Работа сил электростатического поля. Разность потенциалов», 38.51kb.
• Макс Фрай Мой Рагнарёк, 4897.97kb.

Лекция 5

Замечание 2. Если {[a_n,b_n]} система вложенных стягивающихся к нулю отрезков и с[a_n,b_n], то .

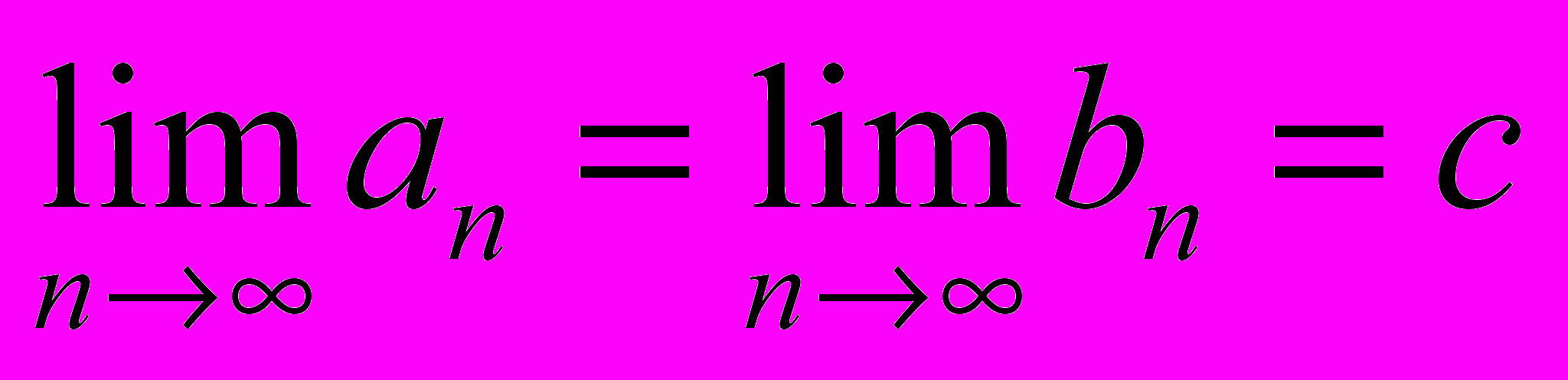Доказательство:



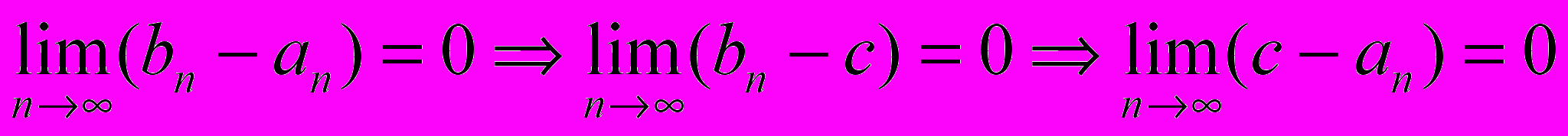
Пример. Число e

Индукцией по n доказывается формула ( Бином Ньютона ):

.

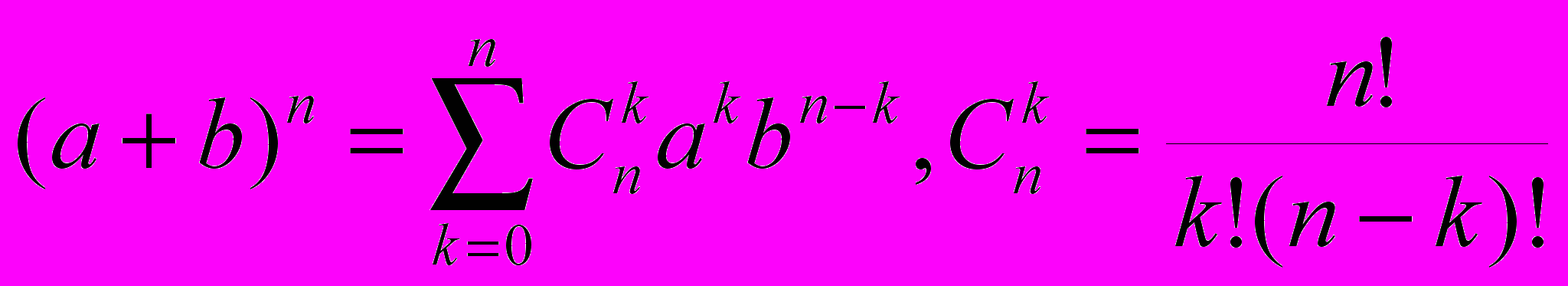Для последовательности x_n=(1+1/n)ⁿ получим





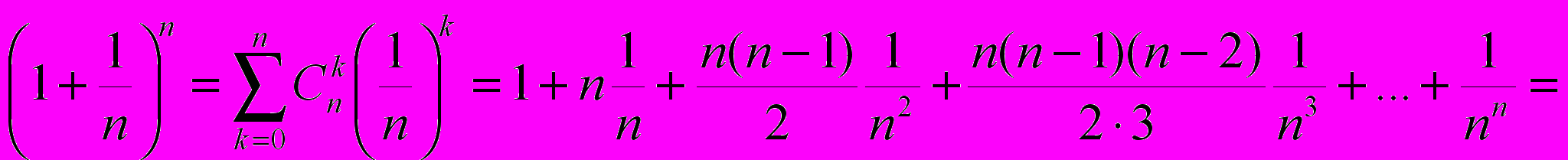
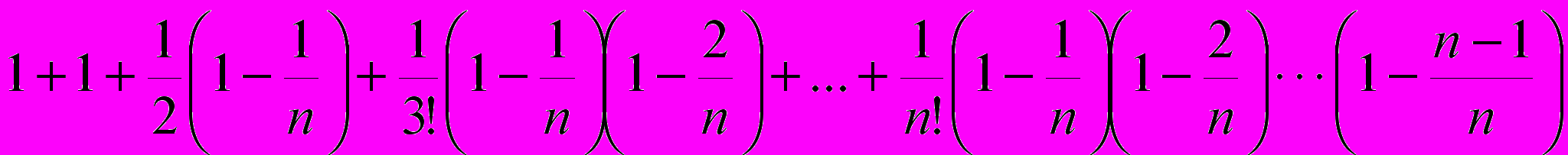
При переходе от n к n+1 каждое слагаемое в этой сумме увеличивается и растет их общее число, поэтому x_n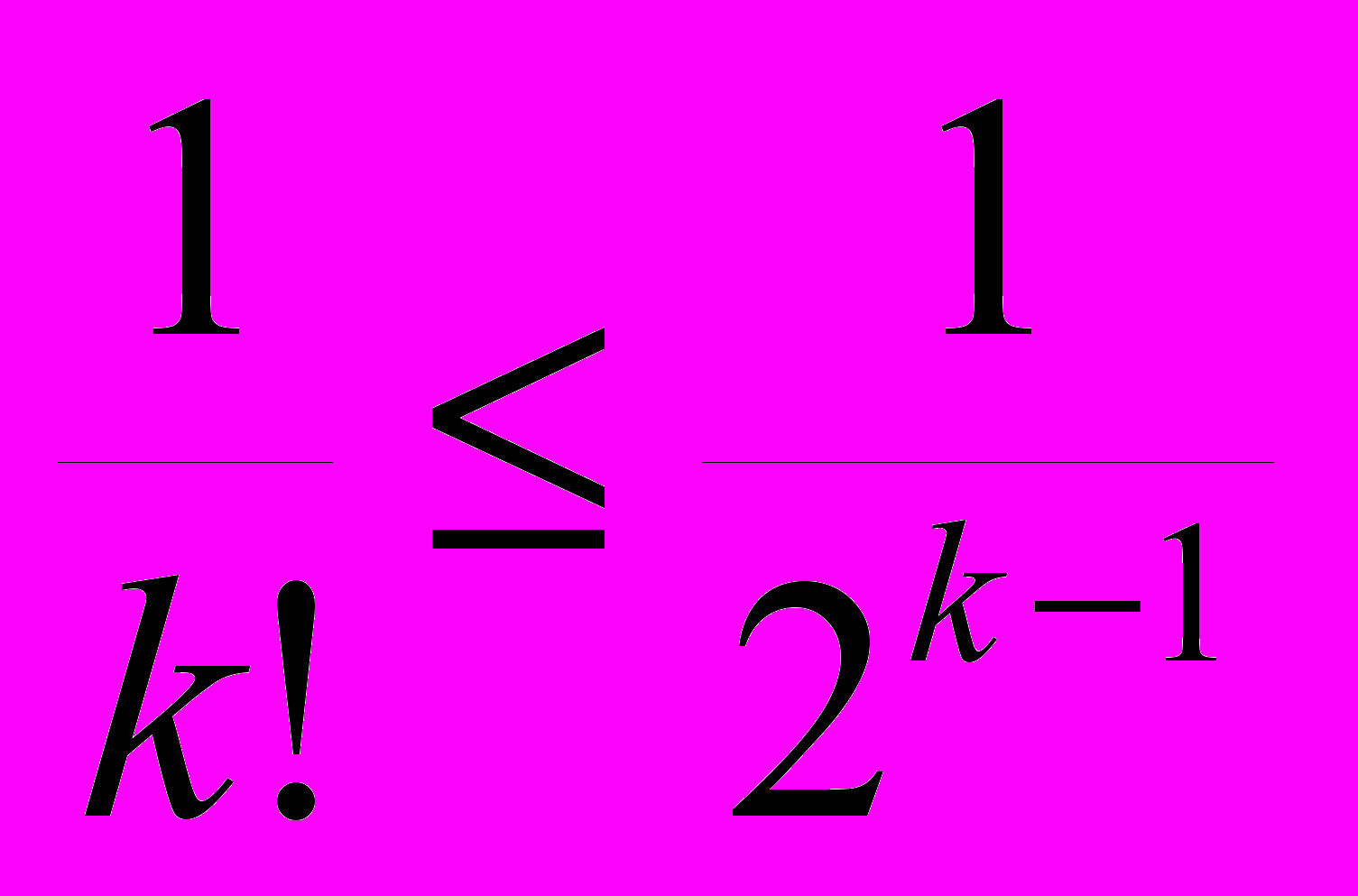n+1. Каждая скобка <1 и , поэтому

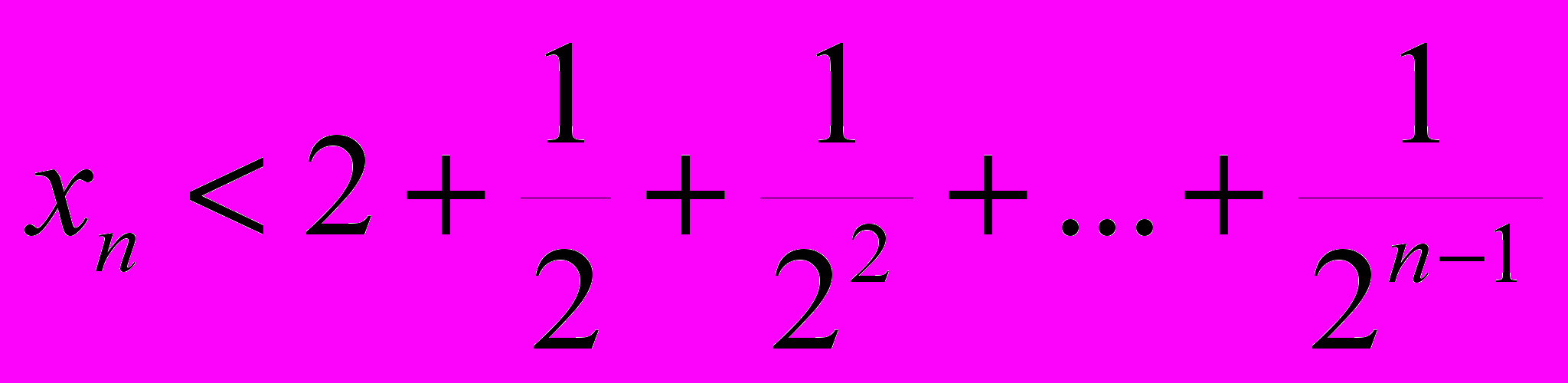. Монотонно возрастающая ограниченная последовательность сходится к некоторому числе, которое обозначается e. Это трансцендентное число называется числом Эйлера e=2.7182818284…


§3. Некоторые свойства последовательностей связанные со свойством непрерывности вещественных чисел

1.Подпоследовательность. Теорема Больцано-Вейерштрасса

Опр. Дана последовательность {x_n} и последовательность натуральных чисел {n_k},1n₁₂<…_kk+1<…

тогда последовательность {y_k}, 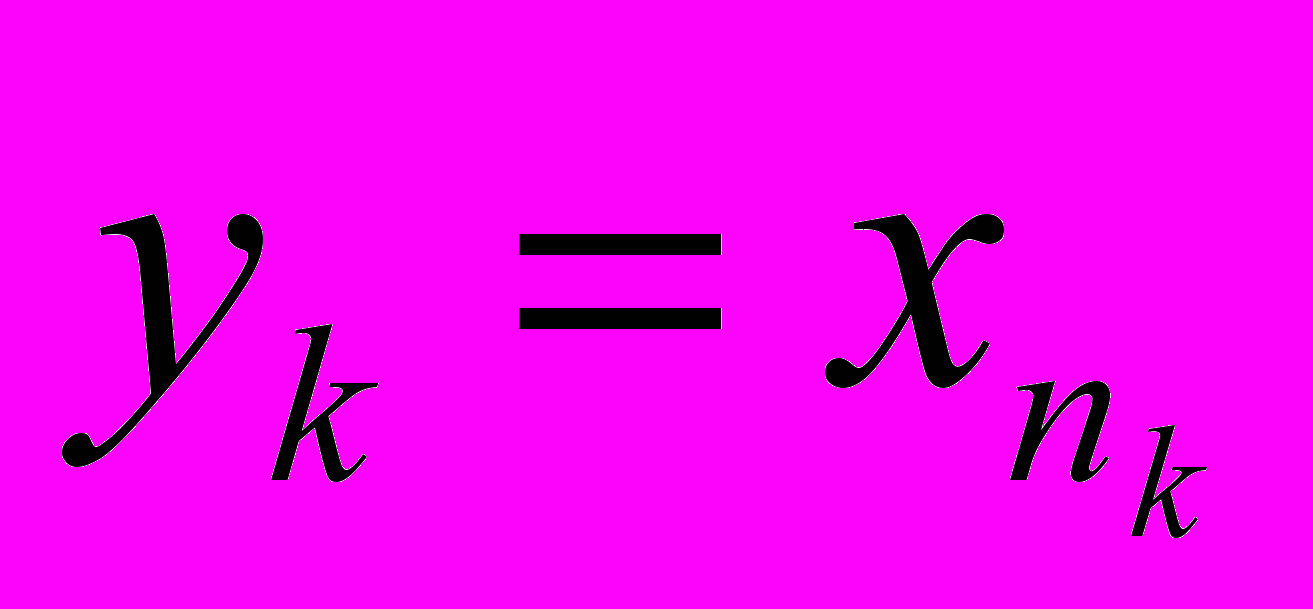называется подпоследовательностью последовательсти {x_n}.

Пример: sin n, sin 2n.

Замечание. Отметим, что n_kk.

Теорема 1. Если 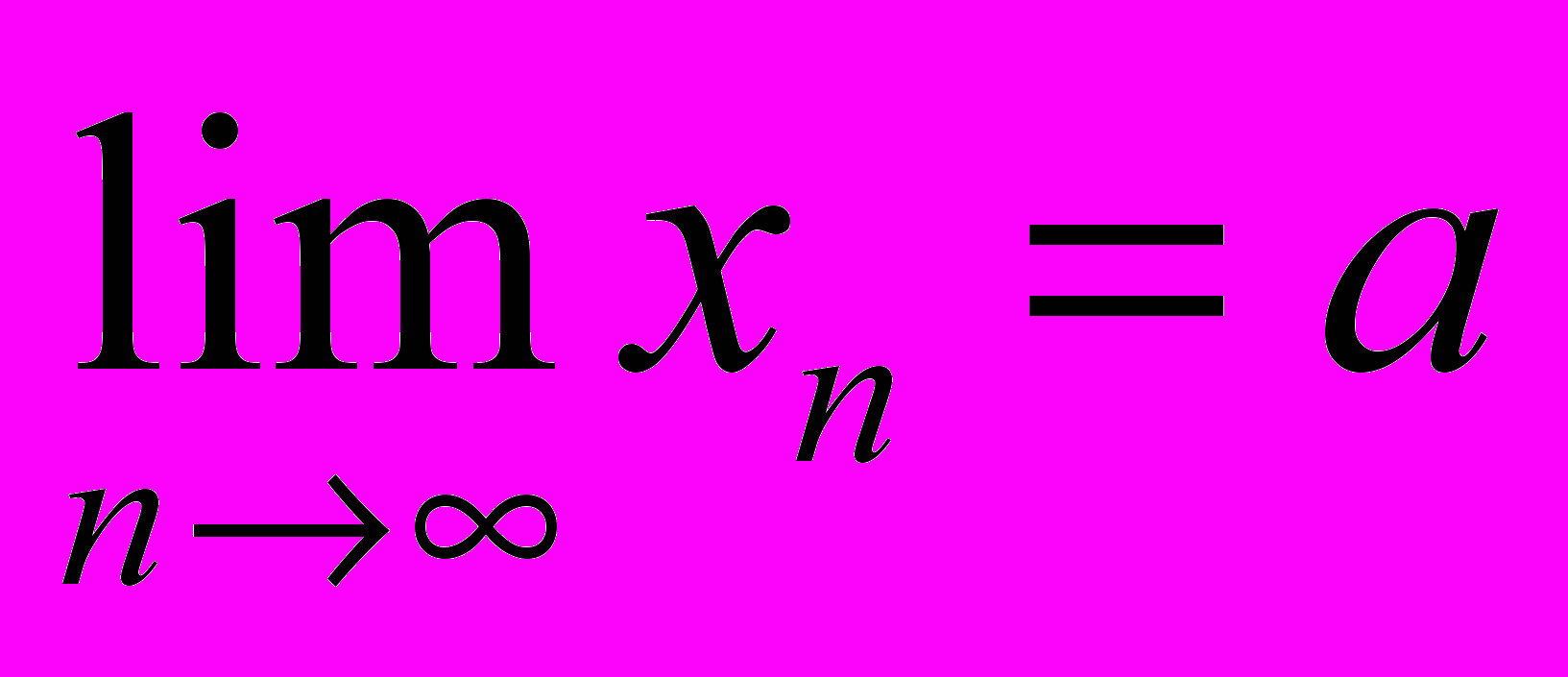(a - число или символ) , то для любой ее подпоследовательности {y_k}, 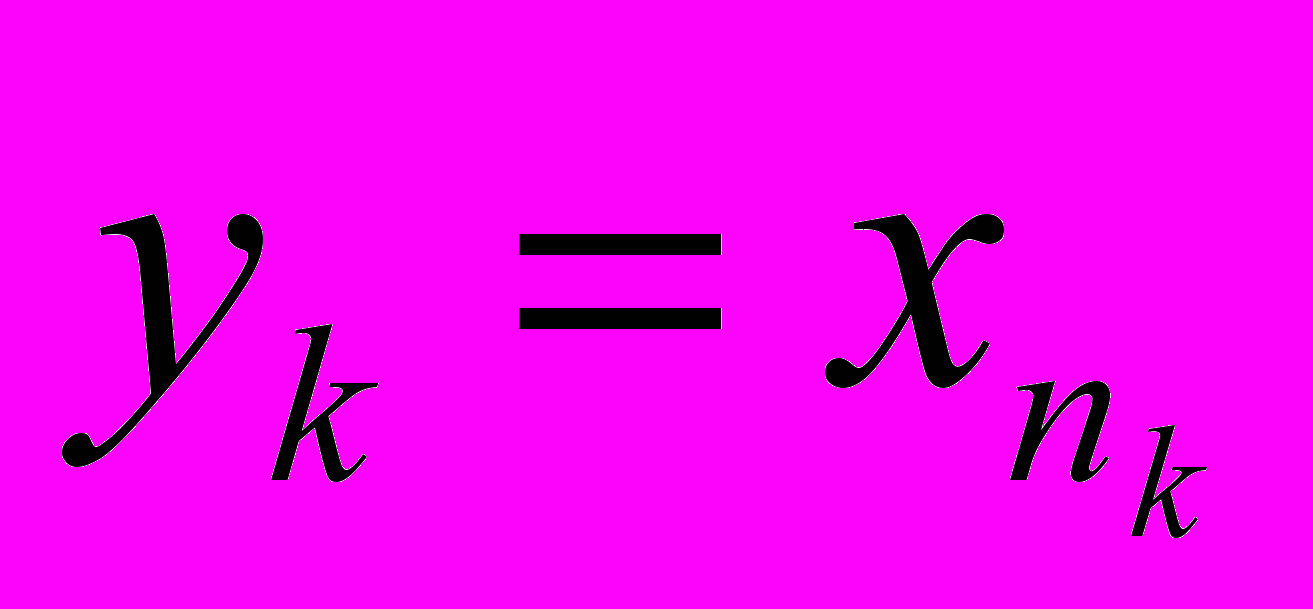,будет .

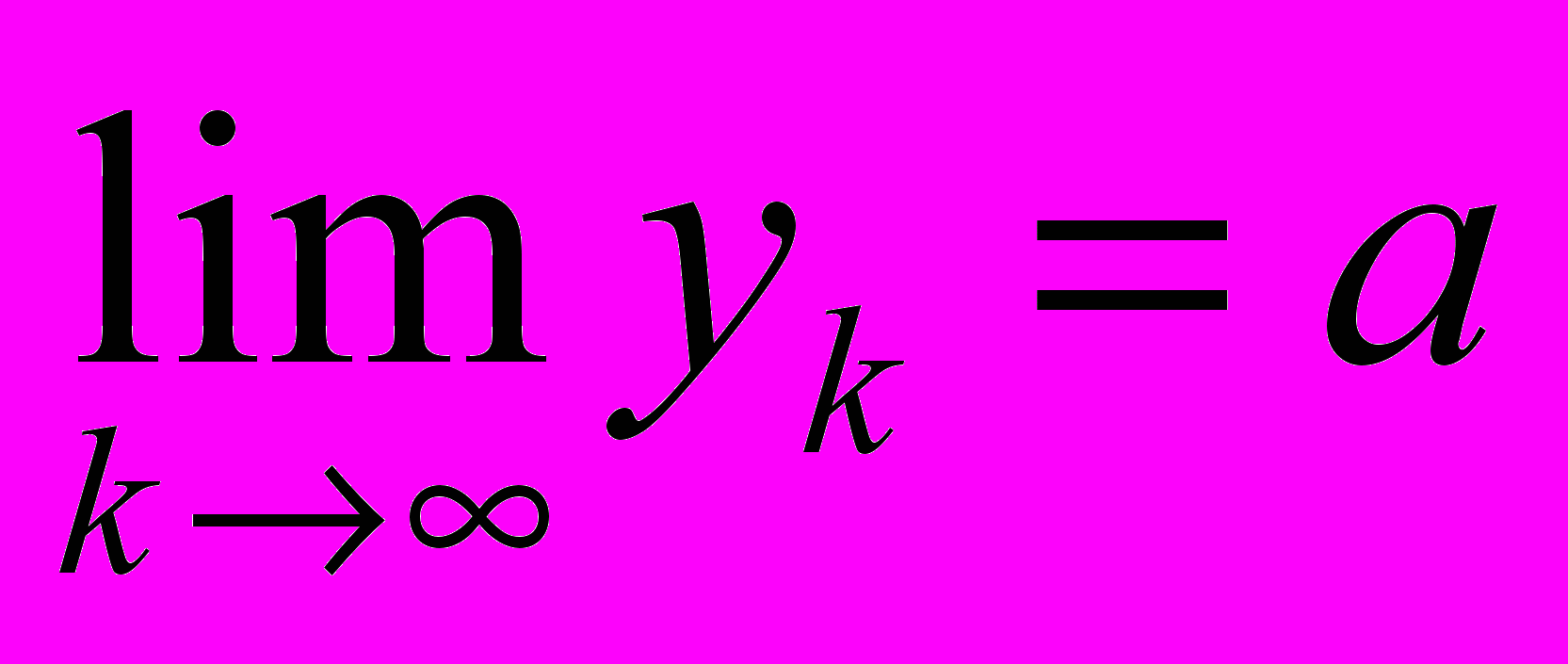Доказательство: Вне любой окрестности a содержится лишь конечное число членов {x_n}, следовательно и конечное число {y_k}.

Теорема 2. (Больцано, Вейерштрасс) Из любой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.

Доказательство. Пусть [a,b]{x_n}.

Разделим отрезок [a,b] пополам, обозначим [a₁,b₁] тот из полученных двух отрезков, который содержит бесконечно много членов последовательности {x_n}. Возьмем какой-нибудь член последовательности, лежащий в [a₁,b₁], его индекс обозначим n_1.

Разделим отрезок [a₁,b₁] пополам, обозначим [a₂,b₂] тот из полученных двух отрезков, который содержит бесконечно много членов последовательности {x_n}. Возьмем какой-нибудь член последовательности, лежащий в [a₂,b₂] и имеющий индекс больший, чем n₁, его индекс обозначим n_2. Продолжая этот процесс, мы построим подпоследовательность . Система отрезков [a_k,b_k] представляет собой систему вложенных, стягивающихся к нулю отрезков ( b_k-a_k=(b-a)/2^k). Общую точку обозначим c. Так как c[a_k,b_k], то 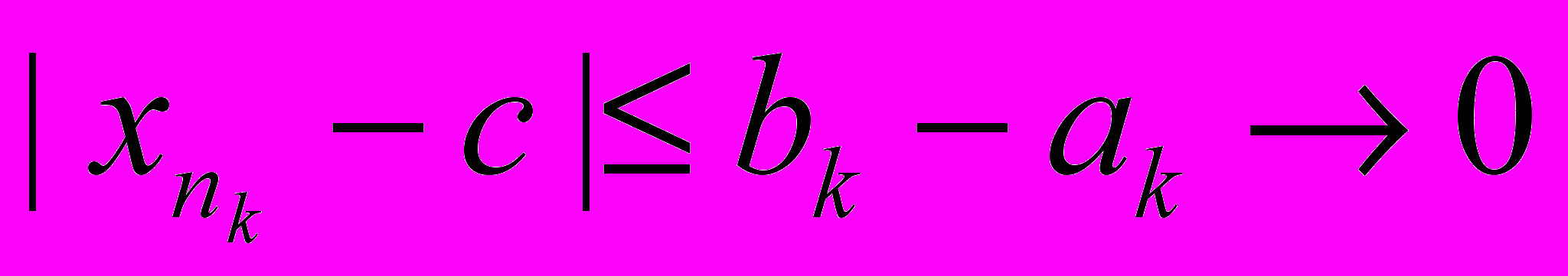. Откуда следует, что (Следствие 2 из Теоремы 4 §2).

Определение. Предел подпоследовательaности называется частичным пределом (в том числе )

Замечание 1. Частичных пределов у последовательности может быть много.

Пример: Последовательность всех рациональных чисел {r_n} имеет своим частичным пределом любое вещественное число.

Замечание 2. Для того, чтобы a (число или символ) было частичным пределом последовательности {x_n} н. и д., чтобы любая окрестность a содержала бесконечно много членов последовательности {x_n}.

Следствие. Если некоторая окрестность a содержит конечное число членов последовательности, то a не является частичным пределом.

Замечание 3. У любой последовательности существует хотя бы один частичный предел (конечный или бесконечный)

Доказательство: Рассмотреть два случая: Ограниченная последовательность (Теорема Больцано-Вейерштрасса). В случае неограниченной последовательности для выделения подпоследовательности имеющей пределом  используется определение 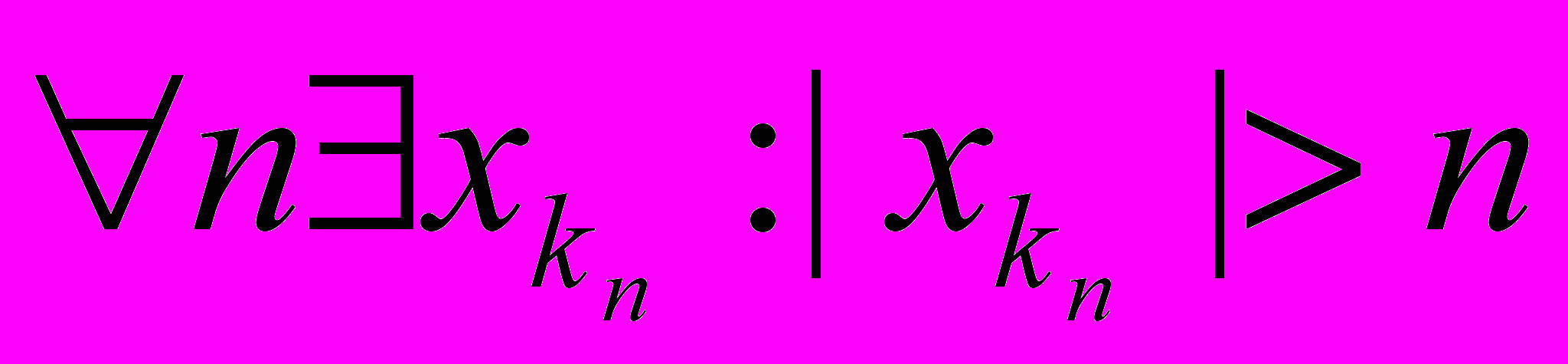и n_k>n_k-1.

2.Верхний и нижний пределы последовательности

Определение. (Наибольший частичная предел последовательности {x_n} называется ее верхним пределом, 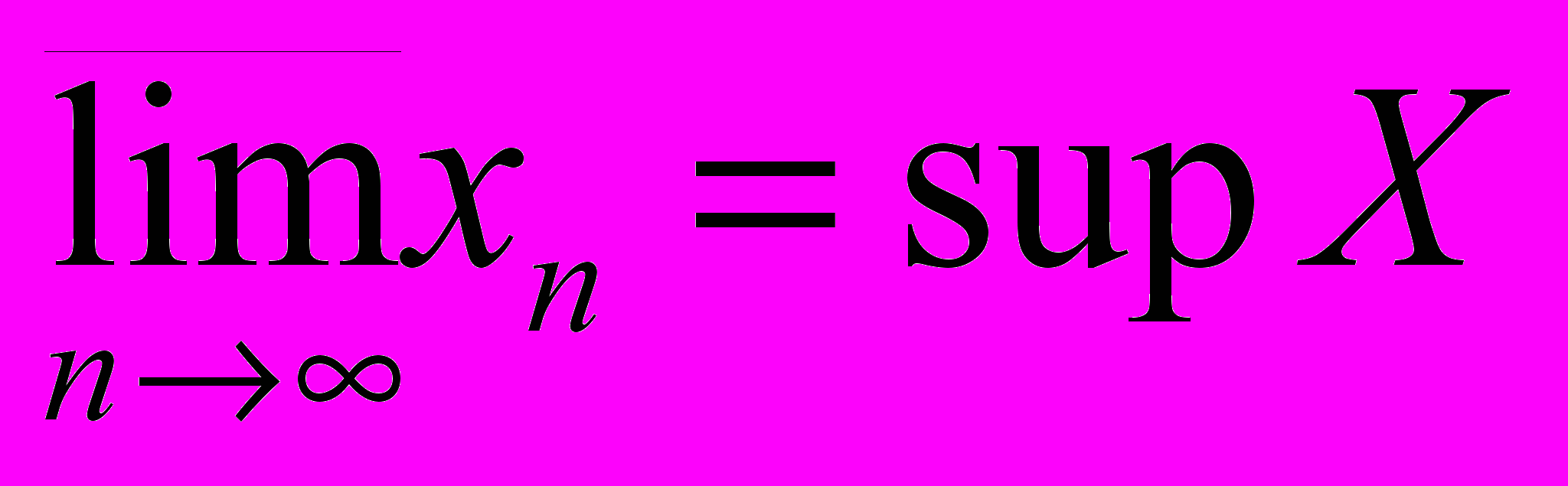, где X – множество всех частичных пределов. Аналогично .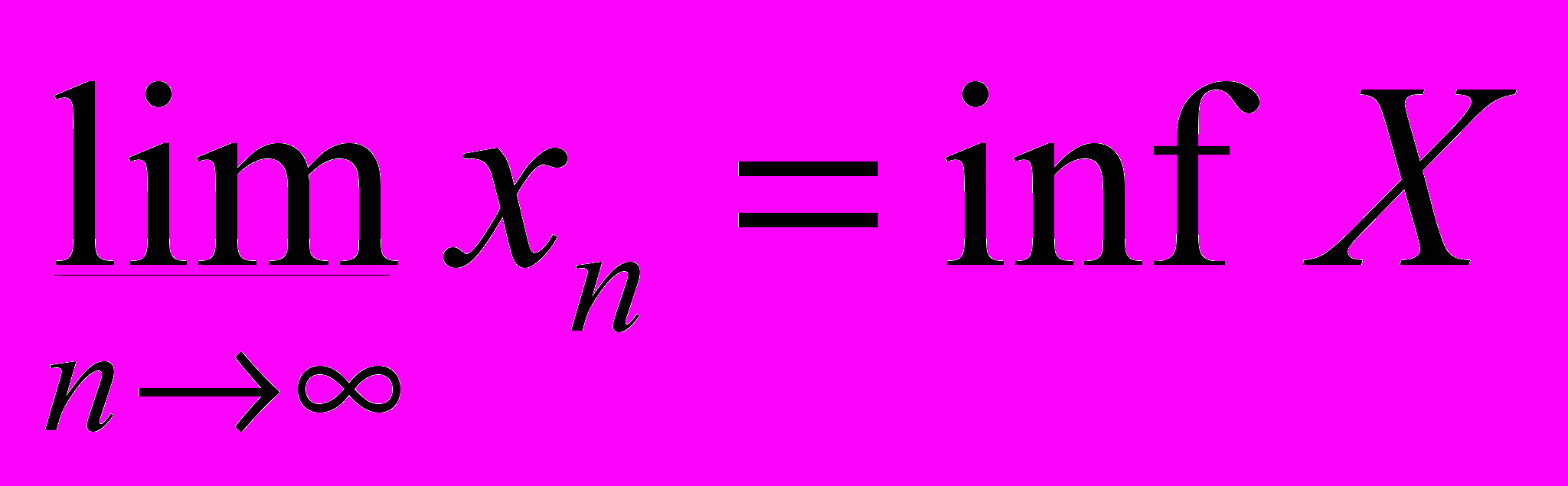