Вопросы, возникшие при знакомстве с квантовой теорией гравитации, и ответы на них

1. Каким образом можно установить экспериментально, что электрон проходит через два отверстия одновременно?

Ответ. Мысль о том, что один электрон может пройти сразу через два отверстия, показалась многим настолько дикой, что её решили проверить экспериментально. Для этого очень сильно уменьшили интенсивность вылетающих из источника электронов (рис. 15). Вылетал в среднем только один электрон за несколько минут. Каждый электрон попадал в какую-то точку на пластинке вроде бы совершенно случайно, но постепенно на пластинке вырисовывалась интерференционная картина. Если бы электрон проходил только через одно отверстие, то такой картины не было бы.

2. Может ли отдельный электрон, находясь в двух виртуальных облаках (волновых пакетах) интерферировать сам с собой? Или же интерференция – это коллективное свойство частиц?

Ответ. Если электрон находится в двух волновых пакетах, то он может интерферировать (взаимодействовать) сам с собой. Но, конечно, при помощи одного электрона интерференционная картина не получится. Поэтому для получения интерференционной картины требуется большое количество электронов. Однако необходимо подчеркнуть, что если бы каждый электрон не взаимодействовал сам с собой, то никакой интерференционной картины не было бы.

3. В чём состоит принципиальная разница между облаком виртуальных электронов и волновой Y-функцией? То есть чем новая интерпретация квантовой механики принципиально отличается от копенгагенской интерпретации?

Ответ. Новая интерпретация квантовой механики является по своей сути наглядной иллюстрацией копенгагенской интерпретации. Облако виртуальных электронов, в котором дискретно движется электрон – это наглядный образ движущегося электрона, а волновая Y-функция – это математическое описание движущегося электрона. Принципиальной разницы между новой интерпретацией и копенгагенской нет. Однако из новой интерпретации вытекает принципиально новый эффект: вблизи большой массы уменьшается неопределённость в движении частиц. А это означает (вопреки общей теории относительности), что время вблизи большой массы “ускоряется”. Следовательно, истинность новой интерпретации можно проверить экспериментально.

4. Будет ли облако виртуальных электронов постоянно расширяться, если нет взаимодействия с “классическим” телом (нет редукции)? Или это облако будет расширяться только до определённых размеров, которые определяются гравитационным потенциалом Вселенной?

Ответ. Гравитационный потенциал Вселенной определяет минимальное действие. Облако виртуальных электронов будет всё время расширяться потому, что ему энергетически выгодно расширяться. В результате пространство оказывается наполненным виртуальными частицами. Известно, что при столкновении высокоэнергетичных частиц рождается много новых частиц. Возможно, новые частицы как раз и появляются за счёт редукции виртуальных частиц. Впрочем, эта тема не исследована.

5. Когда говорят о неполноте квантовой механики, что имеют ввиду?

Ответ. С точки зрения квантовой механики электрон (или другая частица) не имеет определённого местоположения. Он находится с различной плотностью вероятности (а именно: |Y|²) в некоторой области пространства (электронного облака). На заре создания квантовой механики некоторые физики (в том числе и Эйнштейн) считали, что электрон находится в определённом месте пространства и, следовательно, волновая Y-функция не описывает реальное движение электрона, а лишь отражает наше незнание его местоположения. Именно в этом смысле говорилось о неполноте квантовой механики. Главный аргумент, приводимый Эйнштейном в пользу неполноты квантовой механики следующий. Предположим, мы “ловим” электрон в некоторой точке. В тот же момент волновая Y-функция становится равной нулю во всех других точках. Это означает, что существует “мгновенное действие” на расстоянии [2,c.528]. Эйнштейн не допускал возможность такого “действия на расстоянии” и именно поэтому отвергал неопределённость в движении частиц. В настоящее время “мгновенное действие на расстоянии” (нелокальность) – это многократно проверенный экспериментальный факт (см. § 5.5-5.7).

6. Чем редукция волновой Y-функции отличается от коллапса?

Ответ: Редукция означает сокращение, а коллапс – схлопывание. Например, атом излучает фотон, и электрон переходит с одной орбиты на другую. Происходит мгновенное уменьшение размеров электронного облака (так называемый квантовый скачок) – это редукция. А если мы регистрируем электрон в некоторой точке электронного облака, то происходит мгновенное уменьшение размеров облака до нуля – это тоже редукция, которую иногда называют коллапсом.

7. Чем редукция волновой Y-функции принципиально отличается от обычного изменения?

Ответ. Волновая функция непрерывно изменяется во времени. Этот процесс полностью описывается волновым уравнением Шрёдингера. При взаимодействии квантового объекта с классическим происходит редукция. Этот процесс носит случайный характер, и он не описывается волновым уравнением. В этом случае волновое уравнение позволяет только рассчитать вероятность тех или иных возможных скачкообразных изменений в волновой функции. И если взаимодействие произошло, то волновую функцию следует зачеркнуть и написать новую, с учётом произошедших изменений. Таким образом, редукция волновой функции – это мгновенное и скачкообразное изменение волновой функции, которое не описывается волновым уравнением Шрёдингера.

8. Редукция волновой Y-функции происходит вследствие измерения. Но ведь измерение - это не более чем обычное взаимодействие. Например, частица сталкивается с другой частицей. Происходит в этом случае редукция волновой функции или нет? В чём состоит принципиальная разница между измерением и столкновением частицы с другой частицей?

Ответ. Под измерением в квантовой механике подразумевается процесс взаимодействия квантового объекта с классическим. Присутствие экспериментатора необязательно. Если взаимодействуют только квантовые объекты, то редукция может не происходить сколь угодно долго. И все квантовые объекты будут находиться одновременно во всех возможных состояниях. Рассмотрим взаимодействие электрона с прибором. Прибор - это тоже огромное скопление электронов, протонов и нейтронов. Все эти частицы существуют одновременно в различных состояниях и дискретно “прыгают” из одного состояния в другое. Но так как прибор состоит из огромного числа частиц, то для него существуют такие переходы между состояниями (например, из менее упорядоченного состояния в более упорядоченное), вероятность которых ничтожно мала. А значит при возникновении таких состояний, прибор уже не сможет вернуться в начальное состояние (без посторонней помощи). Происходит редукция. Если при этом прибор забрал часть энергии у электрона, то обратно он её уже не отдаст. Устойчивое состояние прибора означает также и устойчивое состояние тех орбит, по которым движутся элементарные частицы, из которых состоит прибор. А устойчивая орбита - это орбита, на которой укладывается целое число волн, т.е. момент импульса на такой орбите кратен постоянной Планка. Поэтому для перехода между любыми устойчивыми состояниями прибора (а только такие состояния прибора наблюдаемы) необходимо действие, кратное величине постоянной Планка. Можно отметить, что энергия фотона как раз и есть та энергия, которая образуется при минимальном действии.

9. В качестве примера необратимости времени на рис. 21 изображена редукция волнового пакета. Почему невозможен обратный процесс?

Ответ. Обратный процесс возможен, но для его осуществления потребуется некоторое время. Невозможен обратный процесс, который будет также быстр, как и прямой. Если повернуть время вспять, то процесс расплывания волнового пакета (который в прямом времени был процессом редукции) будет происходить со сверхсветовой скоростью, что противоречить специальной теории относительности. Именно в этом и проявляется асимметрия времени.

10. Дискретное движение – это остаточное влияние Хаоса. В Хаосе понятие расстояния теряет физический смысл, и поэтому электрон движется в пространстве дискретно. Понятие времени в Хаосе также теряет физический смысл, и поэтому остаточное влияние Хаоса в нашей Вселенной должно проявляться также и в дискретности времени. Означает ли это, что электрон должен двигаться дискретно не только в пространстве, но и во времени?

Ответ. В нашем мире и расстояние, и время непрерывны. По крайней мере, пока не найдены ни минимальная длина, ни минимальное время (можно сказать, что этот вопрос лежит за пределами возможности современных экспериментов). Дискретность (как противопоставление непрерывности) относится к движению, а не отдельно ко времени или расстоянию. Рассмотрим в качестве примера функцию y(x). Эта функция может быть непрерывной или разрывной. В любом случае и непрерывность, и разрывность функции имеют отношение только к зависимости между x и y, но не отдельно к x или отдельно к y.

11. При построении квантовой теории гравитации были использованы экспериментальные данные о постоянстве постоянной тонкой структуры a = е²/сħ » 1/137. Какой физический смысл имеет эта постоянная в квантовой теории гравитации? Почему её величина не изменяется в гравитационном поле?

Ответ. Вблизи большой массы уменьшается неопределённость в движении частиц. Соответственно, уменьшаются радиусы электронных оболочек в атомах. При этом возрастает скорость вращения электронов вокруг ядра, и повышаются частоты излучения в атомных спектрах. В результате возрастает скорость протекания физических процессов, в том числе и скорость распространения электромагнитных колебаний. Давайте сделаем количественные оценки. Величина метра пропорциональна радиусу Бора, который, в свою очередь, пропорционален величине ħ²/m (4.9). Поэтому: 1м ~ ħ²/m. Длительность секунды обратно пропорциональна частоте излучения атомных спектров, которая, в свою очередь пропорциональна величине m/ħ³ (4.28), поэтому: 1с ~ ħ³/m. Скорость света имеет размерность [c] = м/с. Следовательно:

с ~

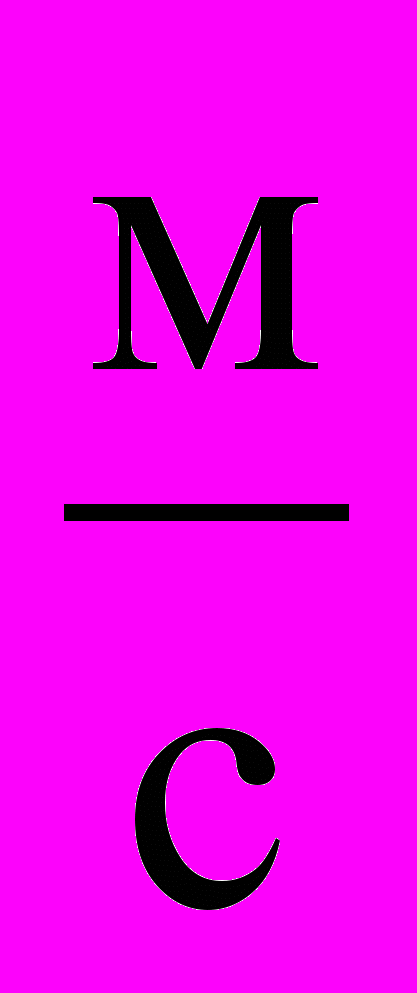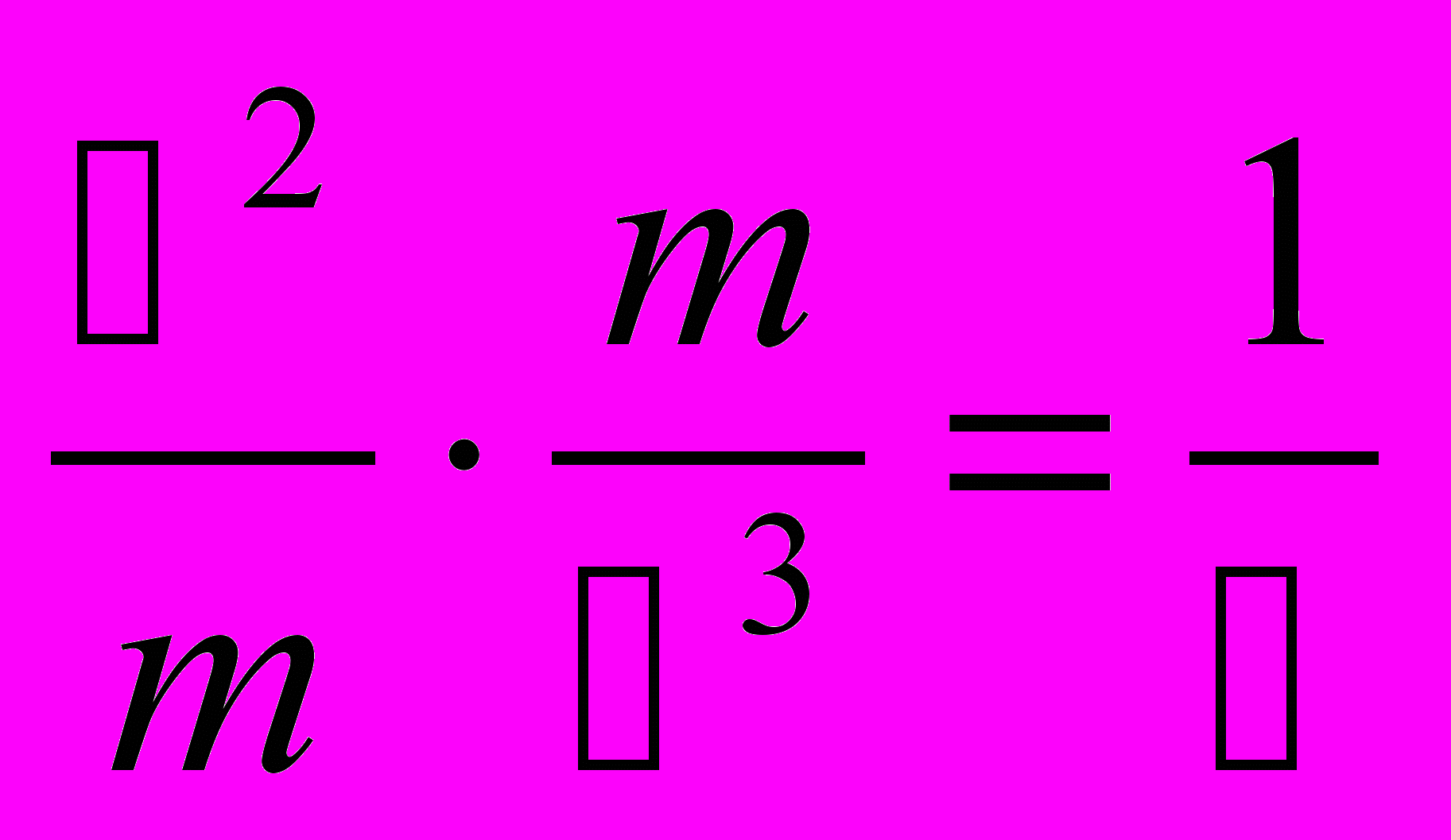(14.1)

Таким образом, мы приходим к выводу, что величина скорости света обратно пропорциональна величине постоянной Планка (2.8), и, следовательно, постоянная тонкой структуры в гравитационном поле не изменяется.

12. Я был уверен в том, что замедление времени вблизи большой массы – это экспериментально установленный факт. Неужели не было прямых экспериментов по измерению скорости времени в гравитационном поле?

Ответ. Когда я понял, что с точки зрения квантовой теории гравитации время вблизи большой массы ускоряется, то, несколько озадачился, так как также был уверен в том, что замедление времени в гравитационном поле – это экспериментально проверенный факт. Однако, исследовав этот вопрос с точки зрения квантовой механики, понял, что время в гравитационном поле должно течь быстрее, вопреки общей теории относительности. Как оказалось, все эксперименты в этой области были косвенные. Кроме того, для интерпретации результатов этих экспериментов использовались дополнительные предположения. Например, предположение о том, что частота фотона, когда он движется в гравитационном поле, не изменяется. Такое предположение очень сомнительно (оно основано на сравнении электромагнитных волн со звуковыми, что некорректно) и также нуждается в экспериментальной проверке.

13. Почему одно и то же выражение для квадрата интервала в гравитационном поле интерпретируется в общей теории относительности как замедление времени, а в квантовой теории гравитации, наоборот, как ускорение? В чём ошибка интерпретации, принятой в общей теории относительности?

Ответ. Рассмотрим выражение (8.4) для квадрата интервала в гравитационном поле, создаваемом массой М:

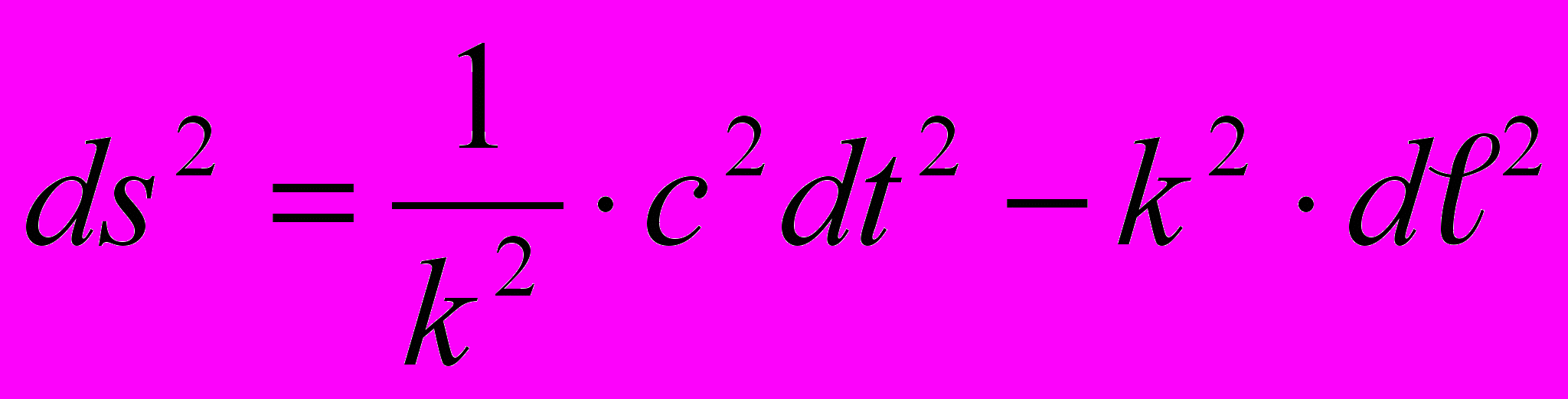(8.4)

Коэффициент k стремится к единице на большом удалении от массы М, а вблизи массы он возрастает. Из этого уравнения следует, что вблизи массы М все расстояния увеличиваются, а все интервалы времени уменьшаются. Эталон длины – это метр, а эталон времени – секунда. Если длина метра уменьшится вблизи большой массы, то все расстояния увеличатся (см. рис. 5). Но если длительность одной секунды уменьшится вблизи большой массы, то все интервалы времени (длительность любого физического процесса) также уменьшатся. Таким образом, из уравнения (8.4) следует, что вблизи большой массы длина метра уменьшается, и длительность секунды также уменьшается. Ошибочность интерпретации, принятой в общей теории относительности состоит в том, что интервал времени рассматривается как расстояние между точками на воображаемой оси времени (по аналогии с обычным расстоянием). Поэтому сокращение интервалов времени вблизи большой массы (8.4) интерпретируется в общей теории относительности как увеличение длительности секунды.

14. С точки зрения квантовой теории гравитации естественный пространственно-временной масштаб (то есть величины c, ħ, m) определяется распределением всей материи во Вселенной. Вблизи большой массы масштаб изменяется, и поэтому траектории движения частиц искривляются. В своих лекциях по гравитации (раздел 5.4 “Принцип Маха в квантовой механике”) Ричард Фейнман, исходя из уравнений общей теории относительности, также пытался рассчитать изменение масштаба, выраженного через величины c, ħ, m, вблизи большой массы. Почему Фейнману не удалось это сделать, несмотря на то, что эта задача с математической точки зрения достаточно проста?

Ответ. Чтобы рассчитать изменение масштаба вблизи большой массы, Фейнман использует компоненту g₀₀ метрического тензора (коэффициент при c²dt² в выражении для квадрата интервала), которая в общей теории относительности равна (смотри уравнение (4.6)):

g₀₀ = 1 -

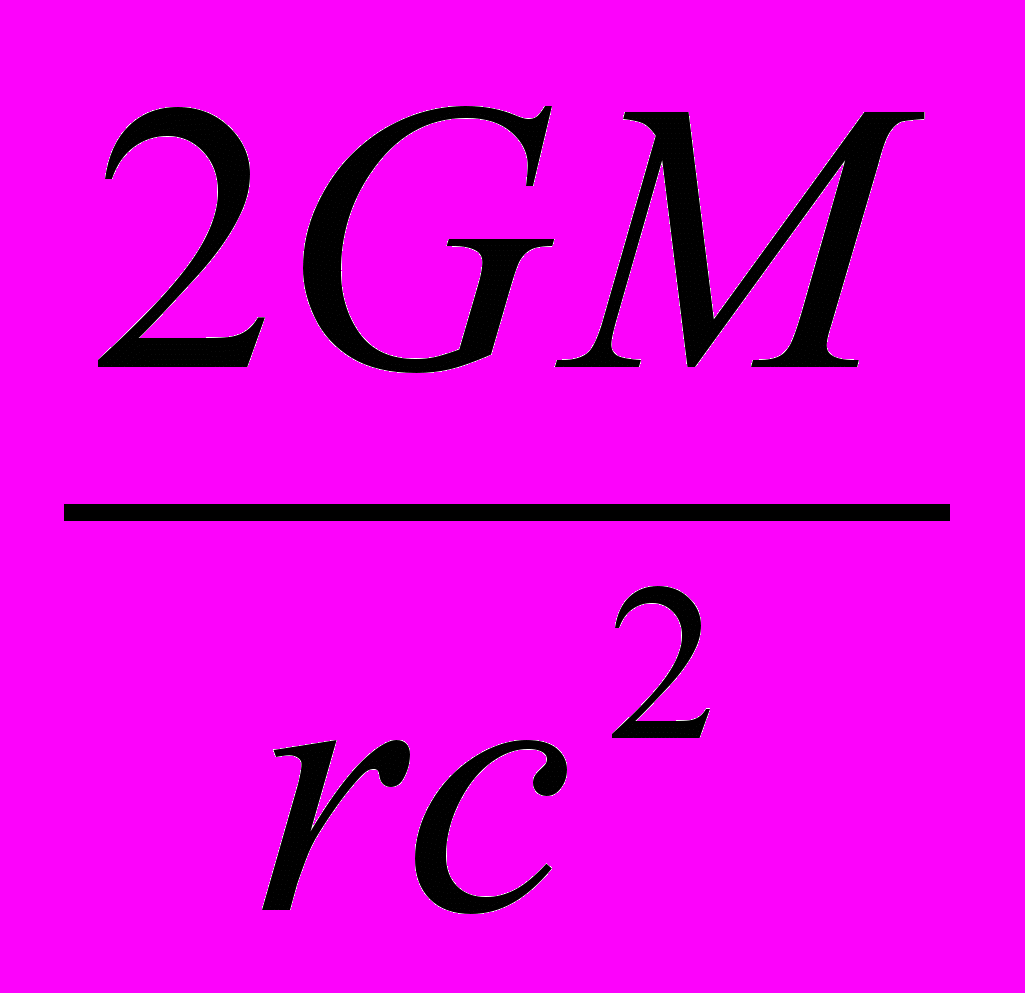(14.2)

Фейнман справедливо полагает, что “единица” в этом уравнении – это масштаб, создаваемый всеми массами во Вселенной, а (-

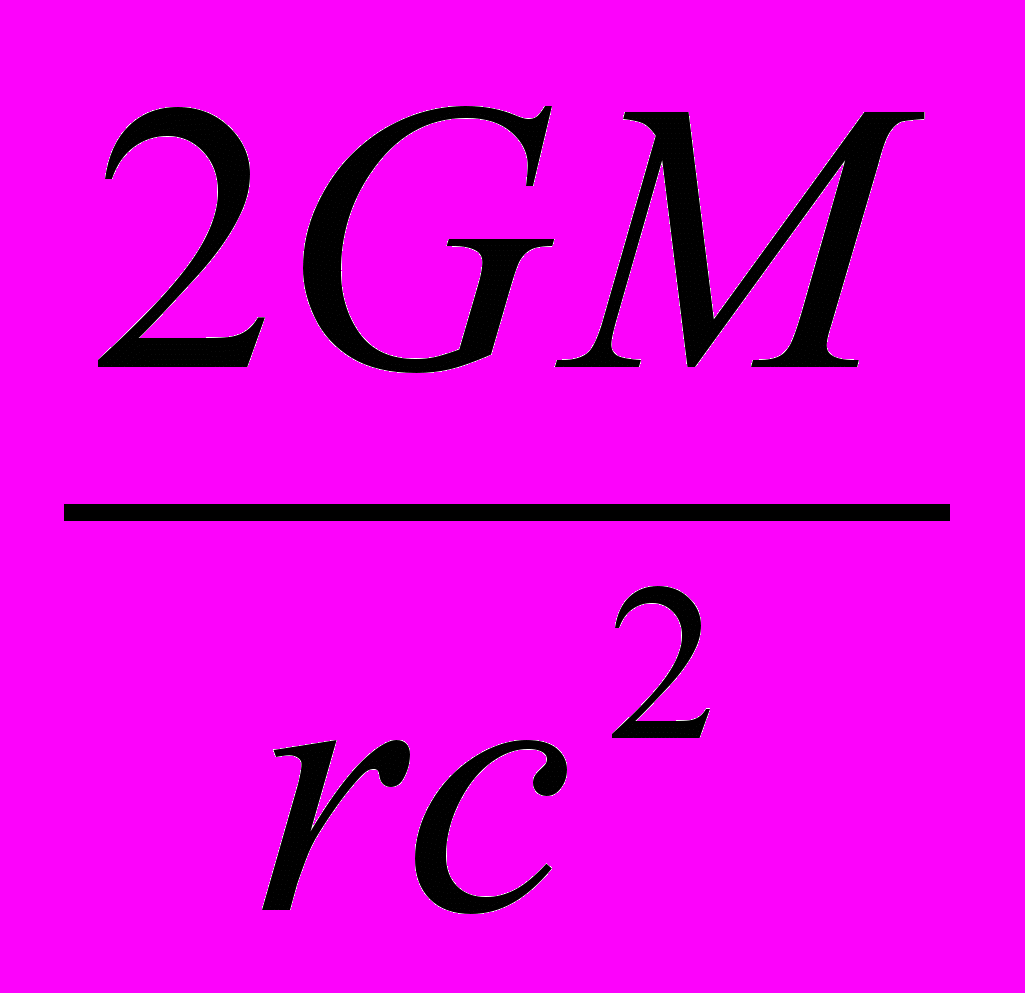) - это изменение масштаба, создаваемое массой M. Очевидно, что в такой постановке эта задача не разрешима, так как изменение масштаба, создаваемое массой М, по неизвестной причине имеет, как это ни странно, противоположный знак, чем масштаб, создаваемый остальными массами (“единица”). В квантовой теории гравитации коэффициент при c²dt² равен (смотри уравнение (7.18)):

. И в такой постановке эта задача легко решается, так как теперь изменение масштаба имеет тот же самый знак, что и “единица”.

Напомним, что в общей теории относительности компонента g₀₀ метрического тензора в случае слабого поля принимается равной: g₀₀ = 1 + 2j/с² = 1 -

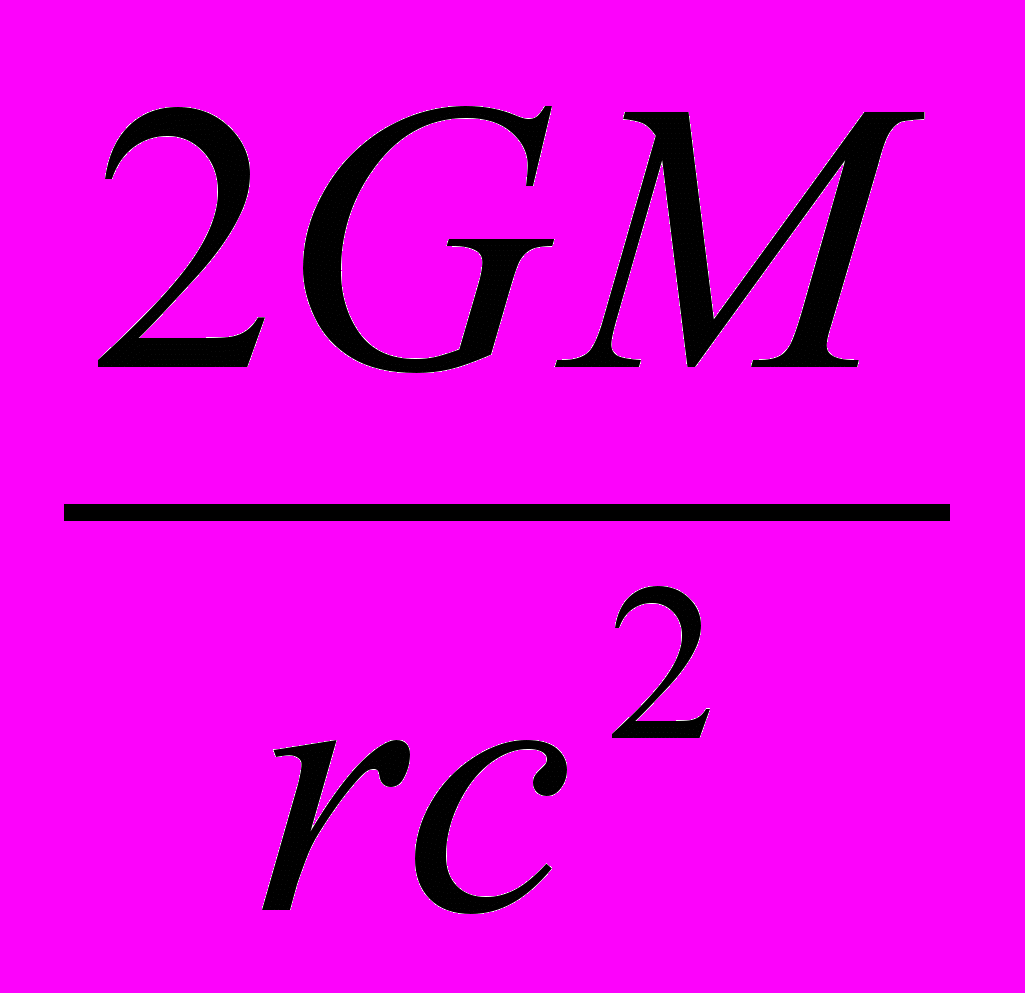только на том основании, чтобы в нерелятивистском пределе (V « c) уравнения движения переходили в ньютоновский закон тяготения [5,§87]. Однако если представить эту компоненту в виде:

g₀₀ =

(14.3)

то полученные уравнения движения также будут в нерелятивистском пределе переходить в ньютоновский закон тяготения (см. § 7.6).

15. В § 4.12 объясняется, почему из эксперимента, проведённого Шапиро, невозможно выяснить, уменьшается или увеличивается скорость света вблизи большой массы. А каким образом можно выяснить, как изменяется скорость света в гравитационном поле?

О
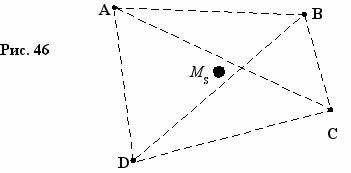
твет. Для того чтобы выяснить, как изменяется скорость света в гравитационном поле, можно, например, провести следующий эксперимент (смотри рис. 46). Четыре спутника A, B, C, D находятся на околосолнечной орбите и непрерывно обмениваются между собой радиосигналами. При этом определяется время, необходимое сигналу, чтобы долететь от одного спутника до другого. При обработке полученной информации мы можем предположить, что скорость света в гравитационном поле не изменяется. И исходя из этого, а также зная интервалы времени Dt_AB (время полёта сигнала от спутника А до спутника В) Dt_BC,Dt_CD,Dt_AD, Dt_AC рассчитать интервал времени Dt_BD. Если реальное время полёта сигнала от B до D окажется меньше расчетного времени Dt_BD, то, значит, скорость света вблизи массы М возрастает. А если реальное время полёта сигнала от В до D окажется больше расчетного времени Dt_BD, то, значит, скорость света вблизи массы М уменьшается.

16. Современная физика – очень сложная наука. Тензора, спиноры, операторы, многомерные гильбертовы пространства вот далеко не полный перечень математических понятий, прочно вошедших в современную физику. Что касается квантовой теории гравитации, то с математической точки зрения – это очень простая теория, вполне доступная человеку без специального математического образования. Разве может такая простая теория быть верной?

Ответ. Когда Бор проходил стажировку у Резерфорда, тот сказал ему примерно следующее: “Если теория представляет собой хоть какую-то ценность, то её можно объяснить даже буфетчице”. Первый раз, услышав эту фразу, невольно думаешь, что Резерфорд немного преувеличил. Ведь получается, что если вы не можете объяснить какую-нибудь из сложных современных теорий буфетчице, то эта теория не просто неверна, она вообще не имеет никакой ценности. Но, на самом деле, если немного подумать, то можно понять – Резерфорд абсолютно прав. Физика – это наука, которая основана исключительно на наблюдениях. А всё, что вы наблюдали (или могли бы наблюдать), сможете рассказать без использования математики даже ребёнку. Если же вы не можете объяснить на пальцах сложную формулу, не обманывайте себя – либо вы её не понимаете, либо она не имеет смысла. Например, если у вас есть тензор – сверните его в скаляр, и разберитесь со скаляром. Но почему теорию надо объяснять именно буфетчице? Резерфорд и здесь прав. Если вы попытаетесь объяснить новую теорию профессору – только зря потратите время. История физики ясно показывает: профессора (за очень редким исключением) не воспринимают новых теорий. Планк, выдвинувший гипотезу о том, что излучение излучается порциями, не воспринял всерьёз идею Эйнштейна о том, что излучение также переносится и поглощается порциями. Он сказал, что Эйнштейн со своей гипотезой о квантах света “зашёл слишком далеко” [28,с.45]. Лоренц скептически относился к принципу относительности Эйнштейна [73,с.321]. Эйнштейн не мог смириться со случайностью в микромире. Возможно, буфетчица потому лучше воспринимает физические теории, что у неё нет собственных идей, которые бы она разрабатывала в течение длительного времени, и от которых было бы жалко отказываться. Так или иначе, но физическая теория в своей основе должна быть простой и понятной [11,с.157].

17. Я недавно разговаривал с одним математиком, и он рассказал следующее. Все трехэтажные математические формулы - это просто формальное представление некоторых объектов, с которыми математик работает в своей голове. Никто в формулах не мыслит. И с этим можно согласиться. Но с другой стороны, математика – это язык физики, и, значит, любое физическое утверждение должно быть выражено в виде математического уравнения. У меня, например, есть знакомый профессор, который не будет читать книгу по физике, если в ней мало формул. Сколько математических формул должно быть в книге по физике?

Ответ. Я тоже думаю, что формулами никто не мыслит. На мой взгляд, математическая формула в физике – это краткая запись какого-то физического процесса. Поэтому я считаю так: необходимо понятно рассказать о физическом процессе на языке наблюдаемых величин, а затем уже привести формулу. В квантовой механике много формул, но там и много новых результатов: технический прогресс 20-го века напрямую связан с исследованием атомной структуры вещества. А в общей теории относительности – куча формул, да ещё в тензорном виде, да ещё в четырёхмерном пространстве, которое к тому же ещё искривлённое и псевдоевклидово. А результатов почти никаких. Единственный новый результат – удвоенное по сравнению с теорией Ньютона отклонение света в гравитационном поле Солнца. Но для объяснения двойки многовато формул. Я не считаю результатом предсказание чёрных дыр или гравитационных волн, так как они пока не обнаружены. И уж тем более не является результатом открытие “белых дыр” или открытие Хокинга о “квантовом испарении чёрных дыр”. Что касается таких теорий, как теория струн и суперструн, теория суперсимметрии и супергравитации и т. п., то здесь ситуация ещё хуже. Огромное количество формул и за много лет ни одного нового экспериментально подтверждённого результата. Получается, что обилие формул предназначено не для того, чтобы поведать о новых результатах, а для того, чтобы скрыть их отсутствие. Таким образом, я думаю, что количество формул в физической теории должно быть пропорционально полученным результатам.

18. Вы утверждаете, что такие теории, как теория струн и суперструн, суперсимметрии, супергравитации и т. д., не имеют физического смысла на том основании, что они не сделали ни одного экспериментально подтверждённого предсказания. Но, возможно, Вы ошибаетесь, и эти теории всё же имеют какой-то физический смысл? Может быть, не стоит высказывать отрицательное отношение к теориям только на том основании, что Вам не понятен их смысл?

Ответ. Я считаю, что любой человек имеет право на ошибку. И если я ошибаюсь, то ничего страшного с этими теориями не случиться. Выражая письменно своё отрицательное отношение к этим теориям, как к физическим теориям, я преследую простую цель. И чтобы понять эту цель, давайте рассмотрим два возможных варианта. Первый вариант. Эти теории имеют некоторый физический смысл. Второй вариант. Эти теории не имеют ни малейшего физического смысла. Допустим, что верен первый вариант, и некто увидит физический смысл в этих теориях. Что произойдёт в этом случае? Этот человек сделает вывод, что Янчилин ошибался, утверждая обратное. И всё. Ничего страшного не произойдёт. А теперь предположим, что верен второй вариант. В этом случае кто-либо, изучая эти теории и пытаясь безуспешно отыскать в них какой-либо физический смысл, может потратить напрасно многие годы своей жизни. А если он узнает о моём отношении к этим теориям, то, возможно, прекратит их изучать и потратит годы своей жизни более осмысленно. Таким образом, если я не прав, то вреда от моих высказываний не будет, а если прав, то польза несомненная. В каком-то смысле, теорию можно сравнить с деревом. За молодым деревом нужно ухаживать и относиться к нему бережно, хотя даже не знаешь, будет ли оно приносить плоды или нет. Но если за деревом уже ухаживают более тридцати лет, а плодов никаких нет, то, следует честно сказать, что дерево декоративное и растёт исключительно для экзотики.

19. В чём Вы видите причину отсутствия развития в фундаментальной физике за последнее время?

Ответ. Основная причина, на мой взгляд, в том, что физики работают не с физическими идеями, а с математическими понятиями. Например, Эйнштейн пытался построить единую теорию поля, манипулируя с метрическим тензором и тензором электромагнитного поля. По этому пути в направлении “великого объединения” и по сей день движется большинство физиков. Очевидно, что такой подход изначально обречён на неудачу. Дело в том, что любая физическая теория может состоять только из физических идей и физических понятий. Она не может строиться на основе математических понятий (хотя может их использовать). Нельзя относиться к тензорам, матрицам, спинорам и прочим математическим объектам так, как будто они существуют реально. Проще говоря, исследуя математические объекты (даже если эти объекты описывают физические явления) невозможно ни на шаг продвинуться в понимании окружающего мира.

20. При первом издании книга называлась “Квантовая теория гравитации”. Почему Вы изменили название?

Ответ. Обычно под квантовой теорией гравитации подразумевается квантование искривлённого пространства-времени в рамках общей теории относительности. Кроме того, читатель, открывая книгу с названием “Квантовая теория гравитации”, ожидает увидеть огромное количество сложных формул. Поэтому, чтобы не пугать напрасно читателя, я решил изменить название.

Blog

Вопросы, возникшие при знакомстве с квантовой теорией гравитации, и ответы на них

Содержание

Вопросы, возникшие при знакомстве с квантовой теорией гравитации, и ответы на них