Правила проведения письменного экзамена Продолжительность экзамена 1,5 часа. (90мин.)

Вид материала

Программа

Содержание Программа экзамена Образцы теоретических вопросов к экзамену

Подобный материал:

• И. о ректора миэм в. П. Кулагин Программа и правила проведения, 36.1kb.
• Программа государственного экзамена бакалавров по направлению 0902 -инженерная механика, 124.98kb.
• Методические материалы по подготовке и проведению егэ в пунктах проведения экзамена, 879.12kb.
• Методические материалы по подготовке и проведению гиа-9 в пунктах проведения экзамена, 688.23kb.
• Примерная программа вступительного экзамена по литературе (сочинение), 36.02kb.
• Испытаний, 83.69kb.
• Темы выпускных сочинений 2007 Комплекты тем сочинений для проведения письменного экзамена, 290.22kb.
• Темы выпускных сочинений 2007 www. MedalSoch ru Темы выпускных сочинений 2007 Комплекты, 252.42kb.
• Комплекты тем сочинений для проведения учреждений письменного экзамена по литературе, 822.53kb.
• Греха, возмездия и покаяния в пьесе А. Н. Островского «Гроза», 92.28kb.

Примечание. Таблица соответствия экзаменационной оценки рейтинговой, при коррекции оценки S₁

Интервал экзаменационных оценок (в баллах)	Соответствующий интервал возможной рейтинговой оценки (в баллах)
36< S2 28236 16228 S216	больше 90 от 71 до 90 от 41 до 70 не больше 40

Правила проведения письменного экзамена

1. Продолжительность экзамена – 1,5 часа. (90мин.)

2. Использование конспектов лекций, учебников, пособий и калькуляторов не разрешается.

3. Каждый экзаменационный билет содержит 4 вопроса. Первый вопрос считается теоретическим (определения, теоремы, следствия и т.п.), остальные три – практическими (задачи). Каждый вопрос оценивается в 10 баллов. За полный ответ на вопрос билета студент получает максимальный балл. Недочёты ответа приводят к уменьшению балла. Отвечать на вопросы билета можно в любой последовательности.


Программа экзамена


1. Числовые последовательности. Бесконечно малые и бесконечно большие последовательности. Предел последовательности.

2. Монотонные последовательности: определение, признак сходимости. Число Эйлера.

3. Приложения последовательностей в экономике: простые и сложные проценты; паутинообразная модель рынка.

4. Функции одной переменной: определение, способы задания, график функции, понятие максимума, минимума функции.
5. Понятие обратной функции. Функции спроса и цены спроса, предложения и цены
предложения, как примеры взаимнообратных.
6. Предел функции в точке. Свойства пределов. Два замечательных предела.
7. Определения непрерывности функции в точке и на промежутках. Свойства непрерывных функций: непрерывность обратной функции, сложной функции; арифметические операции над непрерывными функциями.
8. Теоремы о прохождении непрерывной на отрезке функции через нуль при смене знака
и о прохождении непрерывной на отрезке функции через все промежуточные значения
(теоремы Больцано-Коши).
9. Теоремы об ограниченности и достижении максимума и минимума непрерывной
функции на отрезке (теоремы Вейерштрасса). Точки разрыва функции, их классификация.
10 Определение производной функции в точке. Геометрический смысл производной.
Определение дифференцируемой функции. Дифференциал и его геометрический смысл
11. Производная как показатель мгновенного прироста или скорости изменения функции Простейшие предельные характеристики функций из экономического анализа: предельная выручка, предельные издержки.
12. Дифференцирование основных элементарных функций. Правила дифференцирования.

13. Логарифмическая производная и ее интерпретация как мгновенного темпа прироста функции. Эластичность функции.

14. Основные теоремы дифференциального исчисления: Ферма, Ролля. Лагранжа. Правило Лопиталя.

15. Исследования функций на монотонность, экстремум, выпуклость, вогнутость, точки перегиба. Асимптоты графика функции.

16. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Табличные интегралы. Методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.

Образцы теоретических вопросов к экзамену

1. Критерии монотонности дифференцируемой функции (определение монотонных

функций, необходимые и достаточные условия монотонности).

2. Условия экстремума дифференцируемой функции (определение точек экстремума, необходимое и достаточные условия первого порядка).

3. Условия экстремума дважды дифференцируемой функции (определение точек экстремума, достаточные условия второго порядка).

4. Выпуклые и вогнутые функции (определение через касательные, критерии выпуклости и вогнутости второго порядка).

5. Свойства непрерывных функций на отрезке: прохождение через нуль при смене знака, прохождение через все промежуточные значения, ограниченность и достижение максимума и минимума.

6. Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа).

7. Неопределенный интеграл: определение первообразной и неопределенного интеграла. Основные свойства интеграла.

Образец билета письменного экзамена

1. Непрерывные функции. Основные свойства непрерывных функций на

отрезке

(с доказательством одного из свойств).


2. Исследовать на непрерывность функцию




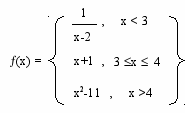
3. Найти интервалы монотонности и локальные экстремумы функции



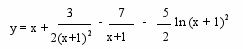
e^3x-5dx

4. Найти интеграл.