Geum.ru

Применение вейвлет-анализа для поддержки задач долгосрочного прогнозирования

Вид материалаДокументы

Содержание


Непрерывное вейвлет-преобразование (НВП)
Программный компонент вейвлет-анализа.
Дискретное вейвлет-преобразование (ДВП).
Подобный материал:
ПРИМЕНЕНИЕ ВЕЙВЛЕТ-АНАЛИЗА ДЛЯ ПОДДЕРЖКИ ЗАДАЧ

ДОЛГОСРОЧНОГО ПРОГНОЗИРОВАНИЯ


Ветрова В.В. (г. Иркутск, ИСЭМ СО РАН)


Рассматривается аппарат вейвлет-преобразований(непрерывное и дискретное) в применении к анализу геоклиматических данных для задач долгосрочного прогнозирования. Приводится технология работы реализованного компонента вейвлет-анализа, позволяющего формировать:
  • сравнительные вейвлетограммы для качественного визуального сопоставления поведения процессов в разных частотно-временных масштабах;
  • спектральные характеристики (с использованием материнского вейвлета Morlet);
  • изменения поведения мер близостей двух исследуемых процессов.



Для решения задач долгосрочного прогнозирования природообусловленных составляющих энергетики в ИСЭМ СО РАН используется информационно-прогностическая система Гипсар[1], основу которой составляют аппроксимативные обучающиеся и нейросетевые методы, опирающиеся на выделение аналогов из конечного набора выборок исследуемых временных рядов. Изменения климата, носящие в настоящее время глобальный характер, приводят к нарушению связей между природными процессами, что влечет за собой отсутствие схожей информации в аналогах. В данных условиях формирование прогнозов будет происходить с большей ошибкой. Для повышения надежности и точности прогнозов необходимо как привлечение дополнительной информации об исследуемых рядах, так и использование современных математических методов.

В ИСЭМ СО РАН была разработана база данных геоклиматических показателей Gi3[2], представленная несколькими климатическими параметрами (показатели температуры, осадков, давления, относительной влажности, циркуляции атмосферы, вертикальной скорости изменения давления и др.). Она включает среднемесячные и суточные данные за период 1948-2008 гг., содержит как приземные показатели, так и данные по разным уровням давления. База поддерживается в актуальном состоянии путем обновления из нескольких источников в сети Интернет (рис. 1). Разработанный Gi3-инструментарий позволяет оперативно формировать временные ряды с выбранной периодичностью (год, месяц, сутки) с последующими методами их обработки (корреляционный, спектральный, регрессионный и др.).






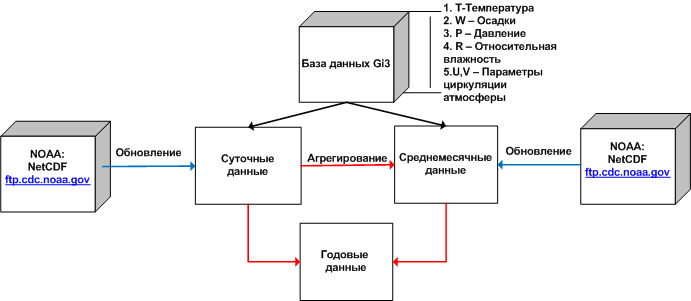
Рис.1. Схема обновления БД Gi3

В настоящее время, для более качественного анализа временных рядов широко применяется математический аппарат вейвлет-преобразований (ВП). ВП позволяет достаточно точно оценивать спектральные характеристики нестационарного процесса, проводить фильтрацию данных, осуществлять анализ в широком диапазоне частотно-временной области и др. Принцип вейвлет-анализа был впервые изложен в работах Гроссмана и Морле в

1984 г. в связи с анализом свойств акустических сигналов. Условно ВП можно разделить на непрерывное и дискретное [3,4] .


Непрерывное вейвлет-преобразование (НВП)

Непрерывное ВП определяется следующей формулой:

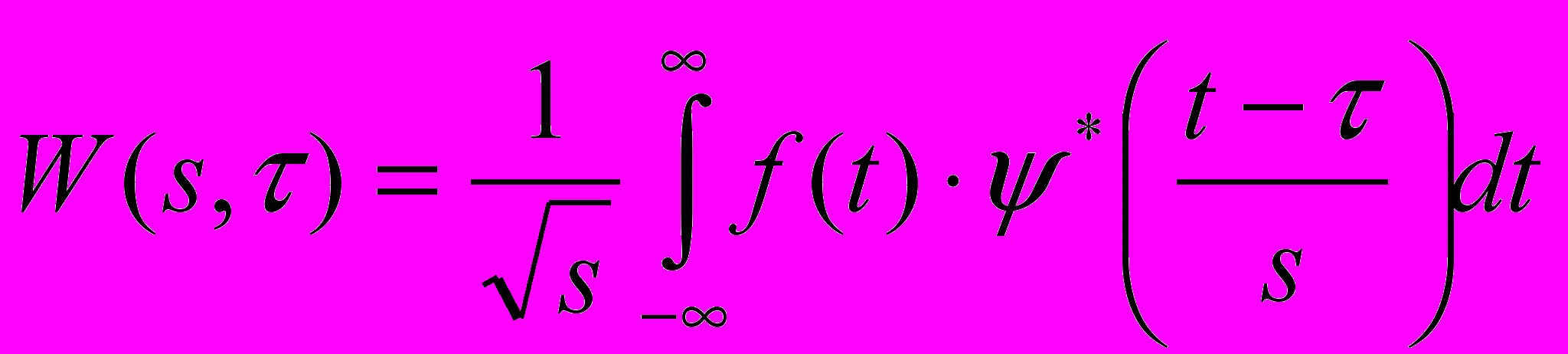, где 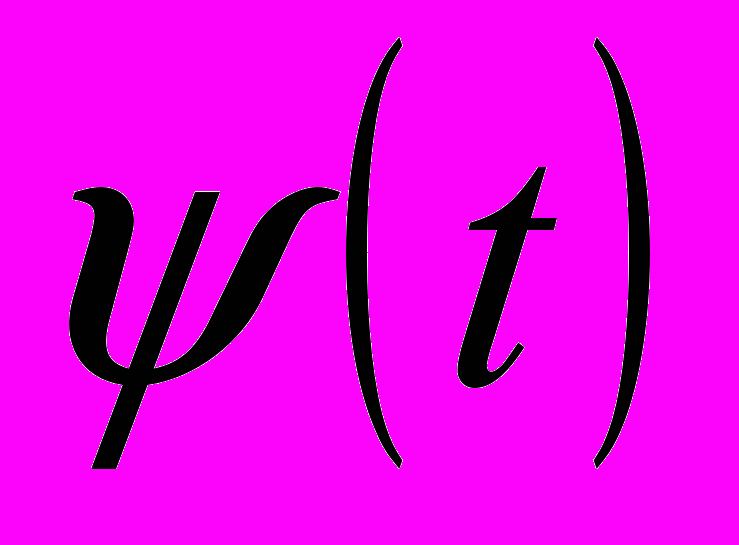– базисная вейвлет-функция (ВФ), 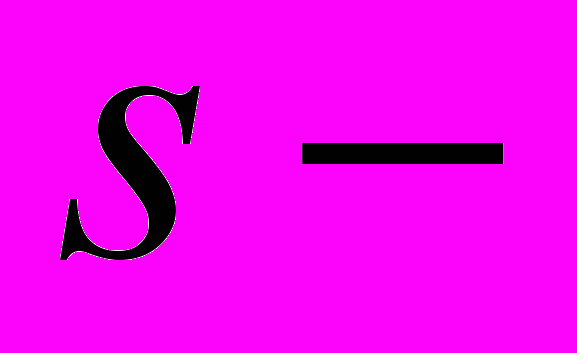масштаб (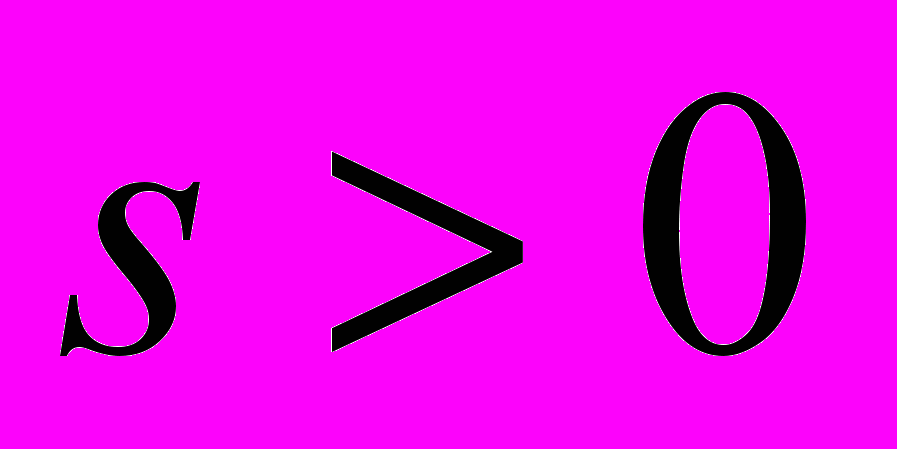, соответствует обратной частоте Фурье-анализа), 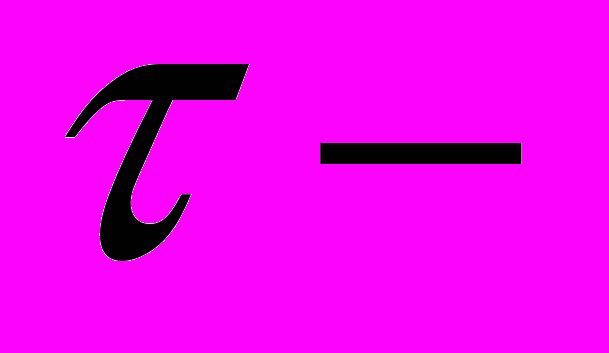временной сдвиг, 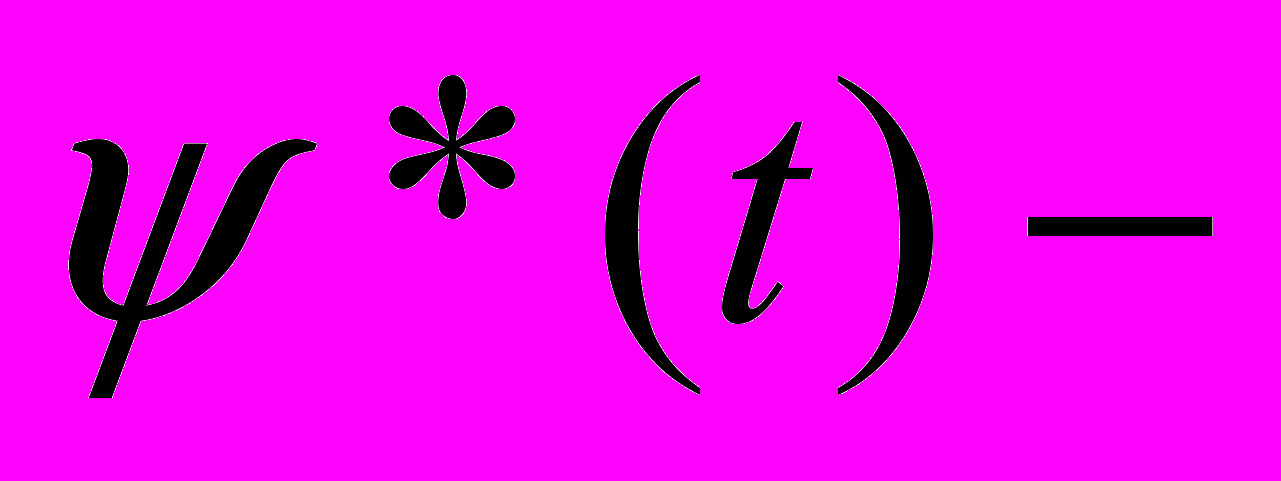функция, комплексно сопряженная с 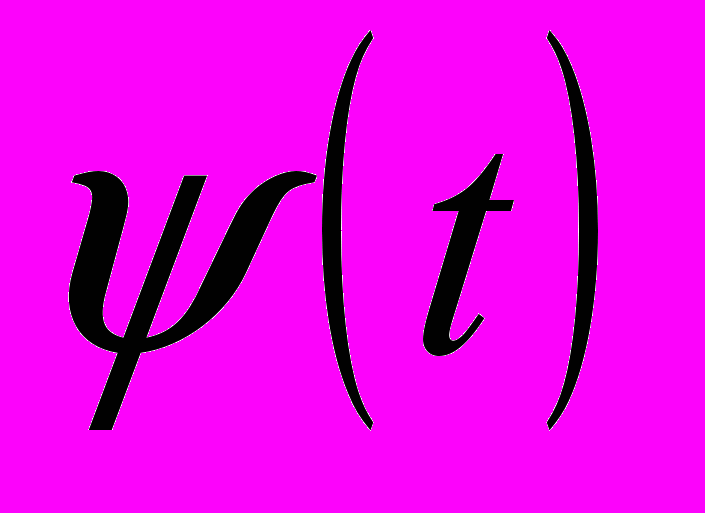. Базисная ВФ должна удовлетворять следующим условиям: , ,.

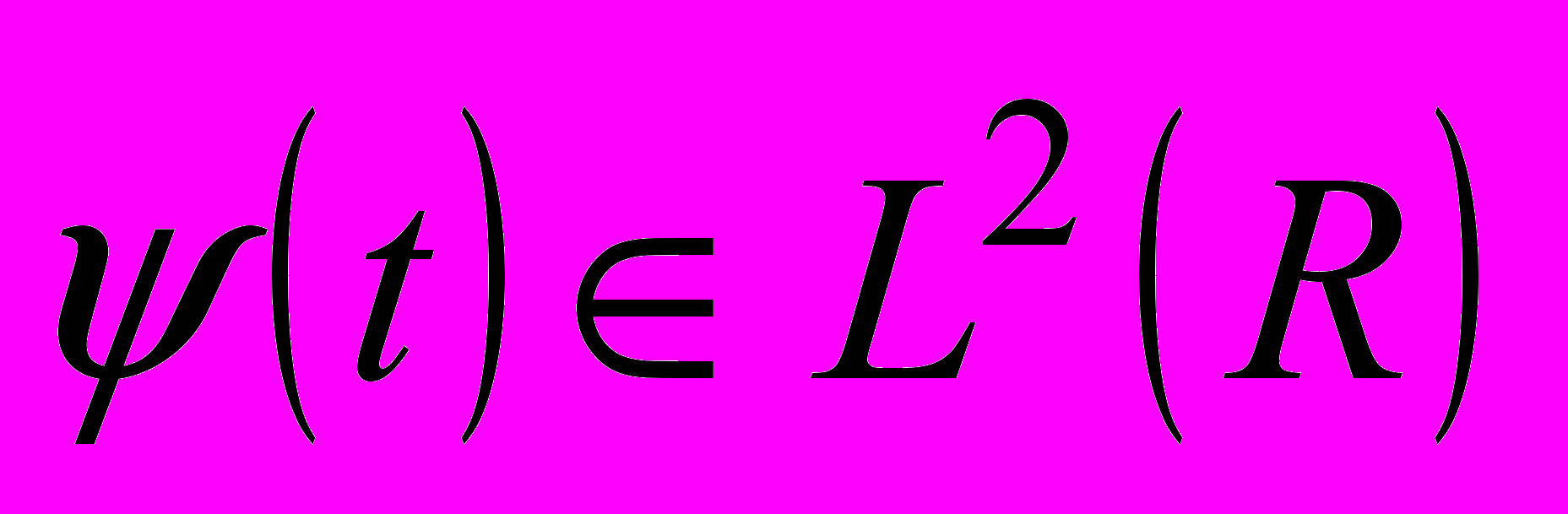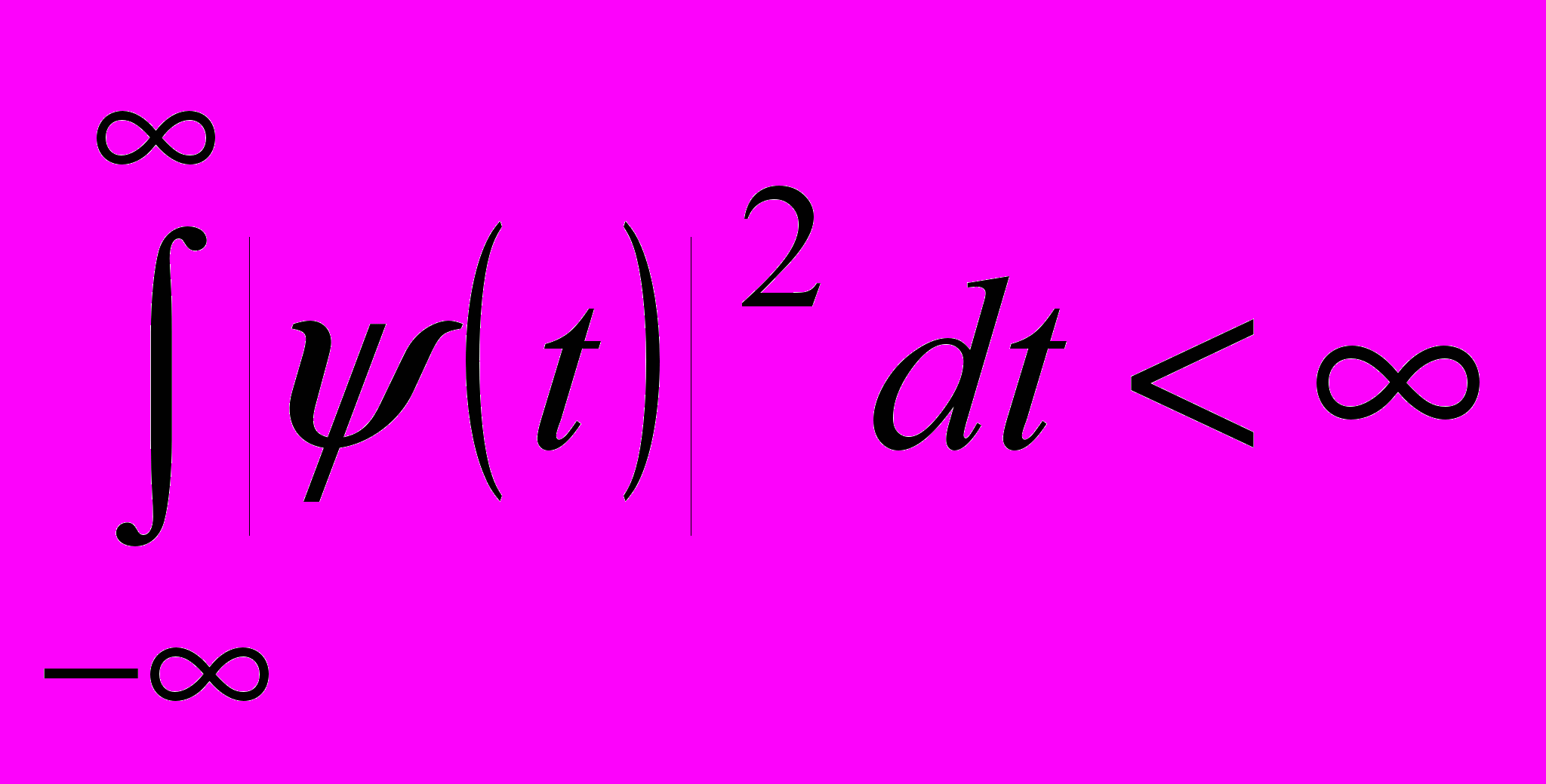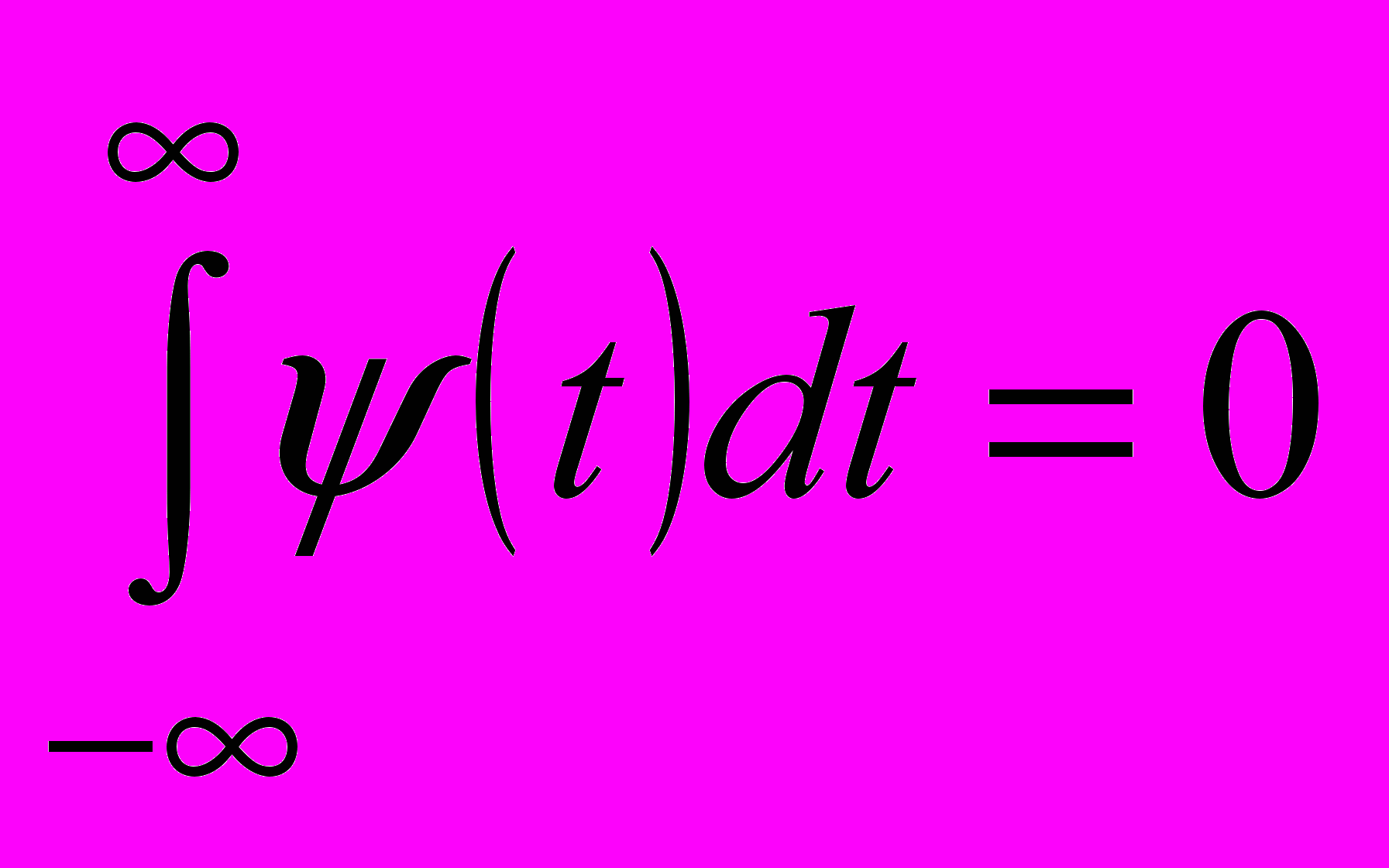Достаточным условием для 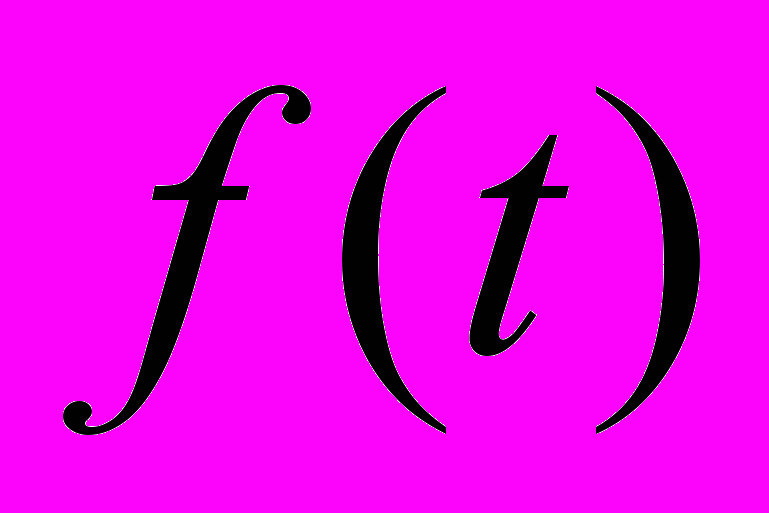является ее ограниченность. ВП характеризуется следующими свойствами:

- линейность: ;

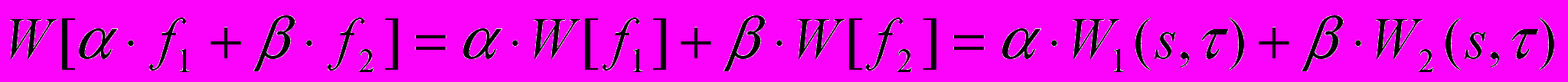- инвариантность относительно сдвига: ;

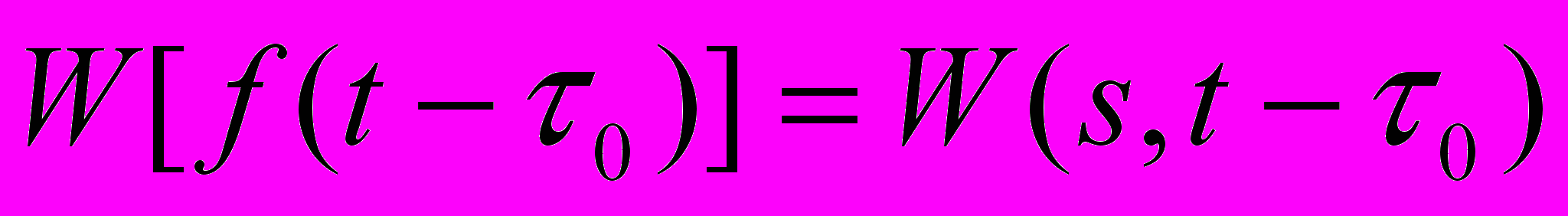- инвариантность относительно растяжения: .

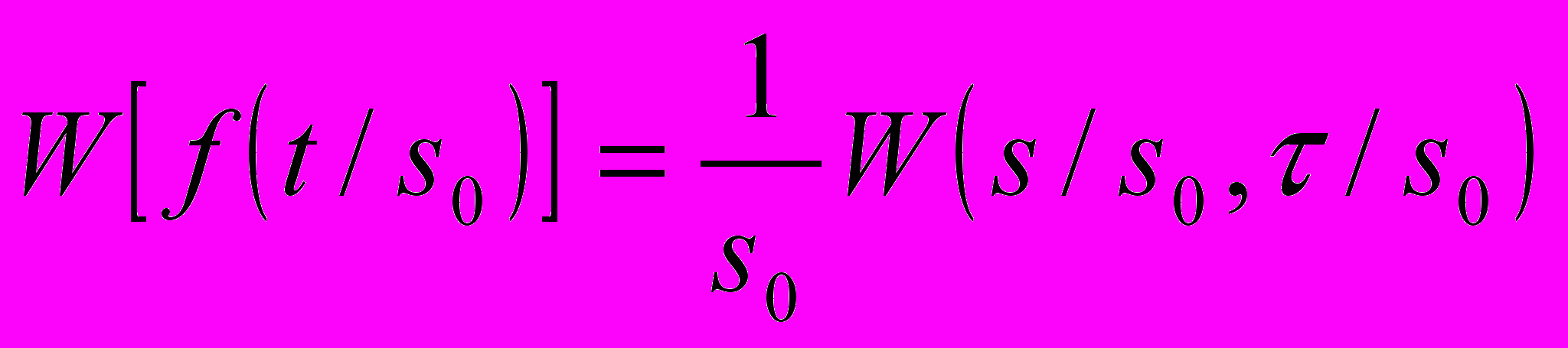Выбор базиса определяется тем, какую информацию необходимо извлечь из временного ряда. Вещественные базисы часто конструируются на основе производных функции Гаусса: 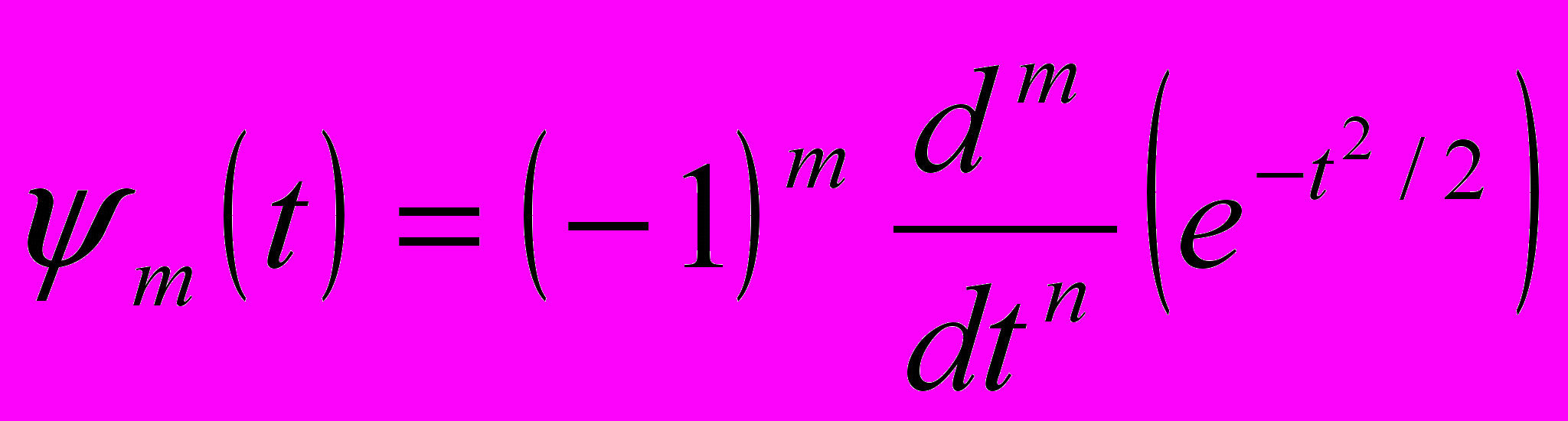. При 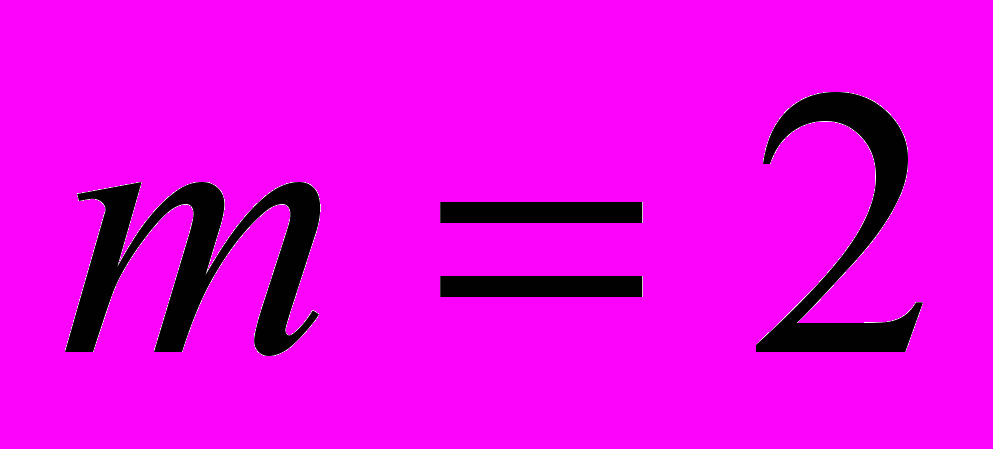, функция 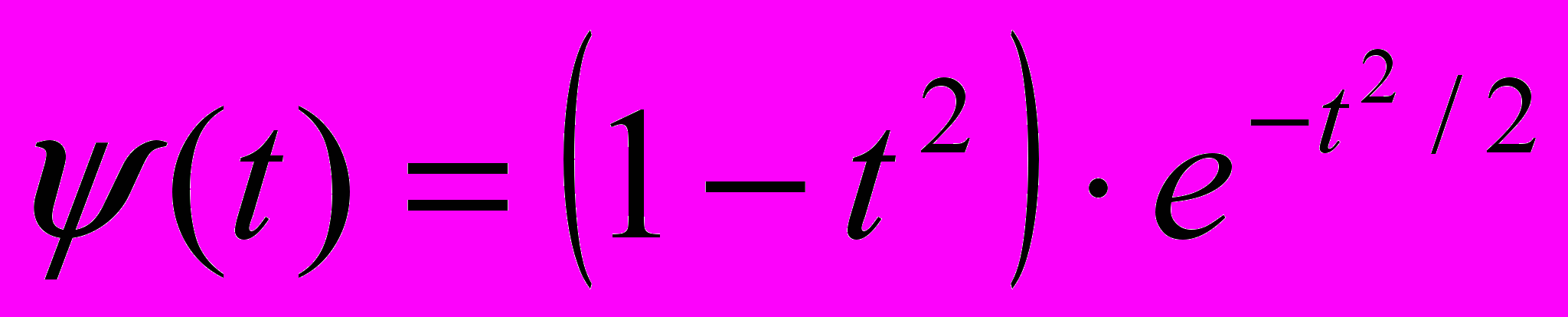называется MHAT-вейвлетом. Она имеет узкий энергетический спектр с хорошей локализацией во времени и пространстве. Для выявления периодичностей в качестве базисной функции часто используется вейвлет Морле: 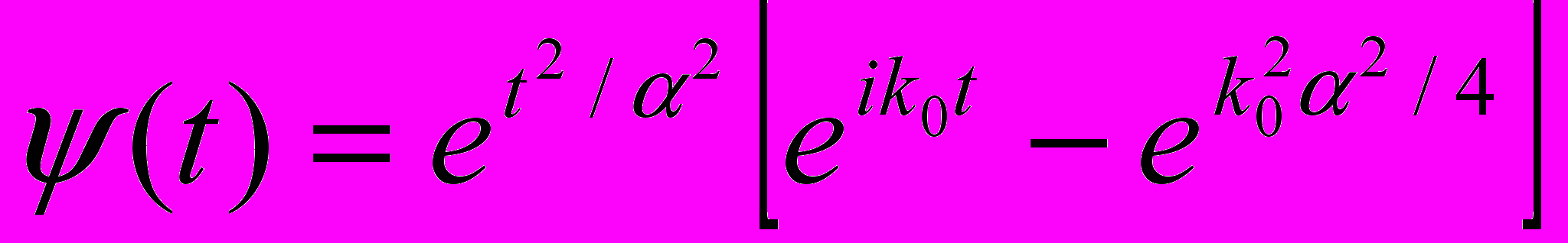, выходящий на предел Гейзенберга [5] (неизменность произведения эффективных ширины спектра и его длительности ). (рис. 2)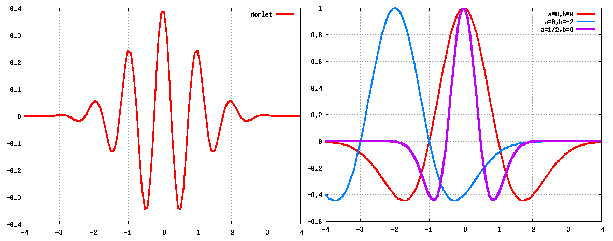




a b

Рис. 2 a) Morlet-вейвлет; b) Mhat-вейвлет

Для анализа с помощью НВП временной ряд 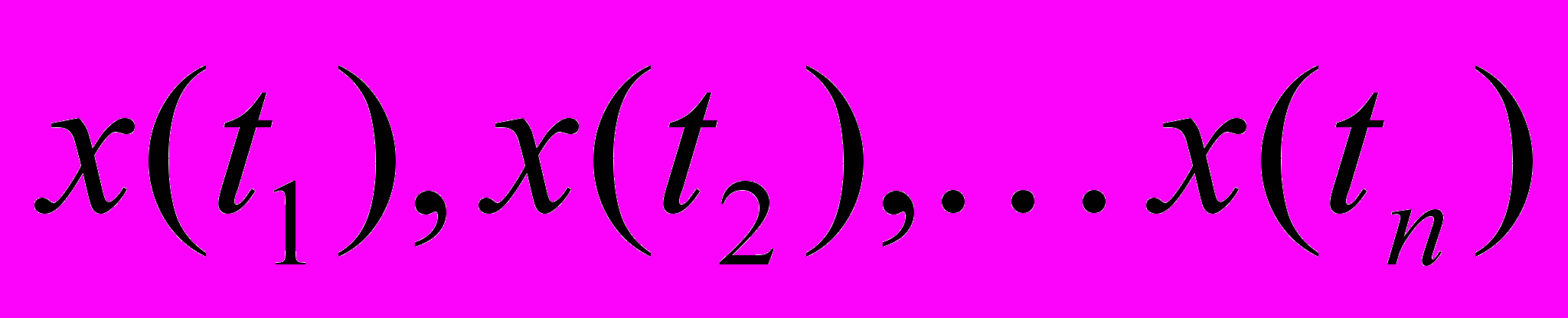представляется в виде:



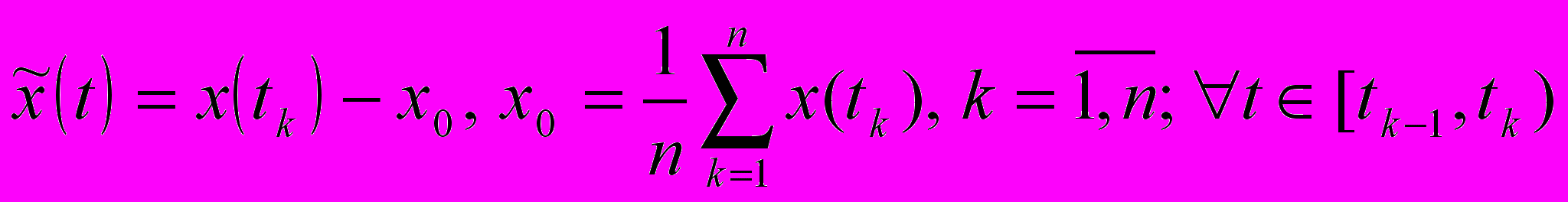(1)

Применив к данному временному ряду НВП, получим:. .

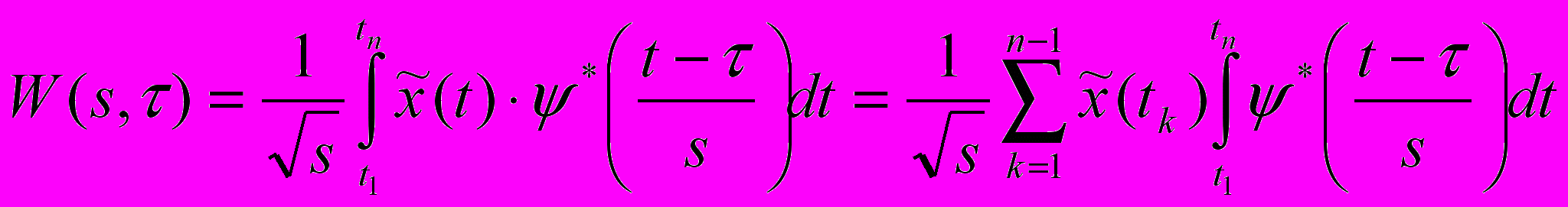Результатом вейвлет-преобразования одномерного ряда является массив амплитуд вейвлет-преобразования - значений коэффициентов 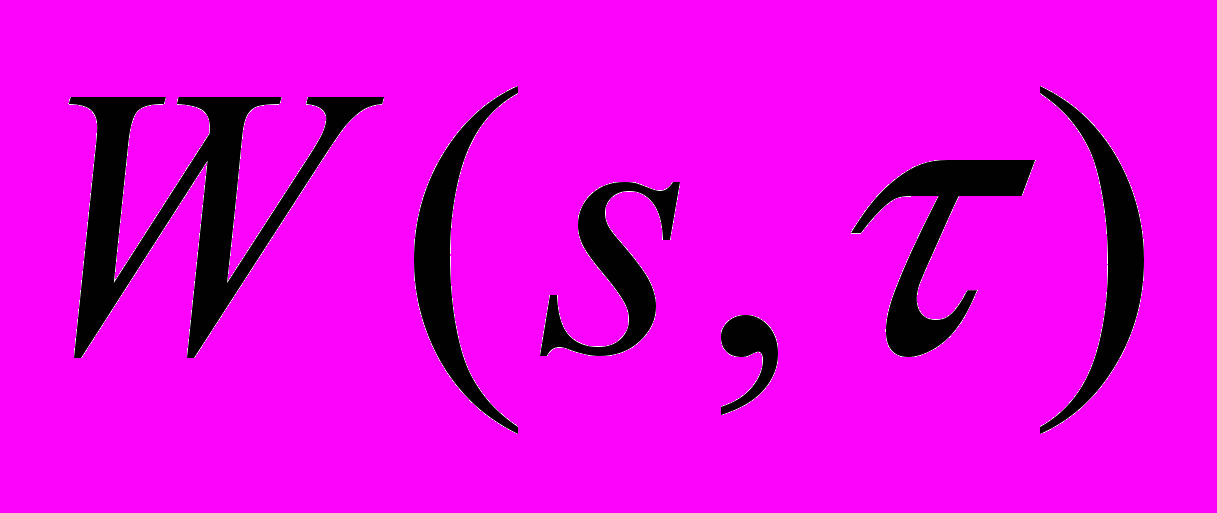. Распределение этих значений в пространстве дает информацию об изменении относительного вклада компонент разной частоты во времени, график данного распределения – вейвлетограмма .

Временная локализация частот также может быть получена с помощью оконного преобразования Фурье 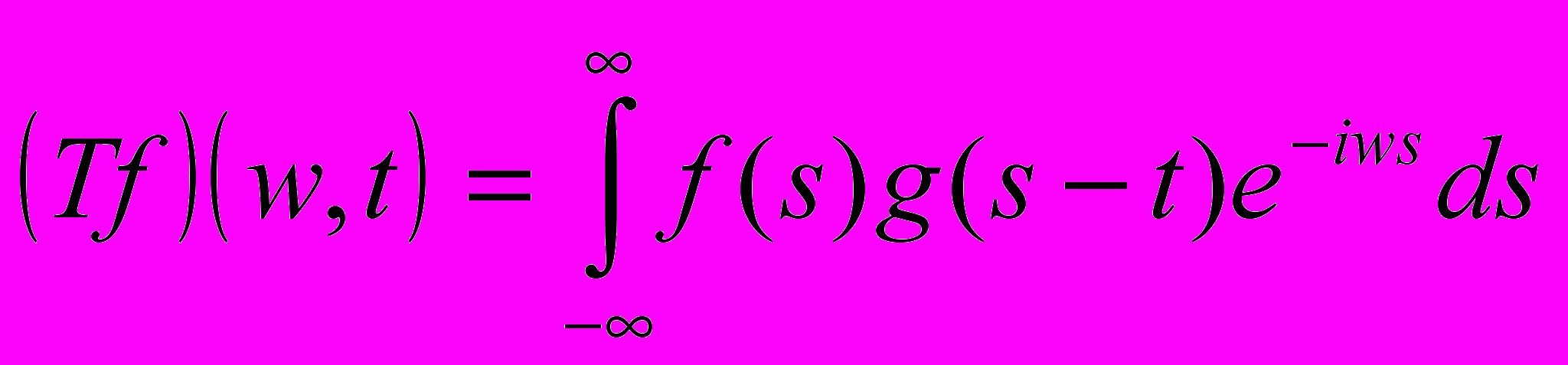, где в качестве функции 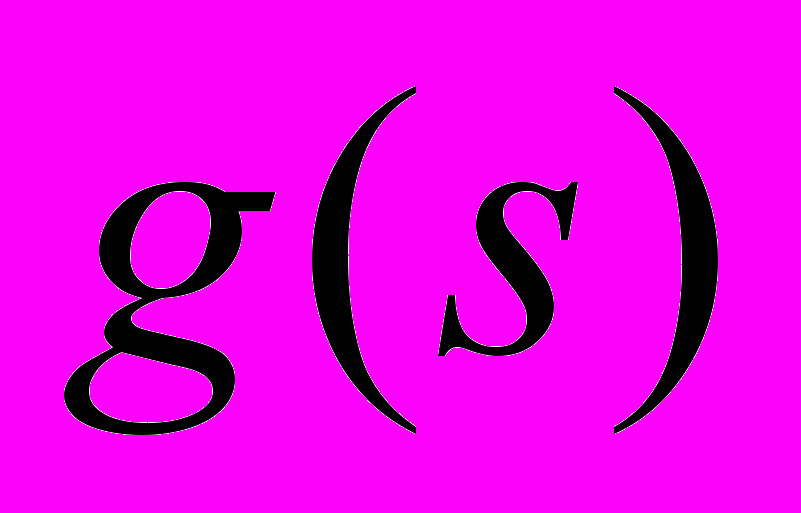часто используется функция Гаусса [4] . Различие между ВП и оконным преобразованием Фурье состоит в форме анализирующих функци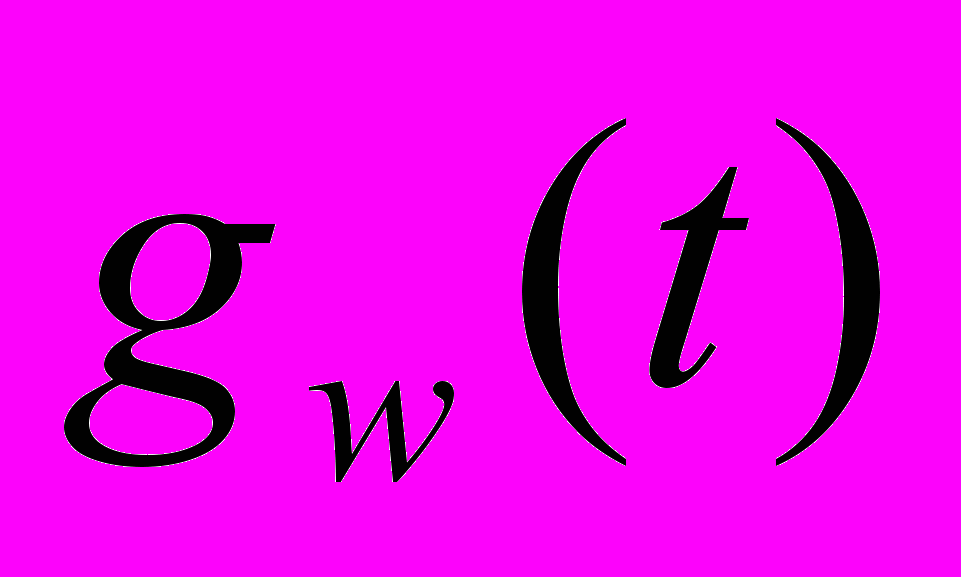й и 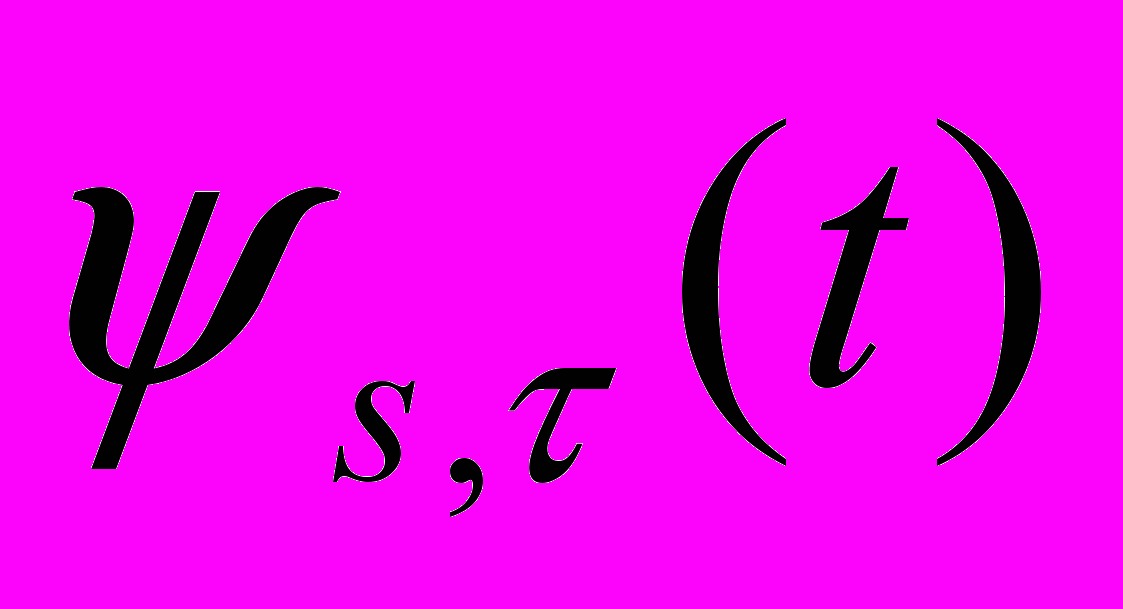. Все функции 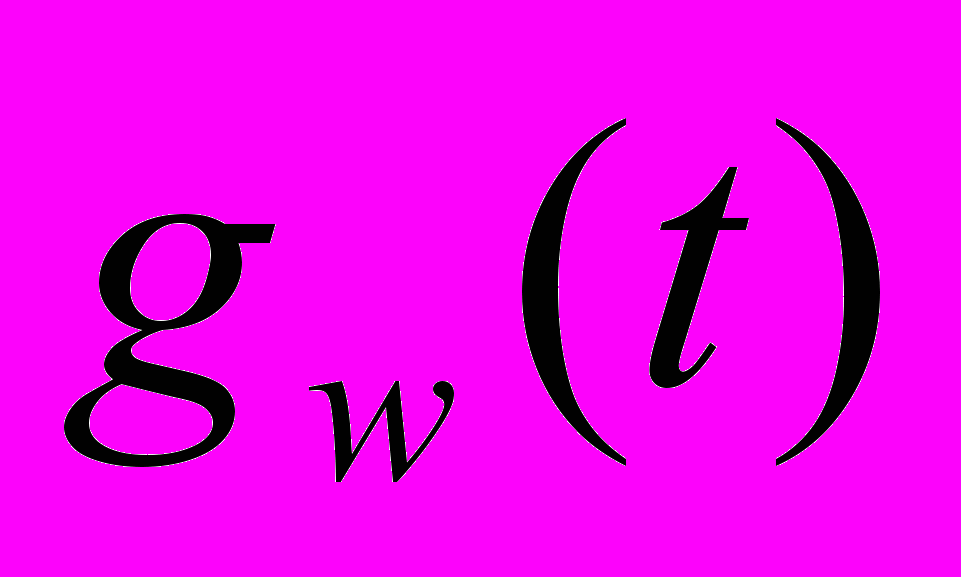состоят из одной и той же оболочки 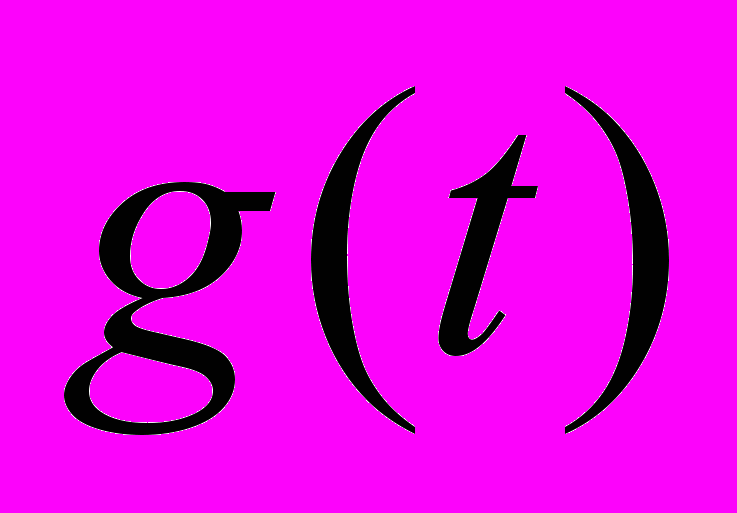, сдвинутой к подходящему расположению во времени и «заполненной» высокочастотными осцилляциями (рис.3). Напротив, 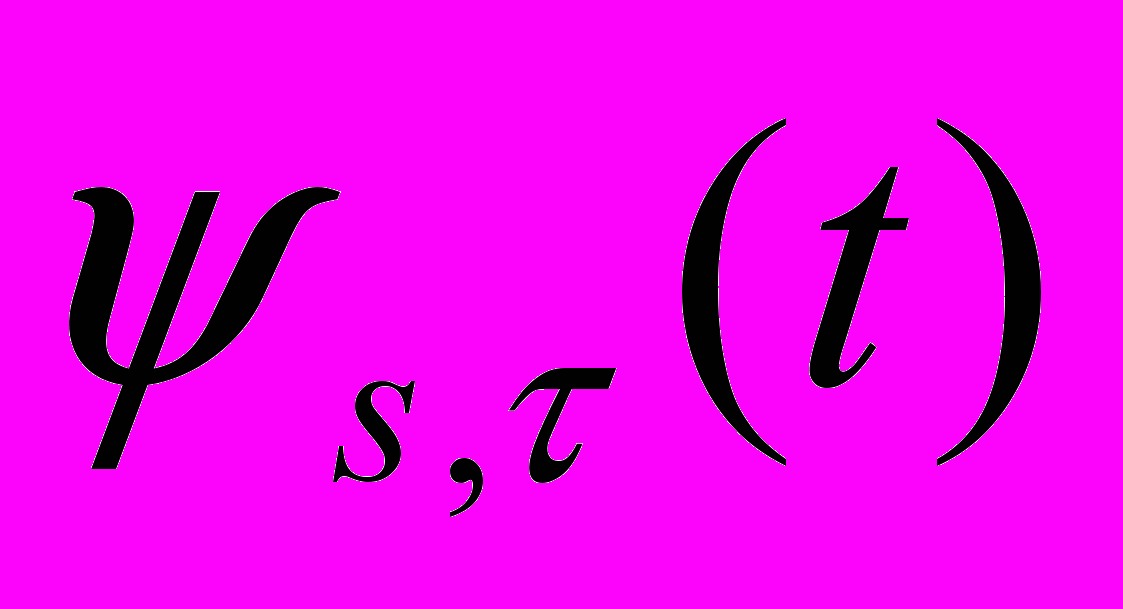имеет ширину во времени, соответствующую частоте, в результате этого ВП дает лучшую возможность рассмотреть высокочастотные явления с коротким периодом существования.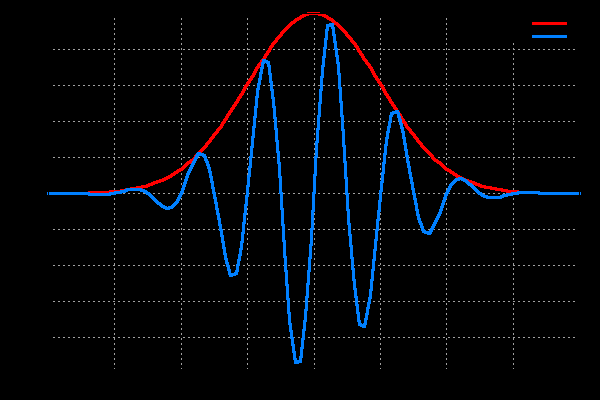



Рис. 3 Функция оконного преобразования Фурье


Для анализа спектральных характеристик и выявления периодичностей используется глобальный спектр энергии: 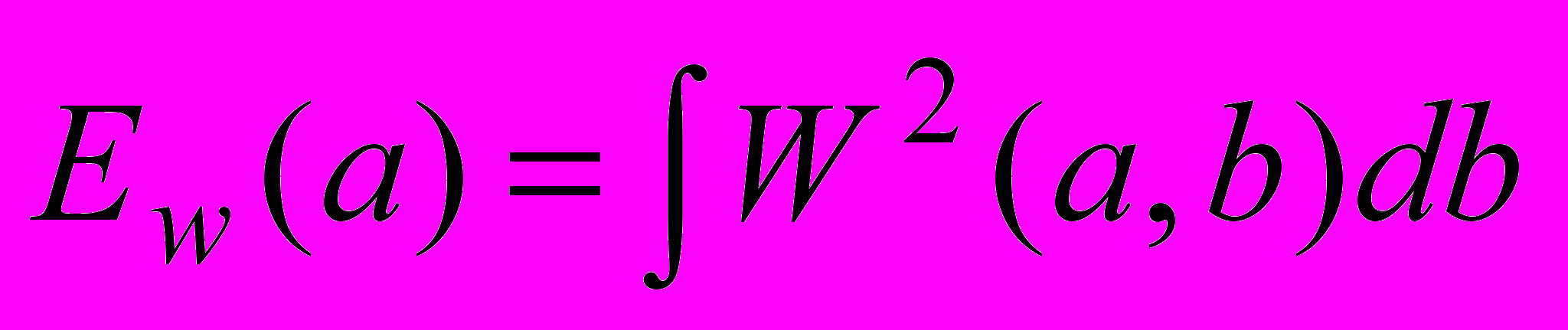. Для сравнения вейвлетограмм двух временных рядов можно использовать различные меры близости. Простейшая мера представляет интеграл разностей вейвлет-коэффициентов в виде: 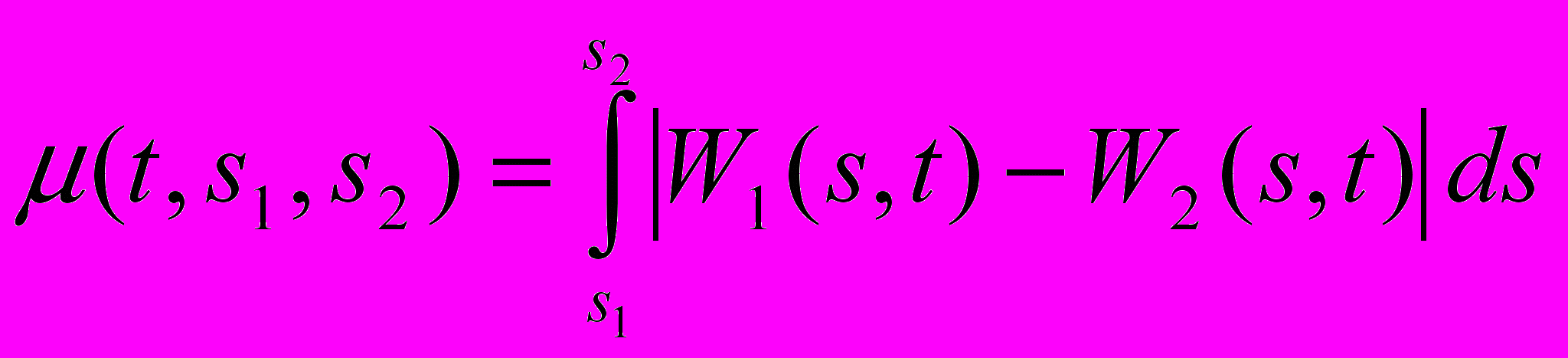, где 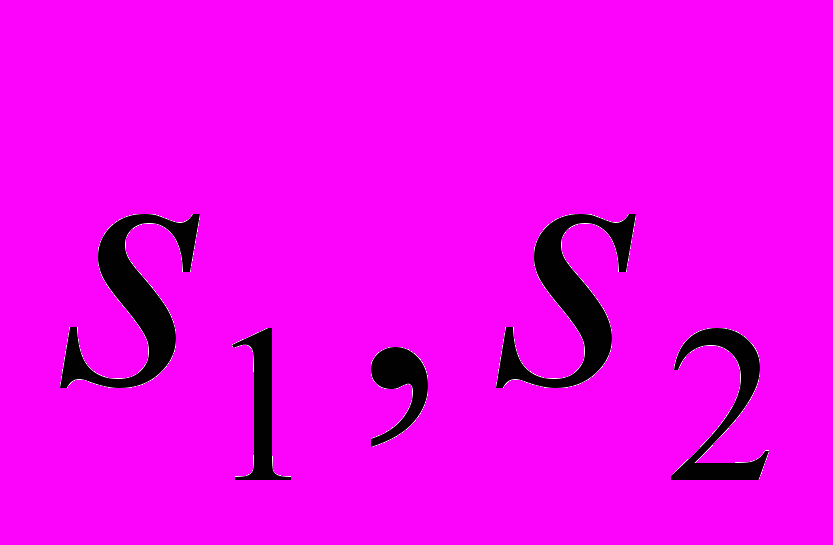- задают диапазон частот для сравнения.

Программный компонент вейвлет-анализа. Для анализа временных рядов, представленных в базе Gi3, реализован компонент вейвлет-анализа (рис. 4). Программный компонент основан на двух составляющих: портабельном и эффективном языке программирования Lua[6] и свободно распространяемой системе построения графиков GnuPlot.



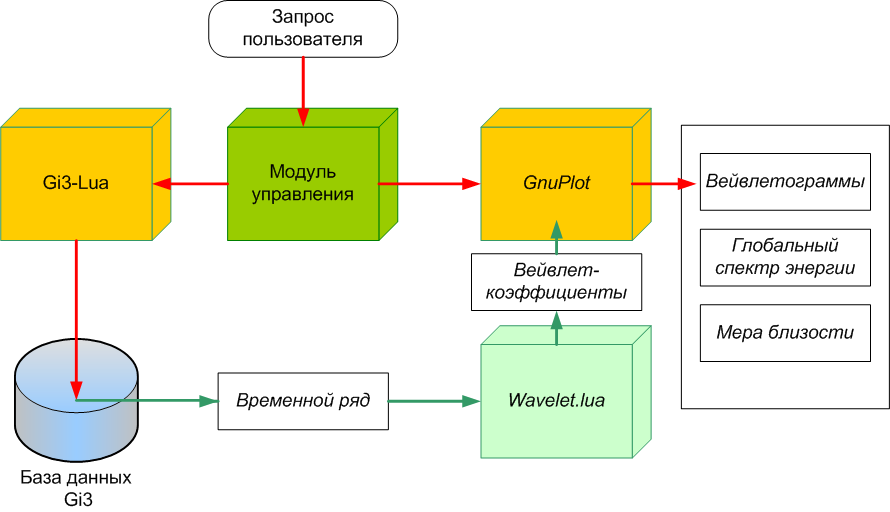
Рис. 4 Технология работы компонента вейвлет-анализа

Данный компонент позволяет получать как вейвлетограмму одного ряда, так и сравнительные вейвлетограммы двух временных рядов, строить график глобального спектра и меры близости. Сначала пользователь формирует запрос, в котором указывает необходимые для анализа наименования: временных рядов или выборок, базисных вейвлетов и типа выводимого результата (вейвлетограмма, глобальный спектр, мера близости и др.). Сформированный в текстовом виде запрос обрабатывается управляющим модулем, который вызывает ядро Gi3-Lua с запросом на выборку данных из геоклиматической базы Gi3. После успешного формирования выборки применяется интегральное вейвлет-преобразование, реализованное в виде скрипта Wavelet.lua. Для базисных вейвлетов MHAT и Wave получены аналитические выражения, а для вейвлета Morlet автоматически проводится дополнительное численное интегрирование. В конечном результате формируется двумерное распределение вейвлет-коэффициентов.

Дискретное вейвлет-преобразование (ДВП). При ДВП временной ряд, представленный в виде (1) разлагается по базису, составленному из масштабных и вейвлет-функций: 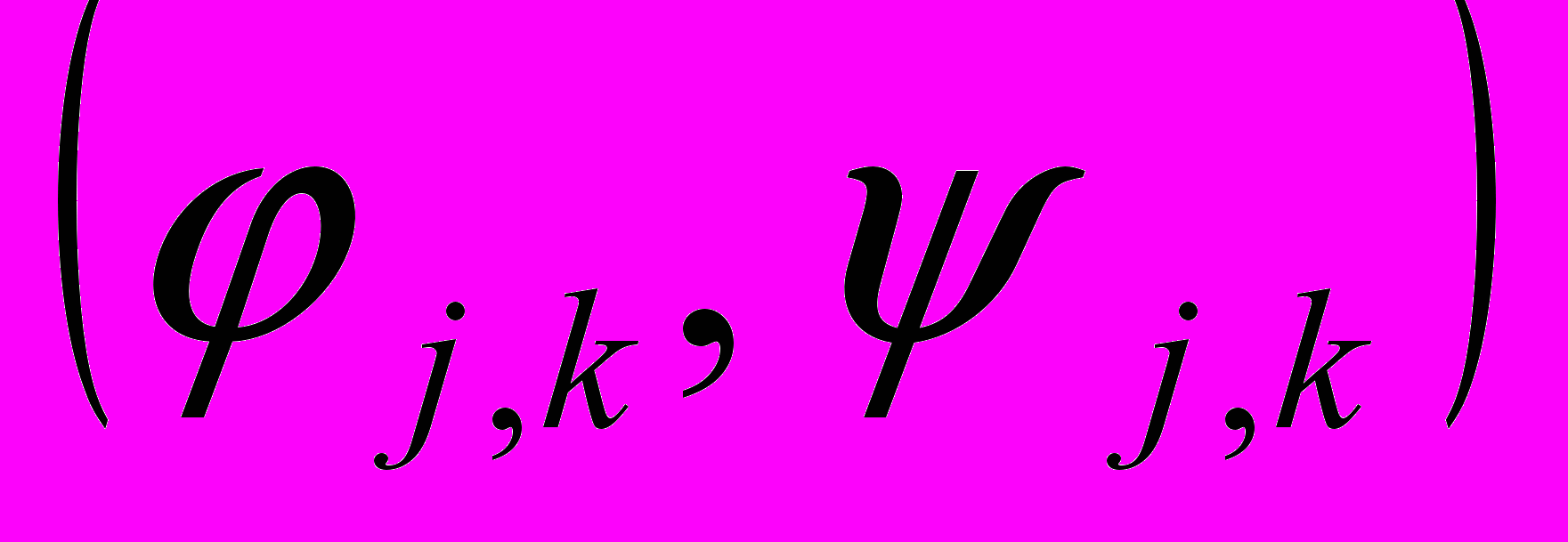. Разложение имеет вид: 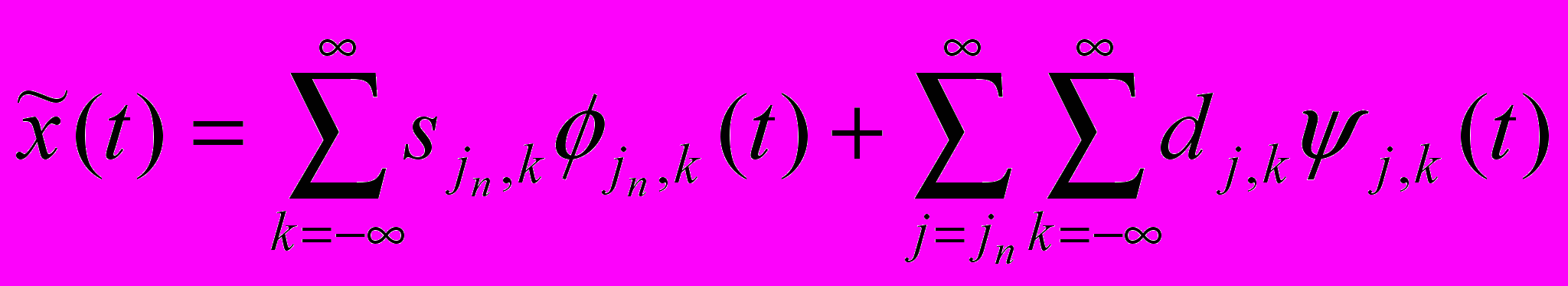, где ­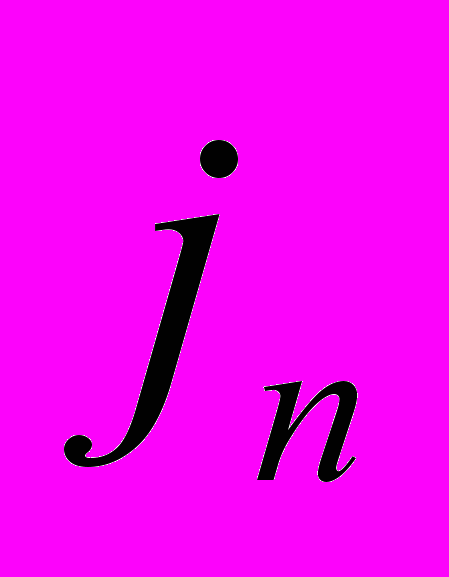 ­– заданный уровень разрешения (сглаживания). 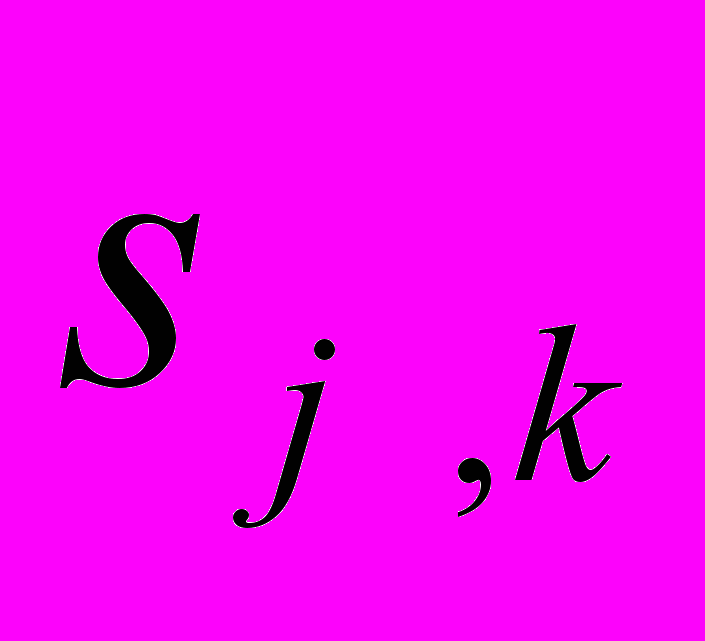представляют собой коэффициенты сглаживания, а 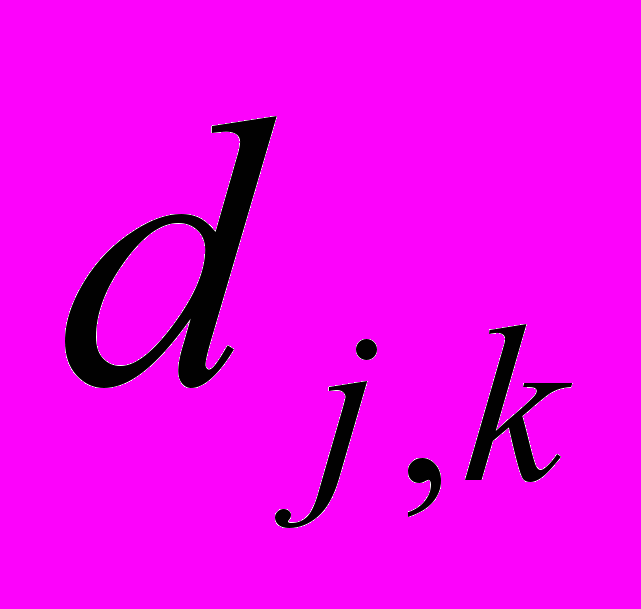– детализирующие, вычисляются по следующим итерационным формулам: 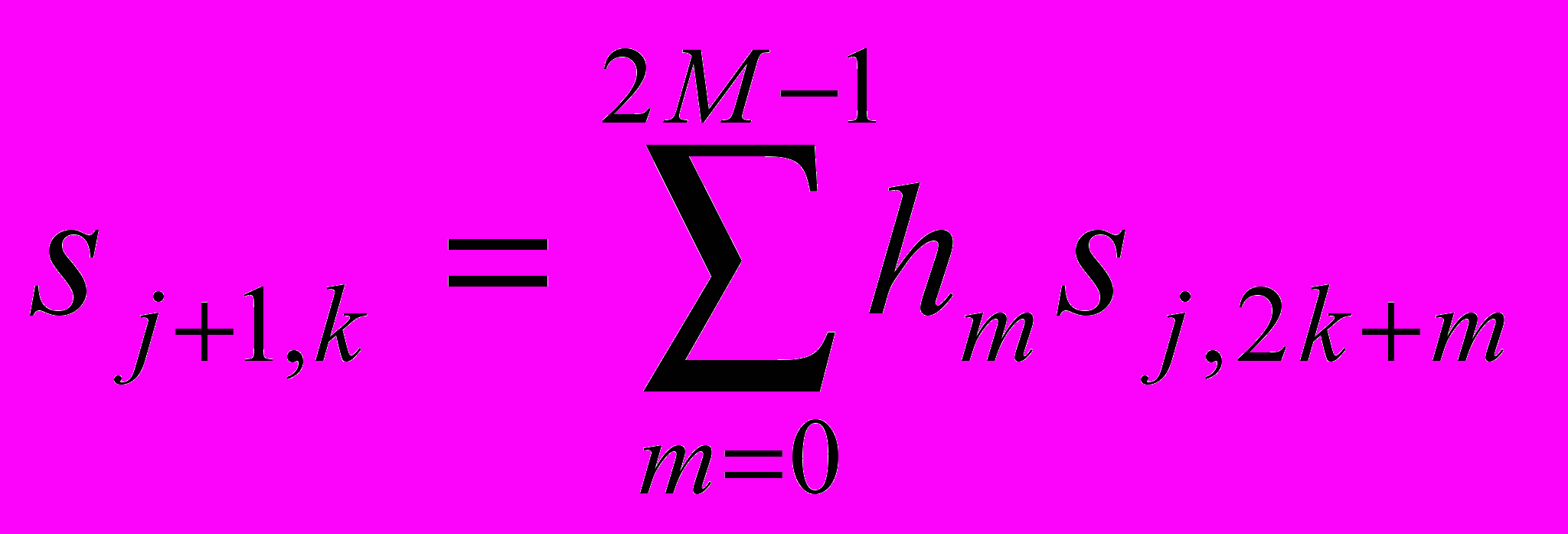, , 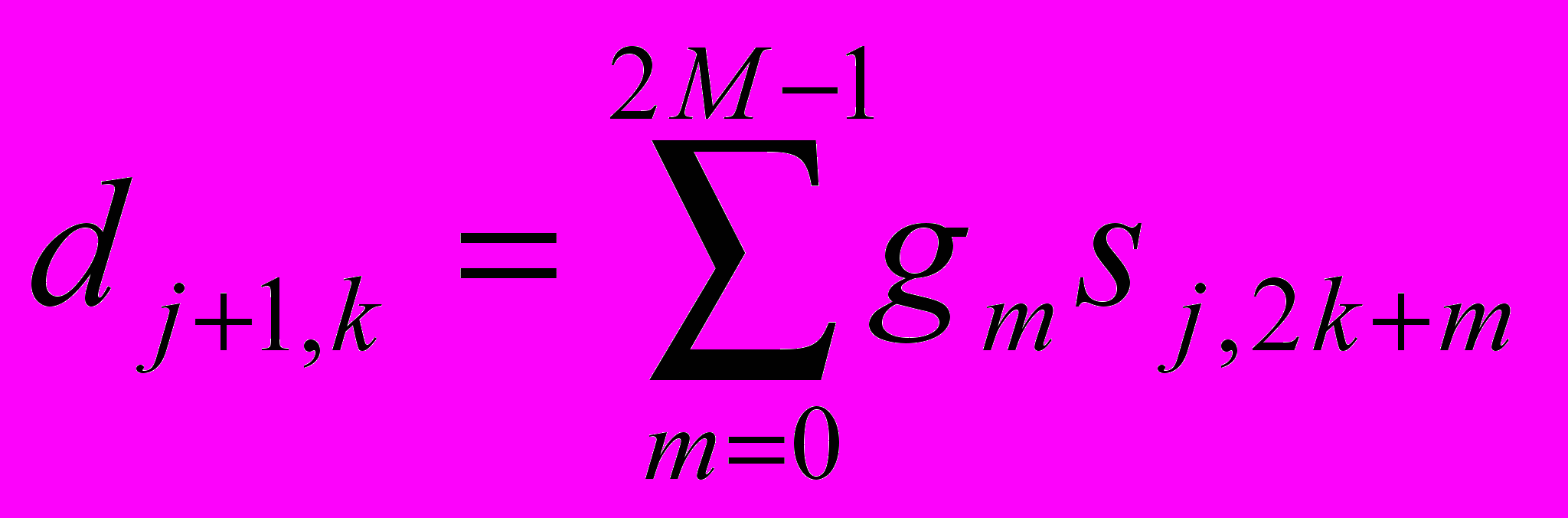, 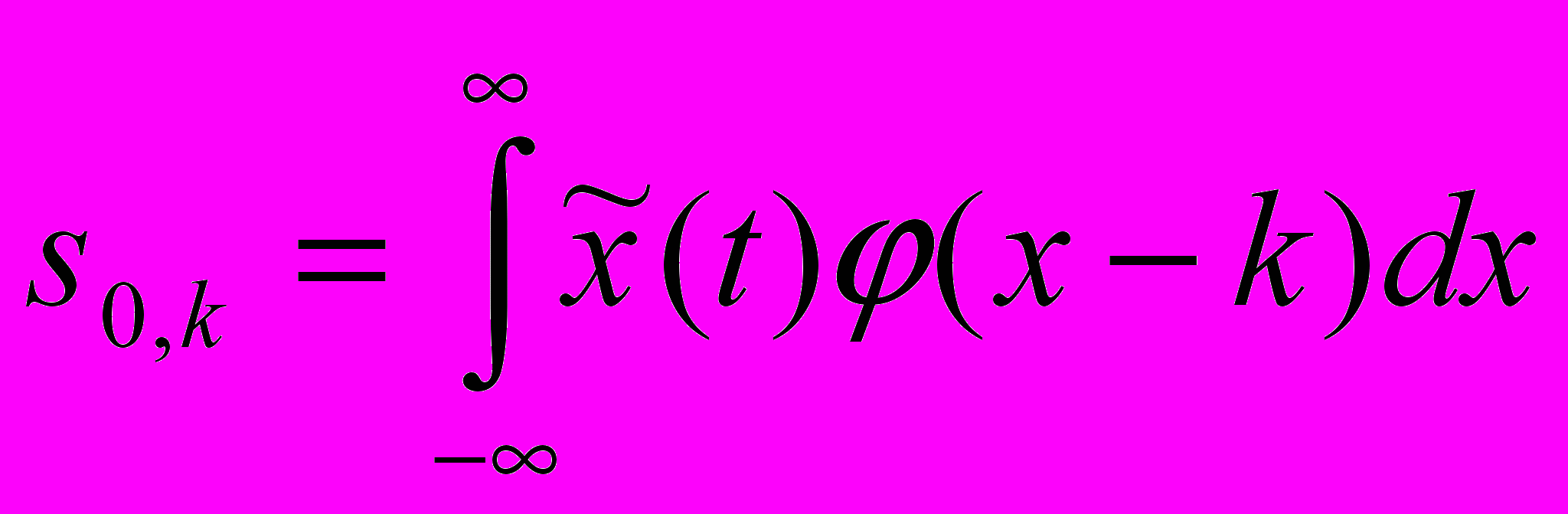где 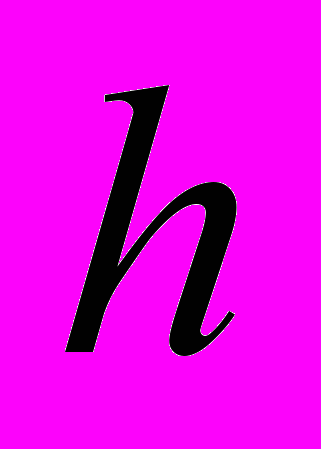– низкочастотный фильтр, а 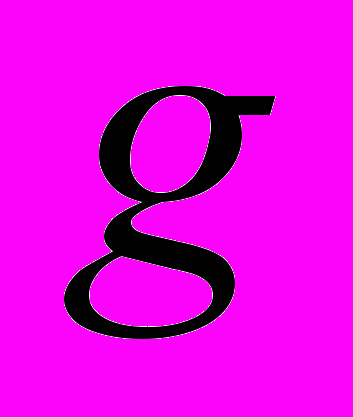– высокочастотный. Фильтры удовлетворяют следующим условиям: 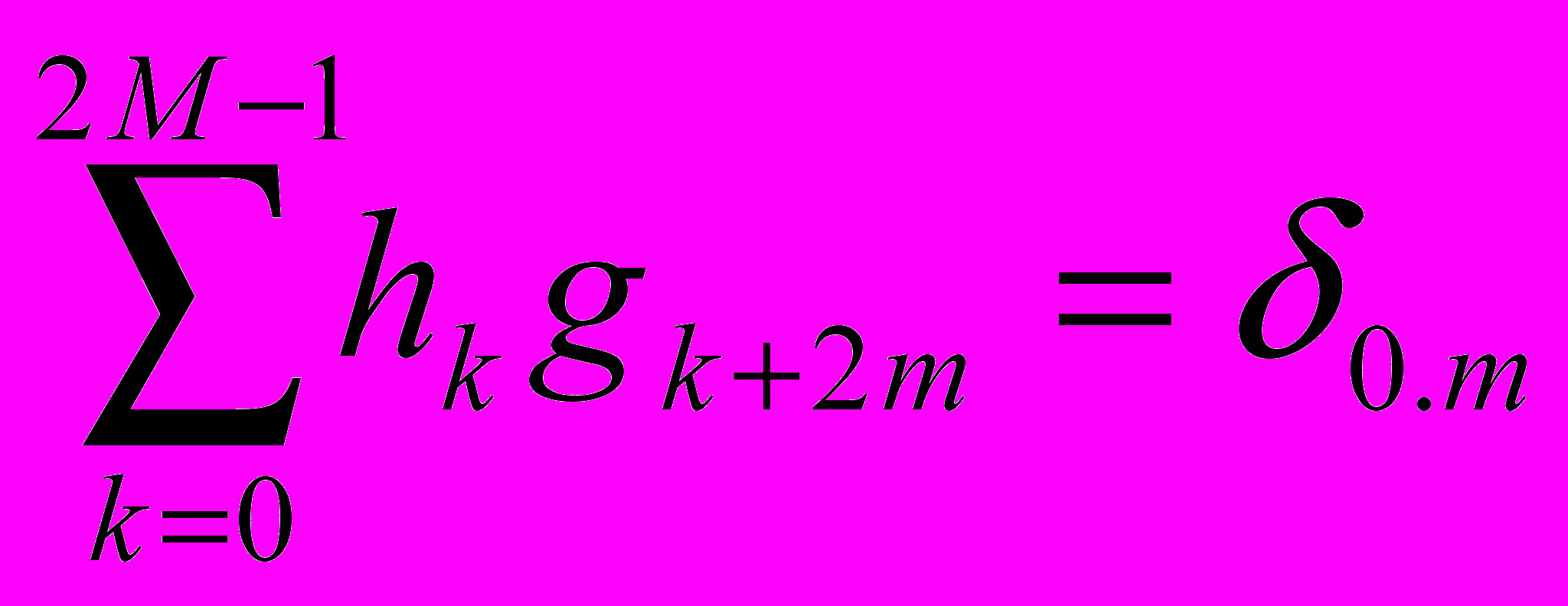, ­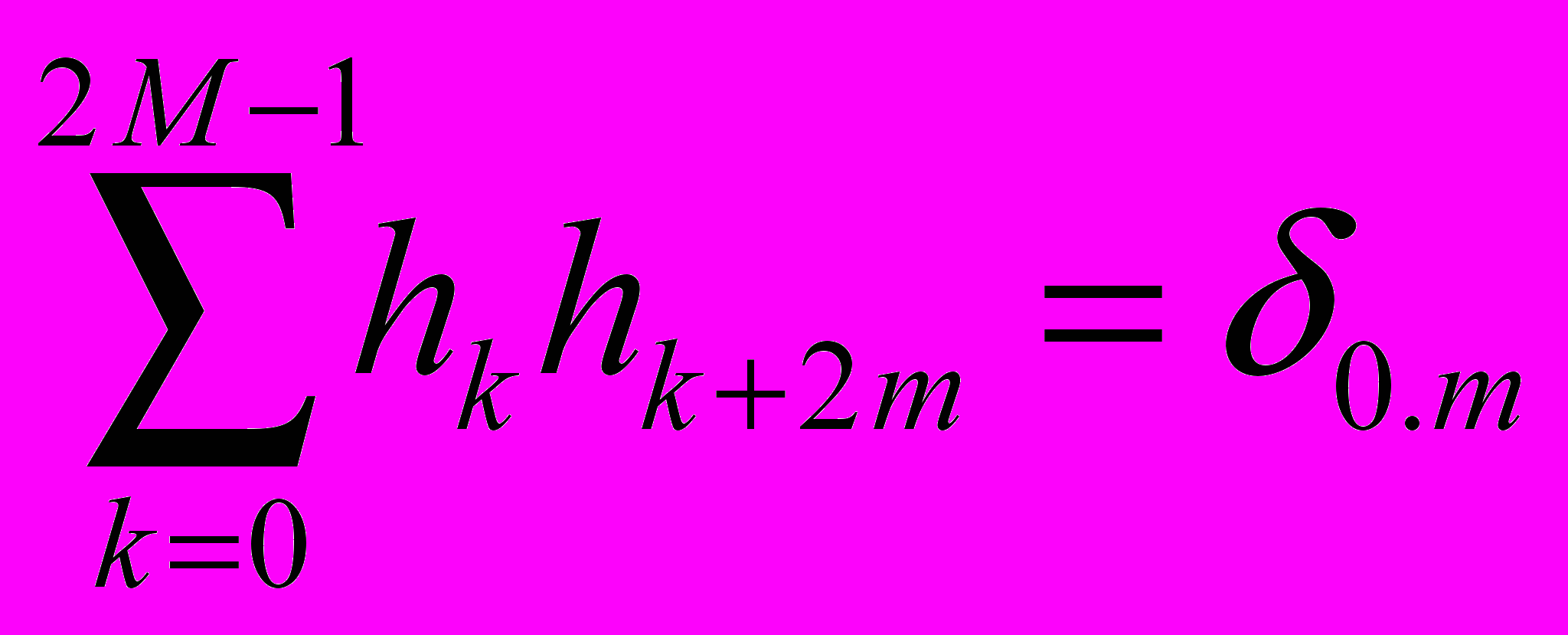– ортогональность; 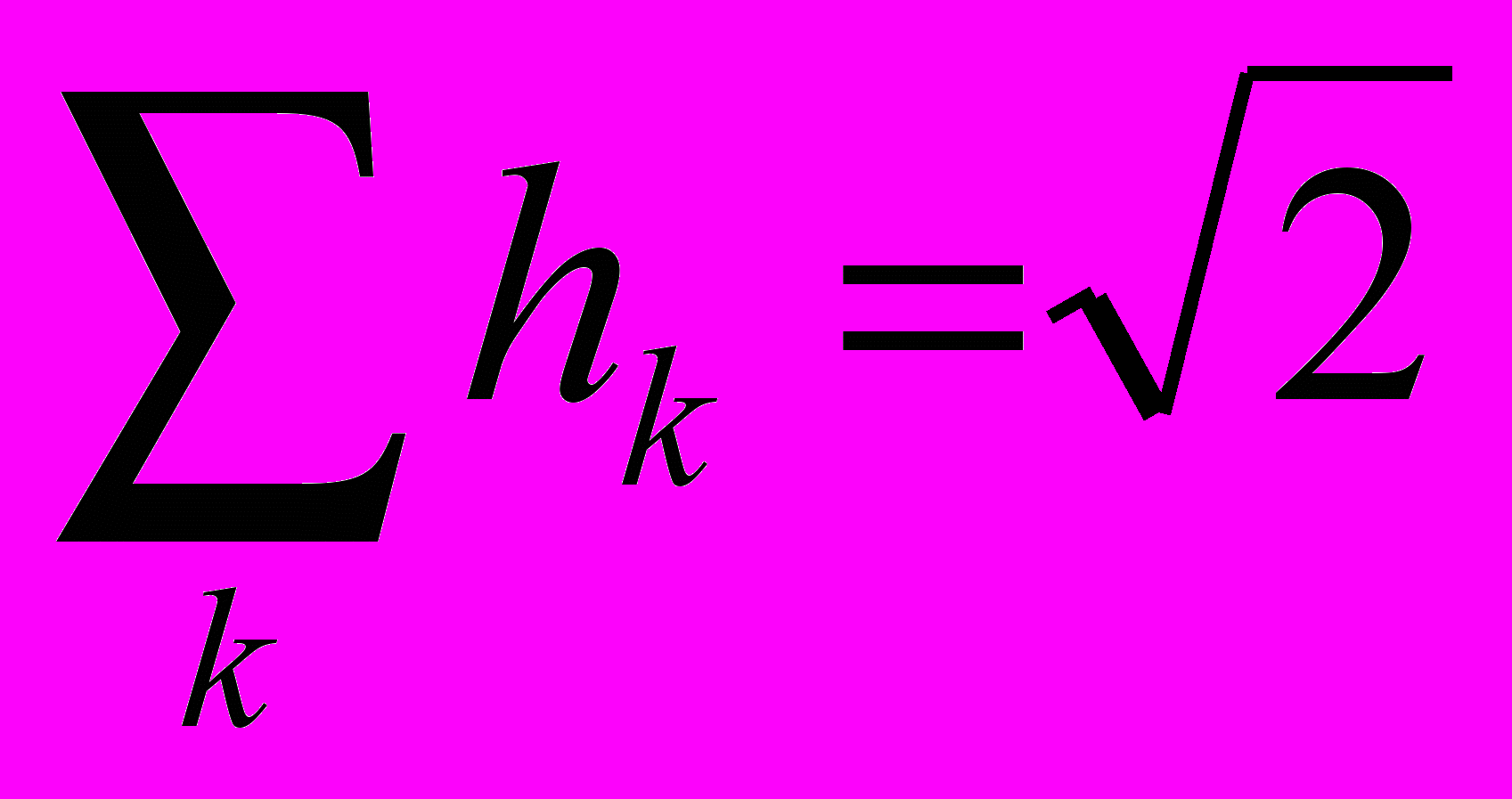– нормировка. Данное преобразование можно разбить на следующие этапы:
  1. Свертка исходного ряда с низкочастотным фильтром, результатом которой является сглаженный ряд, представленный коэффициентами
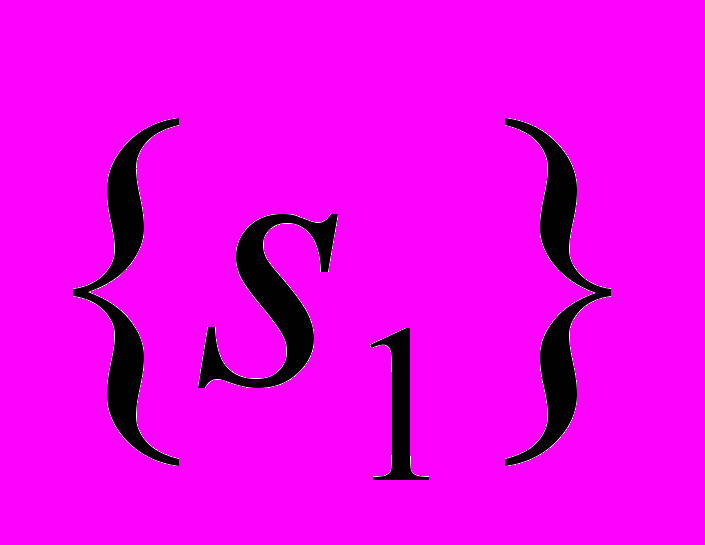
  2. Расчет детализирующих коэффициентов
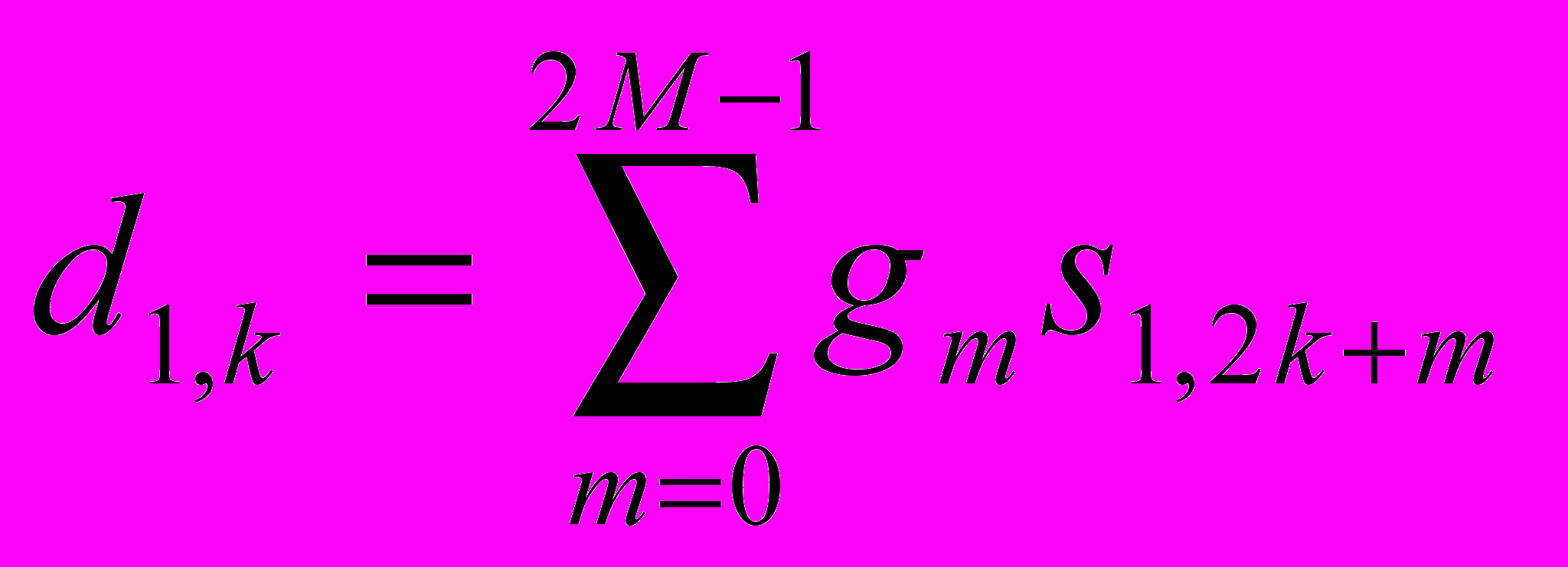
  3. На каждом из следующих уровней сглаживания число коэффициентов уменьшается в два раза (рис. 6)



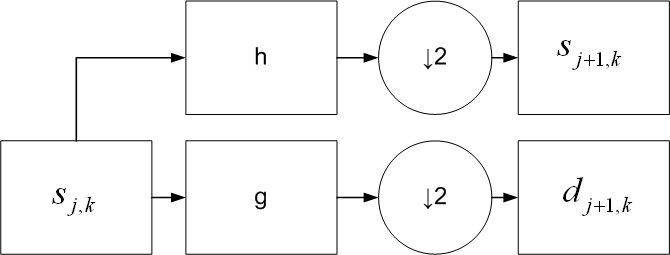
Рис. 5 Вычисление коэффициентов ДВП на уровне j

Для восстановления исходного ряда применяются функции 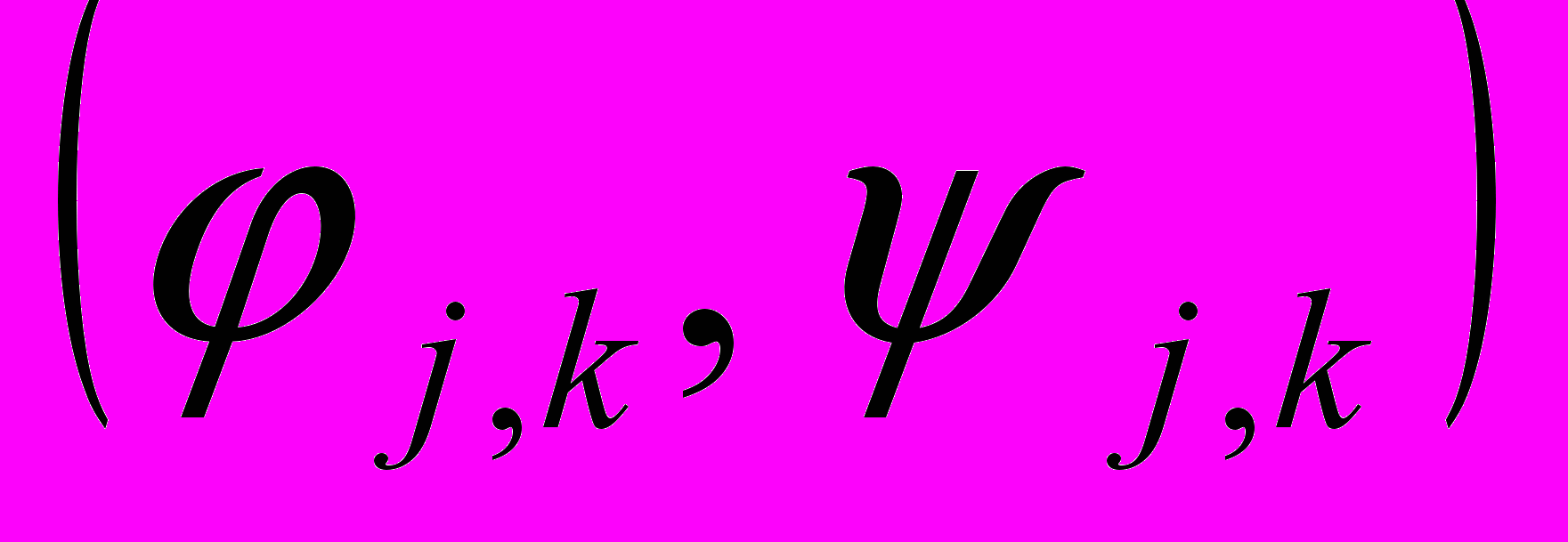, определяемые из следующих условий 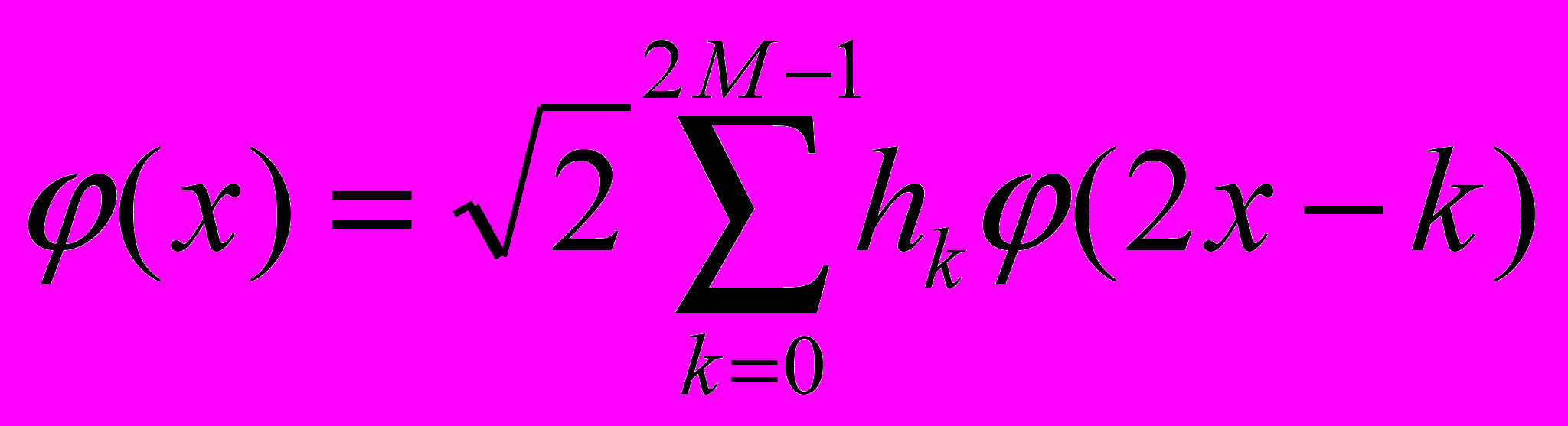, , 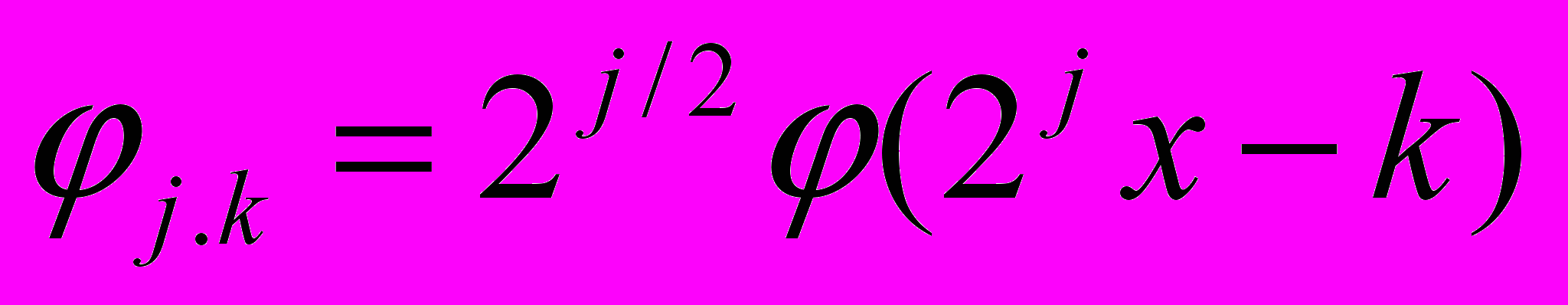, 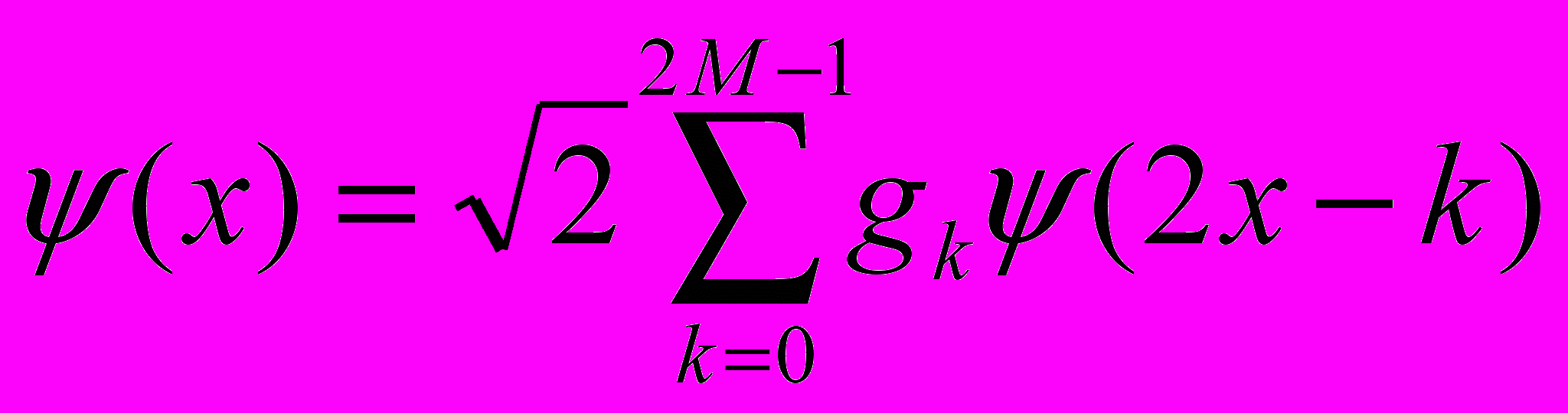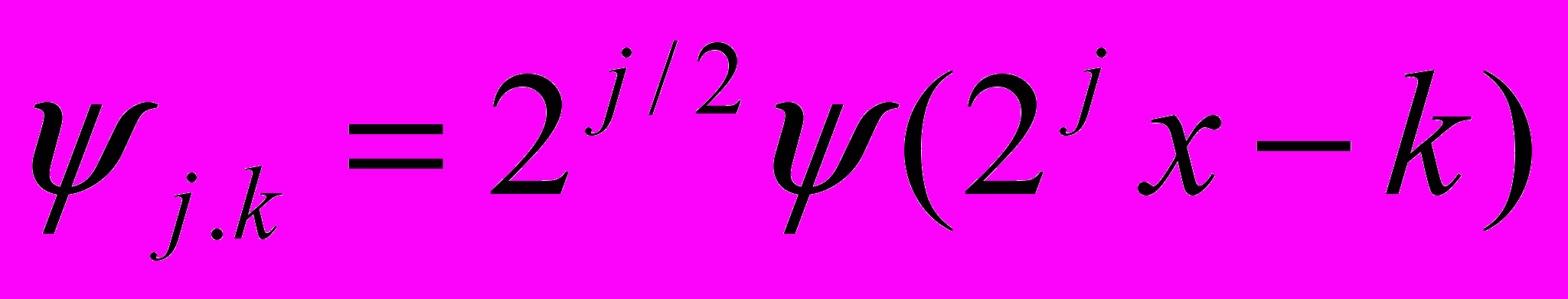. Данное преобразование является прореживающим, т.е. уменьшающим на каждом из этапов число коэффициентов, основным его преимуществом является хранение только достаточной информации для восстановления исходного ряда.

Для применения ВП к прогнозированию временных рядов, оно должно быть инвариантно относительно временного сдвига, т.е. вейвлет-коэффициенты, вычисленные для ряда 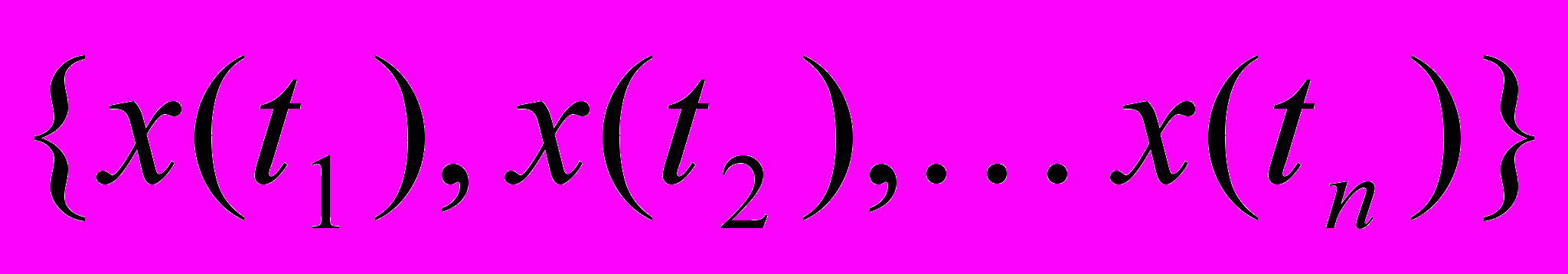, должны совпадать с первыми n коэффициентами для ряда 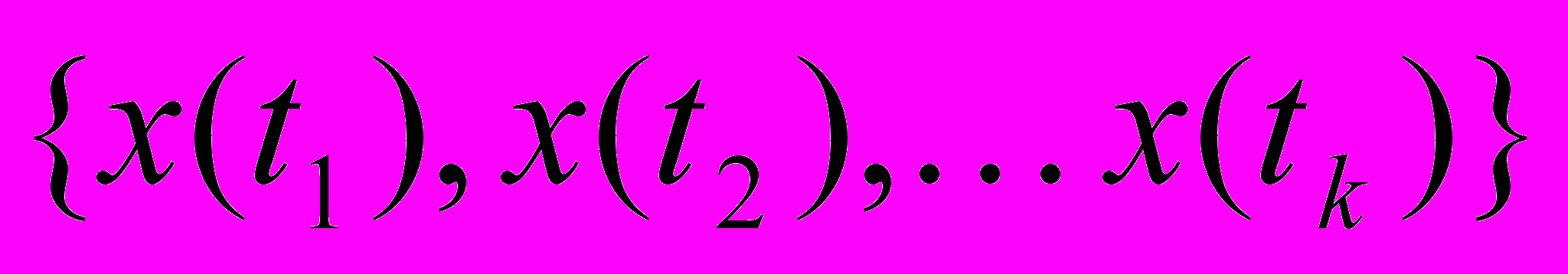, где 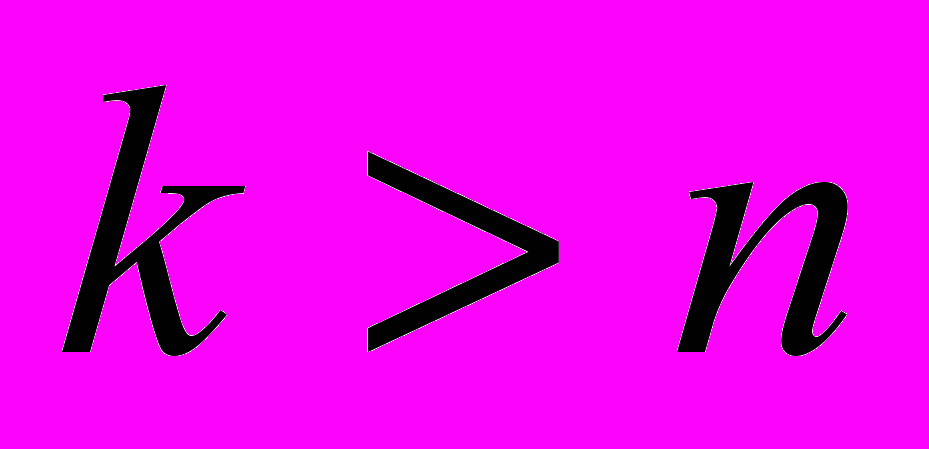. Тогда при обновлении временно ряда нет необходимости заново вычислять ВП для всех точек. Прореживающее вейвлет-преобразование не обладает данным свойством, в отличие от преобразования À trous [7].

ВП À trous заключается также в разложении временного ряда на две составляющие: высокочастотную и низкочастотную. À trous относится к классу избыточных ВП: для временного ряда длины N на каждом из уровней сглаживания содержится N значений.

Данное преобразование можно разделить на следующие этапы:
  1. Исходный временной ряд 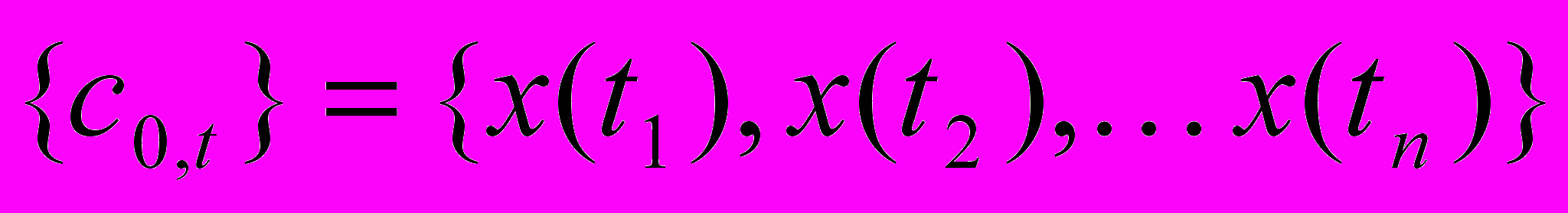представляется как скалярное произведение функции 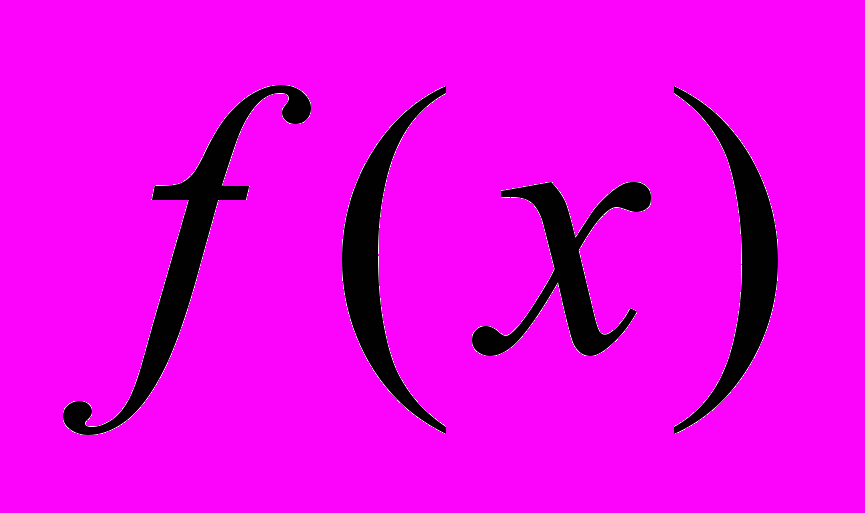и масштабирующей функции 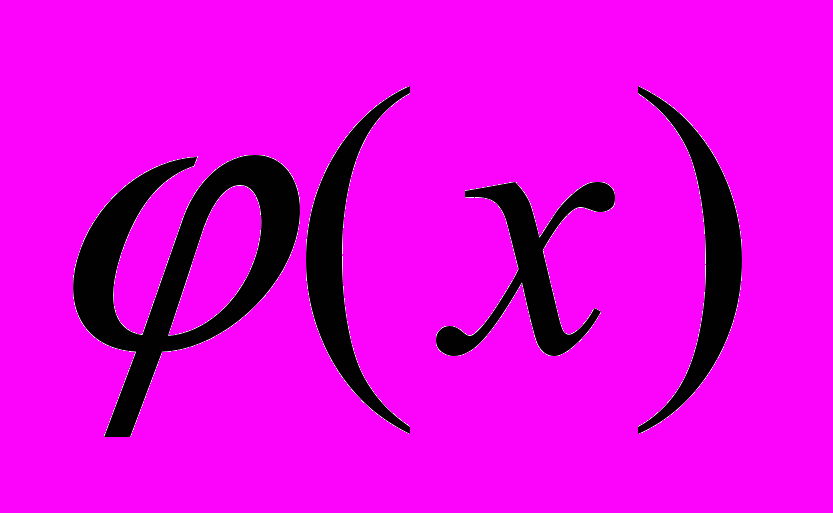: 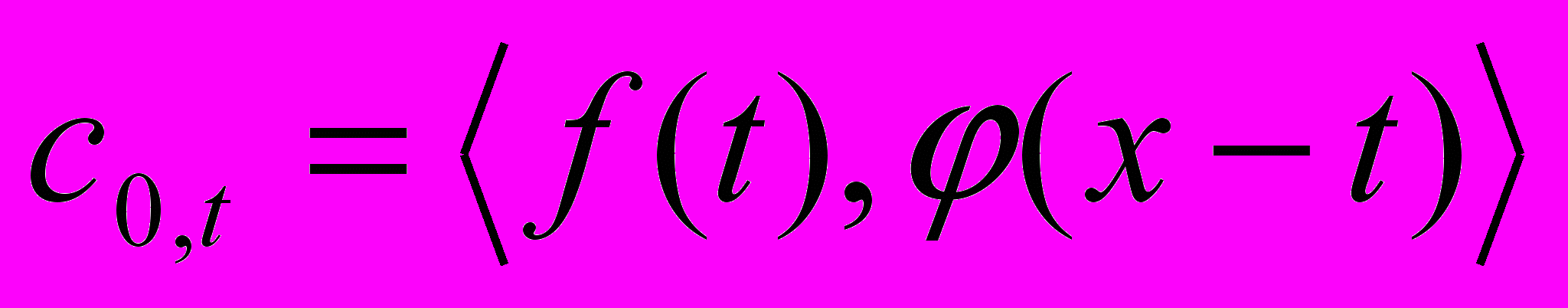. При этом 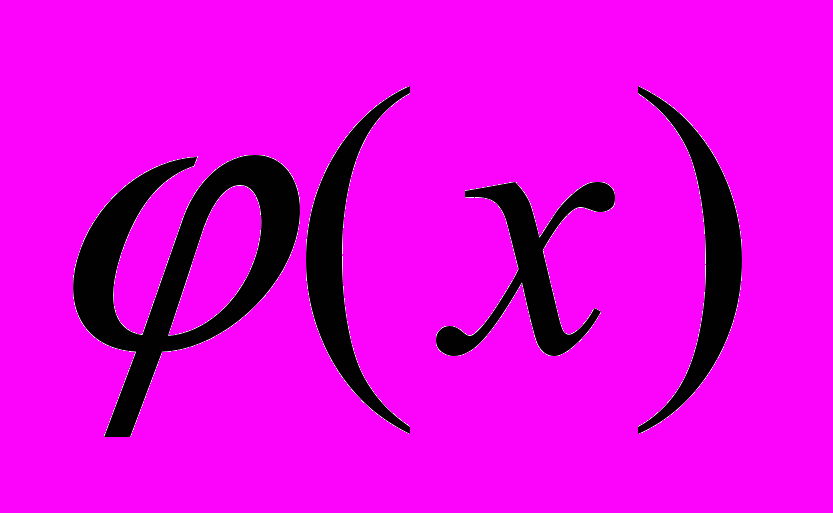удовлетворяет уравнению 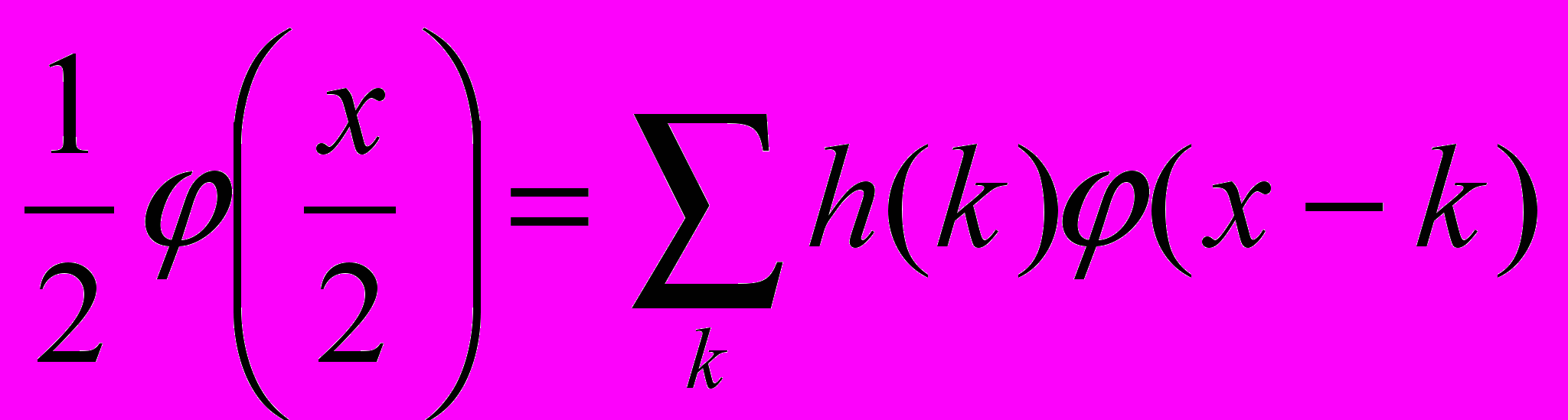, где 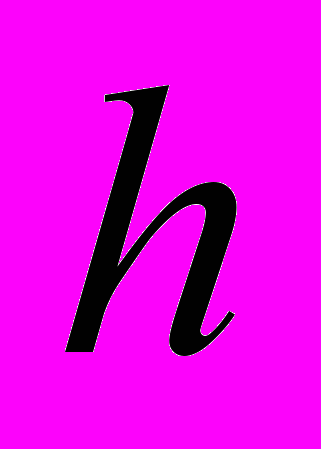- НЧ фильтр.
  2. Значение сглаженного ряда в точке t на данной частоте j определяется формулой: 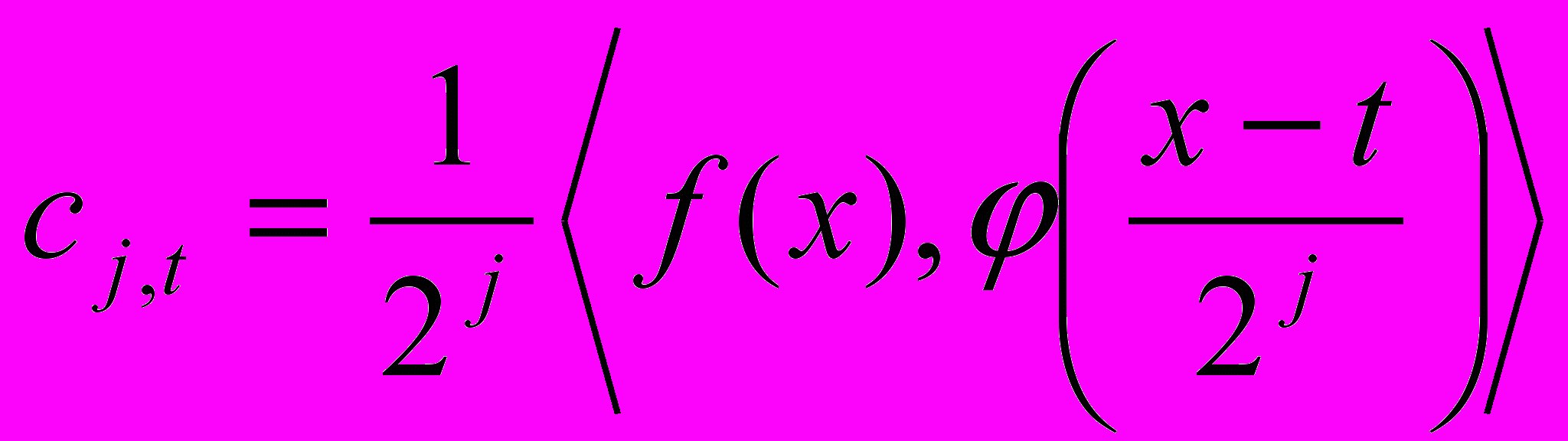, тогда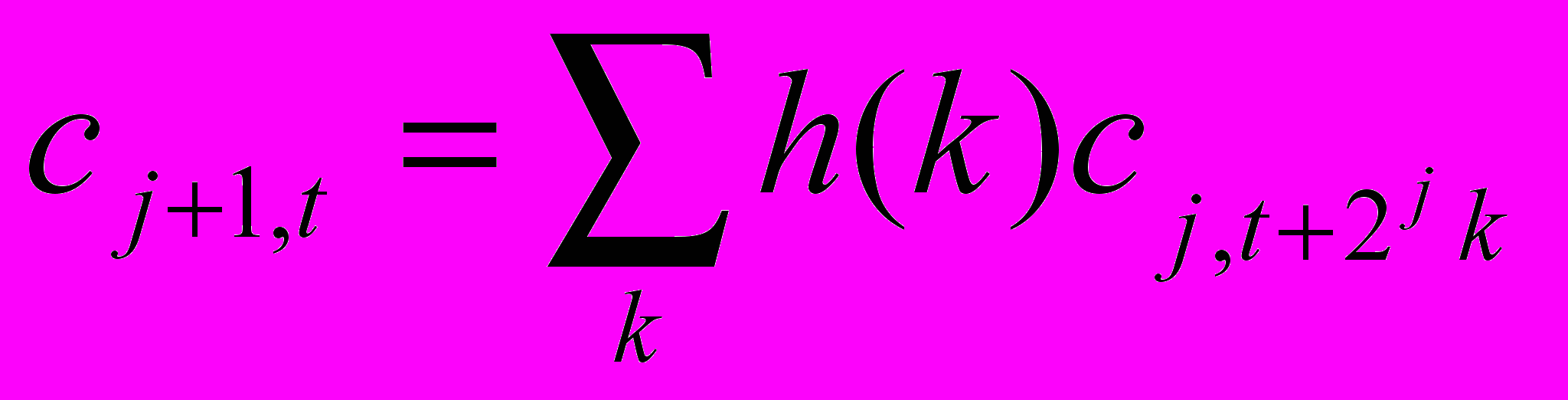
  3. Вейвлет-коэффициенты представляют собой разность между сглаженными рядами на смежных частотах 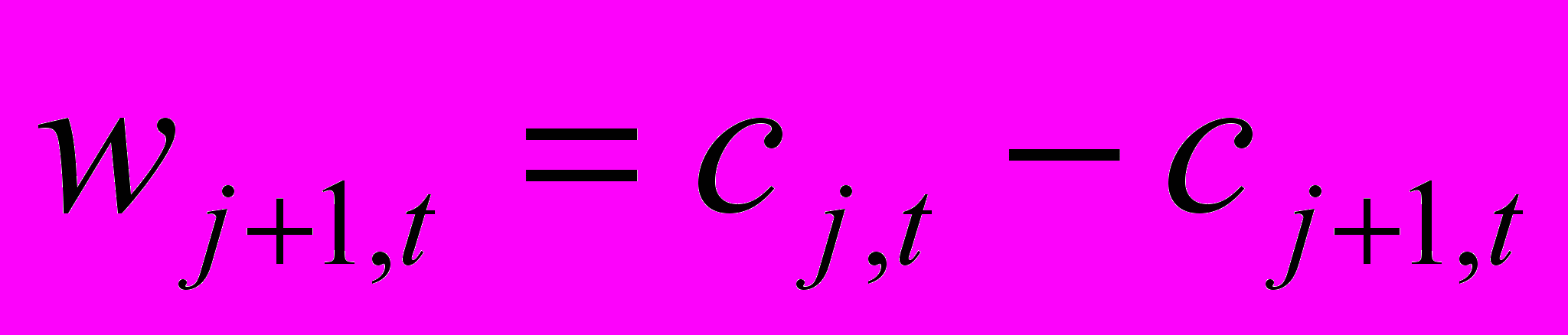. Также ВК можно определить как 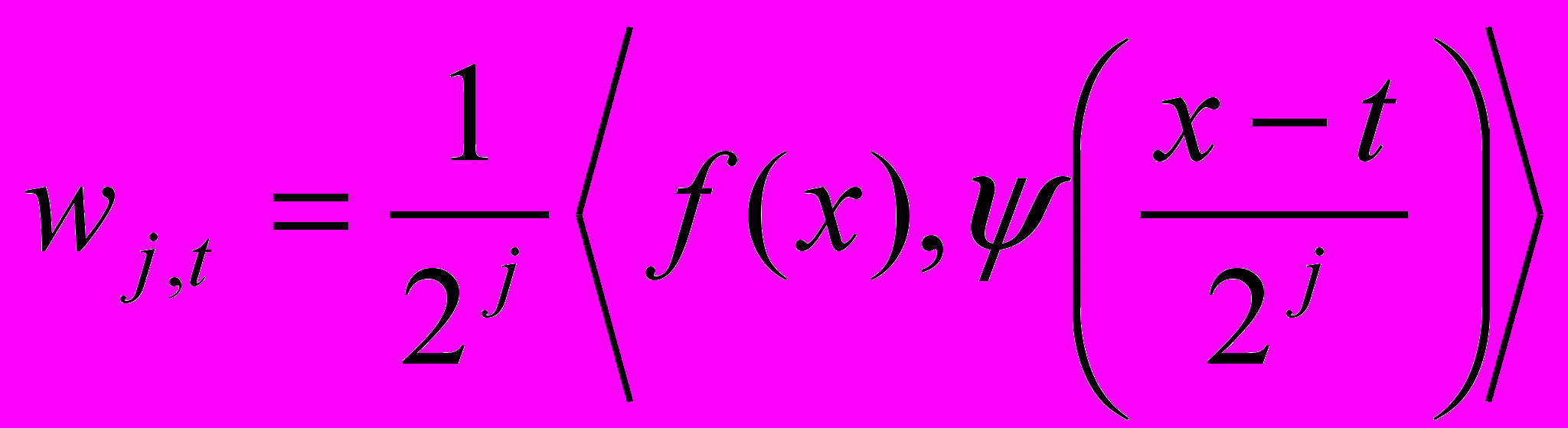, где 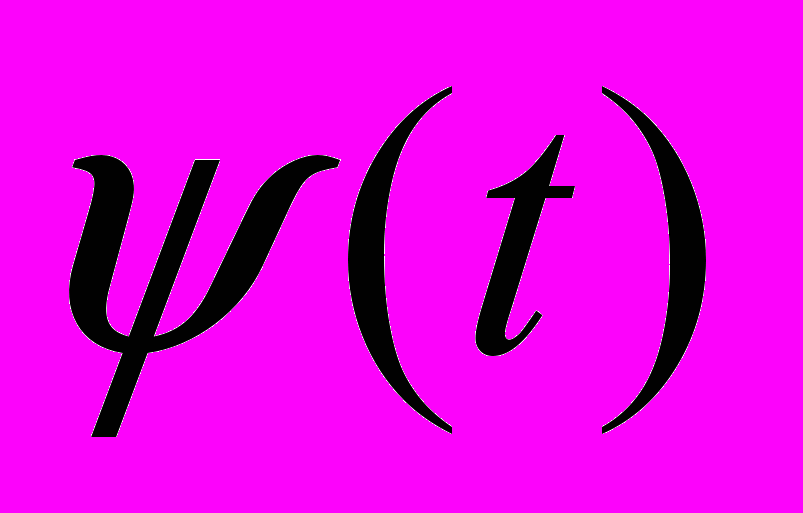- вейвлет-функция, удовлетворяющая уравнению .
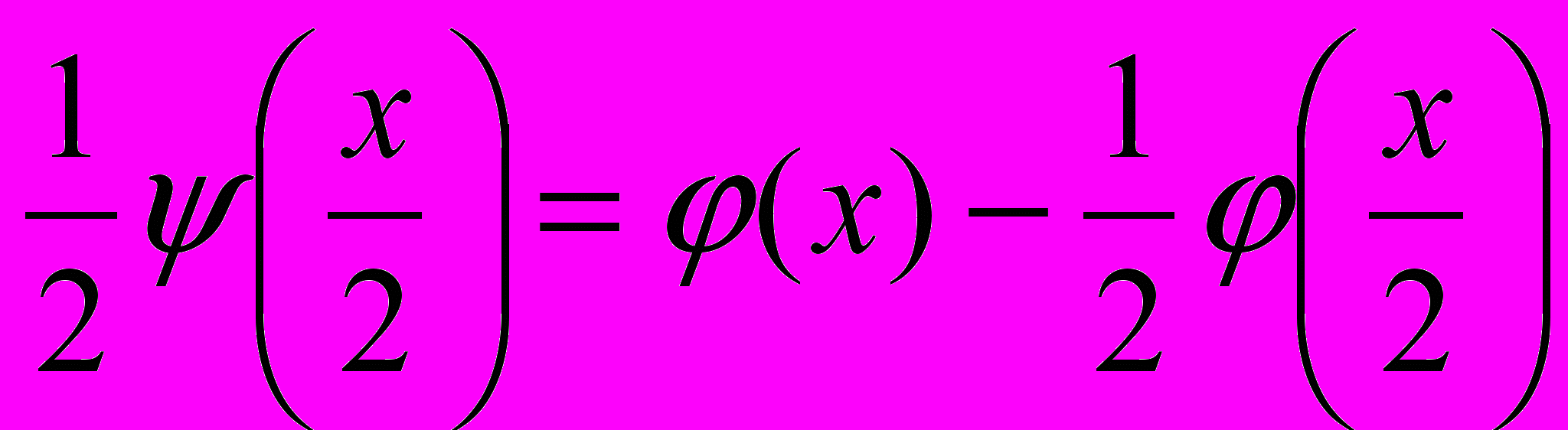  4. Исходный ряд может быть представлен в виде:

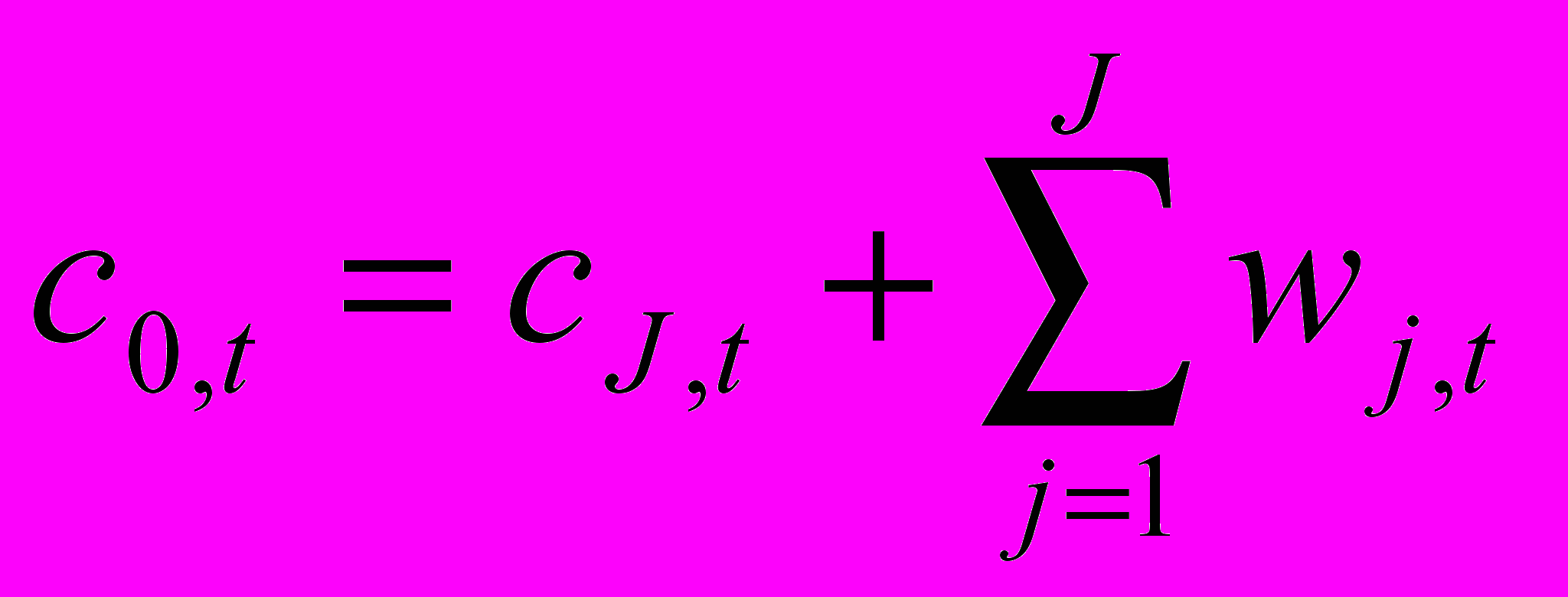
Также важным моментом при прогнозировании является точное вычисление вейвлет-коэффицентов на границе временного ряда: 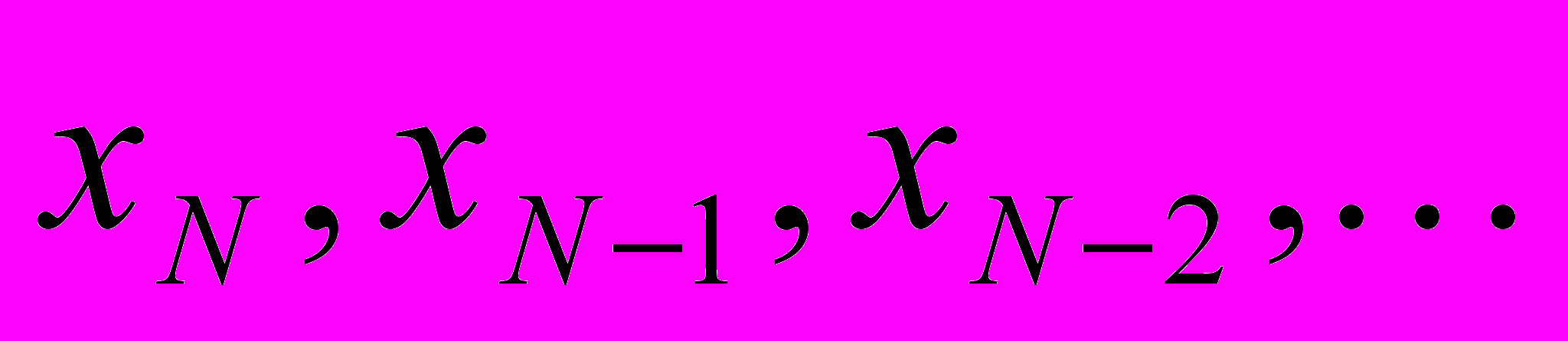[7]. Так, при использовании симметричных фильтров, основанных на функции Гаусса, для заданной частоты s, на границе длиной 3s, вейвлет-коэффициенты будут неточными[5]. Для того, чтобы избежать проблемы учета таких граничных значений может использоваться вейвлет-преобразование À trous с НЧ фильтром Хаара 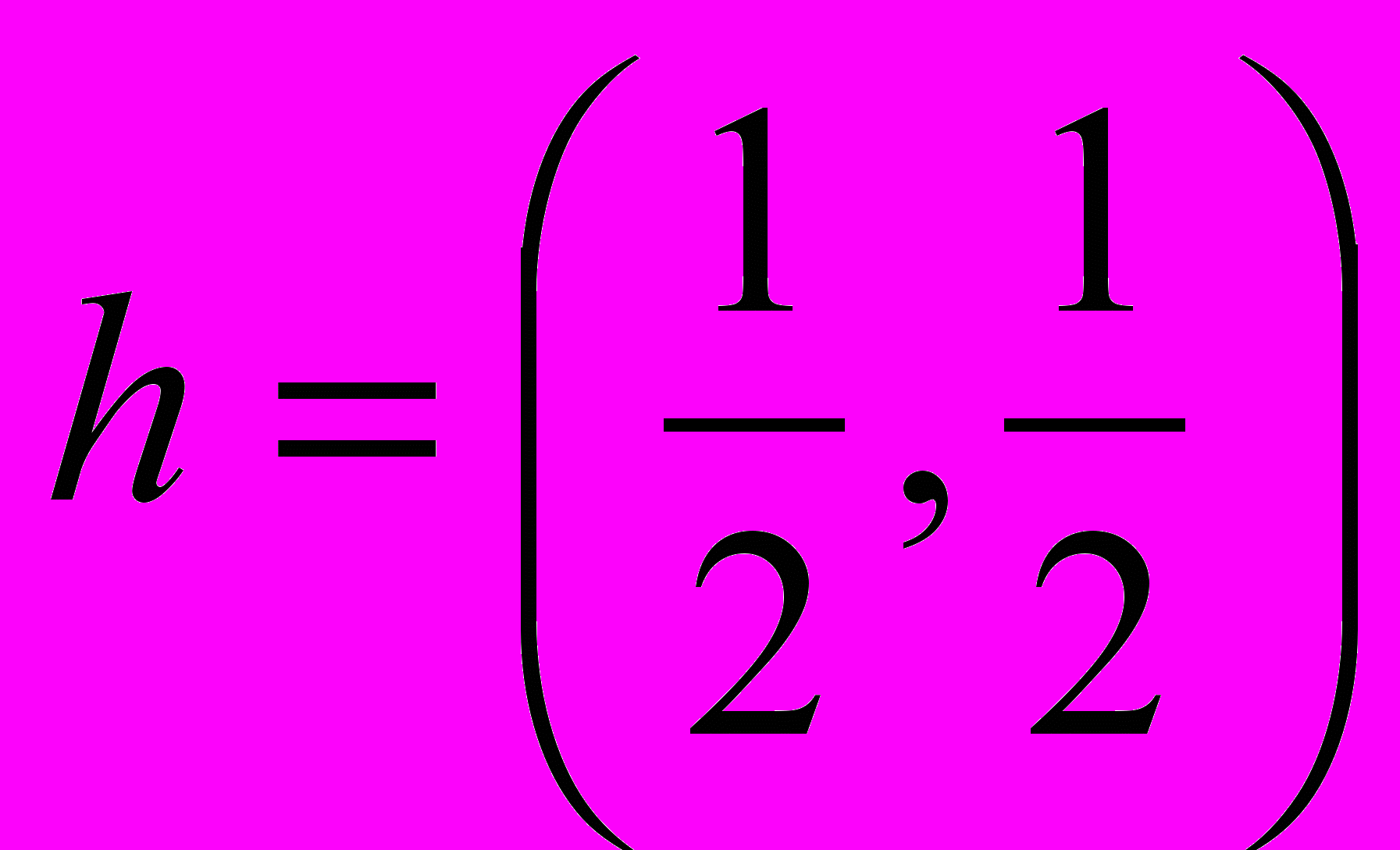, тогда , .

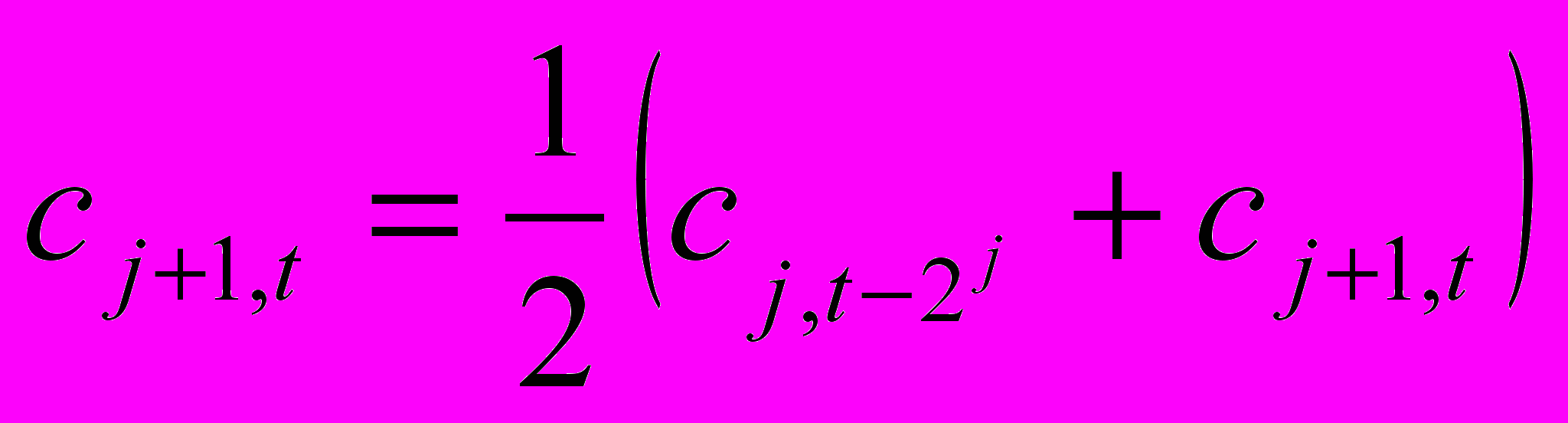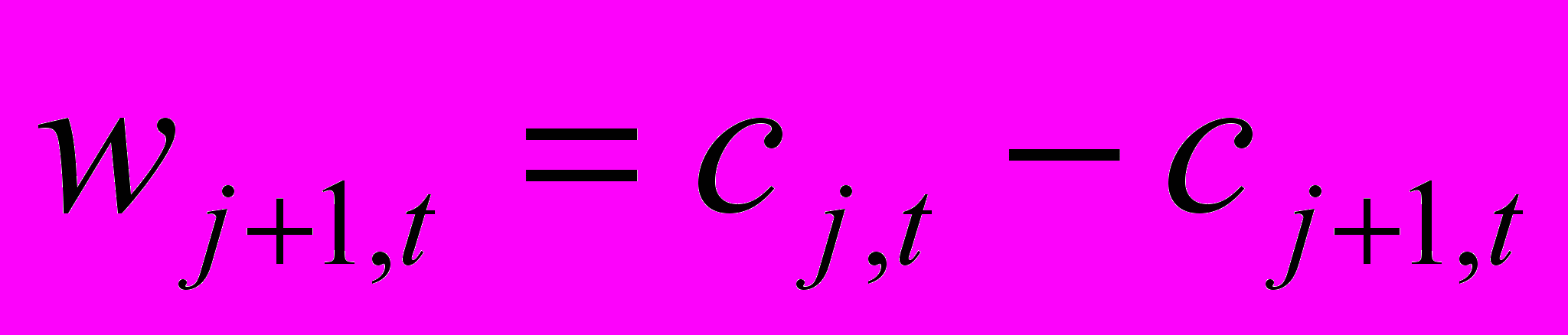Заключение. На основе рассмотренного математического аппарата вейвлет-преобразований разработаны алгоритмы его применения для анализа временных рядов, применяемых для решения задач долгосрочного прогнозирования. Разработан программный инструментарий для формирования вейвлетограмм временных рядов, глобальных энергетических спектров для разных диапазонов частот, сравнения вейвлетограмм на основе задаваемых меры близости. В настоящее время этот инструментарий активно используется для построения моделей прогнозирования природо-обусловленных энергетических факторов (приток воды в Ангарский каскад ГЭС, температура отопительного периода и др.) в условиях глобального изменения климата. Перспективным направлением является разработка новых методов прогнозирования, основанных на процедурах предсказания отдельных вейвлет-коэффициентов (À trous) и построения на их основе итогового прогноза


ЛИТЕРАТУРА

  1. Абасов Н.В., Бережных Т.В., Резников А.П. Долгосрочный прогноз природообусловленных факторов энергетики в информационно-прогностической системе ГИПСАР // Известия РАН, Энергетика, 2000, №6. С. 22-30.
  2. Абасов Н.В., Ветрова В.В. Технология обработки геоклиматических данных // Труды XII Байкальской Всероссийской конф. «Информационные и математические технологии в науке и управлении». Ч. II. – Иркутск: ИСЭМ СО РАН, 2007. С. 85-91.
  3. Чуи Ч. Введение в вейвлеты. М.: Мир, 2001.- 412 с.
  4. Добеши И. Десять лекций по вейвлетам. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2001.­­­– 463 с.
  5. Любушин А.А. Анализ данных систем геофизического и экологического мониторинга. М.: Наука, 2007. – 228 с.
  6. Ierusalimschy R., Figueiredo L.H., Celes W. The implementation of Lua 5.0// Journal of Universal Computer Science 2005, №11_7. P.1159-1176.
  7. Renaud O., Starck J.-L., Murtagh F. Wavelet-Based Combined Signal Filtering and Prediction// IEEE Transactions SMC, Part B, Volume 35, Issue 6, Dec. 2005, P. 1241 - 1251.