Geum.ru

Програмові вимоги 2011

Вид материалаДокументы

Содержание


Математичний аналiз
Подобный материал:




Програмові вимоги - 2011

на державний iспит з математики та iнформатики

(освітньо-кваліфікаційний рівень - бакалавр)

Спеціальність “Інформатика”


1 блок – Математичний аналіз (П.Б. Василишин), Диференціальні рівняння (О.В. Махней), Чисельні методи (О.В.Махней, Т.П.Гой)

2 блок – Алгебра та геометрія (Р.І. Собкович, В.М. Пилипів), Дискретна математика (Р.А. Заторський), Теорія алгоритмів та математична логіка (М.В. Лаврів)

3 блок – Програмування (Б.М. Дрінь, С.В. Шарин, О.Я. Гейко), База даних та інформаційні системи (Б.М. Дрінь), Моделювання економічних, екологічних та соціальних процесів (Л.З.Хрущ), Теорія керування (Л.З.Хрущ)


Математичний аналiз
  1. Множина дійсних чисел. Упорядкованість, щільність, повнота множини дійсних чисел.
  2. Числова послідовність. Види числових послідовностей. Границя послідовності. Властивості збіжних послідовностей.
  3. Нескінченно малі і нескінченно великі послідовності, співвідношення між ними. Леми про нескінченно малі. Границя алгебраїчної суми, добутку, частки.
  4. Відповідність, відображення, функція. Способи задання. Види функцій.
  5. Границя функції в розумінні Гейне та Коші. Еквівалентність означень. Визначні границі: .
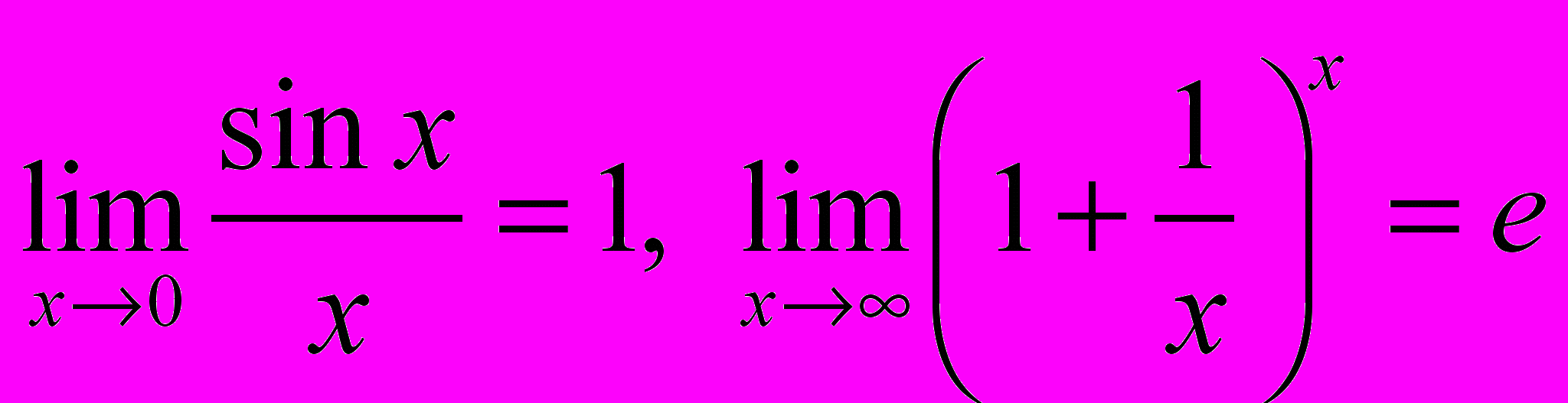  6. Неперервність функції в точці. Різні означення. Одностороння неперервність і її зв’язок з неперервністю в точці. Властивості неперервної функції на сегменті. Теореми Больцано-Коші, Веєрштраса, Кантора.
  7. Задачі, які приводять до поняття похідної. Означення похідної. Таблиця похідних. Геометричний та механічний зміст. Правила відшукання похідних. Похідна композиції функцій.
  8. Застосування похідної до дослідження функції на сталість, монотонність.
  9. Локальний екстремум функції. Необхідна умова. Достатні умови. Знаходження найбільшого і найменшого значення функції на сегменті.
  10. Напрям опуклості графіка функції. Достатні умови. Точка перегину. Необхідна умова перегину. Достатні умови.
  11. Первісна функція (неозначений інтеграл). Таблиця основних інтегралів. Інтегрування підстановкою, частинами.
  12. Інтеграл Рімана. Необхідна і достатня умова інтегрованості. Класи інтегрованих функцій. Теорема Ньютона-Лейбніца.
  13. Основні застосування інтеграла Рімана (знаходження площ, об’ємів, довжин дуг; фізичні застосування).
  14. Функція багатьох змінних. Границя, неперервність.
  15. Частинні похідні, диференційованість функції багатьох змінних. Достатня умова диференційованості. Диференціал функції.
  16. Числові ряди. Збіжні числові ряди. Необхідна умова збіжності. Необхідна і достатня умова збіжності. Ознаки збіжності додатних рядів.

Література
  1. М.І. Шкіль. Математичний аналіз. Т.1,2. К: Вища школа.
  2. Г.Ф. Фихтенгольц. Основы математического анализа. Т.1,2. (будь-яке видання).
  3. В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Т.1,2. М.: Наука.
  4. Л.Д. Кудрявцев. Математический анализ. Т.1,2. М.: Высшая школа.



Диференцiальнi рiвняння
  1. Диференціальні рівняння першого порядку, інтегровані у квадратурах:

  1. Однорідні рівняння та звідні до них.
  2. Лінійні рівняння та звідні до них
  3. Рівняння в повних диференціалах. Інтегрувальний множник.
  4. Рівняння, не розв’язані відносно похідної.
  1. Звичайні диференціальні рівняння вищих порядків:
  1. Рівняння, що допускають зниження порядку.
  2. Лінійні однорідні рівняння зі сталими коефіцієнтами.
  3. Лінійні неоднорідні рівняння (метод варіації довільних сталих, метод невизначених коефіцієнтів).
  4. Лінійні рівняння другого порядку зі змінними коефіцієнтами.
    1. Задача Коші для рівняння струни. Формула Д’аламбера.
    2. Метод Фур'є розв’язання крайових задач для рівнянь струни і теплопровідності.

Література
  1. Перестюк М.О., Маринець В.В. Теорія рівнянь математичної фізики.
  2. Іванчов М.І. Вступ до теорії рівнянь у частинних похідних.
  3. Тихонов А.Н., Самарский А.А. Уравнения математической физики.
  4. Шкіль М.І., Лейфура В.М., Самусенко П.Ф. Диференціальні рівняння.
  5. Самойленко А.М., Перестюк М.О., Парасюк І.О. Диференціальні рівняння.
  6. Степанов В.В. Курс дифференциальних уравнений.


Чисельні методи
  1. Метод ітерації уточнення наближених значень коренів рівнянь: ідея, збіж­ність, оцінка наближення, блок-схе­ма. Зведення рівняння до вигля­ду, зручного для ітерацій.
  2. Метод Гауса розв’язування систем лінійних рівнянь. Схема єдиного ділення. Уточнення коренів.
  3. Постановка задачі інтерполяції. Інтерполяційний поліном у формі Лагранжа (випадок нерівновіддалених і рівновіддалених вузлів). Інтерполяційна формула Лагранжа. Оцінки похибок.
  4. Задача чисельного диференціювання функцій. Чисельне диференціювання функцій, інтерпольованих поліномом Ньютона. Оцінки похибок.
  5. Постановка задачі чисельного інтегрування. Формули прямокутників, трапецій, парабол (Сімпсона) чисельного інтегрування. Оцінки похибок.
  6. Метод Ейлера та його модифікації розв’язування задачі Коші для звичайних диференціальних рівнянь. Розрахункові формули. Геометрична ілюстрація. Оцінки похибок. Блок схеми.


Література
    1. М.Я.Лященко, М.С.Головань. Чисельні методи. – К., Либідь, 1976. – 368 с
    2. Цегелик Г. Чисельні методи. – Львів: Видавничий центр ЛНУ ім. І. Франка, 2004. – 408 с.
    3. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М., Наука, 1970. – 664 с.


Алгебра та геометрiя
  1. Різні способи задання прямих та площин в просторі. Взаємне розміщення двох прямих, прямої та площини.
  2. Основні алгебраїчні структури: група, кільце, поле.
  3. Системи лінійних рівнянь та способи їх розв’язування.
  4. Лiнiйна залежнiсть та ранг системи векторiв.
  5. Векторний простір, його розмірність і базис. Підпростори, теорема про суму їх розмірностей.
  6. Лiнiйнi оператори дійсних векторних просторiв, їх матрицi, ранг і дефект.
  7. Власнi вектори та власнi числа лiнiйних операторiв.


Література
  1. Завало А.В. Курс алгебри. Київ, Вища школа, 1986.
  2. Курош А.Г. Курс высшей алгебры. -., Наука, 1965.- 471с.
  3. Фадеев Д.К., Соминский И.С. Сборник задач по высшей алгебре.- М., Наука, 1964.-304с.
  4. Білоусова В.П. і ін. Аналітична геометрія К., Вища школа, 1973.


Дискретна математика

  1. Множини і дії над ними.
  2. Відношення та їх властивості.
  3. Відношення часткового порядку.
  4. Основні поняття та твердження про графи та орграфи.
  5. Алгоритми Дійкстри.
  6. Алгоритм пошуку в глибину.
  7. Скінченні автомати.

Література


  1. Джеймс Андерсон. Дискретная математика и комбінаторика: Пер. с англ.. – М.: Издательский дом „Вільямс”, 2003. – 960 с.
  2. Андрійчук В.І., Комарницький М.Я., Іщук Ю.Б. Вступ до дискретної математики: Навчальний посібник. – Київ: Центр навчальної літератури, 2004. – 254 с.


Теорія алгоритмів та математична логіка
  1. Висловлювання і операції над ними. Класифікація формул алгебри висловлювань. Основні тавтології алгебри висловлювань. Логічна рівносильність в алгебрі висловлювань
  2. Диз’юнктивна та кон’юнктивні нормальні форми алгебри висловлювань. Подання формул алгебри висловлювань досконалими диз’юнктивними та кон’юнктивними нормальними формами
  3. Булеві функції від n аргументів. Вираження булевих функцій через кон’юнкцію, диз’юнкцію і заперечення.
  4. Системи булевих функцій. Повнота системи. Спеціальні класи булевих функцій
  5. Типові пристрої ЕОМ. Двійковий суматор. Однорозрядний двійковий суматор. Шифратор і дешифратор.

Література
  1. Игошин В.И. Математическая логика и теория алгоритмов.–Саратов: Изд-во Сарат.ун-та,1991.–256 с.
  2. Бондаренко М.Ф., Білоус Н.В., Руткас А.Г. Комп’ютерна дискретна математика: Підручник. – Харків: “Компанія СМІТ”, 2004. – 480 с.
  3. Гуц А.К. Математическая логика и теория алгоритмов: Учебное пособие.–Омск: Издательство Наследие. Диалог-Сибирь, 2003.–108 с.
  4. Марков А. А. Элементы математической логики / Под. ред А.Г. Драгалина.– М.: Узд-во Моск. ун-та, 1984 г. – 80 с.


Програмування
  1. Мови програмування, їхня класифікація та опис мови.
  2. Програми користувача: процедури і функції у мові Pascal.
  3. Оператори умови мови Pascal та їх використання.
  4. Типи даних: масиви, рядки мови Pascal.
  5. Оператори циклу мови Pascal та їх використання.
  6. Процедури і функції роботи з файлами у мові Pascal.
  7. Основні поняття об’єктно-орієнтованого програмування.
  8. Поняття про успадкування та інкапсуляцію.
  9. Механізми підтримки поліморфізму.

Література
  1. Зуєв Е. А. Язык программирования TURBO- PASCAL 6.0. Москва, Унитех, 1992
  2. Вальвачев А. Н., Крисевич В. С. Программирование на языке Паскаль для персональных ЭВМ.Минск: Высш. Школа,1989.
  3. Климов Ю. С., Касаткин Л. И., Мороз С. М Программирования в среде TURBO- PASCAL 6.0.
  4. Себеста Р. Основные концепции языков програмирования.- М., Издательский дом «Вильямс», 2000.
  5. Вирт Н. Алгоритмы+Структуры даных=Програмы.-М., Мир, 1984.



Бази даних та інформаційні системи
  1. Поняття бази і банку даних та їх складових.
  2. Поняття СУБД, її функцій та мовні засоби роботи з даними.
  3. Етапи проектування баз даних.
  4. Поняття інфологічної моделі та її складові.
  5. Поняття агрегації та порядок її виконання.
  6. Представлення запитів в структурованому вигляді відповідним запитувальним зв’язком.
  7. Теорія нормалізації відношень.
  8. Особливості та переваги мови SQL.
  9. Групи команд мови SQL та їх приклади.

Література
  1. Н.В. Єрьоміна. Проектування баз даних: Навч. посібник. – К.:КНЕУ,1998. – 208с.
  2. Н.В. Ситник. Проектування баз і сховищ даних: Навч. посібник. – К.: КНЕУ, 2004.-348с.
  3. Конноли Томас, Каролин Бегг, Страчан Анна. Базы данных: проэктирование, реализация и сопровождение. Теория и практика, 2-е изд., : Пер. с англ. – Изд. Дом “Вильямс”, 2001. – 1120с.


Моделювання економічних, екологічних та соціальних процесів
  1. Порядкові функції корисності. Приклади функцій корисності.
  2. Неокласична модель споживання.
  3. Простір витрат та виробничі функції. Основні типи виробничих функцій.
  4. Неокласична модель однопродуктової фірми.
  5. Міжгалузевий баланс.
  6. Модель Леонтьєва. Модель міжгалузевої залежності цін.
  7. Динамічна модель Леонтьєва.
  8. Модель “хижак-жертва”.
  9. Модель Леслі вікової структури популяції. Темп росту популяції.
  10. Статична модель Леонтьєва-Форда (еколого-економічний баланс).
  11. Модель залежностей цін в еколого-економічному балансі.
  12. Динамічна модель Леонтьєва-Форда.

Література
    1. Пономаренко О.І.,Перестук М.О., Бурим В.М. Основи математичної економіки. – К., Інформтехніка, 1995. – 320 с.
    2. Ляшенко І.М. Економіко-математичні методи та моделі сталого розвитку. – К.: Вища школа, 1999. – 236 с.
    3. Ляшенко І.М., Мукоєд А.П. Моделювання біологічних та екологічних процесів: Навчальний посібник. – К.: ВПЦ „Київський університет”, 2002. – 340 с.


Теорія керування
  1. Приклади систем керування та їх математичних моделей.
  2. Структурні схеми для опису систем керування.
  3. Постановки задач теорії керування.
  4. Постановка та дослідження задач керованості для лінійних нестаціонарних систем.
  5. Керованість лінійних стаціонарних систем. Необхідна та достатня умова для цілком керованості стаціонарної системи 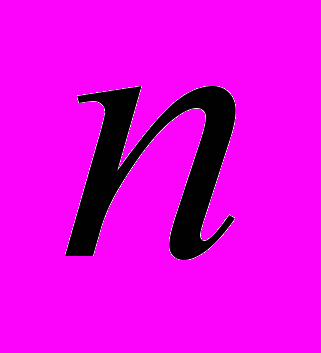-го орядку.
  6. Цілком керованість на заданому проміжку, достатня умова цілком керованості на заданому проміжку.
  7. Властивості стаціонарних систем, коли умова цілком керованості не виконується.
  8. Спостережуваність в лінійних системах керування. Достатні умови для існування розв’язку задачі спостережуваності.
  9. Достатні умови спостережуваності за координатою .
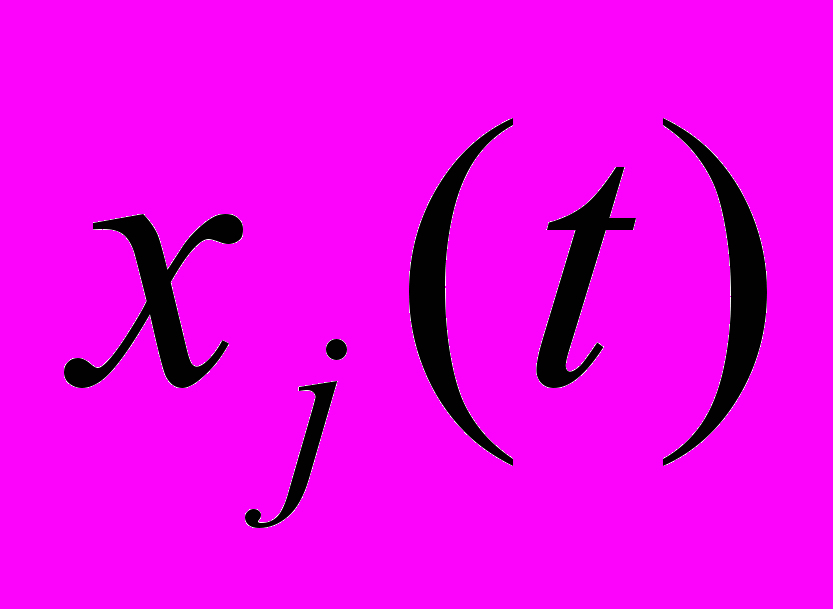  10. Зв’язок між спостережуваністю та керованістю в системах керування. Теорема про зведення задачі спостережуваності до знаходження керування спряженої системи.
  11. Задачі оптимального керування: задача Лагранжа, Майера, Больца. Задача оптимального керування у формі Понтрягіна.
  12. Функція Гамільтона-Понтрягіна. Спряжена система. Принцип максимуму для задачі з оптимального керування з закріпленими кінцями траєкторії і часом.
  13. Метод динамічного програмування. Принцип оптимальності Р. Беллмана.
  14. Метод динамічного програмування в задачі оптимальної швидкодії.

Література
    1. Александров В.В., Болтянский В.Г., Лемак С.С., Парусников Н.А., Тихомиров В.М. Оптимальное управление движением. – М.: Физматлит, 2005. – 276 с.
    2. Бублик Б.Н., Кириченко Н.Ф. Основы теории управления. – К.: Вища школа, 1975. – 328 с.
    3. Васильев Ф.П. Численные методы решения экстремальных задач. -М.: Наука, 1980. -520 с.
    4. Галеев Э.М., Тихомиров В.М. Оптимизация: теория, примеры, задачи. -М.: Эдиториал УРСС, 2000. -320 с.
    5. Егоров А.И. Основы теории управления. -М.: Физматлит, 2004. -504 с.
    6. Малкин И.Г. Теория устойчивости движения. – М.: Наука, 1966. – 532 с.
    7. Моисеев Н.Н. Элементы теории оптимальных систем. – М.: Наука, 1975. – 528 с.