Задачи 10-17стр. Список литературы. 17стр. Введение

Вид материала

Содержание

2. Числа и символы
3. Диофантовы уравнения
Диофант и математики xv–xvi веков
Покупка почтовых марок
Два числа и четыре действия

Подобный материал:

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №92»

Школьная научно-практическая конференция

Диофантовы уравнения

Подготовила:

ученица 10 класса

Сурсина Александра

Руководитель:

учитель математики

Прокопенко О.И.

г.Новокузнецк, 2008г.

Содержание

1. Введение 3стр.

2. Диофант 4-5стр.

3.Числа и символы 6стр.

4.Диофантовые уравнения 7стр.

5. Диофант и математики XV-XVI 7-9стр.

6. Задачи 10-17стр.

7. Список литературы. 17стр.

Введение

В наши дни каждый, кто занимался математикой как профессионал или как любитель, слышал о диофантовых уравнениях и даже о диофантовом анализе. За последние 15–20 лет эта область сделалась «модной» благодаря своей близости к алгебраической геометрии — властительнице дум современных математиков. Между тем, о том, кто дал имя неопределённому анализу, о самом Диофанте, одном из наиболее интересных учёных античности, почти ничего не написано. О его работах даже историки науки имеют самое превратное представление. Большинство из них считает, что Диофант занимался решением отдельных задач, равносильных неопределённым уравнениям, применяя для этого хитроумные, но частные методы.

Между тем простой разбор задач Диофанта показывает, что он не только поставил проблему решения неопределённых уравнений в рациональных числах, но и дал некоторые общие методы их решения. Надо при этом иметь в виду, что в античной математике общие методы никогда не излагались «в чистом виде», отдельно от решаемых задач. Так, например, поступал Архимед: определяя площади эллипса, сегмента параболы, поверхности шара, объёмы шара и других тел, он применял метод интегральных сумм и метод предельного перехода, однако нигде не дал общего абстрактного описания этих методов. Учёным XVI–XVII веков приходилось тщательно изучать и перелагать по-новому его сочинения, чтобы выделить оттуда методы Архимеда. Аналогично обстоит дело и с Диофантом. Его методы были поняты и применены для решения новых задач Виетом и Ферма, т.е. в то же время, когда был разгадан и Архимед.

Заметим ещё, что если история интеграционных методов Архимеда в основном завершается созданием интегрального и дифференциального исчисления Ньютоном и Лейбницем, то история методов Диофанта растягивается ещё на несколько сотен лет, переплетаясь с развитием теории алгебраических функций и алгебраической геометрии. Развитие идей Диофанта можно проследить вплоть до работ Анри Пуанкаре и Андре Вейля. Поэтому-то история диофантова анализа особенно интересна.

Настоящий работа будет посвящена в основном методам Диофанта для решения уравнений в рациональных числах и их истории. Попутно рассмотрим вопрос и о числовой системе, которую применял Диофант, и о его буквенной символике. В этом гораздо более простом вопросе также до сих пор нет ясности: большинство историков науки считает, что Диофант ограничивался областью положительных рациональных чисел и не знал отрицательных чисел. Мы постараемся показать, что это не так, что именно в «Арифметике» Диофанта область чисел была расширена до поля рациональных чисел Q.

1. ДИОФАНТ

Диофант представляет одну из наиболее трудных загадок в истории науки. Нам не известны ни время, когда он жил, ни предшественники его, которые работали бы в той же области. Труды его подобны сверкающему огню среди полной непроницаемой тьмы.

Промежуток времени, когда мог жить Диофант, составляет полтысячелетия! Нижняя грань этого промежутка определяется без труда: в своей книге о многоугольных числах Диофант неоднократно упоминает математика Гипсикла Александрийского, который жил в середине II века до н. э. С другой стороны, в комментариях Теона Александрийского к «Альмагесту» знаменитого астронома Птолемея помещён отрывок из сочинения Диофанта. Теон жил в середине IV века н. э. Этим определяется верхняя грань этого промежутка. Итак, 500 лет!

Французский историк науки Поль Таннери, издатель наиболее полного текста Диофанта, попытался су́зить этот промежуток. В библиотеке Эскуриала он нашёл отрывки из письма Михаила Пселла, византийского учёного XI века, где говорится, что «учёнейший Анатолий, после того как собрал наиболее существенные части этой науки (речь идёт о введении степеней неизвестного и об их обозначениях), посвятил их своему другу Диофанту». Анатолий Александрийский действительно составил «Введение в арифметику», отрывки из которой приводят в дошедших до нас сочинениях Ямблих и Евсевий. Но Анатолий жил в Александрии в середине III века н. э. и даже более точно — до 270 года, когда он стал епископом Лаодакийским. Значит, его дружба с Диофантом, которого все называют Александрийским, должна была иметь место до этого. Итак, если знаменитый александрийский математик и друг Анатолия по имени Диофант составляют одно лицо, то время жизни Диофанта — середина III века н. э.

Сама же «Арифметика» Диофанта посвящена «достопочтенному Дионисию», который, как видно из текста «Введения», интересовался арифметикой и её преподаванием. Хотя имя Дионисий было в то время довольно распространённым, Таннери предположил, что «достопочтенного» Дионисия следует искать среди известных людей эпохи, занимавших видные посты. И вот оказалось, что в 247 году епископом Александрии стал некий Дионисий, который с 231 года руководил христианской гимназией города! Поэтому Таннери отождествил этого Дионисия с тем, которому посвятил свой труд Диофант, и пришёл к выводу, что Диофант жил в середине III века н. э. Мы можем, за неимением лучшего, принять эту дату.

Зато место жительства Диофанта хорошо известно — это знаменитая Александрия, центр научной мысли эллинистического мира.

После распада огромной империи Александра Македонского Египет в конце IV века до н. э. достался его полководцу Птолемею Лагу, который перенёс столицу в новый город — Александрию. Вскоре этот многоязыкий торговый город сделался одним из прекраснейших городов древности. Размерами его превзошёл впоследствии Рим, но долгое время ему не было равного. И вот именно этот город стал на многие века научным и культурным центром древнего мира. Это было связано с тем, что Птолемей Лаг основал Музейон, храм Муз, нечто вроде первой Академии наук, куда приглашались наиболее крупные учёные, причём им назначалось содержание, так что основным делом их были размышления и беседы с учениками. При Музейоне была построена знаменитая библиотека, которая в лучшие свои дни насчитывала более 700 000 рукописей. Неудивительно, что учёные и жаждущие знаний юноши со всего мира устремились в Александрию, чтобы послушать знаменитых философов, поучиться астрономии и математике, иметь возможность в прохладных залах библиотеки углубиться в изучение уникальных рукописей.

Музейон пережил династию Птолемеев. В первые века до н.э. он пришёл во временный упадок, связанный с общим упадком дома Птолемеев в связи с римскими завоеваниями (Александрия была окончательно завоевана в 31 году до н. э.), но затем в первые века н. э. он снова возродился, поддерживаемый уже римскими императорами. Александрия продолжала оставаться научным центром мира. Рим никогда не был в этом отношении её соперником: римской науки (мы имеем в виду естественные науки) просто не существовало, и римляне оставались верными заветам Вергилия, писавшего:

Чтобы исчерпать всё известное о личности Диофанта, приведём дошедшее до нас стихотворение-загадку:

Прах Диофанта гробница покоит; дивись ей — и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребёнком
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей⁾.

Отсюда нетрудно подсчитать, что Диофант прожил 84 года. Однако для этого вовсе не нужно владеть искусством Диофанта! Достаточно уметь решать уравнение 1-й степени с одним неизвестным, а это умели делать египетские писцы ещё за 2 тысячи лет до н. э.

Но наиболее загадочным представляется творчество Диофанта. До нас дошло шесть книг из 13, которые были объединены в «Арифметику». Стиль и содержание этих книг резко отличаются от классических античных сочинений по теории чисел и алгебре, образцы которых мы знаем по «Началам» Евклида, его «Данным», леммам из сочинений Архимеда и Аполлония. «Арифметика», несомненно, явилась результатом многочисленных исследований, которые остались нам совершенно не известны. Мы можем только гадать о её корнях и изумляться богатству и красоте её методов и результатов.

«Арифметика» Диофанта — это сборник задач (их всего 189), каждая из которых снабжена решением (или несколькими способами решения) и необходимыми пояснениями. Поэтому с первого взгляда кажется, что она не является теоретическим произведением. Однако при внимательном чтении видно, что задачи тщательно подобраны и служат для иллюстрации вполне определённых, строго продуманных методов. Как это было принято в древности, методы не формулируются в общем виде, а повторяются для решения однотипных задач.

2. ЧИСЛА И СИМВОЛЫ

Диофант начинает с основных определений и описания буквенных символов, которые он будет применять.

Диофант приводит традиционное определение числа как множества единиц, однако в дальнейшем ищет для своих задач положительные рациональные решения, причём называет каждое такое решение числом .

Но этим дело не ограничивается. Диофант вводит отрицательные числа: он называет их специальным термином — «лейпсис» — производное от глагола — «лейпо», что означает недоставать, не хватать, так что сам термин можно было бы перевести словом «недостаток». Положительное число Диофант называет словом ΰπαρξις — «ипарксис», что означает существование, бытие, а во множественном числе это слово может означать имущество или достояние. Таким образом, терминология Диофанта для относительных чисел близка к той, которую употребляли в Средние века на Востоке и в Европе. Скорее всего, это было просто переводом с греческого на арабский, санскрит, латынь, а затем на различные языки Европы.

Диофант формулирует для относительных чисел правило знаков:

«отрицательное, умноженное на отрицательное, даёт положительное, тогда как отрицательное на положительное даёт отрицательное, и отличительный знак для отрицательного есть

— перевёрнутая и укороченная (буква) ψ».

Далее он пишет:

«После того как я тебе объяснил умножение, становится ясным и деление предложенных членов; теперь будет хорошо приступить к упражнениям над сложением, вычитанием и умножением таких членов. И положительные и отрицательные члены с различными коэффициентами прибавлять к другим членам, которые либо положительны, либо, равным образом, и положительны и отрицательны, и от положительных членов и других отрицательных отнимать другие положительные и, равным образом, положительные и отрицательные».

Заметим, что хотя Диофант ищет только рациональные положительные решения, в промежуточных выкладках он охотно пользуется отрицательными числами.

Мы можем, таким образом, отметить, что Диофант расширил числовую область до поля рациональных чисел, в котором можно беспрепятственно производить все четыре действия арифметики.

В «Арифметике» мы встречаем впервые и буквенную символику. Диофант ввёл следующие обозначения для первых шести степеней x, x², ... , x⁶ неизвестного x:

. 3. ДИОФАНТОВЫ УРАВНЕНИЯ

Но в «Арифметике» поражает не только совершенно новый язык, не только смелое расширение области чисел, но и особенно те проблемы, которые ставит и решает Диофант.

Чтобы понять сущность этих проблем и исследовать методы Диофанта, нам придётся дать некоторые сведения из алгебраической геометрии и теории неопределённых уравнений. В настоящее время задача решения неопределённых уравнений формулируется так: пусть дано m многочленов от n переменных, m < n, f₁(x₁, x₂, ... , x_n), ..., f_m(x₁, x₂, ... , x_n) с коэффициентами из некоторого поля k ⁷⁾. Требуется найти множество M(k) всех рациональных решений системы







f₁(x₁, x₂, ... , x_n) = 0,

· · · · · · · · · ·

f_m(x₁, x₂, ... , x_n) = 0

(1)

и определить его алгебраическую структуру. При этом решение (x₁⁽⁰⁾, ... , x_n⁽⁰⁾) называется рациональным, если все x_i⁽⁰⁾  k.

Множество M(k), разумеется, зависит от поля k. Так, уравнение x² + y² = 3 не имеет ни одного рационального решения в поле Q рациональных чисел, но имеет бесконечно много решений в поле Q(√3), т.е. в множестве чисел вида a+b√3, где a и b — рациональные числа .

Наиболее важными для теории чисел являются случаи, когда 1) k = Q, где Q — поле рациональных чисел, или 2) k есть поле вычетов по простому модулю p. Диофант рассматривал первый из этих случаев. Мы также будем всегда в дальнейшем считать, что k = Q.

Мы ограничимся рассмотрением только таких задач Диофанта, которые сводятся к одному уравнению с двумя неизвестными, т.е. к случаю m=1, n=2:

f (x, y) = 0.

(2)

Однако для целей диофантова анализа (такое название получила область математики, выросшая из задач решения неопределённых уравнений; впрочем, теперь её чаще называют диофантовой геометрией) классификация по порядкам оказалась слишком грубой.

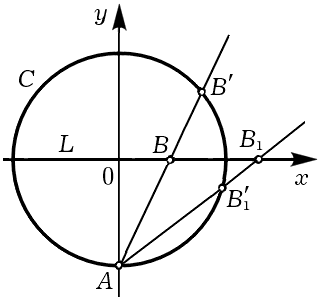
Рис. 1.

Поясним сказанное на примере. Пусть задана окружность C: x² + y² = 1 и любая прямая с рациональными коэффициентами, например, L: y=0. Покажем, что рациональные точки этой окружности и прямой можно поставить во взаимно однозначное соответствие. Это можно сделать, например, так: закрепим точку A(0,–1) окружности и поставим в соответствие каждой рациональной точке B прямой L точку B' окружности C, лежащую на пересечении C и прямой AB (рис. 1). То, что координаты точки B' будут рациональными, предоставим читателю доказать самому либо прочесть аналогичное доказательство у Диофанта (оно будет изложено в следующем параграфе). Очевидно, что такое же соответствие можно установить между рациональными точками любого конического сечения, если на нём лежит хотя бы одна рациональная точка, и рациональной прямой. Мы видим, что с точки зрения диофантова анализа окружность C и прямая L неотличимы: множества их рациональных решений эквивалентны. И это несмотря на то, что порядки обеих кривых различны.

ДИОФАНТ И МАТЕМАТИКИ XV–XVI ВЕКОВ

Комментировать Диофанта начали ещё в древности. Разбору его книг были посвящены труды знаменитой Гипатии, дочери александрийского учёного Теона. Гипатия жила в конце IV – начале V века н. э. в Александрии и славилась там как блестящий оратор и знаток философии Платона.

Сочинения Гипатии до нас, к сожалению, не дошли.

После Гипатии мы не знаем ни одного александрийского математика. Последние греческие учёные Прокл, Исидор и Симпликий развивали своё учение уже не в Александрии, а в Афинах. Но и здесь к началу VII века научная мысль угасла. Античная наука погибла вместе с гибелью античного общества. В IX–XIII веках возникли новые научные центры: Константинополь, а также Багдад и другие города арабского Востока. Отсюда начиная с XII века научная мысль проникала в Европу. Идеи Диофанта шли двумя различными потоками. Первый из них можно назвать алгебраическим, второй — теоретико-числовым или арифметическим. При этом то новое, что внёс Диофант в алгебру, стало известно учёным Европы лет на 300 раньше, чем его арифметические идеи. Это и неудивительно. Новая алгебра и была воспринята как византийскими комментаторами Диофанта (Максим Плануда, Георгий Пахимер, жившие в XIII веке), так и арабскими математиками, особенно Абуль Вафой (X век) и его школой. Правда, арабы не пользовались буквенными символами, а именовали степени неизвестного словами. Кроме того, при наименовании степеней неизвестного они пользовались не аддитивным принципом, как это делал Диофант, а неудобным мультипликативным, т.е., например, x⁶ они называли не «кубо-кубом», как Диофант, а «квадрато-кубом», а для x⁵ они вообще не могли составить название из предыдущих степеней, поскольку 5 — число простое и на множители не раскладывается. Приходилось называть его «глухим» или «первым невыразимым». Аналогично дело обстояло с x⁷, который называли «вторым невыразимым», далее, с x¹¹ и всеми степенями с простыми показателями. Такой принцип обозначения перешёл от арабов в Европу и им пользовались в эпоху Возрождения в Италии, а затем и немецкие алгебраисты, известные под именем коссистов. Исключение составил очень талантливый математик XIII века, современник Данте, Леонардо Пизанский. В своей знаменитой «Книге об абаке» (Liber abaci) он не только применил аддитивный принцип обозначения степеней неизвестного, но и впервые в Европе рассмотрел задачи, сводящиеся к неопределённым уравнениям.

Что касается правил Диофанта оперирования с многочленами и уравнениями, то они повторялись почти всеми алгебраистами средних веков.

Отрицательные числа были восприняты гораздо менее охотно. Арабские математики вообще от них отказались, а европейцы принимали их с большим недоверием. Долгое время они именовали отрицательные числа «ложными числами» и старались обходиться без них.

Но в «Арифметике» Диофанта имелся и другой, гораздо более глубокий круг идей, связанный с решением неопределённых уравнений, с диофантовым анализом. Долгое время о них ничего не знали. В XV–XVI веках в Европе сложилась несколько парадоксальная ситуация: учёные пользовались буквенной алгеброй, восходящей к Диофанту, развивали её дальше, но не были знакомы с трудами Диофанта.

Первым прочёл их, по-видимому, известный астроном XV века Региомонтан (Иоганн Мюллер). Путешествуя по Италии, он открыл рукопись Диофанта в Венеции и сообщил об этом в письме к своему другу. Рукопись поразила его богатством содержания. Он решил перевести её, но не раньше, чем найдёт все 13 книг, о которых пишет Диофант во Введении. Однако, были найдены только 6 книг, те, которые известны и нам, и перевод так и не был сделан.

Прошло ещё 100 лет. За это время ни один из крупных алгебраистов, а их было немало, — достаточно назвать Джироламо Кардано и Николо Тарталья, ничего не знали о Диофанте. Но вот в 1572 году в «Алгебре» Рафаэля Бомбелли, профессора университета в Болонье, вдруг появляются 143 задачи из «Арифметики» Диофанта! В предисловии Бомбелли пишет, что «в прошлом году труд, посвящённый этому предмету, был найден в библиотеке Господа нашего в Ватикане, составленный неким Диофантом, греческим автором, жившим в эпоху Антонина Пия». Заметим, что Антонин Пий был Римским императором в середине II века н. э. Откуда взял своё утверждение о времени жизни Диофанта Бомбелли, абсолютно не известно. Прочтя рукопись, Бомбелли убедился, что автор её «весьма сведущ в науке чисел». И вот «с целью обогатить мир произведением такой важности» Бомбелли принялся совместно с римским математиком Пацци, который первый обнаружил рукопись, за перевод. «Мы перевели пять книг из семи, — сообщает Бомбелли, — но не смогли окончить остальное из-за других работ, которые выпали на нашу долю». О каких семи книгах идёт речь? Ватиканская рукопись содержит их только шесть! Может быть, седьмая была утеряна? Если бы до нас дошёл перевод пяти первых книг, выполненный Бомбелли и Пацци, мы могли бы сравнить их с теми книгами, которые мы имеем, и судить о том, соответствует ли наше разделение задач по книгам тому, которое было у Бомбелли. Но, увы, никаких следов этого перевода не осталось.

«Алгебра» Бомбелли замечательна во многих отношениях. Здесь были усовершенствованы алгебраические обозначения для степеней неизвестного, здесь впервые появились мнимые числа a+bi, где i²=–1, причём очень чётко были сформулированы правила действий с ними. Наконец, с помощью мнимых чисел был исследован так называемый «неприводимый» случай кубического уравнения. Но для нас сейчас книга Бомбелли важна тем, что в ней впервые появились задачи Диофанта, правда, вырванные из контекста. Однако влияние «Арифметики» сказалось на всей книге Бомбелли: в первоначальной рукописи его собственные задачи были облечены в псевдопрактическую форму, в окончательном варианте они формулируются абстрактно, как и у Диофанта. Он изменил и некоторые термины, приблизив их к тем, которые нашёл у Диофанта.

Но уже через три года после выхода в свет «Алгебры» был опубликован первый перевод «Арифметики» на латынь. Он был выполнен известным филологом и философом того времени Ксиландром (настоящее имя его — Гильом Хольцман). Перевод этот был, в целом, хорош, хотя чувствовалось, что он был выполнен человеком, далёким от математики.

После этого задачи четырёх первых книг Диофанта появились в книге известного математика и механика Симона Стевина (1585 год), а во втором издании, подготовленном талантливым алгебраистом Альбером Жираром, — и задачи из последних двух книг.

Но методы Диофанта обрели новую жизнь только в произведениях двух крупнейших математиков Франции XVI–XVII веков — Франсуа Виета и Пьера Ферма.

Задачи.

Вы должны уплатить за купленный в магазине свитер 19 руб. У вас одни лишь трёхрублёвки, у кассира – только пятирублёвки. Можете ли вы при наличии таких денег расплатиться с кассиром и как именно?

Вопрос задачи сводится к тому, чтобы узнать, сколько должны вы дать кассиру трёхрублёвок, чтобы, получив сдачу пятирублёвками, уплатить 19 рублей. Неизвестных в задаче два – число (х) трёхрублёвок и число (у) пятирублёвок. Но можно составить только одно уравнение:

3х-5у=19

Хотя одно уравнение с двумя неизвестными имеет бесчисленное множество решений, но отнюдь ещё не очевидно, что среди них найдётся хоть одно с целыми положительными х и у. Вот почему алгебра разработала метод решения подобных «неопределённых» уравнений. Заслуга введения их в алгебру принадлежит первому европейскому представителю этой науки, знаменитому математику древности Диофанту, отчего такие уравнения часто называют «диофантовыми».

РЕШЕНИЕ

На приведённом примере покажем, как следует решать подобные уравнения.

Надо найти значения х и у в уравнении

3х-5у=19,

зная при этом, что х и у – числа целые и положительные.

Уединим то неизвестное, коэффициент которого меньше, т.е. член 3х; получим:

3х=19+5у,

откуда

х=(19+5у)/3=6+у+(1+2у)/3.

Так как х, 6 и у – числа целые, то равенство может быть верно лишь при условии, что (1+2у)/3 есть также целое число. Обозначим его буквой t. Тогда

Х=6+у+t,

где

t=(1+2у)/3

и, значит,

3t=1+2у, 2у=3t-1.

Из последнего уравнения определяем у:

у=(3t-1)/2=t+(t-1)/2

Так как у и t – числа целые, то и (t-1)/2 должно быть некоторым целым числом t1. Следовательно,

у=t+t1,

причем

t1=(t-1)/2

откуда

2t1=t-1 и t=2t1+1.

Значение t=2t1+1 подставляем в предыдущие равенства:

y=t+t1=(2t1+1)+t1=3t1+1,

x=6+y+t=6+(3t1+1)+(2t1+1)=8+5t1.

Итак для х и у мы нашли выражения1

х=8+5t1,

у=1+3t1.

Числа х и у, мы знаем, - не только целые, но и положительные, т.е. большие чем 0. Следовательно,

8+5t1>0,

1+3t1>0.

Из этих неравенств находим:

5t1>-8 и t1>-(8/5),

3t1>-1 и t1>-(1/3).

Этим величина t1ограничивается; она больше чем –(1/3) (и, значит, подавно больше чем –(8/5). Но так как t1 – число целое, то заключаем, что для него возможны лишь следующие значения:

t 1= 0,1,2,3,4…

Соответствующие значения для х и у таковы:

х=8+5t1=8,13,18,23…,

у=1+3t1=1,4,7,10…,

Теперь мы установили, как может быть произведена уплата: вы либо платите 8 трёхрублёвок, получая одну пятирублёвку сдачи:

8*3-5=19

и т.д.

Теоретически задача имеет бесчисленный ряд решений, практически же число решений ограничено, так как ни у покупателя, ни у кассира нет бесчисленного множества кредитных билетов. Если, например, у каждого всего по 10 биллетов, то расплата может быть произведена только одним способом: выдачей 8 трёхрублёвок и получением 5 рублей сдачи. Как видим, неопределённые уравнения практически могут давать вполне определённые пары решений.

Возвращаясь к нашей задаче, прадлагаем читателю в качестве упражнения самостоятельно решить её вариант, а именно рассмотреть случай, когда у покупателя только пятирублёвки, а у кассира только трёхрублёвки. В результате получится такой ряд решений:

х=5,8,11,000,

у=2,7,12,…

Действительно,

5*5-2*3=19

8*5-7*3=19

11*5-12*3=19

…………..

Мы могли бы получить эти результаты также и из готового уже решения основной задачи, воспользовавшись простым алгебраическим приёмом. Так как давать пятирублёвки и получать трёхрублёвки всё равно, что «получать отрицательные пятирублёвки» и «давать отрицательные трёхрублёвки», то новый вариант задачи решается тем же уравнением, которое мы составили для основной задачи:

3х-5у=19,

но при условии, что х и у – числа отрицательные. Поэтому из равенств

х=8+5t1,

у=1+3t1.

Мы, зная, что х<0 и у<0, выводим:

8+5t11<0,

1+3t11<0.

и, следовательно,

t1<-(8/5).

Принимая t1=-2,-3,-4, и т.д., получаем из предыдущих формул следующие значения для х и у:

t 1=-2,-3,-4,

x=-2,-7,-12,

y=-5,-8,-11.

Первая пара решений, х=-2, у=-5, означает, что покупатель «платит минус 2 трёхрублёвки» и «получает минус 5 пятирублёвок», т.е. в переводе на обычный язык – платит 5 пятирублёвок и получает сдачи 2 трёхрублёвки. Подобным же образом истолковываем и прочие решения.

ЗАДАЧА

При ревизии торговых книг магазина одна из записей оказалась залитой чернилами.

Невозможно было разобрать чило проданных метров, но было несомненно, что число это не дробное; в вырученной сумме можно было различить только последние три цифры, да установить ещё, то перед ними были три какие-то другие цифры.

Может ли ревизионная комиссия по этим следам установить запас?

РУШЕНИЕ

Число, выражаемое тремя залитыми цифрами в записи денежной суммы, обозначим через у. Это, очевидно, число тысяч копеек, а вся сумма в копейках изобразится:

1000у+728.

Имеем уравнение

4936х=1000у+728,

или, после сокращения на 8,

617х-125у=91.

В этом уравнении х и у – числа целые и притом у не больше 999, так как более чем из трёх оно состоять не может. Решаем уравнение, как раньше было указано:

125у=617х-91,

у=5х-1+(34-8х)/125=5х-1+2(17-4х)/125=5х-1+2t

(Здесь мы приняли 617/125=5-(8/125), так как нам выгодно иметь возможно меньше остатки. Дробь.

2(12-4х)/125

есть целое число, а так как 2 не делится на 125, то 17-4х/125 должно быть целым числом, которое мы и обозначим через t.)

Далее из уравнения

(17-4х)/125=t

имеем:

17-4х=125t

x = 4-31t+(1-t)/4=4-31t+t1,

где

t1=(1-t)/4,

и, следовательно,

4t1=1-t;

t=1-4t1;

x = 125t1-27

y = 617t1-134.

Мы знаем, что

100<_y<1000.

Следовательно,

100<_617t1-134<1000.

откуда

t1>_(234/617) и t1<(1134/617).

Очевидно, для t1 существует только одно целое значение:

t 1= 1,

и тогда

x=98, y=483,

т.е. было отпущено 98 метров на сумму 4837 р. 28 коп. Запись восстановлена.

Покупка почтовых марок

ЗАДАЧА

Требуется на один рубль купить 40 штук почтовых марок – копеечных, 4-копеечных и 12-копеечных. Сколько окажется марок каждого достоинства?

РЕШЕНИЕ

В этом случае у нас имеется два уравнения с тремя неизвестными:

х+4у+12z=100,

х+у+z=10.

где х – число копеечных марок, у – 4-копеечных, z-12-копеечных.

Вычитая из первого уравнения второе, получим одно уравнение с двумя неизвестными:

3у+11z=60.

Находим у:

у=20-11(z/3).

Очевидно, z/3 – число целое. Обозначим его через t. Имеем:

y=20-11t,

z=3t.

Подставляем выражение для у и z во второе из исходных уравнений:

х+20-11t+3t=40;

получаем:

х=20+8t.

Так как х>_,y>_0 и z>_0, то нетрудно установить границы для t:

0<_t<_1(9/11),

откуда заключаем, что для t возможны только два целых значения:

t=0 и t=1.

Соответствующие значения х,у и z таковы:

t=	0	1
x=	20	28
y=	20	9
z=	0	3

Проверка :

20*1+20*4+0*12=100,

28*1+9*4+3*12=100.

Итак, покупка марок может быть произведена только двумя способами (а если потребовать, чтобы была куплена хотя бы одна марка каждого достоинства, - то только одним способом).

Умение решать неопределённые уравнения даёт возможность выполнить следующий математический фокус. Вы прадлагаете товарищу умножить число даты его рождения на 12, а номер месяца – на 3. он сообщает вам сумму обоих произведений, и вы вычисляете по ней дату рождения.

Если, например, товарищ ваш родился 9 февраля, то он выполняет следующие выкладки:

9*12=108, 2*31=62, 108+62=170.

Это последнее число, 170, он сообщает вам и вы определяете задуманную дату. Как?

РЕШЕНИЕ

Задача сводится к решению неопределённого уравнения

12х+31у=170

в целых и положительных числах, причём число месяца х не больше 31, а номер месяца у не больше 12.

х=(170-31у)/12=14-3у+(2+5у)/12=14-3у+t,

2+5у=12t,

у=(-2+12t)/5=2t-2*(1-t)/5=2t-2t1.

1-t=5t1, t=1-5t1,

y=2(1-5t1)-2t1=2-12t1,

x=14-3(2-12t1)+1-5t1=9+31t1

Зная, что 31>_x>0 и 12>_y>0, находим границы для t1:

-(9/31)
Следовательно,

t1=0, x=9, y=2.

Дата рождения 9-е число второго месяца, т.е. 9 февраля.

Можно предложить и другое решение, не использующее уравнений. Нам сообщено число а=12х+31у. Так как 12х+24у делится на 12, то числа 7у и а имеют одинаковые остатки от деления на 12. Умножив на 7, найдём, что 49у и 7а имеют одинаковые остатки от деления на 12. Но 49у=48у+у, а 48у делится на 12, значит, у и 7а имеют одинаковые остатки от деления на 12. Иными словами, если а не делится на 12, то у равен остатку от деления числа 7а на 12; если же а делится на 12, то у=12. Этим число у вполне определяется. Ну, а зная у, уже ничего не стоит узнать х.

Маленький совет: прежде чем узнать остаток от деления числа 7а на 12, замените само число а его остатком от деления на 12 – считать будет проще. Например, если а=170, то вы должны произвести в уме следующие вычисления:

170=12*4+2 (остаток, значит равен 2);

2*7=14; 14=12*1+2 (значит, у=2);

х=(170-31у)/12=(170-31*2)/12=108/12=9 (значит, х=2).

Теперь вы можете сообщить товарищу дату его рождения: 9 февраля.

Докажем, что фокус всегда удаётся без отказа, т.е. что уравнение всегда имеет только одно решение в целых положительных числах. Обозначим число, которое сообщил ваш товарищ, через а, так что нахождение даты его рождения сводится к решению уравнения

12х+31у=а.

Станем рассуждать «от противного». Предположим, что это уравнение имеет два различных решения в целых положительных числах, а именно решение х1,у1 и решение х2,у2, причём х1 и х2 не превосходят 31, а у1 и у2 не превосходят 12. Мы имеем:

12х1+31у1=а,

12х2+31у2=а.

Вычитая из первого равенства второе, получим:

12(х1-х2)+31(у1-у2)=0.

Из этого равенства вытекает, что число 12(х1-х2) делится на 31. Так как х1 и х2 – положительные числа, не превосходящие 31, то их разность х1-х2 по величине меньше чем 31. Поэтому число 12(х1-х2) может делиться на 31 только в том случае, когда х1=х2, т.е. когда первое решение совпадает со вторым. Таким образом, предположение о существовании двух различных решений приводит к противоречию.

Два числа и четыре действия

ЗАДАЧА

Эту задачу нужно решать по свободному математическому способу, приводящему к неопределённым уравнениям второй степени.

Вот первая из них.

Над двумя целыми положительными числами были выполнены следующие четыре действия:

их сложили;
вычли из большего меньшее;
перемножили;
разделили большее на меньшее. Полученные результаты сложили – составилось 243. Найти эти числа.

РЕШЕНИЕ

Если большее число х, меньшее у, то

(х+у)+(х-у)+ху+(х/у)=243.

Если это уравнение умножить на у, затем раскрыть скобки и привести подобные члены, то получим:

х(2у+у²+1)=243у.

Но 2у+у²+1=(у+1)². Поэтому

х=243у/(у+1)².

Чтобы х было целым числом, знаменатель (у+1)² должен быть одним из делителей числа 243 (потому что у не может иметь общие множители с у+1). Зная, что 243=3(в 5 степени), заключаем, что 243 делится только на следующие числа, являющиеся точными квадратами: 1,3²,9². Итак, (у+1)² должно быть равно 1,3² или 9², откуда (вспоминая, что у должно быть положительным) находим, что у равно 8 или 2.

Тогда х равно

(243*8)/81 или (243*2)/9.

Итак, искомые числа: 24 и 8 или 54 и 2.

Какой прямоугольник?

ЗАДАЧА

Стороны прямоугольника выражаются целыми числами. Какой длины должны они быть, чтобы периметр прямоугольника числено равнялся его площади?

РЕШЕНИЕ

Обозначив стороны прямоугольника через х и у, составляем уравнение

2х+2у=ху,

откуда

х=2у/(у-2).

Так как х и у должны быть положительными, то положительным должно быть и число у-2, т.е. должно быть больше 2. Заметим теперь, что

х=2у/(у-2)=2(у-2)+4/(у-2)=2+(4/(у-2)).

Так как х должно быть целым числом, то выражение 4/(у-2) должно быть целым числом. Но при у>2 это возможно лишь, если у равно 3,4 или 6. Соответствующие значения х будут 6,4,3.

Итак, искомая фигура есть либо прямоугольник со сторонами 3 и 6, либо квадрат со стороной 4.

Пифагоровы числа

Удобный и очень точный способ, употребляемый землемерами для проведения на местности перпендикулярных линий, состоит в следующем. Пусть через точку А требуется к прямой МN провести перпендикуляр. Откладывают от А по направлению АМ три раза какое-нибудь расстояние а. Затем завязывают на шнуре три узла, расстояния между которми равны 4а и 5а. Приложив крайние узлы к точкам А и В, натягивают шнур за средний узел. Шнур расположится треугольником, в котором угол А – прямой.

Этот древний способ, по-видимому, применявшийся ещё тысячелетия назад строителями египетских пирамид, основан на том, что каждый треугольник, стороны которого относятся, как 3:4:5, согласно общеизвестной теореме Пифагора, - прямоугольный, так как:

3 ² +4² = 5²

Кроме чисел 3,4,5, существует, как известно, бесчисленное множество целых положительных чисел а,b,с, удовлетворяющих соотношению

a²+b²=c²

Они называются пифагоровыми числами. Согласно теореме Пифагора такие числа могут служить длинами сторон некоторого треугольника; поэтому а и b называют «катетами», а с – «гипотенузой».

Ясно, что если а, b, с есть тройка пифагоровых чисел, то и ра, рb, рс, где р – целочисленный множитель, - пифагоровы числа. Обратно, если пифагоровы числа имеют общий множитель, то на этот общий множитель можно их все сократить, и снова получится тройка пифагоровых чисел.

Одна задача из области неопределённых уравнений приобрела громкую известность, так как за её правильное решение было завещено целое состояние: 100000 немецких марок!

Задача состоит в том, чтобы доказать следующее положение, носящее название теоремы, или «великого предложения» Ферма:

Сумма одинаковых степеней двух целых чисел не может быть той же степенью какого-либо третьего целого числа. Исключение составляет лишь вторая степень, для которой это возможно.

Тот же неуспех ожидает вас и при подыскании и примеров для четвёртой, пятой, шестой и т.д. степеней. Это и утверждает «великое предложение Ферма».

Прошло три столетия с тех пор, как она высказана, но математикам не удалось до сих пор найти её доказательства.

Величайшие математики трудились над этой проблемой, однако в лучшем случае им удавалось доказать теорему лишь для того или иного отдельного показателя или для групп показателей, необходимо же найти общее доказательство для всякого целого показателя.

Замечательно, что неуловимое доказательство теоремы Ферма, по-видимому, однажды уже было найдено, но затем вновь утрачено. Австор теоремы, гениальный метематик XVIIв. Пьер Ферма, утверждал, что её доказательство ему известно. Своё «великое предложение» он записал в виде заметки на полях сочинения Диофанта, сопроводив его такой припиской:

«Я нашёл поистине удивительное доказательство этого предложения, но здесь мало места, чтобы его привести».

Ни в бумагах великого математика, ни в его переписке, нигде вообще в другом месте следов этого доказательства найти не удалось.

Последователям Ферма пришлось идти самостоятельным путём.

Вот результаты этих усилий: Эйлер (1797) доказал теорему Ферма для третьей и четвёртой степеней; для пятой степени её доказал Лежандр (1823), для сед\ьмой – Ламе и Лебег (1840). В 1849 году Куммер доказал теорему для обширной группы степеней и, между прочим, - для всех показателей, меньших ста. Эти последние работы далеко выходят за пределы той области математики, какая знакома была Ферма, и становятся загадочным, как мог последний разыскать общее доказательство своего «великого предложения». Впрочем, возможно, он ошибся.

ЛИТЕРАТУРА

Перельман Я.И. Занимательная алгебра. Занимательная геометрия.- М.: Дрофа, 2007.
Диофант Александрийский. Арифметика и книга о многоугольных числах (перевод с древнегреческого И. Н. Веселовского; редакция и комментарии И. Г. Башмаковой). М., «Наука», 1998.
Б. Л. Ван-дер-Варден, Пробуждающаяся наука (перевод И. Н. Веселовского). М., Физматгиз, 1999.
Г. Г. Цейтен, История математики в древности и в средние века (перевод П. Юшкевича). М.–Л., Гостехиздат, 1986
А. В. Васильев, Целое число. Петербург, 1990
И. Г. Башмакова, Диофант и Ферма. В сб. «Историко-математические исследования», вып. 17. М., «Наука», 1986.

Blog

Задачи 10-17стр. Список литературы. 17стр. Введение

Содержание