Влияние неопределенностей в дозах на оценку радиационных рисков Масюк С. В., Шкляр С. В., Кукуш А. Г

Вид материала

Документы

Содержание Берксоновская ошибка. Классическая ошибка. U – случайный независимый от X Сравнение классической и берксоновской ошибок. Методы оценивания риска Оценивание параметров модели с классической ошибкой. Оценивание параметров модели с берксоновской ошибкой. Результаты и обсуждение

Подобный материал:

• Биологические и эпидемиологические эффекты облучения в малых дозах, 5728.53kb.
• Реферат по обж тема: Экологическая безопасность, 429.58kb.
• Нефтегазовые системы, 104.4kb.
• Комплексный план реализации Климатической доктрины Российской Федерации на период, 175.95kb.
• Комплексный план реализации Климатической доктрины Российской Федерации на период, 175.95kb.
• Spider Project – нацеленность на успех, 255.68kb.
• Ирует меры по обеспечению контроля рисков и структуру документации по управлению рисками, 105.94kb.
• Вакцинопрофилактика аллергии, 86.86kb.
• Р. А. Обозов Место систематических финансовых рисков в общей, 49.26kb.
• Главный специалист Отдела оценки рисков Обязанности сотрудника, 19.09kb.

Влияние неопределенностей в дозах на оценку радиационных рисков


Масюк С.В., Шкляр С.В., Кукуш А.Г.^*, Вавилов С.Е.

Институт радиационной защиты АТН Украины, Киев

^* Киевский национальный университет имени Тараса Шевченко


Введение

Как известно, практически все существующие методы моделирования рисков вредного действия радиации на состояние здоровья человека используют некоторые приближения принципиального характера. К такому приближению, в частности, относится предположение об отсутствии распределения индивидуальной дозы (считается, что всякий раз мы имеем детерминированное значение дозы облучения субъекта). Понятно, что такое утверждение принципиально неверно, и неизбежным его следствием является смещение оценок коэффициентов риска и искажение формы кривой “доза-эффект”. Заметим, что к подобным искажениям в оценке рисков приводят не только систематические ошибки в оценках доз, что в принципе очевидно, но и случайные ошибки.

Во всех случаях, когда риск-анализ выполняется с игнорированием вышеперечисленных обстоятельств принципиального характера, аналитик все же получает какие-то оценки рисков. Такие оценки в математическо-статистической литературе [1, 2] принято называть “наивными”. Для краткости будем называть их “Н-оценки”. Также “наивными” называются и методы получения подобных оценок (“Н-методы”). Соответственно оценки радиационного риска, учитывающие влияния ошибок в дозах и методы их получения, называются “ненаивными”. Для обозначения “ненаивных” оценок (методов) в качестве синонима будем использовать термин “корректные” или кратко – “К-оценки” (“К-методы”, “К-подходы”).

В последние годы ведутся интенсивные исследования по включению неопределенностей дозовых оценок в процедуры риск-анализа [3]. Особенную актуальность эта проблема приобрела в связи с эпидемиологическими исследованиями последствий Чернобыльской аварии, когда выполнялись десятки подобных исследований, в которых риск-анализ – основывался на Н-методах. Вследствие этого, полученные Н-оценки оценки рисков характеризуются очень большим разбросом. При этом окончательно неизвестно, связано ли это с “наивностью” методов оценивания рисков или с природой и величиной погрешностей в каждом из названных исследований.

При анализе влияния дозовых ошибок на оценку радиационного риска важно установить механизм возникновения таких ошибок. Существуют две фундаментальные модели ошибок: классическая и берксоновская [1-3]. На практике эти два типа ошибок обычно реализуются совместно. Однако их влияние на оценку радиационного риска кардинально отличается. Поэтому целесообразно рассматривать классическую и берксоновскую ошибки отдельно друг от друга.

Данное сообщение представляет собой попытку установить взаимосвязь между “наивными” и “корректными” риск-оценками, при условии разной степени неопределенности в дозах облучения.

Поскольку ошибки в дозах носят мультипликативный характер, предпочтительнее применять как классическую, так и берсоновскую модель не для самих доз, а для их натуральных логарифмов.

Берксоновская ошибка. Если ошибки в оценке логарифмов доз имеют гауссовское распределение, то можно записать:

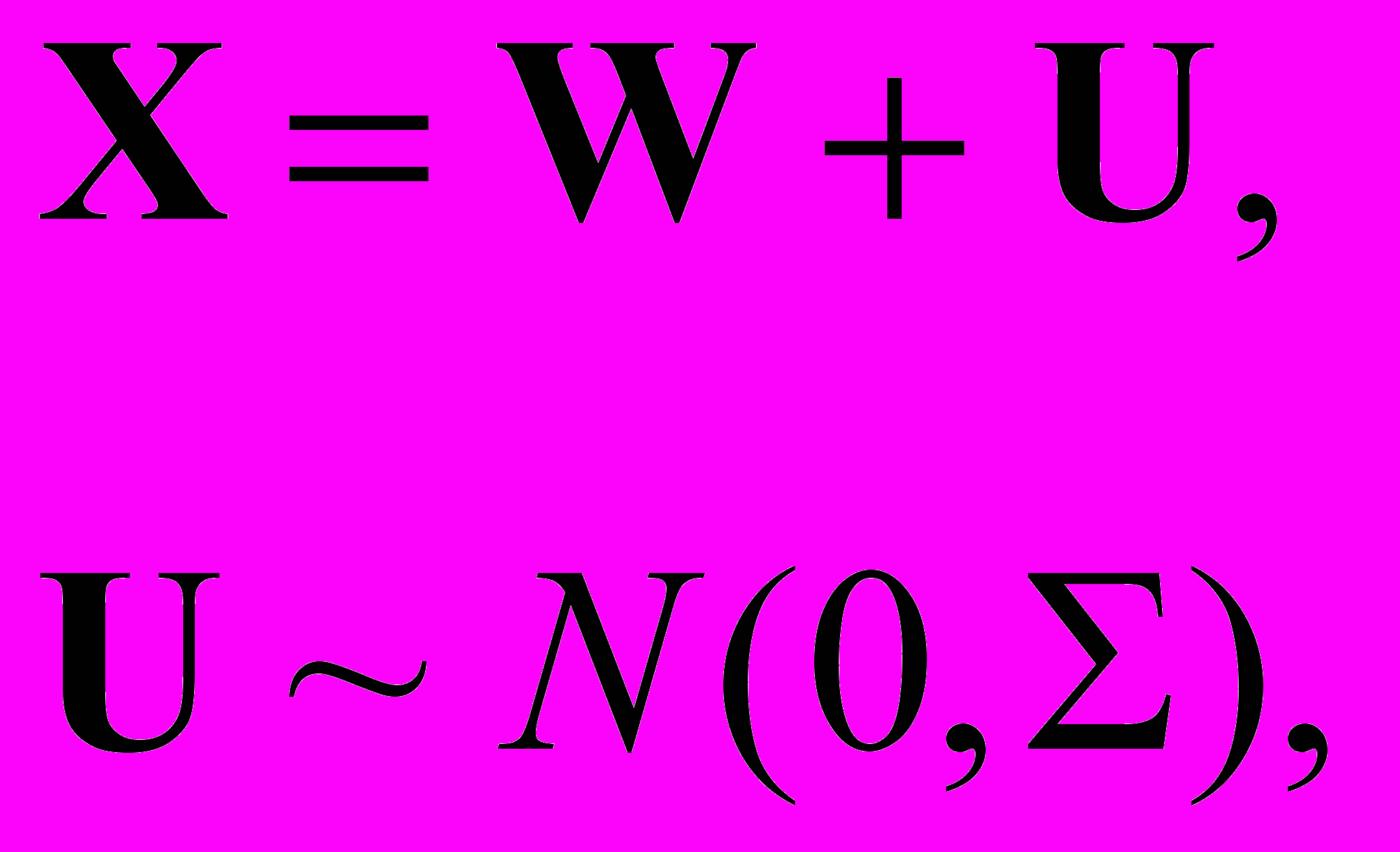(1)

где – известное значение вектора натуральных логарифмов измеренных доз; X – неизвестное значение вектора натуральных логарифмов истинных доз; U – гауссовский случайный вектор ошибок с нулевым математическим ожиданием и известной ковариационной матрицей .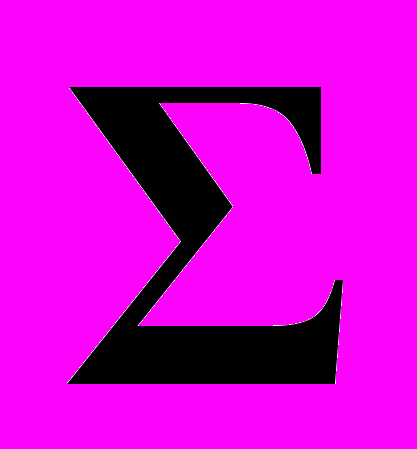

Вектор может быть как случайным, так и детерминированным, но во всех случаях векторы и U стохастически независимы.

В случае берксоновской ошибки определяется условное распределение вектора из логарифмов истинных доз X:

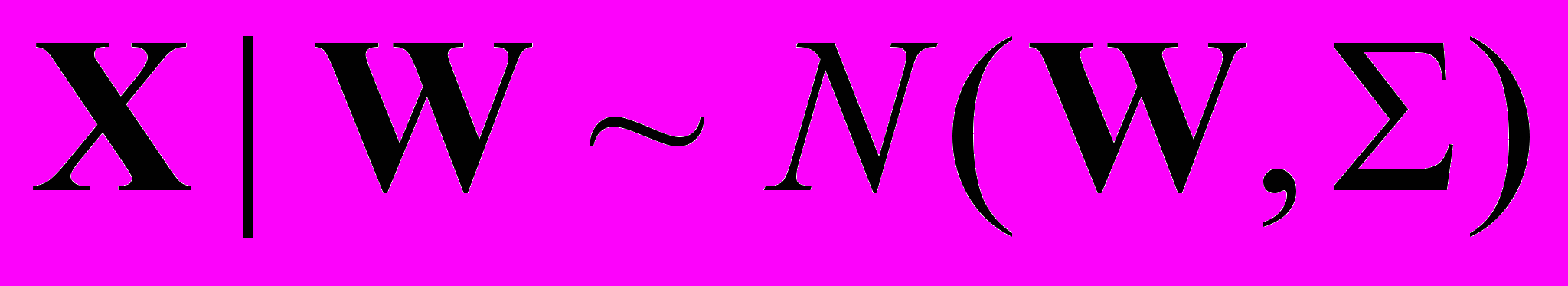, (2)

то есть для каждого наблюдения является известным распределение истинной случайной величины (логарифма дозы), но ее конкретная реализация неизвестна (рис. 1а). Ошибка Берксона возникает всякий раз, когда вместо истинного значения дозы используется ее среднее значение. В частности, если не известны индивидуальные значения доз, но известны их математические ожидания (в том числе средне-групповые оценки индивидуальных доз) полученные, например, с помощью численной Монте-Карло [4-5] процедуры, тогда замена истинных доз их математическими ожиданиями приведет к берксоновской ошибке.



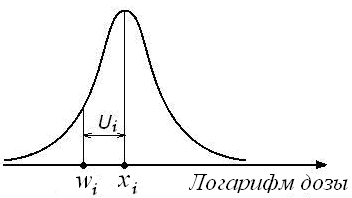
а) б)

Рис. 1 – Иллюстрация к понятиям берксоновской (а) и классической (б) ошибок


Ошибка Берксона (в отличие от классической ошибки) обладает тем удачным свойством, что использование доз с берксоновскими ошибками в линейной (относительно дозы) модели риска практически не приводит к смещению оценок риска [1].

Классическая ошибка. Пусть вектор логарифмов измеренных доз подвержен флуктуациям в связи с классической ошибкой, распределенной по гауссовскому закону. Тогда

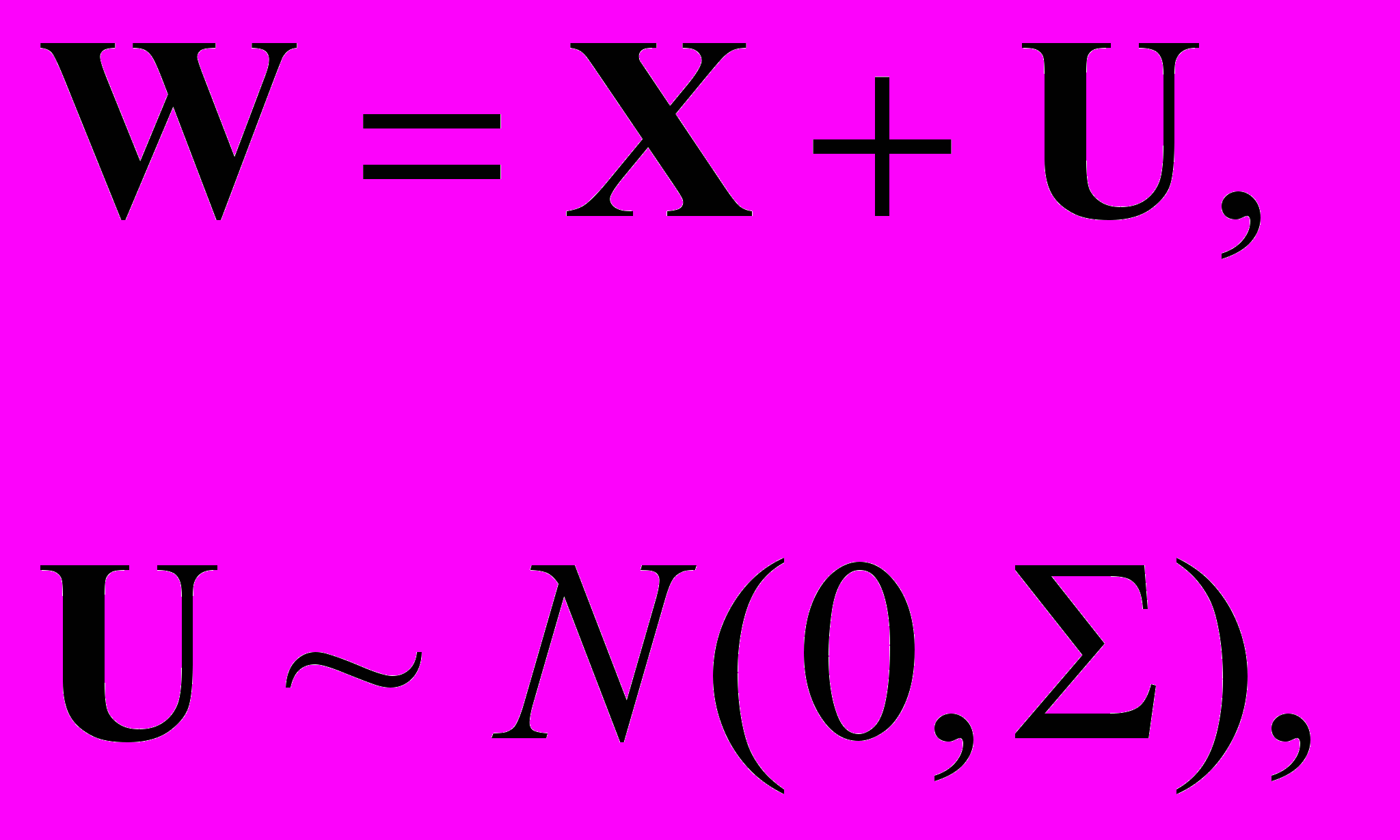(3)

где X – значение вектора натуральных логарифмов истинных доз, которое является неизвестным; – известное значение вектора из натуральных логарифмов измеренных доз; U – случайный независимый от X гауссовский вектор с нулевым математическим ожиданием и известной ковариационной матрицей 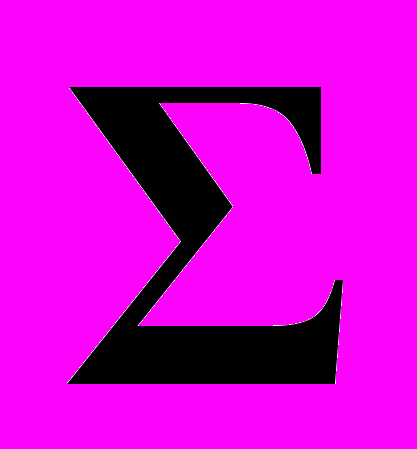(другими словами случайная ошибка).

В случае классической ошибки

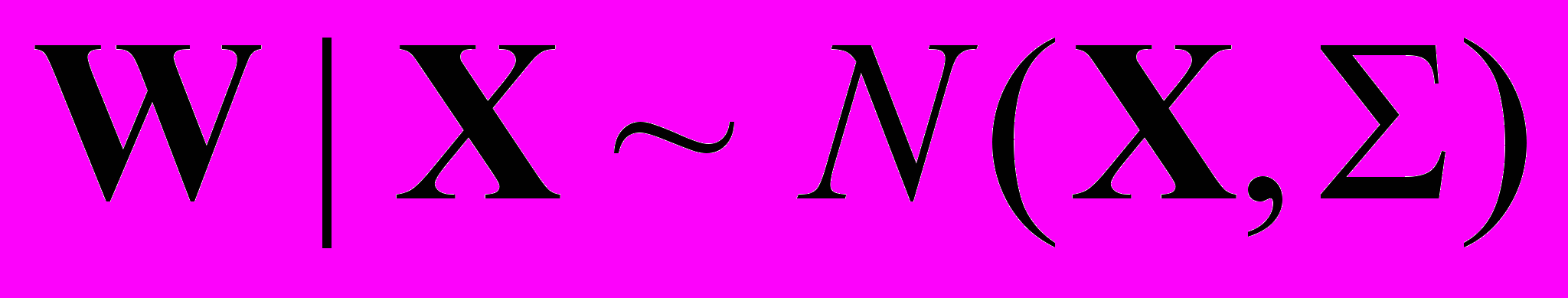. (4)

Из (4) следует, что логарифм измеренной в i-м наблюдении дозы 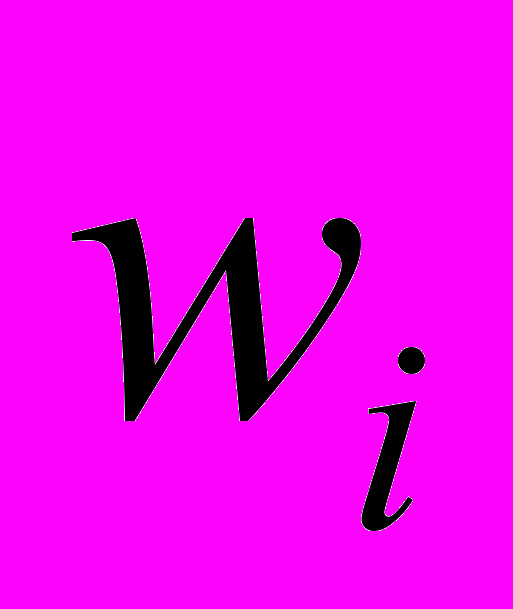имеет условное распределение с известной условной дисперсией и неизвестным условным математическим ожиданием 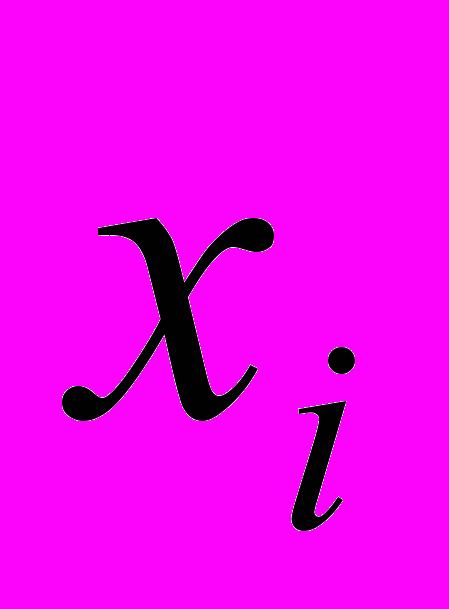, которое рассматривается как логарифм истинной дозы (рис. 1б). Об оценивании в классических моделях с ошибками в переменных см. [1].

Классическая ошибка возникает в случае, когда мы вместо истинного значения дозы используем ее измеренное значение (некоторую рассчетно-инструментальную реализацию подверженную ошибке). Очевидно, что, измерения активности и результаты анкетных опросов флуктуируют как раз из-за наличия классической ошибки.

Сравнение классической и берксоновской ошибок. На первый взгляд, кажется, что классическую ошибку можно получить из берксоновской путем простого переноса величины U в правую часть (1):

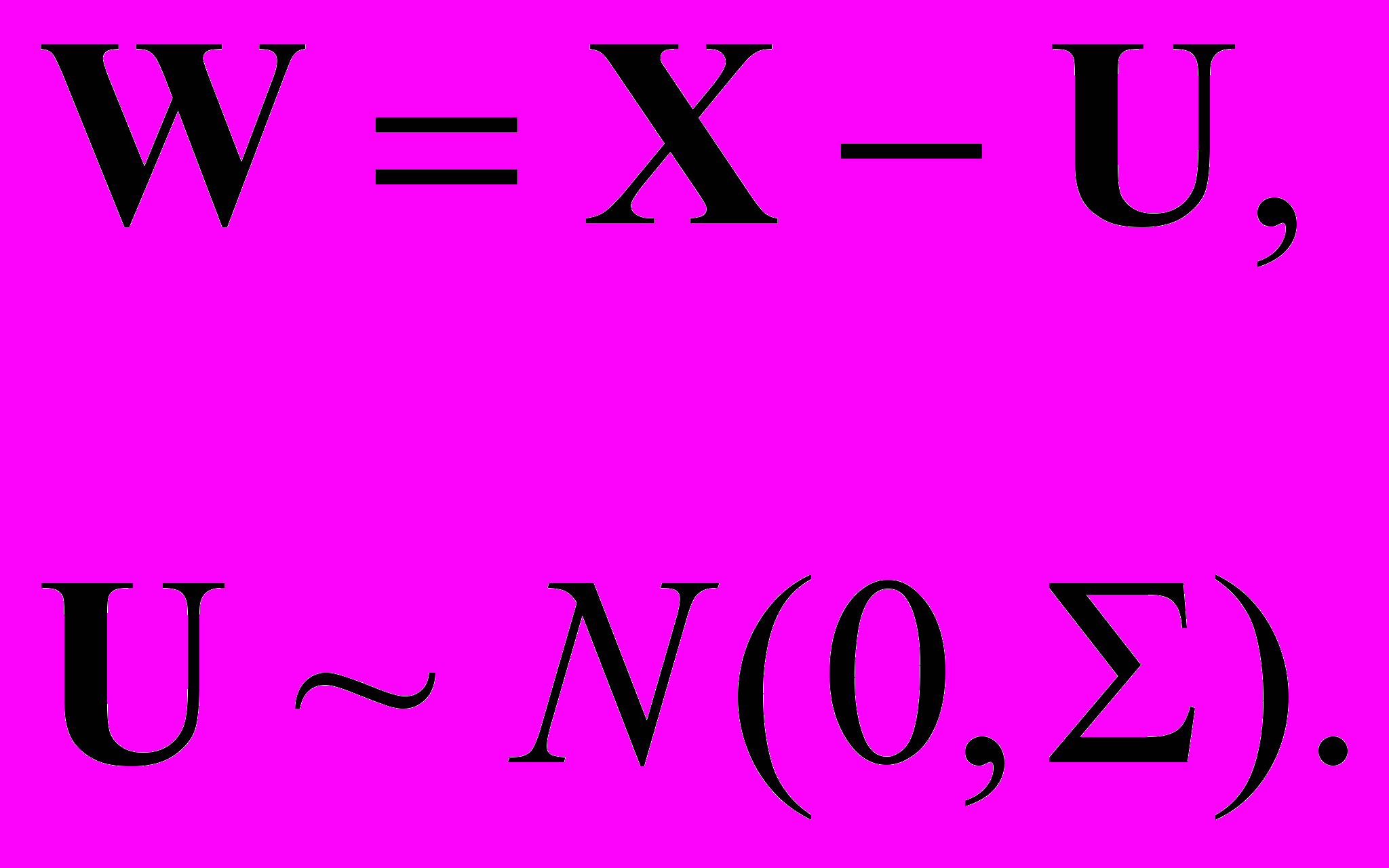(5)

Исходя из того, что U и (-U) одинаково распределены, может показаться, что (5) эквивалентно (3). Однако есть одно существенное отличие: в (3) независимыми величинами являются X и U, a в (5), как и в (1), независимыми являются W и U, что нарушает условие эквивалентности.

Таким образом, при берксоновской ошибке логарифм измеренной дозы W является независимой величиной, характеризующей распределение логарифма истинной дозы, а точнее, является его условным математическим ожиданием. С другой стороны, при классической ошибке логарифм измеренной дозы W является величиной, коррелированной с логарифмом истинной дозой X и ошибкой U.

В случае ошибки Берксона имеется больше информации об истинных дозах, чем в случае классической ошибки. При берксоновской ошибке, по крайней мере, известно условное распределение истинной дозы (или ее логарифма 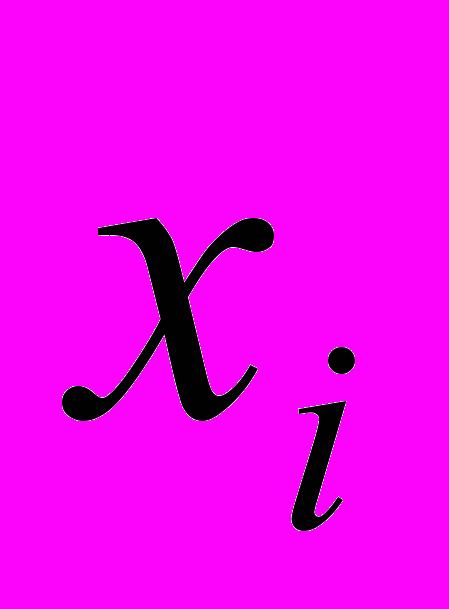) для любого i-го наблюдения. Что касается классической ошибки, то известно лишь отклонение измеренной дозы (или ее логарифма 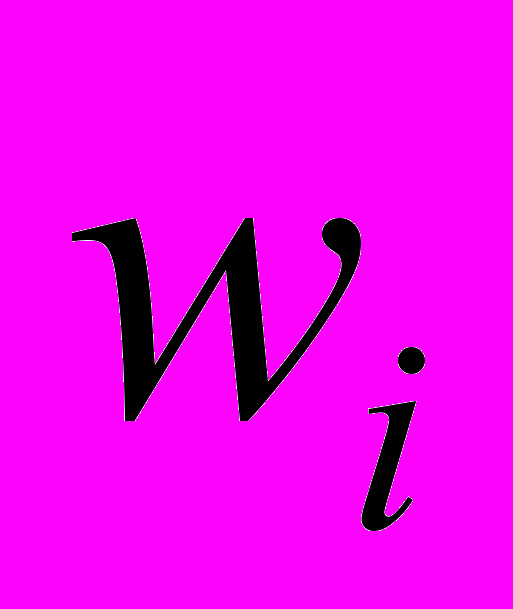) от истинного значения на величину случайной ошибки.


Методы оценивания риска

Для моделирования возникновения случаев рака используется модель с бинарной зависимой переменной Y_i, которая принимает два значения: 0 или 1. Обозначим через P_i вероятность появления единицы (или математическое ожидание Y_i):

P_i = Pr(Y_i = 1) = E(Y_i). (6)

Пусть 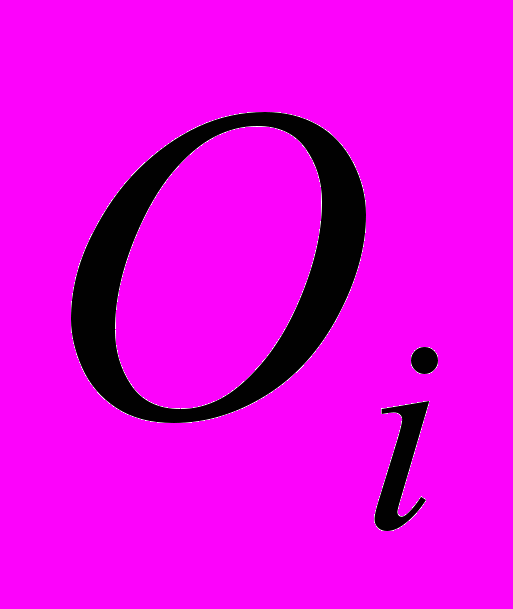(Odds) шанс реализации i-го события – отношение вероятностей Pr(Y_i = 1) и Pr(Y_i = 0), то есть

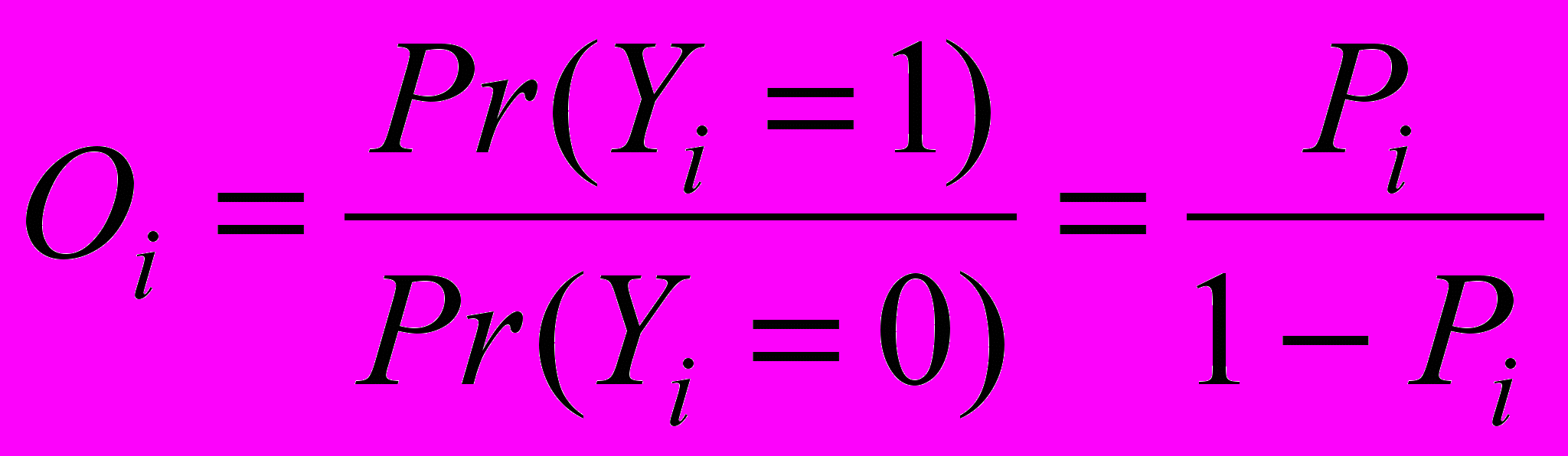. (7)

Пусть шанс является некоторой функцией заболеваемости от переменной x_i и вектора параметров модели b:

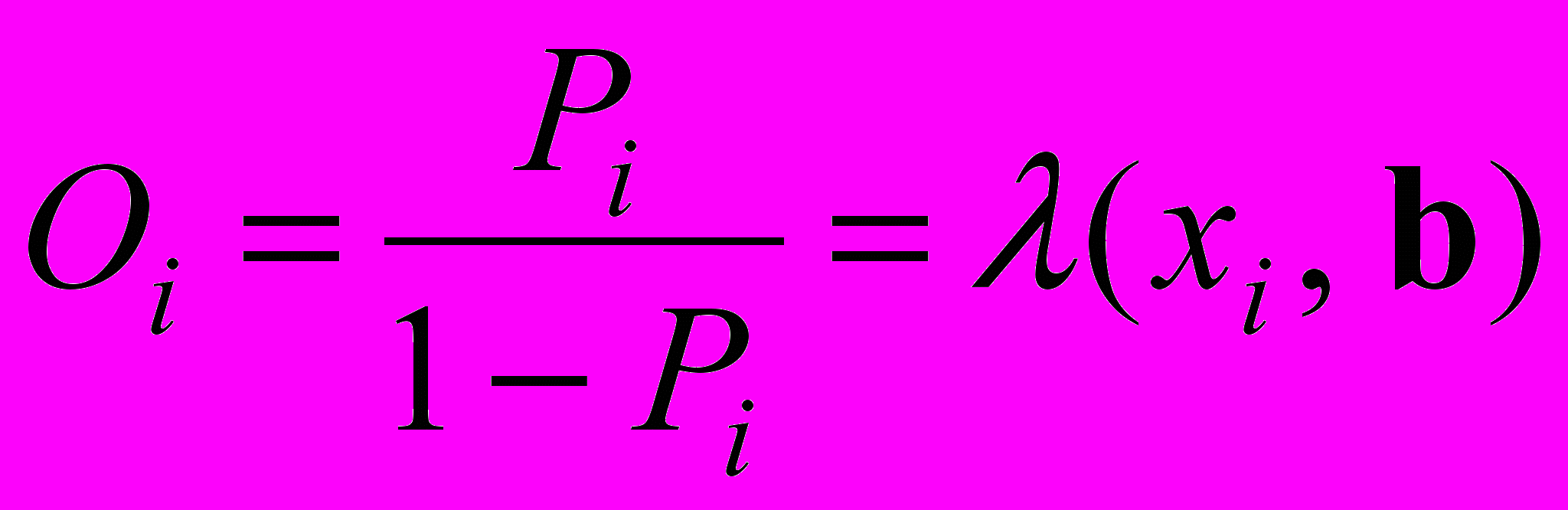. (8)

Легко увидеть, что

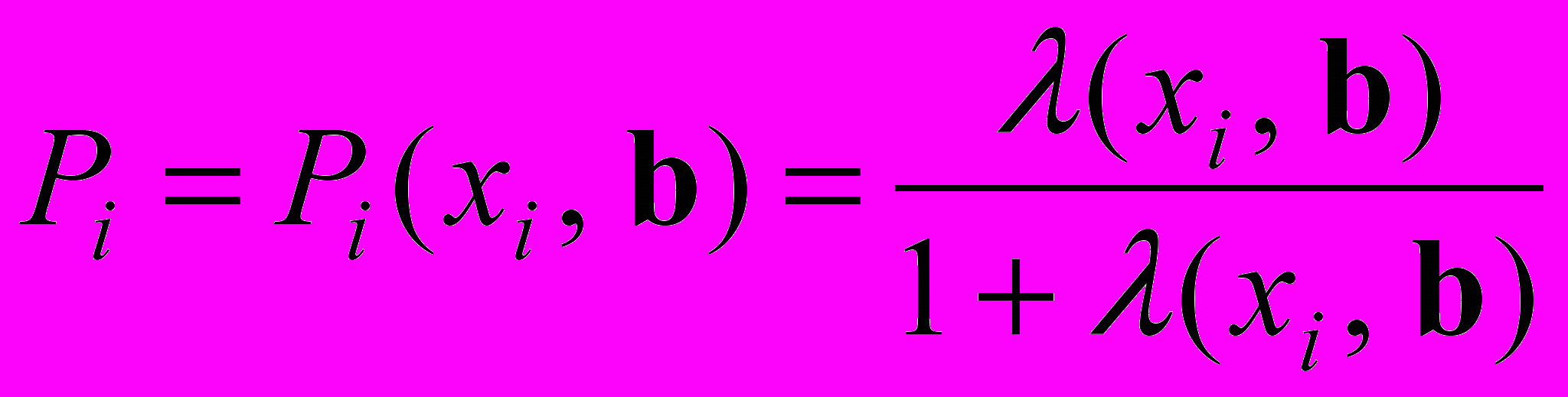. (9)

Функция правдоподобия [6] для бинарной модели определяется формулой:

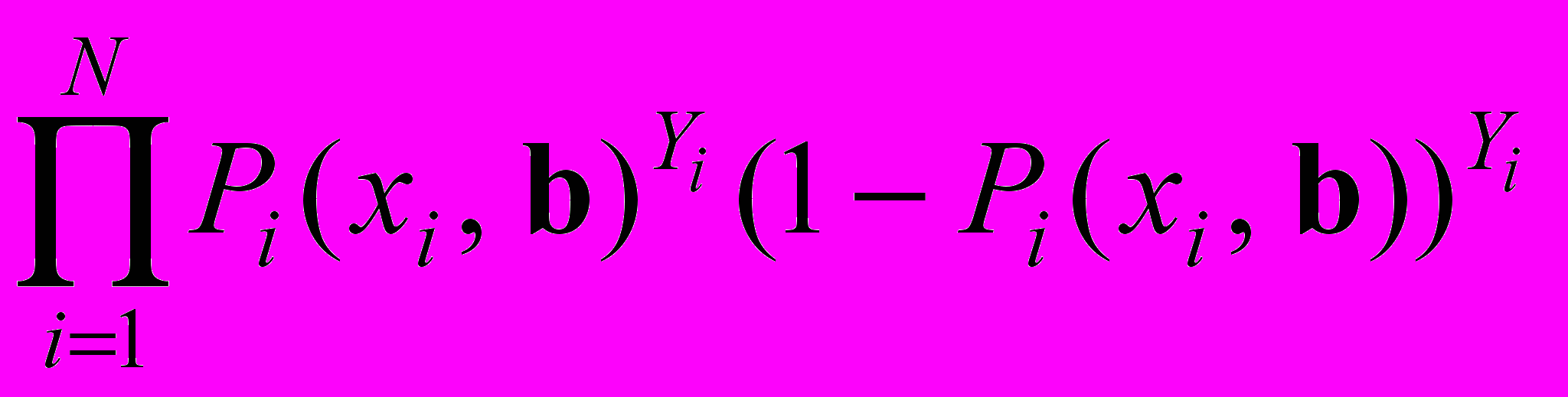, (10)

Логарифмическая функция правдоподобия l соответственно определяется так:

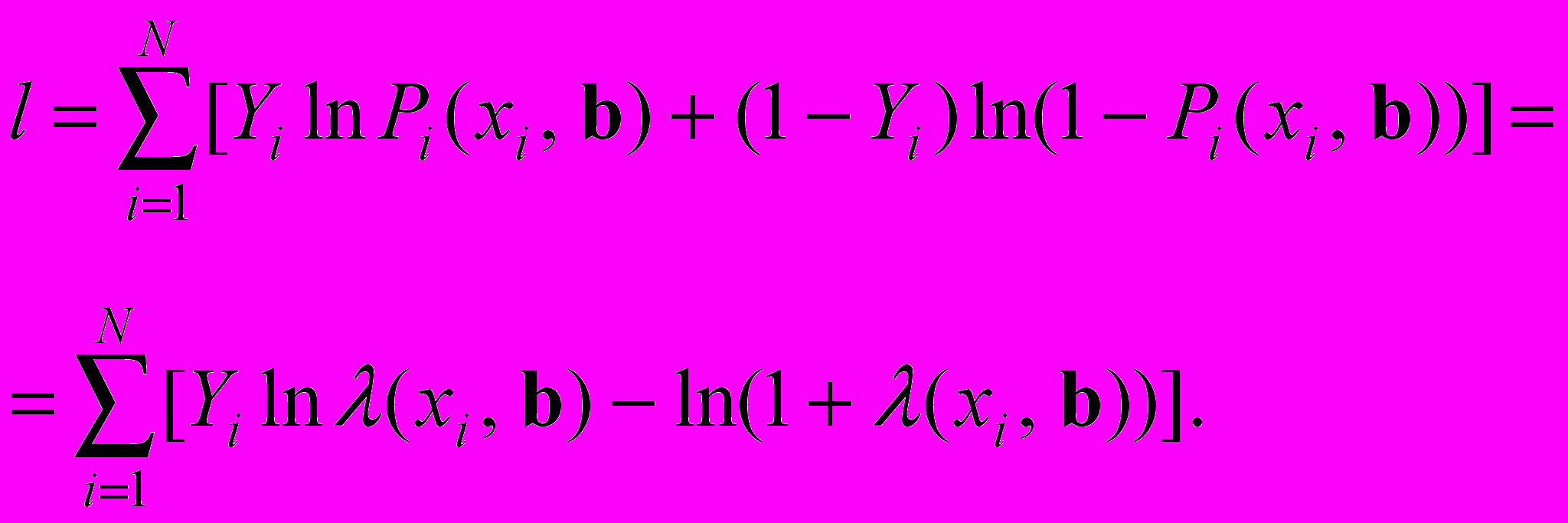(11)

Оценка максимального правдоподобия (ОМП) – это такие значения вектора параметров b, в которых функция (11) достигает своего максимума. Способ получения ОМП оценок называется методом максимального правдоподобия (ММП). Такие оценки обладают хорошими свойствами: они состоятельны, асимптотически нормальны и асимптотически эффективны.

Оценивание параметров модели с классической ошибкой. Пусть вектор регрессоров X наблюдается с классической ошибкой:

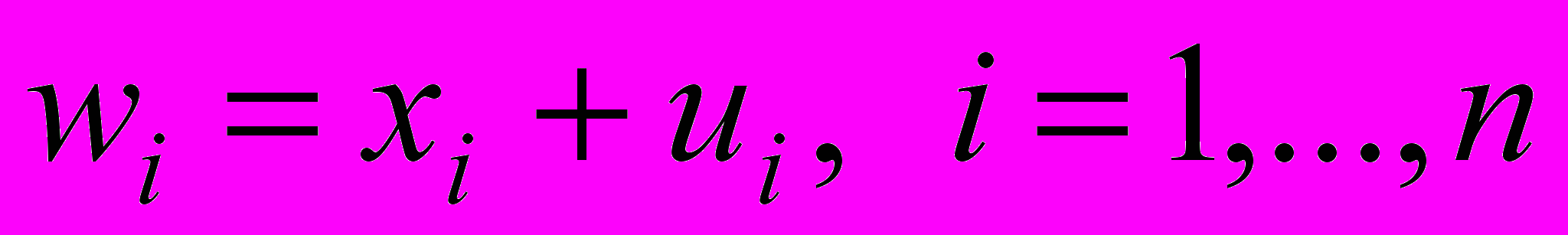, (12)

где x_i – истинное значение независимой переменной (логарифма дозы), w_i – ее измеренное значение, а u_i – случайная ошибка независимая от x_i. Для простоты предположим, что ошибка – нормально распределенная величина 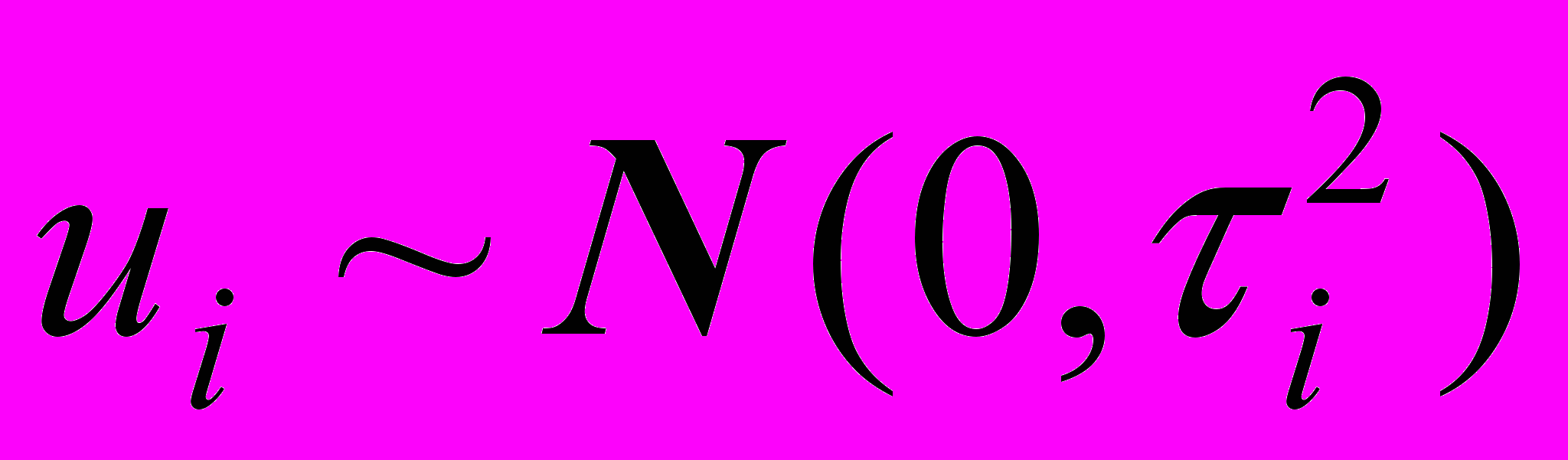с известным параметром τ_i.

Согласно функциональному подходу истинные значения независимой переменной x_i являются детерминированными. Однако мы будем рассматривать нормальную структурную модели ошибки. В рамках этой модели x_i одинаково распределенные случайные величины независимые от ошибок u_i . Кроме того .

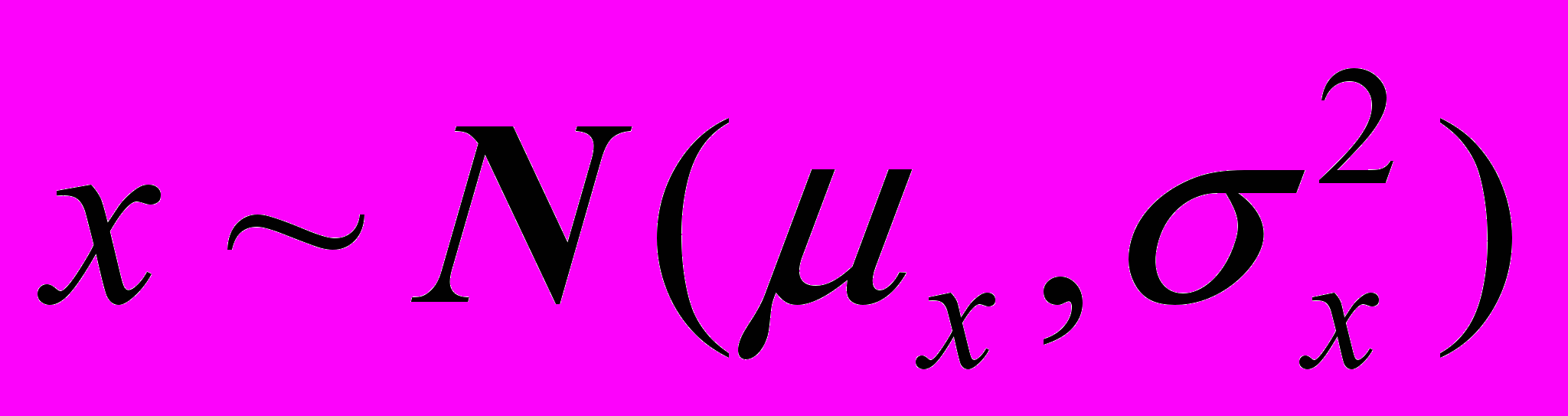Если 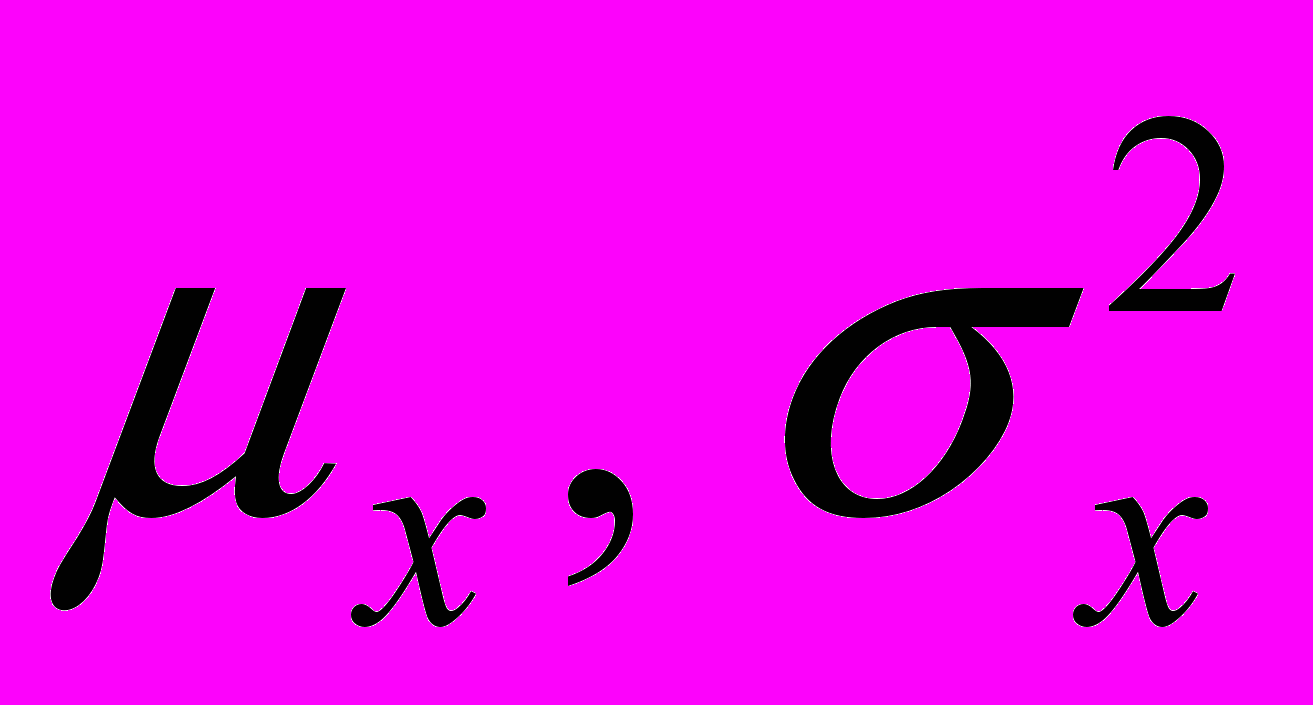неизвестны, их можно оценить исходя из наблюдений w_i:

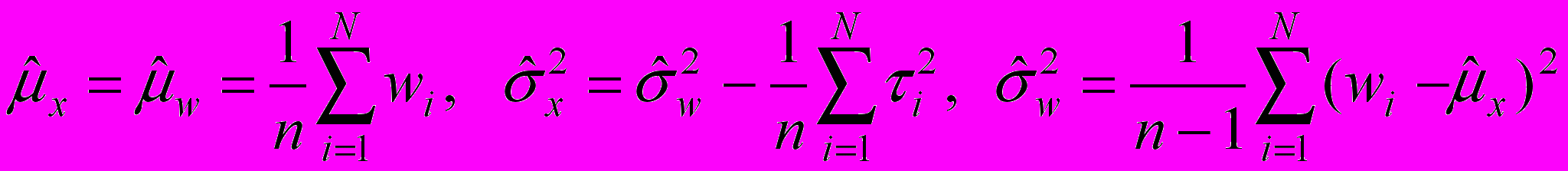(13)

Определим функцию правдоподобия для модели с классической ошибкой. Пусть Pr(Y_i = Y^*, w_i = w^*, x_i = x^*) вероятность произведения событий Y_i = Y^*, w_i = w^*, x_i = x^*. Тогда по формуле условных вероятностей:

Pr(Y_i = Y^*, w_i = w^*, x_i = x^*) = Pr(Y_i = Y^* | w_i = w^*, x_i = x^*) Pr(w_i = w^*, x_i = x^*) = = Pr(Y_i = Y^* | x_i = x^*) Pr(w_i = w^* | x_i = x^*) Pr(x_i = x^*). (14)

Переходя в (14) от вероятностей к функции правдоподобия получим:

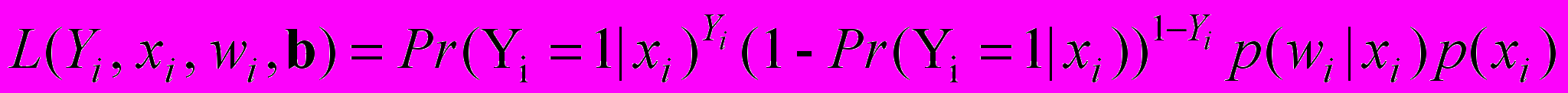(15)

Учитывая (6) а также то, что w_i при условии x_i нормально распределена 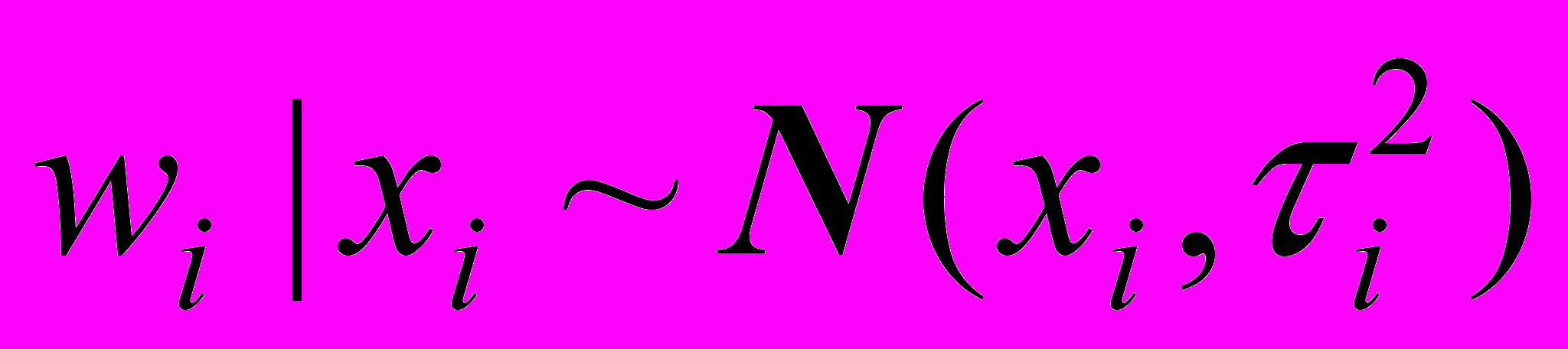, и, находясь в рамках структурной модели 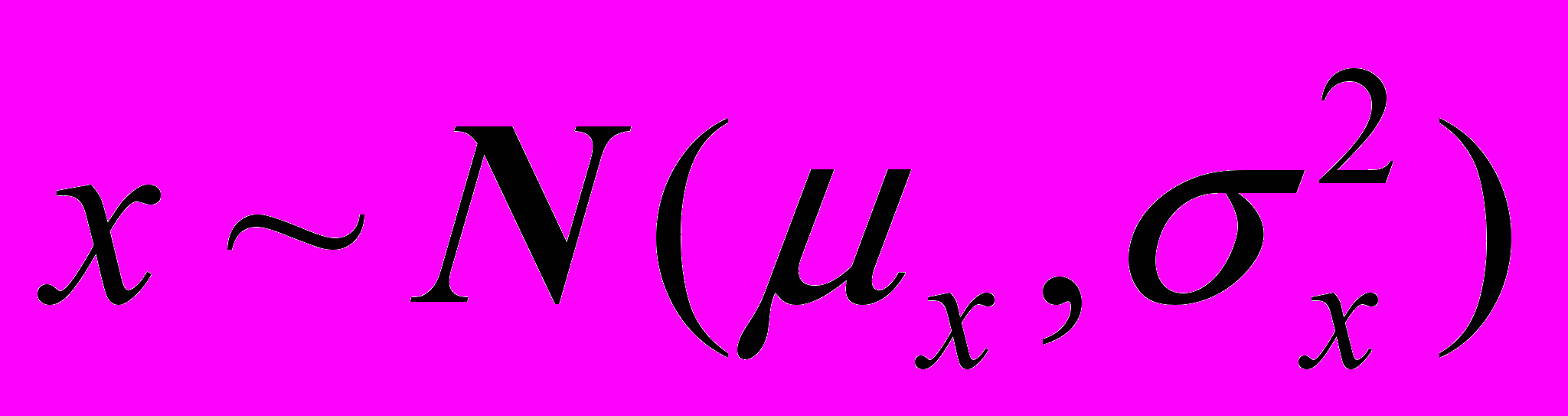, с использованием (9) получим:

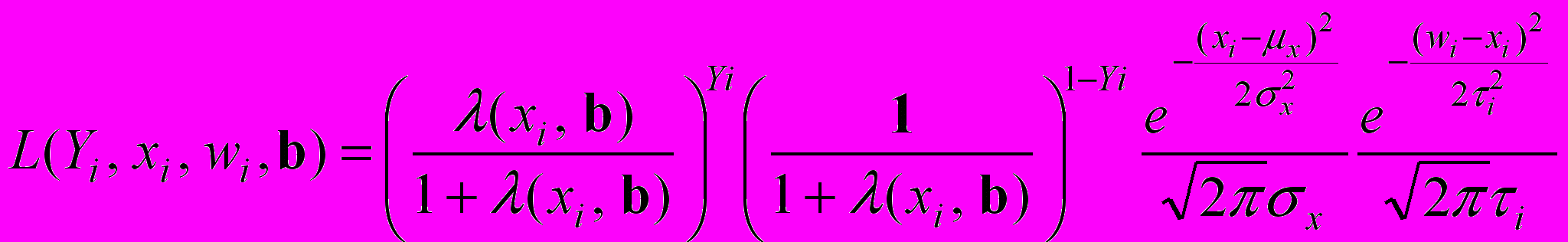. (16)

Для того чтобы избавиться от неизвестной переменной x_i, необходимо по ней сделать свертку:

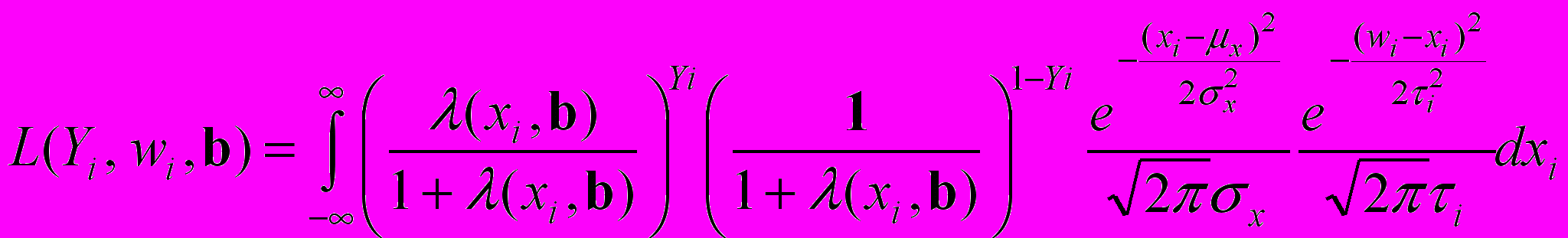. (17)

Таким образом, функция правдоподобия, которая включает вклады всех наблюдений, определяется следующим образом:

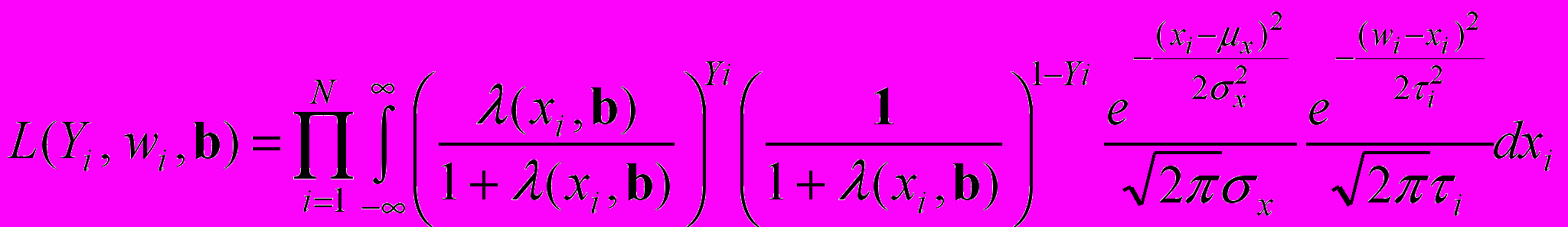, (18)

а, соответствующая логарифмическая функция правдоподобия запишется в виде:

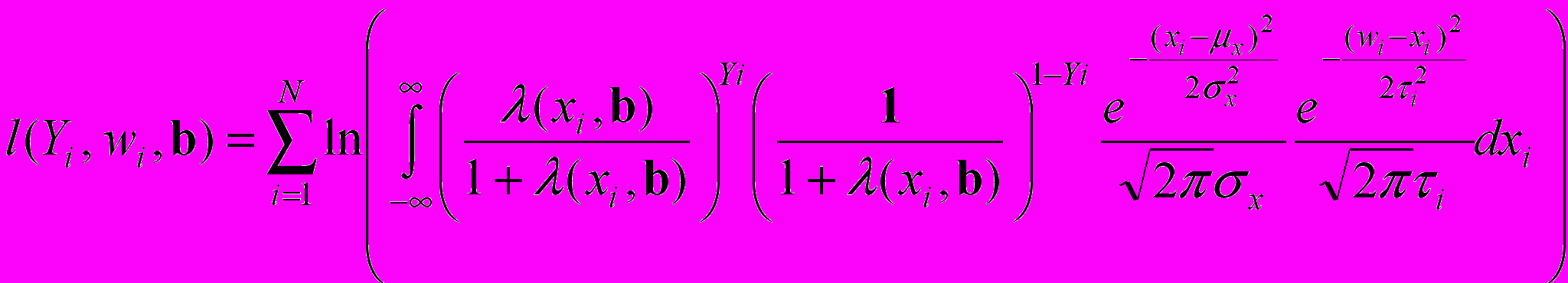(19)

В связи с тем, что переменная Y_i принимает всего два значения (0 и 1), последнее равенство можно записать в виде:

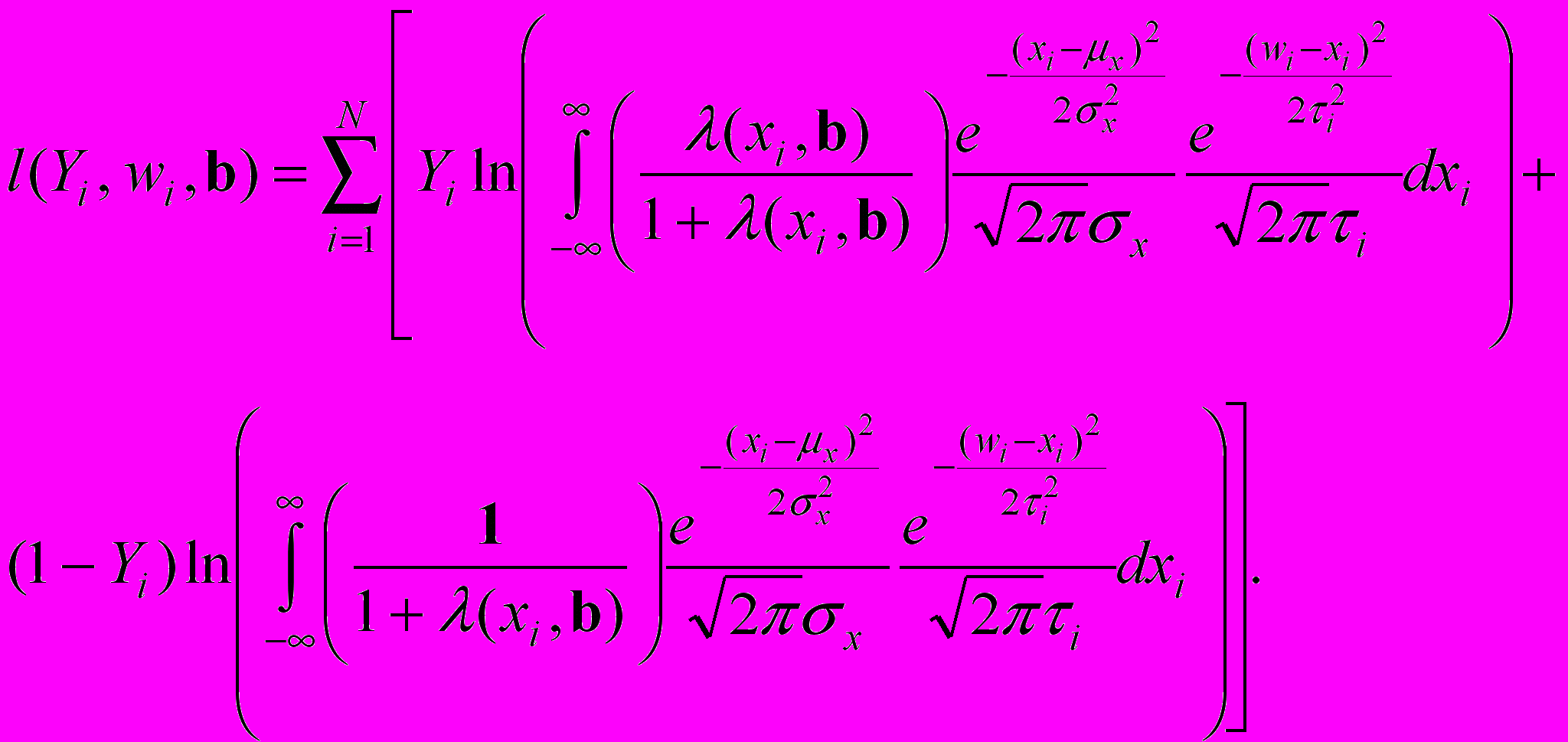(20)

Интеграл в правой части равенства (20) в общем случае невозможно вычислить аналитически, но с достаточно высокой точностью его можно оценить численно, заменив, например, интегральными суммами.

Оценивание параметров модели с берксоновской ошибкой. Пусть вектор регрессоров X подвержен берксоновской ошибке, то есть

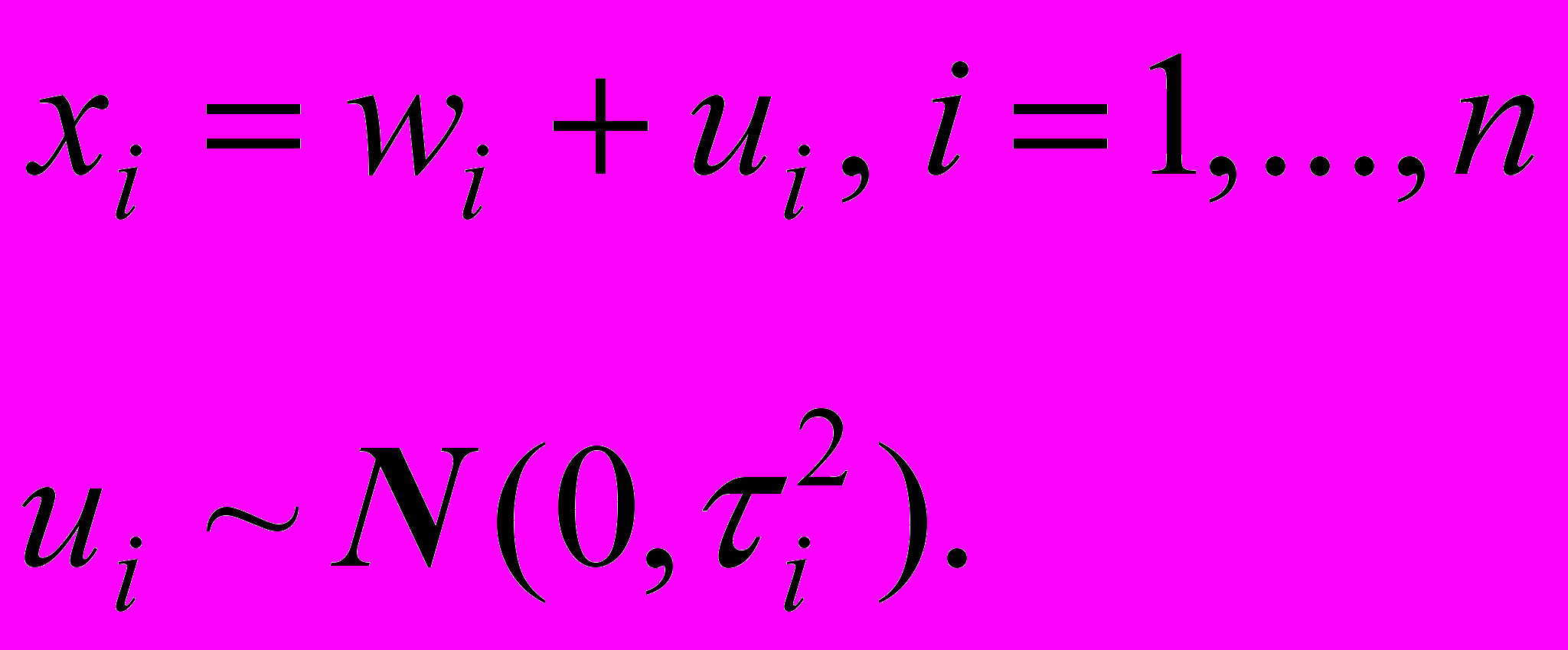(21)

Здесь в отличие от классической ошибки, не нужно делать предположений о распределении истинной переменной x_i. Наблюдаемая переменная w_i может быть величиной как случайной, так и неслучайной, но в любом случае w_i и u_i должны быть независимы.

Определим функцию правдоподобия. Пусть Pr(Y_i = Y^*, w_i = w^*, x_i = x^*) вероятность произведения событий Y_i = Y^*, w_i = w^* и x_i = x^*. Тогда по формуле условных вероятностей получим:

Pr(Y_i = Y^*, w_i = w^*, x_i = x^*)= Pr(Y_i = Y^* | w_i = w^*, x_i = x^*) Pr(w_i = w^*, x_i = x^*) =

= Pr(Y_i = Y^* | x_i = x^*) Pr(w_i = w^* | x_i = x^*)Pr(w_i = w^*). (22)

Так как множитель Pr(w_i = w^*) не несет дополнительной информации о векторе параметров b, то при построении функция правдоподобия его можно опустить.

Переходя в (22) от вероятности к функции правдоподобия будем иметь:

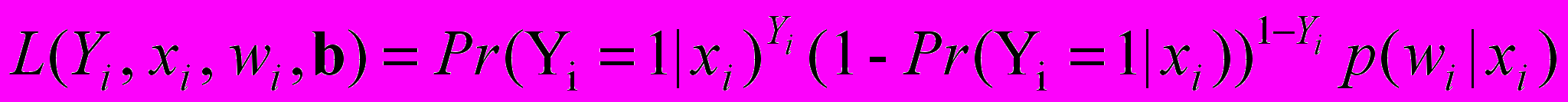. (23)

Учитывая (6), (9) и то, что 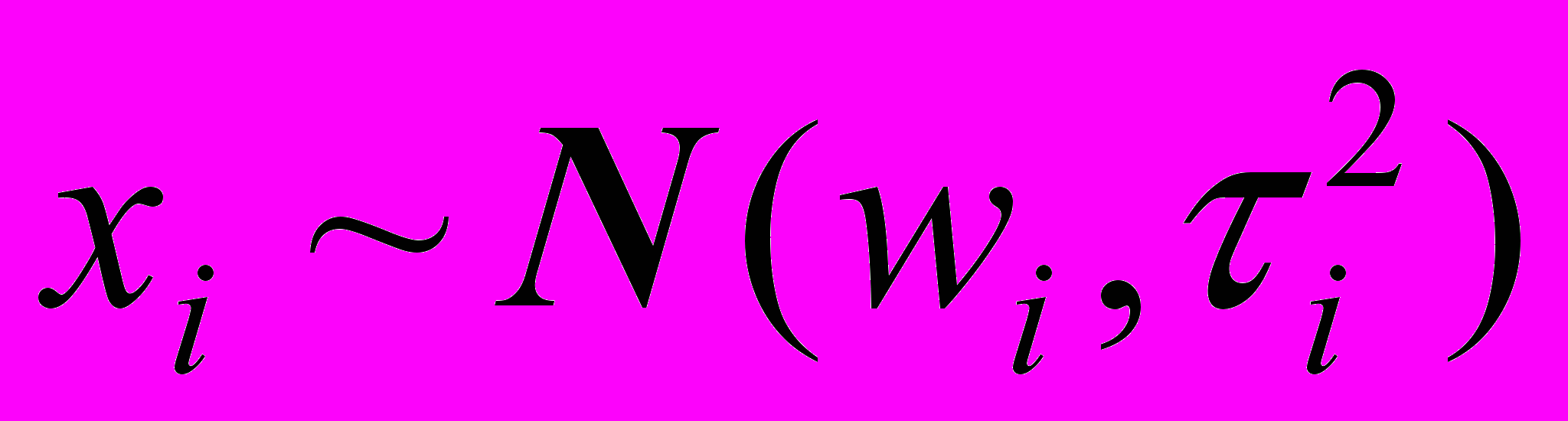, получим:

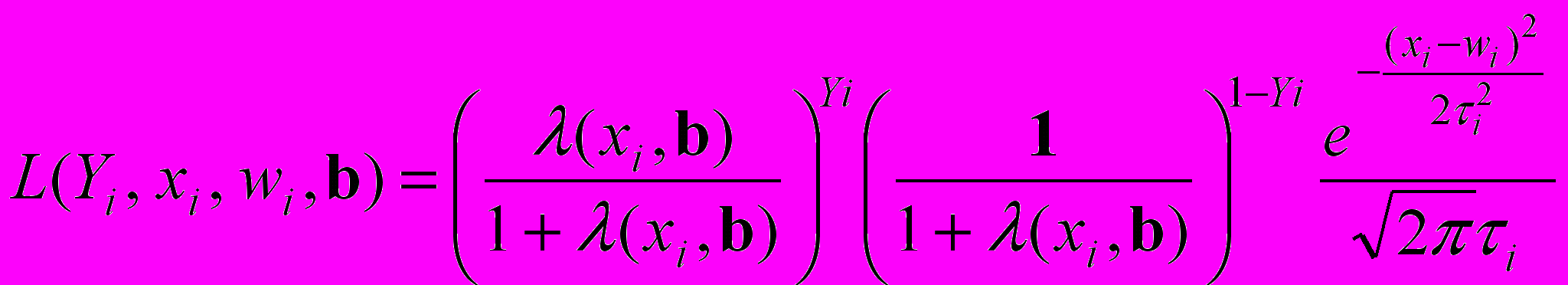. (24)

Чтобы избавиться от неизвестной x_i, сделаем по ней свертку:

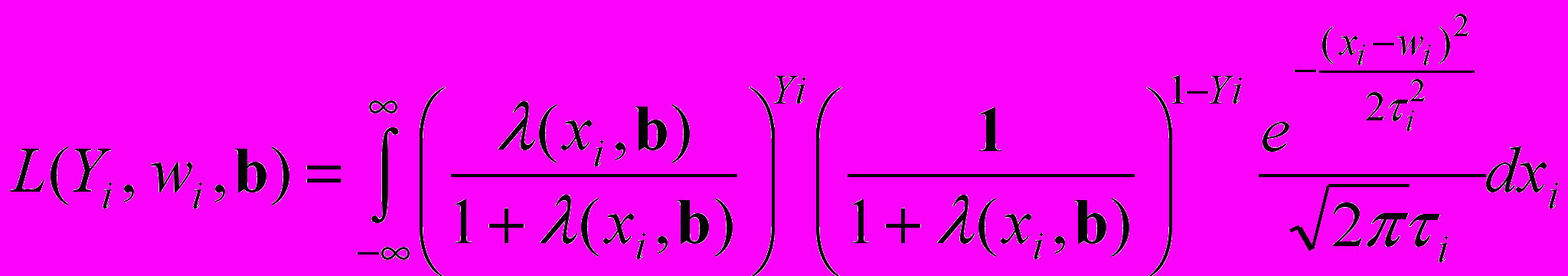. (25)

Логарифмическая функция правдоподобия, учитывающая вклады всех наблюдений равна:

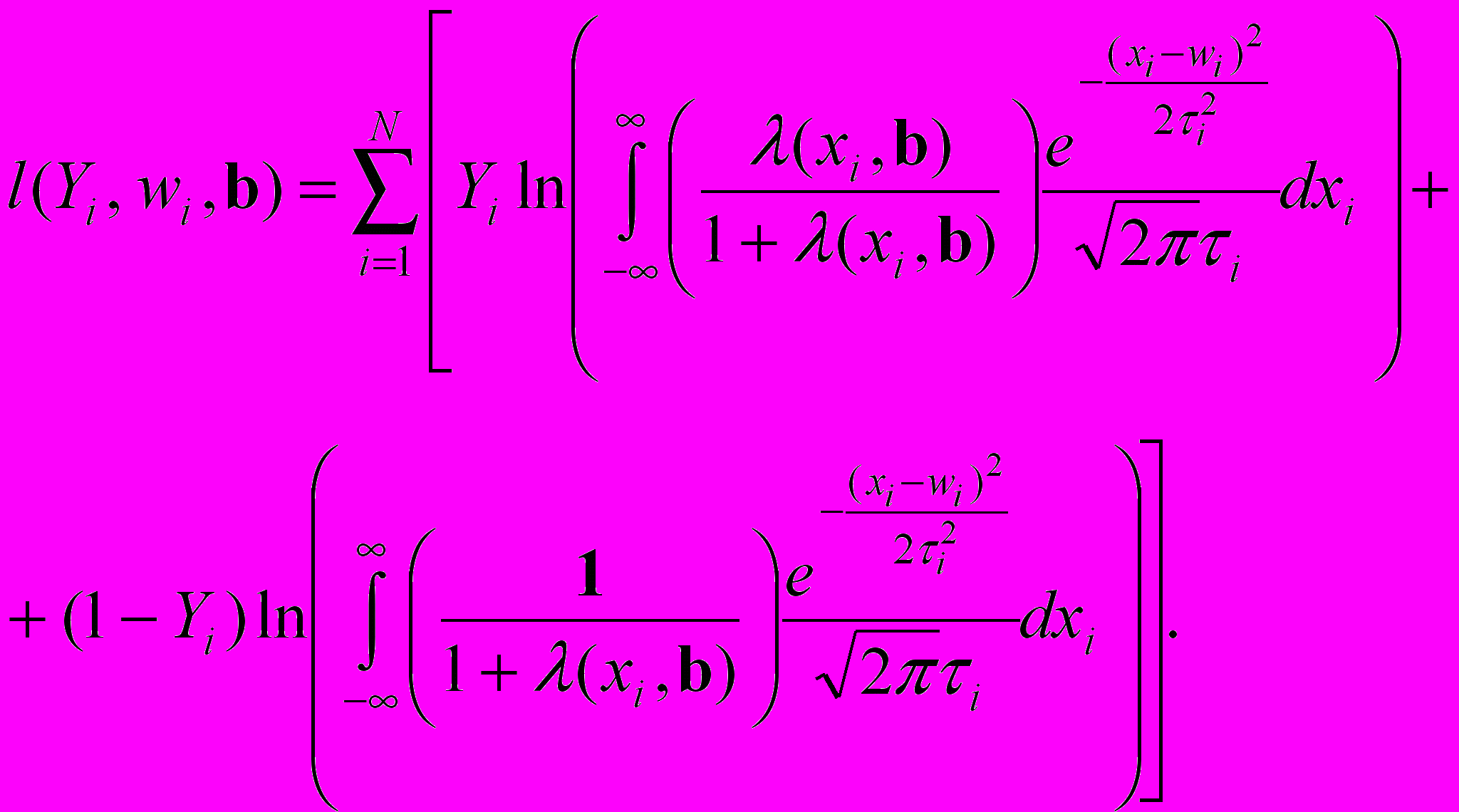(26)


Моделирование

При моделировании использована реальная субпопуляция детей и подростков до 18 лет (всего 301907 человек из 1293 населенных пунктов Житомирской, Киевской и Черниговской областей Украины), разделенная на 36 поло-возрастных групп внутри каждого населенного пункта (НП). Кроме того, внутри каждого НП для каждой поло-возрастной группы использованы полученные в соответствии с [7] средние геометрические дозовые оценки и их стандартные отклонения.

Имитация индивидуальной дозы каждого лица осуществлялась с помощью логнормального [8] генератора случайных величин с соответствующими натурными параметрами распределений:

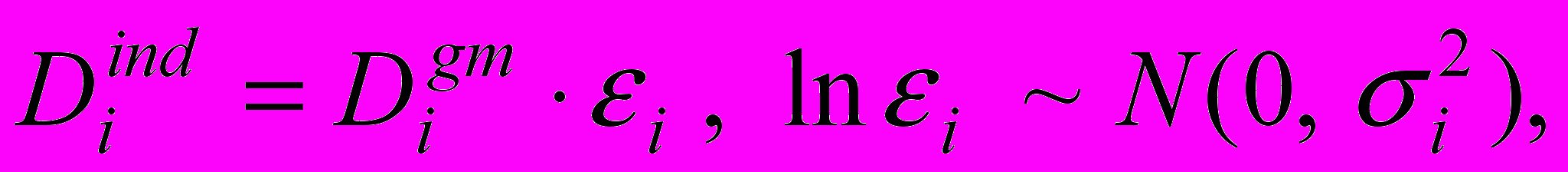(27)

где 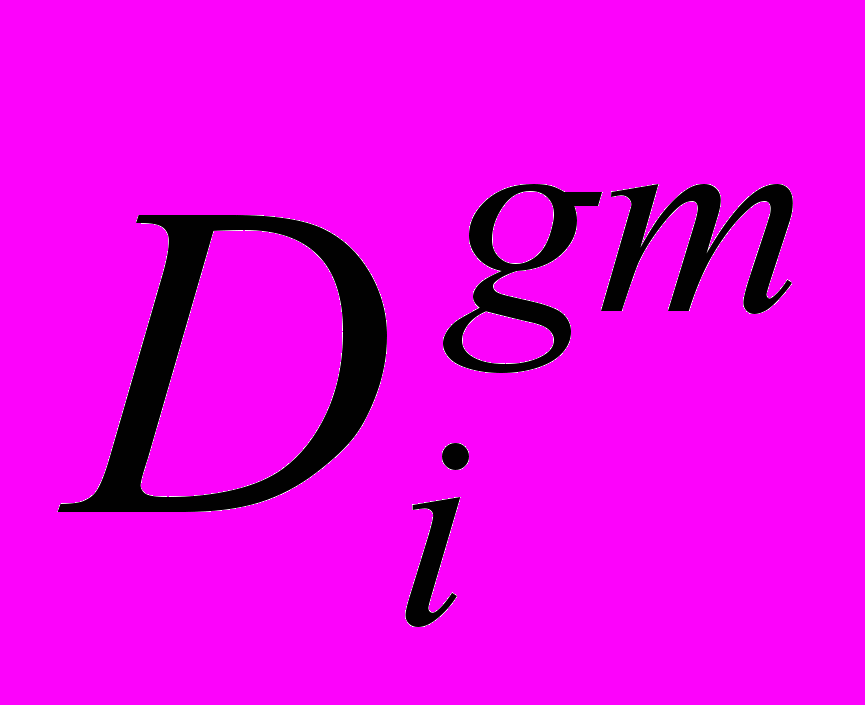– среднегрупповые (средние геометрические – GM) оценки доз; 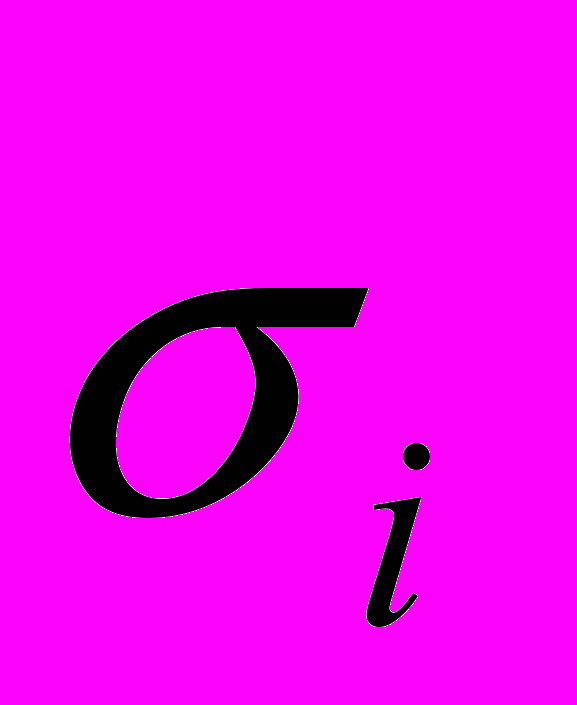– натуральные логарифмы геометрических стандартных отклонений (GSD) этих оценок.

Для генерации случаев рака использовалась простая бинарная модель возникновения этих событий (9) и двухпараметрическая модель заболеваемости;

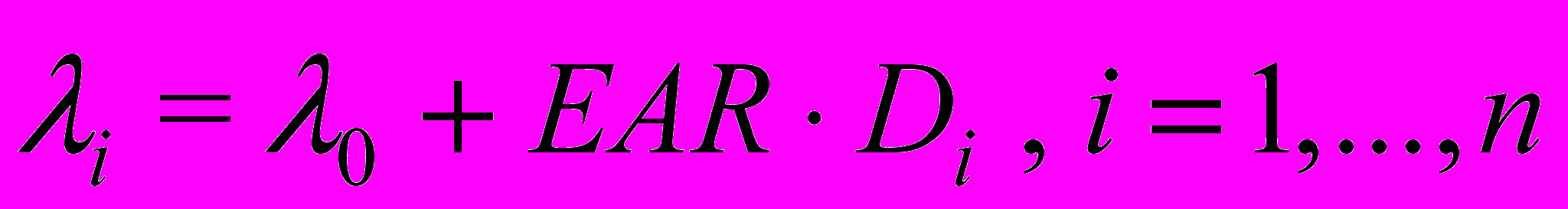(28)

где λ_i – абсолютный радиационный риск; D_i – доза облучения; 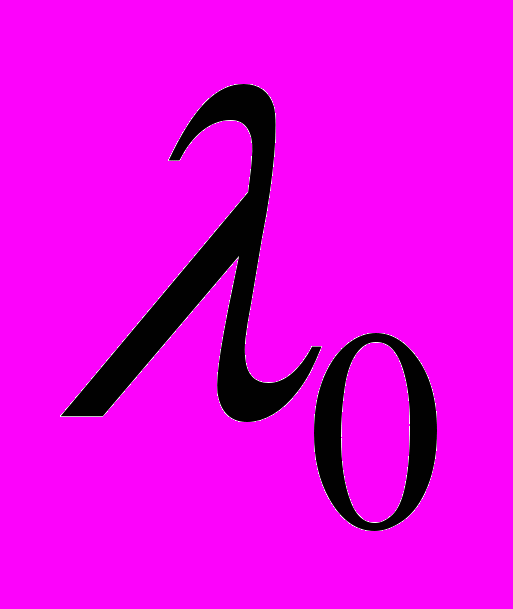– фоновая (в отсутствии дозового фактора) интенсивность заболеваний; EAR – избыточный абсолютный риск.

Параметры модели абсолютного риска (28) задавались значениями близкими к оценкам, полученным в эпидемиологических исследованиях онкологической заболеваемости щитовидной железы в Украине [9-10]:

(29)

При отсутствии ошибок в дозах по наблюдаемой выборке 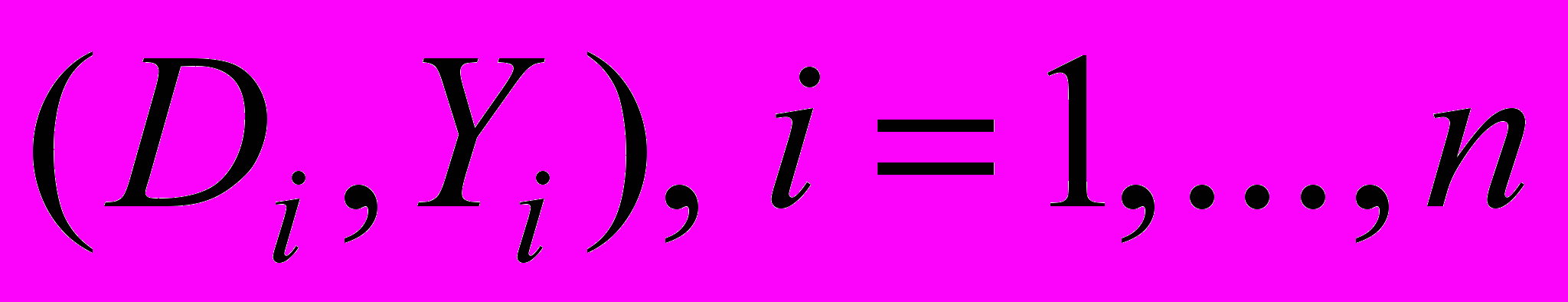на основании классического метода максимального правдоподобия легко строится процедура оценки параметров риска 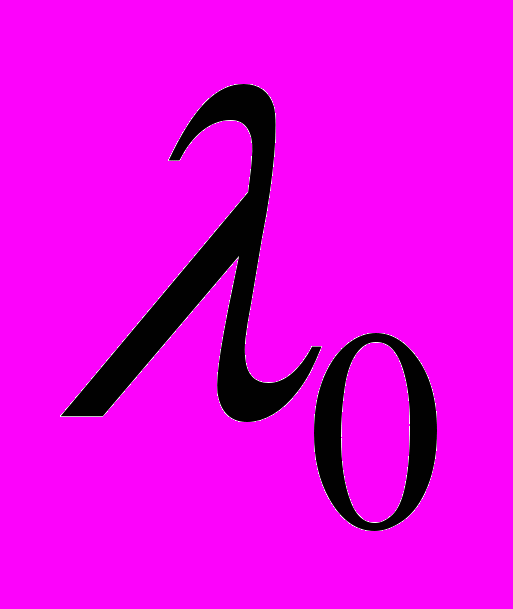и EAR.

Если истинными полагаются индивидуальные дозы, а для оценки параметров модели абсолютного риска используются средние арифметические (по каждой половозрастной группе) оценки этих доз, то имеет место берксоновская ошибка. Если же, наоборот, в качестве истинных доз принимаются среднеарифметические дозы, а для оценки параметров модели использовны индивидуальные дозы, то в этом случае ошибка дозы относится к классическому типу.

Для вычисления оценок радиационных рисков как без учета, так и с учетом ошибок измерения доз использовался специально разработанный пакет программ, оптимизационной основой которого служит описанный выше ММП для К-оценок.

С помощью этого пакета были построены кривые зависимости оценок фоновой заболеваемости и избыточного абсолютного риска от дисперсии ошибок как классического (рис. 2-3), так и берксоновского (рис. 4-5) типов.




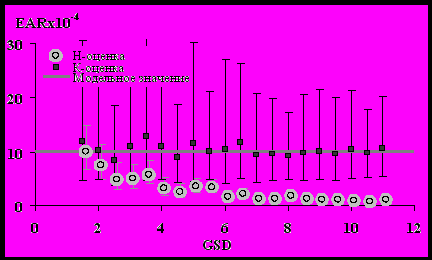
Рис. 2 – Зависимости Н- и К- оценок избыточного абсолютного риска (EAR) от величины классической ошибки в дозе.




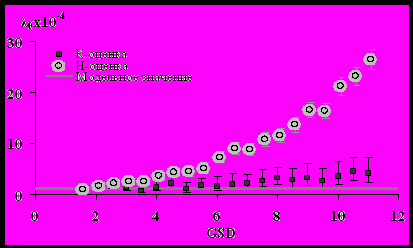
Рис. 3 – Зависимости Н- и К- оценок фоновой заболеваемости от величины классической ошибки в дозе.



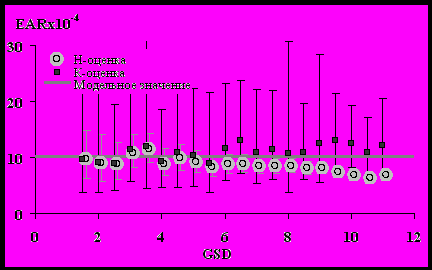
Рис. 4 – Зависимости Н- и К- оценок избыточного абсолютного риска (EAR) от величины берксоновской ошибки в дозе.




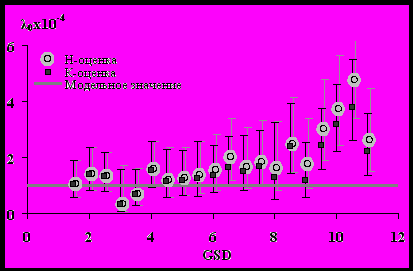
Рис. 5 – Зависимости Н- и К- оценок фоновой заболеваемости от величины ошибки берксоновской в дозе.


Результаты и обсуждение

При наличии классической ошибки в дозе очевиден существенный выигрыш применения “корректного” подхода для оценивания радиационных рисков по сравнению с “наивным” подходом (рис. 2-3). При этом “наивная” оценка избыточного абсолютного риска существенно меньше модельного значения того же параметра. Подобный эффект известен в статистической литературе [1] как “attenuation effect” (“эффект снижения”, “притяжения к нулю”). Степень подобного “притяжения” Н-оценки к нулю возрастает с увеличением дисперсии классической ошибки. В тоже время Н-оценка фоновой заболеваемости при увеличении ошибки, наоборот, существенно (нелинейно) растет. Заметим, что при достаточно больших дисперсиях классической ошибки Н-оценки радиоиндуцированной и спонтанной заболеваемости могут отличаться от модельных (истинных) значений более чем на порядок, причем первые будут занижены, а вторые завышены. К-оценка избыточного абсолютного риска ведет себя достаточно устойчиво и даже при больших дисперсиях практически совпадает с модельным значением, в то время как оценка фоновой заболеваемости имеет тенденцию к незначительному завышению. Вообще говоря, неудивительно, что качество оценок падает с увеличением дисперсии ошибок.

В случае берксоновской ошибки в дозе (рис. 4-5) имеет место схожий эффект занижения Н-оценки для EAR и ее завышения для фоновой заболеваемости. При этом, однако, отклонение Н-оценок от модельных значений параметров значительно меньше, чем в случае классической ошибки. Это объясняется тем, что при берксоновской ошибке в “наивном” методе оценивания используются “неплохие” оценки истинных доз, а именно их математические ожидания. Вместе с тем К-подход дает более точные оценки параметров модели.

Следует заметить, что мы рассматривали линейную регрессионную модель относительно переменной с ошибкой. Нелинейность модели, очевидно, может стать дополнительным источником смещений в оценках рисков.


Выводы

Выполнено имитационно-стохастическое моделирование рисков при разных степенях неопределенности доз облучения щитовидной железы.

Проведено сравнение оценок коэффициентов абсолютного риска, выполненных с одной стороны “наивными”, а с другой “корректными” методами оценивания.

Показано, что с увеличением дисперсии мультипликативных классических ошибок в дозах Н-оценка избыточного абсолютного риска существенно занижается, а оценка фоновой заболеваемости завышается. В то же время как К-оценки приближаются к истинному значению по мере увеличения объема выборки.

В случае ошибки Берксона Н- и К- оценки параметров модели имеют близкие значения, однако К- подход позволяет более точно оценить избыточный абсолютный риск и величину фоновой заболеваемости.

При значительной дисперсии ошибок как берксоновского, так и классического типов, модельное значение избыточного абсолютного риска не попадает внутрь доверительного интервала Н-оценок. В то же время доверительный интервал К-оценок во всех случаях (даже при весьма больших дисперсиях) “покрывает” модельное значение коэффициента риска.

Таким образом, при интерпретации результатов эпидемиологических исследований для предотвращения искажений формы кривой “доза-эффект” и получения более реалистичных оценок радиационных рисков необходимо, по возможности, учитывать наличие величину и тип ошибок в дозах.


Благодарности

Авторы считают своим приятным долгом поблагодарить д.ф.-м.н. проф. И.А. Лихтарева и д.т.н. Л.Н. Ковган за всемерную поддержку данного исследования и помощь в подготовке настоящего сообщения.


Литература

1. Carroll R.J., Ruppert D., Stefanski L.A. Measurement Error in Nonlinear Models. – London: Chapman & Hall, 1995. – 305 p.
   
2. Stefansky L.A., Carrol R.J. Conditional Scores and Optimal Scores for Generalized Linear Measurement Error Models // Biometrika. – 1987. – V.74, N 4. – P. – 703-716.
   
3. E. Ron, F.O. Hoffman. Uncertainties in Radiation dosimetry and their impact on Dose-Response analyses: Proc. of a workshop held September 3-5, 1997 in Bethesda, Maryland. – NIH Publication No. 99-4541, 1999. – 311 p.
   
4. Клейнен. Дж. Статистические методы в имитационном моделировании: В 2-х т. – М.: Статистика, 1978. – 221 c., 335 с.
   
5. Кельтон, В.Д., Лоу А.М. Имитационное моделирование. – СПб.: Питер, 2004. – 847с.
   
6. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М: Наука, 1986. – 544 с.
   
7. Likhtarov, I., Kovgan, L., Vavilov, S., Chepurny, M., Bouville, A., Luckyanov, N., Jacob, P., Voilleque, P., and Voigt, G. Post-Chornobyl thyroid cancers in Ukraine. Report 1: Estimation of thyroid doses. // Rad. Res. – 2005. – V. 163. – P. 125–136.
   
8. Королюк В. С., Портенко Н. И., Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. – М: Наука, 1985. – 640 с.
   
9. P.Jacob, T.Bogdanova, M.Chepurniy et al. Thyroid cancer risk in areas of Ukraine and Belarus affected by the Chernobyl accident // Rad. Res. – 2006. - No 165.– P. 1-8.
   
10. I. Likhtarov, L. Kovgan, S. Vavilov et al. Post-Chornobyl thyroid cancers in Ukraine. Report 2. Risk analysis // Rad. Res. – 2006. - V.166. – P. 375-386.